光的量子性
第七章 光的量子性

Vg应与光强有关,实际却与光的频率有关。 Vg应与光强有关,实际却与光的频率有关。矛盾 应与光强有关
3.照射时间长,积累能量多,只要照射足够长时间,总会有 照射时间长,积累能量多,只要照射足够长时间,
电子逸出,有电流。实际却是若入射光频率ν 电子逸出,有电流。实际却是若入射光频率ν <ν0 ,无论照 入射光频率 射多长时间,无光电流产生。 射多长时间,无光电流产生。 矛盾 光很弱,必须要照射长时间 才能积累足够的能量, 长时间, 积累足够的能量 4.光很弱,必须要照射长时间,才能积累足够的能量,使电 子从金属表面逸出。但实际却只要 不管I 多弱, 子从金属表面逸出。但实际却只要 ν >ν0,不管I0多弱,一 照上去,就有光电流产生。 矛盾 照上去,就有光电流产生。
普适常数就是黑体的单色幅出度。 普适常数就是黑体的单色幅出度。
∴基尔霍夫定律
M(ν ,T ) = Mb (ν ,T ) A(ν ,T )
T=5000k T=3000k
讨论:
1.同样温度下,黑体的辐射最大。 1.同样温度下,黑体的辐射最大。 同样温度下 2.绝对黑体不存在,黑体模型。 2.绝对黑体不存在,黑体模型。 绝对黑体不存在 3.黑体是否一定是黑的? 黑色物体是否就是黑体? 3.黑体是否一定是黑的? 黑色物体是否就是黑体? 黑体是否一定是黑的
一、黑体
黑体—在任何温度状态下全部吸收任何波长的电磁波. 黑体 在任何温度状态下全部吸收任何波长的电磁波. 在任何温度状态下全部吸收任何波长的电磁波 由
∴
Mb (ν ,T ) = f (ν ,T ) Ab (ν ,T )
黑体
Ab (ν , T ) = 1
Mb (ν ,T )
可见光 T=6000k
光的量子性

光的量子性光是一种电磁波,同时也是由一个粒子组成的能量包,这个粒子被称为光子。
在量子物理学中,光的量子性指的是光以离散的能量量子形式传播和吸收的现象,而不是以连续的波浪形式。
光的量子性的概念源于波粒二象性理论,这是量子物理学的基本原则之一。
根据波粒二象性理论,光可以展示出波动性和粒子性。
在光的粒子性方面,每一个光子都携带着离散的能量,其大小由光的频率决定。
光的波长越短,频率越高,每个光子携带的能量就越大。
光子的行为在很多实验中都得到了验证。
例如,光的干涉实验和光的散射实验都可以解释为光粒子之间的相互作用。
在干涉实验中,光的波动性可以解释为不同光子之间相位差的叠加,造成明暗干涉条纹的形成。
在散射实验中,光的粒子性可以解释为光子在物质中与原子或分子之间的相互作用,从而产生散射现象。
光的量子性还可以在单光子实验中得到验证。
通过使用特殊装置,科学家可以将光限制在非常低的能量水平,使得只有一个光子通过。
这种情况下,光呈现出典型的粒子性质,例如光子会在探测器上形成点状的光斑。
光的量子性在现代科技中有着广泛的应用。
例如,在量子通信领域,利用光的量子性可以实现安全的通信。
量子密钥分发协议利用光子的单光子性质,来保证通信的安全性和不可破解性。
此外,量子计算和量子存储等领域也都依赖于光的量子性。
为了更好地理解光的量子性,科学家们不断进行着深入的研究。
通过发展新的实验技术和理论模型,他们希望能够更全面地认识光的本质。
例如,光的单光子实验、光的量子纠缠实验以及光的非经典态实验等都是为了揭示光的微观粒子性质所进行的研究。
光的量子性是现代物理学中一个非常重要的概念,它帮助我们理解和解释光的行为。
从波粒二象性理论出发,我们可以认识到光既有波动性,也具有粒子性。
这种独特的性质使得光在许多领域中都具有广泛的应用潜力。
通过深入研究和探索,我们相信光的量子性将产生更多的新发现和新应用,为人类社会的进步带来更多的可能性。
第七章 光的量子性 第二节 普朗克辐射公式

由于他们的理论没有超出经典物理学的传统概念。 由于他们的理论没有超出经典物理学的传统概念。 所以没有取得完全成功。 所以没有取得完全成功。最具代表性的是维恩公式 和瑞利-金斯公式。 和瑞利-金斯公式。
维恩公式和瑞利- 一. 维恩公式和瑞利-金斯公式
1896年,维恩根据热力学原理,并假设辐射按 年 维恩根据热力学原理, 波长的分布类似于与麦克斯韦速度分布律, 波长的分布类似于与麦克斯韦速度分布律,导 出下列公式: 出下列公式:
ε = hν
普朗克根据上述假设,由玻耳兹曼分布, 普朗克根据上述假设,由玻耳兹曼分布,得出谐振 子的平均能量为: 子的平均能量为:
ε (k , T ) =
ε0
e 1
2πhc 2
hν kT
得出黑体辐射的单色辐出度的表达式为: 得出黑体辐射的单色辐出度的表达式为:
2πhν 1 M B (ν , T ) = hν c 2 e kT 1
2. 与经典物理中能量变化是连续的概念不同,谐振 与经典物理中能量变化是连续的概念不同, 子的能量只能取某些分立值, 子的能量只能取某些分立值,这些分立值是某一最 小能量单元ε的整数倍, 小能量单元ε的整数倍,即ε,2ε,3ε等。这些允许的 ε ε 能量值称为谐振子的能级。 称为能量子。 能量值称为谐振子的能级。 ε称为能量子。所以振子 的能量是不连续的。 的能量是不连续的。 振子从一个能级跃迁到一个能级而辐射或吸收电磁 波时,能量变化也是不连续的, 波时,能量变化也是不连续的,能量的不连续变化 称为能量量子化。 称为能量量子化。 3. 能量子ε与谐振子的频率成正比。 能量子ε与谐振子的频率成正比。 h=6.626×10-34J/s,称为普朗克常数。 = × ,称为普朗克常数。
3
或
第七章光的量子性普朗克公式能量子

第七章光的量子性普朗克公式能量子在经典物理学中,光被认为是一种波动现象,其行为可以用波动方程来描述和解释。
然而,在20世纪初,德国物理学家马克斯·普朗克提出了一个新的理论,即光也具有颗粒性质,被称为“能量子”。
普朗克的研究主要集中在黑体辐射的研究上。
黑体是一种理想化的物体,可以吸收和辐射所有输入的能量。
普朗克试图解释黑体辐射的谱线分布问题,但在经典物理学的框架下,无法得到与实验结果相符的理论。
为了解释黑体辐射谱线的分布,普朗克假设能量可以通过小单位,即“能量子”来传递。
这个假设意味着能量是离散的,而不是连续的。
他还假设能量子的大小与辐射的频率相关,即E = hf,其中E代表能量,h代表普朗克常数,f代表频率。
普朗克的假设得到了与实验结果相符的计算结果,并被后来的实验证实。
这个假设不仅解决了黑体辐射问题,也为后来量子力学的发展奠定了基础。
普朗克公式也被称为第一个量子理论的基本公式,标志着经典物理学的结束和量子物理学的诞生。
根据普朗克公式,光的能量是与频率成正比的,频率越高,能量就越大。
这与经典物理学中光波的能量与振幅平方成正比的关系不同。
相比之下,普朗克公式更加符合大量实验的结果。
普朗克公式的提出不仅在黑体辐射领域产生了广泛的应用,也为后来的量子理论奠定了基础。
后来,爱因斯坦提出了光的光子理论,进一步深化了对光的量子性质的认识。
光子是光的能量量子,它具有波粒二象性,在一些实验中表现为波动性,在另一些实验中表现为粒子性。
普朗克的量子理论不仅推动了对光的理解的发展,也改变了对其他微观粒子行为的理解。
在后来的量子力学中,量子概念被广泛应用于解释微观世界的行为,如电子的行为和原子的结构等。
量子力学的发展对物理学产生了深远的影响,并且在其他领域,如化学、材料科学和计算机科学中也有广泛的应用。
光的量子性
解(1) C (1 cos ) C(1 cos90 ) C
2.431012 m
(2) 反冲电子的动能
Ekmc 2 Nhomakorabea0c2
hc
0
hc
hc
0
(1
0
)
295 eV
(3) 光子损失的能量=反冲电子的动能
解 (1) E h hc 4.421019 J 2.76eV
p h E 1.471027 kg m s1 2.76eV / c
c (2) Ek E A(2.762.28)eV0.48eV (3) hc 5.18107 m 518nm
21.2 光的量子性
1、光电效应(photoelectric effect) (1)光电效应实验的规律
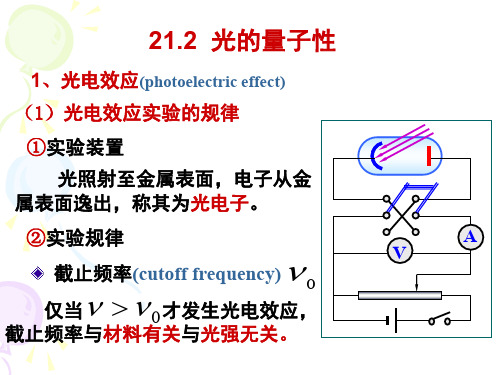
①实验装置
光照射至金属表面,电子从金 属表面逸出,称其为光电子。
②实验规律
截止频率(cutoff frequency) 0 仅当 0才发生光电效应,
截止频率与材料有关与光强无关。
A V
0 0(红限)
Ua k U0
③经典理论遇到的困难
红限问题 按经典理论,无论何种频率的入射光,只要其强度 足够大,就能使电子具有足够的能量逸出金属 .与实 验结果不符。
最大初动能问题 按经典理论,光电子最大初动能取决于光强,应
该和光的频率 无关。与实验结果不符。
瞬时性问题 按经典理论,电子逸出金属所需的能量,需要有 一定的时间来积累,一直积累到足以使电子逸出金属 表面为止.与实验结果不符。
E
3、康普顿效应(Compton effect) 1920年,美国物理学家康普顿在观察X射线被物质
第七章光的量子性光电效应爱因斯坦的量子解释

34
在整个电磁波谱中,射线的波长在0.01nm一下, 14 所以该光子在电子波谱中属于射线。
六. 光压
1
一. 光子
普朗克把能量子的概念只局限于谐振子及其发射 或吸收的机制上,对于辐射场,仍然认为只是一 种电磁波。 爱因斯坦指出,光不仅具有波动性,也具有粒子性。 光是一粒一粒以光速c运动的粒子流,这些光粒子称 光量子,简称光子。每个光子的能量为:
h
不同频率的光其光子能量不同,光子只能整个地被 吸收或发射。
因此,光电倍增管的灵敏度比普通光电管高几百万倍, 微弱的光照就可产生很大的电流。
11
五. 光子的质量和动量
光子不仅具有能量,也具有动量和质量。但光子又是 以光速运动,牛顿力学便不适用。按照狭义相对论的 观点,质量和能量具有如下关系: 2
E mc
因此,光子的质量为:
E h m 2 2 c c
从光子具有动量这一假设出发,还可以解释光压的 作用。即当光子流遇到任何障碍物时,在障碍物上 施加压力,就好像气体分子在容器壁上的碰撞形成 气压的一样。 光压就是光子流产生的压强。 俄罗斯科学家门捷列夫首先 于1900年做了光压的实验, 证实了光压的存在。 光压的存在的事实说明,光不但有能量,而且确实有动 量。这有力地证明了光的物质性,证明了光和电子、原 子、分子等实物一样,是物质的不同形式。
8
阴极可用多种材料制成, 常用的阴极材料有银氧铯 光电阴极、锑铯光电阴极、 铋银氧铯光电阴极等。不 同的阴极材料用于不同波 长范围的光。
为了提高真空光电管的灵敏度,通常在玻璃泡内充入 某种低压惰性气体,光电子在飞向阳极的过程中与气 体分子碰撞,使气体电离,这样可增大光电流,使灵 敏度增加。
光的量子性

光的量子性
(2)入射光频率ν一定时,反向截止电压U0取决于阴极材料,与 入射光强无关.若外加电压是A负K正,则为反向电压.对于固定的入射光 频率和入射光强,随着反向电压的增加,从阴极K逸出并能到达阳极A的 电子会越来越少,A、K间的电流就会越来越小,电流变为0时的电压就 称为反向截止电压.图15- 4(c)中的U0即为不同阴极材料的反向截止电压.
(3)对于给定的阴极材料,反向截止电压正比于入射光频率ν,且 存在一个最低频率,称为红限频率.当入射光频率低于此值时,就不会产 生电流.
光的量子性
(4)光电效应具有瞬时响应特性,即从光照射到阴极表面到产生 电流(有电子从阴极K发出)的时间间隔不大于纳秒数量级.
以上实验结果,除(1)之外的另外三点都无法用经典物理理予 以解释.按照经典物理理论,金属阴极中的电子在光线(电磁波)的照射 下做受迫振动,并吸收电磁场的能量.只要电子吸收足够多的能量,就可 能从金属表面逸出,产生光电效应.因此,只要光强足够强,或者照射的 时间足够长,电子就会积累到足够的能量并从表面逸出,从而发生光电 效应现象.这样,首先,反向截止电压应该与入射光强有关;其次,光电 效应不应该受到频率的限制;最后,电子要积累到足够的能量所需要的 时间应该在毫秒量级,并且这个时间应该随着光强的增加而缩短.
光的量子性
(15- 11) 式(15- 9)和式(15- 11)合在一起称为爱因斯坦关系式, 它们是爱因斯坦光子学说的核心.有趣的是,这两式的左边是能量和 动量,反映了光子粒子性的一面;而右边却与波长和频率相联系, 代表了光子波动性的一面.
光的量子性
三、 康普顿散射
当光照射到某物体时,光线就会向各个方向散开,这 种现象称为光散射.通常而言,光在散射过程中的波长不会 发生变化,这种普通的散射现象在经典物理学中可以得到圆 满解释.1923年,康普顿在用X射线(比紫外线波长更短的 光)进行光散射实验时发现,散射光中除原波长的光线外, 还会出现一些波长更长的光线,这就是康普顿效应.
光的量子性

光子的动量
p h h cc
引入 h 2
k 2 n
2
h
p h n k
11
光子具有动量,显示其有粒子性; 光子具有波长,又说
明其有波动性;这说明,光具有波粒二象性,即在传播过程中
显示它的波动性(如干涉,衍射等),而在光与实物粒子相互
作用时,又显示它的粒子特性。光的波粒二重特性,充分地包
答[ D ]
25
例 15 - 5 设用频率为1,2的两种单色光,先后照射同一种 金属均能产生光电效应,已知金属的红限频率为0 ,测得两次照 射时的遏止电压 |Ua2|=2| Ua1| ,则这两种单色光的频率有如下 关系:
(A)2 10, (B) 2 1+0, (C)2 210, (D) 2 120,
在光子流中,光的能量集中在光子上,电子与光子相遇, 只要hv足够大,电子就可以立刻吸收一个光子的能量而逸出金 属表面,因而不会出现滞后效应。
10
四、光的波粒二象性
描述光的波动性:波长λ,频率ν
描述光的粒子性:能量ε,动量 P
每个光子的能量
h
按照相对论的质能关系 光子无静质量 m0=0
2 p2c2 m02c4
一、光电效应
金属及其化合物在光波的照射下 发射电子的现象称为光电效应,所发 射的电子称为光电子。
1 、实验装置
2 、光电效应的实验规律 ( 1 )饱和光电流强度 Im 与入射 光强成正比(ν不变)。
当光电流达到饱和时,阴极 K 上 逸出的光电子全部飞到了阳极上。
单位时间内从金属表面逸出的光电子 数和光强成正比
4
二、经典物理学所遇到的困难
1、逸出功,初动能与光强、频率的关系
按照经典的物理理论,金属中的自由电子是处在晶格上正电
光的波粒二象性与光的量子性光的粒子性与波动性

光的波粒二象性与光的量子性光的粒子性与波动性光,作为一种电磁波,是人类生活中不可或缺的重要物质。
关于光的性质,科学家们经过长时间的研究,发现了光的波粒二象性和光的量子性,这是光学领域的两个重要概念。
本文将探讨光的波粒二象性以及光的量子性,并对其产生的原因进行简要分析。
一、光的波粒二象性光的波粒二象性是指光既可以表现出波动性,又可以表现出粒子性的特点。
作为一种电磁波,光具有干涉、衍射和折射等波动现象。
当光通过狭缝或物体时,会产生明暗条纹,这就是干涉现象。
而当光通过孔径比它小很多的狭缝时,会发生衍射现象。
这些现象说明了光的波动性。
然而,光也具有粒子性质。
根据普朗克提出的能量量子化理论,光的能量是离散的,而不是连续的。
而爱因斯坦进一步发展了波粒二象性的概念,他通过解释光电效应提出了光的粒子性。
光电效应是指当光照射到金属表面时,产生电子的现象。
根据光的波动性,当光的强度增加,电子的动能应该随之增加。
然而,实验证实,只有当光的频率高于一定的临界值时,才会发生光电效应,而光的强度并不影响电子的动能。
这就表明光是由一定量的能量子(光子)组成的,每个光子的能量与光的频率有关。
这一实验证明了光的粒子性。
二、光的量子性光的量子性是指光的能量是量子化的,光的能量取决于光子的能量量子。
根据爱因斯坦的解释,光的能量 E 与光的频率 f 之间存在着以下关系:E = hf,其中 h 是普朗克常量,约等于6.626×10^(-34) J·s。
这意味着光的能量只能是 hf 的整数倍,而不能是连续变化的。
光的量子性在微观领域有着广泛的应用,如在光谱学中,使用了光的量子性来解释物质与光的相互作用。
光的量子性在现代物理学的发展中起到了重要作用。
基于光的量子性,爱因斯坦提出了激光原理,并导致了现代激光技术的出现。
激光的产生是通过将辐射能量限制在一个模式中,使其与物质系统发生相互作用,并最终产生一种高度聚集的光能。
三、光的粒子性与波动性产生的原因光的波粒二象性以及光的量子性是由光的微观粒子——光子的特性所决定的。
量子光学知识点总结

量子光学知识点总结一、光的基本性质光是一种电磁波,也可以被看作是一种粒子,光子。
在经典光学中,光可以用波动方程来描述,而在量子光学中,光的性质可以用量子理论来解释。
光的基本性质包括:1. 光的量子特性根据量子理论的描述,光可以被看作是一种由光子组成的粒子。
每个光子具有一定的能量和动量,其能量与频率成正比,动量与波长成反比。
光的能量E和频率v之间的关系由普朗克公式E=hv给出,其中h为普朗克常数。
2. 光的波粒二象性光既可以表现出波动性,也可以表现出粒子性。
这就是光的波粒二象性。
在量子光学中,人们可以利用波动方程和光子的概念来解释光的波动性和粒子性。
这一性质常常可以用来解释光的干涉、衍射和光电效应等现象。
二、光场的量子描述在量子光学中,人们通常用量子态和密度算符来描述光场的量子性质。
光场的量子态可以用准确的数学表达式来描述,其中包括了光子的粒子性和光的波动性。
光场的量子态的基本特性包括:1. 光场的量子态在量子光学中,人们通常用Fock态来描述光场的量子态,Fock态可以用来表示不同光子数的态。
例如,n个光子的Fock态可以表示为|n⟩。
光场的量子态还可以用相干态来描述,相干态是一种特殊的量子态,它具有明显的波动性和相干性。
2. 光场的密度算符在量子光学中,人们通常利用密度算符来描述光场的统计性质。
光场的密度算符可以用来描述不同光子数状态的统计分布,以及不同光子数态之间的相干性质。
光场的密度算符还可以用来描述光场的量子纠缠性质。
三、光场与物质的相互作用在实际的光学系统中,光场经常与物质相互作用,产生各种光谱现象和光学效应。
在量子光学中,人们研究了光场与不同类型的物质之间的相互作用规律,包括原子、分子、准粒子等。
光场与物质的相互作用包括:1. 原子的光谱原子在外加光场的作用下,会发生能级跃迁,从而产生吸收、发射光子的现象。
在量子光学中,人们研究了原子的光谱性质,包括原子吸收、发射光子的发射,原子的谐振腔增强等。
第七章光的量子性第二节普朗克辐射公式

第七章光的量子性第二节普朗克辐射公式普朗克辐射公式是描述黑体辐射的经典物理学理论,由德国物理学家马克斯·普朗克在1900年提出。
该公式对于理解光的量子性起到了重要的先导作用,为量子力学的发展提供了关键线索。
本节将从普朗克辐射公式的推导、具体表达形式以及其在物理学中的应用等几个方面进行介绍。
首先,我们来看一下普朗克辐射公式的推导过程。
马克斯·普朗克通过对黑体辐射的研究,提出了一个假设,即黑体辐射的能量不是连续的,而是以一种离散的形式存在,这就是所谓的能量量子化的假设。
根据这个假设,普朗克得出了一个公式,即普朗克辐射公式。
在推导普朗克辐射公式时,普朗克引入了一个新的常数,即普朗克常数h,表示能量的量子。
普朗克辐射公式的具体形式为:E = hv接下来,我们来看一下普朗克辐射公式在物理学中的应用。
首先,普朗克辐射公式为热力学的发展提供了重要的依据。
黑体辐射的研究促进了热力学第二定律的建立,同时也揭示了能量的离散性质。
其次,普朗克辐射公式对量子力学的诞生起到了关键作用。
在推导过程中,普朗克通过引入能量量子化的假设,奠定了光的量子性的基础。
这一假设启发了爱因斯坦等物理学家,从而推动了量子力学的发展。
此外,普朗克辐射公式还在其他领域中得到了广泛的应用,如原子物理学、光学等。
最后,我们来总结一下。
普朗克辐射公式是描述黑体辐射的一个经典物理学理论,通过引入能量量子化的假设,奠定了光的量子性的基础。
普朗克辐射公式的推导过程中,普朗克引入了一个常数h,即普朗克常数,表示能量的量子。
该公式在物理学中得到了广泛的应用,不仅对热力学的发展有重要影响,还对量子力学的建立起到了关键作用。
光的量子性理论

光的量子性理论光的量子性是指光可以通过粒子的方式表现出来。
在经典物理学中,光被视为一种电磁波,可以通过波动理论来解释其传播和性质。
然而,随着物理学的发展,量子力学的出现揭示了光的微粒性质,也就是光子。
光的传播速度相对于真空中的电磁波速度是固定的,但当光与物质相互作用时,其粒子特性变得显著。
光的量子本质可以通过光子的概念来描述。
光子是光的基本粒子,具有能量和动量。
光子的能量由其频率决定,而动量则与其波长有关。
量子力学的理论框架为解释光的量子性提供了基础。
根据量子力学的原理,光的量子性可以通过波-粒二象性解释。
当光传播时,它表现出波动性质,但在某些情况下,比如光与物质相互作用时,光会表现出粒子性质,即光子。
光子的产生可以通过原子或分子的激发态来实现。
当一个原子或分子处于激发态时,它会通过自发辐射的方式向外发射一个光子,将激发态的能量释放出来。
这种光子发射的过程符合量子力学中的概率规律,即光子以概率的形式出现在确定的位置和时间。
光子的性质可以通过光的频率和波长来描述。
根据光的频率和波长,可以确定光子的能量和动量。
量子力学中的能量和动量与经典力学有所不同,它们是离散的,称为能级和量子态。
这意味着光子的能量和动量只能取特定的值,而不是连续变化的。
光的量子性理论在很多领域都有重要的应用。
其中一项突出的应用是光的激光技术。
激光是一种纯净的、高强度的、高方向性的光源,它的特点源于光的量子性质。
激光的产生是通过光子受激辐射的过程实现的,其中一个光子的能级被另一个光子的能级激发,从而产生一系列的光子,并通过光的共振效应放大。
另一个重要的应用领域是量子通信。
量子通信利用光子的量子性质,通过量子态的传输来实现信息的安全和传输。
由于光子的量子态是不可复制和不可观测的,量子通信可以提供高度安全的通信方式,抵御了传统通信中可能存在的窃听和干扰。
总结起来,光的量子性理论揭示了光的微粒性质,即光子。
光子是光的基本粒子,具有能量和动量。
光的量子性

产生光电子数目越多,光电流越大.( 0 时)
光子射至金属表面,一个光子携带的能量 h 将一 次性被一个电子吸收,若 0 ,电子立即逸出,
无需时间积累(瞬时性).
12 – 1 光的量子性
第十二章 量子物理基础
例1 波长为200nm的紫外线射到某种金属的表
解 (1)
E
h
hc
4.42 10 19 J
2.76eV
p
h
E c
1.47
10 27 kg
m s1
2.76eV /
c
(2) Ek E W (2.76 2.29)eV 0.47eV
(3)
hc E
5.18 10 7 m
518 nm
12 – 1 光的量子性
第十二章 量子物理基础
光电效应在近代技术中的应用
2πhc2
5
hc
e kT
* **
**
* *
* *
* 维恩曲线
* *
** *
* *
** *
O
这个公式在长波段与实验曲线相差较大!
12 – 1 光的量子性
第十二章 量子物理基础
瑞利 - 金斯公式(1900-1905年)
M 0 (T )
瑞利 - 金斯曲线
实验曲线
瑞利 - 金斯公式
M 0 (T )
2 π kcT
对同一种金属,W 一定,Ek ,与光强无关
几种金属的逸出功
金属
钠 铝 锌 钨 银铂
W / eV 2.28 4.08 3.34 4.54 4.73 6.35
12 – 1 光的量子性
第十二章 量子物理基础
光的量子性光的能量和频率的关系

光的量子性光的能量和频率的关系在物理学中,光既可以被看作是一种波动,也可以被看作是由许多粒子组成的微粒,即光子。
光子具有量子性质,其能量和频率之间存在着密切的关系。
光的能量与频率之间的关系被描述为普朗克-爱因斯坦关系(Planck-Einstein equation),其公式为E = hv,其中E表示光的能量,h为普朗克常数,v表示光的频率。
普朗克常数h是一个基本物理常数,其数值约等于6.62607015×10^-34 J·s。
这个公式告诉我们,光的能量与其频率成正比,即频率越高,能量越大;频率越低,能量越小。
光的能量可以通过以下公式计算:E = hc/λ,其中c表示光速,λ表示光的波长。
通过该公式,我们可以看出光的能量与波长呈反比关系,即波长越长,能量越小;波长越短,能量越大。
光的频率和波长之间有一个简单的关系:v = c/λ。
这个公式告诉我们,光的频率与波长成反比关系,即波长越长,频率越低;波长越短,频率越高。
根据以上公式和关系,我们可以得出结论:光的能量与频率成正比,与波长成反比。
因此, 高频率的光具有更高的能量,而低频率的光具有更低的能量。
这也意味着光的颜色会随着频率的改变而改变。
以可见光为例,不同颜色的光对应着不同的频率和能量。
红光的频率较低,能量较低;蓝光的频率较高,能量较高。
当频率继续增大时,超出可见光范围的紫外光和伽马射线等具有更高能量的光会出现。
光的能量和频率的关系在实际应用中有着重要的意义。
例如,在光谱学中,我们可以通过测量光的能量和频率来确定物质的成分和性质。
在光电效应中,光的能量足够大时,光子可以将其能量转移给物质中的电子,从而产生电子的逸出。
这种现象在太阳能电池中得到了广泛应用。
总结起来,光的量子性质使得能量和频率之间存在着密切的关系。
光的能量与频率成正比,与波长成反比。
这种关系不仅在理论物理学中发挥着重要作用,也在许多实际应用中得到了广泛应用。
对于深入理解和研究光的本质,以及应用光学的领域,掌握光的量子性质是至关重要的。
光的偏振与光的量子性质

光的偏振与光的量子性质光是一种电磁波,具有波动性和粒子性。
在光的波动性中,一种重要的现象是偏振。
而在光的粒子性中,光子的量子性质起到了关键作用。
本文将从理论和实验两个方面来探讨光的偏振与光的量子性质。
1. 光的偏振光的偏振是指光波中电矢量振动方向的一个特定方向。
在自然界中,大多数光波是不偏振的,即电场矢量在不同平面上、不同方向上等概率地振动。
然而,在某些特定情况下,光波可以具有特定的偏振性质。
一种常见的偏振光是线偏振光。
线偏振光的电场矢量只在一个平面上振动,相当于波动方向被限制在一个特定直线上。
线偏振光可以通过使用偏振片或者其他光学器件来生成。
例如,当自然光穿过偏振片时,只有振动方向与偏振片允许的振动方向相同的光会透过,而垂直方向的光则会被吸收,从而得到线偏振光。
另一种常见的偏振光是圆偏振光。
圆偏振光的电场矢量在垂直于传播方向的平面上旋转,形成一个螺旋状的振动。
圆偏振光可以通过将线偏振光通过一个波片来生成,波片具有特殊的光学性质。
2. 光的量子性质光的量子性质由光子的概念来描述。
光子是光波的粒子性质,可以看作光的离散能量包。
根据量子力学理论,光子具有能量和动量,并且在特定条件下可以表现出波粒二象性。
光子的能量与频率成正比,可以使用普朗克公式来描述:E = hf,其中E为光子的能量,h为普朗克常数,f为光子的频率。
根据这个公式可知,光子的能量是量子化的,且与其频率有直接的关系。
光子还具有动量,其大小可以通过相对论动力学公式p = hf/c得到,其中p为光子的动量,c为光速。
这意味着光子的动量也是量子化的,与其频率和能量相关。
光的量子性在实验中得到了充分的验证。
例如,光电效应实验证明了光子的能量是量子化的,只有能量大于一定阈值的光子才能将电子从金属中解离出来。
另一方面,干涉和衍射现象表明光具有波动性,而光的能量的离散性则反映了光的粒子性。
结论光的偏振性质与光的量子性质是光学中的两个重要概念。
光的偏振性质决定了光的电场矢量的振动方向,可以通过偏振片等光学器件来实现偏振光的生成。
量子力学描述光子的量子特性

量子力学描述光子的量子特性光子是光的基本单位,也是量子力学研究的重要对象之一。
量子力学是描述微观世界的理论框架,通过量子力学可以深入了解光子的量子特性。
本文将从量子力学的角度,详细介绍光子的量子特性。
首先,光子的量子特性可以通过其波粒二象性来描述。
在经典物理学中,光被认为是一种电磁波,具有波动性质。
然而,根据量子力学的观点,光也可以被看作是一种由光子组成的粒子,具有粒子性质。
这种波粒二象性使得光子既可以表现出波动的干涉和衍射现象,又可以表现出粒子的能量量子化和位置不确定性。
其次,光子的能量量子化是其量子特性的重要体现。
根据普朗克的能量量子化假设,光子的能量是离散的,且与其频率成正比。
这意味着光子的能量只能取特定的数值,而不能连续变化。
光子的能量量子化可以通过光子的能量公式E=hf来描述,其中E表示光子的能量,h为普朗克常数,f为光子的频率。
这个公式表明,光子的能量与其频率之间存在着确定的关系,光子的能量只能取整数倍的hf值。
光子的位置不确定性是其量子特性的另一重要方面。
根据海森堡的不确定关系原理,光子的位置和动量不能同时精确确定。
这意味着,我们无法同时知道光子的位置和速度。
当我们试图测量光子的位置时,其动量将变得不确定;当我们试图测量光子的动量时,其位置将变得不确定。
这种位置-动量不确定性关系限制了我们对光子的精确观测,揭示了光子的微观本性。
此外,光子的量子特性还体现在其与其他粒子的相互作用中。
光子是电磁相互作用的媒介,可以与其他粒子发生相互作用。
其中,光子与电子的相互作用尤为重要。
当光子与电子相互作用时,可以发生光电效应、康普顿散射等现象。
这些现象都是光子与电子之间能量和动量的交换结果,进一步证实了光子的量子特性。
最后,量子力学还提供了描述光子的波函数形式。
波函数是量子力学中用来描述粒子状态的数学函数,通过波函数可以计算出光子在不同位置和时间的概率分布。
光子的波函数具有波动性质,可以通过波函数的幅度和相位来描述光子的波动行为。
大学物理知识总结习题答案(第十章)量子物理基础

其中,m为粒子的质量,U为粒子在外力场中的势能函数,E是粒子的总能量。
·在无限深方势阱中的粒子能量为
整数n称为量子数。每一个可能的能量值称为一个能级。
·在势垒有限的情况下,粒子可以穿过势垒到达另一侧,这种现象叫做势垒贯穿。
7.电子运动状态
·量子力学给出的原子中电子的运动状态由以下四个量子数决定
·在不同的热力学温度T下,单色辐射本领的实验曲线存在一个峰值波长 ,维恩从热力学理论导出T和 满足如下关系
其中b是维恩常量。
3.斯忒藩—玻尔兹曼定律
·斯忒藩—玻尔兹曼定律表明黑体的辐射出射度 与温T的关系
其中 为斯忒藩—玻尔兹曼常量。对于一般的物体
称发射率。
4.黑体辐射
·黑体辐射不是连续地辐射能量,而是一份份地辐射能量,并且每一份能量与电磁波的频率 成正比,这种能量分立的现象被称为能量的量子化,每一份最小能量 被称为一个量子。黑体辐射的能量为 ,其中n=1,2,3,…,等正整数,h为普朗克常数。
解:每个光子能量为 ,其中 为普朗克常量且
则,100个波长为550nm的光子的光功率为
10-5(1)广播天线以频率1MHz、功率1kW发射无线电波,试求它每秒发射的光子数;(2)利用太阳常量I0=1.3kW/m2,计算每秒人眼接收到的来自太阳的光子数(人的瞳孔面积约为 ,光波波长约为550nm)。
解:(1)每个光子能量为 ,由
10-7“光的强度越大,光子的能量就越大”,对吗?
答:不对,光的强度是单位时间内照射在单位面积上的光的总能量。一定频率的光强度越大,表明光子数量越多,但每个光子的能量是一定的,只与频率有关,与光子数目无关。
10-8什么是康普顿效应?
答:考察X射线通过物质时向各个方向的散射现象发现,在散射的X射线中,除了存在波长与原有射线相同的成分外,还有波长较长的成分,这种波长改变的散射称为康普顿散射,也称康普顿效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(单位时间内) 取决于T,,物质种类 和表面情况
单位面积
d ,T
d ,T
2、(总)辐出度(总发射本领) 0 (T ) 单位时间内从温度为T 的黑体的单位面积上 所辐射出的各种 波长电磁波的能量总和
0 (T ) d ,T d d E ,T d
即两波的频率(或波长)很接近, 它们合成的波列为
此波的瞬时图像如下图所示,是振辐受到低频 调制高频波列,这调制波列有一系列的最大值, 因而它还算不得是一个典型的波包。要得到一 个真正的波包,需有更多频率和波长相近的波 迭回在一起 。
7.2 经典辐射定律
1. 热辐射
化学发光:在辐射过程中物质内部发生化学变化的; 比如:燃烧 光致发光:用外来的光或任何其他辐射不断地或预先地照 射物质而使之发光的; 比如:荧光、磷光
2 光速的测量与长度单位“米”的定义
真空中光速c不仅是重要的光学常数,也是整个 物理学以及天文学中几个最基本的普适常数之一,对 其数值的精确测定,无疑具有十分重大意义的。 另一个天文学方法是1728年布喇德雷用的光行差 法。在地面上进行光束测定的工作直到十九世纪上半 叶才开始,特别值得提起的有斐索的齿轮法,傅科的 旋转镜法和迈克耳孙的旋转棱镜法。 鉴于光速这一基本常数的重要性,对它的测量工 作几十年来从未中断,在此期间方法不断改进,精确 度不断提高。
傅科(Jean Bernard Leon Foucault 1819~1868)法国实 验物理学家
1834年,英国物理学家 惠斯通利用旋转镜来测定 电火花持续的时间,也想 用此法来测定光速,同时 也想确认一下在拆折射率 更大的介质中,光速是否 更大。惠斯通的思想方法 是正确的,但是他没有完 成。 迈克耳逊继承了傅科的 实验思想,用旋转八面棱 镜法测得光速为299796千 米/秒。
杨氏干涉测波长
激光器的出现把光速的测量推向一个新阶 段。特别是饱和吸收技术的采用,使我们可以得 到频率的稳定性和复现性均十分优良的激光辐射, 并且由于波长可以比原来微波干涉仪法中用的小 三个量级(微米量级),使波长测量的准确度大 为提高,甲烷稳定的3.39μm 氦氖光系统(HeNe:CH4)和碘稳定的633nm氦氖辐射波长的复现 性高百倍以上,比现行的“米”定义86Kr辐射波 长的复现性高百倍以上,因此这不仅是光速的测 量问题了,重新改变“米”的定义问题提上议事 日程。
实验表明: E ,T 之间存在一定的联系 一个黑白花盘子的两张照片
A ,T
室温下,反射光
1100K,自身辐射光
原来白底的地方吸收的少(反射的多),发射 的光强也就弱;
基尔霍夫(Gustav Robert Kirchhoff,1824~1887) 德国物理学家
原来黑花纹的部分吸收的多(反射的少),发射的光强也就强; 基尔霍夫定律 在平衡热辐射时,有规律:
主讲:朱辉
7.1 光速的测定 光的相速度和群速度
1 实验室方法
世界上最早用实验方法测定 光速的是伽利略。他在1607年做 了一个实验。当时,他叫甲乙两 个人在夜间各带一只灯,分立在 两个山顶上,甲先迅速取去灯罩 对乙发出信号,乙在看到信号后, 立即取去灯罩,对甲发出信号。 两山的距离和光往返的时间来计 算光速。由于当时的技术条件限 制,测得的光速很不精确。
1900年从经典电动力学和统计物理学理论(能量均分)推导而得。 该公式在低频段与实验曲线符合得很好。
单位频率间隔驻波数多→ 能量↑ “紫外灾难”!
时, , M
由经典理论导出的 M (T)- 公式都与实验曲线不完全符合!
这正所谓是
“ 物理学晴朗天 空中的一朵乌云!”
1904年诺贝尔物理学奖获 得者 ——瑞利 • Lord Rayleigh • 1842-1919 • 英国人 • 氩的发现
(Wien displacement law)
1893年由理论推导而得
m = C T
C = 5.880×1010 Hz/K
或
Tm b
b 2.898 103 m K
m
-峰值波长
m
m 510nm,
若视太阳为黑体, 测得 定出:
T表面 = 5700K
维恩 (Wilhelm Wien 德国人 1864-1928)
热辐射定律的发现
1911年 诺贝尔物理学奖获得者
斯特藩—玻耳兹曼定律和维恩位移律 是测量高温、遥感和红外追踪等技术 的物理基础。
7 瑞利 —— 金斯公式
辐射的振子模 型
经典物理学遇到的困难 空腔壁产生的热辐射,可想象
成以壁为节点的许多驻波。
2a n n
(n = 1,2)
问题:如何从理论上找到符合实验的函数式?
黑体
,T
=1----‘理想模型’。
空腔小孔吸收与发射
为不透明材料的空腔 开的一个小孔。 黑体能吸收各种频率的电磁波, 也能辐射 各种频率的电磁波 实验表明 辐射能力越强的物体,其吸收能力也越强。
黑体辐射谱(即 E ,T 关系)的规律
1).黑体辐射测量的实验装臵
小孔
T
空腔
s
L1
平ห้องสมุดไป่ตู้光管
L 2 会聚透镜
红外照相机拍摄的人的头部的热图
热的地方显白色,冷的地方显黑色
炼钢的热辐射
红外夜视仪拍的照片
2、辐射出射度和吸收比 1、光谱辐出度(单色辐出度) d ,T
d ,T
空间辐射测试装臵
—单位时间内,从物体单位表面发出的频率在 附近单位 频率间隔内的电磁波的能量。
d E
T
( d )
c
棱镜
热电偶
对黑体加热,会放出热辐射。 通过光栅可得到黑体辐射的频谱。 通过热电偶可得到黑体辐射的光谱辐出度。
黑体辐射谱(实验规律)
可 见 光 区
不同温度下的黑体辐射曲 钨丝和太阳的热辐射 线 曲线与横轴围的面积就是 0 (T ) 曲线
5、斯特藩 —
玻耳兹曼定律
Stefan(德)Boltzman(奥)
一列有限长的波相当于许多单色波列的迭加,通 常把由这样一群单色波组成的波列叫做波包。 当波包通过有色散的媒质时,它的各个单色分量 将以不同的相速前进,整个波包在向前传播的同时, 形状亦随之改变,我们把波包中振辐最大的地方叫做 它的中心,波包中心前进的速度叫做群速,记作υg。
为简单起见,我们考虑由两列波 组成“波包”。设两列波分别为
米定义咨询委员会保证,不管光速的推荐值于1975年 在第十五届国际计量大会上得到正式通过。从此就有可能 利用激光辐射或光速重新定义长度的单位“米”。 1975年第十五届国际计量大会和1979年第十六届国际 计量大会慎重地讨论了重量重新定义米的问题。 考虑到今 后计量学的发展趋势是将物理量的基准建立在基本物理常 数的基础上,米定义咨询委员会通过了一项建议,要求国 际计量委员会考虑一个新的米定义,于1983年提交第十七 届国际计量大会讨论, 这个定义是: “米是平面电磁波在(1/299792458)秒的持续时 间内在真空中传播行程的长度”。
总辐出度M(T)与黑体温度的四次方成正比
(T ) T 4 0
5.67 108 w/m2 K 4
—— 斯特藩 — 玻耳兹曼常量
1879年斯特藩从实验上总结而得到 1884年玻耳兹曼从理论上证明
斯特藩 — 玻耳兹曼定律和维恩位移定律是测量高温、
遥感和红外追踪等的物理基础。
6 维恩位移定律
0 0
单位:w/m2
3、吸收比 (辐射)到某一不透明物体表面 一部分能量被物体散射或反射 能量 d ,T 一部分能量被物体吸收 d' ,T
频率在 d 范围内照射到温度为T的物体单位面积上的辐射能 定义: 吸收比
A ,T d' ,T d ,T
3、基尔霍夫(Kirchhoff)辐射定律:
1
T 2
3
E ,T A ,T
f ( , T )
与材料无关,是一个普适函数! 这表明: 利用利用这个定律可撇开材料的具体性质,来普遍地研究热辐 射本身的规律。 问题提出:是否存在一种这样一种物体其吸收比与频率和温度
无关?
4、
黑体(black body):
黑体
能完全吸收照射到它上面的各种频率电磁波的物体,称为黑体。 黑体的光谱吸收比 维恩设计的黑体:
自从1958年绅鲁姆利用微波干涉仪法得到当时公认的 光速值c=299792.5±0.1km/s以来,所有的光速精密测量 均以公式c=λν为基础,即电磁波在真空中的传播速度等 于其频率与相应真空波长之乘积。当时的不确定度是 3×10的7次方,其主要原因是使用的波长较长(4mm), 因此波长测量的准确度较低,衍射效应带来的误差也较大。
伽利略(Galileo Galilei,15641642),意大利物理学家、天文学 家和哲学家,近代实验科学的先驱 者。
后来,法国物理学家斐索于1849 年用一只旋转的齿轮测量光走过某一 给定距离的时间,齿轮以一定的速度 运动并让光通过齿间。斐索测得的光 速为313000公里/秒。斐索先后研究 了光的干涉、热膨胀等,发明了干涉 仪。他在研究和测量光速问题上作出 了贡献,是第一个不用天文常数、不 借助天文观察来测量光速的人。他是 采用旋转齿轮的方法来测定光速的。 测出的光速为 342539.21千米/秒, 这个数值与当时天文学家公认的光速 值相差甚小。
▲ 著名公式之一:
维恩公式
M (T ) 3e / T
, 为常量
1896年从热力学理论及实验数据的分析而得。
▲
著名公式之二:瑞利 —— 金斯公式 (Rayleigh)
2 2 M (T ) 2 kT c
(Jeans)
k 1.380658 10 23 J K 1
场致发光:由电场作用引起辐射的过程;
