立体图形总复习1

合集下载

立体图形的整理与复习

×
圆柱的体积 = 底面积 ×
高
高
V = Sh
考点四、圆柱和圆锥的表面积和体积
圆锥的体积等于与它等底
等高圆柱体积的三分之一。
1
圆锥的体积=
× 底面积×高
3
1
1
Ⅴ圆锥 = Ⅴ圆柱 = Sh
3
3
4．各种立体图形的表面积和体积计算公式：
立体图形
表面积
体积计算公式
长方体
S＝2(ab＋ah＋bh)
V＝abh
这个圆柱的高是(
)dm。
(6)把一个棱长为4 cm的正方体切成棱长为2 cm的小正方
体，可以得到( )个小正方体，表面积增加了( )cm2。
(7)7.02 m3＝(
)m3(
)dm30.75 L＝(
)mL
2．选择。(将正确答案的字母填在括号里)
(2)把棱长为6 cm的正方体削成一个最大的圆锥，这个
圆锥的体积是(
相等的正方形。
上
前
左下后
右
表面积=棱长×棱长×6
S=6²
正方体的表面积
是6个面的面积和。
长方体的体积 = 长×宽×高
h
厘
米
a厘米
V =ɑbh
长方体的体积 = 底面积×高
V = Sh
考点三：长方体和正方体的表面积和体积
体积是物体所占空间的大小。
长方体的体积=长×宽×高
高( )
V=bh
长( )
圆锥是由一个( 底 )面和一个( 侧 )面组成的。圆锥的
底面是一个( 圆 )，侧面是一个( 曲 )面，侧面展开
得到一个( 扇形 )。从圆锥的顶点到底面圆心的距离是圆
锥的( 高 )，圆锥有( 1 )条高

《基本立体图形》考点讲解复习与同步训练

《8.1 基本立体图形》考点讲解【思维导图】考法一多面体【例1】下列说法正确的是（）A．有一个面是多边形，其余各面都是三角形，由这些面围成的几何体是棱锥B．有两个面平行且相似，其余各面都是梯形的多面体是棱台C．如果一个棱锥的各个侧面都是等边三角形，那么这个棱锥可能为六棱锥D．如果一个棱柱的所有面都是长方形，那么这个棱柱是长方体【一隅三反】1．（多选）下列说法正确的是（）A．如果四棱锥的底面是正方形，那么这个四棱锥的四条侧棱都相等B．五棱锥只有五条棱C．一个棱柱至少有五个面D．棱台的各侧棱延长后交于一点2．列命题正确的是（）A．棱柱的每个面都是平行四边形B．一个棱柱至少有五个面C．棱柱有且只有两个面互相平行D．棱柱的侧面都是矩形3．下列命题中，正确的是（）A．有两个侧面是矩形的棱柱是直棱柱B．底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱C．侧面都是矩形的四棱柱是长方体D．侧面都是等腰三角形的棱锥是正棱锥考法二旋转体【例2】给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是（）A．①②B．②③C．①③D．②④【一隅三反】1．下列说法正确的是（）A．以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥B．以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台C．圆柱、圆锥、圆台的底面都是圆面D．一个平面截圆锥，得到一个圆锥和一个圆台2．下列结论中正确的是（）A．半圆弧以其直径为轴旋转一周所形成的曲面叫做球B．直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥C．夹在圆柱的两个平行截面间的几何体还是一个旋转体D．用一个平面截圆锥底面与截面组成的部分是圆台3．给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台的上、下底面的圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的；⑤圆台所有母线的延长线交于一点其中正确的命题是（）A．①②④B．②③④C．①③⑤D．②④⑤考法三组合体【例3】如图所示的组合体，其结构特征是（）A．由两个圆锥组合成的B．由两个圆柱组合成的C．由一个棱锥和一个棱柱组合成的D．由一个圆锥和一个圆柱组合成的【一隅三反】1．如图的组合体是由（）组合而成.A．两个棱柱B．棱柱和圆柱C ．圆柱和棱台D ．圆锥和棱柱2．将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体是由 ( )A ．一个圆台、两个圆锥构成B ．两个圆台、一个圆锥构成C ．两个圆柱、一个圆锥构成D ．一个圆柱、两个圆锥构成3．观察下列四个几何体，其中可看作是由两个棱柱拼接而成的是_______(填序号).考法四截面问题【例4】（多选）用一个平面截一个正方体，截面图形可以是（）A ．三角形B ．等腰梯形C ．五边形D ．正六边形【一隅三反】1．（多选）一个平面去截正方体，关于截面的形状，下列可能的是（）A ．正三角形B ．正四边形C ．正五边形D ．正六边形 2．已知正方体1111ABCD A B C D -的棱长为2，AB ，AD 中点分别为E ，F ，若过EF 的平面截该正方体所得的截面是一个五边形，则该五边形周长的最大值为（）A BC ．D ．+《8.1 基本立体图形》考点讲解答案解析考法一多面体【例1】下列说法正确的是（）A．有一个面是多边形，其余各面都是三角形，由这些面围成的几何体是棱锥B．有两个面平行且相似，其余各面都是梯形的多面体是棱台C．如果一个棱锥的各个侧面都是等边三角形，那么这个棱锥可能为六棱锥D．如果一个棱柱的所有面都是长方形，那么这个棱柱是长方体【答案】D【解析】选项A，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面围成的多面体是棱锥，即其余各面的三角形必须有公共的顶点，故选项A错误；选项B，棱台是由棱锥被平行于棱锥底面的平面所截而得的，而有两个面平行且相似，其余各面都是梯形的多面体不一定是棱台，因为它的侧棱延长后不一定交于一点，故选项B错误；选项C，当棱锥的各个侧面的共顶点的角之和是360 时，各侧面构成平面图形，构不成棱锥，由此推导出这个棱锥不可能为六棱锥，即选项C错误；选项D，若每个侧面都是长方形，则说明侧棱与底面垂直，又底面也是长方形，符合长方体的定义，即选项D正确．故选：D．【一隅三反】1．（多选）下列说法正确的是（）A．如果四棱锥的底面是正方形，那么这个四棱锥的四条侧棱都相等B．五棱锥只有五条棱C．一个棱柱至少有五个面D．棱台的各侧棱延长后交于一点【答案】CD【解析】四棱锥的底面是正方形，它的侧棱可以相等，也可以不相等，A错误；五棱锥除了五条侧棱外，底面上还有五条棱，故共10条棱，B错误；一个棱柱最少有三个侧面，两个底面，故至少有五个面，C正确；棱台是由平行于棱锥底面的截面截得，故棱台的各侧棱延长后交于一点，D正确.故选：CD.2．下列命题正确的是（）A．棱柱的每个面都是平行四边形B．一个棱柱至少有五个面C．棱柱有且只有两个面互相平行D．棱柱的侧面都是矩形【答案】B【解析】对于A，棱柱的上下底面可以是三角形或者是梯形，故A不正确；对于B，面最少的就是三棱柱，共有五个面，B正确；对于C，长方体是棱柱，但是上下、左右、前后都是互相平行的，C不正确；对于D，斜棱柱的侧面可以不是矩形，D错误.3．下列命题中，正确的是（）A．有两个侧面是矩形的棱柱是直棱柱B．底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱C．侧面都是矩形的四棱柱是长方体D．侧面都是等腰三角形的棱锥是正棱锥【答案】B【解析】对于A，根据直棱柱的概念，侧棱垂直于底面的棱柱是直棱柱，有两个侧面是矩形的棱柱可能是斜棱柱，只有相邻的两个侧面是矩形时，才是直棱柱，故A不正确；对于B，有相邻两个侧面与底面垂直的棱柱，可知侧棱垂直于底面，又底面为正多边形，故B正确；对于C，侧面都是矩形的直棱柱，底面不是矩形，不是长方体，故C不正确；对于D，侧面都是等腰三角形，但底面不是正多边形的棱锥不是正棱锥，故D不正确.故选：B考法二旋转体【例2】给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是（）A．①②B．②③C．①③D．②④【答案】D【解析】由圆柱的母线无论旋转到什么位置都与轴平行，故①错误；圆锥是以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的，故②正确；③中连接的线可能存在与轴异面的情况，而圆台的母线与轴共面，故③错误；④由于圆柱中任意母线均与轴平行，故其中任意两条母线相互平行，故④正确；综上可知②④正确，①③错误.故选：D.【一隅三反】1．下列说法正确的是（）A．以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥B．以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台C．圆柱、圆锥、圆台的底面都是圆面D．一个平面截圆锥，得到一个圆锥和一个圆台【答案】C【解析】以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥，以斜边为轴旋转一周所得的旋转体是是两个同底圆锥的组合体，A错；以直角梯形的直角腰所在直线为轴旋转一周所得的旋转体才是圆台，B错；圆柱、圆锥、圆台的底面都是圆面，正确；平行于圆锥底面平面截圆锥，得到一个圆锥和一个圆台，如果截面不平行于底面，则截得的不是圆锥和圆台，D错.故选：C.2．下列结论中正确的是（）A．半圆弧以其直径为轴旋转一周所形成的曲面叫做球B．直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥C．夹在圆柱的两个平行截面间的几何体还是一个旋转体D．用一个平面截圆锥底面与截面组成的部分是圆台【答案】B【解析】因为半圆弧以其直径为轴旋转一周所形成的曲面叫做球面，球面围成的几何体叫做球，故A错误；当以直角三角形的直角边所在直线为轴旋转时，其余各边旋转形成的面所围成的几何体是圆锥，故B正确；当两个平行截面不平行于上、下两个底面时，两个平行截面间的几何体不是旋转体，故C错误；圆锥的截面不与底面平行时，圆锥底面与截面组成的部分不是圆台，故D错误.故选：B.3．给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台的上、下底面的圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的；⑤圆台所有母线的延长线交于一点其中正确的命题是（）A．①②④B．②③④C．①③⑤D．②④⑤【答案】D【解析】由于圆柱母线所在的直线互相平行且与旋转轴平行，而在圆柱的上、下底面的圆周上各取一点，这两点的连线与旋转轴不一定平行，故①错误，④正确；由圆锥母线的定义知②正确；在圆台的上、下底面的圆周上各取一点，这两点的连线不一定是母线，且圆台所有母线的延长线交于一点，故③错误，⑤正确.故选：D.考法三组合体【例3】如图所示的组合体，其结构特征是（）A．由两个圆锥组合成的B．由两个圆柱组合成的C．由一个棱锥和一个棱柱组合成的D．由一个圆锥和一个圆柱组合成的【答案】D【解析】由图知：该组合体是由一个圆锥和一个圆柱组合成的，故选：D【一隅三反】1．如图的组合体是由（）组合而成.A．两个棱柱B．棱柱和圆柱C．圆柱和棱台D．圆锥和棱柱【答案】B【解析】由图可知该组合体由圆柱和六棱柱组合而成，故选：B2．将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体是由( )A．一个圆台、两个圆锥构成B．两个圆台、一个圆锥构成C．两个圆柱、一个圆锥构成D．一个圆柱、两个圆锥构成【答案】D【解析】旋转体如图，中间是一个圆柱，两端是相同的圆锥构成，故选D．3．观察下列四个几何体，其中可看作是由两个棱柱拼接而成的是________(填序号).【答案】①④【解析】①可看作由一个四棱柱和一个三棱柱组合而成，④可看作由两个四棱柱组合而成.②③显然不是棱柱拼接而成.故答案为：①④考法四截面问题【例4】（多选）用一个平面截一个正方体，截面图形可以是（）A．三角形B．等腰梯形C．五边形D．正六边形【答案】ABCD【解析】如图所示：三角形等腰梯形五边形正六边形故用一个平面去截一个正方体，截面可能是三角形、等腰梯形、五边形、正六边形，故选：ABCD.【一隅三反】1．（多选）（用一个平面去截正方体，关于截面的形状，下列可能的是（）A．正三角形B．正四边形C．正五边形D．正六边形【答案】ABDBDC，故A正确.【解析】如图（1），截面为三角形1如图（2），截面为正方形PQRS ，其中,,,P Q R S 为所在棱的中点，故B 正确.如图（3），截面为正六边形EFGHIJ ，其中,,,,,E F G H I J 为所在棱的中点，故D 正确.如图（4），因为平面11//ADD A 平面11BCC B ，平面KLMNO 平面11=BCC B MN ，平面KLMNO ⋂平面11=ADD A KO ，故//KO MN ，若截面为正五边形，则KO MN =，故四边形OKMN 为平行四边形，但正五边形中不可能存在过4个顶点的平行四边形，故C 错误. 故选：ABD.2．已知正方体1111ABCD A B C D -的棱长为2，AB ，AD 中点分别为E ，F ，若过EF 的平面截该正方体所得的截面是一个五边形，则该五边形周长的最大值为（）A B C ． D ．+【答案】A【解析】将面11BCC B 展开与面11ABB A 处于同一平面要使1l E QC C Q FH H +++最大,则沿面1C QEFH 切才能保证五点共面，在1Rt ECC △中,112,12CC BC BE AB ====,此时1EQ QC +==又1FH HC EQ QC +=+.∴周长()12EF EQ QC =++=故选:A《8.1 基本立体图形（精练）》同步练习【题组一多面体】1．下列几何体中是棱锥的有（）A．0个B．1个C．2个D．3个2．下列命题正确的是（）A．棱柱的底面一定是平行四边形B．棱锥的底面一定是三角形C．棱锥被平面分成的两部分不可能都是棱锥D．棱柱被平面分成的两部分可以都是棱柱3．一个棱锥所有的棱长都相等，则该棱锥一定不是（）A．正三棱锥B．正四棱锥C．正五棱锥D．正六棱锥4．棱台不具备的特点是（）A．两底面相似B．侧面都是梯形C．侧棱都相等D．侧棱延长后都交于一点5．某几何体有6个顶点，则该几何体不可能是（）A．五棱锥B．三棱柱C．三棱台D．四棱台6．下列说法中正确的是（）A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有一个面是多边形，其余各面都是梯形的几何体叫棱台D．有一个面是多边形，其余各面都是有一个公共顶点的三角形的几何体叫棱锥7．下列说法正确的是（）A．棱柱的侧棱都相等，侧面都是全等的平行四边形B．用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台C．若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直D．棱台的侧棱延长后交于一点，侧面是等腰梯形8．下列说法正确的是________(填序号).①底面是正多边形的棱锥为正棱锥；②各侧棱都相等的棱锥为正棱锥；③各侧面都是等腰三角形的棱锥为正棱锥；④各侧面都是全等的等腰三角形的棱锥是正棱锥；⑤底面是正多边形且各侧面全等的棱锥为正棱锥.9．给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.10．下列关于棱锥、棱台的说法中，正确说法的序号是________①用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；②棱台的侧面一定不会是平行四边形；③棱锥的侧面只能是三角形；④棱台的各侧棱延长后必交于一点；⑤棱锥被平面截成的两部分不可能都是棱锥.11．如图，下列几何体中，_______是棱柱，_______是棱锥，_______是棱台(仅填相应序号).【题组二旋转体】1．以下空间几何体是旋转体的是（）A．圆台B．棱台C．正方体D．三棱锥2．给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．其中正确的是（）A．①③B．②④C．①④D．②③3．如图所示，观察下面四个几何体，其中判断正确的是（）A．①是圆台B．②是圆台C．③是圆锥D．④是圆台4．有下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点连线的长度是母线的长度；②圆锥顶点与底面圆周上任意一点连线的长度是母线的长度；③圆柱的任意两条母线所在直线互相平行；④过球上任意两点有且只有一个大圆；其中正确命题的序号是_____ 【题组三组合体】1．说出图中物体的主要结构特征.2．如图，以直角梯形ABCD的下底AB所在直线为轴，其余三边旋转一周形成的面围成一个几何体，说出这个几何体的结构特征.3．如图，说出图中两个几何体的结构特征.4．试指出图中组成各几何体的基本元素.【题组四截面问题】1．如图是一个正方体的表面展开图，则图中“0”在正方体中所在的面的对面上的是（）A．2 B．1 C．高D．考2．如图所示，在三棱台A′B′C′－ABC中，截去三棱锥A′－ABC，则剩余部分是（）A．三棱锥B．四棱锥C．三棱柱D．组合体3．用一个平面去截一个几何体，得到的截面是三角形面，这个几何体不可能是（）A．棱锥B．圆锥C．圆柱D．正方体4．如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面，下底面圆心为顶点的圆锥而得到的组合体，现用一个竖直的平面去截这个组合体，则截面图形可能是（）A．①②B．①③C．①④D．①⑤《8.1 基本立体图形（精练）》同步练习答案解析【题组一多面体】1．下列几何体中是棱锥的有（）A．0个B．1个C．2个D．3个【答案】C【解析】由棱锥的定义可得，只有几何体⑤、⑥为棱锥.故选：C.2．下列命题正确的是（）A．棱柱的底面一定是平行四边形B．棱锥的底面一定是三角形C．棱锥被平面分成的两部分不可能都是棱锥 D．棱柱被平面分成的两部分可以都是棱柱【答案】D【解析】对于选项,A棱柱的底面也可以是三角形，五边形等，不一定是平行四边形，所以该选项错误；对于选项B，棱锥的底面不一定是三角形，也可以是四边形，五边形等，所以该选项错误；对于选项C，棱锥被平面分成的两部分可能都是棱锥，所以该选项错误；对于选项D，棱柱被平面分成的两部分可以都是棱柱，所以该选项正确.故选：D3．一个棱锥所有的棱长都相等，则该棱锥一定不是（）A．正三棱锥B．正四棱锥C．正五棱锥D．正六棱锥【答案】D【解析】因为正六变形的中心到底面顶点的距离等于边长，所以正六棱锥的侧棱必大于底面棱长，故选：D.4．棱台不具备的特点是（）A．两底面相似B．侧面都是梯形C．侧棱都相等D．侧棱延长后都交于一点【答案】C【解析】根据棱台的定义，由平行于棱锥底面的平面截棱锥，截面与底面之间的部分叫棱台．棱台的两底面是相似多边形，A正确；侧面的上下底边平行，侧面都是梯形，B正确；侧棱延长后交于一点，D正确；由于棱锥的侧棱不一定相等，所以棱台的侧棱也不一定相等，C不一定成立，故选：C．5．某几何体有6个顶点，则该几何体不可能是（）A．五棱锥B．三棱柱C．三棱台D．四棱台【答案】D【解析】四棱台有8个顶点，不符合题意.，其他都是6个顶点．故选：D．6．下列说法中正确的是（）A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有一个面是多边形，其余各面都是梯形的几何体叫棱台D．有一个面是多边形，其余各面都是有一个公共顶点的三角形的几何体叫棱锥【答案】D【解析】因为有两个面平行，其余各面是相邻的公共边都相互平行的平行四边形的几何体叫棱柱，所以A、B错误；而一个平行于底面的平面截棱锥，底面与截面之间的部分叫棱台，所以棱台各侧棱的延长线交于一点，所以C错误；因为有一个面是多边形，其余各面都是有公共顶点的三角形的几何体叫棱锥，所以D 正确.故选：D.7．下列说法正确的是（）A．棱柱的侧棱都相等，侧面都是全等的平行四边形B．用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台C．若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直D．棱台的侧棱延长后交于一点，侧面是等腰梯形【答案】C【解析】A. 棱柱的侧棱都相等，侧面是平行四边形,但不一定全等，故错误；B.用一个平面去截棱锥，当棱锥底面与截面平行时，才是棱台，故错误；C.若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直，如正方体共顶点的三个相邻平面，故正确；D.棱台的侧棱延长后交于一点，但侧面不一定是等腰梯形，故错误；故选：C8．下列说法正确的是________(填序号).①底面是正多边形的棱锥为正棱锥；②各侧棱都相等的棱锥为正棱锥；③各侧面都是等腰三角形的棱锥为正棱锥；④各侧面都是全等的等腰三角形的棱锥是正棱锥；⑤底面是正多边形且各侧面全等的棱锥为正棱锥.【答案】⑤【解析】对于①，如果棱锥的顶点在底面上的射影不是正多边形的中心，则此棱锥不是正棱锥，故①错误.对于②，如图（1），棱锥的顶点是圆锥的顶点，而底面多边形是圆锥底面圆的内接非正多边形，此时棱锥满足各侧棱都相等，但不是正棱锥，故②错误.对于③④，如图（2），侧面都是等腰三角形，且它们全等，但该三棱锥不是正棱锥，故③④错误.对于⑤，因为底面是正多边形且各侧面全等的棱锥为正棱锥，故顶点底面上的射影O为正多边形的中心，此时棱锥为正棱锥，故⑤正确.故答案为：⑤9．给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.【答案】②③④【解析】①不正确，根据棱柱的定义，棱柱的各个侧面都是平行四边形，但不一定全等； ②正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二面角；③正确，因为两个过相对侧棱的截面的交线平行于侧棱，又垂直于底面；④正确，如图，正方体1111ABCD A B C D -中的三棱锥1C ABC -，四个面都是直角三角形.故答案为：②③④10．下列关于棱锥、棱台的说法中，正确说法的序号是________①用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；②棱台的侧面一定不会是平行四边形；③棱锥的侧面只能是三角形；④棱台的各侧棱延长后必交于一点；⑤棱锥被平面截成的两部分不可能都是棱锥.【答案】②③④【解析】①错，若平面不与棱锥底面平行，用这个平面去截棱锥，则棱锥底面和截面之间的部分不是棱台；②对，棱台的侧面一定是梯形，而不是平行四边形；③对，由棱锥的定义知棱锥的侧面只能是三角形；④对，棱台是由平行于棱锥底面的平面截得的，故棱台的各侧棱延长后必交于一点； ⑤错，如图所示四棱锥被平面PBD 截成的两部分都是棱锥.故答案为：②③④11．如图，下列几何体中，_______是棱柱，_______是棱锥，_______是棱台(仅填相应序号).【答案】①③④⑥⑤【解析】结合棱柱、棱锥和棱台的定义可知①③④是棱柱，⑥是棱锥，⑤是棱台.故答案为：①③④；⑥；⑤.【题组二旋转体】1．以下空间几何体是旋转体的是（）A．圆台B．棱台C．正方体D．三棱锥【答案】A【解析】由封闭的旋转面围成的几何体叫作旋转体可知，只有A项满足题意故选：A 2．给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．其中正确的是（）A．①③B．②④C．①④D．②③。

上海立体几何配套复习题(一)

专题01空间点、直线、平面之间的位置关系综合题专练一、单选题1．（2021·上海市松江二中高二月考）已知直线a ，b 及平面 α，有下列命题：①//a b a b αα⊥⎧⇒⎨⊥⎩；②//a b a b αα⊥⎧⇒⊥⎨⎩；③//////a b a b αα⎧⇒⎨⎩；④//a b a b αα⎧⇒⊥⎨⊥⎩.则其中正确命题的个数为（）A ．0个B ．1个C ．2个D ．4个2．（2021·上海杨浦·复旦附中高二期中）如图是正方体的平面展开图，在这个正方体中，①BM 与ED 平行；②CN 与BE 是异面直线；③CN 与BM 成60°；④DM 与BN 垂直.以上四个命题中，正确命题的序号是（）A ．①②③B ．②④C ．③④D ．②③④3．（2021·长宁区·上海市延安中学高二期中）已知正方体1111ABCD A B C D -，P 为1CC 中点，对于下列两个命题：（1）过点P 有且只有一条直线与直线AB ，11A D 都相交；（2）过点P 有且只有一条直线与直线AB ，11A D 都成45°角．则以下判断正确的是（）A ．（1）为真命题；（2）为真命题B ．（1）为真命题；（2）为假命题C ．（1）为假命题；（2）为真命题D ．（1）为假命题；（2）为假命题4．（2021·上海普陀·曹杨二中高二月考）下列图形中，一定可以确定一个平面的是（）A ．四边形B ．空间三点C ．两两相交且交点均不相同的四条直线D ．交于同一点的三条直线5．（2021·上海市大同中学）已知a 和b 是成80 角的两条直面直线，则过空间一点且与a b 、都成50 角的直线共有（）A ．2条B ．3条C ．4条D ．无数条6．（2021·上海市杨浦高级中学高二期末）已知直线a 、b 是两条不重合的直线，α、β是两个不重合的平面，则下列命题正确的是（）A ．若a α⊥，a β⊥，则//αβB ．若//a α，//b β，//αβ，则//a bC ．若a b ⊥r r ，b α⊥，//a β，则//αβD ．若//αβ，a 与α所成角和b 与β所成角相等，则//a b7．（2021·上海市洋泾中学高二月考）关于直线l 、m 及平面α、β，下列命题中正确的是（）A ．若//l α，m αβ= ，则//l mB ．若l α⊥，//m α，则l m ⊥C ．若//l α，//m α，则//l mD ．若//l α，m l ⊥，则m α⊥8．（2021·上海市建平中学高二月考）ABC 的三边长分别3､4､5，P 为ABC 所在平面外一点，令集合Q ={P P 为ABC 所在平面外一点，且到三边所在直线的距离都是3}，则集合Q 的子集个数为（）A ．2B ．4C ．8D ．169．（2021·上海市亭林中学高二期中）设直线,a b 与平面α所成的角相等，则直线,a b 的位置关系为（）A ．平行B ．平行或异面C ．平行或相交D ．平行、相交或异面10．（2021·上海市进才中学高二期中）已知平面l αβ= ，B ，C l ∈，A α∈，且A l ∉，D β∈，且D l ∉，则下列叙述错误的是（）A ．直线AD 与BC 是异面直线B ．直线CD 在α上的射影可能与AB 平行C ．过AD 有且只有一个平面与BC 平行D ．过AD 有且只有一个平面与BC 垂直二、填空题11．（2021·上海奉贤区·高二期末）在《九章算术》中定义“底面为直角三角形而有一侧棱垂直于底面的三棱锥为鳖臑”．如图，在鳖臑ABCD 中，侧棱AB ⊥底面BCD ，1AB =，2BC =，1CD =，则异面直线AC 与BD 所成角的大小为______．12．（2021·上海市建平中学高二期中）已知圆锥的轴截面PAB 是等边三角形，C 为底面弧AB 的中点，D 为母线PB 的中点，则异面直线PA 和CD 所成角的大小为________13．（2021·上海静安·高二期末）如图，三棱锥P -ABC 中，PA ⊥底面ABC ，底面ABC 是边长为2的正三角形，且23PA =，若M 是BC 的中点，则异面直线PM 与AC 所成角的大小是__________（结果用反三角函数值表示）14．（2021·上海市复兴高级中学）四面体ABCD 中，2AB CD ==，4AC AD BC BD ====，则异面直线AB 与CD 的距离为________15．（2021·上海普陀区·曹杨二中高二期末）已知空间四边形ABCD ，2AB CD ==，且AB 与CD 所成的角为3π，设E 、F 分别是BC 、AD 的中点，则EF 的长度为______．16．（2021·徐汇区·上海中学高二月考）下列判断中：①三点确定一个平面；②一条直线和一点确定一个平面；③两条直线确定一个平面；④三角形和梯形一定是平面图形；⑤四边形一定是平面图形；⑥六边形一定是平面图形；⑦两两相交的三条直线确定一个平面.其中正确的是___________.17．（2021·上海市中国中学高二月考）一个正方体的展开图如图所示，B 、C 、D 为原正方体的顶点，A 为原正方体一条棱的中点，在原来的正方体中，直线CD 与AB 所成角的余弦值为______．18．（2021·上海市洋泾中学高二月考）如图，1111ABCD A B C D -是棱长为1的正方体，一个质点从A 出发沿正方体的面对角线运动，每走完一条面对角线称为“走完一段”，质点的运动规则如下：运动第i 段与第2i +所在直线必须是异面直线(其中i 是正整数)，质点走完的第99段与第1段所在的直线所成的角是___________.19．（2021·上海徐汇区·位育中学）在棱长为2的正方体1111ABCD A B C D -中，M N 、分别是111A B CC 、的中点，用过D M N 、、三点的平面截正方体，则截面图像的周长为__________20．（2021·上海市建平中学高二月考）已知异面直线,a b 所成角为3π，过空间一点P 有且仅有2条直线与,a b 所成角都是θ，则θ的取值范围是___________.三、解答题21．（2021·上海市松江二中高二月考）在正四棱柱1111ABCD A B C D -中，AB =2，过1A 、1C 、B 三点的平面截去正四棱柱的一个角后，得到如图所示的几何体111ABCD A C D -，且这个几何体的体积为203，点P ，Q 分别是1A D 和AC 的中点.（1）求异面直线1D P 与1C Q 所成角的大小；（2）求直线C 1D 与平面11A C B 所成角的大小.（用反三角函数表示）22．（2021·上海市西南位育中学高二期中）长方体1111ABCD A B C D -中，11,2AB AA AD ===，点E 是棱BC 的中点.（1）求异面直线1BB 与1D E 所成角的大小；（2）求点A 到平面1A DE 的距离.23．（2021·上海杨浦·复旦附中高二期中）已知正方体1111ABCD A B C D -的棱长为2，若M ，N 分別是111,CC A D 的中点，作出过M ，N ，B 三点的截面，并求出这截面的周长.24．（2021·上海市奉贤区奉城高级中学高二期中）如图所示，在长方体1111ABCD A B C D -中，1AB =，2BC =，15CC =，M 为棱1CC 上一点．（1）若132C M =，求异面直线1A M 和11CD 所成角的正切值；（2）若11C M =．试证明：BM ⊥平面11A B M ．25．（2021·宝山区·上海交大附中高二期中）如图，正四棱柱1111ABCD A B C D -的底面是边长为2的正方形，侧棱长为1．（1）求直线1A C 与直线1AD 所成角的余弦值；（2）求二面角11D A C A --平面角大小的余弦值；（3）在直线1A C 上是否存在一个动点P ，使得P 在平面1D AC 的投影恰好为1D AC 的重心，若存在，求线段PC 的长度，若不存在，说明理由．26．（2021·上海市大同中学）如图，在四棱锥P ABCD -中，PA ⊥面ABCD ，2,7AB BC AD CD ====，3,120,PA ABC G =∠=︒为线段PC 上的点.（1）证明：BD ⊥平面PAC ；（2）若G 是PC 的中点，求DG 与平面PAC 所成的角的正切值；（3）在（2）的条件下求异面直线BG 与PD 所成角的余弦值.27．（2021·上海市大同中学）已知长方体ABCD﹣A1B1C1D1中，M，N分别为AA1和AB的中点．求证：（1）D1，M，N，C四点共面；（2）D1M、DA、CN三线共点．28．（2021·上海市中国中学高二月考）已知空间四边形SABC各边及对角线的长都是1．（1）求边SA、BC的距离；（2）求异面直线SB与AC所成角大小．29．（2021·上海市建平中学高二月考）如图，已在正四棱锥P ABCD -，4PA =，底面边长为4，Q 为PB 的中点.（1）求作平面QAD 与正四棱锥P ABCD -的截面；（2）求二面角Q AD B --的大小.30．（2021·上海徐汇区·位育中学）如图所示，在直三棱柱111ABC A B C -中，底面是等腰直角三角形，90ACB ∠= ，12CA CB CC ===.点1D D ，分别是棱11AC A C ，的中点.（1）求证：11、、、D B B D 四点共面；（2）求直线1BC 与平面11DBB D 所成角的大小.。

期末复习专题一：图形与几何—长方体和正方体篇(解析版)人教版

2022-2023学年五年级数学下册典型例题系列之期末复习专题一：图形与几何—长方体和正方体篇（解析版）编者的话：《2022-2023学年五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题、专项练习、分层试卷三大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

分层试卷部分是根据试题难度和掌握水平，主要分为基础卷、提高卷、拓展卷三大部分，其优点在于考点广泛，分层明显，适应性广。

本专题是期末复习专题一：图形与几何—长方体和正方体篇。

本部分内容包括观察立体图形、长方体和正方体的应用、平移和旋转的认识及作图，其中以长方体和正方体内容为主，包括期末常考典型例题，涵盖较广，部分内容和题型比较复杂，建议作为期末复习核心内容进行讲解，一共划分为六大篇目，欢迎使用。

【篇目一】观察立体图形：长方体和正方体。

【知识总览】一、观察物体。

1.从不同位置观察立体图形的形状，一般是从前面、上面、左面三个方向观察，所看到的形状一般是不同的。

2.在画观察到的图形时，遵循三个原则：长对正、高平齐、宽相等。

二、还原立体图形。

1.从上面看到的图形中，小正方形内部的数表示的是在这个位置上所用的小正方体的个数。

2.从正面看到的图形中，视线从前往后，每列中最大的数即为这一列最高层的层数。

3.从左面看到的图形，视线从左往右，每行中最大的数即为这一行最高层的层数。

三、确定小正方体的数量。

1.标数法：根据正面和侧面看到的形状在上面所看到的每个小正方形内标数，然后确定小正方体的个数。

2.分层记数。

根据三视图，了解层数，再分别判断每层的数量，最后把每层数量相加即可。

【典型例题1】观察物体。

一个几何体从上面看到的图形是，图形上的数字表示在这个位置上所用的小正方体的个数，这个几何体从正面看是（），从左面看是（）。

高中数学《立体几何》专题复习 (1)

高中数学《立体几何》专题复习一1．(2018·安徽东至二中段测)将一个等腰梯形绕着它的较长的底边所在直线旋转一周，所得的几何体包括()A．一个圆台、两个圆锥B．两个圆台、一个圆柱C．两个圆台、一个圆锥D．一个圆柱、两个圆锥答案 D解析把等腰梯形分割成两个直角三角形和一个矩形，由旋转体的定义可知所得几何体包括一个圆柱、两个圆锥．故选D.2．以下关于几何体的三视图的论述中，正确的是()A．正方体的三视图是三个全等的正方形B．球的三视图是三个全等的圆C．水平放置的正四面体的三视图都是正三角形D．水平放置的圆台的俯视图是一个圆答案 B解析画几何体的三视图要考虑视角，但对于球无论选择怎样的视角，其三视图总是三个全等的圆．3．如图所示，几何体的正视图与侧视图都正确的是()答案 B解析侧视时，看到一个矩形且不能有实对角线，故A，D排除．而正视时，有半个平面是没有的，所以应该有一条实对角线，且其对角线位置应为B中所示，故选B.4．一个几何体的三视图如图，则组成该几何体的简单几何体为()A．圆柱和圆锥B．正方体和圆锥C．四棱柱和圆锥D．正方体和球答案 C5．(2018·沧州七校联考)三棱锥S－ABC及其三视图中的正视图和侧视图如图所示，则棱SB 的长为()A．16 3 B.38C．4 2 D．211答案 C解析由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形．在△ABC中，AC＝4，AC边上的高为23，所以BC＝4.在Rt△SBC中，由SC＝4，可得SB＝4 2. 6．(2017·衡水中学调研卷)已知一个四棱锥的高为3，其底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形，则此四棱锥的体积为()A．2 2 B．6 2C．1 D. 2答案 A解析因为底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形，所以在直角坐标系中，底面是边长为1和3的平行四边形，且平行四边形的一条对角线垂直于平行四边形的短边，此对角线的长为22，所以该四棱锥的体积为V＝13×22×1×3＝2 2.7.(2018·四川泸州模拟)一个正四棱锥的所有棱长均为2，其俯视图如图所示，则该正四棱锥的正视图的面积为()A. 2B. 3C．2 D．4答案 A解析由题意知，正视图是底边长为2，腰长为3的等腰三角形，其面积为12×2×（3）2－1＝ 2.8．(2018·湖南郴州模拟)一只蚂蚁从正方体ABCD－A1B1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是()A．①②B．③④C．①③D．②④答案 D解析由点A经正方体的表面，按最短路线爬行到达顶点C1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB1A1和平面BCC1B1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过BB1的中点，此时对应的正视图为②；若把平面ABCD和平面CDD1C1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过CD的中点，此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现．故选D.9．某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()答案 D解析依题意，此几何体为组合体，若上、下两个几何体均为圆柱，则俯视图为A；若上边的几何体为正四棱柱，下边几何体为圆柱，则俯视图为B；若上边的几何体为底面为等腰直角三角形的直三棱柱，下边的几何体为正四棱柱时，俯视图为C；若俯视图为D，则正视图中还有一条虚线，故该几何体的俯视图不可能是D，故选D.10．(2018·江西上馓质检)点M，N分别是正方体ABCD－A1B1C1D1的棱A1B1，A1D1的中点，用过平面AMN和平面DNC1的两个截面截去正方体的两个角后得到的几何体如图，则该几何体的正(主)视图，侧(左)视图、俯视图依次为()A．①②③B．②③④C．①③④D．②④③答案 B解析由直视图可知，该几何体的正(主)视图、侧(左)视图、俯视图依次为②③④，故选B. 11．(2018·四川宜宾期中)某几何体的三视图如图所示，则该几何体最长棱的长度为()A．4 B．3 2C．2 2 D．2 3答案 D解析由三视图可知，该几何体为如图所示的四棱锥P－ABCD，由图可知其中最长棱为PC，因为PB2＝PA2＋AB2＝22＋22＝8，所以PC2＝PB2＋BC2＝8＋22＝12，则PC＝23，故选D.12．(2018·北京东城区期末)在空间直角坐标系O－xyz中，一个四面体的顶点坐标分别为(0，0，2)，(2，2，0)，(0，2，0)，(2，2，2)．画该四面体三视图中的正视图时，以xOz平面为投影面，则得到的正视图可以为()答案 A解析设S(2，2，2)，A(2，2，0)，B(0，2，0)，C(0，0，2)，则此四面体S－ABC如图①所示，在xOz平面的投影如图②所示．其中S′是S在xOz平面的投影，A′是A在xOz平面的投影，O是B在xOz平面的投影，SB 在xOz平面的投影是S′O，并且是实线，CA在xOz平面的投影是CA′，且是虚线，如图③. 13．(2018·江西宜春模拟)某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大为()A．2 2 B．4C．2 3 D．2 6答案 C解析由三视图知该几何体为棱锥S－ABD，其中SC⊥平面ABCD，将其放在正方体中，如图所示．四面体S－ABD的四个面中△SBD的面积最大，三角形SBD是边长为22的等边三角形，所以此四面体的四个面中面积最大为34×8＝2 3.故选C.14．(2018·江苏张家港一模)若将一个圆锥侧面沿一条母线剪开，其展开图是半径为2 cm的半圆，则该圆锥的高为________cm.答案 3解析设圆锥的底面圆半径为r cm，则2πr＝2π，解得r＝1 cm，∴h＝22－1＝ 3 cm. 15．(2018·成都二诊)已知正四面体的俯视图如图所示，其中四边形ABCD是边长为2的正方形，则这个四面体的正视图的面积为________．答案2 2解析由俯视图可得，原正四面体AMNC可视作是如图所示的正方体的一内接几何体，则该正方体的棱长为2，正四面体的正视图为三角形，其面积为12×2×22＝2 2.16.(2018·上海长宁区、嘉定区质检)如图，已知正三棱柱的底面边长为2，高为5，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为________．答案13解析将正三棱柱ABC－A1B1C1沿侧棱AA1展开，再拼接一次，如图所示，在展开图中，最短距离是六个矩形形成的大矩形对角线的长度，也即为三棱柱的侧面上所求距离的最小值．由已知求得矩形的长等于6×2＝12，宽等于5，由勾股定理得d＝122＋52＝13.17．某几何体的正(主)视图和侧(左)视图如图1，它的俯视图的直观图是矩形O1A1B1C1如图2，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为________．答案96解析由俯视图的直观图可得y轴与C1B1交于D1点，O1D1＝22，故OD＝42，俯视图是边长为6的菱形，则该几何体是直四棱柱，侧棱长为4，则侧面积为6×4×4＝96. 1．(课本习题改编)如图为一个几何体的三视图，则该几何体是()A．四棱柱B．三棱柱C．长方体D．三棱锥答案 B解析由几何体的三视图可知，该几何体的直观图如图所示，即为一个平放的三棱柱．2．(2018·山东泰安模拟)某三棱锥的三视图如图所示，其侧视图为直角三角形，则该三棱锥最长的棱长等于()A．4 2 B.34C.41 D．5 2答案 C解析根据几何体的三视图，得该几何体是底面为直角三角形，有两个侧面垂直于底面，高为5的三棱锥，最长的棱长等于25＋16＝41，故选C.3．(2018·安徽毛坦厂中学月考)已知一个几何体的三视图如图所示，则这个几何体的直观图是()答案 C解析A项中的几何体，正视图不符，侧视图也不符，俯视图中没有虚线；B项中的几何体，俯视图中不出现虚线；C项中的几何体符合三个视图；D项中的几何体，正视图不符．故选C.4．(2017·山东德州质检)如图是正方体截去阴影部分所得的几何体，则该几何体的侧视图是()答案 C解析此几何体的侧视图是从左边往右边看，故其侧视图应选C.5.(2017·广东汕头中学摸底)如图是一正方体被过棱的中点M，N，顶点A及过N，顶点D，C1的两个截面截去两角后所得的几何体，该几何体的正视图是()答案 B6．(2017·贵州七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤答案 B解析正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③，故选B.7．(2014·课标全国Ⅰ)如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是()A．三棱锥B．三棱柱C．四棱锥D．四棱柱答案 B解析由题知，该几何体的三视图为一个三角形，两个四边形，经分析可知该几何体为三棱柱，故选B.8.用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是()答案 B解析D项为主视图或者侧视图，俯视图中显然应有一个被遮挡的圆，所以内圆是虚线，故选B.9．底面水平放置的正三棱柱的所有棱长均为2，当其正(主)视图有最大面积时，其侧(左)视图的面积为()A．2 3 B．3C. 3 D．4答案 A解析当正视图面积最大时，侧视图是一个矩形，一个边长为2，另一边长是三棱柱底面三角形的高为3，故侧视图面积为2 3.10．(2015·北京，文)某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为()A．1 B. 2C. 3 D．2答案 C解析将三视图还原成几何体的直观图，如图，由三视图可知，底面ABCD是边长为1的正方形，SB⊥底面ABCD，SB＝AB＝1，由勾股定理可得SA＝SC＝2，SD＝SB2＋DB2＝1＋2＝3，故四棱锥中最长棱的棱长为 3.故选C. 11．(2017·南昌模拟)若一几何体的正视图与侧视图均为边长为1的正方形，则下列图形一定不是该几何体的俯视图的是()答案 D解析若该几何体的俯视图为选项D ，则其正视图为长方形，不符合题意，故选D. 12．某几何体的正视图与侧视图如图所示，若该几何体的体积为13，则该几何体的俯视图可以是( )答案 D解析通过分析正视图和侧视图，结合该几何体的体积为13，可知该几何体的底面积应为1，因为符合底面积为1的选项仅有D 选项，故该几何体为一个四棱锥，其俯视图为D. 13．(2018·兰州诊断考试)某几何体的三视图如图所示，且该几何体的体积是3，则正视图中x 的值是( )A ．2 B.92 C.32 D ．3答案 D解析由三视图知，该几何体是四棱锥，底面是一个直角梯形，底面积S ＝12×(1＋2)×2＝3，高h ＝x ，所以其体积V ＝13Sh ＝13×3x ＝3，解得x ＝3，故选D.14．某几何体的三视图如图所示，则该几何体中，最大侧面的面积为( )A.12B.22C.52D.62答案 C解析由三视图知，该几何体的直观图如图所示．平面AED ⊥平面BCDE ，四棱锥A －BCDE 的高为1.四边形BCDE 是边长为1的正方形，则S △AED ＝12×1×1＝12，S △ABC ＝S △ABE ＝12×1×2＝22，S △ACD ＝12×1×5＝52，故选C.15.(2017·山东师大附中月考)如图是各棱长均为2的正三棱柱ABC －A 1B 1C 1的直观图，则此三棱柱侧视图的面积为________．答案 2 3解析依题意，得此三棱柱的侧视图是边长分别为2，3的矩形BB 1D 1D ，故其面积是2 3.16.(2017·北京西城区期末)已知一个正三棱柱的所有棱长均相等，其侧(左)视图如图所示，那么此三棱柱正(主)视图的面积为________．答案 2 3解析由正三棱柱三视图还原直观图可得正(主)视图是一个矩形，其中一边的长是侧(左)视图中三角形的高，另一边是棱长．因为侧(左)视图中三角形的边长为2，所以高为3，所以正视图的面积为2 3.17．用小立方块搭一个几何体，使它的正视图和俯视图如图所示，则它最多需要______个小立方块．答案14解析本题考查了三视图的有关知识．需要小立方块最多则：第一层最多6个，第二层最多5个，第三层最多3个，故最多用14个．18．(2017·湖南株洲质检)已知底面为正方形的四棱锥，其一条侧棱垂直于底面，那么该四棱锥的三视图可能是下列各图中的()答案 C解析通过对以下四个四棱锥的三视图对照可知，只有选项C是符合要求．。

小学六年级复习立体图形

10.立体图形一、填空。

1.张老师在实验室里把2L药水倒入如右图的两个容器中,刚好都倒满。

已知圆柱形和圆锥形容器的底面积相等,则圆柱形容器的容积是( )L,圆锥形容器的容积是( )L。

2.一根长2米,横截面直径是40厘米的圆柱体木头浮在水面上,小华发现它正好有一半露出水面。

这根木头与水接触面的面积是( )平方厘米。

3.种机器零件,圆柱部分和圆锥部分的体积比是( )。

如果圆柱部分的体积是48立方厘米,这个零件的体积是( )立方厘米。

4.如图,把一个体积为720立方厘米的圆柱形木料削成一个蛇螺,陀螺的体积为( )立方厘米。

5. 一个长6厘米,宽4厘米,高12厘米的长方体牛奶盒,装满牛奶。

笑笑在准备喝牛奶时一不小心把盒子弄歪了,洒出一些牛奶,也就是图中的空白部分。

洒出( )毫升牛奶。

6.一个圆柱形油漆桶的侧面贴着商标纸,圆柱底面直径是10cm,高25cm。

这张商标纸展开后是一个长方形,它的长是( )cm。

7. 一个高45厘米的圆锥体容器,盛满水后再倒入和它等底等高的圆柱体容器里,水面的高度是( )厘米。

8.将一张长12cm、宽6cm的长方形纸片围成一个圆柱,这个圆柱的侧面积是( )cm2。

9.一个圆柱的侧面展开后是边长为6.28厘米的正方形,这个圆柱的高是( )厘米,底面半径是( )厘米。

10.一种小桶装的纯净水大约是8L。

这样的一桶纯净水能全部倒入棱长是40厘米的正方体玻璃缸，水高（）厘米。

11．一个圆柱的底面直径是2厘米,高是3厘米,它的侧面积是( )平方厘米。

二、选择。

1. 有一个长26cm、宽18cm、高0.6cm的物体，它可能是 ( )A.冰箱B.黑板擦C.橡皮D.数学书2.把一个棱长为a厘米的正方体锯成两个相同的长方体,表面积增加( )平方厘米。

A 2aB a2 C.2a2 D.无法确定3. 把一个圆柱的底面平均分成若干个扇形,然后拼成一个近似的长方体,表表面积比原来增加了100平方厘米,圆柱的高是10厘米,那么圆柱的侧面积是( )平方厘米。

一轮立体几何复习(文科)

立体几何一、考点分析：考点一：空间几何体的结构、三视图、直观图、表面积和体积了解和正方体、球有关的简单几何体的结构特征，理解柱、锥、台、球的结构特征，能画出简单空间几何体的三视图，会用斜二测画法画出它们的直观图，会用平行投影与中心投影两种方法，画出简单空间几何体的三视图或直观图，了解空间几何体的不同表示形式，能识别上述三视图所表示的空间几何体，理解三视图和直观图的联系，并能进行转化，会计算球、柱、锥、台的表面积和体积（不要求记忆公式）考点二：点、直线、平面的位置关系理解空间中点、线、面的位置关系的定义，了解四个公理及其推论；空间两直线的三种位置关系及其判定；异面直线的定义及其所成角的求法。

考点三：直线与平面、平面与平面平行和垂直的判定与性质掌握线面、面面平行（垂直）的判定与性质定理，能用判定定理证明线面、面面平行，线线、线面、面面垂直，会用性质定理解决线面、面面平行、线面、面面垂直的问题，理解线面角、二面角的概念，能证明一些空间位置关系的简单命题。

二、知识点指导：1、空间基本元素：直线与平面之间位置关系的小结。

如下图：在正棱锥中，要熟记由高PO ，斜高PM ，侧棱PA ，底面外接圆半径OA ，底面内切圆半径OM ，底面正多边形半边长OM ，构成的三棱锥，该三棱锥四个面均为直角三角形。

3、球是由曲面围成的旋转体。

研究球，主要抓球心和半径。

4、立体几何的学习，主要把握对图形的识别及变换（分割，补形，旋转等），因此，既要熟记基本图形中元素的位置关系和度量关系，也要能在复杂背景图形中“剥出”基本图形。

三、典型例题1．空间四边形中，互相垂直的边最多有（） A 、1对 B 、2对 C 、3对 D 、4对 2．底面是正三角形，且每个侧面是等腰三角形的三棱锥是A 、一定是正三棱锥B 、一定是正四面体C 、不是斜三棱锥D 、可能是斜三棱锥 3．(磨中)已知一个正四面体和一个正八面体的棱长相等，把它们拼接起来，使一个表面重合，所得多面体的面数有( )A 、7B 、8C 、9D 、104、一个几何体的三视图如图所示，则这个几何体的体积为。

五年级奥数学练习试卷思维培训资料立体图形(一)

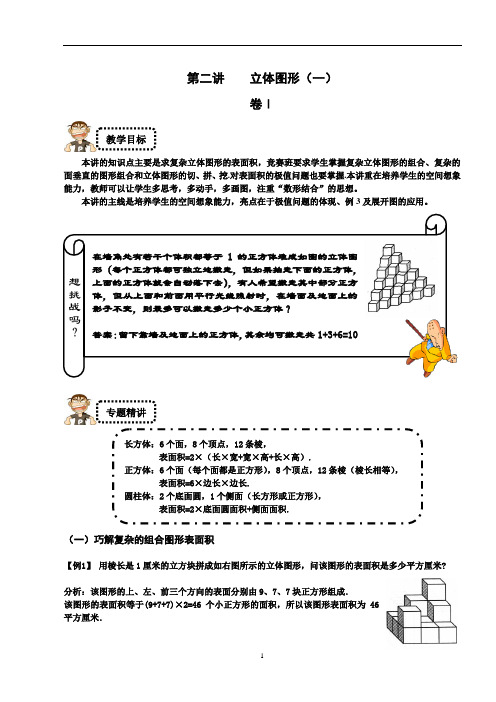
第二讲立体图形（一）卷Ⅰ本讲的知识点主要是求复杂立体图形的表面积，竞赛班要求学生掌握复杂立体图形的组合、复杂的面垂直的图形组合和立体图形的切、拼、挖.对表面积的极值问题也要掌握.本讲重在培养学生的空间想象能力，教师可以让学生多思考，多动手，多画图，注重“数形结合”的思想。

本讲的主线是培养学生的空间想象能力，亮点在于极值问题的体现、例3及展开图的应用。

（一）巧解复杂的组合图形表面积【例1】用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米?分析：该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成．该图形的表面积等于(9+7+7)×2=46个小正方形的面积，所以该图形表面积为46平方厘米．专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形（每个正方体都可独立地搬走，但如果抽走下面的正方体，上面的正方体就会自动落下去），有人希望搬走其中部分正方体，但从上面和前面用平行光线照射时，在墙面及地面上的影子不变，则最多可以搬走多少个小正方体？答案：留下靠墙及地面上的正方体，其余均可搬走共1+3+6=10块.想挑战吗？长方体：6个面，8个顶点，12条棱，表面积=2×（长×宽+宽×高+长×高）.正方体：6个面（每个面都是正方形），8个顶点，12条棱（棱长相等），表面积=6×边长×边长.圆柱体：2个底面圆，1个侧面（长方形或正方形），表面积=2×底面圆面积+侧面面积.【例2】边长为1厘米的正方体，如图这样层层重叠放置，那么当重叠到第5层时，这个立体图形的表面积是多少平方厘米？分析：这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米，该图形的总表面积为90立方厘米．[拓展] 如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？分析：当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木，当拼成一个3×3×3的正方体时，表面积最小，现在要去掉2块小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为54.【例3】（奥数网原创题）按照上题的堆法一直堆到N层（N＞3），要想使总表面积恰好是一个完全平方数，则N的最小值是多少？N N 个小面，总表面积是6个“大面”，所以就增加到分析：每增加一层，每一个“大面”就增加到(1)23N(N+1)个小面，几何题变成数论题，问题转化为“3N(N+1)是一个完全平方数，N的最小值是几（N＞3）？”因为N和N+1互质，所以N和N+1必须有一个是完全平方数，一个是平方数的3倍，但N+1不能是平方数的3倍，因为此时N被3除余2，不可能是完全平方数，所以N是平方数的3倍，N+1是完全平方数，开始试验：当N=3×12=3，不符合题意；当N=3×22=12，N+1=13，不是完全平方数；当N=3×32=27，N+1=28，不是完全平方数；当N=3×42=48，N+1=49，是完全平方数，所以N的最小值是48，即堆到第48层时，总表面积是完全平方数，为3×48×49=842.（二）表面积的最值问题【例4】一个正方体木块，棱长是15．从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体．这个木块剩下部分的表面积最少是多少？分析：截去一个小正方体，表面积不变，只有在截去的小正方体的面相重合时，表面积才会减少，所以要使木块剩下部分的表面积尽可能小，应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示)，这时剩下部分的表面积比原正方体的表面积减少最多．剩下部分的表面积最小是：15×15×6-7×7×2=1252．【例5】边长分别是3、5、8的三个正方体拼在一起，在各种拼法中，表面积最小多少？分析：三个正方体两两拼接时，最多重合3个正方形面，其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形，边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形，三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例6】用10块长7厘米，宽5厘米，高3厘米的长方体积木堆成一个长方体，这个长方体的表面积最小是多少?分析：教师可以先提问：这个长方体的表面积最大是多少?为使表面积最大，要尽量保证10×2个7×5的面成为表面，想要做到这点很容易，只需将7×5面做底面，而后将10个立方体连排，衔接的面选用3×5的面（衔接的面将不能成为表面积），这样得到的长方体表面积最大．同样要想最小，可把7×5面做衔接的面，可得到10个长方体的连排，但此时我们还可以再制造出衔接面，如图：此时增加了2个5×7的面，减少了10个3×7的面，总体来讲表面积减少了．表面积是：2×(7×15+15×10+10×7)=650(平方厘米)，所以这就是最小的表面积．[前铺] 用6块右图所示（单位：cm）的长方体木块拼成一个大长方体，有许多种拼法，其中表面积最小的是多少平方厘米？最大是多少平方厘米？分析：最小：66cm2；最大：（1×2+1×3+2×3）×2×6-1×2×5×2=112．【例7】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？（1）当b=2h时，按图几打包？（2）当b＜2h时，按图几打包？（3）当b＞2h时，按图几打包？分析：图2和图3正面的面积相同，侧面面积=正面周长×长方体长，所以正面的周长愈大表面积越大，图2的正面周长是8h+6b，图3的周长是12h+4b.两者的周长之差为2（b-2h）.当b=2h时，图2和图3周长相等，可随意打包；当b﹤2h时，按图2打包；当b﹥2h时，按图3打包.[前铺] 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体，表面积最小是多少？分析：考虑所有的包装方法，因为6=1×2×3，所以一共有两种拼接方式：第一种按长宽高1×1×6拼接，重叠面有三种选择，共3种包装方法.第二种按长宽高1×2×3拼接，有3个长方体并列方向的重叠面有三种选择，有2个长方体并列方向的重叠面剩下2种选择，一共有6种包装方法.其中表面积最小的包装方法如图所示，表面积为1034.卷Ⅱ（三）立体图形的切、拼、挖【例8】下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为1/4厘米，那么最后得到的立体图形的表面积是多少平方厘米？分析：我们仍然从3个方向考虑．平行于上下表面的各面面积之和：2×2×2＝8（平方厘米）；左右方向、前后方向：2×2×4=16（平方厘米），1×1×4＝4（平方厘米），1/2×1/2×4=1（平方厘米），1/4×1/4×4=1/4 （平方厘米），这个立体图形的表面积为：8+16+4+1+1/4=29又1/4 （平方厘米）．【例9】如图，有一个边长为20厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为2454平方厘米，那么挖掉的小立方体的边长是多少厘米？分析：大立方体的表面积是20×20×6=2400平方厘米．挖掉了三个小正方体，反而多出了6个面，可以计算出每个面的面积：（2454－2400）÷6=9平方厘米，说明小正方体的棱长是3．[拓展1] 图中是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?分析：原正方体的表面积是4×4×6=96(平方厘米)．每一个面被挖去一个边长是1厘米的正方形，同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分．总的来看，每一个面都增加了4个边长是1厘米的正方形．从而，它的表面积是：96+4×6=120平方厘米．[拓展2] 如右图，一个边长为3a厘米的正方体，分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体（都和对面打通）．如果这个镂空的物体的表面积为2592平方厘米，试求正方形截口的边长．分析：原来正方体的表面积为：6×3a×3a＝6×9a2（平方厘米），六个边长为a的小正方形的面积为（减少部分）：6×a×a＝6a2（平方厘米）；挖成的每个长方体空洞增加的侧面积为：a×a×4×2＝8a2（平方厘米）；根据题意可得：54a2－6a2＋3×8a2＝2592，解得a2＝36（平方厘米），故a＝6厘米．【例10】有一个棱长为 5 cm的正方体木块，从它的每个面看都有一个穿透的完全相同的孔（右上图），求这个立体图形的内、外表面的总面积．分析：将此带孔的正方体看做由八个8cm3的正方体（8个顶点）和12个1cm3的正方体（12条棱）粘成的．每个正方体有两个面粘接，减少表面积4cm2，所以总的表面积为：（4×6）×8＋6×12－4×12＝216（cm2）．[拓展] 边长分别是3、5、8的三个正方体拼在一起，在各种拼法中，表面积最小多少？分析：三个正方体两两拼接时，最多重合3个正方形面，其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形，边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形，三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例11】如图，在一个正方体的两对侧面的中心各打通一个长方体的洞，在上下侧面的中心打通一个圆柱形的洞．已知正方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下侧面的洞口是直径为4厘米的圆，求此立体图形的表面积．分析：外侧表面积为：6×10×10-4×4×4-π×22×2=536-8π.内侧表面积为：16×4×3+2× (4×4-π×2)+2×2π×2×3=192+32-8π+24π=224+16π．总表面积=224+16π+536-8π=760+8π=785.12(平方厘米)．【例12】如图，用455个棱长为1 的小正方体粘成一个大的长方体，若拆下沿棱的小正方体，则余下371个小正方体，问：所堆成的大长方体的棱长各是多少？拆下沿棱的小正方体后的多面体的表面积是多少？分析：设长方体棱长为分别为y zx、、.，他们只能取正整数，则有：4554(222)8455371x y zx y z⨯⨯=⎧⎨-+-+-+=-⎩因为4555713=⨯⨯方程组的有序正整数解只有（5，7，13），拆下沿棱的的小正方体后的多面体如图所示，首先计算突出在外面的6个平面，面积是2(11511335)206⨯⨯+⨯+⨯=再计算24个宽都是1的长⨯++=，总面积为358. 条，面积是8(1135)152（三）展开图【例13】在小于16 的自然数中选出6个不同的数，分别写在正方体的6个面上，要求各组相对的两个面上的数的乘积都相等，下图是正方体的展开图，并填上了1，请将其它数填上。

2023年人教版高考数学总复习第一部分考点指导第八章立体几何第一节基本立体图形

3π 27
·x3，
V球 V圆锥
4 ＝
273π·x3
＝75m.06
，解得 m＝33.36 克．
33π·x3
5．(求几何体的体积)某校开展社会实践活动，学生到工厂制作一批景观
灯箱(如图，在直四棱柱上加工，所有顶点都在棱上)，灯箱最上面是正
方形，与之相邻的四个面都是全等的正三角形，灯箱底部是边长为 a 的
【解析】选 D.如图，过 C′作 C′M′∥y′轴，交 x′轴于 M′，
在△C′M′B′中，因为 B′C′与 x′轴垂直且 B′C′＝2 2 ，
∠C′M′B′＝45°，所以 C′M′＝siBn′C45′ ° ＝2
2 2
＝4.由斜二测
2
画法知 CM＝2C′M′＝8，所以△ABC 的边 AB 上的高为 8.
棱柱、棱锥、棱台的侧面分别是平行四边形、三角形、梯形．判断棱台的方法：侧棱延长后是否交于一点．
2．旋转体的结构特征
(1)圆柱：矩形绕其__任__一__边__所在的直线旋转一周形成的轨迹围成的几何体． (2)圆锥：直角三角形绕其_直__角__边__所在的直线旋转一周形成的轨迹围成的几何体． (3)圆台：直角梯形绕其_垂__直__于__底___边__的__腰__所在的直线旋转一周形成的轨迹围成的
表面积 S 表面积＝S 侧＋2S 底
锥体(棱锥和圆锥)
S 表面积＝S 侧＋S 底
台体(棱台和圆台) S 表面积＝S 侧＋S 上＋S 下
球
S＝_4_π_R_2_
体积
V＝_S_h_ V＝13 _S_h_
V＝13 (S 上＋S 下
＋ S上S下 )h
4 R3
V＝__3_______
1.必修二 P106T8

立体图形的复习1

口算
3 = 4×6 ×0.25= 3.14 ×2 ×5 = 18.84÷3.14÷3=
3
2 × 3×5= 3.14 ×8=
1 3 ×3.14 ×2 ×3 = 3
9.42 ×3÷3.14=
思考讨论：
1、长方体和正方体有什么相同点和不同点？它们有什么关系？不同点关系形相同点体面棱点 6个面一般都是长方形，长 6 12 8 相对的面的面积相等；正方方体是个条个相对的棱长度相等。体特殊正 6个面都是相等的正方的长方形；12条棱的长度都相方体体等。
圆柱 6
高
体积
10 12
9.42
圆锥 8 21
141.3
12.56
18
切割问题：
S增=(段数-1)×2×S底
1:把长方体木块切成三段后，它的表面积增加了多少平方米？（单位：米）
（3-1）×2×（3×4）=48（平方米） 4
12
答：它的表面积增加了48平方米
等积变形问题：
把一个底面半径为2米，高为3米圆柱形钢材，锻造成一个长4米，宽1.5米的长方体，长方体的高是多少米？
立体图形
表面积体积一个立体图形的所有的面的物体所占空意义面积总和间的大小计量单位 m2 dm 2 cm 2 …… m3dm 3 cm3 ab+ah+bh) × 2 S=6a2 S=2兀rh+2兀r2
V= abh V=a3 V=兀r 2h
… V= 1/3sh
V = sh
8
答：求铁块的体积是251.2立方厘米
• 判断题： • 1、圆柱体的体积等于圆锥体的3倍。（× ） • 2、一个正方体的棱长是6厘米，它的表面积和体积相等。（ × ） • 3、容器的容积与容器的体积大小不一样。（ √ ）

2020年小升初总复习——小学数学立体图形练习专题(含答案)

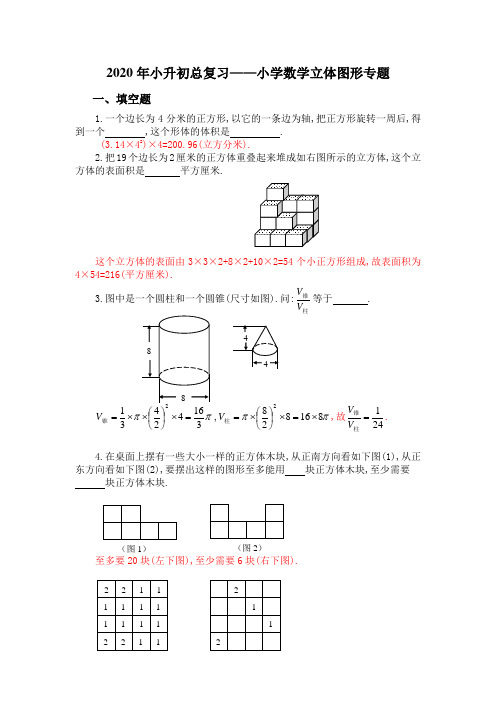
2020年小升初总复习——小学数学立体图形专题一、填空题1.一个边长为4分米的正方形,以它的一条边为轴,把正方形旋转一周后,得到一个 ,这个形体的体积是 .(3.14×42)×4=200.96(立方分米).2.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是平方厘米.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).3.图中是一个圆柱和一个圆锥(尺寸如图).问:柱锥V V 等于 .ππππ816828,316424312⨯=⨯⎪⎭⎫ ⎝⎛⨯==⨯⎪⎭⎫ ⎝⎛⨯⨯=柱锥VV ,故241=柱锥V V .4.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下图(1),从正东方向看如下图(2),要摆出这样的图形至多能用块正方体木块,至少需要块正方体木块.至多要20块(左下图),至少需要6块(右下图).（图1）（图2） 2 1 2 12 2 1 2 1 1 11 1 1 1 1 12 1 15.一个圆柱形玻璃杯中盛有水,水面高2.5厘米,玻璃内侧的底面积是72平方厘米,在这个杯中放进棱长6厘米的正方体的铁块后,水面没有淹没铁块,这时水面高厘米.水的体积为72×2.5=180(cm 2),放入铁块后可以将水看作是底面积为72-6×6=36(cm 2)的柱体,所以它的高为180÷36=5(cm )二、解答题1.一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米.原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?若铁块完全浸入水中,则水面将提高326)3040(203=⨯÷(厘米).此时水面的高小于20厘米,与铁块完全浸入水中矛盾,所以铁块顶面仍然高于水面.设放入铁块后,水深为x 厘米.因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和,故有:x x 20201030403040⨯+⨯⨯=⨯解得x =15,即放进铁块后,水深15厘米.2.雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方形的容器,雨水将它下满要用1小时.有下列(A )-(E )不同的容器(图2),雨水下满各需多少时间(注面是朝上的敞口部分.)2cm 2cm （A ）（B ）（C ）（D ）（E ）雨在例图所示的容器中,容积:按水面积=(10×10×30):(10×30)=10:1,需1小时接满,所以容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满; 容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满; 容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需3小时接满;容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;容器(E):容积:接水面积=20×S:S=20:1(S 为底面积),接水时间为2小时.3、如图是一个立体图形的侧面展开图,求它的全面积和体积.这个立体图形是一个圆柱的四分之一(如图),圆柱的底面半径为10厘米,高为8厘米.它的全面积为: 810281014.32411014.34122⨯⨯+⨯⨯⨯⨯+⨯⨯⨯ 6.4421606.125157=++=(平方厘米).它的体积为:62881014.3412=⨯⨯⨯(立方厘米).。

高三立体几何专题复习

高考立体几何专题复习一．考试要求：〔1〕掌握平面的根本性质，会用斜二测的画法画水平放置的平面图形的直观图，能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。

〔2〕了解空两条直线的位置关系，掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念〔对于异面直线的距离，只要求会计算已给出公垂线时的距离〕。

〔3〕了解空间直线和平面的位置关系，掌握直线和平面平行的判定定理和性质定理，理解直线和平面垂直的判定定理和性质定理，掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念，了解三垂线定理及其逆定理。

〔4〕了解平面与平面的位置关系，掌握两个平面平行的判定定理和性质定理。

掌握二面角、二面角的平面角、两个平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理。

〔5〕会用反证法证明简单的问题。

〔6〕了解多面体的概念，了解凸多面体的概念。

〔7〕了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图。

〔8〕了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图。

〔9〕了解正多面体的概念，了解多面体的欧拉公式。

〔10〕了解球的概念，掌握球的性质，掌握球的外表积、体积公式。

二．复习目标：1．在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的根底上，研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用；在有关问题的解决过程中，进一步了解和掌握相关公理、定理的容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用．2．在掌握空间角(两条异面直线所成的角，平面的斜线与平面所成的角及二面角)概念的根底上，掌握它们的求法(其根本方法是分别作出这些角，并将它们置于*个三角形通过计算求出它们的大小)；在解决有关空间角的问题的过程中，进一步稳固关于直线和平面的平行垂直的性质与判定的应用，掌握作平行线(面)和垂直线(面)的技能；通过有关空间角的问题的解决，进一步提高学生的空间想象能力、逻辑推理能力及运算能力．3．通过复习，使学生更好地掌握多面体与旋转体的有关概念、性质，并能够灵活运用到解题过程中．通过教学使学生掌握根本的立体几何解题方法和常用解题技巧，开掘不同问题之间的在联系，提高解题能力．4．在学生解答问题的过程中，注意培养他们的语言表述能力和"说话要有根据〞的逻辑思维的习惯、提高思维品质．使学生掌握化归思想，特别是将立体几何问题转化为平面几何问题的思想意识和方法，并提高空间想象能力、推理能力和计算能力．5．使学生更好地理解多面体与旋转体的体积及其计算方法，能够熟练地使用分割与补形求体积，提高空间想象能力、推理能力和计算能力．三．教学过程：〔Ⅰ〕根底知识详析高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考察的知识点在20个以. 选择填空题考核立几中的计算型问题, 而解答题着重考察立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着"多一点思考,少一点计算〞的开展.从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探常考常新的热门话题.1．有关平行与垂直(线线、线面及面面)的问题，是在解决立体几何问题的过程中，大量的、反复遇到的，而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的容，因此在主体几何的总复习中，首先应从解决"平行与垂直〞的有关问题着手，通过较为根本问题，熟悉公理、定理的容和功能，通过对问题的分析与概括，掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想，以提高逻辑思维能力和空间想象能力．2．判定两个平面平行的方法：〔1〕根据定义——证明两平面没有公共点；〔2〕判定定理——证明一个平面的两条相交直线都平行于另一个平面；〔3〕证明两平面同垂直于一条直线。

六年级下册数学教案-总复习立体图形复习｜西师大版

六年级下册数学教案总复习立体图形复习｜西师大版教案：六年级下册数学教案总复习立体图形复习｜西师大版一、教学内容本节课的教学内容主要包括教材第六章立体图形的认识和第七章立体图形的计算。

第六章主要介绍了立体图形的概念、特征和分类，包括长方体、正方体、圆柱体、圆锥体等。

第七章主要讲解了立体图形的表面积和体积的计算方法。

二、教学目标通过本节课的教学，使学生能够熟练掌握立体图形的概念、特征和分类，以及立体图形的表面积和体积的计算方法，提高学生的空间想象能力和解决问题的能力。

三、教学难点与重点教学难点：立体图形的表面积和体积的计算方法的灵活运用。

教学重点：立体图形的概念、特征和分类的理解。

四、教具与学具准备教具：多媒体课件、立体模型。

学具：练习本、尺子、圆规、量角器。

五、教学过程1. 实践情景引入：让学生观察教室里的立体物体，如书桌、椅子、窗户等，引导学生发现立体图形的特点。

2. 知识回顾：通过多媒体课件，复习立体图形的概念、特征和分类，以及立体图形的表面积和体积的计算方法。

3. 例题讲解：讲解一道立体图形的相关例题，如长方体的表面积和体积的计算。

4. 随堂练习：让学生独立完成一些立体图形的计算题目，巩固所学知识。

6. 板书设计：板书立体图形的特点和计算方法。

7. 作业设计：布置一些有关立体图形的计算题目，让学生独立完成。

六、作业设计1. 题目：计算下面立体图形的表面积和体积。

（1）长方体：长4cm，宽3cm，高2cm。

（2）正方体：棱长5cm。

2. 答案：（1）长方体的表面积：2×(4×3+4×2+3×2)=52cm²，体积：4×3×2=24cm³。

（2）正方体的表面积：6×(5×5)=150cm²，体积：5×5×5=125cm³。

七、课后反思及拓展延伸通过本节课的教学，学生应该能够掌握立体图形的概念、特征和分类，以及立体图形的表面积和体积的计算方法。

第一章丰富的图形世界重点知识复习

第一章丰富的图形世界重点知识复习1.1 生活中的立体图形一、常见的几何体分类：1、 2、二、图形是由点、线、面构成。

点动成线，线动成面，面动成体。

面与面相交得到线，线与线相交得到点。

面动成体可以通过平移和旋转实现。

例如：五棱柱、圆柱分别可以看作是由五边形或圆沿着竖直方向平移形成。

圆柱又可以看作是矩形绕着一边旋转一周形成。

易错点：1、观察下图，请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( D )2、如图,第二行的图形绕虚线旋转一周便能形成第一行的某个几何体,用线连一连.三、棱柱的特征：1、棱柱的上、下两底面平行且形状相同，大小一样；2、棱柱的侧面形状都是长方形；3、侧面的个数和底面图形的边数相等.4、棱柱的侧棱的长度都相等。

5、n 棱柱有2n 个顶点，3n 条棱，（n+2）个面。

⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧圆台棱台台球圆锥棱锥锥圆柱棱柱柱按“体”分：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧球圆台圆锥圆柱曲面棱台棱锥棱柱平面：按“围成图形的面”分ABCD64 1 2 35 fe d c b a6、n 棱锥（n+1）个顶点，2n 条棱，（n+1）个面。

四、侧面积与表面积计算：柱体的S 侧＝ch （c 为底面周长，h 为高，当柱体为棱柱时，h 为侧棱的长）锥体为棱锥时S 侧＝所有侧面三角形的面积之和；锥体为圆锥时S 侧＝S 扇＝360R n 2（n 为圆心角的度数，R 为圆的半径）柱体的S 表＝S 侧＋S 底（此时S 底为2个）锥体的S 表＝S 侧＋S 底（此时S 底为1个）1.2 展开与折叠一、正方体的展开图（长方体也是类似的展开图）：正方体有12条棱，需要剪7刀才能展开成平面图形。

二、圆柱、圆锥、正三棱锥、正四棱锥、正五棱锥、正三棱柱的展开图：圆柱的底面圆的周长和高分别是侧面展开图中长方体的长与宽，圆锥的侧面展开图是一个扇形，这个扇形的半径就是圆锥的母线（即圆锥的顶点与圆锥底面上任意一点的连线长，而扇形的弧长就是圆锥底面圆的周长。

第01讲平面、立体图形综合一(直线型)(解析版)

例题 5、如图，8 块相同的长方形地砖拼成一个长方形，求每块长方形地砖的长是多少厘米？
60cm
3
随练随练 1、图①的周长大于图②的周长，这种说法对吗？为什么？
随练 2、右边图形的周长是多少？
随练 3、如图，这个多边形任意相邻的两条边都互相垂直，根据图中给出的数（单位：厘米），那么这个多边形周长是__________厘米．
曲线型图形题
课前小测 1、阿呆的高斯积分比阿瓜的多 150 分，且阿呆的高斯积分比阿瓜的 4 倍少 30 分，阿呆和阿瓜分别有多少分？（请用两种方法解答）
2、三块布共长 220 米，第二块布长是第一块的 3 倍，第三块布长是第二块的 2 倍，三块布各有多长？ (列方程解答)
3、司机小王身上带有 1 元、2 元、5 元、10 元四种面值的纸币共 82 元，其中 1 元和 2 元纸币共 22 张，5 元和 10 元纸币共 7 张，2 元纸币的张数是 5 元纸币张数的 2.5 倍．问：小王身上有多少张 10 元纸币？
随练 5、如图， AE : EB 3 : 2 ， CD : DB 7 : 5 ，三角形 ABC 的面积是 60 平方厘米，求三角形 AED 的面积为多少平方厘米．
7
知识精讲一、基本公式
长方体及正方体
二、三视图求表面积在观察物体的时候，我们往往可以从不同的角度进行观察．角度不同，看到的风景就会不同．比如：我们可以从正面看，上面看，左面看，看到的图形分别称为正视图，俯视图和左视图．并且容易发现：正面看和后面看，上面看和下面看，左面看和右面看得到的图形是相同的．对于较复杂的立体图形，通过三视图法往往可以很方便地计算出表面积．
1、分割法就是把图形切开，但是并不移动，使题目便于解答，组合图形中，如多边形、圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，为了计算它们的面积，常常需要用到割补的方法．必要时，我们需要将整个图形切割成最小单元来求解。 2、填补法就是把图形切开，把切下来的那部分移动到其他位置，使题目便于解答；注意：切割下来的面积和要补上的面积要相等．二、常见一半模型下图中阴影部分面积均为长方形面积的一半．其中，A 为长方形长边上任意一点，B 为长方形内部任意一点．

小学六年级立体图形知识复习

v=a3 (三)圆柱体 1、圆柱的认识圆柱的上下两个面叫做底面。圆柱有一个曲面叫做侧面。圆柱两个底面之间的距离叫做高。进一法：实际中，使用的'材料都要比计算的结果多一些，因此，要保存数的时候，省略的位上的是 4 或者比 4 小，都要向前一位进 1。这种取近似值的方法叫做进一法。 2、计算公式 s 侧=ch s 表=s 侧+s 底×2 v=sh/3
侧面展开得到一个扇形。
2、计算公式
v=sh/3
(五)球体
1、认识
球的外表是一个曲面，这个曲面叫做球面。球和圆类似，也有一个球
心，用 O 表示。从球心到球面上任意一点的线段叫做球的半径，用 r 表示，
每条半径都相等。通过球心并且两端都在球面上的线段，叫做球的直径，
Байду номын сангаас
用 d 表示,每条直径都相等,直径的长度等于半径的 2 倍，即 d=2r。
本文格式为 Word 版，下载可任意编辑，页眉双击删除即可。
小学六年级立体图形知识复习
小学六年级立体图形学问复习 (一)长方体
六个面都是正方形;六个面的面积相等;12 条棱，棱长都相等;有 8 个顶点;正方体可以看作特殊的长方体。
2、计算公式 S 表=6a2
1、特征六个面都是长方形(有时有两个相对的面是正方形)。相对的面面积相等，12 条棱相对的 4 条棱长度相等。有 8 个顶点。相交于一个顶点的三条棱的长度分别叫做长、宽、高。两个面相交的边叫做棱。三条棱相交的点叫做顶点。把长方体放在桌面上，最多只能看到三个面。长方体或者正方体 6 个面的总面积，叫做它的外表积。 2、计算公式 s=2(ab+ah+bh) V=sh V=abh (二)正方体 1、特征