医药数理统计第六章习题检验假设和t检验
医用统计学-总体均数的估计与假设检验练习题

医用统计学-总体均数的估计与假设检验练习题二、是非题1.即使变量偏离正态分布,只要样本含量相当大,样本均数也近似正态分布。
()3.两次t检验都是对两样本均数的差别做统计检验,一次P<0.01,另一次0.01<P<0.05,就表明前者两样本均数差别大,后者两样本均数差别小。
()4.对两样本均数的差别做统计检验,两组数据具有方差齐性,但与正态分布相比略有偏离,样本含量都较大,因此仍可做t检验。
()三、最佳选择题2、两样本均数比较的t检验,差别有统计学意义时,P越小,说明()。
A、两样本均数差别越大B、两总体均数差别越大C、越有理由认为两总体均数不同D、越有理由认为两样本均数不同E、越有理由认为两总体均数不同3、甲乙两人分别随机数字表抽得30个(各取两位数字)随机数字作为两个样本,求得X1和S12,X2和S22,则理论上()。
A、X1=X 2B、S12= S22C、作两样本均数的t检验,必然得出无差别的结论D、作两方差齐性的F检验,必然方差齐E、由甲、乙两样本均数之差求出的总体均数的95%可信区间,很可能包括04、在参数未知的正态总体中随机抽样,∣X-μ∣≥()的概率为5%。
A、1.96σB、1.96C、2.58D、t0.05,v SE、t0.05,vsx5、某地1992年随机抽取100名健康女性,算得其血清总蛋白含量的均数为74g/L,标准差为4g/L,则其95%的参考值范围()。
A、74±4×4B、74±1.96×4C、74±2.58×4D、74±2.58×4÷10E、74±1.96×4÷106、关于以0为中心的t分布,错误的是()。
A、t分布是一簇曲线B、t分布是单峰分布C、当ν∝时,t uD、t分布以0为中心,左右对称E、相同ν时,∣t∣越大,P越大7、在两样本均数比较的t检验中,无效假设是()A、两样本均数不等B、两样本均数相等C、两总体均数不等D、两总体均数相等E、两样本均数等于总体均数8、两样本均数比较时,分别取以下检验水准,以()所取第二类错误最小。
中南民族大学医药数理统计第六章和第七章 假设检验.

第六章
假设检验
3. 总体分布未知,但为大样本时的u检验
若总体X的分布未知,均值μ和方差σ2存在, (x1, x2, …, xn)是 来自总体X的一个大样本(n≥50),由独立同分布的中心极限定 理,对任意实数 x,都有 n ⎧ ∑ x − nμ ⎫ 1 2 i x t − 1 x μ − ⎧ ⎫ ⎪ i =1 ⎪ 2 lim P ⎨ e dt ≤ x ⎬ = lim P ⎨ ≤ x⎬ = ∫ n →∞ n →∞ nσ ⎩σ / n ⎭ −∞ 2π ⎪ ⎪ ⎩ ⎭ 当σ2已知,且H0 :μ = μ 0为真时
第六章
假设检验
假设检验 是推断性统计学中的一项重要内容,它是先 对研究总体的参数作出某种假设,然后通过样本的观察来 决定假设是否成立 具 体 的 统 计 方 法
参 数 假 设
样 本 观 察
假 设 检 验
第六章
假设检验
假设检验的基本思想 小概率 事件发生 前提: 承认 原假设
进行一次实验
拒绝 原假设
第六章
假设检验
显著水平与两类错误
第一类错误:弃真(显著水平α) 显著 水平 与 两类 错误
P{拒绝 H 0 H 0 为真 } = α
P{接受 H 0 H 0 不真 } = β
第二类错误:取伪
第六章
假设检验
对于一定的样本容量n ,不能同时做到两 类错误的概率都很小。如果减小α错误, 就会增大犯β错误的机会;若减小β错 误,也会增大犯α错误的机会。
《医学统计学》习题及答案

《医学统计学》习题及答案22.假设检验中的第二类错误是指A.拒绝了实际上成立的0HB.不拒绝实际上成立的0HC.拒绝了实际上成立的1HD.不拒绝实际上不成立的0HE.拒绝0H 时所犯的错误23.方差分析中,组内变异反映的是A. 测量误差B. 个体差异C. 随机误差,包括个体差异及测量误差D. 抽样误差E. 系统误差24.方差分析中,组间变异主要反映A. 随机误差B. 处理因素的作用C. 抽样误差D. 测量误差E. 个体差异25.多组均数的两两比较中,若不用q 检验而用t 检验,则A. 结果更合理B. 结果会一样C. 会把一些无差别的总体判断有差别的概率加大D. 会把一些有差别的总体判断无差别的概率加大E. 以上都不对26.说明某现象发生强度的指标为A.构成比B.相对比C.定基比D.环比E. 率27.对计数资料进行统计描述的主要指标是A.平均数B.相对数C.标准差D.变异系数E.中位数28.构成比用来反映A.某现象发生的强度B.表示两个同类指标的比C.反映某事物内部各部分占全部的比重D.表示某一现象在时间顺序的排列E.上述A 与C 都对29. 样本含量分别为1n 和2n 的两样本率分别为1p 和2p ,则其合并平均率c p 为A. 1p +2pB. (1p +2p )/2C. 21p p ⨯D.212211n n p n p n ++ E.2)1()1(212211-+-+-n n p n p n 30.下列哪一指标为相对比A. 中位数B. 几何均数C. 均数D. 标准差E. 变异系数31.发展速度和增长速度的关系为A. 发展速度=增长速度一1B. 增长速度=发展速度一1C.发展速度=增长速度一100D.增长速度=发展速度一100E.增长速度=(发展速度一1)/10032.SMR 表示A.标化组实际死亡数与预期死亡数之比B.标化组预期死亡数与实际死亡数之比C.被标化组实际死亡数与预期死亡数之比D.被标化组预期死亡数与实际死亡数之比E.标准组与被标化组预期死亡数之比33.两个样本率差别的假设检验,其目的是A.推断两个样本率有无差别B.推断两个总体率有无差别C.推断两个样本率和两个总体率有无差别D.推断两个样本率和两个总体率的差别有无统计意义E.推断两个总体分布是否相同34.用正态近似法进行总体率的区间估计时,应满足A. n 足够大B. p 或(1-p )不太小C. np 或n(1-p)均大于5D. 以上均要求E. 以上均不要求35.由两样本率的差别推断两总体率的差别,若P 〈0.05,则A. 两样本率相差很大B. 两总体率相差很大C. 两样本率和两总体率差别有统计意义D. 两总体率相差有统计意义E. 其中一个样本率和总体率的差别有统计意义36.假设对两个率差别的显著性检验同时用u 检验和2χ检验,则所得到的统计量u 与2χ的关系为A. u 值较2χ值准确B. 2χ值较u 值准确C. u=2χD. u=2χE. 2χ=u37.四格表资料中的实际数与理论数分别用A 与T 表示,其基本公式与专用公式求2χ的条件为A. A ≥5B. T ≥5C. A ≥5 且 T ≥5D. A ≥5 且n ≥40E. T ≥5 且n ≥4038.三个样本率比较得到2χ>2)2(01.0χ,可以为A.三个总体率不同或不全相同B.三个总体率都不相同C.三个样本率都不相同D.三个样本率不同或不全相同E.三个总体率中有两个不同39.四格表2χ检验的校正公式应用条件为A. n>40 且T>5B. n<40 且T>5C. n>40 且 1<T<5D. n<40 且1<T<5E. n>40 且T<140.下述哪项不是非参数统计的优点A.不受总体分布的限定B.简便、易掌握C.适用于等级资料D.检验效能高于参数检验E.适用于未知分布型资料41.秩和检验和t 检验相比,其优点是A. 计算简便,不受分布限制B.公式更为合理C.检验效能高D.抽样误差小E.第二类错误概率小42.等级资料比较宜用A. t 检验B. u 检验C.秩和检验D. 2χ检验E. F 检验43.作两均数比较,已知1n 、2n 均小于30,总体方差不齐且分布呈极度偏态,宜用A. t 检验B. u 检验C.秩和检验D. F 检验E.2χ检验44.从文献中得到同类研究的两个率比较的四格表资料,其2χ检验结果为:甲文)1(01.02χχ>,乙文2)1(05.02χχ>,可认为A.两文结果有矛盾B.两文结果基本一致C.甲文结果更可信D.乙文结果更可信E.甲文说明总体间的差别更大45.欲比较某地区1980年以来三种疾病的发病率在各年度的发展速度,宜绘制A.普通线图B.直方图C.统计地图D.半对数线图E.圆形图46.拟以图示某市1990~1994年三种传染病发病率随时间的变化,宜采用A.普通线图B.直方图C.统计地图D.半对数线图E.圆形图47.调查某地高血压患者情况,以舒张压≥90mmHg 为高血压,结果在1000人中有10名高血压患者,99名非高血压患者,整理后的资料是:A.计量资料B.计数资料C.多项分类资料D.等级资料E.既是计量资料又是分类资料48. 某医师检测了60例链球菌咽炎患者的潜伏期,结果如下。
医学统计学6

《医学统计学》习题集(一)单项选择题1.观察单位为研究中的( )。
A.样本 B. 全部对象C.影响因素 D. 个体2.总体是由()。
A.个体组成 B. 研究对象组成C.同质个体组成 D. 研究指标组成3.抽样的目的是()。
A.研究样本统计量 B. 由样本统计量推断总体参数C.研究典型案例研究误差 D. 研究总体统计量4.参数是指()。
A.参与个体数 B. 总体的统计指标C.样本的统计指标 D. 样本的总和5.关于随机抽样,下列那一项说法是正确的()。
A.抽样时应使得总体中的每一个个体都有同等的机会被抽取B.研究者在抽样时应精心挑选个体,以使样本更能代表总体C.随机抽样即随意抽取个体D.为确保样本具有更好的代表性,样本量应越大越好6.各观察值均加(或减)同一数后()。
A.均数不变,标准差改变B.均数改变,标准差不变C.两者均不变D.两者均改变7.比较身高和体重两组数据变异度大小宜采用()。
A.变异系数B.方差C.极差D.标准差8.以下指标中()可用来描述计量资料的离散程度。
A.算术均数B.几何均数C.中位数D.标准差9.偏态分布宜用()描述其分布的集中趋势。
A.算术均数B.标准差C.中位数D.四分位数间距10.各观察值同乘以一个不等于0的常数后,()不变。
A.算术均数 B.标准差C.几何均数D.中位数11.()分布的资料,均数等于中位数。
A.对称B.左偏态C.右偏态D.偏态12.对数正态分布是一种()分布。
A.正态B.近似正态C.左偏态D.右偏态13.最小组段无下限或最大组段无上限的频数分布资料,可用()描述其集中趋势。
A.均数B.标准差C.中位数D.四分位数间距14.()小,表示用该样本均数估计总体均数的可靠性大。
A. 变异系数B.标准差C. 标准误D.极差15.血清学滴度资料最常用来表示其平均水平的指标是()。
A. 算术平均数B.中位数C.几何均数D. 平均数16.变异系数CV的数值()。
A. 一定大于1B.一定小于1C. 可大于1,也可小于1D.一定比标准差小17.数列8、-3、5、0、1、4、-1的中位数是()。
医药数理统计方法第六版习题答案

医药数理统计方法第六版习题答案
第六版医药数理统计方法习题试题及答案:
1.在哪种研究中,我们可以用t检验来确定两组的时间和数量的组合?
A.单因素分析
B.双因素分析
C.重复测量分析
D.相关分析
答案:C.重复测量分析。
2.下面哪种情况可以用t检验来考察?
A.两个样本的平均数
B.一组数据的中值
C.一组数据的总和
D.两组数据的比例
答案:A.两个样本的平均数。
3.假设检验是用来:
A.检查两组样本是否相等
B.检查一组样本是否具有特定的统计特性
C.确定一组样本的平均数
D.比较一组样本的总和
答案:B.检查一组样本是否具有特定的统计特性。
4.假定检验的目的之一是检查双重限制假设,下列哪种假设是错误的:
A.样本的平均数是不变的
B.样本之间的方差是不变的
C.样本的数量是不变的
D.样本的总和是不变的
答案:D.样本的总和是不变的。
5.下列哪种类型的试验可以用卡方分析来检验?
A.实验室实验
B.研究对照组
C.双因素研究
D.观察法
答案:D.观察法。
6.下列哪种研究不能用卡方分析来检验?
A.对照研究
B.双因素实验
C.回归分析
D.实验室实验
答案:C.回归分析。
7.如何使用非参数统计?。
假设检验与t检验卫生统计学
第七、八章 假设检验
假设检验的原理与步骤 t检验 假设检验与区间估计的关系 假设检验的功效 正态性检验 案例讨论 电脑实验 小结
复习相关概念
抽样误差和标准误 t分布与t界值 小概率事件与小概率事件推断原理
复习相关概念 抽样误差和标准误
24
0.685 0.857 1.318 1.711 2.064 2.492 2.797 3.091 3.467 3.745
25
0.684 0.856 1.316 1.708 2.060 2.485 2.787 3.078 3.450 3.725
复习相关概念
2.t分布特点
v=24
2.5%
-5.4545
2
0.816 1.061 1.886 2.920 4.303 6.965 9.925 14.089 22.327 31.599
3
0.765 0.978 1.638 2.353 3.182 4.541 5.841 7.453 10.215 12.924
4
0.741 0.941 1.533 2.132 2.776 3.747 4.604 5.598 7.173 8.610
5
0.727 0.920 1.476 2.015 2.571 3.365 4.032 4.773 5.893 6.869
6
0.718 0.906 1.440 1.943 2.447 3.143 3.707 4.317 5.208 5.959
7
0.711 0.896 1.415 1.895 2.365 2.998 3.499 4.029 4.785 5.408
第一节 假设检验的原理与步骤
医学统计学方法重点简答题和定义解释

医学统计学方法重点简答题和定义解释本文档旨在提供医学统计学方法的重点简答题和定义解释,帮助读者加深对这一领域的理解。
1. 什么是假设检验?定义解释:假设检验是一种统计推断方法,用于判断样本数据是否支持或反对某个假设。
它涉及两个互补的假设:零假设和备择假设。
通过计算样本数据与零假设之间的距离,以及确定这种距离在统计上的显著性,可以得出结论是否拒绝零假设。
假设检验是一种统计推断方法,用于判断样本数据是否支持或反对某个假设。
它涉及两个互补的假设:零假设和备择假设。
通过计算样本数据与零假设之间的距离,以及确定这种距离在统计上的显著性,可以得出结论是否拒绝零假设。
2. 请解释一下T检验和Z检验的区别是什么?定义解释: T检验和Z检验都是假设检验方法,用于比较两个样本均值的差异。
它们的区别在于所依赖的假设和参数。
T检验和Z检验都是假设检验方法,用于比较两个样本均值的差异。
它们的区别在于所依赖的假设和参数。
T检验适用于小样本(样本量较小)情况,它假设样本数据服从正态分布,并使用样本标准差来估计总体标准差。
T检验通常用于实践中,当总体标准差未知时。
Z检验适用于大样本(样本量较大)情况,它假设样本数据和总体数据都服从正态分布,并使用总体标准差。
Z检验通常用于理论研究中,当总体标准差已知时。
3. 请解释一下卡方检验的用途是什么?定义解释:卡方检验是一种统计检验方法,用于判断两个或多个分类变量之间的关联性。
它通过比较观察到的频数和期望频数之间的差异来评估分类变量之间的独立性。
卡方检验常用于分析有序或无序分类变量之间的关联,例如研究治疗方法对疾病治愈率的影响。
卡方检验是一种统计检验方法,用于判断两个或多个分类变量之间的关联性。
它通过比较观察到的频数和期望频数之间的差异来评估分类变量之间的独立性。
卡方检验常用于分析有序或无序分类变量之间的关联,例如研究治疗方法对疾病治愈率的影响。
4. 请解释一下相关系数是什么?定义解释:相关系数是一种用于衡量两个变量之间关联程度的统计量。
医学统计学题库完整

第一章绪论习题一、选择题1.统计工作和统计研究的全过程可分为以下步骤:(D)A。
调查、录入数据、分析资料、撰写论文B. 实验、录入数据、分析资料、撰写论文C。
调查或实验、整理资料、分析资料D. 设计、收集资料、整理资料、分析资料E. 收集资料、整理资料、分析资料2。
在统计学中,习惯上把(B )的事件称为小概率事件.A. B. 或 C.D。
E.3~8A.计数资料B。
等级资料 C.计量资料 D.名义资料E。
角度资料3。
某偏僻农村144名妇女生育情况如下:0胎5人、1胎25人、2胎70人、3胎30人、4胎14人.该资料的类型是(A)。
4。
分别用两种不同成分的培养基(A与B)培养鼠疫杆菌,重复实验单元数均为5个,记录48小时各实验单元上生长的活菌数如下,A:48、84、90、123、171;B:90、116、124、225、84。
该资料的类型是(C ).5.空腹血糖测量值,属于( C)资料。
6.用某种新疗法治疗某病患者41人,治疗结果如下:治愈8人、显效23人、好转6人、恶化3人、死亡1人。
该资料的类型是(B )。
7。
某血库提供6094例ABO血型分布资料如下:O型1823、A型1598、B型2032、AB型641.该资料的类型是(D )。
8。
100名18岁男生的身高数据属于(C )。
二、问答题1.举例说明总体与样本的概念.答:统计学家用总体这个术语表示大同小异的对象全体,通常称为目标总体,而资料常来源于目标总体的一个较小总体,称为研究总体。
实际中由于研究总体的个体众多,甚至无限多,因此科学的办法是从中抽取一部分具有代表性的个体,称为样本。
例如,关于吸烟与肺癌的研究以英国成年男子为总体目标,1951年英国全部注册医生作为研究总体,按照实验设计随机抽取的一定量的个体则组成了研究的样本.2.举例说明同质与变异的概念答:同质与变异是两个相对的概念.对于总体来说,同质是指该总体的共同特征,即该总体区别于其他总体的特征;变异是指该总体内部的差异,即个体的特异性。
医药数理统计习题答案解析

第一章数据的描述和整理一、学习目的和要求1. 掌握数据的类型及特性;2.掌握定性和定量数据的整理步骤、显示方法;3.掌握描述数据分布的集中趋势、离散程度和分布形状的常用统计量;4.能理解并熟练掌握样本均值、样本方差的计算;5.了解统计图形和统计表的表示及意义;6. 了解用Excel软件进行统计作图、频数分布表与直方图生成、统计量的计算。
二、内容提要(一)数据的分类(二)常用统计量1、描述集中趋势的统计量2、描述离散程度的统计量3、描述分布形状的统计量* 在分组数据公式中,m i , f i 分别为各组的组中值和观察值出现的频数。
三、综合例题解析例1.证明:各数据观察值与其均值之差的平方和(称为离差平方和)最小,即对任意常数C ,有2211()()n ni ii i x x x C ==-≤-∑∑ 证一:设 21()()ni i f C x C ==-∑由函数极值的求法,对上式求导数,得11()2()22, ()2 n ni i i i f C x C x nC f C n =='''=--=-+=∑∑令 f '(C )=0,得唯一驻点11= ni i C x x n ==∑由于()20f x n ''=>,故当C x =时f (C )y 有最小值,其最小值为21()()ni i f x x x ==-∑。
证二:因为对任意常数C 有22222211111222212()()(2)2(2)()0nn n n nii iii i i i i i ni i xx x C x nx x C x nC nx C x nC n x Cx C n x C ======---=---+=-+-=--+=--≤∑∑∑∑∑∑故有2211()()nni ii i x x x C ==-≤-∑∑。
四、习题一解答1.在某药合成过程中,测得的转化率(%)如下:94.3 92.8 92.7 92.6 93.3 92.9 91.8 92.4 93.4 92.6 92.2 93.0 92.9 92.2 92.4 92.2 92.8 92.4 93.9 92.0 93.5 93.6 93.0 93.0 93.4 94.2 92.8 93.2 92.2 91.8 92.5 93.6 93.9 92.4 91.8 93.8 93.6 92.1 92.0 90.8 (1)取组距为0.5,最低组下限为90.5,试作出频数分布表; (2)作频数直方图和频率折线图;(3)根据频数分布表的分组数据,计算样本均值和样本标准差。
(完整版)医学统计学第六版课后答案

第一章绪论一、单项选择题答案 1. D 2. E 3. D 4. B 5. A 6. D 7. A 8. C 9. E 10. D二、简答题1答由样本数据获得的结果,需要对其进行统计描述和统计推断,统计描述可以使数据更容易理解,统计推断则可以使用概率的方式给出结论,两者的重要作用在于能够透过偶然现象来探测具有变异性的医学规律,使研究结论具有科学性。
2答医学统计学的基本内容包括统计设计、数据整理、统计描述和统计推断。
统计设计能够提高研究效率,并使结果更加准确和可靠,数据整理主要是对数据进行归类,检查数据质量,以及是否符合特定的统计分析方法要求等。
统计描述用来描述及总结数据的重要特征,统计推断指由样本数据的特征推断总体特征的方法,包括参数估计和假设检验。
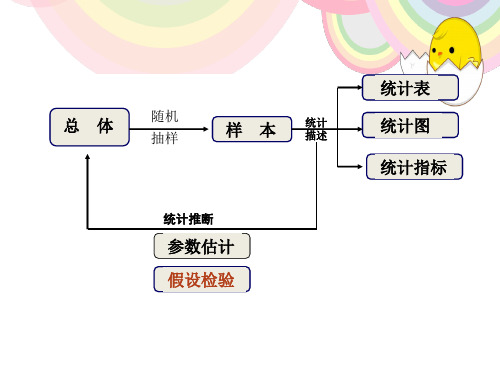
3答统计描述结果的表达方式主要是通过统计指标、统计表和统计图,统计推断主要是计算参数估计的可信区间、假设检验的P 值得出相互比较是否有差别的结论。
4答统计量是描述样本特征的指标,由样本数据计算得到,参数是描述总体分布特征的指标可由“全体”数据算出。
5答系统误差、随机测量误差、抽样误差。
系统误差由一些固定因素产生,随机测量误差是生物体的自然变异和各种不可预知因素产生的误差,抽样误差是由于抽样而引起的样本统计量与总体参数间的差异。
6答三个总体一是“心肌梗死患者”所属的总体二是接受尿激酶原治疗患者所属的总体三是接受瑞替普酶治疗患者所在的总体。
第二章定量数据的统计描述一、单项选择题答案 1. A 2. B 3. E 4. B 5. A 6. E 7. E 8. D 9. B 10. E二、计算与分析2第三章正态分布与医学参考值范围一、单项选择题答案 1. A 2. B 3. B 4. C 5. D 6. D 7. C 8. E 9. B 10. A二、计算与分析12[参考答案] 题中所给资料属于正偏态分布资料,所以宜用百分位数法计算其参考值范围。
又因血铅含量仅过大为异常,故应计算只有上限的单侧范围,即95P 。
t检验例题以及解析

t检验例题以及解析
当进行 t 检验时,我们通常会比较两组数据的平均值,以确定
它们是否存在显著差异。
下面我将以一个例题为例,然后给出解析。
假设我们对一种新药的疗效进行了测试。
我们有两组患者,一
组接受了新药,另一组接受了安慰剂。
我们想知道新药是否比安慰
剂更有效。
假设我们的零假设是,新药的疗效与安慰剂相同,备择假设是,新药的疗效比安慰剂更好。
我们进行了实验,并记录了两组患者的治疗效果数据。
现在我
们要进行 t 检验来确定这两组数据的平均值是否存在显著差异。
首先,我们计算每组数据的平均值和标准差。
然后,我们使用
t 检验的公式计算 t 值。
接下来,我们查找 t 分布表,确定 t 临
界值。
最后,我们将计算得到的 t 值与 t 临界值进行比较,以确
定是否拒绝零假设。
解析:
假设我们进行 t 检验后得到的 t 值为2.31,而自由度为28(假设样本量为30,因此自由度为30-1=29),在显著性水平为0.05的情况下,t 分布表告诉我们 t 临界值为2.045。
因为我们得到的 t 值大于 t 临界值,所以我们可以拒绝零假设,即可以得出结论,新药的疗效与安慰剂存在显著差异。
除了这种数值计算的方法,我们还可以从 t 检验的原理、假设条件、实际应用等多个角度进行解析。
希望这个例题和解析能够帮助你更好地理解 t 检验的应用和原理。
(完整版)医学统计学题库

For personal use only in study and research; not for commercial use第一章 绪论习题一、选择题1.统计工作和统计研究的全过程可分为以下步骤:(D )A . 调查、录入数据、分析资料、撰写论文B . 实验、录入数据、分析资料、撰写论文C . 调查或实验、整理资料、分析资料 D. 设计、收集资料、整理资料、分析资料 E. 收集资料、整理资料、分析资料2.在统计学中,习惯上把(B )的事件称为小概率事件。
A.10.0≤PB. 05.0≤P 或01.0≤PC. 005.0≤PD.05.0≤PE. 01.0≤P 3~8A.计数资料B.等级资料C.计量资料D.名义资料E.角度资料3.某偏僻农村144名妇女生育情况如下:0胎5人、1胎25人、2胎70人、3胎30人、4胎14人。
该资料的类型是( A )。
4.分别用两种不同成分的培养基(A 与B )培养鼠疫杆菌,重复实验单元数均为5个,记录48小时各实验单元上生长的活菌数如下,A :48、84、90、123、171;B :90、116、124、225、84。
该资料的类型是(C )。
5.空腹血糖测量值,属于( C )资料。
6.用某种新疗法治疗某病患者41人,治疗结果如下:治愈8人、显效23人、好转6人、恶化3人、死亡1人。
该资料的类型是(B )。
7.某血库提供6094例ABO 血型分布资料如下:O 型1823、A 型1598、B 型2032、AB 型641。
该资料的类型是(D )。
8. 100名18岁男生的身高数据属于(C )。
二、问答题1.举例说明总体与样本的概念.答:统计学家用总体这个术语表示大同小异的对象全体,通常称为目标总体,而资料常来源于目标总体的一个较小总体,称为研究总体。
实际中由于研究总体的个体众多,甚至无限多,因此科学的办法是从中抽取一部分具有代表性的个体,称为样本。
例如,关于吸烟与肺癌的研究以英国成年男子为总体目标,1951年英国全部注册医生作为研究总体,按照实验设计随机抽取的一定量的个体则组成了研究的样本。
卫生统计学第六章-t检验与假设检验的基本思想

假设检验主要内容单样本 t 检验两独立样本 t 检验 配对资料t 检验假设检验的基本原理与步骤 假设检验的注意事项统 计 分 析统计推断假设检验 hypothesis testing Significance test参 数 估 计统计描述例1 一般健康成年女性血红蛋白的均数为124.7g/L ,某医生在某山区随机抽取了20例健康成年女性,测得她们血红蛋白的均数为115.0g/L ,标准差为12.5g/L ,问:该山区健康成年女性血红蛋白的均数是否与一般健康成年女性不同?山区健康女性血红蛋白 μ≠124.7g/L山区健康女性血红蛋白μ=124.7g/L一种假设另一种假设总体不同假设检验的目的:就是判断差别是由哪种原 因造成的。
抽样误差115.0/=X g L应用场合:当研究结果为一组或两组计量资料( 定量数据)时,要通过该样本推断其总体平均水平是否与某一标准值不同,或这两个样本的总体平均水平是否不同。
应用条件:(1)独立(两样本) (2)正态(3)方差齐,即 t 检验2212σσ=t 检验的3种设计类型t 检验 单样本t 检验(One sample t-test )配对资料的t 检验(paired samples t-test )两个独立样本t 检验(Two independent samples t-test )单样本 t 检验● 单样本 t 检验(one sample/group t -test)即通过样本均数 判断其是否来自某一已知均数μ0 的总体● 已知的总体均数μ0一般为理论值、标准值或经过大量观察所得的稳定值等● 条件:满足正态性● 其检验统计量按下式计算(6.1)X 0,1μυ-==-X t n Sn例1(续)1、建立假设、确定单双侧检验和检验水准αH 0: μ=μ0=124.7g/L , 即该山区健康成年女性血红蛋白均数与一般健康成年女性相同H 1: μ≠μ0, 即该山区健康成年女性血红蛋白均数与一般健康成年女性不同本例为双侧检验,α=0.05单样本 t 检验H 0:μ = μ0H 1:μ ≠ μ0μ = μ0Xμ0μX单样本 t 检验例1(续)2、确定检验方法,计算检验统计量在假定H 0成立的条件下计算检验统计量,按公式(6.1)0115.0124.7 3.47012.5/20120119μυ--===-=-=-=X t S n n 0124.7/,115.0/12.5/μ===S g L g L g X L 单样本 t 检验例1(续)3、确定P 值,作出推断结论查t 界值表,当 时,双侧 ,本例|t |=3.470>2.093,可得P <0.05。
t检验的资料与习题

第四章:定量资料的参数估计与假设检验基础1抽样与抽样误差抽样方法本身所引起的误差。
当由总体中随机地抽取样本时,哪个样本被抽到是随机的,由所抽到的样本得到的样本指标x与总体指标μ之间偏差,称为实际抽样误差。
当总体相当大时,可能被抽取的样本非常多,不可能列出所有的实际抽样误差,而用平均抽样误差来表征各样本实际抽样误差的平均水平。
σx=σ/Sx=S/2t分布t分布曲线形态与n(确切地说与自由度v)大小有关。
与标准正态分布曲线相比,自由度v越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度v愈大,t分布曲线愈接近正态分布曲线,当自由度v=∞时,t分布曲线为标准正态分布曲线。
t=X-u/Sx=X-u/(S/),V=N-1正态分布(normaldistribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
正态分布有两个参数,μ和σ,决定了正态分布的位置和形态。
为了应用方便,常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量u,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standardnormaldistribution),亦称u分布。
根据中心极限定理,通过上述的抽样模拟试验表明,在正态分布总体中以固定n,抽取若干个样本时,样本均数的分布仍服从正态分布,即N(μ,σ)。
所以,对样本均数的分布进行u变换,也可变换为标准正态分布N(0,1) 由于在实际工作中,往往σ是未知的,常用s作为σ的估计值,为了与u变换区别,称为t变换,统计量t值的分布称为t分布。
假设X服从标准正态分布N(0,1),Y服从χ2(n)分布,那么Z=X/sqrt(Y/n)的分布称为自由度为n的t分布,记为Z~t(n)。
特征:1.以0为中心,左右对称的单峰分布;2.t分布是一簇曲线,其形态变化与n(确切地说与自由度ν)大小有关。
自由度ν越小,t分布曲线越低平;自由度ν越大,t分布曲线越接近标准正态分布(u分布)曲线,如图.t(n)分布与标准正态N(0,1)的密度函数对应于每一个自由度ν,就有一条t分布曲线,每条曲线都有其曲线下统计量t的分布规律,计算较复杂。
医学统计学试题:第1题【20分】__t检验

一、两组计量资料比较(20分)题干由试题和相关SPSS分析结果组成1、根据资料选择正确的统计检验方法;2、请写出假设检验步骤:检验假设,检验水准,根据SPSS结果选择正确的统计量值和P值、并作出结果判断。
3、说明:正态性检验提供K-S检验结果;方差齐性检验提供Levene’s检验结果。
正态性检验和方差齐性检验不必列出检验步骤,作出判断即可。
可能包括的内容:●配对设计的两样本均数比较的t检验●成组设计的两样本均数比较的t检验●成组设计的两样本均数比较的近似t检验●配对设计的两样本比较的符号秩和检验●成组设计的两样本比较的秩和检验举例:例2.17 某医生测得18例慢性支气管炎患者及16例健康人的尿17酮类固醇排出量(mg/dl)分别为X1和X2,试问两组的均数有无不同。
X1:3.14 5.83 7.35 4.62 4.05 5.08 4.98 4.22 4.35 2.35 2.89 2.16 5.55 5.94 4.40 5.35 3.80 4.12X2:4.12 7.89 3.24 6.36 3.48 6.74 4.67 7.38 4.95 4.08 5.34 4.27 6.54 4.62 5.92 5.18Test Statistics b-1.334a .182Z Asymp. Sig. (2-tailed)健康者 - 慢支患者Based on negative ranks.a. Wilcoxon Signed Ranks Testb.根据SPSS 分析结果, 对资料分布正态性、方差齐性作出判断。
H 0: μ = μ 0 H 1: μ ≠ μ 0 α = 0.05ν = n1+n2-2=32 本例 t= -1.818, P=0.078>0.05 结论:【答案】jszb1、此资料是计量资料,研究设计为完全随机设计 (又称成组设计);2、根据正态性单样本K-S 检验结果:P 值分别为 0.992、0.987,均大于 0.1,因此两样本均服从正态分布;3、根据方差齐性检验结果:F=0.225、P=0.638,P >0.05,因此两样本总体方差齐性;4、根据以上三点,统计方法选用成组设计两样本 t 检验,其假设检验过程如下: (1)建立假设检验,确立检验水准:H0:u1=u2,即两组的总体均数相同 H1:u1≠u2,即两组的总体均数不同 α=0.05(2)计算检验统计量t 值:ν=18+16-2=32 t = -1.818(3)确定 P 值,做出统计推断:P=0.078>0.05根据α=0.05的检验水准,不拒绝 H0,差异无统计学意义。
医学统计学计算题

医学统计学计算题(一)假设检验的步骤(1)建立假设和检验水准①检验假设或者称无效假设(null hypothesis),用H0表示,H0假设是需要检验的假设,如假设两总体均数相等。
②备择假设(alternative hypothesis),用H1表示。
H1是H0不成立时而被接受的假设,如假设两总体均数不相等。
③检验水准(α)通常α取0.05 。
检验水准就是我们用来区分大概率事件和小概率事件的标准,是人为规定的。
当某事件发生的概率小于α时,则认为该事件为小概率事件,是不太可能发生的事件。
(2)计算统计量根据资料类型与分析目的选择适当的公式计算出统计量,比如t检验计算出t 值。
(3)确定概率值(P)将计算得到的t值与查表得到或tα,ν比较,得到P值的大小。
根据t分布我们知道,如果t >tα/2,ν,则P<α,则拒绝H0,接受H1如果t <tα/2,ν,则P>α,则不拒绝H0(二)单个样本的t检验(1)已知总体均数μ0,但总体标准差σ未知,已知样本含量n,样本标准差S时,选用单样本t检验。
(2)已知总体均数μ0,已知总体标准差σ,已知样本含量n,样本标准差S未知时,选用u 检验。
步骤:1. 建立检验假设,确定检验水准H0:μ=μ0,…与…总体均数相同;H1:μ≠μ0,…与…总体均数不相同;α=0.05。
2. 计算检验统计量在μ=μ0成立的前提条件下,计算统计量为:3. 确定P值,做出推断结论自由度ν=n-1,查附表2,得tα/2,ν=…。
(1)若t <tα/2,ν,故P>α,表明差异无统计学意义,即按α=0.05水准不拒绝H0,根据现有样本信息,尚不能认为…与…总体均数不同。
(2)若t >tα/2,ν,故P<α,表明差异有统计学意义,即按α=0.05水准拒绝H0,接受H1,根据现有样本信息,可以认为…与…总体均数不同。
(三)配对样本t检验1.建立检验假设,确定检验水准H0:μd =0,…和…总体均数差异为0; H1:μd ≠0,…和…总体均数差异不为0;; α=0.05。
医药数理统计方法教学大纲

《医药数理统计方法》教学大纲(供成人专科班使用)(2009年4月修订)I前言《医药数理统计方法》是研究和揭示随机现象中统计规律的数学学科。
数理统计方法的应用广泛,几乎遍及所有科学技术领域,是各学科中分析与解决问题的基本工具。
《医药数理统计方法》课程,是医科各专业的一门重要的基础课,主要程讲述概率论与数理统计的概念和方法,学习的目的旨在培养学生逻辑推理和运算能力、分析问题和解决问题的能力,以学习和掌握统计方法为重点,学会怎样有效地收集、整理和分析带有随机性的数据,以对实际问题做出推断或预测、并为采取一定的决策和行动提供依据和建议。
使学生初步掌握处理随机现象的基本思想与方法,具备分析和处理带有随机性数据的能力,为学习后续相关基础课程与专业课程提供基础理论和相关知识。
本大纲供成人专科班使用。
本大纲使用说明如下:1.大纲按要求分为“了解”、“熟悉”和“掌握”三个层次,“了解”是指对概念和理论方面的要求;“熟悉”和“掌握”是对方法、运算和应用的低层次和较高层次的要求。
2.为使用方便,大纲正文中将重点内容加了下划虚线(如数学期望),将核心内容加了下划线和着重号(如数学期望),使用者要对这部分内容引起足够重视。
3.本课程教学参考时数:36学时。
Ⅱ正文第一章随机事件及其概率一、教学目的学习概率论的目的是为了研究看似无规律的随机现象的数量规律,通过中学所学的频率和排列组合的知识,来理解概率的定义与计算。
古典概型是计算概率最重要的方法之一,要理解并掌握。
事件之间的关系和运算与中学所学的集合论知识极其类似,只是说法和记法有所不同。
古典概型、加法定理、乘法定理、全概率公式与逆概率公式是本单元的核心内容,通过学习要掌握其方法和应用。
1.掌握概率的性质;掌握利用古典概型(率)求事件的概率;掌握概率的加法定理(公式)及其计算;掌握概率的乘法定理(公式)及其计算;掌握全概率公式、逆概率公式及其应用。
2.熟悉事件间的基本关系和运算规律;熟悉两事件独立的充分必要条件。
医学统计学第六章假设检验作业

假设检验1、答:(1)建立假设、确定检验水准α。
H 0:µ1=µ2(两组成年男性的尿2,5-己二酮含量均数相等,吸烟对成年男性尿2,5-己二酮含量无影响)H 1:µ1≠µ2(两组成年男性的尿2,5-己二酮含量均数不相等,吸烟对成年男性尿2,5-己二酮含量有影响)检验水准α=0.05(2)计算检验统计量Z 值计算两均数之差标准误的估计值:067.050/54.1125/56.1//2222212121=+=+=∧-n S n S X X σ 计算Z 值:224.35067.058.2522.232121-=-≈-=-X X X X z σ (3)确定P 值,下结论。
Z<-Z 0.05/2=-1.96,P<0.05,按α=0.05水准,拒绝H0,接受H1,统计结论为差别有统计学意义,可认为吸烟对成年男性尿2,5-己二酮含量有影响。
2、答:根据调查结果,n=1257,p=0.084,有np=105.588,n(1-p)=1151.412,均大于5,已知总体率π0=0.204。
(1)建立假设、确定检验水准α。
H 0:π=0.204(该地6岁以下儿童血清维生素A 缺乏的总体患病率与其它西部边远省份相同)H 1:π≠0.204(该地6岁以下儿童血清维生素A 缺乏的总体患病率与其它西部边远省份不同)检验水准α=0.05(2)计算检验统计量Z 值()()56.101257204.01204.0204.0084.010000-≈--=--=-=n p p z p πππσπ (3)确定P 值,下结论。
Z<-Z 0.05/2=-1.96,P<0.05,按α=0.05水准,拒绝H0,接受H1,统计结论为差别有统计学意义,可认为该地6岁以下儿童血清维生素A 缺乏的总体患病率与其它西部边远省份不同。
3、答:(1)建立假设、确定检验水准α。
H 0:π1=π2(中药和西药的药效无差别)H 1:π1≠π2(中药和西药药效有差别)检验水准α=0.05(2)计算检验统计量Z 值已知n 1=131,p 1=0.962,有效例数(n 1p 1)126例;n 2=124,p 2=0.726,有效例数(n 2p 2)90例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章抽样误差与假设检验练习题一、单项选择题1. 样本均数的标准误越小说明A. 观察个体的变异越小B. 观察个体的变异越大C. 抽样误差越大D. 由样本均数估计总体均数的可靠性越小E. 由样本均数估计总体均数的可靠性越大2. 抽样误差产生的原因是A. 样本不是随机抽取B. 测量不准确C. 资料不是正态分布D. 个体差异E. 统计指标选择不当3. 对于正偏态分布的的总体, 当样本含量足够大时, 样本均数的分布近似为A. 正偏态分布B. 负偏态分布C. 正态分布D. t分布E. 标准正态分布4. 假设检验的目的是A. 检验参数估计的准确度B. 检验样本统计量是否不同C. 检验样本统计量与总体参数是否不同D. 检验总体参数是否不同E. 检验样本的P值是否为小概率5. 根据样本资料算得健康成人白细胞计数的95%可信区间为7.2×109/L~9.1×109/L,其含义是A. 估计总体中有95%的观察值在此范围内B. 总体均数在该区间的概率为95%C. 样本中有95%的观察值在此范围内D. 该区间包含样本均数的可能性为95%E. 该区间包含总体均数的可能性为95%答案:E D C D E二、计算与分析1.为了解某地区小学生血红蛋白含量的平均水平,现随机抽取该地小学生450人,算得其血红蛋白平均数为101.4g/L,标准差为1.5g/L,试计算该地小学生血红蛋白平均数的95%可信区间。
[参考答案]样本含量为450,属于大样本,可采用正态近似的方法计算可信区间。
101.4X=, 1.5S=,450n=,0.07XS===95%可信区间为下限:/2.101.4 1.960.07101.26 XX u Sα=-⨯=-(g/L)上限:/2.101.4 1.960.07101.54 XX u Sα+=+⨯=(g/L)即该地成年男子红细胞总体均数的95%可信区间为101.26g/L~101.54g/L。
2.研究高胆固醇是否有家庭聚集性,已知正常儿童的总胆固醇平均水平是175mg/dl,现测得100名曾患心脏病且胆固醇高的子代儿童的胆固醇平均水平为207.5mg/dl,标准差为30mg/dl。
问题:①如何衡量这100名儿童总胆固醇样本平均数的抽样误差?②估计100名儿童的胆固醇平均水平的95%可信区间;③根据可信区间判断高胆固醇是否有家庭聚集性,并说明理由。
[参考答案]①均数的标准误可以用来衡量样本均数的抽样误差大小,即30S=mg/dl,100n=②样本含量为100,属于大样本,可采用正态近似的方法计算可信区间。
207.5X=,30S=,100n=,3XS=,则95%可信区间为下限:/2.207.5 1.963201.62 XX u Sα=-⨯=-(mg/dl)上限:/2.207.5 1.963213.38 XX u Sα+=+⨯=(mg/dl)故该地100名儿童的胆固醇平均水平的95%可信区间为201.62mg/dl~213.38mg/dl。
③因为100名曾患心脏病且胆固醇高的子代儿童的胆固醇平均水平的95%可信区间的下限高于正常儿童的总胆固醇平均水平175mg/dl,提示患心脏病且胆固醇高的父辈,其子代胆固醇水平较高,即高胆固醇具有一定的家庭聚集性。
(李康)第五章t检验练习题一、单项选择题1. 两样本均数比较,检验结果05P说明.0A. 两总体均数的差别较小B. 两总体均数的差别较大C. 支持两总体无差别的结论D. 不支持两总体有差别的结论E. 可以确认两总体无差别2. 由两样本均数的差别推断两总体均数的差别, 其差别有统计学意义是指A. 两样本均数的差别具有实际意义B. 两总体均数的差别具有实际意义C. 两样本和两总体均数的差别都具有实际意义D. 有理由认为两样本均数有差别E. 有理由认为两总体均数有差别3. 两样本均数比较,差别具有统计学意义时,P值越小说明A. 两样本均数差别越大B. 两总体均数差别越大C. 越有理由认为两样本均数不同D. 越有理由认为两总体均数不同E. 越有理由认为两样本均数相同4. 减少假设检验的Ⅱ类误差,应该使用的方法是A. 减少Ⅰ类错误B. 减少测量的系统误差C. 减少测量的随机误差D. 提高检验界值E. 增加样本含量5.两样本均数比较的t检验和u检验的主要差别是A. t检验只能用于小样本资料B. u检验要求方差已知或大样本资料C. t检验要求数据方差相同D. t检验的检验效能更高E. u检验能用于两大样本均数比较答案:D E D E B二、计算与分析1. 已知正常成年男子血红蛋白均值为140g/L ,今随机调查某厂成年男子60人,测其血红蛋白均值为125g/L ,标准差15g/L 。
问该厂成年男子血红蛋白均值与一般成年男子是否不同? [参考答案]因样本含量n >50(n =60),故采用样本均数与总体均数比较的u 检验。
(1)建立检验假设, 确定检验水平00:μμ=H ,该厂成年男子血红蛋白均值与一般成年男子相同11μμ≠:H ,该厂成年男子血红蛋白均值与一般成年男子不同??0.05(2) 计算检验统计量XX X u μσ-===6015125140-=7.75 (3) 确定P 值,做出推断结论7.75>1.96,故P <0.05,按α=0.05水准,拒绝0H ,接受1H ,可以认为该厂成年男子血红蛋白均值与一般成年男子不同,该厂成年男子血红蛋白均值低于一般成年男子。
2. 某研究者为比较耳垂血和手指血的白细胞数,调查12名成年人,同时采取耳垂血和手指血见下表,试比较两者的白细胞数有无不同。
表 成人耳垂血和手指血白细胞数(10g/L)编号 耳垂血 手指血 1 9.7 6.7 2 6.2 5.4 3 7.0 5.7 4 5.3 5.0 5 8.1 7.5 6 9.9 8.3 7 4.7 4.6 8 5.8 4.2 9 7.8 7.5 10 8.6 7.0 116.15.312 9.9 10.3[参考答案]本题为配对设计资料,采用配对t 检验进行分析 (1)建立检验假设, 确定检验水平H 0:?d =0,成人耳垂血和手指血白细胞数差异为零 H 1:?d ?0,成人耳垂血和手指血白细胞数差异不为零??0.05(2) 计算检验统计量==∑∑2,6.11dd20.360d d d d d t S S μ--===672.312912.0967.0===n S d t dt =3.672>0.05/2,11t ,P < 0.05,拒绝H 0,接受H 1,差别有统计学意义,可以认为两者的白细胞数不同。
3. 分别测得15名健康人和13名Ⅲ度肺气肿病人痰中1α抗胰蛋白酶含量(g/L)如下表,问健康人与Ⅲ度肺气肿病人1α抗胰蛋白酶含量是否不同?表 健康人与Ⅲ度肺气肿患者α1抗胰蛋白酶含量(g/L)健康人Ⅲ度肺气肿患者2.73.6 2.2 3.44.1 3.7 4.35.4 2.6 3.6 1.96.8 1.7 4.7 0.6 2.9 1.9 4.8 1.3 5.6 1.5 4.1 1.7 3.3 1.3 4.31.31.9[参考答案]由题意得,107.1,323.4015.1,067.22211====S X S X ;本题是两个小样本均数比较,可用成组设计t 检验,首先检验两总体方差是否相等。
H 0:?12=?22,即两总体方差相等 H 1:?12≠?22,即两总体方差不等 ?=0.05F =2122S S =22015.1107.1=1.19 ()14,1205.0F =2.53>1.19,F <()14,1205.0F ,故P >0.05,按α=0.05水准,不拒绝H 0,差别无统计学意义。
故认为健康人与Ⅲ度肺气肿病人α1抗胰蛋白酶含量总体方差相等,可直接用两独立样本均数比较的t 检验。
(1)建立检验假设, 确定检验水平210:μμ=H ,健康人与Ⅲ度肺气肿病人1α抗胰蛋白酶含量相同211μμ≠:H ,健康人与Ⅲ度肺气肿病人1α抗胰蛋白酶含量不同??0.05(2) 计算检验统计量2)1()1(212222112-+-+-=n n S n S n S c=1.12 12121212()0||X X X X X X X X t S S -----===5.63(3) 确定P 值,做出推断结论t =5.63> 0.001/2,26t ,P < 0.001,拒绝H 0,接受H 1,差别有统计学意义,可认为健康人与Ⅲ度肺气肿病人α1抗胰蛋白酶含量不同。
4.某地对241例正常成年男性面部上颌间隙进行了测定,得其结果如下表,问不同身高正常男性其上颌间隙是否不同?表 某地241名正常男性上颌间隙(cm )身高 (cm) 例数 均数 标准差 161~ 116 0.2189 0.2351 172~1250.22800.2561[参考答案]本题属于大样本均数比较,采用两独立样本均数比较的u 检验。
由上表可知,1n =116 , 1X =0.2189 , 1S =0.23512n =125 , 2X =0.2280 , 2S =0.2561(1)建立检验假设, 确定检验水平210:μμ=H ,不同身高正常男性其上颌间隙均值相同211μμ≠:H ,不同身高正常男性其上颌间隙均值不同??0.05(2) 计算检验统计量1212X X X X X X u S --==0.91 (3) 确定P 值,做出推断结论u =0.91<1.96,故P >0.05,按α=0.05水准,不拒绝H 0, 差别无统计学意义,尚不能认为不同身高正常男性其上颌间隙不同。
5.将钩端螺旋体病人的血清分别用标准株和水生株作凝溶试验,测得稀释倍数如下表,问两组的平均效价有无差别?表 钩端螺旋体病患者凝溶试验的稀释倍数标准株 100 200 400 400 400 400 800 1600 1600 1600 3200 3200 3200 水生株 100 100 100 200 200 200 200 400 400 800 1600[参考答案]本题采用两独立样本几何均数比较的t 检验。
t =2.689>t 0.05/2,22,P <0.05,拒绝H 0,接受H 1,差别有统计学意义,可认为两组的平均效价有差别。
6.为比较男、女大学生的血清谷胱甘肽过氧化物酶(GSH-Px)的活力是否相同,某医生对某大学18~22岁大学生随机抽查男生48名,女生46名,测定其血清谷胱甘肽过氧化酶含量(活力单位),男、女性的均数分别为96.53和93.73,男、女性标准差分别为7.66和14.97。
问男女性的GSH-Px 是否相同? [参考答案]由题意得 1n =48, =1X 96.53, 1S =7.66 2n =46, 2X =93.73, 2S =14.97本题是两个小样本均数比较,可用成组设计t 检验或t ’检验,首先检验两总体方差是否相等。
