浙江省2020-2021学年高三第一学期9+1高中联盟期中考试数学试题
浙江省9+1高中联盟2021-2022学年高一上学期期中考试数学试题含答案

浙江省9+1高中联盟2021-2022学年高一上学期期中考试数学学科试题考生须知:1.本卷满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息;3.所有答案必须写在答题卷上,写在试卷上无效,考试结束后,只需上交答题卷; 一、选择题1(本大题共8题,每小题5分,共40分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.已知集合{}23A x x =-<<,{}1,2,3,4B =,则(A B ⋂=( ) A.{}1,2B.{}2,3C.{}1,2,3D.{}2,3,42.函数()f x x=的定义域是( )A.{}22x x -<<B.{}02x x <≤ C.{}22x x -≤≤D.{}220x x x -≤≤≠且3.命题“1x ∀>,20x x ->”的否定是( ) A.1x ∃≤,20x x -≤ B.1x ∃>,20x x -≤ C.1x ∀>,20x x -≤D.1x ∀≤,20x x ->4.“1x >”是“11x<”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件D.既不充分也不必要条件5.关于x 的不等式()2110m x mx m +-+-<的解集为∅,则实数m 的取值范围是( )A.1m <-B.m ≥C.m ≤D.m ≤或m ≥6.已知函数()()()f x x a x b =--(其中a b >)的图象如图所示,则函数()2xg x a b =+-的图像是( )A. B.C. D.7.若点(),81m 在幂函数()()2nf x m =-的图象上,则函数()g x 是( )A.⎡⎣B.⎡⎣C.⎤⎦D.[]2,38.定义在R 上的函数()f x 满足()()f x f x -=,且当0x ≥时,()()()122202262x x f x x x x +⎧-≤≤⎪=⎨-+->⎪⎩,若对任意的[]1,x m m ∈-,不等式()()2f x f x m -≤+恒成立,则实数m 的最大值是( )A.2B.23C.-1D.-2二、选择题Ⅱ(本大题共4题,每小题5分,共20分。
浙江省9+1高中联盟2020-2021学年高一上学期期中考试生物+数学试题 含答案

2020学年第一学期9十1高中联盟期中考试高二年级生物学科试题考生须知:1.本卷满分100分,考试时间90分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息;3.所有答案必须写在答题卷上,写在试卷上无效,考试结束后,只需上交答题卷;4.参加联批学校的学生可登陆查询个人分析报告。
一、选择题(本大题共25题,每小题2分,共50分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.下列生物具有细胞核的是A.蓝细菌B.噬菌体C.乳酸菌D.酵母菌2.下列关于化合物的叙述,正确的是A.脂质只含有C、H,O三种元素B.Fe2+是构成某些蛋白质的重要成分C.蔗糖和麦芽糖水解后的产物相同D.细胞吸收无机盐离子的速率取决于膜内外离子的浓度差3.关于等位基因的叙述,正确的是A.分别控制不同性状B.位于同--条染色体上C.位于DNA的两条链上D.有些基因在同源染色体上不存在等位基因4.下列过程中,涉及肽键数量变化的是A.用纤维素酶处理植物细胞B.洋葱表皮细胞的质壁分离C.细胞的有丝分裂D.小肠上皮细胞吸收氨基酸5.下列关于物质检测和鉴定的实验,叙述正确的是A.油脂经苏丹Ⅲ染液染色后就能看到红色颗粒B.常用西瓜等水果作为检测还原糖的实验材料C.若要检测绿叶中的淀粉含量,应先对叶片进行脱色处理D.检测蛋白质时先加人2mL双缩脲试剂A,再加入5mL双缩脲试剂B6.如图为细胞膜结构模式图,下列叙述错误的是A.③为磷脂,它不是动植物体内主要的贮能物质B.动物细胞膜中的胆固醇与膜的流动性大小有关C.结构①一般只存在于细胞膜的外表面D.将一个活细胞放在电子显微镜下,能直接观察到质膜内部的结构7.下列关于成熟玉米叶肉细胞的叙述。
错误的是A.细胞中的线粒体与该细胞有丝分裂相关B.内质网的囊腔和细管彼此相通C.黑暗条件下,叶绿体也能合成有机物D.在电子显微镜下,核糖体呈现微小的悬滴状8.关于细胞的生命历程,下列叙述正确的是A.动物细胞分化仅发生于胚胎发育阶段B.对于某些生物而言,细胞衰老就是个体衰老C.癌细胞容易扩散与转移,这与其细胞膜上的载体蛋白有关D.细胞分化使各种细胞的遗传物质有所差异,导致细胞形态和功能不同9.叶绿体中的色素为脂溶性,液泡中紫红色的花青苷为水溶性。
2020-2021学年浙江省9 1高中联盟高一下学期期中考试数学试卷及答案

绝密★启用前2020-2021学年浙江省91高中联盟高一下学期期中考试数学试题注意事项:1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上一、单项选择题(本题共8小题,每小题5分,共40分.每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.已知集合}{}1,0,2,1{3,2,3A B =-=,,那么A B ⋂=() A .{}1,0-B .{}1,2-C .{}0,3D .{}2,32.已知a 为实数,i 为虚数单位,若()()1a i i +-是纯虚数,则a =() A .2-B .1-C .1D .2 3.已知向量,a b 的夹角为3π,2,1a b ==.则2a b -=() A .2B .23C .4D .434.函数()222cos x xf x x x--=+在[],ππ-的图象大致为() A .B .C .D .5.小明用“五点法”画函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭在某一个周期内的图象时例表并填入了部分数据,如下表:x ωϕ+2π π2πx 12π 712π ()sin y A x ωϕ=+22-请你根据已有信息推算,,A ωϕ的值依次为() A 2,2,3π-B .2,2,6πC .2,,6ππ-D .2,2,3π6.在ABC 中,26A b π==,,则“1a >”是“ABC 有两个解”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.下表中给出的常用对数值有一个是错误的,它是() x0.271.5358lg x632a b -- 3a b c -+ 2a b - a c + 333a c --A .lg1.5B .lg 3C .lg 5D .lg 88.如图所示,在正四棱锥S ABCD -中,635AB SA ==,,它的内切球O 与四个侧面分别相切于点E ,F ,G ,H 处,则四边形EFGH 外接圆的半径为()A .12B .1C .32D .2 二、多项选择题(本题共4小题,每小题5分,共20分.每小题列出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得3分)9.下列命题中正确的是()A .一个棱柱至少有4个面B .平行六面体中相对的两个面是全等的矩形C .有一个面是平行四边形的棱锥一定是四棱锥D .正棱锥的侧面是全等的等腰三角形 10.已知110a b<<,则下列不等式正确的是()A .11a b ab<+B.22ln lna b>C.11b ba a->-D.2a bb a+>11.关于复数z的运算结论正确的有()A.2z z z⋅=B.22z z=C.1122z zz z⎛⎫=⎪⎝⎭D.1122zzz z=12.已知0,2xπ⎛⎫∈ ⎪⎝⎭,函数()cos2f x x xπ=+-,则下列选项正确的是()A.()000,,02x f xπ⎛⎫∃∈>⎪⎝⎭B.()000,,02x f xπ⎛⎫∃∈<⎪⎝⎭C.()000,,02x f xπ⎛⎫∀∈>⎪⎝⎭D.()000,,02x f xπ⎛⎫∀∈<⎪⎝⎭三、填空题(本题共4小题,单空题每空5分,多空题第一空2分,第二空3分,共20分)13.函数223y x x=--的值域是________.14.已知点()1,2P是角θ终边上的一点,则()()5sin cos32sin sin2πθπθπθπθ⎛⎫+--⎪⎝⎭=⎛⎫---⎪⎝⎭________.15.如图所示,在ABC中,6451203AB ABC ADB CD=∠=︒∠=︒=,,,,则AC的长是_____.16.砖雕是江南古建筑雕刻中很重要的一种艺术形式,传统砖雕精致细腻、气韵生动、极富书卷气.如图是一扇环形砖雕,可视为扇形OCD截去同心扇形OAB所得部分.已知扇环周长300cm=,大扇形半径100cmOD=,设小扇形半径cm,OA x AOBθ=∠=弧度,则①θ关于x 的函数关系式()x θ=______;②若雕刻费用关于x 的解析式为()101700x x ω=+,则砖雕面积与雕刻费用之比最大值为______.四、解答题(本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知向量()()21,1,2,a b t =-=-. (Ⅰ)若向量a 与b 共线,求t 的值;(Ⅱ)若3t =,且2a b λ-与a 垂直,求实数λ的值. 18.(本小题满分12分)已知函数()1sincos cos 222x x f x x =+. (1)函数()y f x =图象上所有的点_______,再_______得到()2sin 224g x x π⎛⎫=- ⎪⎝⎭的图象. (Ⅱ)若()g x 在区间()0,m 内是单调函数,求实数m 的最大值.19.(本小题满分12分)如图,在正三棱柱111ABC A B C -中,底面ABC 边长为2,D 为BC 的中点,三棱柱体积33V =.(I )求三棱柱的表面积;(Ⅱ)求三棱锥11B ADC -的体积.20.(本小题满分12分)在ABC 中,A ,B ,C 所对的边分别为,,,cos 3sin a b c a b C b C c -=-. (I )求角B 的大小; (Ⅱ)若3b =,求锐角ABC 周长l 的取值范围.21.(本小题满分12分)新冠肺炎疫情发生以后,口罩供不应求,某口罩厂日夜加班生产,为抗击疫情做贡献.生产口罩的固定成本为200万元,每生产x 万箱,需另投入成本()p x 万元,当产量不大于90万箱时,()992911708p x x x =---;当产量超过90万箱时,()1001002000p x x x =+--,若每箱口罩售价100元,通过市场分析,该口罩厂生产的口罩可以全部销售完. (I )求口罩销售利润y (万元)关于产量x (万箱)的函数关系式; (Ⅱ)当产量为多少万箱时,该口罩生产厂在生产中所获得利润最大? 22.(本小题满分12分)已知函数()10,3a f x x a x ⎛⎫=>> ⎪⎝⎭,点3,3a A ⎛⎫ ⎪⎝⎭,点1,33B a ⎛⎫⎪⎝⎭,和函数()f x 图象上的点()133,P x y x ⎛⎫<<⎪⎝⎭.过B 作直线AP 的垂线,垂足为Q .(I )若2x =,求AP PB ⋅(最后结果用a 表示); (Ⅱ)若53AP PQ a ⋅≤+恒成立,求a 的取值范围. 2020学年第二学期9+1高中联盟期中考试 高一数学A 卷参考答案一、单项选择题(本题共8小题,每小题5分,共40分.每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分)二、多项选择题(本题共4小题,每小题5分,共20分.每小题列出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得3分)三、填空题(本题共4小题,每小题5分,共20分)13.[)0,+∞14.2-1516.21000100100x x x +<<+,(x 的范围不写不扣分);3 四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(I )由题意可知,22t =,解得t =4分 (Ⅱ)()24,6a b λλλ-=+--6分 ∵()2a b a λ-⊥,∴()22100a b a λλ-⋅=+=,解得5λ=-10分18.(1)由已知得()11sin cos 2224f x x x x π⎛⎫=+=+ ⎪⎝⎭2分 向右平移2π个单位长度,再把横坐标缩短为原来的12(纵坐标不变);或横坐标缩短为原来的12(纵坐标不变),再向右平移4π个单位长度6分(任选一种回答正确均给满分)(Ⅱ)()224g x x π⎛⎫=- ⎪⎝⎭. 因为0,x m ∈(),所以2,2444x m πππ⎛⎫-∈-- ⎪⎝⎭,8分 又因为()g x 在区间()0,m 内是单调函数, 所以242m ππ-≤,即38m π≤,故实数m 的最大值为38π12分19.(I )由V =得,高3AA '=2分所以292218S S S =+=⨯+=+侧底6分 (Ⅱ)B ADC B ABD B AA C C ADC V V V V V '''''''----=---8分1132333=⋅-=分20.(1)∴cos sin a b C C c -=-∴sin sin cos sin sin A B C B C C -=-1分cos sin sin sin B C B C C ⇒=-∵sin 0C ≠∴cos 1B B =-3分12sin 1,sin 662B B ππ⎛⎫⎛⎫⇒-=-= ⎪ ⎪⎝⎭⎝⎭∵()0,B π∈ ∴66B ππ-=,即3B π=6分(Ⅱ)由正弦定理可知,2sin sin sin a c bA C B===,故2sin sin a A c C ==,8分所以2sin 2sin l a b c A C =++=++22sin 2sin 3sin 3A A A A π⎛⎫=+-+= ⎪⎝⎭6A π⎛⎫=++ ⎪⎝⎭∵,62A ππ⎛⎫∈⎪⎝⎭,∴sin 62A π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦10分∴(3l ∈12分21.(I )当090x <≤时,()1009917082001508y x x x =---=+3分当90x >时,()10010010020002001800100y x x x x =-+---=--.6分即1508090180010090x x y x x ⎧+<≤⎪=⎨-->⎪⎩,,(Ⅱ)当090x <≤时,1508y x =+令t ⎡=⎣,则291x t =-则221599y t t =-++∴当1t =即90x =时,max 1600y =9分 当90x >时,1800100y x =-- ∴100x =时,max 1800y =.11分综上,当产量为100万箱时,利润最大,最大为1800万元.12分 22.(Ⅰ)当2x =时,2,2a P ⎛⎫ ⎪⎝⎭, 则255551,,632312a a AP PB a ⎛⎫⎛⎫⋅=-⋅-=+ ⎪ ⎪⎝⎭⎝⎭4分 (Ⅱ)∵点P 在()f x 上,记1,33a P x x x ⎛⎫<< ⎪⎝⎭, ∴cos AP PQ AP PB BPQ PB AP ⋅=∠=⋅()211111,33,333333a a a x a x x x a x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--⋅--=--+-- ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭7分记()()21111533333g a a a x x x x ⎛⎫⎛⎫⎛⎫=---+--- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,由题知()0g a ≤恒成立. 令1x =,则241033a a --≤,得113a <≤8分 下面证明当113a <≤时,()0g a ≤恒成立,即()max 0g a ≤.∵()g a 是开口向上的二次函数∴()()max100103g g a g ≤⎧⎪≤⇔⎨⎛⎫≤ ⎪⎪⎝⎭⎩①()1111113323933g x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=--+--- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2211113312332092281x x x x ⎛⎫⎛⎫-+--+- ⎪ ⎪≤+-=-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭10分 ②()()221111811011413333333g x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--+---=-+++- ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 令1102,3t x x ⎡⎫=+∈⎪⎢⎣⎭,则()2210810812203333g t t =-+-≤-+⋅-= 所以当113a <≤时,()0g a ≤恒成立.12分。
2022届浙江省9 1高中联盟高三上学期期中考试数学试题 word版含答案
浙江省9+1高中联盟2022届高三上学期期中考试数学试题 选择题部分(共40分)一.选择题(本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}21,2,3,650A B x x x ==-+<∣,则A B ⋂=( ) A.()1,5B.{}1,3C.{}2,3D.{}1,2,32.复数()2i z a a =+-(,i a ∈R 为虚数单位)在复平面内所对应的点在直线y x =上,则z =( )3.一个正棱柱的正视图和俯视图如图所示(单位:cm ),则该三棱柱侧视图的面积(单位:2cm )是( )C. D.4.函数()222x x f x =-的图象可能是( )A. B.C. D.5.在ABC △中,“角A 为锐角”是“sin cos A A >”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.若P为平面区域0:0x M y x ⎧≥⎪≥⎨⎪+≤⎩内任意一点,则点P 到平面区域M 的边界的距离之和最大值是( )7.用数字1,2,3组成五位数,且数字1,2,3至少都出现一次,这样的五位数共有( )个.8.已知双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12,F F ,过2F 的直线l 交双曲线的右支于,A B 两点.点M 满足12AB AF AM +=,且10AM BF ⋅=.若11cos 4AF B ∠=,则双曲线C 的离心率是( )9.设函数()333f x x x =-+,若0,,a b c >∈R ,且()()()()()f x f a x a x b x c -=---,则1144b c +++的取值范围是( )A.82,136⎛⎤⎥ ⎝⎦B.22,36⎡⎤⎢⎥⎣⎦C.82,135⎛⎤⎥ ⎝⎦D.22,35⎡⎤⎢⎥⎣⎦10.已知数列{}n a 满足()()11*1211,,222121,2,2nn n n a a a a a a n n ++=-=-=--≥∈N ,记数列{}n a 前n 项和为n S ,则( ) A.202178S <<B.202189S <<C.2021910S <<D.20211011S <<非选择题部分(共110分)二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)11.直线1:30l ax y a +-=过定点( ),直线2:210l x y +-=,若12l l ⊥,则a =( ) 12.《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称为阳马.现有阳马P ABCD -,PA ⊥底面ABCD ,底面ABCD 为正方形,且PA AB =,则异面直线PB 与AC 所成角的大小为( )13.袋中装有大小相同的2个红球和1个黄球,小明无放回地连续摸取2次,每次从中摸取1个.记摸到红球的个数为ξ,则()1P ξ==( ),()E ξ=( )14.若()()21,0,0xx f x g x x ⎧-≥⎪=⎨<⎪⎩为奇函数,则()()2f g -=( )15.已知()7,7n nn f x C x n =≤且*n ∈N ,数列{}n a 的通项满足()2n n a f =-,则2a =( ),记{}n a 的前n 项和为n S ,则7S =( )16.已知ABC △,内角,,A B C 所对的边分别是,,,2,a b c c C ∠=的角平分线交AB 于点D .若sin sin 2sin A B ACB ∠+=,则a b +=( ),CD 的取值范围是( ) 17.已知平面向量,,a b c 满足:12,0,12a b a b c a ==⋅=+=,当a c -与b c -所成角θ最大时,则sin θ=( )三、解答题(本大题共5小题,共74分。
2021届浙江省9 1高中联盟高三上学期期中联考数学试题 PDF版
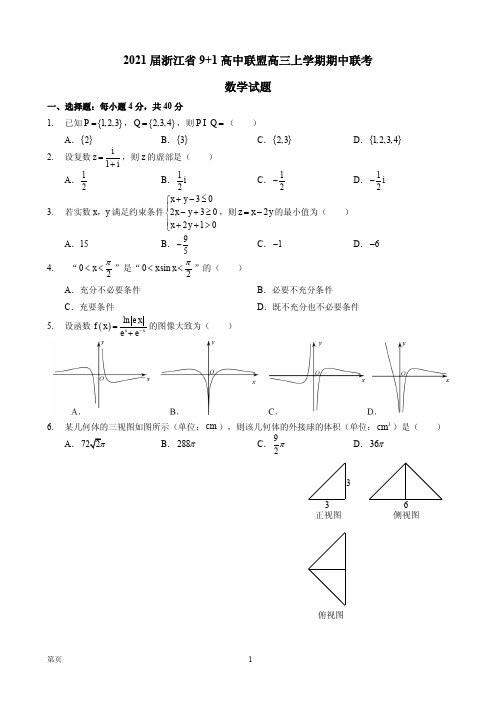
A. 70 10
B. 35 5
C. 35 10
二、填空题:单空题每题 4 分,多空题每题 6 分
11. 2 x5 的展开式中,常数项是
; x2 的系数为
D. 70 5
.
12. 已知等差数列 an 的公差为 d,前 n 项和记为 Sn ,若 S3 9 , a2 a4 8 ,则 d
,
a1
.
13. △ABC 中, cos A B cosC 3 , c2 ab ,则角 C
B.必要不充分条件
C.充要条件
5.
设函数
f
x
ln e x ex ex
的图像大致为(
)
D.既不充分也不必要条件
6. 某几何体的三视图如图所示(单位: cm ),则该几何体的外接球的体积(单位: cm3 )是( )
A. 72 2
B. 288
C. 9 2
D. 36
3
3 正视图
6 侧视图
俯视图
第页
1
7. 袋中有 5 个球,其中 3 个白球,2 个黑球,从袋中随机取球,每次取 1 个,取后放回,取 3 次.在这
3 次取球中,设取到黑球的次数为 X,则 E X ( )
A.1
B.2
C. 6 5
D. 9 5
8. 已知 m 0 ,函数 f x x2 x m ,实数 x1 , x2 满足 x1 0 , x2 0 ,若 f x1 0 , f x2 0 ,则
()
A. x1 x2 m
B. x1 x2 m
, cos Acos B
.
2
14. 已知 a 0 , b 0 , r 0 ,圆 C : x a2 y b2 r2 与 y 轴交于 A0,1 , B0,5 两点,且圆 C 与 x
2020 学年第一学期 9+1 高中联盟期中考试 数学参考答案

4 3
1 (1 2
(1 ) 2
n2)
11 (1 )n1 11
62
6
(15 分)
21.解:(I) 5 ( p) 6 p 2 2
E : y2 4x
(5 分)
(II)设 A(x1, y1), B(x2 , y2 ), N (x0 , y0 )
l1
:
y
kx 1(k y2 4x
0)
k 2 x2
以 㞠 ሺ ሺ 㞠 ၀㞠 . ② 考虑使用零点存在定理,即
㞠ሺ
x + , F (x) ,所以 ၀ ၀ ၀
ሺ,所以 ሺ . 所
၀ሺ . 当 (15 分)
另解:
由 ex1 ln x 0 得 ex1 (x 1) ln x 1 e
记 g(x) ex1 ln x+1
ex1(ln x 1 1)
(2k
4)x
1
0
x1
x2
2k k2
4,
x1 x2
1 k2
AM MB NA NB
x1x1
x2 x0
(x2
x0 )
x1 x2
x1 x2
x0 x0
x0
2 x1 x2 x1 x2
k
1
2
MN
1 k2 k2
又
l2
:
y
1 k
x
1 C (1,
1 k
1)
MC
1
1 k2
SCMN
(7 分)
(Ⅱ) Q
0
x
5 12
,0
2x
5 6
, 6
2x
6
,所以
f
(
x)
浙江省A9协作体2020-2021学年高一上学期期中联考数学试题 Word版含答案

浙江省A9协作体2020学年第一学期期中联考高一数学试题考生须知:1.本卷满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;3.所有答案必须写在答题卷上,写在试卷上无效; 4.考试结束后,只需上交答题卷。
选择题部分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,3,4,5,8}A =,{2,3,5,6,8}B =,若{|C x x A =∈且x B ∉},则集合C = A .{1,2,4,6} B .{3,5,8}C .{1,4}D .{2,6}2.“1x ≥”是“11≤x”的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知(21)1f x x +=-,则(0)f = A .0B .12C .1D .324.命题:p m R ∀∈,一元二次方程210x mx ++=有实根,则 A .:p m R ⌝∀∈,一元二次方程210x mx ++=没有实根 B .:p m R ⌝∃∈,一元二次方程210x mx ++=没有实根 C .:p m R ⌝∃∈,一元二次方程210x mx ++=有实根 D .:p m R ⌝∀∈,一元二次方程210x mx ++=有实根 5.下列函数中是奇函数且在区间(0,)+∞上单调递减的是 A .()||f x x =-B .()f x x=C .3()f x x =D .21()x f x x-=6.函数2145y x x =+-的单调递增区间是A .(,5)-∞-B .(,2)-∞-C .(2,)-+∞D .(1,)+∞7.已知正实数a y x ,,满足axy y x =+2,若y x 2+的最小值为3,则实数a 的值为 A .1B .3C .6D .98.已知()f x 是定义在R 上的奇函数,若12,x x R ∀∈,且12x x ≠,都有1212()(()())0x x f x f x -->成立,则不等式2(1)(2)0x f x x -->的解集是 A .(,1)(1,2)-∞B .(0,1)(1,)+∞C .(,0)(1,2)-∞D .(0,1)(2,)+∞9.已知函数22,()11,x x x af x x a x⎧--≤⎪=⎨->⎪⎩,若函数图像与x 轴有且仅有一个交点,则实数a 的取值范围是A .(,1)-∞-B .(,1)[1,2)-∞-C .[1,2)D .(1,1](2,)-+∞10.已知“函数()y f x =的图像关于点(,)P a b 成中心对称图形”的充要条件为“函数()y f x a b =+-是奇函数”,现有函数:①1224x y x -=-;②1(2)|2|2y x x x =--+;③3(2)1y x x =+--;④2332x x y x -+=-,则其中有相同对称中心的一组是A .①和③B .①和④C .②和③D .②和④非选择题部分二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.已知集合},,2{2x x A =,则A 的子集有 ▲ 个;若A ∈1,则=x ▲ . 12.幂函数254()()mm f x x m Z -+=∈为偶函数且在区间(0,)+∞上单调递减,则m = ▲ ,1()2f = ▲ . 13.已知函数222,0()2,0x x x f x x x x ⎧+<⎪=⎨-+≥⎪⎩,则函数()f x 是 ▲ 函数(填奇偶性);若(())((3))f f a f f <-,则实数a 的取值范围为 ▲ .14.已知,a b 为正实数,若2ab =,则2a b +的最小值为 ▲ ;若23ab a b =-+,则2a b+的最小值为 ▲ .15.函数22153)(x x x f -+-=的值域为 ▲ .16.函数kx x g x x f =-=)(,|1|1)(,若方程()()f x g x =有3个不等的实数根,则实数k 的取值范围为▲ .17.设函数()f x 的定义域和值域分别为D 和M ,记(){()|,,}f A f x x A A D A =∈⊆≠∅,1(){|(),,}f A x f x A A M A -=∈⊆≠∅,现有等式:①1212()()()f A A f A f A =; ②1212()()()f A A f A f A =;③1111212()()()f A A f A f A ---=;④1111212()()()f A A f A f A ---=,则其中正确的等式序号有 ▲ .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)已知集合})4)(2(|{x x y x A -+==,}11|{+<<-=m x x B . (1)若4=m ,求B A ,()R A B ;(2)若A B ⊆,求实数m 的取值范围.19.(本题满分15分)已知函数2()2f x ax x a =--,其中0>a . (1)若函数()f x 在区间)3,1(上单调,求实数a 的取值范围;(2)若方程()0f x =在区间)3,(-∞上有两个不等的实根,求实数a 的取值范围.20.(本题满分15分)已知函数4()f x x x =-,⎩⎨⎧<--≥=1,121),()(x x x x f x g .(1)用定义法证明函数()f x 在区间[1,)+∞上单调递增; (2)若()(1)g a g a <+,求实数a 的取值范围.21.(本题满分15分)设函数2288()||||()f x x x ax a R x x=++-+∈. (1)若函数()f x 为偶函数,求实数a 的值;(2)若关于x 的不等式()16f x x ≤-在区间(0,)+∞上有解,求实数a 的取值范围.22.(本题满分15分)已知函数2()f x ax bx c =++(0,,)a b c R >∈满足1)1()0(==af f . (1)求()f x 的表达式及其单调区间(不出现,b c );(2)设对任意12,[1,3]x x ∈,12()()8f x f x -≤恒成立,求实数a 的取值范围.浙江省A9协作体2020学年第一学期期中联考高一数学参考答案一、选择题:本大题共10小题,每小题4分,共40分. 题号 1 2 3 4 5 6 7 8 9 10 答案CADBDABCBD二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.8;1- 12.32或=m ;4 13.奇;3-<a 14.4,22 15.]3,1[- 16.4>k17.①③ 18.解:(1)]5,1[],4,2[-=-=B A ,则]5,2[-=B A ,()(4,5]R A B =; 7分(2)①当C =∅时,即2m ≤-时,A B ⊆成立;②当C ≠∅时,即2m >-时,11423m m -<+≤⇒-<≤;综上,3m ≤. 14分19.解: (1)321≥a 或121≤a 21610≥≤<⇒a a 或; 7分 (2)因为2180a ∆=+>,所以73037)3(321>⇒⎪⎩⎪⎨⎧>-=<a a f a15分20.解:(1)证明略. 7分(2)因为⎪⎩⎪⎨⎧<--≥-=1,121,4)(x x x xx x g ,在)1,(-∞上单调递减,在),1(+∞上单调递增; ①当0≤a 时,必有()(1)g a g a >+,所以不合题意;②当10<<a 时,131025314112)1()(2<<⇒>-+⇒+-+<--⇒+<a a a a a a a g a g ; ③当1≥a 时,()(1)g a g a <+恒成立.综上,实数a 的取值范围为),31(+∞. 15分21.解:(1)因为()f x 为偶函数(1)(1)16160f f a a a ⇒-=⇒-=+⇒=; 6分(2)①当2x >时,216()1621621f x x x ax x a x x≤-⇔+≤-⇔≤--+有解有解, 所以max 16(21)182a x x≤--+=-; ②当02x <≤时,2161616()16161f x x ax x a x x x≤-⇔+≤-⇔≤--+有解有解, 所以max 21616(1)11a x x≤--+=-; 综上,实数a 的取值范围是182a ≤-. 15分22.解:(1)由1)1()0(==af f 得1)()1)(0(1)(2+-=⇒--=-x ax x f ax x a x f --------------------------------------3分因为0>a ,所以()f x 单调递减区间为)21,(a-∞,()f x 单调递增区间为),21(+∞a ----6分(2)“对任意12,[1,3]x x ∈,12()()8f x f x -≤恒成立”max min ()()8f x f x ⇔-≤.-------------------------------------------------------------------7分 由(1)知1)(2+-=x ax x f①1,[1,3]2a x ≥∈时,()f x 单调递增max min 515()()(3)(1)828424f x f x f f a a a -=-=-≤⇒≤⇒≤≤-----------9分 ②10,[1,3]6a x <≤∈时,()f x 单调递减max min 31()()(1)(3)288046f x f x f f a a a -=-=-≤⇒≥-⇒<≤--------11分③111,[1,]622a xa<<∈时,()f x单调递减;1[,3]2xa∈()f x单调递增max()f x=max{(1),(3)}f f,min11()()24f x fa a==-112(1)()1824311(3)()932824f f aa af f aa a⎧-=-+≤≤⎪⎪⎨⎪-=-+≤≤⎪⎩max min()()8f x f x⇒-≤恒成立11(,)62a⇒∈------14分综上所述:5(0,]4a∈为所求. ---------------------------------------------------------------15分。
浙江省A9协作体2020-2021学年高一上学期期中联考数学试题

9.B
【分析】
讨论 的范围,分别确定 、 上与 轴的交点情况,即可确定实数 的取值范围.
【详解】
∵当 时, ,
∴当 时, 在 与x轴有2个交点;
当 时, 在 与x轴有1个交点;
当 时, 在 与x轴无交点;
∵当 时, ,与x轴有交点时交点为 ,
【详解】
由题意知:有 ,则 当且仅当 时等号成立;
当 ,则有 ,
∴ 当且仅当 时等号成立;
故答案为:4, .
【点睛】
易错点睛:利用基本不等式求最值时,必须满足的三个条件--“一正二定三相等”:
(1)“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
17.设函数 的定义域和值域分别为 和 ,记 , ,现有等式:① ;② ;③ ;④ ,则其中正确的等式序号有________.
四、解答题
18.已知集合 , .
(1)若 ,求 , ;
(2)若 ,求实数 的取值范围.
19.已知函数 ,其中 .
(1)若函数 在区间 上单调,求实数 的取值范围;
(2)若方程 在区间 上有两个不等的实根,求实数 的取值范围.
6.函数 的单调递增区间是()
A. B. C. D.
7.已知正实数 , , 满足 ,若 的最小值为3,则实数 的值为()
A.1B.3C.6D.9
8.已知 是定义在 上的奇函数,若 ,且 ,都有 成立,则不等式 的解集是()
A. B.
C. D.
9.已知函数 ,若函数图象与 轴有且仅有一个交点,则实数 的取值范围是()
2020-2021学年浙江省9+1高中联盟高三(上)期中数学试卷
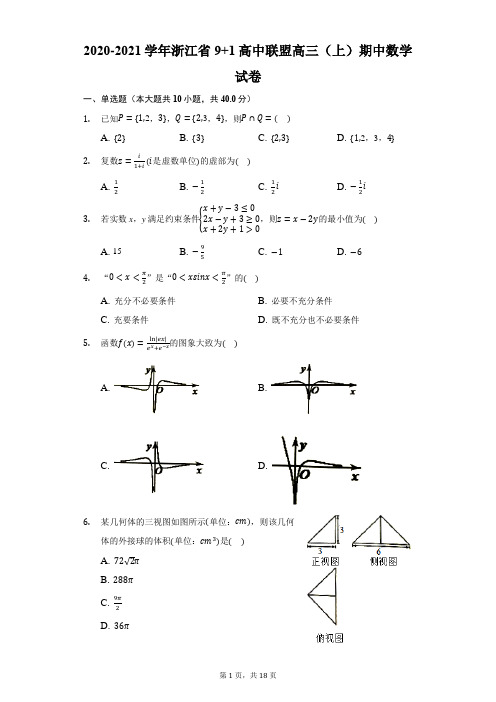
2020-2021学年浙江省9+1高中联盟高三(上)期中数学试卷一、单选题(本大题共10小题,共40.0分)1.已知P={1,2,3},Q={2,3,4},则P∩Q=()A. {2}B. {3}C. {2,3}D. {1,2,3,4}2.复数z=i1+i(i是虚数单位)的虚部为()A. 12B. −12C. 12i D. −12i3.若实数x,y满足约束条件{x+y−3≤02x−y+3≥0x+2y+1>0,则z=x−2y的最小值为()A. 15B. −95C. −1D. −64.“0<x<π2”是“0<xsinx<π2”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.函数f(x)=ln|ex|e x+e−x的图象大致为()A. B.C. D.6.某几何体的三视图如图所示(单位:cm),则该几何体的外接球的体积(单位:cm3)是()A. 72√2πB. 288πC. 9π2D. 36π7. 袋中有5个球,其中3个白球,2个黑球,从袋中随机取球,每次取1个,取后放回,取3次,在这3次取球中,设取到黑球的次数为X ,则E(X)=( )A. 1B. 2C. 65D. 958. 已知m >0,函数f(x)=x 2+x −m ,实数x 1,x 2满足x 1>0,x 2>0,若f(x 1)=0,f(√x 2)=0,则( )A. x 1+x 2<mB. x 1+x 2=mC. x 1+x 2>mD. x 1+x 2与m 的大小关系不能确定9. 已知a ,b ,c ∈[0,1],则a 2b +2b 2c −3c 2a 的最大值为( )A. 43B. 2C. 3D. 8310. 在正四棱锥P −ABCD 中,PA =PB =PC =PD =AB =1,点Q ,R 分别在棱AB ,PC 上运动,当|QR|达到最小值时,|PQ||CQ|的值为( )A. √7010B. √355C. √3510D. √705二、单空题(本大题共7小题,共36.0分)11. (2+x)5的展开式中,常数项是______ ,x 2的系数为______ .12. 已知等差数列{a n }的公差为d ,前n 项和记为S n ,若S 3=9,a 2+a 4=8,则d =______ ,a 1= ______ .13. △ABC 中,cos(A −B)+cosC =32,c 2=ab ,则角C = ______ ,cosAcosB = ______ . 14. 已知a >0,b >0,r >0,圆C :(x −a)2+(y −b)2=r 2与y 轴交于A(0,1),B(0,5)两点,且圆C 与x 轴相切,则a = ______ ,r = ______ . 15. 若椭圆x 2a 2+y 2b 2=1(a >b >0)与双曲线x 2a 12−y 2b 12=1(a 1>0,b 1>0)有相同的焦点F 1,F 2,点P 是两条曲线的一个交点,∠F 1PF 2=π2,椭圆的离心率为e 1,双曲线的离心率为e 2,e 1e 2=2,则e 12+e 22= ______ .16. 已知函数f(x)={x 2+2x +2,x ≤0x +4x,x >0,若关于x 的不等式f(x)≥|ax +1|在R 上恒成立,则实数a 的取值范围是______ .17. 平面向量a ⃗ ,b ⃗ ,c ⃗ ,满足|a ⃗ |=|b ⃗ |≠0,若a ⃗ ⊥b ⃗ ,|c⃗ |=2√2,|c ⃗ −a ⃗ |=1,则|a ⃗ +b ⃗ −c ⃗ |的最大值是______ .三、解答题(本大题共5小题,共74.0分)18. 已知函数f(x)=√34sin2x +14cos2x .(1)求f(x)的最小正周期;(2)求f(x)在区间[0,5π12]上的值域.19.如图,四棱台ABCD−A1B1C1D1,中,底面ABCD为矩形,A1A⊥平面ABCD,A1A=A1D1=1,AB=AD=2.(1)证明:B1B//面ACD1;(2)求直线C1C与平面ACD1所成角的正弦值.20.已知数列{a n},{b n}满足a2+a3=12,b1=1,a n+1a n=2,b n+1−b n=a n,n∈N+.(1)求数列{b n}的通项公式;(2)求证:1b1+1b2+⋯+1b n<116,n∈N+.21. 设抛物线E :y 2=2px 上一点P(5,y 0)到焦点的距离等于6,过M(0,−1)作两条互相垂直的直线l 1和l 2,其中l 1的斜率为k(k >0),且l 1与抛物线交于不同的两点A ,B ,l 2与抛物线的准线交于点C ,若AM ⃗⃗⃗⃗⃗⃗ =λMB ⃗⃗⃗⃗⃗⃗ ,点N 满足NA ⃗⃗⃗⃗⃗⃗ =λNB ⃗⃗⃗⃗⃗⃗ . (1)求抛物线E 的方程; (2)求△CMN 的面积的取值范围.22. 已知函数f(x)=e x−1+λlnx(λ∈R).(1)若λ=1,对于给定的点P(0,t),过点P 恰有两条直线与曲线y =f(x)相切,求实数t 的取值范围;(2)①若函数F(x)=f(x)+λ有两个零点x 1,x 2(0<x 1<x 2),求实数λ的取值范围; ②求证:1e <x 1<1<x 2.答案和解析1.【答案】C【解析】解:∵P ={1,2,3},Q ={2,3,4}, 则P ∩Q ={2,3}, 故选:C .根据集合的交集的定义计算即可.本题考查了集合的交集的运算,是一道基础题.2.【答案】A【解析】解:∵z =i1+i =i(1−i)(1+i)(1−i)=12+12i , ∴z 的虚部为12. 故选:A .直接利用复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.【答案】D【解析】解:由约束条件{x +y −3≤02x −y +3≥0x +2y +1>0作出可行域如图,A(0,3),化目标函数z =x −2y 为y =12x −z2,由图可知,当直线y =12x −z2过A 时, 直线在y 轴上的截距最大,z 有最小值为−6.故选:D.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.本题考查简单的线性规划,考查数形结合的解题思想,是中档题.4.【答案】A【解析】解:0<x<π2时,y=xsinx在(0,π2)递增,故0<xsinx<π2,是充分条件,若“0<xsinx<π2”,推不出0<x<π2,比如:x∈(−π2,0)时,也满足“0<xsinx<π2”,故“0<x<π2”是“0<xsinx<π2”的充分不必要条件,故选:A.根据充分必要条件的定义以及三角函数的性质判断即可.本题考查了充分必要条件,考查三角函数的性质,是一道基础题.5.【答案】B【解析】解:函数的定义为{x|x≠0},f(−x)=ln|ex|e−x+e x=f(x),则函数f(x)为偶函数,其图象关于y轴对称,故排除ACD,故选:B.根据定义可判断函数为偶函数,问题得以解决.本题考查了函数图象的识别,关键掌握函数的奇偶性,属于基础题.6.【答案】D【解析】解:由几何体的三视图知,该几何体是三棱锥P−ABC,底面为等腰△ABC,且侧面PAB⊥底面ABC,如图所示;D为AB的中点,又DA=DB=DC=DP=3,且PD⊥平面ABC,∴三棱锥P−ABC的外接球的球心O在PD上,设OP=R,则OA=R,OD=3−R,∴R2=(3−R)2+32,解得R=3,∴该几何体外接球的表面积是43πR3=36πcm3.故选:D.由三视图知该几何体是底面为等腰直角三角形,且侧面垂直于底面的三棱锥,由题意画出图形,结合图形求出外接球的半径,再计算外接球的表面积.本题考查了利用三视图求几何体外接球的表面积应用问题,是中档题.7.【答案】C【解析】解:袋中有5个球,其中3个白球,2个黑球,从袋中随机取球,每次取1个,取后放回,每次取到黑球的概率都是P=25,取3次,在这3次取球中,设取到黑球的次数为X,则X~B(3,25),∴E(X)=3×25=65.故选:C.每次取到黑球的概率都是P=25,取3次,在这3次取球中,设取到黑球的次数为X,则X~B(3,25),由此能求出E(X).本题考查离散型随机变量的数学期望的求法,考查二项分布的性质等基础知识,考查运算求解能力,是基础题.8.【答案】B【解析】解:∵m>0,函数f(x)=x2+x−m,故函数在(0,+∞)上单调递增,∵实数x1,x2满足x1>0,x2>0,且f(x1)=0,f(√x2)=0,∴x12+x1−m=0,∴x1=√x2⇒x12=x2,∴x1+x2=x12+x1,∴x1+x2=m成立,故选:B.根据已知条件求得x12+x1−m=0以及x12=x2,进而求得结论.本题考查了方程的根与函数的零点之间的关系,考查转化思想,属于中档题.9.【答案】B【解析】解:要想a2b+2b2c−3c2a取最大值,则只需a2b+2b2c取最大值,3c2a取最小值为0,已知a,b,c∈[0,1],所以a和c中有几个为0,由于a2b+2b2c最大,最大值为1,所以b,c,a中有的为1,且仅b为1,①假设b=c=1,a=0时,则0+1+1=2;②假设b=1,a=c=0时,则0+1+0=1;③假设a=b=1,c=0时,则1+0−0=1;故最大值为2.故选:B.直接利用不等式的性质和假设法的应用求出结果.本题考查的知识要点:不等式的性质,假设法的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题.10.【答案】A【解析】解:以P在底面的射影为坐标原点O,作平行于AB,平行于BC的直线为x轴和y轴,以OP为z轴建立空间直角坐标系,因为PA=PB=PC=PD=AB=1,设Q(a,12,0),R(m,n,q), 因为C(12,−12,0),P(0,0,√22),所以PC⃗⃗⃗⃗⃗ =(12,−12,−√22), 又R 在PC 上,所以PR ⃗⃗⃗⃗⃗ =λPC⃗⃗⃗⃗⃗ ,即(m,n,q −√22)=(12λ,−12λ,−√22λ), 所以R(12λ,−12λ,−√22λ), 即QR 2=(a −12λ)2+(12+12λ)2+(−√22λ+√22)2=a 2+λ2−aλ−12λ+34,因为a ∈[−12,12],λ∈[0,1],则(QR 2)′a =2a −λ=0,(QR 2)′λ=2λ−a −12=0, 所以λ=13,a =16时取得最小值, 所以Q(16,12,0),则PQ ⃗⃗⃗⃗⃗ =(16,12,−√22),CQ ⃗⃗⃗⃗⃗ =(−13,1,0),所以PQCQ =(16)+(12)+(−√22)√(−13)2+12=√7010. 故选:A .建立合适的空间直角坐标系,设Q(a,12,0),R(m,n,q),利用PR ⃗⃗⃗⃗⃗ =λPC ⃗⃗⃗⃗⃗ ,求得点R 的坐标,再表示出QR 2的表达式,求出最小值时对应的λ和a 的值,从而得到Q 的坐标,求出PQ ⃗⃗⃗⃗⃗ ,CQ ⃗⃗⃗⃗⃗ 的坐标,求出对应的模的比值即可得到答案.本题考查了多面体和旋转体表面上的最短距离问题,解决此类问题的方法是:折线或曲线的最值问题,通常沿着多面体的棱或旋转体的母线展开成平面图形或曲面,结合平面图形求解.11.【答案】32 80【解析】解:易知(2+x)5的通项为T k+1=25−k ⋅C 5k⋅x k .令k =0,得常数项为T 1=25=32,令k =2,得x 2的系数为23C 52=80.故答案为:32,80.求出展开式的通项,然后分别令x 的指数为0,2,即可求出k 的值,进而求出结果. 本题考查二项式定理,通项法研究展开式中的特定项的方法.属于基础题.12.【答案】1 2【解析】解:等差数列{a n }的公差为d ,前n 项和记为S n ,S 3=9,a 2+a 4=8, ∴{3a 1+3×22d =9a 1+d +a 1+3d =8,解得a 1=2,d =1. 故答案为:1,2.利用等比数列的前n 项和公式和通项公式列出方程组,能求出结果.本题考查等比数列的公差和首项的求法,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.13.【答案】π3 14【解析】解:因为cos(A −B)+cosC =cos(A −B)−cos(A +B)=32, 所以cosAcosB +sinAsinB −cosAcosB +sinAsinB =32, 所以2sinAsinB =32,即sinAsinB =34, 因为c 2=ab ,所以sin 2C =sinAsinB =34,可得sinC =√32,因为C ∈(0,π),且c 不是三角形最大边, 所以C =π3,因为cosC =−cos(A +B)=−cosAcosB +sinAsinB =−cosAcosB +34=12, 所以解得cosAcosB =14. 故答案为:π3,14.利用诱导公式,两角和的余弦公式化简已知等式可得sinAsinB =34,利用正弦定理化简c 2=ab ,可得sinC =√32,结合C ∈(0,π),且c 不是三角形最大边,可求C 的值,进而根据两角和的余弦公式即可求解cos A cos B 的值.本题主要考查了诱导公式,两角和的余弦公式,正弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.14.【答案】√5 3【解析】解:圆C:(x−a)2+(y−b)2=r2与的圆心C(a,b),半径为r,由题意可得a2+(1−b)2=r2,a2+(5−b)2=r2,b=r,解得a=√5,b=3,r=3,故答案为:√5,3.求得圆的圆心和半径,分别代入A,B的坐标,以及圆心到x轴的距离为半径,可得a,b,r的方程,解方程可得圆的方程.本题考查圆的方程的求法,考查方程思想和运算能力,属于基础题.15.【答案】8【解析】解:设焦点为(−c,0),(c,0),可得a2−b2=a12+b12=c2,设P为第一象限的点,|PF1|=m,|PF2|=n,由椭圆的定义可得m+n=2a,由双曲线的定义可得m−n=2a1,解得m=a+a1,n=a−a1,由∠F1PF2=π2,可得m2+n2=4c2,即(a+a1)2+(a−a1)2=4c2,化为a2+a12=2c2,可得a2c2+a12c2=2,即有1e12+1e22=2,又e1e2=2,可得则e12+e22=2(e1e2)2=8,故答案为:8.设焦点为(−c,0),(c,0),P为第一象限的点,|PF1|=m,|PF2|=n,运用椭圆和双曲线的定义,解得m,n,再由勾股定理,可得e1,e2的关系,结合条件e1e2=2,可得所求和.本题考查椭圆和双曲线的定义、方程和性质,以及勾股定理的运用,考查方程思想和运算能力,属于中档题.16.【答案】[0,1516]【解析】解:当x>0时,f(x)≥|ax+1|在R上恒成立,即为|ax+1|≤x+4x,也即−x−4x ≤ax+1≤x+4x,可得−1−1x −4x2≤a≤1−1x+4x2,由y=1−1x +4x2=4(1x−18)2+1516≥1516,可得a≤1516,由y=−1−1x −4x2=−4(1x+18)2−1516<−1516,可得a≥−1516,则−1516≤a≤1516;当x=0时,f(0)=2>|a⋅0+1|恒成立;当x<0时,−(x2+2x+2)≤ax+1≤x2+2x+2,即x+1x +2≤a≤−x−3x−2恒成立,由y=−x−3x −2≥2√−x⋅3−x−2=2√3−2,当且仅当x=−√3时,取得等号,可得a≤2√3−2;由y=x+1x+2≤−2+2=0,当且仅当x=−1取得等号,可得a≥0,则0≤a≤2√3−2,综上可得,a的取值范围是[0,1516].故答案为:[0,1516].运用参数分离和二次函数的性质和不等式的性质,讨论x=0,x>0,x<0时,不等式恒成立时,a的取值范围,求并集可得所求范围.本题考查不等式恒成立问题解法,以及分段函数的运用,考查分类讨论思想和运算能力、推理能力,属于中档题.17.【答案】√7+1【解析】解:a⃗+b⃗ −c⃗=b⃗ −(c⃗−a⃗ ),设n⃗=b⃗ −(c⃗−a⃗ ),当|n⃗|最大时,b⃗ 与(c⃗−a⃗ )反向,∵a⃗⊥b⃗ ,∴a⃗⊥(c⃗−a⃗ ),∴|a⃗|=√(2√2)2−1=√7,故|n⃗|的最大值是:√7+1,即|a⃗+b⃗ −c⃗|的最大值是:√7+1,故答案为:√7+1.根据向量的运算性质求出模的最值即可.本题考查了向量的运算性质,考查了转化思想,是一道中档题.18.【答案】解:(1)因为f(x)=√34sin2x+14cos2x=12(√32sin2x+12cos2x)=12sin(2x+π6),所以f(x)的最小正周期T=2π2=π.(2)因为0≤x≤5π12,所以0≤2x≤5π6,所以π6≤2x+π6≤π,所以f(x)在区间[0,5π12]上的值域为[0,12].【解析】(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=12sin(2x+π6),利用正弦函数的周期公式即可求解.(2)由已知可求范围π6≤2x+π6≤π,利用正弦函数的性质即可求解.本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质的应用,考查了转化思想和函数思想的应用,属于基础题.19.【答案】(1)证明:由题意,延长AA1,BB1,CC1,DD1可交于一点,记为P,连接BD与AC交于O,连接OD1,∵A1D1=1,AD=2,∴D1是PD中点,又O是BD中点,∴PB//D1O,∵PB⊄平面ACD1,D1O⊂平面ACD1,∴PB//平面ACD1,∴B1B//平面ACD1.(2)解:如图建立空间直角坐标系,P(0,0,2),C(2,2,0),∴C 1(1,1,1),∴C 1C ⃗⃗⃗⃗⃗⃗⃗ =(1,1,−1)AC ⃗⃗⃗⃗⃗ =(2,2,0),D(0,2,0), ∴D 1(0,1,1),∴AD 1⃗⃗⃗⃗⃗⃗⃗ =(0,1,1),设n⃗ =(x,y,z)为平面ACD 1的一个法向量, 则{n ⃗ ⋅AC⃗⃗⃗⃗⃗ =0n ⃗ ⋅AD 1⃗⃗⃗⃗⃗⃗⃗ =0,∴{2x +2y =0y +z =0,可取n⃗ =(1,−1,1), 又C 1C ⃗⃗⃗⃗⃗⃗⃗ =(1,1,−1),设直线C 1C 与ACD 1平面所成角为θ,则sinθ=|cos〈C 1C ⃗⃗⃗⃗⃗⃗⃗ ,n ⃗ 〉|=√3√3=13. ∴直线C 1C 与平面ACD 1所成角的正弦值为13.【解析】(1)延长AA 1,BB 1,CC 1,DD 1可交于一点,记为P ,连接BD 与AC 交于O ,连接OD 1,推导出PB//D 1O ,从而PB//平面ACD 1,由此能证明B 1B//平面ACD 1. (2)建立空间直角坐标系,利用向量法能求出直线C 1C 与平面ACD 1所成角的正弦值. 本题考查线面平行的证明,考查线面角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.20.【答案】解:(1)∵a n+1a n=2,所以数列{a n }为等比数列,公比q =2,a 1q +a 1q 2=12, 所以a 1=2,∴a n =2n , 所以b n −b n−1=2n−1, …,b 2−b 1=21, 利用叠加法:b n −b 1=2+22+⃯+2n−1=2n −2 ∴b n =2n −1(2)证明:由(1)得:1b 1+1b 2+⋯+1b n=1+122−1+⋯+12n −1<1+13+122+⋯+12n−1=43+12(1−(12)n−2)=116−(12)n−1<116.【解析】(1)直接利用已知条件和等比数列的应用和叠加法的应用求出结果. (2)利用(1)的结论和放缩法的应用求出结果.本题考查的知识要点:数列的通项公式的求法及应用,放缩法的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.21.【答案】解:(1)根据题意可得5−(−p2)=6,解得p =2,所以抛物线的方程为y 2=4x . (2)设A(x 1,y 1),B(x 2,y 2),N(x 0,y 0) 根据题意可得直线l 1方程为:y =kx −1, 直线l 2方程为:y =−1k x −1,联立直线l 1与抛物线的方程得{y =kx −1y 2=4x ,消掉y 得k 2x 2−(2k +4)x +1=0, 所以x 1+x 2=2k+4k 2,x 1x 2=1k 2,因为{AM ⃗⃗⃗⃗⃗⃗ =λMB ⃗⃗⃗⃗⃗⃗ NA⃗⃗⃗⃗⃗⃗ =λNB ⃗⃗⃗⃗⃗⃗ ,所以{−x 1=λx 2x 1−x 0=λ(x 2−x 0),即λ=−x 1x 2=x 1−x 0x 2−x 0,所以x 0=2x 1x 2x1+x 2=1k+2,所以|MN|=√(x 0−0)2+(y 0+1)2=√x 02+(kx 0−1+1)2=√(1+k 2)|x 0|=√1+k 2k+2, 因为直线l 2方程为:y =−1k x −1, 所以C(−1,1k −1),所以|MC|=√(−1−0)2+(1k −1+1)2=√1+1k 2,所以S △CMN =12|MN||MC|=12√1+k 2k+2√1+1k 2=1+k 22k(k+2)(k >0),f(k)=1+k 2k(k+2)(k >0). 则f′(k)=2k 2−2k−2(k 2+2k)2(k >0),令f′(k)=0,解得k =1±√52,所以f(k)在(0,1+√52)单调递减,在(1+√52,+∞)上单调递增.所以f(k)min =f(1+√52)=√5−12, 所以S △CMN ∈[√5−12,+∞).【解析】(1)由抛物线的定义可得5−(−p2)=6,解得p ,进而可得抛物线的方程. (2)设A(x 1,y 1),B(x 2,y 2),N(x 0,y 0)分别写出直线l 1,l 2方程,联立直线l 1与抛物线的方程消掉y 得关于x 的一元二次方程,结合韦达定理可得x 1+x 2,x 1x 2,由{AM ⃗⃗⃗⃗⃗⃗ =λMB ⃗⃗⃗⃗⃗⃗NA ⃗⃗⃗⃗⃗⃗ =λNB ⃗⃗⃗⃗⃗⃗ ,推出λ=−x 1x 2=x 1−x 0x 2−x 0,即x 0=2x 1x 2x 1+x 2=1k+2,由两点之间的距离公式可得|MN|=√1+k 2k+2,|MC|=√1+1k 2,推出S △CMN =1+k 22k(k+2)(k >0),f(k)=1+k 2k(k+2)(k >0),求导,分析单调性,进而得出取值范围.本题考查直线与抛物线相交问题,解题需要一定运算能力,属于中档题.22.【答案】解(1)当λ=1时,f(x)=e x−1+lnx(x >0),f′(x)=e x−1+1x设切点坐标为Q(x 0,f(x 0)),则曲线过Q 的切线方程为:y =f′(x 0)(x −x 0)+f(x 0)=(e x 0−1+1x 0)(x −x 0)+e x 0−1+lnx 0,由切线经过点P 可得t =(1−x 0)e x 0−1+lnx 0−1,令g(x)=(1−x)e x−1+lnx −1,则g′(x)=−xe x−1+1x g″(x)=−(1+x)e x−1−1x 2<0, 注意到g′(1)=0,且g′(x)在x >0上单调递减, 所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,故g(x)≤g(1)=−1,而当x →0+,g(x)→−∞,当x →+∞,g(x)→−∞, 故若t =g(x)有两个实根,则t 的取值范围是t <−1; (2)①F(x)=f(x)+λ=e x−1+λlnx +λ,F′(x)=e x−1+λx ,当λ≥0时,F′(x)>0,故F (x)在x >0上单调递增,不可能有两个零点, 当λ<0时,令F′(x 0)=0,则e x 0−1+λx 0=0,即λ=−x 0e x 0−1,此时F′(x)=e x−1−x 0xe x 0−1=xe x−1−x 0e x 0−1x所以当0<x <x 0时,F′(x)<0,F(x)单调递减, 当x >x 0时,F′(x)>0,F(x)单调递增,又当x →0+,F(x)→+∞,当x →+∞,F(x)→+∞, 所以要使F(x)在x >0上有两个零点,则F(x 0)<0,即0>F(x 0)=e x 0−1+λlnx 0+λ=−λx 0+λlnx 0+λ=λ(lnx 0−1x 0+1),所以lnx 0−1x 0+1>0,令ℎ(x)=lnx −1x +1,注意到ℎ(x)在(0,+∞)上单调递增,且ℎ(1)=0,所以x 0>1, 所以λ=−x 0e x 0−1<−1.②证明:考虑使用零点存在定理,即F(1e )=e 1e −1>0,F(1)=1+λ<0,当x →+∞,F(x)→+∞,所以1e <x 1<1<x 2, 另解:由e x−1+λlnx +λ=0得−λ=e x−1lnx+1(x ≠1e ), 记g(x)=e x−1lnx+1,g′(x)=e x−1(lnx−1x+1)(lnx+1)2,当x ∈(0,1)且x ≠1e 时g′(x)<0,当x >1时g′(x)>0, 画出g(x)的大致图象,如图示,有两个零点的条件是: −λ>1⇒λ<−1,1e<x 1<1<x 2.【解析】(1)由导数的几何意义可得切线的斜率f′(x 0),进而可得过点Q 的切线方程,再代入点P 可t =(1−x 0)e x 0−1+lnx 0−1,根据题意可得该方程有两个根,令g(x)=(1−x)e x−1+lnx −1,求导分析g(x)的单调性,值域,进而可得t 的取值范围;(2)①根据题意可得F(x)=e x−1+λlnx +λ,求导得F′(x)=e x−1+λx ,分两种情况当λ≥0时,当λ<0时,F′(x)的正负,F(x)的增减性,及值域,使得F(x)有两个零点,进而可得λ的取值范围.②由零点存在定理,得F(1e )>0,F(1)<0,当x →+∞,F(x)→+∞,进而可得1e <x 1<1<x 2.另解:由e x−1+λlnx +λ=0得−λ=e x−1lnx+1(x ≠1e ),记g(x)=e x−1lnx+1,求导,分析g(x)的单调性,作出g(x)的草图,若有两个零点的条件是:λ<−1,即可得出结论1e <x 1<1<x 2.本题考查导数的几何意义,函数的零点,解题中注意分类讨论思想的应用,属于中档题.。
