试题第3和4页

合集下载

2024届福建省泉州市普通高中毕业班质量监测三模语文试题答案

泉州市2024 届普通高中毕业班质量监测（三）语文参考答案2024.03一、现代文阅读（35 分）（一）现代文阅读Ⅰ（本题共5 小题，17 分）1 ．（3 分）A2 ．（3 分）D3 ．（3 分）B4 ．（4 分）①可夯实“夏王朝信史说”这一共同认识基础，使夏文化公共考古传播内容更具科学性。

②可唤醒公众对夏王朝的“历史记忆”，推进夏文化公共考古传播。

答对一点给2 分。

意思答对即可。

其他答案，只要言之成理，可酌情给分。

5 ．（4 分）①改变不重视公共考古的态度，提升公共考古教育的自觉性。

②加强对公众的了解、研究，提高公共考古传播的针对性。

③通过新兴媒体的传播平台，吸引更多公众参与公共考古。

答对一点给2 分，答对两点给满分。

意思答对即可。

其他答案，只要言之成理，可酌情给分。

（二）现代文阅读Ⅱ（本题共4 小题，18 分）6 ．（3 分）B7 ．（3 分）C8 ．（6 分）①由一位战友从回忆的角度来叙述，使叙事更详细；②由亲历事件的战友以第一人称叙事，使故事更真实；③在叙事中融入在场战友切身感受的描述，使故事更有感染力。

答对一点给2 分，意思答对即可。

其他答案，只要言之成理，可酌情给分。

9 ．（6 分）要点：（生活化的笔）①采用现实主义创作手法，以“替写家书”这一平凡小事为线索展开叙事；②用实录笔法写战士们的对话争论；③语言质朴自然、口语色彩鲜明。

（军营里的世态人情）①真实展现了基层官兵日常工作、生活的场景；②塑造了生活常态中朴实、真诚、高尚的军人群体形象；③具体表现了基层战士的奉献精神和军营中深厚纯朴的战友情谊、亲如一家的军民情谊。

答对一个方面给3 分，其中每个要点1 分。

意思答对即可。

其他答案，可根据观点明确、分析合理的程度，酌情给分。

二、古代诗文阅读（35 分）（一）文言文阅读（本题共4 小题，20 分）10 ．（3 分）B11 ．（3 分）C12 ．（10 分）标点：寺在山之阴，山高，月出岭背，比树头发白，夜阑矣。

江苏省盐城市东台市第一教育联盟2021-2022学年五年级上学期数学期中试卷

东台市第一教育联盟2021年秋学期期中质量调研试卷五年级数学（时间：80分钟）得分______等级______一、认真读题，细心填写（每空 1 分，共 28 分）1.一辆汽车向东行驶15千米记作—15千米，那么＋40千米表示这辆汽车向（）行驶了（）千米。

2.在括号里填上合适的数:0.42升＝（）毫升125平方厘米＝（）平方分米5千克40克＝（）千克5.4公顷＝（）平方千米3.已知234×15=3510，那么23.4×15=()，()×15=3.51，4.7.9里面有（）个1和（）个0.1，也就是有（）个0.1。

5.一个数由5个十和95个百分之一组成，这个数写作()，读作（），精确到十分位是（）。

6.某地区去年年末的统计显示：总人口1073600人，生产总值72060000000元。

改写成用“万”作单位，总人口是（）万人；省略“亿”后面的尾数，生产总值约是（）亿元。

7．一个平行四边形比与它等底等高的三角形的面积大12.6平方厘米，这个平行四边形的面积是（）平方厘米。

如果底是6厘米，那么高是（）。

8.如图所示，一个平行四边形相邻的两条边分别是12厘米和8厘米，这个平行四边形的周长是（）厘米，如果高是9厘米，它的面积是（）平方厘米。

9．一个三位小数，精确到百分位是5.70，这个三位小数最大是（），最小是（）。

10．一堆钢管，已知最上层7根，最下层有19根，相邻两层之间相差1根，这堆钢管共有（）根。

11．一个等腰三角形的周长是12厘米，其中一条边是2厘米，另两条边的长分别是（）厘米和（）厘米12.一捆电线长14.85米，电工师傅第一次用去0.75米，第二次又用去1.25米，这时这捆电线比原来短了（）米。

13.小红在计算□－（4.3＋2.6）时错误将括号看漏了，算成了□－4.3＋2.6，这样计算出来的结果比原来正确的结果（）（填“多”或“少”）（）。

8cm12cm学校班级＿＿＿＿＿姓名＿＿＿＿＿测试号＿＿＿＿＿＿＿＿………………………………装……………………………………订………………………………………线…………………………………………二、巧思妙想，明辨是非（对的打“√”，错的打“×”。

中国计量大学801自动控制原理1-2015--2019年考研初试真题

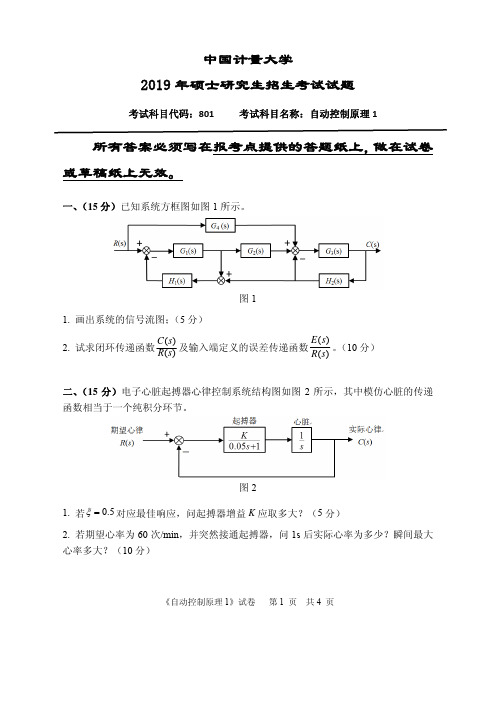
《自动控制原理1》试卷第1 页共4 页中国计量大学2019年硕士研究生招生考试试题考试科目代码：801 考试科目名称：自动控制原理1所有答案必须写在报考点提供的答题纸上，做在试卷或草稿纸上无效。

一、（15分）已知系统方框图如图1所示。

图11. 画出系统的信号流图；（5分）2. 试求闭环传递函数)()(s R s C 及输入端定义的误差传递函数)()(s R s E 。

（10分）二、（15分）电子心脏起搏器心律控制系统结构图如图2所示，其中模仿心脏的传递函数相当于一个纯积分环节。

图21. 若5.0=ξ对应最佳响应，问起搏器增益K 应取多大？（5分）2. 若期望心率为60次/min ，并突然接通起搏器，问1s 后实际心率为多少？瞬间最大心率多大？（10分）《自动控制原理1》试卷第2 页共4 页三、（15分）系统结构图如图3所示，[]()()()e t r t b t =−。

图31. 已知G 1(s )的单位阶跃响应为21e t −−，试求G 1(s )；（5分） 2. 利用求出的G 1(s )，当r (t )=10·1(t )时，试求：①系统的稳态输出；②系统的超调量、调节时间和稳态误差。

（10分）四、（15分）已知系统结构图如图4所示：图41. 绘出K *从0→+∞变化时系统的根轨迹；（8分）2. 确定系统处于欠阻尼条件下的K *范围；（4分）3. 确定系统稳定时的最小阻尼比。

（3分）五、（15分）已知系统传递函数为)52)(2()(2+++=s s s K s G ，1. 画出奈奎斯特图；（10分） 2. 当K =52，利用奈奎斯特稳定判据判断其闭环系统的稳定性。

（5分）六、（15分）已知最小相位开环系统的渐近对数幅频特性如图5所示，试求： 1. 系统的开环传递函数；（4分） 2. 截止频率c ω和相角裕量γ；（8分）3. 若使截止频率s rad c /10=ω，其放大倍数应取多少？（3分）《自动控制原理1》试卷第3 页共4 页七、（20分）已知采样系统结构如图6所示，其中采样周期s T 4.0=。

【三套试卷】【沪教版】小学二年级数学上册第一单元练习试题附答案

第一单元达标检测卷(附答案)学习内容课本第3～4页例2，第6页练习一第1～3题。

学习目标认识长度单位厘米，初步建立1厘米的长度观念。

会用刻度尺量物体的长度（限整厘米）。

课文讲解米和厘米是两个最基本的长度单位，如果孩子对这两个长度单位的实际“大小”形成了较鲜明的表象，就可以正确运用它们进行估测或实测，也容易掌握单位间的进率。

比如，孩子形成了1厘米、1米实际长度的表象，就不至于产生“1米＝10厘米”的错误，才有可能利用表象进行一些简单的估测，如估计窗的宽和高约是几米。

反过来，孩子在进行实际测量的活动中，也能进一步加深和巩固有关长度单位的观念。

为了达到这种相互促进的效果，教材采取了这样一些措施：1.通过多种活动帮助孩子建立厘米和米的长度表象。

比如，教学1厘米时，借助图钉、手指的宽度帮助孩子建立1厘米的表象。

教学1米时，伸开两臂比划1米有多长，体验1米的实际长度。

2.给孩子提供测量实际长度的机会。

如测量铅笔、身高、黑板等各种物体的长度，测量跳远的长度。

让他们认识一些不同的尺子，实际练习读取厘米尺与卷尺等尺上的数值，充实实际测量的经验并巩固长度观念。

3.培养估测意识。

教材在孩子积累了足够的实际测量经验后，给他们提供了先估测再实测的练习，让孩子比较估测与实际测量所得结果的差别，从而修正自己的估测策略。

前面教学统一长度单位的必要性时，已经引出统一的长度单位──正方体（1 立方厘米），但在日常生活中用它来量物体的长度很不方便，为了准确、方便的表示物体的长度，人们发明了带有刻度的尺子，为了便于交流，尺上的刻度作了统一规定。

由此引出厘米尺，并在尺上用不同的颜色标出1厘米的长度，说明前面正方体的一边正好是1厘米。

在此基础上，用一个图钉长度和孩子手指的宽度帮助他建立1厘米的长度观念。

例2，通过量纸条的长度，学习用尺量物体长度的方法。

辅导精要教师拿出一个正方体（1 立方厘米）说：通过昨天的学习知道，测量物体的长度，必须把标准统一起来，并且用正方体测量比较准确，但在日常生活中用它来量物体的长度很不方便，为了准确、方便的表示物体的长度，人们发明了带有刻度的尺子，为了便于交流，尺上的刻度作了统一规定。

浙江农林大学考研试题2014年-2016年902林业信息管理综合

C、森林资源规划设计调查和森林资源作业设计调查
D、全国森林资源清查和森林资源作业设计调查
考试科目：林业信息管理综合
第 2 页，共 4 页
8.森林资源一类调查通常
年进行一次
（）
A、1 年 B、3 年 C、5 年 D、不固定
9.以下描述哪一个是不正确的（）
A.系统分析员 B.程序员 C.数据库管理员 D.操作员
2. 有了模式/内模式映像，可以保证数据和应用程序之间( )。
A．逻辑独立性 B．物理独立性 C．数据一致性 D．数据安全性
3. 数据库的视图、基本表和存储文件的结构分别对应( )。
A．模式、内模式、外模式 B．外模式、模式、内模式
C．模式、外模式、内模式 D．外模式、内模式、模式
三、简答题(每题 5 分，共 50 分) 1.数据库系统由哪几个部分组成？ 2.简述森林资源一类调查。 3.林业信息化的主要内涵是什么？ 4.什么是 GIS？ 5. 请写出 OSI 参考模型的七层。 6. 请给出数据报服务与虚电路服务的 3 个差别。 7. 简要说明 ARP 协议的原理。 8. 什么是单工？什么是半双工？什么是全双工？ 9. 简述集线器、网桥、交换机、路由器等设备所在的层次和功能。 10. 简要说明网络中的一台计算机是如何判断另一个 IP 地址是否与自己同一个网络。
A．层次模型 B．网状模型
C．关系模型 D．面向对象模型
7. 有一个关系：学生(学号，姓名，性别)，规定性别的值域是男或者女，这束
B.参照完整性约束
C.用户自定义完整性约束 D.关键字完整性约束
8.所谓空值就是（）值。
A.数值 0 B.空的字符串 C.未知的值 D.任何值
考试科目：林业信息管理综合

内蒙古呼和浩特市实验中学2024-2025学年七年级上学期11月期中数学试题

内蒙古呼和浩特市实验中学2024-2025学年七年级上学期11月期中数学试题一、单选题1．下列各数中为负数的是（）A ．1B ．2020-C ．0.2D ．122．图中所画的数轴，正确的是（）A ．B ．C ．D ．3．滇池亦称昆明湖、昆明池、滇南泽、滇海，位于昆明市西山区，是云南省面积最大的高原湖泊，也是全国第六大淡水湖，有着“高原明珠”之称，滇池的蓄水量大约为1290000000立方米．数字1290000000用科学记数法可以表示为（）A ．91.2910⨯B ．81.2910⨯C ．100.12910⨯D ．101.2910⨯4．多项式222a b ab ab --的项数及次数分别是（）A ．3，3B ．3，2C ．2，3D ．2，25．下列各对数中数值相等的是（）A ．21-和()21-B ．()3--和3--C ．()32-和32-D ．332-⨯和()332-⨯6．已知a<0、b>0且│a ∣>│b ∣,则a 、b 、-a 、-b 的大小关系是()A ．b>-a>a>-bB ．-b>a>-a>bC ．a>-b>-a>bD ．-a>b>-b >a7．多项式（2x 2+ax ﹣y +4）+（﹣2bx 2+3x ﹣5y +1）的值与字母x 的取值无关，则b ﹣2a 的值是（）A ．﹣5B ．﹣4C ．﹣1D ．78．小琪在一本数学书中看到了这样一个探究活动；对依次排列的两个整式m ，n 按如下规律进行操作：第1次操作后得到整式中m ，n ，n m -；第2次操作后得到整式中m ，n ，n m -，m -；第3次操作后……其操作规则为：每次操作增加的项，都是用上一次操作得到的最末项减去其前一项的差，小强将这个活动命名为“回头差”游戏．则该“回头差”游戏第2024次操作后得到的整式串各项之和是（）A ．2n m-B ．mC ．n m-D ．m n+二、填空题9．如果某超市盈利9%记作“9%+”，那么“亏损8%”应记作．10．单项式272xy π-的系数是，次数是．11．下列各数中：127，-3.1416，0，58-，10%，17，••3.21-，-89，分数有个；非负整数有个．12．如果单项式43m x y 和3n x y -是同类项，则m n -=．13．在数轴上与表示3的点相距4个单位长度的点表示的数是．14．数a 、b 、c 在数轴上对应点的位置如图所示，则|a +b |+|c +b |＝．15．小强有10张写有不同的数的卡片，分别为1+，1-，8-，0，3.5-，4+，7+，9-，2-．3+从中抽取5张卡片，使得这5张卡片的积最小，请问最小的积为．16．我们知道，一个数a 的绝对值|a |即数轴上表示这个数的点到原点的距离，而|a |可以写成|a ﹣0|，推广到一般情况就是，若两个数a 、b 分别对应数轴上两个点A 、B ，则|a ﹣b |即A 、B 两点之间的距离．若x 对应数轴上任意一点P ，则|x +3|﹣|x ﹣5|的最大值是．三、解答题17．计算(1)()()()9936123726-++-+---；(2)()()2320242112126333⎛⎫⎡⎤-+---÷⨯+- ⎪⎣⎦⎝⎭18．先化简，再求值：221523243x xy xy x ⎡⎤⎛⎫--++ ⎪⎢⎥⎝⎭⎣⎦，其中x 、y 满足()21202x y ++-=．19．阅读理解小明在做作业时，遇到如下一道题目：若代数式23x x ++的值为7，则代数式2223x x +-的值为．他的做法如下：由题意，得23x x ++，则24x x +=，所以()22223232435x x x x +-=+-=⨯-=．故答案为5．【方法运用】(1)若代数式21x x ++的值为15，求代数式2223x x --+的值；(2)当2x =时，代数式34ax bx ++的值为11，当2x =-时，求代数式33ax bx ++的值；20．灵宝苹果，河南省三门峡市灵宝市特产，全国农产品地理标志．现有16箱灵宝苹果，以每箱10千克为标准，超过标准的质量记作正数，不足标准的质量记作负数，称量记录如下：与标准质量的差（单位：千克）3-2-1-01 2.5箱数142324(1)这16箱苹果中，最重的一箱比最轻的一箱重千克．(2)与标准质量相比，超过或不足多少千克？(3)若以每千克20元的价格售出，求这16箱苹果一共可以卖多少元？21．在活动课上，有三位同学各拿一张卡片，卡片上分别为A ，B ，C 三个代数式，三张卡片如图所示，其中C 的代数式是未知的．(1)若A 为二次二项式，则k 的值为___________；(2)若A B -的结果为常数，则这个常数是___________，此时k 的值为___________；(3)当1k =-时，2C A B +=，求C ．22．如图1，这是某年11月的月历表，用如图2所示的“Z”字形覆盖住月历表中的五个数，则这五个数从小到大依次为A ，B ，C ，D ，E ．这五个数的和能被5整除吗?为什么?(1)甲同学设A x =，请通过计算得出结论．(2)乙同学说自己设C x =更简单，请你也来试一试．(3)小明受到启发，改编了下面一道题目，请解答：代数式2346A B C D E -++-的值是否为定值若是，请求出它的值：若不是，请说明理由．23．综合性探究：“数形结合”思想解决以下问题．(1)请根据图1中A ，B 两点的位置，分别写出它们所表示的有理数：A ：；B ：；(2)观察数轴，与点A 的距离为4的点表示的数是．(3)若将数轴折叠，使得点A 与表示数2-的点原合，则点B 与表示数的点重合．(4)若数轴上M ，N 两点之间的距离为2024（点M 在点N 的左侧），且M ，N 两点经过（3）中折叠后互相重合，则M ，N 两点表示的数分别是，．(5)点P 与点Q 分别从A ，B 两点同时出发，在数轴上运动，它们的速度分别是2个单位长度/秒，4个单位长度/秒，它们运动的时间为s t ．点P 与点Q 在点A 与点B 之间相向运动，当8PQ =时，直接写出点P 对应的数．(6)《庄子·天下篇》中写道：“一尺之棰，日取其半，万世不竭．”意思是：一根一尺长的木棍，如果每天截取它的一半，永远也取不完．如图2，求231011112222+++⋅⋅⋅+的值．(7)。

华北水利水电大学远程与继续教育学院 C语言程序设计试卷

2. ANSI C 最近发布的标准是(4).
A ANSI 85 B ANSI 86 C ANSI 87 D c99
3. 下列各项_____属于 C 语言的特点。
A 运算符较少 B 结构化语言 C 语法检查严格 D 面向对象
4. 从理论上讲下列语句中_____是构成结构化程序必需的。
A if B goto C union D struct
16. 下述函数交换两个整数,选出无错者_____。
A swap(int * x, int * y) B swap(int * p1, int * p2)
{int temp;
{int *p;
temp = *x;
*p = *p1;
*x = *y;
*p1 = *p2;
*y = temp; }
{*p2 = *temp;
A) 10
B) 1
C) 6
D) 4
23、在 C 语言中,若对函数类型未加明显示说明,则函数的隐含类型是( )类型
A) void
B) double C) int
D) char
24、若有以下说明,且 0<=i<10,则( )是对数组元素地址的正确表示.
int a[ ]={ 1,2,3,4,5,6,7,8,9,10},*p=a, i;
9. 要使字符串变量 str 具有初值”hello!”,正确的语句是_____。
A char str[] = “hello!”; B char str[] = {‘h’,’e’,’l’,’l’,’o’,’!’,’\0’}
C char str[6] = “hello!”; D char str[10] = {“hello!};
输出结果为：

2024年新高考改革适应性练习(3)(九省联考题型)数学卷及答案

2024年新高考改革适应性练习（3）（九省联考题型）数学试题卷（2024.2.6）考生须知1. 本卷共4页，四大题19小题，满分150分，答题时间120分钟；2. 答题时须在答题卡上填涂所选答案（选择题），或用黑色字迹的签字笔规范书写答案与步骤（非选择题），答在本试题卷上或草稿纸上的答案均属无效；3. 考试结束时，考生须一并上交本试题卷，答题卡与草稿纸．一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 设样本空间ΩΩ={1,2,…,6}包含等可能的样本点，且AA={1,2,3,4}，BB={3,4,5,6}，则PP(AABB)= A．13B．14C．15D．162. 若复数zz满足zz2是纯虚数，则|zz−2|的最小值是A．1 B．√2C．2 D．2√23. 算术基本定理告诉我们，任何一个大于1的自然数NN，如果NN不为质数，那么NN可以唯一分解成有限个素因数的乘积的形式．如，60可被分解为 22×31×51，45可被分解为 32×51．任何整除NN的正整数dd都叫作NN的正因数．如，20的正因数有1，2，4，5，10，20．则4200的正因数个数是A．4 B．7 C．42 D．484. 已知点(aa,bb)在直线 2xx+yy−1=0 第一象限的图像上，则1aa+1bb的最小值是A．3+2√2B．2+2√2C．1+2√2D．2√25. 已知函数ff(xx)=sin xx，gg(xx)=cos xx，则ff�gg(xx)�和gg�ff(xx)�都单调递增的一个区间是A．�2ππ5,4ππ5�B．�4ππ5,6ππ5�C．�6ππ5,8ππ5�D．�8ππ5,2ππ�6. 已知直线ll过点(2,1)，且与两坐标轴围成的三角形的面积是6，则满足条件的直线ll共有A．1条B．2条C．3条D．4条7. 我们记ff(nn)(xx)为函数ff(xx)的nn次迭代，即ff(1)(xx)=ff(xx)，ff(2)(xx)=ff�ff(xx)�，…，ff(nn)= ff�ff(nn−1)(xx)�．已知函数gg(xx)=xx|xx|，则gg(2024)(xx)=A．xx3|xx|2021B．xx4|xx|2020C．xx2|xx|2022D．xx20248. 若一四面体恰有一条长度大于1的棱，则这个四面体体积的最大值是A．√33B．12C．13D．√22二、多项选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对一个得3分；若只有3个正确选项，每选对一个得2分．）9. 已知函数ff(xx)=xx3−2xx，下列说法正确的是A．函数gg(xx)=ff(xx)+ff′(xx)无零点B．直线 2xx+yy=0 与yy=ff(xx)相切C．存在无数个aa>0 ，ff(xx)在区间(−aa,aa)上不单调D．存在mm>0 ，使得对于任意nn，ff(nn)≤ff(nn+mm)10. 若一个人一次仅能爬1级或2级台阶，记aa nn为爬nn级台阶时不同的爬法数(nn∈NN∗)．关于数列{aa nn}，下列说法正确的是A．函数ff(nn)=aa nn单调递增B．aa1+aa3+aa5的值为12C．aa1+aa2+⋯+aa10=232D．2aa12+aa22+⋯+aa102=89×14411. 如右图，已知抛物线CC的焦点为FF，准线方程为ll:xx=−1 ，点PP是CC上的一动点．过点PP作ll的垂线，垂足为QQ．过点PP作CC的切线，该切线与xx,yy轴分别交于AA,BB两个不同的点．下列说法正确的是A．抛物线CC的标准方程为yy2=2xxB．QQ,BB,FF三点共线当且仅当|PPFF|=4C．当|PPFF|≠1 时，都有PPAA⊥QQFFD．当|PPFF|≠1 时，△PPAAFF恒为等腰三角形三、填空题（本题共3小题，每小题5分，共15分．）12. 在棱长为1的正方体AABBCCAA−AA1BB1CC1AA1中，三棱锥CC−AABB1AA1的体积是_________．13. 从集合{xx|−4≤xx≤2024}中任选2个不同的非零整数作为二次函数ff(xx)=aaxx2+bbxx的系数，则所有满足ff(xx)的顶点在第一象限或第三象限的有序数对(aa,bb)共有_________组．14. 已知向量aa,bb,cc满足aa+bb+cc=00，(aa−bb)⊥(aa−cc)，|bb−cc|=3 ，则|aa|+|bb|+|cc|的最大值是_________．四、解答题（本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．）15.（13分）已知正方体AABBCCAA−AA1BB1CC1AA1．（1）证明：AAAA1⊥AA1CC；（2）求二面角BB−AA1CC−AA．16.（15分）已知定义在RR上的函数ff(xx)=aaxx4+bbxx3+ccxx2+ddxx(aa≠0)．（1）若原点是ff(xx)的一个极值点，证明：ff(xx)的所有零点也是其所有极值点；（2）若ff(xx)的4个零点成公差为2的等差数列，求ff′(xx)的最大零点与最小零点之差．17.（15分）设点SS(1,1)在椭圆CC:xx2aa2+yy2bb2=1(aa>bb>0)内，直线ll:bb2xx2+aa2yy2−aa2bb2=0 ．（1）求ll与CC的交点个数；（2）设PP为ll PPSS与CC相交于MM,NN两点．给出下列命题：①存在点PP，使得1|PPPP|,1|PPPP|,1|PPPP|成等差数列；②存在点PP，使得|PPMM|,|PPSS|,|PPNN|成等差数列；③存在点PP，使得|PPMM|,|PPSS|,|PPNN|成等比数列；请从以上三个命题中选择一个，证明该命题为假命题．（若选择多个命题分别作答，则按所做的第一个计分．）18.（17分）2024部分省市的高考数学推行8道单选，3道多选的新题型政策．单选题每题5分，选错不得分，多选题每题完全选对6分，部分选对部分分（此处直接视作3分），不选得0分．现有小李和小周参与一场新高考数学题，小李的试卷正常，而小周的试卷选择题是被打乱的，所以他11题均认为是单选题来做．假设两人选对一个单选题的概率都是14，且已知这四个多选题都只有两个正确答案．（1）记小周选择题最终得分为XX，求EE(XX)．（2）假设小李遇到三个多选题时，每个题他只能判断有一个选项是正确的，且小李也只会再选1个选项，假设他选对剩下1个选项的概率是 pp 0�pp 0≥13� ，请你帮小李制定回答4个多选题的策略，使得分最高．19.（17分）信息论之父香农（Shannon ）在1948年发表的论文“通信的数学理论”中指出，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关．香农借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式．设随机变量 XX 所有取值为 1,2,…,nn ，且 PP (xx =ii )=PP ii >0（ii =1,2,…,nn ），PP 1+PP 2+⋯+PP nn =1 ，定义 XX 的信息熵HH (XX )=−�PP ii log 2PP ii nn ii=1（1）当 nn =1 时，求 HH (XX ) 的值；（2）当 nn =2 时，若 PP 1∈�0,12� ，探究 HH (XX ) 与 PP 1 的关系，并说明理由；（3）若 PP 1=PP 2=12nn−1 ，PP kk+1=2PP kk (kk =2,3,⋯,nn ) ，求此时的信息熵 HH (XX ) ．2024年新高考改革适应性练习（3）（九省联考题型）数学参考答案一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）题号 1 2 3 4 5 6 7 8 答案 A B D A D D B C二、多项选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对一个得3分；若只有3个正确选项，每选对一个得2分．具体得分如【附】评分表．）题号91011答案BC ABD BCD【附】评分表三、填空题（本题共3小题，每小题5分，共15分．）题号121314答案132023×2024+4×2024（或 2027×2024）3+3√10四、解答题（本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．）15.（13分）以点AA1为坐标原点，AA1BB1��⃗为xx轴正方向，AA1DD1��⃗为yy轴正方向，AA1AA��⃗为zz轴正方向，建立空间直角坐标系OOxxyyzz，并令正方体AABBAADD−AA1BB1AA1DD1的棱长为1．（1）则AA1(0,0,0)，AA(1,−1,1)，AA1AA��⃗=(1,−1,1)；AA(0,0,1)，DD1(0,−1,0)，AADD1��⃗=(0,−1,−1)．所以AADD1��⃗·AA1AA��⃗=0+1+(−1)=0 ，即AADD1��⃗⊥AA1AA��⃗．故AADD1⊥AA1AA得证．（2）BB(1,0,1)，AA1BB��⃗=(1,0,1)，由（1）得AA1AA��⃗=(1,−1,1)，设平面AA1BBAA的一个法向量nn11=(xx1,yy1,zz1)，则nn11·AA1BB��⃗=nn11·AA1AA��⃗=0 ，即�xx1+zz1=0xx1−yy1+zz1=0令xx1=1 ，则�yy1=0zz1=−1，所以nn11=(1,0,−1)是平面AA1BBAA的一个法向量．同理可求得平面AA1AADD的一个法向量nn22=(0,1,1)，cos<nn11,nn22>=nn11·nn22|nn11|·|nn22|=−12又 <nn11,nn22>∈(0,ππ)，所以 <nn11,nn22>=2ππ3，即平面AA1BBAA与平面AA1AADD的所成角为2ππ3．故二面角BB−AA1AA−DD的大小为2ππ3．16.（15分）（1）ff(xx)=aaxx4+bbxx3+ccxx2+ddxx，ff′(xx)=aaxx3+bbxx2+ccxx+dd，由题意，原点是ff(xx)的一个极值点，即ff′(0)=0 ，代入得dd=0 ，所以ff(xx)=aaxx4+bbxx3+ccxx2=xx2(aaxx2+bbxx+cc)，ff′(xx)=aaxx3+bbxx2+ccxx=xx(aaxx2+bbxx+cc)，所以ff(xx)和ff′(xx)的零点（0除外）都是方程aaxx2+bbxx+cc=0 的根，即ff(xx)和ff′(xx)有共同零点，故ff(xx)的所有零点也是其所有极值点．（2）设ff(xx)的四个零点分别为mm−3 ，mm−1 ，mm+1 ，mm+3 ，则可以设ff(xx)=kk(xx−mm+3)(xx−mm+1)(xx−mm−1)(xx−mm−3)其中kk≠0 ，令tt=xx−mm，则ff(xx)=kk(tt+3)(tt+1)(tt−1)(tt−3)=kk(tt4−10tt+9)=gg(tt)gg′(tt)=kk(4tt3−20tt)=4kk(tt3−5tt)令gg′(tt)=0 得tt1=−√5 ，tt=0 ，tt=√5 ，所以 ff ′(xx )=0 的所有根为 xx 1=mm −√5 ，xx 2=mm ，xx 3=mm +√5 ，所以 ff ′(xx ) 的最大零点与最小零点之差为 |xx 3−xx 1|=2√5 ．17.（15分）（1）因为点 SS (1,1) 在 AA 内，所以 1aa 2+1bb 2<1 ，即 aa 2+bb 2−aa 2bb 2<0 ．联立 ll 与 AA 的方程，得 bb 2(aa 2+bb 2)xx 2−2aa 2bb 4xx +aa 4bb 2(bb 2−1)=0 ．判别式 Δ=4aa 4bb 8−4aa 4bb 4(aa 2+bb 2)(bb 2−1)=4aa 4bb 4(aa 2+bb 2−aa 2bb 2)<0 ，故该二次方程无解，即 ll 与 AA 交点个数为0．（2）可选择命题②或命题③（命题①无法证伪），证明其为假命题．记点 PP ,MM ,NN 的横坐标分别为 xx PP ,xx MM ,xx NN ，不妨设 PP ,MM ,SS ,NN 顺次排列．选择命题②的证明：当直线 MMNN 的斜率不存在时，MMNN :xx =1 ，分别与 ll ,AA 的方程联立可得 PP �1,bb 2−bb 2aa 2� ，MM �1,bb�1−1aa 2�,NN �1,−bb�1−1aa 2� ．若 |PPMM |,|PPSS |,|PPNN | 依次成等差数列，则 bb�1−1aa 2+�−bb�1−1aa 2�=2 ，显然矛盾，不满足题意．当直线 MMNN 的斜率存在时，设其斜率为 kk ，则 MMNN :yy =kk (xx −1)+1 ，与 ll 的方程联立可得 xx PP =aa 2�bb 2+kk−1�aa 2kk+bb 2；与 AA 的方程联立，得 (aa 2kk 2+bb 2)xx 2−2aa 2kk (kk −1)xx +aa 2[(kk −1)2−bb 2]=0 ，由韦达定理⎩⎨⎧xx MM +xx NN =2aa 2kk (kk −1)aa 2kk 2+bb 2xx MM xx NN =aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2则 2|PPSS |−(|PPMM |+|PPNN |)=√1+kk 2(2|xx PP −1|−|xx MM −xx PP |−|xx NN −xx PP |) . 不妨设 xx PP >1 ，则 xx PP >xx MM >1>xx NN ，所以原式=�1+kk 2[2(xx PP −1)−(xx PP −xx MM )−(xx PP −xx NN )]=�1+kk 2(xx MM +xx NN −2)=�1+kk 2⋅−2aa 2kk −2bb 2aa 2kk 2+bb 2<0因此 |PPMM |,|PPSS |,|PPNN | 不能成等差数列，从而②是假命题．选择命题③的证明：当直线 MMNN 的斜率不存在时，MMNN :xx =1 ，分别与 ll ,AA 的方程联立可得 PP �1,bb 2−bb 2aa 2� ，MM �1,bb�1−1aa 2�，NN �1,−bb�1−1aa 2�．若|PPMM |,|PPSS |,|PPNN |成等比数列，则��bb 2−bb 2aa 2�−bb �1−1aa 2�×��bb 2−bb 2aa 2�+bb �1−1aa 2�=��bb 2−bb 2aa2�−1�2即 aa 2+aa 2bb 2−bb 2=0 ，但 aa 2bb 2>aa 2+bb 2 ，因此 aa 2+aa 2bb 2−bb 2>2aa 2>0 ，矛盾，不满足题意．当直线 MMNN 的斜率存在时，设其斜率为 kk ，则 MMNN :yy =kk (xx −1)+1 ，与 ll 的方程联立可得 xx PP =aa 2�bb 2+kk−1�aa 2kk+bb 2；与 AA 的方程联立，得 (aa 2kk 2+bb 2)xx 2−2aa 2kk (kk −1)xx +aa 2[(kk −1)2−bb 2]=0 ，由韦达定理，⎩⎨⎧xx MM +xx NN =2aa 2kk (kk −1)aa 2kk 2+bb 2xx MM xx NN =aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2则|PPSS |2−|PPMM |⋅|PPNN |=�1+kk 2[(xx PP −1)2−(xx PP −xx MM )(xx PP −xx NN )] =�1+kk 2[(xx MM +xx NN −2)xx PP +1−xx MM xx NN ]=�1+kk 2��2aa 2kk (kk −1)aa 2kk 2+bb 2−1�⋅aa 2(bb 2+kk −1)aa 2kk +bb 2+1−aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2�=√1+kk 2aa 2kk 2+bb 2(aa 2+bb 2−aa 2bb 2)<0 因此 |PPMM |,|PPSS |,|PPNN | 不能成等比数列，故③是假命题．18.（17分）（1）由题意，对于单选题，小周每个单选题做对的概率为 14 ，对于多选题，小周每个多选题做对的概率为 12，设小周做对单选题的个数为 XX 1 ，做对多选题的个数为 XX 2 ，则XX 1∼BB �8,1�，XX 2∼BB �3,1� ，所以EE(XX1)=8×14=2 ，EE(XX1)=3×12=32，而小周选择题最终得分为XX=5XX1+3XX2，所以EE(XX)=5EE(XX1)+3EE(XX2)=5×2+3×32=292．（2）由题意他能判断一个选项正确，先把这个正确选项选上，如果他不继续选其他选项肯定能得三分，如果他继续选其它选项的话，设此时他的最终得分为XX3，则XX3的所有可能取值为0，6，则XX3的分布列为：XX30 6PP(XX3)1−pp0pp0那么这个题的得分期望是EE(XX3)=0×(1−pp0)+6pp0=6pp0,�pp0≥13�所以我们只需要比较3和 6pp0的大小关系即可，令 6pp0≥3，解得12≤pp0<1 ，此时四个多选题全部选两个选项得分要高，反之，若13≤pp0<12，此时四个多选只选他确定的那个选项得分最高．19.（17分）（1）若nn=1 ，则ii=1 ，PP1=1 ，因此HH(xx)=−(1×log21)=0 ．（2）HH(XX)与PP1正相关，理由如下：当nn=2 时，PP1∈�0,12�，HH(xx)=−PP1log2PP1−(1−PP1)log2(1−PP1)令ff(tt)=−tt log2tt−(1−tt)log2(1−tt)，其中tt∈�0,12�，则ff′(tt)=−log2tt+log2(1−tt)=log2�1tt−1�>0所以函数ff(tt)在�0,12�上单调递增，所以HH(xx)与PP1正相关．（3）因为PP1=PP2=12nn−1，PP kk+1=2PP kk(kk=2,3,⋯,nn)，所以PP kk =PP 2⋅2kk−2=2kk−22nn−1=12nn−kk+1 (kk =2,3,⋯,nn ) 故PP kk log 2PP kk =12nn−kk+1log 212nn−kk+1=−nn −kk +12nn−kk+1而PP 1log 2PP 1=12nn−1log 212nn−1=−nn −12nn−1于是HH (XX )=nn −12nn−1+�PP kk log 2PP kk nnkk=2=nn −12nn−1+nn −12nn−1+nn −22nn−2+⋯+222+12整理得HH (XX )=nn −12nn−1−nn 2nn +nn 2nn +nn −12nn−1+nn −22nn−2+⋯+222+12 令SS nn =12+222+323+⋯+nn −12nn−1+nn2nn 则12SS nn =122+223+324+⋯+nn −12nn +nn 2nn+1 两式相减得12SS nn =12+122+123+⋯+12nn −nn 2nn+1=1−nn +22nn+1 因此 SS nn =2−nn+22nn，所以 HH (XX )=nn−12nn−1−nn 2nn+SS nn =nn−12nn−1−nn 2nn+2−nn+22nn=2−12nn−2．。

《钢结构制作与安装》试题答案3-4

A.长细比
B.挠度
C.弯矩
D.剪力
密封线密封线
班级
课程
课程
密封线
专业
密封线密封线
专业
专业
.
第 2 页 14.实腹式轴心受压构件应进行( B )。
7．梁整体失稳的方式是（ C ）。
A.强度计算
B.强度、整体稳定、局部稳定和长细比计算
A.剪切失稳
B.扭转失稳
C.弯扭失稳
D. 弯曲失稳
C.强度、整体稳定和长细比计算 D.强度和长细比计算
学号
姓名
班级
密封线
2、门式刚架轻型钢结构的特点及结构形式有哪些？（各说三个即可）刚架特点:
U 形，K 形和 X 形坡口：当焊件厚度 t＞20mm 时采用。
1)采用轻型屋面，不仅可减小梁柱截面尺寸，基础也相应减小；
2)刚架的侧向刚度籍檩条的隅撑保证，省去纵向刚性构件，并减小翼缘宽度；
3)刚架可采用变截面，截面与弯矩成正比；变截面时，根据需要可改变腹板的高
两种承重方案。
4、当不同强度的两种钢材进行连接时，宜采用与低强度相适应的焊条。
例 Q235 和 Q345 两种板材进行焊接时，宜采用 E43
焊条。
5、钢结构的连接方法有焊接连接、螺栓连接和铆钉连接
三种。
6、当构件上螺栓孔的端距大于等于 2d0 连接的板叠总厚度∑t 小于等于 5d
时，可避免端部冲剪破坏；当螺栓时，可避免栓杆受弯破坏。
7、图 1 构件采用三面围焊缝，试在图 2 中用焊缝符号表示（三面围焊缝焊脚尺寸
8、次梁与主梁的连接形式有叠接和平接两种。
9、高强度螺栓的图例符号为
。
10、Q235－A·F 表示屈服强度为 235N/MM2A 级沸腾钢

《汽车整车性能检测》试题库试卷B

A．自校
B．计量检定 Cห้องสมุดไป่ตู้维护
准规定的检验方法测得的汽车百千米燃料消耗量不得大于该车型原厂规定的相应车速等速百千米燃料消耗量的（）作为燃料消耗量限值指标。
22.《机动车运行安全技术条件》（GB 7258—2004）规定，在进行汽车前照灯检测时，发动机的状态为（）。
A．110％
B．103％
C．105％
（）10.汽车燃料经济性，是指汽车以最少的燃料消耗完成单位运输工作量
的能力。
专业：汽车整形技术 10 级 2011－2012－1 《汽车综合性能检测技术》期末考试卷（B 卷）
化技术的汽车计算机监控空燃比、控制排放量、保护三效催化转化器正常工作的
A．一
B．二
C．三
重要信号。
A．CO
B．CO2
C．O2
26.关于检测双怠速尾气排放，下列叙述正确的是（）。
36.某汽车综合性能检测站，提供了一组四灯制汽车前照灯发光强度的检测记录，其中合格的是（）cd。
A．15000，9800，15000，9800 B．15000，15000，9800，9800
备。
（）5.发动机在台架上，按照标准要求只安装部分规定的附件，在曲轴端测
到的相应转速下的发动机输出功率，并按标准大气状态修正得到的功率，称为发
动机最大净功率。
（）6.底盘测功机主要由道路模拟系统，数据采集与控制系统，安全保障系
统及引导系统等组成。
（）7.底盘测功机反拖装置是采用反拖电动机带动底盘测功机的功率吸收装
12.起动电压和起动电流可评价（）。
A．蓄电池技术状况 B．发电机技术状况
C．空调系统技术状况 D．发动机技术状况

北师大版六年级语文上册期末测试题

北师大版六年级语文上册教学质量检测（六）（期末检测）班级_________ 姓名_________ 学号_________成绩_________ 一、日积月累（30分）1．看拼音，写词语。

（5分）zī xún péng bójuéjiàng yāyìshūfā（）（）（）（）（）2．将下列词语填写完整。

（4分）低（）浅唱微不足（）（）堂大笑（）声扫地鞠躬尽（）名不见经（）兴（）勃勃卓尔不（）3．填空。

（5分）（1）你用甘甜的乳汁，___________________。

（胡宏伟《长江之歌》）（2）闻鸡起舞壮筋强骨，___________________。

（谚语）（3）些小吾曹州县吏，___________________。

（郑板桥《墨竹图题诗》）（4）___________________，个个花开淡墨痕。

（王冕《墨梅图题诗》）（5）___________________，同到牵牛织女家。

（刘禹锡《浪淘沙》）4．按要求写句子。

（6分）（1）根据“大方”的不同意思造句。

①不小气 ___________________________________________________②不拘束 ___________________________________________________（2）仿写句子。

秋天的三峡，有时热烈，有时平静；有时明丽，有时朦胧……真是气象万千。

________________________________________________________________ 5．下列句子没有语病的一项是（）。

（3分）A．晚会以后，她那优美的舞姿、动听的歌声还在我的耳边响起。

B．我们要以凌云壮志，用勤奋刻苦的汗水浇开灿烂的理想之花。

C．在学校这条道路上，是一条非常陡的坡。

D．我读了这篇文章，很感到激动。

6．实践活动。

《家畜育种学》试题与答案

《家畜育种学》试题与答案《家畜育种学》试题(A)闭卷适用专业年级:动物科学姓名学号专业班级本试题一共5 道大题，共 4 页，满分100分。

考试时间120分钟。

总分题号一二三四五阅卷人题分 30 15 15 20 20核分人得分注:1.答题前，请准确、清楚地填各项，涂改及模糊不清者、试卷作废。

2.试卷若有雷同以零分计。

一、单项选择题(每题2分，共30分)请把选择题的答案填入下表:题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 1. 选择差除以该性状的标准差称为( )。

A 留种率B 选择反应C 世代间隔D 选择强度2. 伴性快羽公鸡与伴性慢羽母鸡交配后，子一代的母雏为( )。

A丝羽型 B 慢羽型 C 常羽型 D 快羽型3. 选择指数法是针对( )性状的选择方法。

A 单一B 质量C 抗病D 多个4. 发源于一头优秀种公畜的畜群称为( )A 单系B 品族C 近交系D 群系5. 核心群取得的遗传改进扩展到商品群是通过( )实现的。

A 繁育体系B 杂交C 选择D 繁殖6. 下列交配类型中，属于种间杂交的组合是( )。

A 太湖猪×长白猪B 水牛×黄牛C 马×驴D 山羊×绵羊7. 下列那种措施是防止近交衰退最有效的措施( )。

《家畜育种学》试卷第 1 页A 异质选配B 选择+淘汰C 环境控制D 后裔测定 8. 下面哪个因素不会影响选择反应( )。

A 遗传变异B 选择强度C 世代间隔D 留种率9. 在下列品种中，属于原始品种的是( )A 藏鸡B 新疆细毛羊C 荣昌猪D 四川白鹅10. 一般配合力的遗传基础是基因的( )效应。

A显性 B 上位 C加性 D 互作11. 纯合的相同等位基因来自同一个共同祖先的概率称为( )。

A 亲缘系数B 近交系数C 相关系数D 回归系数12. 如果A与B两个体间的亲缘系数是20%，且这两个个体均非近交个体，则这两个个体交配所生后代的近交系数是( )A 40%B 10%C 20%D 12.5% 13. 在下列品系中，采用杂交的方法建立的品系是( )。

2024年天津市高考数学真题试卷及答案

2024年普通高等学校招生全国统一考试（天津卷）数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟．第Ⅰ卷1至3页，第Ⅱ卷4至6页．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上，并在规定位置粘贴考试用条形码．答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效．考试结束后，将本试卷和答题卡一并交回．祝各位考生考试顺利！第Ⅰ卷（选择题）注意事项：1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．2．本卷共9小题，每小题5分，共45分．参考公式：·如果事件A B ，互斥，那么()()()P A B P A P B =+ ．·如果事件A B ，相互独立，那么()()()P AB P A P B =．·球的体积公式34π3V R =，其中R 表示球的半径．·圆锥的体积公式13V Sh=，其中S 表示圆锥的底面面积，h 表示圆锥的高．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.集合{}1,2,3,4A =，{}2,3,4,5B =，则A B = （）A.{}1,2,3,4 B.{}2,3,4 C.{}2,4 D.{}12.设,a b ∈R ，则“33a b =”是“33a b =”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.下列图中，相关性系数最大的是（）A. B.C. D.4.下列函数是偶函数的是（）A.22e 1x x y x -=+ B.22cos 1x x y x +=+ C.e 1x xy x -=+ D.||sin 4e x x x y +=5.若0.30.3 4.24.2 4.2log 0.2a b c -===，，，则a b c ，，的大小关系为（）A.a b c>> B.b a c>> C.c a b>> D.b c a >>6.若,m n 为两条不同的直线，α为一个平面，则下列结论中正确的是（）A .若//m α，n ⊂α，则//m nB.若//,//m n αα，则//m nC.若//,αα⊥m n ，则m n⊥ D.若//,αα⊥m n ，则m 与n 相交7.已知函数()()πsin303f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π．则函数在ππ,126⎡⎤-⎢⎥⎣⎦的最小值是（）A.32B.32-C.0D.328.双曲线22221()00a x y a bb >-=>，的左、右焦点分别为12.F F P 、是双曲线右支上一点，且直线2PF 的斜率为2．12PF F △是面积为8的直角三角形，则双曲线的方程为（）A.22182y x -= B.22184x y -= C.22128x y -= D.22148x y -=9.一个五面体ABC DEF -．已知AD BE CF ∥∥，且两两之间距离为1．并已知123AD BE CF ===，，．则该五面体的体积为（）A.36B.33142+ C.32D.33142-第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．2．本卷共11小题，共105分．二、填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分．10.已知i 是虚数单位，复数))i 2i +⋅=______．11.在63333x x ⎛⎫+ ⎪⎝⎭的展开式中，常数项为______．12.22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合，A 为两曲线的交点，则原点到直线AF的距离为______．13.,,,,A B C D E 五种活动，甲、乙都要选择三个活动参加.（1）甲选到A 的概率为______；已知乙选了A 活动，他再选择B 活动的概率为______．14.在边长为1的正方形ABCD 中，点E 为线段CD 的三等分点，1,2CE DE BE BA BC ==+uur uu r uu u r λμ，则λμ+=______；若F 为线段BE 上的动点，G 为AF 中点，则AF DG ⋅的最小值为______．15.若函数()21f x ax =--+有唯一零点，则a 的取值范围为______．三、解答题：本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤16.在ABC 中，92cos 5163a Bbc ===，，．（1）求a ；（2）求sin A ；（3）求()cos 2B A -．17.已知四棱柱1111ABCD A B C D -中，底面ABCD 为梯形，//AB CD ，1A A ⊥平面ABCD ，AD AB ⊥，其中12,1AB AA AD DC ====．N 是11B C 的中点，M 是1DD的中点．（1）求证1//D N 平面1CB M ；（2）求平面1CB M 与平面11BB CC 的夹角余弦值；（3）求点B 到平面1CB M 的距离．18.已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =．左顶点为A ，下顶点为B C ，是线段OB 的中点，其中ABC S =△．（1）求椭圆方程．（2）过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ，．在y 轴上是否存在点T 使得0TP TQ ⋅≤ 恒成立．若存在求出这个T 点纵坐标的取值范围，若不存在请说明理由．19.已知数列{}n a 是公比大于0的等比数列．其前n 项和为n S ．若1231,1a S a ==-．（1）求数列{}n a 前n 项和n S ；（2）设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩，11b =，其中k 是大于1的正整数．（ⅰ）当1k n a +=时，求证：1n k n b a b -≥⋅；（ⅱ）求1nS ii b =∑．20.设函数()ln f x x x =．（1）求()f x 图象上点()()1,1f 处的切线方程；（2）若()(f x a x ≥-在()0,x ∞∈+时恒成立，求a 的取值范围；（3）若()12,0,1x x ∈，证明()()121212f x f x x x -≤-．2024年普通高等学校招生全国统一考试（天津卷）数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟．第Ⅰ卷1至3页，第Ⅱ卷4至6页．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上，并在规定位置粘贴考试用条形码．答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效．考试结束后，将本试卷和答题卡一并交回．祝各位考生考试顺利！第Ⅰ卷（选择题）注意事项：1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．2．本卷共9小题，每小题5分，共45分．参考公式：·如果事件A B ，互斥，那么()()()P A B P A P B =+ ．·如果事件A B ，相互独立，那么()()()P AB P A P B =．·球的体积公式34π3V R =，其中R 表示球的半径．·圆锥的体积公式13V Sh=，其中S 表示圆锥的底面面积，h 表示圆锥的高．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.集合{}1,2,3,4A =，{}2,3,4,5B =，则A B = （）A.{}1,2,3,4 B.{}2,3,4 C.{}2,4 D.{}1【答案】B 【解析】【分析】根据集合交集的概念直接求解即可.【详解】因为集合{}1,2,3,4A =，{}2,3,4,5B =，所以{}2,3,4A B = ，2.设,a b ∈R ，则“33a b =”是“33a b =”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C 【解析】【分析】说明二者与同一个命题等价，再得到二者等价，即是充分必要条件.【详解】根据立方的性质和指数函数的性质，33a b =和33a b =都当且仅当a b =，所以二者互为充要条件.故选：C.3.下列图中，相关性系数最大的是（）A. B.C. D.【答案】A 【解析】【分析】由点的分布特征可直接判断【详解】观察4幅图可知，A 图散点分布比较集中，且大体接近某一条直线，线性回归模型拟合效果比较好，呈现明显的正相关，r 值相比于其他3图更接近1.故选：A4.下列函数是偶函数的是（）A.22e 1x x y x -=+ B.22cos 1x x y x +=+ C.e 1x xy x -=+ D.||sin 4e x x x y +=【答案】B【分析】根据偶函数的判定方法一一判断即可.【详解】对A ，设()22e 1x x f x x -=+，函数定义域为R ，但()112e 1f ---=，()112e f -=，则()()11f f -≠，故A 错误；对B ，设()22cos 1x x g x x +=+，函数定义域为R ，且()()()()()2222cos cos 11x x x x g x g x x x -+-+-===+-+，则()g x 为偶函数，故B 正确；对C ，设()e 1x xh x x -=+，函数定义域为{}|1x x ≠-，不关于原点对称，则()h x 不是偶函数，故C 错误；对D ，设()||sin 4e x x x x ϕ+=，函数定义域为R ，因为()sin141e ϕ+=，()sin141eϕ---=，则()()11ϕϕ≠-，则()x ϕ不是偶函数，故D 错误.故选：B.5.若0.30.3 4.24.2 4.2log 0.2a b c -===，，，则a b c ，，的大小关系为（）A.a b c >>B.b a c>> C.c a b>> D.b c a>>【答案】B 【解析】【分析】利用指数函数和对数函数的单调性分析判断即可.【详解】因为 4.2x y =在R 上递增，且0.300.3-<<，所以0.300.30 4.2 4.2 4.2-<<<，所以0.30.30 4.21 4.2-<<<，即01a b <<<，因为 4.2log y x =在(0,)+∞上递增，且00.21<<，所以 4.2 4.2log 0.2log 10<=，即0c <，所以b a c >>，故选：B6.若,m n 为两条不同的直线，α为一个平面，则下列结论中正确的是（）A.若//m α，n ⊂α，则//m nB.若//,//m n αα，则//m nC.若//,αα⊥m n ，则m n ⊥D.若//,αα⊥m n ，则m 与n 相交【答案】C 【解析】【分析】根据线面平行的性质可判断AB 的正误，根据线面垂直的性质可判断CD 的正误.【详解】对于A ，若//m α，n ⊂α，则,m n 平行或异面，故A 错误.对于B ，若//,//m n αα，则,m n 平行或异面或相交，故B 错误.对于C ，//,αα⊥m n ，过m 作平面β，使得s βα= ，因为m β⊂，故//m s ，而s α⊂，故n s ⊥，故m n ⊥，故C 正确.对于D ，若//,αα⊥m n ，则m 与n 相交或异面，故D 错误.故选：C .7.已知函数()()πsin303f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π．则函数在ππ,126⎡⎤-⎢⎥⎣⎦的最小值是（）A.32B.32-C.0D.32【答案】A 【解析】【分析】先由诱导公式化简，结合周期公式求出ω，得()sin2f x x =-，再整体求出,126⎡⎤∈-⎢⎥⎣⎦ππx 时，2x 的范围，结合正弦三角函数图象特征即可求解.【详解】()()πsin3sin 3πsin 33f x x x x ωωω⎛⎫=+=+=- ⎪⎝⎭，由2ππ3T ω==得23ω=，即()sin2f x x =-，当,126⎡⎤∈-⎢⎥⎣⎦ππx 时，ππ2,63x ⎡⎤∈-⎢⎥⎣⎦，画出()sin2f x x =-图象，如下图，由图可知，()sin2f x x =-在ππ,126⎡⎤-⎢⎥⎣⎦上递减，所以，当π6x =时，()min π3sin 32f x =-=-故选：A8.双曲线22221()00a x y a bb >-=>，的左、右焦点分别为12.F F P 、是双曲线右支上一点，且直线2PF 的斜率为2．12PF F △是面积为8的直角三角形，则双曲线的方程为（）A.22182y x -= B.22184x y -= C.22128x y -= D.22148x y -=【答案】C 【解析】【分析】可利用12PF F △三边斜率问题与正弦定理，转化出三边比例，设2PF m =，由面积公式求出m ，由勾股定理得出c ，结合第一定义再求出a .【详解】如下图：由题可知，点P 必落在第四象限，1290F PF ∠=︒，设2PF m =，211122,PF F PF F θθ∠=∠=，由21tan 2PF k θ==，求得1sin θ=，因为1290F PF ∠=︒，所以121PF PF k k ⋅=-，求得112PF k =-，即21tan 2θ=，2sin θ=121212::sin :sin :sin 902:1:PF PF F F θθ=︒=则由2PF m =得1122,2PF m F F c ===，由1212112822PF F S PF PF m m =⋅=⋅=得m =，则21122PF PF F F c c =====由双曲线第一定义可得：122PF PF a -==a b ===所以双曲线的方程为22128x y -=.故选：C9.一个五面体ABC DEF -．已知AD BE CF ∥∥，且两两之间距离为1．并已知123AD BE CF ===，，．则该五面体的体积为（）A.36B.33142+ C.32D.33142-【答案】C 【解析】【分析】采用补形法，补成一个棱柱，求出其直截面，再利用体积公式即可.【详解】用一个完全相同的五面体HIJ LMN -（顶点与五面体ABC DEF -一一对应）与该五面体相嵌，使得,D N ；,E M ;,F L 重合，因为AD BE CF ∥∥，且两两之间距离为1．1,2,3AD BE CF ===，则形成的新组合体为一个三棱柱，该三棱柱的直截面（与侧棱垂直的截面）为边长为1的等边三角形，侧棱长为1322314+=+=+=，2132211311422ABC DEF ABC HIJ V V --==⨯⨯⨯=.故选：C.第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．2．本卷共11小题，共105分．二、填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分．10.已知i是虚数单位，复数))i 2i +⋅=______．【答案】7【解析】【分析】借助复数的乘法运算法则计算即可得.【详解】))i 2i 527+⋅=+-+=-.故答案为：7.11.在63333x x⎛⎫+ ⎪⎝⎭的展开式中，常数项为______．【答案】20【解析】【分析】根据题意结合二项展开式的通项分析求解即可.【详解】因为63333x x ⎛⎫+ ⎪⎝⎭的展开式的通项为()63636216633C 3C ,0,1,,63rrr r r r r x T xr x ---+⎛⎫⎛⎫===⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭，令()630r -=，可得3r =，所以常数项为0363C 20=.故答案为：20.12.22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合，A 为两曲线的交点，则原点到直线AF的距离为______．【答案】45##0.8【解析】【分析】先求出圆心坐标，从而可求焦准距，再联立圆和抛物线方程，求A 及AF的方程，从而可求原点到直线AF 的距离.【详解】圆22(1)25-+=x y 的圆心为()1,0F ，故12p=即2p =，由()2221254x y y x⎧-+=⎪⎨=⎪⎩可得22240x x +-=，故4x =或6x =-（舍），故()4,4A ±，故直线()4:13AF y x =±-即4340x y --=或4340x y +-=，故原点到直线AF 的距离为4455d ==，故答案为：4513.,,,,A B C D E 五种活动，甲、乙都要选择三个活动参加.（1）甲选到A 的概率为______；已知乙选了A 活动，他再选择B 活动的概率为______．【答案】①.35②.12【解析】【分析】结合列举法或组合公式和概率公式可求甲选到A 的概率；采用列举法或者条件概率公式可求乙选了A 活动，他再选择B 活动的概率.【详解】解法一：列举法从五个活动中选三个的情况有：,,,,,,,,,ABC ABD ABE ACD ACE ADE BCD BCE BDE CDE ,共10种情况，其中甲选到A 有6种可能性：,,,,,ABC ABD ABE ACD ACE ADE ，则甲选到A 得概率为：63105P ==；乙选A 活动有6种可能性：,,,,,ABC ABD ABE ACD ACE ADE ，其中再选则B 有3种可能性：,,ABC ABD ABE ，故乙选了A 活动，他再选择B 活动的概率为31=62.解法二：设甲、乙选到A 为事件M ，乙选到B 为事件N ，则甲选到A 的概率为()2435C 3C 5P M ==；乙选了A 活动，他再选择B 活动的概率为()()()133524351C 2C C P MN C P N M P M ===故答案为：35；1214.在边长为1的正方形ABCD 中，点E 为线段CD 的三等分点，1,2CE DE BE BA BC ==+uur uu r uu u r λμ，则λμ+=______；若F 为线段BE 上的动点，G 为AF 中点，则AF DG ⋅的最小值为______．【答案】①.43②.518-【解析】【分析】解法一：以{},BA BC 为基底向量，根据向量的线性运算求BE，即可得λμ+，设BF BE k =uu u r uur ，求,AF DG uu u r uuu r ，结合数量积的运算律求AF DG ⋅ 的最小值；解法二：建系标点，根据向量的坐标运算求BE，即可得λμ+，设()1,3,,03F a a a ⎡⎤-∈-⎢⎥⎣⎦，求,AF DG uu u r uuu r ，结合数量积的坐标运算求AF DG ⋅ 的最小值.【详解】解法一：因为12CE DE =，即23CE BA =uur uu r ，则13BE BC CE BA BC =+=+uu u r uur u uu ur r uu u r ，可得1,13λμ==，所以43λμ+=；由题意可知：1,0BC BA BA BC ==⋅=，因为F 为线段BE 上的动点，设[]1,0,13BF k BE k BA k BC k ==+∈，则113AF AB BF AB k BE k BA k BC ⎛⎫=+=+=-+ ⎪⎝⎭，又因为G 为AF 中点，则1111112232DG DA AG BC AF k BA k BC ⎛⎫⎛⎫=+=-+=-+- ⎪ ⎪⎝⎭⎝⎭，可得11111113232AF DG k BA k BC k BA k BC ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⋅=-+⋅-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦22111563112329510k k k k ⎛⎫⎛⎫⎛⎫=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，又因为[]0,1k ∈，可知：当1k =时，AF DG ⋅取到最小值518-；解法二：以B为坐标原点建立平面直角坐标系，如图所示，则()()()()11,0,0,0,0,1,1,1,,13A B C D E ⎛⎫--- ⎪⎝⎭，可得()()11,0,0,1,,13BA BC BE ⎛⎫=-==- ⎪⎝⎭，因为(),BE BA BC λμλμ=+=- ，则131λμ⎧-=-⎪⎨⎪=⎩，所以43λμ+=；因为点F 在线段1:3,,03BE y x x ⎡⎤=-∈-⎢⎥⎣⎦上，设()1,3,,03F a a a ⎡⎤-∈-⎢⎥⎣⎦，且G 为AF 中点，则13,22a G a -⎛⎫-⎪⎝⎭，可得()131,3,,122a AF a a DG a +⎛⎫=+-=--⎪⎝⎭，则()()22132331522510a AF DG a a a +⎛⎫⎛⎫⋅=+---=+- ⎪ ⎪⎝⎭⎝⎭ ，且1,03a ⎡⎤∈-⎢⎥⎣⎦，所以当13a =-时，AF DG ⋅ 取到最小值为518-；故答案为：43；518-.15.若函数()21f x ax =--+有唯一零点，则a 的取值范围为______．【答案】()(1-⋃【解析】【分析】结合函数零点与两函数的交点的关系，构造函数()g x =与()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩，则两函数图象有唯一交点，分0a =、0a >与0a <进行讨论，当0a >时，计算函数定义域可得x a ≥或0x ≤，计算可得(]0,2a ∈时，两函数在y 轴左侧有一交点，则只需找到当(]0,2a ∈时，在y 轴右侧无交点的情况即可得；当0a <时，按同一方式讨论即可得.【详解】令()0f x =，即21ax =--，由题可得20x ax -≥，当0a =时，x ∈R，有211=--=，则22x =±，不符合要求，舍去；当0a >时，则23,2121,ax x a ax ax x a ⎧-≥⎪⎪=--=⎨⎪-<⎪⎩，即函数()g x =与函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩有唯一交点，由20x ax -≥，可得x a ≥或0x ≤，当0x ≤时，则20ax -<，则211ax ax =--=-，即()22441x ax ax -=-，整理得()()()2242121210a xax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦，当2a =时，即410x +=，即14x =-，当()0,2a ∈，12x a =-+或102x a=>-（正值舍去），当()2,a ∈+∞时，102x a =-<+或102x a=<-，有两解，舍去，即当(]0,2a ∈时，210ax -+=在0x ≤时有唯一解，则当(]0,2a ∈时，210ax -+=在x a ≥时需无解，当(]0,2a ∈，且x a ≥时，由函数()23,21,ax x ah x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩关于2x a =对称，令()0h x =，可得1x a =或3x a =，且函数()h x 在12,a a ⎛⎫⎪⎝⎭上单调递减，在23,a a ⎛⎫⎪⎝⎭上单调递增，令()g x y ==，即2222142a x y a a ⎛⎫- ⎪-⎭=⎝，故x a ≥时，()g x 图象为双曲线()222214y x a a -=右支的x 轴上方部分向右平移2a 所得，由()222214y x a a-=的渐近线方程为22a y x x a =±=±，即()g x 部分的渐近线方程为22a y x ⎛⎫=- ⎪⎝⎭，其斜率为2，又(]0,2a ∈，即()23,21,ax x ah x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a ≥时的斜率(]0,2a ∈，令()0g x ==，可得x a =或0x =（舍去），且函数()g x 在(),a +∞上单调递增，故有13a aa a ⎧<⎪⎪⎨⎪>⎪⎩，解得1a <<，故1a <<符合要求；当a<0时，则23,2121,ax x a ax ax x a ⎧-≤⎪⎪=--=⎨⎪->⎪⎩，即函数()g x =与函数()23,21,ax x a h x ax x a ⎧-≤⎪⎪=⎨⎪->⎪⎩有唯一交点，由20x ax -≥，可得0x ≥或x a ≤，当0x ≥时，则20ax -<，则211ax ax =--=-，即()22441x ax ax -=-，整理得()()()2242121210a xax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦，当2a =-时，即410x -=，即14x =，当()2,0a ∈-，102x a =-<+（负值舍去）或102x a=-，当(),2a ∈-∞时，102x a =->+或102x a=>-，有两解，舍去，即当[)2,0a ∈-时，210ax --+=在0x ≥时有唯一解，则当[)2,0a ∈-时，210ax --+=在x a ≤时需无解，当[)2,0a ∈-，且x a ≤时，由函数()23,21,ax x ah x ax x a ⎧-≤⎪⎪=⎨⎪->⎪⎩关于2x a =对称，令()0h x =，可得1x a =或3x a =，且函数()h x 在21,a a ⎛⎫ ⎪⎝⎭上单调递减，在32,a a ⎛⎫ ⎪⎝⎭上单调递增，同理可得：x a ≤时，()g x 图象为双曲线()222214y x a a -=左支的x 轴上方部分向左平移2a 所得，()g x 部分的渐近线方程为22a y x ⎛⎫=-+ ⎪⎝⎭，其斜率为2-，又[)2,0a ∈-，即()23,21,ax x ah x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a <时的斜率[)2,0a ∈-，令()0g x ==，可得x a =或0x =（舍去），且函数()g x 在(),a -∞上单调递减，故有13a aa a⎧>⎪⎪⎨⎪<⎪⎩，解得1a <<-，故1a <<-符合要求；综上所述，()(1a ∈- .故答案为：()(1-⋃.【点睛】关键点点睛：本题关键点在于将函数()f x 的零点问题转化为函数()g x =与函数()23,21,ax x ah x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩的交点问题，从而可将其分成两个函数研究.三、解答题：本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤16.在ABC 中，92cos 5163a Bbc ===，，．（1）求a ；（2）求sin A ；（3）求()cos 2B A -．【答案】（1）4（2）74（3）5764【解析】【分析】（1）2,3a t c t ==，利用余弦定理即可得到方程，解出即可；（2）法一：求出sin B ，再利用正弦定理即可；法二：利用余弦定理求出cos A ，则得到sin A ；（3）法一：根据大边对大角确定A 为锐角，则得到cos A ，再利用二倍角公式和两角差的余弦公式即可；法二：直接利用二倍角公式和两角差的余弦公式即可.【小问1详解】设2,3a t c t ==，0t >，则根据余弦定理得2222cos b a c ac B =+-，即229254922316t t t t =+-⨯⨯⨯，解得2t =（负舍）；则4,6a c ==.【小问2详解】法一：因为B为三角形内角，所以sin 16B ===，再根据正弦定理得sin sin a b A B =，即4sin A =sin 4A =，法二：由余弦定理得2222225643cos 22564b c a A bc +-+-===⨯⨯，因为()0,πA ∈，则sin 4A ==【小问3详解】法一：因为9cos 016B =>，且()0,πB ∈，所以π0,2B ⎛⎫∈ ⎪⎝⎭，由（2）法一知57sin 16B =，因为a b <，则A B <，所以3cos 4A ==，则3sin 22sin cos 2448A A A ==⨯⨯=，2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭()19573757cos 2cos cos 2sin sin 281616864B A B A B A -=+=⨯+⨯=.法二：7337sin 22sin cos 2448A A A ==⨯⨯=，则2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭，因为B为三角形内角，所以57sin 16B ===，所以()9157cos 2cos cos 2sin sin 216816864B A B A B A -=+=⨯+⨯=17.已知四棱柱1111ABCD A B C D -中，底面ABCD 为梯形，//AB CD ，1A A ⊥平面ABCD ，AD AB ⊥，其中12,1AB AA AD DC ====．N 是11B C 的中点，M 是1DD 的中点．（1）求证1//D N 平面1CB M ；（2）求平面1CB M 与平面11BB CC 的夹角余弦值；（3）求点B 到平面1CB M 的距离．【答案】（1）证明见解析（2）22211（3）21111【解析】【分析】（1）取1CB 中点P ，连接NP ，MP ，借助中位线的性质与平行四边形性质定理可得1N//D MP ，结合线面平行判定定理即可得证；（2）建立适当空间直角坐标系，计算两平面的空间向量，再利用空间向量夹角公式计算即可得解；（3）借助空间中点到平面的距离公式计算即可得解.【小问1详解】取1CB 中点P ，连接NP ，MP ，由N 是11B C 的中点，故1//NP CC ，且112NP CC =，由M 是1DD 的中点，故1111122D M DD CC ==，且11//D M CC ，则有1//D M NP 、1D M NP =，故四边形1D MPN 是平行四边形，故1//D N MP ，又MP ⊂平面1CB M ，1D N ⊄平面1CB M ，故1//D N 平面1CB M ；【小问2详解】以A为原点建立如图所示空间直角坐标系，有()0,0,0A 、()2,0,0B 、()12,0,2B 、()0,1,1M 、()1,1,0C 、()11,1,2C ，则有()11,1,2CB =- 、()1,0,1CM =-、()10,0,2BB = ，设平面1CB M 与平面11BB CC 的法向量分别为()111,,m x y z = 、()222,,n x y z =，则有111111200m CB x y z m CM x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩，1222122020n CB x y z n BB z ⎧⋅=-+=⎪⎨⋅==⎪⎩ ，分别取121x x ==，则有13y =、11z =、21y =，20z =，即()1,3,1m = 、()1,1,0n =，则222cos ,11m nm n m n ⋅===⋅，故平面1CB M 与平面11BB CC 的夹角余弦值为22211；【小问3详解】由()10,0,2BB = ，平面1CB M 的法向量为()1,3,1m =，则有121111BB m m ⋅==，即点B 到平面1CB M 的距离为21111.18.已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =．左顶点为A ，下顶点为B C ，是线段OB 的中点，其中ABC S =△．（1）求椭圆方程．（2）过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ，．在y 轴上是否存在点T 使得0TP TQ ⋅≤ 恒成立．若存在求出这个T 点纵坐标的取值范围，若不存在请说明理由．【答案】（1）221129x y +=（2）存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭，使得0TP TQ ⋅≤ 恒成立.【解析】【分析】（1）根据椭圆的离心率和三角形的面积可求基本量，从而可得椭圆的标准方程.（2）设该直线方程为：32y kx =-，()()()1122,,,,0,P x y Q x y T t ，联立直线方程和椭圆方程并消元，结合韦达定理和向量数量积的坐标运算可用,k t 表示TP TQ ⋅，再根据0TP TQ ⋅≤ 可求t 的范围.【小问1详解】因为椭圆的离心率为12e =，故2a c =，b =，其中c 为半焦距，所以()()32,0,0,,0,2A c B C ⎛⎫-- ⎪ ⎪⎝⎭，故13332222ABC S c c =⨯⨯=△，故c =a =，3b =，故椭圆方程为：221129x y +=.【小问2详解】若过点30,2⎛⎫-⎪⎝⎭的动直线的斜率存在，则可设该直线方程为：32y kx =-，设()()()1122,,,,0,P x y Q x y T t ，由22343632x y y kx ⎧+=⎪⎨=-⎪⎩可得()223412270k x kx +--=，故()222Δ144108343245760k kk=++=+>且1212221227,,3434k x x x x k k +==-++而()()1122,,,TP x y t TQ x y t =-=-，故()()121212123322TP TQ x x y t y t x x kx t kx t ⎛⎫⎛⎫⋅=+--=+---- ⎪⎪⎝⎭⎝⎭ ()()22121233122kx x k t x x t ⎛⎫⎛⎫=+-++++ ⎪ ⎪⎝⎭⎝⎭()22222731231342342k k k t t k k ⎛⎫⎛⎫⎛⎫=+⨯--+⨯++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭()2222222327271812332234k k k t t t k k ⎛⎫----++++ ⎪⎝⎭=+()22223321245327234t t k t k ⎛⎫⎡⎤+--++- ⎪⎣⎦⎝⎭=+，因为0TP TQ ⋅≤ 恒成立，故()223212450332702t t t ⎧+--≤⎪⎨⎛⎫+-≤⎪ ⎪⎝⎭⎩，解得332t -≤≤.若过点30,2⎛⎫-⎪⎝⎭的动直线的斜率不存在，则()()0,3,0,3P Q -或()()0,3,0,3P Q -，此时需33t -≤≤，两者结合可得332t -≤≤.综上，存在()30,32T t t ⎛⎫-≤≤⎪⎝⎭，使得0TP TQ ⋅≤ 恒成立.【点睛】思路点睛：圆锥曲线中的范围问题，往往需要用合适的参数表示目标代数式，表示过程中需要借助韦达定理，此时注意直线方程的合理假设.19.已知数列{}n a 是公比大于0的等比数列．其前n 项和为n S ．若1231,1a S a ==-．（1）求数列{}n a 前n 项和n S ；（2）设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩，11b =，其中k 是大于1的正整数．（ⅰ）当1k n a +=时，求证：1n k n b a b -≥⋅；（ⅱ）求1nS ii b =∑．【答案】（1）21n n S =-（2）①证明见详解；②()131419nn S ii n b=-+=∑【解析】【分析】（1）设等比数列{}n a 的公比为0q >，根据题意结合等比数列通项公式求q ，再结合等比数列求和公式分析求解；（2）①根据题意分析可知12,1k k n a b k -==+，()121n k k b -=-，利用作差法分析证明；②根据题意结合等差数列求和公式可得()()1211213143449k k k k i i b k k ---=⎡⎤=---⎣⎦∑，再结合裂项相消法分析求解.【小问1详解】设等比数列{}n a 的公比为0q >，因为1231,1a S a ==-，即1231a a a +=-，可得211q q +=-，整理得220q q --=，解得2q =或1q =-（舍去），所以122112nn n S -==--.【小问2详解】（i ）由（1）可知12n n a -=，且N*,2k k ∈≥，当124kk n a +=≥=时，则111221111k k k k k a n n a a -++⎧=<-=-⎨-=-<⎩，即11k k a n a +<-<可知12,1k k n a b k -==+，()()()1111222121k k k n a k k b b a a k k k k --+=+--⋅=+-=-，可得()()()()1112112122120kn k n k k k k k k k k b k a b ---=--+=--≥--=-⋅≥-，当且仅当2k =时，等号成立，所以1n k n b a b -≥⋅；（ii ）由（1）可知：1211nn n S a +=-=-，若1n =，则111,1S b ==；若2n ≥，则112k k k a a -+-=，当1221k k i -<≤-时，12i i b b k --=，可知{}i b 为等差数列，可得()()()111211112221122431434429k k k k k k k k i i b k kk k k -------=-⎡⎤=⋅+=⋅=---⎣⎦∑，所以()()()232113141115424845431434499nnS n n i i n b n n -=-+⎡⎤=+⨯-⨯+⨯-⨯+⋅⋅⋅+---=⎣⎦∑，且1n =，符合上式，综上所述：()131419nn S ii n b =-+=∑.【点睛】关键点点睛：1.分析可知当1221k k i -<≤-时，12i i b b k --=，可知{}i b 为等差数列；2.根据等差数列求和分析可得()()1211213143449k k k k i i b k k ---=⎡⎤=---⎣⎦∑.20.设函数()ln f x x x =．（1）求()f x 图象上点()()1,1f 处的切线方程；（2）若()(f x a x ≥-在()0,x ∞∈+时恒成立，求a 的取值范围；（3）若()12,0,1x x ∈，证明()()121212f x f x x x -≤-．【答案】（1）1y x =-（2）{}2（3）证明过程见解析【解析】【分析】（1）直接使用导数的几何意义；（2）先由题设条件得到2a =，再证明2a =时条件满足；（3）先确定()f x 的单调性，再对12,x x 分类讨论.【小问1详解】由于()ln f x x x =，故()ln 1f x x ='+.所以()10f =，()11f '=，所以所求的切线经过()1,0，且斜率为1，故其方程为1y x =-.【小问2详解】设()1ln h t t t =--，则()111t h t t t'-=-=，从而当01t <<时()0h t '<，当1t >时()0h t '>.所以()h t 在(]0,1上递减，在[)1,+∞上递增，这就说明()()1h t h ≥，即1ln t t -≥，且等号成立当且仅当1t =.设()()12ln g t a t t =--，则()((ln 12ln f x a x x x a x x a x g ⎛⎫⎫-=-=-=⋅ ⎪⎭⎝.当()0,x ∞∈+的取值范围是()0,∞+，所以命题等价于对任意()0,t ∞∈+，都有()0g t ≥.一方面，若对任意()0,t ∞∈+，都有()0g t ≥，则对()0,t ∞∈+有()()()()112012ln 12ln 1212g t a t t a t a t at a t t t ⎛⎫≤=--=-+≤-+-=+-- ⎪⎝⎭，取2t =，得01a ≤-，故10a ≥>.再取t =，得2022a a a ≤+-=-=-，所以2a =.另一方面，若2a =，则对任意()0,t ∞∈+都有()()()212ln 20g t t t h t =--=≥，满足条件.综合以上两个方面，知a 的取值范围是{}2.【小问3详解】先证明一个结论：对0a b <<，有()()ln 1ln 1f b f a a b b a-+<<+-.证明：前面已经证明不等式1ln t t -≥，故lnln ln ln ln ln ln 1ln 1bb b a a a b a a a b b b b b a b a a --=+=+<+---，且1ln ln ln ln ln ln ln ln 1ln 11a a b b a a b b b a b b a a a a a a b a b a b b⎛⎫--- ⎪--⎝⎭=+=+>=+----，所以ln ln ln 1ln 1b b a aa b b a -+<<+-，即()()ln 1ln 1f b f a a b b a-+<<+-.由()ln 1f x x ='+，可知当10e x <<时()0f x '<，当1ex >时()0f x '>.所以()f x 在10,e⎛⎤ ⎥⎝⎦上递减，在1e ,⎡⎫+∞⎪⎢⎣⎭上递增.不妨设12x x ≤，下面分三种情况（其中有重合部分）证明本题结论.情况一：当1211ex x ≤≤<时，有()()()()()()122122121ln 1f x f x f x f x x x x x x -=-<+-<-<情况二：当1210ex x <≤≤时，有()()()()12121122ln ln f x f x f x f x x x x x -=-=-.对任意的10,e c ⎛⎤∈ ⎥⎝⎦，设()ln ln x x x c c ϕ=--()ln 1x x ϕ=++'.由于()x ϕ'单调递增，且有111111ln 1ln11102e2e ec c ϕ⎛⎫⎪=+<+=-+= ⎪⎝⎭'，且当2124ln 1x c c ≥-⎛⎫- ⎪⎝⎭，2cx >2ln 1c ≥-可知()2ln 1ln 1ln 102c x x c ϕ⎛⎫=++>++=-≥ ⎪⎝⎭'.所以()x ϕ'在()0,c 上存在零点0x ，再结合()x ϕ'单调递增，即知00x x <<时()0x ϕ'<，0x x c <<时()0x ϕ'>.故()x ϕ在(]00,x 上递减，在[]0,x c 上递增.①当0x x c ≤≤时，有()()0x c ϕϕ≤=；②当00x x <<112221e e f f c⎛⎫=-≤-=< ⎪⎝⎭，故我们可以取1,1q c ⎫∈⎪⎭.从而当201cx q <<->()1ln ln ln ln 0x x x c c c c c c qc ϕ⎫=--<--<--=-<⎪⎭.再根据()x ϕ在(]00,x 上递减，即知对00x x <<都有()0x ϕ<；综合①②可知对任意0x c <≤，都有()0x ϕ≤，即()ln ln 0x x x c c ϕ=--.根据10,ec ⎛⎤∈ ⎥⎝⎦和0x c <≤的任意性，取2c x =，1x x =，就得到1122ln ln 0x x x x --≤.所以()()()()12121122ln ln f x f x f x f x x x x x -=-=-≤.情况三：当12101ex x <≤≤<时，根据情况一和情况二的讨论，可得()11e f x f ⎛⎫-≤≤ ⎪⎝⎭，()21e f f x ⎛⎫-≤≤ ⎪⎝⎭而根据()f x 的单调性，知()()()1211e f x f x f x f ⎛⎫-≤- ⎪⎝⎭或()()()1221e f x f x f f x ⎛⎫-≤- ⎪⎝⎭.故一定有()()12f x f x -≤成立.综上，结论成立.【点睛】关键点点睛：本题的关键在于第3小问中，需要结合()f x 的单调性进行分类讨论.。

自考真题11748《商务运营管理》021年04月试卷

机密★考试结束前浙江省2021年4月高等教育自学考试商务运营管理试题课程代码:11748 1.请考生按规定用笔将所有试题的答案涂㊁写在答题纸上㊂ 2.答题前,考生务必将自己的考试课程名称㊁姓名㊁准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上㊂选择题部分注意事项: 每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑㊂如需改动,用橡皮擦干净后,再选涂其他答案标号㊂不能答在试题卷上㊂一㊁单项选择题:本大题共10小题,每小题1分,共10分㊂在每小题列出的备选项中只有一项是最符合题目要求的,请将其选出㊂1.下列哪件商品可以认为是一件定制化产品?A.一辆汽车B.一本书C.一件特别纪念T恤衫D.一部手机2.某企业新建生产线投产后,正常年份固定成本总额为20000元,产品售价为每件10元,单位产品变动成本为6元㊂下列哪个答案是该生产线的盈亏平衡点?A.4000件B.5000件C.6000件D.7000件3.下列哪一项不是∙∙服务质量的维度?A.可靠性B.有形性C.响应性D.耐用性4.项目的一次性”的含义是指下列哪一项?A.项目的持续时间很短B.项目有确定的开始和结束时间C.项目将在未来一个不确定的时间结束D.项目可以在任何时间取消5.假设一个国家与另外一个国家处于同样的发展(人均收入)水平,两国将会有同样的消费水平,下列哪一项统计技术在估算一个国家的需求时会被采用?A.多因素指数法B.回归分析法C.横截面法D.时间序列法6.下列哪一项是持有半成品库存的原因?A.持有半成品库存可以保持存储区域满载B.持有半成品库存作为应对供应变化的缓冲C.持有半成品库存可以在机器故障㊁质量出现问题时保证过程独立运行D.持有半成品库存可以增加公司价值7.海尔集团按照不同客户的需求为其提供冰箱,这做到了下列哪一项运营战略的要素?A.成本B.柔性C.质量D.交货8.下列哪一项最好地描述了生产战略计划?A.生产战略计划包括产能的长期观点㊁工厂选址和流程B.生产战略计划包括产能的中期观点㊁选址和流程C.生产战略计划包括产能的短期观点㊁工厂选址和流程D.生产战略计划包括产能的直接观点㊁选址和流程9.在质量管理中,下列哪一项最好地描述了石川图的作用?A.寻找影响产品质量的主要原因B.分析造成质量问题的原因C.描述产品的统计规律D.寻找质量结果10.下列哪一项活动可以被称为项目?A.汽车制造B.餐馆做一顿饭C.摩天大楼的修建D.保险公司的工作非选择题部分注意事项: 用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上㊂二㊁名词解释题:本大题共5小题,每小题2分,共10分㊂11.全面质量管理12.控制过程13.供应链14.生产战略计划三㊁案例分析题(一):本大题共5小题,第16小题8分,第17小题10分,第18小题10分,第19小题7分,第20小题5分,共40分㊂杭州江南水乡餐饮公司杭州江南水乡餐饮公司(下文简称公司”)是一家定位于家庭聚餐和普通商务宴请的餐饮公司㊂随着生活水平的日益提高,家庭消费能力不容忽视㊂公司主打杭帮菜,菜肴丰富㊁色香味俱全,性价比高,勇于创新,因此赢得了顾客的口碑㊂公司在杭州老城区及城西站稳脚跟后,最近又将经营范围扩大到了杭州滨江区,准备开设新店㊂(案例信息纯属虚构,仅作考试用途㊂)16.结合该公司案例阐述运营管理的含义,并分析服务运营的关键特性㊂17.该公司在杭州老城区及城西所开的店生意兴隆,人气很旺,用餐高峰时段,排队等候的顾客较多㊂请结合排队心理学,列举5个可能的措施,抚慰排队的顾客㊂18.该公司定位于家庭聚餐和普通商务宴请,这与杭帮菜龙头品牌外婆家”起步时期比较接近㊂公司决定以外婆家”餐饮公司为基准,进一步提升竞争力㊂这是哪一种管理方法?详细阐述该公司如何运用这一管理方法提升竞争力㊂19.该公司准备在杭州滨江区开设新店㊂完成这个项目所要做的活动及每个活动的估计完工时间如表1所示㊂绘制关键工序分析图,标出每项活动的最早事件时间和最晚事件时间㊂表1　公司在滨江区开设新店项目必须完成的活动活动代码紧前活动需要时间(周)A 3B A4C A3D B3E B2F B,C1G D,E,F120.根据表1中的信息,解释关键工序,并指出表1中的关键工序㊂选答题(本部分包含四㊁五㊁六㊁七四大题,每大题20分,任选两大题作答,不得多选,多选者只按选答的前两大题计分,共40分㊂)四㊁案例分析题(二):本大题共3小题,第21小题8分,第22小题6分,第23小题6分,共20分㊂华海羽毛球俱乐部每周大约丢失㊁损坏20打羽毛球,羽毛球市场价格是每个5元;俱乐部每月保存羽毛球的费用是采购费用的1.5%并且每次订货需要7元的订货费;由于业务的需要,俱乐部要保持200打的最低库存㊂同时,华海俱乐部决心提高服务质量㊂21.阐述华海俱乐部保持库存的原因,说明可能带来哪几类库存成本㊂22.计算华海俱乐部订购羽毛球的经济批量㊂23.运用SERVQUAL模型分析华海俱乐部服务质量的决定因素㊂五㊁案例分析题(三):本大题共3小题,第24小题10分,第25小题6分,第26小题4分,共20分㊂鸿云科技是一家专业从事APP开发的公司㊂最近,公司业务量急剧增加,开发人员加班加点,疲惫不堪㊂运营经理意识到加强人力资源管理的重要性㊂24.阐述运营经理应该熟悉的主要的人力资源管理事项㊂25.从项目管理基础的角度,阐述APP开发项目需要平衡的三个主要特征㊂26.APP开发过程接近于哪一种制造过程?请陈述你的理由㊂六㊁案例分析题(四):本大题共3小题,第27小题8分,第28小题6分,第29小题6分,共20分㊂益康公司是一家生产智能电视的公司㊂该公司开展了卓有成效的质量管理,进行了全面生产维护,具有较强的竞争优势㊂公司不断开拓产品市场,决定进军欧洲市场㊂27.阐述全面生产维护的含义及主要特征㊂28.解释多因素指数法,并分析益康公司如何运用该方法预测欧洲市场智能电视的需求量㊂29.分析产能管理在益康公司新市场开发中的重要性㊂七㊁案例分析题(五):本大题共3小题,第30小题8分,第31小题6分,第32小题6分,共20分㊂绿源包装制品公司是一家专业生产及销售纸箱纸板等纸制品的企业,公司主要加工食品专用箱㊁邮政纸箱纸盒㊁服装箱㊁物流纸箱㊁快递纸箱等纸制产品㊂随着电子商务的蓬勃发展,公司的发展速度越来越快,高层也日益重视公司的可持续发展㊂30.简述三类不同的制造过程,分析绿源公司所选择的制造过程及原因㊂31.解释柔性的含义,并说明柔性对绿源公司的重要性㊂32.阐述环境管理的必要性,并说明绿源公司如何进行环境评价㊂。

试题第3和4页

2024届福建省泉州市普通高中毕业班质量监测三模语文试题答案

江苏省盐城市东台市第一教育联盟2021-2022学年五年级上学期数学期中试卷

中国计量大学801自动控制原理1-2015--2019年考研初试真题

【三套试卷】【沪教版】小学二年级数学上册第一单元练习试题附答案

浙江农林大学考研试题2014年-2016年902林业信息管理综合

内蒙古呼和浩特市实验中学2024-2025学年七年级上学期11月期中数学试题

华北水利水电大学 远程与继续教育学院 C语言程序设计试卷

2024年新高考改革适应性练习(3)(九省联考题型)数学卷及答案

《钢结构制作与安装》试题答案3-4

《汽车整车性能检测》试题库 试卷B

北师大版六年级语文上册期末测试题

《家畜育种学》试题与答案

2024年天津市高考数学真题试卷及答案

自考真题11748《商务运营管理》021年04月试卷

华北水利水电大学远程与继续教育学院 C语言程序设计试卷

《汽车整车性能检测》试题库试卷B