二次函数中特殊点解析(绝对精品)
二次函数知识点及经典例题详解最终

二次函数知识点总结及经典习题一、二次函数概念:1.二次函数的概念:一般地,形如 y ax 2 bx c ( a ,b ,c 是常数,a 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a 0 ,而b ,c 可以为零.二次函数的定义域是全体实数. 2. 二次函数 y ax 2bxc 的结构特征:⑴ 等号左边是函数,右边是关于自变量 x 的二次式, x 的最高次数是 2. ⑵ a ,b ,c 是常数, a 是二次项系数, b 是一次项系数, c 是常数项.二、二次函数的基本形式1. 二次函数基本形式: y ax 2 的性质:a 00,0x 0 时, y 随 x 的增大而增大; x 0时, y 随x 的增大而减小; x 0 时, y 有最小值0 .a 00,0x 0 时, y 随 x 的增大而减小; x 0时, y 随x 的增大而增大; x 0 时, y 有最大值0 .2a 0 0,cx 0时, y 随 x 的增大而增大; x 0时, y 随x 的增大而减小; x 0 时, y 有最小值c .a 0 0,cx 0 时, y 随 x 的增大而减小; x 0时, y 随x 的增大而增大; x 0 时, y 有最大值c .的性质:a 0h ,0xh 时,y 随x 的增大而增大;x h时,y 随x 的增大而减小;x h 时,y 有最小值0 .a 0h ,0x h 时,y 随x 的增大而减小;x h时,y 随x 的增大而增大;x h 时,y 有最大值0 .的性质:a 0h ,k x h 时,y 随x 的增大而增大;x h时,y 随x 的增大而减小;x h 时,y 有最小值k .a 0 h ,kx h 时,y 随x 的增大而减小;xh时,y 随x 的增大而增大;x h 时,y 有最大值k .三、二次函数图象的平移1.平移步骤:⑴将抛物线解析式转化成顶点式y a x h 2 k,确定其顶点坐标h,k;⑵保持抛物线y ax2 的形状不变,将其顶点平移到h ,k 处,具体平移方法如下:2.平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.四、二次函数y a x h 2 k与y ax2 bx c的比较从解析式上看,y a x h 2 k与y ax2 bx c是两种不同的表达形式,后者通过配方可以得到前者,即y h= -,k五、二次函数y ax2 bx c 的性质当a 0 时,抛物线开口向上,对称轴为- ,顶点坐标为.当x-时,y随x的增大而减小;当x 时,y随x的增大而增大;当x=时,y有最小值 .x- , 顶点坐标为.当x-时,y 随x 的大而增大y;当随x 时,y随 x 的增大而减小;当x=时 , y有最大值.六、二次函数解析式的表示方法1.一般式:y ax2 bx c(a,b,c为常数,a0);2.顶点式:y a(x h)2 k(a,h,k为常数,a0);3.两根式(交点式):y a(x x1 )(x x2 )(a0,x1 ,x2 是抛物线与x轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即b2 4ac 0 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1.二次项系数a⑴当a 0 时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大;⑵当a 0 时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.2.一次项系数b在二次项系数a确定的前提下,b决定了抛物线的对称轴.(同左异右b为0对称轴为y轴)3.常数项c⑴当c 0 时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正;⑵当c 0 时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0 ;⑶当c 0 时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来,c 决定了抛物线与y 轴交点的位置.八、二次函数与一元二次方程:1.二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程ax2 bx c 0 是二次函数y ax2 bx c 当函数值y 0 时的特殊情况. 图象与x 轴的交点个数:①当b2 4ac 0 时,图象与x 轴交于两点A x1,0,B x2,0(x1x2) ,其中的x1,x 2是一元二次方程ax2 bx c 0 a 0的两根.② 0 时,图象与x 轴只有一个交点;③ 0 时,图象与x 轴没有交点.1' 当a 0 时,图象落在x 轴的上方,无论x 为任何实数,都有y 0 ;2 ' 当a 0 时,图象落在x 轴的下方,无论x 为任何实数,都有y 0 .2.抛物线y ax2 bx c 的图象与y 轴一定相交,交点坐标为(0 ,c) ;中考题型例析1.二次函数解析式的确定例1 求满足下列条件的二次函数的解析式(1)图象经过 A(-1,3)、B(1,3)、C(2,6);(2)图象经过 A(-1,0)、B(3,0),函数有最小值-8;(3)图象顶点坐标是(-1,9),与 x 轴两交点间的距离是 6.分析:此题主要考查用待定系数法来确定二次函数解析式.可根据已知条件中的不同条件分别设出函数解析式,列出方程或方程组来求解.(1)解:设解析式为 y=ax2+bx+c,把 A(-1,3)、B(1,3)、C(2,6)各点代入上式得解得∴解析式为 y=x2+2.(2)解法1:由A(-1,0)、B(3,0)得抛物线对称轴为 x=1,所以顶点为(1,-8).设解析式为 y=a(x-h)2+k,即y=a(x-1)2-8.把x=-1,y=0 代入上式得 0=a(-2)2-8, ∴a=2. 即解析式为 y=2(x-1)2-8,即y=2x2-4x-6.解法2:设解析式为 y=a(x+1)(x-3),确定顶点为(1,-8)同上, 把x=1,y=-8 代入上式得-8=a(1+1)(1-3).解得 a=2,∴解析式为 y=2x2-4x-6.解法 3:∵图象过 A(-1,0),B(3,0)两点,可设解析式为:y=a(x+1)(x-3)=ax2-2ax-3a.∵函数有最小值-8.∴ =-8.又∵a≠0,∴a=2.∴解析式为 y=2(x+1)(x-3)=2x2-4x-6.(3)解:由顶点坐标(-1,9)可知抛物线对称轴方程是 x=-1, 又∵图象与 x 轴两交点的距离为 6,即 AB=6.由抛物线的对称性可得 A、B 两点坐标分别为 A(-4,0),B(2,0), 设出两根式y=a(x-x1)·(x-x2),将 A(-4,0),B(2,0)代入上式求得函数解析式为 y=-x2-2x+8.点评:一般地,已知三个条件是抛物线上任意三点(或任意 3 对 x,y 的值)可设表达式为y=ax2+bx+c,组成三元一次方程组来求解; 如果三个已知条件中有顶点坐标或对称轴或最值,可选用 y=a(x-h)2+k 来求解;若三个条件中已知抛物线与 x 轴两交点坐标,则一般设解析式为 y=a(x-x1)(x-x2).⎬2. 二次函数的图象例 2 y=ax 2+bx+c(a ≠0)的图象如图所示,则点 M(a,bc)在( ).A.第一象限B.第二象限C.第三象限D.第四象限分析:由图可知:a>0.抛物线与y 轴负半轴相交 c 0b bc>0.对称轴x2a在y 轴右侧 b∴点 M(a,bc)在第一象限. 答案:A.点评:本题主要考查由抛物线图象会确定 a 、b 、c 的符号.例 3 已知一次函数 y=ax+c 二次函数 y=ax 2+bx+c(a ≠0),它们在同一坐标系中的大致图象是().分析:一次函数 y=ax+c,当 a>0 时,图象过一、三象限;当 a<0 时,图象过二、 四象限;c>0 时, 直线交 y 轴于正半轴; 当 c<0 时, 直线交 y 轴于负半轴; 对于二次函数y= ax 2+bx+c(a ≠0)来讲:开口上下决定a 的正负左同右异(即对称轴在y 轴左侧,b 的符号与a 的符号相同;)来判别b 的符号抛物线与y 轴的正半轴或负半轴相交确定c 的正负解:可用排除法,设当 a>0 时,二次函数 y=ax 2+bx+c 的开口向上,而一次函数 y= ax+c 应过一、三象限,故排除 C;当 a<0 时,用同样方法可排除 A;c 决定直线与 y 轴交点;也在抛物线中决定抛物线与y 轴交点,本题中c 相同则两函数图象在y 轴上有相同的交点,故排除B.答案:D.23. 二次函数的性质例 4 对于反比例函数 y=-与二次函数 y=-x 2+3, 请说出他们的两个相同点:①, ②; 再说出它们的两个不同点:① ,②.分析:本小题是个开放性题目,可以从以下几点性质来考虑①增减性②图象的形状③ 最值④自变量取值范围⑤交点等.解:相同点:①图象都是曲线,②都经过(-1,2)或都经过(2,-1);不同点:①图象形状不同,②自变量取值范围不同,③一个有最大值,一个没有最大值. 点评:本题主要考查二次函数和反比例函数的性质,有关函数开放性题目是近几年命 题的热点.4. 二次函数的应用例 5 已知抛物线 y=x 2+(2k+1)x-k 2+k,(1)求证:此抛物线与 x 轴总有两个不同的交点.(2)设 x 1、x 2 是此抛物线与 x 轴两个交点的横坐标,且满足 x12+x 2=-2k 2+2k+1. ①求抛物线的解析式.②设点 P(m 1,n 1)、Q(m 2,n 2)是抛物线上两个不同的点, 且关于此抛物线的对称轴对称. 求 m+m 的值.分析:(1)欲证抛物线与 x 轴有两个不同交点,可将问题转化为证一元二次方程有两个不相等实数根,故令 y=0,证△>0 即可.(2)①根据二次函数的图象与x 轴交点的横坐标即是一元二次方程的根.由根与系数的关系,求出 k 的值,可确定抛物线解析式;②由 P 、Q 关于此抛物线的对称轴对称得 n 1=n 2, 由 n 1=m 12+m 1,n 2=m 22+m 2 得m 12+m 1=m 22+m 2,即(m 1-m 2)(m 1+m 2+1)=0 可求得 m 1+m 2= - 1.解:(1)证明:△=(2k+1)2-4(-k 2+k)=4k 2+4k+1+4k 2-4k=8k 2+1. ∵8k 2+1>0,即△>0,∴抛物线与 x 轴总有两个不同的交点.(2) ①由题意得 x 1+x 2=-(2k+1), x 1· x 2=-k 2+k. ∵x 1 2+x 2 2=-2k 2+2k+1,∴(x 1+x 2)2-2x 1x 2=- 2k 2+2k+1, 即(2k+1)2-2(-k 2+k)=-2k 2+k+1, 4k 2+4k+1+2k 2-2k= - 2k 2+2k+1. ∴8k 2=0, ∴k=0,∴抛物线的解析式是 y=x 2+x.②∵点 P 、Q 关于此抛物线的对称轴对称, ∴n 1=n 2.2 2 又 n 1=m 12+m 1,n 2=m 2+m 2. ∴m 12+m 1=m2+m 2, 即(m 1-m 2)(m 1+m 2+1)=0. ∵P 、Q 是抛物上不同的点, ∴m 1≠m 2,即 m 1-m 2≠0. ∴m 1+m 2+1=0 即 m 1+m 2=-1.点评:本题考查二次函数的图象(即抛物线)与 x 轴交点的坐标与一元二次方程根与系数的关系.二次函数经常与一元二次方程相联系并联合命题是中考的热点.二次函数对应练习试题一、选择题1. 二次函数 yx 2 4x 7 的顶点坐标是( )A.(2,-11)B.(-2,7)C.(2,11)D. (2,-3)2. 把抛物线 y 2x 2 向上平移 1 个单位,得到的抛物线是( )A. y2(x 1)2B. y2(x 1)2C. y 2x 2 1D. y 2x 2 13.函数 ykx 2k 和 yk(k 0) 在同一直角坐标系中图象可能是图中的( )x4.已知二次函数 y ax 2 bx c ( a 0) 的图象如图所示,则下列结论: ①a,b 同号; ② 当 x1和 x 3时,函数值相等;③ 4 a b 0 ④当 y 2时,x 的值只能取 0.其中正确的个数是( )A.1 个B.2 个C. 3 个D.4 个5.已知二次函数y ax2 bx c(a 0) 的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x 的一元二次方程ax2 bx c 0 的两个根分别是x1 1.3和x()2A.-1.3 B.-2.3 C.-0.3 D.-3.36. 已知二次函数y ax2 bx c 的图象如图所示,则点(ac, bc) 在()A.第一象限B.第二象限C.第三象限D.第四象限7.方程2x x2=的正根的个数为()A.0 个B.1 个C.2 个. 3 个8.已知抛物线过点 A(2,0),B(-1,0),与y 轴交于点 C,且 OC=2.则这条抛物线的解析式为A. y x2 x 2B. y x2 x 2C. y x2 x 2 或y x2 x 2D. y x2x 2 或y x2 x 2二、填空题9.二次函数y x2 bx 3 的对称轴是x 2 ,则b 。
二次函数知识点汇总(全)
二次函数知识点(第一讲)一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
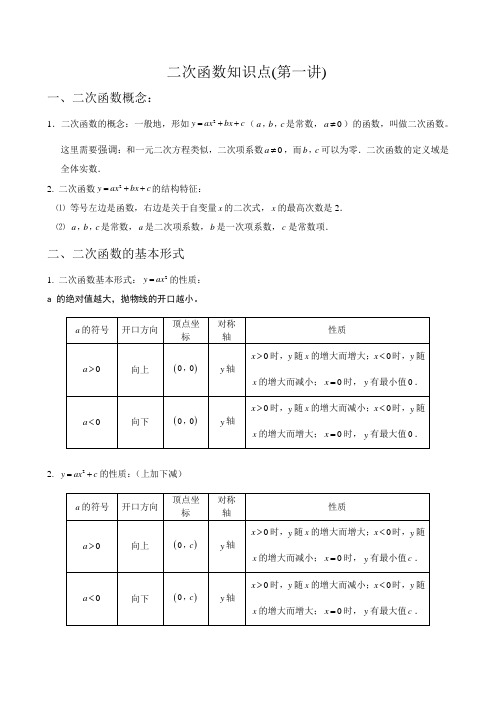
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质:(上加下减)3. ()2y a x h =-的性质:(左加右减)4. ()2y a x h k =-+的性质:三、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k=-+与2y axbx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba -<,即抛物线的对称轴在y 轴左侧;当0b =时,02ba -=,即抛物线的对称轴就是y 轴;当0b <时,02ba->,即抛物线对称轴在y 轴的右侧.⑵ 在0a <的前提下,结论刚好与上述相反,即当0b >时,02ba ->,即抛物线的对称轴在y 轴右侧;当0b =时,02ba -=,即抛物线的对称轴就是y 轴;当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧.总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:二次函数考查重点与常见题型1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2. 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如: 如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )y y y y1 10 x o-1 x 0 x 0 -1 x A B C D3. 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如: 已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x ,求这条抛物线的解析式。
(最新整理)初三数学二次函数知识点总结

初三数学二次函数知识点总结
编辑整理:
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对 文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初三数学二次函数知识点总结) 的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,这将是我们进步 的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以 下为初三数学二次函数知识点总结的全部内容。
五点绘图法:利用配方法将二次函数 y ax2 bx c 化为顶点式 y a(x h)2 k ,确定其开口方
向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:
顶点、与 y 轴的交点 0, c 、以及 0, c 关于对称轴对称的点 2h,c 、与 x 轴的交点 x1 , 0 , x2 , 0 (若与 x 轴没有交点,则取两组关于对称轴对称的点)。
二次函数解析式的确定:
根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解
析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:
1。 一般式: y ax2 bx c ( a , b , c 为常数, a 0 ); 2. 顶点式: y a(x h)2 k ( a , h , k 为常数, a 0 ); 3。 两根式: y a(x x1)(x x2 ) ( a 0 , x1 , x2 是抛物线与 x 轴两交点的横坐标)。 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成
交点式,只有抛物线与 x 轴有交点,即 b2 4ac 0 时,抛物线的解析式才可以用交点式表 示.二次函数解析式的这三种形式可以互化.
—二次函数讲解(精华版)

内容:1、一元一次函数;2、一元二次函数;3、反比例函数★二次函数知识点 一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式:1. 二次函数基本形式:二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中a b ac k a b h 4422-=-=,.2.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2三、二次函数的性质:1、2y ax =的性质:a 的绝对值越大,抛物线的开口越小。
2.2y ax c =+的性质:上加下减。
a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()00,y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0.0a <向下()00,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0.a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()0c ,y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c .3.()2y a x h =-的性质:左加右减。
4.()2y a x h k=-+的性质:5.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.6.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线a b x 2-=. (2)配方法:运用配方法将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点. 四、二次函数图象的平移:0a <向下()0c ,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c .a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()0h ,X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0.0a <向下()0h ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0.a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()h k ,X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值k .0a <向下()h k ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值k .1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k=-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:向右(h >0)【或左(h <0)】平移 |k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向右(h >0)【或左(h <0)】平移|k|个单位向右(h >0)【或左(h <0)】平移|k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向上(k >0)【或向下(k <0)】平移|k |个单位y=a (x-h )2+ky=a (x-h )2y=ax 2+ky=ax 22. 平移规律:在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”.方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)五、二次函数()2y a x h k=-+与2y ax bx c =++的比较从解析式上看,()2y a x h k=-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 六、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠. ⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大. 总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a的大小决定开口的大小.2. 一次项系数b :在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02b a -<,即抛物线的对称轴在y 轴左侧;当0b =时,02b a -=,即抛物线的对称轴就是y 轴;当0b <时,02b a ->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即当0b >时,02ba ->,即抛物线的对称轴在y 轴右侧;当0b =时,02b a -=,即抛物线的对称轴就是y 轴;当0b <时,02b a -<,即抛物线对称轴在y 轴的左侧.总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.(3)ab 的符号的判定:对称轴a bx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异”3. 常数项c :⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. 二次函数解析式的确定:一般来说,有如下几种情况: 1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式. 七、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达1. 关于x 轴对称:2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k=-+关于x 轴对称后,得到的解析式是()2y a x h k=---;2. 关于y 轴对称:2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2y a x h k=-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称:2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-;()2y a x h k=-+关于原点对称后,得到的解析式是()2y a x h k=-+-;4. 关于顶点对称(即:抛物线绕顶点旋转180°):2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a =--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称:()2y a x h k=-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k=-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式. 八、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离2214b acAB x x a-=-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ; 3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系0∆> 抛物线与x 轴有两个交点二次三项式的值可正、可零、可负一元二次方程有两个不相等实根0∆= 抛物线与x 轴只有一个交点二次三项式的值为非负 一元二次方程有两个相等的实数根 0∆<抛物线与x 轴无交点二次三项式的值恒为正 一元二次方程无实数根.九、函数的应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少★二次函数考查重点与常见题型1、考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是( )。
(完整版),初中二次函数知识点详解及典型例题,推荐文档

解一元二次不等式:首先化成一般式,构造函数第二站。
判别式值若非负,曲线横轴有交点。
a正开口它向上,大于零则取两边。
代数式若小于零,解集交点数之间。
方程若无实数根,口上大零解为全。
小于零将没有解,开口向下正相反。
13.1 用公式法解一元二次方程要用公式解方程,首先化成一般式。
调整系数随其后,使其成为最简比。
确定参数abc,计算方程判别式。
判别式值与零比,有无实根便得知。
有实根可套公式,没有实根要告之。
用常规配方法解一元二次方程:左未右已先分离,二系化“1”是其次。
一系折半再平方,两边同加没问题。
左边分解右合并,直接开方去解题。
该种解法叫配方,解方程时多练习。
用间接配方法解一元二次方程:已知未知先分离,因式分解是其次。
调整系数等互反,和差积套恒等式。
完全平方等常数,间接配方显优势【注】恒等式解一元二次方程:方程没有一次项,直接开方最理想。
如果缺少常数项,因式分解没商量。
b、c相等都为零,等根是零不要忘。
b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方。
二次函数:二次方程零换y,二次函数便出现。
全体实数定义域,图像叫做抛物线。
抛物线有对称轴,两边单调正相反。
A定开口及大小,线轴交点叫顶点。
顶点非高即最低。
上低下高很显眼。
如果要画抛物线,平移也可去描点,提取配方定顶点,两条途径再挑选。
列表描点后连线,平移规律记心间。
左加右减括号内,号外上加下要减。
二次方程零换y,就得到二次函数。
图像叫做抛物线,定义域全体实数。
A定开口及大小,开口向上是正数。
绝对值大开口小,开口向下A负数。
抛物线有对称轴,增减特性可看图。
线轴交点叫顶点,顶点纵标最值出。
如果要画抛物线,描点平移两条路。
提取配方定顶点,平移描点皆成图。
列表描点后连线,三点大致定全图。
若要平移也不难,先画基础抛物线,顶点移到新位置,开口大小随基础。
【注】基础抛物线。
二次函数的特征点与特性

二次函数的特征点与特性二次函数是数学中常见的一种函数类型,其形式为y = ax^2 + bx + c,其中a、b、c为常数,且a ≠ 0。
二次函数的图像为抛物线,具有一些特征点和特性,下面将对二次函数的特征点和特性进行详细论述。
1. 零点二次函数的零点是函数图像与x轴相交的点,即使y = 0时的x值。
要求出二次函数的零点,可以通过求解二次方程ax^2 + bx + c = 0来实现。
根据求根公式可知,二次方程的解为x = (-b ± √(b^2 - 4ac)) / 2a。
其中,如果判别式D = b^2 - 4ac > 0,则方程有两个不相等的实根;如果D = 0,则方程有两个相等的实根;如果D < 0,则方程没有实根。
2. 顶点二次函数的顶点是函数图像的最高或最低点,也就是抛物线的顶峰或谷底。
二次函数的顶点的x坐标可以通过公式x = -b / (2a)求得,而y 坐标则可通过将x值代入函数公式y = ax^2 + bx + c计算得出。
3. 对称轴二次函数的对称轴是通过顶点且垂直于x轴的一条直线。
对称轴的方程为x = -b / (2a),其中a和b为二次函数的系数。
关于对称轴,二次函数的图像是左右对称的。
4. 开口方向二次函数的抛物线的开口方向由二次项a的正负决定。
当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。
5. 最值二次函数的最值指的是函数图像的最高点或最低点的y坐标。
当抛物线开口向上时,最小值即为顶点的纵坐标;当抛物线开口向下时,最大值即为顶点的纵坐标。
6. 范围二次函数的范围是指函数图像上所有可能的y值组成的集合。
当二次函数开口向上时,范围为[y0, +∞),其中y0为顶点的纵坐标;当二次函数开口向下时,范围为(-∞, y0]。
7. 正负性二次函数的正负性指的是函数值的正负关系。
根据二次函数的特性,当a > 0时,函数在对称轴两侧是递增的,即当x < -b / (2a)时,函数值为负,当x > -b / (2a)时,函数值为正;当a < 0时,函数在对称轴两侧是递减的,即当x < -b / (2a)时,函数值为正,当x > -b / (2a)时,函数值为负。
二次函数知识点汇总及详细剖析

二次函数知识点汇总及详细剖析函数中,有一种多项式函数形如y=ax^2+bx+c(a,b,c是常数,a≠0),最高次数是2,这种函数,我们称之为二次函数。
二次函数知识点颇多,初高中都会出现,在初中,刚刚出现在一次函数数形结合学习之后,因此,二次函知识点离不开数形结合思想。
二次函数主要有哪些知识点?一、定义与定义表达式:一般地,自变量x和因变量y之间存在如下关系:y=ax^2+bx+c(a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.)则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
二、二次函数的三种表达式一般式:y=ax^2;+bx+c(a,b,c为常数,a≠0)顶点式:y=a(x-h)^2;+k[抛物线的顶点P(h,k)]交点式:y=a(x-x1)(x-x2)[仅限于与x轴有交点A(x1,0)和B(x2,0)的抛物线]注:在3种形式的互相转化中,有如下关系:h=-b/2ak=(4ac-b^2;)/4ax1,x2=(-b±√b^2;-4ac)/2a三、二次函数的图像在平面直角坐标系中作出二次函数y=x2的图像,可以看出,二次函数的图像是一条抛物线。
四、抛物线的性质1.抛物线是轴对称图形。
对称轴为直线:x=-b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
特别地,当b=0时,抛物线的对称轴是y轴(即直线x=0)2.抛物线有一个顶点P,坐标为P[-b/2a,(4ac-b2;)/4a]。
当-b/2a=0时,P在y轴上;当Δ=b^2-4ac=0时,P在x轴上。
3.二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
|a|越大,则抛物线的开口越小。
4.一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右。
(完整版)二次函数知识点及经典例题详解最终
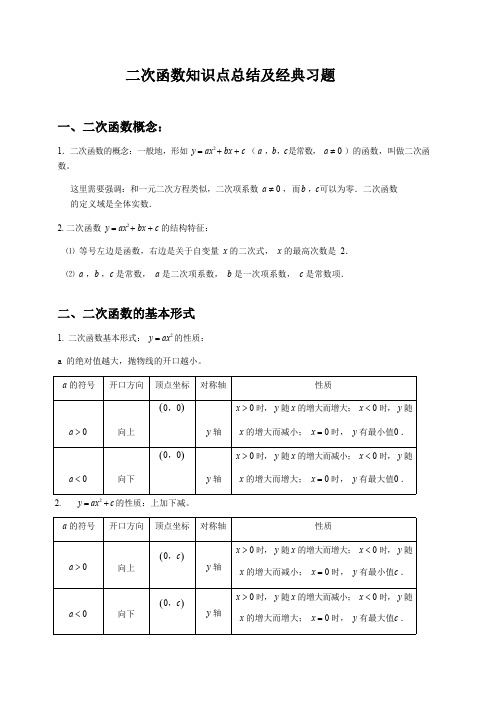
二次函数知识点总结及经典习题一、二次函数概念:1.二次函数的概念:一般地,形如y =ax2 +bx +c (a ,b,c是常数,a ≠ 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a ≠ 0 ,而b ,c 可以为零.二次函数的定义域是全体实数.2. 二次函数y =ax2 +bx +c 的结构特征:⑴等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a ,b ,c 是常数, a 是二次项系数, b 是一次项系数, c 是常数项.二、二次函数的基本形式1.二次函数基本形式:y =ax2 的性质:a 的绝对值越大,抛物线的开口越小。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(0,0)y 轴x > 0 时,y 随x 的增大而增大;x < 0 时,y 随x 的增大而减小;x = 0 时,y 有最小值0 .a < 0向下(0,0)y 轴x > 0 时,y 随x 的增大而减小;x < 0 时,y 随x 的增大而增大;x = 0 时,y 有最大值0 .2.y =ax2 +c 的性质:上加下减。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(0,c)y 轴x > 0 时,y 随x 的增大而增大;x < 0 时,y 随x 的增大而减小;x = 0 时,y 有最小值c .a < 0向下(0,c)y 轴x > 0 时,y 随x 的增大而减小;x < 0 时,y 随x 的增大而增大;x = 0 时,y 有最大值c .3.y = a (x - h )2的性质:左加右减。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(h ,0)X=hx > h 时, y 随 x 的增大而增大; x < h 时, y 随x 的增大而减小; x = h 时, y 有最小值0 .a < 0向下(h ,0)X=hx > h 时, y 随 x 的增大而减小; x < h 时, y 随x 的增大而增大; x = h 时, y 有最大值0 .4.y = a (x - h )2+ k 的性质:a 的符号开口方向顶点坐标对称轴性质a > 0向上(h ,k )X=h x > h 时, y 随 x 的增大而增大;x < h 时, y 随x 的增大而减小; x = h 时, y 有最小值 k .a < 0向下(h ,k )X=hx > h 时, y 随 x 的增大而减小;x < h 时, y 随x 的增大而增大; x = h 时, y 有最大值 k .三、二次函数图象的平移1.平移步骤:⑴ 将抛物线解析式转化成顶点式 y = a (x - h )2+ k ,确定其顶点坐标(h ,k );⑵ 保持抛物线 y = ax 2 的形状不变,将其顶点平移到(h ,k )处,具体平移方法如下:2.平移规律在原有函数的基础上“ h 值正右移,负左移; k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”.四、二次函数 y = a (x - h )2+ k 与 y = ax 2 + bx + c 的比较从解析式上看, y = a (x - h )2+ k 与 y = ax 2 + bx + c 是两种不同的表达形式,后者通过配方可以得到前者,即 y = a +,其中h= - ,k=(b2a )24ac - b 24ab2a 4ac - b 24a 五、二次函数 y = ax 2 + bx + c 的性质当 a > 0 时,抛物线开口向上,对称轴为,顶点坐标为.b2a (‒b 2a ,4ac ‒ b 24a)当x < - 时,y 随x 的增大而减小;b2a当x > - 时,y 随x 的增大而增大;b2a 当x =- 时,y 有最小值 .b 2a 4ac ‒ b 24a 2. 当α<0时,抛物线开口向下,对称轴为x =- , 顶点坐标为.当b2a(‒b 2a ,4ac ‒ b 24a)x < -时, y 随 x 的大而增大y;当随 x > - 时,y 随 x 的增大而减小;当x =- 时 , y 有最大值.b2ab 2a b 2a 4ac ‒ b 24a六、二次函数解析式的表示方法1.一般式: y = ax 2 + bx + c ( a , b , c 为常数, a ≠ 0 );2.顶点式: y = a (x - h )2 + k ( a , h , k 为常数, a ≠ 0 );3.两根式(交点式): y = a (x - x 1 )(x - x 2 ) ( a ≠ 0 , x 1 , x 2 是抛物线与 x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式, 只有抛物线与 x 轴有交点,即b 2 - 4ac ≥ 0 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1.二次项系数 a ⑴ 当 a > 0 时,抛物线开口向上, a 的值越大,开口越小,反之 a 的值越小,开口越大;⑵ 当 a < 0 时,抛物线开口向下, a 的值越小,开口越小,反之 a 的值越大,开口越大.2.一次项系数b 在二次项系数 a 确定的前提下, b 决定了抛物线的对称轴.(同左异右b 为 0 对称轴为 y 轴)3.常数项c⑴ 当c > 0 时,抛物线与 y 轴的交点在 x 轴上方,即抛物线与 y 轴交点的纵坐标为正;⑵ 当c = 0 时,抛物线与 y 轴的交点为坐标原点,即抛物线与 y 轴交点的纵坐标为0 ;⑶ 当c < 0 时,抛物线与 y 轴的交点在 x 轴下方,即抛物线与 y 轴交点的纵坐标为负. 总结起来, c 决定了抛物线与 y 轴交点的位置.八、二次函数与一元二次方程:1.二次函数与一元二次方程的关系(二次函数与 x 轴交点情况):一元二次方程 ax 2 + bx + c = 0 是二次函数 y = ax 2 + bx + c 当函数值 y = 0 时的特殊情况. 图象与 x 轴的交点个数:① 当 ∆ = b 2 - 4ac > 0 时,图象与 x 轴交于两点 A (x 1 ,0),B (x 2 ,0 ) (x 1 ≠ x 2 ) ,其中的 x 1 ,x 2是一元二次方程 ax 2 + bx + c = 0(a ≠ 0)的两根.②当∆= 0 时,图象与x 轴只有一个交点;③当∆< 0 时,图象与x 轴没有交点.1' 当a > 0 时,图象落在x 轴的上方,无论x 为任何实数,都有y > 0 ;2 ' 当a < 0 时,图象落在x 轴的下方,无论x 为任何实数,都有y < 0 .2.抛物线y =ax2 +bx +c 的图象与y 轴一定相交,交点坐标为(0 ,c) ;中考题型例析1.二次函数解析式的确定例 1求满足下列条件的二次函数的解析式(1)图象经过 A(-1,3)、B(1,3)、C(2,6);(2)图象经过 A(-1,0)、B(3,0),函数有最小值-8;(3)图象顶点坐标是(-1,9),与 x 轴两交点间的距离是 6.分析:此题主要考查用待定系数法来确定二次函数解析式.可根据已知条件中的不同条件分别设出函数解析式,列出方程或方程组来求解.(1)解:设解析式为 y=ax 2+bx+c,把 A(-1,3)、B(1,3)、C(2,6)各点代入上式得解得 {3=a ‒b +c 3=a +b +c 6=4a +2b +c {a =1b =0c =2∴解析式为 y=x 2+2.(2)解法1:由 A(-1,0)、B(3,0)得抛物线对称轴为 x=1,所以顶点为(1,-8). 设解析式为 y=a(x-h)2+k,即 y=a(x-1)2-8.把 x=-1,y=0 代入上式得 0=a(-2)2-8,∴a=2. 即解析式为 y=2(x-1)2-8,即 y=2x 2-4x-6.解法2:设解析式为 y=a(x+1)(x-3),确定顶点为(1,-8)同上, 把 x=1,y=-8 代入上式得-8=a(1+1)(1-3).解得 a=2,∴解析式为 y=2x 2-4x-6.解法 3:∵图象过 A(-1,0),B(3,0)两点,可设解析式为:y=a(x+1)(x-3)=ax 2-2ax-3a.∵函数有最小值-8.∴ =-8.4a (‒3a )‒(2a)24a又∵a≠0,∴a=2.⎬∴解析式为 y=2(x+1)(x-3)=2x 2-4x-6.(3)解:由顶点坐标(-1,9)可知抛物线对称轴方程是 x=-1, 又∵图象与 x 轴两交点的距离为 6,即 AB=6.由抛物线的对称性可得 A 、B 两点坐标分别为 A(-4,0),B(2,0), 设出两根式 y=a(x-x 1)·(x-x 2),将 A(-4,0),B(2,0)代入上式求得函数解析式为 y=-x 2-2x+8.点评:一般地,已知三个条件是抛物线上任意三点(或任意 3 对 x,y 的值)可设表达式为y=ax 2+bx+c,组成三元一次方程组来求解; 如果三个已知条件中有顶点坐标或对称轴或最值,可选用 y=a(x-h)2+k 来求解;若三个条件中已知抛物线与 x 轴两交点坐标,则一般设解析式为 y=a(x-x 1)(x-x 2).2.二次函数的图象例 2y=ax 2+bx+c(a≠0)的图象如图所示,则点 M(a,bc)在().A.第一象限B.第二象限C.第三象限D.第四象限分析:由图可知:抛物线开口向上⇒ a>0.抛物线与y 轴负半轴相交 ⇒ c < 0b ⇒ bc>0.对称轴x = - 2a 在y 轴右侧 ⇒ b < 0∴点 M(a,bc)在第一象限. 答案:A.点评:本题主要考查由抛物线图象会确定 a 、b 、c 的符号.例 3 已知一次函数 y=ax+c 二次函数 y=ax 2+bx+c(a≠0),它们在同一坐标o系中的大致图象是().分析:一次函数 y=ax+c,当 a>0 时,图象过一、三象限;当 a<0 时,图象过二、 四象限;c>0 时, 直线交 y 轴于正半轴; 当 c<0 时, 直线交 y 轴于负半轴; 对于二次函数y= ax 2+bx+c(a≠0)来讲:⎧开口上下决定a 的正负⎪左同右异(即对称轴在y 轴左侧,b 的符号⎪⎨与a 的符号相同;)来判别b 的符号⎪抛物线与y 轴的正半轴或负半轴相交确定⎪⎩c 的正负解:可用排除法,设当 a>0 时,二次函数 y=ax 2+bx+c 的开口向上,而一次函数 y= ax+c 应过一、三象限,故排除 C;当 a<0 时,用同样方法可排除 A;c 决定直线与 y 轴交点;也在抛物线中决定抛物线与y 轴交点,本题中c 相同则两函数图象在y 轴上有相同的交点,故排除B.答案:D.3.二次函数的性质例 4对于反比例函数 y=-与二次函数 y=-x 2+3, 请说出他们的两个相同点:2x ①, ②; 再说出它们的两个不同点:① ,②.分析:本小题是个开放性题目,可以从以下几点性质来考虑①增减性②图象的形状③ 最值④自变量取值范围⑤交点等.解:相同点:①图象都是曲线,②都经过(-1,2)或都经过(2,-1);不同点:①图象形状不同,②自变量取值范围不同,③一个有最大值,一个没有最大值. 点评:本题主要考查二次函数和反比例函数的性质,有关函2数开放性题目是近几年命题的热点.4.二次函数的应用例 5 已知抛物线 y=x 2+(2k+1)x-k 2+k,(1)求证:此抛物线与 x 轴总有两个不同的交点.(2)设 x 1、x 2 是此抛物线与 x 轴两个交点的横坐标,且满足 x 12+x 2=-2k 2+2k+1.①求抛物线的解析式.②设点 P (m 1,n 1)、Q(m 2,n 2)是抛物线上两个不同的点, 且关于此抛物线的对称轴对称. 求 m+m 的值.分析:(1)欲证抛物线与 x 轴有两个不同交点,可将问题转化为证一元二次方程有两个不相等实数根,故令 y=0,证△>0 即可.(2)①根据二次函数的图象与x 轴交点的横坐标即是一元二次方程的根.由根与系数的关系,求出 k 的值,可确定抛物线解析式;②由 P 、Q 关于此抛物线的对称轴对称得 n 1=n 2, 由 n 1=m 12+m 1,n 2=m 22+m 2得 m 12+m 1=m 22+m 2,即(m 1-m 2)(m 1+m 2+1)=0 可求得 m 1+m 2= - 1.解:(1)证明:△=(2k+1)2-4(-k 2+k)=4k 2+4k+1+4k 2-4k=8k 2+1.∵8k 2+1>0,即△>0,∴抛物线与 x 轴总有两个不同的交点.(2) ①由题意得 x 1+x 2=-(2k+1), x 1· x 2=-k 2+k.∵x 1 2+x 2 2=-2k 2+2k+1,∴(x 1+x 2)2-2x 1x 2=- 2k 2+2k+1, 即(2k+1)2-2(-k 2+k)=-2k 2+k+1, 4k 2+4k+1+2k 2-2k= - 2k 2+2k+1.∴8k 2=0, ∴k=0,∴抛物线的解析式是 y=x 2+x.22②∵点 P 、Q 关于此抛物线的对称轴对称,∴n 1=n 2.又 n 1=m 12+m 1,n 2=m 2+m 2.∴m 12+m 1=m 2+m 2,即(m 1-m 2)(m 1+m 2+1)=0.∵P 、Q 是抛物上不同的点,∴m 1≠m 2,即 m 1-m 2≠0.∴m 1+m 2+1=0 即 m 1+m 2=-1.点评:本题考查二次函数的图象(即抛物线)与 x 轴交点的坐标与一元二次方程根与系数的关系.二次函数经常与一元二次方程相联系并联合命题是中考的热点.二次函数对应练习试题一、选择题1.二次函数 y = x 2- 4x - 7 的顶点坐标是()A.(2,-11)B.(-2,7)C.(2,11)D. (2,-3)2.把抛物线 y = -2x 2 向上平移 1 个单位,得到的抛物线是()A. y = -2(x +1)2B. y = -2(x -1)2C. y = -2x 2+1D. y = -2x 2-13.函数 y = kx 2- k 和 y = k(k ≠ 0) 在同一直角坐标系中图象可能是图中的()x4.已知二次函数 y = ax 2+ bx + c (a ≠ 0) 的图象如图所示,则下列结论: ①a,b同号;② 当 x = 1和 x = 3时,函数值相等;③ 4a + b = 0 ④当 y = -2时, x 的值只能取0.其中正确的个数是( )A.1 个B.2 个C. 3 个D.4 个5.已知二次函数 y = ax 2+ bx + c (a ≠ 0) 的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于 x 的一元二次方程ax 2+ bx + c = 0 的两个根分别是 x 1 = 1.3和x 2 =()A.-1.3 B.-2.3 C.-0.3 D.-3.36. 已知二次函数 y = ax 2 + bx + c 的图象如图所示,则点(ac , bc ) 在( )A .第一象限B .第二象限C .第三象限D .第四象限7.方程 2x - x 2= 的正根的个数为()2xA.0 个B.1 个C.2 个.3个08.已知抛物线过点 A(2,0),B(-1,0),与 y 轴交于点 C,且 OC=2.则这条抛物线的解析式为A. y = x 2 - x - 2B. y = -x 2+ x + 2C. y = x 2- x - 2 或 y = -x 2+ x + 2 D. y = -x 2- x - 2 或 y = x 2+ x + 2二、填空题9.二次函数 y = x 2+ bx + 3 的对称轴是 x = 2 ,则b = 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数中特殊点解析
【精练】大桥拱形可以近似看作抛物线的一部分.在大桥截面1∶11000的比例图上,跨度AB=5 cm,拱高OC=0.9 cm,线段DE表示大桥拱内桥长,DE∥AB,如图(1).在比例图上,以直线AB为x轴,抛物线的对称轴为y轴,以1 cm作为数轴的单位长度,建立平面直角坐标系,如图(2).
(1)求出图(2)上以这一部分抛物线为图象的函数解析式,写出函数定义域;
(2)如果DE与AB的距离OM=0.45 cm,求大桥拱内实际桥长(备用数据:,计算结果精确到1米).
【知识规律串讲】
二次函数y=ax2+bx+c的顶点坐标,对称轴方程及与坐标轴的交点的坐标,横坐标取±1等都是二次函数的特殊点,也成为近几中考命题的趋势。
1.顶点坐标,对称轴方程。
二次函数的形式有三类:一般形式y=ax2+bx+c,它的顶点坐标为,对称称方程为x=;顶点式y=a(x+h)2+k,它的顶点坐标为(-h,k),对称轴方程为x=-h;交点式y=a(x-x1)(x-x2),它的顶点坐标为,
对称轴方程为x=。
2.与x轴的交点。
当b2-4ac>0时,抛物线与x轴的交点坐标是以方程ax2+bx+c=0的两根为横坐标的两个点;当b2-4ac=0时抛物线与x轴的交点坐标是顶点坐标的横坐标,也是以方程ax2+bx+c=0的一根为横坐标的一个点;当b2-4ac<0时,抛物线与x轴没有交点。
3.与y轴的交点。
抛物线y=ax2+bx+c与y轴的交点坐标总是(0,c),特别的当c=0的时候,抛物线过原点,这也是一个特殊点。
4.横坐标取1时,y=ax2+bx+c的解析式对应的是a+b+c,横坐标取-1时,y=ax2+bx+c 的解析式对应的是a-b+c。
这也是特殊式,用于考察当x=±1时所对应的函数值与0的大小关系。
【典型试题】
例1:已知抛物线与x轴交于A、B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
例2:已知抛物线y=-x2+mx-m+2.
(1)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=,试求m的值;(2)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且△MNC 的面积等于27,试求m的值.
例3:已知:抛物线与x轴的一个交点为A(-1,0).(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5∶2的点,如果点E 在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
(2009•河南)如图,在平面直角坐标系中,已知矩形ABC D的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=a x2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段C D向终点D 运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E.
①过点E作EF⊥A D于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接E Q.在点P、Q运动的过程中,判断有几个时刻使得△C E Q是等腰三角形?请直接写出相应的t值.
(2010•德州)已知二次函数y=ax2+b x+c的图象经过点A(3,0),B(2,-3),C(0,-3).(1)求此函数的解析式及图象的对称轴;
(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t 秒.
①当t为何值时,四边形ABPQ为等腰梯形;
②设P Q与对称轴的交点为M,过M点作x轴的平行线交A B于点N,设四边形AN P Q的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.。
