2016-2017学年甘肃兰州新区舟曲中学高二文上月考二数学试卷
甘肃兰州新区舟曲中学2016-2017学年高二下学期期末考试语文试题+Word版含答案

新舟中学2016-2017学年度第二学期期末考试高二年级语文试卷第Ⅰ卷阅读题一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成下列小题。
阅读微信谨防病态过去总说我们的阅读量低,其实,那要看阅读什么,读书的数量确实不高,可读微信的时间和数量,恐怕在世界上都数一数二。
不妨看看四周,无时无刻不在那里看微信,可以说是任何地方的风景。
开会、上课、听讲,凡是低着头的,十有八九是在读微信;上班时间看微信,已经成了常态行为,更何况微信与工作有关的也不在少数;坐公交、乘火车,等在候车室、候机室、候诊室里,盯着微信的恐怕占大多数,幸亏飞机上不许开手机,否则,读微信的比例大概接近百分之百。
从前纸质媒体独占天下时,蹲厕所看报是一景,今天,上厕所不看微信的还剩下多少?微信的诞生,当然是好事,让阅读大大提速,看什么都变得无比便捷,可这种如潮水一般涌来的微信量也很容易令人沉迷。
须臾离不开微信,一刻不盯着微信就有如失魂落魄,这已经是很多人的生活常态;一家几口各看各的微信,还互转互动,这已经是当今家庭生活的普遍景致。
姑且不说在看微信中度过的生活究竟是好是赖,仅是把阅读都耗费在微信里,就会让原本已经少得可怜的读书时间更无一席之地。
书痴,古往今来向来都是少数,但微信痴如今正与日俱增。
阅读微信一旦成瘾,茶饭无心、睡眠不足、耽误了正事,恐怕就是病态了,不仅无益于身心健康,而且还会带来诸多副作用。
因为这种病态阅读常常是排他的、痴迷的、偏听偏信的,即便谬误就在眼前,也浑然不觉。
尽管读微信也是阅读,好微信就是好文章,好的微信公众号就是一张好报纸、一本好刊物,甚至是一部便携式的好书,可是,阅读那些转来发去的微信时你也会发现,这毕竟有别于书籍、报刊。
个人间转发的微信大多是单向的,很少能看到相左的意见,即使有,往往也难得再次转发到同一个人的手里。
这还不如阅读报刊,起码不同的说法、争论的意见都可以相继呈现;更不如网页,不但有不同的声音,而且还有纠错的跟帖及时出现。
甘肃省兰州2016-2017学年高二数学上册期中考试题

兰州一中2016-2017-1学期高二年级期中考试试题数 学说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间100分钟.答案写在答题卡上,交卷时只交答题卡.第Ⅰ卷(选择题,共40分)一、 选择题(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案写在答题卡上.)1. 已知数列{}n a 满足112,30(),n n a a a n N *+=-+=∈则n a 等于 ( )A .31n -B .31n --C .35n -D .35n -+ 2.若集合2{|1}1A x x=≥-,{|0}B x x =>,则A B 为 ( ) A .(0,1) B .(0,1] C .(0,)+∞ D .[1,)+∞3.已知ABC ∆中,5,3,120,a b C ===则sin A 的值为 ( )A.16 B.16- C.14 D.14- 4. 等差数列{}n a 中,10a >,715S S =,则当n S 取最大值时,n 的值为 ( )A .10B .11C .12D .135.已知0,0a b >>,且满足3a b +=,则14a b+的最小值为 ( )A .1B .2C .3D .46.若不等式组0220x y x y y x y a-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩ 表示的平面区域是一个三角形,则a 的取值范围是( )A .43a ≥B .01a <≤C .413a ≤≤D .01a <≤或43a ≥7.数列{}n a 满足111n na a +=-,且12a =,则2016a 的值为 ( ) A .12 B .1-C .2D .1 8.在ABC ∆中,已知三个内角C B A ,,的对边分别为c b a ,,,若6ABC S a b ∆=+=, cos cos 2cos a B b A C c+=,则c 等于 ( ) A..4 C. D.9.已知1,1x y >->-,且(1)(1)4x y ++=,则x y +的最小值为 ( )A .4B .3C .2D .110.数列{}n a 中,11a =,1(1)2n n n a a n +=+-,对任意的n N *∈, 1()()0n n a p a p +--< 恒成立,则实数p 的取值范围是 ( )A .(1,1)-B .(,1)-∞C .(1,3)-D .(3,)+∞第II 卷(非选择题)二、填空题(每小题4分,共16分,将答案写在答题卡上.)11.设,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩,则2z x y =+的最大值为 .12.已知数列{}n a 中n S 为其前n 项和,1123n a n =++++ ,则100S = . 13.已知数列{}n a 中,11a =,13()23n n n a a n N a *+=∈+,则数列{}n a 的通项公式为 .14.给出下列结论:①若,a b c d >>,则ac bd >;②若a b >,则lg lg a b >; ③若0,0a b >>,则a b +≥④若11a b<,则a b >; ⑤若02παβ<<<,则222ππαβ-<-<.其中正确的结论的序号是 .三、 解答题(本大题共5小题,共44分)15.(本小题8分)(1)n S 为等差数列{}n a 的前n 项和,264,1S S a ==,求5a .(2)在等比数列{}n a 中,若422324,6a a a a -=+=,求通项公式n a .16.(本小题8分)如图,D 是直角三角形ABC 斜边BC 上的一点,AC =.(1)若6DAC π∠=,求角B 的大小;DC 的长.17.(本小题8分)某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m 万件与年促销费用x 万元(0)x ≥满足231m x =-+.已知2017年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每年产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2017年该产品的利润y 万元表示为年促销费用x 万元的函数;(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?18.(本小题10分)已知数列{}n a 的前n 项和n S 满足,2()n n S a n n N *=-∈.(1)求数列{}n a 的通项公式;(2)设,n b n =求数列{}n n a b 的前n 项和n T .19.(本小题10分)已知关于x 的不等式2(4)(4)0,kx k x --->其中k R ∈.(1)当k 变化时,试求不等式的解集A .(2)对于不等式的解集A ,若满足A Z B =(其中Z 为整数集).试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的取值,并用列举法表示集合B ;若不能,请说明理由.兰州一中2016-2017-1学期高二年级期中数学试题(答案)第I 卷(选择题)一、选择题(本大题共10小题,每小题4分,共40分)第II 卷(非选择题)二、填空题(每小题4分,共16分)11. 4 12.101200 13. 123+n 14.③ ⑤三、 解答题(本大题共5小题,共44分)15.(本小题8分)(1)n S 为等差数列{}n a 的前n 项和,264,1S S a ==,求5a .(2)在等比数列{}n a 中,若422324,6a a a a -=+=,求通项公式n a .解:(1)由题意得: ⎩⎨⎧-==⇒⎩⎨⎧=+=+⇒⎪⎩⎪⎨⎧=+⨯+=⨯+27130721325662122111111d a d a d a d a d a d a ∴1)15(275-=--=a ……………………………………………4分 另解:∵)(2054654326a a a a a a S S +=+++==-∴054=+a a ∴145-=-=a a(2)由题意得:311112111124(1)(1)245(1)665a q a q a q q q a a q q a q a q q ⎧⎧-=-+==⎧⎪⎪⇒⇒⎨⎨⎨+=+=⎪⎩⎪⎩=⎩ 121555n n n a --∴=⨯= ……………………………………………4分 16.(本小题8分)如图,D 是直角三角形ABC 斜边BC 上的一点,AC =.(1)若6DAC π∠=,求角B 的大小;DC的长.sin sin CD DAC ADC =∠∠ sin 2ADC ∴∠=又33ADC B BAD B ππ∠=∠+∠=∠+> 23ADC π∴∠= 2()366C ππππ∴=-+= 3B π∴= ……………4分 (2)设CD x=,则在Rt BAC ∆中:sin 33B x == cos 3B ∴=又||AB ===∴在ABD ∆中:22cos 3B ==x ∴=……………4分 17.(本小题8分)某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m 万件与年促销费用x 万元(0)x ≥满足231m x =-+.已知2017年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每年产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2017年该产品的利润y 万元表示为年促销费用x 万元的函数;(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?解:(1)由题意得:161.5(816)(816)28(0)1y m m x x x x =+-+-=--≥+ ……4分 (2)16162829[(1)]292111y x x x x =--=-++≤-=++ 当且仅当16(1)1x x =++即3x =时,等式成立.∴该厂家2017年的促销费用投入3万元时,厂家的利润最大. ……4分18.(本小题10分)已知数列{}n a 的前n 项和n S 满足,2()n n S a n n N *=-∈.(1)求数列{}n a 的通项公式;(2)设,n b n =求数列{}n n a b 的前n 项和n T .解:(1)①当1n =时:11121a S a ==- 11a ∴=②当2n ≥时:1122(1)n n n n n a S S a n a n --=-=--+-121n n a a -∴=+ 112(1)n n a a -∴+=+ 1121n n a a -+∴=+ {1}n a ∴+是以2为首项,2为公比的等比数列. 12n n a ∴+= 21n n a ∴=- ……………5分(2)设n n n c a b =,则2n n c n n =⋅-2312(1222322)(123)n n n T c c c n n ∴=+++=⨯+⨯+⨯++⨯-++++ 令231122232(1)22n n n Q n n -=⨯+⨯+⨯++-⨯+⨯ ①234+12122232(1)22n n n Q n n =⨯+⨯+⨯++-⨯+⨯ ②①-②得: 23+1+1+1212222+222(1)2212n n n n n n Q n n n --=+++-⨯=-⋅=---() +12(1)2n n Q n ∴=+- +1(1)(1)222n n n n T n +∴=--+ ……………5分 19.(本小题10分)已知关于x 的不等式2(4)(4)0,kx k x --->其中k R ∈.(1)当k 变化时,试求不等式的解集A .(2)对于不等式的解集A ,若满足A Z B =(其中Z 为整数集).试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的取值,并用列举法表示集合B ;若不能,请说明理由.解:(1)当0k =时,(,4)A =-∞;当0k >且2k ≠时,4(,4)(,)A k k =-∞++∞; 当2k =时,(,4)(4,)A =-∞+∞; 当0k <时,4(,4)A k k=+ ……………5分 (2)由(1)知,当0k ≥时,集合B 中的元素个数无限;当0k <时,集合B 中的元素个数有限,此时集合B 为有限集. 44[()]4k k k k +=--+≤--,当且仅当2k =-时取等号.∴当2k =-时,集合B 中的元素个数最少.此时(4,4)A =-,故集合{3,2,1,0,1,2,3}B =---.……………5分沁园春·雪 <毛泽东>北国风光,千里冰封,万里雪飘。
甘肃省兰州市2016_2017学年高二数学上学期期中试题理

甘肃省兰州市2016-2017学年高二数学上学期期中试题 理1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分,答题时间2小时。
2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束后,将本试题和答题卡一并交回。
题 号 一 二 三 四 五 总分 得 分 总分人一、选择题(本大题共12小题,每小题5分,共60分。
在每小题列出的四个选项中,选出符合题目要求的一项。
)1.在数列1,1,2,3,5,8,x,21,34,55中,x 等于 ( ) A. 11B. 12C. 13D. 142.设11a b >>>-,则下列不等式中恒成立的是 ( ) A.ba 11< B.ba 11>C. 2a b >D. 22a b >3.已知数列{}n a 中,34,n a n =+若13,n a =则n 等于 ( ) A. 3 B. 4C. 5D. 64.在△ABC 中,a =3,b =2,B =π4,则A = ( )A. π3B. 2π3C. π3或2π3D.6π5.在ABC ∆中,若cos cos A bB a=,则ABC ∆是 ( ) 评卷人 得分A. 等腰或直角三角形B. 等边三角形C. 直角三角形D. 等腰三角形6.已知a ,b ,c ,d 成等比数列,且曲线y =x 2-2x +3的顶点是(b ,c ),则ad 等于( ) A. 3B. 2C. 1D. -27.在△AB C 中,若)())((c b b c a c a +=-+,则∠A= ( ) A. 090 B. 060C. 0120D. 01508.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤x ,x +y ≤1,y ≥-1,且z =2x +y 的最大值和最小值分别为m 和n ,则m -n =( ) A. 5 B. 6C. 7D. 89.在△ABC 中,B =30°,AB =23,AC =2,则△ABC 的面积为 ( )A. 2 3B. 3C. .2 3 或4 3D. 3 或2 310.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cos C 等于 ( )2A.32B.-31C.-3 1D.-411.若数列{a n }满足3a n +1=3a n +1,则数列是 ( )A. 公差为1的等差数列B. 公差为13的等差数列C. 公差为-13的等差数列D. 不是等差数列12.若关于x 的不等式4104822<<>---x a x x 在内有解,则实数a 的取值范围是( )A. 12a <-B. 4->aC. 12->aD. 4a <-二、填空题(本大题共4小题,每题5分,共20分)13.若A =(x +3)(x +7),B =(x +4)(x +6),则A 、B 的大小关系为________. 14.设n S 是等差数列{}n a 的前n 项和,若357=S ,则=4a ___________. 15.设),0(y ,x +∞∈,且1y9x 1=+,则y x +的最小值为___________. 16.船以每小时15km 的速度向东航行,船在A 处看到一个灯塔B 在北偏东60o,行驶4h 后,船到达C 处,看到这个灯塔在北偏东15o,这时船与灯塔的距离为 ___________________km三、解答题(其中17题10分,18、 19、20、21、22每题12分)17. (本题10分)若不等式0252>-+x ax 的解集是⎭⎬⎫⎩⎨⎧<<221x x , (1) 求a 的值;(2) 求不等式01522>-+-a x ax 的解集.评卷人 得分评卷人 得分18.(本题12分)设锐角三角形ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a =2b sin A . (1)求B 的大小;(2)若a =33,c =5,求b .19. (本题12分)已知等差数列{}n a 的前n 项和为n S ,15,555==S a , (1)求数列{}n a 的通项公式; (2)设数列*+∈=N n a a b n n n ,11,求数列{}n b 的前n 项和n S .20. (本题12分)(1)已知x >0,求f (x )=12x+3x 的最小值;(2)已知x <3,求f (x )=4x -3+x 的最大值;21. (本题12分)营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪,1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg 脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?将已知数据列成下表:食物/kg碳水化合物/kg蛋白质/kg脂肪/kgA 0.1050.070.14B 0.1050.140.0722. (本题12分)已知等比数列{a n}中,a1=2,a3+2是a2和a4的等差中项.(1)求数列{a n}的通项公式;(2)记b n=n a n,求数列{b n}的前n项和S n.2016—2017学年第一学期联片期中考试高二数学 参考答案一、选择题(每小题5分,共5×12=60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CCACABCBDDBD二、填空题(每小题5分,共5×4=20分)13.A<B 14.5 15.16 16.230三、解答题(17题10分,19、20、21、22每题12分) 17、(1)依题意,可知方程2520ax x +-=的两个实数根为12和2, 由韦达定理得:12+2=5a - 解得:a =-2 (5分) (2)1{3}2x x -<< (10分) 18 (本题12分)(1)由a =2b sin A ,得sin A =2sin B sin A ,所以sin B =12.由△ABC 为锐角三角形,得B =π6. (6分)(2)根据余弦定理,得b 2=a 2+c 2-2a cos B =27+25-45=7,所以b =7. (12分) 19、(1)设等差数列{a n }的首项为a 1,公差为d .∵a 5=5,S 5=15,∴⎩⎪⎨⎪⎧a 1+4d =5,5a 1+5×5-12d =15,∴⎩⎪⎨⎪⎧a 1=1,d =1,∴a n =a 1+(n -1)d =n . (5分)(2)∴n b =1a n a n +1=1nn +1=1n -1n +1,111......41313121211+-++-+-+-=n n s n=1111+=+-n nn (12分)20.(1)∵x>0,∴f(x)=12x+3x≥212x·3x=12,当且仅当3x=12x,即x=2时取等号.∴f(x)的最小值为12. (6分)(2)∵x<3,∴x-3<0.∴f(x)=4x-3+x=4x-3+x-3+3=-⎣⎢⎡⎦⎥⎤43-x+3-x+3≤-243-x·(3-x)+3=-1,当且仅当43-x=3-x,即x=1时取等号.∴f(x)的最大值为-1. (12分)21.解设每天食用x kg食物A,y kg食物B,总成本为z,那么⎩⎪⎨⎪⎧0.105x+0.105y≥0.075,0.07x+0.14y≥0.06,0.14x+0.07y≥0.06,x≥0,y≥0,⇒⎩⎪⎨⎪⎧7x+7y≥5,7x+14y≥6,14x+7y≥6,x≥0,y≥0.目标函数为z=28x+21y. (4分)作出二元一次不等式组所表示的平面区域,把目标函数z=28x+21y变形为y=-43x+z21,它表示斜率为-43,且随z变化的一族平行直线,z21是直线在y轴上的截距,当截距最小时,z的值最小. (4分)如图可见,当直线z=28x+21y经过可行域上的点M时,截距最小,即z最小.解方程组⎩⎪⎨⎪⎧7x +7y =5,14x +7y =6得M 点的坐标为⎝ ⎛⎭⎪⎫17,47.所以z min =28x +21y =16.答 每天食用食物A 17 kg ,食物B 47 kg ,能够满足日常饮食要求,又使花费最低,最低成本为16元.(12分)22.解 (1)设数列{a n }的公比为q , 由题意知:2(a 3+2)=a 2+a 4,∴q 3-2q 2+q -2=0,即(q -2)(q 2+1)=0. ∴q =2,即a n =2·2n -1=2n. (5分)(2)b n =n ·2n,∴S n =1·2+2·22+3·23+…+n ·2n.① 2S n =1·22+2·23+3·24+…+(n -1)·2n +n ·2n +1.②①-②得-S n =21+22+23+24+…+2n -n ·2n +1=-2-(n -1)·2n +1.∴S n =2+(n -1)·2n +1. (12分)。
甘肃省兰州新区舟曲中学高二数学上学期第一次月考试题

新舟中学2016-2017学年度第一学期第一次月考高二年级 数学试卷一.单项选择题(每题5分)1、对任意等比数列{a n },下列说法一定正确的是( )A .a 1,a 3,a 9成等比数列B .a 2,a 3,a 6成等比数列C .842,,a a a 成等比数列D .963,,a a a 成等比数列2.在△ABC 中,4560B C ==,,1c =,则最短边的边长为( )A ..12C 3.已知{a n }是等差数列,a 3=12,a 6=27,则a 10等于( )A .42B .45C .47D .494.已知等差数列{a n }满足5628a a +=,则其前10项之和为( )A .140B .280C .168D .565.已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和 ,若844S S =,则10S =( )1719...10.1222A B C D6.在等差数列{}n a 中,若,32=a 943=+a a ,则61a a =( )A .18B .14C .2D .277.在△ABC 中,若1=b ,B=30º,则a =( )A .2B .1C .1或2D .28.若(a+b+c)(b+c -a)=3bc,且sinA=2sinBcosC, 那么ΔABC 是 ( )A .直角三角形B .等腰直角三角形C .等腰三角形D .等边三角形9.在△ABC 中, 30,1,3===B b c ,则△ABC 的面积为( ) A. 323或 B. 2343或 C. 343或 D. 3 10.设等差数列{}n a 的前n 项和为n S ,若111-=a ,664-=+a a ,则当n S 取最小值时,n 等于( )A .6B .7C .8D .9 11.在ABC ∆中,若cos cos A b B a=,则ABC ∆是( ) A. 等腰或直角三角形 B. 等边三角形C. 直角三角形D. 等腰三角形12. 若等差数列{}n a 的前n 项和为n S 满足17180,0S S ><,则17121217,,,S S S a a a 中最大的项是( ) A .66S a B .77S a C .88S a D .99Sa二.填空题(每题5分,共20分)13.数列{}n a 的前n 项和*23()n n s a n N =-∈,则5a =14.设n S 是等差数列{}n a 的前n 项和,若357=S ,则=4a ______。
数学---甘肃兰州新区舟曲中学2016-2017学年高二下学期期末考试(文)

甘肃兰州新区舟曲中学2016-2017学年高二下学期期末考试(文)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卡上)1.集合{}4,3,2A ={}63B ,=则=B A ( ) A.{}43,2, B.{}6,3,2 C.{}6,4,3,2 D.{}6,4,3 2.计算 2i -的值为( ) A.1 B.1- C.3 D.03.在等差数列{}n a 中,12a 15a a 754==+,,则=2a ( ) A. 3B.3-C.23D.23-4.函数()⎪⎭⎫⎝⎛+=3x 2sin x f π的最小正周期是( ) A .π4 B .π2 C .π D .2π 5.函数()2x 3-x x f 2+=的零点的个数为 ( ) A .3 B .2 C .1 D .0 6.已知直线020173l =++y x :,则直线l 的倾斜角为( ) A . 150 B . 120 C . 60 D . 30 7. 已知53sin =α,54cos =α,则=α2sin ( ) A.57 B.512 C.2512 D.25248.在△ABC 中,0<AC AB ⋅,则△ABC 是( )A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形 9.如图所示,该程序框图是已知直角三角形的两直角边a 、b ,求斜边c 的算法,其中正确的是( )10. 甲、乙两人下棋,两人下成和棋的概率是21,乙获胜的概率是31,则甲不输的概率是 ( ) A .65 B .32 C .61 D .2111. 某几何体的三视图如图所示,则该几何体的体积是( )A.πB.2πC.4πD.8π12. 已知7tan =α,求αααα223cos cos sin sin ++ 的值为( )A.5056 B.5057 C.5058 D.5059 二、填空题:(本大题共4小题,每小题5分,共20分) 13.抛物线x 2y 2=的准线方程为 . 14.右图所示茎叶统计图表示某城市一台自动售货机的销售额情况,那么这组数据的极差是_____.15. 已知向量a ,b ,1a =,2b =,且()a b a ⊥+,则a 与b的夹角为 .16. 若变量,x y 满足约束条件200220x y x y x y +⎧⎪-⎨⎪-+⎩≥≤≥,则2z x y =-的最小值等于 .三 解答题(本大题共6小题,共70分) 17.(每小题6分,本题满分12分)(1) 计算:883-41n m ⎪⎪⎭⎫ ⎝⎛.(2) 比较大小:8.1log 0.5,7.2log 0.5.18.如图所示,在边长为1的正方体1111D C B A -ABCD 中, (1)判断D BC 1△的形状; (2)求二面角11C -BD -A 的余弦值.19.(本小题满分12分)已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计.先将800人按001,002,…,800进行编号.(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行至第9行)D1C1DCABB1A184 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 60 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54(2)抽取出100人的数学与地理的水平测试成绩如表所示,成绩分为优秀、良好、及格三个等级;横向、纵向分别表示数学成绩与地理成绩,例如:表中数学成绩为良好的共有20+18+4=42人.若在该样本中,数学成绩优秀率是30%,求a ,b 的值;20.(本小题满分12分)已知函数()⎪⎭⎫ ⎝⎛+=6x 2sin 3x f π. (1)求函数()x f 的最值; (2)判断函数()x f 的单调区间.21.(本小题满分12分)一个圆经过点A (5,0)与B (-2,1),圆心在直线x-3y-10=0上,求此圆的方程.[选修4-4:坐标系与参数方程]22. (本小题满分10分)已知在直角坐标系xOy 中,圆的参数方程为⎩⎨⎧=+=θθsin 2cos 21y x (θ为参数).(1)将圆C 的参数方程转化为直角坐标方程;(2)以原点为极点、x 轴正半轴为极轴建立极坐标系,求圆C 的极坐标方程.参考答案1-6.CAACBB ,7-12.DACBAD 13.21-x =14.3915. 120或32π16. 25-17.(1)32-n m 或32n m(2)7.2log 8.1log 0.55.0> 18.(1)等边三角形(2)3119.(1)785,667,199 (2)a=14,b=17 20.(1)最大值3,最小值-3(2)单调递增区间为)(,6,3z k k k ∈⎥⎦⎤⎢⎣⎡++-ππππ,单调递减区间为)(,32,6z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ21.圆的标准方程为()()253122=++-y x 22.(1)()41-x 22=+y (2)3cos 22=-θρρ。
甘肃省兰州市2016_2017学年高二数学上学期期末考试试题文

兰州2016一2017学年第一学期期末试卷高二 数学(文科)一、选择题 (每小题5分共60分)1.设P 是椭圆2169x +2144y =1上一点,F 1、F 2是椭圆的焦点,若|PF 1|等于4,则|PF 2|等于( )A .22B .21C .20D .132.设命题甲:0122>++ax ax 的解集是实数集R;命题乙:10<<a ,则命题甲是命题乙成立的( ) A . 充分非必要条件 B.必要非充分条件 C. 充要条件 D. 既非充分又非必要条件 3.抛物线24y x =-的焦点坐标为( ) A .(1,0)- B .(1,0) C .(0,-116) D .(-116,0) 4.已知双曲线C :12222=-b y a x 的离心率54e =,且其右焦点()25,0F ,则双曲线C 的方程为( )A .13422=-y x B. 191622=-y x C. 116922=-y x D. 14322=-y x 5.已知命题p :存在实数x 使2sin π=x 成立,命题023:2<+-x x q 的解集区间为(1,2).给出下列四个结论:①“p 且q ”真,②“p 且q ⌝”假,③""q p 且⌝真,④“q p ⌝⌝或”假,其中正确的结论是( )A .①②③④B .①②④C .②③`D .②④6.方程222=+ky x 表示焦点在y 轴上的椭圆,则k 的取值范围是 ( ) A .),0(+∞ B .(0,2) C .(1,+∞)D .(0,1)7.已知抛物线的顶点在原点,焦点在y 轴上,抛物线上的点(,2)P m -到焦点的距离为4,则m 的值为( )A .4B .-2C .4或-4D .12或-2命题人:韩蕊8.椭圆12322=+y x 上一点P 到左焦点的距离为23,则P 到右准线的距离为( )A .33B .1059C .29D .239.已知点12,F F 为双曲线C: 221x y -=的左、右焦点,点P 在C 上,1260F PF ∠=o,则12PF PF ⋅=( )A.2B.4C. 6D. 810.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是( ) A.3 B.11 C.22 D.1011.过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于P 、Q 两点,2F 为右焦点,若2PQF ∆为等边三角形,则椭圆的离心率为( )A .22 B .33 C .12 D .1312.过抛物线24y x =的焦点F 作直线l 交抛物线于A ,B 两点,若111,||||2AF BF -=则直线l 的倾斜角(0)2πθθ<<等于( )A .2πB .3πC .4πD .6π二、填空题 (每小题5分共20分)13.若抛物线22(0)y px p =>的准线经过双曲线221x y -=的一个焦点,则p= .14.若过椭圆22164x y +=1内一点(2,1)的弦被该点平分,则该弦所在直线的方程是______ 15.若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为 16.若命题“[]1,1,1240x x x a ∀∈-++⋅<”是假命题,则实数a 的最小值为三、解答题 (本大题共6小题,第17题10分,第18—22题每题12分)17. 已知)0,2(),0,2(B A -,点D C ,依次满足,2=AC ).(AC AB AD +=21求点D 的轨迹.18.设直线y x b =+与椭圆2212x y +=相交于A B ,两个不同的点. (1)求实数b 的取值范围;(2)当1b =时,求AB u u u r.19. 给出两个命题:命题甲:关于x 的不等式x 2+(a -1)x +a 2≤0的解集为Φ,命题乙:函数y =(2a 2-a)x为增函数. 分别求出符合下列条件的实数a 的范围. (1)甲、乙至少有一个是真命题; (2)甲、乙中有且只有一个是真命题.20. 在平面直角坐标系xOy 中,原点为O ,抛物线C 的方程为y x 42=,线段AB 是抛物线C 的一条动弦.(1)求抛物线C 的准线方程和焦点坐标F ; (2)若4-=⋅,求证:直线AB 恒过定点.21. 如图,已知双曲线)0(1:222>=-a y ax C 的右焦点F ,点B A ,分别在C 的两条渐近线上,x AF ⊥轴,BF OB AB ,⊥//OA (O 为坐标原点).求双曲线C 的方程.22. 已知椭圆E :22221(a 0)x y b a b+=>>过点(0,2),且离心率为2.(Ⅰ)求椭圆E 的方程; (Ⅱ)设直线)(,R m my x ∈-=1交椭圆E 于A ,B 两点,判断点G 9(4-,0)与以线段AB 为直径的圆的位置关系,并说明理由.2016---2017学年第一学期期末试卷高二 数学(文科答案)一、 选择题: 题目 1 2 3 4 5 6 7 8 9 10 11 12 答案 ABCBCDCCBDBB二、 填空题:13. 22 ; 14. x +2y -4=0 ; 15. 2; 16. -6 ;三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.【答案】(1) 以原点为圆心,1为半径的圆 解析:(1) 设0000(,),(,),(2,),(4,0).C x yD x y AC x y AB =+=u u u r u u u r00002(3,)(2,),,222x x x yAD x y y y =-⎧=+=+⎨=⎩u u u r 则2222200(2)4, 1.AC x y x y =++=+=u u u r 代入得所以,点D 的轨迹是以原点为圆心,1为半径的圆.18.答案:(1)将y x b =+代入2212x y +=,消去y ,整理得2234220x bx b ++-=.① 因为直线y x b =+与椭圆2212x y +=相交于A B ,两个不同的点,所以2221612(22)2480b b b ∆=--=->,解得33b <<b 的取值范围为(3,3).(2)设11()A x y ,,22()B x y ,,当1b =时,方程①为2340x x +=.解得1240,3x x ==-.相应地1211,3y y ==-. 所以2212124()()23AB x x y y =-+-=u u u r (利用弦长公式也可以)19.答案(1){a|a<-12或a>13};(2){a|13<a ≤1或-1≤a<-12}。
甘肃高二高中数学月考试卷带答案解析

甘肃高二高中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.若集合M={x||x|≤2},N={x|x2-3x=0},则M∩N等于()A.{3}B.{0}C.{0,2}D.{0,3}2.使成立的一个必要不充分条件是 ( )A.B.C.D.3.方程(t为参数)表示的曲线是().A.一条直线B.两条射线C.一条线段D.抛物线的一部分4.使有意义的x的条件是()A.-3≤x<B.<x≤3C.-3≤x< -或D.-3≤x≤35.在同一坐标系中,将曲线变为曲线的伸缩变换是()6.设满足则()A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值7.设点对应的复数为,以原点为极点,实轴正半轴为极轴建立极坐标系,则点的极坐标为()A. (,)B. (,)C. (3,)D. (-3,)8.在符合互化条件的直角坐标系和极坐标系中,直线l:与曲线C:相交,则k的取值范围是().A.B.C.D.但9.不等式|x-1|+|x+2|的解集为( )A.B.C.D.10.若圆的方程为(为参数),直线的方程为(t为参数),则直线与圆的位置关系是().A.相交过圆心B.相交而不过圆心C.相切D.相离11.设a、b、c是互不相等的正数,则下列不等式中不恒成立的是()A.B.C.D.12..已知a,b,c是正实数,且a+b+c=1,则的最小值为( )A.3B.6C.9D.12二、填空题1.在极坐标系中,以为圆心,为半径的圆的极坐标方程是 .2.如图所示,AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8,则CD的长为,cos∠ACB= .3.直线被双曲线截得的弦长为__________4.(1)≥2成立当且仅当a,b均为正数.(2)的最小值是(3)的最大值是(4)|a+|≥2成立当且仅当a≠0.以上命题是真命题的是三、解答题1.(10分)把下列参数方程化为普通方程,并说明它们各表示什么曲线:⑴(为参数);(5分)⑵(为参数)(5分)2.(12分)和的极坐标方程分别为.(Ⅰ)把和的极坐标方程化为直角坐标方程;(Ⅱ)求经过,交点的直线的直角坐标方程.3.(12分)从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.求证:=.4.(12分)已知、满足,求的最值.5.(12分)已知:如图所示,在△ABC中,D是BC的中点,F是BA延长线上的点,FD与AC交于点E.求证:AE·FB=EC·FA.6.(12分)设函数f(x)=∣2x+1∣-∣x-4∣(1)解不等式f(x)>2.(2)求函数y=f(x)的最小值.甘肃高二高中数学月考试卷答案及解析一、选择题1.若集合M={x||x|≤2},N={x|x2-3x=0},则M∩N等于()A.{3}B.{0}C.{0,2}D.{0,3}【答案】B【解析】2.使成立的一个必要不充分条件是 ( )A.B.C.D.【答案】A【解析】即.由得或.故选A3.方程(t为参数)表示的曲线是().A.一条直线B.两条射线C.一条线段D.抛物线的一部分【答案】B【解析】因为所以方程表示的是两条射线.4.使有意义的x的条件是()A.-3≤x<B.<x≤3C.-3≤x< -或D.-3≤x≤3【答案】C【解析】有意义,即解得或.5.在同一坐标系中,将曲线变为曲线的伸缩变换是()【答案】B【解析】变换过程是横坐标伸长为原来的三倍,纵坐标缩短为原来的二分之一.故选B6.设满足则()A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值【答案】B【解析】画出满足的可行域,可得最小值在点(2,0)处取得为2.无最大值.7.设点对应的复数为,以原点为极点,实轴正半轴为极轴建立极坐标系,则点的极坐标为()A. (,)B. (,)C. (3,)D. (-3,)【答案】A【解析】因为,所以点的极坐标为(,).8.在符合互化条件的直角坐标系和极坐标系中,直线l:与曲线C:相交,则k的取值范围是().A.B.C.D.但【答案】A【解析】曲线C:化为直角坐标系下的方程为,圆心(1,0)到直线的距离要小于半径1,即.9.不等式|x-1|+|x+2|的解集为( )A.B.C.D.【答案】D【解析】当原不等式等价于解得;当原不等式等价于解得;当原不等式等价于,无解.所以原不等式的解集为.10.若圆的方程为(为参数),直线的方程为(t为参数),则直线与圆的位置关系是().A.相交过圆心B.相交而不过圆心C.相切D.相离【答案】B【解析】圆的方程为(为参数),化为一般方程是;直线的方程为(t为参数),化为一般方程是不过圆心(-1,3);圆心(-1,3)到直线的距离,所以直线与圆相交且不过圆心.11.设a、b、c是互不相等的正数,则下列不等式中不恒成立的是()A.B.C.D.【答案】D【解析】对于,当时不成立.其他都恒成立.12..已知a,b,c是正实数,且a+b+c=1,则的最小值为( )A.3B.6C.9D.12【答案】C【解析】当且仅当时等号成立.二、填空题1.在极坐标系中,以为圆心,为半径的圆的极坐标方程是 .【答案】【解析】以为圆心,为半径的圆的标准方程是即.所以极坐标方程是.2.如图所示,AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8,则CD的长为,cos∠ACB= .【答案】【解析】在中,,把PC=2,PA=8,代入得;3.直线被双曲线截得的弦长为__________【答案】【解析】直线化为一般式是,与双曲线方程联立消去得,设两交点.则4.(1)≥2成立当且仅当a,b均为正数.(2)的最小值是(3)的最大值是(4)|a+|≥2成立当且仅当a≠0.以上命题是真命题的是【答案】(3)、(4)【解析】≥2成立当且仅当a,b均为正数且时等号成立.故(1)错;当时等号成立.故(2)错;当时等号成立.故(3)对;当时等号成立.故(4)对.三、解答题1.(10分)把下列参数方程化为普通方程,并说明它们各表示什么曲线:⑴(为参数);(5分)⑵(为参数)(5分)【答案】⑴∴曲线是长轴在x轴上且为10,短轴为8,中心在原点的椭圆.⑵,它表示过(0,)和(1, 0)的一条直线.【解析】本题主要是考查参数方程化为普通方程,(1)对两个式子中右边的系数挪到左边,利用三角函数的平方关系式消去整理即得到;(2)可以代入消元或加减消元消去得普通方程.解:⑴.∵∴两边平方相加,得即∴曲线是长轴在x轴上且为10,短轴为8,中心在原点的椭圆.⑵.∵∴由代入,得∴∴它表示过(0,)和(1, 0)的一条直线.2.(12分)和的极坐标方程分别为.(Ⅰ)把和的极坐标方程化为直角坐标方程;(Ⅱ)求经过,交点的直线的直角坐标方程.【答案】以极点为原点,极轴为轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(Ⅰ)即为的直角坐标方程.同理为的直角坐标方程.(Ⅱ),交于点和.过交点的直线的直角坐标方程为.【解析】(1)先建立平面直角坐标系,可得到,.对两边平方就得到直角坐标方程;(2)可以两圆的方程联立,求出交点,写出直线方程.也可以两圆的方程直接相减得直线方程. 以极点为原点,极轴为轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(Ⅰ),,由得.所以.即为的直角坐标方程.同理为的直角坐标方程.(Ⅱ)由解得.即,交于点和.过交点的直线的直角坐标方程为.3.(12分)从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.求证:=.【答案】见解析。
甘肃省兰州20162017学年高二上学期期末考试数学文试题Word版含答案

兰州一中2016-2017-1学期期末考试试题高二数学(文)说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间100分钟.答案写在答题卡上,交卷时只交答题卡.第Ⅰ卷(选择题)一、选择题(本大题共10 小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案写在答题卡上...........) 1. 命题p : 对∀ x ∈R ,x 3-x 2+1≤0,则⌝p 是( ) A.不存在x ∈R ,x 3-x 2+1≤0 B. ∃ x ∈R ,x 3-x 2+1≥0C. ∃ x ∈R ,x 3-x 2+1>0D.对∀ x ∈R ,x 3-x 2+1>02. 抛物线y 2=2px 上横坐标为6的点到焦点的距离是10,则焦点到准线距离是( )3. 下列求导数运算正确的是( ) A. 2'11)1(xx x +=+B. (log 2x )'=2ln 1x C. e xx 3'log 3)3(= D. x x x x sin 2)cos ('2-=4. 若a 、b 为实数, 且a +b =2, 则3a +3b 的最小值为( ) A .6B .18C .23D .2435. 椭圆24x +y 2=1的焦点为F 1、F 2,经过F 1作垂直于x 轴的直线与椭圆的一个交点为P ,则|2PF|等于( ) A.3B. 3C.726.2x 2-5x -3<0的一个必要不充分条件是( ) A .-21<x <3 B .-21<x <0 C .-3<x <21 D .-1<x <67. 过双曲线221169x y 左焦点F 1的弦AB 长为6,则2ABF (F 2为右焦点)的周长是( ) A .28 B .22 C .14 D .128.已知双曲线22221x y a b-= (a >0,b >0)的一条渐近线平行于直线l :y =2x +10,双曲线的一个焦点在直线l 上,则双曲线的方程为( )A. 2233125100x y -=B. 221205x y -=C. 221520x y -=D. 2233110025x y -=9. 椭圆上22221(0)x y a b a b+=>>一点A 关于原点的对称点为B ,F 为其右焦点,若AF BF ⊥,设ABF α∠=,且[,]124ππα∈,则该椭圆离心率的取值范围为( )A .2[B. 26[C. 3[D. 23[ 10. 已知点P 在曲线41x y e =+上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( )A .[0,4π)B .[4π,2π)C .(2π,34π]D .[34π,π)第Ⅱ卷(非选择题)二、选择题(本大题共4小题,每小题4分,共16分,将答案写在答题卡上..........) 11.一个物体运动的方程为s =at 3+3t 2+2t ,其中s 的单位是米,t 的单位是米/秒,若该物体在4秒时的瞬时速度是50米/秒,则a = .12. 已知y x ,满足43035251x y x y x -+≤⎧⎪+≤⎨⎪≥⎩,则z =2x -y 的最小值为 .13. 已知)2,4(P 是直线l 被椭圆193622=+y x 所截得的线段的中点,直线l 的方程为 .14.设双曲线2222b y a x -=1(0<b <a )的半焦距为c ,直线l 经过双曲线的右顶点和虚轴的上端点.已知原点到直线l 的距离为43c ,则双曲线的离心率为 .兰州一中2016-2017-1学期期末考试答题卡高二数学(文)一、选择题(本大题共10 小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题(每小题4分,共16分)11.;12.;13.;14..三、解答题(本大题共5 小题,共44分)15.(本小题8分)己知a,b,c都是正数,且a,b,c成等比数列.求证:a2+b2+c2>(a-b+c)2.16.(本小题8分)已知命题p:函数y=x2+mx+1在(-1,+∞)上单调递增,命题q:对函数y=-4x2+4(2- m)x-1, y≤0恒成立.若p∨q为真,p∧q为假,求m的取值范围.17.(本小题8分)已知曲线C1:y=ax2上点P处的切线为l1,曲线C2:y=bx3上点A(1,b)处的切线为l2,且l1⊥l2,垂足M(2,2),求a、b的值.18.(本小题10分)已知抛物线C:y2=2px(p>0)过点A(1,-2).(1) 求抛物线C的方程,并求其准线方程;(2) 若平行于OA(O为坐标原点)的直线l与抛物线C相交于两点,且直线OA与l的距离等5,求直线l的方程.19. (本小题10分)已知定点1(2,0)F -,动点B 是圆222:(2)12F x y += (F 2为圆心)上一点,线段F 1B 的垂直平分线交BF 2于P . (1)求动点P 的轨迹方程;(2)若直线y =kx +2(k ≠0)与P 点的轨迹交于C 、D 两点.且以CD 为直径的圆过坐标原点,求k 的值.兰州一中2016-2017-1学期期末考试参考答案高二数学(文)一、选择题(本大题共10 小题,每小题4分,共40分)二、填空题(每小题4分,共16分)11.12; 12.-125; 13.082=-+y x ; 1423三、解答题(本大题共5 小题,共44分) 15.(8分)证明:∵a ,b ,c 成等比数列,∴b 2=ac ∵a ,b ,c 都是正数,c a ca acb +<+≤=<∴20 ∴a +c >b , ……………………………4分∴a 2+b 2+c 2-(a -b +c )2=2(ab +bc -ca )=2(ab +bc - b 2)=2b (a +c -b )>0 ∴ a 2+b 2+c 2>(a -b +c )2. ……………………………8分 16.(8分)解:若函数y =x 2+mx +1在(-1,+∞)上单调递增,则-2m≤-2, ∴m ≥2,即p :m ≥2 ……………………………2分 若函数y =-4x 2+4(2- m )x -1≤0恒成立, 则△=16(m -2)2-16≤0,解得1≤m ≤3,即q :1≤m ≤3 ……………………………4分 ∵p ∨q 为真,p ∧q 为假,∴p 、q 一真一假题号 12345678910答案C B B A CD A C B D当p真q假时,由213mm m≥⎧⎨<>⎩或解得:m>3 ……………………………6分当p 假q真时,由213mm<⎧⎨≤≤⎩解得:1≤m<2综上,m的取值范围是{m|m>3或1≤m<2} …………………………8分17.(8分)解:设P(t,at2),则l1斜率k1=2at∴l1:y-at2=2at(x-t)l2斜率k2=3bx2|x=1=3b∴l2:y-b=3b(x-1) …………………………3分∵l1与l2交于点M(2,2),∴222(2)23(21)at at tb b⎧-=-⎨-=-⎩∴242012at atb⎧-+=⎪⎨=⎪⎩①…………………………5分又l1⊥l2∴k1·k2=-1 ∴at=-13②…………………………7分由①②得t=10,a=-130…………………………8分18.(10分)解:(1)将(1,-2)代入y 2=2px ,得(-2)2=2p ·1, 所以p =2.故抛物线方程为y 2=4x ,准线为x =-1. ……………………………3分 (2)设直线l 的方程为y =-2x +t ,由⎩⎪⎨⎪⎧y =-2x +t y 2=4x 得y 2+2y -2t =0. ……………………………5分 因为直线l 与抛物线C 有公共点,所以Δ=4+8t ≥0,解得t ≥-12. ……………………………7分由直线OA 与l 的距离d =55可得|t |5=15, 解得t =±1.因为-1∉[-12,+∞),1∈[-12,+∞),所以直线l 的程为2x +y -1=0. ……………………………10分19.(10分)解:(1)由题意1PF PB =且223PB PF +=,1223PFPF ∴+=22> ∴P 点轨迹是以12,F F 为焦点的椭圆.设其标准方程为22221x y a b+=(0)a b >>223a ∴=即3a =又∴=2c 2221b a c =-=,∴P 点轨迹方程为2213x y +=. ……………………………4分(2)假设存在这样的k ,由222330y kx x y =+⎧⎨+-=⎩得22(13)1290k x kx +++=. 由22(12)36(13)0k k ∆=-+>得21k >.设1122(,),(,)C x y D x y ,则1221221213913k x x k x x k ⎧+=-⎪⎪+⎨⎪=⎪+⎩①, (6)分若以CD 为直径的圆过坐标原点,则有12120x x y y +=,而212121212(2)(2)2()4y y kx kx k x x k x x =++=+++,∴212121212(1)2()40x x y y k x x k x x +=++++= ②,将①式代入②式整理可得2133k =,其值符合0∆>, 故393k =± .………10分。
甘肃省兰州新区舟曲中学2016-2017学年高二上学期第二次月考数学(理)试题Word版含答案

新舟中学2016-2017学年度第一学期第二次月考高二年级 理科 数学试卷 命题人:苏海刚 审题人:李守明一、 选择题:(本大题共12小题,每小题5分,共60分.) 每小题中,只有一项符合题目要求,请将正确答案填在正确的位置.1.在数列,13,10,7,2,1……中,192是这个数列的( )A.第16项B.第24项C.第26项D.第28项2.关于x 的不等式)0(08222><--a a ax x 的解集为),(21x x ,且1512=-x x ,则=a ( )A .25 B. 27 C. 415 D. 215 3.设b a ,是实数,则""b a >是22"b a >的 ( ) A .充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件4. 命题;1sin ,:<∈∀x R x p ;命题.1cos ,:-≤∈∃x R x q 则下列结论是真命题的是 ( )A.q p ∧B.q p ∧⌝C.q p ⌝∨D.q p ⌝∧⌝5.设,,,R c b a ∈则下列命题为真命题的是 ( )A.cb c a b a ->-⇒> B.bc ac b a >⇒> C.22b a b a >⇒> D.22bc ac b a >⇒>6.在△ABC中,若B A sin sin >,则A 与B 的大小关系为 ( )A .B A < B.B A ≥ C.B A > D. A 、B 的大小关系不能确定7.在等差数列{}n a 中,前四项之和为20,最后四项之和为60,前n 项之和是100,则项数n 为 ( )A .9B .10C .11D .128.△ABC 中, ∠A ,∠B ,∠C 所对的边分别为a , b , c .若3,4a b ==,∠C= 60,则c 的值等于 ( ) A. 5 B. 13 C.13 D.379.命题“若4πα=,则1tan =α”的逆否命题是( )A.若4πα≠则1tan ≠α B. 若4πα=则1tan ≠αC. 若1tan ≠α则4πα≠D. 若1tan ≠α则4πα=10.如果}{n a 为递增数列,则}{n a 的通项公式可以为( )A. 32+-=n a n B. 132+-=n n a n C. n n a 21= D. 21log n a n =+11.给出下列命题:①若原命题为真,则这个命题的否命题,逆命题,逆否命题中至少有一个为真;②若p 是q 成立的充分条件,则q 是p 成立的必要条件;③若p 是q 的充要条件,则可记为q p ⇔;④命题“若p 则q ”的否命题是“若p 则q ⌝”.其中是真命题的是 ( )A.①②③B.②③④C.①③④D. ②④12.设ABC ∆的内角C B A ,,所对的边分别为c b a ,,若cc a B 22cos 2+=,则ABC ∆的形状为( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定二、填空题:(本大题4小题,每小题5分,共20分. )请将正确的答案填在横线上。
甘肃省兰州市舟曲中学2016-2017学年高二上学期期末数

2016-2017学年甘肃省兰州市舟曲中学高二(上)期末数学试卷(理科)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.与圆x2+y2=1及圆x2+y2﹣8x+12=0都外切的圆的圆心在()A.一个椭圆上B.双曲线的一支上C.一条抛物线上D.一个圆上2.下列命题中的真命题为()A.∃x0∈Z,使得1<4x0<3 B.∃x0∈Z,使得5x0+1=0C.∀x∈R,x2﹣1=0 D.∀x∈R,x2+x+2>03.已知=(1,﹣3,λ),=(2,4,﹣5),若⊥,则λ=()A.﹣4 B.﹣2 C.2 D.34.原命题“若x≤﹣3,则x<0”的逆否命题是()A.若x<﹣3,则x≤0 B.若x>﹣3,则x≥0 C.若x<0,则x≤﹣3 D.若x ≥0,则x>﹣35.“双曲线渐近线方程为y=±2x”是“双曲线方程为x2﹣=λ(λ为常数且λ≠0)”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知{a,b,c}是空间一个基底,则下列向量可以与向量=+,=﹣构成空间的另一个基底的是()A.B.C.D. +27.椭圆上的点到直线的最大距离是()A.3 B. C. D.8.若正三棱锥的侧面都是直角三角形,则它的侧棱与底面所成角的余弦值为()A .B .C .D .9.抛物线y 2=4x 经过焦点的弦的中点的轨迹方程是( )A .y 2=x ﹣1B .y 2=2(x ﹣1)C .D .y 2=2x ﹣110.设点C (2a +1,a +1,2)在点P (2,0,0),A (1,﹣3,2),B (8,﹣1,4)确定的平面上,则a 的值为( )A .8B .16C .22D .2411.已知,则的最小值是( )A .B .C .D .12.若椭圆C 1: +=1(a 1>b 1>0)和椭圆C 2: +=1(a 2>b 2>0)的焦点相同且a 1>a 2.给出如下四个结论:①椭圆C 1与椭圆C 2一定没有公共点②>③a 12﹣a 22=b 12﹣b 22④a 1﹣a 2=b 1﹣b 2其中所有正确结论的序号是( )A .①②③B .①③④C .①②④D .②③④二、填空题:(本大题共4小题,每小题5分.共20分)13.双曲线4x 2﹣y 2+64=0上一点P 到它的一个焦点的距离等于1,则点P 到另一个焦点的距离等于 .14.已知F 1、F 2为椭圆=1的两个焦点,过F 1的直线交椭圆于A 、B 两点,若|F 2A |+|F 2B |=12,则|AB |= .15.如图所示,空间四边形OABC 中,,,,点M 在OA 上,且,N 为BC 中点,则等于 .16.已知平面内的一条直线与平面的一条斜线的夹角为60°,这条直线与斜线在平面内的射影的夹角为45°,则斜线与平面所成的角为.三.解答题(写出必要的解答过程)17.已知抛物线方程为y2=8x,直线l过点P(2,4)且与抛物线只有一个公共点,求直线l的方程.18.已知椭圆,一组平行直线的斜率是.(1)这组直线何时与椭圆相交?(2)当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.19.已知直线y=kx﹣1与双曲线x2﹣y2=4.(1)当它们没有公共点时,求k取值范围;(2)如果直线与双曲线相交弦长为4,求k的值.20.已知命题p:“方程+=m+2表示的曲线是椭圆”,命题q:“方程+=2m+1表示的曲线是双曲线”.且p∨q为真命题,p∧q为假命题,求实数m的取值范围.21.在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.(1)求证PA∥平面EDB;(2)求二面角C﹣PB﹣D的大小.22.已知椭圆G: +=1(a>b>0)的焦点和一个顶点在圆x2+y2=4上.(1)求椭圆的方程;(2)已知点P(﹣3,2),若斜率为1的直线l与椭圆G相交于A、B两点,试探讨以AB为底边的等腰三角形ABP是否存在?若存在,求出直线l的方程,若不存在,说明理由.2016-2017学年甘肃省兰州市舟曲中学高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.与圆x2+y2=1及圆x2+y2﹣8x+12=0都外切的圆的圆心在()A.一个椭圆上B.双曲线的一支上C.一条抛物线上D.一个圆上【考点】圆与圆的位置关系及其判定.【分析】设动圆P的半径为r,然后根据动圆与圆x2+y2=1及圆x2+y2﹣8x+12=0都外切得|PF|=2+r、|PO|=1+r,再两式相减消去参数r,则满足双曲线的定义,问题解决.【解答】解:设动圆的圆心为P,半径为r,而圆x2+y2=1的圆心为O(0,0),半径为1;圆x2+y2﹣8x+12=0的圆心为F(4,0),半径为2.依题意得|PF|=2+r,|PO|=1+r,则|PF|﹣|PO|=(2+r)﹣(1+r)=1<|FO|,所以点P的轨迹是双曲线的一支.故选B.2.下列命题中的真命题为()A.∃x0∈Z,使得1<4x0<3 B.∃x0∈Z,使得5x0+1=0C.∀x∈R,x2﹣1=0 D.∀x∈R,x2+x+2>0【考点】命题的真假判断与应用.【分析】A,由1<4x0<3,得<x0<,不存在x0∈Z,使得1<4x0<3;B,由5x0+1=0,得,;C由x2﹣1=0,得x=±1,;D,∀x∈R,x2+x+2=(x+1)2+1>0【解答】解:对于A,由1<4x0<3,得<x0<,不存在x0∈Z,使得1<4x0<3,故错;对于B,由5x0+1=0,得,故错;对于C由x2﹣1=0,得x=±1,故错;对于D,∀x∈R,x2+x+2=(x+1)2+1>0,故正确;故选:D3.已知=(1,﹣3,λ),=(2,4,﹣5),若⊥,则λ=()A.﹣4 B.﹣2 C.2 D.3【考点】向量语言表述线线的垂直、平行关系.【分析】由题意可得=(1,﹣3,λ),=(2,4,﹣5),并且⊥,所以结合向量坐标的数量积表达式可得2﹣12﹣5λ=0,进而求出答案.【解答】解:因为=(1,﹣3,λ),=(2,4,﹣5),并且⊥,所以2﹣12﹣5λ=0,解得:λ=﹣2.故选B.4.原命题“若x≤﹣3,则x<0”的逆否命题是()A.若x<﹣3,则x≤0 B.若x>﹣3,则x≥0 C.若x<0,则x≤﹣3 D.若x ≥0,则x>﹣3【考点】四种命题.【分析】直接利用四种命题中题设和结论之间的关系求出结果.【解答】解:原命题“若x≤﹣3,则x<0”则:逆否命题为:若x≥0,则x>﹣3故选:D5.“双曲线渐近线方程为y=±2x”是“双曲线方程为x2﹣=λ(λ为常数且λ≠0)”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据双曲线渐近线方程求出a,b的关系,得到双曲线的方程即可.【解答】解:双曲线渐近线方程为y=±2x,即b=2a,或a=2b,故双曲线方程为x2﹣=λ(λ为常数且λ≠0),是充要条件,故选:C.6.已知{a,b,c}是空间一个基底,则下列向量可以与向量=+,=﹣构成空间的另一个基底的是()A.B.C.D. +2【考点】空间向量的基本定理及其意义.【分析】根据空间向量的一组基底是:任意两个不共线,且不为零向量,三个向量不共面,即可判断出结论.【解答】解:由题意和空间向量的共面定理,结合向量+=(+)+(﹣)=2,得与、是共面向量,同理与、是共面向量,所以与不能与、构成空间的一个基底;又与和不共面,所以与、构成空间的一个基底.故选:C.7.椭圆上的点到直线的最大距离是()A.3 B. C. D.【考点】直线与圆锥曲线的综合问题;点到直线的距离公式.【分析】设椭圆上的点P(4cosθ,2sinθ),由点到直线的距离公式,计算可得答案.【解答】解:设椭圆上的点P(4cosθ,2sinθ)则点P到直线的距离d=;故选D.8.若正三棱锥的侧面都是直角三角形,则它的侧棱与底面所成角的余弦值为()A.B.C.D.【考点】直线与平面所成的角.【分析】根据所给的正三棱锥的特点,根据三垂线定理做出二面角的平面角,在直角三角形中做出要用的两条边的长度,根据三角函数的定义得到角的余弦值即可.【解答】解:正三棱锥P﹣ABC的侧棱两两垂直,过P做地面的垂线PO,在面ABC上,做BC的垂线AD,AO为PA在底面的射影,则∠PAO就是PA与底面ABC所成角,设侧棱长是1,在等腰直角三角形PBC中BC=,PD=,AD=,PA与底面ABC所成角的余弦值为:==.故选:A.9.抛物线y2=4x经过焦点的弦的中点的轨迹方程是()A.y2=x﹣1 B.y2=2(x﹣1)C. D.y2=2x﹣1【考点】抛物线的简单性质;轨迹方程.【分析】先根据抛物线方程求得焦点坐标,进而设出过焦点弦的直线方程,与抛物线方程联立消去y,根据韦达定理表示出x1+x2,进而根据直线方程求得y1+y2,进而求得焦点弦的中点的坐标的表达式,消去参数k,则焦点弦的中点轨迹方程可得.【解答】解:由题知抛物线焦点为(1,0)设焦点弦方程为y=k(x﹣1)代入抛物线方程得所以k2x2﹣(2k2+4)x+k2=0由韦达定理:x1+x2=所以中点横坐标:x==代入直线方程中点纵坐标:y=k(x﹣1)=.即中点为(,)消参数k,得其方程为y2=2x﹣2故选B.10.设点C(2a+1,a+1,2)在点P(2,0,0),A(1,﹣3,2),B(8,﹣1,4)确定的平面上,则a的值为()A.8 B.16 C.22 D.24【考点】共线向量与共面向量.【分析】与不共线,可设=λ+μ,利用平面向量基本定理即可得出.【解答】解:=(2a﹣1,a+1,2),=(﹣1,﹣3,2),=(6,﹣1,4),与不共线,设=λ+μ,则,解得a=16,故选:B.11.已知,则的最小值是()A.B.C.D.【考点】两向量的和或差的模的最值.【分析】求出的坐标,根据向量的模的定义求出的值.【解答】解:∵=(2,t,t)﹣(1﹣t,2t﹣1,0)=(1+t,1﹣t,t ),∴==.故当t=0时,有最小值等于,故选C.12.若椭圆C1: +=1(a1>b1>0)和椭圆C2: +=1(a2>b2>0)的焦点相同且a1>a2.给出如下四个结论:①椭圆C1与椭圆C2一定没有公共点②>③a12﹣a22=b12﹣b22④a1﹣a2=b1﹣b2其中所有正确结论的序号是( )A .①②③B .①③④C .①②④D .②③④ 【考点】椭圆的简单性质.【分析】先由a 12﹣b 12=a 22﹣b 22,从而③a 12﹣a 22=b 12﹣b 22成立,下面从两个方面来看:一方面:a 1>a 2,由上得b 1>b 2,从而①成立;②不成立;另一方面:a 12﹣b 12=a 22﹣b 22⇒(a 1+b 1)(a 1﹣b 1)=(a 2+b 2)(a 2﹣b 2)⇒a 1﹣b 1<a 2﹣b 2,从而④成立;从而得出正确答案.【解答】解:由a 12﹣b 12=a 22﹣b 22,从而③a 12﹣a 22=b 12﹣b 22成立, 一方面:a 1>a 2,由上得b 1>b 2,从而①成立;若在a 12﹣a 22=b 12﹣b 22中,a 1=2,a 2=,b 1=,b 2=1,==,==,有:<,故②不成立;另一方面:a 12﹣b 12=a 22﹣b 22,(a 1+b 1)(a 1﹣b 1)=(a 2+b 2)(a 2﹣b 2) 由于a 1+b 1>a 2+b 2 ∴a 1﹣b 1<a 2﹣b 2, 从而④成立;∴所有正确结论的序号是 ①③④. 故选B .二、填空题:(本大题共4小题,每小题5分.共20分)13.双曲线4x 2﹣y 2+64=0上一点P 到它的一个焦点的距离等于1,则点P 到另一个焦点的距离等于 17 . 【考点】双曲线的定义.【分析】首先将双曲线方程化成标准方程,从而得出参数a 、b 的值,然后根据双曲线的定义得出|PF 1﹣PF 2|=2a ,根据题中的已知数据,可以求出点P 到另一个焦点的距离.【解答】解:将双曲线4x 2﹣y 2+64=0化成标准形式:∴a2=64,b2=16P到它的一个焦点的距离等于1,设PF1=1∵|PF1﹣PF2|=2a=16∴PF2=PF1±16=17(舍负)故答案为:1714.已知F1、F2为椭圆=1的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|=8.【考点】椭圆的简单性质.【分析】运用椭圆的定义,可得三角形ABF2的周长为4a=20,再由周长,即可得到AB的长.【解答】解:椭圆=1的a=5,由题意的定义,可得,|AF1|+|AF2|=|BF1|+|BF2|=2a,则三角形ABF2的周长为4a=20,若|F2A|+|F2B|=12,则|AB|=20﹣12=8.故答案为:815.如图所示,空间四边形OABC中,,,,点M在OA上,且,N为BC中点,则等于.【考点】向量的三角形法则.【分析】画出图形,用、、表示、,从而求出.【解答】解:画出图形,如图:∵,,,点M 在OA 上,且OM=2MA ,N 为BC 的中点,∴==,=(+)=+,∴=﹣=+﹣;故答案为:.16.已知平面内的一条直线与平面的一条斜线的夹角为60°,这条直线与斜线在平面内的射影的夹角为45°,则斜线与平面所成的角为 45° . 【考点】直线与平面所成的角.【分析】由已知中直线a 是平面α的斜线,b ⊂α,a 与b 成60°的角,且b 与a 在α内的射影成45°的角,利用“三余弦定理”,即求出a 与平面α所成的角的余弦值,进而得到答案.【解答】解:题目转化为:直线a 是平面α的斜线,b ⊂α,a 与b 成60°的角,且b 与a 在α内的射影成45°的角,求斜线与平面所成的角. 设斜线与平面α所成的角为θ, 根据三余弦定理可得: cos60°=cos45°×cosθ即=×cosθ则cosθ=则θ=45°故答案为:45°.三.解答题(写出必要的解答过程)17.已知抛物线方程为y2=8x,直线l过点P(2,4)且与抛物线只有一个公共点,求直线l的方程.【考点】直线与抛物线的位置关系.【分析】设出直线方程,与抛物线方程联立,通过直线的斜率是否为0,利用判别式求解即可得到直线方程.【解答】解:由题意,直线l斜率存在,设l为y﹣4=k(x﹣2)代入抛物线y2=8x,得ky2﹣8y﹣16k+32=0,当k=0时,满足题意,此时l为y=4;﹣﹣﹣﹣﹣﹣﹣﹣﹣4分当k≠0时,由△=(8+16k)2﹣4k×32=0,解得k=1,此时l为:x﹣y+2=0﹣﹣﹣﹣﹣﹣﹣﹣﹣10分综上l为:y=4或x﹣y+2=0.18.已知椭圆,一组平行直线的斜率是.(1)这组直线何时与椭圆相交?(2)当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.【考点】直线与圆锥曲线的关系.【分析】(1)设出平行直线的方程:y=x+m,代入椭圆方程,消去y,由判别式大于0,可得m的范围;(2)运用中点坐标公式和参数方程,消去m,即可得到所求的结论.【解答】解:(1)设一组平行直线的方程为y=x+m,代入椭圆方程,可得9x2+4(x2+3mx+m2)=36,即为18x2+12mx+4m2﹣36=0,由判别式大于0,可得144m2﹣72(4m2﹣36)>0,解得﹣3<m<3,则这组平行直线的纵截距在(﹣3,3),与椭圆相交;(2)证明:由(1)直线和椭圆方程联立,可得18x2+12mx+4m2﹣36=0,即有x1+x2=﹣m,截得弦的中点为(﹣m,m),由,消去m,可得y=﹣x.则这些直线被椭圆截得的线段的中点在一条直线y=﹣x上.19.已知直线y=kx﹣1与双曲线x2﹣y2=4.(1)当它们没有公共点时,求k取值范围;(2)如果直线与双曲线相交弦长为4,求k的值.【考点】直线与双曲线的位置关系.【分析】(1)由题意令,得x2﹣(kx﹣1)2=4,整理得(1﹣k2)x2+2kx﹣5=0,当1﹣k2=0,k=±1时,显然符合条件;当1﹣k2≠0时,有△≥0.(2)设直线与双曲线相交于两点A(x1,y1),B(x2,y2).利用|AB|==4,基础即可得出.【解答】解:(1)由题意令,得x2﹣(kx﹣1)2=4,整理得(1﹣k2)x2+2kx ﹣5=0当1﹣k2=0,k=±1时,显然符合条件;当1﹣k2≠0时,有△=20﹣16k2≥0,解得﹣≤k≤.综上,k取值范围是k=±1,﹣≤k≤.(2)设直线与双曲线相交于两点A(x1,y1),B(x2,y2).则x1+x2=,x1•x2=,则|AB|===4,化为:8k2﹣9k﹣1=0,解得k=±.20.已知命题p:“方程+=m+2表示的曲线是椭圆”,命题q:“方程+=2m+1表示的曲线是双曲线”.且p∨q为真命题,p∧q为假命题,求实数m的取值范围.【考点】复合命题的真假.【分析】分别判断出p,q为真时的m的范围,通过讨论p,q的真假,得到关于m的不等式组,解出即可.【解答】解:命题p为真命题时,则有,则有;命题q为真命题时,则有(m﹣1)(m﹣3)<0,则有m∈(1,3),因为p∨q为真命题,p∧q为假命题,所以p和q一真一假.所以.21.在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.(1)求证PA∥平面EDB;(2)求二面角C﹣PB﹣D的大小.【考点】二面角的平面角及求法;直线与平面平行的判定.【分析】(1)连结AC,BD,交于点O,连结OE,则OE∥PA,由此能证明PA∥平面EDB.(2)以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣PB﹣D的大小.【解答】证明:(1)连结AC,BD,交于点O,连结OE,∵底面ABCD是正方形,∴O是AC的中点,∵点E是PC的中点,∴OE∥PA,∵OE⊂平面EBD,PA⊄平面EBD,∴PA∥平面EDB.解:(2)以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,设PD=DC=1,则D(0,0,0),P(0,0,1),B(1,1,0),C(0,1,0),=(0,0,1),=(1,1,0),=(0,1,﹣1),=(1,1,﹣1),设平面PBC的法向量=(x,y,z),平面PBD的法向量=(a,b,c),则,取y=1,得=(0,1,1),,取a=1,得=(1,﹣1,0),设二面角C﹣PB﹣D的大小为θ,则cosθ===,∴θ=60°,∴二面角C﹣PB﹣D的大小为60°.22.已知椭圆G: +=1(a>b>0)的焦点和一个顶点在圆x2+y2=4上.(1)求椭圆的方程;(2)已知点P(﹣3,2),若斜率为1的直线l与椭圆G相交于A、B两点,试探讨以AB为底边的等腰三角形ABP是否存在?若存在,求出直线l的方程,若不存在,说明理由.【考点】椭圆的简单性质.【分析】(Ⅰ)设椭圆G的右焦点为F(c,0),由题意可得:b=c,且b2+c2=8,由此能求出椭圆G的方程.(Ⅱ)以AB为底的等腰三角形ABP存在.设斜率为1的直线l的方程为y=x+m,代入中,得:3x2+4mx+2m2﹣8=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的方程.【解答】解:(Ⅰ)设椭圆G的右焦点为F(c,0),由题意可得:b=c,且b2+c2=8,∴b2=c2=4,故a2=b2+c2=8,∴椭圆G的方程为(Ⅱ)以AB为底的等腰三角形ABP存在.理由如下设斜率为1的直线l的方程为y=x+m,代入中,化简得:3x2+4mx+2m2﹣8=0,①因为直线l与椭圆G相交于A,B两点,∴△=16m2﹣12(2m2﹣8)>0,解得﹣2,②设A(x1,y1),B(x2,y2),则,.③于是AB的中点M(x0,y0)满足=﹣,.已知点P(﹣3,2),若以AB为底的等腰三角形ABP存在,则k PM=﹣1,即=﹣1,④,将M(﹣)代入④式,得m=3∈(﹣2,2)满足②此时直线l的方程为y=x+3.2017年3月23日。
甘肃省兰州新区舟曲中学2017-2018学年高二上学期第二

新舟中学2017-2018学年度第一学期第二次月考高二年级化学试卷一、选择题1.下列变化过程,属于放热反应的是()①液态水变成水蒸气②酸碱中和反应③浓稀释④固体溶于水⑤在中燃烧⑥食物腐败.A.②③④⑤⑥B.②③④C.②⑤⑥D.①③⑤2.已知1白磷变成1红磷放出18.39KJ热量,下面两个反应:4P(白,s) + 5O2(g)=2P2O5(s)△H14P(红,s) + 5O2(g)=2P2O5(s)△H2则△H1和△H2的关系是()A. △H1>△H2B. △H1=△H2C. △H1 < △H2D. 无法确定3.下列关于化学反应速率的说法错误的是()A.化学反应速率是用于衡量化学反应进行快慢的物理量B. 可逆反应达到化学平衡状态时,反应停止,正、逆反应速率都为零C. 决定化学反应速率的主要因素是反应物本身的性质D.增大反应物浓度或升高反应温度都能加快化学反应速率4.反应,经一段时间后的浓度增加了,在这段时间内用表示的反应速率为,则这段时间为()A. B. C. D.5.在中,表示该反应速率最快的是()A. B.C. D.6. 已知298 K时,合成氨反应N 2(g)+3H2(g) 2NH3(g) ΔH=-92.0 kJ·mol-1,将此温度下的1 mol N2和3 mol H2放在一密闭容器中,在催化剂存在时进行反应。
测得反应放出的热量为(假定测量过程中没有能量损失)( )A.一定小于92.0 kJ B.一定大于92.0 kJC.一定等于92.0 kJ D.无法确定7.在一定条件下,对于密闭容器中的反应:,下列说法正确的是()A.增加的量,可以加快反应速率B.当和全部转化为时,反应才达到最大限度C.达到平衡时,和的浓度比一定为D.分别用和来表示该反应的速率时,数值大小相同8.一定温度下在容积恒定的密闭容器中,进行如下可逆反应:当下列物理量不发生变化时,能表明该反应已达到平衡状态的是()①混合气体的密度②容器内气体的压强③混合气体的总物质的量④物质的量浓度.A.①和④B.②和③C.②③④D.只有④9.合成氨所需的氢气可用煤和水作原料经多步反应制得,其中的一步反应为:反应达到平衡后,为提高的转化率,下列措施中正确的是()A.增加压强B.降低温度C.增大的浓度D.更换催化剂10.下列说法中正确的是 ( ) A.凡是放热反应都是能自发进行的反应,而吸热反应都是非自发进行的反应B.自发反应一定是熵增加的反应,非自发反应一定是熵减小或不变的反应C.熵增加且放热的反应一定是自发反应D. 自发反应在任何条件下都可以实现11.下列叙述,正确的是( )A. 液态HCl、固态NaCl均不导电,所以HCl和NaCl均为非电解质B. NH3、SO3的水溶液均导电,所以NH3、SO3是电解质C. 铜丝、石墨均导电,所以它们是电解质D. 蔗糖、酒精在水溶液中或熔融时均不导电,所以它们是非电解质12.下列电离方程式中书写正确的是()A. NaHSO4Na++H++SO42-B. NaHCO3Na++H++CO32-C. HClO=H++ClO-D. H2S H++HS-;HS-H++S2--+H+,要使电离平衡右移且c(H+)增大,13.在醋酸中存在电离平衡:CH应采取的措施是 ( )A.加入NaOH(s) B.加入盐酸C.加蒸馏水 D.升高温度14.在100℃时,水的离子积为10−12,若该温度下某溶液中的c(H+)为1×10−7mol/L,则该溶液( )A. 呈碱性B. 呈酸性C. 呈中性D. c(OH−)=10c (H+)15.(AB层选做)已知反应:①②稀溶液中, ,下下列结论正确的是: ()A. 碳的燃烧热大于110.5kJ/molB. ①的反应热为221kJ/molC. 稀硫酸与稀NaOH溶液反应的中和热为△H=57.3kJ/molD. 稀醋酸与稀NaOH溶液反应生成1 mol水,放出57.3kJ热量15.(C层选做)下列关于反应热的描述中正确的是( )A.CO(g)的燃烧热283.0 kJ·mol-1,则2CO2(g)===2CO(g)+O2(g)反应的ΔH=+2×283.0 kJ·mol-1B.HCl和NaOH反应的中和热ΔH=-57.3 kJ·mol-1,则H2SO4和Ca(OH)2反应的中和热ΔH=2×(-57.3)kJ·mol-1C.反应热有正负之分,燃烧热ΔH全部是正值D.1 mol甲烷燃烧生成气态水和二氧化碳所放出的热量是甲烷的燃烧热16. (AB层选做)下列事实不能用勒夏特列原理解释的是()A. 氯水中有平衡:Cl 2+H2O HCl+HClO,当加入AgNO3溶液后,溶液颜色变浅B. 对CO(g)+NO2(g) CO2(g)+NO(g),平衡体系增大压强可使颜色变深C. 对2NO2(g) N2O4(g),升高温度平衡体系颜色变深D. SO2催化氧化成SO3的反应,往往加入过量的空气16. (C层选做)反应A(g)+2B(g)2C(g) △H>0,达到平衡后,将反应混合物温度降低,下列叙述中,正确的()A. 正反应速率加快,逆反应速率减慢,平衡向正反应方向移动B. 正逆反应速率均减慢,平衡向逆反应方向移动C. 正逆反应速率均加快,平衡不移动D. 正反应速率减慢,逆反应速率加快,平衡向逆反应方向移动17 .(AB层选做) 在一定温度下,固定体积的密闭容器内某一反应中M、N的物质的量随反应时间变化的曲线如图所示,下列表述正确的是( )A. t1时,N的浓度是M浓度的2倍B. t2时,正逆反应速率相等达到平衡C. t3时,正反应速率大于逆反应速率D. 此反应的化学方程式为M 2N17.(C层选做)如图表示工业SO2催化氧化反应过程中的速率(v)与时间(t)的关系曲线,下列叙述正确的是()A. t2- t3,气体总物质的量保持不变(已知该条件下SO3为气体)B. t2时,v(SO2)正和v(O2)逆相等且等于0C. t1时刻,只有正方向的反应没有逆方向的反应D. t2- t3,处于静止状态,反应不再发生18.(AB层选做)对于可逆反应,下列各项对示意图的解释与图象相符的是()A.①压强对反应的影响B.②温度对反应的影响C.③平衡体系增加对反应的影响D.④催化剂对反应的影响18. (C层选做)有一化学平衡mA(g)+nB(g) pC(g)+qD(g),如图所示是A的转化率同压强、温度的关系,分析图可以得出的正确结论是:()A. 正反应吸热,m+n<p+qB. 正反应放热,m+n>p+qC. 正反应吸热,m+n>p+qD. 正反应放热,m+n<p+q二、填空题19.已知下列热化学方程式:①②③④回答下列问题:上述反应中属于放热的是________的燃烧热为________,的燃烧热为________燃烧生成液态水,放出的热量为________燃烧的热化学方程式为____ ____.20. (AB层选做)下表是不同温度下水的离子积数据:试回答以下问题:(1)若25<t1<t2,则a 1×10-14(填“>”、“<”或“=”),作此判断的理由是。
甘肃省兰州新区高二数学上学期期末考试试题 理

甘肃省兰州新区2016-2017学年高二数学上学期期末考试试题 理卷Ⅰ 一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.与圆221x y +=及圆228120x y x +-+=都外切的圆的圆心在( B )A.一个椭圆上B.双曲线的一支上C.一条抛物线上D.一个圆上2.下列命题中的真命题为( D )A.,0Z x ∈∃使得 3410<<xB.,0Z x ∈∃ 使得 0150=+xC.01,2=-∈∀x R xD.02,2>++∈∀x x R x3. 已知()1,3,a λ=-r ,()2,4,5b =-r ,若a b ⊥r r , 则λ= ( C )A .2B .4-C .2-D .34. 原命题“若3x ≤-,则0x <”的逆否命题是( B )A .若3x <-,则0x ≤B .若3x >-,则0x ≥C .若0x <,则3x ≤-D .若0x ≥,则3x >-5.“双曲线渐近线方程为x y 2±=”是“双曲线方程为)0(422≠=-λλλ为常数且y x ”的( C ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件6. 设向量{}c b a ,,是空间一个基底,则一定可以与向量,,b a q b a p -=+=构成空间的另 一个基底的向量是 ( C ) A .a B .b C .c D .a 或b7. 椭圆221164x y +=上的点到直线220x y +-=的最大距离为( D ).A. 311 C. 2108. 若正三棱锥的侧面都是直角三角形,则它的侧棱与底面所成角的余弦值为( A )A.36B.33C.32D. 319. 已知抛物线方程为x y 42=,则经过它的焦点的弦的中点轨迹方程是(B ) A.12-=x y B.)1(22-=x y C.212-=x y D.122-=x y 10.设点)2,1,12(++a a C 在点)4,1,8(),2,3,1(),0,0,2(--B A P 确定的平面上,则a =( A ) A.16 B.4 C.2 D.8 11. 已知1210a t t =--r (,,),(2)b t t =r ,,则||b a -r r 的最小值是( C )A.5B.6 C .2 D.312.若椭圆)0(1:112122121>>=+b a b y a x C 和椭圆)0(1:222222222>>=+b a b y a x C 的焦点相同且21a a >.给出如下四个结论:①椭圆1C 与椭圆2C 一定没有公共点 ②2121b b a a > ③22212221b b a a -=- ④2121b b a a -<-其中所有正确结论的序号是( B )A. ①②③B. ①③④C. ①②④D.②③④卷二二、填空题:(本大题共4小题,每小题5分.共20分)13.双曲线224640x y -+=上一点P 到它的一个焦点的距离等于1,那么点P 到另一个焦点的距离等于 17 . 14.已知21,F F 为椭圆192522=+y x 的两个焦点,过1F 的直线交椭圆于B A ,两点,若12||||22=+B F A F ,则||AB = 8 .15.空间四边形OABC 中,OA a OB b OC c ===u u u r r u u u u r r u u u r r,,. 点M 在OA 上,且OM=2MA ,点N 为BC 的中点,则MN u u u u r 等于211322a b c -++r r r (用a b c r r u r ,,表示) 16.已知平面内的一条直线与平面的一条斜线的夹角为60°,这条直线与斜线在平面内的射影的夹角为45°,则斜线与平面所成的角为45度.三.解答题(写出必要的解答过程)17.(本小题满分10分)已知抛物线方程为x y 82=,直线l 过点)4,2(P 且与抛物线只有一个公共点,求直线l 的方程. 解:由题意,直线l 斜率存在,设l 为)2(4-=-x k y 代入抛物线得0321682=+--k y ky 当0=k 时,满足题意,此时l 为4=y ; ---------4分当100==∆≠k k 得时,由,此时l 为02=+-y x ---------10分综上l 为4=y 或02=+-y x18. (本小题满分12分) 已知椭圆22149x y +=,一组平行直线的斜率是32.(课本试题) (1)这组直线何时与椭圆相交?(2) 当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.19. (本小题满分12分)已知直线1y kx =-与双曲线224x y -=.(课本试题)(1)当它们没有公共点时,求k 取值范围;(2)如果直线与双曲线相交弦长为4,求k 的值.20. (本小题满分12分) 已知命题p :“方程221222+=-+-m my m x 表示的曲线是椭圆”,命题q :“方程123122+=-+-m m y m x 表示的曲线是双曲线”。
甘肃兰州新区舟曲中学2016-2017学年高二数学上学期第二次月考试题 理

甘肃省兰州新区舟曲中学2016-2017学年高二数学上学期第二次月考试题理一、 选择题:(本大题共12小题,每小题5分,共60分.) 每小题中,只有一项符合题目要求,请将正确答案填在正确的位置.1.在数列,13,10,7,2,1……中,192是这个数列的 ( ) A.第16项 B.第24项 C.第26项 D.第28项2.关于x 的不等式)0(08222><--a a ax x 的解集为),(21x x ,且1512=-x x ,则=a ( )A .25 B. 27 C. 415 D. 2153.设b a ,是实数,则""b a >是22"b a >的 ( ) A .充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 4. 命题;1sin ,:<∈∀x R x p ;命题.1cos ,:-≤∈∃x R x q 则下列结论是真命题的是 ( ) A.q p ∧ B.q p ∧⌝ C.q p ⌝∨ D.q p ⌝∧⌝5.设,,,R c b a ∈则下列命题为真命题的是 ( ) A.c b c a b a ->-⇒> B.bc ac b a >⇒> C.22b a b a >⇒> D.22bc ac b a >⇒> 6.在△ABC 中,若B A s i n s i n >,则A 与B 的大小关系为( )A .B A <B.B A ≥C.B A >D. A 、B 的大小关系不能确定7.在等差数列{}n a 中,前四项之和为20,最后四项之和为60,前n 项之和是100,则项数n 为 ( )A .9B .10C .11D .128.△ABC 中, ∠A ,∠B ,∠C 所对的边分别为a , b , c .若3,4a b ==,∠C=60,则c 的值等于( )A. 5B. 13C.13D.37 9.命题“若4πα=,则1t a n =α”的逆否命题是 ( )A.若4πα≠则1tan ≠α B. 若4πα=则1tan ≠αC. 若1tan ≠α则4πα≠ D. 若1tan ≠α则4πα=10.如果}{n a 为递增数列,则}{n a 的通项公式可以为( )A. 32+-=n a n B. 132+-=n n a n C. n n a 21=D. 21log n a n =+ 11.给出下列命题:①若原命题为真,则这个命题的否命题,逆命题,逆否命题中至少有一个为真; ②若p 是q 成立的充分条件,则q 是p 成立的必要条件; ③若p 是q 的充要条件,则可记为q p ⇔; ④命题“若p 则q ”的否命题是“若p 则q ⌝”.其中是真命题的是 ( )A.①②③B.②③④C.①③④D. ②④ 12.设ABC ∆的内角C B A ,,所对的边分别为c b a ,,若cca B 22cos2+=,则ABC ∆的形状为( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定二、填空题:(本大题4小题,每小题5分,共20分. )请将正确的答案填在横线上。
甘肃省兰州市新区舟曲中学高一(上)第二次月考数学试卷
2016-2017学年甘肃省兰州市新区舟曲中学高一(上)第二次月考数学试卷一、选择题(本大题共12小题,每小题5分,共60分)1.已知全集U={0,1,2}且∁U A={2},则集合A的真子集共有()A.3个B.4个C.5个D.6个2.设全集U=R,A={x|x>0},B={x|x>1},则A∩∁U B=()A.{x|0≤x<1}B.{x|0<x≤1}C.{x|x<0}D.{|x>1}3.下列四个图形中,不是以x为自变量的函数的图象是()A.B.C.D.4.当a>1时,在同一坐标系中,函数y=a﹣x与y=log a x的图象为()A. B. C.D.5.7、函数y=log a x,y=log b x,y=log c x,y=log d x的图象如图所示,则a,b,c,d的大小顺序是()A.1<d<c<a<b B.c<d<1<a<b C.c<d<1<b<a D.d<c<1<a<b6.如果函数f(x)=x2﹣(a﹣1)x+5在区间上是减函数,那么实数a的取值范围是()A.a≤2 B.a>3 C.2≤a≤3 D.a≥37.函数f(x)=+的定义域是()A.(﹣∞,﹣1)B.(1,+∞) C.(﹣1,1)∪(1,+∞)D.(﹣∞,+∞)8.方程2x=2﹣x的根所在区间是()A.(﹣1,0) B.(2,3)C.(1,2)D.(0,1)9.函数y=的值域是()A.0,40,4) D.(0,4)10.已知函数f(x)=,则f(﹣10)的值是()A.﹣2 B.﹣1 C.0 D.111.定义在R上的函数f(x),对任意的x∈R都有f(﹣x)=﹣f(x)且当x≥0时f (x)=x2﹣2x,则不等式xf(x)<0的解集为()A.(﹣∞,﹣2)∪(0,2)B.(﹣2,0)∪(0,2)C.(﹣2,0)∪(2,+∞)D.(﹣∞,﹣2)∪(2,+∞)12.用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x,x+2,10﹣x}(x≥0),则f(x)的最大值为()A.4 B.5 C.6 D.7二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=log0.5(﹣x2+4x+5),则f(3)与f(4)的大小关系为.14.对于函数f(x)=x﹣2﹣lnx,我们知道f(3)=1﹣ln3<0,f(4)=2﹣ln4>0,用二分法求函数f(x)在区间(3,4)内的零点的近似值,我们先求出函数值f(3.5),若已知ln3.5=1.25,则接下来我们要求的函数值是f ().15.定义在R上的偶函数f(x)在﹣1,20,+∞)B.C.0,4).故选C.10.已知函数f(x)=,则f(﹣10)的值是()A.﹣2 B.﹣1 C.0 D.1【考点】函数的值.【分析】由题意,代入分段函数求函数的值.【解答】解:f(﹣10)=f(﹣10+3)=f(﹣7)=f(﹣7+3)=f(﹣4)=f(﹣4+3)=f(﹣1)=f(﹣1+3)=f(2)=log22=1.故选D.11.定义在R上的函数f(x),对任意的x∈R都有f(﹣x)=﹣f(x)且当x≥0时f (x)=x2﹣2x,则不等式xf(x)<0的解集为()A.(﹣∞,﹣2)∪(0,2)B.(﹣2,0)∪(0,2)C.(﹣2,0)∪(2,+∞)D.(﹣∞,﹣2)∪(2,+∞)【考点】函数奇偶性的性质.【分析】当x≥0时,不等式xf(x)<0即x(x2﹣2x)<0,解得即可.由于函数f(x)对任意的x∈R满足f(﹣x)=﹣f(x),可得函数f(x)是奇函数.因此当x<0时,f (x)=﹣f(﹣x)=﹣(x2+2x),于是不等式xf(x)<0即﹣x(x2+2x)<0,解出即可.【解答】解:当x≥0时,不等式xf(x)<0即x(x2﹣2x)<0,解得0<x<2.∵函数f(x)对任意的x∈R满足f(﹣x)=﹣f(x),∴函数f(x)是奇函数.当x<0时,f(x)=﹣f(﹣x)=﹣(x2+2x),∴不等式xf(x)<0即﹣x(x2+2x)<0,解得﹣2<x<0.综上可得:不等式xf(x)>0的解集是(﹣2,0)∪(0,2).故选:B.12.用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x,x+2,10﹣x}(x≥0),则f(x)的最大值为()A.4 B.5 C.6 D.7【考点】函数的最值及其几何意义.【分析】在同一坐标系内画出三个函数y=10﹣x,y=x+2,y=2x的图象,以此作出函数f (x)图象,观察最大值的位置,通过求函数值,解出最大值.【解答】解:10﹣x是减函数,x+2是增函数,2x是增函数,令x+2=10﹣x,x=4,此时,x+2=10﹣x=6,如图:y=x+2 与y=2x交点是A、B,y=x+2与y=10﹣x的交点为C(4,6),由上图可知f(x)的图象如下:C为最高点,而C(4,6),所以最大值为6.故选:C二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=log0.5(﹣x2+4x+5),则f(3)与f(4)的大小关系为f(3)<f(4).【考点】对数值大小的比较.【分析】利用函数f(x)=log0.5x在R上单调递减即可得出.【解答】解:∵函数f(x)=log0.5x在R上单调递减,f(3)=log0.58,f(4)=log0.55,∴f(3)<f(4).故答案为:f(3)<f(4).14.对于函数f(x)=x﹣2﹣lnx,我们知道f(3)=1﹣ln3<0,f(4)=2﹣ln4>0,用二分法求函数f(x)在区间(3,4)内的零点的近似值,我们先求出函数值f(3.5),若已知ln3.5=1.25,则接下来我们要求的函数值是f ( 3.25).【考点】二分法求方程的近似解.【分析】函数f(x)=x﹣2﹣lnx在区间(3,4)上连续且单调递增,f(3)=1﹣ln3<0,f(4)=2﹣ln4>0,f(3)f(4)<0,由此可得函数的零点所在的初始区间,再计算函数值f(3.5),即可得出接下来我们要求的函数值.【解答】解:函数f(x)=x﹣2﹣lnx在区间(3,4)上连续且单调递增,f(3)=1﹣ln3<0,f(4)=2﹣ln4>0,f(3)f(4)<0,故用二分法求函数f(x)=x﹣2﹣lnx的零点时,初始的区间大致可选在(3,4)上.又f(3.5)=3.5﹣2﹣ln3.5=0.25>0,∴f(3)f(3.5)<0,零点区间大致可选在(3,3.5)上,则接下来我们要求的函数值是区间(3,3.5)中点的函数值f ( 3.25).故答案为:3.25.15.定义在R上的偶函数f(x)在0,+∞)上单调递减,∴偶函数f(x)在(﹣∞,00,1﹣1,2﹣1,2﹣9,15hslx3y3h.22.某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75%销售.现某茶社要购买这种茶壶x 个,如果全部在甲店购买,则所需金额为y1元;如果全部在乙店购买,则所需金额为y2元.(1)分别求出y1、y2与x之间的函数关系式;(2)该茶社去哪家茶具店购买茶壶花费较少?【考点】函数模型的选择与应用.【分析】(1)根据甲店茶壶的售价不得低于44元/个可知甲店购买所需金额为一个分段函数,若全部在乙店购买,则所需金额为一个一次函数;(2)先求出茶具店购买茶壶花费y一样时所买茶壶个数,然后分段可知该茶社去哪家茶具店购买茶壶花费较少.【解答】解:(1),y2=60x(x∈N+)(2)令﹣2x2+80x=60x解得x=10当0<x<10时,去乙店花费较少当x=10时,甲乙两店一样当x>10时,去甲店花费较少2017年2月11日。
甘肃高二高中数学月考试卷带答案解析

甘肃高二高中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.在△ABC中,已知,,则的值为()A.或B.C.D.\2.在中,若,则等于()A.B.C.D.3.()A.B.C.D.4.已知则的值为()A.B.C.D.5.若,且,则( )A.B.C.D.6.在△ABC 中,,则A等于()A.60°B.45°C.120°D.30°7.在△ABC中,若,则∠A=()A.B.C.D.8.若的内角满足,则()A.B.C.D.9.在中,若的形状一定是()A.等腰直角三角形B.等边三角形C.直角三角形D.等腰三角形10.在中,根据下列条件解三角形,其中有两个解的是()A.,,B.,,C.,,D.,,11..在△ABC中,已知,,则的值为()A.或B.C.D.12.如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB 等于()A.B.C.D.二、填空题1.在中,已知,,,则2.在△中,若,则 .3..函数的图象相邻的两条对称轴之间的距离是4.若,则的形状是三、解答题1.(本题10分)a,b,c为△ABC的三边,其面积S=12,bc=48,b-c=2,求a.△ABC2.(本题12分)在△ABC中,求证:3.(本题12分)在中,已知,判定的形状.4.(本题12分)在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足:2sin(A+B)-=0,求角C的度数,边c的长度.5.(本题12分)设.向量.(Ⅰ) 当时,求函数的值域;(Ⅱ)当时,求函数的单调递减区间.6.(本题10分).在中,,,.(1)求的值;(2)求的值.甘肃高二高中数学月考试卷答案及解析一、选择题1.在△ABC中,已知,,则的值为()A.或B.C.D.\【答案】B【解析】.2.在中,若,则等于()A.B.C.D.【答案】D【解析】因为A:B:C=1:2:3,所以.3.()A.B.C.D.【答案】B【解析】.4.已知则的值为()A.B.C.D.【答案】D【解析】5.若,且,则( )A.B.C.D.【答案】A【解析】对此式两边平方可得, .6.在△ABC 中,,则A等于()A.60°B.45°C.120°D.30°【答案】C【解析】.7.在△ABC中,若,则∠A=()A.B.C.D.【答案】C【解析】因为.8.若的内角满足,则()A.B.C.D.【答案】A【解析】.9.在中,若的形状一定是()A.等腰直角三角形B.等边三角形C.直角三角形D.等腰三角形【答案】D【解析】.所以一定是等腰三角形.10.在中,根据下列条件解三角形,其中有两个解的是()A.,,B.,,C.,,D.,,【答案】C【解析】A为两角一边,B为两边及夹角,都为一解的情况;C、D都为两边及一边对角的情况,但对于D由于b<a,所以只能是一解.故应选C.11..在△ABC中,已知,,则的值为()A.或B.C.D.【答案】B【解析】.12.如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于()A.B.C.D.【答案】A【解析】因为.二、填空题1.在中,已知,,,则【答案】3或6.【解析】由正弦定理可知,,当时,当时,所以a的值为3或6.2.在△中,若,则 .【答案】【解析】因为,所以a:b:c=3:4:5,设a=3x,b=4x,c=5x,则.3..函数的图象相邻的两条对称轴之间的距离是【答案】【解析】,所以f(x)的周期为,所以相邻两条对称轴之间的距离为半个周期的长度.4.若,则的形状是【答案】等腰三角形【解析】,所以的形状是等腰三角形.三、解答题=12,bc=48,b-c=2,求a.1.(本题10分)a,b,c为△ABC的三边,其面积S△ABC【答案】a2=b2+c2-2bccosA=(b-c)2+2bc(1-cosA)=4+2×48×(1-cosA)当A=60°时,a2=52,a=2当A=120°时,a2=148,a=2=12,bc=48,可求出sinA,进而求出cosA,然后再利用【解析】由S△ABC求a值即可.a2=b2+c2-2bccosA=(b-c)2+2bc(1-cosA)=4+2×48×(1-cosA)当A=60°时,a2=52,a=2当A=120°时,a2=148,a=22.(本题12分)在△ABC中,求证:【答案】见解析。
甘肃兰州新区舟曲中学2016-2017学年高二化学上学期第一次月考试题

新舟中学2016—2017学年第一学期第一次月考高二年级化学试卷相对原子质量:Na 23 Al 27 Fe 56 Cu 64 H 1 O 16 C 12 S 16 Cl 35.5(说明:满分100分,考试时间90分钟)Ⅰ卷选择题 (共60分)一单选题 (共15题,每小题4分,总分值60)1. 下列说法中不正确的是 ( )A. 电解水生成氢气和氧气时,电能转变成化学能B. 煤燃烧时,化学能大部分转变成热能C. 绿色植物光合作用过程中,太阳能转变成化学能D. 白炽灯工作时,电能全部转变成光能2. 下列各项与反应热的大小无关的是 ( )A. 反应物的状态B. 生成物的状态C. 反应物的多少D. 表示反应热的单位3. 下列关于燃烧热和中和热的比较中,错误的是 ( )A. 两者对应反应的△H均小于0B. 两者的单位均为kJ·mol-1,但mol-1的含义不同C. 两者的数值均不随反应物用量改变而改变D. 两者的数值均随反应物改变而改变4. 已知在298K时下述反应的有关数据: ( )C (s) + 1/2O2 (g) = CO (g) △H1 = -110.5 kJ• mol-1C (s) + O2 (g) = CO2 (g) △H2= -393.5 kJ• mol-1则C (s) + CO2 (g) = 2CO (g) 的△H为( )A. +283.5 kJ• mol-1B. +172.5 kJ• mol-1C. -172.5 kJ• mol-1D. -504 kJ• mol-15. 分析以下几个热化学方程式,哪个是表示固态碳或气态氢气燃烧时的燃烧热的是( )A. C (s) + O2 (g) =CO (g) ΔH = -110.5 kJ/molB. C (s) + O 2(g) = CO2 (g) ΔH = -393.5 kJ/molC. 2H2 (g) + O2 (g) = 2H2O (l) ΔH = -571.6 kJ/molD. H2 (g)+1/2O2 (g) =H2O (g) ΔH = -241.8 kJ/mol6. 将4molA气体和2molB气体在2L的容器中混合并在一定条件下发生如下反应:2A (g)+B(g) 2C (g),若经2s后测得C的浓度为0.6mol·L-1,现有下列几种说法:①用物质A表示的反应平均速率为0.3mol·(L·s)-1②用物质B表示的反应平均速率为0.6mol·(L·s)-1③2s时物质A的转化率为70% ④2s时物质B的浓度为0.7mol·L-1其中正确的是( )A. ①③B. ①④C. ②③D. ③④7. 对可逆反应4NH3(g)+ 5O2(g) 4NO(g)+ 6H2O(g),下列叙述正确的是( )A. 达到化学平衡时,4υ正(O2)= 5υ逆(NO)B. 若单位时间内生成x mol NO的同时,消耗x mol NH3,则反应达到平衡状态C. 达到化学平衡时,若增大容器体积,则正反应速率减少,逆反应速率增大D. 化学反应速率关系是:2υ正(NH3)= 3υ正(H2O)8. 已知在1×105Pa、298K条件下,2mol氢气燃烧生成水蒸气放出484kJ热量,下列热化学方程式正确的是 ( )A. H2O (g) = H2(g) + 1/2O2 (g) △H=+242kJ/molB. 2H2 (g) + O2 (g) = 2H2O (l) △H=-484kJ/molC. H2 (g) +1/2O2 (g) = 2H2O (g) △H=+242kJ/molD. 2H2 (g) + O2 (g)= 2H2O (g) △H=+484kJ/mol9. 下列热化学方程式书写正确的是 ( )A. 2SO2+O2 2SO3ΔH=-196.6 kJ·mol-1B. H2(g)+ O2(g) = H2O(l) ΔH=-285.8 kJ·mol-1C. 2H2(g)+O2(g) = 2H2O(l) ΔH=-571.6 kJD. C(s)+O2(g) = CO2(g) ΔH=+393.5 kJ·mol-110. 已知反应A(g)+3B(g) 2C(g)+D(g),在某段时间内,以A的浓度变化表示的反应速率为2 mol/(L·s),则以C的浓度变化表示的反应速率为 ( )A. 1 mol/(L·s)B. 3 mol/(L·s)C. 4 mol/(L·s)D. 2 mol/(L·s)11. 强酸与强碱的稀溶液发生中和反应的热效应:H+ (aq) + OH-(aq) = H2O (l) △H=-57.3kJ/mol。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
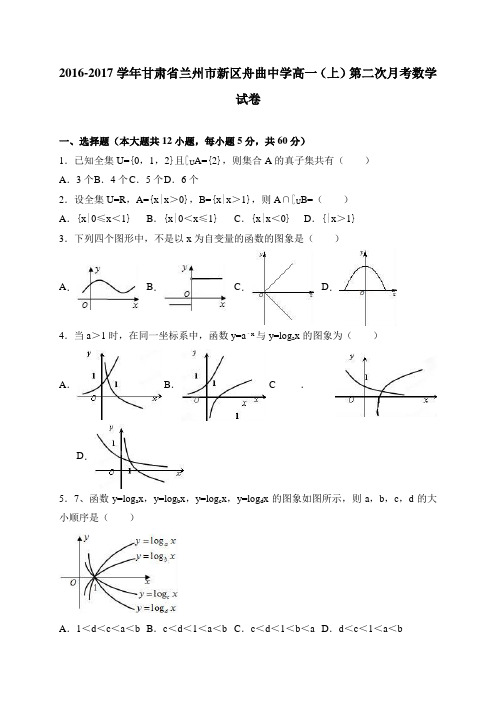
2016-2017学年甘肃兰州新区舟曲中学高二文上月考二数学试卷考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上1.已知全集U ={0,1,2}且U A ={2},则集合A 的真子集共有( ).A .3个B .4个C .5个D .6个2.设全集U =R ,A ={x|x >0},B ={x|x >1},则A ∩U B =( ).A .{x|0≤x <1}B .{x|0<x ≤1}C .{x|x <0}D .{x|x >1}3.下列四个图形中,不是..以x 为自变量的函数的图象是( ).4.当a >1时,在同一坐标系中,函数x y a -=与y =log a x 的图象是( ).5.函数y =log a x ,y =log b x ,y =log c x ,y =log d x 的图象如图所示,则a ,b ,c ,d 的大小顺序是( )A .1<d <c <a <bB .c <d <1<a <bC .c <d <1<b <aD .d <c <1<a <b6.如果函数f(x)=x 2-(a -1)x +5在区间⎪⎭⎫ ⎝⎛121 ,上是减函数,那么实数a 的取值范围是( ).A . a ≤2B .a >3C .2≤a ≤3D .a ≥37.函数f(x)=11x -( ) A .(-∞,-1) B .(1,+∞)C .(-1,1)∪(1,+∞)D .(-∞,+∞)8.方程2x =2-x 的根所在区间是( ).A .(-1,0)B .(2,3)C .(1,2)D .(0,1)9.函数y =x 416-的值域是( ).A .[0,+∞)B .[0,4]C .[0,4)D .(0,4)10.已知函数f(x)=⎩⎨⎧0≤ 30log 2x x f x x ),+(>,,则f(-10)的值是( ). A .-2 B .-1 C .0 D .111.定义在R 上的函数),(x f 对任意的R x ∈都有)()(x f x f -=-且当0≥x 时,2)(2x x x f -= 则不等式0)(<x xf 的解集为( )A .)2,0()2,( --∞B .)2,0()0,2( -C .),2()0,2(+∞-D .),2()2,(+∞--∞12.用min{a ,b ,c}表示a ,b ,c 三个数中的最小值.设f(x)=min{2x ,x +2,10-x}(x≥0),则f(x)的最大值为( )A .4B .5C .6D .713.已知函数f(x)=log 0.5(-x 2+4x +5),则f(3)与f(4)的大小关系为 .14.对于函数f(x)=x -2-ln x ,我们知道f(3)=1-ln 3<0,f(4)=2-ln 4>0,用二分法求函数f(x)在区间(3,4)内的零点的近似值,我们先求出函数值f(3.5),若已知ln 3.5=1.25,则接下来我们要求的函数值是______. 15.定义在R 上的偶函数()f x 在[0,+∞)上单调递减,且102f ⎛⎫= ⎪⎝⎭,则14l o g 0f x ⎛⎫< ⎪⎝⎭的解集为________.16.已知f(x)=(x +1)·|x -1|,若关于x 的方程f(x)=x +m 有三个不同的实数解,则实数m 的取值范围 .17.求值. (Ⅰ)31102log 8)833()32()23(364log 3--+-++-.(Ⅱ)22)2(lg 2lg 2)5(lg -+.18.已知集合},7121|{<-<=x x A 集合},032|{2<--=x x x B(1)求B A ;(2)求()R C A B .19.已知函数f (x)=lg(ax 2+2x +1) .(1)若函数f (x)的定义域为R ,求实数a 的取值范围;(2)若函数f (x)的值域为R ,求实数a 的取值范围.20.设函数xx f 11)(+=. (1)用定义证明函数)(x f 在),(∞+0上为减函数.(2)判断函数)(x f 的奇偶性.21.已知二次函数)(x f 同时满足①)2()0(f f =, ②15)(max =x f ,③方程0)(=x f 的两根的立方和等于17.(立方和公式:))((2233b ab a b a b a+-+=+)(1)求)(x f 的解析式.(2)求函数)(x f 在区间[-1,2]上的值域.22.某品牌茶壶的原售价为80元一个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下的方法促销:如果只购买一只茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…;如果一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个。
乙店一律按原价的75%销售。
现某茶社要购买这种茶壶x 个,如果全部在甲店购买,则所需金额为1y 元;如果全部在乙店购买,则所需金额为2y 元。
(1)分别求出1y 、2y 与x 之间的函数关系式。
(2)该茶社去哪家茶具店购买茶壶花费较少?参考答案1.A【解析】试题分析:由全集U ={0,1,2}且U A ={2}可得{}0,1A =,A 有3个真子集考点:集合运算及子集关系2.B【解析】试题分析:{}{}|1|01R R C B x x A C B x x =≤∴=<≤考点:集合运算3.C【解析】试题分析:函数中每一个自变量x 值只能对应唯一的y 值,因此C 项不能表示函数考点:函数的概念及函数图像4.A【解析】 试题分析:1x x y a a -⎛⎫== ⎪⎝⎭,当1a >时1xx y a a -⎛⎫== ⎪⎝⎭为减函数,y =log a x 为增函数,所以A 图正确考点:函数图像及性质5.B【解析】试题分析:当1a >时函数递增,底数越大图像越靠近x 轴,当01a <<时函数递减,底数越小图像越靠近x 轴,由此可得c <d <1<a <b考点:对数函数性质6.D【解析】 试题分析:函数对称轴为12a x -=,由函数在区间⎪⎭⎫ ⎝⎛121 ,上是减函数1132a a -∴≥∴≥ 考点:二次函数单调性7.C【解析】试题分析:要使函数有意义,需满足10110x x x -≠⎧∴>-⎨+>⎩且1x ≠,定义域为(-1,1)∪(1,+∞)考点:函数定义域8.D【解析】试题分析:方程2x =2-x 变形为220xx +-=,设()22x f x x =+-()()()()0102020,12120010f f f f =+-<=+->∴< ,所以函数在区间()0,1内有零点,即方程2x=2-x 的根分布在()0,1内 考点:函数与方程的转化9.C【解析】试题分析:0416********x x y <≤∴≤-<∴≤< ,函数值域为[0,4)考点:函数值域10.D【解析】试题分析:()()()()()2107412log 21f f f f f -=-=-=-===考点:分段函数求值11.B【解析】试题分析:当x ≥0时,不等式xf (x )<0即x (x 2-2x )<0,解得0<x <2.∵函数f (x )对任意的x ∈R 满足f (-x )=-f (x ),∴函数f (x )是奇函数.当x <0时,f (x )=-f (-x )=-(x 2+2x ),∴不等式xf (x )<0即-x (x 2+2x )<0,解得-2<x <0.综上可得:不等式xf (x )>0的解集是(-2,0)∪(0,2).考点:函数奇偶性单调性解不等式12.C【解析】试题分析:由题意知函数f(x)是三个函数y 1=2x ,y 2=x +2,y 3=10-x 中的最小者,作出三个函数在同一个坐标系下的图象(如图实线部分为f(x)的图象),可知(4,6)为函数f(x)图象的最高点.考点:函数图像及性质13.f(3)<f(4)【解析】试题分析::∵函数f (x )=log 0.5x 在R 上单调递减,f (3)=log 0.58,f (4)=log 0.55,∴f (3)<f (4).考点:对数值大小的比较14.f(3.25)【解析】试题分析:函数f (x )=x-2-lnx 在区间(3,4)上连续且单调递增,f (3)=1-ln3<0,f (4)=2-ln4>0,f (3)f (4)<0,故用二分法求函数f (x )=x-2-lnx 的零点时,初始的区间大致可选在(3,4)上.又f (3.5)=3.5-2-ln3.5=0.25>0,∴f (3)f (3.5)<0,零点区间大致可选在(3,3.5)上,则接下来我们要求的函数值是区间(3,3.5)中点的函数值f ( 3.25).考点:二分法求方程的近似解15.10,2⎛⎫ ⎪⎝⎭∪(2,+∞)【解析】试题分析:因为定义在R 上的偶函数f(x)在[0,+∞)上单调递减,所以在(-∞,0]上单调递增.又12f ⎛⎫ ⎪⎝⎭=0,所以12f ⎛⎫- ⎪⎝⎭=0,由14l o g 0f x ⎛⎫< ⎪⎝⎭可得141log 2x <-或141log 2x >.解得x ∈10,2⎛⎫ ⎪⎝⎭∪(2,+∞).考点:函数单调性奇偶性解不等式16.-1<m <45 【解析】 试题分析:由f(x)=(x +1)|x -1|=221,11,1x x x x ⎧-≥⎨-<⎩得函数y =f(x)的图象(如图).按题意,直线y =x +m 与曲线y =(x +1)|x -1|有三个不同的公共点,求直线y =x +m 在y 轴上的截距m 的取值范围.由21y x y x m⎧=-⎨=+⎩得x 2+x +m -1=0.Δ=1-4(m -1)=5-4m ,由Δ=0,得m =45,易得实数m 的取值范围是-1<m <45. 考点:函数图像与性质与数形结合法17.(Ⅰ)2(Ⅱ)1【解析】试题分析:(Ⅰ)对数式运算首先将底数和真数转化为幂指数形式,指数式运算首先将底数转化为幂指数形式;(Ⅱ)化简时将已知条件变形拼凑lg5lg 2+求解试题解析:(Ⅰ)31log 201382333log 643()(3)22123822-+++--=++--= (Ⅱ)()()()22(lg5)2lg2(lg2)lg5lg2lg5lg22lg2lg5lg22lg2lg5lg21+-=+-+=-+=+=考点:指数式对数式化简18.(1)}31|{<<x x (2)}41|{≥-≤x x x 或【解析】试题分析:(1)两集合的交集为两集合中所有的元素构成的集合;(2)两集合的并集为两集合中所有的元素构成的集合,集合的补集为全集中除去集合中的元素,剩余的元素构成的集合试题解析:由题意解不等式可分别得到{}|14A x x =<<,{}|13B x x =-<<,所以有(1)A B = }31|{<<x x(2){}|14A B x x =-<< ()R C A B ∴= }41|{≥-≤x x x 或考点:集合的交并补运算19.(1) (1,+∞) (2) [0,1]【解析】试题分析:(1)定义域为R 转化为不等式ax 2+2x +1>0对x ∈R 恒成立,结合二次函数性质可求解a 的取值范围;(2)由值域是全体实数可知对数的真数可以取到所有的正数,进而转化为一次函数二次函数求解a 的取值范围试题解析:(1)欲使函数f(x)的定义域为R ,只须ax 2+2x +1>0对x ∈R 恒成立,所以有⎩⎨⎧0 <440a -a >,解得a >1,即得a 的取值范围是(1,+∞); (2)欲使函数 f (x)的值域为R ,即要ax 2+2x +1 能够取到(0,+∞) 的所有值.①当a =0时,a x 2+2x +1=2x +1,当x ∈(-21,+∞)时满足要求; ②当a ≠0时,应有⎩⎨⎧0 ≥440a -a =>Δ⇒ 0<a ≤1.当x ∈(-∞,x 1)∪(x 2,+∞)时满足要求(其中x 1,x 2是方程ax 2+2x +1=0的二根).综上,a 的取值范围是[0,1].考点:函数定义域值域及二次函数性质20.(1)详见解析(2)既不是奇函数也不是偶函数【解析】试题分析:(1)证明函数单调性一般采用定义法,在210x x <<的基础上判断12(),()f x f x 的大小关系,从而确定函数的单调性;(2)判断函数奇偶性,首先看定义域是否对称,在定义域对称的前提下判断()(),f x f x -的关系来确定奇偶函数试题解析:(1)证明:任取210x x << (1分) 21122121)11(11)()(x x x x x x x f x f -=+-+=- (4分) 210x x << 0,02112>>-∴x x x x (5分))()(21x f x f >∴ .),0()(上为减函数在+∞∴x f (6分)(2)0)1(,2)1(=-=f f (10分))1()1()1()1(f f f f -≠--≠且所以)(x f 既不是奇函数也不是偶函数。
