分式与二次根式

合集下载

分式与二次根式的知识点

分式与二次根式的知识点分式与二次根式是数学中的重要知识点，它们在代数运算、方程求解、函数图像等方面都有应用。

本文将逐步介绍分式与二次根式的基本概念、运算规则以及解题思路。

1.分式的基本概念分式是由两个整数或多项式构成的比值形式，通常表示为a/b，其中a为分子，b为分母。

分子和分母可以是整数、多项式或含有变量的表达式。

分式可以表示实数、有理数、无理数等不同类型的数。

2.分式的化简与运算（1）分式的化简：当分式的分子和分母有公约数时，可以通过约分的方式化简分式。

即找到分子和分母的最大公约数，将其约去，使得分子和分母互质。

（2）分式的加减乘除：分式的加减运算可以通过通分的方式进行。

即将两个分式的分母化为相同的数，然后将分子进行加减运算。

分式的乘除运算可以直接对分子和分母进行相应的运算。

3.二次根式的基本概念二次根式是形如√a的表达式，其中a为非负实数。

当a为正实数时，二次根式的值为正实数；当a为零时，二次根式的值为零；当a为负实数时，二次根式的值为虚数。

4.二次根式的化简与运算（1）二次根式的化简：当二次根式内部存在完全平方数因子时，可以将其化简为有理数的形式。

即将完全平方数因子提取出来，使得根号内只剩下非完全平方数。

（2）二次根式的加减乘除：二次根式的加减运算可以通过化简后的形式进行。

即先将二次根式化简为有理数形式，然后进行加减运算。

二次根式的乘除运算可以直接对根号内的数进行相应的运算。

5.解题思路在解题时，我们需要根据具体的问题，灵活运用分式与二次根式的知识。

常见的解题思路包括：（1）化简分式与二次根式，使得问题更加简化。

（2）通过分式与二次根式的运算规则，将复杂的表达式转化为简单的形式。

（3）注意分式与二次根式在方程求解、函数图像等问题中的应用。

分式与二次根式是数学中的重要知识点，掌握了它们的基本概念、运算规则和解题思路，可以帮助我们更好地理解和应用数学知识。

在学习过程中，我们应该多进行练习，加深对分式与二次根式的理解和掌握。

中考总复习：分式与二次根式—知识讲解(提高)与例题讲解

中考总复习：分式与二次根式—知识讲解（提高）【考纲要求】1. 了解分式的概念，会利用分式的基本性质进行约分和通分，会进行分式的加、减、乘、除、乘方运算；能够根据具体问题数量关系列出简单的分式方程，会解简单的可化为一元一次方程的分式方程；2. 利用二次根式的概念及性质进行二次根式的化简，运用二次根式的加、减、乘、除法的法则进行二次根式的运算．【知识网络】【考点梳理】考点一、分式的有关概念及性质1．分式设A、B表示两个整式．如果B中含有字母，式子就叫做分式．注意分母B的值不能为零，否则分式没有意义.2.分式的基本性质（M为不等于零的整式）.3．最简分式分子与分母没有公因式的分式叫做最简分式．如果分子分母有公因式，要进行约分化简.要点诠释：分式的概念需注意的问题：(1)分式是两个整式相除的商，其中分母是除式，分子是被除式，而分数线则可以理解为除号，还含有括号的作用；（2）分式中，A和B均为整式，A可含字母，也可不含字母，但B中必须含有字母且不为0；（3）判断一个代数式是否是分式，不要把原式约分变形，只根据它的原有形式进行判断．（4）分式有无意义的条件：在分式中，①当B≠0时，分式有意义；当分式有意义时，B ≠0．②当B=0时，分式无意义；当分式无意义时，B=0．③当B≠0且A = 0时，分式的值为零．考点二、分式的运算1．基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:（1）加减运算错误！未找到引用源。

±错误！未找到引用源。

=错误！未找到引用源。

同分母的分式相加减，分母不变，把分子相加减.；异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算.（2）乘法运算两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.（3）除法运算两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘.（4）乘方运算（分式乘方）分式的乘方，把分子分母分别乘方．2．零指数.3．负整数指数4．分式的混合运算顺序先算乘方，再算乘除，最后加减，有括号先算括号里面的．5．约分把一个分式的分子和分母的公因式约去，这种变形称为分式的约分．约分需明确的问题：(1)对于一个分式来说，约分就是要把分子与分母都除以同一个因式，使约分前后分式的值相等；(2)约分的关键是确定分式的分子和分母的公因式，其思考过程与分解因式中提取公因式时确定公因式的思考过程相似；在此，公因式是分子、分母系数的最大公约数和相同字母最低次幂的积．6．通分根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通分．通分注意事项：(1)通分的关键是确定最简公分母；最简公分母应为各分母系数的最小公倍数与所有因式的最高次幂的积．(2)不要把通分与去分母混淆，本是通分，却成了去分母，把分式中的分母丢掉．(3)确定最简公分母的方法：最简公分母的系数，取各分母系数的最小公倍数；最简公分母的字母，取各分母所有字母因式的最高次幂的积.要点诠释：分式运算的常用技巧（1）顺序可加法：有些异分母式可加,最简公分母很复杂,如果采用先通分再可加的方法很繁琐.如果先把两个分式相加减,把所得结果与第三个分式可加减,顺序运算下去,极为简便.(2)整体通分法：当整式与分式相加减时,一般情况下,常常把分母为1的整式看做一个整体进行通分,依此方法计算,运算简便.(3)巧用裂项法：对于分子相同、分母是相邻两个连续整数的积的分式相加减，分式的项数是比较多的，无法进行通分，因此，常用分式111(1)1n n n n =-++进行裂项. (4)分组运算法: 当有三个以上的异分母分式相加减时,可考虑分组,原则是使各组运算后的结果能出现分子为常数,且值相同或为倍数关系,这样才能使运算简便.(5)化简分式法：有些分式的分子、分母都异常时如果先通分，运算量很大.应先把每一个分别化简，再相加减.（6）倒数法求值（取倒数法）.（7）活用分式变形求值.(8)设k求值法(参数法)(9)整体代换法.(10)消元代入法.考点三、分式方程及其应用1．分式方程的概念分母中含有未知数的方程叫做分式方程．2．分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程．3．分式方程的增根问题(1)增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根---增根；(2)验根：因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解．4．分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解．另外，还要注意从多角度思考、分析、解决问题，注意检验、解释结果的合理性．要点诠释：解分式方程注意事项：（1）去分母化成整式方程时不要与通分运算混淆；（2）解完分式方程必须进行检验，验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解．列分式方程解应用题的基本步骤：(1)审——仔细审题，找出等量关系；(2)设——合理设未知数；(3)列——根据等量关系列出方程；(4)解——解出方程；(5)验——检验增根；(6)答——答题．考点四、二次根式的主要性质1.0(0)≥≥；a a2.()2(0)a a a =≥； 3.2(0)||(0)a a a a a a ≥⎧==⎨-<⎩； 4. 积的算术平方根的性质：(00)ab a b a b =⋅≥≥，； 5. 商的算术平方根的性质：(00)a a a b b b =≥>，. 6.若0a b >≥，则a b >. 要点诠释：与的异同点：（1）不同点：与表示的意义是不同的，表示一个正数a 的算术平方根的平方，而表示一个实数a 的平方的算术平方根；在中，而中a 可以是正实数，0，负实数．但与都是非负数，即，．因而它的运算的结果是有差别的，，而（2）相同点：当被开方数都是非负数，即时，=；时，无意义，而. 考点五、二次根式的运算1．二次根式的乘除运算(1)运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号.(2)注意知道每一步运算的算理；(3)乘法公式的推广：123123123(0000)n n n a a a a a a a a a a a a ⋅⋅⋅⋅=⋅⋅⋅⋅≥≥≥≥，，，，2．二次根式的加减运算先化为最简二次根式，再类比整式加减运算，明确二次根式加减运算的实质；3．二次根式的混合运算(1)对二次根式的混合运算首先要明确运算的顺序，即先乘方、开方，再乘除，最后算加减，如有括号，应先算括号里面的；(2)二次根式的混合运算与整式、分式的混合运算有很多相似之处，整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.要点诠释：怎样快速准确地进行二次根式的混合运算.1.明确运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的；2.在二次根式的混合运算中，原来学过的运算律、运算法则及乘法公式仍然适用；3.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能收到事半功倍的效果.(1)加法与乘法的混合运算，可分解为两个步骤完成，一是进行乘法运算，二是进行加法运算，使难点分散，易于理解和掌握.在运算过程中，对于各个根式不一定要先化简，可以先乘除，进行约分，达到化简的目的，但最后结果一定要化简. 例如82627⎛⎫+⨯ ⎪ ⎪⎝⎭，没有必要先对827进行化简，使计算繁琐，可以先根据乘法分配律进行乘法运算，884266262327273⎛⎫+⨯=⨯+⨯=+ ⎪ ⎪⎝⎭，通过约分达到化简目的； (2)多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用. 如：()()()()223232321+-=-=，利用了平方差公式. 所以，在进行二次根式的混合运算时，借助乘法公式，会使运算简化.4．分母有理化把分母中的根号化去，分式的值不变，叫做分母有理化.两个含有二次根式的代数式相乘，若它们的积不含二次根式，则这两个代数式互为有理化因式.常用的二次根式的有理化因式：（1）a a 与互为有理化因式；（2）a b a b +-与互为有理化因式；一般地a c b a c b +-与互为有理化因式；（3）a b a b +-与互为有理化因式；一般地c a d b a d b +-与c互为有理化因式.【典型例题】类型一、分式的意义1．若分式211x x -+的值为0，则x 的值等于．【答案】1；【解析】由分式的值为零的条件得2x ﹣1=0，x +1≠0，由2x ﹣1=0，得x =﹣1或x =1，由x +1≠0，得x ≠﹣1， ∴x =1，故答案为1．【总结升华】若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．举一反三：【变式1】如果分式23273x x --的值为0，则x 的值应为 .【答案】由分式的值为零的条件得3x 2-27=0且x-3≠0，由3x 2-27=0，得3（x+3）（x-3）=0， ∴x=-3或x=3，由x-3≠0，得x≠3．综上，得x=-3，分式23273x x --的值为0．故答案为：-3．【分式与二次根式：例1】【变式2】若分式mx x +-212不论x 取何实数总有意义，则m 的取值范围是．【答案】若分式mx x +-212不论x 取何实数总有意义，则分母22x x m -+≠0，设22y xx m =-+，当△＜0即可，440,1m m -＜＞.答案m ＞1.类型二、分式的性质2．已知,b c c a a b abc+++==求()()()abca b b c c a +++的值.【答案与解析】设b c c a a b k abc+++===,所以,,b c ak c a bk a b ck +=+=+= 所以,b c c a a b ak bk ck +++++=++ 所以2()(),()(2)0,a b c k a b c a b c k ++=++++-= 即2k =或()0,a b c ++= 当2k =,所求代数式33118abc abck k ===, 当0a b c ++=,所求代数式1=-. 即所求代数式等于18或1-.【总结升华】当已知条件以此等式出现时，可用设k 法求解. 举一反三：【变式】已知111111111,,,6915abbcac +=+=+=求abcab bc ac++的值. 【答案】因为 111111111,,,6915abbc a c+=+=+=各式可加得1111112,6915abc ⎛⎫++⨯=++ ⎪⎝⎭所以11131180a b c ++=，所以()1180.111()()31abc abc abc ab bc ac ab bc ac abc c a b÷===++++÷++类型三、分式的运算3．已知1,x y zy z z x x y++=+++且0x y z ++≠,求222x y z y z x z x y +++++的值.【答案与解析】因为0x y z ++≠,所以原等式两边同时乘以x y z ++,得:()(().x x y z y x y z z x y z x y z y z z x x y++++++++=+++++）即222()()(),x x y z y y z x z z x y x y z y z y z z x z x x y x y++++++++=++++++++ 所以222(),x y z x y z x y z y z z x x y +++++=+++++ 所以2220.x y z y z z x x y++=+++ 【总结升华】条件分式的求值，如需把已知条件或所示条件分式变形，必须依据题目自身的特点，这样才能到事半功倍的效果，条件分式的求值问题体现了整体的数学思想和转化的数学思想.举一反三：【变式1】已知,,,x y z a b c y z x z x y ===+++且abc o ≠,求111a b ca b c +++++的值. 【答案】由已知得1,y z a x+=所以111,y z x y z a x x ++++=+=即1a x y za x+++=,所以1a xa x y z=+++,同理,,11b y c z b x y z c x y z==++++++ 所以1111a b c x y z x y z a b c x y z x y z x y z x y z++++=++==+++++++++++. 【分式与二次根式：例2】【变式2】已知x ＋y=－4，xy=－12，求+++11x y 11++y x 的值．【答案】原式)1)(1()1()1(22+++++=y x x y =1121222++++++++y x xy x x y y 1)(2)(22)(2++++++-+=y x xy y x xy y x 将x ＋y ＝－4，xy ＝－12代入上式， ∴原式⋅-=+--+-⨯++-=153414122)4(224)4(2类型四、分式方程及应用4．a 何值时,关于x 的方程223242ax x x x +=--+会产生增根? 【答案与解析】方程两边都乘以(2)(2)x x +-,得2(2)3(2).x ax x ++=- 整理得(1)10a x -=-. 当a = 1 时,方程无解. 当1a ≠时,101x a =--. 如果方程有增根,那么(2)(2)0x x +-=,即2x =或2x =-.当2x =时,1021a -=-,所以4a =-; 当2x =-时,1021a -=--,所以a = 6 .所以当4a =-或a = 6原方程会产生增根.【总结升华】因为所给方程的增根只能是2x =或2x =-，所以应先解所给的关于x 的分式方程，求出其根，然后求a 的值.5．甲．乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲．乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？【答案与解析】（1）设乙单独整理x 分钟完工，根据题意得：120204020=++x解得x ＝80，经检验x ＝80是原分式方程的解．答：乙单独整理80分钟完工．（2）设甲整理y 分钟完工，根据题意，得1408030≥+y 解得：y ≥25答：甲至少整理25分钟完工．【总结升华】分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．此题等量关系比较多，主要用到公式：工作总量＝工作效率×工作时间．（1）将总的工作量看作单位1，根据本工作分两段时间完成列出分式方程解之即可；（2）设甲整理y 分钟完工，根据整理时间不超过30分钟，列出一次不等式解之即可．举一反三：【变式】小明乘出租车去体育场，有两条路线可供选择：路线一的全程是25千米，但交通比较拥堵，路线二的全程是30千米，平均车速比走路线一时的平均车速能提高80%，因此能比走路线一少用10分钟到达．若设走路线一时的平均速度为x 千米/小时，根据题意，得（） A ．00253010(18060xx -=+）B ．00253010(180xx-=+）C ．00302510(18060x x -=+） D ．00302510(180x x -=+）【答案】设走路线一时的平均速度为x 千米/小时，00253010(18060x x -=+）故选A ．类型五、二次根式的定义及性质6．要使式子aa 2+有意义，则a 的取值范围为．【答案】a≥－2且a≠0．【解析】根据题意得：a+2≥0且a≠0，解得：a≥－2且a≠0．故答案为：a≥－2且a≠0．【总结升华】本题考查的考点为：分式有意义，分母不为0；二次根式的被开方数是非负数．可以求出x 的范围．类型六、二次根式的运算【分式与二次根式：例3】7．（2015春•泗阳县期末）已知m是的小数部分．（1）求m2+2m+1的值；（2）求的值．【答案与解析】解：依题意得21m=-，则121=+m（1）原式=（m+1）2=2；（2）原式=|1m-|=|﹣1﹣（21+）|=2．m【总结升华】此题考查二次根式的化简求值，掌握完全平方公式和无理数的估算是解决问题的关键．举一反三：【变式】（2018•苏州模拟）计算：．【答案与解析】解：原式=﹣+2=4﹣+2=4+．。

数学中的二次根式与分式方程

数学中的二次根式与分式方程二次根式是数学中的一种重要概念，与之相关的分式方程也是数学中一个常见且有挑战性的问题。

本文将介绍二次根式的定义、性质以及与分式方程的关系，并通过例题进行具体说明。

一、二次根式的定义与性质1. 定义：二次根式是形如√a 的数，其中 a 为非负实数。

其中，√a 可以理解为满足b^2 = a 的非负实数b。

在二次根式中，a 称为根式的被开方数，b 称为根式的值。

2. 性质：（1）二次根式的值是不唯一的，因为一个数的平方可能有两个相反的值。

（2）二次根式的乘法：√a * √b = √(a * b)。

即根式的乘积等于被开方数的乘积的二次根式。

（3）二次根式的除法：√a / √b = √(a / b)。

即根式的商等于被开方数的除法的二次根式。

二、分式方程的概念与解法1. 概念：分式方程是一个含有分式的方程，其中方程中至少有一个变量（未知数）存在于分式中。

2. 解法：解决分式方程的关键是将方程中的分式转化为整式，从而得到更简化的等式。

下面将介绍三种常见的解法。

（1）通分法：将方程中的所有分式的分母找出最小公倍数，并使每个分式的分母都等于最小公倍数，然后将方程两边同乘以最小公倍数，消去分母。

（2）消去法：通过观察可以将分式方程进行简化，将分子或分母中某些数值相同的项通过消去的方式，从而得到一个更简单的等式，进而求解。

（3）代换法：对于某些特定的分式方程，可以通过适当的代换使得方程更加简洁，然后利用已知的数学性质求解。

三、例题分析1. 题目：求解方程 3 / (x+2) + 2 / (x-1) = 1解法：采用通分法解此方程。

首先，找到最小公倍数为 (x+2)*(x-1)，然后将方程两边同时乘以(x+2)*(x-1)，得到 3*(x-1) + 2*(x+2) = (x+2)*(x-1)。

经过展开和整理后，得到 7x - 7 = x^2 + x - 2。

进一步整理后变为 x^2 - 6x + 5 = 0。

数学知识点二次根式与分式的运算

数学知识点二次根式与分式的运算数学知识点：二次根式与分式的运算在数学中，二次根式与分式是常见的运算形式。

二次根式表示被开方数的平方根，而分式则表示数之间的比值。

正确地运用二次根式与分式的运算规则，能够更高效地解决问题。

本文将详细介绍二次根式与分式的运算方法和规则。

一、二次根式的运算二次根式是形如√a的表达式，其中a为非负实数。

在运算二次根式时，常见的操作有合并同类项、分解因式、有理化等。

1. 合并同类项合并同类项是将同一根号内的数合并，然后再进行开方。

例如：√9 + √4 = √(9+4) = √132. 分解因式分解因式是将根号内的数按照倍数的形式分解，以便于提取出根号外的因式。

例如：√12 = √(4×3) = √4 × √3 = 2√33. 有理化有理化是将二次根式中含有根号的分母进行处理，使其变为分母不含根号的形式。

例如：1/√2 = (1/√2) × (√2/√2) = √2/2二、分式的运算分式是形如a/b的表达式，其中a为分子，b为分母。

分式的运算包括四则运算、化简、通分、约分等。

1. 四则运算分式的四则运算与整数的四则运算类似，根据需要进行加、减、乘、除的操作。

例如：(1/2) + (1/3) = (3/6) + (2/6) = 5/62. 化简化简是将分式的分子与分母进行约分，使其达到最简形式。

例如：4/8 = (4÷4) / (8÷4) = 1/23. 通分通分是将分式的分母化为相同的公共分母，以便于进行加减运算。

例如：(1/2) + (1/3) = (3/6) + (2/6) = 5/64. 约分约分是将分数的分子与分母进行化简，使其达到最简形式。

例如：4/8 = (4÷4) / (8÷4) = 1/2三、综合运算在实际问题中，常常需要综合运用二次根式与分式的运算。

例如：例1：计算√(5+2√6) × √(5-2√6) 的值。

二次根式与分式的综合运用

二次根式与分式的综合运用在数学学习中，二次根式与分式是两个重要的概念。

它们在解决实际问题时起到了至关重要的作用。

本文将探讨二次根式与分式的综合运用，揭示其在问题求解中的实际应用。

一、二次根式的综合运用二次根式是指形如√a的表达式，其中a是一个非负实数。

二次根式的运用非常广泛，无论是在几何学还是物理学中，都有其独特的应用。

1. 几何学中的二次根式在几何学中，二次根式被广泛运用于计算图形的周长、面积等属性。

以正方形为例，对于一个边长为a的正方形，其周长可以表示为4a，而面积可以表示为a²。

当我们需要计算边长或面积时，如果给定了周长或面积的数值，就需要通过解二次根式方程来求解。

例如，一块土地的周长为16米，我们需要计算其面积。

假设土地的边长为x，则方程可以表示为4x=16。

通过解方程4x=16，我们可以得到x=4，即土地的边长为4米。

进而，我们可以计算出土地的面积为16平方米。

2. 物理学中的二次根式在物理学领域，二次根式也有广泛的应用。

例如，在求解自由落体问题中，如果知道物体自由落体的时间t，可以通过二次根式来求解它的下落距离。

根据物理学的公式，自由落体的下落距离可以表示为s=1/2gt²，其中g是重力加速度。

如果给定时间t的数值，我们可以通过求解二次根式来计算下落的距离s。

例如，如果一个物体自由落体的时间为2秒，且重力加速度为10米/秒²，我们可以通过计算s=1/2×10×(2²)得出下落的距离为20米。

二、分式的综合运用分式是指形如a/b的表达式，其中a和b都是整数且b不等于零。

分式在数学中广泛应用于比例、概率等问题的解决。

1. 比例中的分式在比例问题中，分式被广泛运用于表示两个量之间的关系。

例如，在解决类似于“甲车每小时行驶100公里，乙车每小时行驶120公里，两车同时出发，多长时间后它们之间的距离将为200公里”的问题时，我们可以通过设置分式来解决。

初中代数学习辅导：分式与二次根式

初中代数学习辅导：分式与二次根式分式与分式方程1指数的扩充2分式和分式的差不多性质设f，g是一元或多元多项式，g的次数高于零次，则称f，g之比f/g 为分式分式的差不多性质分数的分子与分母都乘以或除以同一个不等于0的数，分数的值不变3分式的约分和通分分式的约分是将分子与分母的公因式约去，使分式化简假如一个分式的分子与分母没有一次或一次以上的公因式，且各系数没有大于1的公约数，则此分式成为既约分式既约分式也确实是最简分式关于分母不相同的几个分式，将每个分式的分子与分母乘以适当的非零多项式，使各分式的分母相同，而各分式的值保持不变，这种运算叫做通分4分式的运算5分式方程方程的两遍差不多上有理式，如此的方程成为有理方程假如有理方程中含有分式，则称为分式方程二次根式1根式在实数范畴内，假如n个x相乘等于a，n是大于1的整数，则称x为a的n次方根含有数字与变元的加，减，乘，除，乘方，开方运算，并一定含有变元开方运算的算式成为无理式2最简二次根式与同类根式具备下列条件的二次根式称为最简二次根式:(1)被开方式的每一个因式的指数都小于开方次数(2)根号内不含有分母假如几个二次根式化成最简根式以后，被开方式相同，那么这几个二次根式叫做同类根式3二次根式的运算要练说，先练胆。

说话胆小是幼儿语言进展的障碍。

许多幼儿当众说话时显得可怕：有的结巴重复，面红耳赤；有的声音极低，自讲自听；有的低头不语，扯衣服，扭身子。

总之，说话时外部表现不自然。

我抓住练胆那个关键，面向全体，偏向差生。

一是和幼儿建立和谐的语言交流关系。

每当和幼儿讲话时，我总是笑脸相迎，声音亲切，动作亲昵，排除幼儿恐惧心理，让他能主动的、自由自在地和我交谈。

二是注重培养幼儿敢于当众说话的适应。

或在课堂教学中，改变过去老师讲学生听的传统的教学模式，取消了先举手后发言的约束，多采取自由讨论和谈话的形式，给每个幼儿较多的当众说话的机会，培养幼儿爱说话敢说话的爱好，对一些说话有困难的幼儿，我总是认真地耐心地听，热情地关心和鼓舞他把话说完、说好，增强其说话的勇气和把话说好的信心。

(中考考点梳理)分式与二次根式-中考数学一遍过

考点03 分式与二次根式一、分式 1．分式的定义（1）一般地，整式A 除以整式B ，可以表示成A B 的形式，如果除式B 中含有字母，那么称AB为分式．（2）分式AB中，A 叫做分子，B 叫做分母．【注意】①若B ≠0，则AB有意义；②若B =0，则AB无意义；③若A =0且B ≠0，则AB＝0．学=科网2．分式的基本性质分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式的值不变．用式子表示为(0)A A C C B B C⋅=≠⋅或(0)A A CC B B C ÷=≠÷，其中A ，B ，C 均为整式． 3．约分及约分法则（1）约分把一个分式的分子和分母的公因式约去，这种变形称为分式的约分．（2）约分法则把一个分式约分，如果分子和分母都是几个因式乘积的形式，约去分子和分母中相同因式的最低次幂；分子与分母的系数，约去它们的最大公约数．如果分式的分子、分母是多项式，先分解因式，然后约分．【注意】约分的根据是分式的基本性质．约分的关键是找出分子和分母的公因式． 4．最简分式分子、分母没有公因式的分式叫做最简分式．【注意】约分一般是将一个分式化为最简分式，分式约分所得的结果有时可能成为整式． 5．通分及通分法则（1）通分根据分式的基本性质，把几个异分母的分式分别化为与原来的分式相等的同分母的分式，这一过程称为分式的通分．（2）通分法则把两个或者几个分式通分：①先求各个分式的最简公分母（即各分母系数的最小公倍数、相同因式的最高次幂和所有不同因式的积）；②再用分式的基本性质，用最简公分母除以原来各分母所得的商分别去乘原来分式的分子、分母，使每个分式变为与原分式的值相等，而且以最简公分母为分母的分式；③若分母是多项式，则先分解因式，再通分．【注意】通分的根据是分式的基本性质．通分的关键是确定几个分式的最简公分母．6．最简公分母几个分式通分时，通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母，这样的分母叫做最简公分母．7．分式的运算（1）分式的加减①同分母的分式相加减法则：分母不变，分子相加减．用式子表示为：a c a cb b b±±=．②异分母的分式相加减法则：先通分，变为同分母的分式，然后再加减．用式子表示为：a c ad bc ad bcb d bd bd bd±±=±=．（2）分式的乘法乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母．用式子表示为：a c a cb d b d⋅⋅=⋅．（3）分式的除法除法法则：分式除以分式，把除式的分子、分母颠倒位置后与被除式相乘．用式子表示为：a c a d a db d bc b c⋅÷=⋅=⋅．（4）分式的乘方乘方法则：分式的乘方，把分子、分母分别乘方．用式子表示为：((nn n a a n b b=为正整数，0)b ≠．（5）分式的混合运算含有分式的乘方、乘除、加减的多种运算叫做分式的混合运算．混合运算顺序：先算乘方，再算乘除，最后算加减．有括号的，先算括号里的．二、根式1．二次根式的有关概念（1）二次根式的概念形如)0(≥a a 的式子叫做二次根式．其中符号叫做二次根号，二次根号下的数叫做被开方数．【注意】被开方数a 只能是非负数．即要使二次根式a 有意义，则a ≥0．（2）最简二次根式被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．（3）同类二次根式化成最简二次根式后，被开方数相同的几个二次根式，叫做同类二次根式． 2．二次根式的性质（1）a ≥ 0（a ≥0）；（2）)0()(2≥=a a a ；（3(0)0(0)(0)a a a a a a >⎧⎪===⎨⎪-<⎩；（40,0)a b =≥≥；（50,0)a b ≥>． 3．二次根式的运算（1）二次根式的加减合并同类二次根式：在二次根式的加减运算中，把几个二次根式化为最简二次根式后，若有同类二次根式，可把同类二次根式合并成一个二次根式．（2）二次根式的乘除0,0)a b =≥≥；0,0)a b ≥>．（3）二次根式的混合运算二次根式的混合运算顺序与实数的运算顺序一样，先乘方，后乘除，最后加减，有括号的先算括号内的．在运算过程中，乘法公式和有理数的运算律在二次根式的运算中仍然适用．考向一分式的有关概念1．分式的三要素：（1）形如AB的式子；（2）,A B 均为整式；学科!网（3）分母B 中含有字母． 2．分式的意义：（1）有意义的条件是分式中的字母取值不能使分母等于零，即0B ≠．（2）无意义的条件是分母为0．（3）分式值为0要满足两个条件，分子为0，分母不为0．典例1 x 的取值范围是 A ．x ≠1B ．x ≠0C ．x ＞﹣1且≠0D ．x ≥﹣1且x ≠0【答案】D【解析】根据题意得：100x x +≥⎧⎨≠⎩，解得：x ≥-1且x ≠0．故选：D ．1．若分式21xx-在实数范围内无意义，则x 的取值范围是 A ．x ≠1 B ．x =1C ．x =0D ．x ＞1考向二分式的基本性质分式基本性质的应用主要反映在以下两个方面：（1）不改变分式的值，把分式的分子、分母中各项的系数化为整数；（2）分式的分子、分母与分式本身的符号，改变其中任何两个，分式的值不变．典例2 分式233x yxy+中的x 、y 的值都扩大到原来的2倍，则分式的值为 A ．扩大为原来2倍 B ．缩小为原来的12倍 C ．不变D ．缩小为原来的14倍【答案】B【名师点睛】本题考查了分式的基本概念和性质的相关知识．这类题目的一个易错点是：在没有充分理解题意的情况下简单地通过分式的基本性质得出分式值不变的结论．对照分式的基本性质和本题的条件不难发现，本题不符合分式基本性质所描述的情况，不能直接利用其结论．因此，在解决这类问题时，要注意认真理解题意．2．不改变分式的值，下列变形正确的是A ．2233a ab b -=-- B ．33a ab b -=-- C ．55a a b b=--D ．7744a a b b=- 考向三分式的化简与求值约分与通分的区别与联系：1．约分与通分都是根据分式的基本性质，对分式进行恒等变形，即每个分式变形之后都不改变原分式的值； 2．约分是针对一个分式而言，约分可使分式变得简单；3．通分是针对两个或两个以上的分式来说的，通分可使异分母分式化为同分母分式．典例3 把分式x x y -，y x y +，222x y-的分母化为x 2-y 2后，各分式的分子之和是 A ．x 2＋y 2＋2 B ．x 2＋y 2-x ＋y ＋2 C ．x 2＋2xy −y 2＋2D ．x 2−2xy ＋y 2＋2【答案】C【解析】由平方差公式将x 2−y 2可化简为(x +y )(x −y )，故将xx y-的分母化为x 2−y 2后可得()22x x y x y +-，将y x y+的分母化为x 2−y 2后可得()22y x y x y --，所以分式的x x y -,y x y +,222x y-的分母化为x 2−y 2后,各分式的分子之和为 x (x +y )+y (x -y )+2，展开得x 2+xy +xy −y 2+2合并同类项,得x 2+2xy −y 2+2，故选C.【名师点睛】本题考查了最简公分母，通分的关键是准确求出各个分式中分母的最简公分母，确定最简公分母的方法一定要掌握．求最简公分母的方法是：（i ）将各个分母分解因式；（ii ）找各分母系数的最小公倍数；（iii ）找出各分母中不同的因式，相同因式中取次数最高的. 满足（ii ）（iii ）的因式之积即为各分式的最简公分母．3．下列分式中，是最简分式的是A ．2xyx B ．222x y -C ．22x yx y+- D ．22xx + 考向四分式的运算（1）分式的加减运算：异分母分式通分的依据是分式的基本性质，通分时应确定几个分式的最简公分母．（2）分式的乘除运算：分式乘除法的运算与因式分解密切相关，分式乘除法的本质是化成乘法后，约去分式的分子分母中的公因式，因此往往要对分子或分母进行因式分解（在分解因式时注意不要出现符号错误），然后找出其中的公因式，并把公因式约去．（3）分式的乘方运算，先确定幂的符号，遵守“正数的任何次幂都是正数，负数的偶数次幂是正数，负数的奇数次幂是负数”的原则．（4）分式的混合运算有乘方，先算乘方，再算乘除，有时灵活运用运算律，运算结果必须是最简分式或整式．注意运算顺序，计算准确．典例4 计算(1－1x)÷221x x x -+的结果是A ．x －1B ．11x - C ．1xx -D ．1x x-【答案】B【解析】原式=（x x −1x ）÷()21x x -=1x x -. •()21x x -=11x -，故选B ．4．先化简，再求值：2221()211x x x x x x+÷--+-，其中x =4．考向五二次根式的概念与性质1．二次根式的意义：首先考虑被开方数为非负数，其次还要考虑其他限制条件，这样就转化为解不等式或不等式组问题，如有分母时还要注意分式的分母不为0．2．利用二次根式性质时，如果题目中对根号内的字母给出了取值范围，那么应在这个范围内对根式进行化简，如果题目中没有给出明确的取值范围，那么应注意对题目条件的挖掘，把隐含在题目条件中所限定的取值范围显现出来，在允许的取值范围内进行化简．典例5 下列各式： ①；②；③；；；．其中一定是二次根式的有 A ．4个 B ．3个 C ．2个D ．1个【答案】B5的取值范围是 A ． B． C ．D ．典例6 下列二次根式是最简二次根式的是 ABCD【答案】Cx 1x ≠1x ≥>1x 0x ≥6；．其中是最简二次根式的有 A ．2个 B ．3个C ．4个D ．5个考向六二次根式的运算1．二次根式的运算（1）二次根式的加减法就是把同类二次根式进行合并．（2）二次根式的乘除法要注意运算的准确性；要熟练掌握被开方数是非负数．（3）二次根式混合运算先乘方，再乘除，最后加减，有括号的先算括号里的（或先去括号）． 2．比较分式与二次根式的大小（1）分式：对于同分母分式，直接比较分子即可，异分母分式通常运用约分或通分法后作比较；（2）二次根式：可以直接比较被开方数的大小，也可以运用平方法来比较．典例7 下列计算正确的是A =B 6=C 5+=D 4=【答案】A【解析】A 、原式-B 、原式，错误；C 为最简结果，错误；D 、原式，错误，故选：A ．7．已知x =，y =，则y xx y +=_____________．典例8 比较大小：______5（填“＞，＜，=”）．【答案】＞【解析】因为2228,525==，28＞25，所以＞5．【名师点睛】比较二次根式的大小，可以转化为比较被开方数的大小，也可以将两个数平方，计算出结果，再比较大小．8．设a ，b －1，c ，则a ，b ，c 之间的大小关系是 A ．c ＞b ＞a B ．a ＞c ＞b C ．b ＞a ＞cD ．a ＞b ＞c1．下列根式中属于最简二次根式的是A BCD 2．若分式24x x-的值为0，则x 的值是A ．2或﹣2B ．2C ．﹣2D ．03．如果把分式xyx y+中的x 和y 都扩大2倍，则分式的值 A ．扩大4倍B ．扩大2倍C ．不变D ．缩小2倍4A BCD5．下列关于分式的判断，正确的是A ．当x =2时，12x x +-的值为零 B ．当x ≠3时，3x x-有意义C ．无论x 为何值，31x +不可能得整数值D ．无论x 为何值，231x +的值总为正数6．若x 、y 为实数，且|2|0x +=，则2019x y ⎛⎫⎪⎝⎭的值为A ．2B ．−2C ．1D ．−17的被开方数相同，则a 的值为 A ．1B ．2C ．23D ．328．下列运算中，错误的是 A ．x y y xx y y x--=-++ B ．a ba b--+=−1C −1D a9．已知 1x <，则化简的结果是A ．1x -B ．1x -C ．1x --D ．1x +10．下列分式是最简分式的是A BCD ．22121x x x --+11．若分式11x x -+的值为0，则x 的值为 A ．1 B ．−1 C ．±1D ．无解12 A ．2B ．21x - C ．23x -D ．41x x --13．若x 、y ()2210y +-=，则x y +的值等于A ．1B ．32 C ．2D ．5214a =，则1x x +的值为A ．22a - B ．2a C ．24a -D ．不确定15＝_____________． 16．当x =_____________时，分式323xx -+的值为零．17．比较大小：（填“＞、＜、或=”）18．当a =2_____________．19．已知a ，b 互为倒数，代数式222a ab b a b+++÷11a b ⎛⎫+⎪⎝⎭的值为_____________．20．已知::2:3:4x y z =，则23x y zx y z+--+的值为_____________．21．计算：（1）|1|+（2018−π）0；（2+（（．22．先化简，再求值：221a b a b a b⎛⎫-÷ ⎪--⎝⎭，其中1a =+，1b =-．23．先化简，再求值：2-，其中，．24．先化简，再求值：2212111121m m m m m -⎛⎫-÷- ⎪+--+⎝⎭，其中m 为一元二次方程230x x +-=的根．1．（2018·德阳市）下列计算或运算中，正确的是A ．=B =C ．÷=D ．-=2．（2018·兰州市）下列二次根式中，是最简二次根式的是A BCD3．（2018·绥化市）若y =x 的取值范围是 A ．12x ≤且0x ≠ B ．12x ≠C ．12x ≤D ．0x ≠4．（2018·绥化市）下列运算正确的是A ．2235a a a +=B 5=-C ．3412a a a ⋅=D ．0(π3)1-=5．（2018·曲靖市）下列二次根式中能与合并的是ABCD6．（2018·上海市）的结果是A．4 B．3C．D7．（2018·日照市）计算：（12）−1+tan30°•sin60°=A．﹣32B．2C．52D．728．（2018·莱芜市）若x，y的值均扩大为原来的3倍，则下列分式的值保持不变的是A．2xx y+-B．22yxC．3223yxD．()222yx y-9．（2018·陇南市）有意义的x的取值范围是____________．10．（2018·毕节市）观察下列运算过程：1========-……请运用上面的运算方法计算：+=____________．11．（2018____________．12．（2018·莱芜市）如图，正三角形和矩形具有一条公共边，矩形内有一个正方形，其四个顶点都在矩形的边上，正三角形和正方形的面积分别是和2，则图中阴影部分的面积是____________．13．（2018·镇江市）=____________．14．（2018·梧州市）在实数范围内有意义，则 x 的取值范围是____________．15．（2018·巴彦淖尔市）化简3m m ++269m -÷23m -的结果是____________． 16．（2018·绥化市）当2x =时，代数式211()x x x x x+++÷的值是____________．17．（2018·大连市）计算：+2）2+22-.18．（2018·百色市）已知a 2=19，求22211118a a a --+-的值．19．（2018·福建省b 卷）先化简，再求值：2211(1)m m m m+--÷，其中m ．20．（2018·锦州市）先化简，再求值： 233212,322x x x x x x +-+-÷=++（其中.21．（2018·毕节市）先化简，再求值：22214244aa a a a a ⎛⎫-÷⎪--++⎝⎭，其中a 是方程a 2+a ﹣6=0的解．22．（2018·兰州市）计算：101()(π3)1tan452--+-+-.23．（2018·甘孜州）（1()03.144cos45--π- ；（2）化简：2211x xx x x ÷---.24．（2018·益阳市）化简：2()y x y x y x y x+-+⋅+.25．（2018·莱芜市）先化简，再求值：233(111a aa a a -+÷--+，其中a +1．26．（2018·曲靖市）先化简，再求值（1a b -﹣22b a b -）÷2222+a ab a ab b --，其中a ，b 满足a +b ﹣12=0．27．（2018·梧州市）解不等式组36451102x xx x -≤⎧⎪++⎨<⎪⎩，并求出它的整数解，再化简代数式2321x x x +-+•（3x x +﹣239x x --），从上述整数解中选择一个合适的数，求此代数式的值．28．（2018·抚顺市）先化简，再求值：（1﹣x +31x +）÷2441x x x +++，其中x =tan45°+（12）−1．1．【答案】B 【解析】∵分式21xx-在实数范围内无意义， ∴1﹣x =0，即x =1，故选：B ．3．【答案】D 【解析】A 、2xy x ＝yx，错误； B 、222x y -＝1x y -，错误；C 、22x y x y +-＝1x y -，错误；D 、22xx +是最简分式，正确．故选D ．4．【答案】21x x -；163.【解析】2221()211x x x x x x+÷--+- =2(+1)2(111)()()x x x x x x x --÷-- =2()(+1)111)(x x x x x x -⋅-+ =21x x -，当x =4时，原式=2416413=-． 5．【答案】B【解析】根据二次根式被开方数必须是非负数的条件知，要使．故选B ．6．【答案】B= =， =，∴. 故选：B .8．【答案】D【解析】a −1），b ，c ），＞1，∴a ＞b ＞c ．故选D ． 101x x -≥⇒≥【解析】A、该二次根式符合最简二次根式的定义，故本选项正确；B、该二次根式的被开方数中含有分母，所以它不是最简二次根式，故本选项错误；C、该二次根式的被开方数中含有能开得尽方的因数4，所以它不是最简二次根式，故本选项错误；D、该二次根式的被开方数中含有能开得尽方的因数9，所以它不是最简二次根式，故本选项错误；故选A．【名师点睛】本题考查最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式．2．【答案】A【解析】∵分式24xx-的值为0，∴x2﹣4=0，解得：x=2或﹣2．故选：A．3．【答案】B【解析】把分式xyx y+中的x和y都扩大2倍，则22222x y xyx y x y⋅=++，故选B．5．【答案】D【解析】A选项：当x=2时，该分式的分母20x-=，该分式无意义，故A选项错误．B选项：当x=0时，该分式的分母为零，该分式无意义．显然，x=0满足x≠3．由此可见，当x≠3时，该分式不一定有意义，故B选项错误．C选项：当x=0时，该分式的值为3，即当x=0时该分式的值为整数，故C选项错误．D选项：无论x为何值，该分式的分母x2+1>0，该分式的分子3>0．由此可知，无论x为何值，该分式的值总为正数，故D选项正确．故本题应选D．【名师点睛】本题考查了与分式概念相关的知识．分式有意义的条件是分式的分母不等于零，并不是分母中的x的值不等于零．分式的值为零的条件是分式的分母不等于零且分式的分子等于零．在分式整体的符号为正的情况下，分式值的符号由分子与分母的符号共同确定：若分子与分母同号，则分式值为正数；若分子与分母异号，则分式值为负数．【解析】由非负数的性质可得：x+2=0，y−2=0，即x=−2，y=2，∴2019xy⎛⎫⎪⎝⎭=（−1）2019=−1．故选C．7．【答案】D【解析】31+4,2a a a=-=解得，故选D．8．【答案】D【解析】A．x y y xx y y x--=-++，正确，故不符合题意；B．a ba b--+=−1，正确，故不符合题意；C−1，正确，故不符合题意；D=|a|，错误，故符合题意．故选D．9．【答案】B【解析】∵x＜1，∴x-1＜0x-1|=1-x．故选：B．10．【答案】C【解析】A选项：化简该分式，得()222a ba ab bam am m+++==，故A选项不符合题意．B选项：化简该分式，得623xy xya a=，故B选项不符合题意．C选项：对该分式的分子进行因式分解，得()()222111x xxx x+--=．由此可见，该分式的分子与分母没有公因式，符合最简分式的定义，故C选项符合题意．D选项：化简该分式，得()()()22211112111x xx xx x xx+--+==-+--，故D选项不符合题意．故本题应选C．11．【答案】A【解析】∵分式11x x -+的值为0，∴|x |−1=0，且x +1≠0，解得：x =1．故选A ． 12．【答案】B（13x -−11x -）•（x −3）=13x -•（x −3）−11x -•（x −3）=1−31x x --=21x -．故选B ． 15==． 16．【答案】3【解析】依题意得：3﹣x =0且2x +3≠0．解得x =3，故答案为：3．17．【答案】＜【解析】将两式进行平方可得：(2=12，(2=18，因为12＜18，所以＜18．【答案】3- 【解析】∵()()2121214122121a a a a a a +--==-++，∴当a =2时，原式=1223-⨯=-．故本题应填写：3-．19．【答案】1 【解析】对待求值的代数式进行化简，得22211a ab b a b a b ++⎛⎫÷+ ⎪+⎝⎭()2a b a b a b ab ++⎛⎫=÷ ⎪+⎝⎭()ab a b a b =+⋅+ab =， ∵a ，b 互为倒数，∴ab =1，∴原式=1．故本题应填写：1．20．【答案】411【解析】根据分式的性质（分式的分子和分母同时乘以或除以同一个不为0的整式，分式的值不变）解答．∵::2:3:4x y z =，∴可设234x k y k z k ===、、，∴226444323121111x y z k k k k x y z k k k k +-+-===-+-+，故答案为：411．21．【答案】（1）；（2）【解析】（1）原式−1−+1=．（2）原式=3−−5=2−．22．【答案】化简见解析，结果为．【解析】221a b a b a b ⎛⎫-÷ ⎪--⎝⎭ ()()a b a b a a b a b b+--+=⋅- ()()a b a b b a b b+-=⋅- a b =+，当1a =+，1b =时，原式11++-=23．【答案】8-+．【解析】原式2(2)x y x y =---+22x y x y =--+-2y =-．当34x y ==,时，原式=2−2×4=4 −8． 24．【答案】化简见解析，结果为13．【解析】原式=()()()22122111111m m m m m m m --+--÷++-- =()()()()21121112m m m m m m m ---⋅++-- =()1111m m m m --++=()()11m m m m --+ =()11m m + =21m m +．由m 是方程230x x +-=的根，得到23m m +=，所以原式=13．【名师点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．1．【答案】B【解析】A 、=，此选项错误； B ＝，此选项正确；C 、÷=D 、-=，此选项错误；故选：B ．2．【答案】B【解析】A =不是最简二次根式，错误；B 是最简二次根式，正确；C =不是最简二次根式，错误；D =不是最简二次根式，错误，故选B ．3．【答案】A【解析】由题意可知：1200x x -≥⎧⎨≠⎩，解得：12x ≤且0x ≠，故选A ．4．【答案】D 【解析】A. 23a a +=5a ，故A 选项错误；B. =5，故B 选项错误；C. 347a a a ⋅=，故C 选项错误；D. 0(π3)1-=，故D 选项正确，故选D.5．【答案】B【解析】A ＝，不能与B 合并，故该选项正确；C ＝不能与D 3不能与故选B ．6．【答案】C【解析】，故选C ．7．【答案】C【解析】（12）−1+tan30°•sin60°=2+12 =52，故选C ．9．【答案】x ＞3有意义， ∴x ﹣3＞0，∴x ＞3， ∴x 的取值范围是x ＞3，故答案为：x ＞3．10．【解析】原式=12﹣1）+12+12+ (12)+12=12…）． 11．【答案】6【解析】原式．故答案为：6．12．【答案】2【解析】设正三角形的边长为a ，则12a 2解得a ．则图中阴影部分的面积．故答案是2．13．【答案】2，故答案为2. 14．【答案】x ≥3【解析】由题意可得：x ﹣3≥0，解得：x ≥3，故答案为：x ≥3．15．【答案】1 【解析】3m m ++269m -÷23m - =()()63·3332m m m m m -+++- =333m m m +++ =1，故答案为1.16．【答案】3【解析】原式221()1x x x x x x +=+⋅+ =2(1)1x x x x +⋅+ 1x =+，当2x =时，原式213=+=，故答案为：3．17．【答案】294【解析】原式﹣14=294． 18．【答案】16- 【解析】原式=22121a a a ---（）﹣118 =221a ---118， ∵a 2=19，∴原式=2191--﹣118=﹣318=﹣16．19．【解析】2211(1)m m m m+--÷ =()()2111m m m m m m +-⋅+- =()()111m m m m m +⋅+- =11m -，当m +1时，原式==． 20．【答案】11;12x -- 【解析】原式=()23322)21x x x x ++-⨯+-（， ()()22433221x x x x x +--+=⨯+-，()()21221x x x x -+=⨯+-，11x =-，当x =3时，原式=113-=12-. 21．【答案】13 【解析】22214244a a a a a a ⎛⎫-÷ ⎪--++⎝⎭ =()()()()222222a a a a a a -++⋅+-=2222a a a a a--+⋅- =222a a a a-+⋅-， =2a a +，由a 2+a ﹣6=0，得a =﹣3或a =2，∵a ﹣2≠0，∴a ≠2，∴a =﹣3，当a =﹣3时，原式=32133-+=-． 22．1．【解析】101()(π3)1tan 2--+-+-45°=2111-++1=．（2）2211x x x x x ÷--- =()()211·1x x x x x+---x =x (x +1)-x=x 2.24．【答案】x 【解析】原式=222x y y x y x y x-++⋅+ =2x x y x y x+⋅+ =x ．25．【答案】【解析】当a +1时，原式=()()333111a a a a a a++-+⨯-+=()()4111a a a a a+⨯-+ =41a -. 26．【答案】原式=1a b+=2 【解析】（1a b -﹣22b a b -）÷2222+a ab a ab b -- =()()()()2•a b a b b a b a b a a b -+-+-- =1a b+，由a +b ﹣12=0，得到a +b =12，则原式=112=2． 27．【答案】原式=11x -，当x =2，原式=1．【解析】解不等式 3x ﹣6≤x ，得：x ≤3，解不等式4510x +＜12x +，得：x ＞0，则不等式组的解集为 0＜x ≤3，所以不等式组的整数解为 1、2、3，原式=()231x x +-•[()()2333x x x x --+- ()()333x x x -+-] =()231x x +-•()()()()1333x x x x --+- =11x -， ∵x ≠±3、1，∴x =2，则原式=1．28．【答案】-1 5【解析】原式=（21311xx x-+++）÷()221xx++=()()()2 221·12x x xx x +-+++=22xx -+，当x=tan45°+（12）−1=1+2=3时，原式=231235-=-+。

数学中的二次根式与分式

数学中的二次根式与分式在数学中，二次根式和分式是我们经常会遇到的两个概念。

它们在解决方程、计算和简化表达式等方面都具有重要的作用。

本文将详细介绍二次根式和分式的定义、性质以及它们在数学中的应用。

一、二次根式的定义与性质二次根式是指根号下包含二次项的表达式。

具体地说，对于一个非负实数a和正整数n，我们定义二次根式√a为满足以下条件的实数x：x的n次方等于a，即x^n = a。

其中，n称为根式的指数，而a则是根式的被开方数。

二次根式的性质如下：1. 非负性质：二次根式的值不会小于0，即根号下的被开方数必须为非负实数。

2. 分解性质：对于一个二次根式√ab，可以将其分解为√a * √b。

3. 合并性质：对于两个同类项的二次根式√a和√b，可以合并为√(a+b)。

4. 化简性质：如果被开方数能够整除完全平方数，那么二次根式就可以化简为一个有理数。

二、分式的定义与性质分式是数学中的一种表达形式，通常由分子和分母组成，中间用分数线分隔。

分式可以表示两个数之间的关系，其中分子表示被除数，分母表示除数。

分式的定义如下：对于两个整数a和b（其中b≠0），我们定义分式a/b为两个整数a和b的比值。

在分式中，a被称为分子，b被称为分母。

分式的性质如下：1. 除法性质：分式表示的是除法运算，即a/b = a÷b。

2. 分子和分母的性质：在一个分式中，如果分子和分母乘（或除）以同一个非零实数k，则分式的值不变。

3. 分式的简化：如果分子和分母有一个公因数，那么可以进行约分，将分式化简为最简形式。

4. 分式的加减乘除：两个分式的加减可以通过通分和化简的方法进行，两个分式的乘除可以通过分子乘分子、分母乘分母的方法进行。

三、二次根式与分式的联系与应用二次根式和分式在数学中经常会有联系，并在解决问题中应用到一起。

1. 化简分式时可以利用二次根式的性质进行转化。

比如，在分式中出现二次根式时，可以将其转化为最简形式，使得分母中不存在二次根式。

初中数学分式二次根式知识点归纳

第四节分式与二次根式考点一：分式的概念分式：两个整式相除，且除式中含有字母，这样的代数式叫做分式。

分式中字幕的取值不能使分母为零，当分母为零时，分式就没有意义。

<分式为零的条件>分式为零的条件：当分子为零时，分式的值为零。

<分式有意义的条件>分式有意义的条件：当分母不为零时，分式有意义。

考点二：分式的基本性质与运算<分式的基本性质>分式的分子与分母都乘以（或除以）一个不等于零的整式，粉饰的值不变。

A A×X A A÷M= =B B×X , B B÷M ，（其中M 是不等于零的整式）<约分>分式的约分：把一个分式的分子和分母的公因式约去，叫做分式的约分，约分要约去分子、分母的所有公因式。

分子、分母没有公因式的分式叫做最简分式。

利用分式的约分，可以进行多项式的除法。

把两个多项式相除先表示成分式，然后通过分解因式、约分等把分式简化，用整式或最简分式表示所求的商。

<分式的运算>分式的乘除：分式乘分式，用分子的积做积的分子，分母的积做积的分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。

a c = aca c a d adb d bd , b d bc bc分式的加减：同分母的分式相加减，分式的分母不变，把分子相加减。

a b = a b c c c 通分：把分母不相同的几个分式化成分母相同的分式，叫做痛分，一分母分式的加减就转化为同分母分式的加减，然后按同分母分式的加减法则进行计算。

通分时，一般取各分母的系数的最小公倍数与各分母所有字母的最高词目的积为公分母。

分式方程：只含分式，或分式和整式，并且分母里含有未知数的方程叫做分式方程。

考点三：二次根式<二次根式有意义的条件>二次根式：表示算术平方根的代数式叫做二次根式。

一般地，式子a （ a≥0）叫做二次根式，a 叫做被开方数。

分式与二次根式知识点归纳和考点题型

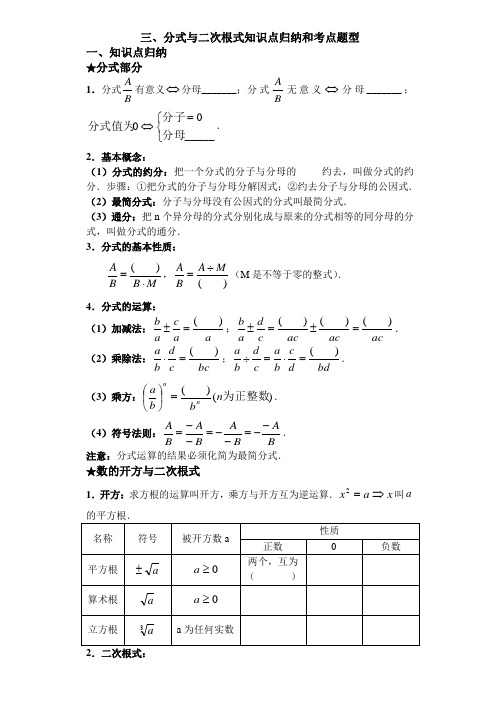
三、分式与二次根式知识点归纳和考点题型一、知识点归纳 ★分式部分1．分式B A 有意义⇔分母_______；分式BA无意义⇔分母_______；⎩⎨⎧=⇔_____0分母分子分式值为． 2．基本概念：（1）分式的约分：把一个分式的分子与分母的_____约去，叫做分式的约分．步骤：①把分式的分子与分母分解因式；②约去分子与分母的公因式．（2）最简分式：分子与分母没有公因式的分式叫最简分式．（3）通分：把n 个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分． 3．分式的基本性质：MB B A ⋅=)(，)(M A B A ÷=（M 是不等于零的整式）． 4．分式的运算：（1）加减法：a a c ab )(=±；acac ac c d a b )()()(=±=±．（2）乘除法：bc c d b a )(=⋅；bdd c b a c d b a )(=⋅=÷．（3）乘方：)()(为正整数n b b a nn=⎪⎭⎫⎝⎛．（4）符号法则：BAB A B A B A --=--=--=．注意：分式运算的结果必须化简为最简分式． ★数的开方与二次根式1．开方：求方根的运算叫开方，乘方与开方互为逆运算．x a x ⇒=2叫a（1）概念：①二次根式：式子a （a _______0）叫二次根式．②最简二次根式：满足①被开方数的因数是整数，因式是整式；②被开方数中不含能开得尽方的因数式因式． ③同类二次根式：化为_________二此根式后被开方数________的二此根式。

④分母有理化：把_____中的根号化去叫做分母有理化． ⑤有理化分式：两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们说这两个代数式互为有理化因式．注：常见的有理化因式有b a +与________，d c b a +与________，a 与___．（2）性质： ①())0(2≥=a a a ；②⎩⎨⎧<-≥==)0()0(2a a a a a a ； ③)0,0(≥≥⋅=b a b a ab ；④)0,0(>≥=b a ba b a （3）运算：①二次根式的加减先化简（化为最简二次根式），后合并（同类二次根式）． ②二次根式的乘除乘法：)0,0(≥≥=⋅b a ab b a多项式的乘法公式适用于二次根式的乘法。

2013届九年级数学总复习四代数式(分式与二次根式)

a
2
a(a 0)
4、最简二次根式：（1）被开方数的因数是整数，因式是整式；（2）被开方数不含有开得尽方的因数或因式。 5、同类二次因式：几个二次根式化成最简二次根式后，被开方数相同。
6、二次根式的运算：（1）、 2 a a 0 a a a a 0
5、如何进行分式的乘除运算？如何进行分式的加减运算？
3 a 1 ，然后请你给a选取一例1、先化简 1 2 a2 a 4
个合适的值，再求化简后的式子的值。
3 a2 4 a2 解:原式= a 2 a 2 a 1 a 1 a 2 a 2 a2 a 1 a2
例5、化简：
x
1 x
x x x 2 x x x
x x x
x
1、由根号内的情况你能判断x的符号吗？
2、这道题应怎样解？
第一步把分子和分母同时乘以x 第二步分母开出来应加绝对值第三步去绝对值
例6化简
a b3 2ab2 a 2b b a 0 ba a
把x=6代入(x-3)(x-5)不为0，所以X=6是原方程的解。
例3、求下列各式的值
2 2
X Y 1、如果x 4 xy 4 y 0, 求的值 X Y x y 7 x2 y 2 2、如果 = ，那么 2 2 3 x 2 xy 3 y 2
解:由条件可得 :
x 2y 0 x 2y 0
（2）
a b
a 0, b 0
a b ab 2 b ab b ab b
a b a b
（3）二次根式的加减：一般把二次根式化为最简二次根式，再合并同类二次根式。（4）二次根式的乘法：

分式方程和二次根式试题和答案

分式方程和二次根式专项讲解一．知识框架二．知识概念1、分式：形如BA，A 、B 是整式，B 中含有未知数且B 不等于0的整式叫做分式。

其中A叫做分式的分子，B 叫做分式的分母。

分式方程的意义:分母中含有未知数的方程叫做分式方程.二次根式：一般地，形如√ā（a≥0）的代数式叫做二次根式。

当a ＞0时，√a 表示a 的算数平方根,其中√0=0 2、分式有意义的条件：分母不等于03、分式的基本性质:分式的分子和分母同时乘以（或除以）同一个不为0的整式，分式的值不变。

用式子表示为：A/B=A*C/B*C A/B=A÷C/B÷C （A,B,C 为整式，且C≠0） 5、最简分式:一个分式的分子和分母没有公因式时,这个分式称为最简分式.约分时,一般将一个分式化为最简分式.6、分式的四则运算：①同分母分式加减法则:同分母的分式相加减,分母不变，把分子相加减.用字母表示为：cba cbc a ±=± ②异分母分式加减法则:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.用字母表示为：bdbcad d c b a ±=± ③分式的乘法法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.用字母表示为：bdacd c b a =* ④分式的除法法则:(1).两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘.bc ad d c b a =÷(2).除以一个分式，等于乘以这个分式的倒数: cd b a d c b a *=÷ 7、理解并掌握下列结论：（1）()0≥a a 是非负数；（2）()()02≥=a a a ；（3）()02≥=a a a ；三、知识讲解【例1】（2009年黔东南州）当x_____时，11+x 有意义．（1-≠x ）★直通中考：1、（2009年漳州）若分式12x -无意义，则实数x 的值是 x=2 ． 2、（2009年天津市）若分式22221x x x x --++的值为0，则x 的值等于 x=2 ．3、（2010安徽芜湖）要使式子a ＋2a有意义，a 的取值范围是（ B ） A ．a ≠0 B ．a ＞－2且a ≠0 C ．a ＞－2或a ≠0 D ．a ≥－2且a ≠0 4、已知有意义，则在平面直角坐标系中，点P （m ，n ）位于第 __四__ 象限．【例2】(2009年成都)分式方程2131x x =+的解是 x=2 ★直通中考：1、(2009年潍坊)方程3123x x =+的解是．（x=9） 2、(2009宁夏)解分式方程：1233x x x +=--．（37=x ）【例3】（2009 年佛山市）化简：2211xyx y x y x y⎛⎫+÷ ⎪-+-⎝⎭ （y 2）★直通中考：1、（2009年湖南长沙）分式111(1)a a a +++的计算结果是（ C ） A ．11a + B ．1a a +C ．1aD ．1a a+ 2、（2009年佳木斯）计算21111a a a ⎛⎫+÷ ⎪--⎝⎭= （1+a a） 3、(2009年成都)化简：22221369x y x y x y x xy y +--÷--+＝_______ （yx y -2） 4、（2010广东广州）若a ＜1，化简2(1)1a --＝（ D ）A ．a ﹣2B ．2﹣aC ．aD ．﹣a5、已知2＜x ＜5，化简2(2)x -+2(5)x -＝________.（3）【例4】(2009年内江市)已知25350x x --=，则22152525x x x x ----＝__________．（528） ★直通中考：1、（2009烟台市）设0a b >>，2260a b ab +-=，则a bb a+-的值等于．（2） 2、（2009年枣庄市）已知a 、b 为实数，且ab =1，设P =11a b a b +++，Q =1111a b +++，则P = Q （填“＞”、“＜”或“＝”）．3、(2011·呼和浩特)若x 2－3x ＋1＝0，则x 2x 4＋x 2＋1的值为________．（81）4、(2011·乐山)若m 为正实数，且m －1m ＝3，则m 2－1m2＝________.（53）5、（2010四川广安）若|2|20x y y -++=，则xy 的值为（ A ） A ．8 B ． 2 C ．5 D ．6-6、已知522+-+-=x x y ，则x y =________．（52）【例5】(2009年河北)已知a = 2，1-=b ，求2221a b a ab --+÷1a的值．解：化简后1++b a ，代入可得2112=+-★直通中考：1、（2009年莆田）先化简，再求值：2244242x x x x x x +++÷---，其中1x =．解：化简后x -，代入可得-12、（2009年衡阳市）先化简，再求值：212)14(-÷-+-a a a a a ，其中31=a ．解：化简后13-a ，代入可得01313=-⨯3、(2011年中考)已知x 是一元二次方程0132=-+x x 的实数根，求代数式⎪⎭⎫ ⎝⎛--+÷--2526332x x x x x 的值．解：化简后)3(31+x x ，因为0132=-+x x 可化为1)3(=+x x ，故原式可得314、（2009湖北省荆门市）已知x =2＋3，y =2-3，计算代数式2211()()x y x y x y x y x y+----+的值．解：化简后xy 4-，代入可得()()34-32324-=-+5、如图，点A 的坐标为（﹣，0），点B 在直线y=x 上运动，当线段AB 最短时点B 的坐为（ A ）A ．（﹣，﹣）B ．（﹣，﹣）C ．（，）D ．（0，0）6、如图所示，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为__4_______．【例6】(2009年安顺)下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格，某公司购买的门票种类、数量绘制的统计图表如下：依据上列图表，回答下列问题：（1）其中观看足球比赛的门票有_50__张；观看乒乓球比赛的门票占全部门票的_20_％；（2）公司决定采用随机抽取的方式把门票分配给100名员工，在看不到门票的条件下，每人抽取一张（假设所有的门票形状、大小、质地完全相同且充分洗匀），问员工小华抽到男篮门票的概率是；（103）（3）若购买乒乓球门票的总款数占全部门票总款数的61，求每张乒乓球门票的价格。

分式与二次根式

分式、二次根式一、考点分析：1. 分式的概念及性质：（1）能确定分式有意义；（2）分式值为零的条件；（3）利用分式的基本性质进行约分和通分。

2. 解分式方程3. 分式的运算：分式的加减乘除运算4. 分式方程的实际应用：（列分式方程解应用题）5.二次根式及其性质：（1）二次根式有意义，则被开方数为非负数；6.二次根式的加、减、乘、除混合运算。

二、考点总结：纵观北京市近三年中考题，对分式的考查内容主要是确定分式有意义或分式值为零的条件，尤其重视对分式方程解法的考查，一般在中考的第14题出现，如果解答题中未出现解分式方程，则在解答题“列方程和方程组解应用题”中会考查分式方程应用题，而对二次根式的考查内容主要是确定二次根式有意义的条件。

其他内容如分式的基本性质、二次根式的运算出题较少，但应引起足够的重视。

三、典型例题：例1：（2011年北京中考）若分式x x 8-的值为0，则x 的值等于___________ 例2：（2010年北京中考）若二次根式12-x 有意义，则x 的取值范围是例3：（2010年房山区一模）在函数12-+=x x y 中，自变量x 的取值范围是例4：（2010年北京中考）解分式方程423-x -2-x x =21例5：（2011年朝阳二模）解分式方程11612+-=-x x x例6：（2008年北京中考）已知x －3y ＝0，求)(2222y x yxy x y x -+-+⋅的值例7：（2011年东城一模）：先化简，再求值：1)1213(22-÷-+-x x xx x x ，其中13-=x例8：（2011北京中考）列方程或方程组解应用题：京通公交快速通道开通后，为响应市政府“绿色出行”的号召，家住通州新城的小王上班由自驾车改为乘坐公交车。

已知小王家距上班地点18千米，他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米，他从家出发到达上班地点，乘公交车方式所用时间是自驾车方式所用时间的73，小王用自驾车方式上班平均每小时行驶多少千米？例9：（2011年东城一模）列方程或方程组解应用题：随着人们节能意识的增强，节能产品进入千家万户，今年1月小明家将天燃气热水器换成了太阳能热水器．去年12月份小明家的燃气费是96元，从今年1月份起天燃气价格每立方米上涨25%，小明家2月份的用气量比去年12月份少10立方米，2月份的燃气费是90元．问小明家2月份用气多少立方米．四、习题巩固：（一）选择题： 1.0312=++-y x ，则2()xy -的值为A.－6B. 9C.6D. －92.若31-+a 在实数范围内有意义，则a 满足的条件是（）A 2=aB 2≥aC 4-≤aD 2≥a 或4-≤a3.下列计算正确的是A ．44a a a ÷=B ．325(2)4a a =C ．223355+=D ．1025÷=4.已知分式 11x x -+的值是零，那么x 的值是 A ．1 B. 0 C. －1 D. 1±（二）填空题1. 若分式2x 4x 2--的值为0，则x 的值为 2. 若分式223x x --有意义,则x 的取值范围是 3. 若x5-有意义时，x 的取值范围是________.（三）计算题1.解分式方程311323162x x -=--2.解分式方程2111x x x =-+-3.已知21(2)02a b -++=，求2()(2)(2)()(32)a b a b a b a b a b +--+++-的值4.当x ＝9，y ＝4时，求代数式3222234141y xy y x xy y x x +++++的值5. 化简：=-+---1)2)(1(31x x x x ，并指出x 的取值范围6. 已知a 2+2a=4，求121111122+-+÷--+a a a a a 的值7. 已知22690x xy y -+=，求代数式2235(2)4x y x y x y +⋅+-的值8.当x ＝2010时，求代数式1x 12x x )12x 1(22-++÷-+的值9.某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．根据以上信息，原来报名参加的学生有多少人？10.列方程（组）解应用题“五一”期间某校学生到相距学校10千米的“老年公寓”开展“献爱心”活动，部分同学骑自行车从学校出发，20分钟后另部分同学乘汽车从学校出发，结果乘汽车的同学比骑自行车的同学提前10分钟到达“老年公寓”．已知汽车速度是自行车速度的4倍，求两种车的速度各是多少？11.列方程或方程组解应用题：根据城市规划设计，某市工程队准备为该城市修建一条长4800米的公路. 铺设600 m后，为了尽量减少施工对城市交通造成的影响，该工程队增加人力，实际每天修建公路的长度是原计划的2倍，结果9天完成任务，该工程队原计划每天铺设公路多少米？12.列方程或方程组解应用题：在2011年春运期间，我国南方发生大范围冻雨灾害，导致某地电路出现故障，该地供电局组织电工进行抢修．供电局距离抢修工地15千米，抢修车装载着所需材料先从供电局出发，15分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的1.5倍，求这两种车每小时分别行驶多少千米．。

初中数学分式与二次根式公式定理_公式总结

初中数学分式与二次根式公式定理_公式总结
第六章分式与二次根式
1 分式与分式方程
11 指数的扩充
12 分式和分式的基本性质
设f,g是一元或多元多项式,g的次数高于零次,则称f,g之比f/g为分式
分式的基本性质分数的分子与分母都乘以或除以同一个不等于0的数,分数的值不变
13 分式的约分和通分
分式的约分是将分子与分母的公因式约去,使分式化简
如果一个分式的分子与分母没有一次或一次以上的公因式,且各系数没有大于1的公约数,则此分式成为既约分式既约分式也就是最简分式
对于分母不相同的几个分式,将每个分式的分子与分母乘以适当的非零多项式,使各分式的分母相同,而各分式的值保持不变,这种运算叫做通分
14 分式的运算
15 分式方程
方程的两遍都是有理式,这样的方程成为有理方程如果有理方程中含有分式,则称为分式方程2 二次根式
21 根式
在实数范围内,如果n个x相乘等于a,n是大于1的整数,则称x为a的n次方根
含有数字与变元的加,减,乘,除,乘方,开方运算,并一定含有变元开方运算的算式成为无理式22 最简二次根式与同类根式
具备下列条件的二次根式称为最简二次根式:(1)被开方式的每一个因式的指数都小于开方次数(2)根号内不含有分母
如果几个二次根式化成最简根式以后,被开方式相同,那么这几个二次根式叫做同类根式
23 二次根式的运算
24 无理方程
根号里含有未知数的方程叫做无理方程。

初中数学教案二次根式与分式的运算

初中数学教案二次根式与分式的运算教案：二次根式与分式的运算引言：本教案主要介绍初中数学中关于二次根式与分式的运算方法。

二次根式与分式是初中数学中常见的数学概念与运算，掌握好相关的运算方法对于学生的数学学习与提高具有重要的意义。

通过本教案的学习，学生将能够掌握二次根式的化简、加减乘除运算以及分式的加减乘除运算方法，从而在解决实际问题时能够熟练灵活地运用相关的知识与技巧。

一、二次根式的概念与性质1. 二次根式的定义二次根式是指具有形如√a（a≥0）的形式的数。

其中，a被称为二次根式的被开方数。

2. 二次根式的化简(1) 化简二次根式的基本原则：- 化简二次根式时，将其写为2次幂的乘积形式；- 若二次根式中包含平方因子，则将其提出；- 若二次根式中包含互质系数的项，则提出一个公因式。

(2) 化简二次根式的步骤：a. 将二次根式的被开方数写成素因数的乘积形式；b. 对每个素因数分别进行如下处理：- 若其次数为偶数，则提出并化为普通数；- 若其次数为奇数，则保留在二次根式中，并继续化简。

3. 二次根式的加减运算(1) 加减运算时，要求二次根式的被开方数相同，然后对应的系数进行加减运算。

(2) 示例：若√a + √b = √c，则有a + b + 2√ab = c.4. 二次根式的乘除运算(1) 乘法运算时，直接对二次根式的被开方数与系数进行乘法运算，并化简结果。

(2) 除法运算时，通过有理化分母的方法，将除法转化为乘法运算进行处理。

二、分式的概念与性质1. 分式的定义分式是指具有形如a/b（b ≠ 0）的形式的数。

其中，a被称为分子，b被称为分母。

2. 分式的化简分式的化简是将一个分式进行约分，使得分子与分母没有共同的约数的过程。

3. 分式的加减运算(1) 加减运算的前提是两个分式的分母相同，然后对应的分子进行加减运算。

(2) 示例：若 a/b ± c/b = (a ± c)/b.4. 分式的乘除运算(1) 乘法运算时，直接对分式的分子与分母进行乘法运算，并化简结果。

2.分式与二次根式

负数，除式是正数．
5．二次根式的双重非负性：对于二次根式，其被开方数 a≥0，它的值 a≥0，所以二次根式具有双重非负性．
上一页返回导航下一页
考点三二次根式的运算 1．二次根式的加减法：将二次根式化为最最简简二二次次根根式式后，把被开方数相同的
二次根式分别合并．
2．二次根式的乘除法： (1)乘法： a· b＝ ab
1．有括号的先算括号内的．
2．分式的分子、分母能因式分解的首先进行因式分解．
3．进行乘除运算(除法可变为乘法)．
4．约分． 5．进行加减运算时，如果是异分母分式先通分，变为不变，分子合并同类项，最终化成最最简简分式．
同同分分母母
分式，此时分母
6．代入求值．
上一页返回导航下一页
温馨提示 1．分式的化简结果必须化为最简分式，再代入数字求值． 2．对于分式化简求值题中所给的值是开放性或多值时，注意选值时应该使原分式与化简过程中的所有分式都有意义.
上一页返回导航下一页
学霸笔记分式运算要注意：运算顺序，如需代值切记未知数的值必须使原分式和运算过程中的所有分式都有意义(即分母均不为 0)．另外，分式化简与解分式方程切勿混淆，化简时不能去分母.
上一页返回导航下一页
学霸笔记对于分式AB：无意义的条件为 B＝0；有意义的条件为 B≠0；值为 0 的条件为： A＝0 且 B≠0；值为正数的条件为 A 与 B 同号；值为负数的条件为 A 与 B 异号．
， .
一个数的平方的算术平方根等于这个数的绝对值．
上一页返回导航下一页
3． ab＝ a· b
(a≥0，b≥0)．
积的算术平方根等于每个因式的算术平方根的乘积，其中的每个因式都是非负数．

第3讲分式与二次根式

第一单元
数与式
第3课时分式与二次根式
知识点一：分式的概念及其性质 1. 分式的概念：形如AB(A，B 都是整式，且 B 中含有字母，B≠0)
的式子，叫做分式，其中 A 叫做分式的(1) 分分子子，B 叫做分式的(2) 分分母母 .
【例 1】下列各式中，是分式的是( C )
3 A. 5
x2－x＋2 B. 3
13. 若(a＋ 2)2 与|b＋1|互为相反数，则b－1 a的值为 2＋＋1 1 ． 14. 当 1＜x＜4 时，|x－4|＋ x2－2x＋1＝ 3 .
15. 计算：(－3)2－51－1＋(－2)0.
解：原式＝9－5＋1＝5.
16. 计算：x－1 4－x2－2x16.
解：原式＝x－1 4－（x－4）2x（x＋4）＝（x－x＋ 4）4－（2xx＋4）＝（x－4）4－（xx＋4）＝－x＋1 4.
ab××dc
ad ＝(23) bc
.
③分式的乘方：把分式的分子、分母分别(24)
an ＝(25) bn .
乘乘方方
. 即：abn
④分式的加减乘除、乘方混合运算：先算(26) 乘方，再算
(27) 乘乘除，最后算(28) 加加减减 . 有括号的先算(29)
括括号号里里的顺序. 要保证最后结果为(30) 最最简简分式 .
有( BB )
A. 1 个
B. 2 个
C. 3 个
D. 4 个
3. 下列各式中，正确的是( DD )
A. －－53yx＝－3x5y
B. －a＋c b＝－ac＋b；
C. －ac－b＝a－c b
D. －b－a a＝a－a b
4. 下列各式中属于最简二次根式的是( A ).

分式与二次根式

分式与二次根式的知识点

中考总复习：分式与二次根式—知识讲解(提高)与例题讲解

数学中的二次根式与分式方程

数学知识点二次根式与分式的运算

二次根式与分式的综合运用

初中代数学习辅导：分式与二次根式

(中考考点梳理)分式与二次根式-中考数学一遍过

数学中的二次根式与分式

初中数学 分式二次根式知识点归纳

分式与二次根式知识点归纳和考点题型

2013届九年级数学总复习四 代数式(分式与二次根式)

分式方程和二次根式试题和答案

分式与二次根式

初中数学分式与二次根式公式定理_公式总结

初中数学教案二次根式与分式的运算

2.分式与 二次根式

第3讲 分式与二次根式

初中数学分式二次根式知识点归纳

2013届九年级数学总复习四代数式(分式与二次根式)

2.分式与二次根式

第3讲分式与二次根式