深圳 朗钛50%吡蚜酮水分散粒剂配方、助剂
电缆参数表(全)

橡套电缆技术参数
产品名称:
产品说明:
本产品适用交流额定电压450/750V及以下家用电器,电动工具和各种移动电器设备。
一、生产执行标准:JB8735.2-1998
二、使用特性
1、额定电压300/500V(YZ型),450/750V(YC)型;
2、线芯的长期允许工作温度应不超过65℃;
3、“W”型电缆具有耐气候和一定的耐油性能,适宜于在户外或接触油污的场合使用;
4、-ZR型电缆具有阻燃性能。
三、型号、名称及主要用途用表1
表1
四、规格范围如表2
表2
五、规格尺寸及技术参数如表3~表5
表3 YQ,YQW型300/300V
表4 YZ,YZW型300/500V
表5 YZ,YZW型300/500V
六、交货要求
1、成圈100M,成盘应大于100M;
2、短段电缆不小于10M,短段电缆的交货数量不超过交货总长度10%,且每个包装件应不超过五段;
3、根据双方协议允许任何长度的电缆交货,长度误差为±0.5%;
4、用户对产品有阻燃特性要求,在合同中需另补充协议。
橡套软电缆。
50-3同轴电缆参数

50-3同轴电缆参数50-3同轴电缆是一种常用的通信电缆,具有一定的特性参数。
本文将从电缆的构造、特性及应用等方面介绍50-3同轴电缆的相关参数。
一、50-3同轴电缆的构造50-3同轴电缆是由内部导体、绝缘层、外部导体和外护层组成的。
内部导体通常由铜或铜合金制成,用于传输信号。
绝缘层一般采用聚乙烯或聚四氟乙烯等材料,用于隔离内部导体和外部导体。
外部导体由铜网或铝箔制成,用于屏蔽外界干扰信号。
外护层则用于保护整个电缆结构,一般采用聚氯乙烯或聚乙烯等材料。
二、50-3同轴电缆的特性参数1. 阻抗:50-3同轴电缆的特性阻抗通常为50欧姆,这是为了与其他通信设备保持匹配,以确保信号传输的质量和稳定性。
2. 衰减:衡量信号传输过程中信号损失的参数,一般以每单位长度的衰减值(dB/m)表示。
50-3同轴电缆的衰减通常较低,适合长距离的信号传输。
3. 带宽:指信号传输的频率范围,一般以MHz为单位。
50-3同轴电缆的带宽一般较宽,可以支持高频率信号的传输。
4. 速度因子:指信号在电缆中传播的速度与真空中光速之比。
50-3同轴电缆的速度因子一般为0.66-0.81之间,根据具体材料和结构有所差异。
5. 电容:指电缆单元长度上的电容值,一般以pF/m为单位。
50-3同轴电缆的电容较低,有利于减少信号传输过程中的能量损失。
三、50-3同轴电缆的应用50-3同轴电缆广泛应用于各种通信系统中,特别是在无线电通信和有线电视系统中。
在无线电通信中,50-3同轴电缆可用于连接天线与信号源,传输射频信号。
在有线电视系统中,50-3同轴电缆可用于传输电视信号,保证图像和声音的传输质量。
总结:50-3同轴电缆是一种常用的通信电缆,具有50欧姆的特性阻抗,衰减低、带宽宽、速度因子适中以及低电容等特点。
它的特性参数使其成为无线电通信和有线电视系统中的理想选择。
通过了解50-3同轴电缆的构造、特性及应用,我们可以更好地理解和应用这种电缆。
黄酮类化合物的构效关系研究进展_赵雪巍

摘 要:天然黄酮类化合物是以 C6-C3-C6 为基本结构骨架,结构亚型多种多样;其在自然界中的分布极为广泛,从水果、 蔬菜到中药中都有发现,生物活性具有多样性,一直是药物研发的热点领域。以天然黄酮类化合物为先导化合物或直接开发
成的药物已经得到广泛应用。由于黄酮类化合物的结构具有极强的规律性,对于该类化合物的构效关系研究也很活跃,也为
(4)取代基种类:Takasawa 等[11]对黄酮类化合 物的构效关系研究表明,C 环 3 位、A 环 7 位羟基 被糖基化或 A 环 6 位羟基甲基化会降低其抗肿瘤 活。López-Posadas 等[12]发现 C 环 3 位糖基化会使 某些黄酮类化合物抗肿瘤活性几乎完全丧失。 Plochmann 等[13]进一步得出黄酮类化合物 A 环各位 点的甲氧基取代和葡萄糖苷化可显著提高化合物的
1
O2
1'
5'
6'
6 5
3 4
O
期为今后黄酮类化合物的研究提供构效依据,为能
2-苯基色原酮
更直接、合理、充分地分离或合成具有更强药理作
图 1 黄酮类化合物母核结构
用的黄酮类先导化合物提供理论参考。Fig. 1 Skelton of flavonoids
收稿日期:2015-05-06 基金项目:国家自然科学基金资助项目(81302664);河北省自然科学基金资助项目(H2013206103);河北医科大学国家级大学生创新性实验
O
O ��
O
OH O ���
O
O ����
O
OH O
�����
O
O ���
OH
O ���
O OH
���
+
铝棒规格表

铝方规格表
规格
6 8 10 12 14 15 16
规格
18 20 22 24 25 26 30
规格
32 35 40 45 50 55 60
规格
65 70 75 80 85 90 95
规格
100 105 110 120 130 140 145
LY12 规格 150 160 170
180
铝板规格表
规格 规格
铝六角棒规格表�LY12�
规格 规格
规格
规格 规格 规格 规格 规格
10
14
22
12
17
24
13
19
2732
42
52
36
45
55
规格
2*20*20 2.5*25*25 2*30*30
铝方管规格表
规格
规格
规格
规格
2*20*40 4*40*40 2*20*30 3*30*30
3*50*50 5*50*50 3*40*30 2.5*80*30
80*160 12*180 16*180 20*180 25*180 30*180 50*180
规格
60*180 90*180 12*200 14*200 20*200 25*200 30*200 50*200 25*210 45*210 10*220 15*220 20*220 25*220 30*220 35*220 65*220
规格 规格 规格 规格 规格 规格 规格 规格
3*0.5 12*1.5 30*3 55*5 96*26
3*1
12*2 32*3 55*10 100*11
4*0.5 4*1 5*0.5 5*1 6*1 7*1 8*0.5 8*1 8*2 9*1 10*1 10*2 12*1
Oceanstor_T3000_G3_产品彩页V1.1

CB、CE、UL、FCC、CCC、ROHS、GOST
SUSE Linux、Windows Server、RedHat Linux、SUN Solaris 提供 ISM 管理软件 支持 IPMI2.0 支持 KVM over LAN,支持 Virtual Media over LAN 支持整机 S3 待机休眠和自动唤醒,唤醒时间小于 30 秒 硬盘缓启动设计,控制启动电流,降低了系统整体功耗需求 指定硬盘休眠技术和自动唤醒功能 智能风扇调速功能,监测环境温度和系统实时温度,自动调节风扇转速
机柜,节省空间,通用性更高;
整机休眠:业界率先支持 S3 待机休眠模式,
可支持整机的待机休眠和自动唤醒;
硬盘缓启动:硬盘缓启动设计,控制启动电流,
降低了系统整体功耗需求;
健康监测:针对关键器件进行健康监测,保 证系统健康绿色;
易维护:主板易维护.、关键部件热插拔,降低
维护成本;
友好:提供 Web 界面的 ISM 管理软件;
10GE,性能大幅提升;
高性能
高性能:采用英特尔 Sandybridge EN 2400 系
列处理器,12 个 DDR3 内存插槽,满足不同应 用对处理能力的需求;
大容量:可支持 3.5’或者 2.5’硬盘规格,提供多
达 25 个 2.5’盘位或 36 个 3.5’盘位,满足大容量 存储的应用需求;
AC,200V~240V 工作模式(平均功耗):<400W S3 待机模式:<50W 4U,175mm(H)*446mm(W)*585mm(D) ≤68kg
。
适用于 NSP、政府、教育、能源、金融等客 户,承担 Web 服务器、文件服务器、Mail 服务器、 数据库服务器等各种应用角色。
渗透压OSMOMAT 030使用说明

提示用户可能是无效结果
error
警告用户可能会损坏渗透压计或威胁本人身体健康
一般注意事项.
Notes, Safety Notices and Warnings | 3
Table of Contents
目录
标志,注意,警告 ................................................................................................................................................... 3
3.3
一般操作方式............................................................................................................... 17
4
OSMOMAT 030 冰点渗透压仪测量渗透压 ..........................................................................................19
4.3
校准液校准系统 ........................................................................................................... 22
4.4
测量样品溶液............................................................................................................... 24
贴片 3014 3020 3528 5050 的定义与区别

贴片3014/3020/3528/5050 的区别3014/3020/3528/5050指的是贴片元件的外形尺寸:3014:元件长3.0mm,宽1.4mm 功率:0.1W 9-13LM一两个LM一个档工作电压:3.0-3.43528:元件长3.5mm,宽2.8mm 功率:0.06W 6-9LM 一个LM一个档工作电压:3.0-3.45050:元件长和宽都是5mm. 功率:0.2W 17-27LM两三个LM一个档工作电压:3.0-3.4尺寸不一样,功率也不一样,各厂家标准都不太一样。
工厂从产品的芯片来源控制,封装用的高导热硅胶体,及采用台湾最前沿的光衰控制技术,环环相扣,从而生产出符合照明灯具高流明、高散热、低光衰的LED 灯珠。
3014灯珠LED日光灯,球泡灯,吸顶灯,面板灯,筒灯专用(3014)灯珠。
从成本,及性能上来看,它更具有目前许多型号无法比似的特点:高流明,高亮度,体积小,散热快,在照明灯具设计上,更加灵活,成本更低,对高要求的客户,能满足一些以往无法达到的高流明要求,目前已获LED日光灯、LED背光,照明灯具方面的厂家的青睐,已经开始大批量在生产,特殊的散热技术,从整灯具成本比较高,3014占有绝对的优势。
因此,目前在LED日光灯散热导上是比较好的产品选择。
3014/3020/3528/5050贴片的区别有以下几点:欢迎大家补充说明一、体积尺寸小:3.0*1.4*0.8mm(长*宽*高)二、散热结构不一样:3014采用独特的LED散热结构,其芯片放置于接脚上,有助于芯片节点的散热,芯片节点温度不会产生累积。
从而保证灯珠的使用寿命和良好使用性,低光衰。
另外3014的热阻低于同类产品,在常温下测试,优于同类产品(3020/3528/5050)。
三、工作的正向电流不一样:3014 IF=30MA3020 IF=20MA3528 IF=20MA5050 IF=60MA更省成本:3014产品芯片具有特殊的散热技术,电流可以在30MA正常使用,灯珠亮度高达9-11LM,相对同类亮度的产品来说,流明更高,使用颗数更少,从整体灯具成本来看,3014具有绝对优势,同时3014在散热方面也比同类产品要好很多,完全可以超越3528等同类产品。
9535中文资料

8-BIT WRITE pulse
INPUT/ OUTPUT PORTS
READ pulse
LP FILTER
I/O0.0 I/O0.1 I/O0.2 I/O0.3 I/O0.4 I/O0.5 I/O0.6 I/O0.7 VINT
INT
NOTE: ALL I/Os ARE SET TO INPUTS AT RESET
The PCA9535 is identical to the PCA9555 except for the removal of the internal I/O pull-up resistor which greatly reduces power consumption when the I/Os are held LOW.
TEMPERATURE RANGE
ORDER CODE
TOPSIDE MARK
24-Pin Plastic SO
-40 to +85 °C
PCA9535D
PCA9535D
24-Pin Plastic TSSOP
-40 to +85 °C
PCA9535PW
PCA9535PW
24-Pin Plastic HVQFN
Philips Semiconductors
16-bit I2C and SMBus, low power I/O port with interrupt
Product data
PCA9535
FEATURES
• Operating power supply voltage range of 2.3 V-5.5 V • 5 V tolerant I/Os • Polarity inversion register • Active LOW interrupt output • Low stand-by current • Noise filter on SCL/SDA inputs • No glitch on power-up • Internal power-on reset • 16 I/O pins which default to 16 inputs • 0 to 400 kHz clock frequency • ESD protection exceeds 2000 V HBM per JESD22-A114, 200 V
四川省成都七中2022-2023学年度上期初一半期数学试题及参考答案

2022-2023学年度上期初2022级半期考试数学参考答案A卷(100分)一.选择题(共8小题,每题4分,满分32分)1.【解答】解:根据“点动成线,线动成面,面动成体”,将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.故选:A.2.【解答】解:流星滑过天空留下一条痕迹,这种生活现象可以反映的数学原理是点动成线.故选:A.3.【解答】解:如果运进粮食20t记作:+20t,那么运出粮食15t记作﹣15t,故选:C.4.【解答】解:将67000吨用科学记数法表示为:6.7×104吨.故选:B.5.【解答】解:从上面看的视图中可以看出最底层小正方体的个数为6,从正面看的视图可以看出小正方体的层数为1、2、1层,从左面看的视图可以看出小正方体的层数为1、2、1层,所以该几何体的正中间是两个小正方体.所以构成这个立体图形的小正方体的个数为6+1=7(个)故选:B.6.【解答】解:∵6+(﹣4)=6﹣4=2,∴A选项符合题意;∵﹣9﹣(﹣4)=﹣9+4=﹣5,∴B选项不符合题意;∵|﹣9|+4=9+4=13,∴C选项不符合题意;∵﹣9﹣4=﹣(9+4)=﹣13,∴D选项不符合题意;故选:A.7.【解答】解:由题意可知:x=±3,y=±6,∵x>y,∴x=3,y=﹣6或x=﹣3,y=﹣6,当x=3,y=﹣6时,x+y2=3+(-6)2=39,当x=﹣3,y=﹣6时,x+y2=﹣3+(﹣6)2=﹣33,故选:B.8.【解答】解:A、ab<0,故A符合题意;B、a+b>0,正确,故B不符合题意;C、a﹣b>0,正确,故C不符合题意;D、|a|﹣|b|>0,正确,故D不符合题意.故选:A.二.填空题(共5小题,每题4分,共20分)9.【解答】解:﹣3<;∵|﹣|=,|﹣|=,>,∴﹣>﹣.故答案为:<;>.10.【解答】解:由n棱柱有3n条棱,所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,而六棱柱有6+2=8个面,故答案为:八.11.【解答】解:在图中添加一个小正方形,使它能折成一个正方体的情况如下:故答案为:4.12.【解答】解:当点B在A的左边时,﹣1﹣3=﹣4,当点B在A的右边时,﹣1+3=2,故答案为:2或﹣4.13.【解答】解:∵(a﹣3)4+|b+7|=0,∴a﹣3=0,b+7=0,∴a=3,b=﹣7,∴a+b=3﹣7=﹣4.故答案为:﹣4.三.解答题(共5小题,共48分)14.计算(20分,每小题4分):【解答】解:(1)原式=﹣2﹣3﹣1+5=﹣1;(2)原式=(﹣+﹣)×(﹣24)=﹣×(﹣24)+×(﹣24)﹣×(﹣24)=18﹣4+15=29;(3)原式=﹣1×2+4÷4=﹣2+1=﹣1;(4)原式=﹣4﹣6+=﹣9;(5)原式=﹣9÷9+6+4=﹣1+6+4=9.15.(6分)【解答】解:如图所示:(各2分)从正面看从左面看从上面看16.(6分)【解答】解:∵a,b互为倒数,c,d互为相反数,x的平方是3∴ab=1,c+d=0,x=3或-3,(3分)则原式=9﹣(1+0)+1=9﹣1+1=9或原式=-9﹣(1+0)+1=-9.(2分)则原式的答案为9或-9.(1分)17.(8分)【解答】 ,,a b c 都是非零有理数,,a b c ∴均为正数或者均为负数或者有一个或两个数为负数因此,分以下四种情况:(1)当,,a b c 均为正数时,则0abc >,则|U +|U +|U +B |BU =+++B B =1+1+1+1=4;(2分)(2)当,,a b c 均为负数时,则0abc <,则|U +|U +|U +B |BU =−+−+−+B −B=-1+(-1)+(-1)+(-1)=-4;(2分)(3)当,,a b c 中有一个数为负数时,不妨设a 为负数,则0abc <,|U +|U +|U +B |BU =−+++B −B =-1+1+1+(-1)=0;(2分)(4)当,,a b c 中有两个数为负数时,不妨设a 和b 为负数,则0abc >,|U +|U+|U +B |BU =−+−++B B =-1+(-1)+1+1=0;(2分)综上,|U +|U +|U +B |BU 的值为0,-4或4.18.(8分)【解答】解:(1)(+100﹣200+400)+3×5000=15300(个).故前三天共生产15300个口罩;(2分)(2)+400﹣(﹣200)=600(个).故产量最多的一天比产量最少的一天多生产600个;(3分)(3)5000×7+(100﹣200+400﹣100﹣100+350+150)=35600(个),0.2×35600=7120(元).(3分)故本周口罩加工厂应支付工人的工资总额是7120元.(不作答-1分)B 卷(50分)一.填空题(共5小题,每题4分,共20分)19.【解答】解:2021的相反数是﹣2021,|﹣2021|=2021.故答案为:2021.20.【解答】解:∵折成正方体后,x,y与其相对面上的数字相等,∴x=﹣2,y=3,∴x y=(﹣2)3=﹣8.故答案为:﹣8.21.【解答】解:|-1|+(-3)+|-5|+(-7)+···+|-97|+(-99)=-2+-2+···+-2两两组合,每一个组合的和为-2,一共有(99-1)/2+1=50个数,共25组,故答案为-50.22.【解答】解:|x+8|+|x−3|表示x到-8的距离与x到3的距离的和,由数形结合可知,x为4或-9.23.【解答】解:由题意可得,当n=26时,第一次输出的结果为:13,第二次输出的结果为:40,第三次输出的结果为:5,第四次输出的结果为:16,第五次输出的结果为:1,第六次输出的结果为:4,第七次输出的结果为:1第八次输出的结果为:4…,∵(2019﹣4)÷2=2015÷2=1007…1,∴第2019次“C运算”的结果是1,故答案为:1.二.解答题(共3小题,共30分)24.(8分)【解答】解:(1)∵3>2>1>0>﹣1>﹣2,(不作答-1分)∴47+3=50(元),47﹣2=45(元),50﹣45=5(元),答:价格最高的一件比价格最低一件多5元;(2分)(2)7×3+6×2+3×1+5×0+4×(﹣1)+5×(﹣2)=22(元),答:总售价超过22元;(3分)(3)(47﹣32)×30=450(元),450+22=472(元),答:赚了472元.(3分)25.(10分)【解答】解:(不作答-1分)(1)V=8×5×6=240(立方厘米)(3分)(2)V=8×5×6﹣π×22×6=240﹣24π(立方厘米).(3分)(3)2×(5×6+5×8+6×8)﹣2π×22+6×2π×2=16π+236(平方厘米)表面积为16π+236平方厘米.(4分)26.(12分)【解答】解:(1)由题意知:OC=120,∴当P运动到点C时,t=120÷4=30(秒);(3分)(2)①当点P、Q还没有相遇时,4t+6t=120﹣60,解得:t=6,(2分)②当点P、Q相遇后,4t+6t=120+60,解得:t=18,(2分)综上所述,经过6秒或18秒P,Q两点相距60cm;(3)∵PA+PB=2|QB﹣QC|=48,∴PA+PB=48,|QB﹣QC|=24,∵在数轴上,点A对应的数为40,点B对应的数为80,点C对应的数为120,∴点P对应的数为36或84(1分),点Q对应的数为88或112,(1分)①点P对应的数为36时,OP=36,t=36÷4=9(s),若点Q对应的数为88时,CQ=120﹣88=32,a=32÷9=,(0.5分)若点Q对应的数为112时,CQ=120﹣112=8,a=8÷9=(舍弃),(0.5分)②点P对应的数为82时,OP=82,t=82÷4=21(s),若点Q对应的数为88时,CQ=120﹣88=32,a=32÷21=,(0.5分)若点Q对应的数为112时,CQ=120﹣112=8,a=8÷21=(舍弃),(0.5分)(舍弃给1分)综上所述,点Q的运动速度为:单位长度/秒或单位长度/秒.。
专题3整式的化简求值专项训练50题

专题3整式的化简求值专项训练50题考试时间:100分钟;满分:100分姓名:___________班级:___________考号:___________ 1.(2020秋•北碚区校级期末)先化简,再求值:若多项式x2﹣2mx+3与13x2+2x﹣1的差与x的取值无关,求多项式4mn﹣[3m﹣2m2﹣6(12−23mn+16n2)]的值.2.(2020秋•高邮市期末)有这样一道题:“求(2x3﹣3x2y﹣2xy2)﹣(x3﹣2xy2+y3)+(﹣x3+3x2y﹣y3)的值,其中x=12021,y=﹣1”.小明同学把“x=12021”错抄成了“x=−12021”,但他的计算结果竟然正确,请你说明原因,并计算出正确结果.3.(2020秋•铜梁区校级期末)有一道数学题:“求(x2+2y2)+3(x2+y2)﹣4x2,其中x=13,y=2.”粗心的小李在做此题时,把“x=13”错抄成了“x=3”,但他的计算结果却是正确的,请你通过计算说明为什么?4.(2020秋•恩施市期末)若代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1)的值与字母x 的取值无关,求代数式5ab2﹣[a2b+2(a2b﹣3ab2)]的值.5.(2020秋•永年区期末)已知:关于x的多项式2ax3﹣9+x3﹣bx2+4x3中,不含x3与x2的项.求代数式3(a2﹣2b2﹣2)﹣2(a2﹣2b2﹣3)的值.6.(2020秋•宛城区校级月考)课堂上李老师把要化简求值的整式(7a2﹣6a2b+3a2b)﹣3(﹣a2﹣2a2b+a2b)﹣(10a2﹣3)写完后,让王红同学任意给出一组a、b的值,老师自己说答案,当王红说完:“a=38,b=﹣32”后,李老师不假思索,立刻就说出答案是3.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”.你相信吗?请你说明其中的道理.7.(2020秋•青羊区校级月考)已知关于x,y的式子(2x2+mx﹣y+3)﹣(3x﹣2y+1﹣nx2)的值与字母x的取值无关,求式子(m+2n)﹣(2m﹣n)的值.8.(2020秋•海珠区校级期中)已知:A=3x2+mx−13y+4,B=6x﹣3y+1﹣3nx2,当x≠0且y≠0时,若3A−13B的值等于一个常数,求m,n的值,及这个常数.9.(2020秋•富县校级期中)已知:A=2x2+6x﹣3,B=1﹣3x﹣x2,C=4x2﹣5x﹣1,当x=−32时,求代数式A﹣3B+2C的值.10.(2020秋•未央区校级期中)有这样一道题,当a=1,b=﹣1时,求多项式:3a3b3−12a2b+b ﹣(4a3b3−14a2b﹣b2)﹣2b2+3+(a3b3+14a2b)的值”,马小虎做题时把a=1错抄成a =﹣1,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.11.(2020秋•成都期末)已知A=a﹣2ab+b2,B=a+2ab+b2.(1)求14(B﹣A)的值;(2)若3A﹣2B的值与a的取值无关,求b的值.12.(2020秋•夏津县期末)已知A=3x2+3y2﹣5xy,B=2xy﹣3y2+4x2.(1)化简:2B﹣A;(2)已知﹣a x﹣2b2与13ab y是同类项,求2B﹣A的值.13.(2020秋•北碚区期末)已知代数式A=2x2+3xy﹣2x﹣1,B=﹣x2+xy﹣1.(1)当x=y=﹣1时,求2A+4B的值;(2)若2A+4B的值与x的取值无关,求y的值.14.(2020秋•淅川县期末)已知M=4x2+10x+2y2,N=2x2﹣2y+y2,求:(1)M﹣2N;(2)当5x+2y=2时,求M﹣2N的值.15.(2020秋•南关区校级期末)已知:A=x−12y+2,B=x﹣y﹣1.(1)化简A﹣2B;(2)若3y﹣2x的值为2,求A﹣2B的值.16.(2020秋•青山湖区月考)已知:A=2ab﹣a,B=﹣ab+2a+b.(1)计算:5A﹣2B;(2)若5A﹣2B的值与字母b的取值无关,求a的值.17.(2020秋•义马市期中)已知A=x2+3xy﹣12,B=2x2﹣xy+y.(1)当x=y=﹣2时,求2A﹣B的值;(2)若2A﹣B的值与y的取值无关,求x的值.18.(2020秋•萧山区月考)已知A=ax2﹣3x+by﹣1,B=3﹣y﹣x+232,且无论x,y为何值时,A﹣3B的值始终不变.(1)分别求a、b的值;(2)求b a的值.19.(2020秋•江汉区月考)先化简再求值,A=2x2−12x+3,B=x2+mx+12.(1)当m=﹣1,求5(A﹣B)﹣3(﹣2B+A);(2)若A﹣2B的值与x无关,求m2﹣[﹣2m2﹣(2m+6)﹣3m].20.(2021秋•株洲期末)已知:A=x2+3y2﹣2xy,B=2xy+2x2+y2.(1)求3A﹣B;(2)若x=1,=−12.求(4A+2B)﹣(A+3B)的值.21.(2020秋•广州期中)已知M=2x2+ax﹣5y+b,N=bx2−32x−52y﹣3,其中a,b为常数.(1)求整式M﹣2N;(2)若整式M﹣2N的值与x的取值无关,求(a+2M)﹣(2b+4N)的值.22.(2020秋•江城区期中)已知多项式A=2x2+mx−12y+3,B=3x﹣2y+1﹣nx2.(1)已知A﹣B的值与字母x的取值无关,求字母m、n的值?(2)在(1)的条件下,求2A+3B的值?23.(2020秋•庐江县期中)数学课上,张老师出示了这样一道题目:“当a=12,b=﹣2时,求多项式7a3+3a2b+3a3+6a3b﹣3a2b﹣10a3﹣6a3b﹣1的值”解完这道题后,小阳同学指出:“a=12,b=﹣2是多余的条件”.师生讨论后,一致认为小阳说法是正确的.(1)请你说明正确的理由;(2)受此启发,老师又出示了一道题目:“无论x,y取任何值,多项式2x2+ax﹣5y+b ﹣2(bx2−32x−52y﹣3)的值都不变,求系数a,b的值”.请你解决这个问题.24.(2020秋•双流区校级期中)已知关于x的代数式2x2−12bx2﹣y+6和ax+17x﹣5y﹣1的值都与字母x的取值无关.(1)求a,b的值.(2)若A=4a2﹣ab+4b2,B=3a2﹣ab+3b2,求4A+[(2A﹣B)﹣3(A+B)]的值.25.(2020秋•温县期中)已知代数式A=x2+12xy﹣2y2,B=32x2﹣xy﹣y2,C=﹣x2+8xy﹣3y2.(1)求2(A﹣B)−12C.(2)当x=2.y=﹣1时,求出2(A﹣B)−12C的值.26.(2020秋•解放区校级期中)已知:A=2x2+3xy﹣2x﹣1,B=﹣x2+xy﹣1.(1)求﹣A﹣2B的值;(2)若﹣A﹣2B的值与x的值无关,求y的值.27.(2020秋•丰城市校级期中)(1)已知,A=2x2+3xy﹣2x﹣1,B=﹣x2﹣xy+1,若3A+6B 的值与x的取值无关,求y的值.(2)定义新运算“@”与“⊕”:a@b=r2,a⊕b=K2.若A=3b@(﹣a)+a⊕(2﹣3b),B=a@(﹣3b)+(﹣a)⊕(﹣2﹣9b),比较A和B的大小.28.(2020秋•江汉区期中)已知:A=2a2+3ab﹣2a﹣1,B=a2+ab﹣1.(1)计算4A﹣(3A+2B);(2)若a=1和a=0时(1)中式子的值相等,求12b﹣2(b−13b2)+(−32b+13b2)的值.29.(2020秋•沙坪坝区校级期中)若A=2x2+xy+3y2,B=x2﹣xy+2y2.(1)若(1+x)2与|2x﹣y+2|为相反数,求2A﹣3(2B﹣A)的值;(2)若x2+y2=4,xy=﹣2,求A﹣B的值.30.(2020秋•滨海新区期中)已知A=2x2+3xy﹣2x﹣1,B=﹣x2+12B+23.(1)当x=﹣1,y=﹣2时,求4A﹣(3A﹣2B)的值;(2)若(1)中式子的值与x的取值无关,求y的值.31.(2020秋•二七区校级期中)已知A=a2+2ab+b2,B=a2﹣2ab+b2.(1)当a=1,b=﹣2时,求14(B﹣A)的值;(2)如果2A﹣3B+C=0,那么C的表达式是什么?32.(2020秋•潮南区期中)已知多项式A=4x2+my﹣12与多项式B=nx2﹣2y+1.(1)当m=1,n=5时,计算A+B的值;(2)如果A与2B的差中不含x和y,求mn的值.33.(2020秋•高邮市期中)已知A=x2﹣2xy,B=y2+3xy.(1)若A﹣2B+C=0,试求C;(2)在(1)的条件下若A=5,求2A+4B﹣2C的值.34.(2020秋•洪山区期中)已知A=2x2+4xy﹣2x﹣3,B=﹣x2+xy+2.(1)求3A﹣2(A+2B)的值;(2)当x取任意数,B+12A的值都是一个定值时,求313A+613B﹣27y3的值.35.(2020秋•平阴县期中)张老师让同学们计算“当a=0.25,b=﹣0.37时,求代数式(13+2a2b+b3)﹣2(a2b−13)﹣b3的值”.解完这道题后,小明同学说“a=0.25,b=﹣0.37是多余的条件”.师生讨论后一致认为这种说法是正确的,老师和同学们对小明敢于提出自己的见解投去了赞赏的目光.(1)请你说明小明正确的理由.(2)受此启发,老师又出示了一道题目:无论x、y取何值,多项式﹣3x2y+mx+nx2y﹣x+3的值都不变.则m=,n=.36.(2020秋•锦江区校级期中)(1)如图:化简|b﹣a|+|a+c|﹣|a+b+c|.(2)已知:ax2+2xy﹣y﹣3x2+bxy+x是关于x,y的多项式,如果该多项式不含二次项,求代数式3ab2﹣{2a2b+[4ab2−13(6a2b﹣9a2)]}﹣(−14a2b﹣3a2)的值.37.(2020秋•武侯区校级期中)已知关于x、y的代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y ﹣1)的值与字母x的取值无关.(1)求a和b值.(2)设A=a2﹣2ab﹣b2,B=3a2﹣ab﹣b2,求3[2A﹣(A﹣B)]﹣4B的值.38.(2021秋•卧龙区期末)数学课上,老师出示了这样一道题目:“当a=12,b=﹣2时,求多项式7a3+3a2b+3a3+6a3b﹣3a2b﹣10a3﹣6a3b﹣1的值”解完这道题后,张恒同学指出:“a=12,b=﹣2是多余的条件”.师生讨论后,一直认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.(1)请你说明正确的理由;(2)受此启发,老师又出示了一道题目:“无论x取任何值,多项式﹣3x2+mx+nx2﹣x+3的值都不变,求系数m、n的值”.请你解决这个问题.39.(2020秋•张店区期末)阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b),“整体思想”是中学教学课题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.(1)尝试应用:把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣5(a﹣b)2+7(a﹣b)2的结果是.(2)已知x2﹣2y=1,求3x2﹣6y﹣5的值.(3)拓展探索:已知a﹣2b=2,2b﹣c=﹣5,c﹣d=9,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.40.(2020秋•天河区期末)已知A=3x2﹣x+2y﹣4xy,B=2x2﹣3x﹣y+xy.(1)化简2A﹣3B;(2)当x+y=67,xy=﹣1,求2A﹣3B的值;(3)若2A﹣3B的值与y的取值无关,求2A﹣3B的值.41.(2020秋•讷河市期末)已知代数式A=2x2+3xy+2y,B=x2﹣xy+x.(1)求A﹣2B;(2)当x=﹣1,y=3时,求A﹣2B的值;(3)若A﹣2B的值与x的取值无关,求y的值.42.(2020秋•路北区期末)已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)(1)化简代数式;(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?43.(2020•路北区三模)已知A=x2﹣mx+2,B=nx2+2x﹣1.(1)求2A﹣B,并将结果整理成关于x的整式;(2)若2A﹣B的结果与x无关,求m、n的值;(3)在(2)基础上,求﹣3(m2n﹣2mn2)﹣[m2n+2(mn2﹣2m2n)﹣5mn2]的值.44.(2020秋•偃师市月考)我们知道,4x﹣2x+x=(4﹣2+1)x=3x.类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.(1)若把(a﹣b)2看成一个整体,则合并4(a﹣b)2﹣8(a﹣b)2+3(a﹣b)2的结果是.(2)已知x2﹣2y=4,求8y﹣4x2+3的值.(3)已知a﹣2b=4,2b﹣c=﹣7,c﹣d=11,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.45.(2020秋•船山区校级月考)一个多项式的次数为m,项数为n,我们称这个多项式为m次多项式或者m次n项式,例如:5x3y2﹣2x2y+3xy为五次三项式,2x2﹣2y2+3xy+2x 为二次四项式.(1)﹣3xy+2x2y2﹣4x3y3+3为次项式.(2)若关于x、y的多项式A=ax2﹣3xy+2x,B=bxy﹣4x2+2y,已知2A﹣3B中不含二次项,求a+b的值.(3)已知关于x的二次多项式,a(x3﹣x2+3x)+b(2x2+x)+x3﹣5在x=2时,值是﹣17,求当x=﹣2时,该多项式的值.46.(2020秋•海州区校级期中)有这样一道题“如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值是多少?”爱动脑筋的吴爱国同学这样来解:原式=2a+2b+8a+4b=10a+6b.我们把5a+3b成一个整体,把式子5a+3b=﹣4两边乘以2得10a+6b=﹣8.整体思想是中学数学解题中的一种重要思想方法,它在多项式的化简与求值中应用极为广泛,仿照上面的解题方法,完成下面问题:【简单应用】(1)已知a2+a=1,则2a2+2a+2020=.(2)已知a﹣b=﹣3,求5(a﹣b)﹣7a+7b+11的值.【拓展提高】(3)已知a2+2ab=﹣5,ab﹣2b2=﹣3,求代数式3a2+92ab+3b2的值.47.(2020秋•海珠区校级期中)已知A=3x2+y2﹣2xy,B=xy﹣y2+2x2,求:(1)2A﹣3B;(2)若|2x﹣3|=1,y2=16,|x﹣y|=y﹣x,求2A﹣3B的值.(3)若x=4,y=﹣8时,代数式ax3+12by+5=18,那么x=﹣128,y=﹣1时,求代数式3ax﹣24by3+10的值.48.(2020秋•宁明县期中)在某次作业中有这样的一道题:“如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值是多少?”小明是这样来解的:原式=2a+2b+8a+4b=10a+6b,把式子5a+3b=﹣4两边同乘以2,得10a+6b=﹣8,仿照小明的解题方法,完成下面的问题:(1)如果a2+a=0,则a2+a+2020=;(2)已知a﹣b=﹣2,求3(a﹣b)﹣5a+5b+6的值;(3)已知a2+2ab=3,ab﹣b2=﹣4,求a2+32ab+12b2的值,49.(2020秋•温江区校级期中)已知代数式2x2+ax﹣y+6−12bx2﹣4x﹣5y﹣1的值与字母x 的取值无关.(1)求出a、b的值.(2)若A=2a2﹣ab+2b2,B=a2﹣ab+b2,求(2A﹣B)﹣3(A﹣B)的值.(3)若P=4x2y﹣5x2y b﹣(m﹣5)x a y3与Q=﹣5x n y4+6xy﹣3x﹣7的次数相同,且最高项的系数也相同,求5m﹣2n的值.50.(2021秋•东城区期末)一般情况下,对于数a和b,2+4≠r2+4(“≠”不等号),但是对于某些特殊的数a和b,2+4=r2+4.我们把这些特殊的数a和b,称为“理想数对”,记作<a,b>.例如当a=1,b=﹣4时,有12+−44=1+(−4)2+4,那么<1,﹣4>就是“理想数对”.(1)<3,﹣12>,<﹣2,4>可以称为“理想数对”的是;(2)如果<2,x>是“理想数对”,那么x=;(3)若<m,n>是“理想数对”,求3[(9−4p−8(−76p]−4−12的值.11。
钢管规格表

三、方管理论重量表四、方管规格:•[19方焊管]19×19×(1.0~2.0):19×19×1.0、19×19×1.1、19×19×1.2、19×19×1.3、19×19×1.4、19×19×1.5、19×19×1.6、19×19×1.7、19×19×1.8、19×19×1.9、19×19×2.0 •[20方焊管]20×20×(1.0~2.0):20×20×1.0、20×20×1.1、20×20×1.2、20×20×1.3、20×20×1.4、20×20×1.5、20×20×1.6、20×20×1.7、20×20×1.8、20×20×1.9、20×20×2.0 •[21方焊管]21×21×(1.0~2.0):21×21×1.0、21×21×1.1、21×21×1.2、21×21×1.3、21×21×1.4、21×21×1.5、21×21×1.6、21×21×1.7、21×21×1.8、21×21×1.9、21×21×2.0 •[25方焊管]25×25×(1.0~2.0):25×25×1.0、25×25×1.1、25×25×1.2、25×25×1.3、25×25×1.4、25×25×1.5、25×25×1.6、25×25×1.7、25×25×1.8、25×25×1.9、25×25×2.0 •[30方焊管]30×30×(1.0~2.0):30×30×1.0、30×30×1.1、30×30×1.2、30×30×1.3、30×30×1.4、30×30×1.5、30×30×1.6、30×30×1.7、30×30×1.8、30×30×1.9、30×30×2.0 •[32方焊管]32×32×(1.0~2.0):32×32×1.0、32×32×1.1、32×32×1.2、32×32×1.3、32×32×1.4、32×32×1.5、32×32×1.6、32×32×1.7、32×32×1.8、32×32×1.9、32×32×2.0 •[40方焊管] 40×40×(1.0~2.0):40×40×1.0、40×40×1.1、40×40×1.2、40×40×1.3、40×40×1.4、40×40×1.5、40×40×1.6、40×40×1.7、40×40×1.8、40×40×1.9、40×40×2.0•[50方焊管]50×50×(1.0~2.0):50×50×1.0、50×50×1.1、50×50×1.2、50×50×1.3、50×50×1.4、50×50×1.5、50×50×1.6、50×50×1.7、50×50×1.8、50×50×1.9、50×50×2.0五、矩形管的规格[20×30毫米矩形管] 20×30×(1.0~2.0):20×30×1.0、20×30×1.1、20×30×1.2、20×30×1.3、20×30×1.4、20×30×1.5、20×30×1.6、20×30×1.7、20×30×1.8、20×30×1.9、20×30×2.0 [20×40毫米矩形管] 20×40×(1.0~2.0):20×40×1.0、20×40×1.1、20×40×1.2、20×40×1.3、20×40×1.4、20×40×1.5、20×40×1.6、20×40×1.7、20×40×1.8、20×40×1.9、20×40×2.0 [30×40毫米矩形管] 30×40×(1.0~2.0):30×40×1.0、30×40×1.1、30×40×1.2、30×40×1.3、30×40×1.4、30×40×1.5、30×40×1.6、30×40×1.7、30×40×1.8、30×40×1.9、30×40×2.0 [25×50毫米矩形管] 25×50×(1.0~2.0):25×50×1.0、25×50×1.1、25×50×1.2、25×50×1.3、25×50×1.4、25×50×1.5、25×50×1.6、25×50×1.7、25×50×1.8、25×50×1.9、25×50×2.0 [30×50毫米矩形管] 30×50×(1.0~2.0):30×50×1.0、30×50×1.1、30×50×1.2、30×50×1.3、30×50×1.4、30×50×1.5、30×50×1.6、30×50×1.7、30×50×1.8、30×50×1.9、30×50×2.0 [40×60毫米矩形管] 40×60×(1.0~2.0):40×60×1.0、40×60×1.1、40×60×1.2、40×60×1.3、40×60×1.4、40×60×1.5、40×60×1.6、40×60×1.7、40×60×1.8、40×60×1.9、40×60×2.0 [25×79毫米矩形管] 25×79×(1.0~2.0):25×79×1.0、25×79×1.1、25×79×1.2、25×79×1.3、25×79×1.4、25×79×1.5、25×79×1.6、25×79×1.7、25×79×1.8、25×79×1.9、25×79×2.0六、不锈钢矩形管规格[20×30毫米矩形管] 20×30×(1.0~2.0):20×30×1.0、20×30×1.1、20×30×1.2、20×30×1.3、20×30×1.4、20×30×1.5、20×30×1.6、20×30×1.7、20×30×1.8、20×30×1.9、20×30×2.0 [20×40毫米矩形管] 20×40×(1.0~2.0):20×40×1.0、20×40×1.1、20×40×1.2、20×40×1.3、20×40×1.4、20×40×1.5、20×40×1.6、20×40×1.7、20×40×1.8、20×40×1.9、20×40×2.0 [30×40毫米矩形管] 30×40×(1.0~2.0):30×40×1.0、30×40×1.1、30×40×1.2、30×40×1.3、30×40×1.4、30×40×1.5、30×40×1.6、30×40×1.7、30×40×1.8、30×40×1.9、30×40×2.0 [25×50毫米矩形管] 25×50×(1.0~2.0):25×50×1.0、25×50×1.1、25×50×1.2、25×50×1.3、25×50×1.4、25×50×1.5、25×50×1.6、25×50×1.7、25×50×1.8、25×50×1.9、25×50×2.0 [30×50毫米矩形管] 30×50×(1.0~2.0):30×50×1.0、30×50×1.1、30×50×1.2、30×50×1.3、30×50×1.4、30×50×1.5、30×50×1.6、30×50×1.7、30×50×1.8、30×50×1.9、30×50×2.0 [40×60毫米矩形管] 40×60×(1.0~2.0):40×60×1.0、40×60×1.1、40×60×1.2、40×60×1.3、40×60×1.4、40×60×1.5、40×60×1.6、40×60×1.7、40×60×1.8、40×60×1.9、40×60×2.0 [25×79毫米矩形管] 25×79×(1.0~2.0):25×79×1.0、25×79×1.1、25×79×1.2、25×79×1.3、25×79×1.4、25×79×1.5、25×79×1.6、25×79×1.7、25×79×1.8、25×79×1.9、25×79×2.0八、方管每米重量方管矩管每米理论重量计算公式正方形和长方形(矩形)截面碳钢:每米重量单位: kg/m(千克/米) & lb/ft(磅/英尺) 公式:kg/m = (Oc - 4Wt) * Wt * 0.00785其中:Oc是外周长,Wt是壁厚;正方形Oc=4*a长方形Oc=2a+2b a,b是边长钢材理论重量基本公式钢材理论重量计算的计量单位为公斤( kg )。
各种电缆穿管管径表-详细

ZLQD
0.6/1KV
电缆标称截面(MM2)
16
25
35
50
70
95
120
150
185
240
焊接钢管(SC)
或水煤气钢管(RC)
最小管径(mm)
电缆穿管长度在30m及以下
直线
32
40
50
70
80
一个弯曲时
40
50
70
80
100
二个弯曲时
50
70
80
100
125
注:适用于三芯、三芯+N及四芯等截面电力电缆.
管材种类
导线规格型号
电话支线穿管对数
1
2
3
4
5
6
7
8
9
最小管径(mm)
导线穿电线管(TC)或聚氯乙烯管(PC)
RVB-2X0.2
2X0。5
16
20
25
32
RVS-2X0.2
2X0.5
20
25
32
40
导线穿焊接钢管(SC)或水煤气钢管(RC)
RVB—2X0.2
2X0。5
15
20
25
RVS—2X0.2
2X0.5
1
2
3
4
5
管材种类
TC SC
RC
TC SC
RC
TC SC
RC
TC SC
RC
TC SC
RC
同轴电缆型号规格
电缆穿管最小管径(mm)
SYV-
SS—
75—5—4
16 15
25 20
25 20
24秋八上【湘教】期中模拟卷01【1-3章】

上学期期中模拟考试01八年级数学(湘教版:第1-3章)(考试时间:120分钟试卷满分:120分)第Ⅰ卷一、选择题:本题共10小题,每小题3分,共30分。
1.实数9的算术平方根是()A .3B .±3C .D .﹣92.代数式25x ,1,22+4,x 2−23,1,+1+2中,属于分式的有()A .2个B .3个C .4个D .5个3.已知x =1是方程2−−1K 2=3的解,那么实数m 的值为()A .﹣2B .2C .﹣4D .44.如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a 的值可以是()A .1B .2C .3D .45.若等腰三角形有一个内角为110°,则这个等腰三角形的底角是()A .70°B .45°C .35°D .50°6.如图,CD ⊥AB 于点D ,已知∠ABC 是钝角,则()A .线段CD 是△ABC 的AC 边上的高线B .线段CD 是△ABC 的AB 边上的高线C .线段AD 是△ABC 的BC 边上的高线D .线段AD 是△ABC 的AC 边上的高线7.下列说法正确的是()A .命题一定有逆命题B .所有的定理一定有逆定理C.真命题的逆命题一定是真命题D.假命题的逆命题一定是假命题8.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为()A.60°B.70°C.75°D.85°9.已知一列均不为1的数a1,a2,a3,…,a n满足如下关系:a2=1+11−1,a3=1+21−2,4=1+31−3,+1=1+1−,若a1=2,则a2023的值是()A.−12B.13C.﹣3D.210.某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设大货车每辆运输x吨,则所列方程正确的是()A.75 K5=50B.75=50K5C.75+5=50D.75=50+5第Ⅱ卷二、填空题:本题共6小题,每小题3分,共18分。
各尺寸相框对应的卡纸尺寸
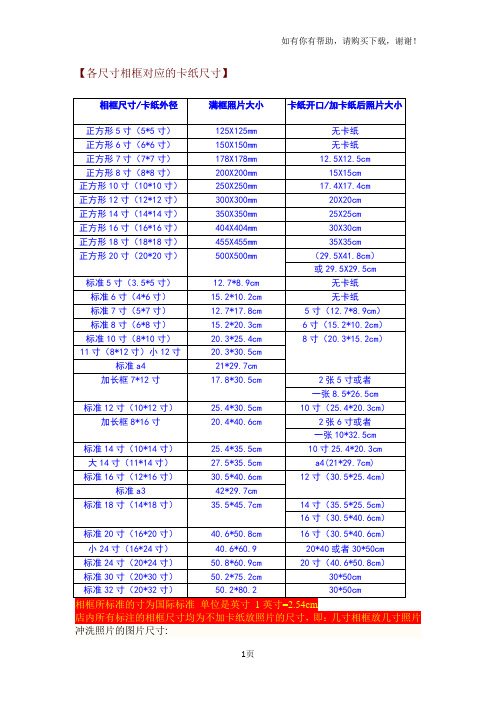
【各尺寸相框对应的卡纸尺寸】1英寸证明照的尺寸应为3.6×2.7厘米;2英寸证明照的尺寸应是3.5×4.5厘米;5英寸(最常见的照片大小)尺寸应为12.7×8.9厘米;6英寸(国际上比较通用的照片大小)尺寸是15.2×10.2厘米;7英寸(放大)照片的尺寸是17.8×12.7厘米;12英寸照片的尺寸是30.5×25.4厘米;(4D照片的尺寸是4.5×6寸)6×8英寸,毫米规格152×2038×10英寸,毫米规格203×2588×12英寸,毫米规格203×3048×14英寸,毫米规格203×356-----------------------------------------------照片规格(英吋) 厘米差(150dpi以下) 好(150dpi 至250dpi) 优(250dpi以上) 5 吋3.5x5 8.9x12.7 850x595以下850x595-1000x700之间1000x700以上5 D 3.75x5 12.7X9.5 850x595以下850x595-1000x700之间1000x700以上6 吋4x6 10.2x15.2 1020x680以下1020x680-1200x800之间1200x800以上6 D 4.5x6 15.2X11.4 1020x680以下1020x680-1200x800之间1200x800以上7 吋5x7 12.7x17.8 1190x850以下1190x850-1400x1000之间1400x1000以上8 吋6x8 15.2x20.3 1360x1020以下1360x1020-1600x1200之间1600x1200以上10吋8x10 20.3x25.4 1700x1360以下1700x1360-2000x1600之间2000x1600以上12吋8x12 20.3x30.5 2040x1700以下2040x1700-2400x2000之间2400x2000以上---------------------------------------------------------1寸2.5*3.5cm 413*295身份证大头照3.3*2.2 390*2602寸3.5*5.3cm 626*413小2寸(护照)4.8*3.3cm 567*3905 寸5x3.5 12.7*8.9 1200x840以上100万像素6 寸6x4 15.2*10.2 1440x960以上130万像素7寸7x5 17.8*12.7 1680x1200以上200万像素8寸8x6 20.3*15.2 1920x1440以上300万像素10寸10x8 25.4*20.3 2400x1920以上400万像素12寸12x10 30.5*20.3 2500x2000以上500万像素15寸15x10 38.1*25.4 3000x2000 600万像素-------------------------------------------------------照片尺寸大全照片尺寸大全1英寸25mm×35mm2英寸35mm×49mm3英寸35mm×52mm港澳通行证33mm×48mm赴美签证50mm×50mm日本签证45mm×45mm大二寸35mm×45mm护照33mm×48mm毕业生照33mm×48mm身份证22mm×32mm驾照21mm×26mm车照60mm×91mm数码相机和可冲印照片最大尺寸对照表500万像素有效4915200,像素2560X1920。
七年级数学下册 专题 解二元一次方程组(计算题50题)(解析版)

七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)−=4,3+=16;(2)−=2,3+5=14.【分析】(1)−=4①3+=16②,由①得:x=y+4,代入②得:3(y+4)+y=16,即可求出y的值,则x的值也就迎刃而解了;(2)−=4①3+5=14②,由①得:y=x﹣2,代入②得:3x+5(x﹣2)=14,即可求出x的值,则y的值也就可以求出了.【解答】解:(1)−=4①3+=16②,由①得:x=y+4,代入②得:3(y+4)+y=16,解得y=1.将y=1代入x=y+4中得x=5,故方程组的解为:=5=1;(2)−=4①3+5=14②,由①得:y=x﹣2,代入②得:3x+5(x﹣2)=14,解得x=3.将x=3代入y=x﹣2,得y=1.故方程组的解为:=3=1.【点评】本题主要考查了二元一次方程组的解法,解题的关键是掌握代入法解方程.2.用代入法解下列方程组:(1)2−=33+2=8;(2)+=103−2=5.【分析】两方程组利用代入消元法求出解即可.【解答】解:(1)2−=3①3+2=8②,由①得:y=2x﹣3③,把③代入②得:3x+2(2x﹣3)=8,解得:x=2,把x=2代入③得:y=4﹣3=1,则方程组的解为=2=1;(2)+=10①3−2=5②,由①得:u=10﹣v③,把③代入②得:3(10﹣v)﹣2v=5,解得:v=5,把v=5代入①得:5+u=10,解得:u=5,则方程组的解为=5=5.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.3.用代入法解下列方程组:(1)3−=2,9+8=17;(2)3−4=10+3=12.【分析】(1)由①得出y =3x ﹣2③,把③代入②得出9x +8(3x ﹣2)=17,求出x ,再把x =1代入③求出y 即可;(2)由②得出x =12﹣3y ③,把③代入①得出3(12﹣3y )﹣4y =10,求出y ,再把y =2代入③求出x 即可.【解答】解:(1)3−=2①9+8=17②,由①,得y =3x ﹣2③,把③代入②,得9x +8(3x ﹣2)=17,解得:x =1,把x =1代入③,得y =3×1﹣2,即y =1,所以原方程组的解是=1=1;(2)3−4=10①+3=12②,由②,得x =12﹣3y ③,把③代入①,得3(12﹣3y )﹣4y =10,解得:y =2,把y =2代入③,得x =12﹣3×2,即x =6,所以原方程组的解是=6=2.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.4.用代入法解下列方程组.(1)+2=4=2−3;(2)−=44+2=−2.【分析】(1)方程组利用代入消元法求出解即可;(2)方程组利用加减消元法求出解即可.【解答】解:(1)+2=4①=2−3②,把②代入①得:x +2(2x ﹣3)=4,解得:x =2,把x =2代入②得:y =4﹣3=1,则方程组的解为=2=1;(2)方程组整理得:−=4①2+=−1②,①+②得:3x =3,解得:x =1,把x =1代入①得:1﹣y =4,解得:y =﹣3,则方程组的解为=1=−3.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.5.用代入法解下列方程组:(1)5+4=−1.52−3=4(2)4−3−10=03−2=0【分析】(1)方程组利用代入消元法求出解即可;(2)方程组利用代入消元法求出解即可.【解答】解:(1)5+4=−1.5①2−3=4②,由②得:x =3r42③,把③代入①得:15r202+4y =﹣1.5,去分母得:15y +20+8y =﹣3,移项合并得:23y =﹣23,解得:y =﹣1,把y =﹣1代入③得:x =12,则方程组的解为=12=−1;(2)方程组整理得:4−3−10=0①=23t ,把②代入①得:83y ﹣3y ﹣10=0,去分母得:8y ﹣9y ﹣30=0,解得:y=﹣30,把y=﹣30代入②得:x=﹣20,则方程组的解为=−20=−30.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.6.用代入法解下列方程组:(1)−=42+=5;(2)3−=29+8=17;(3)3+2=−86−3=−9.【分析】各方程组利用代入消元法求出解即可.【解答】解:(1)−=4①2+=5②,由①得:x=y+4③,把③代入②得:2(y+4)+y=5,解得:y=﹣1,把y=﹣1代入③得:x=﹣1+4=3,则方程组的解为=3=−1;(2)3−=2①9+8=17②,由①得:y=3x﹣2③,把③代入②得:9x+8(3x﹣2)=17,解得:33x=33,解得:x=1,把x=1代入③得:y=3﹣2=1,则方程组的解为=1=1;(3)3+2=−8①2−=−3②,由②得:y=2x+3③,把③代入①得:3x+2(2x+3)=﹣8,解得:x=﹣2,把x=﹣2代入②得:﹣4﹣y=﹣3,解得:y=﹣1,则方程组的解为=−2=−1.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.7.用代入法解下列方程组:(1)3+2=11,①=+3,②(2)4−3=36,①+5=7,②(3)2−3=1,①3+2=8,②【分析】(1)将方程②代入方程①进行求解;(2)将方程②变形为y=﹣5x+7,再代入方程①进行求解;(3)将方程①变形为y=2K13,再代入方程②进行求解.【解答】解:(1)将方程②代入方程①得,3(y+3)+2y=11,解得y=25,把y=25代入②得,x=175,∴该方程组的解为=175=25;(2)将方程②变形为y=﹣5x+7③,把③代入①得,4x﹣3(﹣5x+7)=36,解得x=3,将x=3代入③得,y=﹣5×3+7,解得y=﹣8,∴该方程组的解为=3=−8;(3)将方程①变形为y=2K13③,把③代入②得,3x+2×2K13=8,解得x=2,将x =2代入③得,y =2×2−13,解得y =1,∴该方程组的解为=2=1.【点评】此题考查了利用代入法解二元一次方程组的能力,关键是能直接或将某方程变式后进行代入消元求解.8.用代入法解下列方程组:(1)5+2=15①8+3=−1②;(2)3(−2)=−172(−1)=5−8.【分析】(1)用代入消元法解二元一次方程组即可;(2)用代入消元法解二元一次方程组即可.【解答】解:(1)5+2=15①8+3=−1②,由①得,y =15−52③,将③代入②得,8x +15−52×3=﹣1,解得,x =﹣47,将x =﹣47代入①得,y =125,∴方程组的解为=−47=125;(2)3(−2)=−172(−1)=5−8,整理得,3−=−11①2−5=−6②,由①得,x =3y +11③,将③代入②得,y =﹣28,将y =﹣28代入①得,x =﹣73,∴方程组的解为=−73=−28.【点评】本题考查二元一次方程组的解,熟练掌握代入消元法和加减消元法解二元一次方程组是解题的关键.9.用代入法解下列方程组:(1)=6−53−6=4(2)5+2=15+=6(3)3+4=22−=5(4)2+3=73−5=1【分析】(1)用代入消元法解方程组即可.(2)用代入消元法解方程组即可.(3)用代入消元法解方程组即可.(4)用代入消元法解方程组即可.【解答】解:(1)=6−5s3−6=4②,把①代入②得3(6﹣5y)﹣6y=4,解得y=23,∴x=6−5×23=83,所以方程组的解为=83=23;(2)5+2=15①+=6②,由②得x=6﹣y③,把③代入①,得y=5,∴x=6﹣5=1,所以原方程组的解为=1=5;(3)3+4=2①2−=5②,由②得y=2x﹣5③,把③代入①得,解得x=2,∴y=2×2﹣5=﹣1,所以原方程组的解为=2=−1;(4)2+3=7①3−5=1②,由①得x=7−32③,把③代入②得解得y=1,∴x=7−3×12=2,所以原方程组的解为=2=1.【点评】本题考查二元一次方程组的解法,解题关键是熟知代入消元法解方程组的步骤.10.用代入法解下列方程组:(1)2+=3+2=−6;(2)+5=43−6=5;(3)2−=63+2=2;(4)5+2=113−=−9;【分析】(1)用代入消元法解方程组即可.(2)用代入消元法解方程组即可.(3)用代入消元法解方程组即可.(4)用代入消元法解方程组即可.【解答】解:(1)2+=3①+2=−6②,由①得y=3﹣2x,把y=3﹣2x代入②得x+2(3﹣2x)=﹣6,解得x=4,∴y=3﹣2×4=﹣5.∴方程组的解为=4=−5.(2)+5=4①3−6=5②,由①得x=4﹣5y,把x=4﹣5y代入②得3(4﹣5y)﹣6y=5,解得y=13,∴x=4﹣5×13=73.∴方程组的解为=73=13.(3)2−=6①3+2=2②,由①得y=2x﹣6,把y=2x﹣6代入②得3x+2(2x﹣6)=2,解得x=2,∴y=2x﹣6=2×2﹣6=﹣2.方程组的解为=2=−2.(4)5+2=11①3−=−9②,由②得x=3y+9,把x=3y+9代入①得5(3y+9)+2y=11,解得y=﹣2,∴x=3×(﹣2)+9=3.∴方程组的解为=3=−2.【点评】本题考查二元一次方程组的解法,解题关键是熟知代入消元法解方程组的步骤.1.用加减法解下列方程组:(1)4−=143+=7(2−2=7−3=−8【分析】(1)方程组利用加减消元法求出解即可;(2)方程组利用加减消元法求出解即可.【解答】解:(1)4−=14①3+=7②,①+②得:7x=21,解得:x=3,把x=3代入②得:y=﹣2,则方程组的解为=3=−2;(2−2=7①−3=−8②,①﹣②得:y=15,把y=15代入①得:x=74,则方程组的解为=74=15.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.2.用加减法解下列方程组:(1)2+7=53+=−2(2)5=123=−2(37=127=13【分析】(1)由②得出n=﹣2﹣3m③,把③代入①得出2m+7(﹣2﹣3m)=5,求出m,把m=﹣1代入③求出n即可;(2)②﹣①×2得出13v=﹣26,求出v,把v=﹣2代入①求出u即可;(3)整理后①+②得出28x=35,求出x,②﹣①求出y即可.【解答】解:(1)2+7=5①3+=−2②由②得:n=﹣2﹣3m③,把③代入①得:2m+7(﹣2﹣3m)=5,解得:m=﹣1,把m=﹣1代入③得:n=1,所以原方程组的解是:=−1=1;(2)2−5=12①4+3=−2②②﹣①×2得:13v=﹣26,解得:v=﹣2,把v=﹣2代入①得:2u+10=12,解得:u=1,所以原方程组的解是:=1=−2;(3)整理得:14−6=21①14+6=14②,①+②得:28x=35,解得:x=54,②﹣①得:12y=﹣7,解得:y=−712,所以原方程组的解是:=54=−712.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.3.用加减法解下列方程组:(1)−=53+4=−1.2+=4;(2)−2=3【分析】(1)方程组利用加减消元法求出解即可;(2)方程组利用加减消元法求出解即可.【解答】解:(1)−=5①2+=4②,①+②得:3x =9,解得:x =3,把x =3代入①得:3﹣y =5,解得:y =﹣2,则方程组的解为=3=−2;(2)−2=3①3+4=−1②,①×2+②得:5x =5,解得:x =1,把x =1代入①得:1﹣2y =3,解得:y =﹣1,则方程组的解为=1=−1.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.4.用加减法解下列方程组:(1)4−3=11,2+=13;(2)−=3,2+3(−p =11【分析】(1)方程组利用加减消元法求出解即可;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)4−3=11①2+=13②,①+②×3得:10x =50,解得:x =5,把x =5代入①得:20﹣3y =11,解得:y =3,所以方程组的解为=5=3;(2)方程组整理得:−=3①3−=11②,②﹣①得:2x =8,解得:x =4,把x=4代入①得:4﹣y=3,解得:y=1,所以方程组的解为=4=1.【点评】此题考查了解二元一次方程组,解方程组利用了消元的思想,消元的方法有:代入消元法与加减消元法.5.用加减法解下列方程组:(1)3+2=76−2=11(2)2+=33+=4.【分析】各个方程组利用加减消元法求出解即可.【解答】解:(1)3+2=7①6−2=11②,①+②得:9μ=18,即μ=2,把μ=2代入①得:6+2t=7,解得:t=12,则方程组的解为=2=12;(2)2+=3①3+=4②,②﹣①得:a=1,把a=1代入①得:2+b=3,解得:b=1,则方程组的解为=1=1.【点评】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3−4=04+=8;(2+=3−32=−1.【分析】(1)方程组利用加减消元法求出解即可;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)3−4=0①4+=8②,①+②得:4y=8,解得:y=2,把y=2代入②得:4x+2=8,解得:x=32,则方程组的解为=32=2;(2)方程组整理得:2+=3①−3=−2②,①×3+②得:7x=7,解得:x=1,把x=1代入①得:2+y=3,解得:y=1,则方程组的解为=1=1.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法是代入消元法与加减消元法.7.(2022秋•陕西期末)用加减法解下列方程组:(1)−=33−8=14;(2+2=10=1+r13.【分析】(1)根据加减消元法解二元一次方程组即可求解;(2)将第二个方程去分母化简,然后根据加减消元法解二元一次方程组即可求解.【解答】解:(1)−=3①3−8=14②,①×3﹣②得:﹣3y+8y=9﹣14,解得:y=﹣1,将y=﹣1代入①得:x+1=3,解得:x=2,∴原方程组的解为:=2=−1;(2+2=10①=1+r13②,由②得3x=6+2(y+1),即3x﹣2y③,①﹣③得:4y=2,解得:=12,①+③得:6x=18,解得:x=3,∴原方程组的解为:=3=12.【点评】本题考查了加减消元法解二元一次方程组,掌握解二元一次方程组的方法是解题的关键.8.用加减法解下列方程组:(1)+3=,2(+1)−=6;(2)+=2800,96%+64%=2800×92%.【分析】(1)先用第二个方程减去第一个方程即可得到x 的值,然后将x 的值代入任意一个方程,解方程即可得到y 的值;(2)先对方程组进行化简可得+=2800①3+2=8050②,易得两个方程中y 的系数存在2倍关系,故只需用方程②减去方程①乘2的积即可得到关于x 的方程,解方程即可.【解答】解:(1)+3=,①2(+1)−=6.②②﹣①,得x ﹣1=6,∴x =7,x =7代入①得y =10,所以原方程组的解为=7=10.(2)原方程化简得+=2800,①3+2=8050.②②﹣①×2,得﹣x =﹣2450,∴x =2450,将x =2450代入①得:y =350,∴原方程组的解为:=2450=350.【点评】本题考查二元一次方程组的解法,利用正确的方法求解是本题的关键.9.用加减法解下列方程组:(1)−=5,①2+=4;②(2)−2=1,①+3=6;②(3)2−=5,①−1=12(2−1).②【分析】(1)利用加减消元法解答即可;(2)利用加减消元法解答即可;(3)利用加减消元法解答即可.【解答】解:(1)−=5①2+=4②,①+②得:3x=9,解得:x=3,把x=3代入①得:3﹣y=5,解得:y=﹣2,所以方程组的解为:=3=−2;(2)−2=1①+3=6②,②﹣①得:5y=5,解得:y=1,把y=1代入①得:x﹣2=1,解得:x=3,所以方程组的解为:=3=1;(3)2−=5①−1=12(2−1)②,由②得:2x﹣2y=1③,①﹣③得:y=4,把y=4代入①得:2x﹣4=5,解得:x=92,所以方程组的解为:=92=4.【点评】此题考查了解二元一次方程组,以及解一元一次方程,熟练掌握运算法则是解本题的关键.10.用加减法解下列方程组:(1)+3=62−3=3(2)7+8=−57−=4(3)−1=3(−2)+4=2(+1)(4+4=1−3=−1.【分析】各方程组整理后,利用加减消元法求出解即可.【解答】解:(1)+3=6①2−3=3②,①+②得:3x=9,即x=3,把x=3代入①得:y=1,则方程组的解为=3=1;(2)7+8=−5①7−=4②,①﹣②得:9y=﹣9,即y=﹣1,把y=﹣1代入①得:x=37,则方程组的解为=37=−1;(3)方程组整理得:3−=5①2−=2②,①﹣②得:x=3,把x=3代入①得:y=4,则方程组的解为=3=4;(4)方程组整理得:4+3=12①3−2=−6②,①×2+②×3得:17x=6,即x=617,①×3﹣②×4得:17y=60,即y=6017,则方程组的解为=617=6017.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2−5=14①3+5=16②(加减法).=−t(代入法);(2)2+3=9①【分析】(1)方程组利用代入消元法求出解即可;(2)方程组利用加减消元法求出解即可.【解答】解:(1)把②代入①得:2x+5x=14,解得:x=2,把x=2代入②,得:y=﹣2,则原方程组的解是=2=−2;(2)①×3得:6x+9y=27③,②×2得:6x+10y=32④,④﹣③得:y=5,把y=5代入①得:2x+15=9,解得:x=﹣3,则原方程组的解是=−3=5.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.2.(2022春•安岳县校级月考)解下列方程组:(1)3−=75+2=8(用代入法);(23=104=5(用加减法).【分析】(1)方程组利用代入消元法求出解即可;(2)方程组利用加减消元法求出解即可.【解答】解:(1)3−=7①5+2=8②,由①得:y=3x﹣7③,把③代入②得:5x+2(3x﹣7)=22,解得:x=2,把x=2代入①得:6﹣y=7,解得:y=﹣1,则方程组的解为=2=−1;(2)方程组整理得:3+4=120①4−3=60②,①×3+②×4得:25m=600,解得:m=24,把m=24代入①得:72+4n=120,解得:n=12,则方程组的解为=24=12.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.3.(2022春•大连期中)用指定的方法解下列方程组:(1)−3=42+=13(代入法);(2)5+2=4+4=−6(加减法).【分析】(1)利用代入法解方程组;(2)利用加减消元法解方程组.【解答】解:(1)−3=4①2+=13②,由①得x =3y +4③,把③代入②,得2(3y +4)+y =13,解得y =57,∴x =3×57+4=617,∴方程组的解为=617=57;(2)5+2=4①+4=−6②,①×2﹣②,得9x =14,解得x =149,把x =149代入②,得149+4y =﹣6,解得y =−179.∴方程组的解为=149=−179.【点评】本题考查了解二元一次方程组,做题的关键是掌握加减消元法,和代入消元法解二元一次方程组.4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5−=113+=7(代入消元法);(2)2−5=245+2=31(加减消元法).【分析】(1)由方程①,得b =5a ﹣11,再代入方程②求出未知数a ,进而得出未知数b ;(2)用方程①×2﹣②×5,可消去未知数y ,求出未知数x ,进而得出y 的值.【解答】解:(1)5−=11①3+=7②,由①,得b =5a ﹣11③,把③代入②,得3a +5a ﹣11=7,解得a =94,把a=94代入③,得b=14,故方程组的解为=94=14;(2)2−5=24①5+2=31②,①×2﹣②×5,得29x=203,解得x=7,把x=7代入①,得y=﹣2,故方程组的解为=7=−2.【点评】本题考查了解二元一次方程组,掌握加减消元法和代入消元法是解答本题的关键.5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2+3=11①=+3②(代入消元法);(2)3−2=2①4+=10②(加减消元法).【分析】(1)利用代入消元法进行求解即可;(2)利用加减消元法进行求解即可.【解答】解:(1)2+3=11①=+3②,把②代入①得:2(y+3)+3y=11,解得y=1,把y=1代入②得:x=1+3=4,故原方程组的解是:=4=1;(2)3−2=2①4+=10②,②×2得:8x+2y=20③,①+③得:11x=22,解得x=2,把x=2代入②得:8+y=10,解得y=2,故原方程组的解是:=2=2.【点评】本题主要考查解二元一次方程组,解答的关键是对解二元一次方程组的方法的掌握.6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)−2=22+3=12(代入法);(2)6−5=36+=−15(加减法).【分析】(1)整理后由①得出n =2m ﹣4③,把③代入②得出2m +3(2m ﹣4)=12,求出m ,再把m =3代入③求出n 即可;(2)②﹣①得出6t =﹣18,求出t ,再把t =﹣3代入①求出s 即可.【解答】解:(1)整理得:2−=4①2+3=12②,由①,得n =2m ﹣4③,把③代入②,得2m +3(2m ﹣4)=12,解得:m =3,把m =3代入③,得n =2×3﹣4=6﹣4=2,所以原方程组的解是=3=2;(2)6−5=3①6+=−15②,②﹣①,得6t =﹣18,解得:t =﹣3,把t =﹣3代入①,得6s +15=3,解得:s =﹣2,所以原方程组的解是=−2=−3.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键,解二元一次方程组的方法有代入消元法和加减消元法两种.7.(2022春•泰安期中)用指定的方法解下列方程组(1)3+4=19−=4(代入消元法);(2)2+3=−53−2=12(加减消元法);(3−9)=6(−2)r13=2.【分析】(1)方程组利用代入消元法求出解即可;(2)方程组利用加减消元法求出解即可;(3)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)3+4=19①−=4②,由②得:x =y +4③,把③代入①得:3(y +4)+4y =19,解得:y=1,把y=1代入③得:x=1+4=5,则方程组的解为=5=1;(2)2+3=−5①3−2=12②,①×2+②×3得:13x=26,解得:x=2,把x=2代入①得:4+3y=﹣5,解得:y=﹣3,则方程组的解为=2=−3;(3)方程组整理得:5−6=33①3−4=28②,①×2﹣②×3得:x=﹣18,把x=﹣18代入①得:﹣90﹣6y=33,解得:y=−412,则方程组的解为=−18=−412.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3+2=143+4=17.(加减法)=+3;(代入法)(2)2+3=12【分析】(1)用代入消元法解方程组即可;(2)用加减消元法解方程组即可.【解答】解:(1)3+2=14①=+3②,将②代入①,得3y+9+2y=14,解得y=1,将y=1代入②得x=4,∴方程组的解为=4=1;(2)2+3=12①3+4=17②,①×3得,6x+9y=36③,②×2得,6x+8y=34④,③﹣④,得y=2,将y=2代入①得,x=3,∴方程组的解为=3=2.【点评】本题考查二元一次方程组的解,熟练掌握代入消元法和加减消元法解二元一次方程组的方法是解题的关键.9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)=2−33+2=8(代入法);(2)3+4=165−6=33(加减法).【分析】(1)把①代入②得出x的值,再把x的值代入①求出y的值,从而得出方程组的解;(2)①×3+②×2得出19x=114,求出x,把x=6代入①求出y即可.【解答】解:(1)=2−3①3+2=8②,把①代入②得:3x+2(2x﹣3)=8,解得:x=2,把x=2代入①得:y=1,则原方程组的解是:=2=1.(2)3+4=16①5−6=33②,①×3+②×2得:19x=114,解得:x=6,把x=6代入①得:18+4y=16,解得:y=−12,所以方程组的解=6=−12.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.10.用指定的方法解下列方程组:(1)3+4=19−=4(代入法);(2)2+3=−53−2=12(加减法).【分析】(1)由②得出x=4+y③,把③代入①得出3(4+y)+4y=19,求出y,把y =1代入③求出x即可;(2)①×2+②×3得出13x=26,求出x,把x=2代入①求出y即可.【解答】解:(1)3+4=19①−=4②,由②得:x=4+y③,把③代入①得:3(4+y)+4y=19,解得:y=1,把y=1代入③得:x=4+1=5,所以方程组的解是=5=1;(2)2+3=−5①3−2=12②,①×2+②×3得:13x=26,解得:x=2,把x=2代入①得:4+3y=﹣5,解得:y=﹣3,所以方程组的解=2=−3.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.1.(2022•苏州模拟)用适当的方法解下列方程组.(1)+2=9−3=1;(2−34=1−p−(−4p=4.【分析】(1)利用加减消元法,方程组可化为:7y=28,解得:y=4,将y=4代入①得:x=1;(2)先将方程组化为:8−9=12①8−5=4②,利用加减消元法解得:y=﹣2,将y=﹣2代入①得:=−34.【解答】解:(1)+2=9①−3=1②①×3+②得:7y=28,解得:y=4,将y=4代入①得:x=1,即方程的解为:=1=4;(2)原方程组可化为:8−9=12①8−5=4②,①﹣②得:﹣4y=8,解得:y=﹣2,将y=﹣2代入①得:=−34,即方程的解为:=−34=−2.【点评】本题主要考查的是二元一次方程组的解法,利用合适的方法解方程组即可.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)=2−14+3=7;(2)3+2=22+3=28,.【分析】(1)方程组利用代入消元法求解即可;(2)用方程①×3﹣②×2,可消去未知数y,求出未知数x,进而得出y的值.【解答】解:(1)=2−1①4+3=7②,把①代入②,得4(2y﹣1)+3y=7,解得y=1,把y=1代入①,得x=1,故原方程组的解为=1=1;(2)3+2=2①2+3=28②,①×3﹣②×2,得5x=﹣50,解得x=﹣10,把x=﹣10代入①,得y=16,故原方程组的解为=−10=16.【点评】本题考查了解二元一次方程组,掌握加减消元法和代入消元法是解答本题的关键.3.用适当的方法解下列方程组:(1)+2=0,3+4=6;(2=21)−=11(3)+0.4=40,0.5+0.7=35;(4K4=−14,5(r1)12=2.【分析】(1)由x+2y=0可用y表示x,利用代入消元法求第一个方程组的解.同理解(2)(3)利用加减消元法求方程组的解.(4)对于关于m、n的方程,将其化为整系数方程时,给第一个方程两边同时乘12,给第二个方程两边同时乘12.利用加减消元法求方程组的解.【解答】解:(1)+2=0,①3+4=6;②由①,得x=﹣2y,③把③代入②,得﹣6y+4y=6,解得y=﹣3,把y=﹣3代入①,得x=6.∴原方程组的解为=6=−3;(2=2s1)−=11②由①,得x+1=6y,③把③代入②,得12y﹣y=11,解得y=1.把y=1代入③,得x+1=6,解得x=5.∴原方程组的解为=5=1;(3)+0.4=40,①0.5+0.7=35;②②×2,得x+1.4y=70,③③﹣①,得y=30.把y=30代入①,得x+0.4×30=40,解得x=28.∴原方程组的解为=28=30;(4K4=−14,5(r1)12=2,原方程组化为:+7=−3,①2−5=13,②,①×2﹣②,得19n=﹣19,解得n=﹣1.把n=﹣1代入①,得m﹣7=﹣3,解得m=4.∴原方程组的解为=4=−1.【点评】此题主要考查了解二元一次方程组的方法,灵活运用代入消元法和加减消元法是解题的关键.4.(2022•天津模拟)用适当的方法解下列方程组:(1)+=52−=4;(2=r24−K33=112.【分析】(1)应用代入消元法,求出方程组的解即可.(2)应用加减消元法,求出方程组的解即可.【解答】解:(1)+=5①2−=4②,由①,可得:x=5﹣y③,③代入②,可得:2(5﹣y)﹣y=4,解得y=2,把y=2代入③,可得:x=5﹣2=3,∴原方程组的解是=3=2.(2=r24①−K33=112②,由①,可得:4x﹣3y=2③,由②,可得:3x﹣4y=﹣2④,③×4﹣④×3,可得7x=14,解得x=2,把x=2代入③,可得:4×2﹣3y=2,解得y=2,∴原方程组的解是=2=2.【点评】此题主要考查了解二元一次方程组的方法,注意代入消元法和加减消元法的应用.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2−3=7−3=7.(2)0.3+0.4=40.2+2=0.9.【分析】(1)利用加减法消元法解二元一次方程组即可;(2)先整理方程,再利用加减消元法解二元一次方程组即可.【解答】解:(1)2−3=7①−3=7②,①﹣②得x =0,把x =0代入②得0﹣3y =7,解得y =−73,∴方程组的解为=0=−73;(2)整理原方程组得3+4=40①2−9=−20②,①×2﹣②×3得35q =140,q =4,把q =4代入②得2p ﹣36=﹣20,解得p =8,∴方程组的解为=8=4.【点评】本题考查了解二元一次方程组,做题关键是掌握加减消元法和代入消元法解二元一次方程组.6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)+=52+=8;(2)2+3=73−2=4.【分析】(1)应用代入消元法,求出方程组的解是多少即可.(2)应用加减消元法,求出方程组的解是多少即可.【解答】解:(1)+=5①2+=8②,由①,可得:x =5﹣y ③,③代入②,可得:2(5﹣y )+y =8,解得y =2,把y =2代入③,解得x =3,∴原方程组的解是=3=2.(2)2+3=7①3−2=4②,①×2+②×3,可得13x=26,解得x=2,把x=2代入①,解得y=1,∴原方程组的解是=2=1.【点评】此题主要考查了解二元一次方程组的方法,注意代入消元法和加减消元法的应用.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)+2=93−2=−1(2)2−=53+4=2【分析】(1)利用加减消元法进行求解即可;(2)利用加减消元法进行求解即可.【解答】解:(1)+2=9①3−2=−1②,①+②得:4x=8,解得:x=2,把x=2代入①得:2+2y=9,解得:y=72,故原方程组的解是:=2=72;(2)2−=5①3+4=2②,①×4得:8x﹣4y=20③,②+③得:11x=22,解得:x=2,把x=2代入①得:4﹣y=5,解得:y=﹣1,故原方程组的解是:=2=−1.【点评】本题主要考查解二元一次方程组,解答的关键是熟练掌握解二元一次方程组的方法.8.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2+3=16①+4=13②;(2)2r3=3K28=3.【分析】(1)②×2﹣①得出5y=10,求出y,再把y=2代入②求出x即可;(2)整理后得出得2+=9①3−2=24②,①×2+②得出7s=42,求出s,再把s=6代入①求出t即可.【解答】解:(1)2+3=16①+4=13②,②×2﹣①,得5y=10,解得:y=2,把y=2代入②,得x+8=13,解得:x=5,所以方程组的解为=5=2;(2)整理方程组,得2+=9①3−2=24②,①×2+②,得7s=42,解得:s=6,把s=6代入①,得12+t=9,解得:t=﹣3,所以方程组的解为=6=−3.【点评】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)=2−1+2=−7(2+3=7+2=8【分析】(1)用代入消元解二元一次方程组即可;(2)用加减消元解二元一次方程组即可;【解答】解:(1)=2−1①+2=−7②,把①代入②得,x+2(2x﹣1)=﹣7,解得x=﹣1,将x=﹣1代入①得y=﹣3,∴方程组的解为=−1=−3.(2)整理得3+4=84①2+3=48②,①×2﹣②×3得,﹣y=24,解得y=﹣24,将y=﹣24代入②得x=60,∴方程组的解为=60=−24.【点评】本题考查二元一次方程组的解,熟练掌握加减消元法和代入消元法解二元一次方程组是解题的关键.10.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3+2=9−=8;(2=r25=7.【分析】(1)由②可得x=8+y③,再把③代入①,可得y的值,然后把y的值代入③求出x的值即可;(2)方程组整理后可得+5=0①2−5=7②,利用①+②可得x的值,然后把x的值代入①求出y的值即可.【解答】解:(1)3+2=9①−=8②,由②得,x=8+y③,将③代入①得,3(8+y)+2y=9,解得,y=﹣3,把y=﹣3代入③得,x=5,则方程组的解为=5=−3;(2)方程组整理得:+5=0①2−5=7②,①+②得:3x=7,解得:x=73,把x=73代入①得:y=−715,则方程组的解为=73=−715.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.1.先阅读材料,然后解方程组:材料:解方程组+=4①3(+p+=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以=2=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组−−1=0①4(−p−=5②.【分析】根据阅读材料中的方法求出方程组的解即可.【解答】解:由①得:x﹣y=1③,把③代入②得:4﹣y=5,即y=﹣1,把y=﹣1代入③得:x=0,则方程组的解为=0=−1.【点评】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.2.(2021秋•乐平市期末)解方程组3−2=8⋯⋯⋯①3(3−2p+4=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得=2=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2−3=123(2−3p+5=26.【分析】利用整体代入法的求解方法进行解答即可.【解答】解:2−3=12①3(2−3p+5=26②,把①代入②得:3×12+5y=26,解得y=﹣2,把y=﹣2代入①得:2x+6=12,解得x =3,故原方程组的解是:=3=−2.【点评】本题主要考查解二元一次方程组,解答的关键是对解二元一次方程组的方法的掌握与运用.3.先阅读,然后解方程组.解方程组−−1=0①4(−p −=5②时,可由①得x ﹣y =1.③,然后再将③代入②得4×1﹣y =5,求得y =﹣1,从而进一步求得=0=−1这种方法被称为“整体代入法”,请用这5=0=2+1.【分析】利用整体代入法解方程组即可.5=0①=2+1②,由①得,2x ﹣3y =﹣5,③,把③代入②得,10+37=2y +1,解得,y =37,把y =37代入③得,x =−137,则方程组的解为:=−137=37.【点评】本题考查的是二元一次方程组的解法,掌握整体代入法解方程组的一般步骤是解题的关键.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组−−1=0①4(−p −=5②时,可由①得x ﹣y =1,③然后再将③代入②得4×1﹣y =5,求得y =﹣1,从而进一步求得=0①=−1②这种方法被称为“整体代入法”,2=02=9.【分析】仿照所给的题例先把①变形,再代入②中求出y 的值,进一步求出方程组的解即可.2=0①+2=9②,由①得,2x﹣3y=2③,代入②得2+57+2y=9,解得y=4,把y=4代入③得,2x﹣3×4=2,解得x=7.故原方程组的解为=7=4.【点评】本题考查的是在解二元一次方程组时整体思想的应用,利用整体思想可简化计算.5.先阅读,然后解方程组.解方程组−−1=0①4(−p−=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2−3−2=03(2−3p+=7.【分析】把2x﹣3y看作一个整体,代入第二个方程求出y的值,进而求出x的值即可.【解答】解:2−3−2=0①3(2−3p+=7②,把①变形得:2x﹣3y=2③,③代入②得:6+y=7,即y=1,把y=1代入③得:x=2.5,则方程组的解为=2.5=1.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元方法与加减消元法.1.用换元法解下列方程组+2=12−1=34【分析】方程组利用换元法求出解即可.【解答】解:设1=a,1=b,方程组变形为2+2=12①5−=34②,①+②×2得:12a=2,解得:a=16,把a=16代入②得:b=112,则方程组的解为=16=112,即=6=12.【点评】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.2.用换元法解下列方程组:(1)3(p+2(−p=36(−4(−p=−16(2+r53=2−(+5p=5.【分析】(1)令x+y=m、x﹣y=n得关于m、n的方程组,解得m、n的值,从而可得关于x、y的方程组,求解可得;(2)令x﹣4y=a、x+5y=b得关于a、b的方程组,解该方程组可得a、b的值,从而可得关于x、y的方程组,求解可得.【解答】解:(1)令x+y=m,x﹣y=n,则原方程组可化为:3+2=36−4=−16,解得:=8=6,即+=8−=6,解得:=7=1;(2)令x﹣4y=a,x+5y=b,+3=2−=5,解得:=6=−3,即:−4=6+5=−3,解得:=2=−1.【点评】本题主要考查换元法解方程组的能力,熟练而准确地解方程组是基础,正确找到共同的整体加以换元是关键.3.(2022春•云阳县期中)阅读探索:解方程组(−1)+2(+2)=62(−1)+(+2)=6解:设a﹣1=x,b+2=y原方程组可以化为+2=62+=6,解得=2=2,即:−1=2+2=2∴=3=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(4−1)+2(5+2)=102(4−1)+(5+2)=11;(2)能力运用已知关于x,y的方程组1+1=12+2=2的解为=6=7,求关于m、n的方程组1(−2)+1(+3)=12(−2)+2(+3)=2的解.【分析】(1)仿照“阅读探索“的思路,利用换元法进行计算即可解答;(2)仿照“阅读探索“的思路,利用换元法进行计算即可解答.【解答】解:(1)设4−1=x,5+2=y,∴原方程组可变为:+2=102+=11,解这个方程组得:=4=3,−1=45+2=3,所以:=20=5;(2)设−2=+3=,可得:−2=6+3=7,解得:=8=4.【点评】本题考查了解二元一次方程组,二元一次方程组的解,理解并掌握例题的换元法是解题的关键.4.在学过了二元一次方程组的解法后,+K10=3①−K10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8+2=90③2+8=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即=13=−7小刚:设r6=m,K10=n,则+=3③−=−1④③+④得m=1,③﹣④得m=2,=1=2,所以+=6−=20,所以=13=−7.小芳:①+②得2(rp6=2,即x+y=6.③①﹣②得2(Kp10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y=﹣7,即=13=−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2r37=1−2r37=5.【分析】设3K26=m,2r37=n,方程组整理后求出m与n的值,即可确定出x与y 的值.【解答】解:设3K26=m,2r37=n,方程组整理得:+=1①−=5②,①+②得:2m=6,即m=3,①﹣②得:2n=﹣4,即n=﹣2,=32r3=−2,整理得:3−2=182+3=−14,解得:=2=−6.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(−1)+2(+2)=62(−1)+(+2)=6.解:设a﹣1=x,b+2=y.原方程组可变为+2=62+=6,解这个方程组得=2=2,即−1=2+2=2,所以=3=0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(3−1)+2(5+2)=43(3−1)−(5+2)=5.(3)能力运用已知关于x,y的方程组1+1=12+2=2的解为=3=4,请直接写出关于m、n的方程组1(+2)−1=12(+2)−2=2的解是.【分析】(2)仿照(1)的思路,利用换元法进行计算即可解答;(3)仿照前两个题的思路,利用换元法进行计算即可解答.【解答】解:(2)设3−1=x,5+2=y,∴原方程组可变为:+2=43−=5,解这个方程组得:=2=1,−1=25+2=1,所以:=9=−5;(3)设+2=−=,可得:+2=3−=4,解得:=1=−4.。
小学上册第九次英语第三单元真题

小学上册英语第三单元真题英语试题一、综合题(本题有100小题,每小题1分,共100分.每小题不选、错误,均不给分)1.The ________ was a key document in the founding of modern democracy.2.What is the name of the famous Chinese philosopher?A. ConfuciusB. LaoziC. Sun TzuD. ZhuangziA3.The ______ (彩色的) flowers attract attention.4. A _____ is a place where animals live in the wild.5.What is the capital of Lithuania?A. VilniusB. KaunasC. KlaipedaD. ŠiauliaiA6.What is the term for a scientist who studies plants?A. BotanistB. ZoologistC. MicrobiologistD. EcologistA7.What is the largest mammal in the ocean?A. SharkB. DolphinC. Blue whaleD. Octopus答案:C8.The __________ (沿海城市) is lively and busy.9.The ________ (果树) in our yard gives us delicious apples every fall.10.What do you call the art of making paper flowers?A. OrigamiB. QuillingC. PapercraftD. Floral DesignA11.What is the name of the famous waterfall in Africa?A. Niagara FallsB. Angel FallsC. Victoria FallsD. IguazuFallsC Victoria Falls12.The _____ (海马) is a unique fish that swims upright. 海马是一种独特的鱼,以直立姿势游泳。
太平湖镇中心学校2018-2019学年三年级下学期数学期中模拟试卷含解析

太平湖镇中心学校2018-2019学年三年级下学期数学期中模拟试卷含解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题1.(2分)边长是1米的正方形,面积是1平方米;边长是5米的正方形,面积是()平方米。
A. 5B. 20C. 25【答案】C【考点】正方形的面积【解析】【解答】解:边长是5米的正方形,面积是5×5=25平方米。
故答案为:C。
【分析】正方形的面积=边长×边长。
2.(2分)下面算式和 25 × 18 不相等的是()。
A. 25×2×9B. 25×10×8C. 18×5×5【答案】B【考点】两位数乘两位数【解析】【解答】根据分析可知,和25 × 18 不相等的是25×10×8.故答案为:B.【分析】计算25×18,可以把18分成2×9的形式,也可以把25分成5×5的形式,然后用乘法结合律计算,据此解答.3.(2分)2016年是闰年,下面年份中序号是()的是闰年。
A. 1986B. 2020C. 2014【答案】B【考点】平年、闰年的判断方法【解析】【解答】解:A、1986÷4=496……2,是平年;B、2020÷4=505,是闰年;C、2014÷4=503……2,是平年.故答案为:B【分析】用年份除以4(整百年份除以400),如果没有余数,这一年就是闰年,如果有余数,这一年就是平年.4.(2分)气象站在一天的3点、7点、14点、20点测得的气温分别是8℃、15℃、24℃、17℃,求这天的平均气温。
正确的列式是()。
A. (8+15+24+17)÷4B. (8+15+24+17)÷(3+7+14+20)【答案】A【考点】平均数的初步认识及计算【解析】【解答】解:根据求平均数的含义列式:(8+15+24+17)÷4故答案为:A【分析】平均数=总数÷总份数,因此用四个时段的温度总和除以4即可求出这天的平均气温。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
深圳朗钛提供
50%吡蚜酮水分散粒剂配方、助剂
近一段时间以来,很多客户反映大部分厂家的吡蚜酮原药质量有明显变化,生产50%吡蚜酮水分散粒剂时悬浮率低,造粒时发粘,粒子崩解性差,稀释后有不能分散的残渣等问题,严重影响产品质量。
深圳朗钛公司针对客户和市场的需求,经过上百次试验,对助剂和填料反复筛选,终于成功研制出50%吡蚜酮水分散粒剂,已经提供配方和助剂给生产企业用于工业化生产,目前已成功生产数百吨供应市场,各项指标优异。
该配方适应国内大部分企业的原药,制剂的pH值、水分满足指标要求,崩解快,悬浮率高达95%以上,稀释后没有残渣,不堵塞喷头。
50%吡蚜酮水分散粒剂部分指标(实际生产指标):
崩解时间:<70 秒;悬浮率:≥95%;水分:≤3%;PH:5--8
欢迎有需要的客户来电索取样品和助剂,免费提供配方!。
