2019年广西柳州市中考数学专题训练02:多结论题(含答案)
2019年柳州市数学中考试题含答案

2019年柳州市初中学业水平考试与高中阶段学校招生考试时间:120分钟 满分:120分 第Ⅰ卷(选择题 共36分)一、选择题(共12小题,每小题3分,计36分.每小题只有一个选项是符合题意的)1. 据CCTV 新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为( ) A. 0.1044×106辆 B. 1.044×106辆 C. 1.044×105辆 D. 10.44×104辆2. 如图,这是一个机械零部件,该零部件的左视图是( )第2题图3. 下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )4. 计算:x (x 2-1)=( )A. x 3-1B. x 3-xC. x 3+xD. x 2-x 5. 反比例函数y =2x的图象位于( )A. 第一、三象限B. 第二、三象限C. 第一、二象限D. 第二、四象限 6. 如图,A ,B ,C ,D 是ⅠO 上的点,则图中与ⅠA 相等的角是( ) A. ⅠB B. ⅠC C. ⅠDEB D. ⅠD第6题图 第7题图7. 如图,在▱ABCD 中,全等三角形的对数共有( )A. 2对B. 3对C. 4对D. 5对 阅读【资料】 完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004-2018年中美两国国内生产总值(GDP )的直方图及发展趋势线.(注:趋势线由Excel 系统根据数据自动生成,趋势线中的y 表示GDP ,x 表示年数)2004-2018年中美两国国内生产总值(GDP ,单位:万亿美元)直方图及发展趋势线8. 依据【资料】中所提供的信息,2016—2018年中国GDP 的平均值大约是( ) A. 12.30 B. 14.19 C. 19.57 D. 19.719. 依据【资料】中所提供的信息,可以推算出中国的GDP 要超过美国,至少要到( ) A. 2052年 B. 2038年 C. 2037年 D. 2034年10. 已知A 、B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),则y 关于x 的函数解析式是( )A. y =4x (x ≥0)B. y =4x -3(x ≥34)C. y =3-4x (x ≥0)D. y =3-4x (0≤x ≤34)11. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )A.1325 B. 1225 C. 425 D. 12第11题图12. 定义:形如a +bi 的数称为复数(其中a 和b 为实数,i 为虚数单位,规定i 2=-1),a 称为复数的实部,b 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i )2=12+2×1×3i +(3i )2=1+6i +9i 2=1+6i -9=-8+6i ,因此,(1+3i )2的实部是-8,虚部是6.已知复数(3-mi )2的虚部是12,则实部是( )A. -6B. 6C. 5D. -5第Ⅰ卷(非选择题 共84分)二、填空题(共6小题,每小题3分,计18分) 13. 计算:7x -4x =________.14. 如图,若AB ⅠCD ,则在图中所标注的角中,一定相等的角是________.第14题图15. 柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是________(结果精确到0.01). 16. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为________. 17. 如图,在ⅠABC 中,sinB =13,tanC =22,AB =3,则AC 的长为________.第17题图18. 已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是________.三、解答题(共8小题,计66分.解答时应写出过程) 19. (本题满分6分) 计算:22+|-3|-4+π0.20. (本题满分6分) 已知:ⅠAO B.求作:ⅠA ′O ′B ′,使得ⅠA ′O ′B ′=ⅠAO B. 作法:Ⅰ以O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ; Ⅰ画一条射线O ′A ′,以点O ′为圆心,OC 长为半径画弧,交O ′A ′于点C ′; Ⅰ以点C ′为圆心,CD 长为半径画弧,与第Ⅰ步中所画的弧相交于点D ′; Ⅰ过点D ′画射线O ′B ′,则ⅠA ′O ′B ′=ⅠAO B. 根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出ⅠA ′O ′B ′(请保留作图痕迹);(2)完成下面证明ⅠA ′O ′B ′=ⅠAOB 的过程(注:括号里填写推理的依据). 证明:由作法可知O ′C ′=OC ,O ′D ′=OD ,D ′C ′=________.ⅠⅠC′O′D′ⅠⅠCOD.(________)ⅠⅠA′O′B′=ⅠAO B.(________)第20题图21. (本题满分8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)第21题图22. (本题满分8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=B C.求证:四边形ABCD是平行四边形.第22题图23. (本题满分8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元.已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24. (本题满分10分)如图,直线AB 与x 轴交于点A (1,0),与y 轴交于点B (0,2),将线段AB 绕点A 顺时针旋转90°得到线段AC ,反比例函数y =kx(k ≠0,x >0)的图象经过点C.(1)求直线AB 和反比例函数y =kx(k ≠0,x >0)的解析式;(2)已知点P 是反比例函数y =kx(k ≠0,x >0)图象上的一个动点,求点P 到直线AB 距离最短时的坐标.第24题图25. (本题满分10分)如图,AB 是ⅠO 的直径,弦CD ⅠAB 于点E ,点F 是ⅠO 上一点,且AC ︵=CF ︵,连接FB ,FD ,FD 交AB 于点N .(1)若AE =1,CD =6,求ⅠO 的半径; (2)求证:ⅠBNF 为等腰三角形;(3)连接FC 并延长,交BA 的延长线于点P ,过点D 作ⅠO 的切线,交BA 的延长线于点M .求证:ON ·OP =OE ·OM .第25题图26. (本题满分10分)如图,直线y =x -3交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线y =ax 2+bx +c (a ≠0)经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线y =x -3上的一个动点.(1)求抛物线的解析式; (2)求ⅠBDP 周长的最小值;(3)若动点P 与点C 不重合,点Q 为ⅠF 上的任意一点,当PQ 的最大值等于32CE 时,过P ,Q 两点的直线与抛物线交于M ,N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.第26题图2019年柳州市初中学业水平考试与高中阶段学校招生考试一、选择题1. C 【解析】将一个大于10的数用科学记数法表示,其形式为a ×10n ,其中1≤a <10,n 为原数整数位数减1.故104400=1.044×105.2. C 【解析】从左面看到的图形是一个矩形,里面有一个圆,必须C 符合.3. D 【解析】A 、B 、C 、D 四个选项中只有D 项的图形沿着一条直线折叠,直线两旁的部分能够完全重合,故选D.4. B 【解析】x (x 2-1)=x 3-x .5. A 【解析】反比例函数y =2x ,k =2>0,所以其图象位于第一、三象限,故选A.6. D 【解析】在ⅠO 中,ⅠⅠA 与ⅠD 都是BC ︵所对的圆周角,ⅠⅠA =ⅠD .7. C 【解析】ⅠABD ⅠⅠCDB ,ⅠADO ⅠⅠCBO ,ⅠAOB ⅠⅠCOD ,ⅠABC ⅠⅠCDA ,共4对全等三角形. 8. A 【解析】依据【资料】中所提供的信息,2016、2017、2018年中国GDP 的值分别为11.19万亿美元、12.24万亿美元、13.46万亿美元,2016-2018年中国GDP 的平均值为11.19+12.24+13.463≈12.30万亿美元.9. B 【解析】依据【资料】中所提供的信息,要使中国的GDP 超过美国,则0.468+0.86x >11.778+0.53x ,解得x >37711≈34.3,要使中国的GDP 超过美国至少要到2003+35=2038年. 10. D 【解析】ⅠA 、B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),Ⅰy =3-4x ,其中⎩⎪⎨⎪⎧3-4x ≥0x ≥0,解得0≤x ≤34.11. A 【解析】画树状图如解图:第11题解图共有25种情况,其中和为偶数的有13种,P (小李获胜)=1325.12. C 【解析】根据复数及其各部的名称、四则运算的定义,(3-mi )2=9-m 2-6mi ,Ⅰ(3-mi )2的虚部是12,Ⅰ-6m =12,解得m =-2. Ⅰ(3-mi )2的实部为9-m 2=9-4=5. 二、填空题13. 3x 【解析】7x -4x =(7-4)x =3x .14. Ⅰ1=Ⅰ3 【解析】ⅠAB ⅠCD ,ⅠⅠ1=Ⅰ3(两直线平行,同位角相等).15. 0.95 【解析】经大量实验,频率稳定在0.95,所以这种植物种子在该实验条件下发芽的概率约是0.95.16. 52 【解析】如解图,四边形ABCD 为正方形,BD 为ⅠO 的直径,OA 为半径,则OA =OB =5,OA ⅠOB ,ⅠAB =OA 2+OB 2=52+52=5 2.第16题解图17. 3 【解析】如解图,过点A 作AD ⅠBC 交BC 于点D . ⅠAB =3,sinB =AD AB =13,ⅠAD 3=13,即AD =1. ⅠtanC =AD DC =22,Ⅰ1DC =22,解得DC = 2.ⅠAC =AD 2+DC 2=12+(2)2= 3.第17题解图18. 7 【解析】剩下的两个数的和为5×8-9-8-8=15,其中一个设为x ,则另一个数为15-x ,则15[(8-8)2+(8-8)2+(9-8)2+(x -8)2+(15-x -8)2]=0.4,解得x =7或8.当x =7时,另一个数为15-7=8;当x =8时,另一个数为15-8=7,所以这5个数为7,8,8,8,9,中位数是8,符合题意,所以最小的数是7.三、解答题19. 解:原式=4+3-2+1(4分) =6.(6分)20. 解:(1)如解图所示,ⅠA ′O ′B ′即为所求;第20题解图 (3分)(2)DC ;(4分) SSS ;(5分)全等三角形的对应角相等.(6分)21. 解:(1)42557×45%=19150.65(亿元),(3分)答:义务教育段的经费投入应该是19150.65亿元;(4分) (2)42557(1+9.43%)≈38889.7(亿元),(7分) 答:2016年全国教育经费总投入约为38889.7亿元 .(8分) 22. 证明:如解图,连接BD , 在ⅠABD 与ⅠCDB 中, ⎩⎪⎨⎪⎧AB =CD ,AD =CB ,BD =DB ,ⅠⅠABD ⅠⅠCDB (SSS ).(4分) ⅠⅠ1=Ⅰ2,Ⅰ3=Ⅰ4.(6分) ⅠAB ⅠCD ,AD ⅠB C.Ⅰ四边形ABCD 是平行四边形.(8分)第22题解图23. 解:(1)设大本作业本每本x 元,小本作业本每本(x -0.3)元, 则有8x =5x -0.3,解得x =0.8,(2分)经检验x =0.8是分式方程的根,(3分)答:大本作业本每本0.8元,小本作业本每本0.8-0.3=0.5元;(4分) (2)设大本作业本最多能购买x 本,则小本作业本的数量是2x 本, 则有0.5×2x +0.8x ≤15,(6分) 解得x ≤253.(7分)答:大本作业本最多能购买8本.(8分)24. 解:(1)【思维教练】过点C 作CD Ⅰx 轴于点D ,要求反比例函数的解析式,只需知道其上的一点的坐标,由图形可知,只需求出点C 的坐标,要求点C 的坐标只需求出AD ,CD 的长,而这可由ⅠBAO ⅠⅠACD 证明得到;如解图,过点C 作CD Ⅰx 轴于点D , ⅠⅠCAD +ⅠACD =90°.Ⅰ将线段AB 绕点A 顺时针旋转90°得到线段AC , ⅠAB =AC ,AB ⅠA C. ⅠⅠBAO +ⅠCAD =90°, ⅠⅠBAO =ⅠACD .又ⅠⅠBOA =ⅠADC =90°,ⅠⅠBAO ⅠⅠACD (AAS )(2分)ⅠAD =OB ,OA =CDⅠA (1,0),B (0,2),ⅠOB =2,OA =1,ⅠAD =OB =2, CD =OA =1.ⅠC (3,1).(3分)Ⅰ点C 在反比例函数y =k x(k ≠0,x >0)图象上, Ⅰ1=k 3,解得k =3. Ⅰ反比例函数的解析式为y =3x(x >0).(4分) Ⅰ点B (0,2),Ⅰ直线AB 的解析式为y =kx +2;(5分)Ⅰ点A (1,0)在直线AB 上,Ⅰk +2=0,即k =-2.Ⅰ直线AB 的解析式为y =-2x +2;(6分)第24题解图(2)【思维教练】要在反比例函数图象上找一点,使其到已知直线的距离最短,这个点在平行于已知直线的直线上,当距离最短时,这条直线与反比例函数只有一个交点;设过点P 与AB 平行的直线的解析式为y =-2x +b ,Ⅰ当它与反比例函数只有一个交点时,此交点到AB 的距离最短.Ⅰ方程-2x +b =3x(x >0),只有一个实数根且b >0,(7分) 方程-2x +b =3x可化为2x 2-bx +3=0, 则b 2-4×2×3=0,解得b =26(负值已舍去),(8分)此时-2x +26=3x (x >0),有唯一解,x =62,Ⅰy =6,(9分) Ⅰ点P 的坐标为(62,6)时到AB 的距离最短.(10分) 25. (1)解:如解图Ⅰ,连接OC ,设ⅠO 的半径为r ,ⅠAB 是ⅠO 的直径,弦CD ⅠAB 于点E ,Ⅰ直线AB 垂直平分CD .ⅠCD =6,ⅠCE =3.ⅠAE =1,ⅠOE =r -1.在Rt ⅠCEO 中,ⅠOE 2+CE 2=OC 2,Ⅰ(r -1)2+32=r 2,解得r =5;ⅠⅠO 的半径为5;(3分)第25题解图Ⅰ(2)证明:如解图Ⅰ,连接AF ,ⅠAB 为ⅠO 直径,ⅠⅠ3+Ⅰ1=90°.Ⅰ弦CD ⅠAB ,ⅠAC ︵=AD ︵,ⅠCDF +ⅠDNE =90°.(4分)又ⅠAC ︵=CF ︵,ⅠCF ︵=AD ︵,ⅠⅠ3=ⅠCDF ,ⅠⅠCDF +Ⅰ1=90°.ⅠⅠ1=ⅠDNE ,而ⅠDNE =Ⅰ2,ⅠⅠ1=Ⅰ2,ⅠⅠBNF 是等腰三角形;(6分)第25题解图Ⅰ(3)证明:如解图Ⅰ,连接PD ,OD ,ⅠDM 是切线,ⅠOD ⅠDM ,ⅠⅠDMO +ⅠEOD =90°.ⅠCD ⅠAB ,ⅠⅠEDO +ⅠEOD =90°,ⅠⅠEDO =ⅠDMO .(7分)ⅠⅠEOD =ⅠEOD ,ⅠⅠODE ⅠⅠOMD ,ⅠOD OM =OE OD, 即OD 2=OE ·OM .(8分)ⅠAB 垂直平分CD ,ⅠⅠOPF =ⅠOPD ,ⅠDOA =ⅠDF C.又ⅠⅠDNO =ⅠFNP ,ⅠⅠODN =ⅠOPF .ⅠⅠODN =ⅠOPD .ⅠⅠNOD =ⅠDOP ,ⅠODN =ⅠOPD ,ⅠⅠODN ⅠⅠOPD .(9分)ⅠOD ON =OP OD, ⅠOD 2=ON ·OP ,ⅠON ·OP =OE ·OM .(10分)第25题解图Ⅰ26. (1)解:Ⅰ直线y =x -3交x 轴于点A ,交y 轴于点C ,ⅠA (3,0),C (0,-3).ⅠA 、B 两点为抛物线与x 轴的两个交点,点B 的坐标为(1,0),Ⅰ抛物线的解析式可设为y =a (x -3)(x -1).ⅠC (0,-3)在抛物线的图象上,Ⅰ-3=a (0-3)(0-1),解得a =-1,Ⅰ抛物线的解析式为y =-(x -3)(x -1)=-x 2+4x -3;(3分)(2)如解图Ⅰ,连接BD ,作点D 关于直线AC 对称点D ′,连接D ′B 交AC 于点P ,并连接DP , ⅠCA 垂直平分DD ′,ⅠPD =PD ′,ⅠBD ′+BD 是ⅠBDP 周长的最小值.Ⅰ点A 、点B 关于直线DE 成轴对称,而A (3,0),B (1,0)Ⅰ抛物线的对称轴为x =2,将x =2代入抛物线的解析式y =-(x -3)(x -1),(4分)可得y =1,即点D 的坐标为(2,1),ⅠBD =(2-1)2+(1-0)2= 2.ⅠAD = 2.ⅠAB =2,ⅠAB 2=BD 2+AD 2,ⅠⅠADB 为等腰直角三角形,ⅠADB =90°.(5分)ⅠAD ′=AD =2,ⅠBD ′=BD 2+(DD ′)2=10 .ⅠⅠBDP 周长的最小值=BD ′+BD =10+2;(6分)第26题解图Ⅰ(3)ⅠE (2,0),C (0,-3),ⅠOE =2,OC =3,ⅠCE =OE 2+OC 2=13.ⅠPQ =32CE =3132. 设P (x ,x -3),PQ 若取最大值,则必过点F (-2,0),PF =(2+x )2+(3-x )2.ⅠⅠF 的半径为12CE =132, ⅠQF =132. ⅠPQ =PF +QF =(2+x )2+(3-x )2+132=32CE =3132. 解得x =0或x =1,则P (0,-3)或(1,-2)(8分) Ⅰ动点P 与点C 不重合,ⅠP (1,-2).过点P 、Q 的直线即过点P (1,-2),F (-2,0)的直线,Ⅰ根据P (1,-2),F (-2,0)可得直线为y =-23x -43. 联立⎩⎪⎨⎪⎧y =-x 2+4x -3,y =-23x -43,得⎩⎪⎨⎪⎧x =7+343,y =-26+2349, 或⎩⎪⎨⎪⎧x =7-343,y =234-269.(9分) Ⅰ点M 在点N 的左侧,ⅠM (7-343,234-269),N (7+343,-26+2349). 如解图Ⅰ,连接AN 、BM ,S 四边形ABMN =S ⅠAFN -S ⅠBFM=12×5×26+2349-12×3×26-2349 =26+8349.(10分)第26题解图Ⅰ。
广西柳州2019中考试题-数学(解析版)

广西柳州2019中考试题-数学(解析版)【一】选择题〔本大题共12小题,每题3分,共36分,在每题列出的四个选项中,只有一个选项是正确的,每题选对得3分,选错、不选或多项选择均得零分〕1、李师傅做了一个零件,如图,请你告诉他那个零件的主视图是〔A〕A、B、C、D、【考点】简单组合体的三视图、【专题】推理填空题、【分析】依照主视图的定义,从前面看即可得出答案、【解答】解:依照主视图的定义,从前面看,得出的图形是一个正六边形和一个圆,应选A、【点评】此题考查了简单组合体的三视图的应用,通过做此题培养了学生的理解能力和观看图形的能力,同时也培养了学生的空间想象能力、2、小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是〔D〕A、FGB、FHC、EHD、EF【考点】相似图形、【分析】观看图形,先找出对应顶点,再依照对应顶点的连线即为对应线段解答、【解答】解:由图可知,点A、E是对应顶点,点B、F是对应顶点,点D、H是对应顶点,因此,甲图中的线段AB在乙图中的对应线段是EF、应选D、【点评】此题考查了相似图形,依照对应点确定对应线段,因此确定出对应点是解题的关键、3、如图,直线a与直线c相交于点O,∠1的度数是〔D〕A、60°B、50°C、40°D、30°【考点】对顶角、邻补角、【分析】依照邻补角的和等于180°列式计算即可得解、【解答】解:∠1=180°-150°=30°、应选D、【点评】此题要紧考查了邻补角的和等于180°,是基础题,比较简单、4、如图,小强利用全等三角形的知识测量池塘两端M、N的距离,假如△PQO≌△NMO,那么只需测出其长度的线段是〔B〕A、POB、PQC、MOD、MQ【考点】全等三角形的应用、【分析】利用全等三角形对应边相等可知要想求得MN的长,只需求得其对应边PQ的长,据此能够得到答案、【解答】解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,应选B、【点评】此题考查了全等三角形的应用,解题的关键是如何将实际问题与数学知识有机的结合在一起、5、娜娜有一个问题请教你,以下图形中对称轴只有两条的是〔C〕A、圆B、等边三角形C、矩形D、等腰梯形【考点】轴对称图形、【分析】依照轴对称图形的概念,分别判断出四个图形的对称轴的条数即可、【解答】解:A、圆有许多条对称轴,故本选项错误;B、等边三角形有3条对称轴,故本选项错误;C、矩形有2条对称轴,故本选项正确;D、等腰梯形有1条对称轴,故本选项错误、应选C、【点评】此题考查轴对称图形的概念,解题关键是能够依照轴对称图形的概念正确找出各个图形的对称轴的条数,属于基础题、6、如图,给出了正方形ABCD的面积的四个表达式,其中错误的选项是〔C〕A、〔x+a〕〔x+a〕B、x2+a2+2axC、〔x-a〕〔x-a〕D、〔x+a〕a+〔x+a〕x【考点】整式的混合运算、【分析】依照正方形的面积公式,以及分割法,可求正方形的面积,进而可排除错误的表达式、【解答】解:依照图可知,S正方形=〔x+a〕2=x2+2ax+a2,应选C、【点评】此题考查了整式的混合运算、正方形面积,解题的关键是注意完全平方公式的掌握应用、7、定圆O的半径是4cm,动圆P的半径是2cm,动圆在直线l上移动,当两圆相切时,OP的值是〔A〕A、2cm或6cmB、2cmC、4cmD、6cm【考点】相切两圆的性质、【专题】计算题、【分析】定圆O与动圆P相切时,分两种情况考虑:内切与外切,当两圆内切时,圆心距OP=R-r;当两圆外切时,圆心距OP=R+r,求出即可、【解答】解:设定圆O的半径为R=4cm,动圆P的半径为r=2cm,分两种情况考虑:当两圆外切时,圆心距OP=R+r=4+2=6cm;当两圆内切时,圆心距OP=R-r=4-2=2cm,综上,OP的值为2cm或6cm、应选A【点评】此题考查了相切两圆的性质,两圆相切时有两种情况:内切与外切,当两圆内切时,圆心距等于两半径相减;当两圆外切时,圆心距等于两半径相加、8、你认为方程x 2+2x-3=0的解应该是〔D〕A 、1B 、-3C 、3D 、1或-3【考点】解一元二次方程-因式分解法、【分析】利用因式分解法,原方程可变为〔x+3〕〔x-1〕=0,即可得x+3=0或x-1=0,继而求得答案、【解答】解:∵x 2+2x-3=0,∴〔x+3〕〔x-1〕=0,即x+3=0或x-1=0,解得:x 1=-3,x2=1、应选D 、【点评】此题考查了因式分解法解一元二次方程的知识、此题比较简单,注意掌握十字相乘法分解因式的知识是解此题的关键、9、如图,P 1、P 2、P 3这三个点中,在第二象限内的有〔D〕A 、P 1、P 2、P 3B 、P 1、P 2C 、P 1、P 3D 、P 1【考点】点的坐标、【分析】依照点的坐标的定义,确定出这三个点的位置,即可选择答案、【解答】解:由图可知,P 1在第二象限,点P 2在y 轴的正半轴上,点P 3在x 轴的负半轴上,因此,在第二象限内的有P 1、应选D 、【点评】此题考查了点的坐标,要紧是对象限内的点与坐标轴上点的认识,是基础题、10、如图,小红做了一个实验,将正六边形ABCDEF 绕点F 顺时针旋转后到达A ′B ′C ′D ′E ′F ′的位置,所转过的度数是〔A〕A 、60°B 、72°C 、108°D 、120°【考点】旋转的性质;正多边形和圆、【分析】由六边形ABCDEF 是正六边形,即可求得∠AFE 的度数,又由邻补角的定义,求得∠E ′FE 的度数,由将正六边形ABCDEF 绕点F 顺时针旋转后到达A ′B ′C ′D ′E ′F ′的位置,可得∠EFE ′是旋转角,继而求得答案、【解答】解:∵六边形ABCDEF 是正六边形,∴∠AFE=180°×(6-2)16=120°, ∴∠EFE ′=180°-∠AFE=180°-120°=60°,∵将正六边形ABCDEF 绕点F 顺时针旋转后到达A ′B ′C ′D ′E ′F ′的位置,∴∠EFE ′是旋转角,∴所转过的度数是60°、应选A 、【点评】此题考查了正六边形的性质、旋转的性质以及旋转角的定义、此题难度不大,注意找到旋转角是解此题的关键、11、小芳给你一个如下图的量角器,假如你用它来度量角的度数,那么能精确地读出的最小度数是〔B〕A 、1°B 、5°C 、10°D 、180°【考点】近似数和有效数字、【分析】度量器角的最小的刻度确实是所求、【解答】解:度量器的最小的刻度是5°,因而能精确地读出的最小度数是5°、应选B 、【点评】此题考查了量角器的使用,正确理解:度量器角的最小的刻度确实是能精确地读出的最小度数是关键、12、小兰画了一个函数1a y x=-的图象如图,那么关于x 的分式方程12ax-=的解是〔A〕 A 、x=1B 、x=2C 、x=3D 、x=4【考点】反比例函数的图象、【分析】关于x 的分式方程ax-1=2的解确实是函数y=ax-1中,纵坐标y=2时的横坐标x 的值,据此即可求解、【解答】解:关于x 的分式方程12ax -=的解确实是函数1a y x=-中,纵坐标y=2时的横坐标x 的值、依照图象能够得到:当y=2时,x=1、应选A 、【点评】此题考查了函数的图象,正确理解:关于x 的分式方程12ax-=的解,确实是函数1a y x=-中,纵坐标y=2时的横坐标x 的值是关键、 【二】填空题〔本大题共6小题,每题3分,共18分,请将答案直截了当填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效〕、13、如图,在△ABC 中,BD 是∠ABC 的角平分线,∠ABC=80°,那么∠DBC=40°、【考点】三角形的角平分线、中线和高、【分析】依照角平分线的性质得出∠ABD=∠DBC 进而得出∠DBC 的度数、【解答】解:∵BD 是∠ABC 的角平分线,∠ABC=80°,∴∠DBC=∠ABD=12∠ABC=12×80°=40°,故答案为:40、【点评】此题要紧考查了角平分线的性质,依照角平分线性质得出∠ABD=∠DBC是解题关键、14、如图,x和5分别是天平上两边的砝码,请你用大于号“>”或小于号“<”填空:x<5、【考点】不等式的性质、【分析】托盘天平是支点在中间的等臂杠杆,天平平衡时砝码的质量等于被测物体的质量,依照图示知被测物体x的质量小于砝码的质量、【解答】解:依照图示知被测物体x的质量小于砝码的质量,即x<5;故答案是:<、【点评】此题考查了不等式的相关知识,利用“天平”的不平衡来得出不等关系,表达了“数形结合”的数学思想、15、一元二次方程3x2+2x-5=0的一次项系数是2、【考点】一元二次方程的一般形式、【分析】一元二次方程的一般形式是:ax2+bx+c=0〔a,b,c是常数且a≠0〕,其中a,b,c分别叫二次项系数,一次项系数,常数项、依照定义即可求解、【解答】解:一元二次方程3x2+2x-5=0的一次项系数是:2、故答案是:2、【点评】一元二次方程的一般形式是:ax2+bx+c=0〔a,b,c是常数且a≠0〕特别要注意a ≠0的条件、这是在做题过程中容易忽视的知识点、在一般形式中ax2叫二次项,bx叫一次项,c是常数项、其中a,b,c分别叫二次项系数,一次项系数,常数项、16、一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如下图,那么漏斗的斜壁AB的长度为5cm、【考点】圆锥的计算、【分析】依照题意及图形知此题是圆锥的底面半径及圆锥的高求圆锥的母线长,利用勾股定理即可求得、【解答】解:依照题意知:圆锥的底面半径为3cm,高为4cm,故圆锥的母线长AB=32+42=5cm、故答案为5、【点评】此题考查了圆锥的计算,解题的关键是明白圆锥的底面半径、高及圆锥的母线构成直角三角形、17、某校篮球队在一次定点投篮训练中进球情况如图,那么那个对的队员平均进球个数是6、【考点】加权平均数、【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数、【解答】解:依照题意得:⨯+⨯+⨯+⨯=+++1445184761414,故答案是:6、【点评】此题考查的是加权平均数的求法、此题易出现的错误是求4,5,7,8这四个数的平均数,对平均数的理解不正确、18、:在△ABC 中,AC=a ,AB 与BC 所在直线成45°角,AC 与BC 所在直线形成的夹角的余,那么AC、【考点】解直角三角形、【分析】分两种情况:①△ABC 为锐角三角形;②△ABC 为钝角三角形、这两种情况,都能够首先作△ABC 的高AD ,解直角△ACD 与直角△ABD ,得到BC 的长,再利用余弦定理求解、【解答】解:分两种情况:①△ABC 为锐角三角形时,如图1、作△ABC 的高AD ,BE 为AC 边的中线、∵在直角△ACD 中,AC=a ,cosC=∴a ,AD=5A 、 ∵在直角△ABD 中,∠ABD=45°, ∴BD=AD=,∴A 、在△BCE 中,由余弦定理,得 BE 2=BC 2+EC 2-2BC •EC •cosC22291117254220a a a a =+-⨯= ∴a ;②△ABC 为钝角三角形时,如图2、作△ABC 的高AD ,BE 为AC 边的中线、∵在直角△ACD 中,AC=a ,cosC=∴a ,、∵在直角△ABD 中,∠ABD=45°,∴BD=AD=,∴A 、在△BCE 中,由余弦定理,得BE 2=BC 2+EC 2-2BC •EC •cosC222111125452520a a a a a =+-⨯⨯⨯= ∴a 、综上可知AC边上的中线长是10a或10a 、故答案为10a或10a 、【点评】此题考查了解直角三角形,勾股定理,余弦定理,有一定难度,进行分类讨论是解题的关键、【三】解答题〔本大题共8小题,共66分、解承诺写出文字说明、演算步骤或推理过程、请将解答写在答题卡中相应的区域内,画图或作辅助线时先使用铅笔画出,确定后必需使用黑色字迹的签字笔描黑、在草稿纸、试卷上答题无效〕【考点】二次根式的混合运算、【专题】计算题、【分析】先去括号得到原式=那么得到原式2=【解答】解:原式==2=、【点评】此题考查了二次根式的混合运算:先进行二次根式的乘除运算,再进行二次根式的加减运算;运用二次根式的性质和乘法法那么进行运算、20、列方程解应用题:今年“六•一”儿童节,张红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件? 解:设张红购买甲礼物x 件,那么购买乙礼物x+1件,依题意,得、【考点】一元一次方程的应用、【分析】设张红购买甲种礼物x 件,那么购买乙礼物x+1件,依照“两种礼物共用8.8元”列出方程求解即可、【解答】解:设张红购买甲种礼物x 件,那么购买乙礼物x+1件,依照题意得:1.2x+0.8〔x+1〕=8.8,解得:x=4、答:甲种礼物4件,一种礼物5件、【点评】此题考查了一元一次方程的应用,找到题目中的相等关系是解决此题的关键、21、右表反映了x 与y 之间存在某种函数关系,现给出了几种可能的函数关系式: y=x+7,y=x-5,6y x =,113y x =- x … -6 -5 3 4 … y … 1 1.2 -2 -1.5 … 〔1〕从所给出的几个式子中选出一个你认为满足上表要求的函数表达式:y=-6x ; 〔2〕请说明你选择那个函数表达式的理由、【考点】反比例函数的性质;函数关系式;一次函数的性质、【专题】探究型、【分析】〔1〕依照表中列出的x 与y 的对应关系判断出各点所在的象限,再依照所给的几个函数关系式即可得出结论;〔2〕依照〔1〕中的判断写出理由即可、【解答】解:〔1〕∵由表中所给的x 、y 的对应值的符号均相反,∴所给出的几个式子中只有y=-6x 符合条件,故答案为:y=-6x ;〔2〕∵由表中所给的x 、y 的对应值的符号均相反,∴此函数图象在【二】四象限,∵xy=〔-6〕×1=〔-5〕×1.2=-6,∴所给出的几个式子中只有y=-6x 符合条件、【点评】此题考查的是反比例函数的性质及一次函数的性质,先依照表中xy 的对应值判断出函数图象所在的象限是解答此题的关键、22、在甲、乙两个袋子中分别装有如图点数的牌,假设随机从袋子中抽牌时,每张牌被抽到的机会是均等的、那么分别从两个袋子各抽取1张牌时,它们的点数之和大于10的概率是多少?【考点】列表法与树状图法、【分析】首先依照题意画出树状图,然后由树状图求得所有等可能的结果与它们的点数之和大于10的情况,再利用概率公式求解即可求得答案、【解答】解:画树状图得:∵共有24种等可能的结果,它们的点数之和大于10的有6种情况,∴它们的点数之和大于10的概率是:61244=、 【点评】此题考查的是用列表法或树状图法求概率、注意画树状图法与列表法能够不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比、23、如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD 是一个特别的四边形、〔1〕那个特别的四边形应该叫做菱形;〔2〕请证明你的结论、【考点】菱形的判定与性质、【分析】首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,那么重叠部分为菱形、【解答】解:〔1〕菱形;故答案是:菱形;〔2〕∵四边形ABCD 是用两张等宽的纸条交叉重叠地放在一起而组成的图形, ∴AB ∥CD ,AD ∥BC ,∴四边形ABCD 是平行四边形〔对边相互平行的四边形是平行四边形〕;过点D 分别作AB ,BC 边上的高为DE ,DF 、那么DE=DF 〔两纸条相同,纸条宽度相同〕;∵平行四边形的面积为AB ×DE=BC ×DF ,∴AB=BC 、∴平行四边形ABCD 为菱形〔邻边相等的平行四边形是菱形〕、【分析】此题考查了菱形的判定与性质、注意:“邻边相等的平行四边形是菱形”,而非“邻边相等的四边形是菱形”、24、:抛物线23(1)34y x =--、 〔1〕写出抛物线的开口方向、对称轴;〔2〕函数y 有最大值依旧最小值?并求出那个最大〔小〕值;〔3〕设抛物线与y 轴的交点为P ,与x 轴的交点为Q ,求直线PQ 的函数解析式、【考点】二次函数的性质;待定系数法求一次函数解析式;二次函数的最值;抛物线与x轴的交点、【分析】〔1〕依照二次函数的性质,写出开口方向与对称轴即可;〔2〕依照a 是正数确定有最小值,再依照函数解析式写出最小值;〔3〕分别求出点P 、Q 的坐标,再依照待定系数法求函数解析式解答、【解答】解:〔1〕抛物线23(1)34y x =--, ∵a=34=>0, ∴抛物线的开口向上,对称轴为x=1;〔2〕∵a=34=>0, ∴函数y 有最小值,最小值为-3; 〔3〕令x=0,那么239(01)344y =--=-, 因此,点P 的坐标为〔0,94-〕, 令y=0,那么23(1)304x --=, 解得x 1=-1,x 2=3,因此,点Q 的坐标为〔-1,0〕或〔3,0〕,当点P 〔0,94-〕,Q 〔-1,0〕时,设直线PQ 的解析式为y=kx+b , 那么940b k b ⎧=-⎪⎨⎪-+=⎩,解得k=94-,b=94-, 因此直线PQ 的解析式为9944y x =--, 当P 〔0,94-〕,Q 〔3,0〕时,设直线PQ 的解析式为y=mx+n , 那么9430n m n ⎧=-⎪⎨⎪+=⎩,解得m=34,n=-94-, 因此,直线PQ 的解析式为3944y x =-, 综上所述,直线PQ 的解析式为y=-94x-94或y=34x-94、【点评】此题要紧考查了二次函数的性质,二次函数的最值问题,待定系数法求函数解析式,以及抛物线与x轴的交点问题,是基础题,熟记二次函数的开口方向,对称轴解析式与二次函数的系数的关系是解题的关键、25、如图,AB是⊙O的直径,AC是弦、〔1〕请你按下面步骤画图〔画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑〕;第一步,过点A作∠BAC的角平分线,交⊙O于点D;第二步,过点D作AC的垂线,交AC的延长线于点E、第三步,连接BD、〔2〕求证:AD2=AE•AB;〔3〕连接EO,交AD于点F,假设5AC=3AB,求EOFO的值、【考点】圆的综合题、【专题】综合题、【分析】〔1〕依照差不多作图作出∠BAC的角平分线AD交⊙O于点D;点D作AC的垂线,垂足为点E;〔2〕依照直径所对的圆周角为直角得到∠ADB=90°,DE⊥AC,那么∠AED=90°,又由AD平分∠CAB得到∠CAD=∠DAB,依照相似三角形的判定得到Rt△ADE∽Rt△ABD,依照相似的性质得到AD:AB=AE:AD,利用比例的性质即可得到AD2=AE•AB;〔3〕连OD、BC,它们交于点G,由5AC=3AB,那么不妨设AC=3x,AB=5x,依照直径所对的圆周角为直角得到∠ACB=90°,由∠CAD=∠DAB得到DC DB,依照垂径定理的推论得到OD垂直平分BC,那么有OD∥AE,OG=12AC=32x,同时得到四边形ECGD为矩形,那么CE=DG=OD-OG=52x-32x=x,可计算出AE=AC+CE=3x+x=4x,利用AE∥OD可得到△AEF∽△DOF,那么AE:OD=EF:OF,即EF:OF=4x:52x=8:5,然后依照比例的性质即可得到EOFO的值、【解答】〔1〕解:如图;〔2〕证明:∵AB是⊙O的直径,∴∠ADB=90°,而DE⊥AC,∴∠AED=90°,∵AD平分∠CAB,∴∠CAD=∠DAB,∴Rt△ADE∽Rt△ABD,∴AD:AB=AE:AD,∴AD 2=AE •AB ;〔3〕解:连OD 、BC ,它们交于点G ,如图, ∵5AC=3AB ,即AC :AB=3:5, ∴不妨设AC=3x ,AB=5x , ∵AB 是⊙O 的直径,∴∠ACB=90°, 又∵∠CAD=∠DAB , ∴=DC DB ,∴OD 垂直平分BC ,∴OD ∥AE ,OG=12AC=32x , ∴四边形ECGD 为矩形, ∴CE=DG=OD-OG=52x-32x=x ,∴AE=AC+CE=3x+x=4x , ∵AE ∥OD ,∴△AEF ∽△DOF , ∴AE :OD=EF :OF , ∴EF :OF=4x :52x=8:5,∴851355+==OEOF 、 【点评】此题考查了圆的综合题:平分弦所对的弧的直径垂直平分弦;在同圆或等圆中,相等的圆周角所对的弧相等;直径所对的圆周角为直角;运用相似三角形的判定与性质证明等积式和几何计算;掌握差不多的几何作图、26、如图,在△ABC 中,AB=2,AC=BC=5、〔1〕以AB 所在的直线为x 轴,AB 的垂直平分线为y 轴,建立直角坐标系如图,请你分别写出A 、B 、C 三点的坐标;〔2〕求过A 、B 、C 三点且以C 为顶点的抛物线的解析式;〔3〕假设D 为抛物线上的一动点,当D 点坐标为何值时,S △ABD =12S △ABC ;〔4〕假如将〔2〕中的抛物线向右平移,且与x 轴交于点A ′B ′,与y 轴交于点C ′,当平移多少个单位时,点C ′同时在以A ′B ′为直径的圆上〔解答过程假如有需要时,请参看阅读材料〕、附:阅读材料一元二次方程常用的解法有配方法、公式法和因式分解法,关于一些特别方程能够通过换元法转化为一元二次方程求解、如解方程:y 4-4y 2+3=0、解:令y 2=x 〔x ≥0〕,那么原方程变为x 2-4x+3=0,解得x 1=1,x 2=3、 当x 1=1时,即y 2=1,∴y 1=1,y 2=-1、当x 2=3,即y 2=3,∴y 3=3,y 4=-3、因此,原方程的解是y 1=1,y 2=-1,y 3=3,y 4=-3、再如22x -=y =【考点】二次函数综合题、 【分析】〔1〕依照y 轴是AB 的垂直平分线,那么能够求得OA ,OB 的长度,在直角△OAC 中,利用勾股定理求得OC 的长度,那么A 、B 、C 的坐标即可求解; 〔2〕利用待定系数法即可求得二次函数的解析式;〔3〕首先求得△ABC 的面积,依照S △ABD =12S △ABC ,以及三角形的面积公式,即可求得D 的纵坐标,把D 的纵坐标代入二次函数的解析式,即可求得横坐标、 〔4〕设抛物线向右平移c 个单位长度,那么0<c ≤1,能够写出平移以后的函数解析式,当点C ′同时在以A ′B ′为直径的圆上时有:OC ′2=OA •OB ,据此即可得到一个关于c 的方程求得c 的值、【解答】解:〔1〕∵AB 的垂直平分线为y 轴,∴OA=OB=12AB=12×2=1,∴A 的坐标是〔-1,0〕,B 的坐标是〔1,0〕、 在直角△OAC中,==OC 2,那么C 的坐标是:〔0,2〕;〔2〕设抛物线的解析式是:y=ax 2+b , 依照题意得:02a b b +=⎧⎨=⎩,解得:22a b =-⎧⎨=⎩,那么抛物线的解析式是:222y x =-+;〔3〕∵S△ABC=12AB•OC=12×2×2=2,∴S△ABD=12S△ABC=1、设D的纵坐标是m,那么12AB•|m|=1,那么m=±1、当m=1时,-2x2+2=1,解得:x=±2,当m=-1时,,-2x2+2=-1,解得:x=±2那么D的坐标是:〔2,1〕或〔-2,1-1〕,或〔-1〕、〔4〕设抛物线向右平移c个单位长度,那么0<c≤1,OA′=1-c,OB′=1+C、平移以后的抛物线的解析式是:y=-2〔x-c〕2+B、令x=0,解得y=-2c2+2、即OC′=-2c2+2、当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′,那么〔-2c2+2〕2=〔1-c〕〔1+c〕,即〔4c2-3〕〔c2-1〕=0,解得:c=2,2-〔舍去〕,1,1-〔舍去〕、故平移2或1个单位长度、【点评】此题考查了勾股定理,待定系数法求二次函数的解析式,以及图象的平移,正确理解:当点C′同时在以A′B′为直径的圆上时有:OC′2=OA•OB,是解题的关键、。
2019年广西柳州市中考数学试卷附分析答案

A.∠B
B.∠C
C.∠DEB
D.∠D
【解答】解:∵∠A 与∠D 都是 t所对的圆周角,
∴∠D=∠A.
故选:D.
7.(3 分)如图,在▱ABCD 中,全等三角形的对数共有( )
A.2 对
B.3 对
C.4 对
第 10页(共 24页)
D.5 对
【解答】解:∵四边形 ABCD 是平行四边形, ∴AB=CD,AD=BC;OD=OB,OA=OC; ∵OD=OB,OA=OC,∠AOD=∠BOC; ∴△AOD≌△COB(SAS);① 同理可得出△AOB≌△COD(SAS);② ∵BC=AD,CD=AB,BD=BD; ∴△ABD≌△CDB(SSS);③ 同理可得:△ACD≌△CAB(SSS).④ 因此本题共有 4 对全等三角形. 故选:C. 8.(3 分)阅读【资料】,完成第 8、9 题. 【资料】:如图,这是根据公开资料整理绘制而成的 2004﹣2018 年中美两国国内生产总 值(GDP)的直方图及发展趋势线.(注:趋势线由 Excel 系统根据数据自动生成,趋势 线中的 y 表示 GDP,x 表示年数) 2004﹣2018 年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线
(结果
精确到 0.01).
16.(3 分)在半径为 5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片
的边长应为
.
17.(3 分)如图,在△ABC 中,sinB ,tanC ,AB=3,则 AC 的长为
.
第 4页(共 24页)
18.(3 分)已知一组数据共有 5 个数,它们的方差是 0.4,众数、中位数和平均数都是 8,
求作:∠A′O′B′,使得∠A′O′B′=∠AOB.
【中考真题】2019年广西柳州市中考数学试卷(含参考答案及详细解析)

2019年广西柳州市中考数学试卷一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全4.(3分)计算:x(x2﹣1)=()A.x3﹣1B.x3﹣x C.x3+x D.x2﹣x5.(3分)反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30B.14.19C.19.57D.19.719.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.12.(3分)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6B.6C.5D.﹣5二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.(3分)计算:7x﹣4x=.14.(3分)如图,若AB∥CD,则在图中所标注的角中,一定相等的角是.15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.17.(3分)如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为.18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|﹣+π0.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB 绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB 距离最短时的坐标.25.(10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP=OE•OM.26.(10分)如图,直线y=x﹣3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,抛物线的顶点为点D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,CE的长为半径作圆,点P为直线y=x﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于CE时,过P,Q两点的直线与抛物线交于M,N两点(点M在点N的左侧),求四边形ABMN 的面积.2019年广西柳州市中考数学试卷参考答案与试题解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.【解答】解:104400用科学记数法表示应为1.044×105,故选:C.2.【解答】解:题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C.3.【解答】解:D答案的图形是轴对称图形,故选:D.4.【解答】解:x(x2﹣1)=x3﹣x;故选:B.5.【解答】解:∵k=2>0,∴反比例函数经过第一、三象限;故选:A.6.【解答】解:∵∠A与∠D都是所对的圆周角,∴∠D=∠A.故选:D.7.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形.故选:C.8.【解答】解:由图象可知,2016年至2018年的GDP值分别为:11.19,12.24,13.46.则=≈12.30故选:A.9.【解答】解:由图表信息,联立中美GDP趋势线解析式得解得x=∴2018+(﹣15)=故选:B.10.【解答】解:根据题意得:全程需要的时间为:3÷4=(小时),∴y=3﹣4x(0≤x≤).故选:D.11.【解答】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为;故选:A.12.【解答】解:∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.【解答】解:7x﹣4x=(7﹣4)x=3x,故答案为:3x.14.【解答】解:∵AB∥CD,∴∠1=∠3.故答案为15.【解答】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95.故答案为:0.9516.【解答】解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE=,即a=5.故答案为:5.17.【解答】解:过A作AD⊥BC,在Rt△ABD中,sin B=,AB=3,∴AD=AB•sin B=1,在Rt△ACD中,tan C=,∴=,即CD=,根据勾股定理得:AC===,故答案为:18.【解答】解:∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.【解答】解:原式=4+3﹣2+1=6.20.【解答】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.21.【解答】解:(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38.9亿元,答:2016年全国教育经费总投入约为38.8亿元.22.【解答】证明:连接AC,如图所示:在△ABC和△CDA中,,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.23.【解答】解:(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,依题意,得:=,解得:x=0.5,经检验,x=0.5是原方程的解,且符合题意,∴x+0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.24.【解答】解:(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+b=,∴﹣2x2+bx﹣3=0,当△=b2﹣24=0时,b=,此时点P到直线AB距离最短;∴P(,);25.【解答】解:(1)如图1,连接BC,AC,AD,∵CD⊥AB,AB是直径∴,CE=DE=CD=3∴∠ACD=∠ABC,且∠AEC=∠CEB∴△ACE∽△CEB∴∴∴AB=AE+BE=10∴⊙O的半径为5(2)∵=∴∠ACD=∠ADC=∠CDF,且DE=DE,∠AED=∠NED=90°∴△ADE≌△NDE(ASA)∴∠DAN=∠DNA,AE=EN∵∠DAB=∠DFB,∠AND=∠FNB∴∠FNB=∠DFB∴BN=BF,∴△BNF是等腰三角形(3)如图2,连接AC,CE,CO,DO,∵MD是切线,∴MD⊥DO,∴∠MDO=∠DEO=90°,∠DOE=∠DOE∴△MDO∽△DEO∴∴OD2=OE•OM∵AE=EN,CD⊥AO∴∠ANC=∠CAN,∴∠CAP=∠CNO,∵∴∠AOC=∠ABF∴∠PCO=∠PFB∵四边形ACFB是圆内接四边形∴∠P AC=∠PFB∴∠P AC=∠PFB=∠PCO=∠CNO,且∠POC=∠COE∴△CNO∽△PCO∴∴CO2=PO•NO,∴ON•OP=OE•OM.26.【解答】解:(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),则抛物线的表达式为:y=a(x﹣3)(x﹣1)=a(x2﹣4x+3),则3a=﹣3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+4x﹣3…①;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,连接AB′,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,D(2,1),则点G(2,﹣1),即:BG=EG,即点G是BB′的中点,过点B′(3,﹣2),△BDP周长最小值=BD+B′B=;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,点A、B、C、E、F的坐标为(3,0)、(1,0)、(0,﹣3)、(2,0)、(﹣2,0),则CE=,FQ=CE,则PF=CE﹣CE=,设点P(m,m﹣3),点F(﹣2,0),PF2=13=(m﹣2)2+(m﹣3)2,解得:m=1,故点P(1,﹣2),将点P、F坐标代入一次函数表达式并解得:直线PF的表达式为:y=﹣x﹣…②,联立①②并解得:x=,故点M、N的坐标分别为:(,)、(,),过点M、N分别作x轴的垂线交于点S、R,则S四边形ABMN=S梯形NRSM﹣S△ARN﹣S△SBM=.。
(真题)广西柳州市2019年中考数学试题(有答案)(Word版)

中考数学试卷一、选择题(每题只有一个正确选项,本题共12小题,每题3分,共36分)1.(3.00分)计算:0+(﹣2)=()A.﹣2 B.2 C.0 D.﹣202.(3.00分)如图,这是一个机械模具,则它的主视图是()A.B.C.D.3.(3.00分)下列图形中,是中心对称图形的是()A.正三角形B.圆C.正五边形D.等腰梯形4.(3.00分)现有四张扑克牌:红桃A、黑桃A、梅花A和方块A,将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为()A.1 B.C.D.5.(3.00分)世界人口约7000000000人,用科学记数法可表示为()A.9×107B.7×1010C.7×109D.0.7×1096.(3.00分)如图,图中直角三角形共有()A.1个 B.2个 C.3个 D.4个7.(3.00分)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB==()A.B.C.D.8.(3.00分)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为()A.84°B.60°C.36°D.24°9.(3.00分)苹果原价是每斤a元,现在按8折出售,假如现在要买一斤,那么需要付费()A.0.8a元B.0.2a元C.1.8a元D.(a+0.8)元10.(3.00分)如图是某年参加国际教育评估的15个国家学生的数学平均成绩(x)的扇形统计图,由图可知,学生的数学平均成绩在60≤x<70之间的国家占()A.6.7% B.13.3% C.26.7% D.53.3%11.(3.00分)计算:(2a)•(ab)=()A.2ab B.2a2b C.3ab D.3a2b12.(3.00分)已知反比例函数的解析式为y=,则a的取值范围是()A.a≠2 B.a≠﹣2 C.a≠±2 D.a=±2二、填空题(每题只有一个正确选项,本题共6小题,每题3分,共1836分)13.(3.00分)如图,a∥b,若∠1=46°,则∠2=°.14.(3.00分)如图,在平面直角坐标系中,点A的坐标是.15.(3.00分)不等式x+1≥0的解集是.16.(3.00分)一元二次方程x2﹣9=0的解是.17.(3.00分)篮球比赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,艾美所在的球队在8场比赛中得14分.若设艾美所在的球队胜x场,负y场,则可列出方程组为.18.(3.00分)如图,在Rt△ABC中,∠BCA=90°,∠DCA=30°,AC=,AD=,则BC的长为.三、解答题(每题只有一个正确选项,本题共8小题,共66分) 19.(6.00分)计算:2+3.20.(6.00分)如图,AE 和BD 相交于点C ,∠A=∠E ,AC=EC .求证:△ABC ≌△EDC .21.(8.00分)一位同学进行五次投实心球的练习,每次投出的成绩如表: 投实心球序次 12345成绩(m )10.510.210.310.610.4求该同学这五次投实心球的平均成绩. 22.(8.00分)解方程=.23.(8.00分)如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,且AB=2. (1)求菱形ABCD 的周长; (2)若AC=2,求BD 的长.24.(10.00分)如图,一次函数y=mx +b 的图象与反比例函数y=的图象交于A (3,1),B (﹣,n )两点.(1)求该反比例函数的解析式; (2)求n 的值及该一次函数的解析式.25.(10.00分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.(1)求证:△DAC∽△DBA;(2)过点C作⊙O的切线CE交AD于点E,求证:CE=AD;(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.26.(10.00分)如图,抛物线y=ax2+bx+c与x轴交于A(,0),B两点(点B在点A的左侧),与y轴交于点C,且OB=3OA=OC,∠OAC的平分线AD交y轴于点D,过点A且垂直于AD的直线l交y轴于点E,点P是x轴下方抛物线上的一个动点,过点P作PF⊥x轴,垂足为F,交直线AD于点H.(1)求抛物线的解析式;(2)设点P的横坐标为m,当FH=HP时,求m的值;(3)当直线PF为抛物线的对称轴时,以点H为圆心,HC为半径作⊙H,点Q为⊙H上的一个动点,求AQ+EQ的最小值.中考数学试卷参考答案与试题解析一、选择题(每题只有一个正确选项,本题共12小题,每题3分,共36分)1.(3.00分)计算:0+(﹣2)=()A.﹣2 B.2 C.0 D.﹣20【分析】直接利用有理数的加减运算法则计算得出答案.【解答】解:0+(﹣2)=﹣2.故选:A.【点评】此题主要考查了有理数的加法,正确掌握运算法则是解题关键.2.(3.00分)如图,这是一个机械模具,则它的主视图是()A.B.C.D.【分析】根据主视图的画法解答即可.【解答】解:主视图是从几何体正边看得到的图形,题中的几何体从正边看,得到的图形是并列的三个正方形和一个圆,其中圆在左边正方形的上面,故选:C.【点评】本题考查几何体的三视图画法.根据主视图是从几何体正边看得到的图形解答是关键.3.(3.00分)下列图形中,是中心对称图形的是()A.正三角形B.圆C.正五边形D.等腰梯形【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心进行分析.【解答】解:A、不是中心对称图形,故此选项错误;B、是中心对称图形,故此选项正确;C、不是中心对称图形,故此选项错误;D、不是中心对称图形,故此选项错误;故选:B.【点评】此题主要考查了中心对称图形,关键是掌握中心对称图形的定义.4.(3.00分)现有四张扑克牌:红桃A、黑桃A、梅花A和方块A,将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为()A.1 B.C.D.【分析】利用概率公式计算即可得.【解答】解:∵从4张纸牌中任意抽取一张牌有4种等可能结果,其中抽到红桃A的只有1种结果,∴抽到红桃A的概率为,故选:B.【点评】本题主要考查概率公式的应用,解题的关键是掌握随机事件A的概率P(A)=事件A 可能出现的结果数÷所有可能出现的结果数.5.(3.00分)世界人口约7000000000人,用科学记数法可表示为()A.9×107B.7×1010C.7×109D.0.7×109【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:7000000000=7×109.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.6.(3.00分)如图,图中直角三角形共有()A.1个 B.2个 C.3个 D.4个【分析】根据直角三角形的定义:有一个角是直角的三角形是直角三角形,可作判断.【解答】解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,故选:C.【点评】本题考查了直角三角形的定义,比较简单,掌握直角三角形的定义是关键,要做到不重不漏.7.(3.00分)如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB==()A.B.C.D.【分析】首先利用勾股定理计算出AB长,再计算sinB即可.【解答】解:∵∠C=90°,BC=4,AC=3,∴AB=5,∴sinB==,故选:A.【点评】此题主要考查了锐角三角函数,关键是正确计算出AB的长.8.(3.00分)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为()A.84°B.60°C.36°D.24°【分析】直接利用圆周角定理即可得出答案.【解答】解:∵∠B与∠C所对的弧都是,∴∠C=∠B=24°,故选:D.【点评】本题主要考查圆周角定理,解题的关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.9.(3.00分)苹果原价是每斤a元,现在按8折出售,假如现在要买一斤,那么需要付费()A.0.8a元B.0.2a元C.1.8a元D.(a+0.8)元【分析】根据“实际售价=原售价×”可得答案.【解答】解:根据题意知,买一斤需要付费0.8a元,故选:A.【点评】本题主要考查列代数式,解题的关键是掌握代数式的书写规范及实际问题中数量间的关系.10.(3.00分)如图是某年参加国际教育评估的15个国家学生的数学平均成绩(x)的扇形统计图,由图可知,学生的数学平均成绩在60≤x<70之间的国家占()A.6.7% B.13.3% C.26.7% D.53.3%【分析】根据扇形统计图直接反映部分占总体的百分比大小,可知学生成绩在60≤x<69之间的占53.3%.【解答】解:由图可知,学生的数学平均成绩在60≤x<70之间的国家占53.3%.故选:D.【点评】本题考查了扇形统计图的应用.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.11.(3.00分)计算:(2a)•(ab)=()A.2ab B.2a2b C.3ab D.3a2b【分析】直接利用单项式乘以单项式运算法则计算得出答案.【解答】解:(2a)•(ab)=2a2b.故选:B.【点评】此题主要考查了单项式乘以单项式,正确掌握运算法则是解题关键.12.(3.00分)已知反比例函数的解析式为y=,则a的取值范围是()A.a≠2 B.a≠﹣2 C.a≠±2 D.a=±2【分析】根据反比例函数解析式中k是常数,不能等于0解答即可.【解答】解:由题意可得:|a|﹣2≠0,解得:a≠±2,故选:C.【点评】此题主要考查了反比例函数,关键是根据反比例函数关系式中k的取值范围解答.二、填空题(每题只有一个正确选项,本题共6小题,每题3分,共1836分)13.(3.00分)如图,a∥b,若∠1=46°,则∠2=46°.【分析】根据平行线的性质,得到∠1=∠2即可.【解答】解:∵a∥b,∠1=46°,∴∠2=∠1=46°,故答案为:46.【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等.14.(3.00分)如图,在平面直角坐标系中,点A的坐标是(﹣2,3).【分析】直接利用平面直角坐标系得出A点坐标.【解答】解:由坐标系可得:点A的坐标是(﹣2,3).故答案为:(﹣2,3).【点评】此题主要考查了点的坐标,正确利用平面坐标系是解题关键.15.(3.00分)不等式x+1≥0的解集是x≥﹣1.【分析】根据一元一次不等式的解法求解不等式.【解答】解:移项得:x≥﹣1.故答案为:x≥﹣1.【点评】本题考查了解简单不等式的能力,解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.16.(3.00分)一元二次方程x2﹣9=0的解是x1=3,x2=﹣3.【分析】利用直接开平方法解方程得出即可.【解答】解:∵x2﹣9=0,∴x2=9,解得:x1=3,x2=﹣3.故答案为:x1=3,x2=﹣3.【点评】此题主要考查了直接开平方法解方程,正确开平方是解题关键.17.(3.00分)篮球比赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,艾美所在的球队在8场比赛中得14分.若设艾美所在的球队胜x场,负y场,则可列出方程组为.【分析】根据比赛总场数和总分数可得相应的等量关系:胜的场数+负的场数=8;胜的积分+平的积分=14,把相关数值代入即可.【解答】解:设艾美所在的球队胜x场,负y场,∵共踢了8场,∴x+y=8;∵每队胜一场得2分,负一场得1分.∴2x+y=14,故列的方程组为,故答案为.【点评】本题考查了列二元一次方程组,根据总场数和总分数得到相应的等量关系是解决本题的根据.18.(3.00分)如图,在Rt△ABC中,∠BCA=90°,∠DC A=30°,AC=,AD=,则BC的长为5.【分析】作辅助线,构建直角三角形,先根据直角三角形30度角的性质和勾股定理得:AE=,CE=,及ED的长,可得CD的长,证明△BFD∽△BCA,列比例式可得BC的长.【解答】解:过A作AE⊥CD于E,过D作DF⊥BC于F,Rt△AEC中,∠ACD=30°,AC=,∴AE=,CE=,Rt△AED中,ED===,∴CD=CE+DE==,∵DF⊥BC,AC⊥BC,∴DF∥AC,∴∠FDC=∠ACD=30°,∴CF=CD==,∴DF=,∵DF∥AC,∴△BFD∽△BCA,∴,∴=,∴BF=,∴BC=+=5,故答案为:5.【点评】本题考查了相似三角形的性质和判定、直角三角形30度角的性质及勾股定理,熟练运用勾股定理计算线段的长是关键.三、解答题(每题只有一个正确选项,本题共8小题,共66分)19.(6.00分)计算:2+3.【分析】先化简,再计算加法即可求解.【解答】解:2+3=4+3=7.【点评】考查了二次根式的加减法,关键是熟练掌握二次根式的加减法法则:二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.20.(6.00分)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.【解答】证明:∵在△ABC和△EDC中,,∴△ABC≌△EDC(ASA).【点评】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.21.(8.00分)一位同学进行五次投实心球的练习,每次投出的成绩如表:12345投实心球序次成绩(m)10.510.210.310.610.4求该同学这五次投实心球的平均成绩.【分析】平均数是指在一组数据中所有数据之和再除以数据的个数.【解答】解:该同学这五次投实心球的平均成绩为:=10.4.故该同学这五次投实心球的平均成绩为10.4m.【点评】此题考查了平均数,解题的关键是掌握平均数的计算公式.22.(8.00分)解方程=.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:2x﹣4=x,解得:x=4,经检验x=4是分式方程的解.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.23.(8.00分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.(1)求菱形ABCD的周长;(2)若AC=2,求BD的长.【分析】(1)由菱形的四边相等即可求出其周长;(2)利用勾股定理可求出BO的长,进而解答即可.【解答】解:(1)∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长=2×4=8;(2)∵四边形ABCD是菱形,AC=2,AB=2∴AC⊥BD,AO=1,∴BO=,∴BD=2【点评】本题主要考查菱形的性质,能够利用勾股定理求出BO的长是解题关键.24.(10.00分)如图,一次函数y=mx+b的图象与反比例函数y=的图象交于A(3,1),B(﹣,n)两点.(1)求该反比例函数的解析式;(2)求n的值及该一次函数的解析式.【分析】(1)根据反比例函数y=的图象经过A(3,1),即可得到反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得n=﹣6,把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得一次函数的解析式为y=2x﹣5.【解答】解:(1)∵反比例函数y=的图象经过A(3,1),∴k=3×1=3,∴反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得﹣n=3,解得n=﹣6,∴B(﹣,﹣6),把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得,解得,∴一次函数的解析式为y=2x﹣5.【点评】本题考查了利用图象解决一次函数和反比例函数的问题.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.25.(10.00分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.(1)求证:△DAC∽△DBA;(2)过点C作⊙O的切线CE交AD于点E,求证:CE=AD;(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.【分析】(1)利用AB是⊙O的直径和AD是⊙O的切线判断出∠ACD=∠DAB=90°,即可得出结论;(2)利用切线长定理判断出AE=CE,进而得出∠DAC=∠EAC,再用等角的余角相等判断出∠D=∠DCE,得出DE=CE,即可得出结论;(3)先求出tan∠ABD值,进而得出GH=2CH,进而得出BC=3BH,再求出BC建立方程求出BH,进而得出GH,即可得出结论.【解答】解:(1)∵AB是⊙O直径,∴∠ACD=∠ACB=90°,∵AD是⊙O的切线,∴∠BAD=90°,∴∠ACD=∠DAB=90°,∵∠D=∠D,∴△DAC∽△DBA;(2)∵EA,EC是⊙O的切线,∴AE=CE(切线长定理),∴∠DAC=∠ECA,∵∠ACD=90°,∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,∴∠D=∠DCE,∴DE=CE,∴AD=AE+DE=CE+CE=2CE,∴CE=AD;(3)如图,在Rt△ABD中,AD=6,AB=3,∴tan∠ABD==2,过点G作GH⊥BD于H,∴tan∠ABD==2,∴GH=2BH,∵点F是直径AB下方半圆的中点,∴∠BCF=45°,∴∠CGH=∠CHG﹣∠BCF=45°,∴CH=GH=2BH,∴BC=BH+CH=3BH,在Rt△ABC中,tan∠ABC==2,∴AC=2BC,根据勾股定理得,AC2+BC2=AB2,∴4BC2+BC2=9,∴BC=,∴3BH=,∴BH=,∴GH=2BH=,在Rt△CHG中,∠BCF=45°,∴CG=GH=.【点评】此题是圆的综合题,主要考查了切线的性质,切线长定理,锐角三角函数,相似三角形的判定和性质,勾股定理,求出tan∠ABD的值是解本题的关键.26.(10.00分)如图,抛物线y=ax2+bx+c与x轴交于A(,0),B两点(点B在点A的左侧),与y轴交于点C,且OB=3OA=OC,∠OAC的平分线AD交y轴于点D,过点A且垂直于AD的直线l交y轴于点E,点P是x轴下方抛物线上的一个动点,过点P作PF⊥x轴,垂足为F,交直线AD于点H.(1)求抛物线的解析式;(2)设点P的横坐标为m,当FH=HP时,求m的值;(3)当直线PF为抛物线的对称轴时,以点H为圆心,HC为半径作⊙H,点Q为⊙H上的一个动点,求AQ+EQ的最小值.【分析】(1)求出A、B、C的坐标,利用两根式求出抛物线的解析式即可;(2)求出直线AH的解析式,根据方程即可解决问题;(3)首先求出⊙H的半径,在HA上取一点K,使得HK=,此时K(﹣,﹣),由HQ2=HK•HA,可得△QHK∽△AHQ,推出==,可得KQ=AQ,推出AQ+QE=KQ+EQ,可得当E、Q、K共线时,AQ+QE的值最小,由此求出点E坐标,点K坐标即可解决问题;【解答】解:(1)由题意A(,0),B(﹣3,0),C(0,﹣3),设抛物线的解析式为y=a(x+3)(x﹣),把C(0,﹣3)代入得到a=,∴抛物线的解析式为y=x2+x﹣3.(2)在Rt△AOC中,tan∠OAC==,∴∠OAC=60°,∵AD平分∠OAC,∴∠OAD=30°,∴OD=OA•tan30°=1,∴D(0,﹣1),∴直线AD的解析式为y=x﹣1,由题意P(m,m2+m﹣3),H(m,m﹣1),F(m,0),∵FH=PH,∴1﹣m=m﹣1﹣(m2+m﹣3)解得m=﹣或(舍弃),∴当FH=HP时,m的值为﹣.(3)如图,∵PF是对称轴,∴F(﹣,0),H(﹣,﹣2),∵AH⊥AE,∴∠EAO=60°,∴EO=OA=3,∴E(0,3),∵C(0,﹣3),∴HC==2,AH=2FH=4,∴QH=CH=1,在HA上取一点K,使得HK=,此时K(﹣,﹣),∵HQ2=1,HK•HA=1,∴HQ2=HK•HA,可得△QHK∽△AHQ,∴==,∴KQ=AQ,∴AQ+QE=KQ+EQ,∴当E、Q、K共线时,AQ+QE的值最小,最小值==.【点评】本题考查二次函数综合题、一次函数的应用、一元二次方程、圆的有关知识、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.。
2019年广西柳州市中考数学试卷以及解析版

3.( 3 分) 【分析】 根据轴对称的性质可以判断答案; 【解答】 解: D 答案的图形是轴对称图形, 故选: D . 【点评】 本题考查轴对称的性质;熟练掌握轴对称的性质是解题的关键.
4.( 3 分) 【分析】 根据单项式乘以多项式的法则求解即可;
【解答】 解: x(x 2 1) x3 x ;
故选: A .
求证:四边形 ABCD 是平行四边形.
证明:
第 4 页(共 23 页)
23.( 8 分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小 本作业本贵 0.3 元,已知用 8 元购买大本作业本的数量与用 5 元购买小本作业本的数量相同. (1)求大本作业本与小本作业本每本各多少元? (2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的
6.( 3 分) 【分析】 直接利用圆周角定理进行判断.
【解答】 解: A 与 D 都是 BC 所对的圆周角,
D A. 故选: D . 【点评】 本题考查了圆周角定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等, 这条弧所对的圆心角的一半.
都等于
7.( 3 分) 【分析】 平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出 AO B (请保留作图痕迹) .
(2)完成下面证明 AO B AOB 的过程(注 : 括号里填写推理的依据) .
证明:由作法可知 O C OC , O D OD , D C
,
△ C O D COD (
)
AO B AOB . (
)
21.( 8 分)据公开报道, 2017 年全国教育经费总投入为 42557 亿元,比上年增长 9.43% , 其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.
2019年广西柳州市中考数学专题02:多结论题

结论是
.
图Z2-2
考向互动探究
题型一
[答案]
[解析]
代数类型(13年18题)
②④⑤
∵抛物线的开口向上,∴a>0.∵对称轴在 y 轴的右侧,∴b<0.∵抛物线和 y 轴的负半轴相
交,∴c<0,∴abc>0,故①错误; ∵抛物线 y=ax2+bx+c 过点(-1,0),对称轴为直线 x=1,则抛物线与 x 轴的另一个交点是(3,0),∴9a+3b+c=0. 又 a>0,∴9a+3b+c+a>0,即 10a+3b+c>0,故②正确; 直线 x=4 与直线 x=1 相距 3 个单位长度,直线 x=-3 与直线 x=1 相距 4 个单位长度,根据抛物线的对称性, 有 y2>y1,故③错误;∵抛物线 y=ax2+bx+c 过点(-1,0),∴a-b+c=0,∴b=a+c; ∵抛物线的对称轴为直线 x=1,∴- =1,
2 ������ ������
考向互动探究
题型一 代数类型( 13年18题)
������ ������
∴b=-2a,∴a+c=-2a,∴c=-3a,- =3, ∴无论 a,b,c 取何值,抛物线都经过同一个点(3,0),故④正确. ∵x=m 对应的函数值为 y=am2+bm+c,x=1 对应的函数值为 y=a+b+c. 又∵x=1 时函数取得最小值,∴a+b+c≤am2+bm+c,即 a+b≤am2+bm. ∵b=-2a,∴am2+bm+a≥0.故⑤正确. 综上所述,正确的结论是②④⑤.
2019年广西柳州市中考数学试卷(含解析)完美打印版

2019年广西柳州市中考数学试卷一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全4.(3分)计算:x(x2﹣1)=()A.x3﹣1B.x3﹣x C.x3+x D.x2﹣x5.(3分)反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30B.14.19C.19.57D.19.719.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.12.(3分)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6B.6C.5D.﹣5二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.(3分)计算:7x﹣4x=.14.(3分)如图,若AB∥CD,则在图中所标注的角中,一定相等的角是.15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.17.(3分)如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为.18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|﹣+π0.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.25.(10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP=OE•OM.26.(10分)如图,直线y=x﹣3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y=ax2+bx+c (a≠0)经过A,B,C三点,抛物线的顶点为点D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,CE的长为半径作圆,点P为直线y=x﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于CE时,过P,Q两点的直线与抛物线交于M,N两点(点M在点N的左侧),求四边形ABMN的面积.2019年广西柳州市中考数学试卷参考答案与试题解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n是负数.【解答】解:104400用科学记数法表示应为1.044×105,故选:C.2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.【分析】根据左视图是从几何体左面看得到的图形解答即可.【解答】解:题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全【分析】根据轴对称的性质可以判断答案;【解答】解:D答案的图形是轴对称图形,故选:D.4.(3分)计算:x(x2﹣1)=()A.x3﹣1B.x3﹣x C.x3+x D.x2﹣x 【分析】根据单项式乘以多项式的法则求解即可;【解答】解:x(x2﹣1)=x3﹣x;故选:B.5.(3分)反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限【分析】由反比例函数k>0,函数经过一三象限即可求解;【解答】解:∵k=2>0,∴反比例函数经过第一、三象限;故选:A.6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D 【分析】直接利用圆周角定理进行判断.【解答】解:∵∠A与∠D都是所对的圆周角,∴∠D=∠A.故选:D.7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB =CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形.故选:C.8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30B.14.19C.19.57D.19.71【分析】根据算术平均数的公式即可计算.【解答】解:由图象可知,2016年至2018年的GDP值分别为:11.19,12.24,13.46.则=≈12.30故选:A.9.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年【分析】联立两个一次函数解析式,求解即可【解答】解:由图表信息,联立中美GDP趋势线解析式得解得x=∴2018+(﹣15)=故选:B.10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)【分析】根据路程=速度×时间,容易知道y与x的函数关系式.【解答】解:根据题意得:全程需要的时间为:3÷4=(小时),∴y=3﹣4x(0≤x≤).故选:D.11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.【分析】画出树状图,共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,即可得出答案.【解答】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为;故选:A.12.(3分)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6B.6C.5D.﹣5【分析】先利用完全平方公式得出(3﹣mi)2=9﹣6mi+m2i2,再根据新定义得出复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,由(3﹣mi)2的虚部是12得出m=﹣2,代入9﹣m2计算即可.【解答】解:∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.(3分)计算:7x﹣4x=3x.【分析】根据合并同类项法则计算可得.【解答】解:7x﹣4x=(7﹣4)x=3x,故答案为:3x.14.(3分)如图,若AB∥CD,则在图中所标注的角中,一定相等的角是∠1=∠3.【分析】利用平行线的性质进行判断.【解答】解:∵AB∥CD,∴∠1=∠3.故答案为15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是0.95(结果精确到0.01).【分析】概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概.【解答】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95.故答案为:0.9516.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为5.【分析】先根据题意画出图形,再连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,由垂径定理及正方形的性质得出OE=BE=,再由勾股定理即可求解.【解答】解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE=,即a=5.故答案为:5.17.(3分)如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为.【分析】过A作AD垂直于BC,在直角三角形ABD中,利用锐角三角函数定义求出AD的长,在直角三角形ACD中,利用锐角三角函数定义求出CD的长,再利用勾股定理求出AC的长即可.【解答】解:过A作AD⊥BC,在Rt△ABD中,sin B=,AB=3,∴AD=AB•sin B=1,在Rt△ACD中,tan C=,∴=,即CD=,根据勾股定理得:AC===,故答案为:18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是7.【分析】根据5个数的平均数是8,可知这5个数的和为40,根据5个数的中位数是8,得出中间的数是8,根据众数是8,得出至少有2个8,再根据5个数的和减去2个8和1个9得出前面2个数的和为15,再根据方差得出前面的2个数为7和8,即可得出结果.【解答】解:∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|﹣+π0.【分析】先计算乘方、绝对值、算术平方根和零指数幂,再计算加减可得.【解答】解:原式=4+3﹣2+1=6.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)【分析】(1)根据题意作出图形即可;(2)根据全等三角形的判定和性质即可得到结论.【解答】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)【分析】(1)根据扇形统计图中义务教育段的经费所占的百分比乘以42557亿元即可得到结论;(2)根据题意列式计算即可得到结论.【解答】解:(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38889.7亿元,答:2016年全国教育经费总投入约为38889.7亿元.22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:【分析】连接AC,由SSS证明△ABC≌△CDA得出∠BAC=∠DCA,∠ACB=∠CAD,证出AB∥CD,BC∥AD,即可得出结论.【解答】证明:连接AC,如图所示:在△ABC和△CDA中,,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?【分析】(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,根据数量=总价÷单价结合用8元购买大本作业本的数量与用5元购买小本作业本的数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设大本作业本购买m本,则小本作业本购买2m本,根据总价=单价×数量结合总费用不超过15元,即可得出关于m的一元一次不等式,解之取其中的最大整数值即可得出结论.【解答】解:(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,依题意,得:=,解得:x=0.5,经检验,x=0.5是原方程的解,且符合题意,∴x+0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.【分析】(1)将点A(1,0),点B(0,2),代入y=mx+b,可求直线解析式;过点C作CD⊥x轴,根据三角形全等可求C(3,1),进而确定k;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,当△=h2﹣24=0时,点P到直线AB距离最短;【解答】解:(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,∴﹣2x2+hx﹣3=0,当△=h2﹣24=0时,h=,此时点P到直线AB距离最短;∴P(,);25.(10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP=OE•OM.【分析】(1)连接BC,AC,AD,通过证明△ACE∽△CEB,可得,可求BE的长,即可求⊙O 的半径;(2)通过证明△ADE≌△NDE,可得∠DAN=∠DNA,即可证BN=BF,可得△BNF为等腰三角形;(3)通过证明△ODE∽△ODM,可得DO2=OE•OM,通过证明△PCO∽△CEO,可得CO2=PO•ON,即可得结论.【解答】解:(1)如图1,连接BC,AC,AD,∵CD⊥AB,AB是直径∴,CE=DE=CD=3∴∠ACD=∠ABC,且∠AEC=∠CEB∴△ACE∽△CEB∴∴∴BE=9∴AB=AE+BE=10∴⊙O的半径为5(2)∵=∴∠ACD=∠ADC=∠CDF,且DE=DE,∠AED=∠NED=90°∴△ADE≌△NDE(ASA)∴∠DAN=∠DNA,AE=EN∵∠DAB=∠DFB,∠AND=∠FNB∴∠FNB=∠DFB∴BN=BF,∴△BNF是等腰三角形(3)如图2,连接AC,CE,CO,DO,∵MD是切线,∴MD⊥DO,∴∠MDO=∠DEO=90°,∠DOE=∠DOE∴△MDO∽△DEO∴∴OD2=OE•OM∵AE=EN,CD⊥AO∴∠ANC=∠CAN,∴∠CAP=∠CNO,∵∴∠AOC=∠ABF∵CO∥BF∴∠PCO=∠PFB∵四边形ACFB是圆内接四边形∴∠P AC=∠PFB∴∠P AC=∠PFB=∠PCO=∠CNO,且∠POC=∠COE∴△CNO∽△PCO∴∴CO2=PO•NO,∴ON•OP=OE•OM.26.(10分)如图,直线y=x﹣3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y=ax2+bx+c (a≠0)经过A,B,C三点,抛物线的顶点为点D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,CE的长为半径作圆,点P为直线y=x﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于CE时,过P,Q两点的直线与抛物线交于M,N两点(点M在点N的左侧),求四边形ABMN的面积.【分析】(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),即可求解;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,即可求解;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,即可求解.【解答】解:(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),则抛物线的表达式为:y=a(x﹣3)(x﹣1)=a(x2﹣4x+3),则3a=﹣3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+4x﹣3…①;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,连接AB′,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,D(2,1),则点G(2,﹣1),即:BG=EG,即点G是BB′的中点,过点B′(3,﹣2),△BDP周长最小值=BD+B′B=;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,点A、B、C、E、F的坐标为(3,0)、(1,0)、(0,﹣3)、(2,0)、(﹣2,0),则CE=,FQ=CE,则PF=CE﹣CE=,设点P(m,m﹣3),点F(﹣2,0),PF2=13=(m﹣2)2+(m﹣3)2,解得:m=1,故点P(1,﹣2),将点P、F坐标代入一次函数表达式并解得:直线PF的表达式为:y=﹣x﹣…②,联立①②并解得:x=,故点M、N的坐标分别为:(,)、(,),过点M、N分别作x轴的垂线交于点S、R,则S四边形ABMN=S梯形NRSM﹣S△ARN﹣S△SBM=.。
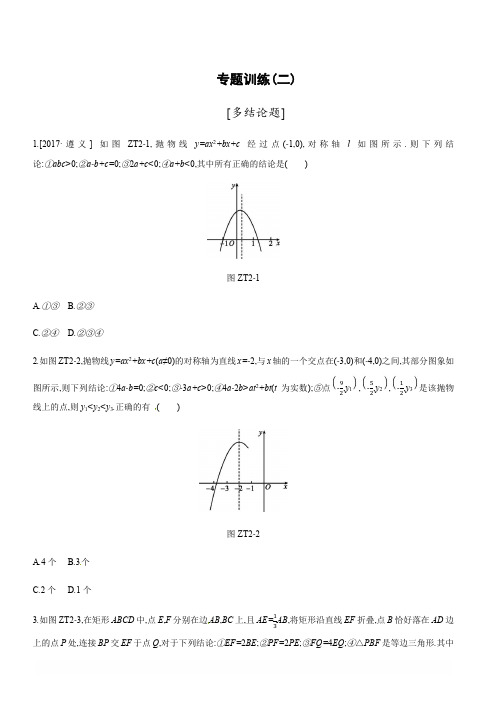
2019年广西柳州市中考数学专题训练02:多结论题含答案
专题训练(二)[多结论题]1.[2017·遵义] 如图ZT2-1,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是()图ZT2-1A.①③B.②③C.②④D.②③④2.如图ZT2-2,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示,则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点-,y1,-,y2,-,y3是该抛物线上的点,则y1<y2<y3.正确的有()图ZT2-2A.4个B.3个C.2个D.1个3.如图ZT2-3,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()图ZT2-3A.①②B.②③C.①③D.①④4.如图ZT2-4,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DF P∽△BPH;③△PFD∽△PDB;④DP2=PH·PC.其中正确的是()图ZT2-4A.①②③④B.②③C.①②④D.①③④5.[2018·宜宾] 如图ZT2-5,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是.(写出所有正确结论的序号)图ZT2-5①当E为线段AB中点时,AF∥CE;②当E为线段AB中点时,AF=;③当A,F,C三点共线时,AE=-;④当A,F,C三点共线时,△CEF≌△AEF.6.[2017·南充] 如图ZT2-6,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是(填写序号).图ZT2-6参考答案1.D[解析] ∵开口向下,∴a<0.∵对称轴与x轴的正半轴相交,∴a,b异号,即b>0.∵抛物线与y轴正半轴相交,∴c>0,即abc<0,结论①错误.∵抛物线y=ax2+bx+c经过点(-1,0),∴a-b+c=0,结论②正确.∵当x=2时,y<0,即4a+2b+c<0,又b=a+c,∴4a+2(a+c)+c<0,即2a+c<0,结论③正确.∵c=b-a,∴a+b<0,结论④正确.2.C[解析] ∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,∴-=-2,∴4a-b=0,故①正确;∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,∴另一个交点位于(-1,0)和(0,0)之间,∴抛物线与y轴的交点在原点的下方,∴c<0.故②正确;∵4a-b=0,∴b=4a.∵抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,∴Δ=b2-4ac=(4a)2-4ac=16a2-4ac>0.∵a<0,∴4a-c<0,∴c>4a,∴-3a+c>-3a+4a=a<0,故③错误;∵4a-b=0,∴b=4a,∴at2+bt-(4a-2b)=at2+4at-(4a-2×4a)=at2+4at+4a=a(t2+4t+4)=a(t+2)2.∵t为实数,a<0,∴a(t+2)2≤0,∴at2+bt-(4a-2b)≤0,∴at2+bt≤4a-2b,即4a-2b≥at2+bt,∴④错误;∵点-,y1,-,y2,-,y3是该抛物线上的点, ∴将它们描在图象上如图:由图象可知:y1<y3<y2,∴⑤错误.综上所述,正确的有2个.故选C.3.D[解析] ∵AE=AB,∴AB=3AE,BE=2AE.由翻折的性质得,PE=BE.∴∠APE=30°,∴∠AEP=90°-30°=60°,∴∠BEF=(180°-∠AEP)=(180°-60°)=60°,∴∠EFB=90°-60°=30°,∴EF=2BE,故①正确; ∵BE=PE,∴EF=2PE.∵EF>PF,∴PF<2PE,故②错误;由翻折可知EF⊥PB,∴∠EBQ=∠EFB=30°,∴BE=2EQ,EF=2BE,∴FQ=3EQ,故③错误;由翻折的性质知,∠EFB=∠EFP=30°,∴∠BFP=30°+30°=60°.∵∠PBF=90°-∠EBQ=90°-30°=60°,∴∠PB F=∠PFB=60°,∴△PBF是等边三角形,故④正确.综上所述,结论正确的是①④.4.C[解析] 在正方形ABCD中,∠A=90°.由△BPC是等边三角形,可得∠CBP=60°,∴∠ABP=30°,∴BE=2AE,即①正确;BD是正方形ABCD的对角线,可得△BCD是等腰直角三角形,∴∠CBD=∠CDB=45°,可得∠PBD=15°.∵CD=CP=CB,∠PCD=30°,可得∠CPD=∠CDP=75°,∴∠BPD=75°+60°=135°,∠FDP=90°-75°=15°,∠PFD=90°-∠PCD=90°-30°=60°,∠FPD=180°-∠PDF-∠PFD=180°-15°-60°=105°,∴∠PBD=∠PDF,∠BPH=∠DFP,∴△DFP∽△BPH,即②正确;∠BPD≠∠DPF,∴③△PFD∽△PDB错误;由∠PDH=∠PDC-∠CDB=75°-45°=30°=∠PCD,∠CPD=∠DPH,可得△PDC∽△PHD,∴DP2=PH·PC,即④正确. 5.①②③[解析] 由折叠的性质可知CF=CB,∠CFE=90°,∠CEB=∠CEF,当E为AB中点时,BE=EF=AE=,∴∠F AE=∠AFE,∵∠FEB=∠F AE+∠AFE,∴∠CEB=∠CEF=∠F AE=∠AFE,∴AF∥CE,故①正确;∵E为AB中点时,BE=,BC=2,∴CE=,过点E作EM⊥AF于点M,∵∠AFE=∠FEC,EM⊥AF,∠CFE=90°,∴AF=2MF,△MFE∽△FEC,∴=,即=,∴MF=,∴AF=,故②正确;当A,F,C三点共线时,∠AFE=90°,AC==,设BE=x,则EF=x,AE=3-x,AF=-2,在Rt△AFE 中,(-2)2+x2=(3-x)2,解得x=-,∴AE=3-x=-,故③正确;∵AF=2,CF=2,∴AF≠CF,∴④错误.6.①②③[解析]①∵正方形的各边相等,各角都是90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.∴△BCE≌△DCG(SAS),∴BE=DG.结论①正确.②如图,设BE交DC于点M,交DG于点O.由△BCE≌△DCG可知∠CBE=∠CDG.又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即BE⊥DG.结论②正确.③连接BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.由勾股定理得BD2+EG2=2a2+2b2.∴DE2+BG2=2a2+2b2.结论③正确.综上所述,正确的结论是①②③.。
2019柳州中考数学试题(卷)(答案解析)

2019年广西市中考一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全4.(3分)计算:x(x2﹣1)=()A.x3﹣1B.x3﹣x C.x3+x D.x2﹣x5.(3分)反比例函数y=2x的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30B.14.19C.19.57D.19.719.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥3 4)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤3 4)11.(3分)小与小做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小获胜,那么,小获胜的概率为()A .1325B .1225C .425D .1212.(3分)定义:形如a +bi 的数称为复数(其中a 和b 为实数,i 为虚数单位,规定i 2=﹣1),a 称为复数的实部,b 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i )2=12+2×1×3i +(3i )2=1+6i +9i 2=1+6i ﹣9=﹣8+6i ,因此,(1+3i )2的实部是﹣8,虚部是6.已知复数(3﹣mi )2的虚部是12,则实部是( )A .﹣6B .6C .5D .﹣5二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.) 13.(3分)计算:7x ﹣4x = .14.(3分)如图,若AB ∥CD ,则在图中所标注的角中,一定相等的角是 .15.(3分)市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据: 种子数n 30 75 130 210 480 856 1250 2300 发芽数m2872 125 200 457 814 1187 2185 发芽频率mn0.93330.96000.96150.95240.95210.95090.94960.9500依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是 (结果精确到0.01).16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .17.(3分)如图,在△ABC 中,sin B =13,tan C =√22,AB =3,则AC 的长为 .18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|−√4+π0.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:23.(8分)小去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=kx(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=kx(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=kx(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.25.(10分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,点F 是⊙O 上一点,且AC ̂=CF ̂,连接FB ,FD ,FD 交AB 于点N . (1)若AE =1,CD =6,求⊙O 的半径; (2)求证:△BNF 为等腰三角形;(3)连接FC 并延长,交BA 的延长线于点P ,过点D 作⊙O 的切线,交BA 的延长线于点M .求证:ON •OP =OE •OM .26.(10分)如图,直线y =x ﹣3交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线y =ax 2+bx +c (a ≠0)经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线y =x ﹣3上的一个动点. (1)求抛物线的解析式; (2)求△BDP 周长的最小值;(3)若动点P 与点C 不重合,点Q 为⊙F 上的任意一点,当PQ 的最大值等于32CE 时,过P ,Q 两点的直线与抛物线交于M ,N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.2019年广西市中考数学试卷参考答案与试题解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆【解答】解:104400用科学记数法表示应为1.044×105,故选:C.2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.【解答】解:题中的几何体从左面看,得到的图形是一个长方形及其部一个圆,如图所示:故选:C.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全【解答】解:D答案的图形是轴对称图形,故选:D.4.(3分)计算:x(x2﹣1)=()A.x3﹣1B.x3﹣x C.x3+x D.x2﹣x 【解答】解:x(x2﹣1)=x3﹣x;故选:B.5.(3分)反比例函数y=2x的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限【解答】解:∵k=2>0,∴反比例函数经过第一、三象限;故选:A.6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D 【解答】解:∵∠A与∠D都是BĈ所对的圆周角,∴∠D=∠A.故选:D.7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形.故选:C.8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A .12.30B .14.19C .19.57D .19.71【解答】解:由图象可知,2016年至2018年的GDP 值分别为:11.19,12.24,13.46. 则 X =11.19+12.24+13.463≈12.30 故选:A .9.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国生产总值(GDP )的直方图及发展趋势线.(注:趋势线由Excel 系统根据数据自动生成,趋势线中的y 表示GDP ,x 表示年数)2004﹣2018年中美两国国生产总值(GDP ,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP 要超过美国,至少要到( ) A .2052年B .2038年C .2037年D .2034年【解答】解:由图表信息,联立中美GDP 趋势线解析式得{y =0.86x +0.468y =0.53x +11.778解得x =34311∴2018+(34311−15)=2037311故选:B .10.(3分)已知A 、B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),则y 关于x 的函数解析式是( ) A .y =4x (x ≥0) B .y =4x ﹣3(x ≥34)C .y =3﹣4x (x ≥0)D .y =3﹣4x (0≤x ≤34)【解答】解:根据题意得:全程需要的时间为:3÷4=34(小时), ∴y =3﹣4x (0≤x ≤34). 故选:D .11.(3分)小与小做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小获胜,那么,小获胜的概率为( )A .1325B .1225C .425D .12【解答】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个, ∴小获胜的概率为1325;故选:A .12.(3分)定义:形如a +bi 的数称为复数(其中a 和b 为实数,i 为虚数单位,规定i 2=﹣1),a 称为复数的实部,b 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i )2=12+2×1×3i +(3i )2=1+6i +9i 2=1+6i ﹣9=﹣8+6i ,因此,(1+3i )2的实部是﹣8,虚部是6.已知复数(3﹣mi )2的虚部是12,则实部是( )A .﹣6B .6C .5D .﹣5【解答】解:∵(3﹣mi )2=32﹣2×3×mi +(mi )2=9﹣6mi +m 2i 2=9+m 2i 2﹣6mi =9﹣m 2﹣6mi ,∴复数(3﹣mi )2的实部是9﹣m 2,虚部是﹣6m , ∴﹣6m =12, ∴m =﹣2,∴9﹣m 2=9﹣(﹣2)2=9﹣4=5. 故选:C .二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.) 13.(3分)计算:7x ﹣4x = 3x . 【解答】解:7x ﹣4x =(7﹣4)x =3x , 故答案为:3x .14.(3分)如图,若AB ∥CD ,则在图中所标注的角中,一定相等的角是 ∠1=∠3 .【解答】解:∵AB ∥CD , ∴∠1=∠3. 故答案为15.(3分)市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据: 种子数n 30 75 130 210 480 856 1250 2300 发芽数m2872 125 200 457 814 1187 2185 发芽频率mn0.93330.96000.96150.95240.95210.95090.94960.9500依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是 0.95 (结果精确到0.01).【解答】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95. 故答案为:0.9516.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 5√2 .【解答】解:如图所示,连接OB 、OC ,过O 作OE ⊥BC ,设此正方形的边长为a , ∵OE ⊥BC , ∴OE =BE =a2, 即a =5√2. 故答案为:5√2.17.(3分)如图,在△ABC 中,sin B =13,tan C =√22,AB =3,则AC 的长为 √3 .【解答】解:过A 作AD ⊥BC , 在Rt △ABD 中,sin B =13,AB =3, ∴AD =AB •sin B =1, 在Rt △ACD 中,tan C =√22, ∴AD CD=√22,即CD =√2, 根据勾股定理得:AC =√AD 2+CD 2=√1+2=√3, 故答案为:√318.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是7.【解答】解:∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|−√4+π0.【解答】解:原式=4+3﹣2+1=6.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)【解答】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)【解答】解:(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38.9亿元,答:2016年全国教育经费总投入约为38.8亿元.22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD 中,AB =CD ,AD =BC . 求证:四边形ABCD 是平行四边形. 证明:【解答】证明:连接AC ,如图所示: 在△ABC 和△CDA 中,{AB =CD AD =CBAC =CA ,∴△ABC ≌△CDA (SSS ),∴∠BAC =∠DCA ,∠ACB =∠CAD , ∴AB ∥CD ,BC ∥AD , ∴四边形ABCD 是平行四边形.23.(8分)小去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同. (1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?【解答】解:(1)设小本作业本每本x 元,则大本作业本每本(x +0.3)元, 依题意,得:8x+0.3=5x,解得:x =0.5,经检验,x =0.5是原方程的解,且符合题意, ∴x +0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤50 6.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=kx(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=kx(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=kx(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.【解答】解:(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=3 x;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x +h =3x, ∴﹣2x 2+hx ﹣3=0,当△=h 2﹣24=0时,h =±2√6,此时点P 到直线AB 距离最短; ∴P (√62,√6);25.(10分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,点F 是⊙O 上一点,且AC ̂=CF ̂,连接FB ,FD ,FD 交AB 于点N . (1)若AE =1,CD =6,求⊙O 的半径; (2)求证:△BNF 为等腰三角形;(3)连接FC 并延长,交BA 的延长线于点P ,过点D 作⊙O 的切线,交BA 的延长线于点M .求证:ON •OP =OE •OM .【解答】解:(1)如图1,连接BC ,AC ,AD ,∵CD ⊥AB ,AB 是直径 ∴AĈ=AD ̂,CE =DE =12CD =3∴∠ACD =∠ABC ,且∠AEC =∠CEB∴△ACE ∽△CEB∴AE CE=CE BE ∴13=3BE∴BE =9∴AB =AE +BE =10∴⊙O 的半径为5(2)∵AĈ=AD ̂=CF ̂ ∴∠ACD =∠ADC =∠CDF ,且DE =DE ,∠AED =∠NED =90°∴△ADE ≌△NDE (ASA )∴∠DAN =∠DNA ,AE =EN∵∠DAB =∠DFB ,∠AND =∠FNB∴∠FNB =∠DFB∴BN =BF ,∴△BNF 是等腰三角形(3)如图2,连接AC ,CE ,CO ,DO ,∵MD 是切线,∴MD ⊥DO ,∴∠MDO =∠DEO =90°,∠DOE =∠DOE∴△MDO ∽△DEO∴OE OD =OD OM∴OD 2=OE •OM∵AE =EN ,CD ⊥AO∴∠ANC =∠CAN ,∴∠CAP =∠CNO ,∵AĈ=CF ̂ ∴∠AOC =∠ABF∵CO ∥BF∴∠PCO =∠PFB∵四边形ACFB 是圆接四边形∴∠P AC =∠PFB∴∠P AC =∠PFB =∠PCO =∠CNO ,且∠POC =∠COE∴△CNO ∽△PCO∴NO CO =CO PO∴CO 2=PO •NO ,∴ON •OP =OE •OM .26.(10分)如图,直线y =x ﹣3交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线y =ax 2+bx +c (a ≠0)经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线y =x ﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP 周长的最小值;(3)若动点P 与点C 不重合,点Q 为⊙F 上的任意一点,当PQ 的最大值等于32CE 时,过P ,Q 两点的直线与抛物线交于M ,N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.【解答】解:(1)直线y =x ﹣3,令x =0,则y =﹣3,令y =0,则x =3,故点A、C的坐标为(3,0)、(0,﹣3),则抛物线的表达式为:y=a(x﹣3)(x﹣1)=a(x2﹣4x+3),则3a=﹣3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+4x﹣3…①;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,连接AB′,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,D(2,1),则点G(2,﹣1),即:BG=EG,即点G是BB′的中点,过点B′(3,﹣2),△BDP周长最小值=BD+B′B=√2+√10;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,点A、B、C、E、F的坐标为(3,0)、(1,0)、(0,﹣3)、(2,0)、(﹣2,0),则CE=√13,FQ=12CE,则PF=32CE−12CE=√13,设点P(m,m﹣3),点F(﹣2,0),PF2=13=(m﹣2)2+(m﹣3)2,解得:m=1,故点P(1,﹣2),将点P、F坐标代入一次函数表达式并解得:直线PF的表达式为:y=−23x−43⋯②,联立①②并解得:x=7±√343,故点M、N的坐标分别为:(7−√343,−26+2√349)、(7+√343,−26−2√349),过点M、N分别作x轴的垂线交于点S、R,则S四边形ABMN=S梯形NRSM﹣S△ARN﹣S△SBM=26+8√349.。
2019广西柳州中考数学解析

2019年广西柳州市初中毕业、升学考试数学(满分120分,考试时间120分钟)一、选择题:本大题共12小题,每小题3分,共36分.不需写出解答过程,请把最后结果填在题后括号内.1.(2019年广西柳州市,1,3分)【答案】C【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.104400用科学记数法表示应为1.044×105,故选:C.【知识点】科学记数法2.(2019年广西柳州市,2,3分)如图,这是一个机械零部件,该零部件的左视图是()A.B. C.D.【答案】C【解析】左视图就是从几何体左边看到的图形,从左看可得一个圆在长方形内,故选C.【知识点】三视图3.(2019年广西柳州市,3,3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑落安全 D .注意安全【答案】D【解析】根据轴对称图形的定义A、B、C都不是轴对称图形,D 是轴对称图形,故选D.【知识点】轴对称图形4.(2019年广西柳州市,4,3分)计算x(x2-1)=( )A.x3-1 B.x3-x C.x3+x D.x2-x【答案】B【解析】根据单项式乘多项式的法则,把单项式与多项式的每一项相乘,x(x2-1)= x3-x,故选B.【知识点】单项式乘多项式5.(2019年广西柳州市,5,3分)反比例函数2yx的图像位于()A.第一、三象限B.第二、三象限C.第一、二象限 D .第二、四象限【答案】A【解析】∵k=2>0,∴反比例函数经过第一、三象限;故选:A.【知识点】反比例函数的图象及性质6.(2019年广西柳州市,6,3分)如图,A 、B 、C 、D 是圆上的点,则图中与∠A 相等的角是( )E OBACDA .∠B B .∠C C .∠DEBD .∠D 【答案】D【解析】:∵∠A 与∠D 都是弧BC 所对的圆周角,∴∠D=∠A .故选:D . 【知识点】圆周角定理7.(2019年广西柳州市,7,3分)如图, ABCD 中,全等三角形的对数共有( )OCDBAA .2对B .3对C .4 对D .5 对 【答案】C 【解析】:∵四边形ABCD 是平行四边形,∴AB=CD ,AD=BC ;OD=OB ,OA=OC ;∵OD=OB ,OA=OC ,∠AOD=∠BOC ;∴△AOD ≌△COB (SAS );①同理可得出△AOB ≌△COD (SAS );②∵BC=AD ,CD=AB ,BD=BD ;∴△ABD ≌△CDB (SSS );③同理可得:△ACD ≌△CAB (SSS ).④因此本题共有4对全等三角形.故选:C .【知识点】平行四边形的性质;全等三角形的判定 阅读【资料】,完成第8、9题【资料】 如图,这是根据公开资料整理绘制而成的2004—2018年中美两国国内生产总值(GDP )的直方图及发展趋势线(注:趋势线由Excel 系统根据数据自动生成,趋势线中的y 表示GDP ,x 表示年数)8.(2019年广西柳州市,8,3分)依据【资料】中所提供的信息,2016—2018年中国GDP 的平均值大约是( )A .12.30B .14.19C .19.57D .19.71【答案】A【解析】从条形统计图中获取2016—2018年中国GDP的值,则这三年的平均值为11.1912.2413.4612.303++≈,故选A.【知识点】平均数;条形统计图9.(2019年广西柳州市,8,3分)依据【资料】中所提供的信息,可以推算出的GDP要超过美国,至少要到()A.2052 B.2038 C.2037 D .2034【答案】B【解析】由统计图得:0.86x+0.468>0.53x+11.778,解得x>34,即到2038年GDP超过美国,因此本题选B.【知识点】折线统计图;一次函数与一元一次不等式10.(2019年广西柳州市,8,3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4 千米/时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0) B.y=4x-3(x≥34) C.y=3-4x(x≥0) D .y=3-4x(0≤x≤34)【答案】D【思路分析】根据实际问题得关系式:余下的路程=相距的路程-已走的路程写出函数关系式,再求出自变量的取值范围.【解题过程】函数关系式为y=3-4x,总用时不超过34小时,∴自变量的取值范围为0≤x≤34,故选D.【知识点】函数关系式;自变量的取值范围11.(2019年广西柳州市,8,3分)小李与小陈做猜拳游戏,规定每人每次至少出一个手指,两人出拳的手指之和为偶数时小李获胜,那么小李获胜的概率为()A.1325B.1225C.425D .12【答案】A【思路分析】画出树状图,共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,由概率公式得出答案.【解题过程】画树状图如下:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为,故选A.【知识点】概率12.(2019年广西柳州市,8,3分)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6 B.6 C.5 D.﹣5【答案】C【思路分析】先利用完全平方公式得出(3﹣mi)2=9﹣6mi+m2i2,再根据新定义得出复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,由(3﹣mi)2的虚部是12得出m=﹣2,代入9﹣m2计算即可.【解题过程】∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.【知识点】完全平方公式;新定义【点评】本题考查了新定义,完全平方公式,理解新定义是解题的关键.二、填空题:本大题共6小题,每小题3分,共18分.不需写出解答过程,请把最后结果填在题中横线上.13.(2019年广西柳州市,13,3分)计算:7x-4x=___________.【答案】3x【解析】根据合并同类项的法则计算,7x-4x=3x,因此本题填3x.【知识点】合并同类项14.(2019年广西柳州市,14,3分)如图,若AB∥CD,则在图中所标注的角中,一定相等的角是___________.321AB CED【答案】∠1=∠3【解析】AB∥CD,根据两直线平行,同位角相等得∠1=∠3,因此本题填∠1=∠3.【知识点】平行线的判定15.(2019年广西柳州市,15,3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果,下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:种子数n 30 75 130 210 480 856 1250 2300发芽数m 28 72 125 200 457 814 1187 2185发芽频率mn0.9333 0.9600 0.9615 0.9524 0.9521 0.9509 0.9496 0.9500依据上面的数据可以估计,这种植物种子在该实验条件下发芽率约是___________(结果精确到0.01).【答案】0.95【解析】在相同实验条件下,频率会逐步稳定在某一个值附近,本题发芽频率的值稳定在0.95附近,所以发芽率约是0.95,因此本题填0.95.【知识点】样本估计总体16.(2019年广西柳州市,16,3分)在半径为5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为___________.【答案】5【解析】先根据题意画出图形,再连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,由垂径定理及正方形的性质得出OE=BE=,再由勾股定理求得a=5.【知识点】正多边形和圆17.(2019年广西柳州市,17,3分)如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为.【答案】【思路分析】过A作AD垂直于BC,在直角三角形ABD中,利用锐角三角函数定义求出AD的长,在直角三角形ACD中,利用锐角三角函数定义求出CD的长,再利用勾股定理求出AC的长.【解题过程】过A作AD⊥BC,在Rt△ABD中,sin B=,AB=3,∴AD=AB•sin B=1,在Rt△ACD中,tan C=,∴=,即CD=,根据勾股定理得:AC===,故答案为:.【知识点】解直角三角形18.(2019年广西柳州市,18,3分)已知一组数据共有5 个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是___________.【答案】7【思路分析】根据5个数的平均数是8,可知这5个数的和为40,根据5个数的中位数是8,得出中间的数是8,根据众数是8,得出至少有2个8,再根据5个数的和减去2个8和1个9得出前面2个数的和为15,再根据方差得出前面的2个数为7和8,即可得出结果.【解题过程】∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7.【知识点】方差、平均数、中位数、众数三、解答题(本大题共8小题,满分66分,解答应写出文字说明、证明过程或演算步骤)19.(2019年广西柳州市,19,6分)计算:22+|﹣3|﹣+π0.【思路分析】先计算乘方、绝对值、算术平方根和零指数幂,再计算加减可得.【解题过程】原式=4+3﹣2+1=6.【知识点】实数的运算20.(2019年广西柳州市,20,6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()【思路分析】(1)根据题目中的作法作出图形;(2)根据SSS得到两个三角形全等,从而得出∠A′O′B′=∠AOB.【解题过程】(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.【知识点】尺规作图,全等三角形的判定和性质21.(2019年广西柳州市,21,8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)【思路分析】(1)根据扇形统计图中义务教育段的经费所占的百分比乘以42557亿元即可得到结论;(2)用2017年全国教育经费总投入42557亿元除以(1+9.43%)得到2016年全国教育经费总投入.【解题过程】(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38.9亿元,答:2016年全国教育经费总投入约为38.8亿元.【知识点】扇形统计图;近似数和有效数字22.(2019年广西柳州市,22,8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:【思路分析】连接AC,由SSS证明△ABC≌△CDA得出∠BAC=∠DCA,∠ACB=∠CAD,证出AB∥CD,BC∥AD,即可得出结论.【解题过程】连接AC,如图所示:在△ABC和△CDA中,,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.【知识点】平行四边形的判定;全等三角形的判定与性质23.(2019年广西柳州市,23,8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?【思路分析】(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,根据数量=总价÷单价结合用8元购买大本作业本的数量与用5元购买小本作业本的数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设大本作业本购买m本,则小本作业本购买2m本,根据总价=单价×数量结合总费用不超过15元,即可得出关于m的一元一次不等式,解之取其中的最大整数值.【解题过程】(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,依题意,得:=,解得:x=0.5,经检验,x=0.5是原方程的解,且符合题意,∴x+0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.【知识点】分式方程的应用;一元一次不等式的应用24.(2019年广西柳州市,24,10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.【思路分析】(1)将点A(1,0),点B(0,2),代入y=mx+b,可求直线解析式;过点C作CD⊥x轴,根据三角形全等可求C(3,1),进而确定k;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+b=,当△=b2﹣24=0时,点P到直线AB距离最短;【解题过程】(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+b=,∴﹣2x2+bx﹣3=0,当△=b2﹣24=0时,b=,此时点P到直线AB距离最短;∴P(,);【知识点】反比例函数的图像与性质;一次函数;旋转;判别式25.(2019年广西柳州市,25,10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP =OE•OM.【思路分析】(1)连接BC,AC,AD,通过证明△ACE∽△CEB,可得,可求BE的长,即可求⊙O的半径;(2)通过证明△ADE≌△NDE,可得∠DAN=∠DNA,即可证BN=BF,可得△BNF为等腰三角形;(3)通过证明△ODE∽△ODM,可得DO2=OE•OM,通过证明△PCO∽△CEO,可得CO2=PO•ON,即可得结论.【解题过程】(1)如图1,连接BC,AC,AD,∵CD⊥AB,AB是直径∴,CE=DE=CD=3∴∠ACD=∠ABC,且∠AEC=∠CEB∴△ACE∽△CEB∴∴∴BE=9∴AB=AE+BE=10∴⊙O的半径为5(2)∵=∴∠ACD=∠ADC=∠CDF,且DE=DE,∠AED=∠NED=90°∴△ADE≌△NDE(ASA)∴∠DAN=∠DNA,AE=EN∵∠DAB=∠DFB,∠AND=∠FNB∴∠FNB=∠DFB∴BN=BF,∴△BNF是等腰三角形(3)如图2,连接AC,CE,CO,DO,∵MD是切线,∴MD⊥DO,∴∠MDO=∠DEO=90°,∠DOE=∠DOE∴△MDO∽△DEO∴∴OD2=OE•OM∵AE=EN,CD⊥AO∴∠ANC=∠CAN,∴∠CAP=∠CNO,∵∴∠AOC=∠ABF∵CO∥BF∴∠PCO=∠PFB∵四边形ACFB是圆内接四边形∴∠PAC=∠PFB∴∠PAC=∠PFB=∠PCO=∠CNO,且∠POC=∠COE∴△CNO∽△PCO∴∴CO2=PO•NO,∴ON•OP=OE•OM.【知识点】圆周角定理;垂径定理;全等三角形的判定与性质;相似三角形的判定和性质26.(2019年广西柳州市,26,10分)如图,直线y=x-3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y=x2+bx+c(a≠0)经过A、B、C三点,抛物线的顶点为D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,12CE的长为半径作圆,点P为直线y=x-3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于32CE时,过PQ两点的直线与抛物线交于MN两点,点M在点N的左侧,求四边形ABMN的面积.【思路分析】(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),代入抛物线的解析式求解;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,用对称求得B′的坐标,进而求出B′B的长,最后求得△BDP周长的最小值;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,P在直线y=x﹣3上,设点P(m,m﹣3),利用PF=CE求出点P的坐标,进而得出直线PF的解析式,求得PF与抛物线的两个交点,则S四边形ABMN=S梯形NRSM减去S△ARN减去S△SBM.【解题过程】(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),则抛物线的表达式为:y=a(x﹣3)(x﹣1)=a(x2﹣4x+3),则3a=﹣3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+4x﹣3…①;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,连接AB′,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,D(2,1),则点G(2,﹣1),即:BG=EG,即点G是BB′的中点,过点B′(3,﹣2),△BDP周长最小值=BD+B′B=;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,点A、B、C、E、F的坐标为(3,0)、(1,0)、(0,﹣3)、(2,0)、(﹣2,0),则CE=,FQ=CE,则PF=CE﹣CE=,设点P(m,m﹣3),点F(﹣2,0),PF2=13=(m﹣2)2+(m﹣3)2,解得:m=1,故点P(1,﹣2),将点P、F坐标代入一次函数表达式并解得:直线PF的表达式为:y=﹣x﹣…②,联立①②并解得:x=,故点M、N的坐标分别为:(,)、(,),过点M、N分别作x轴的垂线交于点S、R,则S四边形ABMN=S梯形NRSM﹣S△ARN﹣S△SBM=.【知识点】二次函数;一次函数;勾股定理;中心对称;最短路线;面积。
2019年广西柳州市中考数学试题(原卷+解析)

2019年广西柳州市中考数学试卷一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆2.(3分)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全4.(3分)计算:x(x2﹣1)=()A.x3﹣1 B.x3﹣x C.x3+x D.x2﹣x5.(3分)反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限6.(3分)如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D7.(3分)如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对8.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30 B.14.19 C.19.57 D.19.719.(3分)阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.12.(3分)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6 B.6 C.5 D.﹣5二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.(3分)计算:7x﹣4x=.14.(3分)如图,若AB∥CD,则在图中所标注的角中,一定相等的角是.15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:种子数n30 75 130 210 480 856 1250 2300 发芽数m28 72 125 200 457 814 1187 2185 发芽频率0.9333 0.9600 0.9615 0.9524 0.9521 0.9509 0.9496 0.9500 依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.17.(3分)如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为.18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:22+|﹣3|﹣+π0.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.25.(10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP=OE•OM.26.(10分)如图,直线y=x﹣3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y=ax2+bx+c (a≠0)经过A,B,C三点,抛物线的顶点为点D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,CE的长为半径作圆,点P为直线y=x﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于CE时,过P,Q两点的直线与抛物线交于M,N两点(点M在点N的左侧),求四边形ABMN的面积.2019年广西柳州市中考数学试卷参考答案与试题解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.【解答】解:104400用科学记数法表示应为1.044×105,故选:C.2.【解答】解:题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C.3.【解答】解:D答案的图形是轴对称图形,故选:D.4.【解答】解:x(x2﹣1)=x3﹣x;故选:B.5.【解答】解:∵k=2>0,∴反比例函数经过第一、三象限;故选:A.6.【解答】解:∵∠A与∠D都是所对的圆周角,∴∠D=∠A.故选:D.7.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形.故选:C.8.【解答】解:由图象可知,2016年至2018年的GDP值分别为:11.19,12.24,13.46.则=≈12.30故选:A.9.【解答】解:由图表信息,联立中美GDP趋势线解析式得解得x=∴2018+(﹣15)=故选:B.10.【解答】解:根据题意得:全程需要的时间为:3÷4=(小时),∴y=3﹣4x(0≤x≤).故选:D.11.【解答】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为;故选:A.12.【解答】解:∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.【解答】解:7x﹣4x=(7﹣4)x=3x,故答案为:3x.14.【解答】解:∵AB∥CD,∴∠1=∠3.故答案为15.【解答】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95.故答案为:0.9516.【解答】解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE=,即a=5.故答案为:5.17.【解答】解:过A作AD⊥BC,在Rt△ABD中,sin B=,AB=3,∴AD=AB•sin B=1,在Rt△ACD中,tan C=,∴=,即CD=,根据勾股定理得:AC===,故答案为:18.【解答】解:∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.【解答】解:原式=4+3﹣2+1=6.20.【解答】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.21.【解答】解:(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38.9亿元,答:2016年全国教育经费总投入约为38.8亿元.22.【解答】证明:连接AC,如图所示:在△ABC和△CDA中,,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.23.【解答】解:(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,依题意,得:=,解得:x=0.5,经检验,x=0.5是原方程的解,且符合题意,∴x+0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.24.【解答】解:(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+b=,∴﹣2x2+bx﹣3=0,当△=b2﹣24=0时,b=,此时点P到直线AB距离最短;∴P(,);25.【解答】解:(1)如图1,连接BC,AC,AD,∵CD⊥AB,AB是直径∴,CE=DE=CD=3∴∠ACD=∠ABC,且∠AEC=∠CEB∴△ACE∽△CEB∴∴∴BE=9∴AB=AE+BE=10∴⊙O的半径为5(2)∵=∴∠ACD=∠ADC=∠CDF,且DE=DE,∠AED=∠NED=90°∴△ADE≌△NDE(ASA)∴∠DAN=∠DNA,AE=EN∵∠DAB=∠DFB,∠AND=∠FNB∴∠FNB=∠DFB∴BN=BF,∴△BNF是等腰三角形(3)如图2,连接AC,CE,CO,DO,∵MD是切线,∴MD⊥DO,∴∠MDO=∠DEO=90°,∠DOE=∠DOE∴△MDO∽△DEO∴∴OD2=OE•OM∵AE=EN,CD⊥AO∴∠ANC=∠CAN,∴∠CAP=∠CNO,∵∴∠AOC=∠ABF∵CO∥BF∴∠PCO=∠PFB∵四边形ACFB是圆内接四边形∴∠PAC=∠PFB∴∠PAC=∠PFB=∠PCO=∠CNO,且∠POC=∠COE∴△CNO∽△PCO∴∴CO2=PO•NO,∴ON•OP=OE•OM.26.【解答】解:(1)直线y=x﹣3,令x=0,则y=﹣3,令y=0,则x=3,故点A、C的坐标为(3,0)、(0,﹣3),则抛物线的表达式为:y=a(x﹣3)(x﹣1)=a(x2﹣4x+3),则3a=﹣3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+4x﹣3…①;(2)过点B作直线y=x﹣3的对称点B′,连接BD交直线y=x﹣3于点P,直线B′B交函数对称轴与点G,连接AB′,则此时△BDP周长=BD+PB+PD=BD+B′B为最小值,D(2,1),则点G(2,﹣1),即:BG=EG,即点G是BB′的中点,过点B′(3,﹣2),△BDP周长最小值=BD+B′B=;(3)如图2所示,连接PF并延长交圆与点Q,此时PQ为最大值,点A、B、C、E、F的坐标为(3,0)、(1,0)、(0,﹣3)、(2,0)、(﹣2,0),则CE=,FQ=CE,则PF=CE﹣CE=,设点P(m,m﹣3),点F(﹣2,0),PF2=13=(m﹣2)2+(m﹣3)2,解得:m=1,故点P(1,﹣2),将点P、F坐标代入一次函数表达式并解得:直线PF的表达式为:y=﹣x﹣…②,联立①②并解得:x=,故点M、N的坐标分别为:(,)、(,),过点M、N分别作x轴的垂线交于点S、R,则S四边形ABMN=S梯形NRSM﹣S△ARN﹣S△SBM=.。
中考数学专题训练02:多结论题(含答案)

专题训练(二)[多结论题]1.如图2-1,抛物线y=ax 2+bx+c 经过点(-1,0),对称轴l 如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )图2-1A .①③B .②③C .②④D .②③④2.如图2-2,抛物线y=ax 2+bx+c (a ≠0)的对称轴为直线x=-2,与x 轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示,则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at 2+bt (t 为实数);⑤点-92,y 1,-52,y 2,-12,y 3是该抛物线上的点,则y 1<y 2<y 3.正确的有 ( )图2-2A .4个B .3个C .2个D .1个3.如图2-3,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且AE=13AB ,将矩形沿直线EF 折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()图2-3A.①②B.②③C.①③D.①④4.如图2-4,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DF P∽△BPH;③△PFD∽△PDB;④DP2=PH·PC.其中正确的是()图2-4A.①②③④B.②③C.①②④D.①③④5.如图2-5,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是.(写出所有正确结论的序号)图2-5①当E为线段AB中点时,AF∥CE;②当E为线段AB中点时,AF=9;5③当A,F,C三点共线时,AE=13-2√13;3④当A,F,C三点共线时,△CEF≌△AEF.6.如图2-6,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是(填写序号).图2-6参考答案1.D[解析] ∵开口向下,∴a<0.∵对称轴与x轴的正半轴相交,∴a,b异号,即b>0.∵抛物线与y轴正半轴相交,∴c>0,即abc<0,结论①错误.∵抛物线y=ax2+bx+c经过点(-1,0),∴a-b+c=0,结论②正确.∵当x=2时,y<0,即4a+2b+c<0,又b=a+c,∴4a+2(a+c)+c<0,即2a+c<0,结论③正确.∵c=b-a,∴a+b<0,结论④正确.2.C[解析] ∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,∴-b=-2,∴4a-b=0,故①正确;2a∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,∴另一个交点位于(-1,0)和(0,0)之间,∴抛物线与y轴的交点在原点的下方,∴c<0.故②正确;∵4a-b=0,∴b=4a.∵抛物线y=ax 2+bx+c (a ≠0)与x 轴有两个交点,∴Δ=b 2-4ac=(4a )2-4ac=16a 2-4ac>0.∵a<0,∴4a-c<0,∴c>4a ,∴-3a+c>-3a+4a=a<0,故③错误; ∵4a-b=0,∴b=4a ,∴at 2+bt-(4a-2b )=at 2+4at-(4a-2×4a )=at 2+4at+4a=a (t 2+4t+4)=a (t+2)2. ∵t 为实数,a<0,∴a (t+2)2≤0,∴at 2+bt-(4a-2b )≤0,∴at 2+bt ≤4a-2b ,即4a-2b ≥at 2+bt ,∴④错误;∵点-92,y 1,-52,y 2,-12,y 3是该抛物线上的点, ∴将它们描在图象上如图:由图象可知:y 1<y 3<y 2,∴⑤错误. 综上所述,正确的有2个.故选C .3.D [解析] ∵AE=13AB ,∴AB=3AE ,BE=2AE. 由翻折的性质得,PE=BE.∴∠APE=30°, ∴∠AEP=90°-30°=60°,∴∠BEF=12(180°-∠AEP )=12(180°-60°)=60°, ∴∠EFB=90°-60°=30°,∴EF=2BE ,故①正确; ∵BE=PE ,∴EF=2PE.∵EF>PF ,∴PF<2PE ,故②错误;由翻折可知EF ⊥PB ,∴∠EBQ=∠EFB=30°,∴BE=2EQ,EF=2BE,∴FQ=3EQ,故③错误;由翻折的性质知,∠EFB=∠EFP=30°,∴∠BFP=30°+30°=60°.∵∠PBF=90°-∠EBQ=90°-30°=60°,∴∠PB F=∠PFB=60°,∴△PBF是等边三角形,故④正确.综上所述,结论正确的是①④.4.C[解析] 在正方形ABCD中,∠A=90°.由△BPC是等边三角形,可得∠CBP=60°,∴∠ABP=30°,∴BE=2AE,即①正确;BD是正方形ABCD的对角线,可得△BCD是等腰直角三角形,∴∠CBD=∠CDB=45°,可得∠PBD=15°.∵CD=CP=CB,∠PCD=30°,可得∠CPD=∠CDP=75°,∴∠BPD=75°+60°=135°,∠FDP=90°-75°=15°,∠PFD=90°-∠PCD=90°-30°=60°,∠FPD=180°-∠PDF-∠PFD=180°-15°-60°=105°,∴∠PBD=∠PDF,∠BPH=∠DFP,∴△DFP∽△BPH,即②正确;∠BPD≠∠DPF,∴③△PFD∽△PDB错误;由∠PDH=∠PDC-∠CDB=75°-45°=30°=∠PCD,∠CPD=∠DPH,可得△PDC∽△PHD,∴DP2=PH·PC,即④正确.5.①②③[解析] 由折叠的性质可知CF=CB,∠CFE=90°,∠CEB=∠CEF,当E为AB中点时,BE=EF=AE=32,∴∠F AE=∠AFE,∵∠FEB=∠F AE+∠AFE,∴∠CEB=∠CEF=∠F AE=∠A FE,∴AF∥CE,故①正确;∵E为AB中点时,BE=32,BC=2,∴CE=52,过点E作EM⊥AF于点M,∵∠AFE=∠FEC,EM⊥AF,∠CFE=90°,∴AF=2MF,△MFE∽△FEC,∴MFEF =EFEC,即MF32=3252,∴MF=910,∴AF=95,故②正确;当A,F,C三点共线时,∠AFE=90°,AC=√22+32=√13,设BE=x,则EF=x,AE=3-x,AF=√13-2,在Rt△AFE中,(√13-2)2+x2=(3-x)2,解得x=2√13-43,∴AE=3-x=13-2√133,故③正确;∵AF=√13-2,CF=2,∴AF≠CF,∴④错误.6.①②③[解析]①∵正方形的各边相等,各角都是90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.∴△BCE≌△DCG(SAS),∴BE=DG.结论①正确.②如图,设BE交DC于点M,交DG于点O.由△BCE≌△DCG可知∠CBE=∠CDG.又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即BE⊥DG.结论②正确.③连接BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG 2.由勾股定理得BD2+EG2=2a2+2b2.∴DE2+BG2=2a2+2b2.结论③正确.综上所述,正确的结论是①②③.。
2019年广西柳州市中考数学试卷-答案

广西柳州市2019年中考试卷数学答案解析一、选择题1.【答案】C【解析】104 400用科学记数法表示应为5⨯,1.04410故选:C。
【提示】科学记数法的表示形式为10na⨯的形式,其中1||10,n为整数。
确定n的值a<时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同。
当<时,n是负数。
原数绝对值1>时,n是正数;当原数的绝对值1【考点】科学记数法—表示较大的数2.【答案】C【解析】题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C。
【提示】根据左视图是从几何体左面看得到的图形解答即可。
【考点】简单组合体的三视图3.【答案】D【解析】D答案的图形是轴对称图形,故选:D 。
【提示】根据轴对称的性质可以判断答案【考点】轴对称图形4.【答案】B【解析】23(1)x x x x -=-;故选:B【提示】根据单项式乘以多项式的法则求解即可;【考点】单项式乘多项式5.【答案】A【解析】20k => ,∴反比例函数经过第一、三象限;故选:A 。
【提示】由反比例函数0k >,函数经过一三象限即可求解;【考点】反比例函数的图象;反比例函数的性质6.【答案】D【解析】A ∠ 与D ∠都是 B C 所对的圆周角,D A ∴∠=∠。
故选:D 。
【提示】直接利用圆周角定理进行判断。
【考点】圆周角定理7.【答案】C【解析】 四边形ABCD 是平行四边形,AB CD ∴=,AD BC =;OD OB =,OA OC =;OD OB = ,OA OC =,AOD BOC ∠=∠;()AOD COB SAS ∴△≌△;①同理可得出()AOB COD SAS △≌△;②BC AD = ,CD AB =,BD BD =;()ABD CDB SSS ∴△≌△;③同理可得:()ACD CAB SSS △≌△。
④因此本题共有4对全等三角形。
故选:C 。
2019年广西柳州市中考数学试卷-答案

OE BC ,
a OE BE ,
2
6 / 18
即a5 2。
故答案为: 5 2 。
【提示】先根据题意画出图形,再连接 OB 、 OC ,过 O 作 OE BC ,设此正方形的边长
10.【答案】D
3 【解析】根据题意得:全程需要的时间为: 3 4 (小时),
4
3 y 3 4x(0x ) 。
4
故选:D。
【提示】根据 路程 速度 时间 ,容易知道 y与 x 的函数关系式。
【考点】函数关系式
11.【答案】A
【解析】画树状图如图:
4 / 18
共有 25 个等可能的结果,两人出拳的手指数之和为偶数的结果有 13 个, 13
【提示】根据合并同类项法则计算可得。
【考点】合并同类项
14.【答案】 1 3
【解析】 AB∥CD ,
1 3.
故答案为 1 3
【提示】利用平行线的性质进行判断。
【考点】平行线的性质
15.【答案】0.95
【解析】概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多 的频率越接近于概率
原数绝对值 1时, n 是正数;当原数的绝对值 1时, n 是负数。
【考点】科学记数法—表示较大的数 2.【答案】C 【解析】题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:
故选:C。 【提示】根据左视图是从几何体左面看得到的图形解答即可。 【考点】简单组合体的三视图 3.【答案】D 【解析】D 答案的图形是轴对称图形,
(3 m i ) 2 的实部是 9 m2 ,虚部是 6m,由 (3 m i ) 2 的虚部是 12 得出 m 2 ,代入 9 m2
2019年广西柳州市中考数学试题及参考答案(word解析版)

2019年柳州市初中学业水平考试与高中阶段学校招生考试试卷数学(考试时间共120分钟,全卷满分120分)第Ⅰ卷(选择题,共36分)一、选择题(本大题共12小题,每小题3分,满分36分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆2.如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.3.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全4.计算:x(x2﹣1)=()A.x3﹣1 B.x3﹣x C.x3+x D.x2﹣x5.反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限6.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D7.如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线8.依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30 B.14.19 C.19.57 D.19.719.依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年10.已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)11.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.12.定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6 B.6 C.5 D.﹣5第Ⅱ卷(非选择题,共84分)二、填空题(本大题共6小题,每小题3分,满分18分)13.计算:7x﹣4x=.14.如图,若AB∥CD,则在图中所标注的角中,一定相等的角是.15.柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).16.在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.17.如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为.18.已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程)19.(6分)计算:22+|﹣3|﹣+π0.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A 顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.25.(10分)如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且=,连接FB,FD,FD交AB于点N.(1)若AE=1,CD=6,求⊙O的半径;(2)求证:△BNF为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON•OP=OE•OM.26.(10分)如图,直线y=x﹣3交x轴于点A,交y轴于点C,点B的坐标为(1,0),抛物线y =ax2+bx+c(a≠0)经过A,B,C三点,抛物线的顶点为点D,对称轴与x轴的交点为点E,点E关于原点的对称点为F,连接CE,以点F为圆心,CE的长为半径作圆,点P为直线y=x ﹣3上的一个动点.(1)求抛物线的解析式;(2)求△BDP周长的最小值;(3)若动点P与点C不重合,点Q为⊙F上的任意一点,当PQ的最大值等于CE时,过P,Q两点的直线与抛物线交于M,N两点(点M在点N的左侧),求四边形ABMN的面积.参考答案与解析第Ⅰ卷(选择题,共36分)一、选择题(本大题共12小题,每小题3分,满分36分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.据CCTV新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为()A.0.1044×106辆B.1.044×106辆C.1.044×105辆D.10.44×104辆【知识考点】学记数法—表示较大的数.【思路分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解题过程】解:104400用科学记数法表示应为1.044×105,故选:C.【总结归纳】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.2.如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.【知识考点】简单组合体的三视图.【思路分析】根据左视图是从几何体左面看得到的图形解答即可.【解题过程】解:题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C.【总结归纳】本题考查几何体的三视图.根据左视图是从几何体左面看得到的图形进行解答是关键.3.下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是()A.当心吊物安全B.当心触电安全C.当心滑跌安全D.注意安全【知识考点】轴对称图形.【思路分析】根据轴对称的性质可以判断答案;【解题过程】解:D答案的图形是轴对称图形,故选:D.【总结归纳】本题考查轴对称的性质;熟练掌握轴对称的性质是解题的关键.4.计算:x(x2﹣1)=()A.x3﹣1 B.x3﹣x C.x3+x D.x2﹣x【知识考点】单项式乘多项式.【思路分析】根据单项式乘以多项式的法则求解即可;【解题过程】解:x(x2﹣1)=x3﹣x;故选:B.【总结归纳】本题考查单项式乘以多项式;熟练掌握单项式乘以多项式的法则是解题的关键.5.反比例函数y=的图象位于()A.第一、三象限B.第二、三象限C.第一、二象限D.第二、四象限【知识考点】反比例函数的图象;反比例函数的性质.【思路分析】由反比例函数k>0,函数经过一三象限即可求解;【解题过程】解:∵k=2>0,∴反比例函数经过第一、三象限;故选:A.【总结归纳】本题考查反比例函数的图象及性质;熟练掌握函数的性质和图象是解题的关键.6.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D【知识考点】圆周角定理.【思路分析】直接利用圆周角定理进行判断.【解题过程】解:∵∠A与∠D都是所对的圆周角,∴∠D=∠A.故选:D.【总结归纳】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.7.如图,在▱ABCD中,全等三角形的对数共有()A.2对B.3对C.4对D.5对【知识考点】全等三角形的判定;平行四边形的性质.【思路分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD =BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).【解题过程】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;∵OD=OB,OA=OC,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵BC=AD,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ACD≌△CAB(SSS).④因此本题共有4对全等三角形.故选:C.【总结归纳】此题考查了平行四边形的性质和全等三角形的判定,三角形全等的条件有时候是直接给的,有时候是根据已知条件推出的,还有时是由已知图形的性质得出的,做题时要全面考虑.阅读【资料】,完成第8、9题.【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线8.依据【资料】中所提供的信息,2016﹣2018年中国GDP的平均值大约是()A.12.30 B.14.19 C.19.57 D.19.71【知识考点】算术平均数.【思路分析】根据算术平均数的公式即可计算.【解题过程】解:由图象可知,2016年至2018年的GDP值分别为:11.19,12.24,13.46.则=≈12.30故选:A.【总结归纳】此题主要考查数据统计算术平均数的计算,关键是根据公式列出算式9.依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到()A.2052年B.2038年C.2037年D.2034年【知识考点】一元二次方程的解.【思路分析】联立两个一次函数解析式,求解即可【解题过程】解:由图表信息,联立中美GDP趋势线解析式得解得x=∴2018+(﹣15)=故选:B.【总结归纳】本题是由图表结合一次函数,利用二元一次方程组求解实际问题的,读懂信息是解题的关键.10.已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)【知识考点】函数关系式.【思路分析】根据路程=速度×时间,容易知道y与x的函数关系式.【解题过程】解:根据题意得:全程需要的时间为:3÷4=(小时),∴y=3﹣4x(0≤x≤).故选:D.【总结归纳】本题主要考查了一次函数的应用,理清“路程、时间、速度”的关系是解答本题的关键.11.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为()A.B.C.D.【知识考点】列表法与树状图法.【思路分析】画出树状图,共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,即可得出答案.【解题过程】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为;故选:A.【总结归纳】本题考查了列表法与树状图法以及概率公式;根据题意画出树状图是解题的关键.12.定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6 B.6 C.5 D.﹣5【知识考点】实数的运算.【思路分析】先利用完全平方公式得出(3﹣mi)2=9﹣6mi+m2i2,再根据新定义得出复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,由(3﹣mi)2的虚部是12得出m=﹣2,代入9﹣m2计算即可.【解题过程】解:∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.【总结归纳】本题考查了新定义,完全平方公式,理解新定义是解题的关键.第Ⅱ卷(非选择题,共84分)二、填空题(本大题共6小题,每小题3分,满分18分)13.计算:7x﹣4x=.【知识考点】合并同类项.【思路分析】根据合并同类项法则计算可得.【解题过程】解:7x﹣4x=(7﹣4)x=3x,故答案为:3x.【总结归纳】本题主要考查合并同类项,合并同类项时要注意以下三点:①要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准:带有相同系数的代数项;字母和字母指数;②明确合并同类项的含义是把多项式中的同类项合并成一项,经过合并同类项,式的项数会减少,达到化简多项式的目的;③“合并”是指同类项的系数的相加,并把得到的结果作为新的系数,要保持同类项的字母和字母的指数不变.14.如图,若AB∥CD,则在图中所标注的角中,一定相等的角是.【知识考点】平行线的性质.【思路分析】利用平行线的性质进行判断.【解题过程】解:∵AB∥CD,∴∠1=∠3.故答案为【总结归纳】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.15.柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:发芽频率依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).【知识考点】利用频率估计概率.【思路分析】概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概.【解题过程】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95.故答案为:0.95【总结归纳】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.16.在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.【知识考点】正多边形和圆.【思路分析】先根据题意画出图形,再连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,由垂径定理及正方形的性质得出OE=BE=,再由勾股定理即可求解.【解题过程】解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE=,即a=5.故答案为:5.【总结归纳】本题考查的是正多边形和圆,解答此类问题的关键是根据题意画出图形,利用数形结合求解.17.如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为.【知识考点】解直角三角形.【思路分析】过A作AD垂直于BC,在直角三角形ABD中,利用锐角三角函数定义求出AD的长,在直角三角形ACD中,利用锐角三角函数定义求出CD的长,再利用勾股定理求出AC的长即可.【解题过程】解:过A作AD⊥BC,在Rt△ABD中,sinB=,AB=3,∴AD=AB•sinB=1,在Rt△ACD中,tanC=,∴=,即CD=,根据勾股定理得:AC===,故答案为:【总结归纳】此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,以及勾股定理,熟练掌握各自的性质是解本题的关键.18.已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.【知识考点】算术平均数;中位数;众数;方差.【思路分析】根据5个数的平均数是8,可知这5个数的和为40,根据5个数的中位数是8,得出中间的数是8,根据众数是8,得出至少有2个8,再根据5个数的和减去2个8和1个9得出前面2个数的和为15,再根据方差得出前面的2个数为7和8,即可得出结果.【解题过程】解:∵5个数的平均数是8,∴这5个数的和为40,∵5个数的中位数是8,∴中间的数是8,∵众数是8,∴至少有2个8,∵40﹣8﹣8﹣9=15,由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..【总结归纳】本题考查了方差、平均数、中位数、众数;熟练掌握方差、平均数、中位数、众数的定义是解题的关键.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程)19.(6分)计算:22+|﹣3|﹣+π0.【知识考点】实数的运算;零指数幂.【思路分析】先计算乘方、绝对值、算术平方根和零指数幂,再计算加减可得.【解题过程】解:原式=4+3﹣2+1=6.【总结归纳】本题主要考查实数的运算,解题的关键是掌握乘方的定义、绝对值性质、算术平方根的定义及零指数幂的规定.20.(6分)已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()【知识考点】全等三角形的判定与性质;作图—基本作图.【思路分析】(1)根据题意作出图形即可;(2)根据全等三角形的判定和性质即可得到结论.【解题过程】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.【总结归纳】本题考查了作图﹣基本作图,全等三角形的判定和性质,正确的作出图形是解题的关键.21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)【知识考点】近似数和有效数字;扇形统计图.【思路分析】(1)根据扇形统计图中义务教育段的经费所占的百分比乘以42557亿元即可得到结论;(2)根据题意列式计算即可得到结论.【解题过程】解:(1)42557×45%=19150.65亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557÷(1+9.43%)≈38.9亿元,答:2016年全国教育经费总投入约为38.8亿元.【总结归纳】本题考查了扇形统计图,熟练掌握扇形统计图的特征是解题的关键.22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:【知识考点】平行四边形的判定.【思路分析】连接AC,由SSS证明△ABC≌△CDA得出∠BAC=∠DCA,∠ACB=∠CAD,证出AB∥CD,BC∥AD,即可得出结论.【解题过程】证明:连接AC,如图所示:在△ABC和△CDA中,,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形.【总结归纳】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定定理,证明三角形全等是解题的关键.23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?【知识考点】分式方程的应用;一元一次不等式的应用.【思路分析】(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,根据数量=总价÷单价结合用8元购买大本作业本的数量与用5元购买小本作业本的数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设大本作业本购买m本,则小本作业本购买2m本,根据总价=单价×数量结合总费用不超过15元,即可得出关于m的一元一次不等式,解之取其中的最大整数值即可得出结论.【解题过程】解:(1)设小本作业本每本x元,则大本作业本每本(x+0.3)元,依题意,得:=,解得:x=0.5,经检验,x=0.5是原方程的解,且符合题意,∴x+0.3=0.8.答:大本作业本每本0.8元,小本作业本每本0.5元.(2)设大本作业本购买m本,则小本作业本购买2m本,依题意,得:0.8m+0.5×2m≤15,解得:m≤.∵m为正整数,∴m的最大值为8.答:大本作业本最多能购买8本.【总结归纳】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.24.(10分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A 顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.(1)求直线AB和反比例函数y=(k≠0,x>0)的解析式;(2)已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,求点P到直线AB距离最短时的坐标.【知识考点】一次函数图象上点的坐标特征;反比例函数的性质;反比例函数图象上点的坐标特征;待定系数法求反比例函数解析式;坐标与图形变化﹣旋转.【思路分析】(1)将点A(1,0),点B(0,2),代入y=mx+b,可求直线解析式;过点C作CD⊥x轴,根据三角形全等可求C(3,1),进而确定k;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,当△=h2﹣24=0时,点P到直线AB 距离最短;【解题过程】解:(1)将点A(1,0),点B(0,2),代入y=mx+b,∴b=2,m=﹣2,∴y=﹣2x+2;过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=AB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;(2)设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,∴﹣2x2+hx﹣3=0,当△=h2﹣24=0时,h=,此时点P到直线AB距离最短;∴P(,)。
2019年广西柳州市中考数学试卷以及逐题解析版

2019年广西柳州市中考数学试卷以及逐题解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV 新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为( )A .60.104410⨯辆B .61.04410⨯辆C .51.04410⨯辆D .410.4410⨯辆2.(3分)如图,这是一个机械零部件,该零部件的左视图是( )A .B .C .D .3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A .当心吊物安全B .当心触电安全C .当心滑跌安全D .注意安全4.(3分)计算:2(1)(x x -= )A .31x -B .3x x -C .3x x +D .2x x - 5.(3分)反比例函数2y x =的图象位于( ) A .第一、三象限 B .第二、三象限 C .第一、二象限 D .第二、四象限6.(3分)如图,A ,B ,C ,D 是O 上的点,则图中与A ∠相等的角是( )A .B ∠ B .C ∠ C .DEB ∠D .D ∠7.(3分)如图,在ABCD 中,全等三角形的对数共有( )A .2对B .3对C .4对D .5对8.(3分)依据【资料】中所提供的信息,20162018-年中国GDP 的平均值大约是( )A .12.30B .14.19C .19.57D .19.719.(3分)依据【资料】中所提供的信息,可以推算出中国的GDP 要超过美国,至少要到( )A .2052年B .2038年C .2037年D .2034年10.(3分)已知A 、B 两地相距3千米,小黄从A 地到B 地,平均速度为4千米/小时,若用x 表示行走的时间(小时),y 表示余下的路程(千米),则y 关于x 的函数解析式是( )A .4(0)y x x =…B .343()4y x x =-…C .34(0)y x x =-…D .334(0)4y x x =-剟 11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )A .1325B .1225C .425D .1212.(3分)定义:形如a bi +的数称为复数(其中a 和b 为实数,i 为虚数单位,规定21)i =-,a 称为复数的实部,b 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如2222(13)1213(3)16916986i i i i i i i +=+⨯⨯+=++=+-=-+,因此,2(13)i +的实部是8-,虚部是6.已知复数2(3)mi -的虚部是12,则实部是( )A .6-B .6C .5D .5-二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.)13.(3分)计算:74x x -= .14.(3分)如图,若//AB CD ,则在图中所标注的角中,一定相等的角是 .15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是 (结果精确到0.01).16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .17.(3分)如图,在ABC ∆中,1sin 3B =,tanC =3AB =,则AC 的长为 .18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是 .三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:202|3|π+-.20.(6分)已知:AOB ∠.求作:AO B ∠''',使得AO B AOB ∠'''=∠.作法:①以O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ;②画一条射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C ';③以点C '为圆心,CD 长为半径画弧,与第②步中所画的弧相交于点D ';④过点D '画射线O B '',则AO B AOB ∠'''=∠.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出AO B ∠'''(请保留作图痕迹). (2)完成下面证明AO B AOB ∠'''=∠的过程(注:括号里填写推理的依据). 证明:由作法可知O C OC ''=,O D OD ''=,D C ''= ,∴△(C O D COD '''≅∆ )AO B AOB ∴∠'''=∠.( )21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD 中,AB CD =,AD BC =.求证:四边形ABCD 是平行四边形.证明:23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24.(10分)如图,直线AB 与x 轴交于点(1,0)A ,与y 轴交于点(0,2)B ,将线段AB 绕点A顺时针旋转90︒得到线段AC ,反比例函数(0,0)k y k x x=≠>的图象经过点C . (1)求直线AB 和反比例函数(0,0)k y k x x=≠>的解析式; (2)已知点P 是反比例函数(0,0)k y k x x=≠>图象上的一个动点,求点P 到直线AB 距离最短时的坐标.25.(10分)如图,AB 是O 的直径,弦CD AB ⊥于点E ,点F 是O 上一点,且AC CF =,连接FB ,FD ,FD 交AB 于点N .(1)若1AE =,6CD =,求O 的半径;(2)求证:BNF ∆为等腰三角形;(3)连接FC 并延长,交BA 的延长线于点P ,过点D 作O 的切线,交BA 的延长线于点M .求证:ON OP OE OM =.26.(10分)如图,直线3y x =-交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线2(0)y ax bx c a =++≠经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线3y x =-上的一个动点.(1)求抛物线的解析式;(2)求BDP ∆周长的最小值;(3)若动点P 与点C 不重合,点Q 为F 上的任意一点,当PQ 的最大值等于32CE 时,过P ,Q 两点的直线与抛物线交于M ,N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.2019年广西柳州市中考数学试卷答案与解析一、选择题(本大题共11小题,每小题3分,满分30分,在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)1.(3分)据CCTV 新闻报道,今年5月我国新能源汽车销量达到104400辆,该销量用科学记数法表示为( )A .60.104410⨯辆B .61.04410⨯辆C .51.04410⨯辆D .410.4410⨯辆【分析】科学记数法的表示形式为10n a ⨯的形式,其中1||10a <…,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数.【解答】解:104400用科学记数法表示应为51.04410⨯,故选:C .【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a ⨯的形式,其中1||10a <…,n 为整数,表示时关键要正确确定a 的值以及n 的值.2.(3分)如图,这是一个机械零部件,该零部件的左视图是( )A .B .C .D .【分析】根据左视图是从几何体左面看得到的图形解答即可.【解答】解:题中的几何体从左面看,得到的图形是一个长方形及其内部一个圆,如图所示:故选:C .【点评】本题考查几何体的三视图.根据左视图是从几何体左面看得到的图形进行解答是关键.3.(3分)下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A .当心吊物安全B .当心触电安全C .当心滑跌安全D .注意安全【分析】根据轴对称的性质可以判断答案;【解答】解:D 答案的图形是轴对称图形,故选:D .【点评】本题考查轴对称的性质;熟练掌握轴对称的性质是解题的关键.4.(3分)计算:2(1)(x x -= )A .31x -B .3x x -C .3x x +D .2x x -【分析】根据单项式乘以多项式的法则求解即可;【解答】解:23(1)x x x x -=-;故选:A .【点评】本题考查单项式乘以多项式;熟练掌握单项式乘以多项式的法则是解题的关键.5.(3分)反比例函数2y x =的图象位于( ) A .第一、三象限 B .第二、三象限 C .第一、二象限 D .第二、四象限【分析】由反比例函数0k >,函数经过一三象限即可求解;【解答】解:20k =>,∴反比例函数经过第一、三象限;故选:A .【点评】本题考查反比例函数的图象及性质;熟练掌握函数的性质和图象是解题的关键.6.(3分)如图,A ,B ,C ,D 是O 上的点,则图中与A ∠相等的角是( )A .B ∠ B .C ∠ C .DEB ∠D .D ∠【分析】直接利用圆周角定理进行判断.【解答】解:A ∠与D ∠都是BC 所对的圆周角,D A ∴∠=∠.故选:D .【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.7.(3分)如图,在ABCD 中,全等三角形的对数共有( )A .2对B .3对C .4对D .5对【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD BC =,AB CD =,AO CO =,DO BO =,再利用“对顶角相等”就很容易找到全等的三角形:()ACD CAB SSS ∆≅∆,()ABD CDB SSS ∆≅∆,()AOD COB SAS ∆≅∆,()AOB COD SAS ∆≅∆.【解答】解:四边形ABCD 是平行四边形,AB CD ∴=,AD BC =;OD OB =,OA OC =;OD OB =,OA OC =,AOD BOC ∠=∠;()AOD COB SAS ∴∆≅∆;①同理可得出()AOB COD SAS ∆≅∆;②BC AD =,CD AB =,BD BD =;()ABD CDB SSS ∴∆≅∆;③同理可得:()ACD CAB SSS ∆≅∆.④因此本题共有4对全等三角形.故选:C .【点评】此题考查了平行四边形的性质和全等三角形的判定,三角形全等的条件有时候是直接给的,有时候是根据已知条件推出的,还有时是由已知图形的性质得出的,做题时要全面考虑.8.(3分)依据【资料】中所提供的信息,20162018-年中国GDP的平均值大约是() A.12.30B.14.19C.19.57D.19.71【分析】根据算术平均数的公式即可计算.【解答】解:由图象可知,2016年至2018年的GDP值分别为:11.19,12.24,13.46.则11.1912.2413.4612.303X++=≈故选:A.【点评】此题主要考查数据统计算术平均数的计算,关键是根据公式列出算式9.(3分)依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到( )A.2052年B.2038年C.2037年D.2034年【分析】联立两个一次函数解析式,求解即可【解答】解:由图表信息,联立中美GDP趋势线解析式得0.860.4680.5311.778 y xy x=+⎧⎨=+⎩解得33411x=332018(3415)20371111∴+-=故选:B.【点评】本题是由图表结合一次函数,利用二元一次方程组求解实际问题的,读懂信息是解题的关键.10.(3分)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )A.4(0)y x x=…B.343()4 y x x=-…C.34(0)y x x=-…D.3 34(0)4 y x x=-剟【分析】根据路程=速度⨯时间,容易知道y与x的函数关系式.【解答】解:根据题意得:全程需要的时间为:3344÷=(小时),334(0)4y x x∴=-剟. 故选:D .【点评】本题主要考查了一次函数的应用,理清“路程、时间、速度”的关系是解答本题的关键.11.(3分)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )A .1325B .1225C .425D .12【分析】画出树状图,共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,即可得出答案. 【解答】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为1325; 故选:A .【点评】本题考查了列表法与树状图法以及概率公式;根据题意画出树状图是解题的关键. 12.(3分)定义:形如a bi +的数称为复数(其中a 和b 为实数,i 为虚数单位,规定21)i =-,a 称为复数的实部,b 称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如2222(13)1213(3)16916986i i i i i i i +=+⨯⨯+=++=+-=-+,因此,2(13)i +的实部是8-,虚部是6.已知复数2(3)mi -的虚部是12,则实部是( ) A .6-B .6C .5D .5-【分析】先利用完全平方公式得出222(3)96mi mi m i -=-+,再根据新定义得出复数2(3)mi -的实部是29m -,虚部是6m -,由2(3)mi -的虚部是12得出2m =-,代入29m -计算即可. 【解答】解:22222222(3)323()969696mi mi mi mi m i m i mi m mi -=-⨯⨯+=-+=+-=--,∴复数2(3)mi -的实部是29m -,虚部是6m -,612m ∴-=, 2m ∴=-,2299(2)945m ∴-=--=-=. 故选:C .【点评】本题考查了新定义,完全平方公式,理解新定义是解题的关键.二、填空题(本大题共6小题,每小题3分,满分18分.请将答案直接填写在答题卡中相应的横线上,在草稿纸、试卷上答题无效.) 13.(3分)计算:74x x -= 3x . 【分析】根据合并同类项法则计算可得. 【解答】解:74(74)3x x x x -=-=, 故答案为:3x .【点评】本题主要考查合并同类项,合并同类项时要注意以下三点:①要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准:带有相同系数的代数项;字母和字母指数;②明确合并同类项的含义是把多项式中的同类项合并成一项,经过合并同类项,式的项数会减少,达到化简多项式的目的;③“合并”是指同类项的系数的相加,并把得到的结果作为新的系数,要保持同类项的字母和字母的指数不变.14.(3分)如图,若//AB CD ,则在图中所标注的角中,一定相等的角是 13∠=∠ .【分析】利用平行线的性质进行判断. 【解答】解://AB CD ,13∴∠=∠.故答案为【点评】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.15.(3分)柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是 0.95 (结果精确到0.01).【分析】概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概.【解答】解:概率是大量重复试验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种种子在此条件下发芽的概率约为0.95.故答案为:0.95【点评】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.16.(3分)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为【分析】先根据题意画出图形,再连接OB 、OC ,过O 作OE BC ⊥,设此正方形的边长为a ,由垂径定理及正方形的性质得出2aOE BE ==,再由勾股定理即可求解. 【解答】解:如图所示,连接OB 、OC ,过O 作OE BC ⊥,设此正方形的边长为a , OE BC ⊥, 2a OE BE ∴==,即a =故答案为:【点评】本题考查的是正多边形和圆,解答此类问题的关键是根据题意画出图形,利用数形结合求解.17.(3分)如图,在ABC ∆中,1sin 3B =,tan 2C =3AB =,则AC【分析】过A 作AD 垂直于BC ,在直角三角形ABD 中,利用锐角三角函数定义求出AD 的长,在直角三角形ACD 中,利用锐角三角函数定义求出CD 的长,再利用勾股定理求出AC 的长即可.【解答】解:过A 作AD BC ⊥, 在Rt ABD ∆中,1sin 3B =,3AB =,sin 1AD AB B ∴==,在Rt ACD ∆中,tan 2C =∴AD CD =,即CD =根据勾股定理得:AC ==【点评】此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,以及勾股定理,熟练掌握各自的性质是解本题的关键.18.(3分)已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是7.【分析】根据5个数的平均数是8,可知这5个数的和为40,根据5个数的中位数是8,得出中间的数是8,根据众数是8,得出至少有2个8,再根据5个数的和减去2个8和1个9得出前面2个数的和为15,再根据方差得出前面的2个数为7和8,即可得出结果.【解答】解:5个数的平均数是8,∴这5个数的和为40,5个数的中位数是8,∴中间的数是8,众数是8,∴至少有2个8,---=,4088915由方差是0.4得:前面的2个数的为7和8,∴最小的数是7;故答案为:7..【点评】本题考查了方差、平均数、中位数、众数;熟练掌握方差、平均数、中位数、众数的定义是解题的关键.三、解答题(本大题共8小题,满分66分,解答时应写出必要的文字说明、演算步骤或推理过程请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后论须使用黑色字的签字笔描黑在草稿纸、试卷上答题无效.)19.(6分)计算:20+-.2|3|π【分析】先计算乘方、绝对值、算术平方根和零指数幂,再计算加减可得.【解答】解:原式43216=+-+=.【点评】本题主要考查实数的运算,解题的关键是掌握乘方的定义、绝对值性质、算术平方根的定义及零指数幂的规定.20.(6分)已知:AOB∠.求作:AO B∠'''=∠.∠''',使得AO B AOB作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O A'',以点O'为圆心,OC长为半径画弧,交O A''于点C';③以点C '为圆心,CD 长为半径画弧,与第②步中所画的弧相交于点D '; ④过点D '画射线O B '',则AO B AOB ∠'''=∠. 根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出AO B ∠'''(请保留作图痕迹). (2)完成下面证明AO B AOB ∠'''=∠的过程(注:括号里填写推理的依据). 证明:由作法可知O C OC ''=,O D OD ''=,D C ''= DC ,∴△(C O D COD '''≅∆ )AO B AOB ∴∠'''=∠.( )【分析】(1)根据题意作出图形即可;(2)根据全等三角形的判定和性质即可得到结论. 【解答】解:(1)如图所示,AO B ∠'''即为所求;(2)证明:由作法可知O C OC ''=,O D OD ''=,D C DC ''=,∴△()C O D COD SSS '''≅∆AO B AOB ∴∠'''=∠.(全等三角形的对应角相等) 故答案为:DC ,SSS ,全等三角形的对应角相等.【点评】本题考查了作图-基本作图,全等三角形的判定和性质,正确的作出图形是解题的关键.21.(8分)据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题. (1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元? (2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)【分析】(1)根据扇形统计图中义务教育段的经费所占的百分比乘以42557亿元即可得到结论;(2)根据题意列式计算即可得到结论.【解答】解:(1)4255745%19150.65⨯=亿元,答:义务教育段的经费总投入应该是19150.65亿元;(2)42557(19.43%)38.9÷+≈亿元,答:2016年全国教育经费总投入约为38.8亿元.【点评】本题考查了扇形统计图,熟练掌握扇形统计图的特征是解题的关键.22.(8分)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB CD=,AD BC=.求证:四边形ABCD是平行四边形.证明:【分析】连接AC,由SSS证明ABC CDA∆≅∆得出BAC DCA∠=∠,ACB CAD∠=∠,证出//AB CD,//BC AD,即可得出结论.【解答】证明:连接AC,如图所示:在ABC∆和CDA∆中,AB CDAD CBAC CA=⎧⎪=⎨⎪=⎩,()ABC CDA SSS∴∆≅∆,BAC DCA ∴∠=∠,ACB CAD ∠=∠, //AB CD ∴,//BC AD ,∴四边形ABCD 是平行四边形.【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定定理,证明三角形全等是解题的关键.23.(8分)小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同. (1)求大本作业本与小本作业本每本各多少元?(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?【分析】(1)设小本作业本每本x 元,则大本作业本每本(0.3)x +元,根据数量=总价÷单价结合用8元购买大本作业本的数量与用5元购买小本作业本的数量相同,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)设大本作业本购买m 本,则小本作业本购买2m 本,根据总价=单价⨯数量结合总费用不超过15元,即可得出关于m 的一元一次不等式,解之取其中的最大整数值即可得出结论.【解答】解:(1)设小本作业本每本x 元,则大本作业本每本(0.3)x +元, 依题意,得:850.3x x=+, 解得:0.5x =,经检验,0.5x =是原方程的解,且符合题意, 0.30.8x ∴+=.答:大本作业本每本0.8元,小本作业本每本0.5元. (2)设大本作业本购买m 本,则小本作业本购买2m 本, 依题意,得:0.80.5215m m +⨯…, 解得:506m …. m 为正整数,m ∴的最大值为8.答:大本作业本最多能购买8本.【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式. 24.(10分)如图,直线AB 与x 轴交于点(1,0)A ,与y 轴交于点(0,2)B ,将线段AB 绕点A 顺时针旋转90︒得到线段AC ,反比例函数(0,0)ky k x x =≠>的图象经过点C .(1)求直线AB 和反比例函数(0,0)ky k x x=≠>的解析式;(2)已知点P 是反比例函数(0,0)ky k x x=≠>图象上的一个动点,求点P 到直线AB 距离最短时的坐标.【分析】(1)将点(1,0)A ,点(0,2)B ,代入y mx b =+,可求直线解析式;过点C 作CD x ⊥轴,根据三角形全等可求(3,1)C ,进而确定k ; (2)设与AB 平行的直线2y x h =-+,联立32x b x-+=,当△2240b =-=时,点P 到直线AB 距离最短;【解答】解:(1)将点(1,0)A ,点(0,2)B ,代入y mx b =+, 2b ∴=,2m =-,22y x ∴=-+;过点C 作CD x ⊥轴,线段AB 绕点A 顺时针旋转90︒得到线段AC , ()ABO CAD AAS ∴∆≅∆,2AD AB ∴==,1CD OA ==,(3,1)C ∴, 3k ∴=,3yx∴=;(2)设与AB平行的直线2y x h=-+,联立32x bx-+=,2230x bx∴-+-=,当△2240b=-=时,b=±,此时点P到直线AB距离最短;P∴;【点评】本题考查反比例函数的图象及性质;熟练掌握反比例函数的图象及性质,当直线与反比例函数有一个交点时,点到直线的距离最短是解题的关键.25.(10分)如图,AB是O的直径,弦CD AB⊥于点E,点F是O上一点,且AC CF=,连接FB,FD,FD交AB于点N.(1)若1AE=,6CD=,求O的半径;(2)求证:BNF∆为等腰三角形;(3)连接FC并延长,交BA的延长线于点P,过点D作O的切线,交BA的延长线于点M.求证:ON OP OE OM=.【分析】(1)连接BC,AC,AD,通过证明ACE CEB∆∆∽,可得AE CECE BE=,可求BE的长,即可求O的半径;(2)通过证明ADE NDE∆≅∆,可得DAN DNA∠=∠,即可证BN BF=,可得BNF∆为等腰三角形;(3)通过证明ODE ODM ∆∆∽,可得2DO OE OM =,通过证明PCO CEO ∆∆∽,可得2CO PO ON =,即可得结论.【解答】解:(1)如图1,连接BC ,AC ,AD ,CD AB ⊥,AB 是直径∴AC AD =,132CE DE CD === ACD ABC ∴∠=∠,且AEC CEB ∠=∠ACE CEB ∴∆∆∽ ∴AE CE CE BE = ∴133BE= 9BE ∴=10AB AE BE ∴=+=O ∴的半径为5(2)AC AD CF ==ACD ADC CDF ∴∠=∠=∠,且DE DE =,90AED NED ∠=∠=︒()ADE NDE ASA ∴∆≅∆DAN DNA ∴∠=∠,AE EN =DAB DFB ∠=∠,AND FNB ∠=∠FNB DFB ∴∠=∠BN BF ∴=,BNF ∴∆是等腰三角形(3)如图2,连接AC ,CE ,CO ,DO ,MD 是切线,MD DO ∴⊥,90MDO DEO ∴∠=∠=︒,DOE DOE ∠=∠MDO DEO ∴∆∆∽ ∴OE OD OD OM= 2OD OE OM ∴=AE EN =,CD AO ⊥ANC CAN ∴∠=∠,CAP CNO ∴∠=∠,AC CF =AOC ABF ∴∠=∠//CO BFPCO PFB ∴∠=∠四边形ACFB 是圆内接四边形PAC PFB ∴∠=∠PAC PFB PCO CNO ∴∠=∠=∠=∠,且POC COE ∠=∠CNO PCO ∴∆∆∽ ∴NO CO CO PO= 2CO PO NO ∴=,ON OP OE OM ∴=.【点评】本题属于圆的综合题,考查了圆周角定理、垂径定理、全等三角形的判定与性质,相似三角形的判定和性质等知识.注意准确作出辅助线是解此题的关键.26.(10分)如图,直线3y x =-交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线2(0)y ax bx c a =++≠经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线3y x =-上的一个动点.(1)求抛物线的解析式;(2)求BDP ∆周长的最小值;(3)若动点P 与点C 不重合,点Q 为F 上的任意一点,当PQ 的最大值等于32CE 时,过P ,Q 两点的直线与抛物线交于M ,N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.【分析】(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,即可求解;(2)过点B 作直线3y x =-的对称点B ',连接BD 交直线3y x =-于点P ,直线B B '交函数对称轴与点G ,则此时BDP ∆周长BD PB PD BD B B =++=+'为最小值,即可求解;(3)如图2所示,连接PF 并延长交圆与点Q ,此时PQ 为最大值,即可求解.【解答】解:(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,则抛物线的表达式为:2(3)(1)(43)y a x x a x x =--=-+,则33a =-,解得:1a =-,故抛物线的表达式为:243y x x =-+-⋯①;(2)过点B 作直线3y x =-的对称点B ',连接BD 交直线3y x =-于点P ,直线B B '交函数对称轴与点G ,连接AB ',则此时BDP ∆周长BD PB PD BD B B =++=+'为最小值,(2,1)D ,则点(2,1)G -,即:BG EG =,即点G 是BB '的中点,过点(3,2)B '-,BDP ∆周长最小值BD B B =+';(3)如图2所示,连接PF 并延长交圆与点Q ,此时PQ 为最大值,点A 、B 、C 、E 、F 的坐标为(3,0)、(1,0)、(0,3)-、(2,0)、(2,0)-,则CE =12FQ CE =,则3122PF CE CE =-, 设点(,3)P m m -,点(2,0)F -,22213(2)(3)PF m m ==-+-,解得:1m =,故点(1,2)P -,将点P 、F 坐标代入一次函数表达式并解得:直线PF 的表达式为:2433y x =--⋯②,联立①②并解得:x ,故点M 、N 的坐标分别为:、, 过点M 、N 分别作x 轴的垂线交于点S 、R ,则ARN SBM ABMN NRSM S S S S ∆∆=--=四边形梯形. 【点评】本题考查的是二次函数综合运用,涉及到一次函数、点的对称性、图形的面积计算等,其中(3),确定PQ 最值时,通常考虑直线过圆心的情况,进而求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(二)
[多结论题]
1.[2017·遵义] 如图ZT2-1,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是()
图ZT2-1
A.①③
B.②③
C.②④
D.②③④
2.如图ZT2-2,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示,则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点-,y1,-,y2,-,y3是该抛物线上的点,则y1<y2<y
3.正确的有()
图ZT2-2
A.4个
B.3个
C.2个
D.1个
3.如图ZT2-3,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD 边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()
图ZT2-3
A.①②
B.②③
C.①③
D.①④
4.如图ZT2-4,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH·PC.其中正确的是()
图ZT2-4
A.①②③④
B.②③
C.①②④
D.①③④
5.[2018·宜宾] 如图ZT2-5,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B 落在矩形内点F处,下列结论正确的是.(写出所有正确结论的序号)
图ZT2-5
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=;
③当A,F,C三点共线时,AE=-;
④当A,F,C三点共线时,△CEF≌△AEF.
6.[2017·南充] 如图ZT2-6,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是(填写序号).
图ZT2-6
参考答案
1.D[解析] ∵开口向下,∴a<0.∵对称轴与x轴的正半轴相交,∴a,b异号,即b>0.∵抛物线与y轴正半轴相交,∴c>0,即abc<0,结论①错误.∵抛物线y=ax2+bx+c经过点(-1,0),∴a-b+c=0,结论②正确.∵当x=2时,y<0,即4a+2b+c<0,又b=a+c,∴4a+2(a+c)+c<0,即2a+c<0,结论③正确.∵c=b-a,∴a+b<0,结论④正确.
2.C[解析] ∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,∴-=-2,∴4a-b=0,故①正确;
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,∴另一个交点位于(-1,0)和(0,0)之间,∴抛物线与y轴的交点在原点的下方,∴c<0.故②正确;
∵4a-b=0,∴b=4a.
∵抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,
∴Δ=b2-4ac=(4a)2-4ac=16a2-4ac>0.∵a<0,∴4a-c<0,∴c>4a,∴-3a+c>-3a+4a=a<0,故③错误;
∵4a-b=0,∴b=4a,∴at2+bt-(4a-2b)=at2+4at-(4a-2×4a)=at2+4at+4a=a(t2+4t+4)=a(t+2)2.
∵t为实数,a<0,∴a(t+2)2≤0,∴at2+bt-(4a-2b)≤0,∴at2+bt≤4a-2b,即4a-2b≥at2+bt,∴④错误;
∵点-,y1,-,y2,-,y3是该抛物线上的点,
∴将它们描在图象上如图:
由图象可知:y1<y3<y2,∴⑤错误.
综上所述,正确的有2个.故选C.
3.D[解析] ∵AE=AB,∴AB=3AE,BE=2AE.由翻折的性质得,PE=BE.∴∠APE=30°,
∴∠AEP=90°-30°=60°,
∴∠BEF=(180°-∠AEP)=(180°-60°)=60°, ∴∠EFB=90°-60°=30°,∴EF=2BE,故①正确; ∵BE=PE,∴EF=2PE.
∵EF>PF,∴PF<2PE,故②错误;
由翻折可知EF⊥PB,∴∠EBQ=∠EFB=30°, ∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质知,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°.
∵∠PBF=90°-∠EBQ=90°-30°=60°,
∴∠PB F=∠PFB=60°,
∴△PBF是等边三角形,故④正确.
综上所述,结论正确的是①④.
4.C[解析] 在正方形ABCD中,∠A=90°.由△BPC是等边三角形,可得∠CBP=60°,∴∠ABP=30°,∴BE=2AE,即①正确;BD是正方形ABCD的对角线,可得△BCD是等腰直角三角形,∴∠CBD=∠CDB=45°,可得∠PBD=15°.∵CD=CP=CB,∠PCD=30°,
可得
∠CPD=∠CDP=75°,∴∠BPD=75°+60°=135°,∠FDP=90°-75°=15°,∠PFD=90°-∠PCD=90°-30°=60
°,∠FPD=180°-∠PDF-∠PFD=180°-15°-60°=105°,∴∠PBD=∠PDF,∠BPH=∠DFP,∴△DFP∽△BPH,
即②正确;∠BPD≠∠DPF,∴③△PFD∽△PDB错误;由∠PDH=∠PDC-∠CDB=75°-45°=30°=∠PCD,∠CPD=∠DPH,可得△PDC∽△PHD,∴DP2=PH·PC,即④正确.
5.①②③[解析] 由折叠的性质可知CF=CB,∠CFE=90°,∠CEB=∠CEF,当E为AB中点时,BE=EF=AE=,∴∠F AE=∠AFE,∵∠FEB=∠F AE+∠AFE,∴∠CEB=∠CEF=∠F AE=∠AFE,∴AF∥CE,故①正确;
∵E为AB中点时,BE=,BC=2,∴CE=,过点E作EM⊥AF于点M,∵∠AFE=∠FEC,EM⊥AF,∠CFE=90°,
∴AF=2MF,△MFE∽△FEC,∴=,即=,∴MF=,∴AF=,故②正确;
当A,F,C三点共线时,∠AFE=90°,AC==,设BE=x,则EF=x,AE=3-x,AF=-2,在Rt△AFE 中,(-2)2+x2=(3-x)2,解得x=-,∴AE=3-x=-,故③正确;
∵AF=2,CF=2,∴AF≠CF,∴④错误.
6.①②③[解析]
①∵正方形的各边相等,各角都是90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.∴△BCE≌△DCG(SAS),∴BE=DG.结论①正确.
②如图,设BE交DC于点M,交DG于点O.由△BCE≌△DCG可知∠CBE=∠CDG.
又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即BE⊥DG.结论②正确.
③连接BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.由勾股定理得BD2+EG2=2a2+2b2.∴DE2+BG2=2a2+2b2.结论③正确.
综上所述,正确的结论是①②③.。
