三偏微分方程的数值离散方法课件
偏微分方程的离散化方法优秀课件

2!
3!
4!
(*)
P(x) xP(x) O(x)
P(x
x) P(x)
x
P(x)
(x/ 2)2
P(x)
(x/ 2)3
P(x)
2
2
2!
3!
P(x) x P(x)O(x)
2
2
1、 一 阶 前 差 商
P P ( x x ) P ( x ) , P Pi1 Pi
x
x
x i
x
2、 一 阶 后 差 商
12
上式两端同除 x 2 ,整理得:
P '' ( x) P(x x) 2P(x) P(x x) O(x 2 ) x 2
忽略二阶截断误差 O(x 2 )
2P x 2
P(x
x)
2P(x) x 2
P(x
x)
,
2P x 2
Pi 1
2 Pi x 2
Pi 1
(用 节 点 位 置 )
i
1、 一种常用二阶差商处理方法
P P ( x x / 2 ) P ( x x / 2 ) , P Pi1 / 2 Pi1 / 2 忽 略 截 断 误 差 O (( x / 2 ) 2 )
x
x
x i
x
1、 二阶差商
将 方 程 (*)正 负 相 加 ,可 得 : P(x x) P(x x) 2P(x) x 2 P '' (x) x 4 P (4) (x) .........
Pn i1
2 Pi n
Pn i1
P n1 i
Pi n
x2
t
P n1 i
(1 2 ) Pi n
(
偏微分方程数值解PPT课件

从(1)得到:
u(ti)u(ti1)hu(ti)O(h)
精选
14
从(2)得到:
u(ti)u(ti1)hu(ti)O(h)
从(1)-(2)得到:
u(ti)u(ti1)2 hu(ti1)O (h2)
从(1)+(2)得到:
u (ti)u (ti 1) 2 u h (2 ti) u (ti 1 ) O (h 2)
精选
15
对经典的初值问题
du
dt
f (t,u )
u ( 0 ) u 0
t (0,T)
满足Lipschitz条件
4
常微分方程的数值解
大气科学中
常微分方程和偏微分方程的关系
1. 大气行星边界层(近地面具有湍流运动特性的大 气薄层,1—1.5km), 埃克曼(V.W.Ekman)(瑞典) 螺线的导出;
2. 1963年,美国气象学家Lorenz在研究热对流的 不稳定问题时,使用高截断的谱方法,由 Boussinesq流体的闭合方程组得到了一个完全确 定的三阶常微分方程组,即著名的Lorenz系统。
2. Curtis F.Gerald and Patrick O., Applied Numerical Analysis, Person Education, Inc., 2004.
3. Eugenia Kalnay, Atmospheric Modeling, Data Assimilation and Predictability, the press Syndicate of the University of Cambridge,2003.
ìïïïïïïïïïíïïïïïïïïî
x1¢=
x
¢
第5章偏微分方程值解ppt课件

t
t nt , x ix , y jy , z kz
总目录
本章目录
5.1
5.2
5.3
5.4
5.2 基本离散化公式
以3对于二阶偏导,我们可以通过对泰勒展开式处 理技术得到下面离散化计算公式:
2u t 2 2u x 2 2u y 2 2u z 2
总目录
本章目录
5.1
5.2
5.3
5.4
5.3 几种常见偏微分方程的离散化计算
例下面介绍3种迭代格式: 1 u (u u u u (1)同步迭代: 4 1 u (u u u u (2)异步迭代: 4 1 u u u ) u (u 4 (3)超松弛迭代:
(5-4) (计算实例VB程序见课本)
总目录
本章目录
5.1
5.2
5.3
5.4
5.3 几种常见偏微分方程的离散化计算
2、一维流动传热传导方程的混合问题 一维流动传热传导方程的混合问题:
2 u u 2 u b f (u, t ) a 2 t x x u t 0 (x), u 0 x x l u x 0 μ1(t)
u
x0
1 (t ),u xt 2 (t )
为初值条件 为边值条件
当该波动方程只提初值条件时,称此方程为波动 方程的初值问题,二者均提时,称为波动方程的 混合问题。
总目录 本章目录
5.1
5.2
5.3
5.4
5.3 几种常见偏微分方程的离散化计算
t t
x
0
x
0
l
(a)初值问题
偏微分方程数值解PPT课件

t
t
n j
tn j1
x x
EXCEL
0.01, x 0.1
t n1 j
t
n j
2(TW
t
n j
)
3
t
n j
t
n j1
x
t n1 j
0.02TW
0.68t
n j
0.3t
n j1
此微分方程,是在不考虑流体本身热传 导时的套管传热微分方程.由计算结果可 知,当计算的时间序列进行到72时,传 热过程已达到稳态,各点上的温度已不 随时间的增加而改变。如果改变套管长 度或传热系数,则达到稳态的时间亦会 改变。
b2 4ac 0 b2 4ac 0 b2 4ac 0
• 物理实际问题的归类:
• 波动方程(双曲型)一维弦振动模型:
2u t 2
2
2u x 2
• 热传导方程(抛物线型)一维线性热传导方程
u t
2u x 2
• 拉普拉斯方程(椭圆型ux22)稳态y2u2 静 电0 场或稳态温度分布场)
第4页/共32页
un i 1
b
un i1
uin
x
f (ix, nt)
ui0
(i x )
un m1
umn
x
0
u0n 1(nt )
(i 1,2, ,m) (n 0,1, 2, ) (n 0,1,2, )
第13页/共32页
一维流动热传导方程
将上式进行处理得到:
un1 i
t
f
(ix, nt )
(a2
t (x)2
1的)偏t )
微
分
采
用
向
后
欧
第5章偏微分方程值解ppt课件

总目录
本章目录
5.1
5.2
5.3
5.4
5.2 基本离散化公式
以三维空间为例,我们将离散化的应变量表示成, 它所表示的真正含义如下 :
uin , j , k u (t , x, y, z ) t nt , x ix , y jy , z kz
1、 波动方程
u 其中:u t 0 ( x), t
( x)
t 0
2 2u 2 u a f ( x, t ) 2 2 t x u ( x) u t 0 ( x), t t 0 u x 0 1 (t ), u x l 2 (t )
t nt , x ix , y jy , z kz 1 n n 1 u in, 2 u u j ,k i , j ,k i , j ,k
t u in1, j ,k 2u in, j ,k u in1, j ,k (x) 2 u in, j 1,k 2u in, j ,k u in1, j ,k (y ) 2 u in, j ,k 1 2u in, j ,k u in, j ,k 1 (z ) 2
同时将边界条件和初始条件也离散化,得到:
ui1 ui0 u ( jx), (ix) t n n u0 1 (nt ), um 2 (nt )
0 i
(i 1,2,, m) (n 1,2,)
(5-3)
由式(5-2),并结合式(5-3),就可以从n时刻的各 点u值,计算得到下一时刻的u值,这样层层递推, 就可以计算出任意时刻,任意位置的u值。
偏微分方程的离散化方法课件

x2 )
从方程可以看出:如果已知第 n(本步时间)的值 Pin ,就可以求得第 n+1
时刻(下步时间)的值
P n1 i
。因此如初始条件,即
n=0
时各网格的
P
值已给定,
就可以依次求得以后各时间的 P 值。这种差分格式是显式差分格式。在显式差分
格式中:只有一个未知数 Pin1 ,由一个方程就可以求出。简单,精度较差,时间
步长受到严格限制,基本不用。
(2)隐式差分:利用 P(x,t)关于 t 的一阶向后差商和关于 x 的二阶差商, 在点(i,n+1)的差分方程:
P n1 i 1
2Pin1 x 2
P n1 i1
P n1 i
Pi n
t
(1
2
) Pi n 1
(
P n1 i1
Pi
n 1 1
)
Pi n
从方程可以看出:如果已知第 n(本步时间)的值 Pin ,为了求得第 n+1 时刻(下
(1)离散空间:把所研究的空间划分成某种类型的网格, 大的空间转化为若干小单元组成,网格之间动态连接,通 常采用矩形网格(正方体)。
(2)离散时间:把研究的时间域分成若干小的时间段, 在每个时间段内,对问题求解,时间段之间有机连接。步 长大小取决于所要解决的实际问题。
离散空间
P
t
离散时间
1、网格系统 它有x,y两个自变量,在平面上用平行线分割成许多网格, 如考虑时间,则。编号:x→i,y→j,t→n。为步长(对三 维z→k)。 节点:网格的交点叫网格节点。取一些与边界s接近的网格 节点,把他们连成折线Sh,Sh所围成的区域记为Dh,Dh 内的节点为内部节点、边界上的节点为边界节点。
偏微分方程及其求解实例ppt课件
(hn1-2.*h(k,n)+h(k,n-1))./dr.^2);
end plot(r(3:n)./ra,p(k,3:n).*theta.*2./rb)
h hi1 hi1 r i 2r
2h hi1 2hi hi1
r 2
r 2
i
P
1 rb 4
1
r
h r
2h r 2
偏微分方程的求解实例2:
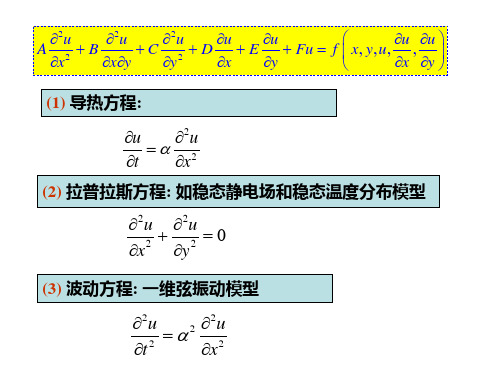
2u A x2
2u B
xy
C
2u y 2
D u x
E u y
Fu
f
x,
y,u,
u x
,
u y
(1) 导热方程:
u 2u
t x2 (2) 拉普拉斯方程: 如稳态静电场和稳态温度分布模型
2u 2u 0
x2 y2
(3) 波动方程: 一维弦振动模型
2u 2 2u
t 2
x2
偏微分方程的边界条件
function PDE1Dd_CrankNicolson % 使用Crank-Nicolson有限差分方法求解一维动态传
热模型
c1 = 100; c2 = 0; a = 10; b = 8; alpha = 2; n = 6; m = 8; U = CrankNicolson(@ic,c1,c2,a,b,alpha,n,m)
h t 3 9c
9c
h3 h33
4h r 4
3
h5 4h4
6h3 4h2 r 4
h1
h t
n
V
r i 2r
2h hi1 2hi hi1
r 2
r 2
i
3h r 3
hi2
2hi1 2hi1 2r 3
偏微分方程的离散化方法PPT精选文档

2!
3!
4!
(*)
P(x) xP(x) O(x)
P(x x) P(x) x P(x) (x/2)2 P(x) (x/2)3 P(x)
2
2
2!
3!
P(x) x P(x)O(x)
2
2
16
1、 一 阶 前 差 商
P P ( x x ) P ( x ) , P Pi1 Pi
x
x
x i
P P ( x x / 2 ) P ( x x / 2 ) , P Pi1 / 2 Pi1 / 2 忽 略 截 断 误 差 O (( x / 2 ) 2 )
x
x
x i
x
17
1、 二阶差商
将 方 程 (*)正 负 相 加 ,可 得 : P(x x) P(x x) 2P(x) x 2 P '' (x) x 4 P (4) (x) .........
x
2、 一 阶 后 差 商
P P ( x ) P ( x x ) , P Pi Pi1
x
x
x i
x
3、 一 阶 中 心 差 商
P P ( x x ) P ( x x ) , P Pi1 Pi1
x
2x
x i
2x
忽 略 截 断 误 差 O(x) 忽 略 截 断 误 差 O(x) 忽 略 截 断 误 差 O (x2)
2
(1)离散空间:把所研究的空间划分成某种类型的网格, 大的空间转化为若干小单元组成,网格之间动态连接,通 常采用矩形网格(正方体)。 (2)离散时间:把研究的时间域分成若干小的时间段, 在每个时间段内,对问题求解,时间段之间有机连接。步 长大小取决于所要解决的实际问题。
最新偏微分方程数值解课件ppt

t
u
u u n
n
i , j,k 1
i , j ,k
z t n t ,x i x ,y j y ,z k z
x
Email: Jansweili@ Phone: 029—85583997
上一页
下一页
回目录
休 息
5.2 离散化公式
对于二阶偏导,我们可以通过对泰勒展开式处理技术得到下面离散化 计算公式:
u
un i 1 , j,k
un i , j ,k
x t n t ,x i x ,y j y ,z k z
x
u
un i , j 1 ,k
un i , j ,k
y
y
t n t ,x i x , y j y ,z k z
u
uin , j,1kuin ,j,k
tt(n1)t,xix,yjy,zkz
下一页
回目录
休 息
5.2 离散化公式推导
将uk+1在uk处按二阶泰勒式展开:
u k 1u kh u x kh 22 ! 2 x u 2 kO (h 3)
将uk-1在uk处按二阶泰勒式展开:
u k 1u kh u x kh 22 ! 2 x u 2 kO (h 3)
二式相加得:
x2u2 uk1
在化工或化学动态模拟方程中,常常有一个自变量是时间, 其它的自变量为空间位置。如果只考虑一维空间,则只有 两个自变量;如果考虑两维空间,则有3个自变量。 许多 化工过程均是通过对偏微分方程的求解进行工艺参数的确 定或数值模拟。
Email: Jansweili@ Phone: 029—85583997
散化,补充方程,启动递推运算
Step4 数值解计算:求解离散系统问题
偏微分(3)分离变量法PPT课件

(
)
sin
ka
L
(t
)sin
k
L
x
d
其中
Bk
(
)
2
ka
L f ( , ) sin k d
0
L
(2.10)
2021/3/22
21
分离变量法:
令
k
u(x, t) Ck(t)sin
k 1
L
x
(2.11)
是混合问题的解。 显见上述函数满足(2.2)。
(2.1)
Ck(t)sin k 1
k
L
x k
从而定出 X (x) 所适合的常微分方程齐次边值问题,以及
T (t) 适合的常微分方程。
本征
求解该常微分方程齐次边值问题,
第二步 求出全部本征值和本征函数,并求
值问 题
出相应的 T (t) 的表达式。
第三步 将所有变量分离形式的特解叠加起来,并
利用初始条件定出所有待定系数。
2021/3/22
12
物理意义
正弦展开的Fourier级数的系数,即
Ak
2 L
L
( ) sin
k
d
0
L
(k 1,2,)
(1.17)
Bk
2
ka
L
( ) sin
k
d
0
L
(1.18)
这样,我们就给出了混合问题(1.1)-(1.4)的形 式解(1.14),其中系数由公式(1.17)和(1.18)给 出。
2021/3/22
10
sin x, sin 2 x, sin k x, 是[0, L]上的正交函数列
[
三偏微分方程的数值离散方法省公开课一等奖全国示范课微课金奖PPT课件

• 非守恒差分格式普通没有对应于原始守恒律“离散守恒律”。
12第12页
3.1.5 守恒型差分格式(续)
• 守恒型差分格式Lax-Wendroff定理: 假如守恒型差分格式
是和守恒律
u n1 j
u n1 j
t x
~f n 1 j 2
~f n 1 j 2
u f (u) 0 t x
相容,且当初间和空间步长趋于零时,差分解一致有界,几乎处处收敛于分 片连续可微函数,则这个收敛函数就是守恒律一个弱解。
比LW更简单,不需要计算函数在半点上值。 LW两步格式和MC各式缺点:定常解误差依赖于时间步长。
19第19页
Mac Cormack格式结构
U F 0
t x
P
:
U
*
U
n
Fn i 1
Fi n
0
t
x
C
U ** :
U *
Fi*
F* i 1
0
t
x
U
n1
1 2
(U
n
U
** )
Taylor exp.
t i1 xi
对于一维单个守恒律:
u f (u) 0 t x 其差分格式如果具有如下形式
u n1 j
u n1 j
t x
~f n j
1
2
~f n j
1
2
则为守恒型差分格式。
其中
~f n j
1
称为数值通量,它是2l个变量的多变量函数:
2
~f n j
1
~f
(u
n j l
1 ,
u
n j l
2,
,
u
n jl
偏微分方程的数值离散方法

偏微分方程的数值离散方法一维抛物方程是一个常见的偏微分方程,可以用来描述热传导问题。
其一般形式为:∂u/∂t=α(∂²u/∂x²)其中,u是温度的函数,t是时间,x是空间坐标,α是热扩散系数。
为了求解这个方程,我们可以使用显式差分法。
首先,在空间上进行离散化,将连续的空间坐标x划分成离散的节点。
然后,在时间上进行离散化,将连续的时间t划分成离散的时间步长。
通过将偏微分方程中的导数近似为差分,我们可以得到一个差分方程来逼近原方程。
在一维抛物方程中,使用中心差分法可以得到如下的差分方程:(u_i^(n+1)-u_i^n)/Δt=α(u_{i+1}^n-2u_i^n+u_{i-1}^n)/Δx²其中,u_i^n表示在节点i和时间步n的温度值,Δt和Δx分别是时间步长和空间步长。
然后,我们可以根据初始条件和边界条件来逐步更新节点的温度值,直到达到预定的时间。
另一个常见的偏微分方程是一维波动方程,可以用来描述波动的传播。
其一般形式为:∂²u/∂t²=ν²∂²u/∂x²其中,u是波动的位移函数,t是时间,x是空间坐标,ν是波速。
对于这个方程,我们可以使用数值离散方法,如有限差分法来求解。
类似于抛物方程,我们首先在空间上和时间上进行离散化。
然后,我们根据差分逼近,得到如下的差分方程:(u_i^{n+1}-2u_i^n+u_i^{n-1})/Δt²=ν²(u_{i+1}^n-2u_i^n+u_{i-1}^n)/Δx²其中,u_i^n表示在节点i和时间步n的位移值。
通过使用适当的初始条件和边界条件,我们可以逐步更新节点的位移值,直到达到预定的时间。
尽管上述方法对于一维问题是有效的,但是对于更复杂的二维或三维问题,就需要使用更高阶的差分方法,如二维抛物方程和二维波动方程中的五点差分法或九点差分法。
此外,还有其他更高级的数值方法,如有限元法和谱方法,可以用于求解偏微分方程。
三偏微分方程的数值离散方法课件.ppt

x3
3u x3
x
(e x 1)u
x
u j1 (e x 1)u ( 2 ) 等价于:
u 1 t t 2
2u t 2
1 t2 6
3u t 3
c
u x
1 x2 6
3u x3
c
2
t
1 2
2u x 2
1 24
4u x 4
(3)
• 差分方程(2)写成算子的形式:
2021/3/6
(三)偏微分方程的数值离散方法
• 3.1 有限差分法 • 3.2 有限体积法 • (有限元,谱方法,谱元,无网格,有限
解析,边界元,特征线)
2021/3/6
1
3.1 有限差分法
• 3.1.1 模型方程的差分逼近 • 3.1.2 差分格式的构造 • 3.1.3 差分方程的修正方程 • 3.1.4 差分方法的理论基础 • 3.1.5 守恒型差分格式 • 3.1.6 偏微分方程的全离散方法
5
3.1.3 差分方程的修正方程 (续)
2021/3/6
t
(e t
1)u
1 2
x
(e x
x
e x )u
1 2
2
e
x
x
2
x
e x
u
(4)
记算子
t
(e t
1)
t
u t
1 t2 2!
2u t2
1 t3 3!
3u t3
则
t
(e t
1)2
t2
2u t2
1 2
1 2
t 3
A n1
2021/3/6
G An 1
(三)偏微分方程数值离散方法

3.1.6.1 两层格式
• Crank-Nicolson格式
u u c 0 t x uin 1 uin c u n u n 1 ( )0 t 2 x x uin 1 uin c 1 n 1 (uin1 uin1 uin 1 ui 1 ) 0 t 4x
u f (u ) 0 t x
相容的,且当时间和空间步长趋于零时,差分解一致有界,几乎处处收敛于 分片连续可微的函数,则这个收敛的函数就是守恒律的一个弱解。
推论:守恒型差分各式的收敛解能自动满足间断关系。 用途: (加上熵条件)可以得到正确的激波,研究中大量使用 例如:Lax-Friedrichs 格式,Lax-Wendroff格式,Mac Cormack格式
3 3
(e (e 可以将t
t
t
t
t
1) 4 t 4
4u t 4
t 表示成(e t 1) l 的级数 t l
t 1 1 3 t t bl e 1 , b1 1, b2 , b3 , b3 t l 1 2 3 8 最后得到 1 x x x t 1 x t bl e x e x 2 e x 2 e x t bl e 1 2 t l 1 2 即有 u ku 2 p 1u 2 pu k k 2 p 1 2 p 1 2 p 2 p t k 1 x x x p 0 p 1 l l
(2)
1 un un j j t t t
u 1 2 2u 1 3 3u t t t 2! t 2 3! t 3
偏微分方程的离散化方法研究 ppt课件

(
Pi
n 1,
j
2Pi
n ,j
Pi
n 1,
j
)
(
Pn i, j
1
2
Pi
n ,j
Pn i, j
1
)
t
x 2
,
t
y 2
,截断误差: O(t
x 2
y 2 )
该线性代数方程组在节点(i,j)列方程式,用到(i,j),(i+1,j),(i-1, j),(i,j+1),(i,j-1)五个点。 —显式:只有一个方程,1 个未知数,简单,精度较差,时间步长受到严格限制, 基本不用。
2P y 2
P t
采用:等距网格差分 (1)显示差分:在点(i,j,n)的差分方程(图示)
Pn i1, j
2
Pi
n ,j
x 2
Pn i1, j
Pn i, j1
2
Pn i, j
y 2
Pn i, j1
P n1 i, j
Pn i, j
t
P n1 i, j
Pn i, j
格式中:只有一个未知数 Pin1 ,由一个方程就可以求出。简单,精度较差,时间
步长受到严格限制,基本不用。
PPT课件
20
(2)隐式差分:利用 P(x,t)关于 t 的一阶向后差商和关于 x 的二阶差商, 在点(i,n+1)的差分方程:
P n1 i 1
2Pin1 x 2
P n1 i1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/9/30
2
3.1.1 模型方程的差分逼近
2020/9/30
3
3.1.2 差分格式的构造
2020/9/30
4
3.1.3 差分方程的修正方程
• 差分方程所精确逼近的微分方程称为修正方程 • 对于时间发展方程,利用展开的方程逐步消去带时间的高阶导数,只留空间导数。 • Warming-Hyett方法:
3u t3
2
1 6
1 2
1 2
t 4
4u t4
t
(e t
1)3
t3
3u t3
1
1 2
t 4
4u t4
t
(e t
1)4
t4
4u t4
可以将
t 表示成
t
(e t
1 ) l 的级数
t
t
t
l1
b l
e
t t
1 l , b 1
1, b 2
1 2
,b3
u
n i
A n e ikx i
u n1 i
A e n 1 ikx i
u A e n
n ikx i1
i1
u
n 1
u
n i
(
u
n i
u
n i
1
)
A e n 1 ikx i A n e ikx i ( A en ikx i A e ) n ikx i1
满足稳定性要求的
amplificat ion factor G
A n1
2020/9/30
G An 1
9
3.1.4 差分方法的理论基础(续)
• Fourier (Von Neumann) 稳定性分(续)
G1eikx 1(coksxisinkx) 1(1coskx)isinkx
G2 1(1coskx)2 2sin2 kx14(1)sin2kx,
2
G1 if 1
u c u 0
(1)
t x
u
n 1 j
u
n j
1 2
u j1 u j1
1 2
2
u j1
2u j
u j1
(2)
Taylor 展开
u n1 j
u
n j
t
u t
1 t2 2!
2u t 2
1 t3 3!
3u t 3
t
(e t 1)u
u
j 1
u
j
x
u x
1 2!
x2
2u x 2
1 3!
1 3
,b3
3 8
最后得到
t
t
b
l
e
t
t
1 l
l1
l
bl
1 2
e
x
x
x
e x
1 2
2
e
x
x
2
x
e x
即有
u
t
k
k 1
ku xk
p0
2 p1
2 p1u x 2 p1
2p
p 1
2pu x2p
(5)
6
3.1.3 差分方程的修正方程(续)
u
t
k
k 1
• 守恒性质:
守恒型差分格式对 j求和 :
j J
u
n j
1
x
jJ
jJ
u
n j1
t
2
~f n J
1
t
2
再对 n求和 :
jJ
u
n j
1
x
jJ
jJ
u
0 j
x
jJ
N k 0
~ f
k
J
1
t
2
N k 0
~ f
k
J
1
t
2
可以看成是积分
u ( x, t )dx xJ1/ 2
x J 1 / 2
(三)偏微分方程的数值离散方法
• 3.1 有限差分法 • 3.2 有限体积法 • (有限元,谱方法,谱元,无网格,有限
解析,边界元,特征线)
2020/9/30
1
3.1 有限差分法
• 3.1.1 模型方程的差分逼近 • 3.1.2 差分格式的构造 • 3.1.3 差分方程的修正方程 • 3.1.4 差分方法的理论基础 • 3.1.5 守恒型差分格式 • 3.1.6 偏微分方程的全离散方法
u n1 j
t x
~f
n j
1
2
~f
n j
1
2
则为守恒型差分格式。
其中
~f
n j
1
称为数值通量,它是
2 l 个变量的多变量函数:
2
~f
n j
1
~f
(u
n jl
1
,
u
n j
l
2,
,
u
n jl
),
2
~f 满足相容性条件 :
2020/9/30
~f (u , u , u ) f (u )
11
3.1.5 守恒型差分格式(续)
• 相容性,稳定性,收敛性 • 等价性定理 • Fourier稳定性分析
2020/9/30
8
3.1.4 差分方法的理论基础(续)
• Fourier (Von Neumann) 稳定性分析
uin 1 tuinc 1 x(uin 1uin)0 , c0(1)
设 c t x
误差的基本解
代入 (1 ) :
• 1 称为CFL条件 (Courant, Friedrichs, Levy)
2020/9/30
10
3.1.5 守恒型差分格式
• 流体力学方程组描述物理量的守恒性;守恒律组:
• 定义
u d f 0
t i1 xi
对于一维单个守恒律:
u f (u) 0 t x 其差分格式如果具有如
下形式
u n1 j
5
3.1.3 差分方程的修正方程 (续)
2020/9/30
t
(e t
1)u
1 2
x
(e x
x
e x )u
1 2
2
e
x
x
2
x
e x
u
(4)
记算子
t
(e t
1)
t
u t
1 t2 2!
2u t2
1 t3 3!
3u t3
则
t
(e t
1)2
t2
2u t2
1 2
1 2
t 3
x3
3u x3
x
(e x 1)u
x
u j1 (e x 1)u ( 2 ) 等价于:
u 1 t t 2
2u t 2
1 t2 6
3u t 3
c
u x
1 x2 6
3u x3
c
2
t
1 2
2u x 2
1 24
4u x 4
(3)
• 差分方程(2)写成算子的形式:
2020/9/30
n 1
xJ 1/ 2 u ( x,0)dx
x J 1 / 2
t 0
n
1
u
(
x
J
1
,
t
)
dt
2
t 0
n
1
u
(
x
J
1
,
t
)
dt
2
该积分代表离散的守恒 律。完全对应于连续的 守恒律:
u ( x, t)dx f (u ( x, t)) dt 0
• 非守恒的差分格式一般没有对应于原始守恒律的“离散守恒律”。
偶次项系数 满足 : ( 1 ) p 2 p 0
对于( 2):
1
c,
2
0, 3
1 6
c(c 2 t2
x2)
4
1 c2t 8
(3c 2 t2 x 2 )
符合 War min g Hyett 稳定性判别条件
. why CFL 1 for scheme (2) ?
2020/9/30
7
3.1.4 差分方法的理论基础
ku xk
基本解为
p0
2 p1
2 p1u x 2 p1
2p
p 1
2pu x2p
e e ( i ) t ikx
( 1 ) p 2 p k 2 p p 1
( 1 ) p 2 p 1 k 2 p 1 p0
格式稳定的充分必要条
件是
( 1 ) p 2 p k 2 p 0 , k p 1
