(整理)少片变截面弹簧的计算.
少片变截面钢板弹簧的设计计算

少片变截面钢板弹簧的设计计算钢板弹簧是一种常见的机械弹簧,在各种机械和设备中得到广泛应用。
它由在轴线方向上并排排列的一系列弯曲的钢板组成,呈螺旋状。
当外力作用于弹簧时,它会发生形变,具有很好的弹性回复能力,是一种具有重要机械性能的弹簧。
一、设计计算1、弹簧基本要素弹簧基本要素包括钢带材料、外直径、内直径、圈数、导程、自由长度和加工工艺。
其中材料是决定弹簧机械性能的关键要素。
通常钢板弹簧采用碳素钢、合金钢等材料,其弹性模量会随材料强度的提高而增大。
2、弹簧设计弹簧的设计需要考虑弹簧的工作条件,计算外力的大小、方向、作用点等,从而确定弹簧材料的选择、外径、圈数等要素。
弹簧设计需要考虑以下几个方面:(1)弹簧的工作负荷:根据机械设备的工作条件和要求确定弹簧承受的最大负荷,以此作为设计的起点。
(2)弹簧的外径和内径:根据弹簧材料、工作负荷和工作环境等要素来确定弹簧的外径和内径大小。
(3)弹簧的圈数和导程:弹簧的圈数和导程直接决定了其刚度和变形量,需要根据实际需求来设计,避免过强或过松。
(4)弹簧自由长度:弹簧自由长度也会影响到其机械性能,需要根据实际工作环境来确定。
二、样例下面以一种常见的钢板弹簧为例,介绍其设计和计算过程。
1、材料选择假设需要设计一种碳素钢的钢板弹簧,采用SWO-A钢带材,其具有以下机械性能:屈服强度:235MPa弹性模量:210GPa泊松比:0.3材料密度:7.85g/cm³2、外径和内径的确定假设弹簧的最大工作负荷为500N,弹簧碳素钢钢带的工作应力取90%时,最大弹簧应变量ρs应该小于σ/2E,即(υ-Dw)/Dw≥0.08。
可根据此公式,确定外径Dw=20mm。
根据设计要求,弹簧的圈数为8,导程为3mm。
当弹簧材料确定且弹簧固定长度生成后,利用弹簧方程(Fs=kρs)推导,得到弹簧直径Di=17.9mm。
3、根据内径、外径和圈数确定性能参数内直径ID=Di-2t,弹簧导程l0=π(Di+Dw)/2,自由长度L0=l0*(n-1)+2*ra+ra-ra*υ/Dw。
弹簧计算公式

胡克弹性定律指出,在弹性极限范围内,弹簧的弹性力f 与弹簧的长度x 成正比,即f =-kx,k 是一个物体的质量弹性系数,该系数由材料的性质决定,负号表示弹簧产生的弹性力与其延伸(或压缩)方向相反弹簧常数: 以k 表示,当弹簧被压缩时,载荷(kgf/mm)增加1mm 的距离,弹簧常数公式(单位: kgf/mm) : k = (g d4)/(8dm3 nc) g = 钢丝的刚度模量: 钢琴丝g = 8000; 不锈钢丝g = 7300; 磷青铜丝g = 4500;黄铜丝g = 3500d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 转速总数弹簧常数的计算例子: 线径= 2.0 mm,外径= 22 mm,总匝数= 5。
5圈,钢丝材料= 钢琴钢丝k = (gxd4)/(8xdm3xnc) = (8000x24)/(8x203x3.5) = 0.571 kg f/mmpull,张力弹簧的k 值与压力弹簧的k 值相同。
张力弹簧的初始张力: 初始张力等于拉开彼此接近的弹簧所需的力,并发生在弹簧轧制成型之后。
在制作张力弹簧时,由于钢丝材质、线径、弹簧指数、静电现象、油脂、热处理、电镀等的不同,使得各张力弹簧的初始张力不均匀。
因此,在安装各种规格的张力弹簧时,应该预张力到平行弯道之间一定距离的力称为初张力。
初始张力= p-(kxf1) = 最大载荷-(弹簧常数x 拉伸长度)扭转弹簧常数: 以k 表示,当弹簧扭转时,载荷(kgf/m)增加1个扭转角。
弹簧常数(单位: kgf/mm) : k = (exd #)/(1167 xdmxpnxr) e = 钢丝的刚度模量: 钢琴线e = 21000,不锈钢线e = 19400,磷青铜线e =11200,黄铜丝e = 11200d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 载荷作用下转臂的总长度= 3.1416。
弹簧参数计算

弹簧参数计算
弹簧参数计算需要考虑以下几个方面:
1. 弹簧的刚度:弹簧的刚度指的是弹簧在受力时所产生的弹性变形,通常用弹性系数表示,单位为牛顿/米。
弹簧的刚度需要根据使用条件和设计要求进行选择和计算。
2. 弹簧材料的选择:弹簧的材料决定了其承受负荷的能力、耐久性和工作温度范围等特性。
常见的弹簧材料包括钢、不锈钢、铜合金、钛合金等。
3. 弹簧的几何参数:弹簧的几何参数包括线径、外径、自由长度、圈数等,这些参数影响着弹簧的刚度和承受负荷的能力。
4. 弹簧的工作条件:弹簧的工作条件包括所受载荷、工作温度、工作环境等,这些条件需要考虑到弹簧的材料和几何参数,以确定其所承受的极限负荷以及使用寿命。
综合以上几个方面,可以进行弹簧参数的计算和选择,以满足设计要求和使用条件。
汽车变截面钢板弹簧的设计计算

汽车变截面钢板弹簧的设计计算东风汽车工程研究院 陈耀明 2006年5月前 言少片变截面钢板弹簧在我国已有多年的制造和使用经验,特别是大、中型客车,采用者相当广泛。
然而,涉及变截面簧的设计计算方法,虽然二十几年前悬架专委会曾做过一些介绍,但资料零散、重复、不完整,尤其是比较常用的加强型变截面簧,资料反而欠缺。
撰写本文的目的,就是为悬架设计者提供变截面簧的比较完整的设计计算资料,主要是刚度计算公式和应力分布计算方法。
变截面簧轮廓线包括梯形和抛物线形两大类,每类又含有根部、端部加厚,或只有根部加厚,或都不加厚等几种变型。
这样,可以说几乎所有的变截面簧轮廓线都可在本文找到计算公式。
此外,本文还介绍了各种轮廓线的选型原则以及若干设计经验等,可供设计人员参考。
附录中列出已有资料中的一些计算公式,并证明了它们和本文公式的一致性。
本文的式(1)~(3)引自日本资料“自动车用重型钢板弹簧”,其它公式(6)~(15)是笔者近期重新推导出来的。
当然,有一些和过去推导出来的公式完全一致。
一、 纵截面为梯形的变截面弹簧这种弹簧的轧锥部分(3l ~4l 段)为梯形,而根部和端部都将厚度增大,称为加强型变截面簧,见图1。
图1为四分之一椭圆钢板弹簧,其刚度计算公式为:654321αααααα+++++=EK ----------------(1)若对称地扩展成为半椭圆钢板弹簧,其总刚度为:6543212αααααα+++++=EK ----------------(2)若弹簧由若干等长、相同轮廓线的叠片所组成,则其合成的总成刚度为:6543212αααααα+++++=nEK ----------------(3)式中 )/(10058.225mm N E ×=为弹性模数n 弹簧片数,单片弹簧1=n313114bt l =α⎥⎦⎤⎢⎣⎡++−+−+−−=1221112121221122212211132ln 223)(22212t t t Al t t l A t Al t t l A t Al t bA α )(43233323l l bt −=α ⎥⎦⎤⎢⎣⎡++−+−+−−=2322322223233223232223234ln 223)(22212t t t Bl t t l B t Bl t t l B t Bl t bB α ⎥⎦⎤⎢⎣⎡++−+−+−−=3423432324244324242234335ln 223)(22212t t t Cl t t l C t Cl t t l C t Cl t bC α )(43536346l l bt −=α而 1212l l t t A −−=3423l l t t B −−=4534l l t t C −−=其中 b 弹簧宽度实际应用中,有些弹簧的轮廓线有所简化,见图2,其刚度计算式也有所变化: 1、增厚转折点急剧变化,2型。
少片变截面弹簧的计算
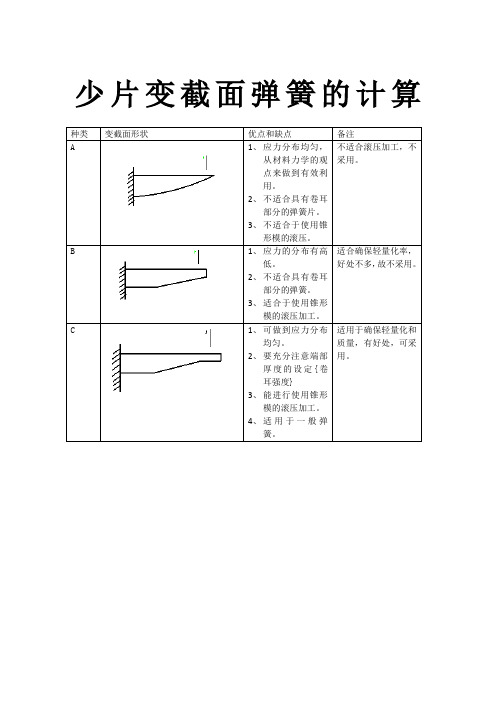
少片变截面弹簧的计算种类变截面形状优点和缺点备注A1、应力分布均匀,从材料力学的观点来做到有效利用。
2、不适合具有卷耳部分的弹簧片。
3、不适合于使用锥形模的滚压。
不适合滚压加工,不采用。
B1、应力的分布有高低。
2、不适合具有卷耳部分的弹簧。
3、适合于使用锥形模的滚压加工。
适合确保轻量化率,好处不多,故不采用。
C1、可做到应力分布均匀。
2、要充分注意端部厚度的设定{卷耳强度}3、能进行使用锥形模的滚压加工。
4、适用于一般弹簧。
适用于确保轻量化和质量,有好处,可采用。
D 1、以减轻C形中心孔部分应力为圆进行改良的。
2、能进行使用锥形模的滚压加工。
适合于小车型车辆用簧。
对确保质量有好处,可采用。
—1—种类变截面形状优点和缺点备注E1、为提高C形卷耳部分的强度,进行了改良。
2、能进行使用锥形模对确保质量有好处,可采用。
3、适用与中型车和大型车{前轴}的弹簧。
F1、是通过把D和E的形态结合在一起,有效地利用材料的形状。
对轻型化确保质量有好处,可采用。
G1、为适合长跨度产品,把F形状的加以改良的,是最有效地利用材料的形状。
2、能进行使用锥形模的滚压加工。
对轻量化有好处,可采用。
少片变截面弹簧的优点:1、应力分布均匀,接近于等应力梁,片数1—4片。
特殊工艺处理而提高其设计应力,从而使边界面弹簧轻量化,同等截面相比可减轻重量30—40%左右。
2、总成簧片在承载时,除端部传力处接触和中部骑马螺栓夹紧部位接触外,无片间接触现象,从而减少摩擦,使动刚度大力降低,提高乘坐舒适性。
3、由于片间接触区大为减少,基本上消除了由于片间接触摩擦磨损引起的使弹簧片早期损坏的疲劳源的产生,从而提高了疲劳寿命。
4、在总成中间平直等厚度的弹簧片,同上下保护垫板之间和簧片之间,插入塑料片或软金属垫片,这样就消除了弹簧总成工作时在中间平直等厚度段片间的直接挤压、摩擦,从而提高寿命。
5、采用喷完处理,中心孔挤压工艺和防锈性能,较好地油漆,这样也提高了疲劳寿命。
弹簧计算公式压簧拉簧扭簧弹力

压簧、拉簧、扭簧弹力计算公式压力弹簧压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;·弹簧常数:以k表示,当弹簧被压缩时,每增加1mm距离的负荷(kgf/mm);·弹簧常数公式(单位:kgf/mm):?G=线材的钢性模数:琴钢丝G=8000,不锈钢丝G=7300,磷青铜线G=4500 ,黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=圈 ,钢丝材质=琴钢丝?拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。
拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不平均的现象。
所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。
·初张力=P-(k×F1)=最大负荷-(弹簧常数×拉伸长度)?扭力弹簧·弹簧常数:以 k 表示,当弹簧被扭转时,每增加1°扭转角的负荷(kgf/mm).·弹簧常数公式(单位:kgf/mm):?E=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=。
弹簧设计基本公式

弹簧设计基本公式
以下是一些常见的弹簧设计公式:
1.线材应力公式:弹簧的线材应力是弹簧所承受的力和弹簧线材的横截面积之比。
线材应力可以通过以下公式计算:
σ=F/A
其中,σ是弹簧线材的应力,F是弹簧所承受的力,A是弹簧线材的横截面积。
2.弹簧刚度公式:弹簧的刚度是用来描述弹簧对外力的抵抗能力。
弹簧刚度可以通过以下公式计算:
k=(Gd^4)/(8nD^3)
其中,k是弹簧的刚度,G是弹簧材料的剪切模量,d是弹簧线材的直径,n是弹簧的有效圈数,D是弹簧的平均直径。
3.弹簧的最大应力和最大变形公式:最大应力和最大变形是弹簧的两个重要性能指标。
最大应力可以通过以下公式计算:
σ_max = 16F / (πd^3)
最大变形可以通过以下公式计算:
δ_max = (8Fn) / (πd^3G)
其中,σ_max 是弹簧的最大应力,δ_max 是弹簧的最大变形。
4.弹簧的自由长度公式:弹簧的自由长度是指弹簧未受到外力时的长度。
自由长度可以通过以下公式计算:
L_free = (n + 2) * d
其中,L_free 是弹簧的自由长度, n 是弹簧的有效圈数, d 是弹簧线材的直径。
这些是弹簧设计中常见的基本公式,通过这些公式可以计算和预测弹簧的各种行为和性能。
然而,弹簧的设计仍然是一个复杂的过程,需要考虑许多其他因素,如应力集中、疲劳寿命等。
因此,在进行弹簧设计时,还需要综合考虑其他相关的因素,以确保弹簧的可靠性和性能。
弹簧基本计算公式

白銅線
4X103
11X103
21X103
硬鋼線SWC
8X103
21X103
不鏽鋼線SUS631
7.5X103
21X103
不鏽鋼線SUS316
7X103
19X103
不鏽鋼線SUS304
7X103
19X103
不鏽鋼線SUS302
7X103
19X103
破銅線
4.5X103
13X103
磷青銅線
4.3X103
10X103
黃銅線
4X103
32
=───M
d3
Ed
=───a
360nd
-
3.符號代號:
d:線材直徑
G:橫彈性係數
D:平均直徑
E:縱彈性係數
n:有效卷數
P:荷重
彈簧材料之彈性係數
材質
橫彈性係數
G值(kg/mm2)
縱彈性係數
E值(kg/mm2)
彈簧鋼SUP
8X103
21X103
鋼琴線SWP
8X103
21X103
油回火線SWOC
8X103
nd2
-
彈簧指數與初張力之關係:
2.扭力彈簧之計算公式。(圓形斷面)
由M (kg~mm)計算
由撓度a計算
由應力(kg/mm2)計算
M (kg~mm)之公式
-
Ed4
M=────a
11520nD
d3
M=───
32
撓度ao之公式
11520nD
a=────M
d4E
-
360nD
a=───
dE
應力(kg/mm2)之公式
弹簧成型计算公式

弹簧成型计算公式弹簧是一种常见的机械零件,广泛应用于各种机械设备中。
它的作用是通过弹性变形储存和释放能量,用于缓冲、支撑或传递力量。
在设计和制造弹簧时,需要考虑弹簧的形状、材料和尺寸等因素,以确保其满足设计要求。
弹簧成型计算公式是设计和制造弹簧时必不可少的工具,它可以帮助工程师准确地计算弹簧的参数,以满足设计要求。
弹簧成型计算公式通常包括弹簧的刚度、变形量、载荷等参数。
其中,弹簧的刚度是指单位变形量所产生的力,通常用弹簧常数(K)表示。
弹簧的刚度可以通过以下公式计算:K = Gd^4 / (8D^3n)。
其中,K为弹簧常数,G为弹簧材料的剪切模量,d为弹簧线径,D为弹簧的螺旋直径,n为弹簧的有效圈数。
通过这个公式,可以根据弹簧的材料和尺寸计算出其刚度,从而确定其在工作时的变形量和载荷。
除了刚度,弹簧的变形量也是设计时需要考虑的重要参数。
弹簧的变形量可以通过以下公式计算:δ = F / K。
其中,δ为弹簧的变形量,F为施加在弹簧上的载荷,K为弹簧的刚度。
通过这个公式,可以根据弹簧的载荷和刚度计算出其变形量,从而确定其在工作时的变形情况。
除了刚度和变形量,弹簧的载荷也是设计时需要考虑的重要参数。
弹簧的载荷可以通过以下公式计算:F = Kδ。
通过这个公式,可以根据弹簧的刚度和变形量计算出其所能承受的最大载荷,从而确定其在工作时的承载能力。
除了上述基本的弹簧成型计算公式,还有一些特殊情况下需要考虑的因素。
例如,当弹簧受到扭转载荷时,需要考虑扭转刚度和扭转变形量。
此时,可以通过以下公式计算弹簧的扭转刚度:Kt = Gd^4 / (32D^3n)。
其中,Kt为弹簧的扭转刚度,G为弹簧材料的剪切模量,d为弹簧线径,D为弹簧的螺旋直径,n为弹簧的有效圈数。
通过这个公式,可以根据弹簧的材料和尺寸计算出其扭转刚度,从而确定其在受到扭转载荷时的变形量和载荷。
总之,弹簧成型计算公式是设计和制造弹簧时必不可少的工具,它可以帮助工程师准确地计算弹簧的参数,以满足设计要求。
汽车变截面钢板弹簧的设计计算

汽车变截面钢板弹簧的设计计算摘要本文介绍了汽车变截面钢板弹簧的设计计算,包括弹簧参数计算、弹簧形状设计及材料组成等方面。
通过对变截面钢板弹簧的物理特性进行分析,结合设计要求,以及材料及工艺的要求,采用MARC建模及软件进行非线性有限元分析,得出变截面钢板弹簧的设计结果。
关键词:变截面钢板弹簧,参数计算,形状设计,MARC建模1. IntroductionVariable-Cross-Section Steel Plate Spring (VCSSPS) is an important part in auto manufacture. VCSSPS can provide smooth and reliable force when it works in enclosed space because ofits advantages of light weight and small size. It has been widely used in body, chassis, engine and suspension systems. VCSSPS contains a variety of parameters such as material, shape, size and load. And its performance is greatly affected by these parameters. Thus, it is very important to design the VCSSPS in a reasonable way.In general, VCSSPS design includes three steps: parameters calculation, shape designing and material selection. First, parameters calculation must be done according to the design requirement. Then, shape should be designed according to parameters carefully. Furthermore, the material and processes should be carefully selected and applied.In this paper, we introduce the VCSSPS design process and analysis. We use MARC software to analyze the VCSSPS under nonlinear finite element environment and get the parameters’ design results. The main contributions include: 1) a conciseintrod uction of VCSSPS design process; 2) analysis of parameters’ effects on VCSSPS; 3) the optimization of geometry design and material selection; 4) the design results of VCSSPS.2 Parameter CalculationThe parameters of VCSSPS mainly include load, length,section size, curvature, number of plate and material. The calculation results of these parameters have significantinfluence on the performance of VCSSPS.2.1 LoadLoad is the product of spring force and displacement, which can be obtained from the static deflection and force performance data provided by the design requirements.2.2 LengthLength of VCSSPS is determined by the static performance. Generally, the distance between the mounting holes should be the same as that of the mating parts.2.3 Section SizeThe section size of VCSSPS can be obtained from the load and displacement provided by the design requirements. Generally, thesection size should be determined according to the static performance.2.4 CurvatureCurvature of VCSSPS is determined by the section size. Generally, the curvature should be designed according to thestatic performance.2.5 Number of PlateThe number of plate is determined by the dynamic performance. Generally, the number of plate should be designed according tothe dynamic performance.2.6 MaterialThe ideal material for VCSSPS is determined by the static, dynamic and temperature requirements. Usually, good strength and modulus of elasticity are preferred.3 Shape DesignThe shape of VCSSPS should be designed according to the parameters calculated above. In general, the shape of VCSSPS should be designed as follows:3.1 Section SizeSection size of VCSSPS should be designed according to the calculated parameters. Generally, the section size should be designed as uniform as possible.3.2 Number of PlateThe number of plate should be designed according to the calculated parameters. Generally, the number of plate should be designed as many as possible.3.3 Geometry。
弹簧计算公式

弹簧应力:弹簧的压缩应力、拉伸 应力等
工作环境:温度、湿度、腐蚀性等
弹簧制造工艺:热处理、表面处理 等
提高弹簧疲劳寿命的方法
选用优质材料: 选用高强度、高 韧性的材料,提 高弹簧的疲劳寿 命
优化设计:优化弹 簧的形状、尺寸和 结构,提高弹簧的 疲劳寿命
控制加工工艺:控 制弹簧的加工工艺, 提高弹簧的疲劳寿 命
计算。
添加标题
弹簧应力和应变 的计算公式:弹 簧应力和应变的 计算公式可以通 过弹簧的弹性模 量、截面尺寸和 弹簧的刚度等参
数来计算。
添加标题
弹簧应力和应变的计算公式
弹簧应力计算公式:σ = F/A 弹簧应变计算公式:ε = ΔL/L 弹簧应力和应变的关系:σ = Eε 弹簧应力和应变的物理意义:应力表示弹簧受力大小,应变表示弹簧形变量大小。
热处理:对弹簧进 行热处理,提高弹 簧的疲劳寿命
润滑:对弹簧进行 润滑,减少摩擦, 提高弹簧的疲劳寿 命
定期维护:定期对 弹簧进行检查和维 护,及时发现和处 理问题,提高弹簧 的疲劳寿命
感谢观看
汇报人:
弹簧应力和应变的影响因素
弹簧的材料:材料 的弹性模量、屈服
强度等
弹簧的形状:弹簧 的直径、长度、线
径等
弹簧的载荷:弹簧 所承受的力大小和
方向
弹簧的温度:温度 对弹簧的弹性模量 和屈服强度的影响
05
弹簧振动频率和阻尼比计算
弹簧振动频率和阻尼比的定义
弹簧振动频率:弹簧在振动过程中,单位时间内振动的次数,单位为赫兹(Hz)。
1/2π√(k/m尼比的应用场景
汽车悬挂系统:弹簧振动频率和阻尼比直接影响汽车的舒适性和操控性 机械设备:弹簧振动频率和阻尼比影响设备的稳定性和寿命 建筑结构:弹簧振动频率和阻尼比影响建筑的抗震性能和稳定性 航空航天:弹簧振动频率和阻尼比影响飞行器的稳定性和操控性
少片变截面钢板弹簧的疲劳寿命分析

少片变截面钢板弹簧的疲劳寿命分析*屈翔张小锋李影杰摘要:少片变截面钢板弹簧在货车、牵引车上逐渐普及运用。
本文建立了某公司少片变截面钢板弹簧的有限元模型,并进行了应力分析,得到其应力从中间向两端先增大后减小的变化趋势,满足材料的许用应力要求;参照国标GB/T 19844-2005中的试验规范,进行了疲劳寿命的有限元分析和试验验证工作:由疲劳寿命云图可知,板簧发生破坏时的载荷循环次数为11.6万次;断裂位置最容易发生在距离板簧中心安装点为116.1mm~145.4mm处,该处正是簧片应力最大的地方;通过疲劳寿命试验,验证了有限元法对建立钢板弹簧模型的正确性。
关键词:少片变截面钢板弹簧;有限元分析;疲劳寿命1.少片变截面钢板弹簧的应力分析1.1 少片变截面钢板弹簧的几何模型根据某公司的产品,该少片变截面板簧由三片变截面式钢板组成,装配体的几何模型导入MD Patran中如图1所示。
图1 几何模型1.2 网格划分对少片变截面钢板弹簧采用实体单元;考虑板簧的结构细节,其应力集中、非线性、大变形的特点,采用精度较好、注重几何细节的8节点六面体单元;由于存在截面尺寸变化的,故每片簧采用3层网格划分,板簧单片高为25mm,宽度方向100mm。
划分好的网格如图2所示,总共有34588个六面体单元[1]。
图2 网格模型1.3 材料属性根据产品图纸,该少片簧材料为50CrVA,热处理温度中淬火温度为1120T,回火温度为770T,淬火介质是油;力学性能:抗拉强度1275 (N/mm2),屈服强度1130(N/mm2),断面收缩率20%[2]。
1.4 载荷及边界条件的确定根据钢板弹簧的安装要求与工作特点,规定其在卷耳的两端处只沿X方向移动,固定其YZ方向的移动;在模型的中间位置只沿Y轴移动,固定其XZ方向的移动[3]。
采用MPC约束,预定接触区域内的单元全定义为接触体,采用deformable body,接触算法选用增强的拉格朗日法;摩擦采用库仑模型,摩擦因数取0.1。
变截面板簧刚度设计与计算

总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
= -w 5 - -f 5= 3. 171- 1. 53= 1. 641, 及式( 19) 解出 -w 6 = 1. 46, 故 w 6 = 1. 46 t = 0. 9m m 。 第七 辊取
w7
弯或负值压弯。 从理论上看压弯量在4. 5mm 以下 可以得到良好矫直, 再大没有必要 , 各辊的分配 也不需严格限定。 5 结语 本文所提供的方法用文献 [ 2] 的实测值验证 是可用的, 其理论简单 , 方法容易, 程序严谨 , 很 具有实用性。 但压弯量计算法的适用性不仅与其 本身的精确性有关 , 也与设备刚度的正确定量有 关, 如矫直辊的弹跳量及压力系统的刚度 值等。 压弯量数学模型的精确化在我国 已具有现实意 义, 文献[ 4] 已经取得初步成果 , 本文作为一种参 与, 愿与同行们共同推进这一工作。
G =
EB = 37. 5 N/ m m 4 K ( i) GD 1= 2G = 75 N/ m m 第一片简图( 如图2 所示) :
图 2 6700后簧第一片
( 转第6 页) — 31 —
总 第 113 期 冶 金 设 备 1999年 2 月第 1期
L L
2
( 2)
dx +
总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
少片变截面弹簧的设计

科学・创新・振兴少片变截面弹簧的设计王宝和(沈阳金杯车辆制造有限公司)目前,少片变截面弹簧在轻型货车和客车上已经获得了广泛地应有,与多片弹簧相比较具有如下的优点:与多片弹簧相比,其重量能降低40%左右,相应地也就减少了对车架和车身的冲击力。
少片变截面弹簧在其片间装置有减磨垫片,显著地降低了片间的摩擦力,从而提高了弹簧的疲劳寿命。
由于为变刚度,所以乘坐的舒适性较大提高。
本文从以下几个方面阐述了少片变截面弹簧的设计:1少片变截面弹簧的构造少片变截面弹簧的叶片数量为l—4片,多数是等宽的,弹簧厚度沿长度方向变化有两种,即纵向截面为直线型和抛物线型。
片闫垫片为减摩材料制成,能降低片间的摩擦力,提高弹簧的疲劳寿命。
2少片变截面弹簧的参数确定2.1弹簧上的载荷w:载荷是根据总布置设计给定的轴荷减去非簧载重部分(前、后轴,车轮,转向节,制动鼓,轮谷,弹簧自重等)2.2弹簧的片数n:片数是根据弹簧上的载荷的大小来选取。
弹簧上的载荷W<1000Kg时,一般采用其1片,1000Kg<W<2000Kg时,一般采用2片,W>2000kg时,一般采用3片或者4片。
2.3弹簧叶片的宽度b:根据总布置来确定,在总布置允许的情况下,应尽量地增加叶片的宽度,以增加弹簧的侧倾角刚度,从而提高整车的横向稳定性。
2.4弹簧的剐度c:静挠度fc需要根据汽车总布置对平顺性的要求,按着固有频率和汽车空载及满载的高度要求,初步地确定静挠度fc和弹刚度C,待弹簧设计完成后再进行精确的计算。
2.5弹簧叶片的长度L:要合理的确定弹簧叶片的长度,弹簧中的应力与长度的平方成反比,故增加弹簧的长度可显著的降低弹簧的应力,提高弹簧的强度,减少了应力的变化幅度,从而提高了弹簧的使用寿命,同时增加了纵向角刚度和纵向稳定性,因此在总布置允许的情况下,应尽量的增加弹簧的长度。
3抛物线形状变截面钢板弹簧的参数计算:3,1纵向载面为抛韧线形状的钢板弹簧,其抛物线方程是顶点为坐标原点并对称于Y轴的抛物线的标准方程:3.2物线钢板弹簧惯性矩3.3抛物线钢板弹簧横截面的R口度3.4抛物线弹簧的应力:3.5抛物线钢板弹簧中部的厚度h:3.6抛物线钢板弹簧的平均应力3.7比应力弹簧的使用寿命在很大程度上取决于弹簧工作时的应力的大小,比应力的大小直接影响弹簧的使用寿命。
少片变截面钢板弹簧的疲劳寿命计算分析

科技资讯 2008 NO. 21
S CI ENCE & TECHNOLOGY I NFORMATI ON
少片变截面钢板弹簧的疲劳寿命计算分析
张劲 松 ( 贵 州省遵 义市遵义 钛厂机 械设备 公司 贵州 遵义 5 6 3 0 0 4 )
摘 要: 根据少片 变截面钢板 弹簧每一 片在自由状 态下的几 何尺寸, 利用 UG软件建 立各片的三 维模型并 进行装配。 在 Hy p e r Me s h 中采
( 下转 7 1 页)
科技资讯 SCI ENCE & TECHNOLOGY I NFORMATI ON
69
工业技术
层及开门由系 统自动控制。 ③无 司机工作方式是系统的自动工作
方式, 考 虑到实际 客梯中乘客 上、下呼梯 的随机性 , 该系统的 选层控制满 足以下要 求: 上 升过程响应 大于等于当 前楼层的 内 呼 和 上 升 外 呼 信号 , 记 忆 其 他 信 号 ; 下 降 过 程 响 应 小 于 等 于 当 前 楼 层 的内 呼 和 下 降 外 呼信 号, 记忆 其他信 号; 在当 前的 行进方 向, 内呼信号 优先响应; 若 无呼梯信号, 轿 厢停在当前楼层; 电梯不用时, 回到一楼。
利 用 三 维 建 模 软 件 UG 建 立 少 片 变 截 面钢板弹 簧各片的几 何模型并 进行装配, 装 配 完 成 后 的 少 片变 截 面 钢 板 弹 簧 总 成 如 图 1 所示。
对包含一个 目标面和一个 接触面, 定义凹 面为目标面, 凸面为接触面。 2 . 3 定 义边 界条件
钢板弹簧的边界条件 主要有位移约束 和自 由 度 耦 合 两 种 方 式 。 板 簧 第 一 片 的 左 端采用固定卷 耳连接, 另 一端采用活 动吊 耳连接, 在卷 耳或吊耳 与转动轴之 间装有 橡胶制成的减 摩衬套, 所 以这两处的 约束 可以 看 成 铰 链 。 应 用 如 下 方 法 对 它 们 进 行 模拟 , 将 卷 耳 内 加 入 一 个 圆 柱 体, 把 它 与 卷 耳相互 粘接 起来 ; 在 固定卷 耳的 一端 ( 左 端) , 把圆 柱体 中轴 线上 的节 点在 x 、y、 z 方 向的自由度都 加以约束; 在浮动卷耳 的一 端( 右端) , 只约束圆柱 体中轴线上节 点在 y、z 方向 的自 由度 。 另外 , 本 文对 中 心螺 栓 的约 束 是 通 过 耦 合 中 心 螺 栓 孔 面 上 节 点 的 所有自由度来实现的 。
少片变截面钢板弹簧的设计计算

少片变截面钢板弹簧的设计计算钢板弹簧是由钢板材料弯曲而成的一种弹簧。
与圆钢弹簧相比,钢板弹簧具有更高的弹性限度和更大的变形能力。
因此,在工程设计中,钢板弹簧得到了广泛的应用。
少片变截面钢板弹簧特指弹簧的板片数量较少且断面形状发生变化的钢板弹簧。
下面将介绍少片变截面钢板弹簧的设计计算。
1.确定设计参数在进行钢板弹簧的设计计算之前,需要确定所需的设计参数。
包括工作负荷F、工作长度L、显微硬度和板片数量n等。
显微硬度是指在微观级别下测量的钢板的硬度。
确定这些参数后,可以通过下列公式计算弹簧的弹性变形:δ=8 × FL^3/En × d^4其中δ表示弹簧的弹性变形,E表示钢板的弹性模量,d表示钢板厚度。
2.确定钢板尺寸和弹簧几何参数在确定设计参数后,可以计算钢板弹簧的几何参数。
包括钢板长度L,钢板宽度b,钢板厚度d,弹簧直径D和板片数量n。
根据这些参数计算出钢板的截面积A和钢板的极径I:A=b × d × nI=b × d^3 × n/123.计算钢板的各个应力和变形在完成钢板的几何参数计算后,可以计算钢板的各个应力和变形。
包括板片的单向弯曲应力σ、截面变形度θ和截面扭转角φ。
单向弯曲应力σ可以通过下面的公式计算:σ=-My/I其中M表示截面转矩,y表示截面离中心轴的距离。
4.校核钢板的疲劳寿命在完成各个应力和变形的计算后,需要对钢板进行疲劳寿命校核。
通常采用S-N曲线法进行疲劳寿命计算。
根据应力幅值和循环次数可以得到S-N曲线,从而计算钢板的疲劳寿命。
总之,少片变截面钢板弹簧的设计计算是一项非常重要的工作,涉及到很多参数和公式的计算。
在实际应用中,需要综合考虑各种因素,确保设计的弹簧满足工程要求。
弹簧计算公式excel

弹簧计算公式excel摘要:1.弹簧计算公式的概述2.弹簧计算公式在Excel 中的应用3.弹簧计算公式的实例解析4.结论正文:1.弹簧计算公式的概述弹簧计算公式是用于计算弹簧的伸长量、压缩量或应力的数学公式。
在工程领域,弹簧经常被用于减震、测量和控制等应用。
弹簧计算公式通常基于弹簧的材料、截面积、线径和长度等参数。
2.弹簧计算公式在Excel 中的应用Excel 是广泛使用的电子表格软件,可以轻松地实现弹簧计算公式的应用。
在Excel 中,可以使用公式函数来计算弹簧的各种参数,如伸长量、压缩量和应力等。
常用的Excel 函数包括SUM、AVERAGE、MAX、MIN 和IF 等,可以结合弹簧计算公式来实现复杂的计算任务。
3.弹簧计算公式的实例解析假设我们有一个圆柱形弹簧,其材料为钢,截面积为10 平方毫米,线径为2 毫米,长度为50 毫米。
我们可以使用以下公式来计算弹簧的伸长量:伸长量= F * x / k其中,F 是施加在弹簧上的力,x 是弹簧的伸长量,k 是弹簧的弹性系数。
在Excel 中,我们可以将上述公式分解为多个步骤来实现。
首先,我们需要计算弹簧的弹性系数k,可以使用以下公式:k = G * (π* d^4) / 8 * L其中,G 是弹簧的剪切模量,d 是弹簧的线径,L 是弹簧的长度。
接下来,我们可以使用IF 函数来判断弹簧是伸长还是压缩,然后根据伸长量或压缩量来计算弹簧所受的力F。
最后,我们可以使用SUM 函数来计算弹簧的伸长量或压缩量。
4.结论弹簧计算公式在Excel 中的应用非常方便,可以实现复杂的弹簧计算任务。
通过使用Excel 的公式函数,可以轻松地计算弹簧的伸长量、压缩量和应力等参数。
弹簧.产品.经典.面积.计算

弹簧.产品.经典的面积.计算:单重=0.04g每公斤约=25000个
如按(外径)公式计算:
圈数61-外径1.1mm-π-线径0.2mm-π-弹簧双截面1.9mm²
61*1.1*π3.1416*0.2*π3.1416+ 1.9=134.35mm²
单个面积=0.0134dm²
按标准(中心线径)公式计算:
先将(外径1.1mm+内径0.7mm)÷2=(求出0.9mm为中心线径)
以圏数61*中心线径0.9mm* 3.1416*0.2mm线径*3.1416
=108.36mm²+弹簧双截面1.9mm²=110.26mm²=单个弹簧面积0.0110dm²
弹簧面积分两部分计算的:面积1+面积2
面积1=弹簧长度*弹簧截面周长
弹簧长度=圈数61*圈周长=圈数61*3.1416*中心线径0.9mm
=172.47mm
弹簧截面周长=π圆周率(Pi)3.1416*线径0.2mm=0.6283mm
所以,面积1=弹簧长度172.47mm*弹簧截面周长0.6283mm=108.36mm²
面积2=两个截面的面积= 3.1416*r2*2
= 3.1416*0.55*0.55*2(r为弹簧半径)=1.9mm²
弹簧面积=面积1:108.36mm²+面积2: 1.9mm²
=110.26mm²=0.0110dm²(单个弹簧面积)。
弹簧重量计算公式

弹簧重量计算公式
弹簧的重量计算公式如下:
弹簧重量= 弹簧线材密度×π×弹簧线径²×弹簧长度÷4
其中,
弹簧线材密度:指弹簧所采用的线材的密度,一般以克/立方厘米表示。
π:圆周率,取值为3.14。
弹簧线径:指弹簧所采用的线材的直径,一般以毫米为单位。
弹簧长度:指弹簧的长度,一般以毫米为单位。
弹簧重量计算公式的解释如下:
弹簧的重量与弹簧线材密度、弹簧线径、弹簧长度等因素有关。
弹簧线材密度越大、弹簧线径越大、弹簧长度越长,弹簧的重量也就越大。
而弹簧重量计算公式中的π是一个常量,其取值为3.14,用于计算弹簧的横截面积。
弹簧线径的平方是弹簧横截面积的大小,弹簧长度除以4是为了计算弹簧体积。
因此,通过弹簧重量计算公式,我们可以很好地估算出弹簧的重量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
少片变截面弹簧的计算
—1—
少片变截面弹簧的优点:
1、应力分布均匀,接近于等应力梁,片数1—4片。
特殊工艺处理而提高其设计应力,从
而使边界面弹簧轻量化,同等截面相比可减轻重量30—40%左右。
2、总成簧片在承载时,除端部传力处接触和中部骑马螺栓夹紧部位接触外,无片间接触现
象,从而减少摩擦,使动刚度大力降低,提高乘坐舒适性。
3、由于片间接触区大为减少,基本上消除了由于片间接触摩擦磨损引起的使弹簧片早期损
坏的疲劳源的产生,从而提高了疲劳寿命。
4、在总成中间平直等厚度的弹簧片,同上下保护垫板之间和簧片之间,插入塑料片或软金
属垫片,这样就消除了弹簧总成工作时在中间平直等厚度段片间的直接挤压、摩擦,从而提高寿命。
5、采用喷完处理,中心孔挤压工艺和防锈性能,较好地油漆,这样也提高了疲劳寿命。
(一)、变刚度弹簧刚度计算推导:
少片变刚度钢板计算:简图如上所示(与单片为例)
t x=t1-(L2-x)(t1-t2)/L1 (1)
I1=bt13/12 (2)
I2=bt23/12 (3)
Ix=btx3/12 (4)
弹簧刚度:
由材料力学悬臂梁理论得到
自由刚度C
2/C=∫0L2-L1[x2/EI2]dx+∫L2L2-L1[X2/EI x]dx+∫L L2[x2/EI1]dx (5)
夹紧刚度
2/C=∫0L2-L1[X2/EI2]d x+∫L2L2-L1[x2/EI X]d x+∫L2L-S/4[X/EI1]d X (6)
以上刚度公式算出的是一片刚度值,如果有几片同样长,乘n即得出总称刚度。
对<5>式积分得:
2/C=[L2-L1]3/3EI2+V+[L3-L32]/3EI1]。
《7》其中:
V=[12L31/Eb(t1-t2)3][m2(1/t12-1/t12)/2L12+2m(1/t2-1/t1)/L1+㏑t1/t2] (8)
式中m=L2t1-L2t2-L1t1
同理得:
2/C=(L2-L1)3/3EI2+V+[(L-S/4)3-L23]/3EI1
距端头x处的应力:σx
σx=PX/W
抗弯断面系数
W x=bt x2/6
(二)、加强型锥形断面图5所示
锥形段位抛物线的变断面单片示意图
1、刚度计算公式
C=6EI/KL3
式中:K=1+(1-λ1)3[1-2(1-ε1)3/2]+(1-λ2)3h
其中:λ1=L1/L λ2=L2/L ε1=(L2-L1)/[L-L1]
η=(t1/t2) 3I=bt13/12
2 、离根部X点处的应力计算公式
0≤X≤L1时σ=(6P/bt22)(L-X)2
L1≤X≤L2时σ=(6P/bt12)(L2-L1)=(6P/bt22)(L-L2)
L2≤X≤L时σ=(6P/bt12)(L-X)
B---片宽
3 总成自由弧高H0的计算
H=H夹c+Q c/C+Δf+ΔH
式中:H夹c:装车夹紧后,满载总成弧高,一般由布置确定。
Q c:满载每付弹簧的负荷C:装车夹紧后的刚度
Δf:总成刚性曲线成形变形量,一般参考同类型的实测值选定。
ΔH:总成装在车桥上夹紧前、后弧高变化量,由于少片变截面弹簧在U型螺栓夹紧部位是平直段,故取ΔH=0
4总成自由半径的计算:R0
①双卷耳结构:
R0=(L0-S/2)2/[2(δ0-r)]{1-(δ0-r)(δ0+5r)/[3(L0-s/2)2]} 式中:δ0=H0+r r---卷耳孔半径
L:总成第一片长度之半s/2:中部平直段长度之半
自由总成第一片曲率示意图
②两端滑板结构的总成见下图
R0=[(L-s/2)2/2H]+H0/2
式中:L:作用弧长之半
自由总成第一片曲率示意图(两端滑板)
5单片自由曲率半径R k,单片自由弧高h ok的计算见图1 图2
①:
1两端为卷耳结构总成
②两端为滑板的总图EQ150前σ01=﹣29.42N/mm2
σ01=﹢29.42N/mm2
②装配成总成前、后,各单片的弧高变化量Δf ok
Δf ok=W kσok/(L ok c ok/2)
{最好满足各片预应力引起的的弯矩之代数和为零}
式中:W 可:各片中部平直段抗弯断面系数
H 01=H 0
H 02=H 01+(t 2-t 1)+T
H 0:总成自由弧高
T :片间衬垫厚度
W k =bt 2k 2/6
σok :各单片装配预应力
C ok :各单片自由刚度
L k :各单片作用长度之半
③各单片的自由弧高H K
H k =H ok +Δf ok
④各单片的自由曲率半径R k 的计算
❶已知作用弦长为L OK -S/2上的弧高H k 时
R k =(L ok -s/2)2/2H k +H k /2
❷已知弧长之半L K 上弧高H 时K
sin αk =2LH/(L 2+H 2)
L:弦长之半H:弧高
单片曲率示意图
α由H k/2L k值查专用表求出,以2L K为弧长H可为弧高的扇形,中心角:2α
b R=2L K/2αK
⑤各单片标注注:自由弧高h k(不计卷耳半径)(考虑中间平直段对h k的影响)
h k=R K{1-cos[(L K-s/2)57.29578/R K]}
式中:L k单片长度之半
⑥各单片标注弧高δk(计入卷耳半径)
δk=h k+r
其中r 卷耳内孔半径
六、少片变截面弹簧特性,强化工艺简介
《一》锥形弹簧片中心孔强化工艺
1.中心孔圆角冲压工艺
所谓中心孔圆角冲压工艺,就是在应力集中孔的拉应力面冲出“R”形塑性变形的中心孔,和用钢球挤压塑性变形的中心孔,这样的目的是为了缓和中心孔的应力集中现象,从而提高疲劳寿命。
如果在拉应力面进行倒角加工后,再进行热处理,最后喷丸处理,也能达到上述目的弹簧中心孔如下进行。
二汽对55SiMnVB 11×75单面双槽扁钢,加工中心孔德工艺方法,经过试验已经成功,钻孔—受拉应力表面锪孔—淬火—回火—受拉应力面喷丸为最后工艺流程。
《二》锥形弹簧片受拉应力表面采用应力喷丸。
目的:使受拉应力表面产生足够大的残余压应力,在钢板弹簧工作时,弹簧片受拉应力表面的拉应力相应地减少,从而提高疲劳寿命。
喷丸处理除了在拉应力表明产生残余压应力外,且在喷丸表明产生0.25mm的硬化层,从而消除和改善簧片的表面缺陷也提高了疲劳寿命。
