变截面钢板弹簧的设计计算
少片变截面钢板弹簧的设计计算

少片变截面钢板弹簧的设计计算钢板弹簧是一种常见的机械弹簧,在各种机械和设备中得到广泛应用。
它由在轴线方向上并排排列的一系列弯曲的钢板组成,呈螺旋状。
当外力作用于弹簧时,它会发生形变,具有很好的弹性回复能力,是一种具有重要机械性能的弹簧。
一、设计计算1、弹簧基本要素弹簧基本要素包括钢带材料、外直径、内直径、圈数、导程、自由长度和加工工艺。
其中材料是决定弹簧机械性能的关键要素。
通常钢板弹簧采用碳素钢、合金钢等材料,其弹性模量会随材料强度的提高而增大。
2、弹簧设计弹簧的设计需要考虑弹簧的工作条件,计算外力的大小、方向、作用点等,从而确定弹簧材料的选择、外径、圈数等要素。
弹簧设计需要考虑以下几个方面:(1)弹簧的工作负荷:根据机械设备的工作条件和要求确定弹簧承受的最大负荷,以此作为设计的起点。
(2)弹簧的外径和内径:根据弹簧材料、工作负荷和工作环境等要素来确定弹簧的外径和内径大小。
(3)弹簧的圈数和导程:弹簧的圈数和导程直接决定了其刚度和变形量,需要根据实际需求来设计,避免过强或过松。
(4)弹簧自由长度:弹簧自由长度也会影响到其机械性能,需要根据实际工作环境来确定。
二、样例下面以一种常见的钢板弹簧为例,介绍其设计和计算过程。
1、材料选择假设需要设计一种碳素钢的钢板弹簧,采用SWO-A钢带材,其具有以下机械性能:屈服强度:235MPa弹性模量:210GPa泊松比:0.3材料密度:7.85g/cm³2、外径和内径的确定假设弹簧的最大工作负荷为500N,弹簧碳素钢钢带的工作应力取90%时,最大弹簧应变量ρs应该小于σ/2E,即(υ-Dw)/Dw≥0.08。
可根据此公式,确定外径Dw=20mm。
根据设计要求,弹簧的圈数为8,导程为3mm。
当弹簧材料确定且弹簧固定长度生成后,利用弹簧方程(Fs=kρs)推导,得到弹簧直径Di=17.9mm。
3、根据内径、外径和圈数确定性能参数内直径ID=Di-2t,弹簧导程l0=π(Di+Dw)/2,自由长度L0=l0*(n-1)+2*ra+ra-ra*υ/Dw。
钢板弹簧设计说明书

目录一、确定断面尺寸及片数 ------------------------------------------------------------------------ 2二、确定各片钢板弹簧的长度 ------------------------------------------------------------------ 4三、钢板弹簧的刚度验算 ------------------------------------------------------------------------ 5四、钢板弹簧总成在自由状态下的弧高及曲率半径计算。
------------------------------- 7H ------------------------------------------------------------------------------------ 71.钢板弹簧总成在自由状态下的弧高02.钢板弹簧各片自由状态下曲率半径的确定 -------------------------------------------------------------------------------- 8五、钢板弹簧总成弧高的核算 ---------------------------------------------------------------- 10六、钢板弹簧的强度验算 ---------------------------------------------------------------------- 11二、(修改)确定各片弹簧长度--------------------------------------------------------------- 12三、(修改)钢板弹簧的刚度验算 ------------------------------------------------------------ 14四、(修改)钢板弹簧总成在自由状态下的弧高及曲率半径计算 --------------------- 15五、(修改)钢板弹簧总成弧高的核算 ------------------------------------------------------ 17六(修改)钢板弹簧的强度验算 ------------------------------------------------------------- 18七、钢板弹簧各片应力计算 ------------------------------------------------------------------- 18八,设计结果 ------------------------------------------------------------------------------------- 20九、参考文献 ------------------------------------------------------------------------------------- 21十、附总成图 ----------------------------------------------------------------- 错误!未定义书签。
变刚度簧设计计算

δ 1.163151365
主簧刚度CM 自由(N/mm) 夹紧(N/mm)
主簧刚度CM 474.6746943 561.4808225
LM=L10 La=L10
900 851 400 351
ZQ6560多片渐变刚度钢板弹簧(伸直长度1350 ZQ6560多片渐变刚度钢板弹簧(伸直长度1350 6560多片渐变刚度钢板弹簧
伸直长度Li' 1350 1350 1190 1030 870 710 600 500
片长之半Li 675 675 595 515 355 300 250
片厚Hi 8 8 8 8 8 8 14 14
片宽Bi 70 70 70 70 70 70 70 70
弧高Hi
∑ Ji 79860.0 159720.0 239580.0 319440.0 399300.0 479160.0 559020.0 638880.0 718740.0 798600.0
2833.543165
弦长之半 (Li"/2) 668.63 668.67 590.68 512.22 433.33 354.10
弦长Li" 1337.3 1337.3 1181.4 1024.4 866.7 708.2
弦长<弧长(伸直长度)
La1=L11
350 301 300 251 250 201 200 151 127 78
力学参数: S= 196 2P1= 5886 2P2= 10594.8 2Pm= 10791
付簧总成参数:
※※Ra0= ※※Ha0=
3055 26.18353078
二、满载挠度计算: f f1 10.48299383 f2 8.618498659 f3 f 0.180782 19.28227
某微车的少片变截面钢板弹簧结构设计分析与验证

( ) = n d [ 1 …t (
d f l 、 用 负 号 ) 由式 ( 9 ) 乘 n减 式 ( 1 0 )得
d ( d , J 、 )= —
) ] ( 用 正 号 ,
( 1 0 )
( 上接第 6 6页 )
6 结 论
( 1 1 )
由 上述 结果 对 比可 知 ,刚 度 、强 度 的结 果 均 比较 接 近 ,台 架耐 久 试 验 也 满 足 了 8万 次 断 裂 的标 准 要 求 。耐 久 性 反 映 了 强
( 2 )辅具结构简单 ,一般 中小型机 械厂都可 以自制 ; ( 3 )辅具可 实现车 间现 场 随 时测量 ,准确 可靠 ,轻巧 耐
用 ,完 全 满 足 生产 现 场 测 量 要 求。
d ( d ) = , n 一 d [ 1 + c 。 t (
d , J 、 用负号 ) 的尺寸 m : ,则
明 了该 设 计 方法 的可 行 性 。
文中主要利用材料力学的简单基础公式对板 簧进行理论计 式 ( 1 2 ) 中 :A d ( △ d 』 J 、 )为被测 圆锥大 、小端直径 ;
n d ( d )为大 ( 小 ) 标 准 圆柱 直径 。
算 ,并未涉及经验之类的系数 ,相对很多其他计算 方法较 为简 洁 明了。并通过 C A E分析验证与台架验证 ,该板簧的理论计算 得 以认证。这一套设计开发流程 ,比较完善地将理论 与实 际结
式 ( 1 1 ) 中 :n可 以取 为 任 意 值 ,在 此 ,笔 者 取 大 、 小标 准 圆 柱 直 径 之 比 ,即 n= n d / d ,代 入式 ( 4) 后 可 得
d ( d , j 、 )= 。 ( 1 2 )
汽车变截面钢板弹簧的设计计算

汽车变截面钢板弹簧的设计计算东风汽车工程研究院 陈耀明 2006年5月前 言少片变截面钢板弹簧在我国已有多年的制造和使用经验,特别是大、中型客车,采用者相当广泛。
然而,涉及变截面簧的设计计算方法,虽然二十几年前悬架专委会曾做过一些介绍,但资料零散、重复、不完整,尤其是比较常用的加强型变截面簧,资料反而欠缺。
撰写本文的目的,就是为悬架设计者提供变截面簧的比较完整的设计计算资料,主要是刚度计算公式和应力分布计算方法。
变截面簧轮廓线包括梯形和抛物线形两大类,每类又含有根部、端部加厚,或只有根部加厚,或都不加厚等几种变型。
这样,可以说几乎所有的变截面簧轮廓线都可在本文找到计算公式。
此外,本文还介绍了各种轮廓线的选型原则以及若干设计经验等,可供设计人员参考。
附录中列出已有资料中的一些计算公式,并证明了它们和本文公式的一致性。
本文的式(1)~(3)引自日本资料“自动车用重型钢板弹簧”,其它公式(6)~(15)是笔者近期重新推导出来的。
当然,有一些和过去推导出来的公式完全一致。
一、 纵截面为梯形的变截面弹簧这种弹簧的轧锥部分(3l ~4l 段)为梯形,而根部和端部都将厚度增大,称为加强型变截面簧,见图1。
图1为四分之一椭圆钢板弹簧,其刚度计算公式为:654321αααααα+++++=EK ----------------(1)若对称地扩展成为半椭圆钢板弹簧,其总刚度为:6543212αααααα+++++=EK ----------------(2)若弹簧由若干等长、相同轮廓线的叠片所组成,则其合成的总成刚度为:6543212αααααα+++++=nEK ----------------(3)式中 )/(10058.225mm N E ×=为弹性模数n 弹簧片数,单片弹簧1=n313114bt l =α⎥⎦⎤⎢⎣⎡++−+−+−−=1221112121221122212211132ln 223)(22212t t t Al t t l A t Al t t l A t Al t bA α )(43233323l l bt −=α ⎥⎦⎤⎢⎣⎡++−+−+−−=2322322223233223232223234ln 223)(22212t t t Bl t t l B t Bl t t l B t Bl t bB α ⎥⎦⎤⎢⎣⎡++−+−+−−=3423432324244324242234335ln 223)(22212t t t Cl t t l C t Cl t t l C t Cl t bC α )(43536346l l bt −=α而 1212l l t t A −−=3423l l t t B −−=4534l l t t C −−=其中 b 弹簧宽度实际应用中,有些弹簧的轮廓线有所简化,见图2,其刚度计算式也有所变化: 1、增厚转折点急剧变化,2型。
少片变截面弹簧的计算
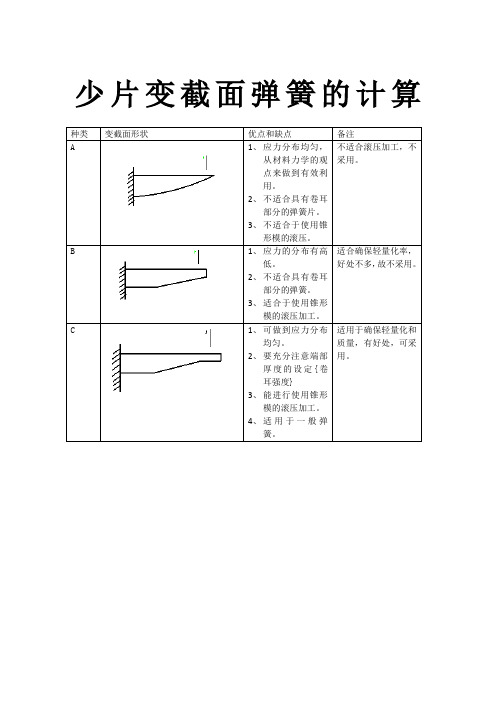
少片变截面弹簧的计算种类变截面形状优点和缺点备注A1、应力分布均匀,从材料力学的观点来做到有效利用。
2、不适合具有卷耳部分的弹簧片。
3、不适合于使用锥形模的滚压。
不适合滚压加工,不采用。
B1、应力的分布有高低。
2、不适合具有卷耳部分的弹簧。
3、适合于使用锥形模的滚压加工。
适合确保轻量化率,好处不多,故不采用。
C1、可做到应力分布均匀。
2、要充分注意端部厚度的设定{卷耳强度}3、能进行使用锥形模的滚压加工。
4、适用于一般弹簧。
适用于确保轻量化和质量,有好处,可采用。
D 1、以减轻C形中心孔部分应力为圆进行改良的。
2、能进行使用锥形模的滚压加工。
适合于小车型车辆用簧。
对确保质量有好处,可采用。
—1—种类变截面形状优点和缺点备注E1、为提高C形卷耳部分的强度,进行了改良。
2、能进行使用锥形模对确保质量有好处,可采用。
3、适用与中型车和大型车{前轴}的弹簧。
F1、是通过把D和E的形态结合在一起,有效地利用材料的形状。
对轻型化确保质量有好处,可采用。
G1、为适合长跨度产品,把F形状的加以改良的,是最有效地利用材料的形状。
2、能进行使用锥形模的滚压加工。
对轻量化有好处,可采用。
少片变截面弹簧的优点:1、应力分布均匀,接近于等应力梁,片数1—4片。
特殊工艺处理而提高其设计应力,从而使边界面弹簧轻量化,同等截面相比可减轻重量30—40%左右。
2、总成簧片在承载时,除端部传力处接触和中部骑马螺栓夹紧部位接触外,无片间接触现象,从而减少摩擦,使动刚度大力降低,提高乘坐舒适性。
3、由于片间接触区大为减少,基本上消除了由于片间接触摩擦磨损引起的使弹簧片早期损坏的疲劳源的产生,从而提高了疲劳寿命。
4、在总成中间平直等厚度的弹簧片,同上下保护垫板之间和簧片之间,插入塑料片或软金属垫片,这样就消除了弹簧总成工作时在中间平直等厚度段片间的直接挤压、摩擦,从而提高寿命。
5、采用喷完处理,中心孔挤压工艺和防锈性能,较好地油漆,这样也提高了疲劳寿命。
弹簧设计计算

弹簧设计计算弹簧在材料选定后,设计时需要计算出弹簧刚度F、中径D、钢丝直径d、有效圈数n、变形量f。
以下面弹簧设计为例;1.计算弹簧受力:假设弹簧端克服1个标准大气压,即推动钢球,则弹簧受力为:F=PA=1×10错误!N/mm错误!×πd1错误!/4其中d1——钢球通道直径弹簧还须克服钢球下降重力:G=mρV=m×4ρπR错误!/3其中R——钢球半径弹簧受合力:F合=F+G考虑制造加工因素,增加1.2倍系数F′=1.2F合2.选材料:(一般选用碳素弹簧钢丝65Mn或琴钢丝)以65Mn为例,钢丝直径d=1.4mm3.查表计算许用应力:查弹簧手册8-10表中Ⅰ类载荷的弹簧考虑(根据阀弹簧受力情况而言) 材料的抗拉强度σb与钢丝直径d有关查表2-30(选用D组): σb=2150~2450Mpa安全系数K=1.1~1.3, 可取K=1.2, 则σb=1791.7~2041.7Mpa因此σb=1791.7Mpa(下限值)查表2-103,取切变模量G=78.8×10错误!Mpa查表8-10,取许用切应力τs==0.5σb=0.3×1791.7=537.51Mpa4.选择弹簧旋绕比C:根据表8-4初步选取C=105.计算钢丝直径:d≥1.6√KFC/[τ]其中K——曲度系数,取K=1.1~1.3F——弹簧受力6.计算弹簧中径:D=Cd7.计算弹簧有效圈数:n=Gd错误!f/8FD错误!则总圈数n总=n+n1(查表8-6) 8.计算试验载荷:Fs=πd错误!τs/8D9.自由高度:H0=nt+1.5d其中:t——初步估计节距t=d+f/n+δ1(δ1=0.1d)查表8-7系列值H0取整数10.节距计算:t=(H0-1.5d)/n11.弹簧螺旋角:(此值一般符合=5°~9°)α=arctan(t/πD)12.弹簧的稳定性验算:(b<5.3,即可满足稳定性要求=b=H0/D13.展开长度:L=πDn1/cosα14.弹簧刚度:F′=Gd错误!/8D错误!n14.弹簧载荷:F=F′×f15.弹簧试验变形:fs=Fs/ F其中在绘制弹簧图纸时,压紧弹簧时的长度L1(即受装配积压时的长度)下弹簧对应受力F1,在阀开启时弹簧压缩的长度L2=L1+f,对应弹簧受力F2 例如:ZYB-1416N15-306H0=68.5mm,装配时弹簧被压缩至37mm,阀开启时再次压缩8mm 则L1=37,L2=37+8=45F1=37×F′F2=45F′验算比较L2与Fs/F的大小:若L2>Fs/F′重新设计刚度;反之设计合理。
某皮卡车少片变截面钢板弹簧后悬架设计讲解

目录1方案论证 (1)1.1悬架结构形式分析 (3)1.1.1 非独立悬架和独立悬架 (3)1.1.2前悬架方案的选择 (4)1.1.3 比较选型 (4)1.2少片变截面钢板板簧结构分析 (5)1.2.1抛物线形叶片弹簧 (5)1.2.2梯形变厚断面弹簧 (8)1.3钢板弹簧的布置方案 (9)2悬架主要部件 (11)2.1钢板弹簧的形式 (11)2.1.1叶片断面形状 (11)2.1.2叶片端部形状 (12)2.2 板簧两端与车架的连接 (12)2.2.1连接的结构形式 (12)2.2.2板簧卷耳与衬套 (13)2.3减震器 (14)2.3.1减振器的作用 (14)2.3.2减振器的结构: (15)2.3.3 减振器工作原理: (15)2.3.4减震器的选择 (15)3 悬架的设计计算 (17)3.1弹性元件的计算 (17)3.2优化设计 (20)3.3变截面钢板弹簧校核 (25)3.3.1校核刚度 (25)3.3.2 弹簧的最大应力点及最大应力 (26)3.4 钢板弹簧总成在自由状态下的弧高及曲率半径 (27)3.5 钢板弹簧各片自由状态下曲率半径的确定 (28)3.6钢板弹簧总成弧高的核算 (29)3.7钢板弹簧强度验算 (29)3.7.1驱动时计算应力 (29)3.7.2.汽车通过不平路面时钢板弹簧的强度 (30)3.8钢板弹簧卷耳和弹簧销的强度核算 (30)3.8.1卷耳应力的验算 (30)3.8.2钢板弹簧销的验算 (31)3.8.3 U形螺栓强度验算 (32)3.9减振器性能参数的选择 (33)3.9.1 相对阻尼系数ψ (33)3.9.2 减振器阻尼系数 的确定 (34)F的确定 (35)3.9.3 最大卸荷力3.9.4计算结果以及减震器的选择 (35)4 CATIA实体建模 (37)4.1CATIA简介 (37)4.2实体建模 (38)4.2.1钢板弹簧的绘制 (38)4.2.2盖板的实体图 (39)4.3主要零件实体图 (39)4.4装配 (42)5 结束语 ................................................................................................ 错误!未定义书签。
少片变厚断面钢板弹簧的设计

公司网址: 电子邮箱:4612757@1为减轻整车重量,使车辆轻量化,改善汽车的平顺性,作为汽车钢板弹簧易损件来说,是实现车辆轻量化的一个不可忽视的零件。
因此,目前国内许多汽车越来越多地开始采用由一片或几片纵向变厚断面弹簧组成的少片弹簧。
(见图一)图一现就宽度不变的抛物线叶片弹簧和梯形变厚叶片弹簧的刚度及其有关应力的计算介绍如下:一、抛物线叶片弹簧(见图二)1、等应力梁实际上抛物线叶片弹簧是一种等应力梁少片变厚断面钢板弹簧的设计公司网址: 电子邮箱:4612757@2设弹簧端部的载荷为P ,弹簧宽度为B ,那么弹簧中央部位A —A 处的应力бA 则为:бA=6P e /Bh 〈1〉弹簧在任一截面ex 处的应力бx 则为:бx=6Pe x /Bh x 〈2〉因弹簧是等应力梁,所以弹簧在任一截面处的应力均相等,由公式:〈1〉和公式〈2〉相等条件得到:hx=h (ex/e ) 〈3〉由上式可看出,欲使弹簧在各截面处的应力相等。
叶片弹簧各点厚度必须沿长度×方向做成抛物线形状。
实际上,理想的抛物线弹簧是无法使用的,这种弹簧在端部不能承受剪应力,卷耳端部强度差,加工难。
所以考虑卷耳端部的强度和弹簧中部实际装车夹紧状况,抛物线叶片弹簧应制成如下:见图三2221公司网址: 电子邮箱:4612757@3图三图中:A 、B 、C 、D 部份弹簧厚度不变,而B 、C 、O 部份弹簧厚度按抛物线变化。
2、抛物线叶片弹簧的刚度: 弹簧在任一截面处的惯性矩分别是 在(O —e 1)范围内J 1为常数 J 1= 式中:n 弹簧片数在(e 1e 2)范围内,断面惯性矩J 2为X 的函数。
J 2= 由公式〈3〉得:J 2= ×( )×n 在(e 2 e 1)范围内,J 3为常数。
J 3= 由于在不同长度范围内惯性矩J 值不同,经整理后刚度值为: C= · ·a式中a 断面修正系数,通常取0.9结论:事实上,抛物线叶片弹簧,在现实的汽车钢板弹簧3 3 3 231 12 ×n ×nBh 1╳nxBh 12 32Bh 12e xe 3 2Bh6E J 3 e (1+( )·K ) e 2 e 3公司网址: 电子邮箱:4612757@4加工中,不能付诸实现,因此较多地采用的是梯形变厚断面代替抛物线变化的梁。
梯形变截面板簧片简易设计方法_整理材料

梯形变截面板簧片的简易设计方法在少片簧设计中,为了节约材料,减轻自重,各板簧片尽可能做成等应力梁,使材料得到充分利用。
抛物线形板簧片属于等应力梁,但制作工艺要求较高,不易控制。
传统的少片簧板簧片采用梯形变截面结构,如果要少片簧设计的最轻,板簧材料得到充分利用,梯形变截面板簧片要设计的尽可能接近等应力梁。
目前梯形变截面板簧片的设计通常有两种方法,一种为试凑法,即根据经验初步选取尺寸参数,然后代入公式验算,经过反复计算,直到选择到最优的参数,这种设计方法不容易获得最佳设计方案,且费工时;另一种为最优化数学方法,将梯形弹簧的各设计参数做为变量,建立一系列函数方程,以理论质量最小作为目标函数,根据各约束要求,求解各参数,该方法虽然能得到最佳方案,但需要进行大量的计算,费工费时。
半 l ,线段NA 等于板簧片厚度h ;若将该梯形变截面板簧片设计的质量最轻,使之接近等应力梁,则线段BC 愈接近曲线OB ,此时梯形NABCO 的面积最小。
建立如下数学建模:由于OA 曲线为抛物线规律变化,则有:5.0⎪⎭⎫⎝⎛=l x h y (1)假设E 点坐标为(x 1,y 1)对(1)式E 点(x 1,y 1)求导可得,E 点的斜率k 为: ⋅=lx h k 12 (2)假设线段OC 长度为OC 则线段BC 的方程为:OC kx y += (3)又线段BC 过E 点(x 1,y 1),111kx y OC -=将(1)式、(2)式带入可得:115.01112x lx hl x h kx y OC -⎪⎭⎫ ⎝⎛=-= =lx h 12 (4) 线段CF 长度:lx h h OC h CF 21-=⋅-= (5)线段l 2长度:1122x l x kCFl -=⋅=(6) 三角形CBF 的面积S 为221l CF S = (7)将(5)式、(6) 式带入(7) 式整理得:()1112221x l x lx hh S -⎪⎪⎭⎫⎝⎛-==lx hx hx l x h 11114+- 若三角形S 面积最大,则梯形NABCO 面积最小,线段ABC 就愈接近抛物线,此时以截面为梯形NABCO 的板簧片就愈接近等应力梁。
汽车钢板弹簧设计计算

1.1单个钢板弹簧的载荷已知汽车满载静止时汽车前轴荷G1=3000kg,非簧载质量Gu1=285kg,则据此可计算出单个钢板弹簧的载荷:Fw1=(G1-Gu1)/2=1357.5 kg (1)进而得到:Pw1=Fw1×9.8=13303.5 N (2)1.2钢板弹簧的静挠度钢板弹簧的静挠度即静载荷下钢板弹簧的变形。
前后弹簧的静挠度都直接影响到汽车的行驶性能[1]。
为了防止汽车在行驶过程中产生剧烈的颠簸(纵向角振动),应力求使前后弹簧的静挠度比值接近于1。
此外,适当地增大静挠度也可减低汽车的振动频率,以提高汽车的舒适性。
但静挠度不能无限地增加(一般不超过240 mm),因为挠度过大,即频率过低,也同样会使人感到不舒适,产生晕车的感觉。
此外,在前轮为非独立悬挂的情况下,挠度过大还会使汽车的操纵性变坏。
一般汽车弹簧的静挠度值通常如表1[2]所列范围内。
本方案中选取fc1=80 mm。
1.3钢板弹簧的满载弧高满载弧高指钢板弹簧装到车轴上,汽车满载时钢板弹簧主片上表面与两端(不包括卷耳孔半径)连线间的最大高度差[3]。
当H0=0时,钢板弹簧在对称位置上工作。
考虑到使用期间钢板弹簧塑性变形的影响和为了在车架高度已限定时能得到足够的动挠度值,常取H0∈10-20mm。
本方案中H01初步定为18mm。
1.4钢板弹簧的断面形状板弹簧断面通常采用矩形断面,宜于加工,成本低。
但矩形断面也存在一些不足。
矩形断面钢板弹簧的中性轴,在钢板断面的对称位置上。
工作时,一面受拉应力,一面受压应力作用,而且上、下表面的名义拉应力和压应力的绝对值相等。
因材料的抗拉性能低于抗压性能,所以在受拉应力作用的一面首先产生疲劳断裂。
除矩形断面以外的其它断面形状的叶片,其中性轴均上移,使受拉应力的一面的拉应力绝对值减小,而受压应力作用的一面的压应力绝对值增大,从而改善了应力在断面上的分布情况,提高了钢板弹簧的疲劳强度并节约了近10%的材料。
汽车钢板弹簧设计计算

1.1单个钢板弹簧的载荷已知汽车满载静止时汽车前轴荷G1=3000kg,非簧载质量Gu1=285kg,则据此可计算出单个钢板弹簧的载荷:Fw1=(G1-Gu1)/2=1357.5 kg (1)进而得到:Pw1=Fw1×9.8=13303.5 N (2)1.2钢板弹簧的静挠度钢板弹簧的静挠度即静载荷下钢板弹簧的变形。
前后弹簧的静挠度都直接影响到汽车的行驶性能[1]。
为了防止汽车在行驶过程中产生剧烈的颠簸(纵向角振动),应力求使前后弹簧的静挠度比值接近于1。
此外,适当地增大静挠度也可减低汽车的振动频率,以提高汽车的舒适性。
但静挠度不能无限地增加(一般不超过240 mm),因为挠度过大,即频率过低,也同样会使人感到不舒适,产生晕车的感觉。
此外,在前轮为非独立悬挂的情况下,挠度过大还会使汽车的操纵性变坏。
一般汽车弹簧的静挠度值通常如表1[2]所列范围内。
本方案中选取fc1=80 mm。
1.3钢板弹簧的满载弧高满载弧高指钢板弹簧装到车轴上,汽车满载时钢板弹簧主片上表面与两端(不包括卷耳孔半径)连线间的最大高度差[3]。
当H0=0时,钢板弹簧在对称位置上工作。
考虑到使用期间钢板弹簧塑性变形的影响和为了在车架高度已限定时能得到足够的动挠度值,常取H0∈10-20mm。
本方案中H01初步定为18mm。
1.4钢板弹簧的断面形状板弹簧断面通常采用矩形断面,宜于加工,成本低。
但矩形断面也存在一些不足。
矩形断面钢板弹簧的中性轴,在钢板断面的对称位置上。
工作时,一面受拉应力,一面受压应力作用,而且上、下表面的名义拉应力和压应力的绝对值相等。
因材料的抗拉性能低于抗压性能,所以在受拉应力作用的一面首先产生疲劳断裂。
除矩形断面以外的其它断面形状的叶片,其中性轴均上移,使受拉应力的一面的拉应力绝对值减小,而受压应力作用的一面的压应力绝对值增大,从而改善了应力在断面上的分布情况,提高了钢板弹簧的疲劳强度并节约了近10%的材料。
汽车变截面钢板弹簧的设计计算

汽车变截面钢板弹簧的设计计算摘要本文介绍了汽车变截面钢板弹簧的设计计算,包括弹簧参数计算、弹簧形状设计及材料组成等方面。
通过对变截面钢板弹簧的物理特性进行分析,结合设计要求,以及材料及工艺的要求,采用MARC建模及软件进行非线性有限元分析,得出变截面钢板弹簧的设计结果。
关键词:变截面钢板弹簧,参数计算,形状设计,MARC建模1. IntroductionVariable-Cross-Section Steel Plate Spring (VCSSPS) is an important part in auto manufacture. VCSSPS can provide smooth and reliable force when it works in enclosed space because ofits advantages of light weight and small size. It has been widely used in body, chassis, engine and suspension systems. VCSSPS contains a variety of parameters such as material, shape, size and load. And its performance is greatly affected by these parameters. Thus, it is very important to design the VCSSPS in a reasonable way.In general, VCSSPS design includes three steps: parameters calculation, shape designing and material selection. First, parameters calculation must be done according to the design requirement. Then, shape should be designed according to parameters carefully. Furthermore, the material and processes should be carefully selected and applied.In this paper, we introduce the VCSSPS design process and analysis. We use MARC software to analyze the VCSSPS under nonlinear finite element environment and get the parameters’ design results. The main contributions include: 1) a conciseintrod uction of VCSSPS design process; 2) analysis of parameters’ effects on VCSSPS; 3) the optimization of geometry design and material selection; 4) the design results of VCSSPS.2 Parameter CalculationThe parameters of VCSSPS mainly include load, length,section size, curvature, number of plate and material. The calculation results of these parameters have significantinfluence on the performance of VCSSPS.2.1 LoadLoad is the product of spring force and displacement, which can be obtained from the static deflection and force performance data provided by the design requirements.2.2 LengthLength of VCSSPS is determined by the static performance. Generally, the distance between the mounting holes should be the same as that of the mating parts.2.3 Section SizeThe section size of VCSSPS can be obtained from the load and displacement provided by the design requirements. Generally, thesection size should be determined according to the static performance.2.4 CurvatureCurvature of VCSSPS is determined by the section size. Generally, the curvature should be designed according to thestatic performance.2.5 Number of PlateThe number of plate is determined by the dynamic performance. Generally, the number of plate should be designed according tothe dynamic performance.2.6 MaterialThe ideal material for VCSSPS is determined by the static, dynamic and temperature requirements. Usually, good strength and modulus of elasticity are preferred.3 Shape DesignThe shape of VCSSPS should be designed according to the parameters calculated above. In general, the shape of VCSSPS should be designed as follows:3.1 Section SizeSection size of VCSSPS should be designed according to the calculated parameters. Generally, the section size should be designed as uniform as possible.3.2 Number of PlateThe number of plate should be designed according to the calculated parameters. Generally, the number of plate should be designed as many as possible.3.3 Geometry。
变截面板簧刚度设计与计算

总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
= -w 5 - -f 5= 3. 171- 1. 53= 1. 641, 及式( 19) 解出 -w 6 = 1. 46, 故 w 6 = 1. 46 t = 0. 9m m 。 第七 辊取
w7
弯或负值压弯。 从理论上看压弯量在4. 5mm 以下 可以得到良好矫直, 再大没有必要 , 各辊的分配 也不需严格限定。 5 结语 本文所提供的方法用文献 [ 2] 的实测值验证 是可用的, 其理论简单 , 方法容易, 程序严谨 , 很 具有实用性。 但压弯量计算法的适用性不仅与其 本身的精确性有关 , 也与设备刚度的正确定量有 关, 如矫直辊的弹跳量及压力系统的刚度 值等。 压弯量数学模型的精确化在我国 已具有现实意 义, 文献[ 4] 已经取得初步成果 , 本文作为一种参 与, 愿与同行们共同推进这一工作。
G =
EB = 37. 5 N/ m m 4 K ( i) GD 1= 2G = 75 N/ m m 第一片简图( 如图2 所示) :
图 2 6700后簧第一片
( 转第6 页) — 31 —
总 第 113 期 冶 金 设 备 1999年 2 月第 1期
L L
2
( 2)
dx +
总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
变截面钢板弹簧的设计计算

变截面钢板弹簧的设计计算
秦志敏;潘宇臣
【期刊名称】《汽车工程》
【年(卷),期】1995(017)002
【摘要】本文从等应力梁的角度,探讨了等宽变截面钢板弹簧的结构型式,并导出这类结构型式钢板弹簧的刚度和质量等设计计算公式。
【总页数】5页(P108-112)
【作者】秦志敏;潘宇臣
【作者单位】不详;不详
【正文语种】中文
【中图分类】U463.334.1
【相关文献】
1.变断面钢板弹簧的设计计算 [J], 彭莫;高军
2.给定条件的变截面等螺旋角蜗卷的弹簧的设计计算 [J], 张成杰
3.少片变截面钢板弹簧的设计计算 [J], 于翔
4.变截面钢板弹簧刚度计算的传递矩阵法 [J], 许昕; 邢庆果; 刚宪约
5.叶片曲率对少片变截面钢板弹簧力学特性的影响 [J], 杨林;于曰伟;周长城;郑伟因版权原因,仅展示原文概要,查看原文内容请购买。
弹簧设计计算公式

弹簧设计计算公式弹簧是一种经过热处理的金属线,具有弹性变形能力。
在工程设计中,弹簧广泛应用于机械、汽车、电器等领域,用于悬挂、减震、传动等功能。
弹簧设计的核心是确定其几何参数和力学性能,以满足特定的工作要求。
弹簧设计的计算公式包括弹簧刚度、变形、工作力和应力等参数。
以下是一些常用的弹簧设计公式:1.弹簧刚度:弹簧刚度是指单位变形时产生的力的大小。
弹簧刚度可以通过以下公式计算:K=Gd^4/8nD^3其中,K表示弹簧刚度,G表示弹簧材料的剪切模量,d表示弹簧线径,n表示弹簧的有效圈数,D表示弹簧的平均直径。
2.弹簧变形:弹簧的变形可以通过以下公式计算:δ=(F×L)/(K×n)其中,δ表示弹簧的变形,F表示作用在弹簧上的力,L表示弹簧自由长度,K表示弹簧刚度,n表示弹簧的有效圈数。
3.弹簧的工作力:弹簧的工作力可以通过以下公式计算:F=K×δ其中,F表示作用在弹簧上的力,K表示弹簧刚度,δ表示弹簧的变形。
4.弹簧的应力:弹簧的应力可以通过以下公式计算:σ=(8×F×L)/(π×d^3×n)其中,σ表示弹簧的应力,F表示作用在弹簧上的力,L表示弹簧自由长度,d表示弹簧线径,n表示弹簧的有效圈数。
需要注意的是,以上公式适用于简单的弹簧设计,如果涉及复杂的弹簧形状或材料,可能需要使用更复杂的计算方法或有限元分析。
弹簧设计时,需要根据实际工作条件和要求,选择合适的弹簧材料和尺寸,以保证弹簧的功能和安全性。
同时,还需要考虑弹簧的寿命、疲劳强度、预紧力等因素,以确保弹簧在长期使用中的可靠性。
除了上述的计算公式,弹簧设计还需要考虑弹簧的安装方式、表面处理、工艺要求等因素。
综合考虑这些因素,可以进行合理的弹簧设计,满足工程需求。
少片变截面钢板弹簧的设计计算

少片变截面钢板弹簧的设计计算钢板弹簧是由钢板材料弯曲而成的一种弹簧。
与圆钢弹簧相比,钢板弹簧具有更高的弹性限度和更大的变形能力。
因此,在工程设计中,钢板弹簧得到了广泛的应用。
少片变截面钢板弹簧特指弹簧的板片数量较少且断面形状发生变化的钢板弹簧。
下面将介绍少片变截面钢板弹簧的设计计算。
1.确定设计参数在进行钢板弹簧的设计计算之前,需要确定所需的设计参数。
包括工作负荷F、工作长度L、显微硬度和板片数量n等。
显微硬度是指在微观级别下测量的钢板的硬度。
确定这些参数后,可以通过下列公式计算弹簧的弹性变形:δ=8 × FL^3/En × d^4其中δ表示弹簧的弹性变形,E表示钢板的弹性模量,d表示钢板厚度。
2.确定钢板尺寸和弹簧几何参数在确定设计参数后,可以计算钢板弹簧的几何参数。
包括钢板长度L,钢板宽度b,钢板厚度d,弹簧直径D和板片数量n。
根据这些参数计算出钢板的截面积A和钢板的极径I:A=b × d × nI=b × d^3 × n/123.计算钢板的各个应力和变形在完成钢板的几何参数计算后,可以计算钢板的各个应力和变形。
包括板片的单向弯曲应力σ、截面变形度θ和截面扭转角φ。
单向弯曲应力σ可以通过下面的公式计算:σ=-My/I其中M表示截面转矩,y表示截面离中心轴的距离。
4.校核钢板的疲劳寿命在完成各个应力和变形的计算后,需要对钢板进行疲劳寿命校核。
通常采用S-N曲线法进行疲劳寿命计算。
根据应力幅值和循环次数可以得到S-N曲线,从而计算钢板的疲劳寿命。
总之,少片变截面钢板弹簧的设计计算是一项非常重要的工作,涉及到很多参数和公式的计算。
在实际应用中,需要综合考虑各种因素,确保设计的弹簧满足工程要求。
钢板弹簧计算

钢板弹簧的计算1. 1 钢板弹簧的布置方案的选择钢板弹簧在汽车上可以纵置也可以横置, 纵向布置时还具有导向传力的作用,并有一定的减震作用,连得因而使的悬架系统结构简化。
而横向布置时因为要传递纵向力,必须设置附加的导向传力装置,使结构复杂、质量加大,所以只在极少数汽车上应用。
如下图所示,它中部用U 型螺栓将钢板弹簧固定在车桥上。
悬架前端为固定铰链,也叫死吊耳。
它由钢板弹簧销钉将钢板弹簧前端卷耳部与钢板弹簧前支架连接在一起,前端卷耳孔中为减少摩损装有衬套。
后端卷耳通过钢板弹簧吊耳销与后端吊耳与吊耳架相连,后端可以自由摆动,形成活动吊耳。
当车架受到冲击弹簧变形时两卷耳之间的距离有变化的可能。
图4.11. 2 钢板弹簧主要参数的确定EQ1042轻型货车相关参数∶悬架静挠c f =72mm ,悬架动挠度c f =80mm ,轴距Z=3300mm, 单个钢板弹簧的载荷111509.8563522w m g F N ⨯=== 1. 2. 1 满载弧高a f满载弧高a f 是指钢板弹簧装到车轴(桥)上,汽车满载时钢板弹簧主片上表面与两端(不包括卷耳孔半径)连线间的最大高度差。
常取a f =10~20mm ,这里取af=10mm.。
1. 2. 2钢板弹簧长度L 的确定钢板弹簧长度L 是指弹簧伸直后两卷耳中心之间的距离,在总布置可能的条件下,应尽可能将钢板弹簧取长些。
在下列范围内选用钢板弹簧的长度: 轿车:L=(0.40~0.55)轴距;货车:前悬架:L=(0.26~0.35)轴距; 后悬架:L=(0.35~0.45)轴距。
应尽可能将钢板弹簧取长些,原因如下:1,增加钢板弹簧长度L 能显著降低弹簧应力,提高使用寿命降低弹簧刚度,改善汽车平顺性。
2,在垂直刚度c 给定的条件下,又能明显增加钢板弹簧的纵向角刚度。
3,刚板弹簧的纵向角刚度系指钢板弹簧产生单位纵向转角时,作用到钢板弹簧上的纵向力矩值。
4,增大钢板弹簧纵向角刚度的同时,能减少车轮扭转力矩所引起的弹簧变形。
