第8讲 幂的运算—尖子班
幂的运算优质课优质课市公开课一等奖省优质课获奖课件
少千米?
105×10 7等于多少呢?
第3页
105×107
=(10×10×···×10)×(10×10×···×10)
5个10
(依据 幂意义 .)
7个10
=10×10×···×10 (依据 乘法结合律 .)
12个10
12
=10
(依据 幂意义
.)
第4页
做一做
1、计算以下各式:
(1)102×103;
(2)105×108;
=102+3.
第6页
(2) 105×10 8
=(10×10×···×10)×(10×10×···×10)
5个10
(依据 幂意义 .)
8个10
=10×10×···×10 依据( 乘法结合律 .)
13个10
=1013 依据( 幂意义 .)
=105+8
第7页
(3) 10m×10 n =(10×10×···×10)×(10×10×···×10)
(3)10m×10n(m,n都是正整数).
你发觉了什么?
2、2m×2n等于什么?( (m,n 都是正整数.)
7)1 m×(
)71 n 呢?
第5页
1.(1)102 ×103 =(10×10)×(10×10×10) (依据 幂意义 .) =10×10×10×10×10 (依据 乘法结合律 .) =105 (依据 幂意义 .)
第18页
课堂
小结
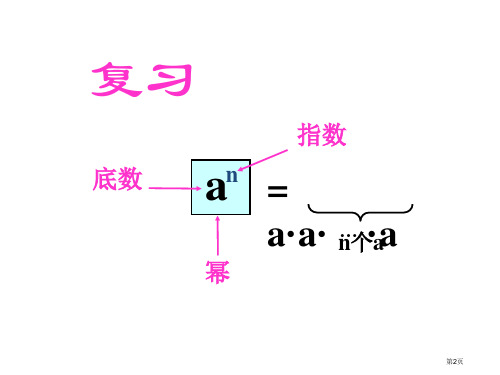
幂意义:
an= a·a·… ·a
n个a
同底数幂乘法性质:
am ·an =am+n(m、n都是正整数)
底数 不变 ,指数 相加 .
第19页
第16页
幂的运算(基础)知识讲解

幂的运算(基础)责编:杜少波【学习目标】1. 掌握正整数幂的乘法运算性质(同底数幂的乘法、幂的乘方、积的乘方);2. 能用代数式和文字语言正确地表述这些性质,并能运用它们熟练地进行运算.【要点梳理】【高清课堂396573 幂的运算 知识要点】要点一、同底数幂的乘法性质+⋅=m n m n a a a (其中,m n 都是正整数).即同底数幂相乘,底数不变,指数相加. 要点诠释:(1)同底数幂是指底数相同的幂,底数可以是任意的实数,也可以是单项式、多项式.(2)三个或三个以上同底数幂相乘时,也具有这一性质,即m n p m n p a a a a ++⋅⋅=(,,m n p 都是正整数).(3)逆用公式:把一个幂分解成两个或多个同底数幂的积,其中它们的底数与原来的底数相同,它们的指数之和等于原来的幂的指数。
即m n m n a a a +=⋅(,m n 都是正整数).要点二、幂的乘方法则()=m n mn a a (其中,m n 都是正整数).即幂的乘方,底数不变,指数相乘.要点诠释:(1)公式的推广:(())=m n p mnp a a(0≠a ,,,m n p 均为正整数) (2)逆用公式: ()()n m mn m n a a a ==,根据题目的需要常常逆用幂的乘方运算能将某些幂变形,从而解决问题.要点三、积的乘方法则()=⋅n n n ab a b (其中n 是正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.要点诠释:(1)公式的推广:()=⋅⋅n n n nabc a b c (n 为正整数).(2)逆用公式:()n n n a b ab =逆用公式适当的变形可简化运算过程,尤其是遇到底数互为倒数时,计算更简便.如:1010101122 1.22⎛⎫⎛⎫⨯=⨯= ⎪ ⎪⎝⎭⎝⎭要点四、注意事项(1)底数可以是任意实数,也可以是单项式、多项式.(2)同底数幂的乘法时,只有当底数相同时,指数才可以相加.指数为1,计算时不要遗漏.(3)幂的乘方运算时,指数相乘,而同底数幂的乘法中是指数相加.(4)积的乘方运算时须注意,积的乘方要将每一个因式(特别是系数)都要分别乘方.(5)灵活地双向应用运算性质,使运算更加方便、简洁.(6)带有负号的幂的运算,要养成先化简符号的习惯.【典型例题】类型一、同底数幂的乘法性质1、计算:(1)234444⨯⨯;(2)3452622a a a a a a ⋅+⋅-⋅;(3)11211()()()()()n n m n m x y x y x y x y x y +-+-+⋅+⋅+++⋅+. 【答案与解析】解:(1)原式234944++==.(2)原式34526177772222a a a a a a a +++=+-=+-=.(3)原式11211222()()()()2()n n m n m n m n m n m x y x y x y x y x y +++-++-+++=+++=+++=+.【总结升华】(2)(3)小题都是混合运算,计算时要注意运算顺序,还要正确地运用相应的运算法则,并要注意区别同底数幂的乘法与整式的加减法的运算法则.在第(2)小题中a 的指数是1.在第(3)小题中把x y +看成一个整体.举一反三:【变式】计算:(1)5323(3)(3)⋅-⋅-;(2)221()()p p p x x x +⋅-⋅-(p 为正整数);(3)232(2)(2)n ⨯-⋅-(n 为正整数).【答案】解:(1)原式532532532103(3)333333++=⋅-⋅=-⋅⋅=-=-. (2)原式22122151()p p p p p p p x xx x x +++++=⋅⋅-=-=-. (3)原式525216222(2)22n n n +++=⋅⋅-=-=-.2、已知2220x +=,求2x 的值.【思路点拨】同底数幂乘法的逆用:22222x x +=⋅ 【答案与解析】解:由2220x +=得22220x ⋅=.∴ 25x =.【总结升华】(1)本题逆用了同底数幂的乘法法则,培养了逆向思维能力.(2)同底数幂的乘法法则的逆运用:m n m n a a a +=⋅.类型二、幂的乘方法则3、计算:(1)2()m a ;(2)34[()]m -;(3)32()m a -.【思路点拨】此题是幂的乘方运算,(1)题中的底数是a ,(2)题中的底数是m -,(3)题中的底数a 的指数是3m -,乘方以后的指数应是2(3)62m m -=-.【答案与解析】解:(1)2()m a 2m a =. (2)34[()]m -1212()m m =-=. (3)32()m a -2(3)62m m a a --==.【总结升华】运用幂的乘方法则进行计算时要注意符号的计算及处理,一定不要将幂的乘方与同底数幂的乘法混淆.幂的乘方法则中的底数仍可以为单个数字、字母,也可以是单项式或多项式.4、(2016春•湘潭期末)已知a x =3,a y =2,求a x +2y 的值.【思路点拨】 直接利用同底数幂的乘法运算法则将原式变形进而将已知代入求出答案.【答案与解析】解:∵a x =3,a y =2,∴a x +2y =a x ×a 2y =3×22=12.【总结升华】本题考查同底数幂的乘法,幂的乘方,解题时记准法则是关键.举一反三:【变式1】已知2a x =,3b x =.求32a b x+的值. 【答案】解:32323232()()238972a b a b a b x x x x x +===⨯=⨯=.【高清课堂396573 幂的运算 例3】【变式2】已知84=m ,85=n ,求328+m n 的值. 【答案】解:因为3338(8)464===m m , 2228(8)525===n n .所以323288864251600+=⨯=⨯=m n m n .类型三、积的乘方法则5、指出下列各题计算是否正确,指出错误并说明原因:(1)22()ab ab =; (2)333(4)64ab a b =; (3)326(3)9x x -=-.【答案与解析】解:(1)错,这是积的乘方,应为:222()ab a b =.(2)对.(3)错,系数应为9,应为:326(3)9x x -=.【总结升华】(1)应用积的乘方时,特别注意观察底数含有几个因式,每个因式都分别乘方.(2)注意系数及系数符号,对系数-1不可忽略.举一反三:【变式】(2015春•铜山县校级月考)(﹣8)57×0.12555.【答案】解:(﹣8)57×0.12555=(﹣8)2×[(﹣8)55×]=﹣64.。
幂的运算ppt课件

=a ·a ·a ·a ·a ·a ·a
=a7 =3+4
可得
m个a
n个a
am·an=(a ·a ·a·… ·a)(a ·a ·a·… ·a)
(m+n)个a
=a ·a ·a·… ·a
=am+n
am·an=am+n(m、n为正整数) 同底数幂相乘,底数不变,指数相加.
例1 计算: (1)103×104;
bn
a
am
an
m
n
情境导入
“盘古开天辟地”的故事:公元前一 百万年,没有天没有地,整个宇宙是混浊 的一团,突然间窜出来一个巨人,他的名 字叫盘古,他手握一把巨斧,用力一劈, 把混沌的宇宙劈成两半,上面是天,下面 是地,从此宇宙有了天地之分,盘古完成 了这样一个壮举,累死了,他的左眼变成 了太阳,右眼变成了月亮,毛发变成了森 林和草原,骨头变成了高山和高原,肌肉 变成了平原与谷地,血液变成了河流.
(1.1×1012)÷(2.2×1010)
怎样计算呢?
探究新知
用你熟悉的方法计算: (1)25÷22=(__2_·_2_·2_·_2_·_2_)__÷__(__2_·2_)_;
=2·2·2 =23 =5-2 (2)107÷103=(__1_0_·_1_0_·_1_0_·1_0_·_1_0_·_1_0_·1_0_)__÷__(__1_0_·_1_0_·_1_0_)__;
(1)[(-x2y)3·(-x2y)2]3; (2)a3·a4·a+(a2)4+(-2a4)2.
=[(-x6y 3)·(x4y2)]3 =(-x10y 5)3
=a8+a8+4a8 =6a8
=-x30y15
七年级数学8.1幂的运算讲解与例题

8.1 幂的运算1.了解幂的运算性质,会利用幂的运算性质进行计算.2.通过幂的运算性质的形成和应用,养成观察、归纳、猜想、论证的能力,提高计算和口算的能力.3.了解和体会“特殊—一般—特殊”的认知规律,体验和学习研究问题的方法,培养思维严谨性,做到步步有据,正确熟练,养成良好的学习习惯.1.同底数幂的乘法(1)同底数幂的意义“同底数幂”顾名思义,是指底数相同的幂.如32与35,(-5)2与(-5)6,(a+b)4与(a+b)3等表示的都是同底数的幂.(2)幂的运算性质1同底数幂相乘,底数不变,指数相加.用字母可以表示为:a m·a n=a m+n(m,n都是正整数).(3)性质的推广运用当三个或三个以上的同底数幂相乘时,也具有这一性质,如:a m·a n·a p=a m+n+p(m,n,p是正整数).(4)在应用同底数幂的乘法的运算性质时,应注意以下几点:①幂的底数a可以是任意的有理数,也可以是单项式或多项式;底数是和、差或其他形式的幂相乘,应把这些和或差看作一个“整体”.②底数必须相同才能使用同底数幂的乘法公式,若底数不同,则不能使用;注意:-a n 与(-a)n不是同底数的幂,不能直接用性质.③不要忽视指数是1的因数或因式.【例1-1】(1)计算x3·x2的结果是______;(2)a4·(-a3)·(-a)3=__________.解析:(1)题中的底数都是x,是两个同底数幂相乘的运算式子,只需运用同底数幂相乘的性质进行运算,即x3·x2=x3+2=x5;(2)应先把底数分别是a,-a的幂化成同底数的幂,才能应用同底数幂的乘法性质,原式=a4·(-a3)·(-a3)=a4·a3·a3=a4+3+3=a10.答案:(1)x5(2)a10正确运用幂的运算性质解题的前提是明确性质的条件和结论.例如同底数幂的乘法,条件是底数相同,且运算是乘法运算,结论是底数不变,指数相加.【例1-2】计算:(1)(x+y)2·(x+y)3;(2)(a-2b)2·(2b-a)3.分析:(1)把(x+y)看作底数,可根据同底数幂的乘法性质来解;(2)题中(a-2b)2可转化为(2b-a)2,或者把(2b-a)3转化为-(a-2b)3,就是两个同底数的幂相乘了.解:(1)原式=(x+y)2+3=(x+y)5;(2)方法一:原式=(2b -a )2·(2b -a )3=(2b -a )5;方法二:原式=(a -2b )2·[-(a -2b )3]=-(a -2b )5.本题应用了整体的数学思想,把(x +y )和(a -2b )看作一个整体,(2)题中的两种解法所得的结果实质是相等的,因为互为相反数的奇次幂仍是互为相反数. 2.幂的乘方(1)幂的乘方的意义:幂的乘方是指几个相同的幂相乘.如(a 5)3是指三个a 5相乘,读作“a 的五次幂的三次方”,即有(a 5)3=a 5·a 5·a 5=a 5+5+5=a 5×3;(a m )n 表示n 个a m 相乘,读作“a 的m 次幂的n 次方”,即有(a m )n =m m m n a a a ⋅⋅⋅L 1442443个=m m m n a a a a a a a a a ⋅⋅⋅⋅⋅⋅⋅⋅⋅L L L L 142431424314243144444424444443个个个个=a mn(m ,n 都是正整数) (2)幂的运算性质2幂的乘方,底数不变,指数相乘.用字母可以表示为:(a m )n =a mn(m ,n 都是正整数).这个性质的最大特点就是将原来的乘方运算降次为乘法运算,即底数不变,指数相乘. (3)性质的推广运用幂的乘方性质可推广为: [(a m )n ]p =a mnp(m ,n ,p 均为正整数).(4)注意(a m )n 与am n的区别 (a m )n 表示n 个a m 相乘,而am n 表示m n 个a 相乘,例如:(52)3=52×3=56,523=58.因此,(a m )n ≠am n .【例2】(1)计算(x 3)2的结果是( ).A .x 5B .x 6C .x 8D .x 9(2)计算3(a 3)3+2(a 4)2·a =__________.解析:(1)根据性质,底数不变,指数相乘,结果应选B ;(2)先根据幂的乘方、同底数幂相乘进行计算,再合并同类项得到结果.3(a 3)3+2(a 4)2·a =3a 3×3+2a 4×2·a =3a 9+2a 8·a =3a 9+2a 9=5a 9.答案:(1)B (2)5a 9防止“指数相乘”变为“指数相加”,同时防止“指数相乘”变为“指数乘方”.如(a 4)2=a 4+2=a 6与(a 2)3=a 23=a 8都是错误的.3.积的乘方(1)积的乘方的意义:积的乘方是指底数是乘积形式的乘方.如(2ab )3,(ab )n等.(2ab )3=(2ab )·(2ab )·(2ab )(乘方意义)=(2×2×2)(a ·a ·a )(b ·b ·b )(乘法交换律、结合律) =23a 3b 3.(ab )n =n ab ab ab ()()()L 1442443个=n a a a (⋅⋅⋅)L 14243个n b b b (⋅⋅⋅⋅)L 14243个=a n b n(n 为正整数).(2)幂的运算性质3积的乘方等于各因式乘方的积.也就是说,先把积中的每一个因式分别乘方,再把所得的结果相乘.用字母可以表示为:(ab )n =a n b n(n 是正整数). (3)性质的推广运用三个或三个以上的乘方也具有这一性质,如(abc )n =a n b n c n(n 是正整数).【例3】计算:(1)(-2x )3;(2)(-xy )2;(3)(xy 2)3·(-x 2y )2;(4)⎝ ⎛⎭⎪⎫-12ab 2c 34.分析:(1)要注意-2x 含有-2,x 两个因数;(2)-xy 含有三个因数:-1,x ,y ;(3)把xy 2看作x 与y 2的积,把-x 2y 看作-1,x 2,y 的积;(4)-12ab 2c 3含有四个因数-12,a ,b 2,c 3,先运用积的乘方性质计算,再运用幂的乘方性质计算.解:(1)(-2x )3=(-2)3·x 3=-8x 3;(2)(-xy )2=(-1)2·x 2·y 2=x 2y 2;(3)(xy 2)3·(-x 2y )2=x 3(y 2)3·(-1)2·(x 2)2y 2=x 3y 6·x 4y 2=x 7y 8;(4)⎝ ⎛⎭⎪⎫-12ab 2c 34=⎝ ⎛⎭⎪⎫-124a 4(b 2)4(c 3)4=116a 4b 8c 12.(1)在计算时,把x 2与y 2分别看成一个数,便于运用积的乘方的运算性质进行计算,这种把某个式子看成一个数或字母的方法的实质是换元法,它可以把复杂问题简单化,它是数学的常用方法.(2)此类题考查积的乘方运算,计算时应特别注意底数含有的因式,每个因式都分别乘方,不要漏掉,尤其要注意系数及系数的符号,对系数是-1的不可忽略.负数的奇次方是一个负数,负数的偶次方是一个正数.4.同底数幂的除法 (1)幂的运算性质4同底数幂相除,底数不变,指数相减.用字母可以表示为:a m ÷a n =a m -n(a ≠0,m ,n 都是正整数,且m >n ).这个性质成立的条件是:同底数幂相除,结论是:底数不变,指数相减.和同底数幂的乘法类似,被除式和除式都是幂的形式且底数一定要相同,商也是一个幂,其底数与被除式和除式的底数相同,商中幂的指数是被除式的指数与除式的指数之差.因为零不能作除数,所以底数a ≠0.(2)性质的推广运用三个或三个以上的同底数幂连续相除时,该性质仍然成立,例如a m ÷a n ÷a p =a m -n -p(a ≠0,m ,n ,p 为正整数,m >n +p ).【例4】计算:(1)(-a )6÷(-a )3;(2)(a +1)4÷(a +1)2;(3)(-x )7÷(-x 3)÷(-x )2. 分析:利用同底数幂的除法性质进行运算时关键要找准底数和指数.(1)中的底数是-a ,(2)中的底数是(a +1),(3)中的底数可以是-x ,也可以是x .解:(1)(-a )6÷(-a )3=(-a )6-3=(-a )3=-a 3;(2)(a +1)4÷(a +1)2=(a +1)4-2=(a +1)2; (3)方法1:(-x )7÷(-x 3)÷(-x )2=(-x )7÷(-x )3÷(-x )2=(-x )7-3-2=(-x )2=x 2. 方法2:(-x )7÷(-x 3)÷(-x )2=(-x 7)÷(-x 3)÷x 2=x 7-3-2=x 2.运用同底数幂除法性质的关键是看底数是否相同,若不相同则不能运用该性质,指数相减是指被除式的指数减去除式的指数;幂的前三个运算性质中字母a ,b 可以表示任何实数,也可以表示单项式和多项式;第四个性质即同底数幂的除法性质中,字母a 只表示不为零的实数,或表示其值不为零的单项式和多项式.注意指数是“1”的情况,如a 5÷a =a 5-1,而不是a 5-0.5.零指数幂与负整数指数幂(1)零指数幂:任何一个不等于零的数的零次幂都等于1.用字母可以表示为:a 0=1(a ≠0).a 0=1的前提是a ≠0,如(x -2)0=1成立的条件是x ≠2.(2)负整数指数幂:任何一个不等于零的数的-p (p 是正整数)次幂,等于这个数的p 次幂的倒数.用字母可以表示为:a -p=1ap (a ≠0,p 是正整数).a -p =1ap 的条件是a ≠0,p 为正整数,而0-2等是无意义的.当a >0时,a p 的值一定为正;当a <0时,a -p 的值视p 的奇偶性而定,如(-2)-3=-18,(-3)-2=19.规定了零指数幂和负整数指数幂的意义后,正整数指数幂的运算性质,就可以推广到整数指数幂了,于是同底数幂除法的性质推广到整数指数幂,即a m ÷a n =a m -n(a ≠0,m ,n 都是整数).如a ÷a 2=a 1-2=a -1=1a;正整数指数幂的某些运算,在负整数指数幂中也能适用.如a -2·a -3=a-2-3=a -5等.【例5】计算:(1)1.6×10-4;(2)(-3)-3;(3)⎝ ⎛⎭⎪⎫-53-2;(4)(π-3.14)0;(5)⎝ ⎛⎭⎪⎫130+⎝ ⎛⎭⎪⎫-13-2+⎝ ⎛⎭⎪⎫-23-1.分析:此题是负整数指数幂和零指数幂的计算,可根据a -p=1ap (p 是正整数,a ≠0)和a 0=1(a ≠0)计算.其中(1)题应先求出10-4的值,再运用乘法性质求出结果.解:(1)1.6×10-4=1.6×1104=1.6×0.000 1=0.000 16.(2)(-3)-3=1-33=-127. (3)⎝ ⎛⎭⎪⎫-53-2=⎝ ⎛⎭⎪⎫-352=925. (4)因为π=3.141 592 6…, 所以π-3.14≠0.故(π-3.14)0=1.(5)原式=1+1⎝ ⎛⎭⎪⎫-132+1⎝ ⎛⎭⎪⎫-231=1+9-32=812.只要底数不为零,而指数是零,不管底数多么复杂,其结果都是1.当一个负整数指数幂的底数是分数时,它等于底数倒数的正整数次幂,即⎝ ⎛⎭⎪⎫a b -p =⎝ ⎛⎭⎪⎫b a p .6.用科学记数法表示绝对值较小的数(1)绝对值小于1的数可记成±a ×10-n的形式,其中1≤a <10,n 是正整数,n 等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法也是科学记数法.(2)把一个绝对值小于1的数用科学记数法表示分两步:①确定a,1≤a <10,它是将原数小数点向右移动后的结果;②确定n ,n 是正整数,它等于原数化为a 后小数点移动的位数.(3)利用科学记数法表示数,不仅简便,而且更便于比较数的大小,如:2.57×10-5显然大于2.57×10-8,前者是后者的103倍.【例6-1】2009年初甲型H1N1流感在墨西哥暴发并在全球蔓延,我们应通过注意个人卫生加强防范.研究表明,甲型H1N1流感球形病毒细胞的直径约为0.000 001 56 m ,用科学记数法表示这个数是( ).A .0.156×10-5B .0.156×105C.1.56×10-6 D.1.56×106解析:本题考查科学记数法,将一个数用科学记数法表示为±a×10-n(1≤a<10)的形式,其中a是正整数数位只有一位的数,所以A、B不正确,n是正整数,n等于原数中第一个有效数字前面的零的个数(包括小数点前面的一个零),所以n=6,即0.000 001 56=1.56×10-6.故选C.答案:Cn的值也等于将原数写成科学记数法±a×10-n时,小数点移动的位数.如本题中将0.000 001 56写成科学记数法表示时,a为1.56,即将原数的小数点向右移动了6位,所以n的值是6.【例6-2】已知空气的单位体积质量为 1.24×10-3 g/cm3,1.24×10-3用小数表示为( ).A.0.000 124 B.0.012 4C.-0.001 24 D.0.001 24解析:因为a=1.24,n=3,因此原数是1前面有3个零(包括小数点前面的一个零),即1.24×10-3=0.001 24.答案:D本题可把1.24的小数点向左移动3位得到原数,也可利用负整数指数幂算出10-3的值,再与1.24相乘得到原数.7.幂的混合运算幂的四个运算性质是整式乘(除)法的基础,也是整式乘(除)法的主要依据.进行幂的运算,关键是熟练掌握幂的四个运算性质,深刻理解每个性质的意义,避免互相混淆.幂的混合运算顺序是先乘方,再乘除,最后再加减,有括号的先算括号里面的.因此,运算时,应先细心观察,合理制定运算顺序,先算什么,后算什么,做到心中有数.(1)同底数幂相乘与幂的乘方运算性质混淆,从而导致错误.如:①a3·a2=a6;②(a3)2=a5.解题时应首先分清是哪种运算:若是同底数幂相乘,应将指数相加;若是幂的乘方,应将指数相乘.正解:①a3·a2=a5;②(a3)2=a6.(2)同底数幂相乘与合并同类项混淆,从而导致错误.如:①a3·a3=2a3;②a3+a3=a6.①是同底数幂相乘,应底数不变,指数相加;②是合并同类项,应系数相加作系数,字母和字母的指数不变.正解:①a3·a3=a6;②a3+a3=2a3.【例7-1】下列运算正确的是( ).A.a4+a5=a9B.a3·a3·a3=3a3C.2a4·3a5=6a9D.(-a3)4=a7解析:对于A,两者不是同类项,不能合并;对于B,结果应为a9;对于C,结果是正确的;对于D,(-a3)4=a3×4=a12.故选C.答案:C【例7-2】计算:(-2x2y)3+8(x2)2·(-x)2·(-y)6÷y3.分析:按照运算顺序,先利用积的乘方化简,即(-2x2y)3=-8(x2)3·y3,8(x2)2·(-x)2·(-y)6=8x4·x2·y6,再利用幂的乘方及同底数幂的乘法化简乘方后的结果,最后合并同类项.解:(-2x2y)3+8(x2)2·(-x)2·(-y)6÷y3=-8(x2)3·y3+8x4·x2·y6÷y3=-8x6y3+8x6y3=0.8.幂的运算性质的逆用对于幂的运算性质的正向运用大家一般比较熟练,但有时有些问题需要逆用幂的运算性质,可以使问题化难为易、求解更加简单.(1)逆用同底数幂的乘法性质:a m +n =a m ·a n (m ,n 为正整数).如25=23×22=2×24.当遇到幂的指数是和的形式时,为了计算的需要,往往逆用同底数幂的乘法性质,将幂转化成几个同底数幂的乘法.但是一定要注意,转化后指数的和应等于原指数.(2)逆用幂的乘方性质:a mn =(a m )n =(a n )m (m ,n 均为正整数).逆用幂的乘方性质的方法是:幂的底数不变,将幂的指数分解成两个因数的乘积,再转化成幂的乘方的形式.如x 6=(x 2)3=(x 3)2,至于选择哪一个变形结果,要具体问题具体分析.(3)逆用积的乘方性质: a n b n =(ab )n (n 为正整数).当遇到指数相差不大,且指数比较大时,可以考虑逆用积的乘方性质解题.注意,必须是同指数的幂才能逆用性质,逆用时一定要注意:底数相乘,指数不变.(4)逆用同底数幂的除法性质: a m -n =a m ÷a n (a ≠0,m ,n 为整数).当遇到幂的指数是差的形式时,为了计算的需要,往往逆用同底数幂的除法性质,将幂转化成几个同底数幂的除法.但是一定要注意,转化后指数的差应等于原指数.【例8-1】(1)已知3a =2,3b =6,则33a -2b的值为__________;(2)若m p =15,m 2q =7,m r =-75,则m 3p +4q -2r的值为__________.解析:(1)因为3a =2,3b=6,所以33a -2b =33a ÷32b =(3a )3÷(3b )2=23÷62=29.(2)m 3p +4q -2r =(m p )3·(m 2q )2÷(m r )2=⎝ ⎛⎭⎪⎫153×72÷⎝ ⎛⎭⎪⎫-752=15.答案:(1)29 (2)15【例8-2】(1)计算:⎝ ⎛⎭⎪⎫18 2 011×22 012×24 024;(2)已知10x =2,10y =3,求103x +2y的值.分析:(1)本题的指数较大,按常规方法计算很难,观察式子特点发现:4 024是2 012的两倍,可逆用幂的乘方性质,把24 024化为(22)2 012,这样再与22 012逆用积的乘方性质,此时发现与⎝ ⎛⎭⎪⎫18 2 011底数互为倒数,但指数不相同,因此逆用同底数幂的乘法及逆用积的乘方性质,简化计算;(2)可逆用幂的乘方,把103x +2y化为条件中的形式.解:(1)原式=⎝ ⎛⎭⎪⎫18 2 011×22 012×(22)2 012(逆用幂的乘方)=⎝ ⎛⎭⎪⎫18 2 011×(2×22)2 012(逆用积的乘方) =⎝ ⎛⎭⎪⎫18 2 011×82 012 =⎝ ⎛⎭⎪⎫18 2 011×82 011×8(逆用同底数幂的乘法) =⎝ ⎛⎭⎪⎫18×8 2 011×8(逆用积的乘方) =8.(2)因为103x =(10x )3=23=8,102y =(10y )2=32=9,所以103x +2y =103x ·102y=8×9=72. 9.利用幂的运算性质比较大小 在幂的运算中,经常会遇到比较正整数指数幂的大小问题.对于一些幂的指数较小的问题,可以直接计算出幂进行比较;但当幂的指数较大时,若通过先计算出幂再比较大小,就会很繁琐甚至不可能.这时可利用幂的运算性质比较幂的大小.比较幂的大小,一般有以下几种方法:(1)指数比较法:利用乘方,将比较大小的各个幂的底数化为相同的底数,然后根据指数的大小关系确定出幂的大小.(2)底数比较法:利用乘方,将比较大小的各个幂的指数化为相同的指数,然后根据底数的大小关系确定出幂的大小.(3)作商比较法:当a >0,b >0时,利用“若a b >1,则a >b ;若a b =1,则a =b ;若a b<1,则a <b ”比较.有关幂的大小比较的技巧和方法除灵活运用幂的有关性质外,还应注意策略,如利用特殊值法、放缩法等.【例9】(1)已知a =8131,b =2741,c =961,则a ,b ,c 的大小关系是( ). A .a >b >c B .a >c >b C .a <b <c D .b >c >a(2)350,440,530的大小关系是( ).A .350<440<530B .530<350<440C .530<440<350D .440<530<350(3)已知P =999999,Q =119990,那么P ,Q 的大小关系是( ).A .P >QB .P =QC .P <QD .无法比较解析:(1)因为a =8131=(34)31=3124,b =2741=(33)41=3123,c =961=(32)61=3122,又124>123>122,所以3124>3123>3122,即a >b >c .故选A .(2)因为350=(35)10=24310,440=(44)10=25610,530=(53)10=12510,而125<243<256,所以12510<24310<25610,即530<350<440.故选B .(3)因为P Q =999999×990119=9×119999×990119=99×119999×990119=1,所以P =Q .故选B . 答案:(1)A (2)B (3)B10.幂的运算性质的实际应用利用幂的运算可以解决一些实际问题,所以要熟练掌握好幂的运算性质,能在实际问题中灵活地运用幂的运算性质求解问题.解决此类问题时,必须认真审题,根据题意列出相关的算式,进而利用幂的运算性质进行运算或化简,特别地,当计算的结果是比较大的数时,一般要写成科学记数法的形式.【例10】卫星绕地球运动的速度(即第一宇宙速度)约为7.9×103m/s ,则卫星运行3×102s 所走的路程约是多少?分析:要计算卫星运行3×102s 所走的路程,根据路程等于时间乘以速度可解决问题.本题实际是一道同底数幂的乘法运算问题.解:因为7.9×103×3×102=(7.9×3)×(103×102)=23.7×105=2.37×106,所以卫星运行3×102 s 所走的路程约为2.37×106m . 11.幂的运算中的规律探究题探究发现型题是指命题中缺少一定的题设或未给出明确的结论,需要经过推断、补充并加以总结.它不像传统的解答题或证明题,在条件和结论给出的情景中只需进行由因导果或由果导因的工作,而是必须利用题设大胆猜想、分析、比较、归纳、推理,或由条件去探索不明确的结论;或去探索存在的各种可能性以及发现所形成的客观规律.规律探索题是指在一定条件下,需要探索发现有关数学对象所具有的规律性或不变性的题目,要解答此类问题,首先要仔细阅读,弄清题意,并从阅读过程中找出其规律,然后进一步利用规律进行计算.【例11】(1)观察下列各式:由22×52=4×25=100,(2×5)2=102=100,可得22×52=(2×5)2;由23×53=8×125=1 000,(2×5)3=103=1 000,可得23×53=(2×5)3;….请你再写出两个类似的式子,你从中发现了什么规律?(2)x2表示两个x相乘,(x2)3表示3个__________相乘,因此(x2)3=__________,由此类推得(x m)n=__________.利用你发现的规律计算:①(x3)15;②(x3)6;③[(2a-b)3]8.解:(1)如:34×54=(3×5)4,45×55=(4×5)5,等等.规律:a n·b n=(ab)n,即两数n次幂的积等于这两个数的积的n次幂.(2)x2x2×3=x6x mn①(x3)15=x45;②(x3)6=x18;③[(2a-b)3]8=(2a-b)24.。
6分钟搞定一种题型丨初中数学专题复习之幂的运算

6分钟搞定一种题型丨初中数学专题复习之幂的运算
每天一起涨知识!
作为整式乘除的前奏,幂的运算看似非常简单,实际运用起来却灵活多变。
不过,只要熟悉运算的一些基本方法原则,问题就迎刃而解了。
而且通过这些方法原则的学习,不但能使我们熟悉幂的运算,还可得到全面的思维训练。
幂的运算的基本知识就四条性质,写作四个公式:
只要理解掌握公式的形状特点,熟悉其基本要义,直接应用一般都容易,即使运用公式求其中的未知指数难度也不大。
如果你还是有所疑惑,那就一起跟傲德老师学习技巧吧~
(建议在WiFi条件下观看)
怎么样?今日份的知识点get了没?
老套路——豆姐会在每周三选择初中某个科目的知识点或者题型,以视频的形式推送给大家。
(所有科目都可以哦,快点来留言啦~)。
第八章幂的运算PPT课件

(1)(105)6=
1030
(2)(a7)3 =
a21
(3)(x5)5 =
x25
(4)(y3)2· (y2)3=
y · y = y 6
2021/7/24
6
12
9
练习三、 计算:
①10m·10m- 1·100=
102m+1
②3×27×9×3m= 3m+6
2021/7/24
10
③(m-n)4·(m-n) 5·(n-m)6=
语言叙述:同底数幂相乘,底
数不变,指数相加。 2021/7/24
4
学习指导二
幂的乘方法则:
字母表示:
(am)n=amn 其中m,n都是正整数
语言叙述:幂的乘方,底
数不变,指数相乘。
2021/7/24
5
想一想:同底数幂的 乘法法则与幂的乘方 法则有什么相同点和 不同点?
2021/7/24
6
同底数幂相乘
个因式分别乘方,再把所得的积相乘。
2021/7/24
18
练习七、计算( 口答) (1) (ab) 2 = a 2 b 2
(2)(ab)3 = a 3 b 3
(3)(ab) = a b 2021/7/24
4
44
19
练习八、 计算:
(1)(2b)3
=23b3 =8b3
(2)(2a)3 =22×(a3)2 =4a6
中,括号内应填写的代数式是
( D)
A、x2m C、x2m+2
B、x2m&5
练习五、 计算:
(1).已知:am=7,bm=4, 求(ab)2m的值。
(2).已知:x+4y-3=0, 求2x●16y的值。
(完整版)幂的运算总结及方法归纳.docx

(完整版)幂的运算总结及方法归纳.docx幂的运算一、知识网络归纳二、学习重难点学习本章需关注的几个问题:●在运用 a m ? a n a m n( m 、 n 为正整数), a m a n a m n (a 0, m 、 n 为正整数且 m > n ), (a m ) n a mn( m 、 n 为正整数), (ab) n a n b n( n 为正整数), a 01(a 0) ,a n1( a 0 ,n为正整数)时,要特别注意各式子成a n立的条件。
◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它还可以表示一个单项式,甚至还可以表示一个多项式。
换句话说,将底数看作是一个“整体”即可。
◆注意上述各式的逆向应用。
如计算0.252004 4 2005,可先逆用同底数幂的乘法法则将42005 写成42004 4 ,再逆用积的乘方法则计算0.25 200442004(0.25 4) 2004120041,由此不难得到结果为1。
◆通过对式子的变形,进一步领会转化的数学思想方法。
如同底数幂的乘法就是将乘法运算转化为指数的加法运算,同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等。
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律” 这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法。
一、同底数幂的乘法1、同底数幂的乘法同底数幂相乘,底数不变,指数相加.公式表示为:a m a n a m n m、n为正整数2、同底数幂的乘法可推广到三个或三个以上的同底数幂相乘,即a m a n a p a m m p (m、 n、 p为正整数 )注意点:(1)同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数 .(2)在进行同底数幂的乘法运算时,如果底数不同,先设法将其转化为相同的底数,再按法则进行计算 .例题:例 1:计算列下列各题(1)a3 a4;( 2) b b2b324;( 3)cc c简单练习:一、选择题1.下列计算正确的是 ( )A.a2+a3=a5B.a2·a3=a5C.3m+2m=5mD.a2+a2=2a42.下列计算错误的是 ( )A.5 x2- x2=4x2B.am+am=2amC.3m+2m=5mD. x·x2m-1=x 2m3.下列四个算式中①a333②x336325·a=2a+x =x③b·b·b=b④p2+p2+p2=3p2正确的有 ( )A.1个B.2个C.3个D.4个4.下列各题中,计算结果写成底数为10 的幂的形式,其中正确的是 ()A.100 × 102=103B.1000× 1010=103C.100 × 103=105D.100×1000=104二、填空题1.a4·a4=_______;a4+a4=_______。
七年级数学下 第八章 幂的运算讲义全

泛 美 教 育 个 性 化 教 学 专 用 教 案学生姓名:科目:数学 七年级 备课时间: 年 月 日讲次:第 讲 授课教师:章老师 授课时间: 年 月 日 至 上课后,学生签字: 年 月 日 教学类型: ■强化基础型 □引导思路型 □错题讲析型 ■督导训练型■效率提升型 □单元测评型 □综合测评型 □应试指导型□专题总结型 □其它:第一讲:幂的运算教学目标:1.学会应用同底数幂的乘法; 2.学会应用同底数幂的除法; 3.掌握幂的乘方; 4. 理解积的乘方。
教学重难点:1. 学会应用同底数幂的乘法;2. 学会应用同底数幂的除法;3. 掌握幂的乘方。
教学内容 :一、同底数幂的乘法(重点)1.运算法则:同底数幂相乘,底数不变,指数相加。
用式子表示为: n m n m a a a +=⋅(m 、n 是正整数)2、同底数幂的乘法可推广到三个或三个以上的同底数幂相乘,即()m n p m m p a a a a m n p ++⋅⋅=、、为正整数注意点:(1) 同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数.(2) 在进行同底数幂的乘法运算时,如果底数不同,先设法将其转化为相同的底数,再按法则进行计算.【典型例题】1.计算(-2)2007+(-2)2008的结果是( )A .22015B .22007C .-2D .-220082.当a<0,n 为正整数时,(-a )5·(-a )2n 的值为( )A .正数B .负数C .非正数D .非负数3.(一题多解题)计算:(a -b )2m -1·(b -a )2m ·(a -b )2m+1,其中m 为正整数.4.(一题多变题)(1)已知x m =3,x n =5,求x m+n . (2)一变:已知x m =3,x n =5,求x 2m+n ;(3)二变:已知x m =3,x n =15,求x n .二、同底数幂的除法(重点)1、同底数幂的除法同底数幂相除,底数不变,指数相减.公式表示为:()0,m n m n a a a a m n m n -÷=≠>、是正整数,且.2、零指数幂的意义任何不等于0的数的0次幂都等于1.用公式表示为:()010a a =≠.3、负整数指数幂的意义任何不等于0的数的-n(n 是正整数)次幂,等于这个数的n 次幂的倒数,用公式表示为()10,n n a a n a-=≠是正整数 4、绝对值小于1的数的科学计数法对于一个小于1且大于0的正数,也可以表示成10n a ⨯的形式,其中110,a n ≤<是负整数.注意点:(1) 底数a 不能为0,若a 为0,则除数为0,除法就没有意义了;(2) ()0,a m n m n ≠>、是正整数,且是法则的一部分,不要漏掉. (3) 只要底数不为0,则任何数的零次方都等于1.【典型例题】一、选择 1.在下列运算中,正确的是( )A .a 2÷a=a 2B .(-a )6÷a 2=(-a )3=-a 3C .a 2÷a 2=a 2-2=0 D .(-a )3÷a 2=-a 2.在下列运算中,错误的是( )A .a 2m ÷a m ÷a 3=a m -3B .a m+n ÷b n =a mC .(-a 2)3÷(-a 3)2=-1D .a m+2÷a 3=a m -1 二、填空题1.(-x 2)3÷(-x )3=_____. 2.[(y 2)n ] 3÷[(y 3)n ] 2=______.3.104÷03÷102=_______. 4.(π-3.14)0=_____.三、解答1.(一题多解题)计算:(a -b )6÷(b -a )3. 2.(巧题妙解题)计算:2-1+2-2+2-3+…+2-2008.3、已知a m =6,a n =2,求a 2m-3n 的值.4.(科外交叉题)某种植物的花粉的直径约为3.5×10-5米,用小数把它表示出来.三、幂的乘方(重点)幂的乘方,底数不变,指数相乘.公式表示为:()()nm mn a a m n =、都是正整数. 注意点:(1) 幂的乘方的底数是指幂的底数,而不是指乘方的底数.(2) 指数相乘是指幂的指数与乘方的指数相乘,一定要注意与同底数幂相乘中“指数相加”区分开.【典型例题】1.计算(-a 2)5+(-a 5)2的结果是( )A .0B .2a 10C .-2a 10D .2a 72.下列各式成立的是( )A .(a 3)x =(a x )3B .(a n )3=a n+3C .(a+b )3=a 2+b 2D .(-a )m =-a m3.如果(9n )2=312,则n 的值是( )A .4B .3C .2D .14.已知x2+3x+5的值为7,那么3x2+9x-2的值是( )A .0B .2C .4D .66.计算:(1)233342)(a a a a a +⋅+⋅ (2)22442)()(2a a a ⋅+⋅补充:同底数幂的乘法与幂的乘方性质比较:幂的运算 指数运算种类 同底数幂乘法乘法 加法 幂的乘方 乘方 乘法四、积的乘方运算法则:两底数积的乘方等于各自的乘方之积。
幂的运算总结及方法归纳

幂的运算一、知识网络归纳二、学习重难点学习本章需关注的几个问题:●在运用n m n m a a a +=•(m 、n 为正整数),n m n m a a a -=÷(0≠a ,m 、n 为正整数且m >n ),mn n m a a =)((m 、n 为正整数),n n n b a ab =)((n 为正整数),)0(10≠=a a ,n n aa 1=-(0≠a ,n 为正整数)时,要特别注意各式子成立的条件。
◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它还可以表示一个单项式,甚至还可以表示一个多项式。
换句话说,将底数看作是一个“整体”即可。
◆注意上述各式的逆向应用。
如计算20052004425.0⨯,可先逆用同底数幂的乘法法则将20054写成442004⨯,再逆用积的乘方法则计算11)425.0(425.02004200420042004==⨯=⨯,由此不难得到结果为1。
◆通过对式子的变形,进一步领会转化的数学思想方法。
如同底数幂的乘法就是将乘法运算转化为指数的加法运算,同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等。
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法。
一、同底数幂的乘法1、同底数幂的乘法同底数幂相乘,底数不变,指数相加.公式表示为:()mnm na a am n +⋅=、为正整数2、同底数幂的乘法可推广到三个或三个以上的同底数幂相乘,即()m n p m m p a a a a m n p ++⋅⋅=、、为正整数注意点:(1) 同底数幂的乘法中,首先要找出相同的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数.(2) 在进行同底数幂的乘法运算时,如果底数不同,先设法将其转化为相同的底数,再按法则进行计算.例题:例1:计算列下列各题(1) 34a a ⋅; (2) 23b b b ⋅⋅ ; (3) ()()()24c c c -⋅-⋅- 简单练习: 一、选择题1. 下列计算正确的是( )A.a2+a3=a5B.a2·a3=a5C.3m +2m =5mD.a2+a2=2a42. 下列计算错误的是( )A.5x2-x2=4x2B.am +am =2amC.3m +2m =5mD.x·x2m-1= x2m3. 下列四个算式中①a3·a3=2a3 ②x3+x3=x6 ③b3·b·b2=b5④p 2+p 2+p 2=3p 2正确的有( )A.1个B.2个C.3个D.4个4. 下列各题中,计算结果写成底数为10的幂的形式,其中正确的是( )A.100×102=103B.1000×1010=103C.100×103=105D.100×1000=104二、填空题1. a4·a4=_______;a4+a4=_______。
七年级下册幂的运算.ppt

指数相加
底数不变 其中m ຫໍສະໝຸດ n都是 指数相乘正整数(am)n=amn
幂的乘方
➢ 练习一 1. 计算:( 口答)
(1) 105×106 1011
(3) a7 ·a3 a10
(5) x5 ·x5
x10 (7) x5 ·x ·x3
x9
(2) (105)6 1030
(4) (a7)3 a21
积的乘方
试猜想:
(ab)n=? 其中 n是正整数
证明:
(ab)n= (1ab4) 4(4ab2) 4 4 (a43b)
n个( )
=(a aa)( • b bb)
n个
n个
= a nbn ∴(ab)n = a nbn (n为正整数)
语言叙述:积的乘方,等于各因数乘方的积.
解(1)(2b)3
=23b3 =8b3
(6) (x5)5
x25
(8)(y3)2·(y2)3
= y 6 ·y 6 = y 12
➢ 练习一 2. 计算:
①10m·10m-1·100= 102m+1 ②3×27×9×3m= 3m+6 ③(m-n)4·(m-n) 5·(n-m)6 = (m-n)15 ④ (x-2y)4·(2y-x) 5·(x-2y)6 = (2y-x)15
=__(_a_a_a_)_•_(_b_b_b_)______________ = a ( 3 )b( 3 ) (3)(ab)4=___(a_b_)_•__(a_b_)_•_(_a_b_)_•_(_a_b_)______ =__(_a_a_a_a_)_•_(_b_b_b_b_)____________ = a ( 4)b(4)
= =1 (3)-82000×(-0.125)=2001
沪科版初中数学七年级下册《8.1 幂的运算精品课件(1)

根据同底数幂的除法运算,得:
32÷35=32-5=3-3;104÷108=104-8=10-4;am÷an=am-n
结论:33
1 33
,104
1 104
, ap
1 ap
(a 0)
于是约定:a p 1 ap
(a 0, p为正整数)
• 语言叙述:任何一个不等于零的数的-p(p为正整数) • 指数幂,等于这个数的p指数幂的倒数。
; 108÷108=108-
;
an÷an=3=a3n0-n=a0 (a≠0) 8=100
结论:30=1, 100=1, a0=1 (a≠0) 于是约定:a0=1 (a≠0)
语言表述:任何一个不等于零的数的零指数幂等于1。
2,根据同底数幂相乘,除法运算及分数约分,得:
32 32 35 = 35
=
32 32 33
选做题:计算:
1, 0.21 2 0 2
2
,
1 x
7
x
5
1 x
3
3
,
3 2
x 1
4 9
, 求x的值
家庭作业:《基础训练》同步。
•谢谢
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
1
33
104 108 =
104
104
108 = 104 104
1 104
am
an=
am an, p n m
32
35
=
32 35
=
32 32
33
1 33
am an = am an
幂的运算-ppt课件

(2)系数应连同它的符号一起乘方,尤其是当系数是-1时,不
可忽略.
感悟新知
知3-练
例 5 计算:
(1)(x·y3)2; (2)(-3×102)3;
(3) -
2;
(4)(-a2b3)3.
解题秘方:运用积的乘方、幂的乘方的运算法则
进行计算.
感悟新知
知3-练
最后结果要符合科
学记数法的要求
(2)(-3×102)3=(-3)3×(102)3=-27×106=-2.7×107;
解:(1)(x·y3)2=x2·(y3)2=x2y6;
(3) -
12
a ;
2=
-
· () 2 =
2
2
=
·(a6)2 =
系数乘方时,要带前面的符号,特
a4n-a6n用a2n表示,再把a2n=3 整体代入求值.
解:a4n-a6n=(a2n)2-(a2n)3=32-33=9-27=-18.
感悟新知
知2-练
4-1.已知10m=3,10n=2,求下列各式的值:
(1)103m;
解:103m=(10m)3=33=27;
(2)102n;
102n=(10n)2=22=4;
感悟新知
知3-练
6-1. [中考·淄博] 计算(-2a3b)2-3a6b2的结果是( C )
A.-7a6b2
B. -5a6b2
C. a6b2
D. 7a6b2
感悟新知
知3-练
6-2. 计算:
(1)(-2anb3n)2+(a2b6)n;
幂的运算课件

幂的运算课件教学目标:1、能说出幂的运算的性质;2、会运用幂的运算性质进行计算,并能说出每一步的依据;3、能说出零指数幂、负整数指数幂的意义,能用熟悉的事物描述一些较小的'正数,并能用科学记数法表示绝对值小于1的数;4、通过具体例子体会本章学习中体现的从具体到抽象、特殊到一般的思考问题的方法,渗透转化、归纳等思想方法,发展合情推理能力和演绎推理能力。
教学重点:运用幂的运算性质进行计算教学难点:运用幂的运算性质进行证明规律教学方法:引导发现,合作交流,充分体现学生的主体地位一、系统梳理知识:幂的运算:1、同底数幂的乘法2、幂的乘方3、积的乘方4、同底数幂的除法:(1)零指数幂(2)负整数指数幂请你用字母表示以上运算法则。
你认为本章的学习中应该注意哪些问题?二、例题精讲:例1 判断下列等式是否成立:①(-x)2=-x2,②(-x3)=-(-x)3,③(x-y)2=(y-x)2,④(x-y)3=(y-x)3,⑤x-a-b=x-(a+b),⑥x+a-b=x-(b-a).解:③⑤⑥成立.例2 已知10m=4,10n=5,求103m+2n的值.解:因为103m=(10m)3=43 =64,102n=(10n)2=52=25.所以103m+2n=103m×102n=64×25=1680例3 若x=2m+1,y=3+4m,则用x的代数式表示y为______.解:∵2m=x-1,∴y=3+4m=3+22m.=3+(2m)2=3+(x-1)2=x2-2x+4.例4设表示正整数n的个位数,例如<3>=3,<21>=1,<13×24>=2,则<210>=______.解 210=(24)222=1624,∴ <210>=<6×4>=4例5 1993+9319的个位数字是( )A.2B.4C.6D.8解1993+9319的个位数字等于993+319的个位数字.∵ 993=(92)469=81469.319=(34)433=81427.∴993+319的个位数字等于9+7的个位数字.则 1993+9319的个位数字是6.三、随堂练习:1、已知a=355,b=444,c=533,则有 ( )A.aC.c2、已知3x=a,3y =b,则32x-y等于 ( )3、试比较355,444,533的大小.4、已知a=-0.32,b=-3-2,c=(-1/3)-2d=(-1/3)0,比较a、b、c、d的大小并用“,〈”号连接起来。
关于幂的运算公式

关于幂的运算公式好的,以下是为您生成的关于“关于幂的运算公式”的文章:咱们在数学的世界里遨游,幂的运算公式那可是相当重要的家伙!就好像是打开数学宝藏的一把把神奇钥匙。
先来说说同底数幂相乘吧,公式是:a^m × a^n = a^(m + n)。
这就好比你有一堆苹果,每堆的数量不一样,但都是同样大小的苹果。
比如说,有一堆是 5 个一堆的(a^5),还有一堆是 3 个一堆的(a^3),把它们放一起,那就是 8 个一堆(a^8)啦。
我记得之前给学生们讲这个知识点的时候,有个小同学一脸迷茫地问我:“老师,这到底有啥用啊?”我笑着跟他说:“你想想看呀,假如咱们要计算边长为 2 的正方形面积,那就是 2 的 2 次幂,也就是 4 对吧。
那如果要算一个正方体的体积呢,边长还是 2 ,这时候就是 2 的 3 次幂,等于 8 啦。
这不就用上了嘛!”这小家伙听了,眼睛一下子亮了起来。
再说说同底数幂相除,公式是:a^m ÷ a^n = a^(m - n) 。
这个就像是把同样大小的苹果堆,从多的里面拿掉少的那部分。
比如说有 8 个一堆的(a^8),拿走3 个一堆的(a^3),那就剩下5 个一堆的(a^5)。
幂的乘方也很有趣,(a^m)^n = a^(mn) 。
这就好像给一堆苹果穿上了好几层“衣服”,每穿一层,数量就跟着变。
比如原本是 2 个一堆的(a^2),给它穿上 3 层“衣服”,那就变成 8 个一堆的(a^8)啦。
积的乘方呢,(ab)^n = a^n × b^n 。
这个就像是不同种类的水果分别打包,然后计算总数。
比如说有一堆苹果(a),每堆 3 个,还有一堆香蕉(b),每堆 4 个,把它们一起打包成 n 份,那苹果就有 3×n 个,香蕉就有 4×n 个。
还记得有一次,学校组织数学竞赛,有一道题就是关于幂的运算的。
题目是这样的:已知 2^m = 3,2^n = 5,求 2^(m + n) 的值。
初中数学人教版 幂的运算 人教版PPT文档19页

60、生活的Байду номын сангаас路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
初中数学人教版 幂的运算 人教版
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
八年级上册——幂的运算(培优难题教案)(K12教育文档)

八年级上册——幂的运算(培优难题教案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级上册——幂的运算(培优难题教案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级上册——幂的运算(培优难题教案)(word版可编辑修改)的全部内容。
幂的运算考点·方法·破译幂的运算性质(其中m 、n 、p 都为正整数):1.m n m n a a a +⋅=2.()m n mn a a =3.()n n n ab a b =4.m n m n a a a -÷=5.011(0)(0)p p a a a a a-=≠=≠, 经典·考题·赏析【例1】下列算式,正确的个数是( )①3412a a a ⋅= ②5510a a a += ③336()a a = ④236(2)6a a -- A .0个B .1个C .2个D .3个【变式题组】 01。
计算212()()n n c c +⋅的结果是( )A .42n c +B .44n c +C .22n c +D .34n c +02.计算100101(2)(2)-+-=_______________03.如果3915()n m a b b a b ⋅=,则m =_________,n =____________04.计算2323()()()n n x y x y +-⋅-=_______________【例2】若2n+12448n +=,求n 的值。
【变式题组】01.若24m =,216n =,求22m n +的值02.若35n x =,求代数式2332(2)4()n n x x -+的值03.若3m x =,6n x =,则32m n x -=________.04.已知33m a =,32n b =,求233242()()m n m n m n a b a b a b +-⋅⋅⋅的值05.已知232122192m m ++-=,求m 的值【例3】552a =-,443b =-,335c =-,226d =-,那么a 、b 、c 、d 的大小关系为( )A .a >b 〉c >dB .a 〉b 〉d >cC .b 〉a >c 〉dD .a >d >b 〉c【变式题组】01.已知3181a =,4127b =,619c =,则a 、b 、c 的大小关系是( )A .a >b 〉cB .a >c 〉bC .a <b <cD .b >c >a 02.已知503a =,404b =,305c =,则a 、b 、c 的大小关系为( )A .a <b 〈cB .c 〈a <bC .c <b 〈aD .b <c <a【例4】求满足200300(1)3x ->的x 的最小正整数【变式题组】01.求满足2003005n <的最大整数值n.02.如果x 、y 是正整数,且2232x y ⋅=,求满足条件的整数x 、y03.求满足22(1)1n n n +--=的整数n 。
幂的运算讲义

③ 。
方法总结:同底数幂相乘,先确定符号,负因数出现奇数个就取负号,出现偶数个就取正号,然后按照同底数幂的乘法法则进行计算。
(2)计算:① ; ② ; ③ ;
④ ;
思路引导:将a+b,x+2看成是一个整体,然后运用同底数幂的乘法法则进行计算;若底数为互为相反数的幂相乘时,可以利用幂确定符号的方法先转化为同底数幂再按法则计算。
解:∵ ,∴ ,∴1+m+n=14 .①
又∵m比n大3,∴m-n=3 .②
①②组成方程组为 ,解得 , ∴mn=8×5=40.
方法总结:解此类问题,首先要根据同底数幂的乘法法则构造方程或方程组,再通过解方程或方程组求出指数中的字母,通过转化和方程组呃综合运用来解决问题。
(4)计算:① ; ② ;
思路引导:先算同底数幂相乘,再合并同类项。
即 也能被13整除。
方法二:∵( - )= = = = ,
∴ 与 也能被13整除,又∵ 能被13整除,∴ 也能被13整除。
题型训练:
计算:1. = 2. = 3. =
4. = 5. = 6.
7. 8. 9.
10. 11.
12. 13.
14. 15.
16. 17. 18.
19. 20.
21. 22.
23. 24.
9. ; 10.4 ; 11. ; 12. ; 13. ; 14. ;
15. ; 16. ; 17. ; 18. ; 19. ; 20. ;
21. ; 22.1; 23. ; 24.1; 25. ; 26.-2y;
能力提升题:1. ; 2. ; 3. ; 4.81;
5. ;
6.b>a>c思路引导: , , ,故 ,即b>a>c;
幂的运算习题课PPT课件

第10页/共25页
3、注意幂的运算法则逆用
am+n=am·an (a≠0,m、n为正整数), amn=(am)n , anbn=(ab)n
第11页/共25页
(1)用于实数计算
计算: 1、(-4)2007×0.252008 2、22006-22005-22004-…-2-1
数学符号表示: (am )n amn
(其中m、n为正整数)
[(am )n ]p amnp (其中m、n、P为正整数)
练习:判断下列各式是否正确。
(a4)4 a44 a8, [(b2)3]4 b234 b24 (x2)2n1 x4n2, (a4)m (am )4 (a2m )2
第2页/共25页
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
第6页/共25页
例、木星是太阳系九大行星中最大的一 颗,木星可以近似地看作球体.已知木星 的半径大约是7×104km,木星的体积大约 是多少km3(∏取3.14)?
分析:球体体积公式 v 4 R3 解: v 4 (7 104 )3 3
3
4 73 1012
(1)如果(x3)6=86,则 x=__—+_2___
(2)小明在计算过程中发现(32)3=(33)2; [(-2)3]4=[(-2)4]3,于是得出结论:(am)n=(an)m (m,n为正整数).同时认为(-am)n=(-an)m也是成立 的。你同意他的观点吗?
(3)计算[( 2 )3]2的值。
第5页/共25页
想一想:
1.下面的计算对吗? 错的请改正:
(1) (43)5=48 ×, 415 (2) (-28)3=(-2)24 ×, 224
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
2003
1 8
2004
(2)
2 3
2001
2
1 4
1000
(3)113
2001
1
1 4
2002
3 5
2003
【巩固】计算:(1)
2x2 y32源自1 2xy 4z
4
(2) 3a2
3
a2
2 2a2
5a3
2
(3)a a3 a4
a2
4
2a4
2
(4)2 x2 3 x3 3x3 3 5x2 x7
比较大小 【例 1】(1)比较 3555 , 4444 , 5333 的大小.
(2)比较 86 与 49 的大小.
第 7 页 共 14 页
让进步看得见
【巩固】(1)若 a 350 ,b 440 ,c 530 ,则 a、b、c 的大小关系为( ).
A.. a b c
B.cab
C .c b a
逆运用 amn am an a p aq m n p q
幂的乘方法则:
幂的乘方,底数不变,指数相乘。
即 am n amn ( m 、 n 都是正整数)
积的乘方法则:
逆运用 amn
am
n
an
m a p q mn pq
积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘
(1) am1 ;
(2) a3n ;
(3) amn2
【巩固】(1)已知, 3n a , 3m b ,则 3mn3 的结果是
.
(2)已知 x2n 5 ,求 1 x6n 5 的值. 5
【例 8】(1)已知 x3 a , x5 b ,你能用含有 a 、 b 的代数式表示 x14 吗?
(2)已知 a3m 3 ,b3n 2 ,求
当 m 偶数时, a bm (b a)m .
a bm ,不论 m 为奇数还是偶数,都有 a bm (b a)m .
第 2 页 共 14 页
让进步看得见
NO.1 同底数幂的乘法 【例1】 下列计算是否正确?错误的指出错误的原因,并加以改正.
(1) a3 a3 a9 ;
(2) a4 a4 2a8 ;
第 4 页 共 14 页
让进步看得见
NO.4 幂的除法 【例 4】(1) t5 t4 t18 t9
【巩固】(1) x3n x2n xn3
(2) xn xn1 xn2
(2) x2 x3 2x2 3 x9 x4
含字母参数的计算——整体思想 【例 5】已知: x 2 y 4 0 ,求: 3x132 y 的值.
【题 2】直接写出结果
(1) m2 (m)2
(2) a2 a2m4
(4) a8n a4
a
2
(2) (m 2n)4 (2n m)2
(3)[(a b)3 ]4
(4)[(2)3 ]4 (22 )6
(5) (2x)2
(6) (4a 2b3 )2
【题 3】已知 x 2 2x 3y 8 0 ,则 x y y2 y x x2
即 abn anbn ( n 为正整数)
逆运用 anbn ab n a2m b3m a2b3 m
同底数幂的除法法则: 同底数幂相除,底数不变,指数相减. 即 am an amn ( m 、 n 都是正整数)
逆运用 amn am an a p aq m n p q
a bm ,当 m 奇数时, a bm (b a)m ;
八年级数学
成长手册
第 1 页 共 14 页
让进步看得见
幂的运算
乘方:求 n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂,在 an 中, a 叫做底
数, n 叫做指数,读作 a 的 n 次幂。
注意: a 2n a2n,,,a 2n1 a2n1
同底数幂的乘除法则 同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加. 即 am an amn ( m 、 n 都是正整数)
【例 2】计算:(1) 102 6
(2)
2 3
3
4
(3)
63
6
第 3 页 共 14 页
让进步看得见
(4) x2 5
(5) am 3
(6) a4 n
【巩固】(1) x3 4 x2
(2)2
x2
n
xn
2
(3)
xm
np
NO.3 积的乘方 【例 3】计算:
(1)
a2m
3
bn
3 a2m bn a4m b2n 的值.
第 6 页 共 14 页
让进步看得见
【巩固】(1)已知10a 5 ,10b 6 ,求102a3b 的值.
(2)若 am 3 , an 4 ,求 a3m2n 的值为多少?
(3)若 x3n 5 ,求代数式 2
x2n
3
4
x3
2n 的值.
(3) x3 x3 x6 ;
(4) y y2 y2 ;
(5) x x3 x4 ;
(6) x2 x3 x6
【巩固】计算:(1)
1 2
2
1 2
3
(2) a10 a2 a ;
(3) x 2y2 2y x3
(4) x y8 y x5 x y4
NO.2 幂的乘方
D .b c a
(2)若 a 8131 ,b 2741 ,c 961 ,则 a、b、c 的大小关系为(
A.. a b c
B.acb
C .a bc
). D .b c a
【例2】 求满足 n200 5300 的最大整数值 n .
【巩固】求满足 x 150 375 的 x 的最大整数值.
【2015-2016 洪山区期末】下列运算正确的是( )
A.(a3)2=a6
B.a3·a2=a6
C.a3+a2=a5
D.(3a)3=9a3
【2015-2016 汉阳区期末】计算: a 2 a 4 (a 2 )3 2a6
第 8 页 共 14 页
让进步看得见
【题 1】填空.
(1) x4m xm (3) n 4n a2nb3n
【巩固】已知: 2x 3y 5 0 ,求: 9x 27y 的值. 【例 6】已知 x3 xa x2a1 x31 ,求 a 的值.
第 5 页 共 14 页
让进步看得见
【巩固】若 x3 xa x2a1 x25 ,则解关于 y 的方程 ay=a 28 .
【例 7】已知 am 2 , an 3 ,求下列各式的值.
