五月试题(理科)
高三5月模拟考试理科综合试卷(含答案)

湖北省高中毕业生五月模拟考试理科综合试卷第Ⅰ卷选择题共21小题,每小题6分,共126分一、选择题:本大题共13小题,每小题6分共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关糖类的叙述,正确的是A.生物组织中的糖类都可斐林试剂检测B.相同质量的糖类中储存的能量比脂肪多C.细胞膜表面的糖类可与蛋白质或脂质结合D.蓝藻细胞中糖类是通过化能合成作用合成2.下列有关人体免疫的叙述,正确的是A.非特异性免疫是通过淋巴细胞发挥作用B.吞噬细胞可参与非特异性免疫和特异性免疫C.细胞直接或间接受抗原刺激可产生淋巴因子D.T细胞可与抗原入侵的宿主细咆接触使其裂解3.《格物粗谈•果品》记载“红柿摘下未熟,毎篮用木瓜三枚放入,得气即发,并无涩味”。
下列叙述正确的是A.文中的“气”是指乙烯,属于生长调节剂B.红柿细胞缺乏相关基因而不能合成乙烯C.木瓜细胞释放的乙烯能促进红柿的成熟D.木瓜细胞释放的乙烯不能促自身的成熟4.下列关于群落的叙述,错误..的是A.群落中所有生物含有的全部基因可构成-个基因库B.群落的物种组成随季节、气候的变化可出现差异C.群落的演替速度与方向可受外来物种入侵的影响D.群落的垂直结构可提高生物利用环境资源的能力5.赫尔希和蔡斯用噬尚体侵染太肠杆菌,离心后,甲组上清液放射性低,沉淀物放射性高;乙组刚好相反。
下列说法正确的是A.甲组的噬菌体是用35S标记其蛋由质B.乙组的噬菌体是用32P标记其蛋白质C.甲组产生的子代吨阐体均含有放射性D.乙组产生的子代噬菌体均不含放射性6.右图为研究酵母菌细胞呼吸的实验装置,排尽注射器中的空气,吸如经煮沸冷却的葡萄糖溶液和酵母菌,在适易温度下进行如图所示实验。
下列分析正确的是A.该实验装置用于研究醉母菌的无氧呼吸B.装置中的气体是在线粒体的基质中产生C.烧杯中加水的主要目的是制造无氧环境D.若升高水温注射器中气体产生速率加快7.我国古代做衣服的主要原料是麻和丝。
高三数学试卷理科答案五月

一、选择题(本大题共12小题,每小题5分,共60分)1. 下列函数中,在其定义域内单调递增的是()A. f(x) = x^2 - 4x + 3B. f(x) = -x^2 + 2x + 1C. f(x) = 2x - 3D. f(x) = x^3 - 3x^2 + 4x - 1答案:C2. 若等差数列{an}的公差为d,且a1 = 3,a3 = 7,则d = ()A. 2B. 3C. 4D. 5答案:A3. 已知函数f(x) = log2(x - 1),其定义域为()A. x > 1B. x ≥ 1C. x < 1D. x ≤ 1答案:A4. 下列命题中,正确的是()A. 若a > b,则a^2 > b^2B. 若a > b,则a - b > 0C. 若a > b,则|a| > |b|D. 若a > b,则|a| < |b|答案:B5. 已知等比数列{an}的公比为q,且a1 = 2,a4 = 32,则q = ()A. 2B. 4C. 8D. 16答案:C6. 已知函数f(x) = x^3 - 6x^2 + 9x,则f'(x) = ()A. 3x^2 - 12x + 9B. 3x^2 - 12x + 3C. 3x^2 - 12xD. 3x^2 - 6x + 9答案:A7. 下列不等式中,正确的是()A. 2x + 3 > 5B. 2x + 3 ≥ 5C. 2x + 3 < 5D. 2x + 3 ≤ 5答案:C8. 已知函数f(x) = x^2 + 2x + 1,其对称轴为()A. x = -1B. x = 0C. x = 1D. x = -2答案:B9. 若复数z = a + bi(a,b∈R),则|z|^2 = ()A. a^2 + b^2B. a^2 - b^2C. a^2 + 2ab + b^2D. a^2 - 2ab + b^2答案:A10. 下列数列中,是等比数列的是()A. 1, 2, 4, 8, 16, ...B. 1, 3, 5, 7, 9, ...C. 1, 4, 9, 16, 25, ...D. 1, 3, 6, 10, 15, ...答案:A11. 已知函数f(x) = e^x - x,则f'(x) = ()A. e^x - 1B. e^x + 1C. e^xD. e^x - x答案:A12. 下列命题中,正确的是()A. 若a > b,则a^2 < b^2B. 若a > b,则a + b > 0C. 若a > b,则|a| < |b|D. 若a > b,则|a| > |b|答案:D二、填空题(本大题共6小题,每小题5分,共30分)13. 若等差数列{an}的公差为2,且a1 = 1,则a10 = _______。
高三5月份理科综合考试试卷

高三5月份理科综合考试试卷
一、选择题
1.下列叙述不正确的是
A.流动性的基础是组成细胞膜的磷脂分子和大多数蛋白质分子是流动的B.在温和的条件下,酶能催化细胞代谢快速进行的原因是不需要活化能C.遗传信息是指DNA中碱基的排列顺序
D.群落中植物种群越多,动物的种群也越多
2.下列关于组成细胞的化合物的叙述,不正确的是
A.可以用如图所示来形象地表示抗体、载体蛋白、蛋白质之间的关系B.蛋白质肽链的盘曲和折叠被解开时,其特定功能并未发生改变
C.棉和麻细胞壁的组成成分主要是纤维素
D.蔗糖和乳糖水解的产物中都有葡萄糖,脂质具有调节生理代谢的功能3.甲至丁为二倍体生物卵巢中的
一些细胞分裂图,图中所示细
胞分裂具有连续性,有关判断
正确的是
A.细胞分裂顺序依次为乙→
丙→
甲→丁
B.乙是初级卵母细胞,丁最可能
为卵细胞
C.若乙的基因组成为AAaaBBbb,则丁的基因组成为AaBb
D.甲、乙、丙细胞中含有的染色体组数目依次为4、2、1
4.下列关于人体内环境的叙述正确的是
A.饮水不足,抗利尿激素增加会导致内环境稳态失调
B.内环境是一个主要由H
2PO-
4
/HPO2-
4
构成的缓冲体系
C.内环境中的血浆、淋巴、组织液等成分稳定时,机体达到稳态
D.细胞内外液Na+、K+分布不均匀是神经纤维兴奋传导的基础
5.关于种群和群落的说法,错误的是
A.生物进化必然伴随着种群基因频率的变化,但不一定形成了新的物种 B.1∶1的性别比例最有利于种群数量增长
C.群落中植物和动物的垂直分布的最终决定性因素都是光照
D.火山喷发后的演替一般属于初生演替。
2023届河南省郑州市重点校高三下学期5月联考理科综合试题

2023届河南省郑州市重点校高三下学期5月联考理科综合试题一、单选题 (共6题)第(1)题已知金属锌的逸出功为3.34 eV。
如图所示为氢原子能级图,氢原子中的电子从能级跃迁到能级可产生a光,从能级跃迁到能级可产生b光。
a光和b光的波长分别为和。
现用a、b两光分别照射金属锌表面均可产生光电效应,遏止电压分别为和。
下列说法正确的是( )A.b光的光子能量为3.4 eVB.C.D.a光照射金属锌表面产生的光电子的最大初动能为6.86 eV第(2)题下图为静电植绒的原理图。
带负电的金属网中盛有绒毛,真空中带负电的绒毛一旦与布匹上的黏合剂接触就粘贴在布匹上,则带负电的绒毛从带负电的金属网到布匹的运动过程中( )A.做加速运动B.做匀速运动C.电势能逐渐增大D.运动经过处各点电势逐渐降低第(3)题下图为气流加热装置的示意图,使用电阻丝加热导气管,视变压器为理想变压器,原线圈接入电压有效值恒定的交流电并保持匝数不变,调节触头P,使输出电压有效值由220V降至110V,调节前后( )A.副线圈中的电流比为B.副线圈输出功率比为C.副线圈的接入匝数比为D.原线圈输入功率比为第(4)题如图所示,金属棒的质量为,通过的电流为,处在磁感应强度大小为的匀强磁场中,磁场方向与导轨平面的夹角为,静止于两根间距为的水平导轨上且与磁场方向垂直。
下列说法正确的是( )A.金属棒受到的安培力大小B.金属棒受到的摩擦力大小C.若只增大磁感应强度,则金属棒对导轨的压力将增大D.若只改变电流方向,则金属棒对导轨的压力将增大第(5)题两波源S1、S2在水槽中形成的波形如图所示,其中实线表示波峰,虚线表示波谷,则( )A.在两波相遇的区域中会产生干涉B.在两波相遇的区域中不会产生干涉C.点的振动始终加强D.点的振动始终减弱第(6)题如图所示,倾角的光滑斜面上,两个质量均为的小球,用长度为的轻绳相连放在斜面上等高且间距为的两点,将两球由静止释放的同时,在轻绳的中点施加的恒力,方向沿斜面向上,重力加速度为.则当两球间距为时,两球的加速度大小为A.B.C.D.二、多选题 (共4题)第(1)题如图所示为某绝缘空心球的示意图,是过球心的水平截面的圆周上六个点等分点,分别在和固定等量的正负电荷,即和,而是球的某一直径且与水平面垂直,设无穷远处为电势零点,则( )A.两点的电场强度相同B.三点的电势分别记为,则C.将一正的试探电荷从点沿圆弧移到点的过程中电场力先做正功再做负功D.若处的电荷仍固定不动,将处的电荷移到处,则电荷的电势能将减小第(2)题如图所示,一半径为R的圆竖直放置,是圆的一条直径,空间有与竖直平面平行的匀强电场,在圆周上A点有一发射器,以相同的初动能平行竖直平面沿不同方向发射带电量为,质量为m的小球,小球会经过圆周上不同的点,在这些点中过C点的小球动能最大,且A、C两点间的距离为,忽略小球间的相互作用,重力加速度为g,下列说法正确的是( )A.电场强度的最小值为B.电场强度的最小值为C.若电场强度取最小时,小球过C点的动能为D.若电场强度取最小时且规定A点电势为0,则C点的电势为第(3)题有研究发现中子衰变后可转化成质子和电子,同时放出质量可视为零的反中微子。
高二5月月考数学(理)试题Word版含答案

眉山中学届5月数学理科月考一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1、复数22i i -+的虚部为( ) A .45i - B .45i C .45- D .352、某小区有125户高收入家庭、280户中等收入家庭、95户低收入家庭。
现采用分层抽样的方法从中抽取100户,对这些家庭社会购买力的某项指标进行调查,则中等收入家庭中应抽选出的户数为( )A 、70户B 、17户C 、56户D 、25户3、下列求导运算错误..的是( ) A.()2424x x '+=+ B.()21log ln 2x x '= C. ()cos sin x x '=- D.211x x '⎛⎫=- ⎪⎝⎭4、A 、B 、C 、D 、E 共5人站成一排,如果A 、B 中间隔一人,那么排法种数共有( ) A . 60种 B .36种 C .48种 D .24种5、曲线1+=x e y 在点(0,2)处的切线与直线0y =和x y -=围成的三角形的面积为( )A .1B .12C .23D .136、在用数学归纳法证明)3,(121...111)(*≥∈<++++=n N n nn n n f 的过程中:假设当)3,(*≥∈=k N k k n 时,不等式1)(<k f 成立,则需证当1+=k n 时,1)1(<+k f 也成立.若)()()1(k g k f k f +=+,则=)(k g ( )A 、221121+++k k B 、k k k 1221121-+++ C 、k k 1221-+ D 、kk 21221-+ 7、 已知函数)(x f 的定义域[-1,5],部分对应值如表,)(x f 的导函数)('x f y =的图象如图所示,x -10 2 4 5 )(x f 1 4 1.5 41 5 -1 O2 4 x y下列关于函数)(x f 的命题:①函数)(x f 的值域为[1,4];②函数)(x f 在[0,2]上是减函数;③如果当],1[t x -∈时,)(x f 的最大值是4,那么t 的最大值为4;④当41<<a 时,函数a x f y -=)(最多有4个零点.其中正确的命题个数为 ( )A .0B .1C .2D .38、已知结论:“在正ABC ∆中,BC 中点为D ,若ABC ∆内一点G 到各边的距离都相等,则2=GDAG ”.若把该结论推广到空间,则有结论:在棱长都相等的四面体ABCD 中,若BCD ∆的中心为M ,四面体内部一点O 到四面体各面的距离都相等,则=OM AO ( ).A 1 .B 2 .C 3 .D 49、设复数),()1(R y x yi x z ∈+-=,若1||≤z ,则x y ≥的概率为( )A 、π2143+B 、π121+C 、π121-D 、π2141- 10、眉山市某高中的5名高三学生计划在高考结束后到北京、上海、杭州、广州等4个城市去旅游,要求每个城市都要有学生去,每个学生只去一个城市旅游,且学生甲不到北京,则不同的出行安排有( )A 、180B 、72C 、216D 、20411、已知定义域为R 的奇函数()x f y =的导函数为()x f y '=,当0≠x 时,()()0>+'x x f x f ,若()⎪⎭⎫ ⎝⎛-=--=⎪⎭⎫ ⎝⎛=21ln 2ln ,22,2121f c f b f a ,则c b a ,,的大小关系正确的是( ).A a c b << .B b c a << .C c b a << .D b a c << 12、设集合}6,5,4,3,2,1{=S ,定义集合对),(B A :S B S A ⊆⊆,,A 中含有3个元素,B 中至少含有2个元素,且B 中最小的元素不小于A 中最大的元素.记满足S B A =⋃的集合对),(B A 的总个数为m ,满足Φ≠⋂B A 的集合对),(B A 的总个数为n ,则n m 的值为 ( ) A 、111 B 、161 C 、221 D 292二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡相应位置.13、如表是某一单位1-4月份用水量(单位:百吨)的一组数据:月份x1 2 3 4 用水量y 4.5 4 3 2.5由散点图可知,用水量y 与月份x 之间有较强的线性相关关系,其线性回归直线方程是ˆˆ0.7yx a =-+,由此可预测该单位第5个月的用水量是 百吨. 14、如图,点A 的坐标为)0,1(,点C 的坐标为)4,2(,函数 2)(x x f =,若在矩形ABCD 内随机取一点,则此点取自阴影部分的 概率等于:15、在安排语文、数学、英语、物理、化学、生物6个学科的6堂考试时,若语文、数学两个学科均安排在生物学科之前,则不同的安排方法共有 种16、有下列命题:①复数z 满足112z z -++=则复数z 所对应点Z 的轨迹是一个椭圆;② 000000/)()(lim )()(lim )(0x x x f x f h x f h x f x f x x h --=-+=→→=hh x f x f h )()(lim 000--→; ③将5封信投入3个邮筒,不同的投法共有35种;④已知一组数据54321,,,,x x x x x 的平均数是2,方差是31,那么另一组数据231-x ,232-x ,233-x ,234-x ,235-x 的平均数和方差分别是4和3;⑤若0,0a b >>,()32422f x x ax bx =--+在1x =处有极值,则ab 的最大值为9其中正确的有:三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17、(本题满分10分) ⑴解方程:22131223x x x C A A +=+;(2)复数z 满足5z ,12z z i-=-求18、(本题满分12分)2017年4月眉山市中小学生田径运动会圆满落幕,市文体局举行表彰大会.某校有男运动员6名,女运动员4名,其中男女队长各1人,从中选5人参加表彰会,下列情形各有多少种选派方法(结果用数字作答).⑴男3名,女2名; ⑵队长至少有1人参加;⑶至少1名女运动员.19、(本题满分12分)已知函数1()(2)lnx 2(0)f x a ax a x=-++≤ (1)当0a =时,求()f x 的极值;(2)当a <0时,讨论()f x 的单调性.20、(本题满分12分)某中学举行一次“地理信息知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分为正整数,满分为100分)作为样本进行统计。
高一5月月考理科综合试题及答案

5月月考高一理科综合能力测试本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I卷注意事项:1. 答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2. 每小题选出答案后,用2B铅笔把答题卡上对应题没有的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效.........。
3. 第I卷共21小题,每小题6分,共126分。
一、选择题:本题共13小题,每小题6分.在每小题给出的四个选项中,只有一项是符合题目要求的。
7.在N2+3H2 2NH3的反应中,经过一段时间后,NH3的浓度增加了0.6 mol/L,在此时间内用NH3表示的反应速率为0.30 mol/(L·s)。
则此一段时间是( )。
A.1秒B.2秒C.0.44秒D.1.33秒8.已知可逆反应2SO2+O2 2SO3是放热反应,下列说法正确的是( )。
A.2 mol SO2与1 mol O2能完全反应生成2 mol SO3,升高温度可以加快此反应的化学反应速率B.2 mol SO2与1 mol O2不能完全反应生成2 mol SO3,升高温度可以加快此反应的化学反应速率C.2 mol SO2与1 mol O2能完全反应生成2 mol SO3,升高温度减慢此反应的化学反应速率D.2 mol SO2与1 mol O2不能完全反应生成2 mol SO3,升高温度减慢此反应的化学反应速率9.对于可逆反应M+N Q 达到平衡时,下列说法中,正确的是( )。
A.M、N、Q三种物质的浓度一定相等B.M、N全部变成了QC.反应混合物各成分的百分组成不再变化D.反应已经停止10.目前世界上最重要的气态化石燃料是( )。
A.水煤气B.一氧化碳C.天然气D.氢气11.下列关于甲烷分子结构的叙述中,正确的是( )。
A .甲烷分子中C 、H 原子间是离子键B .甲烷分子的空间结构是正方体C .甲烷的结构式为CH 4D .甲烷分子中4个碳氢键完全相同12.下列各组物质中,互称为同分异构体的是( )。
黑龙江省部分学校高三5月联考试题理综

2020届黑龙江省部分学校高三5月联考试题理综考生注意:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共300分。
考试时间150分钟。
2.请将各题答案填写在答题卡上。
3.可能用到的相对原子质量:H1 O16 Al27 Si28 S32 Fe56 Cu64 As75第I卷(选择题共126分)一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关实验材料的选择或处理的叙述,错误的是2.细胞通过分裂来增加数量,不同分裂方式的过程中细胞进行的生理活动有所不同。
下列与细胞分裂有关的叙述,错误的是C.同源染色体的联会和分离,只发生在减数分裂过程中3.我国科学家发现,当有稻瘟病菌入侵水稻时,在光照条件下,水稻体内的LHCB5蛋白第24位的苏氨酸就会发生磷酸化,加速向叶绿体中积累,经过一系列的变化,会诱发活性氧的产生。
在活性氧作用下,叶绿体内专门的抗稻瘟病基因表达后,水稻抗稻瘟病的能力会提高。
下列有关叙述错误的是A.阴雨连绵、光照不足的天气更易暴发稻瘟病B.抗稻瘟病基因经转录、翻译形成LHCB5蛋白4.某课题组为研究不同的植物生长调节剂对菠菜根系活力的影响,进行了相关实验,结果如图所示。
下列有关叙述错误的是A.植物生长调节剂具有容易合成、原料广泛、效果稳定等优点B.实验结果表明,不同植物生长调节剂对菠菜根系活力的影响有差异C.实验结果表明,植物生长调节剂对菠菜根系活力的作用具有两重性D.在实验期间,随处理时间延长,所有菠菜根系活力都表现为先增强后减弱的趋势5.人棘状毛囊角质化是一种伴X染色体显性遗传病,下列相关叙述错误的是6.蝗虫繁殖快,对农作物危害大。
我国实施“改治结合、根除蝗害”的战略,取得了良好的效果,即一方面通过化学防治和生物防治降低成年飞蝗密度,一方面改造飞蝗发生地,如修筑堤坝控制水位、耕垦湖滩荒地等。
下列有关叙述正确的是A.降低成年飞蝗密度、改造发生地都有利于降低种群出生率C.飞蝗迁移能力强,调查其幼虫的密度宜用标志重捕法D.控制蝗灾利于调整能量流动方向、提高能量传递效率7.新冠病毒(如图)由蛋白质和核酸组成,核酸由核苷酸组成,核苷酸的单体由五碳糖、磷酸基和含氮碱基构成。
2023年高三5月大联考(全国乙卷)理科数学试题及参考答案

2023届高三5月大联考(全国乙卷)理科数学试题及参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}022<--=x x x M ,{}012>+∈=x Z x N ,则=N M ()A .⎥⎦⎤ ⎝⎛-2321,B .⎥⎦⎤ ⎝⎛-121C .{}2,1,0D .{}1,02.在复平面内,设复数21,z z 对应的点分别为()()1,12021-Z Z ,,,则=21z z ()A .2B .3C .2D .13.映射由德国数学家戴德金在1887年提出,曾被称为“基础数学中最为美妙的灵魂”,在计算机科学、数学以及生活的方方面面都有重要的应用.例如,在新高考中,不同选考科目的原始分要利用赋分原则,映射到相应的赋分区间内,转换成对应的赋分后再计入总分.下面是某省选考科目的赋分规则:若小华选考政治的原始分为82,对应等级A,且等级A 的原始分期间为[81,87],则小华的政治成绩对应的赋分为()A .91B .92C .93D .94等级原始分占比赋分区间A 3%[91,100]B+7%[81,90]B 16%[71,80]C+24%[61,70]C 24%[51,60]D+16%[41,50]D 7%[31,40]E3%[21,30]4.已知不共线的平面向量b a ,满足a b 2=,()a b a⊥+,则平面向量b a ,的夹角为()A.6πB .3πC .2πD .32π5.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≥-≤--010201y x y x y x ,则y x z +=2的最大值为()A .1B .2C .3D .316.学校安排老师到小区对指定的学生进行家访.甲、乙两位老师被安排从A,B,C,D,E 五个小区中各选两个小区进行家访,且甲、乙两位老师选择的小区最多可以有一个相同.若甲必须去A 小区,则甲、乙两位老师不同的安排方法有()A .48种B .36种C .32种D .24种7.已知函数()x f 在[]2,2-上的图象如图所示,则()x f 的解析式可能是()A .()x e x f --=22B .()22--=x x x fC .()xex x f -=22D .()()122ln 2-+-=x x x f 8.某几何体的三视图如图所示,则该几何体各个面中,面积最大的面的面积为()A .28B .36C .64D .89.设等差数列{}n a 的前n 项和为n S ,84=a ,3612=S ,则满足n n a S >的正整数n 的最大值为()A .16B .15C .12D .810.已知椭圆C :()012222>>=+b a by a x 的左、右焦点分别为21,F F ,O 为坐标原点,点P在椭圆C 上且位于第一象限,直线PO 与椭圆C 的另一个交点为A ,直线2PF 与椭圆C 的另一个交点为B .若直线AB 平行于x 轴,且213PF PF =,则椭圆C 的离心率为()A .21B .22C .23D .4211.已知函数()()ϕω+=x x f cos 2()00<<->ϕπω,,()30=f ,且()x f 在[]π,0上有且只有三个极值点,则下列说法不正确的个数是()①存在ω值,使得函数()x f 在[]π,0上有两个极小值点;②ω的取值范围为⎦⎤⎝⎛619613,;③函数()x f 在⎪⎭⎫⎝⎛50π,上单调递增;④若Z ∈ω,则函数()x f 图象的一个对称中心为⎪⎭⎫⎝⎛092π.A .1B .2C .3D .412.已知正三棱锥ABC S -的底面ABC ∆的中心为O ,M 为棱SC 的中点,⊥OG 平面SAC ,且GM AG 2=.若MAB ∆的面积为6,则正三棱锥ABC S -外接球的表面积为()A .π12B .π64C .π26D .π8二、填空题:本题共4小题,每小题5分,共20分.13.曲线xxy ln =在1=x 处的切线方程为.14.若等比数列{}n a 的前n 项和为n S ,222341+==S a a ,,则等比数列{}n a 的公比为.15.在立德学校举办的春季运动会上,甲、乙两位教师进行某项比赛,采取七局四胜制(当一人赢得四局时就获胜,比赛结束).根据甲、乙两人多次比赛的成绩统计,每局甲获胜的概率为32,乙获胜的概率为31.设各局比赛结果相互独立,则乙在第一局负的情况下获胜的概率是.16.已知双曲线C :()0,012222>>=-b a b y a x 的焦距为c 2,过双曲线C 的左焦点F 作圆M :04222=+++b cx y x 的切线,切点为B ,该切线交双曲线C 的右支于点A ,若FB F A 4=,则双曲线C 的离心率为.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.(12分)在ABC ∆中,交C B A ,,所对的边分别为c b a ,,,且A c C a Cb cos cos 32cos 22+=.(1)若2π≠C ,求a b的值;(2)若32π=C ,ABC ∆的面积为23,求c 的值.18.(12分)如图,在正四棱柱1111D C B A ABCD -中,AB AA 21=,G F E ,,分别为棱BC DD AD ,,1的中点,M 为线段G D 1上一点.(1)求证:∥AM 平面CEF ;(2)当12MD GM =时,求二面角C EF M --的正弦值.19.(12分)已知抛物线C :()022>=p px y ,M 是其准线与x 轴的交点,过点M 的直线l 与抛物线C 交于B A ,两点,当点A 的坐标为()0,4y 时,有BA MB =.(1)求抛物线C 的方程;(2)设点A 关于x 轴的对称点为点P ,证明:直线BP 过定点,并求出该定点坐标.20.(12分)已知函数()0ln 12≠--=a x a x ex f ,.(1)求函数()x f 的单调区间;(2)当1=a 时,若关于x 的方程()m x f =(m 为实数)有两个不相等的实数根21,x x ,且21x x <,求证:()112+<-m e x x .21.(12分)某公司生产B A ,两种型号的盲盒,每一种型号的盲盒又12款形态各异的玩偶,买家拆封之前,不知道盲盒里玩偶的款式.(1)小明看中了A 型号盲盒,12款玩偶中有2款他特别喜欢,1款他不喜欢,另有3款他已经拥有.小明从中随机购买2款,若他购买到1宽他特别喜欢的玩偶,积3分;购买到1款他不喜欢的玩偶,积-3分;购买到1款他已经拥有的玩偶,积-1分;购买到1款其他款式的玩偶,积1分.记X 表示小明购买的2款玩偶的总积分,求X 的分布列和数学期望;(2)五一前,该公司推出D C ,两种新型号盲盒,现规定每一名爱好者一次只能购买其中一种型号的盲盒.据统计,爱好者第一次购买D C ,两种型号盲盒的概率都是21.如果上次购买C 型号盲盒,则这次购买C 型号盲盒的概率为32,购买D 型号盲盒的概率为31;如果上次购买D 型号盲盒,那么这次购买D C ,型号盲盒的概率都为21.如此重复,设一名爱好者第n 次购买C 型号盲盒的概率为n P .(1)求n P ;(2)如果这名爱好者长期购买D C ,型号盲盒,试判断该爱好者购买C 型号盲盒的概率能否达到53.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(10分)【选修4-4:坐标系与参数方程】在直角坐标系xOy 中,直线l 的参数方程为⎪⎩⎪⎨⎧+==ααsin 21cos t y t x (t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为⎪⎭⎫ ⎝⎛+=4sin 22πθρ.(1)写出曲线C 的直角坐标方程;(2)已知点P 的直角坐标为⎪⎭⎫ ⎝⎛210,,若直线l 与曲线C 交于N M ,两点,求PN PM -的最大值.23.(10分)【选修4-5:不等式选讲】已知c b a ,,都是正实数..(1)若1=ac ,求证:()()b c b b a 4≥++;(2)若1112121=++++cb a ,求c b a ++的最小值.参考答案一、选择题1.D解析:由已知得{}21<<-=x x M ,⎭⎬⎫⎩⎨⎧->∈=21x Z x N ,∴=N M {}1,0.2.C解析:由题意,知i z 21=,i z -=12,∴i i i z z +-=-=11221,∴221=z z .3.C解析:根据赋分公式得9110081828287--=--T T,解得935.92≈=T .4.D 解析:设向量b a ,的夹角为θ,∵()a b a ⊥+,∴()0=⋅+a b a ,即2a b a -=⋅,∴2cos a b a -=⋅θ ,∴212cos 22-=⋅-=⋅-=a a a b a aθ.∵[]πθ,0∈,∴向量b a ,的夹角为32π.5.B 解析:作出不等式组⎪⎩⎪⎨⎧≤-+≥-≤--010201y x y x y x 所表示的平面区域如图中阴影部分所示.由y x z +=2得z x y +-=2.作出直线x y 2-=,然后平移该直线,当直线经过点()01,A 时,z 取得最大值,即2012max =+⨯=z .6.B解析:(1)若甲、乙两位老师选择的家访小区完全不同,则有2314C C 种安排方法.(2)若甲、乙两位老师选择的家访小区有一个相同:①若甲、乙两位老师选择了A 小区,则有24A 种安排方法;②若甲、乙两位老师选择的相同小区不是A 小区,则有1314C C 种安排方法.综上,甲、乙两位老师不同的安排方法有361314242314=++C C A C C 种.7.C解析:由题图知函数()x f 的图象关于y 轴对称,∴函数是偶函数,故排除A;对于B,()⎪⎩⎪⎨⎧<-+≥--=0,20,222x x x x x x x f ,虽然函数()x f 为偶函数且在⎪⎭⎫⎝⎛210,上单调递减,在⎪⎭⎫ ⎝⎛221上单调递增,但()02=f ,与图象不吻合,排除B;对于D,∵()()()x f x x x f -=-+-=122ln 2,∴函数()x f 是偶函数,但()012ln 2<-=f ,与图象不吻合,排除D;对于C,函数()x f 为偶函数,图象关于y 轴对称,下面只分析y 轴右侧部分.当()+∞∈,0x 时,()xe x xf -=22,()xe x xf -='4,令()xe x x -=4ϕ,求导得()xe x -='4ϕ.当()4ln ,0∈x 时,()0>'x ϕ,()x f '单调递增,当()2,4ln ∈x 时,()0<'x ϕ,()x f '单调递减,∴()x f '在4ln =x 处取得最大值.又∵()00<'f ,()04ln >'f ,()02>'f ,∴()4ln ,00∈∃x ,使得()00='x f ,当()0,0x x ∈时,()0<'x f ,()x f 为减函数,当()2,0x x ∈时,()0>'x f ,()x f 为增函数,与图象吻合,故选C.8.A解析:如图,在棱长为4的正方体中,C 为棱的中点,三棱锥BCD A -即为该几何体.其中ABD ∆为直角三角形,BD AB BD AB ⊥==,,424,∴其面积为2824421=⨯⨯;BCD ∆为等腰三角形,4==BD CD BC ,,点C 到边BD 的距离为4,∴其面积为84421=⨯⨯;ABC ∆为等腰三角形,2452===AB AC BC ,,∴点C 到边AB 的距离为32,∴其面积为64243221=⨯⨯;ACD ∆为等腰三角形,3452===AD CD AC ,,∴点C 到边AD 的距离为22,∴其面积为64243221=⨯⨯;综上,该几何体各个面中面积最大的面为ABD ∆,其面积为28.9.B解析:设等差数列{}n a 的公差为d ,则⎩⎨⎧=+=+3666128311d a d a ,解得⎩⎨⎧-==2141d a ,∴n n S n a n n 152162+-=-=,.由n n a S >得n n n 216152->+-,即016172<+-n n ,解得161<<n ,∴正整数n 的最大值为15.10.B 解析:由椭圆的对称性,知点A 与点P 关于原点对称.∵直线AB 平行于x 轴,∴点B 与点A 关于y 轴对称,∴点P 与点B 关于x 轴对称,即2PF ⊥x 轴,∴a b PF 22=.又213PF PF =,∴a b PF 213=.又a PF PF 221=+,∴a b a b a 2232+=,即2122=a b ,∴椭圆C 的离心率22122=-==ab ac e .11.C 解析:∵()30=f ,∴23cos =ϕ.∵0<<-ϕπ,∴6πϕ-=.当[]π,0∈x 时,⎥⎦⎤⎢⎣⎡--∈-6,66πωπππωx ,∵()x f 在[]π,0上有且只有三个极值点,∴ππωππ362<-≤得619613<≤ω,∴根据图象可以判断,()x f 在[]π,0上有两个极大值点,一个极小值点,∴①错误,②错误;当⎪⎭⎫ ⎝⎛∈5,0πx 时,6566ππωπωππ-<-≤-,显然065>-ππω,不符合题意∴③错误;由Z ∈ω得3=ω,∴()⎪⎭⎫ ⎝⎛-=63cos 2πx x f ,令Z k k x ∈+=-,263πππ,得Z k k x ∈+=,923ππ,当0=k 时,92π=x ,∴④正确.故选C.12.A 解析:如图,连接SG 并延长交AC 于点D ,连接BD ∵GM AG 2=,∴M G A ,,三点共线,且GM AG 2=.又∵AM 为SAC ∆的中线,∴G 为SAC ∆的重心,∴D 为AC 的中点,且GD SG 2=.又O 为正三角形ABC 的中心,∴B O D ,,三点共线,且OD BO 2=,∴BS OG ∥,且BS OG 31=,∵⊥OG 平面SAC ,∴⊥SB 平面SAC ,∴SA BS SC BS ⊥⊥,.又∵三棱锥ABC S -为正三棱锥,∴SA SC ⊥.设a SA 2=,则a MB MA a AB 522===,.在MAB ∆中,512cos 222=⋅⋅-+=∠MB MA AB MB MA AMB ,∴562sin =∠AMB ,∴265625521sin 21a a a AMB MB MA S MAB =⋅⋅⋅=∠⋅⋅⋅=∆,即662=a ,解得1=a .由SB SA SB SC SA SC ⊥⊥⊥,,,且2===SC SB SA ,知正三棱锥ABC S -的外接球即是棱长为2的正方体的外接球,棱长为2的正方体的体对角线长32即为外接球的直径,∴正三棱锥ABC S -的外接球的半径3=R ,表面积为ππ1242=R .二、填空题13.01=--y x 解析:2ln 1xxy -=',当1=x 时,1='y .又当1=x 时,0=y ,∴曲线xxy ln =在1=x 处的切线方程为1-=x y ,即01=--y x .14.3解析:设等比数列{}n a 的公比为q ,由2234+=S a 得()22211131+++=qa q a a q a .又21=a,∴032223=---q q q ,即0323223=--+-q q q q ,∴()()0132=++-q q q ,解得3=q .15.72973解析:由题意,乙在第一局负的情况下获胜,则乙还需要胜四局比赛.若再比赛四局乙获胜,则概率为811314=⎪⎭⎫⎝⎛,若再比赛五局乙获胜,则概率为24383132414=⎪⎭⎫ ⎝⎛⨯⨯C ,若再比赛六局乙获胜,则概率为7294031324225=⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯C .综上,一在第一局负的情况下获胜的概率是72973729402438811=++.16.5解析:圆M :04222=+++b cx y x 可化为42222a y c x =+⎪⎭⎫ ⎝⎛+,∴圆心为⎪⎭⎫⎝⎛-0,2c M ,半径2a r =.连接BM ,则AF BM ⊥.设双曲线C 的离心率为e ,右焦点为F ',连接F A '.∵c F F c FM 22='=,,∴41='F F FM .又FB F A 4=,∴41=F AFB ,∴F AFBF F FM =',∴A F MB '∥,∴a MB A F 24==',︒='∠90AF F ,即AF F A ⊥'.根据双曲线的定义,得a a A F F A 42=+'=.在F AF Rt '∆中,由勾股定理得222F F A F F A'='+,∴()()()222224c a a =+,即225c a =,∴5222==e ac ,∴双曲线C 的离心率为5.三、解答题(一)必考题:共60分17.解:(1)由A c C a Cb cos cos 32cos22+=得()A c C a C b cos cos 3cos 1+=+.由正弦定理得:()A C C A C B cos sin cos sin 3cos 1sin +=+,∴()C A C A C B B ++=+sin cos sin 2cos sin sin ,∵()B C A sin sin =+,∴C A C B cos sin 2cos sin =.∵2π≠C ,∴0cos ≠C ,∴A B sin 2sin =,∴a b 2=,∴2=ab.(2)由(1)知a b 2=.∵32π=C ,ABC ∆的面积为23,∴232332sin 212==a ab π,解得12=a ,即1=a ,∴22==a b .由余弦定理得724132cos2222=++=-+=πab b a c ,∴7=c .18.解:(1)如图,连接AG AD ,1,∵F E ,分别为棱1DD AD ,的中点,∴EF AD ∥1.∵⊄1AD 平面CEF ,⊂EF 平面CEF ,∴1AD ∥平面CEF ,∵BC AD ∥,且BC AD =,G E ,分别为棱BC AD ,的中点,∴CG AE ∥且CG AE =,∴四边形AECG 为平行四边形,∴CE AG ∥.∵⊄AG 平面CEF ,⊂CE 平面CEF ,∴AG ∥平面CEF .又∵A AG AD = 1,⊂AG AD ,1平面G AD 1,∴平面G AD 1∥平面CEF .∵⊂AM 平面G AD 1,∴∥AM 平面CEF .(2)如图,以1,,DD DC F A 所在的直线分别为z y x ,,轴建立如图所示的空间直角坐标系.设()c b a M DA ,,2,=,则()()()020021001,,,,,,,,C G E ,()()4002001,,,,,D F .∵12MD GM =,∴132GD GM =,即()()4,2,132,2,1--=--c b a ,解得383231===c b a ,,,∴⎪⎭⎫ ⎝⎛38,32,31M ,∴()()⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛-=-=-=32323138,32,32220021,,,,,,,,,FM EM FC EC .设平面MEF 的法向量为()1111,,z y x n =,则⎪⎩⎪⎨⎧=⋅=⋅0011n FM n EM ,∴⎪⎪⎩⎪⎪⎨⎧=++=++-03232310383232111111z y x z y x ,令11=z ,则2211-==y x ,,∴平面MEF 的一个法向量为()1,2,21-=n.设平面CEF 的法向量为()2222,,z y x n =,在⎪⎩⎪⎨⎧=⋅=⋅0022n FC n EC ,∴⎩⎨⎧=-=+-022022222z y y x ,令12=y ,则1222==z x ,,∴平面CEF 的一个法向量为()1,1,22=n.∴66633,cos 212121==⋅=n n n n n n.设二面角C EF M --的平面角为θ,∴630661,cos1sin 2212=⎪⎪⎭⎫ ⎝⎛-=-=n nθ,即二面角C EF M --的正弦值为630.19.解:(1)设()B B y x B ,,由BA MB =得B 诶线段MA 的中点.∵⎪⎭⎫ ⎝⎛-0,2p M ,∴⎪⎩⎪⎨⎧=-=02242y y p x B B ,∴⎪⎪⎩⎪⎪⎨⎧=-=2420y y p x B B ,即⎪⎭⎫ ⎝⎛-2,420y p B ,把⎪⎭⎫ ⎝⎛-2,420y p B 代入px y 22=中,得⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛422220p p y ,把()0,4y A 代入px y 22=中,得p y 820=,∴p p p 2422=⎪⎭⎫⎝⎛-.又0>p ,∴4=p ,∴抛物线C 的方程为x y 82=.(2)由题意,知直线l 的斜率存在且不为0,∵()02,-M ,∴可设直线l 的方程为2-=my x .设()()2211,,y x B y x A ,,则点()11,y x P -.由⎩⎨⎧=-=xy my x 822消去x 得01682=+-my y ,∴0>∆,根据根与系数的关系得1682121==+y y m y y ,.直线BP 的斜率12212212121288y y y y y y x x y y k -=-+=-+=,直线BP 的方程为()21228x x y y y y --=-,∴()()()221222122122128181********y y y y y y y x y y y y y y x ++--=+---=()28112+-=y y y ,即直线BP 的方程可表示为()28112+-=y y y x .∴直线BP 过定点,且定点坐标为()02,.20.解:(1)()exaex x a e x f -=-='22.①当0<a 时,()0>'x f 恒成立,∴()x f 在()∞+,0上单调递增;②当0>a 时,令()0>'x f ,解得2ae x >,令()0<'x f ,解得20aex <<,∴()x f 在⎪⎭⎫ ⎝⎛20ae ,上单调递减,在⎪⎭⎫⎝⎛+∞,2ae 上单调递增.综上所述,当0<a 时,()x f 的单调递增区间为()∞+,0,无单调递减区间;当0>a 时,()x f 的单调递减区间为⎪⎭⎫ ⎝⎛20ae ,,单调递增区间为⎪⎭⎫⎝⎛+∞,2ae .(2)当1=a 时,()x x ex f ln 12--=,由(1)可知()x f 的单调递减区间为⎪⎭⎫ ⎝⎛20ae ,,单调递增区间为⎪⎭⎫⎝⎛+∞,2ae .∵方程()m x f =有两个不相等的实数根21,x x ,且21x x <,因此2120x ex <<<.由于2x 时()m x f =的实数根,∴m x x e=--22ln 12,整理得()2221ln x m e x e x -+=-.令()x e x x h ln -=,且2ex >,则()x e x x e x h -=-='1,令()0>'x h ,解得e x >,令()0<'x h ,解得e x e<<2,∴()x h 在⎪⎭⎫⎝⎛e e ,2上单调递减,在()∞+,e 上单调递增,∴()()0ln =-=≥e e e e h x h ,即0ln 22≥-x e x ,∴()012≥-+x m e ,而01>x ,因此()0112>+-+x x m e ,即()112+<-m e x x .21.解:(1)由题意知X 的所有可能取值为-4,-2,0,2,4,6,且()221663421213===-=C C X P ;()22366922122316==+=-=C C C X P ;()331066200212121613==+==C C C C X P ;()22766212212261213==+==C C C C X P ;()112661242121612====C C C X P ;()661621222===C C X P ,∴X 的分布列为:∴()()()16616112422723310022322214=⨯+⨯+⨯+⨯+⨯-+⨯-=X E .(2)①记一名爱好者第1+n 次购买C 型号盲盒的概率为1+n P ,则()n n n P P P -+=+121321,即21611+=+n n P P ,∴⎪⎭⎫ ⎝⎛-=-+5361531n n P P .∵211=P ,∴⎭⎬⎫⎩⎨⎧-+531n P 是以101531-=-P 为首项,61为公比的等比数列,∴16110153-⎪⎭⎫⎝⎛⋅-=-n n P ,即53611011+⎪⎭⎫⎝⎛⋅-=-n n P .②∵5353611011<+⎪⎭⎫⎝⎛⋅-=-n n P ,∴这名爱好者购买C 型号盲盒的概率不能达到53.(二)选考题22.解:(1)∵⎪⎭⎫ ⎝⎛+=4sin 22πθρ,∴θθρcos 2sin 2+=,即θρθρρcos 2sin 22+=.X -4-2246P2212233310227112661又θρcos =x ,θρsin =y ,222ρ=+y x ,∴曲线C 的直角坐标方程为02222=--+y x y x .(2)依题意,将直线l 的参数方程代入曲线C 的直角坐标方程得:()043cos 2sin 2=-+-t t αα.设点N M ,所对应的参数分别为21,t t ,则43cos 2sin 2121-=+=+t t t t ,αα.∵点P 的直角坐标为⎪⎭⎫ ⎝⎛210,,∴1t PM =,2t PN =.∵021<t t ,∴2121t t t t PN PM +=-=-()ϕααα+=+=sin 5cos 2sin ,其中552sin 55cos ==ϕϕ,.由()03cos 2sin 2>++=∆αα,得R ∈α,∴当()1sin ±=+ϕα时,PN PM -最大,且最大值为5.23.解:(1)∵c b a ,,都是正实数,∴02>≥+ab b a ,02>≥+bc c b ,∴()()bc ab c b b a 22⋅≥++,当且仅当1===c b a 时,等号成立,即()()ac b c b b a 4≥++.又∵1=ac ,∴()()b c b b a 4≥++.(2)∵1112121=++++c b a ,∴12212422=++++cb a .由柯西不等式,得()()[]()22122212142221242++≥⎪⎭⎫⎝⎛++++++++c b a c b a ,即()22215222+≥+++c b a ,即222+≥++c b a ,当且仅当()c b a 21222=+=+,即222222+===c b a ,,时等号成立,∴c b a ++的最小值为222+.。
2019-2020学年下学期高三5月月考测试卷理科综合能力测试

2019-2020学年下学期高三5月月考测试卷理科综合能力测试注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.考试结束后,请将本试题卷和答题卡一并上交。
相对原子质量:H 1 C 12 N14 O16 Cl35.5 Fe 56Mn55 Ba137第Ⅰ卷(选择题,共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在生物教材当中出现了很多有关小泡的叙述,下面说法错误的是A.内质网膜会形成小泡,把附在其上的核糖体中合成的蛋白质包裹起来,随后小泡离开内质网向高尔基体移动并最后与之融合B.在动物、真菌和某些植物的细胞中,含有一些由高尔基体断裂形成的,由单位膜包被的小泡,称为溶酶体C.在植物有丝分裂的前期,核膜开始解体,形成分散的小泡,到了有丝分裂的末期,这些小泡会聚集成一个细胞板,进而形成新的细胞壁D.刚分裂形成的植物细胞中只有很少几个分散的小液泡,随着细胞的长大,这些小液泡就逐渐合并发展成一个大液泡2.如图所示,某种化合物与细胞膜表面受体识别并结合后,受体便通过G蛋白调控并打开离子通道,离子的跨膜流动导致膜电位的改变。
下列相关叙述错误的是A.细胞外Na+内流是产生静息电位的基础B.该过程体现了细胞膜具有信息交流的功能C.构成细胞膜的基本支架是磷脂双分子层D.Na+通过协助扩散的方式进入细胞内3.菊花的重瓣是一种突变性状,研究表明有三个突变基因可能与重瓣性状有关。
相对于野生基因,突变基因Ⅰ增添了1个碱基对,突变基因Ⅱ替换了1个碱基对,突变基因Ⅲ缺失了1个碱基对。
下列叙述不正确的是A.野生基因与突变基因可位于一对同源染色体的两条染色体上B.野生基因与突变基因可位于一条染色体的两条姐妹染色单体上C.野生基因突变形成三个突变基因说明基因突变具有普遍性D.突变基因Ⅱ控制合成相应蛋白质中的氨基酸数可能改变多个4.人体感染新型冠状病毒(SARS-CoV-2)之初一般会引起发热、乏力、干咳等症状。
5月份月考高三化学理科综合试卷(含答案)

批扯州址走市抄坝学校5月份月考理科综合试卷〔化学〕相对原子质量:H-1 C-12 N-14 O-16 Na-23 S-32 Ca-40 Fe-56 Cu-64 Ba-137第I卷一、选择题〔此题共7小题。
在每题给出的四个选项中,只有一个选项符合题目要求〕6.以下表达正确的选项是A.汽油、柴油和植物油都是碳氢化合物B.乙醇可以被氧化为乙酸,二者都能发生酯化反C.甲烷、乙烯和苯在工业上都可通过分馏得到D.棉、麻、丝、毛及合成纤维完全燃烧都只生成CO2和H2O7.假设NA代表阿伏加德罗常数,以下说法正确的选项是A.4LCO2中含有的原子数为0.3NAB.状况下,2.24L Cl2与足量的Mg充分反,转移的电子数目为0.2NAC.18g重水〔2H2O〕含有10N A个电子D.1 L 0.5mol·L-1 Na2CO3溶液中含有的CO32-数目为0.5N A8.在以下溶液中,一.能够大量共存的离子组是A.pH为1的溶液:Ca2+、Na+、Mg2+、NO3-B.滴加石蕊试液显的溶液:Fe3+、NH4+、C1-、SCN-C.常温下,由水电离出的c(H+)=l0-14mo1·L-1的溶液中:CO32-、SO42-、Na+、K+D.与铝反放出氢气的溶液:Fe2+、SO42-、NO3-、Na+9.有M、R两种主族元素,M2-离子与R+离子核外电子数之和为20,那么以下说法不正确的选项是.......A.M与R的质子数之和一于19B.M、R可能分别处于第二周期和第三周期C.M、R可能分别处于第三周期和第二周期D.M与R的质子数之差可能于710.将物质的量的X、Y气体充入一个密闭容器中,在一条件下发生如下反并达平衡:X(g)+Y(g) 2Z(g);△H<0。
当改变某个条件并到达平衡后,以下表达不.正确的选项是......A.升高温度,X的体积分数增大B.保持容器体积不变,充入一量的惰性气体,Y的浓度不变C.增大压强〔缩小容器体积〕,Z的浓度不变D.保持容器体积不变,充入一量的Z,X的转化率减小11.生物燃料电池〔BFC〕是以有机物为燃料,直接或间接利用酶作为催化剂的一类特殊的燃料电池,其能量转化效率高,是一种真正意义上的绿色电池,其工作原理如下图。
高三5月月考数学(理)试题+Word版含答案
高三五月月考试卷 数 学(理)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{|10},{1,0,1}A x x B =+>=-,则AB =A.{1}B.{1}-C. {0,1}D. {1,0}- 2.若复数,其中为虚数单位,则下列结论正确的是A. 的虚部为B.C. 的共轭复数为D. 为纯虚数3.已知m ,n 为两条不重合直线,α,β为两个不重合平面,下列条件中,一定能推出//αβ 的是A.//,,m n m n αβ⊂⊂B. //,,m n m n αβ⊥⊥C. ,//,//m n m n αβ⊥D. ,,m n m n αβ⊥⊥⊥4.空气质量指数AQI 是反映空气状况的指数, AQI 指数值越小, 表明空气质量越好, 其对应关系如下表:下图是某市10月1日 - 20日AQI 指数变化趋势,下列叙述错误的是A.这20天中AQI 指数值的中位数略高于100B.这20天中的中度污染及以上的天数占1/4C.该市10月的前半个月的空气质量越来越好D.总体来说,该市10月上旬的空气质量比中旬的空气质量好5.已知向量a , b 满足||2,||2a b ==,且(2)a a b ⊥+, 则b 在a 方向上的投影为A .1B .CD .1-6.若某空间几何体的三视图如图所示,则该几何体的表面积是A.48+πB.48-πC.48+2πD.48-2π7.十九世纪末,法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?” 贝特朗用“随机半径”、 “随机端点”、 “随机中点”三个合理的求解方法,但结果都不相同. 该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化. 已知“随机端点”的方法如下:设A 为圆O 上一个定点,在圆周上随机取一点B ,连接AB ,所得弦长AB 大于圆O 的内接等边三角形边长的概率. 则由“随机端点”求法所求得的概率为A.14 B.13 C.128.已知ξ服从正态分布2(1,),N a σ∈R ,则“()0.5P a ξ>=”是“关于x 的二项式321()ax x + 的展开式的常数项为3”的 A. 充分不必要条件 B. 必要不充分条件 C. 既不充分又不必要条件 D. 充要条件9.函数的大致图象为A. B.C. D.10.已知双曲线22221(0,0)x y a b a b-=>>的左右两个焦点分别为12,,,F F A B 为其左、右两个顶点,以线段12F F 为直径的圆与双曲线的渐近线在第一象限的交点为M ,且30AMB ∠=︒,则该双曲线的离心率为C.D. 11.已知ABC △的边AB ,AC 的长分别为2,3,120BAC ∠=︒,则ABC △的角平分线AD 的长为A.3B.5C.6D.5 12.已知函数1ln ,1,()11,1,22x x f x x x +≥⎧⎪=⎨+<⎪⎩ 若12x x ≠,且12()()2f x f x +=,则12x x +的取值范围是 A.[2,)+∞ B. [1,)e -+∞ C. [32ln 2,)-+∞ D. [32ln3,)-+∞ 二、填空题:本题共4小题,每小题5分,共20分。
武汉市五月模拟数学理科试卷及答案

武汉市五月模拟数学理科试卷及答案一、选择题(每题5分,共40分)1. 若函数 f(x) = x² - 2x + 1 在区间(-∞,a]上的值域为[-1,+∞),则实数a的取值范围是()A. [-1, +∞)B. (-∞, 1]C. [1, +∞)D. (-∞, 2]2. 设集合 A = {x | x² - 3x + 2 = 0},B = {x | x - 2 < 0},则A∩B = ()A. {1}B. {2}C. {1, 2}D. ∅3. 函数 y = x² - 4x + 3 的图像与x轴的交点坐标为()A. (1, 0) 和 (3, 0)B. (2, 0) 和 (2, 0)C. (1, 0) 和 (-3, 0)D. (3, 0) 和 (-1, 0)4. 若等差数列 {an} 的前n项和为 Sn,且满足 Sn =2an - 1,则首项 a1 = ()A. 1B. 2C. 3D. 45. 若等比数列 {an} 的公比为q,且 a1 + a2 = 5,a1 a2 = 4,则 q = ()A. 2B. -2C. 1D. -16. 已知函数 y = f(x) 在 x = 2 处的导数为 3,则函数y = f(x) + 2 在 x = 2 处的导数为()A. 3B. 4C. 5D. 67. 若函数 f(x) = x² - 2x + 1 在区间[1, +∞) 上单调递增,则实数 a 的取值范围是()A. [1, +∞)B. (1, +∞)C. (-∞, 1]D. (-∞, 1)8. 若函数 y = f(x) 的图像关于直线 x = 1 对称,则函数 y = f(x + 1) 的图像关于()A. 直线 x = 0 对称B. 直线 x = 1 对称C. 直线 x = 2 对称D. 直线 x = -1 对称二、填空题(每题5分,共30分)9. 若函数 y = f(x) 的图像经过点 (2, 3),且 f(x) = x² + bx + c,则 b + c = _______。
高三数学5月联考试题 理 试题

毛坦厂中学2021届高三数学5月联考试题理考生注意:1.本套试卷分第一卷(选择题)和第二卷(非选择题)两局部,一共150分.考试时间是是120分钟.2.请将各题答案填在试卷后面的答题卡上.3.本套试卷主要考试内容:高考全部内容.第一卷一、选择题:此题一共12小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.1.设集合A={x|x2<5},B={x|1<x<4},那么A∪B=A.{x|1<x<5}B.{x|-<x<4}C.{x|1<x<}D.{x|-5<x<4}2.假设复数z=,那么励志赠言经典语录精选句;挥动**,放飞梦想。
厚积薄发,一鸣惊人。
关于努力学习的语录。
自古以来就有许多文人留下如头悬梁锥刺股的经典的,而近代又有哪些经典的高中励志赠言出现呢?小编筛选了高中励志赠言句经典语录,看看是否有些帮助吧。
好男儿踌躇满志,你将如愿;真巾帼灿烂扬眉,我要成功。
含泪播种的人一定能含笑收获。
贵在坚持、难在坚持、成在坚持。
功崇惟志,业广为勤。
耕耘今天,收获明天。
成功,要靠辛勤与汗水,也要靠技巧与方法。
常说口里顺,常做手不笨。
不要自卑,你不比别人笨。
不要自满,别人不比你笨。
高三某班,青春无限,超越梦想,勇于争先。
敢闯敢拼,**协力,争创佳绩。
丰富学校体育内涵,共建时代校园文化。
奋勇冲击,永争第一。
奋斗冲刺,誓要蟾宫折桂;全心拼搏,定能金榜题名。
放心去飞,勇敢去追,追一切我们为完成的梦。
翻手为云,覆手为雨。
二人同心,其利断金。
短暂辛苦,终身幸福。
东隅已逝,桑榆非晚。
登高山,以知天之高;临深溪,以明地之厚。
大智若愚,大巧若拙。
聪明出于勤奋,天才在于积累。
把握机遇,心想事成。
奥运精神,永驻我心。
“想”要壮志凌云,“干”要脚踏实地。
**燃烧希望,励志赢来成功。
楚汉名城,喜迎城运盛会,三湘四水,欢聚体坛精英。
乘风破浪会有时,直挂云帆济沧海。
五月理综试题

五月理综试题可能用到的相对原子质量 H--1 C--12 N--14 O--16 Fe--56 Na--23 Si--28 P-- 31 S--32 Cl--35.5 Cu—64 lg2 = 0.3--------------------------------------第I卷(选择题,共132分)每小题只有一个答案符合题意,每小题6分,共132分1、用放射性同位素标记的某种氨基酸培养胰腺细胞,最后测出细胞分泌带有放射性的胰岛素。
假如用仪器测试放射性在细胞中显现的顺序,那个顺序最可能是()①线粒体②核糖体③中心体④染色体⑤高尔基体⑥细胞膜⑦细胞核A.①③④⑦⑥ B.⑥②⑤⑥ C.②③⑦④⑤ D.⑥②⑦④⑤2、如图所示为物质代谢过程中光合作用与呼吸作用两者间的关系,请问供给绿色植物各种生命活动所需能量最多的过程和各种生物体都能进行的过程分别是哪些部分()A.1和5 B.5和3 C.2和3 D.3和53、下列关于细胞分裂的说法,不正确的是()A.精原细胞一定不进行有丝分裂 B.蛙的红细胞进行无丝分裂C.某些生物能够通过有丝分裂繁育后代 D.在极核形成过程中要通过减数分裂4、紫茉莉是一种花斑植物,这种植物同时生有绿色、白色和花斑二种枝条,用这三种枝条上的花作为母本,分别授以白色、绿色、花斑枝条上的花粉,结果白色枝条上的任何杂交种子都长成白色,绿色枝条上的任何杂交种子都长成绿色,而花斑枝条上的杂交种子有的长成绿苗,有的长成白苗,有的长成花斑,下列说明正确的是()A.此现象属于无性生殖 B.此现象不属于遗传物质的操纵C.此现象符合自由组合规律 D.此现象是由细胞质基因所操纵的遗传5、假设右图所示食物网中水稻固定的太阳能为N,能量传递效率为10%,则人类获得的能量( )A .等于10-1N B.等于10-2NC .少于10-1 ND .多于10-1N6、已知下列氧化剂均能氧化+4价的硫(元素),为了除去稀硫酸中的少量亚硫酸,宜选用的氧化剂是( )A 、KMnO 4B 、Cl 2C 、H 2O 2 D 、Na 2O 27、某一种固体X 与浓H 2SO 4共热能生成一种酸性气体;把氨水加入X 溶液中,能生成白色沉淀,连续加氨水,沉淀消逝。
高三数学5月测试试题 理 试题

卜人入州八九几市潮王学校黄梅国际育才高级2021届高三数学5月测试试题理 考生注意:1.考试时量为120分钟,总分值是为150分。
2.在答题之前,答题卡上面本卷须知。
3.所有题目答案均写在答题卡上。
1.i R y x ,,∈是虚数单位,假设yi x +与i i ++13互为一共轭复数,那么=+y x A.O2.集合A={0352|2≤--x xx },B={2|≤∈x Z x },那么B A 中的元素个数为A.2B.3C.43.,由此得到以下说法,其中表达正确的选项是A.近1年以来,我国HY 储藏月增长量最大的月份是2021B.2021年4月至10月,我国HY 储藏连续下降C.2021年底,我国HY 储藏降至近年来最低D.截止2021年3月末,我国HY 储藏连续第五个月上升 4.双曲线C:12222=-b y a x (a>b>0)的离心率45=e ,且其右焦点F2(5,0),那么双曲线 的C 方程为 A.13422=-y x B.191622=-y x C.116922=-y x D.14322=-y x 5.)'(,cos 41)(2x f x x x f +=为)(x f 的导函数,那么)'(x f 的图象是 6.函数)42sin(2)(π+=x x f 向右平移)>0(ϕϕ个单位后,得到x y 2cos =的图象,那么ϕ的最小值为A.87πB.85πC.83πD.8π 7.某三棱锥的三视图如图,那么该三棱锥的四个面中,面积最大的面的面积是B.23C.32D.78.等差数列{n a }的第8项是二项式4)1(y xx ++展开式的常数项,那么=-11931a a A.32 B . 2C. 4D. 6 9.抛物线:0)>(22p py x =的焦点为F ,准线为l ,点P(4,0y 〕在抛物线上,K 为l 与y 轴的交点,且||2||PF PK =,那么0y 的取值为B.2C.32D.2 10.甲、乙、丙3人进展擂台赛,每局2人进展单打比赛,另1人当裁判,每一局的输方当下一局的裁判,由原来裁判向胜者挑战,比赛完毕以后,经统计,甲一共打了5局,乙一共打了6局,而丙一共当了2局裁判,那么整个比赛一共进展了A.13局B. 11局 C . 9局 D. 8局11.数列{n a }中,0>),2,(2||,12111a n N n a a a n n n ≥*∈=--=--,假设数列{12-n a }单调递减,数列{n a 2}单调递增,那么=2019aA.3122019-B.3122019+C.3122019+-D.3122019+- P(a,b)能且只能向函数t tx x x f ()(3-=为给定的正常数〕的图象作两条切线,那么22)1(-+=b a z 的最小值为A.211t +B.211t +C.21t +D.21t +二、填空题〔本小题一共4题,每一小题5分,一共20分。
高三下学期五月月考数学(理)试题及答案

密学校 班级姓名 学号密 封 线 内 不 得 答 题高三下学期五月月考 数学(理)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24小题,共150分,考试时间120分钟。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内;2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米的黑色字迹的签字笔书写,字体工整、笔迹清楚;3.请按照题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效;4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑;5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A = {0 , 1} ,则满足条件 A B = {2 , 0 , 1 , 3}的集合 B 共有( )A .1 个B .2 个C .3 个D .4 个2.已知复数i m z 21+=,i z 432-=若21z z为实数,则实数m 的值为( )A .38B .23C .38- D .23- 3.如图所示程序框图,其输出结果是111,则判断框中所填的条件是( )A .5≥nB .6≥nC .7≥nD .8≥n 4.已知 x ∈ R ,则 x ≥ 1是| x +1| + | x -1|= 2 | x | 的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分也非必要条件5.设数列{}n a 为等差数列,其前n 项和为n S ,已知14725899,93a a a a a a ++=++=,若对任意*n N ∈都有k n S S ≤成立,则k 的值为( ) A .22 B .21 C .20 D .196.已知点1)0,0)(,(22=+>>y x C b a b a M :是圆内任意一点,点),(y x P 是圆上任意一点,则实数1-+by ax ( )A.一定是负数B.一定等于0C.一定是正数D.可能为正数也可能为负数 7.已知圆O 的半径为2,A 、B 是圆上两点,32π=∠AOB ,MN 是圆O 的一条直径,点C 在圆内且满足()()101<<-+=λλλOB OA OC ,则⋅的最小值为()A .-2 B.-1C .-3D .-48.已知0>ω,函数)4sin()(πω+=x x f 在区间[ππ,2]上单调递减,则实数ω的取值范围是( ) A. [ 210219.现需编制一个八位的序号,规定如下:序号由4个数字和2个x 、1个y 、1个z 组成;2个x 不能连续出现,且y 在z 的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( ) A .12600 B .6300 C .5040 D .252010.已知方程sin xk x=在(0,)+∞有两个不同的解,αβ(αβ<),则下面结论正确的是: A .1tan()41πααα++=- B .1tan()41πααα-+=+ C .1tan()41πβββ++=- D .1tan()41πβββ-+=+ 11.在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,12.已知函数)1(+=x f y 的图象关于点)0,1(-对称,且当)0,(-∞∈x 时,0)()(<'+x f x x f 成立(其中)(x f '是)(x f 的导函数),若0.30.33311(3)(3),(log 3)(log 3),(log )(log )99a fb fc f ππ=⋅=⋅=⋅,则a ,b ,c 的大小关系为( )A . a > c >bB .c>a>bC .c> b > aD . b >a> c第Ⅱ卷二、填空题:本大题共4个小题,每小题5分。
青海省2022届高三五月大联考理科数学试题(高频考点版)

一、单选题二、多选题三、填空题四、解答题1. 命题“是第一象限角”的否定是( )A .是第一象限角B.不是第一象限角C.是第一象限角D.不是第一象限角2. 已知分别是双曲线的左、右焦点,P 是该双曲线上的点,且,则( )A .3B .15C .3或15D .6或123. 设,则的大小关系( )A.B.C.D.4. 第19届亚运会将于2023年9月23日至10月8日在杭州举行,甲、乙等4名杭州亚运会志愿者到游泳、射击、体操三个场地进行志愿服务,每名志愿者只去一个场地,每个场地至少一名志愿者,若甲不去游泳场地,则不同的安排方法共有( )A .12种B .18种C .24种D .36种5. 已知条件,条件的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件6. 在△ABC 中,角A 、角C 、角C 所对的边为a 、b 、c ,若,则△ABC 是( )A .等边三角形B .等腰直角三角形C .有一个内角是30°的直角三角形D .有一个内角是30°的等腰三角形7.若,则以下结论正确的是( )A.B.C.D.8. 已知点F 为椭圆C:,的左焦点,过原点O 的直线l 交椭圆于P ,Q 两点,点M 是椭圆上异于P ,Q 的一点,直线MP ,MQ 的斜率分别为,,椭圆的离心率为e ,若,,则( )A.B.C.D.9. i 是虚数单位,纯虚数z满足,则实数m 的值为________.10. 已知,则___________.11.若函数在区间上为增函数,则实数的取值范围是_______.12.如果随机变量,且,,则等于___________.青海省2022届高三五月大联考理科数学试题(高频考点版)青海省2022届高三五月大联考理科数学试题(高频考点版)13. 已知等差数列的前项和为,且.(1)求的通项公式;(2)试求出所有的正整数,使得对任意正整数,均有.14. 2022年北京冬奥会防寒服中的“神奇内芯”—仿鹅绒高保暖絮片,是国家运动员教练员比赛服装的保暖材料.该“内芯”具有超轻超薄、湿态保暖、高蓬松度等特点,其研发是国家重点研发计划“科技冬奥”重点专项之一,填补了国内空白.为了保证其质量,厂方技术员从生产的一批保暖絮片中随机抽取了100处,分别测量了其纤维长度(单位:)的均值,并制成如下频率分布直方图:(1)估计该批保暖絮片纤维长度的平均数和样本方差(同一组数据用该区间的中点值作代表);(2)该批保暖絮片进入成品库之前需进行二次检验,从中随机抽取15处测量其纤维长度均值,数据如下:31.8,32.7,28.2,34.3,29.1,34.8,37.2,30.8,30.6,25.2,32.9,28.9,33.9,29.5,34.5.请问该批保暖絮片是否合格?(若二次抽检纤维长度均值满足,则认为保暖絮片合格,否则认为不合格).15. 已知,数列的前n项和为,点在曲线上()且,.(1)求数列的通项公式;(2)数列的前n项和为,且满足,确定的值使得数列是等差数列.16. 已知的一个顶点,且,的角平分线所在直线的方程依次是,,求的三边所在直线的方程.。
2023届河南省郑州市重点校高三下学期5月联考理科综合试题

2023届河南省郑州市重点校高三下学期5月联考理科综合试题一、单选题 (共6题)第(1)题一定质量的理想气体,从状态a经bcd又回到状态a,其循环过程的p-V图像如图所示。
已知气体在状态a的温度为T0。
则下列说法正确的是( )A.气体在状态c的温度为6T0B.气体由a到b和由c到d的两个过程中,对外做的功相等C.气体完成1次循环过程,一定从外界吸收热量D.气体由a到b的过程中,吸收的热量小于内能的增加量第(2)题如图(a)所示,四旋翼无人机下方通过悬杆连接一质量为m的相机。
取竖直向上为正方向,某段时间内该无人机沿竖直方向运动的位移x随时间t变化的图线如图(b)所示,该图线为抛物线的一部分,时对应图线的顶点。
已知重力加速度为g,下列说法正确的是( )A.内,相机处于超重状态;内,相机处于失重状态B.内,相机处于失重状态;内,相机处于超重状态C.时,悬杆对相机的拉力大小为D.时,悬杆对相机的拉力小于第(3)题如图,使甲、乙两条形磁铁隔开一段距离,静止于水平桌面上,甲的N极正对着乙的S极,甲的质量大于乙的质量,两者与桌面之间的动摩擦因数相等。
现同时释放甲和乙,在它们相互接近过程中的任一时刻( )A.甲的加速度大小比乙的大B.甲和乙的动量之和为零C.甲、乙的速度大小相等D.甲的动量大小比乙的小第(4)题历经7年水下考古调查勘探,长江口二号古船于2022年11月21日露出水面,时隔150多年重见天日。
科学家团队对古船中稻壳进行了碳十四测年,验证出了长江口二号古船的“年龄”。
已知植物存活期间,因其新陈代谢等生命活动,其体内14C的含量不变,生命活动结束后,14C能自发进行β衰变成为14N,14C的比例持续减少,下列说法正确的是( )A.14C发生一次β衰变,它的中子数减少一个,质子数增加一个B.14C衰变为14N的过程中,电荷数守恒,质量也守恒C.14C核的比结合能大于14N核的比结合能D.2g14C经过两个半衰期就会全部发生衰变第(5)题如图所示,有一固定的闭合导体圆环L,一条形磁铁垂直于圆环所在的平面,且其中心在圆环圆心处。
2023届河南省郑州市重点校高三下学期5月联考理科综合试题
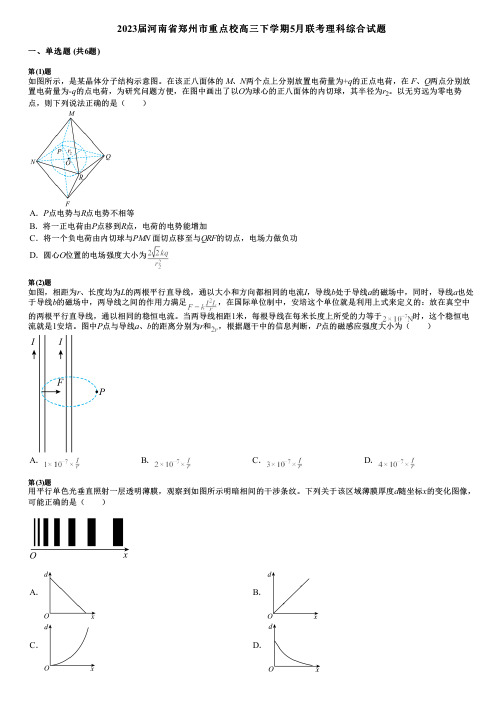
2023届河南省郑州市重点校高三下学期5月联考理科综合试题一、单选题 (共6题)第(1)题如图所示,是某晶体分子结构示意图。
在该正八面体的M、N两个点上分别放置电荷量为+q的正点电荷,在 F、Q两点分别放置电荷量为-q的点电荷,为研究问题方便,在图中画出了以O为球心的正八面体的内切球,其半径为r2。
以无穷远为零电势点,则下列说法正确的是( )A.P点电势与R点电势不相等B.将一正电荷由P点移到R点,电荷的电势能增加C.将一个负电荷由内切球与PMN 面切点移至与QRF的切点,电场力做负功D.圆心O位置的电场强度大小为第(2)题如图,相距为r、长度均为L的两根平行直导线,通以大小和方向都相同的电流I,导线b处于导线a的磁场中,同时,导线a也处于导线b的磁场中,两导线之间的作用力满足,在国际单位制中,安培这个单位就是利用上式来定义的:放在真空中的两根平行直导线,通以相同的稳恒电流。
当两导线相距1米,每根导线在每米长度上所受的力等于时,这个稳恒电流就是1安培。
图中P点与导线a、b的距离分别为r和,根据题干中的信息判断,P点的磁感应强度大小为( )A.B.C.D.第(3)题用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹。
下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( )A.B.C.D.第(4)题如图所示,将可视为质点的小球置于空心管的正上方处,空心管长度一定,小球与管的轴线重合。
将小球先由静止释放,间隔一小段时间后再将管由静止释放(此时小球还没有进入管内),假设空间足够大,空心管不会碰到地面,不计空气阻力,则下列判断正确的是()A.越大,小球穿过管的时间越长B.无论为多少,小球穿过管的时间保持不变C.一定时,越小,小球穿出管时管子的速度越大D.一定时,越小,小球穿过管的时间越短第(5)题汽车紧急刹车后,停止运动的车轮在水平地面上滑动直至停止,在地面上留下的痕迹称为刹车线。
由刹车线的长短可知汽车刹车前的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三五月诊断考试 数学(理科)试卷
第I 卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题
目要求的.
1、已知集合{}
0,2|>==x y y M x
,{}
2
|lg(2)N x y x x ==-,则N M 为( )
A .(1,2)
B . ),1(+∞
C . ),2[+∞
D . ),1[+∞
2.已知角α2的顶点在原点, 始边与x 轴非负半轴重合, 终边过⎪⎪
⎭
⎫
⎝⎛-
23,21, )[πα2,02∈ 则=αtan ( )
A. 3-
B. 3
C.
33
D. 3
3±
3.已知等差数列{}n a 的前n 项和为n S ,且
4
24S S =,则64
S S =( ) A .94 B .32 C .5
3
D .4
4.若直线x y 2=上存在点(x,y)满足约束条件30230x y x y x m +-≤⎧⎪
--≤⎨⎪≥⎩则实数m 的最大值为( )
A.-1 B.1 C.2
3
D.2
5. 命题p :,R x ∈∃使得x x
>3;命题q :若函数)1(-=x f y 为偶函数,则函数)(x f y = 关
于直线1=x 对称,则( )
A. q p ∨真
B. q p ∧真
C. p ⌝真
D. q ⌝假
6.多面体MN-ABCD 的底面ABCD 为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视
图为等腰梯形,侧(左)视图为等腰三角形,则AM 的长等于( )
(A
(B
(C
(D
)
7. 在棱长都相等的正三棱柱111C B A ABC -中,点D 是侧面C C BB 11的中心,则AD 与平面
C C BB 11所成角的大小为( )
A.
60 B.
45 C.
30 D.
90
8.对于任意给定的实数m ,直线03=+-m y x 与双曲线
0(12
2
22>=-a b y a x ,)0>b 最多有一个交点,则双曲线的离心率等于( )
A .2
B .2
C .3
D .10
9.程序框图如图所示,该程序运行后输出的S 的值是 ( )
A .2
B .12-
C .3-
D .13
10.计划在4个不同的体育馆举办排球、篮球、足球3个项目的比赛,每个项目的比赛只能安排在一个体育馆进行,则在同一个体育馆比赛的项目不超过2个的安排方案共有( ) (A )60种 (B )42种 (C )36种 (D )24种
11.已知抛物线x y 42
=;直线l 过点M(-1,0)与抛物线交于A,B 两点;点C 和点B 关于x 轴对称。
则直线AC 必过点( )
A.(-2,0)
B.(0,0)
C.(2,0)
D.(1,0) 12.函数3
2,(0,1)x y a
a a +=->≠的图像恒过定点 A ,若点 A 在直线
1,x y
m n
+=-上且m,n>0则 3m+n 的最小值为 ( )
A .13
B .16
C .11+
D .28
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分.
13.已知 {}n a 为等比数列,若4617373910,2a a a a a a a a +=++则的值为
14. 51
(21)(1)x x
+-的展开式的常数项是__________.(填写具体数字)
15. 若a=3
1
3
12,2log =b , c=21
)31(-
,则a,b,c 按由小到大的顺序排列为: (用“<”
连接起来)
16. 已知三个向量a 、b 、c ,其中每两个之间的夹角为120°,若|a
|=3,|b |=2,
|c |=1,则a 用b 、c
表示为
三、解答题:解答应写出文字说明.证明过程或演算步骤
17.( 12分) 已知,A B 是ABC ∆的两个内角,向量,sin )22
A B A B
a +-= ,且
||a = (1)证明:tan tan A B 为定值;
(2)若,26
A A
B π
=
=,求边BC 上的高AD 的长度。
18.(12分)某品牌电视专卖店,在“五一”期间设计一项有奖促销活动:每购买一台电视,
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,产生20组随机数组,每组3个数,试验结果如下所示:
235,145,124,754,353,296,065,379,118,247, 520,356,218,954,245,368,035,111,357,265.
(1)在以上模拟的20组数中,随机抽取3组数,至少有一组获奖的概率;
(2)根据上述模拟试验的结果,将频率视为概率,若本次活动平均每台电视的奖金不超过260
元,求m 的最大值。
19 .(本小题12分)在如图所示的几何体中, 四边 形ABCD 为平行四边形,∠ ACB=90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC, AB=2EF
(Ⅰ)若M是线段AD的中点,
求证:GM∥平面ABFE; (Ⅱ)若AC=BC=2AE,
求二面角A---BF---C的大小.
20.(12分) 已知椭圆C :22x a +22y b =1(a >b >0)的一个焦点在直线:l 1=x 上,离心率为2
1。
设P,Q 为椭圆上不同的两点,且弦PQ 的中点T 在直线:l 1=x 上,点R (
4
1
,0). (1) 求椭圆的方程; (2) 试证:对于所有满足条件的P,Q,恒有RQ RP =; (3) 试判断PQR ∆能否为等边三角形?证明你的结论 21. (本小题满分12分)已知函数f (x )=x ln x (x ∈(0,+∞)). (Ⅰ)求(+1)
()+1
f x
g x x x =
-(x ∈(-1,+∞))的单调区间与极大值; (Ⅱ)任取两个不等的正数x 1、x 2,且x 1<x 2,若存在x 0>0使21021
()()
()f x f x f x x x -'=
-成立,
求证:x 1<x 0<x 2;
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分,做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题满分10分)选修4-1:几何证明选讲. 如图,PA 是圆O 的切线,PE 过圆心O , AC 为圆O 的
直径,PC 与圆O 相交于B 、C 两点,连结AB 、CD .
(1) 求证:PAD CDE ∠=∠; (2) 求证:2PA BD
PC PE AD
=
⋅. 23.(本小题满分10分)选修4-4:坐标系与参数方程选讲.
在极坐标系内,已知曲线1C 的方程为22(cos 2sin )40ρρθθ--+=,以极点为原点,极轴方向为x 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线2C 的参数方程为
5145183x t
y t
=-⎧⎨
=+⎩(t 为参数).(1) 求曲线1C 的直角坐标方程以及曲线2C 的普通方程; (2) 设点P 为曲线2C 上的动点,过点P 作曲线1C 的两条切线,求这两条切线所成角余弦值的取值范围.
24. (本小题满分10分)选修4-5:不等式选讲
已知函数)|2||12(|log )(2m x x x f -+++=. (1)当4=m 时,求函数)(x f 的定义域;
(2)若关于x 的不等式1)(≥x f 的解集是R ,求m 的取值范围。
