反比例函数面积专题
反比例函数求面积公式大全

反比例函数求面积公式大全《反比例函数求面积公式大全》引言:反比例函数是数学中的一种特殊函数,其特点是当自变量x增加时,因变量y会以相反的趋势减小。
在数学和实际应用中,使用反比例函数可以描述许多重要的关系,尤其是与面积相关的问题。
本文将为读者提供一份反比例函数求面积的公式大全,帮助读者更好地理解和应用反比例函数。
一、长方形1. 长方形的面积与其长度(l)和宽度(w)成反比例关系,即S = k/(l×w),其中k为常数。
二、正方形1. 正方形的面积与其边长(s)的平方成反比例关系,即S = k/s²,其中k为常数。
三、圆1. 圆的面积与其半径(r)的平方成反比例关系,即S = πr²,其中π为圆周率,约等于3.14159。
四、椭圆1. 椭圆的面积与其长轴(2a)和短轴(2b)的乘积成反比例关系,即S = πab,其中a和b分别为长轴和短轴的半长。
五、三角形1. 三角形的面积与其底(b)和高(h)的乘积成反比例关系,即S = (1/2)bh。
六、平行四边形1. 平行四边形的面积与其底(b)和高(h)的乘积成反比例关系,即S = bh。
七、等腰梯形1. 等腰梯形的面积与其上底(a)、下底(b)和高(h)的关系为S = (a + b)h/2。
八、圆环1. 圆环的面积与其外半径(R)、内半径(r)和π的关系为S = π(R² - r²)。
结论:通过反比例函数求面积的公式大全,读者可以更加方便地计算各种几何形状的面积。
这些公式对于数学学习、几何推导以及实际生活中的建模和计算都具有重要意义。
希望读者能够掌握这些公式,并在实际中运用自如,提高数学应用的能力和解决问题的水平。
反比例函数中的面积问题(共26张PPT)

课后精练
解:(1)如图,过点 D 作 DH⊥x 轴于点 H, ∵直线 AB 的解析式为 y=-2x+4,∴B 点坐标为(0,4), A 点坐标为(2,0). ∵∠OAB+∠DAH=90°,∠ADH+∠DAH=90°, ∴∠BAO=∠ADH. 又∵∠BOA=∠AHD,∴△AOB∽△DHA. ∴ADOH=ABOH=AADB=12.∴D2H=A4H=12,解得 DH=4,AH=8. ∴D(10,4),则 k=10×4=40. 故答案为:40.
③若 M 点的横坐标为 1,△OAM 为等边三角形,则 k=2+ 3;
7.如图,函数 y=kx(k 为常数,k>0)的图象与过原点的 O 的直线 相交于 A,B 两点,点 M 是第一象限内双曲线上的动点(点 M 在点 A 的左侧),直线 AM 分别交 x 轴,y 轴于 C,D 两点,连接 BM 分别 交 x 轴,y 轴于点 E,F.现有以下四个结论:
课后精练
∵D(10,4),∴D′(10,-4). 设直线 CD′的解析式为 y=ax+d, 则180a+a+dd==8- ,4,解得da==-566. , 故直线 CD′的解析式为 y=-6x+56. 当 y=0 时,x=238,故 P 点坐标为238,0. 延长 CD 交 x 轴于 Q,此时|QC-QD|的值最大, ∵CD∥AB,D(10,4),∴直线 CD 的解析式为 y=-2x+24. ∴Q(12,0).∴PQ=12-238=83. 故 P 点坐标为238,0,Q 点坐标为(12,0),线段 PQ 的长为83.
专题2 反比例函数中的面积问题
考点解读
反比例函数中的面积类问题是最能体现数形结合思想 方法的一类问题,几何中的函数问题使图形性质代数 化,函数中的几何问题使代数知识图形化,利用“数”
反比例函数背景下的应用题(面积问题)

反比例函数背景下的应用题(面积问题)
反比例函数背景下与面积相关的问题往往围绕着以下三个结论展开:①反比例函数上任意一点与坐标轴围成的矩形面积;②反比例函数上任意一点与坐标轴围成的三角形面积;③反比例函数上任意两点与原点围成的三角形面积.
解法分析:对于平面直角坐标系中三角形面积的求法问题有如下的解法策略:①当三角形的一边在坐标轴上或平行于坐标轴上时,可以直接求三角形面积;②当三角形中的任意一边不在坐标轴或不平行于坐标轴时,利用割补法(补成/分割成规则图形)面积进行求解。
本题中的△ABC的一边AC//x轴,则可以直接求解,需要注意的是当用点表示线段长度时,要加上绝对值。
解法分析:本题可以直接求三角形的面积,△MPQ的底PQ是可求的定值,而高是点M和点P横坐标差的绝对值,要注意M点可能在第二象限,也可能在第四象限,加上绝对值后就可以避免漏解了。
解法分析:本题首先需要联立正比例函数和反比例函数的解析式求出A、B两点的坐标,然后过A、B两点作x轴垂线构造梯形,求梯形面积即可。
解法分析:本题可以用代数法或几何法解决。
综合利用直角三角形的性质,三角形的面积比解决。
同时还要能够利用点的坐标表示线段的长度,灵活运用。
解法分析:本题主要考察了反比例函数上的点与坐标轴围成的矩形面积。
对于第2、3问,需要分类讨论,即P在B左侧或P在B右侧,进行计算。
解法分析:本题是反比例函数和正方形背景下的问题。
△BCE的面积可以直接求解,主要表示出E的坐标,再求出B'E的长度,即可求出△BCE的面积。
反比例函数面积问题专题

反比例函数面积问题专题反比例函数面积问题是数学中的一个重要问题,也是中学数学中常见的题型之一、这种问题涉及到两个变量的关系,其中一个变量的值与另一个变量的值成反比例关系。
在解决这类问题时,需要通过分析问题的条件和利用数学公式,找出两个变量之间的关系,并求解出所要求的面积。
首先,让我们来梳理一下反比例函数的基本概念。
反比例函数也被称为倒数函数或者比例函数的倒数。
当两个变量的乘积为常数时,我们就可以称它们之间存在反比例关系。
即当一个变量的值增大时,另一个变量的值就会减小,反之亦然。
反比例函数可以用以下的公式来表示:y=k/x其中,y和x分别代表两个变量的值,k为常数,表示两个变量的乘积。
通过这个公式,我们可以求出y与x的关系,也可以表示成x与y的关系。
反比例函数在数学学科中有着广泛的应用,并且有很多技巧可以帮助我们解决相关的问题。
接下来,让我们来讨论解决反比例函数面积问题的思路。
对于这类问题,我们通常需要求解一个围成面积的最大或者最小值。
我们可以按照以下的步骤来解决这类问题:1.确定问题的条件:首先,我们需要明确给定的条件,包括一些已知的数值和问题的限定条件。
2.建立模型并画图:根据给定条件,我们可以建立一个函数模型来描述两个变量的关系,同时我们还可以画出一个图形,以便更好地理解问题。
3.确定所要求的值:根据问题的要求,我们需要确定所要求的面积,是最大的还是最小的。
4.利用数学方法求解:根据问题的要求和模型函数,我们可以通过求导、解方程等数学方法,求得所要求的面积的最大或最小值。
最后,让我们来看几个实际的例子,以更好地理解反比例函数面积问题。
例子1:一个矩形的长和宽成反比例关系,如果矩形的周长为60,求矩形的最大面积。
解决思路:首先根据周长的公式可以得到l + w = 30,然后利用面积公式S = lw,将w表示成l的函数,即w = 30 - l。
将这个表达式代入面积公式中,得到S = l(30 - l) = 30l - l^2、这是一个二次函数,即S = -l^2 + 30l。
反比例函数面积问题专题

反比例函数面积问题专题【围矩形】1.如图所示,点P是反比例函数图象上一点,过点P分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是()A. B.C..D.2.反比例函数的图象如图所示,则k的值可能是()A. -1B.C. 1D. 23.如图,A、B是双曲线上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为()A. 1B. 2C. 3D. 44.如图,在反比例函数y=(x>0)的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则S1+S2+S3=()A. 1B. 1.5C. 2D. 无法确定5.如图,两个反比例函数y=和y=(其中k1>0>k2)在第一象限内的图象是C1,第二、四象限内的图象是C2,设点P在C1上,PC⊥x轴于点M,交C2于点C,PA⊥y轴于点N,交C2于点A,AB∥PC,CB∥AP相交于点B,则四边形ODBE的面积为()A. |k1﹣k2|B.C. |k1•k2|D.6.如图,A、C是函数y=的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则()A. S1>S2B. S1<S2C. S1=S2D. 关系不能确定7.如图,过y轴上任意一点p,作x轴的平行线,与反比例函数的图象交于A点,若B为x轴上任意一点,连接AB,PB则△APB的面积为()A. 1 B. 2 C. 3 D. 48.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为()A. 1 B. 2 C. -1 D. -29.反比例函数y=与y=在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为()A. B. 2 C. 3 D. 110.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=﹣和y=的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为() A. 3 B . 4 C . 5 D . 1011.双曲线y1=与y2=在第一象限内的图象如图.作一条平行于x轴的直线交y1,y2于B、A,连OA,过B作BC∥OA,交x轴于C,若四边形OABC的面积为3,则k=()A. 2B. 4 C .3 D . 512.如图,直线l和双曲线交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则()A. S1<S2<S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S313.如图是反比例函数和在第一象限内的图象,在上取点M分别作两坐标轴的垂线交于点A、B,连接OA、OB,则图中阴影部分的面积为.14.如图,直线y=kx(k>0)与双曲线y=交于A,B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=.其中正确结论的个数为()个 A. 1 B . 2 C . 3 D . 415.如图,直y=mx与双曲线y=交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是()A. 1 B. m﹣1 C. 2 D. m16.正比例函数y=x与反比例函数y=的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D,如图,则四边形ABCD的面积为()A. 1B.C. 2D.17.如图,A,C是函数y=(k≠0)的图象上关于原点对称的任意两点,AB,CD垂直于x轴,垂足分别为B,D,那么四边形ABCD的面积S是()A. B. 2k C. 4k D. k18.如图,反比例函数y=﹣的图象与直线y=﹣x的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为()A. 8B. 6C. 4D. 2【三角形叠梯形】19.如图,点A和B是反比例函数y=(x>0)图象上任意两点,过A,B分别作y轴的垂线,垂足为C和D,连接AB,AO,BO,△ABO的面积为8,则梯形CABD的面积为()A. 6B. 7C. 8D. 1020.如图,△ABO的顶点A和AB边的中点C都在双曲线y=(x>0)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k=()A. 2 B. 3 C. 4 D.21.如图,A、B是双曲线上任意两点,过A、B两点分别作y轴的垂线,垂足分别为C、D,连接AB,直线OB、OA分别交双曲线于点E、F,设梯形ABCD的面积和△EOF的面积分别为S1、S2,则S1与S2的大小关系是()A. S1=S2 B. S1>S2 C. S1<S2 D. 不能确定【截矩形】22.如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=(x>0)的图象于点A、B,则四边形BOAP的面积为()A. 3 B. 3.5 C. 4 D. 523.如图,双曲线y=(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则k=.24.函数y=和y=在第一象限内的图象如图,点P是y=的图象上一动点,PC⊥x轴于点C,交y=的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=AP.其中所有正确结论的序号是()A. ①②③B. ②③④C. ①③④D. ①②④25.两个反比例函数和(k1>k2>0)在第一象限内的图象如图,P在C1上,作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1﹣k2③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中正确的是()【截直角三角形】26.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为()A. 20B. 18C. 16D. 1227.如图,双曲线经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.则△AOC的面积为()A. 9 B. 6 C. 4.5 D. 328.如图,已知矩形ABCO的一边OC在x轴上,一边OA在y轴上,双曲线交OB的中点于D,交BC边于E,若△OBC的面积等于4,则CE:BE的值为()A. 1:2 B . 1:3 C. 1:4 D. 无法确定29.如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值()A. 2B.C.D. 无法确定30.如图,反比例函数的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为()A. 1B. 2C. 3D. 4反比例函数【围矩形】1.解:由题意得:矩形面积等于|k|,∴|k|=4又∵反比例函数图象在二、四象限.∴k<0∴k=﹣4∴反比例函数的解析式是y=﹣.故选C.2.解:∵反比例函数在第一象限,∴k>0,∵当图象上的点的横坐标为1时,纵坐标小于1,∴k<1,故选B.3.解:∵S1+S2=4,∴S1=S2═2,∵S3=1,∴S1+S3=1+2=3,∴k=3故选C.4.解:由题意可知点P1、P2、P3、P4坐标分别为:(1,2),(2,1),(3,),(4,).∴由反比例函数的几何意义可知:S1+S2+S3=2﹣1×==1.5.故选B.5.解:∵AB∥PC,CB∥AP,∠APC=90°,∴四边形APCB是矩形.设P(x,),则A(,),C(x,),∴S矩形APCB=AP•PC=(x﹣)(﹣)=,∴四边形ODBE的面积=S矩形APCB ﹣S矩形PNOM﹣S矩形MCDP﹣S矩形AEON=﹣k1﹣|k2|﹣|k2|=.故选D.【围三角形】6.解:结合题意可得:A、C都在双曲线y=上,反比例函数系数k的几何意义有S1=S2;故选C.7.解:依题意得:△APB的面积S=|k|=×|4|=2.故选B8.解:如图,连OA,∵AB⊥x轴,∴AB∥OP,∴S△OAB=S△PAB=1,∴|k|=2×1=2,∵反比例函数图象过第二象限,∴k=﹣2.故选D.9.解:分别过A、B作x轴的垂线,垂足分别为D、E,过B作BC⊥y轴,点C为垂足,∵由反比例函数系数k的几何意义可知,S四边形OEAC=6,S△AOE=3,S△BOC=,∴S△AOB=S四边形OEAC﹣S△AOE﹣S△BOC=6﹣3﹣=.故选A.10.解:设P(a,0),a>0,则A和B的横坐标都为a,将x=a代入反比例函数y=﹣中得:y=﹣,故A(a,﹣);将x=a代入反比例函数y=中得:y=,故B(a,),∴AB=AP+BP=+=,则S△ABC=AB•x P的横坐标=××a=5.故选C11.解:由题意得:S四边形OABC=|k1|﹣|k2|=|6|﹣|k|=3;又由于反比例函数位于第一象限,k>0;k=3.故选C.12.解:结合题意可得:AB都在双曲线y=上,则有S1=S2;而AB之间,直线在双曲线上方;故S1=S2<S3故选D.13.解:∵在上取点M分别作两坐标轴的垂线交于点A、B,∴S△AOC=×5=2.5,S△BOD=×5=2.5 S矩形MDOC=3∴S阴影=S△AOC+S△BOD﹣S矩形MDOC=5﹣3=2故答案为2.【对称点】14.解:①反比例函数与正比例函数若有交点,一定是两个,且关于原点对称,所以正确;②根据A、B关于原点对称,S△ABC为即A点横纵坐标的乘积,为定值1,所以正确;③因为AO=BO,OD∥BC,所以OD为△ABC的中位线,即D是AC中点,所以正确;④在△ADO中,因为AD和y轴并不垂直,所以面积不等于k的一半,不等于,错误.故选C.15.解:由图象上的点A、B、M构成的三角形由△AMO和△BMO的组成,点A与点B关于原点中心对称,∴点A,B的纵横坐标的绝对值相等,∴△AMO和△BMO的面积相等,且为,∴点A的横纵坐标的乘积绝对值为1,又因为点A在第一象限内,所以可知反比例函数的系数k为1.故选A.16.解:根据反比例函数的对称性可知:OB=OD,AB=CD,∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2.故选C.17.解:∵A,C是函数y=(k≠0)的图象上关于原点对称的任意两点,∴若假设A点坐标为(x,y),则C点坐标为(﹣x,﹣y).∴BD=2x,AB=CD=y,∴S=S△ABD+S△CBD=BD•AB+BD•CD=2xy=2k.故四边形ABCD的面积S是2k.故选B.四边形ABCD18.解:由于点A、B在反比例函数图象上关于原点对称,则△ABC的面积=2|k|=2×4=8.故选A.【三角形叠梯形】19.解:过点B向x轴作垂线,垂足是G.由题意得:矩形BDOG的面积是|k|=3,∴S△ACO=S△BOG=.所+S梯形ABDC﹣S△ACO﹣S△BOG=8,以△AOB的面积=S矩形BDOG则梯形CABD的面积=8﹣3+3=8.故选C20.解:过点A作AM⊥OB于M,设点A坐标为(x,y),∵顶点A在双曲线y=(x>0)图象上,∴xy=k,∴S△AMO=OM•AM=xy=k,设B的坐标为(a,0),∵中点C在双曲线y=(x>0)图象上,CD⊥OB于D,∴点C坐标为(,),∴S△CDO=OD•CD=••=k,∴ay=3k,∵S△AOB=S△AOM+S△AMB =k+•(a﹣x)y =k+ay﹣xy=k+×3k﹣k =k,又∵C为AB中点,∴△AOC的面积为×k=3,∴k=4,故选C.21.解:∵直线OB、OA分别交双曲线于点E、F,∴S2=S△AOB,∵S1=S△AOC+S△AOB﹣S△BOD,而S△AOC=S△BOD=k,∴S1=S△AOB,∴S1=S2.故选A.【截矩形】22.解:∵B、A两点在反比例函数y=(x>0)的图象上,∴S△DBO=S△AOC=×2=1,∵P(2,3),∴四边形DPCO的面积为2×3=6,∴四边形BOAP的面积为6﹣1﹣1=4,故选:C.23.解:连接OE,设此反比例函数的解析式为y=(k≠0),C(c,0),则B(c,b),E(c,),设D(x,y),∵D和E都在反比例函数图象上,∴xy=k,=k,即S△AOD=S△OEC=×c×,∵梯形ODBC的面积为3,∴bc﹣×c×=3,∴bc=3,∴bc=4,∴S△AOD=S△OEC=1,∵k>0,∴k=1,解得k=2,故答案为:2.24.解:∵A、B是反比函数y=上的点,∴S△OBD=S△OAC=,故①正确;当P的横纵坐标相等时PA=PB,故②错误;=4,∵P是y=的图象上一动点,∴S矩形PDOC=S矩形PDOC﹣S△ODB﹣﹣S△OAC=4﹣﹣=3,故③正确;∴S四边形PAOB连接OP,===4,∴AC=PC,PA=PC,∴=3,∴AC=AP;故④正确;综上所述,正确的结论有①③④.故选C.25.解:①∵A、B两点都在y=上,∴△ODB与△OCA的面积都都等于,故①正确;②S矩形OCPB﹣S△AOC﹣S△DBO=|k2|﹣2×|k1|÷2=k2﹣k1,故②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选B.【截直角三角形】26.解:∵点A的坐标为(﹣8,6),O点坐标为(0,0),∴斜边OA的中点D的坐标为(﹣4,3),把D(﹣4,3)代入y=得k=﹣4×3=﹣12,∴反比例函数的解析式为y=﹣,∵AB⊥x轴,∴C点和横坐标为点A相同,都为﹣8,把x=﹣8代入y=﹣得y=,∴C点坐标为(﹣8,),∴AC=6﹣=,∴△AOC的面积=AC•OB=××8=18.故选B.27.解:∵OA的中点是D,双曲线y=﹣经过点D,∴k=xy=﹣3,D点坐标为:(x,y),则A点坐标为:(2x,2y),∴△BOC的面积=|k|=3.又∵△AOB的面积=×2x×2y=12,∴△AOC的面积=△AOB的面积﹣△BOC的面积=12﹣3=9.故选:A.28.解:设D点的坐标是(x,y).∵点D是线段OB的中点,∴B点的坐标是(2x,2y);∵△OBC的面积等于4,∴×2x×2y=4,即xy=﹣2,∴k=﹣2;又∵点E在双曲线上,∴点E的坐标为(2x,);∴CE:BE=:(2y﹣)=:(2×﹣)=1:3;故选B.29.解:方法1:设B点坐标为(a,b),∵OD:DB=1:2,∴D点坐标为(a,b),根据反比例函数的几何意义,∴a•b=k,∴ab=9k①,∵BC∥AO,AB⊥AO,C在反比例函数y=的图象上,∴设C点横坐标为m,则C点坐标为(m,b)将(m,b)代入y=得,m=,BC=a﹣,又因为△OBC的高为AB,所以S△OBC=(a﹣)•b=3,所以(a﹣)•b=3,(a﹣)b=6,ab﹣k=6②,把①代入②得,9k﹣k=6,解得k=.方法2:延长BC交y轴于E,过D作x轴的垂线,垂足为F.由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,可知,△ODF的面积=梯形DFAB=△BOC的面积=,即k=,k=.故选B.30.解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则++6=4k,k=2.故选B.。
反比例函数与面积问题(基础篇)九年级数学下册基础知识专项讲练(人教版)

专题26.8反比例函数与面积问题(基础篇)(专项练习)一、单选题1.如图,点P 是反比例函数(0)ky k x=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M ,若POM 的面积等于3,则k 的值等于()A .6-B .6C .3-D .32.如图,在同一平面直角坐标系中,直线y =t (t 为常数)与反比例函数y 14x=,y 21x =-的图象分别交于点A ,B ,连接OA ,OB ,则△OAB 的面积为()A .5tB .52tC .52D .53.如图:点A 、B 是双曲线y =6x上的点,分别过点A 、B 做x 轴和y 轴的垂线段,若图中阴影部分的面积为2,这两个空白矩形的面积和为()A .12B .10C .9D .84.如图所示,在平面直角坐标系Oxy 中,四边形OABC 为矩形,点A 、C 分别在x 轴、y 轴上,点B 在函数14(0)y x x=>的图象上,边AB 与函数22(0)y x x =>的图象交于点D ,则阴影部分ODBC 的面积为()A .2B .3C .4D .55.如图,点P 是反比例函数()0,0ky k x x=≠<的图象上一点,过点P 作PA ⊥y 轴于点A ,点B 是点A 关于x 轴的对称点,连接PB ,若△PAB 的面积为6,则k 的值为()A .-3B .6C .-6D .-126.如图,正方形ABCD 的相邻两个顶点C 、D 分别在x 轴、y 轴上,且满足BD ∥x 轴,反比例函数y =kx(x <0)的图象经过正方形的中心E ,若正方形的面积为8,则该反比例函数的解析式为()A .y =4xB .y =-4xC .y =8xD .y =-8x7.如图,反比例函数()0k y x x=>的图象上有一点P ,PA x ⊥轴于点A ,点B 在y 轴上,PAB △的面积为6,则k 的值为()A .12-B .12C .6D .6-8.如图,在平面直角坐标系中,点P 在反比例函数ky x=(0k >,0x >)的图象上,其纵坐标为2,过点P 作PQ //y 轴,交x 轴于点Q ,将线段QP 绕点Q 顺时针旋转60°得到线段QM .若点M 也在该反比例函数的图象上,则k 的值为()AB C .D .49.如图,点A 在反比例函数ay x=第一象限内的图象上,点B 在x 轴的正半轴上,OA =AB ,△AOB 的面积为2,则a 的值为()A .12-B .12C .2D .110.如图,反比例函数()0k y x x=>的图象与矩形OABC 的边分别交于点E 、F ,且AE =BE ,点A 、C 分别在x 、y 轴上,若△OEF 的面积为3,则k 的值为()A .3B .4C .5D .6二、填空题11.如图,点A 是反比例函数3y x=图像上一点,过点A 分别作x 轴,y 轴的垂线,垂足为B ,C ,则四边形ABOC 的面积为______.12.如图,OAB 是等边三角形,点A 在x 轴的正半轴上12y x=0x >)的图象上,则OAB 的面积为______.13.如图,点A 是反比例函数y =kx(x >0)图象上的任意一点,过点A 作垂直x 轴交反比例函数y =1x(x >0)的图象于点B ,连接AO ,BO ,若ΔABO 的面积为1.5,则k 的值为____________14.如图所示,矩形ABCD 顶点A 、D 在y 轴上,顶点C 在第一象限,x 轴为该矩形的一条对称轴,且矩形ABCD 的面积为6.若反比例函数ky x=的图象经过点C ,则k 的值为_________.15.如图,已知点P 是y 轴正半轴上一点,过点P 作EF ∥x 轴,分别交反比例函数3y x=(x >0)和(0)ky x x=<图象的于点E 和点F ,以EF 为对角线作平行四边形EMFN .若点N 在x 轴上,平行四边形EMFN 的面积为8,则k 的值为_____.16.如图,在平面直角坐标系中,正方形ABOC 和正方形DOFE 的顶点B ,F 在x 轴上,顶点C ,D 在y 轴上,且3ADF S = ,反比例函数()0k y x x=>的图像经过点E ,则k =______________.17.如图,A 、B 是双曲线ky x=上的两点,过点A 作AC x ⊥轴于点C ,交OB 于点D ,且D 为AC 的中点,若AOD △的面积为2,点B 的坐标为(,1)m ,则m 的值为________.18.如图,函数()0ky x x=>的图象过矩形OBCD 一边的中点,且图象过矩形OAPE 的顶点P ,若阴影部分面积为6,则k 的值为______.三、解答题19.如图,在平面直角坐标系中,O 为坐标原点,Rt △OAB 的直角边OB 在x 轴的正半轴上,点A 的坐标为(6,4),斜边OA 的中点D 在反比例函数y kx=(x >0)的图象上,AB 交该图象于点C ,连接OC .(1)求k 的值;(2)求△OAC 的面积.20.如图,过反比例函数2(0)y x x=>的图象上任意两点A 、B ,分别作x 轴的垂线,垂足为','A B ,连接OA ,OB ,'AA 与OB 的交点为P ,记△AOP 与梯形''PA B B 的面积分别为12,S S ,试比较12,S S 的大小.21.如图,直线x=t(t>0)与双曲线y=1k x (k 1>0)交于点A ,与双曲线y=2k x(k 2<0)交于点B ,连接OA ,OB .(1)当k 1、k 2分别为某一确定值时,随t 值的增大,△AOB 的面积_______(填增大、不变、或减小)(2)当k 1+k 2=0,S △AOB =8时,求k 1、k 2的值.22.如图,正比例函数y1=﹣3x 的图象与反比例函数y2=kx的图象交于A 、B 两点.点C 在x 轴负半轴上,AC=AO ,△ACO 的面积为12.(1)求k 的值;(2)根据图象,当y1>y2时,写出x 的取值范围.23.如图,是反比例函数1k y x=和2ky x =(k 1>k 2)在第一象限的图象,直线A B ∥x 轴,并分别交两条曲线于A 、B 两点.(1)若点A 的纵坐标是3,则可得点B 的纵坐标是.(2)若4AOB S ∆=,则1k 与2k 之间的关系是.24.如图,反比例函数的图象过点A (2,3).(1)求反比例函数的解析式;(2)过A 点作AC ⊥x 轴,垂足为C .若P 是反比例函数图象上的一点,求当△PAC 的面积等于6时,点P 的坐标.参考答案1.A【分析】根据12P P POM x y =⋅ 即可求得答案.解:由题意得,132POM S PM OM =⋅= ,则6PM OM ⋅=,=P PM y ,P OM x =,点P 在第三象限,0P y ∴>,0P x <6P P k x y ∴=⋅=-,故选A .【点拨】本题考查了反比例函数k 的几何意义,熟练掌握k 的几何意义是解题的关键.2.C【分析】由反比例函数ky x=中的k 的几何意义直接可得特定的三角形的面积,从而可得答案.解:如图,记直线y =t 与y 轴交于点,M 由反比例函数的系数k 的几何意义可得:1111,42,222OBM OAM S S =⨯-==⨯= 152,22AOB S ∴=+= 故选:.C 【点拨】本题考查的是反比例函数的系数k 的几何意义,掌握反比例函数的系数k 与特定的图形的面积之间的关系是解题的关键.3.D【分析】根据反比例函数k 值得几何意义,转变成矩形面积代入求解即可.解:∵点A 、B 是双曲线y =6x上的点,∴S 矩形ACOG =S 矩形BEOF =6,∵S 阴影DGOF =2,∴S 矩形ACDF +S 矩形BDGE =6+6﹣2﹣2=8,故选:D .【点拨】本题考查反比例函数k 值的几何意义,关键在于牢记相关性质.4.B【分析】根据反比例函数k 的几何意义可知:△AOD 的面积为1,矩形ABCO 的面积为4,从而可以求出阴影部分ODBC 的面积.解:∵D 是反比例函数22y x=(x >0)图象上一点,∴根据反比例函数k 的几何意义可知:△AOD 的面积为12×2=1.∵点B 在函数14(0)y x x=>的图象上,四边形OABC 为矩形,∴根据反比例函数k 的几何意义可知:矩形ABCO 的面积为4.∴阴影部分ODBC 的面积=ABCO 的面积-△AOD 的面积=4-1=3.故选:B .【点拨】本题考查了反比例函数k 的几何意义,解题的关键是正确理解k 的几何意义.5.C【分析】过点P 作PD ⊥x 轴交点D ,PB 与x 轴的交点记为E ,推出S △OBE =S △PDE ,得到6PDOA S k ==四边形,于是得到结论.解:如图,过点P 作PD ⊥x 轴交点D ,PB 与x 轴的交点记为E ,∵点B 是点A 关于x 轴的对称点,∴OA =OB ,∴PD =OB ,又∵∠PED =∠BEO ,PD ⊥x 轴,OB ⊥x 轴,∴△OBE ≌△DPE (AAS ),∴S △OBE =S △PDE ,∴6PAB PDOA S S k === 四边形,∵反比例函数的图象在第二象限,∴k =-6,故选:C .【点拨】本题考查了反比例函数比例系数k 的几何意义,把三角形的面积转化为四边形的面积是解题的关键.6.B【分析】根据正方形的性质以及反比例函数系数k 的几何意义即可求得S △CDE =12|k |=2,解得即可.解:∵正方形的面积为8,∴S △CDE =2,∵正方形ABCD 的相邻两个顶点C 、D 分别在x 轴、y 轴上,BD ∥x 轴,∴S △CDE =12|k |,∴|k |=4,∵k <0,∴k =-4,∴该反比例函数的解析式为y =-4x ,故选:B .【点拨】本题考查了正方形的性质,反比例函数系数k 的几何意义,得到关于k 的方程是解题的关键.7.A【分析】设P 的坐标是(m ,n ),则mn =k ,PA =-n ,△ABP 中,AP 边上的高是|m |=m ,根据△PAB 的面积即可求解.解:设P 的坐标是(m ,n ),则mn =k ,PA =-n ,△ABP 中,AP 边上的高是m ,∵△PAB 的面积为6,∴12m ⋅(-n )=6,∴12mn =-,∴k =mn =-12.故选:A .【点拨】本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k |.8.C【分析】作MN ⊥x 轴交于点N ,分别表示出ON 、MN ,利用k 值的几何意义列式即可求出结果.解:作MN ⊥x 轴交于点N ,如图所示,∵P 点纵坐标为:2,∴P 点坐标表示为:(2k ,2),PQ =2,由旋转可知:QM =PQ =2,∠PQM =60°,∴∠MQN =30°,∴MN =112QM =,QN ∴ON MN k = ,即:2k k =,解得:k =故选:C .【点拨】本题主要考查的是k 的几何意义,表示出对应线段是解题的关键.9.C【分析】过点A 作AC OB ⊥于点C ,设点A 的坐标为(),A m n ,则,OC m AC n ==,先根据等腰三角形的三线合一可得22OB OC m ==,再根据三角形的面积公式可得2mn =,由此即可得.【详解】解:如图,过点A 作AC OB ⊥于点C ,设点A 的坐标为(),A m n ,则,OC m AC n ==,OA AB = ,22OB OC m ∴==,△AOB 的面积为2,112222OB AC m n ∴⋅=⨯⋅=,整理得:2mn =,将点(),A m n 代入反比例函数a y x =得:2a mn ==,故选:C .【点睛】本题考查了求反比例函数的系数、等腰三角形的三线合一,熟练掌握反比例函数的图象是解题关键.10.B【分析】连接OB .先根据反比例函数的比例系数的几何意义得出S △AOE =S △COF=2k ,然后由三角形任意一边上的中线将三角形的面积二等分及矩形的对角线将矩形的面积二等分,得出F 是BC 的中点,则124BEF BOF k S S == ,最后由S △OEF =S 矩形AOCB ﹣S △AOE ﹣S △COF ﹣S △BEF =3,代入即可求得k =4.解:如图,连接OB .∵E 、F 是反比例函数()0k y x x =>的图象上的点,EA ⊥x 轴于A ,FC ⊥y 轴于C ,∴S △AOE =S △COF=2k ,∵AE=BE ,∴S △BOE =S △AOE =2k ,S △BOC =S △AOB =k ,∴S △BOF =S △BOC ﹣S △COF =k -2k =2k ,∴F 是BC 的中点,∴124BEF BOF k S S == ,∴S △OEF =S 矩形AOCB ﹣S △AOE ﹣S △COF ﹣S △BEF =23224k k k k ---=,解得k =4,故选:B .【点拨】此题考查了反比例函数的比例系数k 与其图象上的点与远点所连的线段、坐标轴向坐标轴作垂线所围成的直角三角形面积的关系,即2k S =,得出F 是BC 的中点是解题的关键.11.3【分析】根据反比例函数解析式中比例系数k 的几何意义即可解决.解:由反比例函数解析式中比例系数k 的几何意义知,四边形ABOC 的面积为33k ==,故答案为:3.【点拨】本题考查了反比例函数的比例系数k 的几何意义,掌握它是解决问题的关键.12.12【分析】过点A 作AH ⊥OB 于点H ,根据反比例函数的几何意义,得到6AOH S = ,再根据等边三角形的性质,可得到2OAB AOH S S = ,即可求解.解:如图,过点A 作AH ⊥OB 于点H ,∵点A 在x 轴的正半轴上12y x=(0x >)的图象上,∴11262AOH S =⨯= ,∵OAB 是等边三角形,AH ⊥OB ∴12OH BH OB ==,∴22612OAB AOH S S ==⨯= .故答案为:12.【点拨】本题主要考查了反比函数的几何意义,熟练掌握本题主要考查了反比例函数()0k y k x=≠中k 的几何意义,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积等于k 是解题的关键.13.-2【分析】设AB 交x 轴于点C 解:设AB 交x 轴于点C ,如图,根据题意得:12BOC S ∆=,12AOC S k ∆=,∵ΔABO 的面积为1.5,∴ 1.5BOC AOC S S ∆∆+=,∴11 1.522k +=,解得:2k =,∵反比例函数y =k x(x >0)的图象位于第四象限,∴0k <,∴2k =-.故答案为:-2【点拨】本题主要考查反比例函数系数的几何意义,理解反比例函数系数的几何意义是得出正确答案的关键.14.3【分析】由图得,x 轴把矩形平均分为两份,即可得到上半部分的面积,利用矩形的面积公式即3C C x y ⋅=,又由于点C 在反比例函数图象上,则可求得答案.解:x 轴为该矩形的一条对称轴,且矩形ABCD 的面积为6,632C C x y ∴⋅==,3C C k x y ∴=⋅=,故答案为3.【点拨】本题考查了反比例函数k 的几何意义,熟练掌握k x y =⋅是解题的关键.15.-5【分析】连接OE 、OF ,利用反比例函数系数k 的几何意义可得S △FOP =12|k |,S △EOP =3322=,再根据同底等高的三角形面积相等,得到S △EFN =S △EFO ,由平行四边形的面积为8可求出S △EFN =12S ▱FNEM =4,进而求出答案.解:连接OF 、OE ,∵EF ∥x 轴,∴S △EFN =S △EFO ,又∵四边形FNEM 是平行四边形,EF 为对角线,∴S △EFN =12S ▱FNEM =12×8=4,由反比例函数系数k 的几何意义得,S △FOP =12|k |,S △EOP =3322=,又∵S △EFO =S △FOP +S △EOP =12|k |+32=4,解得k =﹣5,k =5>0(舍去),故答案为:﹣5.【点拨】本题考查反比例函数系数k 的几何意义,理解反比例函数系数k 的几何意义是正确应用的前提.16.6【分析】设正方形ABOC 的边长为a ,正方形DOFE 的边长为b ,利用面积法得:()()221113222b a b a b a b a +⋅+=⋅+++,所以26a =,然后利用k 的几何意义得到k 的值.解:如图,设正方形ABOC 的边长为a ,正方形DOFE 的边长为b ,∴AB BO a ==,DE DO OF EF b ====,90ABO BOC ∠=∠=︒,90DEF ∠=︒,ED y ⊥轴,EF x ⊥轴,∵ABF ADF DEF DOFE ABOD S S S S S +=++△△△正方形梯形,∴()()221113222b a b a b a b a +⋅+=⋅+++,∴26a =,∴26k a ==,∴6k =或6k =-(负值不合题意,舍去)故答案为:6.【点拨】本题考查反比例函数系数k 的几何意义:在反比例函数k y x=图像中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值k .本题涉及正方形的性质和等积变换等知识点.理解和掌握反比例函数系数k 的几何意义是解题的关键.17.8【分析】由D 为AC 的中点,可得出24AOC AOD S S == ,再由反比例函数系k 的几何意义,可得出k =8,进而得出双曲线的表达式8y x =,把点B 的坐标代入双曲线的表达式,即可得出m =8.解:设点A 的坐标为(b ,d ),∵D 为AC 的中点,∴AC =2AD ,∵△AOD 的面积为2,142AD OC ∴∙=,∴AD ·OC =4,11124222AOC S bd AC OC AD OC ∴==∙=⨯∙= ,∴bd =8,∵A 是双曲线k y x =上的点,∴k d b=,∴8k bd ==,∴双曲线k y x =的表达式为8y x=,∵B 是双曲线k y x =上的点,点B 的坐标为(m ,1),∴81m=,∴m =8.故答案为:8【点拨】本题考查了反比例函数系数k 的几何意义,关键是由D 为AC 的中点,可得出24AOC AOD S S == .18.6【分析】分两种情况讨论,设函数图象过BC 的中点,中点坐标为(m ,k m),则C (m ,2k m),根据阴影的面积可以求出k 的值;若函数图象过CD 的中点,同理可以求出k 的值.解:设函数图象过BC 的中点,中点坐标为(m ,k m ),则C (m ,2k m ),∴S 阴影=S 矩形OBCD -S 矩形OAPE =2k -k =6,∴k =6;若函数图象过CD 的中点,中点坐标为(m ,k m ),则C (2m ,k m),∴S 阴影=S 矩形OBCD -S 矩形OAPE =2k -k =6,∴k =6.综上,k 的值为6.故答案为:6.【点拨】本题考查反比例函数系数k 的几何意义,解题的关键是利用过某个点,这个点的坐标应适合这个函数解析式;所给的面积应整理为和反比例函数上的点的坐标有关的形式.19.(1)6(2)9【分析】(1)根据线段中点的坐标的确定方法求得点D 的坐标,再根据反比例函数图象上点的坐标特征求出k ;(2)由反比例函数解析式求出点C 的纵坐标,进而求出AC 的长,再根据三角形的面积公式计算即可.(1)解: 点A 的坐标为(6,4),点D 为OA 的中点,∴点D 的坐标为(3,2), 点D 在反比例函数k y x =的图象上,326k ∴=⨯=;(2)解:由题意得,点C 的横坐标为6,∴点C 的纵坐标为:616=,413AC ∴=-=,OAC ∴∆的面积16392=⨯⨯=.【点拨】本题考查的是反比例函数系数k 的几何意义、反比例函数图象上点的坐标特征,掌握反比例函数的性质、解题的关键是正确求出AC 的长度.20.12S S =【分析】利用图形面积关系可得:,,AOP AOA A OP BOB A OP A PBB S S S S S S ''''''=-=- 梯形再利用反比例函数的k 的几何意义可得:1,AOA BOB S S ''== 从而可得答案.解:12S S =【点拨】本题考查的是反比例函数的系数k 的几何意义,解题的关键是掌握反比例函数系数k 与过反比例函数图象上任意一点向两轴作垂线所形成的矩形的面积之间的关系.21.(1)不变;(2)k 1=8,k 2=﹣8.【分析】(1)根据反比例函数系数k 的几何意义即可得出答案;(2)由题意可知S△AOB=12k1﹣12k2,然后与k1+k2=0构成方程组,解之即可.解:(1)不变.∵S△AOC=12|k1|,S△BOC=12|k2|,∴S△AOB=S△AOC+S△BOC=12(|k1|+|k2|),∵k1,k2分别为某一确定值,∴△AOB的面积不变.故答案为:不变;(2)由题意知:k1>0,k2<0,∴S△AOB=12k1﹣12k2=8,∵k1+k2=0,∴k1=8,k2=﹣8.【点拨】本题考查的是反比例函数系数k的几何意义,属于常考题型,熟知反比例函数系数k的几何意义是解题的关键.22.(1)k=-12;(2)x<﹣2或0<x<2.解:(1)过点A作AD垂直于OC,由,得到,确定出△ADO与△ACO面积,即可求出k的值;(2)根据函数图象,找出满足题意x的范围即可.解:(1)如图,过点A作AD⊥OC,∵AC=AO,∴CD=DO,∴S△ADO=S△ACD=6,∴k=-12;(2)根据图象得:当y1>y2时,x的范围为x<﹣2或0<x<2.k k-=.23.(1)3,(2)128解:(1)平行线间的距离处处相等,B到x轴的距离也是3.(2)由图像知1k与2k都大于0,延长AB交y轴于C,△AOC的面积等于二分之一乘以K1,△BOC的面积二分之一乘以K 2,这两个三角形面积相减等于△AOB 的面积=4,解得128k k -=.考点:反比例函数图像性质24.(1)y =6x;(2)(6,1),(﹣2,﹣3).【分析】(1)把点A 的坐标代入反比例函数解析式,列出关于系数m 的方程,通过解方程来求m 的值;(2)设点P 的坐标是(a ,6x),然后根据三角形的面积公式来求点P 的坐标.解:(1)设反比例函数为y =m x,∵反比例函数的图象过点A (2,3).则2m =3,解得m =6.故该反比例函数的解析式为y =6x ;(2)设点P 的坐标是(a ,6x).∵A (2,3),∴AC =3,OC =2.∵△PAC 的面积等于6,∴12×AC ×|a ﹣2|=6,解得:|a ﹣2|=4,∴a 1=6,a 2=﹣2,∴点P 的坐标是(6,1),(﹣2,﹣3).【点拨】本题考查了反比例函数的面积问题,涉及的知识点有:待定系数法求函数解析式,坐标和图形性质,以及反比例函数的图像和性质,熟练掌握反比例函数的几何意义是解题的关键。
专题、反比例函数的面积问题 (经典问题)

专题、反比例函数中的面积问题一、反比例与矩形面积的关系1、如图,若过双曲线()0≠=k xky 上一点()y x P ,作x PA ⊥于A 点, 作y PB ⊥于B 点,则矩形PABO 的面积为k xy y x PB PA S ==⋅=⋅=. 2、k 的几何意义对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论, 可得出对应的面积的结论为:结论1:如图1,在直角三角形ABO 中,k S AOB 21=∆; 结论2:如图2,在矩形ABOC 中,k S OABC =矩形; 结论3:如图3,在ABM ∆中,x AM ⊥轴,k S ABM =∆;结论4:如图4,在ABC ∆中,x BC y AC //,//,则k S ABC 2=∆;结论5:如图5,ACE BPE OACB OAPB S S S S △△梯形梯形),()(==21; 结论6:如图6,x PA ⊥轴,x CD ⊥轴,()()2211,,,y x C y x P ,则()()2222121x x y y AD CD PA S S PADC OPC -⨯+=⨯+=⨯+==高下底上底梯形△;二、中点坐标公式(1)在平面直角坐标系上,点()11,y x A 与点()22,y x B 的中点是()00,y x C ,则⎪⎩⎪⎨⎧=+=+02102122y y y x x x .图4图5图6图3图2图1考点一、已知面积,求反比例函数的解析式(或比例系数k ) 例1、(1)如图1,直线OA 与反比例函数()0≠=k xky 的图象在第一象限交于A 点,x AB ⊥轴于点B ,OAB ∆的面积为2,则=k .(2)如图2,已知双曲线()0>=x xky 经过矩形OABC 的边BC AB ,的中点E F ,,且四边形OEBF 的面积为2,则=k .如图,矩形ABOD 的顶点A 是函数xky =与函数()1+--=k x y 在第二象限的交点,x AB ⊥轴于y AD B ⊥,轴于D ,且矩形ABOD 的面积为3. (1)求两函数的解析式.(2)求两函数的交点C A ,的坐标.(3)若点P 是y 轴上一动点,且5=∆APC S ,求点P 的坐标.考点二、已知反比例函数解析式,求图形的面积 (1) 在反比例函数xy 4=的图象中,阴影部分的面积不等于4的是( )(2)如图,点B A ,是双曲线xy 3=上的点,分别经过B A ,两点向x 轴、y 轴作垂线段,若1=阴影S ,则=+21S S .图1图2.A .B.C.D考点三、利用点的坐标及面积公式求面积例3、如图,已知()()4,2,4--B n A ,是一次函数b kx y +=的图像和反比例函数xmy =的图像的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线AB 与x 轴的交点C 的坐标及三角形AOB 的面积.如图,直线b kx y +=与反比例函数()0<=x xky 的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为()4,2-,点B 的横坐标为4-.(1)试确定反比例函数的关系式; (2)求AOC ∆的面积.考点四、利用对称性求反比例函数有关的面积问题 例4、已知, E D C B A ,,,,是反比例函数()016>=x xy 图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数xy 2=的图象上,则图中阴影部分的面积等于 .考点五、反比例函数有关的动点问题 例5、如图,点P 为函数()016>=x xy 的图象上一点,且到两坐标轴距离相等,⊙P 半径为()0,3,2A ,()0,6B 点Q 是⊙P 上的动点,点C 是QB 的中点,则AC 的最小值是 .随堂练习1、如图1,已知21211,A A P OA P ∆∆都是等腰直角三角形,点21,P P 都在函数()04>=x xy 的图象上,斜边211,A A OA 都在x 轴上.则点2A 的坐标为 .1、如图2,已知n n n A A P A A P A A P OA P 132321211,,,,-∆∆∆∆ 都是等腰直角三角形,点n P P P P ,,,,321 都在函数()04>=x xy 的图象上,斜边n n A A A A A A OA 132211,,,,- 都在x 轴上.则点10A 的坐标为 .2、已知点()2,0A 和点()2,0-B ,点P 在函数xy 1-=的图像上,如果PAB ∆的面积为6,求P 点的坐标.图1图23、如图 所示,反比例函数xky =的图象经过点()b A ,3-,过点A 作AB 垂直x 轴于点AOB B ∆,,的面积为3.(1)求k 和b 的值;(2)若一次函数1+=ax y 的图象经过点A ,并且与x 轴相交于点M ,求OM AB :的值.4、如右图,已知点()3,1在函数()0>=x xky 的图像上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的中点,函数()0>=x xky 的图象又经过E A ,两点,点E 的横坐标为m ,解答下列各题 (1)求k 的值;(2)求点C 的横坐标(用m 表示); (3)当oABD 45=∠时,求m 的值.1、已知:如图,矩形ABCD 的边BC 在x 轴上,E 是对角线BD AC ,的交点,反比例函数()02>=x xy 的图象经过E A ,两点,点E 的纵坐标为m .(1)求点A 坐标(用m 表示)(2)是否存在实数m ,使四边形ABCD 为正方形,若存在,请求出m 的值;若不存在,请说明理由2、在平面直角坐标系中,已知()()1,0,0,1B A ,矩形OMPN 的相邻两边ON OM ,分别在y x ,轴的正半轴上,O 为原点,线段AB 与矩形OMPN 的两边NP MP ,的交点分别为BOE AOF F E ∆∆~,,(顶点依次对应).(1)求FOE ∠; (2)求证:矩形OPMN 的顶点P 必在某个反比例函数图像上,并写出该函数的解析式.1、如图,在平面直角坐标系中,直线1+-=x y 分别交x 轴、y 轴于B A ,两点,点()b a P ,是反比例函数xy 21=在第一象限内的任意一点,过点P 分别作x PM ⊥轴于点y PN M ⊥,轴于点PN PM N ,,分别交直线AB 于F E ,,有下列结论:①BE AF =;②图中的等腰直角三角形有4个;③()121-+=∆b a S OEF ;④o EOF 45=∠.其中结论正确的序号是 .2、已知反比例函数xky 2=和一次函数12-=x y ,其中一次函数的图象经过()()2,,,+++k b k a b a 两点.(1)求反比例函数的解析式;(2)求反比例函数与一次函数两个交点B A ,的坐标:(3)根据函数图象,求不等式122->x xk的解集; (4)在(2)的条件下,x 轴上是否存在点P ,使AOP ∆为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由。
专题:反比例函数中的面积问题

微专题 反比例函数中的面积问题
模型一 一点一垂线
反比例函数图象上一点与坐标轴垂线、另一坐标轴上一点(含原点)围成的三 角形面积= |k|.
1
S△ABC= 2 |k|
S△ABC=12 |k|
1
S△AOC= 2 |k|
1. 如图,点A在反比例函数y=- 4 的图象上,AM⊥y轴于点M,点P是x轴上的一
方法一:S△EOF=S△EOD-S△FOD. 方法二:作EM⊥x轴于点M,交OF于点B,FA⊥x轴于点A,则S△OEB=S四边形 BMAF(划归到模型一),则S△EOF=S直角梯形EMAF.
类型一 两交点在反比例函数同一支上
Байду номын сангаас
方法一:当
BE CE
或
BFFA=m时,则S四边形OFBE=m|k|.
方法二:作EM⊥x轴于点M,
A. 1
B. m-1
C. 2
D. m
第3题图
模型四 两点两垂线
反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形 面积=2|k|.
SABC 2 | k |
易得四边形ANBM是平行四边形, ∴S四边形ANBM=AM·NM=AM·2OM=2|k|
模型四 两点两垂线 反比例函数与正比例函数的交点及由交点向坐标轴所作两条垂线围成的图形
= =
1
2
1
OM·AM+12 OM·BC |k|+1 |k|=|k|
22
S△ABM=S△ADM+S△MDB
=
1 2
MD·|yB-yA|
S△ABM=S△BMO+S△AMO
=
1 2
MO·|xB-xA|
3. 如图,直线y=mx与双曲线y=k (k≠0)交于点A,B,过点A作
反比例函数常见的面积类型

反比例函数常见的面积类型
反比例函数是数学中的一种基本函数类型。
在实际应用中,反比例函数常常涉及到面积问题。
下面列举一些常见的反比例函数面积类型。
1. 长方形面积
如果一个长方形的宽是固定的,而长度是随着宽的增加而减小的,那么它的面积就可以用反比例函数来表示。
设长方形宽为x,长度为y,则长方形面积为S=xy,即S与x成反比例关系,S=k/x。
其中,k 为比例常数。
2. 圆形面积
圆的半径和面积之间也存在反比例关系。
设圆的半径为r,圆的面积为S,则圆的面积可以表示为S=k/r^2。
其中,k为比例常数。
3. 梯形面积
如果一个梯形的高是固定的,而底边长度是随着高的增加而减小的,那么它的面积也可以用反比例函数来表示。
设梯形的高为h,上底为a,下底为b,则梯形面积为S=(a+b)h/2,即S与h成反比例关系,S=k/h。
其中,k为比例常数。
4. 等腰三角形面积
如果一个等腰三角形的底边长度是固定的,而高是随着底边长度增加而减小的,那么它的面积也可以用反比例函数来表示。
设等腰三角形的底边长度为b,高为h,则等腰三角形面积为S=bh/2,即S与b成反比例关系,S=k/b。
其中,k为比例常数。
综上所述,反比例函数在实际应用中常常涉及到面积问题,这些常见的反比例函数面积类型包括长方形面积、圆形面积、梯形面积和等腰三角形面积。
人教版反比例函数与面积问题

(1)求这个一次函数的解析式
(2)求△AOB的面积.
A
解
:
(2)
y
6 x
,
y x 1.
解得 xy3,2或xy3.2,
y
N M
O
x B
A (2,3)B ,(3,2) .
曲直结合
y y 4 x
⑴直线OA与双曲线的 另一交点B的坐标.
A(2, 2)
B(-2,-2)
O
C
B
D
x
⑵△BDA的面积是多少?
作x轴,y轴的垂线,垂足分别为E, F,
若设矩形OEPF和正 方形OABC不重合部 分的面积为S,写出S 关于m的函数关 系 式.
G
总结提高 一个性质:反比例函数的面积不变性
两种思想:分类讨论和数形结合
变式练习
已知:如图,反比例函数
y
6 x
与一次函数
y=kx+1的图像交于A、B两点,点A的纵坐标是3.
y
∟
P
s1
Q
∟
∟
s2
O
x
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
趁热打铁,大显身手
如图,P1、P2、P3是双曲线上的三点.过这三点分 别作y轴的垂线,得到三个三角形P1A10、P2A20、 P3A30,设它们的面积分别是S1、S2、S3,则 ( ).
A.S1<S2<S3
B.S2<S1<S3
(1)若A(2,3),求K的值 (2)在(1)的条件下,若点B的横坐标为3, y
连接OA,OB,AB,求△OAB的面积。 D A E
B
o
Cx
如图,已知,A,B是双曲线 y k (k 0) 上的两点, x
反比例函数背景下的面积问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数

模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图,直线AB 与反比例函数k y x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低2.如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
【例1】.如图,反比例函数y=在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是8.过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,∴x=2时,y=3;x=6时,y=1,=S△OBD=3,故S△ACOS四边形AODB=×(3+1)×4+3=11,故△AOB的面积是:11﹣3=8.故答案为:8.变式训练【变1-1】.如图,点A在反比例函数(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,△AOB的面积为12,则k的值为()A.4B.6C.10D.12解:如图,过点A作AD⊥x轴,垂足为D,∵OC∥AD,,∴,∴,k>0,∴k=12,故选:D.【变1-2】.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,=4,则k的值为16.若E是AB的中点,S△BEF解:设E(a,),则B纵坐标也为,∵E是AB中点,∴F点坐标为(2a,),∴BF=BC﹣FC=﹣=,=4,∵S△BEF∴a•=4,∴k=16.故答案是:16.【例2】.如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为12.解:解法一:过点A作x轴的垂线,交CB的延长线于点E,∵BC∥x轴,∴AE⊥BC,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为6,4,∴A(,6),B(,4),∴AE=2,BE=﹣=,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE===1,∴k=1,∴k=12.解法二:同理知:BE=1,设A(a,6),则B(a+1,4),∴6a=4(a+1),∴a=2,∴k=2×6=12.故答案为12.变式训练【变2-1】.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是()A.9B.8C.7D.6解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,∴A(4,3),B(2,6),作AD⊥y轴于D,BE⊥y轴于E,=S△BOE=×12=6,∴S△AOD=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,∵S△OAB=(4+2)×(6﹣3)=9,∴S△AOB故选:A.【变2-2】.如图,在直角坐标系中,O为坐标原点,函数y=与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=a﹣.(结果用a,b表示)解:设B(m,),A(,n),则P(m,n),∵点P为曲线C1上的任意一点,∴mn=a,=mn﹣b﹣b﹣(m﹣)(n﹣)∴阴影部分的面积S△AOB=mn﹣b﹣(mn﹣b﹣b+)=mn﹣b﹣mn+b﹣=a﹣.故答案为:a﹣.1.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.2.如图,OC交双曲线y=于点A,且OC:OA=5:3,若矩形ABCD的面积是8,且AB ∥x轴,则k的值是()A.18B.50C.12D.解:延长DA、交x轴于E,∵四边形ABCD是矩形,且AB∥x轴,∴∠CAB=∠AOE,∴DE⊥x轴,CB⊥x轴,∴∠AEO=∠ABC∴△AOE∽△CAB,∴=()2,∵矩形ABCD的面积是8,OC:OA=5:3,∴△ABC的面积为4,AC:OA=2:3,∴=()2=,=9,∴S△AOE∵双曲线y=经过点A,=|k|=9,∴S△AOE∵k>0,∴k=18,故选:A.3.如图,已知点A,B分别在反比例函数y1=﹣和y2=的图象上,若点A是线段OB 的中点,则k的值为()A.﹣8B.8C.﹣2D.﹣4解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=﹣的图象上,∴ab=﹣2;∵B点在反比例函数y2=的图象上,∴k=2a•2b=4ab=﹣8.故选:A.4.如图,点A(m,n),B(4,)在双曲线y=上,且0<m<n.若△AOB的面积为,则m+n=()A.7B.C.D.3解:∵点A(m,n),B(4,)在双曲线y=上,∴mn=4×=k,∴mn=k=6,∴双曲线为y=,∴n=,作AD⊥x轴于D,BE⊥x轴于E,=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB,∵S△AOB∴(+)(4﹣m)=,解得m1=1,m2=﹣16,∵0<m<n.∴m=1,∴n=6,∴m+n=7,故选:A.5.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴=3,则S△于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCDAOC为()A.2B.3C.4D.6解:在Rt△BCD中,∵×CD×BD=3,∴×CD×3=3,∴CD=2,∵C(2,0),∴OC=2,∴OD=4,∴B(4,3),∵点B是反比例函数y=(x>0)图象上的点,∴k=12,∵AC⊥x轴,==6,∴S△AOC故选:D.6.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y 轴上的动点,则△ABC的面积为()A.k1﹣k2B.(k1﹣k2)C.k2﹣k1D.(k2﹣k1)解:由题意可知,AB=﹣,AB边上的高为x,=×(﹣)•x=(k1﹣k2),∴S△ABC故选:B.7.已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=与边BC交于点D、与对角线OB交于中点E,若△OBD的面积为10,则k的值是()A.10B.5C.D.解:设E点的坐标是(x,y),∵E是OB的中点,∴B点的坐标是(2x,2y),则D点的坐标是(,2y),∵△OBD的面积为10,∴×(2x﹣)×2y=10,解得,k=,故选:D.8.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=()A.6B.9C.D.解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b)∵D、E在反比例函数的图象上,∴=k,设E的坐标为(a,y),∴ay=k∴E(a,),=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣k﹣k﹣••(b﹣)=12,∵S△ODE∴4k﹣k﹣+=12k=故选:D.9.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=8.解:∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=8÷2=4,又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,∴△AOC的面积=|k|,∴|k|=4,∵k>0,∴k=8.故答案为8.10.如图,若反比例函数y=的图象经过等边三角形POQ的顶点P,则△POQ的边长为2.解:如图,过点P作x轴的垂线于M,∵△POQ为等边三角形,∴OP=OQ,OM=QM=OQ,∵反比例函数的图象经过点P,∴设P(a,)(a>0),则OM=a,OQ=OP=2a,PM=,在Rt△OPM中,PM===a,∴=a,∴a=1(负值舍去),∴OQ=2a=2,故答案为:2.11.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x 轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.则△OAP 的面积为5.解:过P作MN⊥x轴于M,交AB于N,过A作AD⊥x轴于D,∵A(4,3),∴AD=3,OD=4,∴AO==5,∵AB=AO,∴AB=5,∵AB∥x轴,点B的横坐标是4+5=9,纵坐标是3,即点B的坐标是(9,3),设直线OB的解析式是y=ax,把B点的坐标(9,3)代入得:3=9a,解得:a=,即y=x,∵AB∥x轴,∴MN⊥AB,把A(4,3)代入y=,得k=12,即y=,解方程组得:或,∵点P在第一象限,∴点P的坐标是(6,2),∵A(4,3),AB∥x轴,P(6,2),∴MN=AD=3,PN=3﹣2=1,﹣S△APB=3﹣=5,∴△OAP的面积是S△ABO故答案为:5.12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC 面积的最小值为6.解:方法一:设A(a,),B(b,),则C(a,).将y=x+m代入y=,得x+m=,整理,得x2+mx﹣3=0,则a+b=﹣m,ab=﹣3,∴(a﹣b)2=(a+b)2﹣4ab=m2+12.=AC•BC∵S△ABC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+12)=m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为6.方法二:因为y=x+m斜率为1,且BC∥x轴,AC∥y轴,∴∠ABC=∠BAC=45°,∴△ABC为等腰直角三角形,∴AC=BC=AB,=AC•BC=AB2,∴S△ABC当AB最小时,m=0,直线为y=x,联立方程,解得或,∴A(,),B(﹣,﹣),AB=×2=2,=×4×6=6.∴S△ABC最小故答案为:6.13.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线=6,则k的值为8.段AB于点D,连接CD,OD.若S△OCD解:根据题意设B(m,m),则A(m,0),∵点C为斜边OB的中点,∴C(,),∵反比例函数y=(k>0,x>0)的图象过点C,∴k=•=,∵∠OAB=90°,∴D的横坐标为m,∵反比例函数y=(k>0,x>0)的图象过点D,∴D的纵坐标为,作CE⊥x轴于E,=S△AOD,∵S△COES△OCD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE,S△OCD=6,∴(AD+CE)•AE=6,即(+)•(m﹣m)=6,∴m2=32,∴k==8,故答案为:8.解法二:作CE⊥OA于E,∵C为AB的中点,OA=AB,∠OAB=90°,=S△AOD=k,S△AOB=2k,∴S△OEC=k,∴S△BOD∵C为斜边OB的中点,=S△BCD=S△BOD=6,∴S△OCD∴×k=6,∴k=8.故答案为:8.14.如图,在平面直角坐标系中,▱OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD,▱OABC的面积为15,则k的值为18.解:过点D作DN⊥y轴于N,过点B作BM⊥y轴于M,设OC=a,CN=2b,MN=b,∵▱OABC的面积为15,∴BM=,∴ND=BM=,∴A,D点坐标分别为(,3b),(,a+2b),∴•3b=(a+2b),∴b=a,∴k=•3b=•3×a=18,故答案为:18.15.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x 轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.16.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)请直接写出不等式x+b的解.解:(1)∵反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m),∴k1=8,B(﹣4,﹣2),解方程组,解得;(2)由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),=×6×4+×6×1=15;∴S△AOB(3)﹣4≤x<0或x≥1.17.如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB=,反比例函数y=的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为.(1)求反比例函数的解析式;(2)求直线EB的解析式;.(3)求S△OEB解:(1)∵A点的坐标为(a,6),AB⊥x轴,∴AB=6,∵cos∠OAB==,∴,∴OA=10,由勾股定理得:OB=8,∴A(8,6),∴D(8,),∵点D在反比例函数的图象上,∴k=8×=12,∴反比例函数的解析式为:y=;(2)设直线OA的解析式为:y=bx,∵A(8,6),∴8b=6,b=,∴直线OA的解析式为:y=x,则,x=±4,∴E(﹣4,﹣3),设直线BE的解式为:y=mx+n,把B(8,0),E(﹣4,﹣3)代入得:,解得:,∴直线BE的解式为:y=x﹣2;=OB•|y E|=×8×3=12.(3)S△OEB18.如图,直线y=x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=.(1)求反比例函数的解析式;(2)求点B的坐标;.(3)求S△OAB解:(1)∵直线y=x与反比例函数的图象交于点A(3,a),∴a=×3=4,∴点A的坐标为(3,4),∴k=3×4=12,∴反比例函数解析式y=.(2)∵点B在这个反比例函数图象上,设点B坐标为(x,),∵tanα=,∴=,解得:x=±6,∵点B在第一象限,∴x=6,∴点B的坐标为(6,2).(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,解得:k=,∴OB直线解析式为:y=x.过A点做AC⊥x轴,交OB于点C,如图所示:则点C坐标为(3,1),∴AC=3.S△OAB的面积=S△OAC的面积+S△ACB的面积=×|AC|×6=9.∴△OAB的面积为9.19.已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比=4.例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB (1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.=•|x A|•y B,解:(1)由题意得:S△AOB即×2×y B=4,y B=4,∴B(2,4),设反比例函数的解析式为:y=,把点B的坐标代入得:k=2×4=8,∴y=,设直线AB的解析式为:y=ax+b,把A(﹣2,0)、B(2,4)代入得:,解得:,∴y=x+2;(2)由题意得:x+2=,解得:x1=﹣4,x2=2,∴D(﹣4,﹣2),=S△OAD+S△OAB=×2×2+4=6.∴S△ODB20.如图,在平行四边形OABC中,,点A在x轴上,点D是AB 的中点,反比例函数的图象经过C,D两点.(1)求k的值;(2)求四边形OABC的面积.解:(1)过点C作CE⊥x轴于E,∵∠AOC=45°,∴OE=CE,∴OE2+CE2=OC2∵OC=2,∴OE=CE=2,∴C(2,2),∵反比例函数的图象经过点C点,∴k=2×2=4;(2)过点D作DF⊥x轴于F,∵四边形OABC是平行四边形,∴AB=OC=2,∠DAF=∠AOC=45°,又∵点D是AB的中点,∴AD=,AF=DF,∴AF2+DF2=AD2,∴AF=DF=1,∴D点的纵坐标为1,∵反比例函数的图象过点D点,∴D(4,1),∴OF=4,OA=OF﹣AF=4﹣1=3,∴平行四边形OABC的面积S=OA•CE=3×2=6.21.如图,直线y=6x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标为2.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB,求△AOB的面积.解:(1)将x=2代入y=6x,得:y=12,∴点A的坐标为(2,12),将A(2,12)代入y=,得:k=24,∴反比例函数的解析式为y=;(2)在y=中y=6时,x=4,∴点B(4,6),而A(2,12),如图,过A作AC⊥y轴,BD⊥x轴,交于点E,则OD=4,OC=12,BD=6,AC=2,AE=2,BE=6,=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB=4×12﹣×2×12﹣×4×6﹣×2×6=48﹣12﹣12﹣6=18.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点.(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)若D(x,0)是x轴上原点左侧的一点,且满足,求x的取值范围.解:(1)∵B(2,﹣4)在反比例函数y=的图象上,∴m=﹣8,∴反比例函数的表达式为y=﹣.∵A(﹣4,n)在y=﹣的图象上,∴n=2,∴A(﹣4,2).∵y=kx+b经过A(﹣4,2)和B(2,﹣4),∴,解得∴一次函数的表达式为y=﹣x﹣2.(2)当y=﹣x﹣2=0时,解得x=﹣2.∴点C(﹣2,0),∴OC=2,=S△AOC+S△COB∴S△AOB=×2×2+×2×4=6.(3)根据函数的图象可知:若D(x,0)是x轴上原点左侧的一点,当﹣4<x<0时,满足kx+b﹣<0.23.如图,一次函数y=k1x+b的图象与反比例函数y=(x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).(1)求此一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.解:(1)∵反比例函数y=(x<0)的图象经过点A(﹣1,2),∴k2=﹣1×2=﹣2,∴反比例函数表达式为:y=﹣,∵反比例y=﹣的图象经过点B(﹣4,n),∴﹣4n=﹣2,解得n=,∴B点坐标为(﹣4,),∵直线y=k1x+b经过点A(﹣1,2),点B(﹣4,),∴,解得:,∴一次函数表达式为:y=+.(2)设直线AB与x轴的交点为C,如图1,当y=0时,x+=0,x=﹣5;∴C点坐标(﹣5,0),∴OC=5.S△AOC=•OC•|y A|=×5×2=5.S△BOC=•OC•|y B|=×5×=.S△AOB=S△AOC﹣S△BOC=5﹣=;(3)如图2,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,∵点A′和A(﹣1,2)关于x轴对称,∴点A′的坐标为(﹣1,﹣2),设直线A′B的表达式为y=ax+c,∵经过点A′(﹣1,﹣2),点B(﹣4,)∴,解得:,∴直线A′B的表达式为:y=﹣x﹣,当y=0时,则x=﹣,∴P点坐标为(﹣,0).24.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b>0的解集.解:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),∴C点坐标为(6,4),∵A点坐标为(3,2),∴k1=3×2=6,∴反比例函数解析式为y=;把x=6代入y=得x=1,则F点的坐标为(6,1);把y=4代入y=得x=,则E点坐标为(,4),把F(6,1)、E(,4)代入y=k2x+b,得,解得,,∴直线EF的解析式为y=﹣x+5;﹣S△ODE﹣S△OBF﹣S△CEF(2)△OEF的面积=S矩形BCDO=4×6﹣×4×﹣×6×1﹣×(6﹣)×(4﹣1)=;(3)由图象得:不等式k2x+b﹣>0的解集为<x<6.25.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P,连结OP、OQ.求△OPQ的面积.解:(1)反比例函数y=(m≠0)的图象经过点(1,4),解得m=4,故反比例函数的表达式为y=.一次函数y=﹣x+b的图象与反比例函数的图象相交于点Q(﹣4,n),所以,解得n=﹣1,b=﹣5.∴一次函数的表达式y=﹣x﹣5;(2)由,解得或.∴点P(﹣1,﹣4),在一次函数y=﹣x﹣5中,令y=0,得﹣x﹣5=0,解得x=﹣5,故点A(﹣5,0),S△OPQ=S△OP A﹣S△OAQ=×5×4−×5×1=7.5.26.如图,在平面直角坐标系中,边长为4的等边△OAB的边OB在x轴的负半轴上,反比例函数y=(x<0)的图象经过AB边的中点C,且与OA边交于点D.(1)求k的值;(2)连接OC,CD,求△OCD的面积;(3)若直线y=mx+n与直线CD平行,且与△OAB的边有交点,直接写出n的取值范围.解:(1)∵等边△OAB,∴AB=BO=AO=4,∠ABO=∠BOA=∠OAB=60°,∵点C是AB的中点,∴BC=AC=2,过点C作CM⊥OB,垂足为M,在Rt△BCM中,∠BCM=90°﹣60°=30°,BC=2,∴BM=1,CM=,∴OM=4﹣1=3,∴点C 的坐标为(﹣3,),代入y =得:k =﹣3答:k 的值为﹣3;(2)过点A 作AN ⊥OB ,垂足为N ,由题意得:AN =2CM =2,ON =OB =2,∴A (﹣2,2),设直线OA 的关系式为y =kx ,将A 的坐标代入得:k =﹣,∴直线OA 的关系式为:y =﹣x ,由题意得:,解得:舍去,,∴D (﹣,3)过D 作DE ⊥OB ,垂足为E ,S △OCD =S CMED +S △DOE ﹣S △COM =S CMED =(+3)×(3﹣)=3,答:△OCD 的面积为3.(3)①当与直线CD 平行的直线y =mx +n 过点O 时,此时y =mx +n 的n =0,②当与直线CD 平行的直线y =mx +n 经过点A 时,设直线CD 的关系式为y =ax +b ,把C 、D 坐标代入得:,解得:a =1,b =3+∴直线CD 的关系式为y =x +3+,∵y =mx +n 与直线y =x +3+平行,∴m =1,把A (﹣2,2)代入y =x +n 得:n =2+2因此:0≤n ≤2+2且n .答:n 的取值范围为:0≤n ≤2+2且n ≠3+.。
专题07 反比例函数K值与几何面积综合中考数学专题复习
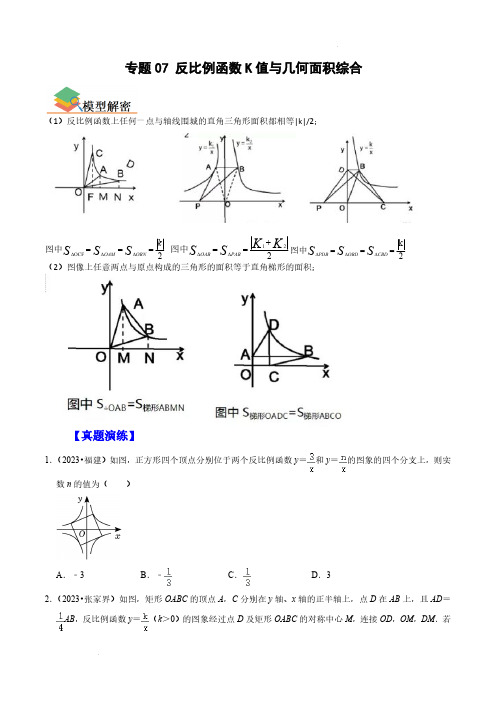
专题07 反比例函数K 值与几何面积综合(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;【真题演练】1.(2023•福建)如图,正方形四个顶点分别位于两个反比例函数y =和y =的图象的四个分支上,则实数n 的值为( )A .﹣3B .﹣C .D .32.(2023•张家界)如图,矩形OABC 的顶点A ,C 分别在y 轴、x 轴的正半轴上,点D 在AB 上,且AD =AB ,反比例函数y =(k >0)的图象经过点D 及矩形OABC 的对称中心M ,连接OD ,OM ,DM .若△ODM的面积为3,则k的值为( )A.2B.3C.4D.53.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是( )A.﹣6B.﹣12C.﹣D.﹣94.(2023•宜宾)如图,在平面直角坐标系xOy中,点A、B分别在y、x轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为( )A.B.C.D.5.(2022•日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )A.3B.﹣3C.D.6.(2022•郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )A.3B.5C.6D.107.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )A.36B.18C.12D.98.(2022•黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )A.2B.1C.﹣1D.﹣29.(2023•连云港)如图,矩形OABC的顶点A在反比例函数y=(x<0)的图象上,顶点B、C在第一象限,对角线AC∥x轴,交y轴于点D.若矩形OABC的面积是6,cos∠OAC=,则k= .10.(2023•枣庄)如图,在反比例函数(x>0)的图象上有P1,P2,P3,…P2024等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2023,则S1+S2+S3+…+S2023= .11.(2023•朝阳)如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接PA,PB.若△ABP的面积等于3,则k的值为 .12.(2023•衢州)如图,点A,B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF,反比例函数y=(k>0)的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为 .13.(2023•锦州)如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC 的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为 .14.(2023•黄石)如图,点A(a,)和B(b,)在反比例函数y=(k>0)的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为 ;若△AOB的面积为,则= .15.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为 6 .16.(2023•绍兴)如图,在平面直角坐标系xOy中,函数(k为大于0的常数,x>0)图象上的两点A (x1,y1),B(x2,y2),满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 .17.(2022•烟台)如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .18.(2022•黄石)如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k= .19.(2022•衢州)如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC=6,则k= .20.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM 分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为 .21.(2022•鄂尔多斯)如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .22.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为 .23.(2022•绍兴)如图,在平面直角坐标系xOy 中,点A (0,4),B (3,4),将△ABO 向右平移到△CDE 位置,A 的对应点是C ,O 的对应点是E ,函数y =(k ≠0)的图象经过点C 和DE 的中点F ,则k 的值是 .24.(2022•内蒙古)如图,在平面直角坐标系中,Rt △OAB 的直角顶点B 在x 轴的正半轴上,点O 与原点重合,点A 在第一象限,反比例函数y =(x >0)的图象经过OA 的中点C ,交AB 于点D ,连接CD .若△ACD 的面积是1,则k 的值是 .专题07 反比例函数K 值与几何面积综合(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;【真题演练】1.(2023•福建)如图,正方形四个顶点分别位于两个反比例函数y=和y=的图象的四个分支上,则实数n的值为( )A.﹣3B.﹣C.D.3【答案】A【解答】解:连接正方形的对角线,由正方形的性质知对角线交于原点O,过点A,B分别作x轴的垂线.垂足分别为C、D,点B在函数y=上,如图:∵四边形是正方形,∴AO=BO,∠AOB=∠BDO=∠ACO=90°,∴∠CAO=90°﹣∠AOC=∠BOD,∴△AOC≌△BOD(AAS),∴S△AOC=S△OBD==,∵点A在第二象限,∴n=﹣3,故选:A.2.(2023•张家界)如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,点D在AB上,且AD=AB,反比例函数y=(k>0)的图象经过点D及矩形OABC的对称中心M,连接OD,OM,DM.若△ODM的面积为3,则k的值为( )A.2B.3C.4D.5【答案】C【解答】解:解法一:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵矩形OABC的对称中心M,∴延长OM恰好经过点B,M(,),∵点D在AB上,且AD=AB,∴D(,b),∴BD=a,∴S△BDM=BD•h=×a×(b﹣)=ab,∵D在反比例函数的图象上,∴ab=k,∵S△ODM=S△AOB﹣S△AOD﹣S△BDM=ab﹣k﹣ab=3,∴ab=16,∴k=ab=4,解法二:连接BM,因为点M是矩形的对称中心,∴三角形DMO的面积=三角形DMB的面积,则三角形DBO的面积为6,∵AD=1/4AB,∴AD:DB=1:3,∴三角形ADO的面积:三角形DBO的面积为1:3,即三角形ADO的面积为2,∴K=4.故选:C.3.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是( )A.﹣6B.﹣12C.﹣D.﹣9【答案】C【解答】解:设BC与y轴的交点为F,B(b,),则A(﹣b,﹣),b>0,由题意知,AO=BO,即O是线段AB的中点,过A作AE⊥BC于点E,∵AC=AB,AE⊥BC,∴BE=CE,AE∥y轴,∴CF=3BF=3b,∴C(﹣3b,),∴D(﹣3b,),∴CD=,BC=4b,∴S△BCD=,∴k=﹣.故选:C.4.(2023•宜宾)如图,在平面直角坐标系xOy中,点A、B分别在y、x轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为( )A.B.C.D.【答案】B【解答】解:如图,过点N作NQ⊥x轴于点Q,过C作CT⊥y轴交y轴于T,交NQ于K,设OA=a,OP=b,BM=c,N(m,n),∵OP:BP=1:4,BM=CM,∴A(0,a),B(5b,0),M(5b,c),C(5b,2c),∵∠NCK=∠ACT,∠NKC=90°=∠ATC,∴△NKC∽△ATC,∴==,∵NC=2AN,∴CK=2TK,NK=AT,∴,解得,∴,∴,,∴,∵△APN的面积为3,∴S梯形OANQ﹣S△AOP﹣S△NPQ=3,∴,∴2ab+bc=9,将点M(5b,c),代入得:,整理得:2a=7c,将2a=7c代入2ab+bc=9得:7bc+bc=9,∴,∴,故选:B.5.(2022•日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )A.3B.﹣3C.D.【答案】B【解答】解:∵y1、y2的图象均在第一象限,∴k1>0,k2>0,∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,∴S△OAM=S△OCN=k1,∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,∴S矩形OABC=k2,∴S四边形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,∴k2﹣k1=3,∴k1﹣k2=﹣3,故选:B.6.(2022•郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )A.3B.5C.6D.10【答案】B【解答】解:∵点A在函数y=(x>0)的图象上,∴S△AOC=×2=1,又∵点B在反比例函数y=﹣(x<0)的图象上,∴S△BOC=×8=4,∴S△AOB=S△AOC+S△BOC=1+4=5,故选:B.7.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )A.36B.18C.12D.9【答案】B【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图象上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B.8.(2022•黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD 的面积是5,则k的值是( )A.2B.1C.﹣1D.﹣2【答案】D【解答】解:设B(a,),∵四边形OBAD是平行四边形,∴AB∥DO,∴A(,),∴AB=a﹣,∵平行四边形OBAD的面积是5,∴(a﹣)=5,解得k=﹣2,故选:D.9.(2023•连云港)如图,矩形OABC的顶点A在反比例函数y=(x<0)的图象上,顶点B、C在第一象限,对角线AC∥x轴,交y轴于点D.若矩形OABC的面积是6,cos∠OAC=,则k= ﹣ .【答案】﹣.【解答】解:作AE⊥x轴于E,∵矩形OABC的面积是6,∴△AOC的面积是3,∵∠AOC=90°,cos∠OAC=,∴,∵对角线AC∥x轴,∴∠AOE=∠OAC,∵∠OEA=∠AOC=90°,∴△OEA∽△AOC,∴,∴,∴S△OEA=,∵S△OEA=|k|,k<0,∴k=﹣.故答案为:﹣.10.(2023•枣庄)如图,在反比例函数(x>0)的图象上有P1,P2,P3,…P2024等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2023,则S1+S2+S3+…+S2023= .【答案】.【解答】解:∵P1,P2,P3,...P2024的横坐标依次为1,2,3, (2024)∴阴影矩形的一边长都为1,将除第一个矩形外的所有矩形向左平移至y轴,∴S 1+S2+S3+…+S2023=,把x=2024代入关系式得,y=,即OA=,∴S矩形OABC=OA•OC=,由几何意义得,=8,∴=8﹣=.故答案为:.11.(2023•朝阳)如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接PA,PB.若△ABP的面积等于3,则k的值为 6 .【答案】6.【解答】解:设反比例函数的解析式为y=,∵△AOB的面积=△ABP的面积=3,△AOB的面积=|k|,∴|k|=3,∴k=±6;又∵反比例函数的图象的一支位于第一象限,∴k>0.∴k=6.故答案为:6.12.(2023•衢州)如图,点A,B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF,反比例函数y=(k>0)的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为 24 .【答案】见试题解答内容【解答】解:设OA=4a,∵AO=2AB,∴AB=2a,∴OB=AB+OA=6a,则B(6a,0),由于在正方形ABEF中,AB=BE=2a,∵Q为BE中点,∴BQ=AB=a,∴Q(6a,a),∵Q在反比例函数y=(k>0))上,∴k=6a×a=6a2,∵四边形OACD是正方形,∴C(4a,4a),∵P在CD上,∴P点纵坐标为4a,∵P在反比例函数y=(k>0)上,∴P点横坐标为:x=,∴P(,4a),∵作PM⊥x轴于点M,QN⊥y轴于点N,∴四边形OMNH是矩形,∴NH=,MH=a,∴S矩形OMHN=NH×MH=×a=6,则k=24,故答案为:24.13.(2023•锦州)如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为 4 .【答案】4.【解答】解:过点C作CD⊥y轴于点D,如图:设点C的坐标为(a,b),点A的坐标为(0,c),∴CD=a,OA=c,∵△AOC的面积是6,∴,∴ac=12,∵点C(a,b)在反比例函数(x>0)的图象上,∴k=ab,∵点B为AC的中点,∴点,∵点B在反比例函数(x>0)的图象上,∴,即:4k=a(b+c),∴4k=ab+ac,将ab=k,ac=12代入上式得:k=4.故答案为:4.14.(2023•黄石)如图,点A(a,)和B(b,)在反比例函数y=(k>0)的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为 ;若△AOB的面积为,则= 2 .【答案】,2.【解答】解:因为点A(a,)在反比例函数y=的图象上,则,又a>0,解得k=5.根据k的几何意义可知,.过点B作x轴的垂线,垂足为D,则S△OBD+S梯形ACDB=S△AOC+S△AOB,又根据k的几何意义可知,S△OBD=S△AOC,则S梯形ACDB=S△AOB.又△AOB的面积为,且A(a,),B(b,),所以,即.解得.又a>b>0,所以.故答案为:,2.15.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为 6 .【答案】6.【解答】解:如图,延长CD交y轴于E,连接OD,∵矩形ABCD的面积是8,∴S△ADC=4,∵AC=2AO,∴S△ADO=2,∵AD∥OE,∴△ACD∽△OCE,∴AD:OE=AC:OC=2:3,∴S△ODE=3,由几何意义得,=3,∵k>0,∴k=6,故答案为:6.16.(2023•绍兴)如图,在平面直角坐标系xOy中,函数(k为大于0的常数,x>0)图象上的两点A (x1,y1),B(x2,y2),满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 2 .【答案】2.【解答】解:如图,延长CA交y轴于E,延长CB交x轴于点F,∴CE⊥y轴,CF⊥x轴,∴四边形OECF为矩形,∵x2=2x1,∴点A为CE的中点,由几何意义得,S△OAE=S△OBF,∴点B为CF的中点,∴S△OAB=S矩形OECF=6,∴S矩形OECF=16,∴S△ABC=×16=2.故答案为:2.217.(2022•烟台)如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 6 .【答案】见试题解答内容【解答】解:因为D为AC的中点,△AOD的面积为3,所以△AOC的面积为6,所以k=12=2m.解得:m=6.故答案为:6.18.(2022•黄石)如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k= 8 .【答案】8.【解答】解:如图,过点E作EH⊥BC于H,设点A(a,),C(c,0),∵点E是矩形ABCD的对角线的交点,∴E(,),∵点E在反比例函数y=的图象上,∴=k,∴c=3a,∵△OCE的面积为6,∴OC•EH=c•=×3a•=6,∴k=8,故答案为:8.19.(2022•衢州)如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC=6,则k= .【答案】.【解答】解:如图,作CM⊥AB于点M,DN⊥AB于点N,设C(m,),则OM=m,CM=,∵OE∥CM,AE=CE,∴==1,∴AO=m,∵DN∥CM,CD=2BD,∴===,∴DN=,∴D的纵坐标为,∴=,∴x=3m,即ON=3m,∴MN=2m,∴BN=m,∴AB=5m,∵S△ABC=6,∴5m•=6,∴k=.故答案为:.20.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为 9 .【答案】9.【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图,∵△OMN是边长为10的等边三角形,∴OM=ON=MN=10,∠MON=∠M=∠MNO=60°设OC=b,则BC=,OB=2b,∴BM=OM﹣OB=10﹣2b,B(b,b),∵∠M=60°,AB⊥OM,∴AM=2BM=20﹣4b,∴AN=MN﹣AM=10﹣(20﹣4b)=4b﹣10,∵∠AND=60°,∴DN==2b﹣5,AD=AN=2b﹣5,∴OD=ON﹣DN=15﹣2b,∴A(15﹣2b,2b﹣5),∵A、B两点都在反比例函数y=(x>0)的图象上,∴k=(15﹣2b)(2b﹣5)=b•b,解得b=3或5,当b=5时,OB=2b=10,此时B与M重合,不符题意,舍去,∴b=3,∴k=b•b=9,故答案为:9.21.(2022•鄂尔多斯)如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= 10 .【答案】见试题解答内容【解答】解:作EH⊥y轴于点H则四边形BCHE、AEHO都为矩形,∵∠ECF=45°,∴∠OCD+∠OCF=45°,∵∠DOC+∠OCF=45°,∴∠BCE=∠OCD,∵BC=OC,∠B=∠COD,∴△BCE≌△OCD(ASA),∴S△BCE=S△COD=5,∴S△CEH=5,S矩形BCHE=10,∴根据反比例函数系数k的几何意义得:k1﹣k2=S矩形BCHE=10,故答案为:10.22.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为 y=﹣ .【答案】y=﹣.【解答】解:如图,作AD⊥x轴于D,BC⊥x轴于C,∴∠ADO=∠BCO=90°,∵∠AOB=90°,∴∠AOD+∠BOC=90°,∴∠AOD+∠DAO=90°,∴∠BOC=∠DAO,∵OB=OA,∴△BOC≌△OAD(AAS),∵点B在反比例函数y=(x>0)的图象上,∴S△OBC=,∴S△OAD=,∴k=﹣1,∴经过点A的反比例函数解析式为y=﹣.故答案为:y=﹣.23.(2022•绍兴)如图,在平面直角坐标系xOy中,点A(0,4),B(3,4),将△ABO向右平移到△CDE位置,A的对应点是C,O的对应点是E,函数y=(k≠0)的图象经过点C和DE的中点F,则k的值是 6 .【答案】6.【解答】解:过点F作FG⊥x轴于点G,FH⊥y轴于点H,过点D作DQ⊥x轴于点Q,如图所示,根据题意可知,AC=OE=BD,设AC=OE=BD=a,∴四边形ACEO的面积为4a,∵F为DE的中点,FG⊥x轴,DQ⊥x轴,∴FG为△EDQ的中位线,∴FG=DQ=2,EG=EQ=,∴四边形HFGO的面积为2(a+),∴k=4a=2(a+),解得:a=,∴k=6.故答案为:6.24.(2022•内蒙古)如图,在平面直角坐标系中,Rt△OAB的直角顶点B在x轴的正半轴上,点O与原点重合,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C,交AB于点D,连接CD.若△ACD的面积是1,则k的值是 .【答案】.【解答】解:连接OD,过C作CE∥AB,交x轴于E,∵∠ABO=90°,反比例函数y=(x>0)的图象经过OA的中点C,∴S△COE=S△BOD=k,S△ACD=S△OCD=1,∵CE∥AB,∴△OCE∽△OAB,∴△OCE与△OAB得到面积比为1:4,∴4S△OCE=S△OAB,∴4×k=1+1+k,∴k=.故答案为:.。
反比例函数中的面积问题专题课程教案

反比例函数中的面积问题专题课程教案第一章:反比例函数的概念与性质1.1 反比例函数的定义引导学生回顾反比例函数的定义,即形如y = k/x (k ≠0) 的函数。
强调反比例函数中k 的作用,k 表示函数在x 轴和y 轴上的截距。
1.2 反比例函数的性质分析反比例函数的图像特征,如双曲线、渐近线等。
探讨反比例函数的单调性、奇偶性等性质。
第二章:反比例函数图像的绘制2.1 绘制反比例函数图像的基本方法介绍利用坐标轴、点斜式等方法绘制反比例函数图像。
强调反比例函数图像的中心对称性和轴对称性。
2.2 利用尺规作图绘制反比例函数图像引导学生运用尺规作图的方法,绘制特定k 值的的反比例函数图像。
讨论不同k 值对图像形状和位置的影响。
第三章:反比例函数中的面积问题3.1 反比例函数图像的面积计算引入反比例函数图像中任意三角形、四边形的面积计算方法。
强调利用函数值和坐标轴围成的封闭区域的面积计算公式。
3.2 反比例函数图像与坐标轴围成的面积引导学生探讨反比例函数图像与坐标轴围成的封闭区域的面积。
分析不同k 值对封闭区域形状和面积的影响。
第四章:反比例函数图像的交点问题4.1 反比例函数图像与直线交点的求解引导学生运用解析几何方法,求解反比例函数图像与直线的交点。
强调运用韦达定理、判别式等工具解题。
4.2 反比例函数图像与圆的交点问题探讨反比例函数图像与圆的交点个数和位置关系。
引导学生运用代数方法解反比例函数与圆的交点问题。
第五章:反比例函数图像的应用问题5.1 反比例函数图像在实际问题中的应用引入实际问题,如面积、距离、速度等,运用反比例函数图像解决。
强调反比例函数图像在实际问题中的直观性和实用性。
5.2 反比例函数图像的综合应用问题引导学生运用反比例函数图像解决综合应用问题,如平面几何、物理等。
强调运用反比例函数图像解决问题的方法和技巧。
第六章:反比例函数图像的变换6.1 反比例函数图像的平移讲解反比例函数图像如何通过平移实现变换,包括上下左右平移。
反比例函数求面积

反比例函数求面积反比例函数是数学中一种常见的函数形式,其表达式为y =k/x,其中k为常数。
反比例函数具有一定的特点,其中最常见的应用就是求解面积相关问题。
在几何学中,很多问题可以通过反比例函数来求解面积,以下将介绍几个常见的例子。
1. 矩形的面积:可以将矩形的长记为x,宽记为y,则矩形的面积为S = xy。
如果已知矩形的面积S和宽y,可以通过反比例函数求解矩形的长x。
我们知道xy = S,对上式两边同时取倒数,得到yx = 1/S,可以看到yx符合反比例函数的形式,因此可以通过反比例函数求解矩形的长。
2. 圆的面积:圆的面积公式为S = πr²,其中r为圆的半径。
如果已知圆的面积S,可以通过反比例函数求解圆的半径r。
我们知道S = πr²,对这个式子两边同时取倒数,得到1/S = 1/(πr²),可以看到1/S符合反比例函数的形式,因此可以通过反比例函数求解圆的半径。
3. 三角形的面积:三角形的面积公式为S = 1/2bh,其中b为底边的长度,h为高的长度。
如果已知三角形的面积S和底边长度b,可以通过反比例函数求解高h。
我们知道S = 1/2bh,对这个式子两边同时取倒数,得到1/S = 2/bh,可以看到1/S符合反比例函数的形式,因此可以通过反比例函数求解三角形的高。
在实际问题中,反比例函数也有着广泛的应用。
例如,汽车行驶的时间和速度之间就存在着反比例关系。
假设一辆汽车行驶的距离为d,速度为v,行驶的时间为t。
根据定义,速度等于距离除以时间,即v = d/t。
如果我们已知汽车行驶的距离d和行驶的时间t,可以通过反比例函数求解汽车的速度v。
在数学教育中,反比例函数也是一个重要的概念,它可以帮助学生理解函数的性质和图像的变化。
学生可以通过绘制函数图像、计算函数的值等方式来探究反比例函数的特点,并且可以通过实际应用问题来加深对反比例函数的理解。
综上所述,反比例函数是求解面积问题常用的数学工具之一。
反比例函数面积问题

反比例函数面积问题
反比例函数面积问题通常是指与反比例函数相关的图形面积的计算
问题。
例如,给定反比例函数y=k/x的图像与坐标轴所围成的区域,要求该区域的面积。
解决这类问题通常需要应用积分学知识,因为反比例函数的图像通常是一个双曲线,与坐标轴围成的区域是一个不规则图形。
通过积分,我们可以求出这个不规则图形的面积。
具体地,如果要求反比例函数y=k/x在第一象限内与x轴、y轴所围成的区域面积,可以先求出该函数在第一象限内的图像与x轴之间的面积,然后再乘以2(因为反比例函数在第一、三象限内是对称的)。
这个面积可以通过定积分来计算,积分区间是从0到正无穷大,被积函数是y=k/x。
需要注意的是,由于反比例函数的图像在x轴和y轴上都趋于无穷大,
因此所求得的面积也是无穷大的。
但是,在某些特定情况下,例如给定一个特定的矩形区域,我们可以通过计算该矩形区域内反比例函数图像的面积来得到一个有限的数值。
总之,反比例函数面积问题需要根据具体情况进行具体分析,通常需要应用积分学知识和几何知识来解决。
以上是对于反比例函数面积问题5的回答,希望对你有所帮助。
专题10 由面积求反比例函数比例系数的4种常见压轴题型全攻略(原卷版)

专题10由面积求反比例函数比例系数的4种常见压轴题型全攻略【考点导航】目录【典型例题】 (1)【考点一由三角形面积求反比例的比例系数】..............................................................................................1【考点二由四边形面积求反比例的比例系数】..............................................................................................2【考点三由其它面积问题求反比例函数解析式】 (2)【考点四反比例函数中求面积问题的拓展提高】.........................................................................................3【过关检测】. (4)【典型例题】【例题1】如图所示(图象在第二象限),点A 是反比例函数ky x=上的一点,AM x ⊥轴于点M ,AMO 的面积为2,则k 的值为()A .2B .2-C .4D .4-【变式1】如图,点P 是反比例函数()10k y k x-=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M ,若POM 的面积等于3,则k 的值是()A .6B .5C .5-D .6-【变式2】如图,A 是反比例函数ky x=的图象上一点,AB y ⊥轴于B ,点C 在x 轴上,若ABC 面积为2,则k 的值为()A .4-B .1C .2D .4【变式3】如图,点A 是反比例函数()0ky x x=<图象上一点,过点A 作AB y ⊥轴于点D ,且点D 为线段AB 的中点.若点C 为x 轴上任意一点,且ABC 的面积为12,则求k 的值为()A .12-B .8-C .6-D .6【考点二由四边形面积求反比例的比例系数】【例题2】如图,过双曲线上任意一点P 分别作x 轴,y 轴的垂线PM ,PN ,交x 轴、y 轴于点M 、N ,所得矩形PMON 的面积为8,则k 的值是()A .4B .4-C .8D .8-【变式1】如图,四边形ABCD 是平行四边形,CD 在x 轴上,点B 在y 轴上,反比例函数(0)ky x x=>的图象经过第一象限点A ,且ABCD Y 的面积为6,则k =().A .6B .3C .9D .12【变式2】如图,A 、B 两点在反比例函数1k y x =的图象上,C ,D 两点在反比例函数2ky x=的图象上,AC y ⊥轴于点E ,BD y ⊥轴于点F ,5AC =,3BD =,EF 的长度为8,则12k k -的值是()A .8B .11C .15D .16【变式3】如图,点A B ,是反比例函数()0k y x x=>图像上的点,点,C D 分别在x 轴,y 轴正半轴上.若四边形ABCD 为菱形,BD x ∥轴,6ABCD S =菱形,则k 的值()A .3B .6C .12D .24【考点三由其它面积问题求反比例函数解析式】【例题3】如图,点A ,B 分别在函数()0ay a x=>图象的两支上(A 在第一象限),连接AB 交x 轴于点C .点D ,E 在函数by x=(0b <,0x <)图象上,AE x 轴,BD y ∥轴,连接DE ,BE .(1)若2AC BC =,ABE 的面积为9,则a b -的值为.(2)在(1)的条件下,若四边形ABDE 的面积为14,则经过点D 的反比例函数解析式为.【变式1】如图,点B 是反比例函数()0k y x x=>上一点,矩形OABC 的周长是16,正方形BCGH 和正方形OCDF 的面积之和为56,则反比例函数的解析式是.【变式2】如图,已知点(),0A a ,()0,B b ,且a 、b 满足()2130a a b ++++=,平行四边形ABCD 的边AD 与y 轴交于点E ,且E 为AD 中点,双曲线ky x=经过C 、D 两点.(1)=a ______,b =______;(2)求反比例函数表达式;【考点四反比例函数中求面积问题的拓展提高】【例题4】如图,在反比例函数()0ky x x =>的图像上,有点1P ,2P ,3P ,4P ,它们的横坐标依次为1,2,3,4.分别过这些点作垂直于x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S ,2S ,3S ,若1233S S S ++=,则k 的值为()A .2.5B .3C .4D .无法确定【变式1】如图,点A ,B 依次在反比例函数1k y x=(常数10k >,0)x >的图象上,点C ,D 依次在反比例函数2k y x=(常数20k <,0)x >的图象上,4AC BD =,AC BD y ∥∥轴,AE ,CF 分别垂直y 轴于点E ,F ,BG AC ⊥于点G ,DH AC ⊥于点H .若2EO FO =,阴影部分面积为8,则12k k ,的值分别为.【变式2】如图,反比例函数()60y x x=-<的图象经过点A ,反比例函数()0ky x x =<的图象经过点B ,AB所在直线垂直x 轴于点C ,M 是y 轴上一点,连接MA ,MB ,若95MAB S =△,则k 的值等于.【变式3】如图,在平面直角坐标系中,点A 、B 为反比例函数()0ky k x=≠上两点,且点B 横坐标为点A 横坐标的两倍,分别过点A 作x 轴平行线,过点B 作y 轴平行线,两直线交于点C ,若S 6OAB = ,则S ABC =.【过关检测】一、单选题1.如图,点A ,B 分别在反比例函数1y x=和4y x=的图象上,且AB x ∥轴,连接OB 与反比例函数1y x =的图象交于点C ,连接AC ,则ABC 的面积为()A .34B .98C .32D .32.如图,平行于x 轴的直线与函数6(0)y x x =>,()0>0>,ky k x x=的图象分别相交于A ,B 两点,点A 在点B 的右侧,C 为x 轴上的一个动点,若ABC 的面积为2.则k 的值为()A .4B .4-C .2D .2-3.如图,Rt BOC 的一条直角边OC 在x 轴正半轴上,双曲线ky x=过BOC 的斜边OB 的中点A ,与另一直角边BC 相交于点D .若BOD 的面积是6,则k 的值是()A .6-B .4-C .4D .64.如图,点A 在反比例函数4y x =的图象上,点B 在反比例函数()0ky k x=≠的图象上,过点A 、B 分别作x 轴、y 轴的垂线,垂足分别为D 、C 、E 、F ,且OC BE =,连接BC 恰好经过点D ,则k 的值是()A .4B .8C .8-D .10-二、填空题5.如图,A 是反比例函数ky x=的图象上一点,AB y ⊥轴于点B ,若ABO 的面积为2,则k 的值为.6.如图,点P 是第二象限内的一点,且在反比例函数ky x=的图象上,过点P 作PA x ⊥轴于点A ,若PAO 的面积为5,则k 的值为.7.如图,反比例函数与正比例函数的图象相交于A 、B 两点,过点A 作AC x ⊥轴于点C .若ABC 的面积是4,则这个反比例函数的解析式为.8.双曲线()1:0,0k C y k x x =≠>和()21:0C y x x=>如图所示,A 是双曲线1C 上一点,过点A 作AB x ⊥轴,垂足为B ,交双曲线2C 于点C ,连接,OA OC ,若AOC 的面积为2,则k =.9.如图,在平面直角坐标系中,点O 为坐标原点,ABCD Y 的顶点()1,A b 在双曲线()20=>y x x上,顶点B 在双曲线ky x=(0k <,且0x <)上,边CD 在x 轴上.①若4k =-,则CD 的长度为;②若ABCD Y 的面积是7,则k 的值是.10.如图,直线l 与x 轴,y 轴分别交于A ,B 两点,且与反比例函数(0)k y x x=>的图象交于点C ,若5AOB COB S S ==△△,则k =.11.如图,点A ,B 是函数0)ky x x =<(图象上两点,过点A 作AC x ⊥轴,垂足为点C ,AC 交OB 于点D .若ADO △的面积为3,点D 为OB 的中点,则k 的值为.12.如图,点P 是双曲线(0)k y x x=>上的一点,点A ,B 是x 轴正半轴上的不同点,连接AP ,BP ,已知:1:2OA AB =,AP BP =,AOP 的面积为3,则k =.13.直线6y =与双曲线3y x=,()0my m x=<相交于点A ,B ,作AC x ⊥轴于点C ,作BD x ⊥轴于点D ,四边形ACDB 的面积为5,则m 的值为.14.如图,A ,B 两点在反比例函数m y x =的图像上,C ,D 两点在反比例函数ny x=的图像上,AC y ⊥轴于点E ,BD y ⊥轴于F ,3AC =,2BD =,5EF =,则m n -的值是.15.如图,点A 是反比例函数()0ky x x=>的图象上一点,过点A 作AC x ⊥轴,垂足为点C ,延长AC 至点B ,使2BC AC =,点D 是y 轴上任意一点,连接AD ,BD ,若ABD △的面积是6,则k =.16.如图,过点O 作直线与双曲线()0ky k x=≠交于A ,B 两点,过点B 作BC x ⊥轴于点C ,作BD y ⊥轴于点D ,在x 轴、y 轴上分别取点E ,F ,使点A ,E ,F 在同一条直线上,且AE AF =,设图中矩形ODBC 的面积为1S ,EOF 的面积为2S ,则1S ,2S 的数量关系是.17.如图,点5,A a a ⎛⎫⎪⎝⎭和5,B b b ⎛⎫ ⎪⎝⎭在反比例函数()0k y k x =>的图象上,其中0a b >>.过点A 作AC x ⊥轴于点C ,若AOB 的面积为154,则a b =.18.在直角坐标平面内,函数(0)ky k x=≠的图像在同一个象限内经过A 、B 两点,且(2,4)A .过点B 作y 轴垂线,垂足为点C ,连接AC 、AB 、CB ,若2ABC S =△,则点B 的坐标是.三、解答题19.如图,A ,D 关于原点对称,B 为反比例函数ky x=图象上异于D 的一个点.过D 作DC 垂直于y 轴于点C .11(1)若D 的坐标为()2,3--,则A 的坐标为______;(2)若ODC 的面积为2,则k 的值为______;(3)在(1)的条件下,若B 的纵坐标为1-,求ABO 的面积.20.如图,在平面直角坐标系中,Rt ABC △的斜边BC 在x 轴上,坐标原点是BC 的中点,30ABC ∠=︒,4BC =,双曲线k y x=经过点A .(1)求k ;(2)直线AC 与双曲线33y x=-在第四象限交于点D .求ABD △的面积.21.已知,矩形OCBA 在平面直角坐标系中的位置如图所示,点C 在x 轴的正半轴上,点A 在y 轴的正半轴上,已知点B 的坐标为(4,2),反比例函数k y x=的图象经过AB 的中点D ,且与BC 交于点E ,连接OD ,OE .(1)反比例函数k y x=的表达式是______,点E 的坐标为______;(2)点M 为y 轴正半轴上一点,若MBO △的面积等于ODE 的面积,求点M 的坐标;(3)点P 为x 轴上一点,点Q 为反比例函数k y x=图象上一点,是否存在点P 、Q 使得以点P ,Q ,D ,E 为顶点的四边形为平行四边形?若存在,求出点Q 的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数面积专题一、选择题(共5小题)1、(2012•泸州)如图,在△OAB中,C就就是AB得中点,反比例函数y= (k>0)在第一象限得图象经过A、C两点,若△OAB面积为6,则k得值为()A、2B、4C、8D、162、(2010•无锡)如图,已知梯形ABCO得底边AO在x轴上,BC∥AO,AB⊥AO,过点C得双曲线交OB于D,且OD:DB=1:2,若△OBC得面积等于3,则k得值()A、等于2B、等于C、等于D、无法确定3、(2010•内江)如图,反比例函数得图象经过矩形OABC对角线得交点M,分别与AB、BC相交于点D、E、若四边形ODBE得面积为6,则k得值为()A、1B、2C、3D、44、(2010•抚顺)如图所示,点A就就是双曲线y=(x>0)上得一动点,过A作AC⊥y轴,垂足为点C,作AC得垂直平分线双曲线于点B,交x轴于点D、当点A在双曲线上从左到右运动时,四边形ABCD得面积()A、逐渐变小B、由大变小再由小变大C、由小变大再有大变小D、不变5、(2006•绵阳)如图,梯形AOBC得顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC得面积为()A、3B、C、﹣1D、+1二、填空题(共8小题)6、(2012•福建)如图,点A在双曲线上,点B在双曲线上,且AB∥y轴,点P就就是y轴上得任意一点,则△PAB得面积为_________、7、(2012•常州)如图,已知反比例函数y=(k1>0),y=(k2<0)、点A在y轴得正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数得图象交于点B与C,连接OC、OB、若△BOC得面积为,AC:AB=2:3,则k1= _________,k2=_________ 、8、(2011•遵义)如图,已知双曲线,,点P为双曲线上得一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线于D、C两点,则△PCD得面积为_________、9、(2011•孝感)如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它得面积为_________、10、(2010•衡阳)如图,已知双曲线y=(k>0)经过直角三角形OAB斜边OB得中点D,与直角边AB相交于点C、若△OBC得面积为3,则k=_________、11、如图,Rt△ABC得直角边BC 在x轴正半轴上,斜边AC边上得中线BD反向延长线交y轴负半轴于E,双曲线(x>0)得图象经过点A,若S△BEC=10,则k等于_________、12、如图,直角梯形OABC,AB∥OC,反比例函数y=(x>0)得图象经过B点与BC得中点D,且梯形OABC得面积为2,则该反比例函数得解析式为_________ 、13、如图(1),在Rt△ABC得边AB得同侧,分别以三边为直径作三个半圆,大半圆以外得两部分面积分别为S1、S3,三角形得面积为S2;如图(2),两个反比例函数与在第一象限内得图象如图所示,点P在得图象上,PC⊥x轴于点C,PD⊥y轴于点D,交得图象于分别于点A,B,当点P在得图象上运动时,△BOD,四边形OAP B,△AOC得面积分别为S1、S2、S3;如图(3),点E为▱ABCD边AD上任意一点,三个三角形得面积分别为S1、S2、S3;如图(4),梯形ABCD中,AB∥CD,∠DAB+∠ABC=90°,AB=2CD,以AD、DC、CB为边作三个正方形得面积分别为S1、S2、S3、在这四个图形中满足S1+S3=S2有_________ (填序号)、2012年9月窗户得初中数学组卷参考答案与试题解析一、选择题(共5小题)1、(2012•泸州)如图,在△OAB中,C就就是AB得中点,反比例函数y= (k>0)在第一象限得图象经过A、C两点,若△OAB面积为6,则k得值为()A、2B、4C、8D、16考点: 反比例函数系数k得几何意义;三角形中位线定理。
分析:分别过点A、点C作OB得垂线,垂足分别为点M、点N,根据C就就是AB得中点得到CE为△ADE得中位线,然后设MN=NB=a,CN=b,AM=2b,根据OM•AM=ON•CN,得到OM=a,最后根据面积=3a•2b÷2=3ab=6求得ab=2从而求得k=a•2b=2ab=4、解答:解:分别过点A、点C作OB得垂线,垂足分别为点M、点N,如图,∵点C为AB得中点,∴CE为△AMB得中位线,∴MN=NB=a,CN=b,AM=2b,∵又因为OM•AM=ON•CN∴OM=a∴这样面积=3a•2b÷2=3ab=6,∴ab=2,∴k=a•2b=2ab=4,故选B、点评:本题考查了反比例函数得比例系数得几何意义及三角形得中位线定理,解题得关键就就是正确得作出辅助线、2、(2010•无锡)如图,已知梯形ABCO得底边AO在x轴上,BC∥AO,AB⊥AO,过点C得双曲线交OB于D,且OD:DB=1:2,若△OBC得面积等于3,则k得值()A、等于2B、等于C、等于D、无法确定考点:反比例函数系数k得几何意义。
专题:数形结合。
分析:先设出B点坐标,即可表示出C点坐标,根据三角形得面积公式与反比例函数得几何意义即可解答、解答:解:方法1:设B点坐标为(a,b),∵OD:DB=1:2,∴D点坐标为(a,b),根据反比例函数得几何意义,∴a•b=k,∴ab=9k①,∵BC∥AO,AB⊥AO,C在反比例函数y=得图象上,∴设C点横坐标为m,则C点坐标为(m,b)将(m,b)代入y=得,m=,BC=a﹣,又因为△OBC得高为AB,所以S△OBC=(a﹣)•b=3,所以(a﹣)•b=3,(a﹣)b=6,ab﹣k=6②,把①代入②得,9k﹣k=6,解得k=、方法2:延长BC交y轴于E,过D作x轴得垂线,垂足为F、由△OAB得面积=△OBE得面积,△ODF得面积=△OCE得面积,可知,△ODF得面积=梯形DFAB=△BOC得面积=,即k=,k=、故选B、点评:本题考查了反比例系数k得几何意义、此题还可这样理解:当满足OD:DB=1:2时,当D在函数图象上运动时,面积为定值、3、(2010•内江)如图,反比例函数得图象经过矩形OABC对角线得交点M,分别与AB、BC相交于点D、E、若四边形ODBE得面积为6,则k得值为( )A、1B、2C、3D、4考点:反比例函数系数k得几何意义。
分析:本题可从反比例函数图象上得点E、M、D入手,分别找出△OCE、△OAD、□OABC得面积与|k|得关系,列出等式求出k值、解答:解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线得交点,则S矩形ABCO=4S□ONMG=4|k|, 由于函数图象在第一象限,k>0,则++6=4k,k=2、故选B、点评:本题考查反比例函数系数k得几何意义,过双曲线上得任意一点分别向两条坐标轴作垂线,与坐标轴围成得矩形面积就等于|k|、本知识点就就是中考得重要考点,同学们应高度关注、4、(2010•抚顺)如图所示,点A就就是双曲线y=(x>0)上得一动点,过A作AC⊥y轴,垂足为点C,作AC得垂直平分线双曲线于点B,交x轴于点D、当点A在双曲线上从左到右运动时,四边形ABCD得面积()A、逐渐变小B、由大变小再由小变大C、由小变大再有大变小D、不变考点: 反比例函数系数k得几何意义。
专题:数形结合;几何变换。
分析:四边形ABCD得面积等于×AC×BD,AC、BC可以用A点得坐标表示,即可求解、解答:解:设A点得坐标就就是(m,n),则m•n=1,则D点得横坐标就就是,把x=代入y=,得到y=,即BD=、∴四边形ABCD得面积=AC×BD=×m×=1、即四边形ABCD得面积不随C点得变化而变化、故选D、点评:本题主要考查得就就是利用反比例函数系数k得几何意义求对角线互相垂直得四边形面积得计算方法、5、(2006•绵阳)如图,梯形AOBC得顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC得面积为( )A、3B、C、﹣1 D、+1考点:反比例函数系数k得几何意义;梯形。
专题:综合题。
分析:四边形AOEC得面积=梯形AOBC得面积﹣三角形OBE得面积、根据AO∥BC,且直线BC经过E(2,0),用待定系数法求出BE得解析式,再求出B、C两点得坐标、根据C点坐标得出反比例函数解析式为y=,解方程组,求出A点坐标、根据勾股定理求出OA、BC得长度,易求梯形AOBC得高,从而求出梯形AOBC得面积、△OBE 就就是等腰直角三角形,腰长就就是2,易求其面积、解答:解:因为AO∥BC,上底边OA在直线y=x上, 则可设BE得解析式为y=x+b,将E(2,0)代入上式得,b=﹣2,BE得解析式为y=x﹣2、把y=1代入y=x﹣2,得x=3,C点坐标为(3,1), 则反比例函数解析式为y=,将它与y=x组成方程组得:,解得x=,x=﹣(负值舍去)、代入y=x得,y=、A点坐标为(,),OA==,BC==3,∵B(0,﹣2),E(2,0),∴BE=2,∴BE边上得高为,∴梯形AOBC高为:,梯形AOBC面积为:×(3+)×=3+,△OBE得面积为:×2×2=2,则四边形AOEC得面积为3+﹣2=1+、故选D、点评:此题综合考查了梯形与函数得有关知识,此题难度较大,考查了函数与方程得关系,交点坐标与方程组得解得关系,以及反比例函数系数k得几何意义、要用梯形、三角形得面积公式及勾股定理来计算、二、填空题(共8小题)6、(2012•福建)如图,点A在双曲线上,点B在双曲线上,且AB∥y轴,点P就就是y轴上得任意一点,则△PAB得面积为1、考点: 反比例函数系数k得几何意义。
专题: 探究型。
分析:设A(x,),则B(x,),再根据三角形得面积公式求解、解答:解:设A(x,),∵AB∥y轴,∴B(x,),∴S△ABC=AB•x=(﹣)×x=1、故答案为:1、点评:本题考查得就就是反比例函数系数k得几何意义,先根据设出A点坐标,再由AB∥y轴得出B点坐标就就是解答此题得关键、7、(2012•常州)如图,已知反比例函数y=(k1>0),y=(k2<0)、点A在y轴得正半轴上,过点A 作直线BC∥x轴,且分别与两个反比例函数得图象交于点B与C,连接OC、OB、若△BOC得面积为,AC:AB=2:3,则k1=2,k2=﹣3、考点: 反比例函数系数k得几何意义。
