初二下反比例函数与面积和动点问题小综合
反比例函数小题综合

期末专题07 反比例函数小题综合(江苏专用)一、单选题1.(2022春·江苏淮安·八年级统考期末)矩形的面积为20平方米,它的长y 米,宽x 米之间的函数表达式是( )A .20y x=B .20y x =C .20y x =+D .20y x=-2.(2022春·江苏宿迁·八年级统考期末)若反比例函数ky x=的图象经过点()3,4A -,则下列各点中也在这个函数图象的是( )A .()2,3-B .()4,3-C .()6,2--D .38,2æöç÷èø3.(2022春·江苏宿迁·八年级统考期末)若点()36A ,在反比例函数()0ky k x=¹的图像上,则k 的值为( )A .18-B .2-C .18D .24.(2022春·江苏南京·八年级期末)已知点(-2,a )(2,b )(3,c )在函数22k y x +=(k 为常数)的图像上,则下列判断正确的是( )A .a <c <bB .b <a <cC .a <b <cD .c <b <a5.(2022春·江苏无锡·八年级统考期末)古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N 和0.5m ,小明最多能使出500N 的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )A .至多为1.6mB .至少为1.6mC .至多为0.625mD .至少为0.625m6.(2022春·江苏无锡·八年级统考期末)已知点A (﹣2,y 1)、B (1,y 2)、C (3,y 3)三点都在反比例函数y kx= (k <0) 的图像上,则下列关系正确的是( )A .y 2<y 3<y 1B .y 3<y 2<y 1C .y 1<y 3<y 2D .y 1<y 2<y 37.(2022春·江苏扬州·八年级统考期末)若点()211,a y --、()222,a y --、()231,a y +都在反比例函数6y x=-的图象上,则1y 、2y 、3y 的大小关系是( )A .213y y y <<B .321y y y <<C .312y y y <<D .123y y y <<8.(2022春·江苏扬州·八年级统考期末)已知反比例函数3y x=,下列结论中不正确的是( )A .其图像经过点(1,3)--B .其图像分别位于第一、第三象限C .当0x <时,y 随x 的增大而增大D .当1x >时,03y <<9.(2022春·江苏无锡·八年级统考期末)反比例函数1y x=的图象与一次函数2y x =+的图象交于点(),A a b ,则a ab b --的值是( )A .3B .-3C .-1D .110.(2022春·江苏宿迁·八年级统考期末)如图,在平面直角坐标系中,将一块含有45°角的直角三角板按如图所示的方式放置,直角顶点C 的坐标为(2,0),顶点A 的坐标为(0,4),顶点B 恰好落在第一象限内,反比例函数ky x=的图像经过点B ,则k 的值为( )A .4B .6C .8D .1211.(2022春·江苏盐城·八年级校联考期末)在同一直角坐标系中,函数y kx k =-与(0)ky k x=¹的图象大致是( )A .B .C .D .12.(2022春·江苏无锡·八年级校考期末)已知A (1x ,1y )、B (2x ,2y )、C (3x ,3y )是反比例函数y =5x的图象上三点,且1y <2y <0<3y ,则下列结论正确的是( )A .1x <2x <3xB .2x <1x <3xC .2x <3x <1xD .3x <2x <1x 13.(2022春·江苏扬州·八年级校联考期末)如图,△AOB 和△ACD 均为正三角形,且顶点B 、D 均在双曲线6y x=(x >0)上,连接BC 交AD 于P ,连接OP ,则图中OBP S △是( )A B .3C .6D .1214.(2022春·江苏苏州·八年级校考期末)如图,已知点(3,0)A ,(0,4)B ,C 是y 轴上位于点B 上方的一点,AD 平分OAB Ð,BE 平分ABC Ð,直线BE 交AD 于点D .若反比例函数(0)ky x x=<的图象经过点D ,则k 的值是( )A .8-B .9-C .10-D .12-15.(2022春·江苏无锡·八年级统考期末)如图,点O 为坐标原点,菱形OABC 的边OC 在x 轴的正半轴上,对角线AC 、BD 交于点D ,反比例函数()0ky x x=>的图象经过点A和点D ,若菱形OABC 的面积为A 的坐标为( )A .2ö÷÷øB .(C .34æçèD .æççè二、填空题16.(2022春·江苏淮安·八年级统考期末)若反比例函数1m y x+=的图象在二、四象限,则m 的取值范围为____________.17.(2022春·江苏宿迁·八年级统考期末)如图,在平面直角坐标系中,O 为坐标原点,OABC Y 的顶点A 在反比例函数2(0)y x x=>的图像上,顶点B 在反比例函数8(0)y x x =>的图像上,顶点C 在x 轴的正半轴上,则OABC Y 的面积是______________.18.(2022春·江苏宿迁·八年级统考期末)若一次函数1y k x =的图象与反比例函数2k y x=的图象相交于两点,且其中一个交点坐标为(-,则另一个交点坐标为________.19.(2022春·江苏宿迁·八年级统考期末)若点A (2,1y ),B (1,2y )都在反比例函数(0)ky k x=<的图像上,则1y _____________2y (填“>、<或=”).20.(2022春·江苏南京·八年级期末)如图,正比例函数y =ax 与反比例函数y =bx的图像交于A ,B 两点,BC ∥x 轴,AC ∥y 轴,若S △ABC =12,则b =_________.21.(2022春·江苏宿迁·八年级统考期末)如图,四边形OABC 是矩形,四边形ADEF 是正方形,点A 、D 在x 轴的负半轴上,点C 在y 轴的正半轴上,点F 在AB 上,点B 、E 在反比例函数ky x=(k 为常数,0k ¹)的图像上,正方形ADEF 的面积为4,且2BF AF =,则k 值为_____________.22.(2022春·江苏淮安·八年级统考期末)如图,Rt ABC △的一个顶点B 在原点,BC 在y 轴上,直角边1AC =,2BC =,把Rt ABC △绕点B 逆时针旋转90°,顶点A 的对应点为A ¢.若反比例函数my x=的图象经过点A ¢,则m 的值为________.23.(2022春·江苏南京·八年级校联考期末)如图,一次函数1y k x b =+与反比例函数2k y x =的图象交于点A ,B ,其横坐标分别为1,5.则关于x 的不等式21k k x b x+>与的解集是________.24.(2022春·江苏扬州·八年级统考期末)如图,点A 、D 分别在函数3(0)k y k y x x=<=、的图像上,点B 、C 在x 轴上,且2OB OC =.若四边形ABCD 为矩形,点D 在第一象限,则k =______.25.(2022春·江苏南京·八年级期末)已知一次函数1y =kx +b (k ≠0)与反比例函数2y =m x (m <0)相交于点A (-3,a ),B (-1,c ),不等式kx >mx-b 的解集是_________.26.(2022春·江苏无锡·八年级统考期末)如图,点A 、B 在某双曲线的两个分支上,且AB 经过原点,点A 的坐标为(2,4),以AB 为一边作正方形ABCD ,则点C 的坐标为______.27.(2022春·江苏无锡·八年级统考期末)已知点A (x 1,y 1)和点B (x 2,y 2)在反比例函数y =5x上,且x 1<x 2<0,则y 1与y 2的大小关系是______.28.(2022春·江苏无锡·八年级统考期末)如图,在平面直角坐标系中,()1,3A ,()3,1B .已知反比例函数()0ky k x=¹的图像与线段AB 有公共点,则k 的取值范围是______.29.(2022春·江苏宿迁·八年级统考期末)已知点1,12A a a æö-+ç÷èø、1,12B b b æö-+ç÷èø是反比例函数ky x=图像上的两个点,且0a <,0b >,则a b +=_____.30.(2022春·江苏苏州·八年级校考期末)如图,在平面直角坐标系中,C ,A 分别为x轴、y 轴正半轴上的点,以OA ,OC 为边,在第一象限内作矩形OABC ,且OABC S =矩形将矩形OABC 翻折,使点B 与原点O 重合,折痕为MN ,点C 的对应点C ′落在第四象限,过M 点的反比例函数()0ky k x=¹的图像恰好过MN 的中点,点C ′的坐标为________.。
八年级反比例函数综合(含答案)
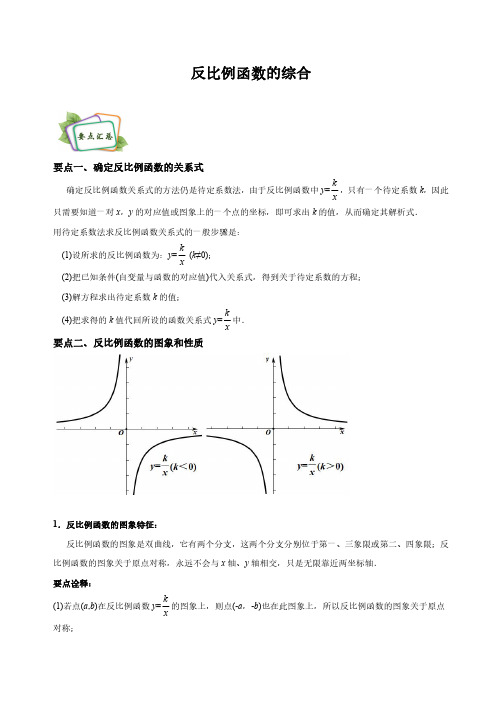
反比例函数的综合要点一、确定反比例函数的关系式确定反比例函数关系式的方法仍是待定系数法,由于反比例函数中y=kx,只有一个待定系数k,因此只需要知道一对x,y的对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.用待定系数法求反比例函数关系式的一般步骤是:(1)设所求的反比例函数为:y=kx(k≠0);(2)把已知条件(自变量与函数的对应值)代入关系式,得到关于待定系数的方程;(3)解方程求出待定系数k的值;(4)把求得的k值代回所设的函数关系式y=kx中.要点二、反比例函数的图象和性质1.反比例函数的图象特征:反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限;反比例函数的图象关于原点对称,永远不会与x轴、y轴相交,只是无限靠近两坐标轴.要点诠释:(1)若点(a,b)在反比例函数y=kx的图象上,则点(-a,-b)也在此图象上,所以反比例函数的图象关于原点对称;(2)在反比例函数y =k x(k 为常数,k ≠0)中,由于x ≠0且y ≠0,所以两个分支都无限接近但永远不能达到x 轴和y 轴.2.反比例函数的性质(1)如图1,当k >0时,双曲线的两个分支分别位于第一、三象限,在每个象限内,y 值随x 值的增大而减小.(2)如图2,当k <0时,双曲线的两个分支分别位于第二、四象限,在每个象限内,y 值随x 值的增大而增大.要点诠释:反比例函数的增减性不是连续的,它的增减性都是在各自的象限内的增减情况,反比例函数的增减性都是由反比例系数k 的符号决定的;反过来,由双曲线所在的位置和函数的增减性,也可以推断出k 的符号.要点三、反比例函数y =k x(k ≠0)中的比例系数k 的几何意义过双曲线y =k x (k ≠0)上任意一点作x 轴、y 轴的垂线,所得矩形的面积为|k|.过双曲线y =k x (k ≠0)上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为||2k .要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.例1.两个反比例函数y =3x ,y =6x在第一象限内的图象如图所示,点P 1,P 2,P 3……P 2020在反比例函数y =6x 图象上,它们的横坐标分别是x 1,x 2,x 3……x 2020,纵坐标分别是1,3,5,…,共2020个连续奇数,过点P 1,P 2,P 3……P 2020分别作y 轴的平行线,与反比例函数y =3x的图象交点依次是Q 1(x 1,y 1),Q 2(x 2,y 2),Q 3(x 3,y 3)……Q 2020(x 2020,y 2020),则y 2020等于()A .2019.5B .2020.5C .2019D .4039例2.如图,直线y =k 1x +b 与双曲线y =2k x A ,B 两点,其横坐标分别为1和5,则不等式k 1x <2k x +b 的解集是.1.一次函数y 1=k 1x +b 和y 2=2k x (k 2>0)相交于A (1,m ),B (3,n )两点,则不等式k 1x +b >2k x的解集为()A.1<x<3B.x<1或x>3C.x<0或x>3D.1<x<3或x<02.反比例函数y=kx和正比例函数y=mx的图象如图.由此可以得到方程kx=mx的实数根为()A.x=﹣2B.x=1C.x1=2,x2=﹣2D.x1=1,x2=﹣2例3.如图,点A在双曲线y=kx的第一象限的那一支上,AB垂直y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.1.如图,在反比例函数y=4x的图象上有一点A向x轴作垂线交x轴于点C,B为线段AC的中点,又D点在x轴上,且OD=3OC,则△OBD的面积为.例4.在平面直角坐标系xOy中,反比例函数y=kx(k≠0,x>0)的图象经过点A(1,-4),直线y=-2x+m与x轴交于点B(1,0).(1)求k,m的值;(2)已知点P(n,-2n)(n>0),过点P作平行于x轴的直线,交直线y=-2x+m于点C,过点P作平行于y轴的直线交反比例函数y=kx(k≠0,x>0)的图象于点D,当PD=2PC时,结合函数的图象,求出n的值.1.如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=kx的图象在同一直角坐标系中,若y3>y2>y1,则自变量x的取值范围是()A.x<﹣1B.﹣1<x<0或x>1.6C.﹣1<x<0D.x<﹣1或0<x<12.设函数y1=kx,y2=kx (k>0),当2≤x≤3时,函数的y1最大值是a,函数y2的最小值是a﹣4,则ak=()A.4B.6C.8D.103.已知反比例函数y=8x和y=3x在第一象限内的图象如图所示,则△AMN的面积为.4.如图,P1是反比例函数y=kx(k>0)图象在第一象限上的一点,点A1的坐标为(2,0).(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?逐渐减少.(2)若点P2在反比例函数图象上,点A2在x轴上,△P1OA1与△P2A1A2均为等边三角形,①求次反比例函数的解析式;②求点A2的坐标.5.如图,反比例函数y=kx图象和一次函数y=ax+b经过M(1,6)和N(2,a).(1)求一次函数解析式;(2)一次函数y=ax+b与x轴交于点B,与y轴交于点A,求证:AM=BN.6.已知:A (a ,y 1).B (2a ,y 2)是反比例函数y =k x (k >0)图象上的两点.(1)比较y 1与y 2的大小关系;(2)若A 、B 两点在一次函数y =43x+b 第一象限的图象上(如图所示),分别过A 、B 两点作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,且S △OAB =8,求a 的值;(3)在(2)的条件下,如果3m =-4x +24,3n =32x ,求使得m >n 的x 的取值范围.7.如图,在平面直角坐标系xOy 中,函数y =k x(x <0)的图象经过点A (﹣1,6),直线y =mx ﹣2与x 轴交于点B (﹣1,0).(1)求k ,m 的值;(2)过第二象限的点P (n ,﹣2n )作平行于x 轴的直线,交直线y =mx ﹣2于点C ,交函数y =k x(x <0)的图象于点D .①当n =﹣1时,判断线段PD 与PC 的数量关系,并说明理由;②若PD ≥2PC ,结合函数的图象,直接写出n 的取值范围.8.在平面直角坐标系xOy中,函数y=mx(x>0)的图象G与直线l:y=kx-4k+1交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.(1)求m的值;(2)横、纵坐标都是整数的点叫做整点.记图象G与直线l围成的区域(不含边界)为W.①当n=5时,求k的值,并写出区域W内的整点个数;②若区域W内恰有5个整点,结合函数图象,求k的取值范围.【经典例题1】A【解析】解:∵P n 的纵坐标为:2n -1,∴P 2020的纵坐标为2×2020-1=4039.∵y =与y =在横坐标相同时,y =的纵坐标是y =的纵坐标的2倍,∴y 2020=×4039=2019.5.∴A 答案正确.【经典例题2】-5<x <-1或x >0【解析】解:根据一次函数平移和反比例函数的对称性可得,直线y =k 1x -b 与双曲线y =2k x 交于第三象限点的坐标为(-5,-1)和(-1,-5),如下图所示,∴不等式k 1x <2k x +b ,即k 1x -b <2k x 的解集,即当直线y =k 1x -b 的图象在反比例函数y =2k x 图象的下方对应的自变量x 的取值范围为:-5<x <-1或x >0.【举一反三1】D【解析】解:如图,由图象可得:不等式k 1x +b >2k x 的解集是1<x <3或x <0.故选:D .【举一反三2】C【解析】解:如图,反比例函数y =和正比例函数y =mx 相交于点A (﹣2,1),∴另一个交点为:(2,﹣1),∴方程=mx 的实数根为:x 1=2,x 2=﹣2.故选:C .【经典例题3】163【解析】解:连DC ,∵AE =3EC ,S △ADE =3,∴S △CDE =1.∴S △ADC =4.设A (a ,b ),则AB =a ,OC =2AB =2a .∵D 为OB 的中点,∴BD =OD =12b .∵S 梯形OBAC =S △ABD +S △ADC +S △ODC ,12(a +2a )·b =12a ·12b +4+12·2a ·b ,∴ab =163.把A (a ,b )代入y =,得k =ab =163.【举一反三1】3【解析】解:设A (x 、y ),由反比例函数y =4x可知xy =4,BC =AC =y ,OD =3OC =3x ,∴S △OBD =BC ×OD =×y ×3x =xy =×4=3.故答案为:3.【经典例题4】【解析】解:(1)把A(1,-4)代入y=k x,得k=1×(-4)=-4;把B(1,0)代入y=-2x+m,得-2+m=0,解得m=2;(2)反比例函数解析式为y=-(x>0),一次函数解析式为y=-2x+2,如图,当y=-2n时,-2x+2=-2n,解得x=n+1,则C(n+1,-2n),∴PC=n+1-n=1,当y=-2n时,y=-=,∴D(n,-),∴PD=|-2n+|,∵PD=2PC,∴|-2n+|=2,当-2n+=2时,解得n1=-2(舍去),n2=1,当-2n+=-2时,解得n1=-1(舍去),n2=2,综上所述,当PD=2PC时,n=1或n=2.【自我检测1】B【解析】解:由图象可知,当﹣1<x<0或x>1.6时,双曲线y3落在直线y2上方,且直线y2落在直线y1上方,即y3>y2>y1,所以若y3>y2>y1,则自变量x的取值范围是﹣1<x<0或x>1.6.故选:B.【自我检测2】C【解析】解:∵k>0,2≤x≤3,∴y1随x的增大而减小,y2随x的增大而增大,∴当x=2时,y1取最大值,最大值为=a①;当x=2时,y2取最小值,最小值为﹣=a﹣4②;由①②得a=2,k=4,∴ak=8,故选:C.【自我检测3】25 16【解析】解:设A(a,),则M(a,),N(,),∴AN=a﹣=,AM=﹣=,∴△AMN的面积=AN×AM=××=25 16,故答案为:25 16.【自我检测4】【解析】解:(1)△P1OA1的面积逐渐减少;(2)作P1C⊥OA1于C,∵△P1OA1为等边三角形,A1(2,0),∴OC=1,P1C3P1(1,3).∴反比例函数的解析式为y=3 x.(3)作P2D⊥A1A2于D,如上图,设A1D=x,则OD=2+x,P2D3x,∴P2(2+x3x).将点P2代入y=3x,得y332x=+.x2+2x-1=0,解得x1=-2,x2=-12<0(舍).∴x=-2,OA2=2+x+x=2+2x=2+2(-2)=22.∴A2(22,0).【自我检测5】【解析】解:(1)∵点M(1,6)在反比例函数y=图象上,∴k=1×6=6,∴反比例函数的关系式为y=,把N(2,a)代入得,a==3,∴N(2,3).∵点M(1,6)和N(2,3)在一次函数y=ax+b的图象上,∴a+b=6,2a+b=3,解得a=﹣3,b=9,∴一次函数的关系式为y=﹣3x+9;(2)过点M、N分别作MC⊥OA,ND⊥OB,垂足分别为C、D,当x=0时,y=9,当y=0时,x=3,∴一次函数y=﹣3x+9与x轴的交点B(3,0),与y轴的交点A(0,9),由于A(0,9),B(3,0),M(1,6),N(2,3),∴MC=1,AC=9﹣6=3,ND=3,BD=3﹣2=1,∴MC=BD=1,AC=ND=3,又∵∠ACM=∠NDB=90°,∴△ACM≌△NDB(SAS),∴AM=BN.【自我检测6】【解析】解:(1)∵A、B是y=kx(k>0)图象上的两点,∴a≠0.当a>0时,A、B在第一象限,a<2a,∴此时y1>y2,同理,a<0时,y1<y2.(2)∵A(a,y1)、B(2a,y2)在y=kx(k>0)图象上,∴AC=y1=,BD=y2=.∴y1=2y2.又A (a ,y 1)、B (2a ,y 2)在y =a +b 图象上,∴y 1=a +b ,y 2=a +b .∴a +b =2(a +b ),得b =4a .∵S △AOC +S 梯形ACDB =S △AOB +S △BOD ,又S △AOC =S △BOD ,∴S 梯形ACDB =S △AOB ,即[(a +b )+(a +b )]•a =8.∴a 2=4,由a >0,得a =2.(3)由(2)知,一次函数y =x +8,反比例函数y =.∵A 、B 两点的横坐标分别为2,4,且m =x +8,n =,∴使得m >n 的x 的范围,是反比例函数的图象在一次函数图象下方的点的横坐标取值范围.∴由图可知,2<x <4或x <0.【自我检测7】【解析】解:(1)∵函数y =k x (x <0)的图象经过点A (﹣1,6),∴k =﹣6.∵直线y =mx ﹣2与x 轴交于点B (﹣1,0),∴m =﹣2.(2)①判断:PD =2PC .理由如下:当n =﹣1时,点P 的坐标为(﹣1,2),∵y =﹣2x ﹣2交于于点C ,且点P (﹣1,2)作平行于x 轴的直线,∴点C 的坐标为(﹣2,2),∵函数y =k x(x <0)的图象于点D ,且点P (﹣1,2)作平行于x 轴的直线,点D 的坐标为(﹣3,2).∴PC =1,PD =2.∴PD =2PC .②当PD=2PC时,有两种情况,分别为:y=2,或者y=6.若PD≥2PC,0<y≤2,或y≥6即0<﹣2n≤2,或﹣2n≤6解得﹣1≤n<0.或n≤﹣3【自我检测8】【解析】(1)解:把A(4,1)代入y=mx(x>0),得m=4×1=4;(2)①当n=5时,把B(1,5)代入直线l:y=kx-4k+1得,5=k-4k+1,解得k=4 3-,如图所示,区域W内的整点有(2,3),(3,2),有2个;(3)直线l:y=kx-4k+1过(1,6)时,k=53-,区域W内恰有4个整点,直线l:y=kx-4k+1过(1,7)时,k=-2,区域W内恰有5个整点,∴区域W内恰有5个整点时,k的取值范围是-2≤k<5 3-.。
2020-2021学年八年级数学苏科版下册反比例函数与几何综合题专题练习(2)

2021八年级下册反比例函数与几何综合解答题专题练习(2)1.如图,在平面直角坐标系中,四边形ABCD 是平行四边形,点A 、B 在x 轴上,点C 、D 在第二象限,点M 是BC 中点.已知AB=6,AD=8,∠DAB=60°,点B 的坐标为(-6,0).(1)求点D 和点M 的坐标;(2)如图∠,将□ABCD 沿着x 轴向右平移a 个单位长度,点D 的对应点D 和点M 的对应点M '恰好在反比例函数ky x=(x>0)的图像上,请求出a 的值以及这个反比例函数的表达式; (3)如图∠,在(2)的条件下,过点M ,M '作直线l ,点P 是直线l 上的动点,点Q 是平面内任意一点,若以,B C '',P 、Q 为顶点的四边形是矩形,请直接写出所有满足条件的点Q 的坐标. 2.如图,正方形AOCB 的边长为4,反比例函数的图象过点()3,4E .(1)求反比例函数的解析式;(2)反比例函数的图象与线段BC 交于点D ,直线12y x b =-+过点D ,与线段AB 相交于点F ,求点F 的坐标;(3)连接,OF OE ,探究AOF ∠与EOC ∠的数量关系,并证明.3.阅读理解:己知:对于实数a≥0,b≥0,满足 a = b 时,等号成立,此时取得代数式a+b 的最小值.根据以上结论,解决以下问题:(1)拓展:若a>0,当且仅当a=___时,a+1a有最小值,最小值为____; (2)应用:∠如图1,已知点P 为双曲线y=4x(x>0)上的任意一点,过点P 作PA∠x 轴,PB 丄y 轴,四边形OAPB 的周长取得最小值时,求出点P 的坐标以及周长最小值: ∠如图2,已知点Q 是双曲线y=8x(x>0)上一点,且PQ∠x 轴, 连接OP 、OQ ,当线段OP 取得最小值时,在平面内取一点C ,使得以0、P 、Q 、C 为顶点的四边形是平行四边形,求出点C 的坐标.4.在平面直角坐标系第一象限中,已知点A 坐标为()1,0,点D 坐标为()1,3,点G 坐标为()1,1,动点E 从点G 出发,以每秒1个单位长度的速度匀速向点D 方向运动,与此同时,x 轴上动点B 从点A 出发,以相同的速度向右运动, 两动点运动时间为:(02)t t <<, 以AD AB 、分别为边作矩形ABCD , 过点E 作双曲线交线段BC 于点F ,作CD 中点M ,连接BE EF EM FM 、、、 (1)当1t =时,求点F 的坐标.(2)若BE 平分AEF ∠, 则t 的值为多少? (3)若EMF ∠为直角, 则t 的值为多少?5.如图,在直角坐标系xOy 中,矩形ABCD 的DC 边在x 轴上,D 点坐标为(6,0)-边AB 、AD 的长分别为3、8,E 是BC 的中点,反比例函数ky x=的图象经过点E ,与AD 边交于点F .(1)求k 的值及经过A 、E 两点的一次函数的表达式;(2)若x 轴上有一点P ,使PE PF +的值最小,试求出点P 的坐标;(3)在(2)的条件下,连接EF 、PE 、PF ,在直线AE 上找一点Q ,使得QEF PEF S S ∆∆=直接写出符合条件的Q 点坐标.6.如图,在平面直角坐标系中,直线12y x =-与反比例函数ky x=的图象交于A ,B 两点(点A 在点B 左侧),已知A 点的纵坐标是2.(1)求反比例函数的表达式;(2)点A 上方的双曲线上有一点C ,如果ABC 的面积为30,直线BC 的函数表达式.7.如图,双曲线y 1=1k x与直线y 2=2x k 的图象交于A 、B 两点.已知点A 的坐标为(4,1),点P (a ,b)是双曲线y 1=1k x上的任意一点,且0<a <4. (1)分别求出y 1、y 2的函数表达式;(2)连接PA 、PB ,得到∠PAB ,若4a =b ,求三角形ABP 的面积; (3)当点P 在双曲线y 1=1k x上运动时,设PB 交x 轴于点E ,延长PA 交x 轴于点F ,判断PE 与PF 的大小关系,并说明理由.8.已知边长为4的正方形ABCD ,顶点A 与坐标原点重合,一反比例函数图象过顶点C ,动点P 以每秒1个单位速度从点A 出发沿AB 方向运动,动点Q 同时以每秒4个单位速度从D 点出发沿正方形的边DC→CB→BA 方向顺时针折线运动,当点P 与点Q 相遇时停止运动,设点P 的运动时间为t .∠求出该反比例函数解析式;∠连接PD ,当以点Q 和正方形的某两个顶点组成的三角形和∠PAD 全等时,求t 值;9.如图,在平面直角坐标系中有Rt ABC ,90BAC ∠=︒,AB AC =,(3,0)A -,(0,1)B ,(,)C m n . (1)请直接写出C 点坐标.(2)将ABC 沿x 轴的正方向平移t 个单位,'B 、'C 两点的对应点、正好落在反比例函数ky x=在第一象限内图象上.请求出t ,k 的值.(3)在(2)的条件下,问是否存x轴上的点M和反比例函数kyx图象上的点N,使得以'B、'C,M,N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.10.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=(k>0,x>0)的图象上,点D的坐标为(4,3).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.11.如图,A、B是双曲线y=kx上的两点,过A点作AC∠x轴,交OB于D点,垂足为C,过B点作BE∠x轴,垂足为E.若∠ADO的面积为1,D为OB的中点,(1)求四边形DCEB的面积.(2)求k 的值.12.如图,在∠ABC 中,AC=BC ,AB∠x 轴于A ,反比例函数y=kx(x >0)的图象经过点C ,交AB 于点D ,已知AB=4,BC=52. (1)若OA=4,求k 的值.(2)连接OC ,若AD=AC ,求CO 的长.13.如图,一次函数y kx b =+与反比例函数6(0)y x x=>的图象交于(),6A m ,()3,B n 两点.(1)求一次函数的解析式; (2)根据图象直接写出60kx b x+-<的x 的取值范围; (3)求AOB的面积.14.已知一次函数()10y kx n n =+<和反比例函数()20,0my m x x=>>.(1)如图1,若2n =-,且函数1y 、2y 的图象都经过点()3,4A . ∠求m ,k 的值;∠直接写出当12y y >时x 的范围;(2)如图2,过点()1,0P 作y 轴的平行线l 与函数2y 的图象相交于点B ,与反比例函数()30ny x x=>的图象相交于点C .∠若2k =,直线l 与函数1y 的图象相交点D .当点B 、C 、D 中的一点到另外两点的距离相等时,求m n -的值;∠过点B 作x 轴的平行线与函数1y 的图象相交于点E .当m n -的值取不大于1的任意实数时,点B 、C 间的距离与点B 、E 间的距离之和d 始终是一个定值.求此时k 的值及定值d . 15.如图,已知一次函数y=32 x−3与反比例函数y=kx的图象相交于点A(4,n),与x 轴相交于点B .(1)填空:n 的值为___,k 的值为___;(2)以AB 为边作菱形ABCD ,使点C 在x 轴正半轴上,点D 在第一象限,求点D 的坐标; (3)观察反比例函数y=kx的图象,当y∠−2时,请直接写出自变量x 的取值范围。
反比例函数中及面积有关的问题

反比例函数中与面积有关的问题知识点回忆由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进展考察。
这种考察方式既能考察函数、反比例函数本身的根底知识内容,又能充分表达数形结合的思想方法,考察的题型广泛,考察方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的几种类型归纳如下:利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,那么两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k故S=|k|从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于以下三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|类型之一k与三角形的面积k〔k>0〕经过直角三角形OAB斜边OB的中点D,与直※1、如图,双曲线y=x角边AB相交于点C.假设△OBC的面积为6,那么k=______.最正确答案过D点作DE⊥x轴,垂足为E,1k,由双曲线上点的性质,得S△AOC=S△DOE=2∵DE⊥x轴,AB⊥x轴,∴DE∥AB,∴△OAB∽△OED,又∵OB=2OD,∴S△OAB=4S△DOE=2k,由S△OAB-S△OAC=S△OBC,得2k-21k=6,解得:k=4.故答案为:4.2、如图1-ZT-1,分别过反比例函数y=x2018(x>0)的图象上任意两点A、B作x 轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S 1、S2,,比拟它们的大小,可得A.S1>S2B.S1=S2C.S1<S2D.S1、S2大小不确定。
反比例函数中的面积问题

解得 k=2 评注:第①小题中由图形所在象限可确定k>0,应用结论可直接求k值。 第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相 等,列出含k的方程求k值。
例2(2008贵州省黔南州)如图,矩形ABOD的顶点A是函数 与函数 在第二象限的交点, 轴于B, 轴于D,且矩形ABOD的பைடு நூலகம்积为3. (1)求两函数的解析式. (2)求两函数的交点A、C的坐标.
图象上,∴
解得x=1从而所求面积为π 评注:对于较复杂的图形面积计算问题,先应观察图形的特征,若具有 对称特征,则应用对称关系可以简化解题过程。
四、 讨论与面积有关的综合问题 例8.(2008山东省)(1)探究新知:
如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由. (2)结论应用:
与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4. (1)试确定反比例函数的关系式; (2)求△AOC的面积.
.解:(1)∵点A(-2,4)在反比例函数图象上 ∴k=-8 ∴反比例函数解析式为y=
(2)∵B点的横坐标为-4, ∴纵坐标为y=2 ∴B(-4,2) ∵点A(-2,4)、 点B(-4,2)在直线y=kx+b上 ∴ 4=-2k+b 且2=-4k+b 解得 k=1 b=6 ∴直线AB为y=x+6 与x轴的交点坐标C(-6,0)
(3)若点P是y轴上一动点,且 , 求点P的坐标.
解:(1)由图象知k<0,由结论及已知条件得 -k=3 ∴
∴反比例函数的解析式为 ,一次函数的解析式为 (2)由 ,解得 ,
∴点A、C的坐标分别为(
,3),(3, ) (3)设点P的坐标为(0,m) 直线 与y轴的交点坐标为M(0,2) ∵
苏科版初中八年级数学下册期末反比例函数与几何综合巩固训练题含答案

苏科版初中八年级数学下册期末反比例函数与几何综合巩固训练题含答案一、单选题(共6小题)1.(2019春•南京期末)如图,在平面直角坐标系中,点是轴正半轴上的一个定点,点是双曲线上的一个动点,轴于点,当点的横坐标逐渐增大时,四边形的面积将会( )A .逐渐增大B .不变C .逐渐减小D .先增大后减小【解答】解:设点的坐标为, 轴于点,点是轴正半轴上的一个定点,四边形是个直角梯形,四边形的面积, 是定值,四边形的面积是个减函数,即点的横坐标逐渐增大时四边形的面积逐渐减小. 故选:.2.(2019春•玄武区期末)如图,点是反比例图数图象上一点,轴于点,与反比例函数图象交于点,,连接、,若的面积为2,则A x P 3(0)y x x=>PB y ⊥B P OAPB P 3(,)x xPB y ⊥B A x ∴OAPB ∴OAPB 11333331()()222222AO AO PB AO BO x AO x x x =+=+=+=+AO ∴OAPB P OAPB C A (0)m y x x=<AC x ⊥C (0)n y x x=<B 2AB BC =OA OB OAB ∆(m n +=)A .B .C .D .【解答】解:设, ,, ,的面积为2,根据反比例函数的几何意义可知:的面积为,的面积为, 的面积为, ,,,,故选:.3-4-6-8-(,)n B a a (,)m A a a2AB BC =∴3m n a a=3m n ∴=OAB ∆∴k AOC ∆2m -BOC ∆2n -AOB ∴∆222m n -+=4n m ∴-=34n n ∴-=2n ∴=-6m ∴=-8m n ∴+=-D3.已知四边形是矩形,边在轴上,边在轴上,双曲线与边交于点、与对角线交于点中点,若的面积为10,则的值是A .10B .5C .D . 【解答】解:设点的坐标是,是的中点,点的坐标是,则点的坐标是,, 的面积为10,, 解得,, 故选:.4.(2019春•盐城月考)如图,在第一象限内,点,是双曲线上OABC OA x OC y k y x=BC D OB E OBD ∆k ()103203E (,)x y E OB B ∴(2,2)x y D (2k y2)y OBD ∆∴1(2)21022k x y y⨯-⨯=203k =D (2,3)P (,2)M a (0)k y k x=≠的两点,轴于点,轴于点,与交于点,则的面积为A .B .C .2D . 【解答】解:把,代入得,解得,, 设直线的解析式为,把代入得,解得, 所以直线的解析式为,当时,, 所以点坐标为, 所以的面积. 故选:.5.(2019春•赣榆区期末)如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,,将沿直线翻折,点的对应点恰好落在双曲线上,则的值为PA x ⊥A MB x ⊥B PA OM C OAC ∆()324383(2,3)P (,2)M a k y x=232k a =⨯=6k =3a =OM y mx =(3,2)M 32m =23m =OM 23y x =2x =24233y =⨯=C 4(2,)3OAC ∆1442233=⨯⨯=B y (0,4)B x A 30BAO ∠=︒AOB ∆AB O C (0)k y k x=≠k ()A .B .C .D .【解答】解:过点作轴,垂足为,由折叠得:,,在中,,,, ,代入得:故选:.6.(2019春•姑苏区期末)如图,四边形和四边形都是正方形,反比例函数在第一象限的图象经过点,若两正方形的面积差为12,则的值为A .12B .6C .D .8【解答】解:设正方形、的边长分别为和,则,,所以, 8-16---C CD y ⊥D 4OB BC ==30OAB BAC ∠=∠=︒60OBA CBACBD ∴∠=∠=︒=∠Rt BCD ∆30BCD∠=︒122BD BC ∴==CD =(C ∴-6)6k =-=-D OABC BDEF k y x=E k ()12-OABC BDEF a b (,)D a a b -(,)F a b a +(,)k E a b a b++所以, ,,两正方形的面积差为12,.故选:.二、填空题(共5小题)7.(2019春•苏州期末)如图,直线与轴轴分别相交于点、,四边形是正方形,曲线在第一象限经过点.则 .【解答】解:作轴,垂足为,连.,,,又,,,.k a b a b=-+()()a b a b k ∴+-=22a b k ∴-=12k ∴=A 22y x =-+x y A B ABCD k y x=D k=DE x ⊥E OD 90DAE BAO ∠+∠=︒90OBA BAO ∠+∠=︒DAE OBA ∴∠=∠BOA AED ∠=∠AB DA =()BOA AED HL ∴∆≅∆OA DE ∴=,可知,,,,, . 故答案为:3.8.(2019春•锡山区校级期末)如图,在的面积为6,,,反比例函数的图象经过点与点,则的值为 .【解答】解:过点作轴的平行线交过点与轴的平行线于点,过点作轴,22y x =-+(0,2)B (1,0)A 1OA DE ∴==123OE OA AE ∴=+=+=11331222DOE S OE DE ∆∴==⨯⨯=3232k ∴=⨯=ABCD (4,)A a (6,)Bb k y x=A C k C x y H A AM x ⊥,则,,,,,,故点,即:①,连接,过点分别作、轴的垂线于点、,②, 联立①②并解得:,,,故答案为4.9.(2019春•东海县期末)如图,直线与双曲线交于、两点,为上轴一点,连接交轴与点,若恰好为中点,且的面积为6,则点坐标为 .【解答】解:过点作轴,垂足为,点是的中点,//OA BC BCN AOM ∠=∠OA BC =90CNB AMO ∠=∠=︒()OAM CBN AAS ∴∆≅∆NB AM a ∴==4CN OM ==(2,)C b a -2()4b a a -=⋯CA C x y G H ()()1142322AOC ABCDACGM S S a b a S ∆==+-⨯-==⋯梯形1a =3b =44k a ==y mx =k y x=A B D x BD y C (0,2)C -BD ABD ∆B B BE y ⊥E 90BEC DOC ∴∠=∠=︒C BD,, 故答案为:,10.(2019春•赣榆区期末)如图,点为函数图象上一点过点作轴、轴的平行线,分别与函数的图象交于点,,则的面积为 .【解答】解:作轴于,设轴于,BC DC ∴=OCD ECB ∠=∠BEC DOC ∴∆≅∆BE OD ∴=2EC OC ==6ABD S OD OE ∆==⨯32OD ∴=3(2A ∴-34)(2B 4)-3(2B 4)-P 4(0)y x x=>P x y 8(0)y x x=>A B AOB∆AD x ⊥D PB x ⊥E点为函数图象上一点,过点作轴、轴的平行线, 设,则,, 点、在函数的图象上, ,,, 故答案为6.11.(2019春•玄武区期末)如图,在反比例函数的图象上有点,,,,,它们的横坐标依次为1,2,3,,,,分别过点,,,,,作轴,轴的垂线,图中所构成的阴影部分面积从左到右依次为,,,,,则 .(用含的代数式表示) P 4(0)y x x=>P x y ∴4(,)P m m 4(2,)A m m 8(,)B m mA B 8(0)y x x=>OBE OAD S S ∆∆∴=AOB OAD OBE ABOD ABOD ABED S S S S S S ∆∆∆=-=-=四边形四边形梯形184()(2)62AOB S m m m m∆∴=+-=9(0)y x x=>1P 2P 3P n P ⋯1n P +⋯n 1n +1P 2P 3P ⋯n P 1n P -x y 1S 2S 3S 4S ⋯n S =n【解答】解:当时,的纵坐标为9,当时,的纵坐标4.5,当时,的纵坐标3,当时,的纵坐标, 当时,的纵坐标,则;;; ;; 故答案为.1x =1P 2x =2P 3x =3P 4x =4P 945x =5P 95⋯11(9 4.5)9 4.5S =⨯-=-21(4.53) 4.53S =⨯-=-3991(3)344S =⨯-=-499991()4545S =⨯-=-⋯9991(1)n S n n n n =-=++9(1)n n +三、解答题(共2小题)12.(2019春•滨湖区期末)如图在平面直角坐标系中位于第二象限的点在反比例函数的图象上,点与点关于原点对称,直线经过点,且与反比例函数的图象交于点. (1)当点的横坐标是,点坐标是时,分别求出、的函数表达式;(2)若点的横坐标是点的横坐标的4倍,且的面积是16,求的值.【解答】解:(1)把点代入得: , 当时,代入,,点与点关于原点对称,把,代入得:,解得:,, xOy A 1(0)k y x x=<B A O 2y mx n =+B 1k y x =C A 2-C (8,2)-1y 2y C A ABC ∆k (8,2)C -1k y x =16k =-116y x∴=-2x =-116y x =-8y =(2,8)A ∴-B A O (2,8)B ∴-(2,8)B -(8,2)C -2y mx n =+2882m n m n +=-⎧⎨-+=⎩1m =-6n =-,答:、的函数表达式分别为,. (2)过、分别作轴的平行线与过作轴的平行线相交于、,设,则,, 此时,,,,,,,, 即:,, 解得:, 答:的值为.13. (2019春•锡山区校级期末)(1)如图,已知点、在双曲线上,轴与,轴于点,与交于点,是的中点,点的横坐标为.26y x ∴=--1y 2y 116y x=-26y x =--A C y B x M N (,)k A a a (4,)4k C a a (,)k B a a--2k k k AN a a a =+=2BN a a a =--=-45BM a a a =--=-544k k k CM a a a =+=43MN a a a =-+=-16ABC CMNA ABN BCM S S S S ∆∆∆=+-=111()16222CM AN MN AN BN CM BM ++-=()32CM AN MN AN BN CM BM ++-=5225()(3)(2)(5)3244k k k k a a a a a a a+⨯-+⨯--⨯-=6415k =-k 6415-A B (0)k y x x=>AC x ⊥C BD y ⊥D AC BD P P AC B b A与的坐标分别为 、 .(用与表示),由此可以猜想与的数量关系是 .(2)四边形的四个顶点分别在反比例函数与的图象上,对角线轴,且于点,是的中点,点的横坐标为4.①当,时,判断四边形的形状并说明理由.②四边形能否成为正方形?若能,直接写出此时,之间的数量关系;若不能,试说明理由.【解答】解:(1)轴于,轴于点,,由题意,,, ,, ,,故答案为:,,,.(2)①当时,, B b k DP BP ABCD m y x =(0,0)n y x m n x=><<//BD y BD AC ⊥P P AC B 4m =20n =ABCD ABCD mn AC x ⊥C BD y ⊥D AC BD ∴⊥(,)k B b b1(2A b 2)k b 12PD b ∴=BD b =2BD PD ∴=DP BP ∴=1(2A b 2)k b (,)k B b bDP BP =4x =41y x==点的坐标为;当时,, , 点为线段的中点,设,则, ,,, ,,,, 点的坐标为,,, .,四边形为平行四边形.又,四边形为菱形.②四边形能成为正方形.当四边形为正方形时,设. 当时,, ∴B (4,1)4x =205y x==(4,5)D ∴P AC 4(,)A a a 4(5,)C a aPA PC ∴=(5)24a a ∴+÷=43a ∴=4(3A ∴3)20(3C 3)∴P (4,3)48433PA ∴=-=208433PC =-=PA PC ∴=PB PD =∴ABCD BD AC ⊥∴ABCD ABCD ABCD (0)PA PB PC PD t t ====≠4x =4m m y x ==点的坐标为, 点的坐标为. 点在反比例函数的图象上, ,化简得:, 点的纵坐标为, 点的坐标为, ,整理,得:. 即四边形能成为正方形,此时.∴B (4,)4m ∴A (4,)4m t t -+A m y x =(4)()4m t t m ∴-+=44m t =-∴D 22(4)84444m m m m t +=+-=-∴D (4,8)4m -4(8)4m n ∴⨯-=32m n +=ABCD 32m n +=。
初二数学之反比例函数图象与图形面积问题.doc

初二数学之反比例函数图象与图形面积问
题
利用临界点求反比例函数图象与图形面积问题
例1.
分析:
由于AB∥x轴,BC⊥x轴,易知△ABC是直角三角形,由于反比例函数在第一象限,k>0,则当经过点A时,其横纵坐标的乘积最小,k值最小,经过点C时,其横纵坐标的乘积最大,k值最大.据此可得出k的取值范围.解答:
过点A,则k=2
过点C,则k=16,2≤k≤16,选C
例2:
分析:
首先,我们可以根据点C的横坐标,求出点C的坐标,继而求出点A和点B的坐标,以及直线AB的解析式,易知AB⊥OC,设AB与OC交点为D,且D必为AB中点.根据反比例函数的轴对称性,其中的一条对称轴是y=-x,显然,当图象过点A时,也必然过点B,当图象过中点D时,与AB只有一个交点.
解答:
总结:
例1及例2,均是求反比例k的取值范围,那么只需关注临界点的情况.
如例1,考虑的是过点作坐标轴垂线段,两条垂线段与坐标轴围成面积的最大值和最小值,发现点A和点C是临界点.而例2,则借助对称性,发现点A是临界点,AB的中点也是.因此,看到这样的题目,不要慌,找出关键临界点,计算下横纵坐标的积,k就解出来了!。
八年级下学期数学专题反比例函数综合

八年级数学反比例函数综合一、反比例函数与几何综合1、如图,11POA ∆、212P A A ∆都是等腰直角三角形,点1P 、2P 在函数4y x=(0x >)的图像上,斜边1OA 、12A A 、都在x 轴上,求点2A 的坐标.2、如图所示,()()111222P x y P x y ,,,,……,()n n n P x y ,在函数()90y x x=>11OP A ∆,212P A A ∆,323P A A ∆,…,1n n n P A A -∆,…都是等腰直角三角形,斜边1121n n OA A A A A -,,…,都在x 轴上,则12n y y y +++=…______________.3、如图,如果函数y x =-与4y x=-的图像交于A ,B 两点,过点A 作AC 足为点C ,求BOC ∆的面积.4、如图,一次函数y kx b =+的图像与反比例函数my x=的图像交于(21)(1)A B n -,,,两点. (1)试确定上述反比例函数和一次函数的表达式; (2)求AOB ∆的面积.5、如图,直线y kx b =+与反比例函数()0k y x x =<′的图象相交于点A 点C ,其中点A 的坐标为()24-,,点B 的横坐标为4-.(1)试确定反比例函数的关系式; (2)求AOC ∆的面积.6、如图,在直角坐标系xOy 中,一次函数1y k x b =+于()()143A B m ,,,两点. (1)求一次函数的解析式; (2)求AOB ∆的面积.7、两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x =的图象上,PC x ⊥轴于点C ,交1y x =的图象于点A ,PD y ⊥轴于点D ,交1y x=的图象于点B ,当点P 在ky x=的图象上运动时,以下结论: ①ODB ∆与OCA ∆的面积相等; ②四边形PAOB 的面积不会发生变化; ③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是8、如图,点A 、B 在反比例函数k y x =(0k >)的图象上,且点A 2a (0a >)AC x ⊥轴,垂足为C ,AOC ∆的面积为2.(1)求反比例函数的解析式;(2)若点(a -,1y ),(2a -,2y )也在反比例函数的图象上,试比较1y 与2y 的大小; (3)求AOB ∆的面积.9、已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E .(1)求证:AOE △与BOF △的面积相等;(2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.10、如图,反比例函数8y x=的图象过矩形OABC 的顶点B ,OA 、OC正半轴上,:2:1OA OC =.(1)设矩形OABC 的对角线交于点E ,求出E 点的坐标; (2)若直线2y x m =+平分矩形OABC 面积,求m 的值.11、两个反比例函数1k y x =和()2120ky k k x=>>在1k y x =的图象上,PC x ⊥轴于点C ,交2ky x=的图象于点A ,交2k y x=的图象于点B . ⑴求证:四边形PAOB 的面积是定值; ⑵当23PA PC =时,求DBBP的值; ⑶若点P 的坐标为()52,,OAB ABP ∆∆,的面积分别记为OAB S ∆、ABP S ∆,设ABP OAB S S S ∆∆-=.①求1k 的值;②当2k 为何值时,S 有最大值,最大值为多少?k 2x12、如图,已知正方形OABC 的面积为9,点O 为坐标原点,点A 在x 轴上,点C 在y 轴上,点B 在函数ky x=(0k >,0x >)的图像上,点P (m ,n )为其双曲线上的任一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S .⑴求B 点的坐标和k 的值;⑵当92S =时,求P 点坐标;⑶写出S 关于m 的函数关系式.13、若一次函数21y x =-和反比例函数2ky x=的图象都经过点(1,1). (1)求反比例函数的解析式;(2)已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标; (3)利用(2)的结果,若点B 的坐标为(2,0),且以点A O B P ,,,为顶点的四边形是平行四边形,请你直接写出点P 的坐标.14、如图,点()1A m m +,,()31B m m +-,都在反比例函数ky x=的图象上. (1)求m k ,的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A B M N ,,,为顶点的四边形是平行四边形,试求直线MN 的函数表达式.15、已知(1)A m -,与(2B m +,是反比例函数ky x=图象上的两个点. (1)求k 的值;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.16、如图,已知反比例函数12y x=的图象和一次函数7y kx =-求这个一次函数的解析式;②如果等腰梯形ABCD 的顶点A B ,点C D ,在这个反比例函数图象上,两底AD ,BC 与y 轴平行,且A 和2a +,求a 的值。
初二数学人教版(下册)反比例函数综合练习(附答案)
反比例函数综合练习一、选择题1.反比例函数y= -2/x的图象位于()A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限2.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为()、. 若双曲线y=6/x 经过点A(m,3),则m的值为()A.2 B.-2 C.3 D.-33. 如图,过原点的一条直线与反比例函数y=k/x(k<0)的图像分别交于A、B两点,若A、、点的坐标为(a,b),则B点的坐标为()A.(a,b) B.(b,a) C.(-b,-a) D.(-a,-b)4、下列关系中,两个量之间为反比例函数关系的是()A 、 正方形的面积S 与边长a 的关系B 、 正方形的周长L 与边长a 的关系C 、 长方形的长为a ,宽为20,其面积S 与a 的关系D 、 长方形的面积为40,长为a ,宽为b ,a 与b 之间的关系 5、在同一直角坐标系中,函数x y 3=与xy 1-=的图象大致是( )6、设()()2211,,,y x B y x A 是反比例函数xy 2-=图象上和两点,若1x <2x <0则1y 与2y 之间的关系是( )A 、2y <1y <0B 、1y <2y <0C 、2y >1y >0D 、1y >2y >0 7、函数k kx y +=与xky =在同一坐标系中的图象如图所示,则k 的取值范围为( ) A 、k >0 B 、k <0 C 、-1<k <0 D 、k <-18、(2006年兰州市)如图1所示,P 1、P 2、P 3是双曲线上的三点,过这三点分别作y 轴的垂线,得到三个三角形△P 1A 1O 、△P 2A 2O 、△P 3A 2O ,设它们的面积分别是S 1、S 2、S 3,则( ) A 、S 1<S 2<S 3 B 、S 2<S 1<S 3 C 、S 1<S 3<S 2 D 、S 1=S 2=S 3yOxyOxyOxO xyx二、填空题9.在函数xky =中,当2=x 时,3-=y 。
八年级数学下册 11.3 用反比例函数解决问题 如何处理函数中的动点问题素材 苏科版(2021学年

八年级数学下册11.3 用反比例函数解决问题如何处理函数中的动点问题素材 (新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级数学下册11.3 用反比例函数解决问题如何处理函数中的动点问题素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级数学下册11.3 用反比例函数解决问题如何处理函数中的动点问题素材(新版)苏科版的全部内容。
如何处理函数中的动点问题?难易度:★★★★关键词:反比例函数应用-动点.答案:利用反比例函数的图像和性质,根据点的移动确定函数的解析式,从而做出所求问题.【举一反三】典题:如图,已知A、B是反比例函数y= (y>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→"所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )A、B、C、 D、思路导引:本题考查了反比例函数的综合题和动点问题的函数图象,解题的关键是根据点的移动确定函数的解析式,从而确定其图象.当点p在OA上运动时,此时S随t的增大而增大,当点P在AB上运动时,S不变,当点P在BC上运动时,S随t的增大而减小,根据以上判断做出选择即可.标准答案:解:当点p在OA上运动时,此时S随t的增大而增大,当点P在AB上运动时,S不变,∴B、D淘汰;当点P在BC上运动时,S随t的增大而逐渐减小,∴C错误.故选A.以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
反比例函数____动点、面积专题(附详细讲解)
反比例函数 ---动点、面积专题(附详解)一、解答题(共7小题)1、已知反比例函数y=的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.2、已知:反比例函数经过点B(1,1).(1)求该反比例函数解析式;(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;(3)若该反比例函数图象上有一点F(m,)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是,求代数式的值.3、如图,M点是正比例函数y=kx和反比例函数的图象的一个交点.(1)求这两个函数的解析式;(2)在反比例函数的图象上取一点P,过点P做PA垂直于x轴,垂足为A,点Q是直线MO上一点,QB垂直于y轴,垂足为B,直线MO上是否存在这样的点Q,使得△OBQ的面积是△OPA的面积的2倍?如果存在,请求出点Q的坐标,如果不存在,请说明理由.4、如图,已知:一次函数:y=﹣x+4的图象与反比例函数:(x>0)的图象分别交于A、B两点,点M是一次函数图象在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M1、M2,设矩形MM1OM2的面积为S1;点N为反比例函数图象上任意一点,过N分别向x轴、y轴作垂线,垂足分别为N1、N2,设矩形NN1ON2的面积为S2;(1)若设点M的坐标为(x,y),请写出S1关于x的函数表达式,并求x取何值时,S1的最大值;(2)观察图形,通过确定x的取值,试比较S1、S2的大小.5、如图,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P (﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由.6、如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.7、如图,点P(a,b)和点Q(c,d)是反比例函数y=图象上第一象限的两个动点(a<b,a≠c),且始终有OP=OQ.(1)求证:a=d,b=c;(2)P1是点P关于y轴的对称点,Q1是点Q关于x轴的对称点,连接P1Q1分别交OP、OQ于点M、N.①求证:PQ∥P1Q1;②求四边形PQNM的面积S能否等于?若能,求出点P的坐标;若不能,请说明理由.反比例动点与面积答案与评分标准一、解答题(共7小题)1、已知反比例函数y=的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x 轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.考点:反比例函数综合题;待定系数法求反比例函数解析式;旋转的性质。
苏科版数学八年级下册复习《反比例函数和图形面积》
初二数学复习《反比例函数与图形面积》例题1:如图在平面直角坐标系xOy 中,函数)0(41>=x xy 的图象与一次函数k kx y -2=的图象的交点为A (m ,2). (1)求一次函数的解析式;(2)观察图像直接写出使得21y y ≥的x 的取值范围; (3)设一次函数y=kx-k 的图象与y 轴交于点B , ①求△AOB 的面积②若点P 是y 轴上一点,且满足△PAB 的面积是4,求点P 的坐标;若点P 是x 轴上呢?直接写出P 点的坐标.练习1:如图,A 、B 是反比例函数y=(k >0)图象上关于原点O 对称的两点,直线AC 经过点C (0,﹣2)与x 轴交于点D ,若C 为AD 中点,△ABD 的面积是5, (1) 求点B 的坐标;(2)在xky =的图像上是否存在一点Q , 使ABD △△S S QOD =,若存在求Q 点坐标例题2:如图,直线y =6x 、y =23x 分别与双曲线y =kx在第一象限内交于点A 、B , 若S △OAB =8,求K 的值。
练习2:如图,函数x y 1=(x >0)和xy 3=(x >0)的图象分别是l 1和l 2.设点P 在l 2上,PA ∥y 轴,交l 1于点A ,PB ∥x 轴,交l 1于点B ,求△PAB 的面积.提高:如图,正方形OABC 的面积为4,点O 为坐标原点,点B 在函数y =kx(k<0,x<0)的图象上,点P(m ,n)是函数y =kx(k<0,x<0)的图象上异于点B 的任意一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为点E 、F .(1)设矩形OEPF 的面积为S 1,判断S 1与点P 的位置是否有关(不必说明理由);(2)从矩形OEPF 的面积中减去其与正方形OABC 重合的面积,剩余面积记为S 2,写出S 2与m 的函数关系式,并标明m 的取值范围.反比例函数中K 与面积的关系反比例函数问题,许多都是与三角形、四边形等图形的面积联系在一起的,其中常见的有已知反比例函数的解析式,求其图象围成的某一图形的面积;或已知某一图形的面积,求符合条件的反比例函数的解析式等题型。
八年级下册反比例函数面积专题

反比例函数面积专题二【反比例函数的性质】1.当0>k 时,图象分别位于第一、三象限,同一个象限内,y 随x 的增大而减小;当0<k 时,图象分别位于二、四象限,同一个象限内,y 随x 的增大而增大。
2.因为在)0(≠=k xky 中,x 不能为0,y 也不能为0,所以反比例函数的图象不可能与x 轴相交,也不可能与y 轴相交。
3. 在一个反比例函数图象上任取两点P ,Q ,过点P ,Q 分别作x 轴,y 轴的平行线,与坐标轴围成的矩形面积为S 1,S 2,则S 1=S 2=|k |4. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴 x y x y -==,(即第一三,二四象限角平分线),对称中心是坐标原点。
5.若设正比例函数mx y =与反比例函数xny =交于A 、B 两点(m 、n 同号),那么A 、 B 两点关于原点对称。
6.k 值相等的反比例函数重合,k 值不相等的反比例函数永不相交。
【知识准备】1、如图,点A 在反比例函数(0)ky k=≠的图象上,AM x ⊥轴于点M,AMO △的面积为3,则k = .2、如图,一次函数y kx b=+的图象与反比例函数my x=的图象交于(21)(1)A B n -,,,两点. (1)求上述反比例函数和一次函数的表达式;(2)求AOB △的面积.3、如图,在直角坐标系中,一次函数b kx y +=的图像与反比例函数xmy =的图像交于A (1,4)、B (3,n )两点. (1)求一次函数的解析式;(2)求△AOB 的面积4、如图,过原点的直线与反比例函数xy 7-=的图像交于A 、C ,自点A 和C 做x 轴的垂线,垂足分别为B 和D ,则四边形ABCD 的面积等于 【典型例题】例1、如图,已知反比例函数)0(>=x xky 经过矩形OABC 边AB 的中点F 且交BC 于点第1题图第2题图第3题图 第4题图四边形OEBF 的面积为2,则k =例2、如图,已知直线x y 21=与反比例函数)0(>=k x ky 交于A 、B 两点,且A 点的横坐标是4. (1)求k 的值; (2)若反比例函数)0(>=k xky 上一点C 纵坐标为8,求△(3)过原点O 的另一条直线l 交)0(>=k xky 与P 、Q 两点(P 点在第一象限),若四边形ABPQ 的面积为24,求P 的坐标.【巩固练习】1、如图:函数kx y =与x y 4-=的图象交于点A 、B ,AC ⊥Oy , BD ⊥Oy.则四边形ACBD 面积=2)0(2>=x xy 的图像上,有点P 1,P 2,P 3,P 4,它们的横坐标分别是1,2,3,4,分别过这些点做x 轴、y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为S 1,S 2,S 3,则S 1+S 2+S 3= 3、如图,Rt △ABO 的顶点A 是双曲线y=k x 与直线y =-x -(k +1)在第二象限的交点.AB ⊥x 轴于B ,且S △ABO =3. (1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A 、C 的坐标和△AOC 的面积.4、如图,在矩形AOBC 中,OB =4,OA =3,分别以OB 、OA 所在直线为x 轴和y 轴,F 是边BC 上的一个动点(不与B 、C 重合),过F 的反比例函数)0(>=k xky 的图像与AC 边交于E .(1)记S =S OEF -S △ECF ,当k 为何值时,S 有最大值,最大值为多少?(2)情探索:是否存在这样的点F ,使得△CEF 沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.x题图2题图。
反比例函数与 面积 动点问题

一. 求函数解析式例1. 如图1,P 是反比例函数图象在第二象限上的一点,且矩形PEOF 的面积为3。
求这个反函数的解析式。
二例,2),三. 例(四. 例A. C.五. 求参数的值例5. 如图5,已知反比例函数x12y =的图象和一次函数7kx y -=的图象都经过点P (m ,2)。
(1)求这个一次函数的解析式;(2)如果等腰梯形ABCD 的顶点A 、B 在这个一次函数图象上,顶点C 、D 在这个反比例函数图象上,两底AD ,BC 与y 轴平行,且A 和B 的横坐标分别为a 和a+2,求a 的值。
一、反比例函数与特殊四边形结合 1.如图1,已知双曲线y =xk(k >0)与直线y =k′ x 交于A ,B 两点,点A 在第一象限.试解答下列问题: (1)若点A 的坐标为(4,2)则点B 的坐标为_____________;若点A 的横坐标为m ,则点B 的坐标可表示为_____________; (2)如图2,过原点O 作另一条直线l ,交双曲线y =xk(k >0)于P ,Q 两点,点P 在第一象限. ①说明四边形APBQ 一定是平行四边形;②设点A ,P 的横坐标分别为m ,n ,四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,直接写出m ,n 应满足的条件;若不可能,请说明理由.2如图,x3(1(2(33AOC =31,点B 的坐标为(m ,-2). (1)求反比例函数的解析式; (2)求一次函数的解析式;(3)在y 轴上存在一点P ,使得△PDC 与△ODC 相似,请你求出P 点的坐标.4.如图,是反比例函数y =-x 2和y =-x 8在第二象限中的图像,点A 在y =-x 8的图像上,点A 的横坐标为m (m <0),AC ∥y 轴交y =-x2的图像于点C ,AB 、CD 均平行于x 轴,分别交y =-x 2、y =-x8的图像于点B 、D .(1)用m 表示A 、B 、C 、D 的坐标;(2)求证:梯形ABCD 的面积是定值;(3)若△ABC 与△ACD 相似,求m 的值.k2.在平面直角坐标系中,函数y =xm(x >0,m 是常数)的图象经过点A (1,4)、点B (a ,b ),其中a >1.过点A 作x 轴的垂线,垂足为C ,过点B 作y 轴的垂线,垂足为D ,AC 与BD 相交于点M ,连结AD 、DC 、CB 与AB . (1)求m 的值;(2)求证:DC ∥AB ;(3)当AD =BC 时,求直线AB 的函数解析式 3.如图,一次函数y =kx -7的图象与反比例函数y =-x12的图象交于A (m ,2)、B 两点. (1)求一次函数的解析式和点B 的坐标;(2)等腰梯形CDEF 的顶点C 、D 在反比例函数的图象上,顶点E 、F 在一次函数的图象上,DE ∥CF ∥y 轴,且C 、D 的横坐标分别为a 、a -2,求a 的值.4C ,轴于H1P 运2①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?3速度(((4;点P1、APE=2、如图,在矩形ABCD 中,AB =12以1厘米/秒的速度移动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图所示,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在直线y=x 上,其中点A的横坐标为1,且AB∥x轴,AC∥y轴,若双曲线y=k/x(k≠0)与△ABC有交点,则k的取值范围是_________
2、如图,已知△ABO的顶点A和AB边的中点C都在双曲线y= 4/x(x>0)
的一个分支上,点B在x轴上,CD⊥OB于D,则△AOC的面积为()A、2 B、3 C、4 D、32
3、已知点A、B是反比例函数y=2x(x>0)的图象上任两点,过A、B两
点分别作y轴的垂线,垂足分别为C、D,连接AB,AO,BO,
则S四边形ABCD:S△AOB等于()
4、在平面直角坐标系中,有反比例函数y= 1x与y=- 1x的图象和正方形ABCD,原点O与对角线AC、BD的交点重叠,且如图所示的阴影部分面积为8,则
AB=__________
5、反比例函数y=- 5x的图象如图所示,P是图象上的任意点,过点P分
别做两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是对角线OP上的
动点,连接DA、DB,则图中阴影部分的面积是____________
6、如图,点A,C在反比例函数y= 3x(x<0)的图象上,B,D在x轴
上,△OAB,△BCD均为正三角形,则点C的坐标是____________
7、如图所示,P1(x1,y1)、P2(x2,y2),…P n(x n,y n)在函数
y= 9x(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3…△P n A n-1A n…
都是等腰直角三角形,斜边OA1,A1A2…A n-1A n,都在x轴上,则
y1+y2+…y n=________
8、如图,在直角坐标平面内,函数y=mx(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
(1)若△ABD的面积为4,求点B的坐标;
(2)求证:DC∥AB;
(3)当AD=BC时,求直线AB的函数解析式.
9、如图,直线y=k 1x+b 与反比例函数 y=k2x 的图象交于A (1,6),B (a ,3)两点. (1)求k 1、k 2的值.
(2)直接写出 k1x+b-k2x >0时x 的取值范围;
(3)如图,等腰梯形OBCD 中,BC ∥OD ,OB=CD ,OD 边在x 轴上,过点C 作CE ⊥OD 于点E ,CE 和反比例函数的图象交于点P ,当梯形OBCD 的面积为12时,请判断PC 和PE 的大小关系,并说明理由.
10、已知(1)A m -,
与(2B m +,是反比例函数k
y x
=图象上的两个点. (1)求k 的值;
(2)若点(10)C -,,则在反比例函数k
y x
=
图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.
11、如图12,已知直线12y x =与双曲线(0)k
y k x
=>交于A B ,两点,且点A 的横坐标为4.
(1)求k 的值; (2)若双曲线(0)k
y k x
=
>上一点C 的纵坐标为8,求AOC △的面积; (3)过原点O 的另一条直线l 交双曲线(0)k
y k x
=
>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.
图12。
