【优质文档】高二数学圆锥曲线专(文科)
高中文科数学 圆锥曲线专题

高二文科数学 寒假作业 圆锥曲线专题一、选择题1 .(2013年高考湖北卷(文))已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的( )A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等2 .(2013年高考四川卷(文))从椭圆22221(0)x y a b a b +=>>上一点P 向x 轴作垂线,垂足恰为左焦点1F ,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且//AB OP (O 是坐标原点),则该椭圆的离心率是( )A. B .12 C. D.3 .(2013年高考课标Ⅰ卷(文))O 为坐标原点,F为抛物线2:C y =的焦点,P 为C 上一点,若||PF =,则POF ∆的面积为 ( )A .2B.C. D .44 .(2013年高考课标Ⅰ卷(文))已知双曲线2222:1x y C a b -=(0,0)a b >>,则C 的渐近线方程为 ( )A .14y x=± B .13y x=± C .12y x=± D .y x =±5 .(2013年高考福建卷(文))双曲线122=-y x 的顶点到其渐近线的距离等于 ( )A .21B .22C .1D .26 .(2013年高考广东卷(文))已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是( )A .14322=+y xB .13422=+y xC .12422=+y xD .13422=+y x7 .(2013年高考四川卷(文))抛物线28y x =的焦点到直线0x =的距离是 ( )A.B .2CD .18 .(2013年高考课标Ⅱ卷(文))设椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为12,,F F P 是C 上的点21212,30PF F F PF F ⊥∠=︒,则C 的离心率为 ( )A .B .C .D .9.(2013年高考大纲卷(文))已知抛物线2:8C y x =与点()2,2M -,过C 的焦点且斜率为k 的直线与C 交于,A B 两点,若0MA MB =,则k =( )A .12 B. CD .210.(2013年高考安徽(文))直线250x y +-+=被圆22240x y x y +--=截得的弦长为 ( ) A .1B .2C .4D.二、填空题11.(2013年高考陕西卷(文))双曲线221169x y -=的离心率为________.12.(2013年高考辽宁卷(文))已知F 为双曲线22:1916x y C -=的左焦点,,P Q 为C 上的点,若PQ 的长等于虚轴长的2倍,点()5,0A 在线段PQ 上,则PQF ∆的周长为____________.13.(2013年高考北京卷(文))若抛物线22y px =的焦点坐标为(1,0)则p =____;准线方程为_____.14.(2013年高考天津卷(文))已知抛物线28y x=的准线过双曲线22221(0,0)x ya ba b-=>>的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为______.三、解答题15.(2013年高考课标Ⅱ卷(文))在平面直角坐标系xOy中,己知圆P在x轴上截得线段长为2,在Y轴上截得线段长为2.(Ⅰ)求圆心P的轨迹方程;(Ⅱ)若P点到直线y=x的距离为,求圆P的方程.16.(2013年高考陕西卷(文))已知动点M(x,y)到直线l:x = 4的距离是它到点N(1,0)的距离的2倍.(Ⅰ) 求动点M的轨迹C的方程;(Ⅱ) 过点P(0,3)的直线m与轨迹C交于A, B两点. 若A是PB的中点, 求直线m的斜率.17.(2013年高考大纲卷(文))已知双曲线()221222:10,0x y C a b F F a b -=>>的左、右焦点分别为,,离心率为3,直线2y C =与(I)求,;a b ; (II)2F l C A B 设过的直线与的左、右两支分别相交于、两点,且11,AF BF =证明:22AF AB BF 、、成等比数列18.(2013年高考天津卷(文))设椭圆22221(0)x y a b a b +=>>的左焦点为F, , 过点F 且与x(Ⅰ) 求椭圆的方程;(Ⅱ) 设A, B 分别为椭圆的左右顶点, 过点F 且斜率为k 的直线与椭圆交于C, D 两点. 若··8AC DB AD CB +=, 求k 的值.19.(2013年高考福建卷(文))如图,在抛物线2:4E y x =的焦点为F ,准线l 与x 轴的交点为A .点C 在抛物线E 上,以C 为圆心OC为半径作圆,设圆C 与准线l 的交于不同的两点,M N .(1)若点C 的纵坐标为2,求MN;(2)若2AF AM AN=⋅,求圆C 的半径.20.(2013年高考广东卷(文))已知抛物线C的顶点为原点,其焦点()()0,0F c c>到直线:20 l x y--=的距离为2.设P为直线l上的点,过点P作抛物线C的两条切线,PA PB,其中,A B为切点. (1) 求抛物线C的方程;(2) 当点()00,P x y为直线l上的定点时,求直线AB的方程;(3) 当点P在直线l上移动时,求AF BF⋅的最小值.高二文科数学 寒假作业 圆锥曲线专题 参考答案选择题 1. D 2. C 3. C 4. C 5. B 6. D 7. D 8. D 9. D 10C填空题 11. 45 12. 44 13. 2,1x =- 14. 2213y x -=解答题15.【答案】16.【答案】解: (Ⅰ) 点M(x,y)到直线x=4的距离,是到点N(1,0)的距离的2倍,则134)1(2|4|2222=+⇒+-=-y x y x x .所以,动点M 的轨迹为 椭圆,方程为13422=+y x(Ⅱ) P(0, 3), 设212122113202),,(B ),,(A y y x x y x y x +=+=,由题知:椭圆),3-,0()3,0(和的上下顶点坐标分别是经检验直线m 不经过这2点,即直线m 斜率k 存在.3:+=kx y m 方程为设直线.联立椭圆和直线方程,整理得:221221224324,432402424)43k x x k k x x kx x k +=⋅+-=+⇒=+++(232924)43()24(252)(2212221212211221±=⇒=⋅+-⇒=⋅⋅-+⇒+=+k k k x x x x x x x x x x 所以,直线m 的斜率23±=k17.【答案】(Ⅰ)由题设知3c a =,即2229a b a +=,故228b a =. 所以C 的方程为22288x y a -=.将y=2代入上式,求得,x =由题设知,=解得,21a =.所以1,a b ==(Ⅱ)由(Ⅰ)知,1(3,0)F -,2(3,0)F ,C 的方程为2288x y -=. ① 由题意可设l 的方程为(3)y k x =-,||k <,代入①并化简得,2222(8)6980k x k x k --++=.设11(,)A x y ,22(,)B x y ,则 11x ≤-,21x ≥,212268k x x k +=-,2122988k x x k +∙=-. 于是11||(31)AF x ===-+,12||31BF x ==+由11||||AF BF =得,12(31)31x x -+=+,即1223x x +=-.故226283k k =--,解得245k =,从而12199x x ∙=-.由于21||13AF x ===-,22||31BF x ===-,故2212||||||23()4AB AF BF x x =-=-+=,221212||||3()9-116AF BF x x x x ∙=+-=.因而222|||||AB|AF BF ∙=,所以2||AF 、||AB 、2||BF 成等比数列.18.【答案】19.【答案】解:(Ⅰ)抛物线24y x =的准线l 的方程为1x =-, 由点C 的纵坐标为2,得点C 的坐标为(1,2)所以点C 到准线l 的距离2d =,又||CO =.所以||2MN ===.(Ⅱ)设200(,)4y C y ,则圆C 的方程为242220000()()416y y x y y y -+-=+, 即22200202y x x y y y -+-=. 由1x =-,得2202102y y y y -++=设1(1,)M y -,2(1,)N y -,则: 222000201244(1)240212y y y y y y ⎧∆=-+=->⎪⎪⎨⎪=+⎪⎩由2||||||AF AM AN =⋅,得12||4y y = 所以2142y +=,解得0y =,此时0∆>所以圆心C的坐标为3(2或3(,2从而233||4CO =,||CO =,即圆C20.【答案】(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P , 由24x y =,即214y x ,=得y '=12x .∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= .∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ①同理,20202y x x y -=. ②综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程y x xy -=002.∵经过1122(,),(,)A x y B x y 两点的直线是唯一的,∴直线AB 的方程为yx xy -=002,即00220x x y y --=;第 11 页 共 11 页 11 (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x yx x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-=0020x y --= ()222200000021=221A F B F y y x y y y ∴⋅=-++-+++2200019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y=-时,AF BF ⋅取得最小值为92。
高二数学圆锥曲线专(文科)

高二数学(文科)专题复习(十二)圆锥曲线一、选择题1. 设双曲线以椭圆192522=+y x 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为( )A .2±B .34±C .21±D .43±2. 过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于5,则这样的直线( )A .有且仅有一条B .有且仅有两条C .有无穷多条D .不存在3.从集合{1,2,3…,11}中任选两个元素作为椭圆方程12222=+ny m x 中的m 和n,则能组成落在矩形区域B={(x ,y)| |x |<11且|y|<9}内的椭圆个数为( )A .43B . 72C . 86D . 90 4. 设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是( )(A (B (C )2 (D 1 5. 已知双曲线22163x y -=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为( )(A) (B) (C) 65 (D) 566.已知双曲线22a x -22b y =1(a >0,b >0)的右焦点为F ,右准线与一条渐近线交于点A ,△OAF 的面积为22a (O 为原点),则两条渐近线的夹角为( )7.直线y =x +b (b ≠0)交抛物线212y x =于A 、B 两点,O 为抛物线的顶点,OA OB •u u u r u u u r=0,则b =_______.8.椭圆221mx ny +=与直线10x y +-=相交于,A B 两点,过AB 中点M 与坐标原点的直线的斜率为,则mn的值为9.过抛物线24y x =的焦点作直线交抛物线于1122(,),(,)A x y B x y 两点,若12y y +=则AB 的值为10.以下四个关于圆锥曲线的命题中: ①设A 、B 为两个定点,k 为非零常数,||||PA PB k -=u u u r u u u r,则动点P 的轨迹为双曲线;②过定圆C 上一定点A 作圆的动点弦AB ,O 为坐标原点,若1(),2OP OA OB =+u u u ru u ur u u u r 则动点P 的轨迹为椭圆;③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率;④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点. 其中真命题的序号为 (写出所有真命题的序号)三、解答题11.抛物线顶点在原点,它的准线过双曲线22221(0,0)x y a b a b-=>> 的一个焦点,且抛物线与双曲线的一个交P (3212.已知抛物线y 2=2px(p>0)的焦点为F,A 是抛物线上横坐标为4、且位于x 轴上方的点,A 到抛物线准线的距离等于5,过A 作AB 垂直于y 轴,垂足为B,OB 的中点为M. (1)求抛物线方程;(2)过M 作MN ⊥FA, 垂足为N,求点N 的坐标;(3)以M 为圆心,MB 为半径作圆M.当K(m,0)是x 轴上一动点时,讨论直线AK 与圆M 的位置关系.高二数学专题复习(十三)圆锥曲线(文科)一、选择题1.已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,若过点F 且倾斜角为60o的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )A .(1,2]B .(1,2)C .[2,)+∞D .(2,)+∞2.若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) A .2- B .2 C .4- D .43.已知双曲线9322=-y x ,则双曲线右支上的点P 到右焦点的距离与点P 到右准线的距离之比等于( )A. 2B.332 C. 2 D.4 4.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC 的周长是 ( )A .2 3B .6C .4 3D .12 5.已知两定点()()2,0,1,0A B -,如果动点P 满足2PA PB =,则点P 的轨迹所包围的图形的面积等于( )A .9πB .8πC .4πD .π6.直线3y x =-与抛物线24y x =交于,A B 两点,过,A B 两点向抛物线的准线作垂线,垂足分别为,P Q ,则梯形APQB 的面积为( )A .48B .56C .64D .727.抛物线24y x =的经过焦点弦的中点轨迹方程是8. 以y=为渐近线的双曲线的离心率为____________9.抛物线C :28y x =,一直线:(2)l y k x =-与抛物线C 相交于A 、B 两点,设,m AB = 则m 的取值范围是10.对于椭圆191622=+y x 和双曲线19722=-y x 有下列命题: ①椭圆的焦点恰好是双曲线的顶点;②双曲线的焦点恰好是椭圆的顶点; ③双曲线与椭圆共焦点; ④椭圆与双曲线有两个顶点相同.其中正确命题的序号是 . 三、解答题11.已知三点P (5,2)、1F (-6,0)、2F (6,0)。
高中文科数学圆锥曲线教案

高中文科数学圆锥曲线教案
学科:数学
年级:高中
课时:1课时
教学目标:
1. 了解圆锥曲线的基本概念和性质;
2. 掌握圆、椭圆、双曲线和抛物线的方程及其图像特征;
3. 能够通过方程判断图像种类和位置。
教学内容:
1. 圆锥曲线的定义和分类;
2. 圆的方程和图像特征;
3. 椭圆的方程和图像特征;
4. 双曲线的方程和图像特征;
5. 抛物线的方程和图像特征。
教学步骤:
一、导入(5分钟)
1. 引导学生回顾基础知识,复习圆的相关概念;
2. 提出问题:“什么是圆锥曲线?有哪些种类?”
二、讲解(20分钟)
1. 解释圆锥曲线的概念和分类;
2. 介绍圆、椭圆、双曲线和抛物线的方程和图像特征;
3. 分别讲解每种圆锥曲线的方程及其图像形状。
三、练习(20分钟)
1. 给学生练习一些简单的题目,让他们通过方程确定图像的种类;
2. 提示学生注意每种圆锥曲线的特征,做好区分。
四、总结(10分钟)
1. 总结本节课学习的重点内容,强调圆锥曲线的分类和特征;
2. 提醒学生在以后的学习中要注意圆锥曲线的应用。
五、作业布置(5分钟)
1. 布置相关练习题目,巩固今天学习的知识;
2. 提醒学生复习圆锥曲线的相关理论。
教学反思:
本节课内容相对简单,主要是让学生掌握圆锥曲线的基本概念和特征。
教学中应注意引导学生运用所学知识解决问题,培养他们的思维能力和分析能力。
同时,也要注重引导学生合理安排学习时间,将知识运用到实际问题中,提高学习效果。
圆锥曲线高二文科知识点

圆锥曲线高二文科知识点圆锥曲线是高中数学中的一个重要内容,也是文科生需要掌握的知识点之一。
圆锥曲线包括圆、椭圆、双曲线和抛物线四种形态,每种形态都有其独特的性质和应用。
下面将逐一介绍这些知识点。
一、圆圆是由平面上到一个固定点距离相等的所有点构成的集合。
圆的特点是:1. 圆心:圆上所有点到圆心的距离相等;2. 半径:圆心到圆上任一点的距离。
圆的方程可以表示为:(x - a)² + (y - b)² = r²,其中(a, b)是圆心的坐标,r是半径的长度。
圆的性质可以应用于日常生活中的测量、建筑等方面。
在几何中,圆的相关定理也是很重要的内容。
二、椭圆椭圆是圆锥曲线中的一种形态,其特点是:1. 两个焦点F₁和F₂:椭圆上任意一点到两个焦点的距离之和等于两个固定值2a;2. 短轴:过圆心的直径,一般记为2b;3. 长轴:连接两个焦点并通过圆心的直径,一般记为2a。
椭圆的标准方程可以表示为:(x - h)²/a² + (y - k)²/b² = 1,其中(h, k)是椭圆的中心坐标。
椭圆在几何学、天文学等领域有广泛的应用。
如行星运动的轨道、航天器发射中的轨迹分析等。
三、双曲线双曲线是圆锥曲线中的一种形态,其特点是:1. 两个焦点F₁和F₂:双曲线上任意一点到焦点距离之差等于两个固定值2a;2. 短轴:通过两个焦点且垂直于连接两焦点的直线的直径,一般记为2b。
双曲线的标准方程可以表示为:(x - h)²/a² - (y - k)²/b² = 1,其中(h, k)是双曲线的中心坐标。
双曲线在物理学、天文学等领域有广泛应用,例如天体运动轨迹、电磁场分布等。
四、抛物线抛物线是圆锥曲线中的一种形态,其特点是:1. 焦点F:抛物线上任意一点到焦点的距离等于该点到准线的垂直距离;2. 准线:与抛物线对称轴平行且与焦点的距离相等的直线。
高二上文科数学圆锥曲线专题复习

高二上文科数学圆锥曲线专题复习知识梳理:1.椭圆与双曲线23若直线b kx y l +=:与圆锥曲线0),(:=y x F r 相交于),(),,(2211y x B y x A 两点, 则弦长=||AB ;特别的,若圆锥曲线为抛物线时,则过抛物线焦点的弦长=||AB ;复习作业:1.已知椭圆121022=-+-m y m x 的焦距为4,则m 等于( ) A. 4 B. 8 C. 4或8 D.以上均不对2.若椭圆19822=++y k x 的离心率为21=e ,则k 等于( ) A. 4 B. 45-C. 4或45- D.以上均不对 3.“21<<m ”是“方程13122=-+-my m x 表示焦点在y 轴上的椭圆”的( )条件 A.充分不必要 B. 必要不充分 C. 充要 D.既不充分也不必要4.以椭圆的焦点为顶点,离心率为的双曲线的方程 ( ) AB C 或 D 以上都不对 5.设椭圆)0(1:2222>>=+b a b y a x C 的左右焦点分别为21,F F ,P 是C 上的点,且02121230,=∠⊥F PF F F PF ,则C 的离心率为( )A.63 B.31 C. 21D.33 6.若双曲线17222=---my m x 的焦距为6,则实数m 为( ) A. 9 B. 0 C. 0或9 D.0或9-7. .椭圆1244922=+y x 上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直,则△21F PF 的面积为 ( ) A 20 B 22 C 28 D 248.过双曲线)0,0(12222>>=-b a by a x 的一个焦点F 引它的一条渐近线的垂线,垂足为M ,并且交y 轴于点E ,若M 为EF 的中点,则该双曲线的离心率为( )A.3B.2C.3D.29.过点)1,1(M 的直线与椭圆13422=+y x 交于B A ,两点,且点M 平分弦AB ,则直线AB 的方程为( )A.0734=-+y xB.743-+y xC.0143=+-y xD.0134=--y x1162522=+y x 21481622=-y x 127922=-y x 1481622=-y x 127922=-y x10..已知点)1,2(A ,抛物线x y 42=的焦点F ,若抛物线上存在一点P ,使得PF PA +最小,则P 点的坐标为( )A.)1,2(B.)1,1(C.)1,21(D.)1,41(11.双曲线的焦点到渐近线的距离等于 . 12.设抛物线28y x =上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是 ________13. 过双曲线228x y -=的左焦点1F 有一条弦PQ 在左支上,若||PQ =7,2F 是双曲线的右焦点,则2PF Q ∆ 的周长是 .14. 方程22141x y k k +=--表示的曲线为C ,若曲线C 为圆,则_______k =;若曲线C 表示焦点在x 轴 上的椭圆,则k 的取值范围为______________;若曲线C 表示双曲线,则k 的取值范围为_______________. 15. 已知抛物线24y x =上有一点P ,且点P 到直线03=+-y x 的距离最短,则最短距离为________. 16.若动圆P 经过定点)0,3(A ,且与定圆16)3(:22=++y x B 外切,则动圆圆心的轨迹方程为17.(1)已知双曲线)0,0(12222>>=-b a b y a x 与椭圆14922=+y x 有相同的焦点,且双曲线的渐近线方程为x y 2±=,求双曲线的标准方。
高二文科期末复习圆锥曲线

圆锥曲线解题注意点:1. 椭圆中,a ,b ,c 的关系为————;离心率e=————;准线方程为————;焦点到相应准线距离为———— 双曲线中,a ,b ,c 的关系为————;离心率e=————;准线方程为————;焦点到相应准线距离为————2. 解题时,将方程转化为标准形式,注意焦点位置;若焦点位置不定须先讨论3.在利用圆锥曲线统一定义解题时,两个定义常常结伴而用,有时对我们解题有很大的帮助,有关过焦点弦问题用第二定义0,||>=e e dPF 可能更为方便.4.在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式0≥∆的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在0>∆下进行).5. 解析几何中解题关键就是把题目中的几何条件代数化,特别是一些很不起眼的条件,有时起着关键的作用:如:点在曲线上、相交、共线、以某线段为直径的圆经过某点、夹角、垂直、平行、中点、角平分线、中点弦问题等.数形结合是解决解几问题的重要思想方法,要记得画图分析.典型例题:一.求三种圆锥曲线的方程 1. 求满足下列条件的椭圆方程(1) 椭圆的两个顶点坐标分别为),(03-,),(03,且短轴是长轴的31; (2)两个焦点的坐标是),),(,(2020-,并且椭圆经过点),(2523-2.根据下列条件,求双曲线方程。
(1)与双曲线116y 9x 22=-有共同渐近线,且过点(-3,32); (2)与双曲线14y 16x 22=-有公共焦点,且过点(23,2).3. 分别求满足下列条件的抛物线的标准方程(1)过点(-3,4);(2) (4)定点在原点,以坐标轴为对称轴,焦点到准线的距离为25二.圆锥曲线的简单几何性质1. 设F1、F2为椭圆14y9x22=+的两个焦点,P为椭圆上一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求|PF||PF|21的值.2. 已知21,F F 是双曲线)0,0(1x 2222>>=-b a by a 的两焦点,以线段21F F 为边作正三角形21F MF ,若边1MF 的中点在双曲线上,求双曲线的离心率3.已知抛物线x y 62=,定点)3,2(A ,F 为抛物线的焦点,P 为抛物线的动点,求PA PF +的最小值三.两种圆锥曲线相结合的综合问题1.抛物线顶点在原点,它的准线过双曲线22221(,)x y ao bo a b-=的一个焦点并与双曲线实轴垂直,已知抛物线与双曲线的交点为32⎛ ⎝,求抛物线和双曲线的方程2. 已知抛物线1C 的顶点在坐标原点,它的准线经过双曲线2C :22221x y a b-=的一个焦点1F 且垂直于2C 的两个焦点所在的轴,若抛物线1C 与双曲线2C 的一个交点是2(,33M .(1)求抛物线1C 的方程及其焦点F 的坐标;(2)求双曲线2C 的方程及其离心率e .四.直线与圆锥曲线的位置关系1. 已知椭圆2222 1 (0)y x a b a b +=>>的上、下焦点分别为12,F F ,离心率e =,一条准线方程为2y =。
(完整)圆锥曲线知识点梳理(文科),推荐文档

S 积为 F1PF2
b2 tan . 2
且 PF1
PF2
2b2 1 cos
x2
2.设 P 点是双曲线
a2
y2 b2
x0
(3)设抛物线的标准方程为 y 2 =2px(p>0),则抛物线的焦点到其顶点的距离为 p ,顶点到准线的距离 p ,焦点到准线的距离
2
2
为 p.
(4)已知过抛物线 y 2 =2px(p>0)焦点的直线交抛物线于 A、B 两点,则线段 AB 称为焦点弦,设 A(x1,y1),B(x2,y2),则弦长
在圆 C 上,|MC|>r 点 M 在圆 C 内,其中|MC|= (x 0 - a)2 (y0 - b) 2 。
(4)直线和圆的位置关系:①直线和圆有相交、相切、相离三种位置关系:直线与圆相交 有两个公共点;直线与圆相切 有一个公共点;直线与圆相离 没有公共点。
Aa Bb C
②直线和圆的位置关系的判定:(i)判别式法;(ii)利用圆心 C(a,b)到直线 Ax+By+C=0 的距离 d
e 的点的轨迹.(e>1)
与定点和直线的距离相等的点的 轨迹.
轨迹条件
点集: ({M||MF1+|MF2|=2a,|F
1F2|<2a=
点集:{M||MF1|-|MF2|. =±2a,|F2F2|>2a}.
点集{M| |MF|=点 M 到直线 l 的距离}.
图形
方 标准 方程
程
x 2 y 2 1( a b >0) a2 b2
与半径 r 的大
A2 B2
小关系来判定。
二、圆锥曲线的统一定义:
平面内的动点 P(x,y)到一个定点 F(c,0)的距离与到不通过这个定点的一条定直线 l 的距离之 比是一个常数 e(e>0),则动点的轨 迹叫做圆锥曲线。其中定点 F(c,0)称为焦点,定直线 l 称为准线,正常数 e 称为离心率。当 0<e<1 时,轨迹为椭圆;当 e=1 时, 轨迹为抛物线;当 e>1 时,轨迹为双曲线。
高二文科圆锥曲线专题复习(含答案)

圆锥曲线文科专题复习知识回顾:一、圆锥曲线的两个定义:1、椭圆:第一定义:椭圆中,与两个定点F,F的距离的和等于常数,且此常数一定要大于,(当常数等于时,轨迹是线段FF;当常数小于时,无轨迹)第二定义:与定点和直线的距离之比为定值e的点的轨迹.(0<e<1)2、双曲线:第一定义:双曲线中,与两定点F,F的距离的差的绝对值等于常数,且此常数一定要小于|F-F|,(定义中的“绝对值”与<|F-F|不可忽视。
若=|FF|,则轨迹是以F,F为端点的两条射线;若﹥|FF|,则轨迹不存在;若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
)第二定义:与定点和直线的距离之比为定值e的点的轨迹.(e>1)3、抛物线:与定点和直线的距离相等的点的轨迹.二、圆锥曲线的标准方程(1)椭圆:焦点在轴上时()(为参数),焦点在轴上时=1()(2)双曲线:焦点在轴上: =1,焦点在轴上:=1()。
(3)抛物线:开口向右时, 开口向左时,开口向上时, 开口向下时。
三:圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):(1)椭圆:由,分母的大小决定,焦点在分母大的坐标轴上。
如已知方程表示焦点在y轴上的椭圆,则m的取值范围是__(答:)(2)双曲线:由,项系数的正负决定,焦点在系数为正的坐标轴上;(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
【特别提醒】在椭圆中,最大,,在双曲线中,最大,。
四、圆锥曲线的几何性质:(1)椭圆(以()为例):①范围:;②焦点:两个焦点;③对称性:两条对称轴,一个对称中心(0,0),四个顶点,其中长轴长为2,短轴长为2;④准线:两条准线;⑤离心率:,椭圆,(越小,椭圆越圆;越大,椭圆越扁。
)(2)双曲线(以()为例):①范围:或;②焦点:两个焦点;对称性:两条对称轴,一个对称中心(0,0),两个顶点,其中实轴长为2,虚轴长为2,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为;④准线:两条准线;⑤两条渐近线:⑥离心率:,双曲线,(越小,开口越小,越大,开口越大;)(3)抛物线(以为例)-----的几何意义是:焦点到准线的距离:①范围:;②焦点:一个焦点,③对称性:一条对称轴,没有对称中心,只有一个顶点(0,0);④准线:一条准线;⑤离心率:,抛物线。
高二文科数学圆锥曲线(基础篇)

高二文科数学圆锥曲线基础训练1.k 为何值时,直线y=kx+2和椭圆632x 22=+y 有两个交点 ( ) A .—36<k<36 B .k>36或k< —36 C .—36≤k ≤36 D .k ≥36或k ≤ —36 2.抛物线4x y 2=上一点M 到焦点的距离为1,则点M 的纵坐标是 ( ) A. 0 B. 1516 C. 78 D. 17163.过点(0,1)与双曲线221x y -=仅有一个公共点的直线共有 ( ) A.1条 B.2条 C.3条 D.4条4.椭圆的一个顶点和两个焦点构成等腰直角三角形,则此椭圆的离心率为( ) A.21 B.23 C.22 D.33 5.若椭圆)0(122>>=+n m ny m x 和双曲线)0(122>>=-b a b y a x 有相同的焦点1F 、2F ,P 是两曲线的一个公共点,则||||21PF PF ⋅的值是( )A .m-aB .)(21a m - C .22a m - D .a m - 6.已知点)0,4(1-F 和)0,4(2F ,曲线上的动点P 到1F 、2F 的距离之差为6,则曲线方程为()A.17922=-y x B .)0(17922>=-y x y C .17922=-y x 或17922=-x y D .)0(17922>=-x y x 7.已知k <4,则曲线14922=+y x 和14922=-+-ky k x 有 ( ) A. 相同的准线 B. 相同的焦点C. 相同的离心率D. 相同的长轴8.抛物线)0(2<=a ax y 的焦点坐标是( ) A .⎪⎭⎫ ⎝⎛0,21a B.⎪⎭⎫ ⎝⎛a 21,0 C.⎪⎭⎫ ⎝⎛a 41,0 D.⎪⎭⎫ ⎝⎛-a 41,0 9.抛物线212y x =的准线与双曲线的两条渐近线所围成的三角形面积等于( ) A. B.C.210.已知椭圆)0(12222>>=+b a by a x 的左、右两焦点分别为21,F F ,点A 在椭圆上,0211=⋅F F AF , 4521=∠AF F ,则椭圆的离心率e 等于 ( )A.33 B.12- C.13- D. 215-11.中心在原点,焦点在x 轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的标准方程为___________ 12.过椭52x +42y =1的右焦点作一条斜率为2的直线与椭圆交于A 、B 两点,O 为坐标原点,求弦AB 的长_______ 13.过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 作一条渐近线的垂线,若垂足恰在线段OF (O 为原点)的垂直平分线上,则双曲线的离心率为 .14.过点(1,2)总可作两条直线与圆2222150x y kx y k ++++-=相切,则实数k 的取值范围是 .15.已知抛物线2:2(0)C x py p =>上一点(,4)A m 到其焦点的距离为5,则m = .16.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点12,F F 在x 轴上,离心率为2。
文科圆锥曲线专题练习及答案

文科圆锥曲线1.设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点,P 为直线32ax =上一点,12PF F ∆是底角为30的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34()D 45【答案】C【命题意图】本题主要考查椭圆的性质及数形结合思想,是简单题.【解析】∵△21F PF 是底角为030的等腰三角形, ∴322c a =,∴e =34,∴0260PF A ∠=,212||||2PF F F c ==,∴2||AF =c ,2.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,AB =;则C 的实轴长为( )()A ()B ()C 4 ()D 8【命题意图】本题主要考查抛物线的准线、直线与双曲线的位置关系,是简单题.【解析】由题设知抛物线的准线为:4x =,设等轴双曲线方程为:222x y a -=,将4x =代入等轴双曲线方程解得y =,∵||AB =a =2,∴C 的实轴长为4,故选C.3.已知双曲线1C :22221(0,0)x y a b a b -=>>的离心率为2.若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为2,则抛物线2C 的方程为(A) 2x y =(B) 2x y = (C)28x y = (D)216x y = 考点:圆锥曲线的性质解析:由双曲线离心率为2且双曲线中a ,b ,c 的关系可知a b 3=,此题应注意C2的焦点在y 轴上,即(0,p/2)到直线x y 3=的距离为2,可知p=8或数形结合,利用直角三角形求解。
4.椭圆的中心在原点,焦距为4,一条准线为4x =-,则该椭圆的方程为(A )2211612x y += (B )221128x y += (C )22184x y += (D )221124x y += 【命题意图】本试题主要考查了椭圆的方程以及性质的运用。
【精品】高二文科数学圆锥曲线复习共65页

56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
高考文科数学圆锥曲线专题复习.doc

圆锥曲线专题复习知识归纳: 名称椭圆图 象平面内到两定点F 1 ,F 2 的距离的和为常数(大于 F 1F 2 )的动点的轨迹叫椭 圆即 MF 1MF 2 2a定 义c 时,轨迹是椭圆,当 2 a ﹥ 2 当 2 a = 2 c 时 , 轨 迹 是 一 条 线 段F 1 F 2当 2 a ﹤ 2 c 时,轨迹不存在双曲线平面内到两定点F 1, F 2 的距离的差的绝对值为常数(小于F 1 F 2 )的动点的轨迹叫双曲线即MF 1 MF 2 2a当 2 a ﹤ 2 c 时,轨迹是双曲线当 2 a = 2 c 时,轨迹是两条射线当 2 a ﹥ 2 c 时,轨迹不存在焦点在 x 轴上时:x 2y 2ab1x 2y222焦点在 x 轴上时:1a 2b 2标 准 焦点在 y 轴上时: y 2 x2方 程1焦点在 y 轴上时: y2x 2a2b21注:根据分母的大小来判断焦点在哪一a 2b 2坐标轴上常 数a,b,ca 2 c 2b 2 , a b 0 ,c 2a 2b 2 ,c a 0的 关 a 最大, cb, c b, cbc 最大,可以 a b, ab,ab系焦点在 x 轴上时:xy渐 近a b线焦点在 y 轴上时:yx 0a b抛物线:图形yOFl yxFO xl方 22 px( p0)y22 px( p0) x 22 py( p 0)x 22 py( p 0)y 程焦p,0) ( p,0)(0, p)(0, p )(点2222 准px pypyp x2222线(一)椭圆1. 椭圆的性质:由椭圆方程x 2y 2 ab 0)a1(2b 2( 1)范围:a xa ,- bx a ,椭圆落在 xa yb 组成的矩形中。
,( 2)对称性 : 图象关于 y 轴对称。
图象关于 x 轴对称。
图象关于原点对称。
原点叫椭圆的对称中心,简称中心。
x 轴、 y 轴叫椭圆的对称轴。
从椭圆的方程中直接可以看出它的范围,对称的截距。
高考文科数学圆锥曲线专题复习

高三文科数学专题复习之圆锥曲线 名 称 椭圆双曲线图 象xOyxOy定 义平面内到两定点的距离的和为常数(大于)的动点的轨迹叫椭圆即当2﹥2时,轨迹是椭圆,当2=2时,轨迹是一条线段当2﹤2时,轨迹不存在 平面内到两定点的距离的差的绝对值为常数(小于)的动点的轨迹叫双曲线即当2﹤2时,轨迹是双曲线 当2=2时,轨迹是两条射线 当2﹥2时,轨迹不存在标准方 程 焦点在轴上时:焦点在轴上时:注:根据分母的大小来判断焦点在哪一坐标轴上焦点在轴上时:焦点在轴上时:常数的关 系,, 最大,,最大,可以渐近线焦点在轴上时:焦点在轴上时:抛物线:图形方程焦点准线(一)椭圆1. 椭圆的性质:由椭圆方程(1)范围:,椭圆落在组成的矩形中。
(2)对称性:图象关于y轴对称。
图象关于x轴对称。
图象关于原点对称。
原点叫椭圆的对称中心,简称中心。
x轴、y轴叫椭圆的对称轴。
从椭圆的方程中直接可以看出它的范围,对称的截距。
(3)顶点:椭圆和对称轴的交点叫做椭圆的顶点椭圆共有四个顶点:,。
加两焦点共有六个特殊点。
叫椭圆的长轴,叫椭圆的短轴。
长分别为。
分别为椭圆的长半轴长和短半轴长。
椭圆的顶点即为椭圆与对称轴的交点。
(4)离心率:椭圆焦距与长轴长之比。
椭圆形状与的关系:,椭圆变圆,直至成为极限位置圆,此时也可认为圆为椭圆在时的特例。
椭圆变扁,直至成为极限位置线段,此时也可认为是椭圆在时的特例。
2. 椭圆的第二定义:一动点到定点的距离和它到一条定直线的距离的比是一个内常数,那么这个点的轨迹叫做椭圆。
其中定点叫做焦点,定直线叫做准线,常数就是离心率。
椭圆的第二定义与第一定义是等价的,它是椭圆两种不同的定义方式3. 椭圆的准线方程对于,左准线;右准线对于,下准线;上准线焦点到准线的距离(焦参数)(二)双曲线的几何性质:1. (1)范围、对称性由标准方程,从横的方向来看,直线x=-a,x=a之间没有图象,从纵的方向来看,随着x的增大,y的绝对值也无限增大,所以曲线在纵方向上可无限伸展,不像椭圆那样是封闭曲线。
高二数学圆锥曲线(完整版)
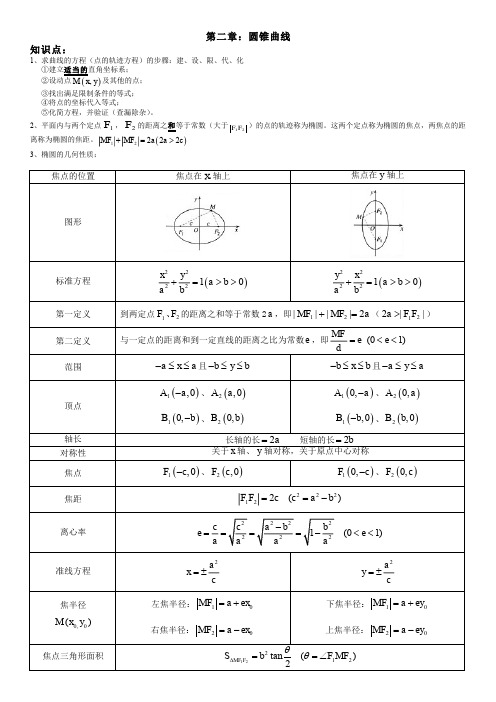
第二章:圆锥曲线知识点:1、求曲线的方程(点的轨迹方程)的步骤:建、设、限、代、化①建立适当的直角坐标系;),M x y 及其他的点; ③找出满足限制条件的等式; ④将点的坐标代入等式;⑤化简方程,并验证(查漏除杂)。
2、平面内与两个定点1F ,2F 的距离之和等于常数(大于12F F)的点的轨迹称为椭圆。
这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距。
()12222MF MF a a c +=> 3、椭圆的几何性质:焦点在x 轴上4、设M 是椭圆上任一点,点M 到F 对应准线的距离为1d ,点M 到F 对应准线的距离为2d ,则1212F F e d d M M ==。
5、平面内与两个定点1F ,2F 的距离之差的绝对值等于常数(小于12F F )的点的轨迹称为双曲线。
这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距。
()12222MF MF a a c -=< 6、双曲线的几何性质:7、实轴和虚轴等长的双曲线称为等轴双曲线。
x129、平面内与一个定点F和一条定直线l的距离相等的点的轨迹称为抛物线.定点F称为抛物线的焦点,定直线l称为抛物线的准线.11、焦半径公式:若点()00,x y P 在抛物线()220y px p =>上,焦点为F ,则02p F x P =+;、若点()00,x y P 在抛物线()220y px p =->上,焦点为F ,则02pF x P =-+;若点()00,x y P 在抛物线()220x py p =>上,焦点为F ,则02p F y P =+;若点()00,x y P 在抛物线()220x py p =->上,焦点为F ,则02p F y P =-+.12、抛物线的几何性质:关于抛物线焦点弦的几个结论:设AB 为过抛物线22(0)y px p =>焦点的弦,1122(,)(,)A x y B x y 、,直线AB 的倾斜角为θ,则⑴ 221212,;4p x x y y p ==- ⑵ 22;sin p AB θ= ⑶ 以AB 为直径的圆与准线相切; ⑷ 焦点F 对A B 、在准线上射影的张角为2π;⑸112.||||FA FB P+= 知识储备1、 直线的方程形式:① 点斜式:已知直线过点(x0,y0),斜率为k,则直线方程为y -y0=k(x -x0),它不包括垂直于x 轴的直线;② 斜截式:已知直线在y 轴上的截距为b,斜率为k,则直线方程为y =kx +b,它不包括垂直于x 轴的直线;③ 两点式:已知直线经过P1(x1,y1),P2(x2,y2)两点,则直线方程为x-x1/x2-x1=y-y1/y2-y1,它不包括垂直于坐标轴的直线; ④ 截距式:已知直线在x 轴和y 轴上的截距为a,b,则直线方程为x/a +y/b =1,它不包括垂直于坐标轴的直线和过原点的直线;⑤ 一般式:任何直线均可写成Ax +By +C =0(A,B 不同时为0)的形式.2、 与直线相关的重要内容:① 倾斜角与斜率k :倾斜角与斜率k :② 点到直线的距离d : 夹角公式:③ 弦长公式:④ 两条直线的位置关系:。
(完整版)高二数学(文科)圆锥曲线的题目型地总结,推荐文档

方程是
(B)
A.x=3
B.y=-4
C.x=3 或 y=-4 D.x=4 或 y=-3
7.直线 y=kx+1 与椭圆 x 2 y 2 1 恒有公共点,则 m 的取值范围是 5m
(D)
解析:直线过定点(0,1),把点代入要不大于 1,且 m 不等于 5(等于 5 不是椭圆)
8.一动圆与两圆: x2 y2 1和 x2 y2 8x 12 0 都外切,则动圆心的轨迹为( D )
()
A.(0,1)
B.(0,5)
C.[1,+ )
D.[1,5 ) (5,)
8.一动圆与两圆: x2 y2 1和 x2 y2 8x 12 0 都外切,则动圆心的轨迹为( )
(A)圆弧
(B)圆
(C)椭圆
(D)双曲线的一支
9.已知点 P 是抛物线 y 2 4x 上的动点,点 P 在 y 轴上的射影是点 Q,抛物线外一点 A(4,5)则
|PA|+|PQ|的最小值是
.
10.如图,过抛物线 y 2 2 px( p 0) 的焦点 F 的直线与抛物线相交于 M、N 两点,自 M、N 向准线 l
作垂线,垂足分别为 M1、N1. (I)求证:FM1⊥FN1;
(II)记△FMM1、△FM1N1、△FNN1
的面积分别为
S1、S2、S3,试判断
实用标准文案
高二数学(文)圆锥曲线复习
1.已知动圆过点(1,0),且与直线 x=一 l 相切,则动圆圆心的轨迹方程为
()
A.x2+y2=l
B.x2-y2=1
C.y2=4x
D.x=0
2.已知椭圆 x2 y2 1a b 0,双曲线 x2 y2 1a 0,b 0和抛物线 y2 2 px
高考文科数学圆锥曲线专题复习

圆锥曲线专题复习知识概括: 名称椭圆y图 象Ox平面内到两定点 F 1 ,F 2 的距离的和为常数(大于F 1F 2 )的动点的轨迹叫椭 圆 即 MF 1MF 22a定 义当 2 a ﹥ 2 c 时,轨迹是椭圆,当 2 a = 2 c 时 , 轨 迹 是 一 条 线 段F 1 F 2当 2 a ﹤ 2 c 时,轨迹不存在双曲线yOx平面内到两定点F 1, F 2 的距离的差的绝对值为常数(小于F 1 F 2 )的动点的轨迹叫双曲线即MF 1 MF 2 2a当 2 a ﹤ 2 c 时,轨迹是双曲线当 2 a = 2 c 时,轨迹是两条射线当 2 a ﹥ 2 c 时,轨迹不存在焦点在 x 轴上时:x 2 y2a1x2y22b21焦点在 x 轴上时:b 2 标 准y 2x2a 2方 程焦点在y 轴上时:1焦点在 y 轴上时: y2x 2a2b21注:依据分母的大小来判断焦点在哪一a 2b 2坐标轴上常 数a,b,ca 2c 2b 2 , ab 0 ,c 2a 2b 2 ,c a 0的 关 a 最大, cb, c b, cbc 最大,能够 a b, ab,ab系焦点在 x 轴上时:xy 0渐 近a b线焦点在 y 轴上时:yx 0ab抛物线:图形yOF lyxFO xl方 22 px( p0)y22 px( p 0)x 22 py( p 0)x 22 py( p 0)y程焦 p,0)( p,0) (0, p)(0, p )(点 2222 准 p x pypypx2222线(一)椭圆x 2y 2 a b 0)1. 椭圆的性质:由椭圆方程1(a 2b 2( 1)范围: a xa ,- bx a ,椭圆落在 xa ,yb 构成的矩形中。
( 2)对称性 : 图象对于 y 轴对称。
图象对于 x 轴对称。
图象对于原点对称。
原点叫椭圆的对称中心,简称中心。
x 轴、 y 轴叫椭圆的对称轴。
从椭圆的方程中直接能够看出它的范围,对称的截距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 ,则 m 的值为
2
n
优秀学习资料 欢迎下载
9. 过抛物线 y2 4 x 的焦点作直线交抛物线于 A( x1, y1 ), B( x2, y2 ) 两点,若
y1 y2 2 2, 则 AB 的值为
10.以下四个关于圆锥曲线的命题中:
①设 A 、 B 为两个定点, k 为非零常数, | PA | | PB | k ,则动点 P 的轨迹为双曲线;
P,Q ,则梯形 APQB 的面积为(
)
A. 48 B . 56
C
. 64
D
. 72
题号
1
2
3
4
5
6
答案
二、填空题
7. 抛物线
2
y
4 x 的经过焦点弦的中点轨迹方程是
8. 以 y= 3 x,为渐近线的双曲线的离心率为 ____________
9. 抛物线 C: y2 8x , 一直线 l : y k( x 2) 与抛物线 C 相交于 A、 B 两点 , 设 m AB ,
3
x 轴,则 F1 到直线 F2 M 的距离为
56 (B)
6
6 (C)
5
5 (D)
6
x2 y2 6.已知双曲线 a 2 - b2 =1( a> 0, b> 0)的右焦点为 F,右准线与一条渐近线交于点
A ,△ OAF 的面
积为 a 2 ( O 为原点),则两条渐近线的夹角为(
)
2
A .30o
题号
1
答案
x2 a2
y2 b2
1(a
0, b
0) 的右焦点为 F,若过点
与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
F 且倾斜角为 (
60o 的直线
)
A. (1,2]
B. (1,2)
C. [2, )
D. (2, )
2
2
2.若抛物线 y2 2 px 的焦点与椭圆 x y 1 的右焦点重合,则 p 的值为( )
②过定圆 C 上一定点 A 作圆的动点弦 AB ,O 为坐标原点,若 OP
椭圆;
1 (OA OB ), 则动点 P 的轨迹为
2
③方程 2x 2 5 x 2 0 的两根可分别作为椭圆和双曲线的离心率;
x2
④双曲线
y2
1与椭圆 x 2
y 2 1有相同的焦点 .
25 9
35
其中真命题的序号为 三、解答题
(写出所有真命题的序号)
11. 抛物线顶点在原点, 它的准线过双曲线
x2 a2
y2 b2
1(a
0, b
0) 的一个焦点, 且抛物线与双曲线的一
个交
P(
3 ,
6 )点,求抛物线和双曲线方程。
2
12.已知抛物线 y2=2px(p>0) 的焦点为 F,A 是抛物线上横坐标为
4、且位于 x 轴上方的点 ,A 到抛物线准线的
距离等于 5,过 A 作 AB 垂直于 y 轴,垂足为 B,OB 的中点为 M.
62
A. 2
B
.2
C. 4
D
.4
3.已知双曲线 3 x2 y2 9 , 则双曲线右支上的点 P 到右焦点的距离与点 P 到右准线的距离之比等于
()
优秀学习资料 欢迎下载
A. 2
B. 2 3 3
C. 2
D.4
4.已知△ ABC的顶点 B、 C 在椭圆 x2+ y2= 1 上,顶点 A 是椭圆的一个焦点,且椭圆的另外一个焦点在
(1) 求抛物线方程 ;
(2)过 M 作 MN ⊥ FA, 垂足为 N, 求点 N 的坐标 ; (3)以 M 为圆心 ,MB 为半径作圆 M.当 K(m,0) 是 x 轴上一动点时 ,讨论直线 AK 与圆 M 的位置关系 .
高二数学专题复习 ( 十三 )
圆锥曲线 ( 文科 )
一、选择题
1.已知双曲线
BC
3
边上,则△ ABC的周长是 ( )
A. 2 3
B
.6
C.4 3
D. 12
5.已知两定点 A 2,0 , B 1,0 ,如果动点 P 满足 PA 2 PB ,则点 P 的轨迹所包围的图形的面积等
于( )
A. 9 B . 8 C . 4 NhomakorabeaD.
6.直线 y x 3 与抛物线 y 2 4 x 交于 A, B 两点,过 A, B 两点向抛物线的准线作垂线,垂足分别为
则 m的取值范围是
2
x
10.对于椭圆
16
2
2
y 1和双曲线 x
9
7
2
y 1有下列命题: 9
①椭圆的焦点恰好是双曲线的顶点 ;
②双曲线的焦点恰好是椭圆的顶点 ;
③双曲线与椭圆共焦点 ;
④椭圆与双曲线有两个顶点相同 .
其中正确命题的序号是
.
三、解答题
11.已知三点 P( 5, 2)、 F1 (- 6, 0)、 F2 ( 6, 0)。
(Ⅰ)求以 F1 、 F2 为焦点且过点 P 的椭圆的标准方程;
(Ⅱ)设点
P、 F1 、 F 2 关于直线 y=x 的对称点分别为
P
、
F
' 1
、
F2'
,求以
F1'
、
F
' 2
为焦点且过点
P 的双
曲线的标准方程。
12.
已知椭圆
x2
C 1:
4
y 2 1 ,抛物线 C2: ( y m) 2 2 px( p 0) ,且 C1、C2 的公共弦 AB 过椭圆 C1 的右焦 3
直线(
)
A .有且仅有一条
B.有且仅有两条
C .有无穷多条
D .不存在
3.从集合 {1,2,3 …, 11} 中任选两个元素作为椭圆方程
x2 y2 m 2 n 2 1 中的 m 和 n,则能组成落在矩形区域
B={( x,y)| |x|<11 且|y|<9} 内的椭圆个数为(
)
A .43
B. 72
C. 86
二、填空题
B. 45o 2
7.直线 y= x+ b( b≠ 0) 交抛物线 y
C. 60o
3
4
D . 90o
5
6
1 x2 于 A、B 两点, O为抛物线的顶点, OA OB = 0,则 b= _______. 2
8. 椭圆 mx2 ny2 1 与直线 x y 1 0 相交于 A, B 两点,过 AB 中点 M 与坐标原点的直线的斜率为
优秀学习资料 欢迎下载
高二数学 ( 文科 ) 专题复习 ( 十二 ) 圆锥曲线
一、选择题
x2
1. 设双曲线以椭圆
y 2 1 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜
25 9
率为(
)
A. 2
4
B.
3
1
C.
2
3
D.
4
2. 过抛物线 y 2 4 x 的焦点作一条直线与抛物线相交于 A 、B 两点,它们的横坐标之和等于 5,则这样的
D . 90
4. 设椭圆的两个焦点分别为 F1、、 F2,过 F2 作椭圆长轴的垂线交椭圆于点 P,若△ F1PF2
为等腰直角三角形,则椭圆的离心率是(
)
( A) 2 2
21
(B)
2
( C) 2 2 (D ) 2 1
x2 5. 已知双曲线
6 ()
36 (A)
5
y2 1的焦点为 F1 、 F2 ,点 M 在双曲线上且 MF1
