数 学 2011年广东省初中毕业生学业考试
2011年广东省初中毕业生学业考试模拟试题(二)

2011年广东省初中毕业生学业考试模拟试题(二)英 语第一卷 语言知识与技能 (共85分)一、听力理解(本大题分为A 、B 、C 、D 四部分,共25小题,25分)A 、听句子(本题有5小题,每小题1分,共5分)根据所听句子的内容和所提的问题,选择符合题意的图画回答问题,并将最佳选项的字母编号填写在答卷相应题目的答题位置上。
若用答题卡答题,则将答题卡上对应题目所选选项涂黑。
每小题听一遍。
( )1. What does the girl want to buy?A B C( )2. What does Jim like playing?A B C( )3. When is the woman arriving?A B C( )4. How much is the MP3?A.B. C.( )5. Where is her pen pal from?A B CB 、听对话(本题有10小题,每小题1分,共l0分)回答每段对话后面的问题,在各题所给的三个选项中选出一个最佳答案。
并将其字母编号填写在答卷相应题目的答题位置上。
若用答题卡答题,则将答题卡上对应题目所选的选项涂黑。
每段对话听两遍。
听第一段对话,回答第6小题。
( )6. Where does the conversation probably take place ?A.In a cinema .B.In a bookshop .C.In a post office .听第二段对话,回答第7小题。
( )7. What does the man think of the food in Green House ?A.Good .B.Bad .C.So—so .听第三段对话,回答第8小题。
( )8. How much is the jacket now ?A.30 dollars .B.60 dollars .C.120 dollars .听第四段对话,回答第9小题。
2011年广东广州中考数学试卷及答案 -new

第1页2011年广州市初中毕业生学业考试数学本试卷共5页,分两部分,共25小题,满分150分。
考试用时120分钟。
注意事项:1、答卷前,考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;同时填写考场试室号、座位号,再用2B 铅笔把对应这两号码的标号涂黑。
2、选择题答案用2B 铅笔填涂;将答题卡上选择题答题区中对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;答案不能答在试卷上。
3、非选择题答案必须用黑色字迹的钢笔或签字笔写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,改动后的答案也不能超出指定的区域;不准使用铅笔、圆珠笔和涂改液。
不按以上要求作答的答案无效。
4、考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
第一部分 选择题(共30分)一、选择题(每小题3分,共30分) 1、四个数-5,-0.1,21,3中为无理数的是( ) (A )-5 (B )-0.1 (C )21(D )32、已知□ABCD 的周长为32,AB =4,则BC =( )(A )4 (B )12 (C )24 (D )283、某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( ) (A )4 (B )5 (C )6 (D )104、将点A (2,1)向左平移2个单位长度得到点A ',则点A '的坐标是( ) (A )(0,1) (B )(2,-1) (C )(4,1) (D )(2,3)5、下列函数中,当x >0时,y 值随x 值增大而减小的是( ) (A )2x y = (B )1-=x y (C )x y 43=(D )xy 1= 6、若a <c <0<b ,则abc 与0的大小关系是( )(A )abc <0 (B )abc =0 (C )abc >0 (D )无法确定 7、下面的计算正确的是( )(A )2221243x x x =⋅ (B )1553x x x =⋅ (C )34x x x =÷ (D )725)(x x =第2页8、如图所示,将矩形纸片先沿虚线AB 按箭头方向向右..对折,接着对折后的纸片沿虚线CD 向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )9、当实数x 的取值使得2-x 有意义时,函数y=4x+1中y 的取值范围是( ) (A ) y ≥-7 (B ) y ≥9 (C ) y >9 (D ) y ≤910、如图,AB 切⊙O 于点B ,OA =23,AB =3,弦BC//OA ,则劣弧BC 的弧长为( )(A )π33 (B ) π23 (C ) π (D ) π23二、填空题:(每小题3分,共18分) 11、9的相反数是______。
2011年广东省初中毕业生学业考试数学(附答案)(高清扫描版)

一、2011年广东省初中毕业生学业考试数学参考答案一、1-5、DBACB二、6、-27、___ x ≥2__8、___12__9、__25º__ 10、2561 三、11、原式=-6 12、x ≥3 13、由△ADF ≌△CB E ,得AF =C E ,故得:AE=CF14、(1)⊙P 与⊙P 1外切。
(2)∏-215、(1)c > 21 (2)顺次经过三、二、一象限。
因为:k >0,b=1>0四、16、解:设该品牌饮料一箱有x 瓶,依题意,得6.032626=+-x x 化简,得013032=-+x x解得 131-=x (不合,舍去),102=x经检验:10=x 符合题意答:略.17、略解:AD=25(3+1)≈68.3m18、(1)“班里学生的作息时间”是总体(2)略(3)10%19、略解:(1)∠BDF =90º;(2)AB=BD ×sin60°=6.五、20、略解:(1)64,8,15;(2)n 2-2n+2,n 2,(2n-1);(3)第n 行各数之和:)12)(1()12(222222-+-=-⨯++-n n n n n n n 21、略解:(1)、△HAB △HGA ;(2)、由△AGC ∽△HAB ,得AC/HB=GC/AB ,即9/y=x/9,故y=81/x (0<x<29)(3)因为:∠GAH = 45①当∠GAH = 45°是等腰三角形.的底角时,如图(1):可知CG =x =29/2 ②当∠GAH = 45°是等腰三角形.的顶角时, 如图(2):由△HGA ∽△HAB 知:HB= AB=9,也可知BG=HC ,可得:CG =x =18-29图(1)B (D )A FE G(H ) C图(2) 22、略解:(1)易知A(0,1),B(3,2.5),可得直线AB 的解析式为y =121+x (2) )30(41545)121(14174522≤≤+-=+-++-=-==t t t t t t MP NP MN s (3)若四边形BCMN 为平行四边形,则有MN =BC ,此时,有25415452=+-t t ,解得11=t ,22=t 所以当t =1或2时,四边形BCMN 为平行四边形.①当t =1时,23=MP ,4=NP ,故25=-=MP NP MN , 又在Rt △MPC 中,2522=+=PC MP MC ,故MN =MC ,此时四边形BCMN 为菱形②当t =2时,2=MP ,29=NP ,故25=-=MP NP MN , 又在Rt △MPC 中,522=+=PC MP MC ,故MN ≠MC ,此时四边形BCMN 不是菱形. B(D )A F E G HC。
2011年广东省初中毕业生学业考试

2011年中考数学模拟试题(一)参考答案一、1. A 2.B 3.C 4.B 5.A二、6. 7.26×1010元 7.5,021==x x 8.2.5 9.[]2)1()1(1100x x ++++=50010. 217三、11.解:原式=3+(-3)-2×21+1…………5分 =0………………6分12.解:)(2222y x y xy x y x -+-+……………1分 =)()(22y x y x y x --+……………3分 =yx y x -+2……………4分 当03=-y x 时,y x 3=…………5分原式=272736==-+y y y y y x ……………6分 13.解:①………2分②………4分路线长:π2……6分14.(1)证明:连结DE ,BE …………1分∵AB 是直径∴BE ⊥AC …………2分∵D 是BC 的中点∴DE=DB∴∠DBE=∠DEB 又0E=0B ∴∠0BE=∠0EB∴∠DBE+∠OBE=∠DEB+∠OEB即∠ABD=∠OED 但∠ABC=900,∴∠OED=900∴DE 是⊙O 的切线…………4分(2) ∵AC=346)32(2222=+=+BC AB∴BE=334632=⋅=⋅AC BC AB ∴AE=391222=-=-BE AB ………………6分15.解:(1) ∵OA=OB=OD=1,∴点A 、B 、D 的坐标分别为A(-1,0),B(0,1),D(1,0).………3分(2) ∵点A 、B 在一次函数y=kx+b(k ≠0)的图象上,∴⎩⎨⎧==⎩⎨⎧==+-11,10b k b b k 解得∴一次函数的解析式为y=x+1.…………………………4分∵点C 在一次函数y=x+l 的图象上,且CD ⊥x 轴.∴点C 的坐标为(1,2).……………………………………5分又∵点C 在反比例函数)0(≠=m xm y 的图象上,m=2. ∴反比例函数的解析式为xy 2=……………6分 四、1,1),(2,2),(3,3)共3种,P (两数差为0)=41123=…………4分 (2)不公平,改为小明每次得1分,小华每次得3分。
广东省2011年初中毕业生学业考试数学试卷(含答案)(WORD版)

2011年广东省初中毕业生学业考试数 学 试 题全卷共6页,考试用时100分钟,满分为120分。
一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的, 1.-3的相反数是( )A .3B .31C .-3D .31-2.如图,已知∠1 = 70º,如果CD ∥BE ,那么∠B 的度数为( )A .70ºB .100ºC .110ºD .120º3.某学习小组7位同学,为玉树地震灾区捐款,捐款金额分别为5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( ) A .6,6B .7,6C .7,8D .6,84.左下图为主视方向的几何体,它的俯视图是( )5.下列式子运算正确的是( )A .123=-B .248=C .331=D .4321321=-++二、填空题(本大题5小题,每小题4分,共20分)6. 据中新网上海6月1日电:世博会开园一个月来,客流平稳,累计至当晚19时,参观者已超过8000000人次。
试用科学记数法表示8000000=_______________________。
7.化简:11222---+-y x y xy x=_______________________。
8.如图,已知Rt △ABC 中,斜边BC 上的高AD=4,cosB=54,则AC=____________。
9.已知一次函数b x y -=与反比例函数xy 2=的图象,有一个交点的纵坐标是2,则b 的值为________。
10.如图(1),已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1;把正方形A 1B 1C 1D 1边长按原法延长一倍得到正方形A 2B 2C 2D 2(如图(2));以此下去···,则正方形A 4B 4C 4D 4的面积为__________。
2011年广东省初中毕业生学业考试试题(有答案)

2011年广东省初中毕业生学业考试历史说明:1.全卷共5页,满分为100分,考试用时为50分钟。
2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡上填写字迹的准考证号、姓名、试室号、座位号。
用2B铅笔把对应号码的标号涂黑。
3.单项选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
4.综合题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡个体指定区域内相应位置上。
如需改动,先划掉原来的答案,然后再写上新的答案,不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
5.考生务必保持答题卡的整洁。
考试结束时,将试卷和答题卡一并交回。
一、单项选择题(本大题共25小题,每小题3分,共75分。
在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑。
)1.我国古代有许多抗击自然灾害的英雄传说,其中,一心治水,在外多年,三国家门而不入的“英雄”是()A.黄帝B.尧C.舜D.禹2.秦统一后,为维护皇权,巩固统治,加强了对官员的监察管理。
其中,中央分管监察百官的是()A.博士B.丞相C.太尉D.御史大夫3.19世纪末,德国地质学家里希霍芬将我国西汉以来逐渐形成的贯穿欧亚的路上通到称为“丝绸之路”。
下列对“丝绸之路”的表述,错误的是()A.丝绸之路”的起点是玉门关B.经河西走廊向西最远到达欧洲C.丝绸是“通道”上运输的主要商品D.促进了东西方经济、文化交流4.小龙在图书馆借了一本《贞观政要》。
在这本书中,他可以查到下列哪位皇帝在位期间的“治世”史实()A.秦始B.唐太宗C.唐玄宗D.明太祖5.我国古代四大发明对人类的文明与进步产生了巨大影响。
其中,在促进不同区域的文化交流中最先发挥作用的是()A.造纸术B.指南针C.火药D.印刷术6.如果你有机会到宝岛台湾一游,建议你到台南市参观当地的名胜古迹——赤嵌楼。
这里敬奉着一位民族英雄,他是()A.邓世昌B.戚继光C.郑成功D.左宗棠7.明太祖认为,秦朝设置丞相,却很快亡国。
2011广东中考数学试卷(word版,有答案)

广州四中2011年初三第一次模拟测试数学答案及评分标准命题教师: 谢敏娜 审题科组长:周文辉一、单项选择题(每题3分,共30分) 1-5CACBB 6-10 DBDBB二、填空题(每题3分,共18分)11、 2 12、 65 ︒或115 ︒ 13、 20 14、 14/16/26 15、 12 16、 1011 三、解答题(共9小题,共102分) 17、(本小题9分)a b a b =--+-……7分2b =-……9分18、(本小题9分)解:(1)由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的马按上、中、下顺序出阵时,田忌的马按下、上、中的顺序出阵,田忌才能取胜.……2分 (2)当田忌的马随机出阵时,双方马的对阵情况如下表: 齐王的马 上中下 上中下 上中下 上中下 上中下 上中下 田忌的马上中下上下中中上下中下上下上中下中上··················································································································· 6分双方马的对阵中,总有一种对抗情况田忌能赢,所以田忌获胜的概率16P =. ············· 9分19、(本题10分)解:设AB x =cm ,BC y =cm , 根据题意,得2214,2x y x x y y +=⎧⎪⎨-=-⎪⎩ ························································································ (5分) 解得4,3.x y =⎧⎨=⎩···························································································· (9分)答:AB=4,BC=3.…………………………………………………………………………(10分) 20、(本题10分)(1)证明:90ABC DE AC ∠=°,⊥于点F , ABC AFE ∴∠=∠. ································ (1分)AC AE EAF CAB =∠=∠,, ABC AFE ∴△≌△ ································· (2分)D CB AFAB AF ∴=. ········································· (3分) 连接AG , ·············································· (4分) AG AG AB AF ==,, Rt Rt ABG AFG ∴△≌△. ······················ (5分) BG FG ∴=. ········································· (6分) (2)解:AD DC DF AC =,⊥,1122AF AC AE ∴==. ··········································································· (7分)30E ∴∠=°.30FAD E ∴∠=∠=°, ············································································ (8分)3AF ∴=.·························································································· (9分) 3AB AF ∴==. ··············································································· (10分) 21、(本题12分)(1)证明:∵AB 是直径,AM 、BN 是切线, (加下划线的字一定要出现) ∴AM AB BN AB ⊥,⊥,∴AM BN ∥. ··············· (2 分)(2)过点D 作 DF BC ⊥于F ,则AB DF ∥. 由(1)AM BN ∥,∴四边形ABFD 为矩形. ∴2DF AB ==,BF AD x ==. ··························· (3 分)∵DE 、DA ,CE 、CB 都是切线, ∴根据切线长定理,得 DE DA x ==,CE CB y ==. ······························ (4 分) 在Rt DFC △中,2DF DC DE CE x y CF BC BF y x ==+=+=-=-,,,∴222()2()x y y x +=+-, ······································································ (6 分) 化简,得1(0)y x x=>. ··········································································· (7分) (3)由(1)、(2)得,四边形的面积111()222S AB AD BC x x ⎛⎫=+=⨯⨯+ ⎪⎝⎭, 即1(0)S x x x=+>. ··············································································· (9分) ∵2111220x x x x x x ⎛⎫⎛⎫+-=-+=- ⎪ ⎪⎝⎭⎝⎭≥,当且仅当1x =时,等号成立. ∴12x x+≥,即2S ≥. ······································································· (12分) 第三小问的第二解法:O A DEM CB N图9 F()221122122s x xx x x x x x=++-+=-=+≥22、(本题12分)解:(1)当4060x <≤时,令y kx b =+,则404602k b k b +=⎧⎨+=⎩,解得1108.k b ⎧=-⎪⎨⎪=⎩, ∴1810y x =-+.同理,当60100x <<时,1520y x =-+. ························································ 4分 18(4060)1015(60100)20x x y x x ⎧-+<⎪⎪∴=⎨⎪-+<<⎪⎩,≤ (直接写出这个函数式也记4分.)(2)设可以安排a 人()15040(508)0.251551040a a --⨯+--==…………………………………………(7分)(3)当4060x <≤时,()()214080.25801510160510l x x x ⎛⎫=--+-⨯- ⎪⎝⎭=--+……………………………………(9分)当60100x <<时,()()214050.258015201701020l x x x ⎛⎫=--+-⨯- ⎪⎝⎭=--+…………………………………(11分)由此当x=70时利润最大10万元,80 ÷10=8…………………………………(12分)所以最早8个月可以还清贷款。
广东省2011年中考数学试题(含解析)

广东省2011年中考数学试卷一、选择题(本大题5小题,每小题3分,共15分)1、(2011•广东)﹣2的倒数是()A、﹣B、C、2D、﹣2考点:倒数。
分析:根据倒数的定义,即可得出答案解答:解:根据倒数的定义,∵﹣2×(﹣)=1,∴﹣2的倒数是﹣点评:本题主要考查了倒数的定义,比较简单2、(2011•广东)据中新社北京2010年12月8日电,2010年中国粮食总产量达到546400000吨,用科学记数法表示为()A、5.464×107吨B、5.464×108吨C、5.464×109吨D、5.464×1010吨考点:科学记数法—表示较大的数。
专题:常规题型。
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:将546400000用科学记数法表示为5.464×108.故选B.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3、(2011•广东)将下图中的箭头缩小到原来的,得到的图形是()A、B、C、D、考点:相似图形。
专题:应用题。
分析:根据相似图形的定义,结合图形,对选项一一分析,排除错误答案.解答:解:∵图中的箭头要缩小到原来的,∴箭头的长、宽都要缩小到原来的;选项B箭头大小不变;选项C箭头扩大;选项D的长缩小、而宽没变.故选A.点评:本题主要考查了相似形的定义,联系图形,即图形的形状相同,但大小不一定相同的变换是相似变换.4、(2011•广东)在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为()A、B、C、D、考点:概率公式。
【VIP专享】2011年广东省初中毕业生学业考试数学试卷及答案

页
1
C.
2
C
.
5
C.
8
C.140º
(共
A
7
页)
÷2
D
.
D. 1 2
D.5.464×1010 吨
3
D.
8
D.144º
答案
10.如图(1),将一个正六边形各边延长,构成一个正六角星形 AFBDCE,它的面积为 1; 取△ABC 和△DEF 各边中点,连接成正六角星形 A1F1B1D1C1E1,如图(2)中阴影部分; 取△A1B1C1 和△D1E1F1 各边中点,连接成正六角星形 A2F2B2D2C2E2,如图(3)中阴影部 分;如此下去…,则正六角星形 A4F4B4D4C4E4 的面积为_______ 题 10 图(1)
A
EF
CB
三、解答题(一)(本大题 5 小题,每小题 6 分,共 30 分)
11.计算: ( 2011 1)0 18 sin 45 22 .
12.解不等式组:
2x 1 3,
8
2x
x
F1
B1
A
A1
D1
D 题 10 图(2)
1
A.
5
5.正八边形的每个内角为( )
A.120º
1
B.
3
B.135º
二、填空题(本大题 5 小题,每小题 4 分,共 20 分)请将下列各题的正确答案填写在答题
卡相应的位置上.
6.已知反比例函数 y k 的图象经过(1,-2),则 k ____________. x
7.使 x 2 在实数范围内有意义的 x 的取值范围是______ _____.
学记数法表示为( )
2011年广东省中考数学试卷及答案(WORD版)
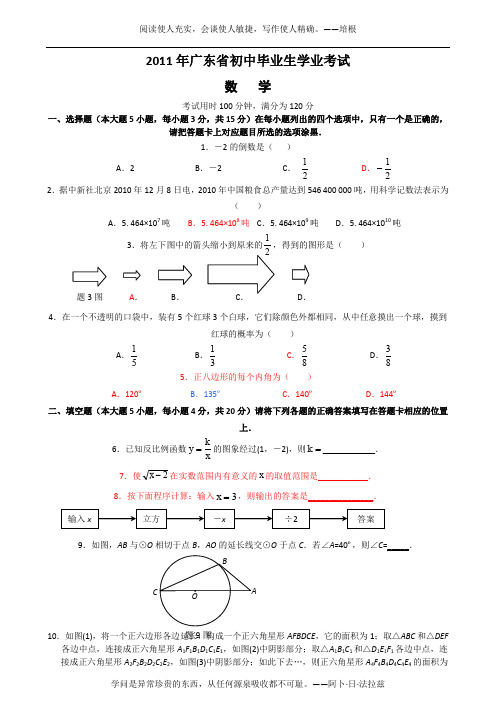
2011年广东省初中毕业生学业考试数 学考试用时100分钟,满分为120分一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1.-2的倒数是( )A .2B .-2C . 21D .21- 2.据中新社北京2010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为( )A .5.464×107吨B .5.464×108吨C .5.464×109吨D .5.464×1010吨3.将左下图中的箭头缩小到原来的1,得到的图形是( ) 4.在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )A .51B .31C .85D .83 5.正八边形的每个内角为( )A .120ºB .135ºC .140ºD .144º二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上.6.已知反比例函数xk y =的图象经过(1,-2),则=k ____________. 7.使2-x 在实数范围内有意义的x 的取值范围是______ _____.8.按下面程序计算:输入3=x ,则输出的答案是_______________.9.如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C .若∠A =40º,则∠C =_____.10.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ABC 和△DEF各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…,则正六角星形A 4F 4B 4D 4C 4E 4的面积为A .B . D . 题3图 题9图 BC O A_________________.三、解答题(一)(本大题5小题,每小题6分,共30分)11.计算:20245sin 18)12011(-︒+-.12.解不等式组:⎩⎨⎧-≤-->+128,312x x x ,并把解集在数轴上表示出来.13.已知:如图,E 14.如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系;(2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A ,B ,求劣弧AB 与弦AB 围成的图形的面积(结果保留π).15.已知抛物线c x x y ++=221与x 轴没有交点. (1)求c 的取值范围;(2)试确定直线1+=cx y 经过的象限,并说明理由.四、解答题(二)(本大题4小题,每小题7分,共28分)16.某品牌瓶装饮料每箱价格26元.某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,则题13图 B C DA F E 题14图题10图(1) E E C E 题10图(2) 题10图(3)买一箱送三瓶,这相当于每瓶比原价便宜了0.6元.问该品牌饮料一箱有多少瓶?17.如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l ,AB 是A 到l 的小路. 现新修一条路AC 到公路l . 小明测量出∠ACD =30º,∠ABD =45º,BC =50m . 请你帮小明计算他家到公路l 的距离AD 的长度(精确到0.1m ;参考数据:414.12≈,732.13≈).18.李老师为了解班里学生的作息时间表,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?19.如图,直角梯形纸片ABCD 中,AD //BC ,∠A =90º,∠C =30º.折叠纸片使BC 经过点D ,点C 落在点E处,BF 是折痕,且BF =CF =8.(1)求∠BDF 的度数;(2)求AB 的长.五、解答题(三)(本大题3小题,每小题9分,共27分)20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 2526 27 28 29 30 31 32 33 34 35 36…………………………(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;(2)用含n 的代数式表示:第n 行的第一个数是___________________,最后一个数是________________,第n 行共有_______________个数;第17题图 ) 题19图 B CED AF 题18图(3)求第n 行各数之和.21.如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与DE 重合,AB =AC =EF =9,∠BAC =∠DEF =90º,固定△ABC ,将△DEF 绕点A 顺时针旋转,当DF 边与AB 边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE ,DF (或它们的延长线)分别交BC (或它的延长线) 于G ,H 点,如图(2)(1)问:始终与△AGC 相似的三角形有及 ;(2)设CG =x ,BH =y ,求y 关于x 的函数关系式(只要求根据图(2)的情形说明理由)(3)问:当x 为何值时,△AGH 是等腰三角形.22.如图,抛物线1417452++-=x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x (1(2)动点P 在线段OC 点M ,交抛物线于点N . 设点P 移动的时间为t 出t (3)设在(2)的条件下(不考虑点P 与点O BCMN 为平行四边形?问对于所求的t 2011一、1-5、DBACB二、6、-27、___ x ≥2__8、___12__9、__25º__ 10、2561 三、11、原式=-6 12、x ≥3 13、由△ADF ≌△CB E ,得AF =C E ,故得:AE=CF14、(1)⊙P 与⊙P 1外切。
广东省13市2011年中考数学试题分类解析汇编(12份)-7

广东2011年中考数学试题分类解析汇编专题2:代数式和因式分解一、选择题1.(佛山3分)在①42a a ⋅;②23()a -;③122a a ÷;④23a a ⋅中,计算结果为6a 的个数是A 、1个B 、2个C 、3个D 、4个【答案】A 。
【考点】同底幂乘法运算法则,幂的乘方运算法则,同底幂除法运算法则。
【分析】根据同底幂乘、除法运算法则和幂的乘方运算法则,有①42426==a a a a +⋅;②23236()==a a a ⨯---;③12212210==a a a a -÷;④23235==a a a a +⋅。
故选A 。
2.(广州3分)下面的计算正确的是21世纪教育网A 、3x 2•4x 2=12x 2B 、x 3•x 5=x 15C 、x 4÷x =x 3D 、(x 5)2=x 7【答案】C 。
【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方;单项式乘单项式。
【分析】根据单项式的乘法、同底数幂的乘法和除法、幂的乘方等知识点进行判断:A 、3x 2•4x 2=12x 4,故本选项错误;B 、x 3•x 5=x 8,故本选项错误;C 、正确;D 、(x 5)2=x 10,故本选项错误。
故选C 。
3.(河源3分)下列各式运算正确的是()32352352331025A. B. C. D. a a a a a a ab a b a a a +⋅==÷= = 【答案】B 。
【考点】合并同类项,同底幂乘法、积和幂的乘方、同底幂除法运算法则。
【分析】根据合并同类项,同底幂乘法、积和幂的乘方、同底幂除法运算法则,A.指数不同不可以相加,选项错误;B.选项正确;C.()3236ab a b =,选项错误;D.1028 a a a ÷=选项错误。
故选B 。
[来源:21世纪教育网]4.(清远3分)下列选项中,与x y 2是同类项的是A .—2x y 2B .2x 2yC .x yD .x 2y 2【答案】A 。
2011年广州试题答案(word)+试题扫描

2011年广州市初中毕业生学业考试数 学本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分,考试用时102分钟 注意事项:1.答卷前,考生务必在答题卡第1面、第三面、第五面上用黑色字迹的钢笔或签字笔走宝自已的考生号、姓名;走宝考场室号、座位号,再用2B 铅笔把对应这两个号码的标号涂黑。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图,答案必须写在答题卡各题目指定区域内的相应位置上,如需改动,先划掉原来的答案,然后再写上新的答案,改动的答案也不能超出指定的区域,不准使用铅笔,圆珠笔和涂改液,不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共30分)一、选择题(每小题3分,共30分)1.四个数-5,-0.1,21,3中为无理数的是( ) A. -5 B. -0.1 C. 21D. 32.已知□ABCD 的周长为32,AB=4,则BC=( )A. 4B. 121C. 24D. 283.某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( ) A. 4 B. 5 C. 6 D. 104.将点A (2,1)向左平移2个单位长度得到点A ',则点A '的坐标是( ) A. (0,1) B. (2,-1) C. (4,1) D. (2,3)5.下列函数中,当x>0时,y 值随x 值增大而减小的是( ) A.2x y = B. 1-=x y C. x y 43=D. xy 1= 6.若a<c<0<b ,则abc 与0的大小关系是( )A. abc<0B. abc=0C. abc>0D. 无法确定 7.下面的计算正确的是( )A. 2221243x x x =⋅ B. 1553x x x =⋅ C. 34x x x =÷ D. 725)(x x =8.如图所示,将矩形纸片先沿虚线AB 按箭头方向向右..对折,接着对折后的纸片沿虚线CD 向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )9.当实数x 的取值使得2-x 有意义时,函数y=4x+1中y 的取值范围是( ) A.y ≥-7 B. y ≥9 C. y>9 D. y ≤910.如图,AB 切⊙O 于点B ,OA=23,AB=3,弦BC//OA ,则劣弧BC 的弧长为( )A.π33 B. π23 C. π D. π23 二、填空题:(每小题3分,共18分) 11.9的相反数是______12.已知α∠=260,则α∠的补角是______度。
广东省2011年中考数学试卷(含答案)

2011年广东省初中毕业生学业考试1.21-的相反数是( ) A .2 B .-2 C .21 D .21- 2.如图,已知AB∥CD,直线EF 分别交AB ,CD 于点E ,F ,EG 平分∠BEF ,若∠1=5O°,则∠2的度数为( ). A.50° B.55° C.60° D.65° 3.将左下图中的箭头缩小到原来的21,得到的图形是( )4、下列计算中,正确的是( )A 、xy y x 532=+B 、 3632)(y x y x -=- C 、428x x x =÷D 、()9322+=+x x5.正六边形的每个内角为( )A .120ºB .135ºC .140ºD .108º 6.因式分解 =-x x 283______ _________ ___ 7.使21-x 在实数范围内有意义的x 的取值范围是______ _____.8.如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C . 若∠A =50º,则∠C =___ __. 9.按下面程序计算:输入3=x ,则输出的答案是_______________.10、如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________11.计算:2201221145cos 18)12012(-⎪⎭⎫ ⎝⎛-+-︒+- A .B .D .题3图题8图BCO12.解不等式组:⎪⎩⎪⎨⎧-≥-->--125,121x x x x ,并把解集在数轴上表示出来.13.已知:如图,E ,F 在AC 上,AD //CB 且AD =CB ,∠D =∠B .求证:AE =CF .14.如图,在平面直角坐标系中,点P 的坐标为(-4⊙P 的半径为2,将⊙P 沿x 轴向右平移4(1)画出⊙P 1,直接判断⊙P 与⊙P 1的位置关系; (2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A ,B ,求劣弧AB 与弦AB 围成的图形的面积(结果保留π).15.甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜。
广东省珠海市2011年学业考试数学试题与答案

2011年珠海市初中毕业生学业考试数 学一、选择题(本小题5分,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡对应题目所选的选项涂黑. 1.(11·珠海)-34的相反数是A .-43B .-34C .-43D .34【答案】D2.(11·珠海)化简(a 3)2的结果是 A .a 6 B .a 5C .a 9D .2a 3【答案】A3.(11·珠海)圆心角为60°,且半径为3的扇形的弧长为 A .π2B .πC .3π2D .3 π【答案】B4.(11·珠海)已知一组数据:4,-1,5,9,7,6,7,则这组数据的极差是 A .10 B .9C .8D .7【答案】A 5.(11·珠海)若分式2aa +b中的a 、b 的值同时扩大到原来的10倍,则此分式的值 A .是原来的20倍 B .是原来的10倍 C .是原来的110D .不变【答案】D二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上6.(11·珠海)分解因式ax 2-4a =_ ▲ . 【答案】a (x +2)(x -2)7.(11·珠海)方程组⎩⎨⎧x +y =62x -y =3的解为_ ▲ .【答案】⎩⎨⎧x =3y =38.(11·珠海)写出一个图象位于第二、第四象限的反比例函数的解析式_ ▲ . 【答案】y =- 1x(答案不唯一)9.(11·珠海)在□ABCD 中,AB =6cm ,BC =8cm ,则□ABCD 的周长为_ ▲ cm .B【答案】2810.(11·珠海)不等式组⎩⎨⎧2x -6<4x >2的解集为_ ▲ .【答案】2<x <5三、解答题(一)(本大题5小题,每小题6分,共30分)11.(11·珠海)(本题满分6分)计算:|-2|+(13)-1-(π-5)0-16.【答案】原式=2+3-1-4……………………4分=0 ……………………6分12.(11·珠海)(本题满分6分)某校为了调查学生视力变化情况,从该校2008年入校的学生中抽取了部分学生进行连续三年的视力跟踪调查,将所得数据处理,制成拆线统计图和扇形统计图,如图所示:(1)该校被抽查的学生共有多少名?(2)现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2010年有多少名学生视力合格.【答案】(1)被抽查的学生共有:80÷40%=200(人) ……………………3分(2)视力合格人数约有:600×(10%+20%)=180(人)……………………6分13.(11·珠海)(本题满分6分)如图,在Rt △ABC 中,∠C =90°.(1)求作:△ABC 的一条中位线,与AB 交于D 点,与BC 交于E 点.(保留作图痕迹,不写作法) (2)若AC =6,AB =10,连结CD ,则DE =_ ▲ ,CD =_ ▲ .【答案】(1)作出BC 的垂直平分线 ……………………3分 答:线段DE 即为所求 ……………………4分)被抽取学生视力在5.0以下人数变化情况统计图 被抽取学生视力在2010的视力分布情况统计图视力分组说明: A :5.0以下 B :5.0~5.1 C :5.2~5.2 D :5.2以上 每组数据只含最低值,不含最高值.(2)3,5 ……………………6分14.(11·珠海)(本题满分6分)八年级学生到距离学校15千米的农科所参观,一部分学生骑自行车先走,过了40分钟后,其余同学乘汽车出发,结果两者同时到达.若汽车的速度是骑自行车同学速度的3倍,求骑自行车同学的速度.【答案】解:设骑自行车同学的速度为x 千米/小时,由题意得 ……………………1分15x - 153x =4060 ……………………3分 解之得:x =15 ……………………4分 经验,x =15是原方程的解 ……………………5分 答:骑自行车同学的速度为15千米/小时. ……………………6分15.(11·珠海)(本题满分6分)如图,在正方形ABC 1D 1中,AB =1.连接AC 1,以AC 1为边作第二个正方形AC 1C 2D 2;连接AC 2,以AC 2为边作第三个正方形AC 2C 3D 3. (1)求第二个正方形AC 1C 2D 2和第三个正方形的边长AC 2C 3D 3; (2)请直接写出按此规律所作的第7个正方形的边长.【答案】(1)解:∵四边形ABC 1D 1是正方形,∠ABC =120°∴∠B =90°,BC 1=AB =1;∴AC 1=12+12= 2即第二个正方形AC 1C 2D 2的边长为2. ……………………2分 ∵四边形AC 1C 2D 2是正方形,∴∠AC 1C 2=90°,C 1C 2=AC 1=2;∴AC 2=(2)2+(2)2=2;即第二个正方形AC 2C 3D 3的边长为2. ……………………4分(2)解:∵第7个正方形的边长8. ……………………6分四、解答题(二)(本大题4小题,每小题7分,共28分)A C 1C 2C 3D 3D 2 D 1 BA 16.(11·珠海)(本题满分7分)如图,在鱼塘两侧有两棵树A 、B ,小华要测量此两树之间的距离.他在距A 树30 m 的C 处测得∠ACB =30°,又在B 处测得∠ABC =120°.求A 、B 两树之间的距离(结果精确到0.1m )(参考数据:2≈1.414,3≈1.732)【答案】解:作BD ⊥AC ,垂足为点D 1分∵∠C =30°,∠ABC =120°,∴∠A =30°;∴AB =BC 2分 ∴AD =CD =12AC =12×30=15 3分在Rt △ABD 中,∵cos A =ADAB , ……………………4分∴AB =AD cos A =1532=103≈17.3 ……………………6分答:A 、B 两树之间的距离约为17.3m . ……………………7分17.(11·珠海)(本题满分7分)某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有A 、B 两个盒子,里面都装有一些乒乓球,你只能选择在其中一只盒子中摸球.”获将规则如下:在A 盒中有白色乒乓球4个,红色乒乓球2个,一人只能摸一次且一次摸出一个球,若为红球则可获得玩具熊一个,否则不得奖;在B 盒中有白色乒乓球2个,红色乒乓球2个,一人只能摸一次且一次摸出两个球,若两球均为红球则可获得玩具熊一个,否则不得奖.请问小军在哪只盒子内摸球获得玩具熊的机会更大?说明你的理由.【答案】解:小军在A 盒中摸球获得玩具熊的机会更大 ……………………1分把小军从A 盒中抽出红球的概率记为P A , 那么:P A =24+2=13……………………3分 把B 盒中的两个白球记为白1,白2,两个红球记为红1,红2,小军从B 盒中摸出两球的所有可能出现的结果为:白1白2;白1红1;白1红2;白2红1;白2红2;红1红2;且六种结果出现的可能性相等,把小军从B 盒中抽出两个红球的概率记为P B ,那么P B =16; ……………………6分因为P A >P B ,所以小军在A 盒内摸球获得玩具熊的机会更大 ………………7分A18.(11·珠海)(本题满分7分)如图,Rt △OAB 中,∠OAB =90°,O 为坐标原点,边OA 在x 轴上,OA =AB =1个单位长度.把Rt △OAB 沿x 轴正方向平移1个单位长度后得△AA 1B . (1)求以A 为顶点,且经过点B 1的抛物线的解析式;(2)若(1)中的抛物线与OB 交于点C ,与y 轴交于点D ,求点D 、C 的坐标.【答案】解:(1)由题意,得A (1,0),A 1 (2,0),B 1 (2,1). ……………………1分 设以A 为顶点的抛物线的解析式为y =a (x -1)2 ∵此抛物线过点B 1 (2,1),∴1=a (2-1)2. ∴a =1.∴抛物线的解析式为y =(x -1)2. ……………………3分(2)∵当x =0时,y =(0-1)2=1.∴D 点坐标为 (0,1). ……………………4分 由题意,得OB 在第一象限的角平分线上,故可设C (m ,m ),代入y =(x -1)2,得m =(m -1)2, ……………………5分 解得m 1=3-52<1,m 1=3+52>1(舍去). ……………………6分 19.(11·珠海)(本题满分7分)如图,将一个钝角△ABC (其中∠ABC =120°)绕点B 顺时针旋转得△A 1BC 1,使得C 点落在AB 的延长线上的点C 1处,连结AA 1. (1)写出旋转角的度数; (2)求证:∠A 1AC =∠C 1.【答案】(1)解:旋转角的度数为60°.……………………2分 (2)证明:由题意可知:△ABC ≌△A 1BC 1, ∴A 1B =AB ,∠C =∠C 1, 由(1)知:∠ABA 1=60°, ∴△A 1BA 为等边三角形.∠BAA 1=60° ……………………4分 而∠CBC 1=60°,∴∠BAA 1=∠CBC 1, ……………………5分 ∴AA 1∥BC ∴∠A 1AC =∠C .C 1A 1A B C又∵∠C =∠C 1,∴∠A 1AC =∠C 1 ……………………7分五、解答题(三)(本大题3小题,每小题9分,共27分) 20.(11·珠海)(本题满分9分)阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+22=(1+2)2,善于思考的小明进行了以下探索:设a +b 2=(m +n 2)2(其中a 、b 、m 、n 均为整数),则有a +b 2=m 2+2n 2+2mn 2. ∴a =m 2+2n 2,b =2mn .这样小明就找到了一种把部分a +b 2的式子化为平方式的方法.请我仿照小明的方法探索并解决下列问题:(1)当a 、b 、m 、n 均为正整数时,若a +b 3=(m +n 3)2,用含m 、n 的式子分别表示a 、b ,得a =_ ▲ ,b =_ ▲ ;(2)利用所探索的结论,找一组正整数a 、b 、m 、n ,填空:_ ▲ +(_ ▲ +2; (3)若a +43=(m +n 3)2,且a 、m 、n 均为正整数,求a 的值.【答案】(1)a =m 2+3n 2,b =2mn ……………………2分(2)4,2,1,1(答案不唯一) ……………………4分(3)解:由题意,得⎩⎨⎧a =m 2+3n 24=2mn……………………5分∵4=2mn ,且m 、n 为正整数,∴m =2,n =1或m =1,n =2. ……………………7分 ∴a =22+3×12=7或a =12+3×22=13. ……………………9分21.(11·珠海)(本题满分9分)已知:如图,锐角△ABC 内接于⊙O ,∠ABC =45°;点D 是⌒BC上一点,过点D 的切线DE 交AC 的延长线于点E ,且DE ∥BC ;连结AD 、BD 、BE ,AD 的垂线AF 与DC 的延长线交于点F . (1)求证:△ABD ∽△ADE ;(2)记△DAF 、△BAE 的面积分别为S △DAF 、S △BAE ,求证:【答案】证明:(1)连结OD . ∵DE 是⊙O 的切线,∴OD ⊥DE . 又∵DE ∥BC , ∴OD ⊥BC .∴ ⌒BD = ⌒CD . ……………………2分 ∴∠BAD =∠EAD .O AB CDPE FM NA ∵∠BDA =∠BCA ,DE ∥BC , ∴∠BDA =∠DEA . ∴∠BAD =∠EAD ,∴△ABD ∽△ADE . ……………………5分 (2)由(1)得AB AD =ADAE,即AD 2=AB ·AE 设在△ABE 中,AE 边上的高为h ,则: ∴S △ABE = 12h ·AE ,且h <AB .由∠ABC =45°,AD ⊥AF 可推得△ADF ∴S △DAF =12 AD 2. ……………………8分∴S △DAF =S △BAE∴△DAF >△BAE . ……………………9分22.(11·珠海)(本题满分9分)如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =AB =1,BC =2.将点A 折叠到CD 边上,记折叠后A 点对应的点为P (P 与D 点不重合),折痕EF 只与边AD 、BC 相交,交点分别为E 、F .过点P 作PN ∥BC 交AB 于N 、交EF 于M ,连结P A 、PE 、AM ,EF 与P A 相交于O .(1)指出四边形PEAM 的形状(不需证明);(2)记∠EPM =a ,△AOM 、△AMN 的面积分别为S 1、S 2.① 求证:S 1tan a 2=18 P A 2.② 设AN =x ,y =S 1-S 2tan a 2,试求出以x 为自变量的函数y 的解析式,并确定y 的取值范围.【答案】(1)四边形AMPE 为菱形 ……………………2分(2)证明:∵四边形AMPE 为平行四边形, EPM =a∴∠MAP =12a S 1=12OA ·OM . ……………………4分∵在Rt △OM 中,tan a 2=OM OA ,∴OM =OA ·tan a2.S 1tan a 2=12OA ·OM OM OA =12OA ·OM ×OA OM =12OA 2=12×(12P A )2=18P A 2.……………………5分 (3)过D 作DH 垂直于BC 于H ,交NP 于点K ,则:DK ⊥PN ,BH =AB =AD =DH =1,DK =AN =x . ∵CH =BC -BH =2-1=1,∴CH =DH .∴∠NPD =∠BCD =45°. ∴PK =DK =x . ∴PN =1+x . 在Rt △ANP 中,AP 2=AN 2+PN 2=x 2+(1+x )2=2x 2+2x +1. ……………………6分 过E 作PM 的垂线EG (垂足为G ),令△EGM 的面积为S . ∵△EGM ∽△AOM , ∴S S 1=(EG AO )2=x 214AP 2=4x 2AP 2. 则S =4x 2AP2 S 1.∵四边形ANGE 的面积等于菱形AMPE 的面积, ∴2S 1=S 2+S .∴S 1-S 2=S -S 1=4x 2AP 2 S 1-S 1=(4x 2AP 2-1)S 1.∴y =S 1-S 2tan a 2=(4x 2AP 2-1)×S 1tan a 2=(4x 2AP 2-1)×18 P A 2=18 (4x 2-AP 2). ∴y =14x 2-14x -18.。
2011广州市中考数学试题及完整答案(word)

广州四中2011年初三第一次模拟测试数学答卷第 I 卷(48分)一、单项选择题(每题3分,共30分,请你把选择题的答案填涂到答题卡上) 二、填空题(每题3分,共18分,请你把答案写在下列对应题号的横线上)11、 12、 13、14、 15、 16、第II 卷(102分)三、解答题(本大题共9小题,解答应写出文字说明、证明过程或演算步骤)17、(本小题9分)解:18、(本小题9分) 解:题号 一 二 17 18 19 20 21 22 23 24 25 总分 分数密 封 线 内 不 要 答 题学校: 班别: 姓名: 考号: 试室号: 座位号:19、(本小题10分)解:D G CFAE B(第19题)20、(本小题10分) 解:DCEB GA(20题)F21、(本小题12分) 解:座位号:OA D EMC B N图2122、(本小题12分) 解:42 1 40 6080x(元) (万件) y O23、(本小题12分)解:(3)图(1) AC DB P α α ββ图(2)ACDB1P2P第23题图图(3)AC DB图(4)ACDB(1)(2)24、(本小题14分(1)证明:G AB CD PQE EABC DPQQPDCB A 25、(本小题14分)① ②。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机密★启用前数学2011年广东省初中毕业生学业考试说明:1.全卷共6页,考试用时100分钟,满分为120分。
2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、试室号、座位号。
用2B铅笔把对应该号码的标号涂黑。
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试题上。
4.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
5.考生务必保持答题卡的整洁。
考试结束时,将试卷和答题卡一并交回。
一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑。
1.25的算术平方根是A.5 B.±5 C.5D.±52.从长度分别为3、5、7、9的4条线段中任取3条作边,能组成三角形的概率为()(A)34(B)12(C)13(D)143.如左下图所示的几何体的正视图是()A. B. C. D.4.下列运算正确的是()A.3412a a a⋅=B.339()y y-=C.222264x x x-+=D.3252()m n m n=5. 如图1,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32o,那么∠2的度数是()(A) 32o; (B) 58o; (C) 68o; (D) 60o.二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上。
6. 分解因式:324a ab-= .7.请写出一个以直线3-=x为对称轴,且在对称轴右侧部分是下降的抛物线的表达式,这条抛物线图9的表达式可以是 .8. 成功、精彩、难忘的中国2010年上海世博会,众多境外参观者纷至沓来。
国家统计局上海调查总队调查显示:上海世博会境外参观者近4250000人次.4250000人次可用科学记数法表示为 人次.9.某盏路灯照射的空间可以看成如图9所示的圆锥,它的 高AO = 8米,母线AB 与底面半径OB 的夹角为α,34tan =α, 则圆锥的底面积是 平方米(结果保留π).10.如图,在ABC ∆中,α=∠A ,ABC ∠的平分线与ACD ∠的平分线交于点1A ,得1A ∠,则1A ∠= .BC A 1∠的平分线与CD A 1∠的平分线交于点2A ,得2A ∠,……,BC A 2009∠的平分线与CD A 2009∠的平分线交于点2010A ,得2010A ∠,则2010A ∠= .三、解答题(一)(本大题5小题,每小题6分,共30分) 11. 计算12. 解不等式组31422x x x ->-⎧⎨<+⎩,并把它的解集表示在数轴上.13.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;(2)画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;14.如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.求证:(1)△ABC≌△DEF;(2)BE=CF.15.如图,已知一次函数)(01≠+=k b kx y 与反比例函数()02≠=m x my 的图象交于A 、D 两点,且与y 轴交于点C .AB 垂直于y 轴,垂足为B ,CO =BC=1,1=∆AOB S . 求两个函数的表达式.四、解答题(二)(本大题4小题,每小题7分,共28分)16.为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图9所示(其中男生收看3次的人数没有标出). 根据上述信息,解答下列各题:(1) 该班级女生人数是 ▲ ,女生收看“两会”新闻次数的中位数是 ▲ ; (2) 对于某个群体,我们把一周内 收看某热点新闻次数不低于3次的人 数占其所在群体总人数的百分比叫做 该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻 的“关注指数”比女生低5%,试求 该班级男生人数;(3) 为进一步分析该班级男、女生 收看“两会”新闻次数的特点,小明 给出了男生的部分统计量(如表1).根据你所学过的统计知识,适当 计算女生的有关统计量,进而比较该 班级男、女生收看 “两会”新闻次数 的波动大小.(图9)(表1)17.如图,在梯形ABCD 中,AB ∥CD ,E 是BC 的中点,AE ,DC 的延长线相交于点F ,连结AC ,BF . (1)求证:AB =CF ;(2)四边形ABFC 是什么四边形?说明你的理由.18.一开口向上的抛物线与x 轴交于A ,B 两点,C (m ,2 )为抛物线顶点,且AC ⊥BC . (1)若m 是常数,求抛物线的解析式;(2)设抛物线交y 轴正半轴于D 点,抛物线的对称轴交x 轴于E 点。
问是否存在实数m ,使得 △E OD 为等腰三角形?若存在,求出m 的值;若不存在,请说明理由.ABCDE F19.小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的1.6倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.五、解答题(三)(本大题3小题,每小题9分,共27分)20.如图6,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连结BE交AC于点P.(1)求AP的长;(2)若以点A为圆心,AP为半径作⊙A,试判断线段BE与⊙A的位置关系并说明理由;(3)已知以点A为圆心,r1为半径的动⊙A,使点D在动⊙A的内部,点B在动⊙A的外部.①求动⊙A的半径r1的取值范围;②若以点C为圆心,r2为半径的动⊙C与动⊙A相切,求r2的取值范围.21.阅读材料,解答下列问题.例:当0a >时,如6a =,则66a ==,故此时a 是它本身;当0a =时,0a =,故此时a 是零;当0a <时,如6a =-,则66(6)a =-==--,故此时a 是它的相反数. 综上所述,a 可分三种情况,即 0000a a a a a a >⎧⎪==⎨⎪-<⎩当当当 这种分析方法渗透了数学的分类讨论思想.问:(1)请仿照例中的分类讨论的方法,分析二次根式2a 的各种展开的情况.(2)猜想2a 与a 的大小关系是a . (3)当21<<x 时,试化简:()221-+-x x .22.如图,在等腰梯形OABC中,CB∥OA,∠COA=60°BC=2,OA=4,且与x轴重合.(1)直接写出点A、B、C的坐标.(2)求经过点O、A、B的抛物线解析式,并判断点C是否在抛物线上.(3)在抛物线的OCB段,是否存在一点P(不与O、B重合),使得四边形OABP的面积最大,若存在,求出此时P点的坐标,若不存在,请说明理由.x参考答案:一、选择题1.A2.A3.B4.C 5.B ; 二、填空题6.()()22a a b a b +-; 7、答案不唯一 8.64.2510⨯; 9. 36 π10.三、解答题(一) 11.解:原式=2+1-2×22+2-1 =2+1-2+2-1 =212.解:31422x x x ->-⎧⎨<+⎩12x x >-⎧⇒⎨<⎩12x ⇒-<<. ∴原不等式组的解集是12x -<<. 在数轴上表示为:13. (1)从三角形的各点向对称轴引垂线并延长相同单位得到各点的对应点,顺次连接即可,然后从坐标中读出各点的坐标.(2)让三角形的各顶点都绕点O 顺时针旋转90°后得到对应点,顺次连接即可. 解:(1)点C 1的坐标(-1,-3).(2)C2(3,1).14. 证明:(1)∵AC∥DF,∴∠ACB=∠F,在△ABC和△DEF中,A= DACB= F AB=DE∠∠⎧⎪∠∠⎨⎪⎩,∴△ABC≌△DEF(AAS);(2)∵△ABC≌△DEF,∴BC=EF,∴BC-CE=EF-CE , 即BE=CF .15.依题意有:12121==⋅xy OB AB ,即121=m ,∴2±=m又∵反比例函数的图象在二、四象限,∴xy 22-=∵CO =BC =1,∴OB=2, ∴AB=1 ∴A(-1,2),C(0,1)∴⎩⎨⎧==+-12b b k解得⎩⎨⎧=-=11b k∴11+-=x y四、解答题(二) 16.(1)20 , 3;(2)由题意:该班女生对“两会”新闻的“关注指数”为%65%1002013=⨯ 所以,男生对“两会”新闻的“关注指数”为%60 设该班的男生有x 人则 %60)631(=++-x x , 解得:25=x答:该班级男生有25人.(3)该班级女生收看“两会”新闻次数的平均数为3202554635221=⨯+⨯+⨯+⨯+⨯,女生收看“两会”新闻次数的方差为:101320)53(2)43(5)33(6)23(5)13(222222=-+-+-+-+-因为2>1013,所以男生比女生的波动幅度大. 17.证明:(1)∵AB ∥CD ,∴∠1=∠2 ∵E 是BC 的中点,∴CE=BE 又∵∠3=∠4 ∴△ABE ≌△FCE ∴AB =CF(2)四边形ABFC 是平行四边形。
理由:ABCD E F1234∵AB =CF , AB ∥DF∴四边形ABFC 是平行四边形18、解:(1)设抛物线的解析式为:2()2y a x m =--∵AC ⊥BC ,由抛物线的对称性可知:△ACB 为等腰直角三角形,又AB =4, ∴B (m +2,0)代入,得a =12.∴解析式为:2211222y x mx m =-+-.(2)由(1)得D (0,12m 22-),设存在实数m ,使得△E OD 为等腰三角形.∵△E OD 为直角三角形,∴只能OD =O E .∴当点E 在x 轴正半轴,即m >0时,12m 2-2=m.解得m=1或m=1. 当点E 在x 轴负半轴,即m <0时,12m 2-2=m -.当解得m=1-m=1-(舍);当点E 在原点,即m =0时, B 、O 、D 三点共线(不合题意,舍)综上所述:存在实数m=1m=1-E OD 为等腰三角形.19.解:设小明乘坐动车组到上海需要x 小时 依题意,得6.1621602160⨯+=x x . 解得 10=x .经检验:10x =是方程的解,且满足实际意义. 答:小明乘坐动车组到上海需要10小时五、解答题(三) 20.(本题满分12分,每小题4分) 解:(1)∵四边形ABCD 是矩形,∴AE ∥BC , ∵AB =8, BC =6,∴AC =10, ∵AP AECP CB=,即15106AP AP =- 解得:507AP =.(2)∵AB =8,AE =15,∴BE =17. 作AH ⊥BE ,垂足为H ,则AB AE BE AH ⋅=⋅,∴8151201717AB AE AH BE ⋅⨯===. ∵50120717>,∴⊙A 与BE 相交. (3)①168r << ,②224r <<,或21618r <<.21.解:(1)当0a >时,如3=a ,则3322==a ,故此时2a 的结果是它本身;当0a =时,02=a ,故此时2a 的结果是零;当0a <时,如3-=a ,则)()(33322--==-=a ,故此时2a 的结果是它的相反数.综上所述,2a 的结果可分三种情况,即⎪⎩⎪⎨⎧<-=>=)0( )0( 0)0(2a a a aa a(2)a .(3)∵21<<x ,∴ 01>-x ,02<-x , ∴ 2)2(1-+-x x =)2(1x x -+-=122.解:(1)()04,A ,),(33B ,),(31C(2)依题意设)(4-=x ax y ,又),(33B 在该函数图象上, ∴33=-a解得:33-=a ∴x x y 334332+-=当x=1时,3=y ,故点),(31C 在该函数图象上。
