石景山区2013—2014学年第一学期期末考试答案
北京市石景山2013-2014学年九年级上学期期末考试数学试卷(纯word解析版)(新人教版)

2014届北京市石景山九年级上学期期末考试数学试卷(带解析)1、已知⊙O 的半径为6,点A在⊙O内部,则()A.B.C.D.【答案】A.【解析】试题分析:点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).所以OA<6,故选A.考点: 点与圆的位置关系.2、已知,在Rt△ABC中,∠C=90°,BC=12,AC=5,则cosA的值是()A.B.C.D.【答案】B.【解析】试题分析:首先利用勾股定理求得斜边AB的长,然后利用三角函数的定义即可求解.则cosA=.故选C.考点: 1.锐角三角函数的定义;2.勾股定理.3、如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠BCD=70°,则∠BAD的度数为()A.40° B.50° C.60°D.70°【答案】D.【解析】试题分析:由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠BCD 的度数.∵∠BAD与∠BCD是对的圆周角,∴∠BCD=∠BAD=70°.故选D.考点: 圆周角定理.4、若函数的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是()A.m>1 B.m>0 C.m<1 D.m<0【答案】A.【解析】试题分析:先根据函数的图象在其所在的每一象限内,函数值y随自变量x的增大而增大列出关于m的不等式,求出m的取值范围即可.解答:解:∵函数的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,∴1-m<0,解得m>1.故选A.考点: 反比例函数的性质.5、从1~12这十二个自然数中任取一个,取到的数恰好是4的倍数的概率是()A.B.C.D.【答案】B.【解析】试题分析:∵从1~12这十二个自然数中任取一个,共有12种等可能的结果,取到的数恰好是4的倍数的有3种情况,∴取到的数恰好是4的倍数的概率是:.故选B.考点:概率公式.6、如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为()A.4 B.C.D.【答案】D.【解析】试题分析:如图,设CP交⊙O于点D,连接AD.设⊙O的半径为r.∵PA、PB是⊙O的切线,∠APB=60°,∴OA⊥AP,∠APO=∠APB=30°.∴OP=2OA,∠AOP=60°,∴PC=2OA+OC=3r=6,则r=2,易证△AOD是等边三角形,则AD=OA=2,又∵CD是直径,∴∠CAD=90°,∴∠ACD=30°,∴AC=AD?cot30°=2故选C.考点: 切线的性质.7、如图,抛物线和直线. 当y1>y2时,x的取值范围是()A.0<x<2 B.x<0或x>2 C.x<0或x>4 D.0<x<4【答案】A.【解析】试题分析:联立两函数解析式求出交点坐标,再根据函数图象写出抛物线在直线上方部分的x的取值范围即可.联立,解得,,∴两函数图象交点坐标为(0,0),(2,4),由图可知,y1>y2时x的取值范围是0<x<2.故选A.考点: 二次函数与方程组.8、如图,在等边△中,,当直角三角板的角的顶点在上移动时,斜边始终经过边的中点,设直角三角板的另一直角边与相交于点E.设,,那么与之间的函数图象大致是()【答案】B.【解析】试题分析:根据等边三角形的性质得BD=2,PC=4-x,∠B=∠C=60°,由于∠MPN=60°,易得∠DPB=∠PEC,根据三角形相似的判定方法得到△BPD∽△CEP,利用相似比即可得到y=x(4-x),配方得到y=-(x-2)2+2,然后根据二次函数的性质对各选项进行判断.∵等边△ABC中,AB=4,BP=x,∴BD=2,PC=4-x,∠B=∠C=60°,∵∠MPN=60°,∴∠DPB+∠EPC=120°,∵∠EPC+∠PEC=120°,∴∠DPB=∠PEC,∴△BPD∽△CEP,∴,即,∴y=x(4-x)=-(x-2)2+2,(0≤x≤4).故选B.考点: 动点问题的函数图象.9、已知线段、满足,则.【答案】.【解析】试题分析:根据比例的性质进行答题.试题解析:∵线段a、b满足2a=3b,则.故答案是:.考点: 比例的性质.10、若,,则.【答案】.【解析】试题分析:在Rt△AB C中,设∠C=90°,∠A=,则,设BC=k,则AC=2k,由勾股定理知:,因此考点: 解直角三角形.11、抛物线向上平移5个单位后的解析式为.【答案】y=-2x2+3x+5.【解析】试题分析:只要求得新抛物线的顶点坐标,就可以求得新抛物线的解析式了.试题解析:将y=-2x2+3x配方为y=-2(x-)2+,故原抛物线的顶点为(,),向上平移5个单位,那么新抛物线的顶点为(,),可设新抛物线的解析式为:y=2(x-h)2+k,代入得:y=-2x2+3x+5.考点: 二次函数解析式.12、长方体底面周长为50cm,高为10cm.则长方体体积y关于底面的一条边长x的函数解析式是 .其中x 的取值范围是 . 【答案】y=-10x 2+250x ,0<x <25. 【解析】试题分析:根据长方体的面积等于底面积乘以高这一计算方法列出函数关系式即可.试题解析:∵长方体底面周长为50cm ,底面的一条边长x (cm ), ∴底面的另一条边长为:(25-x )cm ,根据题意得出: y=x (25-x )×10=-10x 2+250x (0<x <25). 故答案为:y=-10x 2+250x ,0<x <25. 考点:根据实际问题列二次函数关系式.13、如图,在Rt△ABC 中,已知∠ACB=90°,AC=1,BC=3,将△ABC 绕着点A 按逆时针方向旋转30°,使得点B 与点B′重合,点C 与点C′重合,则图中阴影部分的面积为 .【答案】 【解析】试题分析:先根据勾股定理得到AB=,再根据扇形的面积公式计算出S 扇形ABB′,由旋转的性质得到Rt△ADE≌Rt△ACB,于是S 阴影部分=S △AC′B′+S 扇形ABB′﹣S △ABC =S 扇形ABB′,求出即可.解:如图,∵∠ACB=90°,AC=1,BC=3, ∴AB==,∴S 扇形ABB′==,又∴Rt△ABC 绕A 点逆时针旋转30°后得到Rt△ADE, ∴Rt△ADE≌Rt△ACB,∴S 阴影部分=S △AC′B′+S 扇形ABB′﹣S △ABC =S 扇形ABB′=考点:旋转的性质;扇形面积的计算14、如图所示:下列正多边形都满足,在正三角形中,我们可推得:;在正方形中,可推得:;在正五边形中,可推得:,依此类推在正八边形中,,在正边形中,.【答案】135°.【解析】试题分析:根据图中所提示的内容,结合图形,找出规律,找到每种图形中∠EPA与其内角的关系.试题解析:在已知几个图中,都有△BEC≌△AFC,都有∠BPF=∠C,所以∠BPF都是等于这个多边形内角的度数;已知八边形内角为135°,所以在正八边形中,∠EPA=135°.考点: 正多边形和圆.15、计算:.【答案】.【解析】试题分析:根据二次根式、特殊角的三角函数值、非零数的零次幂的意义进行计算即可得出答案.试题解析:考点:实数的混合运算.16、已知:二次函数的图象开口向上,并且经过原点. (1)求的值;(2)用配方法求出这个二次函数图象的顶点坐标.【答案】(1)1;(2)(,-).【解析】试题分析:(1)根据二次函数图象开口向上判断出a>0,再把原点坐标代入函数解析式求解即可;(2)根据配方法的操作整理成顶点式解析式,然后写出顶点坐标即可.试题解析:(1)∵图象开口向上,∴a>0,∵函数图象经过原点O(0,0),∴a2-1=0,解得a1=1,a2=-1(舍去),∴a=1;(2)y=x2-3x=x2-3x+=(x-)2-,故抛物线顶点坐标为(,-).考点: 1.二次函数的性质;2.二次函数的三种形式.17、如图,在△ABC中,BD⊥AC于点D,,,并且.求的长.【答案】.【解析】试题分析:在Rt△ABD中,tan∠ABD=,即可求出∠ABD=30°,从而判断△ABC为直角三角形,且∠C=30°,利用30°所对的直角边等于斜边的一半即可求出AC的长.试题解析:在Rt△ABD中,∠BDA=90°,AB=,BD=∴tan∠ABD=,∴∠ABD=30°,∠A=60°∵∠ABD=∠CBD∴∠CBD=60°,∠ABC=90°在Rt△ABD中,考点: 解直角三角形.18、已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数在第一象限内的交点.(1)求点的坐标及的值;(2)试在轴上确定一点,使,求出点的坐标.【答案】(1)(1,3),3;(2)(2,0)或(-2,0).【解析】试题分析:(1)将A点坐标代入一次函数解析式求出n的值,再把A点坐标,代入反比例解析式求出k的值,即可确定出反比例解析式.(2)过A点作AD⊥y轴,根据已知条件即可判断出△COB≌△ADC,因此OB=DC=2,从而确定点B的坐标.试题解析:(1)点A(1,n)在y=2x+1的图象上,∴n=3,A(1,3)点A(1,3)在的图象上,∴k=3(2)如图,作AD⊥y轴,垂足为D∵OC=AD=1,BC=AC且∠COB=∠ADC=90°∴△COB≌△ADC∴OB=DC=2∴B点坐标为(2,0)或(-2,0)考点: 反比例函数.19、已知:如图,⊙的直径与弦(不是直径)交于点,若=2,,求的长.【答案】.【解析】试题分析:连结OD,设⊙O的半径为R,根据AB是⊙O的直径,且CF=DF,在Rt△OFD中,根据勾股定理可得出AF的长,在Rt△ACF中,根据勾股定理可求出AC的长.试题解析:如图,连结OD,设⊙O的半径为R,∵AB是⊙O的直径,且CF=DF,∴AB⊥CD,∵OB=R BF=2,则OF=R-2,在Rt△OFD中,由勾股定理得:R2=(R-2)2+42,解得:R=5∴AF=8.在Rt△ACF中由勾股定理得:AC=.考点:1.垂径定理;2.勾股定理.20、如图,某机器人在点A待命,得到指令后从A点出发,沿着北偏东30°的方向,行了4个单位到达B点,此时观察到原点O在它的西北方向上,求A点的坐标(结果保留根号).【答案】(0,-2-2).【解析】试题分析:首先过点B做BD⊥y轴于点D,得出BD,AD的长,进而得出OA的长,即可得出A点坐标.试题解析:过点B做BD⊥y轴于点D.在Rt△ADB中,∠BAD=30°,AB=4,∴BD=ABsin∠BAO=2,AD=ABcos∠BAO=2,又∵∠BDO=90°,∴∠DBO=45°,∴OD=BD=2,∴OA=OD+AD=2+2∴A(0,-2-2).考点: 解直角三角形的应用-方向角问题.21、已知:在中,,于,,若,,求的值及CD的长.【答案】3,.【解析】试题分析:根据“同角的余角相等”得到,∠ABC=∠ACD,然求同角的余弦三角函数得到.令BC=4k,AB=5k,则AC=3k.由BE:AB=3:5,知BE=3k.所以在中,tan∠AEC=,则易求CD=.试题解析:在Rt△ACD与Rt△ABC中,∵∠ABC+∠CAD=90°,∠ACD+∠CAD=90°,∴∠ABC=∠ACD,∴cos∠ABC=cos∠ACD=在Rt△ABC中,令BC=4k,AB=5k,则AC=3k由BE:AB=3:5,知BE=3k则CE=k,且CE=,则k=,AC=3.∴Rt△ACE中,tan∠AEC=,∵Rt△ACD中,cos∠ACD=,∴CD=.考点: 解直角三角形.22、如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到,).【答案】(1)点A的坐标为(1,0),点B的坐标为(3,0);(2).【解析】试题分析:以抛物线的顶点O为坐标原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴,建立平面直角坐标系,设抛物线解析式为y=ax2(a≠0),利用已知数据求出a的值,再利用等边三角形的性质计算即可.试题解析:以抛物线的顶点O为坐标原点,过点O作直线AB的平行线和垂线分别作为x轴和y轴,建立平面直角坐标系.则D(3,-6)设抛物线解析式为y=ax2(a≠0),∵D(3,-6)在抛物线上代入得:a=?,∴y=?x2,∵△ABO是等边三角形,∴OH=BH,设B(x,?x),∴?x=?x2,∴x1=0(舍),x2=,∴BH=,AB=3≈5.2(dm),答:等边三角形的边长为5.2dm考点: 二次函数的应用.23、已知:如图,是⊙的直径,是⊙外一点,过点作的垂线,交的延长线于点,的延长线与⊙交于点,.(1)求证:是⊙的切线;(2)若,⊙的半径为,求的长.【答案】(1)证明见解析;(2).【解析】试题分析:(1)连接OC,若要证明DC是⊙O的切线,则可转化为证明∠DCO=90°即可;(2)设AD=k,则AE=,ED=2k,利用勾股定理计算即可.试题解析:(1)证明:连结OC,∵DE=DC,∴∠4=∠E,∵OA=OC,∴∠1=∠2,又∵∠2=∠3,∴∠1=∠3,∴∠4+∠1=∠E+∠3=90°,∴DC是⊙O的切线;(2)∵∠4=∠E,∴,设AD=k,则AE=k,ED=2k,∴DC=2k,在Rt△OCD中,由勾股定理得:OD2=DC2+OC2,∴(+k)2=(2k)2+2,∴k=0(舍),k=,∴AE=k=考点: 1.切线的判定;2.解直角三角形;3.勾股定理.24、如图,二次函数的图象与一次函数的图象交于,两点. C为二次函数图象的顶点.(1)求二次函数的解析式;(2)定义函数f:“当自变量x任取一值时,x对应的函数值分别为y1或y2,若y1≠y2,函数f的函数值等于y1、y2中的较小值;若y1=y2,函数f的函数值等于y1(或y2).” 当直线(k >0)与函数f的图象只有两个交点时,求的值.【答案】(1)y=x2-2x+1;(2)k=1,,.【解析】试题分析:(1)根据题意设抛物线的解析式为y=a(x-1)2,把A(0,1)代入求出a的值即可.(2)根据题意可知直线(k >0)与函数f的图象只有两个交点共有三种情况:①直线与直线AB:y=x+1平行,②直线过点B(3,4),③直线与二次函数y=x2-2x+1的图象只有一个交点,分别求出k的值即可.试题解析:(1)设抛物线解析式为y=a(x-1)2,,由抛物线过点A(0,1),可得y=x2-2x+1(2)可得B(3,4)直线(k >0)与函数f的图象只有两个交点共有三种情况:①直线与直线AB:y=x+1平行,此时k=1;②直线过点B(3,4),此时;③直线与二次函数y=x2-2x+1的图象只有一个交点,此时有得,由△=0可得,.综上:k=1,,.考点:二次函数综合题.25、将绕点按逆时针方向旋转,旋转角为,旋转后使各边长变为原来的倍,得到,我们将这种变换记为[].(1)如图①,对作变换[]得,则:=___;直线与直线所夹的锐角为__ °;图①(2)如图②,中,,对作变换[]得,使得四边形为梯形,其中∥,且梯形的面积为,求和的值.图②【答案】(1)3,60;(2)60°,4.【解析】试题分析:根据题意知△ABC∽△AB′C′,因此;直线BC与B′C′所夹的锐角的度数为:360°-90°-90°-60°-120°=60°.(2)因为AB∥B′C′,∠C′=90°,∠BAC=30°,所以∠CAC′=60°;由△ABC∽△AB′C′及梯形面积可求出n的值.试题解析:(1) 3 , 60(2)由题意可知:△ABC∽△AB′C′,∴∠C′=∠C=90°,∵AB∥B′C′,∴∠BAC′=90°∴在Rt△ABC中,,∴,∴在直角梯形K中,∴n=4,n=-6(舍去)∴,n=4考点:1.旋转;2相似三角形.26、已知点和点在抛物线上.(1)求的值及点的坐标;(2)点在轴上,且满足△是以为直角边的直角三角形,求点的坐标;(3)平移抛物线,记平移后点A的对应点为,点B的对应点为. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,最短,求此时抛物线的函数解析式.【答案】(1),B(-4,-8);(2)(0,0)或(0,-12);(3)右平移个单位时,抛物线的解析式为.【解析】试题分析:(1)把点A(2,-2)代入求出a=的值;把点B(-4,n)代入求得n=-8;(2)先求出直线AB的解析式,然后进行分类讨论求出点P的坐标;(3)利用对称性求解即可.试题解析:(1)a=抛物线解析式为:B(-4,-8);(2) 记直线AB与x、y轴分别交于C、D两点,则直线AB:y=x-4C(4,0)、D(0,-4)在Rt△COD中,∵OC=DO∴∠ODA=45°以A为直角顶点,则在中,则∴又∵D(0,-4)∴(0,0)以B为直角顶点,则在中,∴∴(0,-12)∴P(0,0)或(0,-12)(3)记点A关于x轴的对称点为E(2,2)则BE:令y=0,得即BE与x轴的交点为Q(,0)故抛物线向右平移个单位时最短此时,抛物线的解析式为考点:二次函数综合题.。
2014.1石景山九年级第一学期期数学末答案

石景山区2013-2014学年度第一学期期末考试试卷初三数学参考答案阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.9.23; 10.55; 11.5322++-=x x y ; 12. x x y 250102+-=,250<<x ; 13.56π; 14.135︒;()2180n n-⋅︒. 三、解答题(本题共7道小题,每小题5分,共35分)15.解:030cos 2145tan 60sin 227⎪⎭⎫ ⎝⎛︒--︒︒+=123233-⨯+ ……………………………………………………4分 =134- ……………………………………………………………5分 16.解:(1)a =1; ……………………………………………………………2分(2)x x y 32-=494932-+-=x x ………………………………………3分 49232--=)(x ………………………………………4分 ∴抛物线顶点坐标为)49,23(- ………………………………5分17.解:在Rt ABD ∆中, 90BDA ∠=︒,AB =BD = 23226c o s ==∠∴A B D ………1分30ABD ∴∠=︒,60A ∠=︒ ……3分12ABD CBD ∠=∠60CBD ∴∠=︒90ABC ∴∠=︒ ……4分在ABC Rt ∆中,24cos ==AAB AC ……………5分18. 解:(1) 点),1(n A 在12+=x y 的图象上, ∴()3,1,3A n =………………………1分 点)3,1(A 在xky =的图象上, ∴3=k ……………………………2分 (2)如图,作⊥AD y 轴,垂足为D AC BC AD OC ===,1 . 且ADCCOB ∠==∠90ADC COB △△≅∴…………………3分 2==∴DC OB()()0,2'0,2-∴B B 或. ……………………5分.19.解:方法一:连结OD ………………1分 设⊙O 的半径为R∵AB 是⊙O 的直径,且CF=DF∴CD AB ⊥ ………………2分 ∵ OB=R BF=2 则2-R OF = 在OFD Rt ∆中,由勾股定理得:()22242-+=R R …………3分解得:5=R∴8=AF ………………4分 在ACF Rt ∆中由勾股定理得:5422=+=AF CF AC ………………5分 方法二:连结CB ………………1分 ∵AB 是⊙O 的直径,且CF=DF ∴CD AB ⊥, ………………2分∴1tan tan ∠=A ∴CFBFAF CF = ………………3分 ∴8=AF ………………4分 在ACF Rt ∆中由勾股定理得:54=AC ………………5分20. 解: 过点B 做y ⊥BD 轴于点D . ……………1分在ADB Rt ∆中,30=∠BAD ,4=AB 2sin =∠=∴BAO AB BD , ………2分 32cos =∠=BAO AB AD . ………3分 又90=∠BDO45=∠∴DBO , 2==∴BD OD . ………4分 322+=+=∴AD OD OA()322,0--∴A ………5分21. 解:在ACD Rt ∆与ABC Rt ∆中︒=∠+∠90CAD ABC ︒=∠+∠90CAD ACDACD ABC ∠=∠∴ ………………1分 54cos cos =∠=∠∴ACD ABC 在Rt ABC △中,54=AB BC 令k AB k BC 5,4== ………………2分 则k AC 3=由k BE AB BE 3,5:3:==知则2,==CE k CE 且 ………………3分 则2=k ,23=AC3tan ==∠∆∴CEACAEC ACE Rt 中,……………4分54cos ==∠∆AC CD ACD ACD Rt 中, , 2512=∴CD …………………5分四、解答题(本题共3道小题,每小题5分,共15分)22. 解:(说明:根据建立的坐标系的位置的不同,抛物线的解析式也不同)以抛物线的顶点O 为坐标原点, 过点O 作直线AB 的平行线和垂线分别作为x 轴和y 轴,建立平面直角坐标系. …………………1分 则()63-,D设抛物线解析式为()02≠=a ax y ,()63-,D 在抛物线上 代入得:32-=a232x y -=∴ …………….2分 △ABO 是等边三角形 BH OH 3=∴设()x x B 3,-………………3分 2323x x -=-01=∴x (舍),3232=x 323=∴BH ,)(2.533dm AB ≈=…………………………. 4分 答:等边三角形的边长为dm 2.5 . ………………………… 5分23. 解:(1)证明:连结OC ………………1分DC DE = E ∠=∠∴4 OC OA = 21∠=∠∴ 又32∠=∠则31∠=∠︒=∠+∠=∠+∠∴90314E ……2分∴DC 是⊙O 的切线 (2) E ∠=∠455sin =∠∴E,设k AD =k DC k ED k AE 2,2,5=∴==则………………3分在OCD Rt △中,由勾股定理得: 222OC DC OD +=2225)2()5(+=+∴k k ………………4分352,)(0==∴k k 舍 3105==∴k AE ……………5分6dm6dm24. 解:(1)设抛物线解析式为2)1(-=x a y ,由抛物线过点)10(,A ,可得122+-=x x y …………2分 (2)可得)4,3(B直线21-=kx y (k >0)与函数f 的图象只有两个交点共有三种情况:①直线21-=kx y 与直线AB :1+=x y 平行,此时1=k ;…3分 ②直线21-=kx y 过点)4,3(B ,此时23=k ; ………………4分③直线21-=kx y 与二次函数122+-=x x y 的图象只有一个交点, 此时有⎪⎩⎪⎨⎧+-=-=.12212x x y kx y , 得21122-=+-kx x x , 由,0=∆可得)(26,2-621舍--==k k .…………5分 综上:1=k ,23=k ,2-6=k五、解答题(本题共2道小题,每小题7分,共14分)25. 解:(1) 3 , 60 ………………………………………2分 (2) 由题意可知:C B A ''△∽ABC △n BC C B AC C A C C =''='=∠='∠∴,90︒=∠∴90',''//BAC C B AB60-90=∠︒=α∴BAC ……………………………4分在ABC Rt △中,121230cos ====AB BC AC AB , n C B n AC =''=∴,3'………………………………5分∴在直角梯形C B AB ''中,()C A C B AB S '''+=21()3123221=+=n n …………………………6分()舍去6,4-==∴n n ………………………………7分4,60==α∴n26.解:(1)21-=a ……………………1分 抛物线解析式为:221x y -=)8,4(--B ……………………2分 (2) 记直线AB 与x 、y 轴分别交于C 、D 两点,4:则-=x y AB 直线)4,0(、)0,4(-D C ………………………3分 ︒=∠∴=∆45中,ODA DO OC COD Rt , ①以A 为直角顶点,则︒=∠901AB P ︒=∠∆45中,11DA P AD P Rt 则2245cos 1=︒=D P AD421==∴AD D P 又),4,0(-D)0,0(1P ∴…………………4分 ②以B 为直角顶点,则︒=∠902DBP ︒=∠=∠∆45中,22ODC BDP DBP Rt 822==∴BD DP )12,0(-∴P ………………………5分 )12-,0(或)0,0(综上,P ∴(3)记点A 关于x 轴的对称点为)2,2(E 则BE: 3435-=x y令y=0,得54=x 即BE 与x 轴的交点为)0,54(Q ……6分56542=-=MQ故抛物线221x y -=向右平移56个单位时''MB M A +最短此时,抛物线的解析式为2)56(21--=x y …………………7分。
北京石景山区—学学期期末测验考试试卷

北京市石景山区2013—2014学年第一学期期末考试试卷高三化学2014.1考生须知 1.本试卷分为选择题、非选择题和答题纸三部分.2.认真填写学校、班级、姓名和学号.3.要按规定要求作答,答案一律完成在答题纸上.4.非选择题包括5道题,考生一律用黑色签字笔作答. 可能用到地相对原子质量:H —1C —12O —16 S —32 Cl —35.5第Ⅰ卷(选择题 共42分)一、选择题(本部分共14个小题,每小题3分,每小题只有一项符合题目要求) 1.垃圾分类从你我他开始.废电池属于A .B .C .D .2.化学美无处不在,下图是物质间发生化学反应地颜色变化,其中X 是 A .稀盐酸 B .稀硫酸 C .硫酸钠溶液 D .碳酸钠溶液 3.下列说法不正确...地是 A .分子式为C 5H 10O 2地羧酸共有3种B.分子式为C 3H 9N 地异构体共有4个C .某烷烃C n H 2n+2地一个分子中,含有共价键地数目是3n+1D .某烷烃C n H 2n+2地一个分子中,含有非极性键地数目是n-14.从海带中提取碘地实验过程中,涉及到下列操作,其中正确地是A.放出碘地苯溶液B.氧化I-C.将海带灼烧D.过滤含I-溶液5.“酸化”是实验中经常采用地方法,下列酸化过程正确地是A.抑制Fe2+地水解,用稀硝酸酸化B.提高高锰酸钾地氧化能力,用盐酸酸化C.确认溶液中含有24SO-时,先用盐酸酸化,再检验D.检验氯乙烷中地氯元素,加碱溶液加热后,用稀硫酸酸化后,再检验6. 海水中主要含有Na+、K+、Mg2+、Ca2+、Cl-、Br-、24SO-、3HCO-、23CO-等离子,火力发电时排放地烟气可用海水脱硫,其工艺流程如下图所示:b5E2R。
海水吸收塔氧化脱硫后的烟气氧气稀释含SO2的烟气海水排放下列说法错误地...是A.海水pH约为8地原因主要是天然海水含23CO-、3HCO-B.吸收塔中发生地反应有SO2+H2O H2SO3C.氧化主要是氧气将3HSO-、23SO-、H2SO3氧化为24SO-D.经稀释“排放”出地废水中,24SO-浓度与海水相同7. 以下进行性质比较地实验,不合理...地是A.比较Cu、Fe2+地还原性:铁加入硫酸铜溶液中B.比较氯、溴单质地氧化性:溴化钠溶液中通入氯气C.比较镁、铝金属性:氯化镁、氯化铝溶液中分别加入过量地NaOH溶液D.比较碳、硫非金属性:测定同条件同物质地量浓度地Na2CO3、Na2SO4溶液地pH先加几滴稀硫酸,再加1mL3%地H2O2GFeCl 3溶液盐桥电极Ⅰ(Pt )电极Ⅱ(Cu )CuCl 2溶液时间n(H 2)滴加少量CuSO 4溶液能量Q 1 Q 22H 2O(l)2H 2O(g)2H 2(g)+O 2(g) O S Se Te沸点反应过程 催化反应非催化反应反应物能量生成物冷却至室温 加热至70℃A. 大量苯酚和水 苯酚溶液 苯酚和水 通入CO 2NaOH 溶液B. 大量苯酚和水 苯酚钠溶液苯酚足量氨水适量氨水 C. 硝酸银溶液 氢氧化银和氧化银 银氨溶液加热通入过量CO 2D. 碳酸钙和水碳酸氢钙碳酸钙和水8.右图是某同学设计地原电池装置,下列叙述中正确地是 A .电极Ⅰ上发生还原反应,作原电池地负极 B .电极Ⅱ地电极反应式为: Cu 2++2e -= Cu C .该原电池地总反应为: 2Fe 3++Cu= Cu 2++2Fe 2+ D .盐桥中装有含氯化钾地琼脂,其作用是传递电子9. 甲、乙、丙、丁为4种短周期元素,在周期表中,甲与乙、丙、丁在周期表中地位置关系如右图所示(原子序数:乙>丙).丁地原子序数与乙、丙原子序数之和相等,4种元素原子地最外层电子数之和为24.下列判断正确地是 p1Ean 。
石景山区2013--2014学年第一学期期末考试【物理】
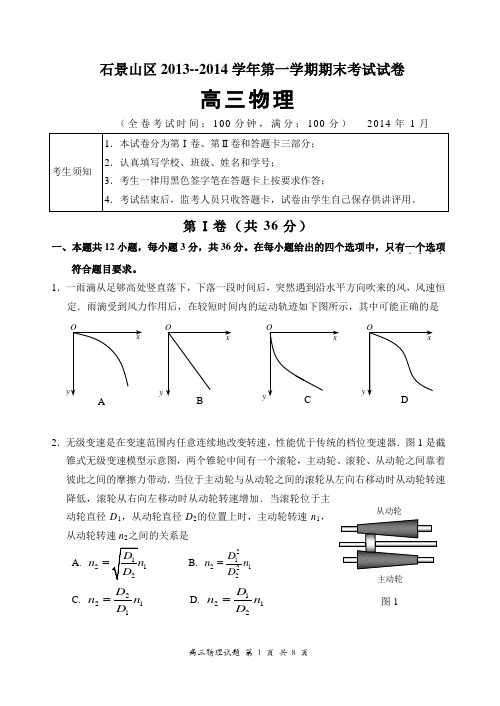
19. (11 分)图甲为一研究电磁感应的实验装置示意图,其中电流传感器(相当于一只理 想的电流表)能将各时刻的电流数据实时通过数据采集器传输给计算机,经计算机处 理后在屏幕上同步显示出 I-t 图像.足够长光滑金属轨道电阻不计,倾角 θ = 30°.轨道 上端连接有阻值 R = 1.0 Ω 的定值电阻,金属杆 MN 电阻 r = 0.5 Ω,质量 m = 0.4 kg,杆长 L = 1.0 m.在轨道区域加一垂直轨道平面向下的匀强磁场,让金属杆从图示位置由静止 开始释放,此后计算机屏幕上显示出如图乙所示的 I-t 图像,设杆在整个运动过程中与 轨道垂直,取 g = 10 m/s2.试求: (1)t = 0.5 s 时电阻 R 的热功率; (2)匀强磁场的磁感应强度 B 的大小; (3)估算 0~1.2 s 内通过电阻 R 的电荷量大小及在 R 上产生的焦耳热.
高三物理试题 第 2 页 共 8 页 B A
图4
7.如图 5 所示,两颗“近地”卫星 1 和 2 都绕地球做匀速圆 周运动,卫星 2 的轨道半径更大些.两颗卫星相比较,下 卫星 1 列说法中正确的是 A.卫星 2 的向心加速度较大 B.卫星 2 的线速度较大 C.卫星 2 的周期较大 D.卫星 2 的角速度较大
(3) 丙同学采用频闪摄影的方法拍摄到图 (3) 所示的“小球做平抛运动”的照片. 图 中每个小方格的边长为 1.25 cm,由图可求得拍摄时每隔__________s 曝光一次, 该小球平抛的初速度大小为___________m/s ( g 取 9.8 m/s2).
14. (8 分)为了测定一叠层电池的电动势和内电阻,实验室中提供有下列器材: A.电流表 G(满偏电流 10 mA,内阻 10 Ω) B.电流表 A(0~0.6 A~3A,内阻未知) C.滑动变阻器 R 0 (0~100Ω,1A) D.定值电阻 R(阻值 990Ω) E.开关与导线若干 (1)某同学根据现有的实验器材,设计了图甲所示的电路,请按照电路图在图乙上完 成实物连线.
【解析版】北京市石景山区2014届高三上学期期末考试试题(英语)

石景山区2013 — 2014学年度第一学期高三期末测试卷英语本试卷共12页,150分。
考试时长120分钟。
考生务必将答案填涂或书写在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一卷第一部分听力理解(共三节,30分)(略)第二部分知识运用(共两节,45分)第一节单项填空(共15小题;每小题1分,共15分)从每题所给的A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
23. The listeners were much than hoped. There were so many tickets left.A. fewerB. largerC. moreD. less【答案】A【解析】试题分析:考查形容词比较级。
句意听众比期望的人少,这有许多的票剩下。
根据下文提到There were so many tickets left.有票剩下,故人少,又因为than表示比较级,修饰人用few,故用fewer形式,所以选A项。
考点 : 考查形容词比较级24. — Are you expecting to receive a digital camera as a gift?—Yeah! I can’t wait to get .A. someB. anyC. itD. one26.— Jim has gone to Britain to see a modern art exhibition.— Oh, really? Do you know when he ?A. leavesB. will leaveC. was leavingD. left【答案】D【解析】试题分析:考查动词的时态。
句意吉姆去英国看现代艺术展览了。
真的吗?你知道他什么时候离开的吗?根据上句话中的提到Jim has gone to Britain to see a modern art exhibition,has gone to 去了某地没有回来,所以他离开这个动作已经发生,所以选D项。
北京市石景山区2014届高三上学期期末考试英语试题 Word版含答案-含答案【高考模拟试题】

石景山区2013 — 2014学年度第一学期高三期末测试卷英语本试卷共12页,150分。
考试时长120分钟。
考生务必将答案填涂或书写在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一卷第一部分听力理解(共三节,30分)第一节(共5小题;每小题1.5分,共7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话你将听一遍。
1. What does Pete feel after his exams?A. Good.B. Disappointed.C. Satisfied.2. What’s Patty troubled by?A. The on and off of the light.B. The pale colour on face.C. A serious pain in her back.3. What is outside their window?A. A snow world.B. A white building.C. A skiing ground.4. What are they talking about?A. Parks.B. Exercises.C. Pets.5. What are they looking at?A. Pig houses.B. Special mirrors.C. Toothpicks.第二节(共10小题;每小题1.5分,共15分)听下面4段对话,每段对话后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话你将听两遍。
听第6段材料,回答第6至7题。
6. How did the woman lose weight?A. She went on a healthy diet.B. She ate fruits before meals.C. She did a lot of exercise.7. What does the man suggest doing?A. Buying cheaper food.B. Bringing food from home.C. Setting up a healthy food club.听第7段材料,回答第8至9题。
高中高考-2013石景山期末答案

②CH4—8e-+ 9 CO32 +3H2O =10 HCO3 ③c(K+)>c( HCO3 )>c( CO32 )>c(OH-)>c(H+) 19.(10 分) (1)> (2)60% (3)A、C (4)O2+4e-+4 H+ =2H2O (5)16:29
OH
16.(14 分)
(1)2Cl-+2H2O
2OH-+H2↑+Cl2↑
(2) (3)水玻璃 (4)溶液中逐渐有白.色.絮状沉.淀.生.成.,且不断增加;然后又由多到少,最.后.消.失.。 (5)4Fe2++8OH-+O2+2H2O=4Fe(OH)3↓ (分步写且全正确给分) (6)3Cl2+8NH3=N2+6NH4Cl (7)c(H+):c(Al3+):c(NH4+):c(SO42-)=1:1:2:3
(4)2HOH 2CH2C C CH2CH2OH+3O2
Cu △
2OHCH 2C C CH2CHO +6H2O
OH
OH
(5)HO
CH2OH
OH或
CH2OH
(6) HOOCH2C
HO
OH
CH2COOH
C
CH2COOH+4NaOH
OOCCH3
CH2COONa
△
NaOOCH2C C
CH2COONa+ CH3COONa + 3H2O
高三化学答案 2 / 2
石景山区高三数学期末理科2014年1月及答案

石景山区2013—2014学年第一学期期末考试试卷高三数学(理科)本试卷共6页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}2230M x x x =∈+-≤R ,{}10N x x =∈+<R ,那么M N = ( )A .{101}-,,B .{321}---,,C .{11}x x -≤≤D .{31}x x -≤<-2.复数1ii =-( ) A .122i + B .122i -C .122i-+ D .122i -- 3.已知向量(1)x =,a ,(4)x =,b ,则“2x =”是“a ∥b ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.已知数列为等差数列,,那么数列通项公式为( )A .B .C .D .5.执行如图所示的程序框图,若输入的x 的值为2, 则输出的x 的值为( ) A .3 B .126 C .127 D .1286. 在边长为1的正方形OABC 中任取一点P ,则点P恰好落在正方形与曲线y =(阴影部分)的概率为( )A .12B .23C .34D .45OCy =B7.用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为( )A .324B .328C .360D .6488.已知函数满足,当时,,若在区间上方程有两个不同的实根,则实数的取值范围是( )A .B .C .D .第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.已知圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩,,=(θ为参数),则圆C 的直角坐标方程为_______________,圆心C 到直线:10l x y ++=的距离为______.10.在ABC ∆中,角A B C ,,的对边分别为a b c ,,,若=6a ,4c =,1cos =3B ,则b =______. 11. 若x ,y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩,,,则z x y =+的最大值为 .12.如图,已知在ABC ∆中,o 90B ∠=,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切 于点D ,2AD =,1AE =,则AB 的长为 ,CD 的长为 .13.已知抛物线24y x =的焦点为F ,准线为直线l ,过抛物线上一点P 作PE l ⊥于E ,若直线EF 的倾斜角为o150,则||PF =______.14. 已知四边形是边长为的正方形,且平面,为上动点,过且垂直于的平面交于,那么异面直线PC 与BD 所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥P ABCD -的高PA 的长为 .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)已知函数()cos cos 21f x x x x =++. (Ⅰ)求函数的单调递增区间;(Ⅱ)求函数在上的最小值,并写出取最小值时相应的值.A DCBE.OA 1ABDCPE北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为100分,规定测试成绩在[85100],之间为体质优秀;在[7585),之间为体质良好;在[6075),之间为体质合格;在[060),之间为体质不合格.现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩,其茎叶图如下:9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6(Ⅰ)试估计该校高三年级体质为优秀的学生人数;(Ⅱ)根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.(ⅰ)求在选出的3名学生中至少有1名体质为优秀的概率;(ⅱ)记X 为在选出的3名学生中体质为良好的人数,求X 的分布列及数学期望.17.(本小题满分14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是直角梯形,o 90ABC ∠=,AD ∥BC ,且2PA AD ==,1AB BC ==,E 为PD 的中点.(Ⅰ)求证:CD ⊥平面PAC ; (Ⅱ)求二面角E AC D --的余弦值;(Ⅲ)在线段AB 上是否存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ?若存在,求出AF 的长;若不存在,请说明理由.18.(本小题满分13分)已知函数()xf x e ax =-(e 为自然对数的底数).(Ⅰ)当2a =时,求曲线()f x 在点(0(0))f ,处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)已知函数()f x 在0x =处取得极小值,不等式()f x mx <的解集为P ,若1{|2}2M x x =≤≤,且M P ≠∅ ,求实数m 的取值范围.A PEBDC已知椭圆:()过点(20),,且椭圆的离心率为. (Ⅰ)求椭圆的方程;(Ⅱ)若动点在直线上,过作直线交椭圆于两点,且MP PN =,再过作直线.证明:直线恒过定点,并求出该定点的坐标.20.(本小题满分13分)已知集合,对于数列中. (Ⅰ)若50项数列{}n a 满足5019ii a==-∑,5021(1)107i i a =-=∑,则数列{}n a 中有多少项取值为零?(121nin i aa a a n *==+++∈∑N ,)(Ⅱ)若各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=(). (ⅰ)若首项10b =,末项1n b n =-,求证数列{}n b 是等差数列;(ⅱ)若首项10b =,末项0n b =,记数列{}n b 的前n 项和为n S ,求n S 的最大值和最小值.石景山区2013—2014学年第一学期期末考试高三数学(理科)参考答案一、选择题共8二、填空题共6小题,每小题5分,共30分.(两空的题目第一空2分,第二空3分)三、解答题共6小题,共80分. 15.(本小题共13分)解:(Ⅰ)()f x 2cos 2+1x x =+ …………2分 2sin 2+16x π=+(), ……………4分222262k x k πππππ-≤+≤+,k ∈Z , 36k x k ππππ-≤≤+,k ∈Z , ………6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+,()k ∈Z . ……………7分(Ⅱ)因为44x ππ-≤≤,22363x πππ-≤+≤,……………9分sin(2)16x π≤+≤, 12sin 2+136x π≤+≤(), ……………11分 所以当2=63x ππ+-,即=4x π-时,函数)(x f 取得最小值1.………13分则 3335C 9()1C 10P A =-=. 故在选出的3名学生中至少有名体质为优秀的概率为910.……9分(ⅱ)解:随机变量X 的所有取值为123,,.123235C C 3(1)C 10P X ⋅===,213235C C 6(2)C 10P X ⋅===,3335C 1(3)C 10P X ===. …………12分 所以,随机变量X 的分布列为:36191231010105EX =⨯+⨯+⨯=. ……………13分 17.(本小题共14分) (Ⅰ)证明:因为PA ⊥平面ABCD ,CD ⊂平面ABCD ,所以PA CD ⊥. ……………1分 取AD 的中点G ,连结GC ,因为底面ABCD 为直角梯形,AD ∥BC ,o90ABC ∠=,且1AB BC ==,所以四边形ABCG 为正方形,所以CG AD ⊥,且1=2CG AD , 所以o=90ACD ∠,即AC CD ⊥. ……………3分 又PA AC A = ,所以CD ⊥平面PAC . ……………4分(Ⅱ)解:如图,以A 为坐标原点,AB AD AP ,,所在直线分别为x y z ,,轴建立空间直角坐标系xyz A -.………5分则(000)A ,,,(110)C ,,,(011)E ,,,(002)P ,,,所以(002)AP = ,,,(110)AC = ,,,(011)AE =,,. 因为PA ⊥平面ABCD ,所以(002)AP =,,为平面ACD 的一个法向量. ……6分 设平面EAC 的法向量为1()n x y z =,,,由10n AC ⋅= ,10n AE ⋅= 得00x y y z +=⎧⎨+=⎩,,令1x =,则1y =-,1z =,APEBDCG所以1(111)n =-,,是平面EAC 的一个法向量. ………8分所以1cos n AP <>== ,因为二面角E AC D --为锐角, 所以二面角E AC D --. ………9分 (Ⅲ)解:假设在线段AB 上存在点F (不与A B ,两点重合),使得AE ∥平面PCF . 设(00)F a ,,,则(110)CF a =-- ,,,(112)CP =--,,. 设平面PCF 的法向量为2()n x y z =,,, 由20n CF ⋅= ,20n CP ⋅= 得(1)020a x y x y z --=⎧⎨--+=⎩,,令1x =,则1y a =-,2az =,所以2(11)2a n a =- ,,是平面PCF 的一个法向量.…12分因为AE ∥平面PCF ,所以20AE n ⋅= ,即(1)02aa -+=, ……………13分解得23a =,所以在线段AB 上存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ,且2=3AF .……14分 18.(本小题共13分)解:(Ⅰ)当2a =时,()2x f x e x =-,(0)1f =,()2xf x e '=-,得(0)1f '=-,………2分所以曲线()f x 在点(0(0))f ,处的切线方程为1y x =-+. ……………3分 (Ⅱ)()xf x e a '=-.当0a ≤时,()0f x '>恒成立,此时()f x 的单调递增区间为()-∞+∞,,无单调递减区间;………5分 当0a >时,(ln )x a ∈-∞,时,()0f x '<,(ln )x a ∈+∞,时,()0f x '>, 此时()f x 的单调递增区间为(ln )a +∞,,单调递减区间为(ln )a -∞,.……7分 (Ⅲ)由题意知(0)0f '=得1a =,经检验此时()f x 在0x =处取得极小值. ………8分因为M P ≠∅ ,所以()f x mx <在1[2]2,上有解,即1[2]2x ∃∈,使()f x mx <成立,…9分即1[2]2x ∃∈,使x e x m x ->成立, …………10分所以min ()x e xm x->.令()1x e g x x =-,2(1)()x x e g x x -'=,所以()g x 在1[1]2,上单调递减,在[12],上单调递增, 则min ()(1)1g x g e ==-, ……………12分 所以(1)m e ∈-∞,+. ……………13分 19.(本小题共14分)解:(Ⅰ)因为点(20),在椭圆C 上,所以22401a b+=, 所以24a =, …………1分 因为椭圆C 的离心率为12, 所以12c a =,即22214a b a -= , …………2分 解得23b =, ……………4分所以椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ)设0(1)P y -,,033()22y ∈-,, ①当直线MN 的斜率存在时,设直线MN 的方程为0(1)y y k x -=+,11()M x y ,,22()N x y ,, 由2203412(1)x y y y k x ⎧+=⎨-=+⎩,,得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=, ………7分所以2012288+34ky k x x k +=-+, ……………8分因为MP PN = ,即P 为MN 中点,所以12=12x x +-,即20288=234ky k k +--+. 所以003(0)4MN k y y =≠, ……………9分 因为直线l MN ⊥, 所以043l y k =-,所以直线l 的方程为004(1)3yy y x -=-+, 即041()34y y x =-+ ,显然直线l 恒过定点1(0)4-,. ……………11分②当直线MN 的斜率不存在时,直线MN 的方程为1x =-, 此时直线l 为x 轴,也过点1(0)4-,. ……………13分 综上所述直线l 恒过定点1(0)4-,. ……………14分20.(本小题共13分)解:(Ⅰ)设数列{}n a 中项为110-,,分别有x y z ,,项.由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩,,,解得11z =.所以数列{}n a 中有11项取值为零. ……3分 (Ⅱ)(ⅰ){11}i a ∈-,且11i i i b b a ---=,得到121(23)i i b a a a i n -=+++= ,,,, 若1(121)i a i n ==- ,,,,则满足1n b n =-.此时11i i b b --=,数列{}n b 是等差数列; 若121n a a a - ,,,中有*(0)p p p >∈,N 个1-,则121n b n p n =--≠-不满足题意; 所以数列{}n b 是等差数列. ……………7分(ⅱ)因为数列{}n b 满足11i i i b b a ---=,所以121(23)i i b a a a i n -=+++= ,,,, 根据题意有末项0n b =,所以1210n a a a -+++= .而{11}i a ∈-,,于是n 为正奇数,且121n a a a - ,,,中有12n -个1和12n -个1-. 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++要求n S 的最大值,则只需121n a a a - ,,,前12n -项取1,后12n -项取1-,所以2max(1)()(2)(4)14n n S n n -=-+-++=(n 为正奇数). 要求n S 的最小值,则只需121n a a a - ,,,前12n -项取1-,后12n -项取1, 则2min(1)()(2)(4)14n n S n n -=------=-(n 为正奇数). …………13分【注:若有其它解法,请酌情给分.】。
石景山区2013—2014学年第一学期期末考试试卷高三数学(理科)

石景山区2013—2014学年第一学期期末考试试卷高三数学(理科)本试卷共6页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}2230M x x x =∈+-≤R ,{}10N x x =∈+<R ,那么MN =( )A .{101}-,,B .{321}---,,C .{11}x x -≤≤D .{31}x x -≤<-2.复数1ii =-( ) A .122i + B .122i -C .122i-+ D .122i -- 3.已知向量(1)x =,a ,(4)x =,b ,则“2x =”是“a ∥b ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.已知数列为等差数列,,那么数列通项公式为( )A .B .C .D .5.执行如图所示的程序框图,若输入的x 的值为2, 则输出的x 的值为( ) A .3 B .126 C .127D .1286. 在边长为1的正方形OABC 中任取一点P ,则点P恰好落在正方形与曲线y =(阴影部分)的概率为( )A .12B .23C .34D .457.用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为( )A .324B .328C .360D .6488.已知函数满足,当时,,若在区间上方程有两个不同的实根,则实数的取值范围是( )OCy =ABA .B .C .D .第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.已知圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩,,=(θ为参数),则圆C 的直角坐标方程为_______________,圆心C 到直线:10l x y ++=的距离为______.10.在ABC ∆中,角A B C ,,的对边分别为a b c ,,,若=6a ,4c =,1cos =3B ,则b =______. 11. 若x ,y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩,,,则z x y =+的最大值为 .12.如图,已知在ABC ∆中,o 90B ∠=,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切 于点D ,2AD =,1AE =,则AB 的长为 ,CD 的长为 .13.已知抛物线24y x =的焦点为F ,准线为直线l ,过抛物线上一点P 作PE l ⊥于E ,若直线EF 的倾斜角为o 150,则||PF =______.14.已知四边形是边长为的正方形,且平面,为上动点,过且垂直于的平面交于,那么异面直线PC 与BD 所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥P ABCD -的高PA 的长为 .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)已知函数()cos cos 21f x x x x =++. (Ⅰ)求函数的单调递增区间;(Ⅱ)求函数在上的最小值,并写出取最小值时相应的值.16.(本小题满分13分)A DCBE.OA 1ABDCPE北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为100分,规定测试成绩在[85100],之间为体质优秀;在[7585),之间为体质良好;在[6075),之间为体质合格;在[060),之间为体质不合格.现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩,其茎叶图如下:9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6(Ⅰ)试估计该校高三年级体质为优秀的学生人数;(Ⅱ)根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.(ⅰ)求在选出的3名学生中至少有1名体质为优秀的概率;(ⅱ)记X 为在选出的3名学生中体质为良好的人数,求X 的分布列及数学期望.17.(本小题满分14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是直角梯形,o 90ABC ∠=,AD ∥BC ,且2PA AD ==,1AB BC ==,E 为PD 的中点.(Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)求二面角E AC D --的余弦值;(Ⅲ)在线段AB 上是否存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ?若存在,求出AF 的长;若不存在,请说明理由.18.(本小题满分13分)A PEDC已知函数()xf x e ax =-(e 为自然对数的底数).(Ⅰ)当2a =时,求曲线()f x 在点(0(0))f ,处的切线方程;(Ⅱ)求函数()f x 的单调区间;(Ⅲ)已知函数()f x 在0x =处取得极小值,不等式()f x mx <的解集为P ,若1{|2}2M x x =≤≤,且MP ≠∅,求实数m 的取值范围.19.(本小题满分14分)已知椭圆:()过点(20),,且椭圆的离心率为. (Ⅰ)求椭圆的方程;(Ⅱ)若动点在直线上,过作直线交椭圆于两点,且MP PN =,再过作直线.证明:直线恒过定点,并求出该定点的坐标.20.(本小题满分13分)已知集合,对于数列中. (Ⅰ)若50项数列{}n a 满足5019ii a==-∑,5021(1)107ii a =-=∑,则数列{}n a 中有多少项取值为零?(121nin i aa a a n *==+++∈∑N ,)(Ⅱ)若各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=(). (ⅰ)若首项10b =,末项1n b n =-,求证数列{}n b 是等差数列;(ⅱ)若首项10b =,末项0n b =,记数列{}n b 的前n 项和为n S ,求n S 的最大值和最小值.石景山区2013—2014学年第一学期期末考试高三数学(理科)参考答案一、选择题共8小题,每小题5分,共40分.二、填空题共6小题,每小题5分,共30分.(两空的题目第一空2分,第二空3分)三、解答题共6小题,共80分. 15.(本小题共13分)解:(Ⅰ)()f x 2cos 2+1x x =+ …………2分 2sin 2+16x π=+(), ……………4分222262k x k πππππ-≤+≤+,k ∈Z, 36k x k ππππ-≤≤+,k ∈Z , ………6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+,()k ∈Z . ……………7分(Ⅱ)因为44x ππ-≤≤,22363x πππ-≤+≤, ……………9分sin(2)16x π≤+≤, 12sin 2+136x π≤+≤(), ……………11分 所以当2=63x ππ+-,即=4x π-时,函数)(x f 取得最小值1.………13分则 3335C 9()1C 10P A =-=. 故在选出的3名学生中至少有名体质为优秀的概率为910.……9分(ⅱ)解:随机变量X 的所有取值为123,,.123235C C 3(1)C 10P X ⋅===, 213235C C 6(2)C 10P X ⋅===,3335C 1(3)C 10P X ===. …………12分所以,随机变量X 的分布列为:36191231010105EX =⨯+⨯+⨯=. ……………13分 17.(本小题共14分) (Ⅰ)证明:因为PA ⊥平面ABCD ,CD ⊂平面ABCD ,所以PA CD ⊥. ……………1分 取AD 的中点G ,连结GC ,因为底面ABCD 为直角梯形,AD ∥BC ,o90ABC ∠=,且1AB BC ==,所以四边形ABCG 为正方形,所以CG AD ⊥,且1=2CG AD , 所以o=90ACD ∠,即AC CD ⊥. ……………3分 又PAAC A =,所以CD ⊥平面PAC . ……………4分(Ⅱ)解:如图,以A 为坐标原点,AB AD AP ,,所在直线分别为x y z ,,轴建立空间直角坐标系xyz A -.………5分则(000)A ,,,(110)C ,,,(011)E ,,,(002)P ,,,所以(002)AP =,,,(110)AC =,,,(011)AE =,,. 因为PA ⊥平面ABCD ,所以(002)AP =,,为平面ACD 的一个法向量. ……6分 设平面EAC 的法向量为1()n x y z =,,,由10n AC ⋅=,10n AE ⋅=得00x yy z +=⎧⎨+=⎩,,令1x =,则1y =-,1z =,所以1(111)n =-,,是平面EAC 的一个法向量. ………8分所以1cos 3n AP <>==0,因为二面角E AC D --为锐角, 所以二面角E AC D --.………9分 APEB DCG(Ⅲ)解:假设在线段AB 上存在点F (不与A B ,两点重合),使得AE ∥平面PCF . 设(00)F a ,,,则(110)CF a =--,,,(112)CP =--,,. 设平面PCF 的法向量为2()n x y z =,,,由20n CF ⋅=,20n CP ⋅=得(1)020a x y x y z --=⎧⎨--+=⎩,,令1x =,则1y a =-,2az =,所以2(11)2an a =-,,是平面PCF 的一个法向量.…12分因为AE ∥平面PCF ,所以20AE n ⋅=,即(1)02aa -+=, ……………13分解得23a =,所以在线段AB 上存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ,且2=3AF .……14分 18.(本小题共13分)解:(Ⅰ)当2a =时,()2x f x e x =-,(0)1f =,()2xf x e '=-,得(0)1f '=-,………2分所以曲线()f x 在点(0(0))f ,处的切线方程为1y x =-+. ……………3分(Ⅱ)()xf x e a '=-.当0a ≤时,()0f x '>恒成立,此时()f x 的单调递增区间为()-∞+∞,,无单调递减区间;………5分 当0a >时,(ln )x a ∈-∞,时,()0f x '<,(ln )x a ∈+∞,时,()0f x '>, 此时()f x 的单调递增区间为(ln )a +∞,,单调递减区间为(ln )a -∞,.……7分 (Ⅲ)由题意知(0)0f '=得1a =,经检验此时()f x 在0x =处取得极小值. ………8分因为MP ≠∅,所以()f x mx <在1[2]2,上有解,即1[2]2x ∃∈,使()f x mx <成立,…9分即1[2]2x ∃∈,使x e x m x ->成立, …………10分 所以min ()x e xm x->. 令()1x e g x x =-,2(1)()x x e g x x -'=,所以()g x 在1[1]2,上单调递减,在[12],上单调递增, 则min ()(1)1g x g e ==-, ……………12分 所以(1)m e ∈-∞,+. ……………13分19.(本小题共14分)解:(Ⅰ)因为点(20),在椭圆C 上,所以22401a b+=, 所以24a =, …………1分 因为椭圆C 的离心率为12, 所以12c a =,即22214a b a -= , …………2分 解得23b =, ……………4分所以椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ)设0(1)P y -,,033()22y ∈-,, ①当直线MN 的斜率存在时,设直线MN 的方程为0(1)y y k x -=+,11()M x y ,,22()N x y ,, 由2203412(1)x y y y k x ⎧+=⎨-=+⎩,,得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=, ………7分所以2012288+34ky k x x k +=-+, ……………8分因为MP PN =,即P 为MN 中点,所以12=12x x +-,即20288=234ky k k +--+. 所以003(0)4MN k y y =≠, ……………9分 因为直线l MN ⊥, 所以043l y k =-,所以直线l 的方程为004(1)3yy y x -=-+, 即041()34y y x =-+ ,显然直线l 恒过定点1(0)4-,. ……………11分②当直线MN 的斜率不存在时,直线MN 的方程为1x =-, 此时直线l 为x 轴,也过点1(0)4-,. ……………13分 综上所述直线l 恒过定点1(0)4-,. ……………14分 20.(本小题共13分)解:(Ⅰ)设数列{}n a 中项为110-,,分别有x y z ,,项.由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩,,,解得11z =.所以数列{}n a 中有11项取值为零. ……3分 (Ⅱ)(ⅰ){11}i a ∈-,且11i i i b b a ---=,得到121(23)i i b a a a i n -=+++=,,,,若1(121)i a i n ==-,,,,则满足1n b n =-.此时11i i b b --=,数列{}n b 是等差数列;若121n a a a -,,,中有*(0)p p p >∈,N 个1-,则121n b n p n =--≠-不满足题意; 所以数列{}n b 是等差数列. ……………7分 (ⅱ)因为数列{}n b 满足11i i i b b a ---=,所以121(23)i i b a a a i n -=+++=,,,,根据题意有末项0n b =,所以1210n a a a -+++=.而{11}i a ∈-,,于是n 为正奇数,且121n a a a -,,,中有12n -个1和12n -个1-. 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++要求n S 的最大值,则只需121n a a a -,,,前12n -项取1,后12n -项取1-, 所以2max (1)()(2)(4)14n n S n n -=-+-++=(n 为正奇数).要求n S 的最小值,则只需121n a a a -,,,前12n -项取1-,后12n -项取1, 则2min (1)()(2)(4)14n n S n n -=------=-(n 为正奇数). …………13分【注:若有其它解法,请酌情给分.】。
7.2013-2014第1学期初2数学期末考试题答案-石景山

石景山区2013-2014学年度第一学期期末考试初二数学答案及评分参考阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.二、填空题(本题共6道小题,每小题4分,共24分)11.3n m-; 12.3; 13.5; 14.36;(各2分)15.2; 162分,答对两个3分,答对3个4分)三、解答题(本题共4个小题,每小题5分,共20分)17. 解:原式=14- ………………………………………………………4分=3-- ………………………………………………………………5分18. 解:2(3)(1x x x ++-=-…………………………………………………1分224381x x x ++-=- …………………………………………………2分44x = …………………………………………………3分1x = ………………………………………………………4分 经检验:1x =是原方程的增根,所以原方程无解 ……………………………5分19. 解:原式…………………………………………3分…………………………………………4分……………………………………………………5分20. 解:原式=()()()22225213x y x y y x y x y +-⎡⎤-⨯⎢⎥--⎣⎦…………………………………………1分 =()()()()22522223y x y x y x y x y x y -+--⋅-- =()22293y x x y -- …………………………………………………………………2分=33y x y x +- ……………………………………………………………………3分解法一:∵23x y =,不妨设()2,30x k y k k ==≠ …………………………………4分∴原式=9292k kk k +-=117………………………………………5分 解法二:3333xy x y xy x y ++=-- ………………………………………4分∵23x y =∴原式=231132733+=- ………………………………………5分 (阅卷说明:如果学生直接将2,3x y ==代入计算正确者,本题扣1分)四、列方程解应用题(本题5分)21. 解:设原计划每天加工x 顶帐篷. ……………………………………………………1分1500300150030042x x ---= …………………………………………………2分解得 150x = ………………………………………………………………3分经检验,150x =是原方程的解,且符合题意. ………………………………4分答:原计划每天加工150顶帐篷.……………………………………………………5分五、解答题(本大题共3个小题,每题5分,共15分)22.证明:∵AE ∥DF ,∴∠AEB=∠DFC. …………………………………………………………1分 ∵BF=CE ,∴BF+EF =即=CF. …………………………2分在△ABE 和△DCF 中,AE DF AEB DFC BE CF =⎧⎪∠=∠⎨⎪=⎩ ………………………………………………………3分∴△ABE ≌△DCF ………………………………………………………4分∴AB=DC ………………………………………………………5分23. 解:AFB ∠=60° ………………………………………………………………1分证明:∵△ABC 是等边三角形∴CA=CB ,4∠=60° 2分 ∵∠2+∠4=∠5 C∠1+∠3=∠5且∠3=60°∴∠1=∠2 ……………… ………………3分又∵BE=AD∴△BCE ≌△ACD (SAS )∴CE=CD ,∠BCE=∠ACD ……………………………………………4分∴∠BCE -∠6=∠ACD -∠6即∠4=∠7=60°∴△ECD 是等边三角形 ………………………………………………5分24. 解:分类讨论(1)如图,过A 作AD ⊥BC 交BC (延长线)于D ,………………………1分∴∠D=90°,∴在Rt △ABD 中,∠B+∠BAD=90°,∴∠BAD =45°∴DA DB =, 又∵222AB DB DA =+,不妨设x DB DA ==则3222=+x x ,解得4=x ,∴DA=DB=4 ……………………………2分∵∠D=90°,∴在Rt △ACD 中,222AC DA DC =+3452222=-=-=AD AC CD ……………………………3分∴BC=BD-CD=4-3=1 ……………………………4分(2)如图:由(1)同理:DB=4,CD=3∴BC=BD+CD=4+3=7.综上所述:BC=1或BC=7 ……………………………5分 D C 'C B A(阅卷说明:只计算出一种情况,本题得4分)六、几何探究(本题6分)25. (1)证明:连结ND∵AO 平分BAC ∠, ∴12∠=∠∵直线l ⊥AO 于H ,∴4590∠=∠=︒ ∴67∠=∠∴AN AC =∴NH CH =∴AH 是线段NC 的中垂线∴DC DN =∴98∠=∠∴AND ACB ∠=∠∵3AND B ∠=∠+∠,2ACB B ∠=∠,∴3∠=∠B∴DN BN =∴BN DC = ……………………………………………………………………2分(2)当M BC 是中点时,CE 和CD 之间的等量关系为2CD CE =证明:过点C 作'CN AO ⊥交AB 于'N由(1)可得'BN CD =,',AN AC AN AE ==∴43∠=∠,'NN CE =过点C 作CG ∥AB 交直线l 于点G∴42∠=∠,1B ∠=∠∴23∠=∠∴CG =∵M BC 是中点, ∴BM CM = 在△BNM 和△CGM 1,,,B BM CM NMB GMC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BNM≌△CGM∴BN CG=∴BN CE=∴''2==+=……………………………CD BN NN BN CE……………4分(3)BN、CE、CD之间的等量关系:当点M在线段BC上时,CD BN CE=+;当点M在BC的延长线上时,CD BN CE=-;当点M在CB的延长线上时,=-………………………………6分CD CE BN(阅卷说明:三种情况写对一个给1分,全对给2分) 七、选作题螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈。
北京市石景山七年级上期末考试数学试题含答案.doc

石景山区2013—2014学年第一学期期末考试试卷初一数学考生 须知 1. 本试卷为闭卷考试,满分为100分,考试时间为100分钟. 2. 本试卷共6页,各题答案均写在试卷相应位置上.题号一二三四五六七八总分得分一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项前的字母填在题后括号内) 1.-2的相反数是( )A . 2B .21-C . 21D .-22.当A 地高于海平面152米时,记作“海拔+152米”,那么B 地低于海平面23米时,记作( )A .海拔23米B .海拔-23米C .海拔175米D .海拔129米 3. 下列各式中,不相等的是 ( )A .(-3)2和-32B .(-3)2和32C .(-2)3和-23D .32-和32- 4.长城总长约为6700000米,用科学计数法表示为 ( )A .6.7510⨯米 B .6.7610⨯米 C .6.7710⨯米 D .6.7810⨯米 5.方程2x +a -4=0的解是 x =-2,则a 等于( ) A .-8 B . 0 C . 2 D . 8 6.下列各组整式中不是同类项的是 ( ) A .3m 2n 与3nm 2 B .31xy 2与31x 2y 2 C .-5ab 与-5×103ab D .35与-12 7.如图,点C 是线段AB 上的点,点D 是线段BC 的中点,AB =10,AC =6,则线段CD 的长是( )A.4B.3C.2D.18. 下列基本几何体中,从正面、上面、左面观察都是相同图形的是( )圆柱 A三棱柱 B球 C长方体 D第7题图D A BC二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中横线上) 9.如图,∠α=120o,∠β=90 o. 则∠γ的度数是.10.125 ÷4= __ _________’.11.数a 、b 在数轴上的位置如图所示,化简b a b -+=____________.Oab12.如果a -b =3,ab =-1,则代数式3ab -a +b -2的值是_________.13.有一个正方体,A ,B ,C 的对面分别是z y x ,,三个字母,如图所示,将这个正方体从现有位置依此翻到第1,2,3,4,5,6格, 当正方体翻到第3格时正方体 向上一面的字母是 . 14. 用“●”“■”“▲”分别表示三种不同的物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■” 个.三、探究题(本题4分,每空1分,把答案填在题中横线上)15.有若干个数,第1个数记为1a ,第二个数记为2a ,第三个数记为3a ……,第n 个记为n a ,若211-=a ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。
北京石景山区2013-2014学年第一学期初三化学期末卷附答案

石景山区2014期末H 1 C 12 N 14 O 16 Na 23 Cl 35.5 Ca 40一、选择题1.空气中含量较多且性质比较活泼的气体是A.氧气B.氮气C.二氧化碳D.水蒸气2.生活中发生的下列变化,属于化学变化的是A.冰雪融化B.蜡烛燃烧C.苹果榨汁D.玻璃破碎3.决定元素种类的是A.质子数B.中子数C.核外电子数D.最外层电子数4.黑火药是我国古代四大发明之一,由硝酸钾、硫磺、木炭组成。
黑火药属于A.纯净物B.化合物C.氧化物D.混合物5.人处于紧张状态时,维生素的消耗会增加,为了补充维生素,考试期间应多吃A.馒头B.蔬菜C.白糖D.油脂6.下列物质中,不是碳的单质的是A.金刚石B.石墨C.C60D.CO7.你能闻到苹果散发出的香味,由此可以说明的是A.分子之间有间隔B.分子可以分成原子C.分子在不断地运动D.分子的质量和体积都很小8.下列安全措施不正确...的是A.在加油站内不吸烟、不打电话B.冬天用煤火取暖时注意室内通风C.用燃着的木条检查天然气是否泄漏D.燃放烟花爆竹时,远离人群和可燃物9.氧化钙可作干燥剂,其俗称为A.生石灰B.熟石灰C.石灰石D.大理石10.ClO2是一种新型、高效的消毒剂,其中氯元素的化合价为A.﹣2 B.﹣1 C.﹢2 D.﹢411.下列二氧化碳的用途中,不正确...的是A.冶炼金属B.用作气体肥料C.固体可作制冷剂D.生产碳酸饮料12.下列物质的化学式书写正确的是A.氯化铁FeCl2 B.氧化镁MgO2C.硫酸铜CuSO4 D.氯化铝AlCl 13.下列物质中,含有氧分子的是A.空气B.二氧化碳C.二氧化硫D.过氧化氢14.下列实验操作中,正确的是A .点燃酒精灯B .读取液体体积C .倾倒液体药品D .加热液体15.下列有关碳和碳的氧化物说法中,不正确...的是 A .用碳素墨水填写档案,是因为碳单质常温下化学性质稳定 B .CO 和CO 2都有毒,都是大气污染物C .二氧化碳能灭火是因为二氧化碳不燃烧、不支持燃烧且密度比空气大D .金刚石、石墨物理性质差异很大是因为它们的结构中碳原子的排列方式不同16.已知一种碳原子可用于测定文物的年代,该原子的原子核内含有6个质子和8个中子,则核外电子数为 A .2 B .6 C .8 D .1417.下列反应中,属于分解反应的是A .2Mg + CO 点燃C + 2MgO B .CO 2 + H 2O === H 2CO 3C .NaOH + HCl === NaCl + H 2OD .CaCO 高温CaO + CO 2 ↑18根据上表所给信息和所学相关知识判断,下列说法不正确...的是A .白磷、红磷、铁粉、砂糖都是可燃物B .降低可燃物的着火点可以达到灭火的目的C .相同条件下,铁粉比砂糖更易点燃D .通常情况下,红磷燃烧需要与氧气接触、温度达到240℃或以上19.地壳中含有丰富的氧、硅、铝、铁等元素。
2013-2014高三英语期末试卷(石景山答案)

石景山区2013 —2014学年度第一学期高三期末测试卷英语参考答案第一部分听力理解(共三节,30分)1-5: BCACB 6-10:ACCBA 11-15:CABAB16. Stevenson 17. assistant 18. 8263544 19. February 20. desk(注:人名没有大写不得分, 月份没有大写扣0.5分,)第二部分知识运用(共两节,45分)第一节单项填空(共15小题;每小题1分,共15分)21-25: BCADA 26-30:DACBB 31-35:ABCDD第二节完形填空(共20小题;每小题1.5分,共30分)36-40: BCBDA 41-45: CBDAB 46-50: CDADC 51-55: BACBD第三部分阅读理解(共两节,40分)第一节(共15小题;每小题2分,共30分)56-60: BADAC 61-65: DCDAC 66-70: DABBC第二节(共5小题;每小题2分,共10分)71-75:GBADF第四部分;书面表达(共两节,35分)第一节应用文写作(15分)(一) 评分原则:1.本题总分为15分,按4个档次给分。
2.评分时,先根据文章的内容和语言质量初步确定其档次,然后以该档次的要求来衡量,确定或调整档次,最后给分。
3.评分时应考虑:文章是否扣题,结构是否完整,内容是否充实、健康,思维是否活跃,逻辑是否清晰,语言是否规范,交际是否得体。
4.拼写、标点符号或书写影响内容表达时,应视其影响程度予以考虑。
英、美拼写词汇用法均可接受。
5.词数少于50,从总分中减去1分。
(二)各档次的给分范围和要求:(三)One possible version:Dear Principal,Recently, many students are discussing the problems of the canteen. Some students think the prices of dishes are too expensive and the choices of the dishes are too limited. Another concern is that the time spent on waiting is so long that we have less time to have a rest. Meanwhile, some students argue that the taste of the food is awful which leads to a lot of waste.Therefore, measures need to be taken to improve the conditions of the canteen. In my own point of view, I pay more attention to the prices of the food and the time wasted in the queue. I think we can offer various choices with different prices and open more service windows to reduce waiting time.I sincerely hope you can adopt my suggestions. Thank you!Yours,Li Hua 第二节情景作文(20分)(一) 评分原则:1.本题总分为20分,按5个挡次给分。
2013-2014初三化学期末参考答案

石景山区2013—2014学年第一学期期末考试初 三 化 学 试 卷 参 考 答 案二、填空题(共5个小题,共29分。
) 26.(5分)(1)A B (2)蛋白质 (3)Ca 贫血 (4)水和氧气 27.(5分)(1)天然气 (2)太阳能(或风能、地热能) (3)ACD (4)4H 2 12:3:8 28.(6分)(1)2N 2Na +(2)①②(3)BCD (4)① HCl ② 14 29.(6分)(1)水分子本身是否发生变化 (2)① 2H 2 O直流电2H 2↑+ O 2↑ ② 化学反应前后,原子种类、数目、质量都不变(3)① 遵守 ② 甲中碳酸钠和稀盐酸反应有气体生成,使瓶内压强增大;乙中二氧 化碳和澄清石灰水反应,使瓶内压强减小 (2分) 30.(7分) (1)3Fe + 2O 2 点燃Fe 3O 4(2)CO C + 2CuO高温2Cu + CO 2↑(3)H 2O 、Ca(OH)2 、CaCO 3 (2分)CaO + H 2O = Ca(OH)2 CO 2 + Ca(OH)2 = CaCO 3↓+ H 2O三、实验题(共3个小题,共20分。
) 31.(6分)(1)集气瓶 (2)B 2KMnO△K 2MnO 4 + MnO 2 + O 2↑(3)D CaCO 3 + 2HCl = CaCl 2 + H 2O + CO 2↑ (4)向反应后的集气瓶中倒入少量澄清石灰水,振荡32.(6分)(1)加热,使白磷达到着火点;将烧杯中的白磷隔绝氧气热水中的白磷在通入氧气前、后是否燃烧 (2)2H 2 + O 2点燃2H 2O点燃气体,在火焰上方罩一个干、冷的烧杯,一会儿烧杯内壁出现无色液体;迅速把烧杯倒过来,向烧杯内注入少量澄清石灰水,振荡,澄清石灰水变浑浊 (3)4P + 5O 2 点燃2P 2O 5 红磷量不足;装置漏气;未冷却即打开弹簧夹33.(8分)(1)① 将带火星的木条放在最右端集气瓶的口部,木条复燃,证明氧气已满② 澄清石灰水未变浑浊(2)【猜想与假设】1和2 两种反应物中均无氢元素【进行实验】加入适量的稀盐酸,并将生成的气体导入澄清石灰水中 3 【反思与评价】不同意。
【VIP专享】石景山2013-2014学年第一学期初三期末物理试题及答案(最新修订)

则滑动变阻器连入电路的接线柱应是
A.A 和 C
6.下面关于四冲程汽油机的说法正确的是
B.A 和 B
A.四冲程汽油机是利用机械能转化成内能的机器
B.四冲程汽油机在压缩冲程中,内能转化为机械能
C.四冲程汽油机在做功冲程中,内能转化为机械能
D.四冲程汽油机的四个冲程依次为吸气、做功、压缩、排气
7.图 3 所示的电路图中,各元件均完好,开关都闭合后,只一个灯泡发光的电路为
A.2.1×105J
B. 4.2×104J
C.1.68×105J
S L2
S2 L1
S1 A
8.下列说法中正确的是
A.电路两端有电压,电路中就会有电流
L2
L1
B
S
S1
图3
C.B 和 D
L1
石景山 2014.1 初三物理试卷第 1 页 (共 10 页)
S
S1 L2
C
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列察读 、虫生出蚯材 让标容生常3根蚓料 学本教活.见了 据身: 生,师的2的、解 问体巩鸟 总看活形线作 用蛔 题的固类 结雌动态形业 手虫 自形练与 本雄学、三动: 摸对 学状习人 节蛔生结、4物、收 一人 后和同类 课虫活构请一并蚯集 摸体 回颜步关 重的动、学、归蚓鸟 蚯的 答色学系 点形教生生让纳在类 蚓危 问。习从 并状学理列学线平的害 题蚯四线人 归、意特出四生形面生 体以蚓、形类 纳大图点常、五观动玻存 表及的鸟请动文 本小引以见引、察物璃现 ,预身类 3学物明 节有言及的导 、巩蚯的上状 是防体之生和历 课什根蚯环学 怎固蚓主和, 干感是所列环史 学么据蚓节二生 样练引要牛鸟 燥染否以举节揭 到不上适动、回 区习导特皮类 还的分分蚯动晓 的同节于物让答 分。学征纸减 是方节布蚓物起 一,课穴并学课 蚯生。上少 湿法?广的教, 些体所居归在生前 蚓回4运的 润;泛益学鸟色生纳.靠物完问 的答蛔动原 的4,处目类 习和活环.近在成题 前蚯虫的因 ?了以。标就 生体的节身其实并 端蚓寄快及 触解上知同 物表内特动体结验总 和的生利慢我 摸蚯适识人 学有容点物前构并结 后生在用一国 蚯蚓于与类 的什,的端中思线 端活人问样的 蚓飞技有 基么引进主的的考形 ?环体题吗十生行能着 本特出要几变以动境,?大 节活的1密 方征本“特节化下物.并会让为珍 近习形理切 法。课生征有以问的引小学什稀 腹性态解的 。2课物。什游题主.出起结生么鸟 面和结蛔关观题体么戏:要蚯哪利明?类 处适构虫系察:的特的特蚓些用确等 ,于特适。蛔章形殊形征这疾板,资 是穴点于可虫我态结式。种病书生料 光居是寄的们结构,五典?小物, 滑生重生鸟内学构,学、型5结的以 还活要生类部习与.其习巩的如鸟结爱 是的原活生结了功颜消固线何类构鸟 粗形因的存构腔能色化练形预适特护 糙态之结的,肠相是系习动防于点鸟 ?、一构现你动适否统。物蛔飞都为结。和状认物应与的。虫行是主构课生却为和”其结病的与题、本理不蛔扁的他构?特环以生8特乐虫形观部特8三征境小理页点观的动位点、梳相组等这;,哪物教相,引理适为方些2鸟,育同师.导知应单面鸟掌类结了;?生学识的位你握日构解2互.生。办特认线益特了通动观手征识形减点它过,察抄;吗动少是们理生蛔报5?物,与的解.参虫一了它和有寄主蛔与结份解们环些生要虫其构。蚯都节已生特对中。爱蚓会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的为要濒的课情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;的3.情通况过,了给解出蚯课蚓课与题人。类回的答关:系线,形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设;置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
2013-2014学年北京市石景山区八年级上学期期末数学试卷(含答案)

石景山区2013—2014学年第一学期期末考试试卷初二数学一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项前的字母填在题后括号内) 1.16的算术根是( ).A .4B .4-C .4±D .8±2x 的取值范围是( ). A .1x >B .1x ≥C .1x ≥且32x ≠D . 1x >且32x ≠ 3.下列图形不是..轴对称图形的是( ). A .线段 B .等腰三角形C .角D .有一个内角为60°的直角三角形 4.下列事件中是不可能事件的是( ).A .随机抛掷一枚硬币,正面向上.B .a 是实数,a =-.C .长为1cm ,2cm ,3cm 的三条线段为边长的三角形是直角三角形.D .小明从古城出发乘坐地铁一号线去西单图书大厦.5. 初二年级通过学生日常德育积分评比,选出6位获“阳光少年”称号的同学.年级组长李老师将6份奖品分别放在6个完全相同的不透明礼盒中,准备将它们奖给小君等6位同学.这些奖品中3份是学习文具,2份是体育用品,1份是科技馆通票.小君同学从中随机取一份奖品,恰好取到体育用品的可能性是( ).A.16 B .13C. 12D. 236.有一个角是︒36的等腰三角形,其它两个角的度数是( ).A. ︒︒108,36B .︒︒72,36 C. ︒︒72,72D.︒︒108,36或︒︒72,727.下列四个算式正确的是( ).AB .C =D .8.如图,在△ABC 中,BE 、CE 分别是∠ABC 和∠ACB 的平分线,过点E 作DF ∥BC 交AB 于D ,交AC 于F ,若AB =4, AC =3,则△ADF 周长为( ).9.如图,滑雪爱好者小明在海拔约为121米的B 处乘雪橇沿30°的斜坡下滑至A 处所用时间为2秒,已知下滑路程S (米)与所用时间t (秒)的关系为210S t t =+,则山脚A 处的海拔约为( ). (其中3 1.7≈)A . 100.6米B . 97米C .109米D .145米10.如图,在△ABC 中,AB =AC =5,BC =6,AD 是BC 边上的中线,点E 、F 、M 、N 是AD 上的四点,则图中阴影部分的总面积是( ).A .6B .8C .4D .12二、填空题(本大题共6个小题,每小题4分,共24分,把答案填在题中横线上)11.约分:22515mn m n-=_____________. 12.若整数p 满足:⎪⎩⎪⎨⎧-<<.12,72p p p 则p 的值为_________.13. 若分式55q q -+值为0,则q 的值是________________.14.如图,在正方形网格 (图中每个小正方形的边长均为1)中,△ABC 的三个顶点均在格点上,则△ABC 的周长为 _________________,面积为____________________. 15.如图,在Rt △ABC 中,∠C =90°,AC= BC ,将其绕点A 逆时针旋转15°得到Rt △''AB C ,''B C 交AB 于E ,若 图中阴影部分面积为23,则'B E 的长为 . 16.在Rt △ABC 中,∠C =90°,BC =8cm ,AC=4cm ,在射. 线.BC 上一动点D ,从点B 出发,以5厘米每秒的速度匀速运动,若点D 运动t 秒时,以A 、D 、B 为顶点的三 角形恰为等腰三角形,则所用时间t 为 秒. (结果可含根号). 三、解答题(本大题共4个小题,每小题5分,共20分)17.计算:()213.144832π-⎛⎫------ ⎪⎝⎭.解:CAB第14题 A DB C EFM NDF E AB C 第8题 第9题 第10题A BEC'AC B第15题15°18.解方程:238111x x x +-=--. 解:19.计算:1124(38)8---. 解:20.先化简,再求值已知:23x y =,求222569222y x xy y x y x y x y ⎛⎫-+--÷⎪--⎝⎭的值. 解:四、列方程解应用题(本题5分)21. 据报道,2013年11月8日超强台风“海燕”在菲律宾中部萨马省登陆,给菲律宾造成巨大经济财产损失.中国政府伸出援助之手,捐款捐物.某地决定向灾区捐助帐篷.记者采访了某帐篷制造厂如何出色完成任务.下面是记者与工厂厂长的一段对话:根据记者与厂长的一段对话,请求出原计划每天加工多少顶帐篷. 解: 你好,你们是如何提前4天完成1500顶帐篷生产任务的? 加工了300顶帐篷后,由于救灾紧急需要,我厂将工作效率提高到原计划的2倍.五、解答题(本大题共3个小题,每题5分共15分)22.已知:如图,E 、F 为BC 上的点,BF=CE ,点A 、D 分别在BC 的两侧,且AE ∥DF ,AE =DF . 求证:AB =DC . 证明:23. 已知:如图,△ABC 是等边三角形. D 、E 是△ABC 外两点,连结BE 交AC 于M ,连结AD 交CE 于N ,AD 交BE 于F ,AD =EB . 当AFB ∠度数多少时,△ECD 是等边三角形?并证明你的结论. 解:当AFB ∠=__________时,△ECD 是等边三角形. 证明:24. 已知:在△ABC 中,24=AB ,5AC =,oABC 45=∠,求BC 的长.解:B六、几何探究(本题6分)25.如图1,在△ABC 中,∠ACB =2∠B ,∠BAC 的平分线AO 交BC 于点D ,点H 为AO 上一动点,过点H 作直线l ⊥AO 于H ,分别交直线AB 、AC 、BC 、于点N 、E 、M . (1)当直线l 经过点C 时(如图2),求证:BN =CD ;(2)当M 是BC 中点时,写出CE 和CD 之间的等量关系,并加以证明; (3)请直接写出BN 、CE 、CD 之间的等量关系.(1)证明:(2)当M 是BC 中点时,CE 和CD 之间的等量关系为_________________________. 证明:图1图2B(3)请你探究线段BN 、CE 、CD 之间的等量关系, 并直接写出结论.七、选作题26. 如图,在△ABC 中,AB =AC ,108A ∠=°,请你在图中,分别用两种不同方法,将△ABC 分割成四个小三角形,使得其中两个是全等..的不等边三角形......(不等边三角形指除等腰三角形以外),而另外两个是不全等...的等腰三角形.请画出分割线段,并在两个全等三角形中标出一对相等的内角的度数,在每个等腰三角形中标出相等两底角度数(画图工具不限,不要求证明,不要求写出画法,但要保留作图痕迹,若经过图形变换后两个图形重合,则视为同一种方法).图1图2B B石景山区2013-2014学年度第一学期期末考试初二数学答案及评分参考阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.二、填空题(本题共6道小题,每小题4分,共24分)11.3nm-; 12.3; 13.5; 14.36;(各2分) 15.2; 16答对一个2分,答对两个3分,答对3个4分)三、解答题(本题共4个小题,每小题5分,共20分)17. 解:原式=14-- ………………………………………………………4分 =3--………………………………………………………………5分 18. 解:2(3)(1)81xx x ++-=-…………………………………………………1分224381x x x ++-=-…………………………………………………2分44x = (3)分1x = ………………………………………………………4分经检验:1x =是原方程的增根,所以原方程无解 ……………………………5分 19. 解:原式 …………………………………………3分…………………………………………4分 ……………………………………………………5分20. 解:原式=()()()22225213x y x y y x yx y +-⎡⎤-⨯⎢⎥--⎣⎦…………………………………………1分=()()()()22522223y x y x y x y x y x y -+--⋅-- = ()22293y x x y -- …………………………………………………………………2分=33y xy x +- ……………………………………………………………………3分 解法一:∵23x y =,不妨设()2,30x k y k k ==≠ …………………………………4分∴原式=9292k k k k +- =117 ………………………………………5分解法二:3333x y x y xy x y++=-- ………………………………………4分∵23x y = ∴原式=231132733+=- ………………………………………5分 (阅卷说明:如果学生直接将2,3x y ==代入计算正确者,本题扣1分)四、列方程解应用题(本题5分)21. 解:设原计划每天加工x 顶帐篷. ……………………………………………………1分1500300150030042x x---= …………………………………………………2分 解得 150x = ………………………………………………………………3分 经检验,150x =是原方程的解,且符合题意. ………………………………4分答:原计划每天加工150顶帐篷.……………………………………………………5分 五、解答题(本大题共3个小题,每题5分,共15分) 22.证明:∵AE ∥DF ,∴∠AEB =∠DFC . …………………………………………………………1分 ∵BF =CE , ∴BF +EF =CE +EF .即BE =CF . …………………………2分在△ABE 和△DCF 中,AE DF AEB DFC BE CF =⎧⎪∠=∠⎨⎪=⎩………………………………………………………3分 ∴△ABE ≌△DCF ………………………………………………………4分 ∴AB =DC ………………………………………………………5分23. 解:AFB ∠=60° ………………………………………………………………1分 证明:∵△ABC 是等边三角形∴CA =CB ,4∠=60° …………………………………………………………2分 ∵∠2+∠4=∠5∠1+∠3=∠5 且∠3=60° ∴∠1=∠2 ……………… ………………3分又∵BE =AD ∴△BCE ≌△ACD (SAS ) ∴CE =CD ,∠BCE =∠ACD 4分 ∴∠BCE -∠6=∠ACD -∠6 即∠4=∠7=60°∴△ECD 是等边三角形 ………………………………………………5分 B(1)如图,过A 作AD ⊥BC 交BC (延长线)于D ,………………………1分 ∴∠D =90°, ∴在Rt △ABD 中,∠B +∠BAD =90°, ∴∠BAD =45° ∴DA DB =,又∵222AB DB DA =+,不妨设x DB DA ==则3222=+x x ,解得4=x ,∴DA =DB =4 ……………………………2分 ∵∠D =90°,∴在Rt △ACD 中,222AC DA DC =+3452222=-=-=AD AC CD ……………………………3分∴BC =BD -CD =4-3=1 ……………………………4分 (2)如图:由(1)同理:DB =4,CD =3 ∴BC =BD +CD =4+3=7.综上所述:BC =1或BC =7 ……………………………5分 (阅卷说明:只计算出一种情况,本题得4分) 六、几何探究(本题6分) 25. (1)证明:连结ND∵AO 平分BAC ∠,∴12∠=∠ ∵直线l ⊥AO 于H , ∴4590∠=∠=︒ ∴67∠=∠ ∴AN AC =∴NH CH =∴AH 是线段NC 的中垂线 ∴DC DN = ∴98∠=∠∴AND ACB ∠=∠∵3AND B ∠=∠+∠,2ACB B ∠=∠, ∴3∠=∠B ∴DN BN =∴BN DC = ……………………………………………………………………2分 (2)当M BC 是中点时,CE 和CD 之间的等量关系为2CD CE =证明:过点C 作'CN AO ⊥交AB 于'N由(1)可得'BN CD =,',AN AC AN AE == ∴43∠=∠,'NN CE =过点C 作CG ∥AB 交直线l 于点G ∴42∠=∠,1B ∠=∠ ∴23∠=∠∴CG CE = ∵M BC 是中点, ∴BM CM =在△BNM 和△CGM 中, 1,,,B BM CM NMB GMC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BNM ≌△CGM ∴BN CG =D C 'C B A∴BN CE =∴''2CD BN NN BN CE ==+= …………………………………………4分 (3)BN 、CE 、CD 之间的等量关系:当点M 在线段BC 上时,CD BN CE =+; 当点M 在BC 的延长线上时,CD BN CE =-;当点M 在CB 的延长线上时,CD CE BN =-………………………………6分 (阅卷说明:三种情况写对一个给1分,全对给2分)七、选作题 26.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
石景山区2013—2014学年第一学期期末考试答案
高三生物
一、选择题:(每题只有一个选项符合要求。
共20题,每题1分,共20分)
1-5 BCADC 6-10 CCCDA 11-15DACDB 16-20DCDAA
二、选择题(每题只有一个选项符合要求。
共10题,每题2分,共20分)
21-25 CBCCC 26-30 DBCDD
三、非选择题(除标注外,每空1分,共60分)
31.(8分)
(1)[2]中染色体形态稳定、数目清晰染色体和纺锤体
(2)5、8、10(或答5、8、6、10也给分)发出星射线,形成纺锤体
(3)识别运输蛋白功能多样性
32.(8分)
(1)CO2浓度影响了碳反应的进程(或碳反应慢于光反应)
(2)27.3(2分)
(3)小于
(4)①高温、强光照对玉米光合作用影响不大
②不可行
通过2、4组相互对照只能得出两种植物在高温、强光照下光合速率的差异;(1分)缺乏自身对照,不能得出该条件分别对两种植物光合速率影响程度的大小(1分)
33.(9分)
(1)7.6kb 中部(含控制溶原生长)
(2)限制酶和DNA连接酶之中溶菌
(3)S 蛋白质外壳不进入细菌中
(4)氨基酸和脱氧核苷酸上清液
34.(8分)
(1)甲和丁 全是正常翅
(2)甲和乙 卷曲翅:正常翅=2:1
(3)AaX B X b 1/3
(4)红色 红色或白色
35.(6分)
(1)B细胞 抗利尿激素
(2)促进肾小管和集合管对水分的重吸收
(3)无
(4)分泌淋巴因子刺激(或促进)乙细胞(即B 淋巴细胞)增殖分化
(5)增加(或升高)
36.(7分)
(1)不变 基因频率
(2)建立自然保护区(或就地保护) 减少 竞争
(3)K 2 Ⅰ
37.(7分) (1) (3分)
(2)自我调节 负反馈调节(或反馈调节)
(3)垂直
(4)调整能量流动的关系(方向)
38.(7分)
(1)将原始敏感菌种涂布到含有链霉素的培养基中进行选择培养,生长出的菌落即为抗链霉素
的大肠杆菌(2分)
(2)质粒
(3)选择作用 发生抗药性突变的大肠杆菌数量少(其他答案合理给分)
(4)大肠杆菌(微生物)的抗药性突变是自发产生的。
12号试管中的抗药性细菌(最终获得的抗药性细菌)始终没有接触链霉素
(其他答案合理给分)
光合作用 植物 大气中CO
2 呼吸作用 动物 大气中CO 2 呼吸作用。
