08 立体图形上的最短路径问题
勾股定理立体图形中最短路径

勾股定理应用——最短路径问题
学习目标:1.认识平面图形和立体图形的关系,会图形间的互相转化。
2.能在平面图形中构建勾股定理模型解决实际问题。
一、尝试练习、联系生活
1.两点之间,最短!
2.一个圆柱体的侧面展开图是,它的一边长是圆柱的,
它的另一边长是圆柱的.
二、合作交流、探究新知
例1:如图所示,圆柱体的底面周长为6cm,高AC为4cm,一只蚂蚁从A点出发,沿着圆柱的侧面爬行到点B,试求出爬行的最短路程.
三、变式训练、拓展延伸
变式1:有一圆柱形油罐,油罐底面周长是12米,高AB是5米,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?
变式2:如果圆柱换成棱长为1cm的正方体盒子,蚂蚁沿着表面从A点爬行到B 点需要的最短路程又是多少呢?
变式3:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
四、方法迁移、自我检测
1、如果盒子换成长为40cm,宽为30cm,高为120cm的金鱼缸,如果鱼缸中的A 点有一条金鱼,它想尽快吃到B点的食物,那么金鱼游的最短路程又是多少呢?
2、如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A 和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少?。
立体图中的最短路

变一变:若将立方体改为长方体,长为6宽为4,高 为3,则蚂蚁沿长方体的表面行的问题;如图,圆锥
的底面半径为1,母线长为4,一只蚂蚁从圆锥底面圆周上 一点A出发,要沿着圆锥的侧面爬过一圈到达母线PA的中 点B,问蚂蚁爬行的最短路程是多少?
若蚂蚁沿着圆锥的侧面爬过一圈重新回到A处,则爬 行的最短路程是多少?
小结: 数学思想:转化思想 依据:两点之间线段最短 策略:利用几何体的侧面或表面展开图
立体图中的最短路线
溪口初中
陆志军
作业本; “转化”是一种重要的数学思想,将空间问题转化为平面问题是转化思 想的一个重要方面.例如如图(1),一个立方体的棱长为1.有一只蚂 蚁从A点出发沿着立方体的表面爬行到G点,沿怎样的路线爬行路程 最短?要解决这个问题,我们可以把立方体展开(如图2,3)把空 间两个面上的A,G之间的最短路线问题转化为同一个面上两点之间 距离的问题,根据“两点之间线段最短”,可知蚂蚁应沿线段AG爬 行.最短路程为
练一练:圆锥的底面半径为1,母线长为3,一只蚂蚁 从圆锥底面圆周上一点A出发,要沿着圆锥的侧面爬 到对面的母线PC中点B,问蚂蚁爬行的最短路程是多 少?
议一议:如图,一圆柱的底面周长为24cm,高AB 为4cm,BC是直径,一只蚂蚁从A点出发沿着圆柱 体侧面爬行到C点的最短路程大约是( )
A .6 cm B.12 cm C.13cm D. 16cm
想一想:如图,一只蚂蚁欲从圆柱形的桶外点A爬到桶内点 B,去寻找食物,已知点A到桶口的距离AC为12cm,点B到 桶口的距离BD为8cm,弧CD的长为15cm,问蚂蚁的爬行 的最短路线是多少?
想一想:如图,一只蚂蚁欲从圆柱形的桶外点A爬到桶内点 B,去寻找食物,已知点A到桶口的距离AC为12cm,点B到 桶口的距离BD为8cm,弧CD的长为15cm,问蚂蚁的爬行 的最短路线是多少?
立体图形中的最短路径问题

128教育版■文/师:3cm 处吃食物,生:方体:是利用转化思想,转化成平面问题;2.方法:(1)展开;(2)运用两点之间线段最短找到最短路径;(3)运用勾股定理解决问题;3.思想:转化思想;建模思想;分类讨论思想。
三、结尾:举一反三,过关训练。
四、教学反思:本节微课是学生通过自主学习,以获得解决问题经验和培养实践能力的课程。
它可以弥补数学学科实践能力的不足,加强实践环节,重视数学思维的训练,促进学生兴趣、个性、特长等自主和谐的发展,从而全面提高学生的数学素质。
(单位:临江市宝山中学)知识点描述:《数鸭子》是一首颇具说唱风格、形象生动、活泼有趣的童谣歌曲。
歌词描述了小朋友看到鸭群游过大桥、兴奋地数鸭子的情景。
歌曲前后皆有数板,说唱结合,表现出儿童活泼可爱的天性,童趣盎然。
教学目标:1.知识:在歌曲学唱过程中,认识四分休止符,并能准确地运用;2.过程:能随音乐用轻巧活泼的声音表情演唱《数鸭子》,能积极主动、自信有表情地参与表演,从中感受乐趣;3.情感:通过歌曲《数鸭子》的教学,让学生与同伴之间友好相处,保护小动物。
适用对象:小学一年级学生。
设计思路:我本着推行教学民主的理念,从主宰变为主导,发挥学生主体作用,形成良好的合作关系。
从全面提高学生素质出发,为学生创造良好的教学氛围。
在教学方法上变繁为简,变被动为主动,做到既能促进学生智能最大限度地发展,又不加重学生负担,特别在情感上使学生的学习积极性得到激发,让每个学生享受到成功的快乐。
教学过程:一、片头(30秒以内) 大家好,我是吉林省临江市宝山中学教师吴宛姗,我带来的课程是人民音乐出版社出版,义务教育教科书音乐,一年级下册第三课手拉手,歌曲《数鸭子》。
17秒。
二、正文讲解 (8分钟左右)(一)发声练习:12345 555 小鸡怎样叫叽叽叽,小鸭怎样叫嘎嘎嘎,小猫怎样叫喵喵喵。
9分钟;(二)新课讲授:1.出示课题,欣赏歌曲播放《数鸭子》,感受音乐节奏和情绪。
立体图形中的距离最短问题
立体图形中的距离最短问题根据新课程标准,培养学生的空间观念主要表现在:“能由实物的形状想像出几何图形,由几何图形想像出实物的形状,进行几何体与其三视图、展开图之间的转化;能根据条件做出立体模型或画出图形;……”。
空间图形的建立需要有一个循序渐进的过程,从小学到初中,再到高中,渐渐加强,作为一个初、高中的知识衔接模块,让学生在初中阶段能理解空间图形,特别是空间图形的展开图,夯实基础,显得尤为重要。
立体图形上点点之间的距离最短问题,通过把立体图形转化为平面图形,然后再运用“两点之间,线段最短”来解决。
解决这一类距离最短的问题,可以利用轴对称或平移或旋转等几何图形的变换,把两条或多条线段和最短的问题转化为平面上两点之间的距离最短的问题来解决。
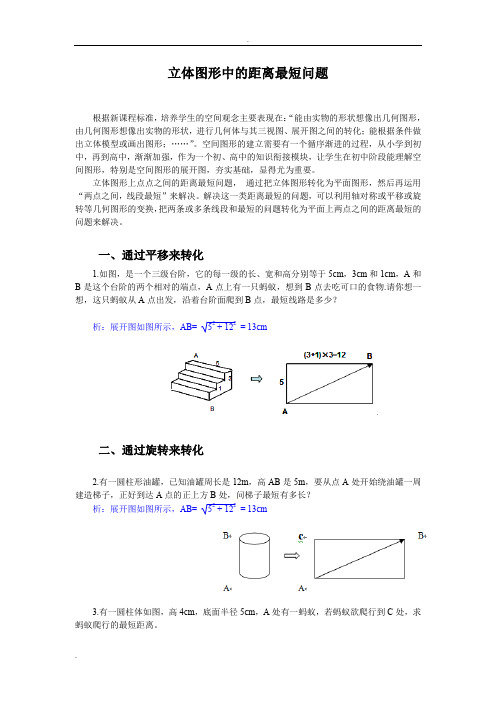
一、通过平移来转化1.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?析:展开图如图所示,AB= 52 + 122= 13cm二、通过旋转来转化2.有一圆柱形油罐,已知油罐周长是12m,高AB是5m,要从点A处开始绕油罐一周建造梯子,正好到达A点的正上方B处,问梯子最短有多长?析:展开图如图所示,AB= 52 + 122= 13cm3.有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离。
AB = 4,BC 为底面周长的一半 即BC = 5πAC = AB 2 + BC 2 = 42 + (5π)2= 16 + 25π24.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线--螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm ,绕一圈升高(即圆柱的高)40cm ,则它爬行一圈的路程是多少?(2)如果树干的周长为80cm ,绕一圈爬行100cm ,它爬行10圈到达树顶,则树干高多少?(1)如图,⊙O 的周长为30cm ,即AC=30cm , 高是40cm ,则BC=40cm ,由勾股定理得AB =50cm . 故爬行一圈的路程是50cm ;(2)⊙O 的周长为80cm ,即AC=80cm ,绕一圈爬行100cm ,则AB = 100cm ,高BC = 60cm .∴树干高=60×10=600cm=6m . 故树干高6m5.已知O 为圆锥顶点,OA 、OB 为圆锥的母线,C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A ,另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线的痕迹如右图所示.若沿OA 剪开,则得到的圆锥侧面展开图为 ( )要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线.A .B .C .D .故选C6.如图,一直圆锥的母线长为QA=8,底面圆的半径r=2,若一只小蚂蚁从A点出发,绕圆锥的侧面爬行一周后又回到A点,则蚂蚁爬行的最短路线长是______(结果保留根式)。
立体图形中的最短线问题

立体图形中的最短线问题立体图形中的最短线问题,大都直接来源于生活.这类问题集知识性、实践性和趣味性于一“题”,因而倍受中考命题者的青睐.在近几年考题中频频出现,现选取几例分析如下,供同学们参考.一、长方体上的最最短线问题例1:如图1是一个长8m 、宽6m 、高5m 的仓库,在其内壁的A (长的四等份点)处有一只壁虎,B (宽的三等份点)处有一只蚊子,则壁虎爬到蚊子处的最短距离为 m .分析与解:壁虎从A 处爬到B 处,所有可能最短路径有三种:①→③;②→③;①→④.(1)从①→③,展开使A 、B 两点同在一个平面内,如图2—①所示,由题意知AC =10m ,BC =5m .由勾股定理222BC AC AB +=,得5551022=+=AB (m ); (2)从②→③,展开使A 、B 两点同在一个平面内,如图2—②所示,由题意知AC =11m ,BC =4m .由勾股定理222BC AC AB +=,得13741122=+=AB (m ); (3)从①→④,展开使A 、B 两点同在一个平面内,如图2—③所示,由题意知AC =6m ,BC =9 m .由勾股定理222BC AC AB +=,得1339622=+=AB (m ).综合上述(1)、(2)、(3)可得,壁虎爬到蚊子处的最短距离为133 m .B图2—② A C图1—③二、正方体上的最短线问题例2:如图2,一个无盖的正方体盒子的棱长为10cm ,顶点C 1处有一只昆虫甲,在盒子的内部顶点A 处有一只昆虫乙.(盒壁的厚度忽略不计) 1(1)假设昆虫甲在顶点C 1处静止不动,如图3,在盒 子的内部我们先取棱BB 1中点E ,再连结AE 、E C 1,昆虫 乙如果沿路径A →E →C 1爬行,那么可以在最短的时间内捕 捉到昆虫甲.仔细体会其中的道理,并在图3中画出另一条 路径,使昆虫乙从顶点A 沿这条路径爬行,同样可以在最短 AB 的时间内捕捉到昆虫甲;(2)假设昆虫甲从顶点C 1以1 cm∕s 的速度在盒子的 图2内部沿棱C 1C 向下爬行,同时昆虫乙从顶点A 以2 cm∕s 的速度在盒壁上爬行,那么昆虫乙至少需要多少时间才能捕捉到昆虫甲?(精确到1s )解:(1)可取DD 1中点E 1,DC 中点E 2,BC 中点E 3,将这些中点与A 和C 1相连,则A →E i →C 1(i=1,2,3)均为所求的路径,见图3.(2)所有可能费时最短的路径有如图四种:可以看出,图3—①与图3—②中的路径相等,图3—③与图3—④中的路径相等. 1F F图3—① 图3—②D 1 C 1F D C F C 1D CA B B 1A B图3—③ 图3—④设昆虫甲从顶点C 1沿棱C 1C 向F 爬行的同时,昆虫乙从顶点A 按路径A →E 1→F 爬行捕捉到昆虫甲需x s .如图3—①,在RtΔACF 中,22220)10()2(+-=x x ,解得x =10;设昆虫甲从顶点C 1沿棱C 1C 向顶点C 爬行的同时,昆虫乙从顶点A 按路径A →E 2→F 爬行捕捉到昆虫甲需y s .如图3—③,在RtΔABF 中,22210)20()2(+-=x y ,解得8≈y .∴昆虫乙顶点A 爬行捕捉到昆虫甲需8 s .四、圆柱体上的最短线问题例4:如图4,一个蚂蚁要从树干(看做圆柱)底面的A 点沿表面爬到与A 点相对的B 点,已知从A 点到B 点升高了3米,树干底面的半径为1.27米,这只蚂蚁爬行的最短路程是(精确到1米,π取3.14) ( )A .4米B .5米C .6米D . 6.5 米A A 图4—①分析与解:圆柱的侧面展开图为矩形,如图4—①所示.连结AB ,则A 、B 两点之间的最短距离就是A B 的长.由题意知BC =3米,AC =1.27π米,由勾股定理222BC AC AB +=,得53)271(22≈+=⋅πAB 米.故选B .五、圆锥体上的最短线问题例5:如图5,有一圆锥形粮堆,其正视图是边长为6米.的正三角形A BC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时,小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路线是 米.(结果不取近似值)APC B图5 图5—①分析与解:圆锥的侧面展开图为扇形,如图5—①所示.连结B P ,则B 、P 两点之间的最短距离就是BP 的长.由已知条件可得圆锥的侧面积为18π米2,∴2618360n π⨯=π,解得n =180º,则∠BAP =90º,又AB =6米,AP =3米,由勾股定理得53=BP 米.从以上几例可以看出,解决立体图形中的最短线问题的主要思想是:把立体图形平面化;具体方法是:把立体图形的侧面展开,根据“两点之间线段最短”,利用勾股定理,直接求出平面上两点之间的距离.。
3.3勾股定理的应用举例——立体图形中最短路径问题

归●纳5:、圆柱答展开转化为平面图形,利用两点之间
线段最短找到最短路径,然后运用勾股定理求
解。圆柱体的展开图是一个长方形,但需要注
意展开后点的位置的确定。
变式训练:最短路径问题——圆柱
1、有一圆柱形糖罐, 底面周长是12厘米,高AB是5厘米,蚂蚁从
BC
=
16
×
1 2
= 8,
由勾股定理得
AB2= AC2+ BC2=1100
∴AB=10(m) .
最短路径问题——长方体
如图:长方体的长、宽、高分别是12,8,30,在 AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去 吃,有无数种走法,则最短路程是( )
A.15
B.25
C.35
D.45
最短路径问题——长方体 例3.如图是一块长,宽,高分别是 4cm,2cm和1cm的长方体木块一只 蚂蚁要从长方体木块的一个顶点A 处,沿着长方体的表面到长方体上 和A相对的顶点B处吃糖,那么它需 要爬行的最短路径的长是(B )
因为每个面的 大小相同,展 开后长方形的 长宽不变,所 以结果相同。
ቤተ መጻሕፍቲ ባይዱ
无论什么立方体,都必须通过展开后得到平面图形,利用两点 之间线段最短得到最短的距离,再运用勾股定理求出结果。
课堂总结:
知识:立体图形中的最短路径问题
转化
方法:1、展开; 平面图形
2、找起点、终点 3、运用两点之间线段最短找到最短路径; 4、运用勾股定计算。 5、答
勾股定理的应用 立体图形中最短路径问题
立体图形中的最短路径
最短路径问题——圆柱
B
例1、有一个圆柱,它 我怎 的高为12cm,底面半径为 么走
人教版八下数学 第17章 勾股定理 微专题三 立体图形中的最短线路问题

人教版八下数学第17章勾股定理微专题三立体图形中的最短线路问题1.如图,圆柱的底面半径为6cm,高为10cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米(结果保留小数点后一位)?2.如图,圆柱的底面周长是14cm,圆柱高为24cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为( )A.14cm B.15cm C.24cm D.25cm3.如图,透明的圆柱形容器(容器厚度忽路不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且在离容器上部3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路程是( )A.13cm B.2√61cm C.√61cm D.2√34cm4.如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A.13cm B.12cm C.10cm D.8cm5.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是尺.6.如图①,圆柱的底面半径为4cm,圆柱高AB为2cm,BC是底面直径,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:路线1:高线AB+底面直径BC,如图①所示,设长度为l1.路线2:侧面展开图中的线段AC,如图②所示,设长度为l2.请按照小明的思路补充下面解题过程:(1) 解:l1=AB+BC=2+8=10,l2=√AB2+BC2=√22+(4π)2=√4+16π2;∵l12−l22=.(2) 小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为2cm,高AB为4cm”继续按前面的路线进行计算.(结果保留π)①此时,路线1:l1=;路线2:l2=.②选择哪条路线较短?试说明理由.答案1. 【答案】答图略,将圆柱展开,侧面为矩形,∴AB=√(6π)2+102≈21.3(cm).答:蚂蚁从点A爬到点B的最短路程约是21.3cm.2. 【答案】D3. 【答案】A4. 【答案】A5. 【答案】256. 【答案】(1) 96−16π2(2) ① 8;2√4+π2② ∵l12−l22=82−(16+4π2)=48−4π2=4(12−π2)>0.∴l12>l22,即l1>l2.所以选择路线2较短.【解析】(1) l1=AB+BC=2+8=10,l2=√AB2+BC2=√22+(4π)2=√4+16π2,∵l12−l22=102−(4+16π2)=96−16π2=16(6−π2)<0,∴l12<l22,即l1<l2,所以选择路线1较短.。
立体图形与路径最短问题

A
最短路径:
AB
h r
2 2
2
情况二解决
B
如图,展开上底面,沿 AB爬行是此种情况的最短 路径. 最短路径为:h+2r
A
B
比较与总结
比较
2
h r
2 2 2 2
2
和 h+2r的大小
h r
=h+2r
h
2
4 r 4
当h
2
当h
当h
2
4 r时,沿侧面爬行路径最 短 4
①
②
③
④
⑤
⑥
⑦
⑧
⑨
相对的两个面不是 ⑩ 11 相间,就是 Z的两端
问题情境一
在棱长为1的立方体
的左下角A处有一只蚂蚁,
欲从立方体的外表面爬行
B
去吃右上角B处的食物,
问怎样爬行路径最短,最
短路径是多少?它有几种
爬行方法?(注:除下面 A 外,每一个面均能爬行)
知识准备
1、什么是线段公理?
两点之间,线段最短
2
4 r时,两种路径情况一样 4
4 r时,沿A向上再沿上底直径爬行 最短 4
因此最短路径为侧面爬行的 4
2
是否所有的情况下都是侧面爬行路径最短吗? 高和底面半径换一些数据试一试.
延伸问题
在底面半径为r、 高为h的圆柱体的左 下角A处有一只蚂 蚁,欲爬行去吃右
B
上角B处的食物,问
怎样爬行路径最短, 最短路径是多少?
A
情况一
从A点向上剪开,则侧面展开图如图所示, 连接AB,则AB为爬行的最短路径.
A B
最短路径是多少?
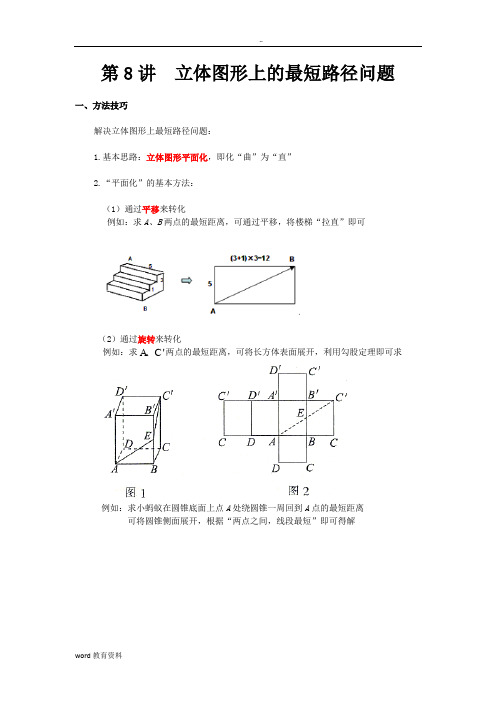
立体图形上的最短路径问题
第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1.基本思路:立体图形平面化,即化“曲”为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4.解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,13AB cm ==所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C ’处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC ’(在面ADD ’A ’上爬行是一样的).将四棱柱剪开铺平使矩形AA ’B ’B 与BB ’C ’C 相连,连接AC ’,使E 点在AC ’上(如图2))(412810')('2222cm CC BC AB AC =+=++= 所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可.试题解析:解:如下图所示,把圆柱的半侧面展开成矩形,点S ,F 各自所在的母线为矩形的一组对边上下底面圆的半周长为矩形的另一组对边.该矩形上的线段SF 即为所求的最短路线. 过点S 作点F 所在母线的垂线,得到SEF Rt ∆.34SF cm ==【难度】较易【例题4】(2015·红河期末)如下图,有一圆锥形粮堆,其主视图是边长为6m 的正三角形ABC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路程是__________m (结果不取近似值)【答案】【解析】试题分析:求小猫经过的最短距离,首先应将其侧面展开,将问题转化为平面上两点间的距离的问题,根据展开图中扇形的弧长与圆锥底面周长相等可求展开图的扇形圆心角度数,故可得出展开图中90BAP ∠=︒,即可用勾股定理求出小猫经过的最短距离BP 长.试题解析:解:作出圆锥侧面展开后的扇形图如下图,设该扇形的圆心角度数为n , 由展开扇形圆弧长等于底面圆周长,可得180n AC BC ππ⋅=⋅, 再由6AC BC m ==,可得180n =︒, 故在展开的平面图形中,1180902BAC ∠=⨯︒=︒点B 到P 的最短距离为 )BP m ===【难度】一般类型三 通过轴对称来转化【例题5】桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A 处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B 处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在位置?【答案】15厘米【解析】试题分析:把圆柱展开,得到矩形形状,A B 、的最短距离就是线段'BA 的长,根据勾股定理解答即可 试题解析:解:如图所示,作A 点关于杯口的对称点'A则'15BA ==厘米【难度】较易三、实战演练类型一 通过平移来转化1.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm 、3dm 、2dm .A 和B 是这个台阶上两个相对的端点,点A 处有一只蚂蚁,想到点B 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B 的最短路程为 dm .【答案】25dm【解析】试题分析:先将图形平面展开,再根据勾股定理进行解答试题解析:解:如图,三级台阶平面展开图为长方形,长为20dm ,宽为(2+3)×3dm ,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B 点最短路程为xdm ,由勾股定理可得x 2=202+[(2+3)×3]2,解得x =25.即蚂蚁沿着台阶面爬行到点B 的最短路程为25dm .【难度】较易类型二 通过旋转来转化2.(2015·陕西)有一个圆柱形油罐,已知油罐周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周造梯子,正好到达A 点的正上方B 处,问梯子最短有多长?【答案】13m【解析】试题分析:把圆柱沿AB 侧面展开,连接AB ,再根据勾股定理得出结论试题解析:解:展开图如图所示,12AC m =,5BC m =13AB m ===【难度】较易3.有一个圆柱体,如图,高4cm ,底面半径5cm ,A 处有一小蚂蚁,若蚂蚁欲爬行到C 处蚂蚁爬行的最短距离 .)cm【解析】试题分析:圆柱展开就是一个长方形,根据两点之间线段最短可求试题解析:解:∵4AB =,BC 为底面周长的一半,即5BC π=∴)AC cm ===【难度】较易4.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线-螺旋前进的,难道植物也懂得数学? 阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm ,绕一圈升高(即圆柱的高)40cm ,则它爬行一周的路程是多少?(2)如果树干的周长是80cm ,绕一圈爬行100cm ,它爬行10圈到达树顶,则树干高多少?【答案】(1)50cm ;(2)6m【解析】试题分析:(1)如下图,将圆柱展开,可知底面圆周长,即为AC 的长,圆柱的高即为BC 的长,求出AB 的长即为葛藤树的最短路程(2)先根据勾股定理求出绕行1圈的高度,再求出绕行10圈的高度,即为树干高 试题解析:解:(1)如图,O 的周长为30cm ,即AC =30cm高是40cm ,则BC =40cm ,由勾股定理得50AB cm ==故爬行一周的路程是50cm(2)O 的周长为80cm ,即AC =80cm绕一圈爬行100cm ,则AB=100cm ,高BC =60cm∴树干高=60×10=600cm =6m故树干高6m【难度】一般5.(2015·江阴市)如图,一个无盖的正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从盒外的B 点沿正方形的表面爬到盒内的M 点,蚂蚁爬行的最短距离是 ( )A B C .1 D .2+【答案】B【解析】试题分析:根据已知得出蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是如图BM的长度,进而利用勾股定理求出试题解析:解:∵蚂蚁从盒外的B点沿正方体的表面爬到盒内的M点∴蚂蚁爬行的最短距离是如图BM的长度∵无盖的正方体盒子的棱长为2,BC的中点为M∴1224A B=+=11A M=∴BM=故选:B【难度】较易6.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示,若沿OA剪开,则得到的圆锥侧面展开图为()【答案】C【解析】试题分析:要求小蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线. 试题解析:解:∵C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A∴侧面展开图BO 为扇形对称轴,连接AC 即是最短路线∵另一只小蚂蚁绕着圆锥侧面爬行到点B ,作出C 关于OA 的对称点,再利用扇形对称性得出关于BO 的另一对称点,连接即可.故选C【难度】一般7.(2014·枣庄)图①所示的正方体木块棱长为6cm ,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A 爬行到顶点B 的最短距离为 cm .【答案】(cm【解析】试题分析:要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果试题解析:解:如答图,易知△BCD 是等腰直角三角形,△ACD 是等边三角形,在Rt △BCD 中,CD ==,∴12BE CD ==,在Rt △ACE 中,AE ==,∴从顶点A 爬行到顶点B 的最短距离为(cm【难度】一般8.一个圆锥的母线长为QA =8,底面圆的半径r =2,若一只小蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到A 点,则蚂蚁爬行的最短路线长是________(结果保留根式)【答案】【解析】解:设圆锥的展开图扇形’QAA 的中心角'AQA ∠的度数为n ,则 822180n ππ⨯⨯⨯=,解得:90n = 即'90AQA ∠=在'Rt AQA 中,根据勾股定理'AA =【难度】一般9.如图,圆锥的主视图是等边三角形,圆锥的底面半径为2cm ,假若点B 有一只蚂蚁只能沿圆锥的表面爬行,它要想吃到母线AC 的中点P 处的食物,那么它爬行的最短路程是多少?【答案】【解析】试题分析:根据圆锥的主视图是等边三角形可知,展开图是半径是4的半圆,点B 是半圆的一个端点,而点P 是平分半圆的半径的中点,根据勾股定理就可求出两点B 和P 在展开图中的距离,就是这只蚂蚁爬行的最短距离试题解析:解:设圆锥的展开图的圆心角为n , 则422180n ππ⨯⨯⨯=, 解得:180n =︒ 即'180CAC ∠=︒在展开图中,'BA CC ⊥,4BA =,2AP =由勾股定理得,BP =点评:本题主要考查了圆锥的侧面展开图的计算,正确判断蚂蚁爬行的路线,把曲面的问题化为平面的问题是解题的关键【难度】较难10.(1)如图○1,一个无盖的长方体盒子的棱长分别为3BC cm =,4AB cm =,15AA cm =,盒子的内部顶点1C 处有一只昆虫甲,在盒子的内部顶点A 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点1C 处静止不动,请计算A 处的昆虫乙沿盒子内壁爬行到昆虫甲1C 处的最短路程,并画出其最短路径,简要说明画法(2)如果(1)问中的长方体的棱长分别为6AB BC cm ==,114AA cm =,如图○2,假 设昆虫甲从盒内顶点1C 以1厘米/秒的速度在盒子的内部沿棱1C C 向下爬行,同时昆虫乙从盒内顶点A 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕 捉到昆虫甲?【答案】(1)1A E C →→就是最短路径 (2)5秒【解析】解:(1)如图二,将上表面展开,使上表面与前表面在同一平面内,即11A A D 、、三点共线,111538AA A D +=+= 114D C =根据勾股定理得1AC =如图三,将右侧面展开,使右侧面与下面在同一平面内,即1A B B 、、三点共线1459AB BB +=+=,113B C =根据勾股定理得1AC =如图四,将右侧面展开,使右侧面与前表面在同一平面内,即A B C 、、三点共线. 437AB BC +=+=,15CC =根据勾股定理得1AC.在图四中,∵1ABE ACC ∽ ∴1BE AB CC AC= ∴457BE =,207BE =如图一,在1BB 上取一点E ,使207BE =,连接AE ,1EC ,1A E C →→就是最短路径 (2)如图五,设1C F x =,则3AF x =,5CF x =-在Rt ACF 中,根据勾股定理得222AF AC CF =+即:()()()22236614x x =++-解得:15x =,2172x =- ∵0x >∴5x =所以,昆虫至少需要5秒才能捉到昆虫甲.点评:在长方体中,经过它的表面,从一个顶点到另一个与它相对的顶点的最短距离是:在 长、宽、高中,以较短的两条边的和作为一条直角边,最长的边作为另一条直角边,斜边即 为最短路线长【难度】较难11.如图,A 是高为10cm 的圆柱底面圆上一点,一只蜗牛从A 点出发,沿30°角绕圆柱侧面爬行,当他爬到顶上时,他沿圆柱侧面爬行的最短距离是( )A. 10cmB. 20cmC. 30cmD. 40cm【答案】B试题分析:将圆柱侧面展开,连接AB ,根据三角函数求出AB 的长即可试题解析:解:根据题意得,10BC cm =,30BAC ∠=︒ ∴13010202A BC Sin cmB =÷︒=÷= 故选B .【难度】一般12.如图,是一个长4m ,宽3m ,高2m 的有盖仓库,在其内壁的A 处(长的四等分)有一只壁虎,B 处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为( )A .4.8B .5 D 【答案】C【解析】有两种展开方法:①长方体展开成如图所示,连接A B 、,②将长方体展开成如图所示,连接A B 、【难度】较易13.(2015-2016·内蒙古包头)如图,长方体的长为15 cm,宽为10 cm,高为20cm,点B 距离C点5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是cm.【答案】25【解析】试题分析:要求正方体中两点之间的最短路径,最直接的作法就是将正方体展开,然后利用两点之间线段最短解答.试题解析:解:如图:(1(2(3所以需要爬行的最短距离是25.【难度】较难14.已知:如图,一个玻璃材质的长方体,其中6,4,8===BF BC AB ,在顶点E 处有一块爆米花残渣,一只蚂蚁从侧面BCSF 的中心沿长方体表面爬行到点E .则此蚂蚁爬行的最短距离为 .【解析】试题分析:要求蚂蚁爬行的最短距离,需要将立体图形转化为平面图形,将E 、O (设面BCSF 的中心为点O )所在的两个面展开,但展开图并非只有一种,而是两种,需要利用“两点之间,线段最短”,来一一求出线段EO 的长度,然后比较两种情况的结果,找出最短路径试题解析:解:设面BCSF 的中心为点O ,根据题意,最短路径有下列两种情况:○1如图1,沿SF 把长方体的侧面展开,蚂蚁爬行的最短距离==○2如图2,沿BF 把长方体的侧面展开,蚂蚁爬行的最短距离==∵【难度】较难15.如图,圆柱形容器中,高为1.2m ,底面周长为1m ,在容器内壁..离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁..,离容器上沿0.3m 与蚊子相对..的点A 处,则壁虎捕捉蚊子的最短距离为 m (容器厚度忽略不计).【答案】1.3m【解析】试题分析:将容器侧面展开,建立A 关于EF 的对称点A ’,根据两点之间线段最短可知A ’B 的长度即为所求试题解析:解:要求壁虎捉蚊子的最短距离,实际上是求在EC 上找一点P ,使PA+PB 最短, 过点A 作EC 的对称点A ’,连结A ’B ,则A ’B 与EF 的交点P 就是所求的点P因为两点之间,线段最短,A ’B 的长即为壁虎捕捉蚊子的最短距离∵底面周长为1m∴'0.5A D m =, 1.2BD m =' 1.3A B m =【难度】一般类型三 通过轴对称来转化16.一只蚂蚁欲从圆柱形桶外的A 点爬到桶内的B 点处寻找食物,已知点A 到桶口的距离AC 为12cm ,点B 到桶口的距离BD 为8cm ,CD 的长为15cm ,那么蚂蚁爬行的最短路程是多少?【答案】25cm【解析】试题分析:如图,作点B 关于CD 的对称点B ’,连结AB ’, 交CD 于点P ,连结PB ,则最短路线应该 是沿AP 、PB ’ 即可试题解析:解:如下图所示,作点B 关于CD 的对称点'B ,连结'AB ,交CD 于点P ,则蚂蚁的爬 行路线'A P B →→ 为最短,且'AP PB AP PB +=+在'Rt AEB 中,15AE CD ==,''=12820EB ED DB AC BD =++=+=由勾股定理知 '25AB =所以,蚂蚁爬行的最短路程是25cm【难度】一般。
立体图形与路径最短问题.PPT资料39页

问题情境一
在棱长为1的立方体 的右下角A处有一只蚂蚁,
B
欲从立方体的外表面爬行
去吃右上角B处的食物,
问怎样爬行路径最短,最
短路径是多少?它有几种
爬行方法?(注:每一个
面均能爬行)
A
知识准备
1、什么是线段公理? 两点之间,线段最短
2、勾股定理 在Rt△ABC中,两直角边为a、b,斜边为c,则 a2+b2=c2.
角B处的食物,问怎样爬
行路径最短,最短路径是 4
多少?
3
A5
思维分析
1、长方体和立方体的情况一样吗?它们有什么 相同和不同点呢?
和A相连的面是左面、前面和下面; 和B相连的面是上面、右面和后面. 共有六种不同的选择路径
这六种不同选择的路径大小相同吗?
思维方法和过程
前面
后面
A点 左面
右面
B点
下面
上面
B
路径.
最短路径为:4
A
比较选择最短路径
两个最短路径 4 2 和4哪一个最小呢?
比较大小: 4 2 4
因此最短路径为侧面爬行的 4 2
是否所有的情况下都是侧面爬行路径最短吗? 高和底面半径换一些数据试一试.
延伸问题五
在底面半径为r、高
为h的圆柱体的左下角A
处有一只蚂蚁,欲爬行去
A
则AB6为最短路径 由勾股定理得
AB6= 2212 5
B6
总结
B 从A到B共有六种最短路径
最短路径为 5
A
问题情境二
在底面半径为1、高
为2的圆柱体的左下角A
处有一只蚂蚁,欲从圆柱
B
体的侧面爬行去吃右上角
立体图形中的距离最短问题

立体图形中的距离最短问题根据新课程标准,培养学生的空间观念主要表现在:“能由实物的形状想像出几何图形,由几何图形想像出实物的形状,进行几何体与其三视图、展开图之间的转化;能根据条件做出立体模型或画出图形;……”。
空间图形的建立需要有一个循序渐进的过程,从小学到初中,再到高中,渐渐加强,作为一个初、高中的知识衔接模块,让学生在初中阶段能理解空间图形,特别是空间图形的展开图,夯实基础,显得尤为重要。
立体图形上点点之间的距离最短问题,通过把立体图形转化为平面图形,然后再运用“两点之间,线段最短”来解决。
解决这一类距离最短的问题,可以利用轴对称或平移或旋转等几何图形的变换,把两条或多条线段和最短的问题转化为平面上两点之间的距离最短的问题来解决。
一、通过平移来转化1.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?析:展开图如图所示,AB= 52 + 122= 13cm二、通过旋转来转化2.有一圆柱形油罐,已知油罐周长是12m,高AB是5m,要从点A处开始绕油罐一周建造梯子,正好到达A点的正上方B处,问梯子最短有多长?析:展开图如图所示,AB= 52 + 122= 13cm3.有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离。
AB = 4,BC为底面周长的一半即BC = 5πAC = AB2 + BC2=42 + (5π)2= 16 + 25π24.藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线--螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?(2)如果树干的周长为80cm,绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?(1)如图,⊙O的周长为30cm,即AC=30cm,高是40cm,则BC=40cm,由勾股定理得AB =50cm.故爬行一圈的路程是50cm;(2)⊙O的周长为80cm,即AC=80cm,绕一圈爬行100cm,则AB = 100cm,高BC = 60cm.∴树干高=60×10=600cm=6m.故树干高6m5.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示.若沿OA剪开,则得到的圆锥侧面展开图为()B CBACAA.B.C.D.要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线. 故选C6.如图,一直圆锥的母线长为QA=8,底面圆的半径r=2,若一只小蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到A 点,则蚂蚁爬行的最短路线长是______(结果保留根式)。
08 立体图形上的最短路径问题
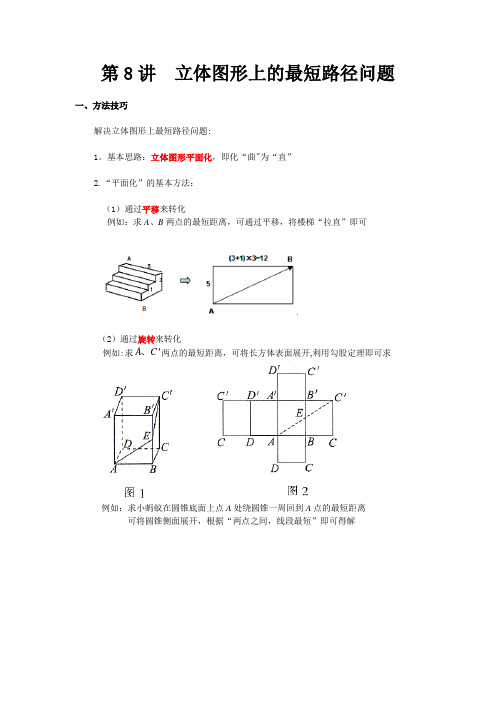
第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1。
基本思路:立体图形平面化,即化“曲"为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4。
解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,2251213AB cm =+=所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C'处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC'(在面ADD'A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与BB’C’C 相连,连接AC’,使E 点在AC'上(如图2))(412810')('2222cm CC BC AB AC =+=++=所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1.基本思路:立体图形平面化,即化“曲”为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4.解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,13AB cm ==所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C’处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC’(在面ADD’A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与BB’C’C 相连,连接AC’,使E 点在AC’上(如图2))(412810')('2222cm CC BC AB AC =+=++= 所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可.试题解析:解:如下图所示,把圆柱的半侧面展开成矩形,点S ,F 各自所在的母线为矩形的一组对边上下底面圆的半周长为矩形的另一组对边.该矩形上的线段SF 即为所求的最短路线. 过点S 作点F 所在母线的垂线,得到SEF Rt ∆.34SF cm ==【难度】较易【例题4】(2015·红河期末)如下图,有一圆锥形粮堆,其主视图是边长为6m 的正三角形ABC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路程是__________m (结果不取近似值)【答案】【解析】试题分析:求小猫经过的最短距离,首先应将其侧面展开,将问题转化为平面上两点间的距离的问题,根据展开图中扇形的弧长与圆锥底面周长相等可求展开图的扇形圆心角度数,故可得出展开图中90BAP ∠=︒,即可用勾股定理求出小猫经过的最短距离BP 长.试题解析:解:作出圆锥侧面展开后的扇形图如下图,设该扇形的圆心角度数为n , 由展开扇形圆弧长等于底面圆周长,可得180n AC BC ππ⋅=⋅, 再由6AC BC m ==,可得180n =︒, 故在展开的平面图形中,1180902BAC ∠=⨯︒=︒点B 到P 的最短距离为 )BP m ===【难度】一般类型三 通过轴对称来转化【例题5】桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A 处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B 处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在位置?【答案】15厘米【解析】试题分析:把圆柱展开,得到矩形形状,A B 、的最短距离就是线段'BA 的长,根据勾股定理解答即可 试题解析:解:如图所示,作A 点关于杯口的对称点'A则'15BA ==厘米【难度】较易三、实战演练类型一 通过平移来转化1.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm 、3dm 、2dm .A 和B 是这个台阶上两个相对的端点,点A 处有一只蚂蚁,想到点B 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B 的最短路程为 dm .【答案】25dm【解析】试题分析:先将图形平面展开,再根据勾股定理进行解答试题解析:解:如图,三级台阶平面展开图为长方形,长为20dm ,宽为(2+3)×3dm ,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B 点最短路程为xdm ,由勾股定理可得x 2=202+[(2+3)×3]2,解得x =25.即蚂蚁沿着台阶面爬行到点B 的最短路程为25dm .【难度】较易类型二 通过旋转来转化2.(2015·陕西)有一个圆柱形油罐,已知油罐周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周造梯子,正好到达A 点的正上方B 处,问梯子最短有多长?【答案】13m【解析】试题分析:把圆柱沿AB 侧面展开,连接AB ,再根据勾股定理得出结论试题解析:解:展开图如图所示,12AC m =,5BC m =13AB m ===【难度】较易3.有一个圆柱体,如图,高4cm ,底面半径5cm ,A 处有一小蚂蚁,若蚂蚁欲爬行到C 处蚂蚁爬行的最短距离 .)cm【解析】试题分析:圆柱展开就是一个长方形,根据两点之间线段最短可求试题解析:解:∵4AB =,BC 为底面周长的一半,即5BC π=∴)AC cm ===【难度】较易4.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线-螺旋前进的,难道植物也懂得数学? 阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm ,绕一圈升高(即圆柱的高)40cm ,则它爬行一周的路程是多少?(2)如果树干的周长是80cm ,绕一圈爬行100cm ,它爬行10圈到达树顶,则树干高多少?【答案】(1)50cm ;(2)6m【解析】试题分析:(1)如下图,将圆柱展开,可知底面圆周长,即为AC 的长,圆柱的高即为BC 的长,求出AB 的长即为葛藤树的最短路程(2)先根据勾股定理求出绕行1圈的高度,再求出绕行10圈的高度,即为树干高 试题解析:解:(1)如图,O 的周长为30cm ,即AC =30cm高是40cm ,则BC =40cm ,由勾股定理得50AB cm ==故爬行一周的路程是50cm(2)O 的周长为80cm ,即AC =80cm绕一圈爬行100cm ,则AB=100cm ,高BC =60cm∴树干高=60×10=600cm =6m故树干高6m【难度】一般5.(2015·江阴市)如图,一个无盖的正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从盒外的B 点沿正方形的表面爬到盒内的M 点,蚂蚁爬行的最短距离是 ( )A B C .1 D .2+【答案】B【解析】试题分析:根据已知得出蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是如图BM的长度,进而利用勾股定理求出试题解析:解:∵蚂蚁从盒外的B点沿正方体的表面爬到盒内的M点∴蚂蚁爬行的最短距离是如图BM的长度∵无盖的正方体盒子的棱长为2,BC的中点为M∴1224A B=+=11A M=∴BM=故选:B【难度】较易6.已知O为圆锥顶点,OA、OB为圆锥的母线,C为OB中点,一只小蚂蚁从点C开始沿圆锥侧面爬行到点A,另一只小蚂蚁绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示,若沿OA剪开,则得到的圆锥侧面展开图为()【答案】C【解析】试题分析:要求小蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B ,它们所爬行的最短路线. 试题解析:解:∵C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A∴侧面展开图BO 为扇形对称轴,连接AC 即是最短路线∵另一只小蚂蚁绕着圆锥侧面爬行到点B ,作出C 关于OA 的对称点,再利用扇形对称性得出关于BO 的另一对称点,连接即可.故选C【难度】一般7.(2014·枣庄)图①所示的正方体木块棱长为6cm ,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A 爬行到顶点B 的最短距离为 cm .【答案】(cm【解析】试题分析:要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果试题解析:解:如答图,易知△BCD 是等腰直角三角形,△ACD 是等边三角形,在Rt △BCD 中,CD ==,∴12BE CD ==,在Rt △ACE 中,AE ==,∴从顶点A 爬行到顶点B 的最短距离为(cm【难度】一般8.一个圆锥的母线长为QA =8,底面圆的半径r =2,若一只小蚂蚁从A 点出发,绕圆锥的侧面爬行一周后又回到A 点,则蚂蚁爬行的最短路线长是________(结果保留根式)【答案】【解析】解:设圆锥的展开图扇形’QAA 的中心角'AQA ∠的度数为n ,则 822180n ππ⨯⨯⨯=,解得:90n = 即'90AQA ∠=在'Rt AQA 中,根据勾股定理'AA =【难度】一般9.如图,圆锥的主视图是等边三角形,圆锥的底面半径为2cm ,假若点B 有一只蚂蚁只能沿圆锥的表面爬行,它要想吃到母线AC 的中点P 处的食物,那么它爬行的最短路程是多少?【答案】【解析】试题分析:根据圆锥的主视图是等边三角形可知,展开图是半径是4的半圆,点B 是半圆的一个端点,而点P 是平分半圆的半径的中点,根据勾股定理就可求出两点B 和P 在展开图中的距离,就是这只蚂蚁爬行的最短距离试题解析:解:设圆锥的展开图的圆心角为n , 则422180n ππ⨯⨯⨯=, 解得:180n =︒ 即'180CAC ∠=︒在展开图中,'BA CC ⊥,4BA =,2AP =由勾股定理得,BP =点评:本题主要考查了圆锥的侧面展开图的计算,正确判断蚂蚁爬行的路线,把曲面的问题化为平面的问题是解题的关键【难度】较难10.(1)如图○1,一个无盖的长方体盒子的棱长分别为3BC cm =,4AB cm =,15AA cm =,盒子的内部顶点1C 处有一只昆虫甲,在盒子的内部顶点A 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点1C 处静止不动,请计算A 处的昆虫乙沿盒子内壁爬行到昆虫甲1C 处的最短路程,并画出其最短路径,简要说明画法(2)如果(1)问中的长方体的棱长分别为6AB BC cm ==,114AA cm =,如图○2,假 设昆虫甲从盒内顶点1C 以1厘米/秒的速度在盒子的内部沿棱1C C 向下爬行,同时昆虫乙从 盒内顶点A 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕 捉到昆虫甲?【答案】(1)1A E C →→就是最短路径 (2)5秒【解析】解:(1)如图二,将上表面展开,使上表面与前表面在同一平面内,即11A A D 、、三点共线,111538AA A D +=+= 114D C =根据勾股定理得1AC =如图三,将右侧面展开,使右侧面与下面在同一平面内,即1A B B 、、三点共线 1459AB BB +=+=,113B C =根据勾股定理得1AC =如图四,将右侧面展开,使右侧面与前表面在同一平面内,即A B C 、、三点共线. 437AB BC +=+=,15CC =根据勾股定理得1AC.在图四中,∵1ABE ACC ∽ ∴1BE AB CC AC= ∴457BE =,207BE =如图一,在1BB 上取一点E ,使207BE =,连接AE ,1EC ,1A E C →→就是最短路径 (2)如图五,设1C F x =,则3AF x =,5CF x =-在Rt ACF 中,根据勾股定理得222AF AC CF =+即:()()()22236614x x =++-解得:15x =,2172x =- ∵0x >∴5x =所以,昆虫至少需要5秒才能捉到昆虫甲.点评:在长方体中,经过它的表面,从一个顶点到另一个与它相对的顶点的最短距离是:在 长、宽、高中,以较短的两条边的和作为一条直角边,最长的边作为另一条直角边,斜边即 为最短路线长【难度】较难11.如图,A 是高为10cm 的圆柱底面圆上一点,一只蜗牛从A 点出发,沿30°角绕圆柱侧面爬行,当他爬到顶上时,他沿圆柱侧面爬行的最短距离是( )A. 10cmB. 20cmC. 30cmD. 40cm【答案】B试题分析:将圆柱侧面展开,连接AB ,根据三角函数求出AB 的长即可试题解析:解:根据题意得,10BC cm =,30BAC ∠=︒ ∴13010202A BC Sin cmB =÷︒=÷= 故选B .【难度】一般12.如图,是一个长4m ,宽3m ,高2m 的有盖仓库,在其内壁的A 处(长的四等分)有一只壁虎,B 处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为( )A .4.8B .5 D【答案】C【解析】有两种展开方法:①长方体展开成如图所示,连接A B 、,②将长方体展开成如图所示,连接A B 、【难度】较易13.(2015-2016·内蒙古包头)如图,长方体的长为15 cm,宽为10 cm,高为20 cm,点B 距离C点5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是cm.【答案】25【解析】试题分析:要求正方体中两点之间的最短路径,最直接的作法就是将正方体展开,然后利用两点之间线段最短解答.试题解析:解:如图:(1(2(3所以需要爬行的最短距离是25.【难度】较难14.已知:如图,一个玻璃材质的长方体,其中6,4,8===BF BC AB ,在顶点E 处有一块爆米花残渣,一只蚂蚁从侧面BCSF 的中心沿长方体表面爬行到点E .则此蚂蚁爬行的最短距离为 .【解析】试题分析:要求蚂蚁爬行的最短距离,需要将立体图形转化为平面图形,将E 、O (设面BCSF 的中心为点O )所在的两个面展开,但展开图并非只有一种,而是两种,需要利用“两点之间,线段最短”,来一一求出线段EO 的长度,然后比较两种情况的结果,找出最短路径 试题解析:解:设面BCSF 的中心为点O ,根据题意,最短路径有下列两种情况:○1如图1,沿SF 把长方体的侧面展开,蚂蚁爬行的最短距离==○2如图2,沿BF 把长方体的侧面展开,蚂蚁爬行的最短距离==∵【难度】较难15.如图,圆柱形容器中,高为1.2m ,底面周长为1m ,在容器内壁..离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁..,离容器上沿0.3m 与蚊子相对..的点A 处,则壁虎捕捉蚊子的最短距离为 m (容器厚度忽略不计).【答案】1.3m【解析】试题分析:将容器侧面展开,建立A 关于EF 的对称点A’,根据两点之间线段最短可知A ’B 的长度即为所求试题解析:解:要求壁虎捉蚊子的最短距离,实际上是求在EC 上找一点P ,使P A+PB 最短, 过点A 作EC 的对称点A ’,连结A ’B ,则A ’B 与EF 的交点P 就是所求的点P因为两点之间,线段最短,A’B 的长即为壁虎捕捉蚊子的最短距离∵底面周长为1m∴'0.5A D m =, 1.2BD m =' 1.3A B m =【难度】一般类型三 通过轴对称来转化16.一只蚂蚁欲从圆柱形桶外的A 点爬到桶内的B 点处寻找食物,已知点A 到桶口的距离AC 为12cm ,点B 到桶口的距离BD 为8cm ,CD 的长为15cm ,那么蚂蚁爬行的最短路程是多少?【答案】25cm【解析】试题分析:如图,作点B 关于CD 的对称点B’,连结AB ’, 交CD 于点P ,连结PB ,则最短路线应该 是沿AP 、PB ’ 即可试题解析:解:如下图所示,作点B 关于CD 的对称点'B ,连结'AB ,交CD 于点P ,则蚂蚁的爬 行路线'A P B →→ 为最短,且'AP PB AP PB +=+在'Rt AEB 中,15AE CD ==,''=12820EB ED DB AC BD =++=+=由勾股定理知 '25AB =所以,蚂蚁爬行的最短路程是25cm【难度】一般。
