数值分析插值算法源程序
数值分析插值法

数值分析插值法插值法是数值分析中的一种方法,用于通过已知数据点的函数值来估计介于这些数据点之间的未知函数值。
插值法在科学计算、数据处理、图像处理等领域中得到广泛应用。
插值法的基本思想是通过已知数据点构造一个函数,使得该函数逼近未知函数,并在已知数据点处与未知函数值相等。
插值法的关键是选择适当的插值函数,以保证估计值在插值区间内具有良好的近似性质。
常用的插值法有拉格朗日插值法、牛顿插值法和埃尔米特插值法等。
以下将分别介绍这些插值法的原理及步骤:1. 拉格朗日插值法:拉格朗日插值法通过构造一个多项式函数来逼近未知函数。
假设已知n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn),其中x0, x1, ..., xn为给定的节点,y0, y1, ..., yn为对应的函数值。
拉格朗日插值多项式的一般形式为:L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中l0(x), l1(x), ..., ln(x)为拉格朗日基函数,定义为:li(x) = (x - x0)(x - x1)...(x - xi-1)(x - xi+1)...(x - xn) / (xi - x0)(xi - x1)...(xi - xi-1)(xi - xi+1)...(xi - xn)拉格朗日插值法的步骤为:a. 计算基函数li(xi)的值。
b.构造插值多项式L(x)。
c.计算L(x)在需要估计的插值点上的函数值f(x)。
2.牛顿插值法:牛顿插值法通过构造一个差商表来逼近未知函数。
差商表的第一列为已知数据点的函数值,第二列为相邻数据点的差商,第三列为相邻差商的差商,以此类推。
最终,根据差商表中的数值,构造一个差商表与未知函数值相等的多项式函数。
牛顿插值法的步骤为:a.计算差商表的第一列。
b.计算差商表的其他列,直至最后一列。
c.根据差商表构造插值多项式N(x)。
数值分析第五章插值法

数值分析第五章插值法插值法是数值分析中常用的一种数值逼近方法,它的目的是通过已知数据点之间的插值多项式来逼近未知数据点的函数值。
插值法可以在信号处理、图像处理、计算机图形学等领域中广泛应用。
在插值法中,最常用的方法有拉格朗日插值法和牛顿插值法。
拉格朗日插值法是一种利用拉格朗日插值多项式来逼近函数的方法。
对于n个已知数据点(xi, yi),拉格朗日插值多项式L(x)可以表示为:L(x) = ∑(yi * li(x))其中,li(x)表示拉格朗日基函数,定义为:li(x) = ∏[(x - xj)/(xi - xj)] (j≠i)可以证明,在给定的n个数据点上,拉格朗日插值多项式L(x)满足:L(xi) = yi牛顿插值法是另一种常用的插值方法,它利用差商的概念来逼近函数。
对于n个已知数据点(xi, yi),差商可以定义为:f[xi] = yif[xi, xi+1] = (f[xi+1] - f[xi]) / (xi+1 - xi)f[xi, xi+1, ..., xi+k] = (f[xi+1, ..., xi+k] - f[xi, ...,xi+k-1]) / (xi+k - xi)通过差商的递归定义,可以得到牛顿插值多项式N(x)的表达式,其中:N(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...与拉格朗日插值法类似,牛顿插值多项式N(x)也满足:N(xi) = yi这两种插值方法都有自己的优点和缺点。
拉格朗日插值法简单易懂,计算量小,但当数据点较多时,多项式的次数会很高,容易出现龙格现象。
而牛顿插值法可以通过求差商一次次递推得到插值多项式,计算效率较高,且具备局部逼近性,不易出现龙格现象。
除了拉格朗日插值法和牛顿插值法,还有其他插值方法,如分段线性插值、样条插值等。
分段线性插值是利用线性多项式逼近函数,将数据点之间的区间分为若干段,每段内使用一条线性多项式进行插值。
数值分析第二章 插值法

(j,k=0,1,…,n)
( x x0 )( x xk 1 )( x xk 1 )( x xn ) lk ( x ) ( xk x0 )( xk xk 1 )( xk xk 1 )( xk xn )
n1 ( x ) ( x xk ) n1 ' ( xk )
n
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
• 性质 (2)k阶均差可重新写为:
f [ x1 , x2 ,, xk ] f [ x0 , x1 , xk 1 ] f [ x0 , x1 , xk ] xk x0
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
类似地称 2 f k f k 1 f k 为 xk 处的二阶差分. 一般地称 n f k n1 f k 1 n1 f k 为 xk 处的n阶差分.
• 均差与差分关系
• 牛顿前插公式
n f k (1) f nk j , j 0 j
求5、6月份的日照时间的变化规律。 • 多项式插值的存在唯一性
一、引言
2.多项式插值
• 一个例子 日照时间的变化设为 y(x)=a0+ a1x + a2x2, 根据三组数据: (1, 13.53), (31, 14.21),(61, 14.40), 导出关于a0,a1,a2的线性方程组
a0 a1 a2 13.53 2 a0 31a1 (31) a2 14.21 2 a0 61a1 (61) a2 14.40
三、均差与牛顿插值
3.差分形式的牛顿插值公式
若x0,x1,…,xn 为等距节点,即xk=x0+kh (k=0,1,...,n) 时,可将牛顿插值公式简化
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
数值分析所有代码

实验一:拉格朗日插值多项式命名(源程序.cpp及工作区.dsw):lagrange问题:4//Lagrange.cpp#include <stdio.h>#include <conio.h>#define N 4int checkvalid(double x[], int n);void printLag (double x[], double y[], double varx, int n);double Lagrange(double x[], double y[], double varx, int n);void main (){double x[N+1] = {0.4, 0.55, 0.8, 0.9, 1};double y[N+1] = {0.41075, 0.57815, 0.88811, 1.02652, 1.17520};double varx = 0.5;if (checkvalid(x, N) == 1){printf("\n\n插值结果: P(%f)=%f\n", varx, Lagrange(x, y, varx, N));}else{printf("结点必须互异");}getch();}int checkvalid (double x[], int n){int i,j;for (i = 0; i < n; i++){for (j = i + 1; j < n+1; j++){if (x[i] == x[j])//若出现两个相同的结点,返回-1{return -1;}}}return 1;}double Lagrange (double x[], double y[], double varx, int n) {double fenmu;double fenzi;double result = 0;int i,j;printf("Ln(x) =\n");for (i = 0; i < n+1; i++){fenmu = 1;for (j = 0; j < n+1; j++){if (i != j){fenmu = fenmu * (x[i] - x[j]);}}printf("\t%f", y[i] / fenmu);fenzi = 1;for (j = 0; j < n+1; j++){if (i != j){printf("*(x-%f)", x[j]);fenzi = fenzi * (varx - x[j]);}}if (i != n){printf("+\n");}result += y[i] / fenmu * fenzi;}return result;}运行及结果显示:实验二:牛顿插值多项式命名(源程序.cpp及工作区.dsw):newton_cz问题:4//newton_cz.cpp#include<stdio.h>#include<iostream.h>#include<conio.h>#define N 4int checkvaild(double x[],int n){int i,j;for(i=0;i<n+1;i++){for(j=i+1;j<n+1;j++)if(x[i]==x[j])return -1;}return 1;}void chashang(double x[],double y[],double f[][N+1]){int i,j,t=0;for(i=0;i<N+1;i++){f[i][0]=y[i];//f[0][0]=y[0],f[1][0]=y[1];f[2][0]=y[2];f[3][0]=y[3];f[4][0]=y[4] }for(j=1;j<N+1;j++)// 阶数j{for(i=0;i<N-j+1;i++) //差商个数if[i][j]=(f[i+1][j-1]-f[i][j-1])/(x[t+i+1]-x[i]);//一阶为f[0][1]~f[3][1];二阶为f[0][2]~f[2][2]//三阶为f[0][3]~f[1][3];四阶为f[0][4]t++;}}double compvalue(double t[][N+1],double x[],double varx){int i,j,r=0;double sum=t[0][0],m[N+1]={sum,1,1,1,1};printf("i\tXi\t F(Xi)\t 1阶\t 2阶\t\t3阶\t 4阶\n");printf("--------------------------------------------------------------------------------");for(i=0;i<N+1;i++){r=i;printf("x%d\t%f ",i,x[i]);for(j=0;j<=i;j++){printf("%f ",t[r][j]);r--;}printf("\n");}printf("--------------------------------------------------------------------------------");/**/ printf("N(x) =\n");printf(" %f\n",t[0][0]);for(i=1;i<N+1;i++){for(j=0;j<i;j++)m[i]=m[i]*(varx-x[j]);m[i]=t[0][i]*m[i];sum=sum+m[i];}for(i=1;i<N+1;i++){ printf(" +%f*",t[0][i]);for(j=0;j<i;j++)printf("(x-%f)",x[j]);printf("\n");}return sum;}void main(){double varx,f[N+1][N+1];double x[N+1]={0.4,0.55,0.8,0.9,1};double y[N+1]={0.41075,0.57815,0.88811,1.02652,1.17520};checkvaild(x,N);chashang(x,y,f);varx=0.5;if(checkvaild(x,N)==1){chashang(x,y,f);printf("\n\n牛顿插值结果: P(%f)=%f\n",varx,compvalue(f,x,varx));}elseprintf("输入的插值节点的x值必须互异!");getch();} 运行及结果显示:实验三:自适应梯形公式命名(源程序.cpp 及工作区.dsw ):autotrap ][n T问题:计算⎰+=10214dx x π的近似值,使得误差(EPS )不超过610- //autotrap.cpp #include<stdio.h> #include<conio.h> #include<math.h> #define EPS 1e-6 double f(double x) { return 4/(1+x*x); } double AutoTrap(double(*f)(double),double a,double b,double eps) { double t2,t1,sum=0.0; int i,k; t1=(b-a)*(f(a)+f(b))/2; printf("T(%4d)=%f\n",1,t1); for(k=1;k<11;k++) { for(i=1;i<=pow(2,k-1);i++) sum+=f(a+(2*i-1)*(b-a)/pow(2,k)); t2=t1/2+(b-a)*sum/pow(2,k); printf("T(%4d)=%f\n",(int)pow(2,k),t2); if(fabs(t2-t1)<EPS) break; else t1=t2; sum=0.0; } return sum; } void main(){ double s;s=AutoTrap(f,0.0,1.0,EPS);getch();} 运行及结果显示:实验四:龙贝格算法命名(源程序.cpp 及工作区.dsw ):romberg问题:求⎰+=10214dx x π的近似值,要求误差不超过610-//romberg.cpp #include <stdio.h> #include <conio.h> #include <math.h> #define N 20 #define EPS 1e-6 double f(double x){return 4/(1+x*x);} double Romberg(double a,double b,double (*f)(double),double eps) { double T[N][N],p,h;int k=1,i,j,m=0;T[0][0]=(b-a)/2*(f(a)+f(b));do{p=0;h=(b-a)/pow(2,k-1);for(i=1;i<=pow(2,k-1);i++)p=p+f(a+(2*i-1)*h/2);T[0][k]=T[0][k-1]/2+p*h/2;for(i=1;i<=k;i++){j=k-i;T[i][j]=(pow(4,i)*T[i-1][j+1]-T[i-1][j])/(pow(4,i)-1); }k++; p=fabs(T[k-1][0]-T[k-2][0]);}while(p>=EPS);k--; while(m<=k){for(i=0;i<=m;i++) printf("T(%d,%d)=%f ",i,m-i,T[i][m-i]);m++;printf("\n");}return T[k][0]; } void main() {printf("\n\n 积分结果 = %f",Romberg(0,1,f,EPS)); getch(); } 运行及结果显示:实验五:牛顿切线法问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //newton_qxf.cpp#include <math.h>#include<conio.h>#include <stdio.h>#define MaxK 1000#define EPS 0.5e-3double f(double x){return x*x*x-x-1;}double f1(double x){return 3*x*x-1;}int newton(double (*f)(double), double (*f1)(double), double &x0, double eps) {double xk, xk1;int count = 0;printf("k\txk\n");printf("-----------------------\n");xk = x0;printf("%d\t%f\n", count, xk);do{if((*f1)(xk)==0)return 2;xk1 = xk - (*f)(xk) / (*f1)(xk);if (fabs(xk - xk1) < eps){count++;xk = xk1;printf("%d\t%f\n", count, xk);x0 = xk1;return 1;}count++;xk = xk1;printf("%d\t%f\n", count, xk);}while(count < MaxK);return 0;}void main(){for(int i=0;i<2;i++){double x=0.6;if(i==1)x=1.5;printf("x0初值为%f:\n",x);if (newton(f, f1, x, EPS) == 1){printf("-----------------------\n");printf("the root is x=%f\n\n\n", x);}else{printf("the method is fail!");}}getch();}实验六:牛顿下山法命名(源程序.cpp 及工作区.dsw ):newton_downhill 问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //newton_downhill.cpp #include <stdio.h> #include <conio.h> #include <math.h> #include <stdlib.h> #define Et 1e-3//下山因子下界 #define E1 1e-3//根的误差限 #define E2 1e-3//残量精度 double f(double x) { return x * x * x - x - 1; } double f1(double x) { return 3 * x * x - 1; } void errormess(int b){char *mess;switch(b){case -1:mess = "f(x)的导数为0!";break;case -2:mess = "下山因子已越界,下山处理失败";break;default:mess = "其他类型错误!";}printf("the method has faild! because %s", mess);}int Newton(double (*f)(double), double (*f1)(double), double &x0) {int k = 0;double t;double xk, xk1;double fxk, fxk_temp;printf("k t xk f(xk)\n");printf("----------------------------------------------------------\n");printf("%-20d", k);xk = x0;printf("%-15f", x0);fxk = (*f)(xk);printf("%-20f", fxk);printf("\n");for (k = 1; ; k++){t = 1;while(1){printf("%-10d", k);printf("%-10f", t);if((*f1)(xk) != 0){xk1 = xk - t * (*f)(xk) / (*f1)(xk);}else{return -1;}printf("%-15f", xk1);fxk_temp = (*f)(xk1);printf("%-20f", fxk_temp);if(fabs(fxk_temp) >fabs(fxk)){t = t / 2;printf("\n");if (t < Et){return -2;}}else{printf("下山成功\n");break;}}if (fabs(xk-xk1)<E1){x0 = xk1;return 1; } xk = xk1; } }void main() {int b;double x0; x0 = 0.6;b = Newton(f, f1, x0); if (b == 1) printf("\nthe root x=%f\n", x0); else errormess(b); getch(); }运行及结果显示:实验七:埃特金加速算法命名(源程序.cpp 及工作区.dsw ):aitken问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //aitken.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define MaxK 100 #define EPS 0.5e-3double g(double x) {return x * x * x - 1; }int aitken (double (*g)(double), double &x, double eps) {int k;double xk = x, yk, zk, xk1;printf("k xk yk zk xk+1\n");printf("-------------------------------------------------------------------\n"); for (k = 0;k<MaxK; k++) { yk = (*g)(xk); zk = (*g)(yk);xk1 = xk - (yk - xk) * (yk - xk) / (zk - 2 * yk + xk); printf("%-10d%-15f%-15f%-15f%-15f\n", k, xk, yk, zk, xk1); if (fabs(yk-xk)<=eps) { x = xk1; return k + 1; } xk = xk1; }return -1; }void main () {double x = 1.5; int k;k = aitken(g, x, EPS); if (k == -1) printf("迭代次数越界!\n"); else printf("\n 经k=%d 次迭代,所得方程根为:x=%f\n", k, x); getch(); }运行及结果显示:实验八:正割法问题:求方程01)(3=--=x x x f 在5.1=x 附近的根(精度0.5e-8) //ZhengGe.cpp #include <math.h> #include <stdio.h> #include <conio.h>#define MaxK 1000 #define EPS 0.5e-8double f(double x) {return x*x*x-x-1;}int ZhengGe(double (*f)(double), double x0, double &x1, double eps) {printf("k xk f(xk)\n");printf("---------------------------------------------\n");int k;double xk0, xk, xk1;xk0 = x0;printf("%-10d%-15f%-15f\n", 0, x0, (*f)(x0));xk = x1;for (k=1;k<MaxK;k++){if((*f)(xk)-(*f)(xk0)==0)return -1;xk1 = xk - (*f)(xk) / ( (*f)(xk) - (*f)(xk0) ) * (xk - xk0);printf("%-10d%-15f%-15f\n", k, xk, (*f)(xk));if (fabs(xk1 - xk)<=eps){printf("%-10d%-15f%-15f\n\n", k + 1, xk1, (*f)(xk1));printf("---------------------------------------------\n\n");x1 = xk1;return 1;}xk0 = xk;xk = xk1;}return -2;}void main (){double x0 = 1, x1 = 2;if (ZhengGe(f, x0, x1, EPS) == 1){printf("the root is x = %f\n", x1);}else{printf("the method is fail!");}getch();}实验九:高斯列选主元算法命名(源程序.cpp 及工作区.dsw ):colpivot问题:求解方程组并计算系数矩阵行列式值 ⎪⎩⎪⎨⎧=-+=+-=-+2240532321321321x x x x x x x x x//colpivot.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define N 3static double aa[N][N]={{1,2,-1},{1,-1,5},{4,1,-2}}; static double bb[N+1]={3,0,2};void main() {int i,j;double a[N+1][N+1],b[N+1],x[N+1],det;double gaussl(double a[][N+1],double b[],double x[]); for(i=1;i<=N;i++) { for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1]; b[i]=bb[i-1]; }det=gaussl(a,b,x); if(det!=0) { printf("\n 方程组的解为:"); for(i=1;i<=N;i++) printf(" x[%d]=%f",i,x[i]); printf("\n\n 系数矩阵的行列式值=%f",det); }else printf("\n\n 系数矩阵奇异阵,高斯方法失败 !:"); getch(); }double gaussl(double a[][N+1],double b[],double x[])//a传入增广矩阵(有效元素为a[1,1]...a[n,n+1]),x负责传入迭代初值并返回解向量//(有效值为x[1]...x[n]);返回值:系数矩阵行列式值detA{double det=1.0,F,m,temp;int i,j,k,r;void disp(double a[][N+1],double b[]);printf("消元前增广矩阵:\n");disp(a,b);for(k=1;k<N;k++){temp=a[k][k];r=k;for(i=k+1;i<=N;i++){if(fabs(temp)<fabs(a[i][k])){temp=a[i][k];r=i;}//按列选主元,即确定ik}if(a[r][k]==0)return 0;//如果aik,k=0,则A为奇异矩阵,停止计算if(r!=k){for(j=k;j<=N;j++){a[k][j]+=a[r][j];a[r][j]=a[k][j]-a[r][j];a[k][j]-=a[r][j];}b[k]+=b[r];b[r]=b[k]-b[r];b[k]-=b[r];det=-det;//如果ik!=k,则交换[A,b]第ik行与第k行元素printf("交换第%d, %d行:\n",k,r);disp(a,b);}for(i=k+1;i<=N;i++){m=a[i][k]/a[k][k];for(j=1;j<=k;j++)a[i][j]=0.0;for(j=k+1;j<=N;j++)a[i][j]-=m*a[k][j];b[i]-=m*b[k];}printf("第%d次消元:\n",k);disp(a,b);det*=a[k][k];} //大FOR循环结束x[N]=b[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=i+1;j<=N;j++)F+=a[i][j]*x[j];x[i]=(b[i]-F)/a[i][i];}det*=a[N][N];return det;}void disp(double a[][N+1],double b[])//显示选主元及消元运算中间增广矩阵结果 {int i,j;for(i=1;i<=N;i++) {for(j=1;j<=N;j++)printf("%10f\t",a[i][j]); printf("%10f\n",b[i]); } }运行及结果显示:实验十:高斯全主元消去算法 命名(源程序.cpp 及工作区.dsw ):fullpivot问题:利用全主元消去法求解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----9555.04525.015.0201.0321x x x //fullpivot.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define N 3 double x[N+1];static double aa[N][N]={{0.01,2,-0.5},{-1,-0.5,2},{5,-4,0.5}}; static double bb[N]={-5,5,9};void main(){int i,j;double a[N+1][N+1],b[N+1],x[N+1],det;int t[N+1];//引入列交换保存x向量的各分量的位置顺序double gaussl(double a[][N+1],double b[],double x[],int t[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];}for(i=1;i<=N;i++)t[i]=i;det=gaussl(a,b,x,t);if(det!=0){ printf("\n方程组的解为:");for(i=N;i>=1;i--){printf(" x[%d]=%f",t[i],x[i]);if(i>1)printf(" -->");}printf("\n\n系数矩阵的行列式值=%f",det);}else printf("\n\n系数矩阵奇异阵,高斯方法失败!:");getch();}double gaussl(double a[][N+1],double b[],double x[],int t[])//a传入增广矩阵(有效元素为a[1,1]...a[n,n+1]),x负责传入迭代初值并返回解向量//(有效值为x[1]...x[n]);返回值:系数矩阵行列式值detA{double det=1.0,F,m,temp;int i,j,k,r,s;void disp(double a[][N+1],double b[],int x[]);// printf("消元前增广矩阵:\n");//disp(a,b,t);for(k=1;k<N;k++){temp=a[k][k];r=k;s=k;for(i=k;i<=N;i++)for(j=k;j<=N;j++)if(fabs(temp)<fabs(a[i][j])){temp=a[i][j];r=i;s=j;}//选主元,选取ik,jkif(a[r][s]==0)return 0;if(r!=k){for(j=k;j<=N;j++){a[k][j]+=a[r][j];a[r][j]=a[k][j]-a[r][j];a[k][j]-=a[r][j];}b[k]+=b[r];b[r]=b[k]-b[r];b[k]-=b[r];det=-det;printf("交换第%d, %d行:\n",k,r);disp(a,b,t);}if(s!=k){for(i=0;i<=N;i++){a[i][k]+=a[i][s];a[i][s]=a[i][k]-a[i][s];a[i][k]-=a[i][s];}t[k]+=t[s];t[s]=t[k]=t[s];t[k]-=t[s];det=-det;printf("交换第%d, %d列:\n",k,s);disp(a,b,t);}for(i=k+1;i<=N;i++){m=a[i][k]/a[k][k];for(j=1;j<=k;j++)a[i][j]=0.0;for(j=k+1;j<=N;j++)a[i][j]-=m*a[k][j];b[i]-=m*b[k];} //消元计算printf("第%d次消元:\n",k);disp(a,b,t);det*=a[k][k];} //大FOR循环结束x[N]=b[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=i+1;j<=N;j++)F+=a[i][j]*x[j];x[i]=(b[i]-F)/a[i][i];}//回代计算det*=a[N][N];return det;}void disp(double a[][N+1],double b[],int x[])//显示选主元及消元运算中间增广矩阵结果{int i,j;for(i=1;i<=N;i++){for(j=1;j<=N;j++)printf("%f\t",a[i][j]);printf("| x%d = %f\n",x[i],b[i]);}}运行及结果显示:实验十一:LU 分解算法命名(源程序.cpp 及工作区.dsw ):LU问题:利用LU 法求解方程组 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡472111312613321x x x //LU.cpp#include<math.h> #include<stdio.h> #include<conio.h> #define N 3static aa[N][N]={{3,1,6},{2,1,3},{1,1,1}}; static bb[N]={2,7,4};void main() {int i,j;double a[N+1][N+1],b[N+1];void solve(double a[][N+1],double b[N+1]); int LU(double a[][N+1]); for(i=1;i<=N;i++) { for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1]; b[i]=bb[i-1]; }if(LU(a)==1){printf("矩阵L如下\n");for(i=1;i<=N;i++){for(j=1;j<=i;j++)if(i==j)printf("%12d ",1);else printf("%12f",a[i][j]);printf("\n");}printf("\n矩阵U如下\n");for(i=1;i<=N;i++){for(j=1;j<=N;j++)if(i<=j)printf("%12f",a[i][j]);else printf("%12s","");printf("\n");}solve(a,b);for(i=1;i<=N;i++)printf("x[%d]=%f ",i,b[i]);printf("\n");}else printf("\nthe LU method failed!\n");getch();}int LU(double a[][N+1])//对N阶矩A阵进行LU分解,结果L、U存放在A的相应位置{int i,j,k,s;double m,n;for(i=2;i<=N;i++)a[i][1]/=a[1][1];for(k=2;k<=N;k++){for(j=k;j<=N;j++){m=0;for(s=1;s<k;s++)m+=a[k][s]*a[s][j];a[k][j]-=m;}if(a[k][k]==0){printf("a[%d][%d]=%d ",k,k,0);return -1;//存在元素akk为0}for(i=k+1;i<=N;i++){n=0;for(s=1;s<k;s++)n+=a[i][s]*a[s][k];a[i][k]=(a[i][k]-n)/a[k][k];}}return 1;//正常结束}void solve(double a[][N+1],double b[N+1])//利用分解的LU求x//回代求解,L和U元素均在A矩阵相应位置;b存放常数列,返回时存放方程组的解{double y[N+1],F;int i,j;y[1]=b[1];for(i=2;i<=N;i++){F=0.0;for(j=1;j<i;j++)F+=a[i][j]*y[j];y[i]=b[i]-F;}b[N]=y[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=N;j>i;j--)F+=a[i][j]*b[j];b[i]=(y[i]-F)/a[i][i];}}运行及结果显示:实验十二:Guass-Sediel 算法命名(源程序.cpp 及工作区.dsw ):GS问题:利用G -S 法求解方程组 ⎪⎩⎪⎨⎧=+--=-+-=--2.453.82102.7210321321321x x x x x x x x x (精度为41021-⨯)//Guass_sediel.cpp#include "iostream.h"#include "math.h"#include "stdio.h"#include<conio.h>#define N 3 //方程的阶数#define MaxK 100 //最大迭代次数#define EPS 0.5e-4 //精度控制static double aa[N][N]={{10,-1,-2},{-1,10,-2},{-1,-1,5}};static double bb[N]={7.2,8.3,4.2};void main(){int i,j;double x[N+1];double a[N+1][N+1],b[N+1];int GaussSeidel(double a[][N+1],double b[],double x[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++)a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];x[i]=0;}if(GaussSeidel(a,b,x)==1){printf("the roots is:");for(i=1;i<=N;i++)printf(" x[%d]=%f ",i,x[i]);printf("\n");}else printf("\nthe G-S method failed!\n");getch();}int GaussSeidel(double a[][N+1],double b[],double x[])//a传入系数矩阵(有效元素为a[1,1]...a[n,n]),b为方程组右边常数列,x传入迭代初值并返回解向量//x**(k+#x)=Gx**(k)+f{int k=1,i,j;double m,max,t[N+1];while(true){printf("k=%d:",k);max=0.0;for(i=1;i<=N;i++){if(a[i][i]==0)return -1;//存在元素akk为0m=0.0;t[i]=x[i];for(j=1;j<=N;j++)if(j!=i)m+=a[i][j]*x[j];x[i]=(b[i]-m)/a[i][i];if(max<fabs(x[i]-t[i]))max=fabs(x[i]-t[i]);printf(" x[%d]=%f ",i,x[i]);}printf("\n");if(max<EPS)return 1;//正常结束elsek++;if(k>MaxK)return -2;//迭代次数越界}}运行及结果显示:实验十三:SOR 算法命名(源程序.cpp 及工作区.dsw ):sor问题:利用SOR 法求解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----111141111411114111144321x x x x (精度为51021-⨯) //SOR.cpp#include "math.h"#include "stdio.h"#include "conio.h"#define N 4#define MaxK 1000#define EPS 0.5e-5static double aa[N][N]={{-4,1,1,1},{1,-4,1,1},{1,1,-4,1},{1,1,1,-4}}; static double bb[N]={1,1,1,1};void main(){int i,j;double x[N+1];double a[N+1][N+1],b[N+1];int Sor(double a[][N+1],double b[],double w,double x[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++)a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];x[i]=0;}if(Sor(a,b,1.3,x)==1){printf("the roots is:");for(i=1;i<=N;i++)printf(" x[%d]=%f ",i,x[i]);printf("\n");}else printf("\nthe G-S method failed!\n");getch();}int Sor(double a[][N+1],double b[],double w,double x[]) {int i,j,k;double loft,comb;for(k=0;k<=N;k++)x[k]=0;for(i=1;i<=MaxK && fabs(comb)>EPS;i++){printf("k=%d:\t",i);comb=0;for(k=1;k<=N;k++){loft=b[k];for(j=1;j<N+1;j++)loft-=a[k][j]*x[j];if(a[k][k]==0)return -1;else loft=w*loft/a[k][k];x[k]=x[k]+loft;printf("x[%d]=%10f \t",k,x[k]);if(fabs(loft)>comb)comb=fabs(loft);}printf("\n");}if(i>MaxK)return -2;elsereturn 1;}运行结果(w=1)=。
数值分析实验报告(插值法)

武汉理工大学学生实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导老师姓名学生姓名学生专业班级2010—2010学年第一学期实验课程名称:数值分析第二部分:实验调试与结果分析(可加页)一、调试过程(包括调试方法描述、实验数据记录,实验现象记录,实验过程发现的问题等)(1)用拉格朗日插值法计算时,输入及运行结果如下:拉格朗日插值法牛顿插值法(2)利用二次插值计算时,输入及运行结果如下:拉格朗日插值法牛顿插值法(3)用艾尔米特插值法计算时,f(x)的插值多项式H5(x)=(1+4*x)*(x-0.5)*(x-0.5)*(x-2)*(x-2)+(3.90807-6.03838*x)*(x-2)*(x-2)*x*x+(2.34573-4.16674*x)*x*x*(x-0.5)*(x-0.5)(4)各插值算法的精度差异比较经过比较,拉格朗日插值法要比牛顿插值法算法的计算量多一些,拉格朗日插值法后一次计算时用到了前一次计算的结果,提高了运算的效率,但拉格朗日插值法在构造艾尔米特插值法时很方便,将坐标点和对应的导数结合起来的精度比线性插值的精度又要高一些。
但从实验数据来看,在坐标不是很多的情况下,已知的点越多精度也就相对较高。
对于实验要求的第二组数据用拉格朗日插值法(或者牛顿插值法)实验结果如下:一下分别是二阶、三阶、四阶、五阶插值得到的结果以上只是实验结果的一部分,改变插值的位置时,得到的实验结果精度也是有所不同的。
由以上结果分析可知,插值次数并不是越多越好,多了反而会让结果更加偏离真实结果,这充分说明了高次插值存在“病态性质”,在已知点很多的情况下应该采用分段低次插值,将拉格朗日插值法和牛顿插值法运用到分段低次插值法当中,这样得到的结果可能胡更加精确。
数值分析中的(插值法)

三、多项式插值问题中需要研究的问题
满足插值条件的多项式 Pn 是x否存在?唯一?
若满足条件的 Pn 存x在,又如何构造? 用 Pn 近x似代替 f的 x误 差估计?
数值分析 第二章 插值法
李庆扬 王能超 易大义编
Anhui University of Science and Technology DEPARTMENT OF MATHEMATICS PHYSICS
理学院
2.‹#›
(4)若引入记号
n1(x) (x x0 )(x x1) (x xn ) 则
n
1
(xk
)
(xk
x0 )
(xk
xk 1)(xk
xk 1)
(xk
xn )
于是
Ln(x)
n
yklk (x)
k 0
n
yk
k 0
(x
n1(x) xk )n1(xk )
Li(x)为插值基函数。
数值分析 第二章 插值法
李庆扬 王能超 易大义编
Anhui University of Science and Technology DEPARTMENT OF MATHEMATICS PHYSICS
理学院
2.‹#›
注:(1) 插值基函数l i(x) (i=0,1, …,n)仅由插值节点 xi (i=0,1, … ,n)确定,与被插函数 f(x)无关.
Rn ( x) f ( x) Ln ( x) K ( x)n1( x) 可知:x0 , x1, , xn和x是 (t) 在区间[a,b]上的n+2个 互异零点, 因此根据罗尔(Rolle)定理, 至少存在一点
数值分析中的(插值法)

插值法可以与其他数值分析方法结合使用,以获得更准确和可靠的估计结果。例如,可以 考虑将插值法与回归分析、时间序列分析等方法结合,以提高数据分析的效率和精度。
THANKS
感谢观看
多项式的阶数
根据数据点的数量和分布情况,选择适当的多项式阶数,以确保多 项式能够更好地逼近真实数据。
计算多项式的系数
通过已知的数据点和多项式阶数,计算出多项式的系数,从而得到 完整的插值多项式。
计算插值多项式的导数
导数的计算
在某些应用中,需要计算插值多项式的导数,例如在 曲线拟合、数值微分等场景中。
总结词
牛顿插值法是一种基于差商的插值方法,通过构造差商表来逼近未知点的数值。
详细描述
牛顿插值法的基本思想是通过构造差商表来逼近未知点的数值,差商表中的每一 项都是根据前一项和后一项的差来计算的。该方法在数值分析中广泛应用于数据 拟合、函数逼近等领域。
样条插值法
总结词
样条插值法是一种通过已知的离散数据点来构造一个样条函 数,用于估计未知点的数值的方法。
常见的插值法
拉格朗日插值法
总结词
拉格朗日插值法是一种通过已知的离散数据点来构造一个多项式,用于估计未 知点的数值的方法。
详细描述
拉格朗日插值法的基本思想是通过构造一个多项式来逼近已知数据点,使得该 多项式在每个数据点的取值与实际值相等。该方法在数值分析中广泛应用于数 据拟合、函数逼近等领域。
牛顿插值法
增加采样点的数量可以减小离散化误差,提高插值结果的稳定
性。
选择合适的插值方法
02
根据具体情况选择适合的插值方法,如多项式插值、样条插值
等,以获得更好的逼近效果和稳定性。
引入阻尼项
数值分析插值法

解 由上表可得过前三点的二次牛顿插值多项式为
故
又
可得过前四点的三次牛顿插值多项式
可得N3(x)的截断误差
差分与等距节点的牛顿插值多项式
设函数y=fx在等距节点xi=x0+ih i=01 …n上的函数值为fi=fxih为步长
定义2 fi=fi+1-fi 和 fi=fi-fi-1 分别称为函数fx在点xi处的一阶向前差分和一阶向后差分
求f2.8用牛顿后插公式且由 2.8=3+0.5t 得 t= -0.4
第四节 埃尔米特Hermite插值
一、 埃尔米特插值多项式
为了使插值函数能更好的切合原来的函数许多问题不但要求节点上的函数值相等还要求导数值相同甚至高阶导数也相等这类插值问题称为埃尔米特插值
xi[a, b] (i=0,1, …, n) 为n+1个互异节点,考虑函数值 与导数个数相等的情况。
二、误差估计
定理4 设fx在包含x0、x1的区间ab内存在四阶导数则当x∈ab时有
且与x有关)
例1 已知fx=x1/2在X=121和144时的函数值及其一阶导数的数据见下表用埃尔米特插值公式计算1251/2的近似值并估计其截断误差.
得
由
可求得
例2
第五节 分段低次插值
解 (1) 用线性插值
第三节 均差与牛顿插值公式
一、差商及其基本性质
定义1 称
为 f x在x0、x1点的一阶差商.一阶差商的差商
称为函数f x在x0、x1 、x2 点的二阶差商.
一般地n-1阶差商的差商
称为f x在x0 x1 … xn点的 n 阶差商
差商的计算步骤与结果可列成差商表如下
xk
函数值
一阶差商
数值分析第三章 插值法

+ (0.3367 − 0.32)(0.3367 − 0.36) × 0.333487 (0.34 − 0.32)(0.34 − 0.36)
+ (0.3367 − 0.32)(0.3367 − 0.34) × 0.352274 = 0.330374
(0.36 − 0.32)(0.36 − 02.36 4)
x x0 x1 y 01
一次插值多项式y = P1 (x)可以由两个基本插值多项 式 l0 (x)、l1 (x) 与函数值y0、y1的线性组合来表示
6
6
线性插值
例3.2.1:已知y = f (x)的函数表
x13 y12
求线性插值多项式,并计算x=1.5的函数值
解:已知两点的线性插值多项式
Rn (x) = f (x) − Pn (x)
定理3.2:设f (n)(x)在区间[a, b]上连续,f (n + 1)(x) 在[a, b]上存在,x0, x1,…, xn是[a, b]上互异的节 点,记插值问题的余项为 Rn (x) = f (x) − Pn (x) , 那么,当x ∈ [a, b]时,有如下估计
≈
P2 (115)
=
(115 (100
− 121)(115 − 144) − 121)(100 − 144)
× 10
+ (115 − 100)(115 − 144) ×11 (121 − 100)(121 − 144)
+ (115 − 100)(115 − 121) ×12 (144 − 100)(144 − 121)
P1 ( x)
=
x−3 1−3
×1+
x −1× 3−1
2
(完整版)数值分析插值法

第二章插值法2.在区间[-1,1]上分别取n=10,20用两组等距节点对龙哥函数f(x)=1/(1+25*x^2)做多项式插值及三次样条插值,对每个n值,分别画出插值函数及f(x)的图形。
(1)多项式插值①先建立一个多项式插值的M-file;输入如下的命令(如牛顿插值公式):function [C,D]=newpoly(X,Y)n=length(X);D=zeros(n,n)D(:,1)=Y'for j=2:nfor k=j:nD(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1));endendC=D(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)))m=length(C);C(m)= C(m)+D(k,k);end②当n=10时,我们在命令窗口中输入以下的命令:clear,clf,hold on;X=-1:0.2:1;Y=1./(1+25*X.^2);[C,D]=newpoly(X,Y);x=-1:0.01:1;y=polyval(C,x);plot(x,y,X,Y,'.');grid on;xp=-1:0.2:1;z=1./(1+25*xp.^2);plot(xp,z,'r')得到插值函数和f(x)图形:③当n=20时,我们在命令窗口中输入以下的命令:clear,clf,hold on;X=-1:0.1:1;Y=1./(1+25*X.^2);[C,D]=newpoly(X,Y);x=-1:0.01:1;y=polyval(C,x);plot(x,y,X,Y,'.');grid on;xp=-1:0.1:1;z=1./(1+25*xp.^2);plot(xp,z,'r')得到插值函数和f(x)图形:(2)三次样条插值①先建立一个多项式插值的M-file;输入如下的命令:function S=csfit(X,Y,dx0,dxn)N=length(X)-1;H=diff(X);D=diff(Y)./H;A=H(2:N-1);B=2*(H(1:N-1)+H(2:N));C=H(2:N);U=6*diff(D);B(1)=B(1)-H(1)/2;U(1)=U(1)-3*(D(1));B(N-1)=B(N-1)-H(N)/2;U(N-1)=U(N-1)-3*(-D(N));for k=2:N-1temp=A(k-1)/B(k-1);B(k)=B(k)-temp*C(k-1);U(k)=U(k)-temp*U(k-1);endM(N)=U(N-1)/B(N-1);for k=N-2:-1:1M(k+1)=(U(k)-C(k)*M(k+2))/B(k);endM(1)=3*(D(1)-dx0)/H(1)-M(2)/2;M(N+1)=3*(dxn-D(N))/H(N)-M(N)/2;for k=0:N-1S(k+1,1)=(M(k+2)-M(k+1))/(6*H(k+1));S(k+1,2)=M(k+1)/2;S(k+1,3)=D(k+1)-H(k+1)*(2*M(k+1)+M(k+2))/6;S(k+1,4)=Y(k+1);end②当n=10时,我们在命令窗口中输入以下的命令:clear,clcX=-1:0.2:1;Y=1./(25*X.^2+1);dx0= 0.0739644970414201;dxn= -0.0739644970414201; S=csfit(X,Y,dx0,dxn)x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')结果如图:②当n=20时,我们在命令窗口中输入以下的命令:clear,clcX=-1:0.1:1;Y=1./(25*X.^2+1);dx0= 0.0739644970414201;dxn= -0.0739644970414201; S=csfit(X,Y,dx0,dxn)x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')结果如图:第三章函数逼近与快速傅里叶变换2. 由实验给出数据表x 0.0 0.1 0.2 0.3 0.5 0.8 1.0y 1.0 0.41 0.50 0.61 0.91 2.02 2.46试求3次、4次多项式的曲线拟合,再根据数据曲线形状,求一个另外函数的拟合曲线,用图示数据曲线及相应的三种拟合曲线。
数值分析常用的插值方法

数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。
下面将对这些插值方法进行详细介绍。
一、线性插值(linear interpolation)线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值,通过这两个点之间的直线来估计中间点的函数值。
线性插值公式为:f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中,f(x)表示要求的插值点的函数值,f(x0)和f(x1)是已知的两个点上的函数值,x0和x1是已知的两个点的横坐标。
二、拉格朗日插值(Lagrange interpolation)拉格朗日插值是一种基于多项式的插值方法。
它通过多个已知点的函数值构造一个多项式,并利用这个多项式来估计其他点的函数值。
拉格朗日插值多项式的一般形式为:f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中,f(x)表示要求的插值点的函数值,f(xi)是已知的多个点的函数值,Li(x)是拉格朗日基函数。
拉格朗日基函数的表达式为:Li(x) = Π[(x-xj)/(xi-xj)] (i≠j,i,j=0,1,2,...,n)三、分段线性插值(piecewise linear interpolation)分段线性插值是一种逐段线性近似函数的方法。
通过将整个插值区间分成多个小段,在每个小段上使用线性插值来估计函数的值。
分段线性插值的过程分为两步:首先确定要插值的点所在的小段,在小段上进行线性插值来估计函数值。
四、Newton插值(Newton interpolation)Newton插值也是一种基于多项式的插值方法。
利用差商的概念来构造插值多项式。
Newton插值多项式的一般形式为:f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中,f(x)表示要求的插值点的函数值,f(x0)是已知的一个点的函数值,f[xi,xi+1,...,xi+k]是k阶差商。
数值分析分段线性插值样条插值Runge函数Newton-Lagrange-Chebyshev插值多项式Runge现象matlab源程序代码
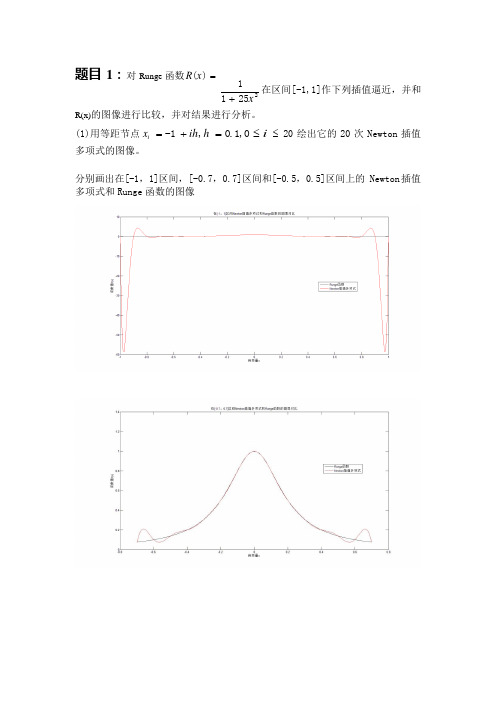
题目1:对Runge 函数R(x ) =1在区间[-1,1]作下列插值逼近,并和1 + 25x 2R(x)的图像进行比较,并对结果进行分析。
= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点xi多项式的图像。
分别画出在[-1,1]区间,[-0.7,0.7]区间和[-0.5,0.5]区间上的 Newton 插值多项式和Runge 函数的图像从图中可以看出: 1)在[-0.5,0.5]区间 Newton 插值多项式和 Runge 函数的图像偏差较小,这说 明 Newton 插值多项式在此区间上可以较好的逼近 Runge 函数; 2)在边界(自变量 x=-1 和 x=1)附近,Newton 插值多项式和 Runge 函数的图像 偏差很大,Newton 插值多项式出现了剧烈的震荡。
(Runge 现象) (2)用节点 x = cos(2i + 1π)(, i = 0,1,2,⋅ ⋅ ⋅ ,20),绘出它的 20 次 Lagrangei 42 插值多项式的图像。
画出在[-1,1]区间上的 Lagrange 插值多项式和 Runge 函数的图像从图中可以看出:使用 Chebyshev 多项式零点构造的 Lagrange 插值多项式和 Runge 函数的图 像偏差较小,没有出现 Runge 现象。
(3)用等距节点 x i 的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数画出在[-1,1]区间上分段线性插值函数和 Runge 函数的图像从图中可以看出:使用分段线性插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象,只在自变量 x=0 处有稍许偏差。
(4)用等距节点 x i 函数的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值画出在[-1,1]区间上三次自然样条插值函数和 Runge 函数的图像从图中可以看出:使用三次自然样条插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象。
数值分析 实验三Newton插值多项式

数学与软件科学学院实验报告学期:至第学期年月日课程名称:___计算机数值方法_ 专业:信心与计算科学 08 级 6班实验编号:3 实验项目Newton插值多项式指导教师__张莉_姓名:田文晓学号:2008060632 实验成绩:一、实验目的及要求实验目的:掌握Newton插值多项式的算法,理解Newton插值多项式构造过程中基函数的继承特点,掌握差商表的计算特点。
实验要求:1. 给出Newton插值算法2. 用C语言实现算法二、实验内容1. 用下列插值节点数据,构造Newton插值多项式,并计算2. 用下列插值节点数据,构造一个三次Newton插值多项式,并计算f(1.2)的值。
三、实验步骤(该部分不够填写.请填写附页)步骤1:算法描述:输入n值,及(x_i,y_i),i=0,1,2,…n;记f(x_i)=y_i;For i=0,1,2…n计算差商f[x0,x1,x2,…x_k]=(f[x1,x2,…x_k]-f[x0,x1,x_k-1])/(x_k-x0) 其中 f[x_i]=f(x_i);对给定的x ,由N_n(x)=f(x0)+(x-x0)f[x0,x1]+(x-x0)(x-x1)f[x0,x1.x2]+...(x-x0)(x-x 1)(x-x2)...(x-x_n-1)f[x0,x1,...x_n]计算出N_n(x)的值输出N_n(x)的值步骤2:程序代码如下:#include<stdio.h>#define MAX_N 30typedef struct tagPOINT /*the structer of point */{double x;double y;}POINT;int main(){int n,i,j;POINT points[MAX_N+1];double tmp,newton=0;double diff[MAX_N+1];double x;clrscr();printf("\nInput n value :"); /*the number of the points inserted*/scanf("%d",&n);if(n>MAX_N){printf("The input n is larger than MAX_N,please redefine the MAX_N.\n");return 1;}if(n<=0){printf("Please input a number between 1 and %d.\n",MAX_N);return 1;}printf("Now input the (x_i,y_i),i=0,...%d:\n",n);for(i=0;i<=n;i++)scanf("%lf %lf",&points[i].x,&points[i].y);printf("Now input the x value:"); /*the value of x*/scanf("%lf",&x);for(i=0;i<=n;i++) diff[i]=points[i].y;for(i=0;i<n;i++){for(j=n;j>i;j--){diff[j]=(diff[j]-diff[j-1])/(points[j].x-points[j-1-i].x); }}tmp=1;newton=diff[0];for(i=0;i<n;i++){tmp=tmp*(x-points[i].x);newton=newton+tmp*diff[i+1];}printf("newton(%f)=%f\n",x,newton);return 0;}四,实验结果与分析:当输入x=0.9时,利用牛顿二次插值得到结果如下:Input n value :2Now input the (x_i,y_i),i=0,...2:0 11 22 19Now input the x value:0.9newton(0.900000)=1.180000当输入x=0.9时,利用牛顿三次插值得到结果如下:Input n value :3Now input the (x_i,y_i),i=0,...3:-2 170 12 191 2Now input the x value:0.9newton(0.900000)=1.303750输入当x=1.2时,得到结果如下:Input n value :3Now input the (x_i,y_i),i=0,...3:-1.00 3.002.00 5.003.00 7.004.005.00Now input the x value:1.2newton(1.200000)=2.401600注:实验成绩等级分为(90-100分)优,(80-89分)良,(70-79分)中,(60-69分)及格,(59分)不及格。
数值分析各算法流程图

01,,n1,,n1,,)n x及数值分析各算法流程图一、插值1、 拉格朗日插值流程图:( 相应程序:lagrintp(x,y,xx))2,,n ,,j n 1,2,,n 1,,)n 2、 牛顿插值流程图(1)产生差商表的算法流程图(相应程序:divdiff(x,y))注:1、另一程序divdiff1(x,y),输出的矩阵包含了节点向量。
而divdiff(x,y)不含节点向量。
2、另一程序tableofdd(x,y,m),输出的是表格形式,添加了表头。
1,,),,n m 及1,,m (2)非等距节点的牛顿插值流程图(相应程序:newtint11(x,y,xx,m)) 、注:1、虽然程序newtint11(x,y,xx,m)考虑了多种情形,看上去很复杂,但基本流程结构还是如上图所示。
2、程序中调用的子程序是divdiff 。
若调用的子程序是divdiff1的话,流程图中的第三,第四,第五步要相应的改一下数字。
2,3,,1m +1,,j1,2,,n=1,2,,)n m 及(3)求差分表的流程图(相应程序:difference(y,m))注:1、difference 输出的是矩阵D 。
而另一程序tableofd(y,m),输出的是带有表头的差分表。
n x m1,,),,1,,m注:1、程序newtforward1(x,y,xx,m))的结构与上述流程图一致,xx可以是数组。
2、另一程序newtforward(x,y,xx,m))先求出插值多项式,再求插值多项式在插值点的函数值。
基本结构还是和上面的流程图一样。
n x m1,,),,-x x1,,m注:1、程序newtbackward1(x,y,xx,m))的结构与上述流程图一致,xx可以是数组。
2、另一程序newtbackward(x,y,xx,m))先求出插值多项式,再求插值多项式在插值点的函数值。
基本结构还是和上面的流程图一样。
1,2,,n1,2,,n ,2,,)n x及3、Hermite 插值流程图(1) 已知条件中一阶导数的个数与插值节点的个数相等时的Hermite 插值流程图。
MATLAB数值实验一(数据的插值运算及其应用完整版)

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 插值法与数据拟合 专业班级 机械工程 姓 名 余红杰 学 号 2111505010 指导教师 陈剑 成 绩 日 期 月 日一、实验目的1、学会Lagrange 插值、牛顿插值和三次样条插值等基本插值方法;2、讨论插值的Runge 现象3、学会Matlab 提供的插值函数的使用方法,会用这些函数解决实际问题。
二、实验原理1、拉格朗日插值多项式2、牛顿插值多项式3、三次样条插值 三、实验步骤1、用MA TLAB 编写独立的拉格朗日插值多项式函数2、用MA TLAB 编写独立的牛顿插值多项式函数3、用MA TLAB 编写独立的三次样条函数(边界条件为第一、二种情形)4、已知函数在下列各点的值为:根据步骤1,2,3编好的程序,试分别用4次拉格朗日多项式4()L x 、牛顿插值多项式4()P x 以及三次样条函数()S x (自然边界条件)对数据进行插值,并用图给出 {(,),0.20.08,0,1,2,,10i i i x y x i i =+= },4()L x 、4()P x 和()S x 。
5、在区间[-1,1]上分别取10,2n =用两组等距节点对龙格函数21(),(11)125f x x x =-≤≤+作多项式插值,对不同n 值,分别画出插值函数及()f x 的图形。
6、下列数据点的插值可以得到平方根函数的近似,在区间[0,64]上作图。
(1)用这9个点作8次多项式插值8()L x 。
(2)用三次样条(第一边界条件)程序求()S x 。
7、对于给函数21()125f x x =+在区间[-1,1]上取10.2(0,1,,10)i x i i =-+= ,试求3次曲线拟合,试画出拟合曲线并打印出方程,与第5题的结果比较。
四、实验过程与结果:1、Lagrange 插值多项式源代码:function ya=lag(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 ya=0; mu=1; %初始化%循环方式求L 系数,并求和: for i = 1:length(y) for j = 1:length(x) if i ~= jmu = mu * (xa - x(j) ) / ( x(i) - x(j) ); else continue end endya = ya + y(i) * mu ; mu = 1; end2、Newton 源代码:function ya = newton(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 %建立系数零矩阵D 及初始化:D = zeros(length(x)-1);ya = y(1);xi = 1;%求出矩阵D,该矩阵第一行为牛顿插值多项式系数:for i=1:(length(x)-1)D(i,1) = (y(i+1) -y(i))/(x(i+1) -x(i));endfor j=2:(length(x)-1)for i=1:(length(x)-j)D(i,j) = (D(i+1,j-1) - D(i,j-1)) / (x(i+j) - x(i)); endend%xi为单个多项式(x-x(1))(x-x(2))...的值for i=1:(length(x)-1)for j=1:ixi = xi*(xa - x(j));endya = ya + D(1,i)*xi;xi = 1;end3、三次样条插值多项式(1)(第一边界条件)源代码:function y=yt1(x0,y0,f_0,f_n,x) _____________(1)%第一类边界条件下三次样条插值;%xi 所求点;%yi 所求点函数值;%x 已知插值点;%y 已知插值点函数值;%f_0左端点一次导数值;%f_n右端点一次导数值;n = length(x0);z = length(y0);h = zeros(n-1,1);k=zeros(n-2,1);l=zeros(n-2,1);S=2*eye(n);for i=1:n-1h(i)= x0(i+1)-x0(i);endfor i=1:n-2k(i)= h(i+1)/(h(i+1)+h(i));l(i)= 1-k(i);end%对于第一种边界条件:k = [1;k]; _______________________(2)l = [l;1]; _______________________(3)%构建系数矩阵S:for i = 1:n-1S(i,i+1) = k(i);S(i+1,i) = l(i);end%建立均差表:F=zeros(n-1,2);for i = 1:n-1F(i,1) = (y0(i+1)-y0(i))/(x0(i+1)-x0(i));endD = zeros(n-2,1);for i = 1:n-2F(i,2) = (F(i+1,1)-F(i,1))/(x0(i+2)-x0(i));D(i,1) = 6 * F(i,2);end%构建函数D:d0 = 6*(F(1,2)-f_0)/h(1); ___________(4)dn = 6*(f_n-F(n-1,2))/h(n-1); ___________(5)D = [d0;D;dn]; ______________(6)m= S\D;%寻找x所在位置,并求出对应插值:for i = 1:length(x)for j = 1:n-1if (x(i)<=x0(j+1))&(x(i)>=x0(j))y(i) =( m(j)*(x0(j+1)-x(i))^3)/(6*h(j))+...(m(j+1)*(x(i)-x0(j))^3)/(6*h(j))+...(y0(j)-(m(j)*h(j)^2)/6)*(x0(j+1)-x(i))/h(j)+... (y0(j+1)-(m(j+1)*h(j)^2)/6)*(x(i)-x0(j))/h(j) ; break;else continue;endendend(2)(自然边界条件)源代码:仅仅需要对上面部分标注的位置做如下修改:__(1):function y=yt2(x0,y0,x)__(2):k=[0;k]__(3):l=[l;0]__(4)+(5):删除—(6):D=[0:D:0]4、——————————————PS:另建了一个f 方程文件,后面有一题也有用到。
插值法VB源程序
第四章 插值方法VB一、线性插值应用实例VB1已知:169的平方根为13,196的平方根为14,编程求175的平方根。
Private Sub Command1_click()Dim x(1 To 2),y(1 To 2) As Singlex(1)=169:y(1)=13x(2)=196:y(2)=14x0=175y0=F(x,y,x0)a=Format$(y0,"###.##")Text1.Text="y0=" & Str$(a)End SubPrivate Function F(x,y,x0)F=y(1)+(y(2)-y(1))/(x(2)-x(1))*(x0-x(1))End Function线性插值应用实例VB2已知水的温度与密度和关系如下:试编程计算温度为6、13、16、19、23、26 o C 时的密度。
Private Sub Command1_click()N = 6X = Array(0, 5, 10, 15, 20, 25, 30)Y = Array(0, 0.999965, 0.9997, 0.999099, 0.998203, 0.997044, 0.995646) xc = Array(0, 6, 13, 16, 19, 23, 26)List1.AddItem " x0" & " y0"For I = 1 To 6X0 = xc(I)Y0 = f(N, X, Y , X0)List1.AddItem Str$(X0) & Str$(Y0)Next IEnd SubPrivate Function f(N, X, Y , X0)For I = 1 To NIf X0 <= X(I) ThenW = I0.990.990.990.990.9970.9999密度30.0 25.0 20.0 15.0 10.0 5.0 温度Exit ForEnd IfNext IW = W - 1If W <= 1 ThenW = 1: End IfIf W >= N ThenW = N - 1: End Iff = Y(W) + (Y(W + 1) - Y(W)) / (X(W + 1) - X(W)) * (X0 - X(W))End Function二、拉格朗日三点插值实例例:实验测得25O C 乙醇溶液的平均摩尔体积v 与乙醇的摩尔分数xi 的关系数据如下表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include<stdio.h>
#include<math.h>
float f(float x) //计算ex的值
{
return (exp(x));
}
float g(float x) //计算根号x的值
{
return (pow(x,0.5));
}
void linerity () //线性插值
{
float px,x;
float x0,x1;
printf("请输入x0,x1的值\n");
scanf("%f,%f",&x0,&x1);
printf("请输入x的值: ");
scanf("%f",&x);
px=(x-x1)/(x0-x1)*f(x0)+(x-x0)/(x1-x0)*f(x1);
printf("f(%f)=%f \n",x,px);
}
void second () //二次插值
{
float x0,x1,x2,x,px;
x0=0;
x1=0.5;
x2=2;
printf("请输入x的值:");
scanf("%f",&x);
px=((x-x1)*(x-x2))/((x0-x1)*(x0-x2))*f(x0)+((x-x0)*(x-x2))/((x1-x0)*(x1-x2))*f(x1)+((x-x0)* (x-x1))/((x2-x0)*(x2-x1))*f(x2);
printf("f(%f)=%f\n",x,px);
}
void Hermite () //Hermite插值
{
int i,k,n=2;
int flag1=0;
printf("Hermite插值多项式H5(x)=");
for(i=0;i<=n;i++)
{
int flag=0;
flag1++;
if(flag1==1)
{
printf("y%d[1-2(x-x%d)*(",i,i);
}
else
{
printf("+y%d[1-2(x-x%d)*(",i,i);
}
for(k=0;k<=n;k++)
{
if(k!=i)
{
flag++;
if(flag==1)
{
printf("(1/x%d-x%d)",i,k);
}
else
{
printf("+(1/x%d-x%d)",i,k);
}
}
}
printf(")]*(");
for(k=0;k<=n;k++)
{
if(i!=k)
{
printf("[(x-x%d)/(x%d-x%d)]2",i,k,i);
}
}
printf(")");
}
printf("\n");
}
void sectionl () //分段线性插值
{
float x[5]={2.0,2.1,2.2,2.3,2.4};
float y;
printf("请输入y:");
scanf("%f",&y);
if(y>=2.0&&y<2.1)
{
float px;
px=((y-x[1])/(x[0]-x[1]))*g (x[0])+((y-x[0])/(x[1]-x[0]))*g (x[1]);
printf("f(%f)=%f\n",y,px);
}
else if(y>=2.1&&y<2.2)
{
float px;
px=((y-x[2])/(x[1]-x[2]))*g (x[1])+((y-x[1])/(x[2]-x[1]))*g (x[2]);
printf("f(%f)=%f\n",y,px);
}
else if(y>=2.2&&y<2.3)
{
float px;
px=((y-x[3])/(x[2]-x[3]))*g (x[2])+((y-x[2])/(x[3]-x[2]))*g (x[3]);
printf("f(%f)=%f\n",y,px);
}
else if(y>=2.3&&y<2.4)
{
float px;
px=((y-x[4])/(x[3]-x[4]))*g (x[3])+((y-x[3])/(x[4]-x[3]))*g (x[4]);
printf("f(%f)=%f\n",y,px);
}
else if(y>2.4) printf("**********ERROR!******************\n"); }
void sectionp ()
{
int i;
float a[5]={2.0,2.1,2.2,2.3,2.4};
float x,y;
printf("input the data: x?\n");
scanf("%f",&x);
if(x<a[1])
{i=1;goto loop;}
if(x>a[4])
{i=4;goto loop;}
i=1;
loop1:i++;
if(x>a[i])goto loop1;
if(fabs(x-a[i-1])<=fabs(x-a[i]))i=i-1;
loop:y=g(a[i-1])*(x-a[i])*(x-a[i+1])/((a[i-1]-a[i])*(a[i-1]-a[i+1]));
y=y+g(a[i])*(x-a[i-1])*(x-a[i+1])/((a[i]-a[i-1])*(a[i]-a[i+1]));
y=y+g(a[i+1])*(x-a[i-1])*(x-a[i])/((a[i+1]-a[i-1])*(a[i+1]-a[i]));
printf("f(%f)=%f\n",x,y);
}
int main()
{
char flag1='y';
while(flag1=='y')
{
int flag=0;
printf("*******[1]:线性插值***************\n");
printf("*******[2]:二次插值***************\n");
printf("*******[3]:Hermite插值************\n");
printf("*******[4]:分段线性插值***********\n");
printf("*******[5]:分段抛物线插值*********\n");
printf("请输入:");
scanf("%d",&flag);
switch(flag)
{
case 1:
linerity ();break;
case 2:
second ();break;
case 3:
Hermite ();break;
case 4:
sectionl ();break;
case 5:sectionp ();break;
default:
printf("error!!\n");
}
printf("是否继续?y/n \n");
getchar();
scanf("%c",&flag1);
}
return 0;
}。
