数值分析中的(插值法)

合集下载

数值分析插值法

数值分析插值法插值法是数值分析中的一种方法，用于通过已知数据点的函数值来估计介于这些数据点之间的未知函数值。

插值法在科学计算、数据处理、图像处理等领域中得到广泛应用。

插值法的基本思想是通过已知数据点构造一个函数，使得该函数逼近未知函数，并在已知数据点处与未知函数值相等。

插值法的关键是选择适当的插值函数，以保证估计值在插值区间内具有良好的近似性质。

常用的插值法有拉格朗日插值法、牛顿插值法和埃尔米特插值法等。

以下将分别介绍这些插值法的原理及步骤：1. 拉格朗日插值法：拉格朗日插值法通过构造一个多项式函数来逼近未知函数。

假设已知n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，其中x0, x1, ..., xn为给定的节点，y0, y1, ..., yn为对应的函数值。

拉格朗日插值多项式的一般形式为：L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中l0(x), l1(x), ..., ln(x)为拉格朗日基函数，定义为：li(x) = (x - x0)(x - x1)...(x - xi-1)(x - xi+1)...(x - xn) / (xi - x0)(xi - x1)...(xi - xi-1)(xi - xi+1)...(xi - xn)拉格朗日插值法的步骤为：a. 计算基函数li(xi)的值。

b.构造插值多项式L(x)。

c.计算L(x)在需要估计的插值点上的函数值f(x)。

2.牛顿插值法：牛顿插值法通过构造一个差商表来逼近未知函数。

差商表的第一列为已知数据点的函数值，第二列为相邻数据点的差商，第三列为相邻差商的差商，以此类推。

最终，根据差商表中的数值，构造一个差商表与未知函数值相等的多项式函数。

牛顿插值法的步骤为：a.计算差商表的第一列。

b.计算差商表的其他列，直至最后一列。

c.根据差商表构造插值多项式N(x)。

数值分析实验报告--实验2--插值法

1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。

显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式的次数增加时，是否也更加靠近被逼近的函数。

龙格（Runge ）给出一个例子是极著名并富有启发性的。

设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。

实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。

(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。

(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。

1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。

1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。

Matlab 脚本文件为Experiment2_1_1fx.m 。

可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。

数值分析第五章插值法

数值分析第五章插值法插值法是数值分析中常用的一种数值逼近方法，它的目的是通过已知数据点之间的插值多项式来逼近未知数据点的函数值。

插值法可以在信号处理、图像处理、计算机图形学等领域中广泛应用。

在插值法中，最常用的方法有拉格朗日插值法和牛顿插值法。

拉格朗日插值法是一种利用拉格朗日插值多项式来逼近函数的方法。

对于n个已知数据点(xi, yi)，拉格朗日插值多项式L(x)可以表示为：L(x) = ∑(yi * li(x))其中，li(x)表示拉格朗日基函数，定义为：li(x) = ∏[(x - xj)/(xi - xj)] (j≠i)可以证明，在给定的n个数据点上，拉格朗日插值多项式L(x)满足：L(xi) = yi牛顿插值法是另一种常用的插值方法，它利用差商的概念来逼近函数。

对于n个已知数据点(xi, yi)，差商可以定义为：f[xi] = yif[xi, xi+1] = (f[xi+1] - f[xi]) / (xi+1 - xi)f[xi, xi+1, ..., xi+k] = (f[xi+1, ..., xi+k] - f[xi, ...,xi+k-1]) / (xi+k - xi)通过差商的递归定义，可以得到牛顿插值多项式N(x)的表达式，其中：N(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...与拉格朗日插值法类似，牛顿插值多项式N(x)也满足：N(xi) = yi这两种插值方法都有自己的优点和缺点。

拉格朗日插值法简单易懂，计算量小，但当数据点较多时，多项式的次数会很高，容易出现龙格现象。

而牛顿插值法可以通过求差商一次次递推得到插值多项式，计算效率较高，且具备局部逼近性，不易出现龙格现象。

除了拉格朗日插值法和牛顿插值法，还有其他插值方法，如分段线性插值、样条插值等。

分段线性插值是利用线性多项式逼近函数，将数据点之间的区间分为若干段，每段内使用一条线性多项式进行插值。

数值分析插值法

图形见图2-3. 称 lk ( x) 及 lk 1 ( x) 为线性插值基函数，
11
图2-3
12
பைடு நூலகம் 2.
n次插值多项式
根据插值的定义 Ln ( x) 应满足
Ln ( x j ) y j ( j 0,1, , n).
为构造 Ln ( x)，先定义 n 次插值基函数.
13
定义1 若 n 次多项式 L j ( x ) ( j 0,1, , n) 在 n 1 个节点
L1 ( xk 1 ) yk 1.
8
其几何意义就是通过两点( xk , yk ), ( xk 1 , yk 1 ) 的直线. 如图2-2.
图2-2
9
由 L1 ( x) 的几何意义可得到表达式
L1 ( x ) y k y k 1 y k ( x xk ) xk 1 xk
5
因为线性方程组的系数行列式
1 1 . . 1 xn ...
n xn
x0 x1
... ...
n x0 n x1
0
所以线性方程组的解存在且唯一。
6
定理1
在次数不超过 n 的多项式集合 H n 中，满足条
件的
插值多项式 L ( x) H是存在唯一的. n n
7
2.3
1. 线性插值
拉格朗日插值
y
k 0
n
k
l k ( x ).
Ln ( x j ) yk lk ( x j ) y j
( j 0,1, , n).
称为拉格郎日（Lagrange)插值多项式而线性插值与抛物线插值是 n=1 和 n=2 的特殊情形
若引入记号

数值分析与计算方法第一章插值法

同理： (t) 至少有n 个互异零点；
(t) 至少有n 1 个零点；
(n1) (t ) 至少有一个零点；即 (a ，b)，
(n1) (
)
R(n1) n
(
)
K ( x)n1(n1) (
)
R(n1) n
(
)
K ( x) (n
1)!
f (n1) ( ) K ( x) (n 1)! 0
x x0 x1 x2 xn ， y f ( x)？ y y0 y1 y2 yn
（1）有的函数没有表达式，只是一种表格函数，而我们需要的函数值可能不在该表格中。
（2）如果函数表达式本身比较复杂，计算量会很大；
对于这两种情况，我们都需要寻找一个计算方便且表达简单
的函数 P x来近似代替 f ( x)，求 P x 的方法称为插值法。
Ln1( x)
为此我们考虑对Lagrange插值多项式进行改写； ——由唯一性，仅是形式上的变化
期望：Ln ( x) 的计算只需要对Ln1( x)作一个简单的修正.
考虑 h( x) Ln ( x) Ln1( x) h( x) 是次数 n 的多项式，且有
h( x j ) Ln ( x j ) Ln1( x j ) 0 ，j 0 ，1，2 ，L ，n 1 ；
)
3
)
1 2
(x
(
4
6
6
)( x
)(
4
3
)
3
)
1
(
x
6
)(
x
4
)
2
(
3
6
)(
3
4
)
3 2

数值分析第2章插值法

0.32 0.34
0.34 0.32
0.330365.
截断误差为：R1x
f
1
2！
2
x
M2 2
x
x0 x
x1 ，其中：
M2
max
x0 x x1
f x，f x sin x，f x
sin x，M2
sin x1
0.3335
R1 0.3367
sin0.3367
L1 0.3367
x a, b,插值余项Rn x
f x Ln x
f n1 n 1!
n1
x
,
其
中
a,
b,
与x有关,n1x
n
x
k0
xk
.
n
性质： lk x 1. k0
5
例1、证明： ( xi x)2 li ( x) 0, 其中li ( x)是关于点x0 , x1 ,, x5的插值 i0
基函数.
2.2 拉格朗日插值
2.2.1、线性插值与抛物插值
1、线性插值：
设 yk f xk ， yk1 f xk1 ， xk xk1 求一次多项式 L1 x，满足：L1 xk yk，L1 xk1 yk1
L1 x
yk
yk1 xk1
yk xk
x xk
求n次插值多项式Ln x, 满足：Ln xi yi i 0，1，2，，n
Ln
x
n
lk
x
yk
k0
lk
xj
1，k j
kj 0，k j
j 0，1，2，，n
lk x
x

数值分析中的插值算法及其应用

数值分析中的插值算法及其应用数值分析是研究解决数学问题的数值方法的一门学科。

其中，插值算法是数值分析中重要的方法之一。

插值是指在给定一些数据点的情况下，用一些方法建立一个函数，该函数可以在给定区间内的任何一点上计算出函数值。

插值方法有很多种，其中比较常用的有拉格朗日插值法、牛顿插值法和埃尔米特插值法。

1. 拉格朗日插值法拉格朗日插值法是一种将一个多项式函数p(x)与一系列已知数据点相联系的方法。

假设给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn)，其中x1 < x2 < ... < xn，那么可以构造一个次数小于等于n-1的多项式函数p(x)满足p(xi) = yi，i=1,2,...,n。

设p(x)的表达式为：p(x) = Σyi li(x)其中，li(x)为拉格朗日基函数。

每个基函数都满足：li(xi) = 1, li(xj) = 0, j≠i基函数的表达式为：li(x) = Π[j≠i] (x - xj) / (xi - xj)利用拉格朗日插值法，可以在给定数据点的情况下，快速计算函数在其他点上的值。

2. 牛顿插值法牛顿插值法是一种利用差商的方法建立插值多项式的方法。

相比于拉格朗日插值法，牛顿插值法更注重于递推计算。

给定n个数据点(x1, y1), (x2, y2), ..., (xn, yn)，牛顿插值法可以建立一个关于x的n次多项式。

首先，定义一个差商：f[xi] = yif[xi, xi+1, ..., xj] = (f[xi+1, ..., xj] - f[xi, ..., xj-1]) / (xj - xi)差商f[xi, xi+1, ..., xj]是由区间(xi, xj)内的函数值f(xi), f(xi+1), ..., f(xj)所计算得到的。

定义一个新的多项式qk(x)，其中：qk(x) = f[x0, x1, ..., xk] + (x - xk) qk-1(x)其中q0(x) = f[x0]。

《数值分析》第二讲插值法PPT课件

1 xn xn2 xnn Vandermonde行列式
即方程组（2）有唯一解 (a0, a1, , an)
所以插值多项式
P (x ) a 0 a 1 x a 2 x 2 a n x n
存在且唯一
第二章：插值
§2.2 Lagrange插值
y
数值分析
1、线性插值
P 即(x)ykx yk k 1 1 x yk k(xxk)
l k ( x k 1 ) 0 ,l k ( x k ) 1 ,l k ( x k 1 ) 0 l k 1 ( x k 1 ) 0 ,l k 1 ( x k ) 0 ,l k 1 ( x k 1 ) 1
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) lk(x)((xx k x xk k 1 1))((x xkxx k k1)1)
第二章：插值
数值分析
3、Lagrange插值多项式
令 L n ( x ) y 0 l 0 ( x ) y 1 l 1 ( x ) y n l n ( x )
其中，基函数
lk (x ) (x ( k x x x 0 ) 0 ) (( x x k x x k k 1 1 ) )x x k ( ( x x k k 1 ) 1 ) (( x x k x n x )n )
因此 P (x ) lk (x )y k lk 1 (x )y k 1
且
P (x k ) y k P (x k 1 ) y k 1
lk(x), lk1(x) 称为一次插值基函数
数值分析
第二章：插值
2、抛物线插值令
y (xk , yk )
f (x)
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) p( x) (xk1,yk1)

数值分析插值法

系数行列式（n+1阶范德蒙行列式）
1 1 1
x0 x1 xn
2 x0 2 x1
n x0 n x1

0 i j n
2 xn n xn

( x j xi ) 0
, an .
由克莱默法则知，方程组有唯一解 a0 , a1 ,
§2 Lagrange Polynomial
唯一性的另一证明满足 P( xi ) yi , i 0, ... , n 的 n 阶插值多项式是唯一存在的。
f (x)
(x0 ,y0)
(x1 ,y1)
P1(x)
x0
x1
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
§2 Lagrange Polynomial
y1 y0 直线方程为: y y0 x x ( x x0 ) 1 0
记 P 1 ( x) L 1 ( x) ，上式等价变形为:
化简得到
L2 ( x ) l0 ( x ) y0 l1 ( x ) y1 l2 ( x ) y2 l i ( x ) yi .
i 3
成立:
l 0 ( x0 ) 1 l ( x ) 0 0 1 l 0 ( x 2 ) 0
l1 ( x 0 ) 0 l ( x ) 1 1 1 l1 ( x 2 ) 0
l 2 ( x0 ) 0 l ( x ) 0 2 1 l 2 ( x 2 ) 1
将以上思路推广到n+1个节点情形，即可得到类似的插值基函数和插值多项式表示形式。
§2 Lagrange Polynomial
2-3 Lagrange插值多项式

数值分析中的(插值法)

与其他方法的结合
插值法可以与其他数值分析方法结合使用，以获得更准确和可靠的估计结果。例如，可以考虑将插值法与回归分析、时间序列分析等方法结合，以提高数据分析的效率和精度。
THANKS
感谢观看
多项式的阶数
根据数据点的数量和分布情况，选择适当的多项式阶数，以确保多项式能够更好地逼近真实数据。
计算多项式的系数
通过已知的数据点和多项式阶数，计算出多项式的系数，从而得到完整的插值多项式。
计算插值多项式的导数
导数的计算
在某些应用中，需要计算插值多项式的导数，例如在曲线拟合、数值微分等场景中。
总结词
牛顿插值法是一种基于差商的插值方法，通过构造差商表来逼近未知点的数值。
详细描述
牛顿插值法的基本思想是通过构造差商表来逼近未知点的数值，差商表中的每一项都是根据前一项和后一项的差来计算的。该方法在数值分析中广泛应用于数据拟合、函数逼近等领域。
样条插值法
总结词
样条插值法是一种通过已知的离散数据点来构造一个样条函数，用于估计未知点的数值的方法。
常见的插值法
拉格朗日插值法
总结词
拉格朗日插值法是一种通过已知的离散数据点来构造一个多项式，用于估计未知点的数值的方法。
详细描述
拉格朗日插值法的基本思想是通过构造一个多项式来逼近已知数据点，使得该多项式在每个数据点的取值与实际值相等。该方法在数值分析中广泛应用于数据拟合、函数逼近等领域。
牛顿插值法
增加采样点的数量可以减小离散化误差，提高插值结果的稳定
性。
选择合适的插值方法
02
根据具体情况选择适合的插值方法，如多项式插值、样条插值
等，以获得更好的逼近效果和稳定性。
引入阻尼项

数值分析插值法

解由上表可得过前三点的二次牛顿插值多项式为
故
又
可得过前四点的三次牛顿插值多项式
可得N3(x)的截断误差
差分与等距节点的牛顿插值多项式
设函数y=fx在等距节点xi=x0+ih i=01 …n上的函数值为fi=fxih为步长
定义2 fi=fi+1-fi 和 fi=fi-fi-1 分别称为函数fx在点xi处的一阶向前差分和一阶向后差分
求f2.8用牛顿后插公式且由 2.8=3+0.5t 得 t= -0.4
第四节埃尔米特Hermite插值
一、埃尔米特插值多项式
为了使插值函数能更好的切合原来的函数许多问题不但要求节点上的函数值相等还要求导数值相同甚至高阶导数也相等这类插值问题称为埃尔米特插值
xi[a, b] (i=0,1, …, n) 为n+1个互异节点,考虑函数值与导数个数相等的情况。
二、误差估计
定理4 设fx在包含x0、x1的区间ab内存在四阶导数则当x∈ab时有
且与x有关)
例1 已知fx=x1/2在X=121和144时的函数值及其一阶导数的数据见下表用埃尔米特插值公式计算1251/2的近似值并估计其截断误差.
得
由
可求得
例2
第五节分段低次插值
解 (1) 用线性插值
第三节均差与牛顿插值公式
一、差商及其基本性质
定义1 称
为 f x在x0、x1点的一阶差商.一阶差商的差商
称为函数f x在x0、x1 、x2 点的二阶差商.
一般地n-1阶差商的差商
称为f x在x0 x1 … xn点的 n 阶差商
差商的计算步骤与结果可列成差商表如下
xk
函数值
一阶差商

数值分析中常用的插值方法

数值分析中常用的插值方法在数值计算中，许多问题都可以用插值方法来近似求解，比如曲线拟合、函数逼近和图像重建等。

插值方法是指在已知数据点的情况下，通过一些数值计算技巧，在每个数据点处构造一个多项式函数，使得该函数在每个数据点处都能通过数据点。

在数据点之间计算函数值时，就可以使用这个多项式函数进行估算。

接下来，我们就来详细介绍一些常见的插值方法。

一、拉格朗日插值法拉格朗日插值法是一个经典的插值方法，它的思想是通过给定的数据点，构造一个经过这些点的多项式函数进行逼近。

具体来讲，拉格朗日插值法会首先构造一个基函数，该函数满足只在其对应的数据点处等于1，其余的数据点处等于0。

然后，根据基函数和数据点，构造一个多项式函数，使得该函数在每个数据点处都能通过数据点。

最终得到的多项式函数就是插值函数。

优点：简单易懂，使用较为广泛。

缺点：多项式次数较高时造成的误差会较大，且在数据点密集的区域可以出现龙格现象，使得插值函数在某些区间内呈现大幅度振荡。

二、牛顿插值法牛顿插值法是一种递推式的插值方法，它通过利用已知的数据点和前面已经计算出来的差商，得到一个逐步逼近的插值函数。

具体来讲，牛顿插值法会先将已知的数据点连成一条曲线，然后逐个向这条曲线添加新的数据点，每次添加一个新的数据点后，将差商计算出来并加入到之前的差商序列中，最终得到一个多项式函数，它在每个数据点处都能通过数据点。

牛顿插值法的优缺点与拉格朗日插值法相似，但是由于牛顿插值法是递推式的，可以方便的添加新的数据点，因此在数据点多变的情况下，牛顿插值法具有很大的优势。

三、分段插值法分段插值法是一种将插值区间划分为多个子区间的插值方法，在每个子区间内使用插值方法进行插值，然后将所有子区间内的插值函数拼接起来，得到最终的插值函数。

分段插值法主要分为两种：线性分段插值和三次样条插值。

1.线性分段插值线性分段插值的思路很简单，即在每个数据点处构造两条直线，在数据点之间的区间内使用一条直线作为插值函数。

数值分析-插值法的讲解

y=P(X) y=f(x)
称P(x)为f(x)的插值函数，x为插值节点，[a,b]为插值区间，求插值函数P(x)的方法为插值法。
若P(x)=a0+a1x+▪▪▪+anxn，称 P(x)为插值多项式。若P(x)为分段多项式，就称之为分段插值。
若P(x)为三角多项式，就称之为三角插值。
枪管膛线－－－－→
1.插值多项式的存在唯一性 P(x)=a0+a1x+▪▪▪+anxn, P(x) ∈Hn a0+a1x0+…+anx0n=y0 a0+a1x1+…+anx1n=y1
. . .
a0+a1xn+…+anxnn=yn
1 x x ... x Vn(x0,x1,…,xn)= 1 x x ... x ... 1 x x ... x
k 1 k 1 k 1 k 1

y
( x xk 1)( x xk 1)
k
( xk xk 1)( xk xk 1)
T H A N K Y O U !
( x xk 1)( x xk ) ( xk 1 xk 1)( xk 1 xk )
k k k 1
l
l
2
k
k 1
( x xk )( x xk 1) ( x x )( x x ) y ( )( ) L ( x) yk 1 x x x x ( xk 1 xk )( xk 1 xk 1)
k 1
x
x xk
k 1
k ห้องสมุดไป่ตู้1
k
xk
L1(x)=
x x y x x y x x x x

数值分析--第2章插值法

数值分析--第2章插值法第2章插值法在科学研究与工程技术中，常常遇到这样的问题：由实验或测量得到一批离散样点，要求作出一条通过这些点的光滑曲线，以便满足设计要求或进行加工。

反映在数学上，即已知函数在一些点上的值，寻求它的分析表达式。

此外，一些函数虽有表达式，但因式子复杂，不易计算其值和进行理论分析，也需要构造一个简单函数来近似它。

解决这种问题的方法有两类：一类是给出函数)(x f 的一些样点，选定一个便于计算的函数)(x ϕ形式，如多项式、分式线性函数及三角多项式等，要求它通过已知样点，由此确定函数)(x ϕ作为)(x f 的近似，这就是插值法；另一类方法在选定近似函数的形式后，不要求近似函数过已知样点，只要求在某种意义下在这些样点上的总偏差最小。

这类方法称为曲线（数据）拟合法。

设已知函数f 在区间],[b a 上的1+n 个相异点ix 处的函数值(),0,,iif f x i n ==，要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈，使得()(),0,1,,iiix f x f i n ϕ=== (2-1) 这类问题称为插值问题。

称f 为被插值函数；()x ϕ为插值函数；nx x ,,0 为插值节点；(2-1)为插值条件。

若插值函数类{()}x ϕ是代数多项式，则相应的插值问题为代数插值。

若{()}x ϕ是三角多项式，则相应的插值问题称为三角插值。

若{()}x ϕ是有理分式，则相应的插值问题称为有理插值。

§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f 在1+n 个相异点01,,,nx x x 上的值n i x f f ii ,,1,0),( ==是已知的，在次数不超过n 的多项式集合n P 中，求()nL x 使得(),0,1,,n i iL x f n n == (2-2) 定理2.1 存在惟一的多项式nn P L ∈满足插值条件(2-2)。

数值分析中的插值方法

数值分析中的插值方法在数值分析中，插值是一种通过在已知数据点之间估计未知数据点的方法。

它是一种常见的数据处理技术，用于填补数据间的空白，揭示数据间的关联性，或者建立数据模型。

在本文中，我们将讨论数值分析中的几种常见的插值方法。

一、拉格朗日插值拉格朗日插值是一种基于多项式的插值方法。

假设有n个离散数据点，我们想要在这些点之间插值得到未知数据点的值。

拉格朗日插值可以通过构建一个n次多项式来实现。

例如，给定三个数据点(x0, y0)，(x1, y1)，(x2, y2)，我们可以假定插值多项式为：P(x) = y0 * L0(x) + y1 * L1(x) + y2 * L2(x)其中，L0(x)，L1(x)，L2(x)是拉格朗日插值多项式的基函数，由以下公式得到：L0(x) = (x - x1) * (x - x2) / ((x0 - x1) * (x0 - x2))L1(x) = (x - x0) * (x - x2) / ((x1 - x0) * (x1 - x2))L2(x) = (x - x0) * (x - x1) / ((x2 - x0) * (x2 - x1))利用这些基函数，我们可以得到插值多项式P(x)，从而计算出未知点的值。

二、牛顿插值牛顿插值是另一种常见的插值方法，也是基于多项式的。

与拉格朗日插值不同的是，牛顿插值使用了差商的概念来构建插值多项式。

差商是一种表示数据间差异的指标，它可以用于计算插值多项式的系数。

对于n个数据点，差商可以由以下递归公式计算得到：f[x0] = f(x0)f[x0, x1] = (f[x1] - f[x0]) / (x1 - x0)f[x0, x1, ..., xn] = (f[x1, x2, ..., xn] - f[x0, x1, ..., xn-1]) / (xn - x0)基于差商，我们可以得到牛顿插值多项式的表达式：P(x) = f[x0] + f[x0, x1] * (x - x0) + f[x0, x1, x2] * (x - x0) * (x - x1) + ...利用牛顿插值，我们可以通过已知数据点构建插值多项式，进而估计未知点的值。

数值分析-插值法

数值分析-插值法我们能得到⼀个函数f在区间[a,b]上某些点的值或者这些点上的⾼阶导数我们就能通过插值法去得到⼀个函数g，g与f是⾮常相近的⼀般来说g分为三类，⼀类是n次多项式 a n*x n +a n-1*x n-1 + .......+a0，⼀类是三⾓多项式，最后⼀类是分段n次多项式多项式插值这个可以说是最简单的插值了对于a n*x n +a n-1*x n-1 + .......+a0，我们有n+1个未知数，我只需要知道n+1个点的函数值就可以解出这n+1个未知数将解出的值带⼊即可优点:简单粗暴缺点:要解n+1个⽅程，时间复杂度较⾼，n不好确定，若n过⼤，容易过拟合，若n过⼩，容易⽋拟合拉格朗⽇插值先说⼀阶多项式我们有两点式f(x) = y k*(x k+1 - x) / (x k-x k+1) + y k+1*(x-x k) / (x k+1 - x k)此两点式可以看做∂ * y k + (1-∂) * y k+1那么⾃然的在x=x k的时候 ∂=0 在x=x k+1的时候∂=1这⾥的∂其实是与x相关的⼀阶多项式再说⼆阶多项式对于⼀个⼆次函数，我们有三个点(x k-1,y k-1) ,(x k,y k) ,(x k+1,y k+1)我们有l k-1,l k,l k+1f(x) = l k-1*y k-1 + l k*y k + l k+1*y k+1其中l是与x相关的⼆次多项式我们可以把l当作基函数这样的话就有x = x k-1 时l k-1 = 1, l k=0, l k+1 = 0x = x k时 l k-1 = 0, l k=1, l k+1 = 0x = x k+1时l k-1 = 0, l k=0, l k+1 = 1那么这个插值基函数是很好求的因为每个插值函数都有两个零点对于l k-1来说有零点x k,x k+1那么lk-1就可以表⽰为l k-1 = A*(x-x k)*(x-x k+1)因为x=xk-1时l k-1 = 1所以A = 1 / (（x k-1 - x k）* (x k-1 - x k+1) )那么同理l k和l k+1也能求出来了那我们得到⼆阶的拉格朗⽇插值多项式现在将⼆阶推⼴到n阶得到n接的拉格朗⽇插值多项式余项:R n(x) = f(x) - L n(x) R n(x)表⽰n次拉格朗⽇多项式的插值余项R n(x) = f n+1(e)/(n+1)! * w n+1(x) e属于[a,b]且依赖与x w n+1(x) = (x-x0)(x-x1).......(x-x n)优点:算法较为简单缺点:⽆法处理动态增加节点的情况⽜顿插值还是先从⼀阶到⼆阶进⾏说明我先得到了⼀阶差值多项式P1(x),P1(x) 满⾜过点(x1, f(x1)), (x2,f(x2))假设现在有第三个点(x3,f(x3))我们要通过这个点去得到⼆阶差值多项式P2(x) 使得P2(x)过这三个点可以设P2(x) = P1(x) + a2*(x-x0)*(x-x1)通过第三个点解出a2就⾏了推⼴到多阶那么可以得到P n(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + a3(x-x0)(x-x1)(x-x2) + ......求这个插值多项式的值可以通过递推⼀步⼀步的求这样就实现了动态增删可以看到计算a k需要计算(k-1)2次，那么⽜顿插值法就是⼀个快速的计算⽅法均差⼀阶均差 f[x0, x k] = ( f(x k) - f(x0) ) / (x k - x0)⼆阶均差 f[x0, x1, x2] = (f[x0, x2] -f[x0, x1] ) / (x2 - x1)可以看到⼀阶均差就是简单的求斜率⼆阶均差就是对⼀阶均差求斜率那么k阶均差就是f[x0, x1,,,,,,x k] = (f[x0,,,,,x k-2, x k] -f[x0, ,,,,,,,x k-2,x k-1] ) / (x k - x k-1)f[x0, x1,,,,,,x k] = f n(ε) / n!均差的性质k阶均差可表⽰为f(x0),f(x1), f(x2),,,,,,,,, f(x k)的线性组合⽜顿插值中的a就是均差，可以从⼀阶开始推，然后使⽤数学归纳法证明那么⽜顿插值多项式就是：在计算f[x0,x1,,,,,,,,,,x n]时，⼀般使⽤均差表均差表的计算⽅式为a[i,j] = ( a[i-1][j] - a[i-1][j-1] ) / (末尾的x - 最开始的x)误差:误差为最后⼀阶的均差 * w(x)优点:可动态增删节点缺点:⽆法处理要求导数相同的情况埃尔⽶特插值法实验报告⼀个点，多个导数:⽜顿插值中的均差在xi->x0时其实分别是i阶导数，这样就是我们熟悉的泰勒多项式此时的插值函数就是泰勒多项式两个点，⼀个导数我们有三个条件，也就是说我们能求出三次插值多项式这时我们先写出过这两个点的⽜顿插值多项式在这个多项式的基础上我们再加上⼀个三次项搞定，可以观察到，这三个项数其实可以算是正交的，因为当x=x1或者x=x2时最后⼀项是0满⾜条件的两个点，两个导数这也是题⽬所要求的情况因为有两个导数，所以⽜顿插值法⽆法解决，这⾥只能使⽤基函数⽅法设插值函数为H(x), 点与导数分别为(x1,y1,m1),(x2,y2,m2)H(x)满⾜：H(x1) =y1, H(x2) = y2, H(x1)’ = m1,H(x2)=m2H(x) = a1*x1 + a2*x2 + b1*m1 + b2*m2其中 a1, a2, b1, b2均为三层插值多项式X=x1时 a1(x1) = 1,a2(x1) = 0, b1(x1) = 0,b2(x1) = 0,a1’(x1) = 1,a2’(x1) = 0X=x2时 a1(x2) = 0,a2(x2) = 1, b1(x2) = 0,b2(x2) = 0,a1’(x2) = 1,a2’(x2) = 0X=x1时 b1’(x1) = 1,b2’(x1) = 0X=x2时b1’(x1) = 0,b2’(x1) = 1然后⽤了⼀个很巧妙的⽅法设基函数，解出来值和就是这样⼦的R3(x) = 1/4! * (x-x k)2(x-x k+1)2*f4(ε)两个点，两个导数2直接使⽤泰勒多项式，并把将余项改为未知数，使⽤多余的⼀个条件去求余项的值例如:求次数⼩于等于3的多项式P(x)，使满⾜条件P(x0)=f(x0)，P'(x0)=f'(x0)，P"(x0)=f"(x0)，P(x1)=f(x1)。

数值分析常用的插值方法

数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。

下面将对这些插值方法进行详细介绍。

一、线性插值（linear interpolation）线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值，通过这两个点之间的直线来估计中间点的函数值。

线性插值公式为：f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中，f(x)表示要求的插值点的函数值，f(x0)和f(x1)是已知的两个点上的函数值，x0和x1是已知的两个点的横坐标。

二、拉格朗日插值（Lagrange interpolation）拉格朗日插值是一种基于多项式的插值方法。

它通过多个已知点的函数值构造一个多项式，并利用这个多项式来估计其他点的函数值。

拉格朗日插值多项式的一般形式为：f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中，f(x)表示要求的插值点的函数值，f(xi)是已知的多个点的函数值，Li(x)是拉格朗日基函数。

拉格朗日基函数的表达式为：Li(x) = Π[(x-xj)/(xi-xj)] (i≠j，i,j=0,1,2,...,n)三、分段线性插值（piecewise linear interpolation）分段线性插值是一种逐段线性近似函数的方法。

通过将整个插值区间分成多个小段，在每个小段上使用线性插值来估计函数的值。

分段线性插值的过程分为两步：首先确定要插值的点所在的小段，在小段上进行线性插值来估计函数值。

四、Newton插值（Newton interpolation）Newton插值也是一种基于多项式的插值方法。

利用差商的概念来构造插值多项式。

Newton插值多项式的一般形式为：f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中，f(x)表示要求的插值点的函数值，f(x0)是已知的一个点的函数值，f[xi,xi+1,...,xi+k]是k阶差商。

数值分析——插值法

当精确函数 y = f(x) 非常复杂或未知时，在一系列节点 x0 … xn 处测得函数值 y0 = f(x0), … yn = f(xn)，由此构造一个简单易算的近似函数 g(x) f(x)，满足条件g(xi) = f(xi) (i = 0, … n)。这里的 g(x) 称为f(x) 的插值函数。
然而,方程组的求解也并不是一件容易的事。
对于线性插值的两种形式解进行适当的分析, 从中寻求规律而得到启发,就有了所谓的拉格朗日插值法(公式)和牛顿插值(公式).
我们先来看看如何得到二次拉格朗日插值公式（和牛顿插值公式（为讨论方便，留待后述））.
称为拉氏基函数，满足 li(xj)=ij 首先, 线性插值的两点式可看作是两个特殊的一次式的一种线性组合. 两点式 P1 ( x ) =
x - x1 y + x 0 - x1 0 x - x0 y = x1 - x 0 1
1.2.2 基函数法
l ( x) y
i =0 i
1
i
l0(x) l1(x) 这里， l0(x)和l1(x)具有如下性质：显然有l0(x)+ l0(x)≡1. 实质上 l（（ 0 x）和 l 1 x）即是满足函数表
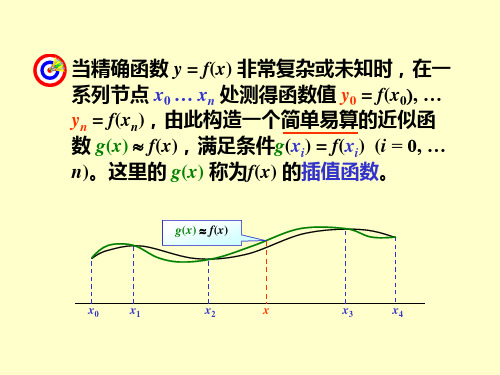
g(x) f(x)
x0
x1
x2
x
x3
x4
根据实际需要，可以用各种不同的函数来近似原来的函数。
最常用的插值函数是多项式： …?
代数多项式最简单，计算其值只需用到加、减乘运算，且积分和微分都很方便；所以常用它来近似表示表格函数(或复杂函数),这样的插值方法叫做代数插值法，简称插值法。
§1 拉格朗日多项式
求 n 次多项式 Pn ( x) = a0 a1 x an x n 使得

(完整版)数值分析插值法

第二章插值法2.在区间[-1,1]上分别取n=10,20用两组等距节点对龙哥函数f(x)=1/(1+25*x^2)做多项式插值及三次样条插值，对每个n值，分别画出插值函数及f（x）的图形。

（1）多项式插值①先建立一个多项式插值的M-file；输入如下的命令（如牛顿插值公式）：function [C,D]=newpoly(X,Y)n=length(X);D=zeros(n,n)D(:,1)=Y'for j=2:nfor k=j:nD(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1));endendC=D(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)))m=length(C);C(m)= C(m)+D(k,k);end②当n=10时，我们在命令窗口中输入以下的命令：clear,clf,hold on;X=-1:0.2:1;Y=1./(1+25*X.^2);[C,D]=newpoly(X,Y);x=-1:0.01:1;y=polyval(C,x);plot(x,y,X,Y,'.');grid on;xp=-1:0.2:1;z=1./(1+25*xp.^2);plot(xp,z,'r')得到插值函数和f（x）图形：③当n=20时，我们在命令窗口中输入以下的命令：clear,clf,hold on;X=-1:0.1:1;Y=1./(1+25*X.^2);[C,D]=newpoly(X,Y);x=-1:0.01:1;y=polyval(C,x);plot(x,y,X,Y,'.');grid on;xp=-1:0.1:1;z=1./(1+25*xp.^2);plot(xp,z,'r')得到插值函数和f（x）图形：（2）三次样条插值①先建立一个多项式插值的M-file；输入如下的命令:function S=csfit(X,Y,dx0,dxn)N=length(X)-1;H=diff(X);D=diff(Y)./H;A=H(2:N-1);B=2*(H(1:N-1)+H(2:N));C=H(2:N);U=6*diff(D);B(1)=B(1)-H(1)/2;U(1)=U(1)-3*(D(1));B(N-1)=B(N-1)-H(N)/2;U(N-1)=U(N-1)-3*(-D(N));for k=2:N-1temp=A(k-1)/B(k-1);B(k)=B(k)-temp*C(k-1);U(k)=U(k)-temp*U(k-1);endM(N)=U(N-1)/B(N-1);for k=N-2:-1:1M(k+1)=(U(k)-C(k)*M(k+2))/B(k);endM(1)=3*(D(1)-dx0)/H(1)-M(2)/2;M(N+1)=3*(dxn-D(N))/H(N)-M(N)/2;for k=0:N-1S(k+1,1)=(M(k+2)-M(k+1))/(6*H(k+1));S(k+1,2)=M(k+1)/2;S(k+1,3)=D(k+1)-H(k+1)*(2*M(k+1)+M(k+2))/6;S(k+1,4)=Y(k+1);end②当n=10时，我们在命令窗口中输入以下的命令：clear,clcX=-1:0.2:1;Y=1./(25*X.^2+1);dx0= 0.0739644970414201;dxn= -0.0739644970414201; S=csfit(X,Y,dx0,dxn)x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')结果如图：②当n=20时，我们在命令窗口中输入以下的命令：clear,clcX=-1:0.1:1;Y=1./(25*X.^2+1);dx0= 0.0739644970414201;dxn= -0.0739644970414201; S=csfit(X,Y,dx0,dxn)x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')结果如图：第三章函数逼近与快速傅里叶变换2. 由实验给出数据表x 0.0 0.1 0.2 0.3 0.5 0.8 1.0y 1.0 0.41 0.50 0.61 0.91 2.02 2.46试求3次、4次多项式的曲线拟合，再根据数据曲线形状，求一个另外函数的拟合曲线，用图示数据曲线及相应的三种拟合曲线。

数值分析中的(插值法)

数值分析插值法

数值分析实验报告--实验2--插值法

数值分析第五章插值法

数值分析 插值法

数值分析与计算方法 第一章 插值法

数值分析第2章插值法

数值分析中的插值算法及其应用

《数值分析》第二讲插值法PPT课件

数值分析 插值法

数值分析中的(插值法)

数值分析插值法

数值分析中常用的插值方法

数值分析-插值法的讲解

数值分析--第2章 插值法

数值分析中的插值方法

数值分析-插值法

数值分析常用的插值方法

数值分析——插值法

(完整版)数值分析插值法

数值分析插值法

数值分析与计算方法第一章插值法

数值分析插值法

数值分析--第2章插值法