matlab第二讲
合集下载
Matlab第二讲

2.2.3字符串 在Matlab中,字符串是用单引号括起来的字 符序列。MATLAB将字符串当作一个行向 量,每个元素对应一个字符。 例:>>str1=‘hello’ >>str2=‘I like ’’Matlab’’’ %重复单引号 来输入含单引号的字符串须 >>str3=‘你好!’ Matlab存储字符串,一个字符占用2 Byte。
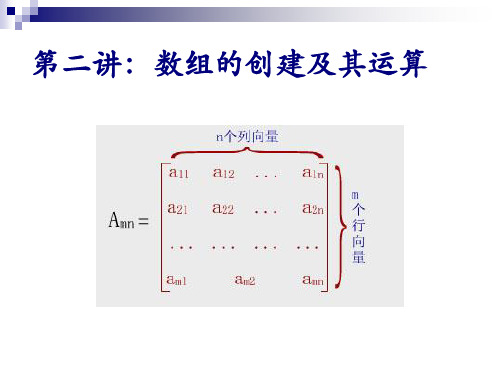
2.2 矩阵和数组
2.2.1矩阵输入 Matlab中的矩阵表示的基本规则: (1)矩阵元素用“[ ]”括住; (2)每行内的元素用逗号或空格隔开; (3)行与行之间用分号或回车键隔开; (4)元素可以是数值或表达式;
通过显式元素输入矩阵: 例:>>c=[1 2;3 4;5 6]或c=[1,2;3,4;5,6] 通过语句生成矩阵: 语句 from: step: to(开始值: 步长: 结束值) step省略时默认步长为1;step省略或step>0 而from>to时为空矩阵,step<0而from<to时 也为空矩阵。 例:x1=2:5 x2=2:0.5:5 x3=5:-1:2 x4=2:-1:3 x5=2:-1:0.5 x6=[1:2:5;1:3:7]
(3)矩阵和数组的除法 矩阵:A\B和A/B分别表示左除和右除。 X=A\B是方程A*X=B的解,A\B=A-1*B X=A/B是方程X*A=B的解,A/B=A*B-1 数组:A.\B和A./B分别表示数组的左除和右除, 表示数组相应元素相除。 例:>>A=[2 -1 3;3 1 -5;4 -1 1] >>B=[5;5;9] >>X=A\B (4)矩阵和数组的乘方 P48 矩阵:A^B 数组:A.^B
MATLAB课件-第二讲
A(r,c)
访问A的由r指定行和c指定列上元素构 成的子数组;r,c可取多行或列
A(r, :)
访问A的r指定行上全部元素构成的子 数组;此处冒号表示全部列
A(:,c)
访问A的c指定列上全部元素的子数 组;此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组,以形成更大 的数组
在总元素数不变的前提下,改变数组的“行数、列 数” 以数组“水平中线”为对称轴,交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴,交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数,导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.
MATLAB讲义第2讲

4
2013-7-27
2.2 命令窗口 (续)
>>who
Your variables are: circle_len area radius
>>whos
Name Size Bytes Class area 1x1 8 double array circle_len 1x1 8 double array radius 1x1 8 double array Grand total is 3 elements using 24 bytes
Matlab Language
20
பைடு நூலகம்
2013-7-27
2.1 数值表示、变量及表达式 (续)
Matlab预定义的变量
变量名 ans eps pi inf i或j NaN 意义 最近的计算结果的变量名 MATLAB定义的正的极小值=2.2204e-16 圆周率π ∞值,无限大 虚数单元,sqrt(-1) 非数,0/0、∞/ ∞
11
2.6 获取在线帮助
MATLAB提供的帮助信息有两类
简单纯文本帮助信息
help
lookfor(条件比较宽松)例:inverse
窗口式综合帮助信息(文字、公式、图形)
doc
helpwin
2013-7-27
Matlab Language
12
〘功能演示-1〙求方程的根
5 3 2 求方程 2 x 3 x 71 x 9 x 13 0 的全部根。
2013-7-27
Matlab Language
6
2.2 命令窗口 (续)
数值显示格式设置 缺省显示格式:简洁的短(short g,7位有效数字)格式 窗口命令及语法格式:format 显示格式关键字 如:format long %15位数字显示 常见通用命令 命令 clc clear who或whos dir cd type help或doc quit或exit
2013-7-27
2.2 命令窗口 (续)
>>who
Your variables are: circle_len area radius
>>whos
Name Size Bytes Class area 1x1 8 double array circle_len 1x1 8 double array radius 1x1 8 double array Grand total is 3 elements using 24 bytes
Matlab Language
20
பைடு நூலகம்
2013-7-27
2.1 数值表示、变量及表达式 (续)
Matlab预定义的变量
变量名 ans eps pi inf i或j NaN 意义 最近的计算结果的变量名 MATLAB定义的正的极小值=2.2204e-16 圆周率π ∞值,无限大 虚数单元,sqrt(-1) 非数,0/0、∞/ ∞
11
2.6 获取在线帮助
MATLAB提供的帮助信息有两类
简单纯文本帮助信息
help
lookfor(条件比较宽松)例:inverse
窗口式综合帮助信息(文字、公式、图形)
doc
helpwin
2013-7-27
Matlab Language
12
〘功能演示-1〙求方程的根
5 3 2 求方程 2 x 3 x 71 x 9 x 13 0 的全部根。
2013-7-27
Matlab Language
6
2.2 命令窗口 (续)
数值显示格式设置 缺省显示格式:简洁的短(short g,7位有效数字)格式 窗口命令及语法格式:format 显示格式关键字 如:format long %15位数字显示 常见通用命令 命令 clc clear who或whos dir cd type help或doc quit或exit
第二讲 MATLAB基础PPT课件
3、MATLAB常用用户文件格式
• M文件:程序文件。文件扩展名为.m。可在File 菜单中创建或打开。也可从历史命令窗口生成。
• MAT文件:数据文件。文件扩展名为.mat。用 于保存工作空间中(内存中)的数据变量。可 用“save”命令生成。
• FIGURE文件:图形文件。文件扩展名为.fig。 可由MATLAB的绘图命令生成,也可在File菜 单中创建或打开。
save — 将全部变量保存到数据文件中 save a b— 将变量a,b保存到数据文件中 save a b-append— 将变量a,b添加到中 clear —— 从内存中删除变量 clear a b —— 从内存中删除变量a,b (clc —— 清屏 ) who —— 显示内存中的变量(只显示变量名) load —— 将变量从 .mat 数据文件中装入内存
Current Directory Browser 窗口
• Workspace Browser(工作空间浏览器窗口)
也是在左上方,可与目录浏览器窗口切换。又称内存浏 览器窗口。用于显示MATLAB工作空间中所有变量的变量名、 数据结构、数据类型、大小和字节数。并可以对变量进行观 察、编辑、提取、保存和图形显示等操作。
Clear Command History % 清除历史命令窗口中的内容
Clear Workspace
% 清除工作空间中的内容
• Desktop: Undock Workspace % 将工作空间窗口从主界面中分离
…ቤተ መጻሕፍቲ ባይዱ
Desktop Layout
% 主界面布局
Command Window % 打开(或关闭)命令窗口
在左上方。可显示当前目录下的M(程序)、 FIG(图形)、 MAT(数据)等文件信息,如文件 类型、文件名、最后修改时间等,并可复制、编辑 和运行M文件以及装载MAT数据文件。选中窗口中 列出的某个文件,单击鼠标右键,即可对其进行打 开、运行、装载等处理和创建、重命名、删除、复 制等常规操作。
MATLAB第二讲__数值计算和符号计算

(4)数值运算中必须先对变量赋值;符号运算无须事先对变 量赋值,但必须先定义,运算结果以标准的符号表达 式形式给出。
Matlab基础应用 21
2.2.2 符号运算中的运算符
(1)基本运算符 符号矩阵:‚+”,‚-”,‚*‛,‚\”, ‚/”, ‚^”, ‚ ’ ” 符号数组:‚.*”,‚./”,‚.\‛,‚.^”, ‚.’ ” (2)关系运算符 运算符只有‚==”,‚~=”。
Matlab基础应用 7
1.3.4 多项式乘除运算(续)
例4: a(x)=x2+2x+3; b(x)=4x2+5x;求c=a(x)*b(x)。 解: >>a=[1 2 3];b=[4 5 0]; >>c=conv(a,b) c= 4 13 22 15 0 >>[d,r]=deconv(c,a) d= 4 5 0 r= 0 0 0 0 0
注意: 方法一只创建了符号表达式,没有创建符号变量; 而方法二既创建了符号表达式,又创建符号变量.
Matlab基础应用 19
2.1.3 创建符号矩阵
使用sym和syms命令创建
例4: A=sym(‘[a,b;c,d]’) A= [ a, b] [ c, d] syms f g h k B=[f,g;h,k] B=
%方法二
Name Size Bytes Class a 1x1 126 sym object b 1x1 126 sym object c 1x1 126 sym object f2 1x1 146 sym object x 1x1 126 sym object Grand total is 20 elements using 650 bytes
matlab-第2讲

函数使用说明: (1) 三角函数以弧度为单位计算。 (2) abs函数可以求实数的绝对值、复数的模、字符串的ASCII 码值. (3) 用于取整的函数有fix、floor、ceil、round,要注意它们的 区别。
• • • •
fix():向0方向靠拢取整 floor():向左取整,即向负无穷方向取整 ceil():返回大于等于指定表达式的最小整数,即向正无穷方向取整 round ():四舍五入 rem(x,y)=x-y.*fix(x./y) mod(x,y) )=x-y.*floor(x./y) rem(x,y)和mod(x,y)要求x,y必须为相同大 小的实矩阵或为标量。
A=
1 1 1 1 8 4 2 1 27 9 3 1 125 25 5 1
(3) 希尔伯特矩阵 在MATLAB中,生成希尔伯特矩阵的函数是hilb(n)。 使用一般方法求逆会因为原始数据的微小扰动而产生不可靠 的计算结果。MATLAB中,有一个专门求希尔伯特矩阵的逆 的函数invhilb(n),其功能是求n阶的希尔伯特矩阵的逆矩阵。
2.1.3 内存变量的管理
1.内存变量的删除与修改 工作空间窗口(Workspace)专门用于内存变量的管理。在 Workspace窗口中可以显示所有内存变量的属性。 当选中某些变量后,再单击Delete按钮,就能删除这些变 量。 当选中某些变量后,再单击Open按钮,将进入变量编辑器。 通过变量编辑器可以直接观察变量中的具体元素,也可修 改变量中的具体元素。
1 4 2 5 3 6
Ex:1. 写出完成下列操作的命令。
a. b.
c.
d. e.
将矩阵A 第2~5 行中的第1,3,5列元素赋给矩阵B。 删除矩阵A的第7号元素。 将矩阵A的每个元素值加30。 求矩阵A的大小和维数(提示:用size函数和ndims函数)。 将含有12个元素的向量x转换成3×4矩阵。
matlab 第二讲

字符与字符串
字符与字符串运算是各种高级语言不可缺少的 部分,Matlab具有强大的字符处理能力。
字符串和字符数组
字符串必须用单引号括起来
str1='Matrix Laboratory'
字符串是由多个字符组成的字符行向量
str2=['M','a','t','r','i','x']
字符数组必须是方的,即每行的字符个数必须相等
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定,也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
例:>> x=[0:pi/10:2*pi];
>> y=sin(x); >> plot(x,y);
Matlab 二维作图
基本形式
plot(x,y) x, y 都是向量,则以 x 中元素为横坐标, y 中元素为 纵坐标作平面曲线。此时 x, y 必须具有相同长度。 x, y 都是矩阵,则将 x 的列和 y 中相应的列相组合, 绘制多条平面曲线。此时 x, y 必须具有相同的大小。 x 是向量, y 是矩阵,若 x 的长度与 y 的行数相等, 则将 x 与 y 中的各列相对应,绘制多条平面曲线;否 则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各 行相对应,绘制多条平面曲线。此时 x 的长度必须等 于 y 的行数或列数。
字符与字符串运算是各种高级语言不可缺少的 部分,Matlab具有强大的字符处理能力。
字符串和字符数组
字符串必须用单引号括起来
str1='Matrix Laboratory'
字符串是由多个字符组成的字符行向量
str2=['M','a','t','r','i','x']
字符数组必须是方的,即每行的字符个数必须相等
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定,也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
例:>> x=[0:pi/10:2*pi];
>> y=sin(x); >> plot(x,y);
Matlab 二维作图
基本形式
plot(x,y) x, y 都是向量,则以 x 中元素为横坐标, y 中元素为 纵坐标作平面曲线。此时 x, y 必须具有相同长度。 x, y 都是矩阵,则将 x 的列和 y 中相应的列相组合, 绘制多条平面曲线。此时 x, y 必须具有相同的大小。 x 是向量, y 是矩阵,若 x 的长度与 y 的行数相等, 则将 x 与 y 中的各列相对应,绘制多条平面曲线;否 则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各 行相对应,绘制多条平面曲线。此时 x 的长度必须等 于 y 的行数或列数。
Matlab 第二讲:Matlab中的函数

15
MATLAB is column dominant, so when sort is used with a 2-D matrix, each column is sorted in ascending order
16
查看矩阵的大小
查看矩阵的大小:size、length
size(A) size(A,1) size(A,2)
Matlab中的函数
1
函数取值
函数作用在矩阵上的取值
设 x 是变量, f 是一个函数
当 x = a 是标量时,f(x) = f(a) 也是一个标量 当 x = [x1, x2, … , xn ] 是向量时,则 f(x) = [ f(x1), f(x2), … , f(xn)] 是一个与 x 长度相同的向量
f 作用在 x 的每个分量上!
若 A 是矩阵,则 f (A) 是一个与 A 同形状的矩阵
2
函数取值
f ( a11 ) f (a ) 21 f ( A) f ( am1 ) f ( a12 ) f ( a22 ) f ( am 2 ) f ( a1n ) f ( a2 n ) f ( amn )
若参数 x 是矩阵, 则作用在其各列上
6
Function Input can be either scalars or matrices
7
内置函数的使用
Functions consist of
Name Input argument(s) Output In MATLAB sqrt (x)= result sqrt(4) ans = 2
log(x) % ln(x) 自然对数 (以 e 为底) log2(x) % 以 2 为底的对数 log10(x) % 以 10 为底的对数 sqrt(x) abs(x) % 平方根 % 绝对值
第2讲 MATLAB初步

(2) 范得蒙矩阵 范得蒙(Vandermonde)矩阵最后一列全为1, 倒数第二列为一个指定的向量,其他各列 是其后列与倒数第二列的点乘积。可以用 一个指定向量生成一个范得蒙矩阵。在 MATLAB中,函数vander(V)生成以向量V 为基础向量的范得蒙矩阵。例如, A=vander([1;2;3;5])即可得到上述范得蒙矩 阵。
各种 format 格式
格式 解释 例
format
format short format long
短格式(缺省显示格式),同short
短格式(缺省显示格式),只显示5位 长格式,双精度数15位,单精度数7位
3.1416
3.1416 3.14159265358979
format short e
format long e format short g format long g format compact format loose
(5) 伴随矩阵 MATLAB生成伴随矩阵的函数是 compan(p),其中p是一个多项式的系数向 量,高次幂系数排在前,低次幂排在后。 例如,为了求多项式的x3-7x+6的伴随矩阵, 可使用命令: p=[1,0,-7,6]; compan(p)
(6) 帕斯卡矩阵 我们知道,二次项(x+y)n展开后的系数随n 的增大组成一个三角形表,称为杨辉三角 形。由杨辉三角形表组成的矩阵称为帕斯 卡(Pascal)矩阵。函数pascal(n)生成一个n阶 帕斯卡矩阵。
2.1.3 内存变量的管理 1.内存变量的删除与修改
clear命令用于删除MATLAB工作空间中的变 量。who和whos这两个命令用于显示在 MATLAB工作空间中已经驻留的变量名清 单。who命令只显示出驻留变量的名称, whos在给出变量名的同时,还给出它们的 大小、所占字节数及数据类型等信息。
Matlab软件入门(第二讲)

p= 3.14159065358969
elapsed_time = 0.1710
数学建模工作室 2011-3-7
Matlab软件入门讲义 Matlab软件入门讲义
第10页 mecca_zj@
函数文件
MATLAB的内部函数是有限的,有时为了研究某 的内部函数是有限的, 的内部函数是有限的 一个函数的各种性态,需要为MATLAB定义新函数, 定义新函数, 一个函数的各种性态,需要为 定义新函数 为此必须编写函数文件. 函数文件是文件名后缀为M 为此必须编写函数文件 函数文件是文件名后缀为 的文件,这类文件的第一行必须是一特殊字符 的文件,这类文件的第一行必须是一特殊字符 function开始,格式为: 开始, 开始 格式为: function 因变量名 函数名(自变量名) 因变量名=函数名 自变量名) 函数名( 函数值的获得必须通过具体的运算实现, 函数值的获得必须通过具体的运算实现,并赋给因变 量.
plotxy?r?xzg0?10806040202040608数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第16页meccazj163com符号函数显函数隐函数和参数方程画图ezplotezplotxtyttmintmax表示在区间tminttmax绘制参数方程ezplotfxab表示在axb绘制显函数ffx的函数图ezplotfxyxminxmaxyminymax表示在区间xminxxmax和yminyymax绘制隐函数fxy0的函数图数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第17页meccazj163com在0pi上画ycosx的图形解输入命令ezplotsinx0pi解输入命令ezplotcost3sint302pi输入命令ezplot?expxsinxy?20502星形图数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第18页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第19页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第20页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第21页meccazj163comezplotezplotfunctionftuoyuanxy3535数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第22页meccazj163comfplot注意
elapsed_time = 0.1710
数学建模工作室 2011-3-7
Matlab软件入门讲义 Matlab软件入门讲义
第10页 mecca_zj@
函数文件
MATLAB的内部函数是有限的,有时为了研究某 的内部函数是有限的, 的内部函数是有限的 一个函数的各种性态,需要为MATLAB定义新函数, 定义新函数, 一个函数的各种性态,需要为 定义新函数 为此必须编写函数文件. 函数文件是文件名后缀为M 为此必须编写函数文件 函数文件是文件名后缀为 的文件,这类文件的第一行必须是一特殊字符 的文件,这类文件的第一行必须是一特殊字符 function开始,格式为: 开始, 开始 格式为: function 因变量名 函数名(自变量名) 因变量名=函数名 自变量名) 函数名( 函数值的获得必须通过具体的运算实现, 函数值的获得必须通过具体的运算实现,并赋给因变 量.
plotxy?r?xzg0?10806040202040608数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第16页meccazj163com符号函数显函数隐函数和参数方程画图ezplotezplotxtyttmintmax表示在区间tminttmax绘制参数方程ezplotfxab表示在axb绘制显函数ffx的函数图ezplotfxyxminxmaxyminymax表示在区间xminxxmax和yminyymax绘制隐函数fxy0的函数图数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第17页meccazj163com在0pi上画ycosx的图形解输入命令ezplotsinx0pi解输入命令ezplotcost3sint302pi输入命令ezplot?expxsinxy?20502星形图数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第18页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第19页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第20页meccazj163com数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第21页meccazj163comezplotezplotfunctionftuoyuanxy3535数学建模工作室2018810matlabmatlab软件入门讲义软件入门讲义第22页meccazj163comfplot注意
第二讲 MATLAB基本操作

三、矩阵及其运算
(四)矩阵的基本数值运算
(1)矩阵与常数的四则运算(同向量与数的四则运算) 矩阵与常数的四则运算(同向量与数的四则运算) 矩阵与常数的四则运算是指矩阵各元素与常 数之间的四则运算。 数之间的四则运算。 例如: 例如 a=[1,2,3;4,5,6;7,8,9]; 求: c=a+2; d=a-2; e=a*2; f=a/2;
(一)矩阵的生成
矩阵的生成有多种方式,通常使用的有四种: 矩阵的生成有多种方式,通常使用的有四种: (1)在命令窗口中直接输入矩阵; 在命令窗口中直接输入矩阵; 把矩阵的元素直接排列到方括号中, 把矩阵的元素直接排列到方括号中,每行 内的元素用空格或逗号相隔, 内的元素用空格或逗号相隔,行于行之间的内 容用分号相隔。 容用分号相隔。 通过语句和函数产生矩阵; (2)通过语句和函数产生矩阵; 文件中建立矩阵; (3)在M文件中建立矩阵; 从外部的数据文件中导入矩阵; (4)从外部的数据文件中导入矩阵; 例如: 例如 a=[1 2 3;4 5 6;7 8 9], b=[2,4,6,8;1,3,5,7;1,2,3,4],
四、数组及其运算
(一)数组的生成
(1)在命令窗口中直接输入向量 格式:a=[a1,a2,a3, …an ] 格式: (2)等差元素向量的生成 生成法: 格式: (i)冒号“:”生成法: 格式:a=a1:m:an )冒号“ (ii)使用线性等分向量函数 )使用线性等分向量函数linspace法: 法 格式: 格式:a=linspace(a1,an,n)
三、矩阵及其运算
(三)矩阵中元素的操作
的第r行 (1)提取矩阵 的第 行:A(r,:) )提取矩阵A的第 ( ,:) 的第r列 (:,r) (2)提取矩阵 的第 列:A(:, ) )提取矩阵A的第 (:, 的每一列, 拉伸为一个列向量: (:) (3)依次提取矩阵 的每一列,将A拉伸为一个列向量:A(:) )依次提取矩阵A的每一列 拉伸为一个列向量 (4)取矩阵 的第 1~i2行、第j1~j2列构成新矩阵 的第i 列构成新矩阵:A(i1:i2, j1:j2) )取矩阵A的第 的第i 构成新矩阵:A(i2:-1:i1,:) (5)以逆序提取矩阵 的第 1~i2行,构成新矩阵 )以逆序提取矩阵A的第 : 的第j 构成新矩阵:A(:, j2:-1:j1 ) (6)以逆序提取矩阵 的第 1~j2列,构成新矩阵 )以逆序提取矩阵A的第 : 的第i 构成新矩阵:A(i1:i2,: ] ,:)=[ (7)删除 的第 1~i2行,构成新矩阵 )删除A的第 的第j 构成新矩阵:A(:, (8)删除 的第 1~j2列,构成新矩阵 :, j1:j2)=[ ] )删除A的第 拼接成新矩阵: (9)将矩阵 和B拼接成新矩阵:[A B];[A;B] )将矩阵A和 拼接成新矩阵 ; ;
matlab讲稿 第二讲

A(i,j,k,:)
A(:)
2.5 操作和特殊字符
3.特殊字符
[] 用于形成向量和矩阵,空格用于行元素的间 隔,分号或回车表示一行的结束。 []内还可以采用矩阵和向量, 例如只要A、B、C 的维数适当,就可利用D=[A B; C]产生更大的 矩阵。
A=[]表示产生空矩阵A A(m, :)=[]表示从A中删去第m行 A(:, n)=[]表示从A中删去第n列 A(:)表示将A重新排列成列向量
2.5 操作和特殊字符
A′可求出矩阵转置, 对复数阵A, 则可 求出其复共轭转置; A.′可求出阵列转置, 对复数阵A也不涉 及到共轭运算。
2.5 操作和特殊字符
2. 冒号(∶) 冒号是MATLAB中最常用的操作符之一, 它 可用于建立向量、 下标阵列和迭代。
表 2.3 冒号使用格式(1) 格式 j:k j:k j:i:k j:i:k 功 能 当j<=k时,等同 于[j, j+1,…,k] 当j>k时为空 等同于[ j+i, j+2i, …, k] j, 当i>0且j>k, 或者 i<0且j<k时为空
4.关系操作符 关系操作符可完成两个阵列之间元素对元素的比 较,其结果为同维数的阵列。当关系成立时相应 的元素置为逻辑真(1),否则置为逻辑假(0)。 操作符<、<=、>、>=只用于比较操作数的实部, 而==、~=用于比较实部和虚部。 测试两个字符串是否相同可采用strcmp, 这时 可比较不同长度的字符串。 strcmpi将忽略大小写 strncmp,strncmpi可以比较前n个字符
2.6 基本矩阵和矩阵操作
阵 作 矩 操 diag reshape rot90 fliplr flipud tril triu cat repmat 功 能 对 矩 角 阵和 阵 矩 的对 角 化 阵 列重 新排 列 矩 阵旋 转90° 矩 阵左 右翻 转 矩 阵上 下翻 转 矩 的下三 阵 阵 角 矩 的上三 阵 阵 角 阵列 接 连 复 并平铺 列 制 阵
matlab课件--第2讲-数组和矩阵

Matlab 软件实习
矩阵的创建
1) 矩阵的直接定义
键入:A=[1 2 3;4 5 6]
输出:A= 123 456
或键入:A=[1 2 3 4 5 6]
第9页,共66页。
Matlab 软件实习
>> A=[1 2 3;4 5 6;7 8 9]
A= 123 456
789
第10页,共66页。
Matlab 软件实习
第15页,共66页。
Matlab 软件实习
c. 三角矩阵
命令
triu(A) triu(A,k) tril(A) tril(A,k)
运行结果
生成一个和A维数相同的上三角矩阵。该矩 阵主对角线及以上元素取自A中相应元素。 其余元素为0。
生成一个和A维数相同的上三角矩阵。该矩 阵第k条对角线及以上元素取自A中相应元 素。其余元素为0。
max(v) min (v) sum(v) mean(v) sort(v)
求最大值
求最小值
求和
求平均值
按升序排列
第5页,共66页。
Matlab 软件实习
矩阵的创建
标量的创建
直接输入:
>>x = 7 x=
7
第6页,共66页。
Matlab 软件实习
行、列向量的创建
1、逐个元素输入法
❖ >> x=[2 pi/2 3+5i]
第20页,共66页。
Matlab 软件实习
用于专门学科的特殊矩阵
(1) 魔方矩阵 魔方矩阵有一个有趣的性质,其每行、
每列及两条对角线上的元素和都相等。对于 n阶魔方阵,其元素由1,2,3,…,n2共n2个整数 组成。MATLAB提供了求魔方矩阵的函数 magic(n),其功能是生成一个n阶魔方阵。
第2讲_matlab 绘图

线条之间的空挡填充颜色,沿z轴按每一网
格变化
调用格式: surf(x,y,z) —— 与mesh的调用方式相同 例: [X,Y,Z]=peaks(30) ※peaks为matlab 自动生成的三维测 试图形 surf(X,Y,Z)
surfc(X,Y,Z) — 带等高线的曲面图 [X,Y,Z]=peaks(30);surfc(X,Y,Z)
mesh(X,Y,Z) mesh(Z) —— Z为n×m的矩阵, 默认x=1:n, y=1:m
meshc —— 生成网格线,在xoy面上
生成曲面的等高线图形
meshz —— 生成网格线,在曲面下面 加上一个长方形的台柱
mesh,meshc,meshz的调用方式相 同
例:
x=1:0.1:3; y=1:0.1:4; [X,Y]=meshgrid(x,y); Z=ones(size(X)); mesh(X,Y,Z)
第二讲 matlab 绘图
——matlab语言丰富的图形表 现方法,使得数学计算结果可 以方便地、多样性地实现了可 视化,这是其它语言所不能比 拟的。
一、二维绘图
plot —— 最基本的二维图形指令,绘制线 性图形(描点、连线)
plot的调用格式
plot(x) —— 缺省自变量绘图格式,x为 向量, 以x元素值为纵坐标,以相应元素 下标为横坐标绘图 plot(x,y) —— 基本格式,以y(x)的函数 关系作出直角坐标图。P36
在图形的顶端加注文字作为图名
在当前图形的x轴旁边加注文字 在当前图形的y轴旁边加注文字 在当前图形的z轴旁边加注文字
图形标注 text (x, y, ‘String’) 在(x,y)处加文字‘String’(二维图 形) text (x, y, z, ‘String’) 在(x,y,z)处…(三维图形) gtext (‘String’) 在鼠标指定位置上标注
格变化
调用格式: surf(x,y,z) —— 与mesh的调用方式相同 例: [X,Y,Z]=peaks(30) ※peaks为matlab 自动生成的三维测 试图形 surf(X,Y,Z)
surfc(X,Y,Z) — 带等高线的曲面图 [X,Y,Z]=peaks(30);surfc(X,Y,Z)
mesh(X,Y,Z) mesh(Z) —— Z为n×m的矩阵, 默认x=1:n, y=1:m
meshc —— 生成网格线,在xoy面上
生成曲面的等高线图形
meshz —— 生成网格线,在曲面下面 加上一个长方形的台柱
mesh,meshc,meshz的调用方式相 同
例:
x=1:0.1:3; y=1:0.1:4; [X,Y]=meshgrid(x,y); Z=ones(size(X)); mesh(X,Y,Z)
第二讲 matlab 绘图
——matlab语言丰富的图形表 现方法,使得数学计算结果可 以方便地、多样性地实现了可 视化,这是其它语言所不能比 拟的。
一、二维绘图
plot —— 最基本的二维图形指令,绘制线 性图形(描点、连线)
plot的调用格式
plot(x) —— 缺省自变量绘图格式,x为 向量, 以x元素值为纵坐标,以相应元素 下标为横坐标绘图 plot(x,y) —— 基本格式,以y(x)的函数 关系作出直角坐标图。P36
在图形的顶端加注文字作为图名
在当前图形的x轴旁边加注文字 在当前图形的y轴旁边加注文字 在当前图形的z轴旁边加注文字
图形标注 text (x, y, ‘String’) 在(x,y)处加文字‘String’(二维图 形) text (x, y, z, ‘String’) 在(x,y,z)处…(三维图形) gtext (‘String’) 在鼠标指定位置上标注
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、矩阵的创建
例3、编制一个名为exno1.m的M文件。 %exno1.m %创建一个M文件,用以输入大规模矩阵 Matrix=[12 23 34 25 27 47 46; 21 344 566 43 45 65 45; 423 45 21 23 67 855 45;
123 452 642 64 632 34 26]
四、矩阵的生成
triu(A)——生成一个和A大小相同的上三角矩阵。该矩阵 的主对角线及以上元素取自A中相应元素,其余元素都为 零。 triu(A,k)——生成一个和A大小相同的上三角矩阵。该矩 阵的第k条对角线及以上元素取自A中相应元素,其余元 素都为零。命令triu(A,0)等同于命令triu( A )。 tril(A)——生成一个和A大小相同的下三角矩阵。该矩阵 的主对角线及以下元素取自A中相应元素,其余元素都为 零。 tril(A,k)——生成一个和A大小相同的下三角矩阵。该矩 阵的第k条对角线及以下元素取自A中相应元素,负数k表 示主对角线下的对角线。其余元素都为零。命令 tril(A,0)等同于命令tril(A)
一、矩阵的创建 符号的作用:
逗号和分号的作用 逗号和分号可作为指令间的分隔符,matlab允许多条语句 在同一行出现。 分号如果出现在指令后,屏幕上将不显示结果。 使用逗号时,命令语句的运行结果将显示。 注意:只要是赋过值的变量,不管是否在屏幕上显示过, 都存储在工作空间中,以后可随时显示或调用。变量名尽 可能不要重复,否则会覆盖 。
二、数组的生成
注:以上关于数组生成的命令经常用于作 图,如: x=linspace(0,pi); %生成数组 y=sin(x); %计算函数 plot(x,y); %作图
三、矩阵的裁剪 A(:,j) 返回矩阵A中第j列列向量。 A(i,:) 返回矩阵A中第i行行向量。 A(:,j:k) 返回由矩阵A中的第j列,第j+1列,直到第k列 列向量组成的子阵。 A(i:k,:) 返回由矩阵A中的第i行,第i+1行,直到第k行 行向量组成的子阵。 A(i:k,j:l) 返回由矩阵A中的第i行到第k行行向量和 第j列到第l列列向量组成的子阵。 A(:) 将矩阵A中的每列合并成一个长的列向量。 A(j:k) 返回一个行向量,其中的元素为A(:)中的从第j 个元素到第k个元素。
一、矩阵的创建 2、通过函数创建数值矩阵
MATLAB提供了许多生成和操作矩阵的函数,可 以利用它们去建立矩阵。
例1:x=[0,pi/6,pi/3;pi/2,2*pi/3,5*pi/6]; >> y=sin(x) y= 0 0.5000 0.8660 1.0000 0.8660 0.5000 例2:reshape函数和diag函数等。 reshape函数用于建立数值矩阵。 diag函数用于产生对角阵。
4.导入数据创建矩阵
一、矩阵的创建 1、直接输入 >>a=[1,2,3;4,5,6]; 注:1.必须使用方括号 2.当一行输不完时可以用续行“„” 3.行与行之间用分号或回车符分隔 4.同行元素用空格或逗号分隔 5.矩阵元素可以是任何matlab表达式,可以是 实数,也可是复数,复数可用特殊函数i,j 输入 6.该方法只适合创建小型矩阵
二、数组的生成
2、用Linspace函数构造数组 用Linspace函数构造数组需要指定首尾值和元素总个数。 linspace(a,b) 在区间[a,b]上创建一个有1 0 0个元素 的向量,这1 0 0个数把整个区间线性分隔。 linspace(a,b,n) 在区间[a,b]上创建一个有n个元素的 向量。 这个命令和冒号表示形式相近,但是它直接定义了数 据的个数。
四、矩阵的生成
fliplr(A)——将二维矩阵A左右翻转。这里的‘lr’是 ‘left - right’的缩写。 flipud(A)——将二维矩阵A上下翻转。这里的‘ud’是‘up - down’的缩写。 flipdim(A,n)——沿指定方向翻转矩阵。 注意:这里n=1或2,当=1相当flipud,当n=2相当fliplr. transpose(A) ——沿主对角线翻转矩阵。 ctranspose(A) ——转置矩阵。 rot90(A)——生成一个由矩阵A逆时针旋转90°而得的新阵。 rot90(A,k)——生成一个由矩阵A逆时针旋转k×90°而得到 的新阵。
可以用聚合的方法创建矩阵甚至更多维数组,但不能生成不 规则的形状,必须是矩形的。如果是水平生成矩阵,则每个 子矩阵必须具有相同的行数;如果是垂向生成矩阵,则每个 子矩阵必须具有相同的列数。
四、矩阵的生成
用repmat函数可以利用已有矩阵的多个拷贝来创建矩 阵。键入下面的命令行:
repmat(M,v,h)
四、矩阵的生成
rand——产生在0~1之间均匀分布的随机数;每调用一次 给一个新的数值。 rand+i*rand——产生一个复数随机数。 rand(n)——产生一个nxn的矩阵,其元素为0~1之间均匀 分布随机数。 rand(m,n)——产生一个mxn的矩阵,其元素是0~1之间均 匀分布的随机数。 randn——产生零均值、单位方差的正态分布随机数。 randn(n)——产生一个n×n的矩阵,其元素为零均值、单 位方差的正态分布随机数。 randn(m,n)——产生一个m×n的矩阵,其元素为零均值、 单位方差的正态分布随机数。
四、矩阵的生成
hilb(n)——生成一个n×n的希尔伯特矩阵。 invhilb(n)——生成一个n×n的希尔伯特矩阵的逆矩阵, 其元素都为整数。 magic(n)——给出一个n×n的魔方矩阵。 pascal(n)——返回一个n×n的Pascal矩阵,它是对称、 正定的矩阵,它的元素由Pascal三角组成。它的逆矩阵的 所有元素是整数。 vander(x) ——生成范德蒙矩阵。 如:>>x=[1 2 3 4 5] >>A=vander(x)
三、矩阵的裁剪 A([j1 j2 „ ]) 返回一个行向量,其中的元素为A ( : )中的第j1、j2„元素。 A(:,[j1 j2„]) 返回矩阵A的第j1列、第j2列等的 列向量。 A([i1 i2„] ,:) 返回矩阵A的第i1行、第i2行等 的行向量。 A([i1 i2...],[j1 j2...]) 返回矩阵第i1行、第 i2行等和第j1列、第j2列等的元素。
例如,要将work文件夹中的exno2.xls调入MATLAB中, 可以如下操作。
二、数组的生成
Matlab中的数组在外观上与矩阵毫无差别,也就是说矩阵的 输入方法可以直接移植到数组的输入上。同样,下述关于数 组的生成方法也可以用来生成矩阵。 X=[0 2 3 6 7 8]就构成了一个有6个元素的数组X。 除直接构造外,还有一些常用的构造方法,以下介绍两种: 1、用增量法构造数组 例3、A=10:15 B=-2.5:2.5 默认时,Matlab创建序列时增量总是1.即使最后的值不是 整数。 例4、A=1:6.3
>>a=zeros(4)
>>b=hilb(4) >>a(2,3)=b(2,3) >>a(:,2)=b(:,4) (exno25)
Matlab语言程序设计
理学院
徐屹
东北电力大学
Northeast Dianli College
第二讲 矩阵的输入与生成
ห้องสมุดไป่ตู้一 二
矩阵的创建 数组的生成 矩阵的裁剪
三 3
四 4
矩阵的生成
第二讲 矩阵的输入与生成
一、矩阵的创建
1.直接输入矩阵
矩阵的 创建
2.通过函数创建数值矩阵 3.通过M文件创建矩阵
四、矩阵的生成
diag(A)——生成一个由矩阵A主对角线元素组成的列向量。 主对角线总是从矩阵左上角开始。对于方阵来说它结束 于矩阵的右下角。 diag(x)——生成一个n维的方阵,它的主对角线元素值取 自向量x,其余元素的值都为0。 diag(A ,k)——生成一个由矩阵A第k条对角线的元素组成 的列向量。k=0为主对角线;k<0为下第k对角线;k>0为 上第k对角线。 diag(x ,k)——生成一个(n+abs(k))维的方阵,该矩阵的 第k条对角线元素取自向量x,其余元素都为零。
四、矩阵的生成
矩阵聚合是通过连接一个或多个矩阵来形成一个新的矩阵。 符号[]不仅是一个矩阵构造符,它还是一个Matlab聚合 运算符。表达式C=[A B]在水平方向上聚合矩阵A和B, 表达式C=[A;B]在垂向上聚合它们。 例如:A=ones(2,5)*6, %2*5的矩阵,元素为6. B=rand(3,5), %3*5的矩阵,元素为随机数 C=[A;B] %垂向聚合A和B (exno22)
一、矩阵的创建
例如:>>a3=[2 4 6 8 10];
>>a2=[2,4 6,8,10];
>>a1=[2;4;6;8;10];
Matlab可以在行和列向量之间进行转置,使用“`”,如在 本例中,可以使用如下命令实现上述3个向量的转置,在 “命令”窗口中输入如下命令,并按Enter键确认。
>>a3’ >>a2’ >>a1’
(exno21)
一、矩阵的创建
3、通过M文件建立矩阵 直接输入一个规模比较大的矩阵是很艰苦的工作, 而且出错也不容易修改,这里利用M文件的特点 将所要输入的矩阵按格式先写到一个文本文件中, 然后,将此文件以M为扩展名命名,这就是M文 件。在MATLAB命令窗口中输入此M文件名,则 要输入的大型矩阵就被直接输入到内存中了。
Matlab将矩阵M在垂向上复制v次,在水平方向上复制 h次。例如,下面将已有矩阵A复制到新矩阵B中。
A=[8 1 6;3 5 7;4 9 2]
B=repmat(A,2,4)
(exno23)
四、矩阵的生成
用blkdiag函数创建块对角矩阵
