2013习题解答
机械制图2013习题解答(1-5章)

a″ b″ c″ d″
e″
(1)先求特殊点 (2)再求一般点 (3)判别可见性; (4)顺次光滑连接
3.纬圆法或素线法求圆锥表面曲线的另 两面投影。
(1)先求特殊点 (2)再求一般点 (3)判别可见性 (4)顺次光滑连接
4.圆锥表面取线
(1)先求特殊点 (2)再求一般点 (3)判别可见性 (4)顺次光滑连接
平 面 图 形 的 线 段 分 析
已知线段 连接线段
1-8 基本绘图练习 100
平
φ20
面 2×φ16 图
形
的
作
R15
R10
图
步
骤
R10
30
70
46 70
R32 R20 R20
1-8 基本绘图练习
平 面 中间线段 图 形 的 线 段 分 析
已知线段
已知线段 连接线段
1-8 基本绘图练习 30
平
E不在△ABC上
a″ d″
l″ b″
c″
l d
4.已知△ABC的两面投影,求其侧面投影, 并在△ABC内取一点K,使点K距V面12mm, 距H面15mm。
5.已知△ABC在平面EFGH内,补画其正面投
影。
c′ a′
b′
6.在△ABC上作正平线和水平线,正平线 在V 面之前14mm,水平线在H面之上18mm。
c″
b′
3.求直线与平面的交点,并判断可见性。
4.求直线与平面的交点,并判断可见性
pv 3′ 4′
2 1
5 求平面与平面的交线,并判断可见性。 QV a′ e′
PV b′ 3 n′ m′
f′
X
g′ 4
c′
2013_晶体结构习题-答案

晶体结构习题1. 对于面心立方点阵:(1) 写出 {111} 晶面族包含的所有晶面的晶面指数;(2) 在一个晶胞中画出 {111} 晶面族所有晶面(每个晶面为三角形); (3) 在以上图中,标出所有晶面交线(三角形三条边)的晶向指数。
1、(1){111}=(111)+(T11)+(1T1)+(11T )+(TTT )+(1TT )+ (T1T )+(TT1) (2)略(3)<110>= [110]+[101]+[011]+[T10]+[T01]+[0T1]+[TT0]+[T0T]+ [0TT]+[1T0]+[10T]+[01T]2. 对于面心点阵,计算回答下列问题 (1) [111] 与 [011] 的晶向夹角 ; (2) (101) 与( 111 )晶面的夹角 ;(3) (100) 、 (110) 、 (111) 面是否属于同一晶带轴。
2、(1) 解:3/623110cos 232221232221332211=⋅++=++⋅++++=⋅⋅=bb b a a a b a b a b a ba ba φ()3/6arccos =φ (2)解:()3/6arccos =φ(3)不属于同一晶带。
3. 对于立方晶系,证明 (hkl) 晶面与 [hkl] 晶向垂直。
证明:由晶带定律可知:对于任一属于(hkl)晶面的 [uvw] 晶向,应满足: hu+kv+lw =0对于两晶向[hkl]与[uvw]的夹角为0cos 232221232221332211=++⋅++++=⋅⋅=bb b a a a b a b a b a ba ba φ故(hkl) 晶面与 [hkl] 晶向垂直4. 分别计算面心立方、体心立方点阵 {001} 、 {011} 、 {111} 面的面间距。
解:面心立方,当(hkl)不为全奇或全偶时,有附加面:{001} 、 {011} d(001)=a a5.0001212=++d(011)=221a d(111)=3a体心立方,当h+k+l=奇数时,有附加面:{001} 、{111} d(001)=a a5.0001212=++d(011)=2ad(111)=32a5. Cu 的密度为 8.96 g/cm3, 计算 CU 的点阵常数与原子半径。
2013年司法考试三卷练习题:主物与从物

【真题研习】根据民法中物的分类标准,下列物中哪些属于主物与从物的关系?A.锁与钥匙 B.上衣与裤子
C.电视机与遥控器 D.房屋与窗户
【答案】AC
【例1】甲向乙出售某房屋,已办理过户登记。
交付房屋前,甲着手拆除厕所和猪圈,以将所得砖瓦另作他用。
乙知悉后前往制止,甲辩称房屋买卖合同并未就厕所和猪圈的归属作出约定,自己有权拆除。
①厕所、猪圈属于从物。
②房屋所有权移转时,厕所、猪圈的所有权亦归乙所有。
故甲无权拆除。
【例2】甲因不对乙支付到期的汽车修理费,乙对汽车行使留置权。
由于汽车上没有工具箱和备胎,乙要求甲交出工具箱和备胎。
①工具箱和备胎均为汽车的从物。
②《担保法解释》第114条规定:如果债务人未将从物移交留置权人占有,则留置权的效力不能及于留置物的从物。
③故乙对未占有的工具箱和备胎不享有留置权。
2013考研数学一真题解析

则|A|=
。
【考点分析】:伴随矩阵。
【求解过程】:-1
从题目条件 aij + Aij = 0 得知 Aij = −aij ,根据 A 和它的伴随矩阵之间的关系得知
A* = −AT (1)
再根据公式 AA* =| A | E = −AAT ,两边取行列式 − | A |2 =| A |3 解得:
| A |= 0 或| A |= -1
得 y(0)=1,因此极限的值为 1.
【方法总结】: lim n[ f ( 1) −1] 为 0* 型的极限,此类极限求法为先将其化作 0 型或者
n→
n
0
型,然后使用洛必达法则,等价无穷小代换或者泰勒公式求得。
10.已知 y1=e3x –xe2x,y2=ex –xe2x,y3= –xe2x 是某二阶常系数非齐次线性微分方程的 3 个解, 则该方程的通解 y= 。 【考点分析】:二阶常系数微分方程求解。
【求解过程】:1− 1 。 e
PY a +1 Y a
dy dx
=
dt dx
=
sin t
+ t cos t cos t
− sin t
=t,
dt
d2y dx2
=
d (dy ) dx dx
=
d(dy ) dx dt
•
dt dx
=
sec t
,带入
t
的值,原式=
2。
【方法总结】:对于参数方程求导和反函数求导的题目,需要掌握求导的过程,特别对于其
中二阶倒数甚至更高阶导数的求法,更需认真对待。
x→ 1+ x
1
= 0 − 0 + 0 − (− ln 2)
数据结构1-3章习题答案2013

while(p->next!=NULL)
p=p->next;
temp=p->data;
delete p;
return temp;
}
4、数据结构简单地说是指数据以及相互之间的联系。
5、算法应具备以下5个特性:有穷性、正确性、可行性、输入和输出。
6、在分析各种算法的时间复杂度时,一般只讨论相应的数量级,用f(素的个数远远少于零元素的个数。
8、的运算规则为后进先出,队列的运算规则为先进先出。
C.(rear+1) %n= =frontD. (rear-1)%n= = front
5、下列是顺序存储线性表排序的算法
void Sort(List& L)
{
int i,j;
ElemType x;
for(i=1;i<L.size;i++)
{
x=L.list[i];
for(j=i-1;j>=0;j--)
}
不考虑健壮性条件,写出下列出队算法中缺失的语句:
ElemType OutQueue(struct QueueSq* Q)
{…
Q->front=(Q->front+1)%Q->MaxSize;
return Q->queue[Q->front];
…
}
参考以上两算法和数据结构,写出队满的条件:
(Q->rear+1)%Q->MaxSize==Q->front
和队空的条件:
Q->front==Q->rear
六、用f(n)=2n为例,说明栈与递归算法之间的关系。
概率统计练习册习题解答

概率统计练习册习题解答苏州科技学院概率论与数理统计》活页练习册习题解答信息与计算科学系概率论与数理统计教材编写组2013 年12 月习题1-1 样本空间与随机事件1选择题(1)设A,B,C为三个事件,则A,B,C中至少有一个不发生”这一事件可表示为(D)(A)AB IJ AC U BC(B)A U B U C(C )AB CU A B C UA BC(D )AUBUC(2)设三个元件的寿命分别为T1,T2,T3,并联成一个系统,则只要有一个元件正常工作则系统能正常工作,事件系统的寿命超过t”可表示为(D)A ;T1T2T3kB ITT2T3 t?C :min 汀,T2,T3? t? D;max:T1,T2,T3i >t?2•用集合的形式表示下列随机试验的样本空间「与随机事件A:对目标进行射击,击中后便停止射击,观察射击的次数;事件A表示射击次数不超过5次”。
解:Q = {l,2,3,,}; A = {1,2,3,4,}。
3•设某工人连续生产了4个零件,A i表示他生产的第i个零件是正品(i=123,4 ),试用A表示下列各事件:(1 )只有一个是次品;(2)至多有三个不是次品;卜- A- A3 一A4习题1-2 随机事件的概率及计算1填空题(1)已知 A B,P(A)=0.4,P(B)=0.6,贝P(A)二—0.6,P(AB)二二0 ,P(AB)二0.4。
P(A B)(2)设事件A与B互不相容,P(A) =0.4, P(B) = 0.3,则P(AB)=0.3 ,P(AU B)= 0.6 。
2 •选择题(1)如果P(AB) =0,则(C )(A) A与B互不相容(B) A 与B互不相容(C) P(A_B)二P(A) (D) P(A_B) =P(A) _P(B)(2)两个事件A与B是对立事件的充要条件是(C )(A) P(AB) = P(A) P(B) (B) P(AB) =0 且P(A B) =1(C) AB二•一且 A B 二■1(D) AB 二一3.—批晶体管共40只,其中3只是坏的,今从中任取5只,求(1) 5只全是好的的概率; (2) 5只中有两只坏的的概率; (3) 5只中至多有一只坏的概率P 2=弩(2)C 40=0.03544. ( 1)教室里有r 个学生,求他们的生日都不相同的概率;(2)房间里有四个人,求至少两个人的生日在同一 个月的概率.解:(1)设A 二“他们的生日都不相同”,则P(A)崇;(2)设B 二“至少有两个人的生日在同一个月4112-p 441 96习题1-3 条件概率1.选择题:(1)设A,B为两个相互对立事件, 且P(A) 0,P(B) 0,(B) P(A B) = P(A) (C) P(A B) =0 (D)(A) P(BA)»OP(AB)二 P(A)P(B)(2) —种零件的加工由两道工序组成,第一道工序的废品率为p,第二道工序的废品率为q,则该零件加工的成品率为(|c )(A) 1»q ( B) 1 - pq (C) 1 - p - q pq (D)(1-P) (1-q)2 •填空题:(1)已知P(A) =0.5, P(AUB) =0.6,若A、B 互不相容,贝P(B) = 0 .1_ ;若A、B 相互独立,则P(B)=—0 . 2(2)一射手对同一目标独立地进行四次射击,若至少命中一次的概率为80/81,该射手的命中率2——p=3—。
传感器课后习题答案2013

返回
上页
下页
图库
第2章
2.5 解:①图 2-32(c)
6 2 2 A R r 59 . 7 10 ②圆桶截面积
应变片 1,2,3,4 感受的是纵向应变,有
1 2 3 4 x
应变片 5,6,7,8 感受的是纵向应变,有
5 6 7 8 y
返回
上页
下页
图库
第2章
2.5 一个量程为10kN的应变式测力传感器,其弹 性元件为薄壁圆筒轴向受力,外径20mm,内径18mm, 在其表面粘贴八各应变片,四个沿周向粘贴,应 变片的电阻值均为120Ω ,灵敏度为2.0,波松比为 0.3,材料弹性模量E=2.1×1011Pa。要求: 1) 绘出弹性元件贴片位置及全桥电路; 2) 计算传感器在满量程时,各应变片电阻变化; 3) 当桥路的供电电压为10V时,计算传感器的输出 电压。
nxi yi xi yi nxi (xi ) 2
2
2
6 182.54 21 42.23 208.41 1.98 6 91 21 21 105
91 42.23 21 182.54 9.59 0.09 6 91 21 21 105
第1章
1.5
某传感器为一阶系统,当受阶跃函数作用时,在 t=0时,输出为10mV;t→∞时,输出为100mV;在t=5s时, 输出为50mV,试求该传感器的时间常数。
解:此题与炉温实验的测飞升曲线类似:
y t 10 90(1 e t / T )
5 8.51 由 y 5 50 T 5 ln 9
返回 上页
解:
2.10题图
概率统计练习册习题解答

苏州科技学院 《概率论与数理统计》活页练习册习题解答信息与计算科学系 概率论与数理统计教材编写组2013年12月习题1-1 样本空间与随机事件1.选择题(1)设,,A B C 为三个事件,则“,,A B C 中至少有一个不发生”这一事件可表示为( D ) (A )ABAC BC (B )A B C (C )ABC ABC ABC (D )A B C(2)设三个元件的寿命分别为123,,T T T ,并联成一个系统,则只要有一个元件正常工作则系统能正常工作,事件“系统的寿命超过t ”可表示为( D )A {}123T T T t ++>B {}123TT T t >C {}{}123min ,,T T T t >D {}{}123max ,,T T T t >2.用集合的形式表示下列随机试验的样本空间Ω与随机事件A :对目标进行射击,击中后便停止射击,观察射击的次数;事件A 表示“射击次数不超过5次”。
解:{} ,,,=321Ω;{}54321A ,,,,=。
3.设某工人连续生产了4个零件,i A 表示他生产的第i 个零件是正品(4,3,2,1=i ),试用i A 表示下列各事件:(1)只有一个是次品;(2习题1-2 随机事件的概率及计算1.填空题(1)已知B A ⊂,4.0)(=A P ,6.0)(=B P ,则)(A P)(AB P=)(B A P 0 ,)(B A P(2)设事件A 与B 互不相容,()0.4,()0.3P A P B ==,则()P AB ()P A B 0.62.选择题(1)如果()0P AB =,则( C )(A) A 与B 互不相容 (B) A 与B 互不相容(C) ()()P A B P A -= (D) ()()()P A B P A P B -=- (2) 两个事件A 与B 是对立事件的充要条件是( C )(A ) )()()(B P A P AB P = (B )1)(0)(==B A P AB P 且 (C ) Ω=∅=B A AB 且 (D )∅=AB 3.一批晶体管共40只,其中3只是坏的,今从中任取5只,求 (1)5只全是好的的概率; (2)5只中有两只坏的的概率; (3)5只中至多有一只坏的概率。
2013年中考数学复习习题集答案

习题集部分第一部分 数与代数 第一章 数与式 第1讲 实数1.B 2.A 3.D 4.D 5.B 6.D 7.3 8.<9.C 解析:0.000 021=2.1×10-5. 10.解:原式=5-1+(2-3)+1=4.11.C 解析:根据数轴表示数的方法得到a <0<b ,数a 表示的点比数b 表示的点离原点远,则-a >-b ,b -a >0,|a |>|b |.∴选项A 、B 、D 正确,选项C 不正确.故选C.12.1.6×10-6 13.2 314.解:原式=3 3-2×32-14+1=2 3+34.15.解:原式=-4+3-2×12+3=1.16.517.解:(1)19×11 12×11911⎛⎫- ⎪⎝⎭(2)1(2n -1)×(2n +1) 12×112121n n ⎛⎫- ⎪-+⎝⎭(3)a 1+a 2+a 3+a 4+…+a 100=12×113⎛⎫- ⎪⎝⎭+12×1135⎛⎫- ⎪⎝⎭+12×1157⎛⎫- ⎪⎝⎭+…+12×11199201⎛⎫- ⎪⎝⎭=12×1111111133557199201⎛⎫-+-+-- ⎪⎝⎭…+ =12×11201⎛⎫- ⎪⎝⎭=12×200201=100201. 18.2(a +b )ab 解析:∵1⊕2=2⊕1=3=2×1+2×21×2,(-3)⊕(-4)=(-4)⊕(-3)=-76=2×(-3)+2×(-4)(-3)×(-4),(-3)⊕5=5⊕(-3)=-415=2×5+2×()-35×(-3),…∴a ⊕b =2(a +b )ab.第2讲 代数式1.B 2.D 3.B 4.A5.A 解析:根据题意,x -2+(y +1)2=0,两个非负数的和为0,必须这两个数同时为0,所以得:x -2=0,y +1=0,解得x =2,y =-1,所以x -y =3.6.1 7.1.25b +a 8.5 9.n -m 10.解:由2x -1=3得,x =2,又(x -3)2+2x (3+x )-7=x 2-6x +9+6x +2x 2-7=3x 2+2,∴当x =2时,原式=14.11.B 解析:a 2-b 2=(a -b )·(a +b ),得到14=12·(a +b ),即可得到:(a +b )=12,所以选择B答案.12.m +43 1 解:m 2-163m -12=()m +4()m -43()m -4=m +43;当m =-1时,原式=-1+43=1.13.B 14.A15.解:A 2-B 2=(2x +y )2-(2x -y )2 =4x ·2y =8xy .16.A 解析:∵3x =4,9y =7,∴3x -2y=3x 32y =3x 9y =47.17.(-1)n a 3n -1n18.解:原式=x -y x ÷x 2-2xy +y 2x =x -y x ·x (x -y )2=1x -y .当x =2 009,y =2 010时,原式=12 009-2 010=-1.19.C 解析:根据题意得出矩形的面积是(a +1)2-(a -1)2,求出即可.矩形的面积是(a +1)2-(a -1)2=a 2+2a +1-(a 2-2a +1)=4a (cm 2).第3讲 整式与分式 第1课时 整式1.A 2.B 3.D 4.D 5.D 6.D 7.D 8.C9.(1)2 (2)2a 3 (3)-12a 4+2a10.解:原式=a 2+2ab +b 2+a 2-2ab =2a 2+b 2. 11.A 12.D13.解:原式=4a 2-4ab +b 2-b 2 =4a 2-4ab ,将a =-2,b =3代入上式得:上式=4×(-2)2-4×(-2)×3=16+24=40. 14.解:原式=a 2-b 2+2a 2=3a 2-b 2. 代入a =1,b =2,原式得3-(2)2=1.15.解:原式=4x 2-9-4x 2+4x +x 2-4x +4=x 2-5. 当x =-3时,原式=(-3)2-5=3-5=-2. 16.B17.解:由2x -y +|y +2|=0,得2x -y =0,y +2=0,∴x =-1,y =-2. 又[(x -y )2+(x +y )(x -y )]÷2x=(x 2-2xy +y 2+x 2-y 2)÷2x =x -y . ∴x -y =-1-(-2)=1.18.解:(1)4×6-52=24-25=-1;(2)答案不唯一.如n (n +2)-(n +1)2=-1;(3)成立.因为n (n +2)-(n +1)2=n 2+2n -(n 2+2n +1) =n 2+2n -n 2-2n -1=-1.19.2 解析:3·9m ·27m =3·32m ·33m =31+2m +3m =311, ∴1+2m +3m =11.解得m =2. 第2课时 因式分解1.C 2.B 3.C 4.(a +b )(a -b )5.(m -3)2 6.2x (2x -1) 7.2(x +2)(x -2) 8.2(x +1)2 9.C 10.211.解:能,因为(n +11)2-n 2=(n +11+n )(n +11-n )=11(2n +11)为11的倍数,所以可以被11整除.12.a (1-3b )2 13.ab (b +2)(b -2) 14.x (x +2)(x -6)15.D 解析:首先把x -1看做一个整体,观察发现符合完全平方公式,直接利用完全平方公式进行分解即可.(x -1)2-2(x -1)+1=(x -1-1)2=(x -2)2.16.解:原式=()x -y 2()x +y ()x -y =x -yx +y.当x =3+1,y =3-1时,原式=()3+1-()3-1()3+1+()3-1=22 3=33.17.6 解析:∵a =2,a +b =3,∴a 2+ab =a (a +b )=2×3=6. 18.-3219.(x +y )(x -y -3)20.解:等腰或直角三角形 ∵a 2c 2-b 2c 2=a 4-b 4,∴c 2(a +b )(a -b )=(a 2+b 2)(a 2-b 2), ∴c 2(a +b )(a -b )=(a 2+b 2)(a +b )(a -b ). ∵a ,b 为三角形边长,∴a +b ≠0. ∴c 2(a -b )=(a 2+b 2)(a -b ),∴a -b =0或c 2=a 2+b 2,即a =b 或c 2=a 2+b 2, ∴△ABC 是等腰或直角三角形. 21.x (x +2)(x -2) 第3课时 分式1.B 2.C 3.(1)4xab (2)a +b 4.7z 36x 2y x +3x +1 5.326.-1 7.解:x 2-1x +1÷x 2-2x +1x 2-x =(x +1)(x -1)x +1÷(x -1)2x (x -1)=x .8.解:x 2x -1+11-x =x 2-1x -1=x +1,代入求值(除x =1外的任何实数都可以).9.-1410.m -6 11.C12.解:234211x x x +⎛⎫- ⎪--⎝⎭÷x +2x 2-2x +1=3x +4-2x -2(x +1)(x -1)·(x -1)2x +2 =x +2(x +1)(x -1)·(x -1)2x +2=x -1x +1. 13.解:原式=2111(11)x x x x ⎛⎫-+ ⎪++-⎝⎭())(·x +1x -1 =x x +1·x +1x -1=xx -1. 当x =2时,原式=2.14.解:原式=a -2a 2-1÷(a +1)(a -1)-2a +1a +1=a -2a 2-1÷a 2-2a a +1=a -2(a +1)(a -1)×a +1a (a -2) =1a 2-a. ∵a 是方程x 2-x =6的根,∴a 2-a =6.∴原式=16.15.解:原式=a (b +1)(b +1)(b -1)+b -1(b -1)2=a b -1+1b -1=a +1b -1. 由b -2+36a 2+b 2-12ab =0, 得b -2+(6a -b )2=0,∴b =2,6a =b ,即a =13,b =2.∴a +1b -1=13+12-1=43. 16.解:由x 2-3x -1=0知x ≠0,则x 2-1=3x ,两边同除以x 得x -1x=3.原式=21x x ⎛⎫- ⎪⎝⎭+2=1117.-4 解析:由xy x +y=-2,得x +y xy =-12,裂项得1y +1x =-12.同理1z +1y =43,1x +1z =-43.所以,1y +1x +1z +1y +1x +1z =-12+43-43=-12,1z +1y +1x =-14.于是xy +yz +zx xyz =1z +1y +1x =-14,所以xyzxy +yz +zx=-4.第4讲 二次根式1.C 2.B 3.D 4.C 5.A 6.3 3 7.2 2 8.4949.710.解:原式=3×33-1+2 2-2+1=2+1.11.C12.B13.C解析:由m=1+2,n=1-2,得m+n=2,mn=-1,则m2+n2-3mn=(m+n)2-5mn=22-5×(-1)=9=3.故选C.14.5解析:先将20n化为最简二次根式,即20n=2 5n,因此要使5n是整数,正整数n的最小值为5.15.D 16.解:原式=-212⎛⎫⎪⎝⎭+1-(3 2-3)+3188⎡⎤⎛⎫⨯- ⎪⎢⎥⎝⎭⎣⎦=4+1-3 2+3-1=7-3 2.17.D解析:因为x-2y+9与|x-y-3|互为相反数,所以x-2y+9=0,|x-y-3|=0.可得290,30x yx y-+=⎧⎨--=⎩⇒15,12xy=⎧⎨=⎩⇒x+y=27.18.-2解析:∵1+x-(y-1)1-y=0,∴1+x+(1-y)1-y=0.又∵由被开方数为非负数的二次根式有意义的条件,得1-y≥0,∴根据算术平方根为非负数的性质,要使两个非负数之和等于0,必须这两个数同时为0,即1+x=0,1-y=0,即x=-1,y=1.∴x2 011-y2 011=(-1)2 011-12 011=-2.19.A解析:首先根据二次根式有意义的条件求出x的值,然后代入式子求出y的值,最后求出2xy的值.根据二次根式被开方数必须是非负数的条件,要使y=2x-5+5-2x-3在实数范围内有意义,必须250,520xx-≥⎧⎨-≥⎩⇒x=52.∴y=-3.∴2xy=2·52·(-3)=-15.第二章方程与不等式第1讲方程与方程组第1课时一元一次方程与二元一次方程组1.A 2.D 3.B 4.A 5.4 6.1,1 xy=⎧⎨=-⎩7.20 000-3x=5 0008.解:设中国人均淡水资源占有量为x m3,美国人均淡水资源占有量为y m3.根据题意,得5,13800.y xx y=⎧⎨+=⎩解得2300,11500.xy=⎧⎨=⎩答:中、美两国人均淡水资源占有量各为2 300 m3,11 500 m3.9.1解析:由于-2x m-1y3与12xn y m+n是同类项,所以有1,3,m nm n-=⎧⎨=+⎩由m-1=n,得-1=n-m.所以(n-m)2 012=(-1)2 012=1.10.C解析:把2,1xy=⎧⎨=⎩代入8,1,mx nynx my+=⎧⎨-=⎩得⎩⎪⎨⎪⎧2m+n=8,2n-m=1,解得⎩⎪⎨⎪⎧m=3,n=2.所以2m-n=6-2=4,4的算术平方根是2.故选C.11.1 10012.解:原方程组可化为⎩⎪⎨⎪⎧4x-y=5,①3x+2y=12,②①×2+②,得11x=22,∴x=2.把x=2代入①,得y=3.∴方程组的解为⎩⎪⎨⎪⎧x=2,y=3.13.解:(1)当x=1时,y=1+1=2,∴b=2.(2)⎩⎪⎨⎪⎧x=1,y=2.(3)∵直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b),∴当x=1时,y=m+n=b=2.∴当x=1时,y=n+m=2,∴直线l3:y=nx+m也经过点P.14.解:这天萝卜的单价是x元/斤,排骨的单价是y元/斤.根据题意,得⎩⎪⎨⎪⎧3x+2y=45,31+50%x+21+20%y=36.解得⎩⎪⎨⎪⎧x=3,y=18.答:这天萝卜、排骨的单价是3元/斤、18元/斤.15.解:⎩⎪⎨⎪⎧x-y=2,①x2-2xy-3y2=0,②方程①变形为y=x-2.③把③代入②,得x2-2x(x-2)-3(x-2)2=0.整理,得x2-4x+3=0.解这个方程,得x1=1,x2=3.将x1=1,x2=3代入③,分别求得y1=-1,y2=1.所以原方程组的解为⎩⎪⎨⎪⎧x1=1,y1=-1或⎩⎪⎨⎪⎧x2=3,y2=1.16.B解析:关于x,y的二元一次方程组⎩⎪⎨⎪⎧x+y=5k,x-y=9k,得⎩⎪⎨⎪⎧x=7k,y=-2k.将之代人方程2x+3y =6,得k=34.第2课时分式方程1.D 2.D 3.B 4.C 5.C6.1解析:原方程求解,得x=1或-1.经检验,x=-1是原方程的增根,所以x=1是原方程的根.7.2 200元解析:设条例实施前此款空调的售价为x元,由题意列方程,得10 000x(1+10%)=10 000x-200,解得x=2 200元.8.解:方程两边同时乘以(x+1)(x-1),得2+(x -1)=(x +1)(x -1).解得x =2或-1. 经检验:x =-1是方程的增根. ∴原方程的解为x =2.9.解:由题意列方程,得3-x 2-x -1x -2-=3,解得x =1.经检验x =1是原方程的根.10.解:设一片国槐树叶一年的平均滞尘量为x 毫克,则一片银杏一年的平均滞尘量为(2x -4)毫克,根据题意,得1 0002x -4=550x .解得x =22.经检验,x =22是方程的解.答:一片国槐树叶一年的平均滞尘量为22毫克.11.A 解析:∵a ⊕b =1b -1a ,∴2⊕(2x -1)=12x -1-12=1.∴12x -1=32,解得x =56.检验,合适.故选A.12.0 解析:去分母,得2-x -m =2(2-x ),解得x =6-m 3.由原方程有增根,所以6-m3=2,解得∴m =0.13.解:设文学书的单价是x 元/本,则科普书的单位为(x +4)元/本.依题意,得12 000x +4=8 000x .解得x =8.经检验x =8是方程的解,并且符合题意. ∴科普书的单价为:x +4=12(元).∴去年购进的文学书和科普书的单价分别是8元和12元. 15.解:(1)设商铺标价为x 万元,则:按方案一购买,则可获投资收益(120%-1)×x +x ×10%×5=0.7x .投资收益率为0.7xx×100%=70%.按方案二购买,则可获投资收益(120%-0.85)×x +x ×10%×(1-10%)×3=0.62x .投资收益率为0.62x0.85x×100%≈72.9%.∴投资者选择方案二所获得的投资收益率更高. (2)由题意,得0.7x -0.62x =5. 解得x =62.5(万元).∴甲投资了62.5万元,乙投资了53.125万元. 14.解:设该校九年级学生有x 人.根据题意,得 1 936x ×0.8=1 936x +88, 整理,得0.8(x +88)=x . 解得x =352.经检验x =352是原方程的解. 答:这个学校九年级学生有352人.16.解:设B 车间每天生产x 件,则A 车间每天生产1.2x .由题意,得4 400x +1.2x+4 400x =20.解得x =320.经检验x =320 是原方程的根.A 车间每天生产的件数=1.2x =320×1.2=384(件).答:A 车间每天生产384件,B 车间每天生产320件. 第3课时 一元二次方程1.C 2.C 3.D 4.B 5.C 6.B7.B 解析:∵关于x 的一元二次方程x 2+2x -a =0有两个相等的实数根,∴Δ=22+4a =0.解得a =-18.c >9 9.289(1-x )2=256 10.解:(x -3)2+4x (x -3)=0, 因式分解,得(x -3)(x -3+4x )=0, 整理,得(x -3)(5x -3)=0. 于是得x -3=0或5x -3=0.解得x 1=3,x 2=35.11.D 解析:x 1+x 2=-2a =3,a =-32;x 1x 2=b =1.12.B 13.314.-1 解析:将原代数式去括号,因式分解,整理, 得(a -b )(a +b -2)+ab . ①由一元二次方程根与系数关系,得a +b =2,ab =-1, ①式=0-1=-1.15.解:(1)设每千克核桃应降价x 元.根据题意,得(60-x -40)⎝⎛⎭⎫100+x2×20=2 240. 化简,得x 2-10x +24=0,解得x 1=4,x 2=6. 答:每千克核桃应降价4元或6元.(2)由(1)可知,每千克核桃可降价4元或6元.因为要尽可能让利于顾客,所以每千克核桃应降价6元.此时,售价为:60-6=54(元),5460×100%=90%.答:该店应按原售价的九折出售.16.解:设AB =x m ,则BC =(50-2x ) m. 根据题意可,得x (50-2x )=300. 解得x 1=10,x 2=15.当x =10时,BC =50-10-10=30>25, 故x 1=10(不合题意,舍去).答:可以围成AB 的长为15米,BC 为20米的矩形.17.D 解析:由题意,得⎩⎨⎧(2k +1)2-4k >0,2k +1≥0,k ≠0.解得-12≤k <12且k ≠0.18.4 解析:∵α,β是一元二次方程x 2+3x -7=0的两个根,∴α+β=-3,α2+3α=7.∴α2+4α+β=α2+3α+α+β=7-3=4.故α2+4α+β的值为4.19.10 解析:解方程x 2-6x +8=0,得x 1=2,x 2=4. ∴三角形的三条边的长只能是4,4,2 .∴该三角形的周长是10. 第2讲 不等式与不等式组1.B 2.C 3.B 4.B 5.2<x <3 6.m ≤27.m >2 解析:由第一象限点的坐标的特点可得⎩⎪⎨⎪⎧m >0,m -2>0.解得m >2.8.-1,0,1 解析:解原不等式组,得-32<x ≤1,所以x 取-1,0,1.9.解:⎩⎪⎨⎪⎧3x -2<x +2, ①8-x ≥1-3(x -1). ②由不等式①,得x <2, 由不等式②,得x ≥-2.∴不等式组的解集为-2≤x <2.10.解:(1)牛奶盒数为(5x +38)盒.(2)根据题意,得⎩⎪⎨⎪⎧5x +38-6(x -1)<5,5x +38-6(x -1)≥1.∴不等式组的解集为39<x ≤43. ∵x 为整数,∴x 取40,41,42,43.答:该敬老院至少有40名老人,最多有43名老人.11.A 解析:由题意得,点M 关于x 轴对称的点的坐标为(1-2m,1-m ).又∵M (1-2m ,m -1)关于x 轴的对称点在第一象限,∴⎩⎪⎨⎪⎧1-2m >0,1-m >0.解得⎩⎪⎨⎪⎧m <12,m <1. 在数轴上表示为.故选A.12.B 解析:设购进这种水果a 千克,进价为y 元/千克,这种水果的售价在进价的基础上应提高x ,则售价为(1+x )y 元/千克.由题意,得0.9a (1+x )y -ayay ×100%≥20%.解得x ≥13.∵超市要想至少获得20%的利润,∴这种水果的售价在进价的基础上应至少提高33.4%.13.a <4 解析:⎩⎪⎨⎪⎧2x >3x -3, ①3x -a >5. ②由①得,x <3,由②得,x >5+a3.∵此不等式组有实数解, ∴5+a 3<3,解得a <4.14.解:(1)设甲票价为4x 元,则乙为3x 元. ∴3x +4x =42,解得x =6.∴4x =24,3x =18.∴甲、乙两种票的单价分别是24元、18元. (2)设甲票有y 张,根据题意,得 ⎩⎪⎨⎪⎧24y +18(36-y )≤750,y >15. 解得15<y ≤17.∵x 为整数,∴y =16或17.∴有两种购买方案:甲种票16张,乙种票20张;甲种票17张,乙种票19张.15.解:⎩⎨⎧x 2+x +13>0, ①x +5a +43>43(x +1)+a . ②解不等式①,得x >-25.解不等式②,得x <2a .由该不等式有实数解,得该不等式组的解集为-25<x <2a .又由该不等式恰有两个整数解,得1<2a ≤2.解得12<a ≤1.∴实数a 的取值范围为12<a ≤1.16.解:(1)设有x 人生产A 种板材,则有(210-x )人生产B 种板材.根据题意列方程,得 48 00060x =24 00040(210-x ). 化简,得6x =8(210-x ). 解得x =120.经检验x =120是原方程的解.生产B 种板材的人数为210-x =210-120=90(人).(2)设生产甲型板房m 间,则生产乙型板房为(400-m )间.根据题意,得 ⎩⎪⎨⎪⎧108m +156(400-m )≤48 000,61m +51(400-m )≤24 000.解得300≤m ≤360. 设400间板房能居住的人数为W .则有 W =12m +10(400-m ),W =2m +4 000.∵k =2>0,∴当m =360时,W 最大值=2×360+4 000=4 720(人). 答:这400间板房最多能安置4 720人. 17.a <418.解:(1)(2 420+1 980)×13%=572(元).(2)①设冰箱采购x 台,则彩电采购(40-x )台.根据题意,得 ⎩⎪⎨⎪⎧2 320x +1 900(40-x )≤85 000,x ≥56(40-x ).解不等式组,得18211≤x ≤2137.因为x 为整数,所以x =19或20或21. 方案一:冰箱购买19台,彩电购买21台; 方案二:冰箱购买20台,彩电购买20台; 方案一:冰箱购买21台,彩电购买19台. ②设商场获得总利润为y 元,则y =(2 420-2 320)x +(1 980-1 900)(40-x ) =20x +3 200.∵k =20>0,∴y 随x 的增大而增大.∴当x =21时,y 最大=20×21+3 200=3 620. 第三章 函数第1讲 函数与平面直角坐标系 1.B 2.B 3.C 4.B 5.B6.B 解析:顶点A 的坐标是(-2,3),△ABC 向右平移4个单位后得到△A 1B 1C 1的顶点A 1的坐标是(2,3),△A 1B 1C 1关于x 轴对称图形△A 2B 2C 2的顶点A 2的坐标是(2,-3).7.C 解析:根据以原点O 为位似中心,图形的坐标特点得出,对应点的坐标应乘以-2,故点A 的坐标是(1,2),则点A ′的坐标是(-2,-4).8.C 9.C 10.(-1,-2) 11.(1,3)12.⎝⎛⎭⎫72,0 解析:如下图D37,取B (3,-1)关于x 轴的对称点为B ′,则B ′的坐标为(3,1).作直线AB ,它与x 轴的交点即为所求的点M .使用待定系数法求得直线AB 的解析式为y =-2x +7,令y =0,得-2x +7=0,解得x =72,所以点M 的坐标为⎝⎛⎭⎫72,0.图D3713.210 解析:如图可知,每个拐角形阴影部分的面积等于两个正方形面积的差,其面积分别为:22-12,42-32,62-52,…,202-192,因此其面积和为:2+1+4+3+6+5+…+20+19=20×(1+20)2=210. 14.(16,1+3) 解析:可以求得点A (-2,-1-3),则第一次变换后点A 的坐标为A 1(0,1+3),第二次变换后点A 的坐标为A 2(2,-1-3),可以看出每经过两次变换后点A 的y 坐标就还原,每经过一次变换x 坐标增加2.因而第九次变换后得到点A 9的坐标为(16,1+3).15.(1)△ABC 如图D38 14(2)直角三角形 解析:(1)因为点A 的坐标为(1,2),所以点A 关于y 轴的对称点B 的坐标为(-1,2),关于原点的对称点C 的坐标为(-1,-2).连AB ,BC ,AC ,作△ABC.图D38设AB 交y 轴于D 点,如图D38, D 点坐标为(0,2), ∵OD ∥BC ,∴△ADO ∽△ABC . ∴S △ADO S △ABC =AD 2AB 2=14. (2)∵ab ≠0,∴a ≠0,且b ≠0, ∴点A 不在坐标轴上, ∴AB ∥x 轴,BC ⊥x 轴. ∴∠ABC =90°.∴△ABC 是直角三角形.16.解:(1)∵四边形ONEF 是矩形, ∴点M 是OE 的中点.∵O (0,0),E (4,3),∴点M 的坐标为⎝⎛⎭⎫2,32. (2)设点D 的坐标为(x ,y ).若以AB 为对角线,AC ,BC 为邻边构成平行四边形,则AB ,CD 的中点重合∴⎩⎨⎧ 1+x 2=-1+324+y 2=2+12,解得,⎩⎪⎨⎪⎧x =1y =-1.若以BC 为对角线,AB ,AC 为邻边构成平行四边形,则AD ,BC 的中点重合∴⎩⎨⎧ -1+x 2=1+322+y 2=4+12,解得,⎩⎪⎨⎪⎧x =5y =3.若以AC 为对角线,AB ,BC 为邻边构成平行四边形,则BD ,AC 的中点重合∴⎩⎨⎧3+x 2=-1+121+y 2=2+42,解得,⎩⎪⎨⎪⎧x =-3y =5.综上可知,点D 的坐标为(1,-1)或(5,3)或(-3,5).17.D 解析:过小正方形的一个顶点D 3作FQ ⊥x 轴于点Q ,过点A 3作A 3F ⊥FQ 于点F . ∵正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3, ∴∠B 3C 3E 4=60°,∠D 1C 1E 1=30°,∠E 2B 2C 2=30°,∴D 1E 1=12D 1C 1=12,∴D 1E 1=B 2E 2=12,∴cos30°=B 2E 2B 2C 2=12B 2C 2,解得:B 2C 2=33.∴B 3E 4=36,cos30°=B 3E 4B 3C 3.解得:B 3C 3=13.则D 3C 3=13.根据题意得出: ∠D 3C 3Q =30°,∠C 3D 3Q =60°,∠A 3D 3F =30°,∴D 3Q =12×13=16,FD 3=D 3A 3·cos30°=13×32=36.则点A 3到x 轴的距离FQ =D 3Q +FD 3=16+36=3+16.第2讲 一次函数1.D 2.D 3.D 4.A 5.D 6.C 7.B 8.减小 9.210.解:(1)120×150=18 000(元). (2)由图象知,y 与x 之间的函数是一次函数.设函数关系式为:y =kx +b (k ≠0).将(205,1 000),(275,1 280)两点坐标代入得:⎩⎪⎨⎪⎧ 205k +b =1 000,275k +b =1 280,解得⎩⎪⎨⎪⎧k =4,b =180.则y 与x 之间的函数关系式为y =4x +180.11.B 解析:∵函数图象经过二、四象限,∴m -1<0,解得m <1.故选B.12.B 解析:∵一次函数y =mx +|m -1|的图象过点(0,2),∴|m -1|=2,∴m -1=2或m -1=-2,解得m =3或m =-1,∵y 随x 的增大而增大,∴m >0,∴m =3.13.B 解析:由函数图象可知,当x <2时y 1<y 2.14.-8 解析:∵y =kx +b 的图象与正比例函数y =2x 的图象平行,∴k =2.∵y =kx +b 的图象经过点A (1,-2),∴2+b =-2,解得b =-4,∴kb =2×(-4)=-8. 15.解:(1)y =(1-0.5)x -(0.5-0.2)(200-x ) =0.8x -60(0≤x ≤200);(2)根据题意得:30×(0.8x -60)≥2 000,解得x ≥15813.故小丁每天至少要卖159份报纸才能保证每月收入不低于2 000元.16.⎝⎛⎭⎫75,-65 解析:如图D39,当AB 最短时AB ⊥直线y =2x -4,设直线与x 轴、y 轴的交点分别为点C ,D ,过点B ,作BE ⊥AC 于E ,易知△ABC ∽△DOC ,对应线段成比例,即CA CD =BCOC,AC =3,易求OC =2,CD =2 5,可以求出BC =35 5,又有△ABC ∽△BEC ,根据EC BC =BCAC,可求出CE =35,所以点B 的横坐标为2-35=75,代入表达式中就可以求出点B 的纵坐标为-65.所以点B 的坐标为⎝⎛⎭⎫75,-65. 图D3917.解:(1)当售价定为每件30元时,一个月可获利: (30-20)×[105-5(30-25)]=800(元).(2)设售价为每件x 元时,一个月的获利为y 元 由题意得:y =(x -20)[105-5(x -25)] =-5x 2+330x -4 600 =-5(x -33)2+845当x =33时,y 的最大值是845.故当售价定为每件33元时,一个月获利最大,最大利润是845元. 18.解:(1)设商家购买彩电x 台,则购买洗衣机(100-x )台. 由题意,得2 000x +1 000(100-x )=160 000, 解得x =60.则100-x =40(台),所以,商家可以购买彩电60台,洗衣机40台. (2)设购买彩电a 台,则购买洗衣机为(100-2a )台. 根据题意,得 ⎩⎪⎨⎪⎧2 000a +1 600a +1 000(100-2a )≤160 000,100-2a ≤a , 解得3313≤a ≤37.5,因为a 是整数,所以a =34,35,36,37. 因此,共有四种进货方案.设商店销售完毕后获得利润为w 元.则w =(2 200-2 000)a +(1 800-1 600)a +(1 100-1 000)(100-2a )=200a +10 000. ∴w 随a 的增大而增大. ∴当a =37时,w 最大值=200×37+10 000=17 400(元), 所以商店获得的利润最大为17 400元.19.解:将(-1,1)代入y =kx +3,得1=-k +3,所以k =2.所以2x +3<0.解得x <-32.20.解:(1)(2 420+1 980)×13%=572(元).(2)设冰箱采购x 台,则彩电采购(40-x )台,根据题意得 ⎩⎪⎨⎪⎧2 320x +1 900(40-x )≤85 000,x ≥56(40-x ), 解不等式组得18211≤x ≤2137,因为x 为整数,所以x =19,20,21,方案一:冰箱购买19台,彩电购买21台, 方案二:冰箱购买20台,彩电购买20台, 方案一:冰箱购买21台,彩电购买19台, 设商场获得总利润为y 元,则y =(2 420-2 320)x +(1 980-1 900)(40-x ) =20x +3 200∴当x =21时,y 最大值=20×21+3 200=3 620(元).∴商场购买冰箱21台,彩电19台时获利最大,最大利润是3 620元. 第3讲 反比例函数 1.B 2.D3.A 解析:将y =k x 代入y =x +2中,得k x =x +2,由于函数y =kx与y =x +2的图象没有交点,则kx=x +2无解,得出k 的值. 4.C 解析:∵直线y =ax (a ≠0)与双曲线y =kx(k ≠0)的图象均关于原点对称,∴它们的另一个交点坐标与(2,6)关于原点对称.∴它们的另一个交点坐标为:(-2,-6).5.A 解析:先根据反比例函数的图象经过第一、三象限得到关于m 的不等式,求出m 的取值范围即可.∵双曲线y =m -1x的图象经过第一、三象限,∴m -1>0.∴m >1.6.B 解析:双曲线与直线的交点坐标适合两者的解析式,利用y =2x +1可以求出交点坐标为(-1,-1),进而求出k =1.7.C 解析:由矩形的面积知xy =9,可知它的长x 与宽y 之间的函数关系式为y =9x(x >0),是反比例函数图象,且其图象在第一象限.故选C.8.A 解析:由图象观察可知,一次函数与反比例函数相交于点(-2,-2)、(1,4)两点,进一步观察当-2<x <0时,一次函数的函数值大于反比例函数的函数值即y 1>y 2;当x >1时,一次函数的函数值大于反比例函数的函数值即y 1>y 1,因此A 满足条件.9.-2 解析:根据图象上的点满足函数解析式,即-2=k1,所以k =-2.10.-311.解:(1)∵点A (m,6)、B (n,3)在函数y =6x的图象上,∴m =1,n =2.∴A (1,6),B (2,3).∴⎩⎪⎨⎪⎧ k +b =6,2k +b =3.∴⎩⎪⎨⎪⎧k =-3,b =9.∴一次函数的解析式为y =-3x +9. (2)由图象知:1<x <2.12.A 解析:由反比例函数的增减性可知,当x <0时,y 随x 的增大而增大,所以当x 1<x 2<0时,0<y 1<y 2.又C (x 3,y 3)在第四象限,则y 3<0,所以y 3<y 1<y 2.故选A.13.C 14.-5<x <-1或x >0 15.-416.解:(1)在y 1=k 1x +1中,当x =0时,y =1, ∴点A 的坐标为(0,1). 设B 点的坐标为(b,0) 由△AOB 的面积为1,得 12b ×1=1,∴b =2.∴点B 的坐标为(2,0) 又∵点B 在一次函数y 1=k 1x +1的图象上,有0=2k 1+1,∴k 1=-12.∴一次函数的解析式为y 1=-12x +1.由点M 在一次函数y 1=k 1x +1的图象上,点M 纵坐标为2,得2=-12x +1,解得x =-2,点M 坐标为(-2,2).代入y 2=k 2x 中,得2=k 1-2.∴k 1=-4.∴反比例函数的解析式的解析式为y 2=-4x.由图象可知,点N 坐标为(4,-1)y 1>y 2时x 的取值范围为x <-2或0<x <4.17.三 k >0 解:(1)根据反比例函数图象与性质得到:双曲线y =kx的一支在第一象限,则k>0,得到另一支在第三象限;(2)∵梯形AOBC 的边OB 在x 轴的正半轴上,AC ∥OB ,BC ⊥OB ,而点C 的坐标标为(2,2),∴A 点的纵坐标为2,E 点的横坐标为2,B 点坐标为(2,0),把y =2代入y =k x 得x =k2;把x =2代入y =k x 得y =k2,∴A 点的坐标为⎝⎛⎭⎫k 2,2,E 点的坐标为⎝⎛⎭⎫2,k 2. ∴S 阴影=S △ACE +S △OBE =12×⎝⎛⎭⎫2-k 2×⎝⎛⎭⎫2-k 2+12×2×k 2=18k 2-12k +2=18(k -2)2+32. 当k -2=0,即k =2时,S 阴影部分最小,最小值为32;∴E 点的坐标为(2,1),即E 点为BC 的中点.∴当点E 在BC 的中点时,阴影部分的面积S 最小.(3)设D 点坐标为⎝⎛⎭⎫a ,k a ,∵OD OC =12,∴OD =DC ,即D 点为OC 的中点.∴C 点坐标为⎝⎛⎭⎫2a ,2k a ,把y =2k a 代入y =k x 得x =a2,确定A 点坐标为⎝⎛⎭⎫a 2,2k a ,∵S △OAC =2,∴12×⎝⎛⎭⎫2a -a 2×2k a =2,解得k =43.双曲线的解析式为y =43x . 18.解:(1)510-200=310(元).(2)p =200x,∴p 随x 的增大而减小.(3)购x 元(200≤x <400),在甲商场的优惠额是100元,乙商场的优惠额是x -0.6x =0.4x . 当0.4x <100,即200≤x <250时,选甲商场优惠; 当0.4x =100,即x =250时,选甲乙商场一样优惠; 当0.4x >100,即250<x <400时,选乙商场优惠;19.解:(1)把A (2,3)代入y 2=mx,得m =6.把A (2,3),C (8,0)代入y 1=kx +b ,得⎩⎪⎨⎪⎧3=2k +b ,0=8k +b ,解得⎩⎪⎨⎪⎧k =-12,b =4.∴这两个函数的解析式为:y 1=-12x +4,y 2=6x.(2)由题意得⎩⎨⎧y =-12x +4,y =6x,解得⎩⎪⎨⎪⎧ x 1=6,y 1=1或⎩⎪⎨⎪⎧x 2=2,y 2=3.∴当x <0或2<x <6时,y 1>y 1.20.解:(1)设反比例函数解析式为y =kx,将(25,6)代入解析式得,k =150.所以y =150x(x ≥15).将y =10代入解析式得,10=150x.x =15.故A (15,10),则正比例函数解析式为y =150x(x ≥15).设正比例函数解析式为y =nx ,将A (15,10)代入上式即可求出n 的值,n =23.则正比例函数解析式为y =23x (0≤x ≤15).(2)150x=2,解之得x =75(分钟).答:从药物释放开始,师生至少在75分钟内不能进入教室. 第4讲 二次函数1.D 2.A 3.D 4.C 5.D 6.D 7.C 8.A 9.(1,-4) 10.-1<x <3 11.解:(1)画图(如图D40).图D40(2)当y <0时,x 的取值范围是x <-3或x >1. (3)平移后的图象所对应的函数关系式为y =-12(x -2)2+2⎝⎛⎭⎫或写成y =-12x 2+2x . 12.C 13.D 14.D 15.D 16.解:(1)10+x 500-10x(2)设月销售利润为y 元.根据题意, 得y =(10+x )(500-10x ), 整理得y =-10(x -20)2+9 000当x =20时,y 有最大值9 000(元),此时篮球的售价为:20+50=70(元). 答:8 000元不是最大利润,最大利润是9 000元,此时篮球售价应为70元. 17.解:(1)∵抛物线y =ax 2+bx +3与x 轴相交于点A (-3,0),B (-1,0), ∴⎩⎪⎨⎪⎧ 9a -3b +3=0,a -b +3=0,解得⎩⎪⎨⎪⎧a =1,b =4. ∴抛物线的解析式为:y =x 2+4x +3.(2)由(1)知,抛物线解析式为:y =x 2+4x +3, ∵令x =0,得y =3,∴C (0,3).∴OC =OA =3,则△AOC 为等腰直角三角形.∴∠CAB =45°.∴cos ∠CAB =22.在Rt △BOC 中,由勾股定理得:BC =12+32=10. 如图D41所示,连接O 1B ,O 1C ,由圆周角定理得:∠BO 1C =2∠BAC =90°. ∴△BO 1C 为等腰直角三角形.∴⊙O 1的半径O 1B =22BC =22×10= 5.图D41图D42(3)抛物线y =x 2+4x +3=(x +2)2-1,∴顶点P 坐标为(-2,-1),对称轴为x =-2.又∵A (-3,0),B (-1,0),可知点A ,B 关于对称轴x =2对称.如图D42所示:由圆及抛物线的对称性可知:点D ,点C (0,3)关于对称轴对称, ∴D (-4,3).又∵点M 为BD 中点,B (-1,0),∴M ⎝⎛⎭⎫-52,32. ∴BM =⎣⎡⎦⎤-52-(-1)2+⎝⎛⎭⎫322=322. 在△BPC 中,B (-1,0),P (-2,-1),C (0,3),由两点间的距离公式得:BP =2,BC =10,PC =2 5. ∵△BMN ∽△BPC ,∴BM BP =BN BC =MN PC ,即3 222=BN 10=MN2 5. 解得:BN =3210,MN =3 5.设N (x ,y ),由两点间的距离公式可得:⎩⎨⎧(x +1)2+y 2=⎝⎛⎭⎫32102,⎝⎛⎭⎫x +522+⎝⎛⎭⎫y -322=(35)2,解之得,⎩⎨⎧ x 1=72,y 1=32,⎩⎨⎧x 2=12,y 2=-92.∴点N 的坐标为⎝⎛⎭⎫72,-32或⎝⎛⎭⎫12,-92. 18.(1)证明:∵二次函数y =mx 2+nx +p 图象的顶点横坐标是2,∴抛物线的对称轴为x =2,即-n2m=2,化简得:n +4m =0.(2)解:∵二次函数y =mx 2+nx +p 与x 轴交于A (x 1,0),B (x 2,0),x 1<0<x 2,∴OA =-x 1,OB =x 2;x 1+x 2=-n m ,x 1·x 2=pm.令x =0,得y =p ,∴C (0,p ).∴OC =|p |.由三角函数定义得:tan ∠CAO =OC OA =|p |-x 1=-|p |x 1,tan ∠CBO =OC OB =|p |x 2.∵tan ∠CAO -tan ∠CBO =1,即-|p |x 1-|p |x 2=1,化简得:x 1+x 2x 1·x 2=-1|p |.将x 1+x 2=-n m ,x 1·x 2=pm 代入得:-n m p m=-1|p |,化简得:n =p|p |=±1.由(1)知n +4m =0,∴当n =1时,m =-14;当n =-1时,m =14.∴m ,n 的值为:m =14,n =-1(此时抛物线开口向上)或m =-14,n =1(此时抛物线开口向下).(3)解:由(2)知,当p >0时,n =1,m =-14,∴抛物线解析式为:y =-14x 2+x +p .联立抛物线y =-14x 2+x +p 与直线y =x +3解析式得到:-14x 2+x +p =x +3,化简得:x 2-4(p -3)=0.∵二次函数图象与直线y =x +3仅有一个交点, ∴一元二次方程根的判别式等于0,即△=02+16(p -3)=0,解得p =3.∴抛物线解析式为:y =-14x 2+x +3=-14(x -2)2+4.当x =2时,二次函数有最大值,最大值为4.∴当p >0且二次函数图象与直线y =x +3仅有一个交点时,二次函数的最大值为4. 19.解:(1)当m =3时,y =-x 2+6x .令y =0得-x 2+6x =0,解得,x 1=0,x 2=6. ∴A (6,0).当x =1时,y =5.∴B (1,5).∵抛物线y =-x 2+6x 的对称轴为直线x =3,且B ,C 关于对称轴对称,∴BC =4. (2)过点C 作CH ⊥x 轴于点H (如图D43) 由已知得,∠ACP =∠BCH =90°, ∴∠ACH =∠PCB .又∵∠AHC =∠PBC =90°,∴△ACH ∽△PCB . ∴AH CH =PB BC. ∵抛物线y =-x 2+2mx 的对称轴为直线x =m ,其中m >1,且B ,C 关于对称轴对称, ∴BC =2(m -1).∵B (1,2m -1),P (1,m ),∴BP =m -1.又∵A (2m,0),C (2m -1,2m -1),∴H (2m -1,0). ∴AH =1,CH =2m -1,∴12m -1=m -12()m -1,解得m =32.图D43图D44(3)存在.∵B ,C 不重合,∴m ≠1.当m >1时,BC =2(m -1),PM =m ,BP =m -1, ①若点E 在x 轴上如图D43, ∵∠CPE =90°,∴∠MPE +∠BPC =∠MPE +∠MEP =90°,PC =EP . ∴△BPC ≌△MEP ,∴BC =PM ,即2(m -1)=m ,解得m =2. 此时点E 的坐标是(2,0).②若点E 在y 轴上如图D44,过点P 作PN ⊥y 轴于点N ,易证△BPC ≌△NPE ,∴BP =NP =OM =1,即m -1=1,解得,m =2. 此时点E 的坐标是(0,4).当0<m <1时,BC =2(1-m ),PM =m ,BP =1-m , ①若点E 在x 轴上如图D45, 易证△BPC ≌△MEP ,∴BC =PM ,即2(1-m )=m ,解得,m =23.此时点E 的坐标是(43,0).图D45图D46②若点E 在y 轴上如图D46,过点P 作PN ⊥y 轴于点N ,易证△BPC ≌△NPE , ∴BP =NP =OM =1,即1-m =1,∴m =0(舍去). 综上所述,当m =2时,点E 的坐标是(0,2)或(0,4),当m =23时,点E 的坐标是⎝⎛⎭⎫43,0. 20.解:(1)在y =-38x 2-34x +3中,令y =0,即-38x 2-34x +3=0,解得x 1=-4,x 2=2.∵点A 在点B 的左侧,∴A ,B 点的坐标为A (-4,0),B (2,0).(2)由y =-38x 2-34x +3得,对称轴为x =-1.在y =-38x 2-34x +3中,令x =0,得y =3.∴OC =3,AB =6,S ΔACB =12AB ·OC =12×6×3=9.在Rt △AOC 中,AC =OA 2+OC 2=42+32=5,∴sin ∠OCA =45.设△ACD 中AC 边上的高为h ,则有12AC ·h =9,解得h =185.如图D47,在坐标平面内作直线平行于AC ,且到AC 的距离h =185,这样的直线有2条,分别是L 1和L 2,则直线与对称轴x =-1的两个交点即为所求的点D.图D47设L 1交y 轴于点E ,过点C 作CF ⊥L 1于点F ,则CF =h =185,∴CE =CF sin ∠CEF =CFsin ∠OCA =18545=92.设直线AC 的解析式为y =kx +b , 将点A (-4,0),点C (0,3)坐标代入,得⎩⎪⎨⎪⎧-4k +b =0,b =3,解得⎩⎪⎨⎪⎧k =34,b =3.∴直线AC 解析式为y =34x +3.直线L 1可以看做直线AC 向下平移CE 长度单位⎝⎛⎭⎫92个长度单位而形成的, ∴直线L 1的解析式为y =34x +3-92=34x -32.则D 1的纵坐标为34×()-1-32=-94.∴D 1⎝⎛⎭⎫-1,-94. 同理,直线AC 向上平移92个长度单位得到L 2,可求得D 2⎝⎛⎭⎫-1,274. (3)如图D48,以AB 为直径作⊙F ,圆心为F .过E 点作⊙F 的切线,这样的切线有2条.图D48连接FM ,过M 作MN ⊥x 轴于点N .∵A (-4,0),B (2,0),∴F (-1,0),⊙F 半径FM =FB =3. 又FE =5,则在Rt △MEF 中,ME =52-32=4,sin ∠MFE =45,cos ∠MFE =35.在Rt △FMN 中,MN =FN ·sin ∠MFE =3×45=125,FN =FM ·cos ∠MFE =3×35=95,则ON =45,∴M 点坐标为⎝⎛⎭⎫45,125.直线l 过M ⎝⎛⎭⎫45,125,E (4,0),设直线l 的解析式为y =k 1x +b 1,则有⎩⎪⎨⎪⎧45k +b =125,4k +b =0,解得⎩⎪⎨⎪⎧k =-34,b =3.∴直线l 的解析式为y =-34x +3.同理,可以求得另一条切线的解析式为y =34x -3.综上所述,直线l 的解析式为y =-34x +3或y =34x -3.第二部分 空间与图形 第四章 三角形与四边形 第1讲 相交线和平行线1.B 2.C 3.C 4.A 5.C 6.B 7.D 8.121° 9.98 10.35 11.360 12.解:∵∠1=∠2,∴AB ∥CD (同位角相等,两直线平行). ∴∠3=∠4=75°(两直线平行,内错角相等). 13.A 14.B15.解:(1)2 (2)6 (3)12 (4)(n -1)n (5)4 030 05616.解:(1)∠MON =∠COM -∠CON =12∠AOC -12∠BOC =12×120°-12×30°=45°.(2)∠MON =∠COM -∠CON =12∠AOC -12∠BOC =12(α+30°)-12×30°=12α.(3)∠MON =∠COM -∠CON =12∠AOC -12∠BOC =12(90°+β)-12β=45°.(4)∠MON 的大小等于∠AOB 的一半,与∠BOC 的大小无关. 17.解:(1)∵m ∥n ,∴点C ,P 到直线n 间的距离与点A ,B 到直线m 间的距离相等. 又∵同底等高的三角形的面积相等,∴图D49(1)中符合条件的三角形有:△CAB 与△P AB 、△BCP 与△APC ,△ACO 与△BOP . (2)∵m ∥n ,∴点C ,P 到直线n 间的距离是相等的.∴△ABC 与△P AB 的公共边AB 上的高相等. ∴总有△P AB 与△ABC 的面积相等.(1)(2)图D49(3)如图D49(2)连接EC ,过点D 作直线DM ∥EC 交BC 的延长线于点M ,连接EM ,线段EM 所在的直线即为所求的直线.第2讲 三角形 第1课时 三角形1.C 2.D 3.B 4.B 5.D 6.B 7.C 8.A 9.3 10.证明:∵BD ⊥AC ,CE ⊥AB , ∴∠ADB =∠AEC =90°. 在△ABD 和△ACE 中,⎩⎪⎨⎪⎧∠A =∠A ,∠ADB =∠AEC ,AB =AC ,∴△ABD ≌△ACE (AAS).∴BD =CE .11.证明:∵AD =EB ,∴AD -BD =EB -BD ,即AB =ED . 又∵BC ∥DF ,∴∠CBD =∠FDB . ∴∠ABC =∠EDF .又∵∠C =∠F ,∴△ABC ≌△EDF .∴AC =EF .12.解:(1)如果①②,那么③;如果①③,那么②; (2)若选择如果①②,那么③. 证明:∵AE ∥DF ,∴∠A =∠D .∵AB =CD ,∴AB +BC =BC +CD ,即AC =DB . 在△ACE 和△DBF 中, ⎩⎪⎨⎪⎧∠E =∠F ,∠A =∠D ,AC =DB ,∴△ACE ≌△DBF (AAS).∴CE =BF . 若选择如果①③,那么②.证明:∵AE ∥DF ,∴∠A =∠D . 在△ACE 和△DBF 中,⎩⎪⎨⎪⎧∠E =∠F ,∠A =∠D ,EC =FB ,∴△ACE ≌△DBF (AAS).∴AC =DB .∴AC -BC =DB -BC ,即AB =CD . 13.解:∵∠CMD =90°,∴∠CMA +∠DMB =90°. 又∵∠CAM =90°,∴∠CMA +∠ACM =90°. ∴∠ACM =∠DMB . 又∵CM =MD ,∴Rt △ACM ≌Rt △BMD ,∴AC =BM =3. ∴他到达点M 时,运动时间为3÷1=3(s). 答:这个人运动了3 s. 14.13 15.D16.7 解析:因为△ABC 折叠,使点C 与点A 重合,折痕为DE ,所以EC =AE ,故△ABE 的周长为AB +BE +AE =AB +BE +EC =AB +BC =3+4=7.17.解:(1)①结论:BD =CE ,BD ⊥CE . ②结论:BD =CE ,BD ⊥CE .理由如下:∵∠BAC =∠DAE =90°,∴∠BAD -∠DAC =∠DAE -∠DAC ,即∠BAD =∠CAE . 在△ABD 与△ACE 中,∵⎩⎪⎨⎪⎧AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE .∴BD =CE .延长BD 交AC 于点F ,交CE 于点H . 在△ABF 与△HCF 中,∵∠ABF =∠HCF ,∠AFB =∠HFC , ∴∠CHF =∠BAF =90°.∴BD ⊥CE .(2)结论:乙.AB ∶AC =AD ∶AE ,∠BAC =∠DAE =90°. 18.(1)证明:在Rt △AFD 和Rt △CEB 中, ∵AD =BC ,AF =CE ,∴Rt △AFD ≌Rt △CEB . (2)解:∵∠ABH +∠CBE =90°,∠ABH +∠BAH =90°,∴∠CBE =∠BAH . 又∵AB =BC ,∠AHB =∠CEB =90°, ∴△ABH ≌△BCE .同理,得△ABH ≌△BCE ≌△CDG ≌△DAF . ∴S 正方形ABCD =4S △ABH +S 正方形HEGF=4×12×2×1+1×1=5.(3)解:由(1),知△AFD ≌△CEB ,故h 1=h 3, 由(2),知△ABH ≌△BCE ≌△CDG ≌△DAF , ∴S 正方形ABCD =4S △ABH +S 正方形HEGF=4×12(h 1+h 2)·h 1+h 22 =2h 21+2h 1h 2+h 22.第2课时 等腰三角形与直角三角形 1.C 解析:分顶角为40°或底角为40°两种情况. 2.B 3.C 4.A5.D 解析:∠B =∠EFC =90°-∠CEF =40°. 6.B 7.2 8.59.如果三角形三条边的边长a ,b ,c ,满足a 2+b 2=c 2,那么这个三角形是直角三角形 10.解:∵在Rt △BDC 中,∠BDC =45°,BD =10 2, ∴BC =CD =10. ∵∠C =90°,AB =20,∴∠A =30°.11.(1)解:∵AB =AC ,∴∠B =∠C =30°. ∵∠C +∠BAC +∠B =180°, ∴∠BAC =180°-30°-30°=120°. ∵∠DAB =45°,∴∠DAC =∠BAC -∠DAB =120°-45°=75°. (2)证明:∵∠DAB =45°, ∴∠ADC =∠B +∠DAB =75°.∴∠DAC =∠ADC . ∴DC =AC .∴DC =AB . 12.解:(1)AC ⊥BD .∵△DCE 由△ABC 平移而成,∴BE =2BC =6,DE =AC =3,∠E =∠ACB =60°.∴DE =12BE .∴BD ⊥DE .∵∠E =∠ACB =60°,∴AC ∥DE .∴BD ⊥AC . (2)在Rt △BED 中,∵BE =6,DE =3,∴BD 2=BE 2-DE 2=62-32,解得BD =3 3. 13.C 14.10+2 13 15.解:(1)如图D50:图D50(2)2 55 5 (3)直角 10 (4)1216.49217.解:(1)(x +0.7)2+22=2.52, 0.8,-2.2(舍去),0.8. (2)①不会是0.9米,若AA 1=BB 1=0.9,则A 1C =2.4-0.9=1.5, B 1C =0.7+0.9=1.6,1.52+1.62=4.81,2.52=6.25, ∵A 1C 2+B 1C 2≠A 1B 1 2 , ∴该题的答案不会是0.9米. ②有可能.设梯子顶端从A 处下滑x 米,点B 向外也移动x 米, 则有(x +0.7)2+(2.4-x )2=2.52, 解得:x =1.7或x =0(舍去).∴当梯子顶端从A 处下滑1.7米时,点B 向外也移动1.7米,即梯子顶端从A 处沿墙AC 下滑的距离与点B 向外移动的距离有可能相等.第3讲 四边形与多边形第1课时 多边形与平行四边形 1.B 2.A 3.C 4.C 5.300° 6.3 7.4 8.6 9.5 10.证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD .∴∠P AE =∠PCF .∵点P 是□ABCD 的对角线AC 的中点, ∴P A =PC .在△P AE 和△PCE 中,⎩⎪⎨⎪⎧∠P AE =∠PCF ,P A =PC ,∠APE =∠CPF ,∴△P AE ≌△PCE (ASA).∴AE =CF .11.解:添加的条件是BE =DF .证明如下: ∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC . ∵BE =DF ,∴AF =CE , 即AF =CE ,AF ∥CE .∴四边形AECF 是平行四边形. 12.证明:∵AE ⊥AD ,CF ⊥BC , ∴∠EAD =∠FCB =90°. ∵AD ∥BC ,∴∠ADE =∠FBC ,在Rt △AED 和Rt △CFB 中, ∵⎩⎪⎨⎪⎧∠EAD =∠FCB ,∠ADE =∠FBC ,AE =CF ,∴Rt △AED ≌Rt △CFB .∴AD =BC .又∵AD ∥BC ,∴四边形ABCD 是平行四边形. 13.B14.证明:(1)∵四边形ABCD 是平行四边形, ∴∠DAB =∠BCD .∴∠EAM =∠FCN . 又∵AD ∥BC ,∴∠E =∠F . 在△AEM 与△CFN 中,。
《线性代数》(经科社2013版)习题解答

5. A2 − 2A − 4E = O ⇒ A2 − 2A − 3E = E ⇒ (A + E )(A − 3E ) = E , 故(A + E )−1 = (A − 3E ).
3(A − E )−1 A = 3(A−1 (A − E ))−1 = 3(E − A−1 )−1 , 其中A−1 = 9. AA∗ = |A|E ⇒ 10.
−1 1
2
1 (4)A31 + A32 + A33 + A34 = 3 1
2 3 1
−3 6 3 1 3 1 .
3 4 1 8 3.(1)第i行减去末行的ai 倍(i = 1, 2, · · · , n), 再按末列展开. (2)仿教材例1.4.4. (3)从第一行开始, 上一行的x倍加到下一行, 再按末行展开. (4)按末列展开. 4.(1)见《线性代数学习指导》P25例25. (2)见《线性代数学习指导》P26例26. 或: 第一行减去第二行, 按第一行展开, 得递推关系式; 列同样 处理. 联立解之. 注: ::::::::: 此题较难,::::::::::: 可不作要求. (3)从第一行开始, 用上一行消下一行, 化为上三角行列式. 1 5. M11 + M21 + M31 + M41 = A11 − A21 + A31 − A41 = −1 1 −1 1 A11 + A12 + A13 + A14 = 1 −1 1 1 3 1 0 1 1 −5 3 −3 . −5 1 3 −4 2 0 1 1 −5 3 .
i=1 i=1 i=1
注: :::::::::::::::::::::::::::::::::: 要牢记矩阵乘法的口诀“前行乘后列”.
2013年高频习题解答

反馈系数
固有谐振电导
接入系数
折合到ce两端的总电导为
起振条件为
其中 ,
故
4-9图示是一电容反馈振荡器的实际电路,已知C1=50 pF,C2=100 pF,C3= 10~260pF,要求工作在波段范围,即f=10~1OMHz,试计算回路电感L和电容C。设回路无载Q。=100,负载电阻R=1kΩ,晶体管输入电阻Ri=500Ω.若要求起振时环路增益K。KF=3,问要求的跨gs。和静态工作电流IcQ必须多大?
3-8高频功放的欠压、临界、过压状态是如何区分的?各有什么特点?当UC、UBB、Ub、RL四个外界因素只变化其中的一个时,高频功放的工作状态如何变化?
答3-8
当晶体管工作在线性区时的工作状态叫欠压状态,此时集电极电流随激励而改变,电压利用率相对较低。如果激励不变,则集电极电流基本不变,通过改变负载电阻可以改变输出电压的大,输出功率随之改变;该状态输出功率和效率都比较低。
题3-1图
解3-2:
根据已知条件可知,能够忽略中和电容和yre的影响。得:
品质因数
3dB带宽
(2)放大器的电压增益
中和电容
答:品质因数QL为40.4,带宽为11.51kHz,谐振时的电压增益为-309,中和电容值为1.615pF
3-3高频谐振放大器中,造成工作不稳定的王要因素是什么?它有哪些不良影响?为使放大器稳定工作,可以采取哪些措施?
(2)利用功放放大振幅调制信号时,功放应选在欠压状态,并为乙类工作。
(3) 利用功放放大等幅度的信号时,功放应选在过压状态,此时输出电压幅度比较稳定。
3-16改正图示线路中的错误,不得改变馈电形式,重新画出正确的线路。
题3-16图
解3-16:
2013-化工基础复习题及解答(高分子)
绪论一.选择题1.下面那个过程属于动量传递过程?(B )A、萃取B、过滤C、蒸发D、干燥2.下列哪个单位为SI单位(A )A、温度/KB、温度/℃C、体积/m3D、力/N二.填空1.请列举出化工中常用的5个SI单位(格式要求-量的名称/单位符号)长度/m、质量/kg、时间/s、热力学温度/K、物质的量/mol。
2.质量衡算、能量衡算与动量衡算是化学工程课程中分析问题的基本方法。
质量守恒定律是质量衡算的依据;能量守恒定律是能量衡算的依据;动量守恒定律是动量衡算的依据。
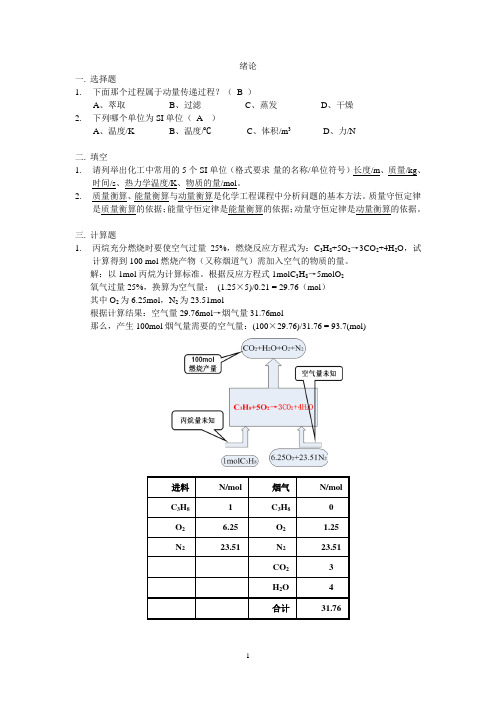
三.计算题1.丙烷充分燃烧时要使空气过量25%,燃烧反应方程式为:C3H8+5O2→3CO2+4H2O,试计算得到100 mol燃烧产物(又称烟道气)需加入空气的物质的量。
解:以1mol丙烷为计算标准。
根据反应方程式1molC3H8→5molO2氧气过量25%,换算为空气量:(1.25×5)/0.21 = 29.76(mol)其中O2为6.25mol,N2为23.51mol根据计算结果:空气量29.76mol→烟气量31.76mol那么,产生100mol烟气量需要的空气量:(100×29.76)/31.76 = 93.7(mol)2.在换热器里将平均比热为3.56 kJ/(kg·°C)的某溶液自25°C加热到80°C,溶液流量为1.0 kg/s,加热介质为120°C的饱和水蒸气,其消耗量为0.095 kg/s,蒸气冷凝成同温度的饱和水排出。
试计算此换热器的热损失占水蒸气所提供热量的百分数。
(120°C饱和水蒸气的焓值为2708.9 kJ/kg,120°C饱和水的焓值为503.67 kJ/kg。
)解:根据题意画出流程图基准:单位时间1s;在图中虚线范围内作热量衡算:在此系统中输入的热量:∑ Q I = Q1 + Q2(Q = mc PΔt)蒸气带入的热量:Q1 = 0.095 × 2708.9 = 257.3 kJ溶液带入的热量:Q2 = 1.0 × 3.56 × (25-0) = 89 kJ∑ Q I = Q1 + Q2 =257.3+89 = 346.3 kJ在此系统中输出的热量:∑ Q o = Q3 + Q4冷凝水带出的热量:Q3 = 0.095 × 503.67 = 47.8 kJ溶液带出的热量:Q4 = 1.0 × 3.56 × (80-0) = 284.8 kJ∑ Q o = Q3 + Q4 =47.8 +284.8 = 332.6 kJ热量损失= ∑ Q I - ∑ Q o = 346.3 - 332.6 = 13.7 kJ热量损失的百分数= 13.7/(257.3 - 47.8)= 6.5%3.P6例0-1;P7例0-2;P10例0-3第一章流体流动与输送一.选择题1.流体的输送方式通常有四种。
2013复式记账习题答案解析

一:目的:练习资金投入企业的核算:某企业200*年7月发生资金投入的各项经济业务如下:1.收到投资者投入资金400 000元存入银行,2.接受A单位投入生产设备一台,价值150 000元,3.向银行借入临时借款50 000元,存入银行,借款期为3个月,4.临时借款50 000元到期,以银行存款归还。
【答案】1.借:银行存款 400 000贷:实收资本 400 0002.借:固定资产150 000贷:实收资本150 0003. 借:银行存款 50 000贷:短期借款 50 0004.借:短期借款 50 000贷:银行存款 50 000二.某企业200*年7月内发生的有关材料采购的经济业务:1.采购员**预支差旅费500元,以现金支付2.购进下列原材料,增殖税17%,已验收入库,货款以商业承兑汇票结算甲材料1600千克单价10元计16 000元乙材料800千克单价16元计12 800元应交增值税 4 896元合计33 696元3.以银行存款支付上述材料运费480元,以现金支付运达仓库的装卸费240元,计甲材料480元,乙材料240元4.上述材料按实际成本入账,计甲材料16 480元,乙材料13 040元5.商业汇票到期,以银行存款支付上述材料款33 696元6.从外地购入材料11 100元,计甲材料550千克,单价10元,乙材料350千克,单价16元,应交增值税1887元,货款以银行存款支付,材料未到7.上述材料已到,以现金支付运费180元,以银行存款支付装卸费540元,计甲材料440元,乙材料280元8.上述材料按实际成本11 820元转账,计甲材料5 940元,乙材料5 880元要求:编制会计分录【答案】1.借:其他应收款 500贷:库存现金 5002.借:在途物资——甲材料16 000——乙材料12 800应交税费——应交增值税(进项)4 896贷:应付票据33 6963.借:在途物资——甲材料480——乙材料240贷:银行存款 480库存现金 2404.借:原材料——甲材料16 480——乙材料13 040贷:在途物资——甲材料16 480——乙材料13 0405.借:应付票据 33 696贷:银行存款 33 6966.借:在途物资——甲材料5500——乙材料5600应交税费——应交增值税(进项)1887贷:银行存款 129877.借:在途物资——甲材料440——乙材料280贷:库存现金 180银行存款 5408.借:原材料——甲材料 5 940——乙材料 5 880贷:在途物资——甲材料 5 940——乙材料 5 880三:练习企业生产过程核算:某企业200*年7月内发生的经济业务内容如下:L生产车间从仓库领用各种原材料进行产品生产,计用于生产A产品甲材料150千克,每千克10.50元,乙材料100千克,每千克16.50元,用于生产B产品甲材料120千克,每千克10.50元,乙材料80千克,每千克16.50元。
张宇2013考研数学辅导讲义高等数学第1,2章习题详解(理工类)

"
+
$ ) # $ 0 , 1 ) $ " # . / 0 ) & , " ! ) + , ! + $ & ) ( ) ( $ 6 7 ( ( 6 7 ) ) "& ) & $ " , - &! ! + % ) ($ 6 7 " & ( ) " " " "# % + 1 " # & "# " " "# % + 1 " # & "# " * 改为) * ! # " 题目中) + , -$ + , -$ % & & "( ( "( ( " " " " "# % + 1 " # & "# $" 分析 ! ! ! 3 % + , ! ( !设 & "( ( "
/" "# " "# $ 原式! + , ! $ /( % "( ( & &
令"! ! 得. # (代入原式得. /# ! " /" ( ! & % ' . " "# # " ' + , -. & ! " % "( ( " 分析 " ! % " " 8 9 . : 8 1 ' "# "# !原式!
+
2013四川大学生物反应工程练习题及部分解答

2013四川大学生物反应工程练习题及部分解答化工学院一、动力学基础1.为什么pH值会影响酶反应的速度?解释温度对酶反应的影响。
答:pH----酶分子上有许多酸性和碱性的氨基酸侧链基团,如果酶要表现活性,则这些基团必须有一定的解离形式。
随着pH的变化,这些基团可处在不同的解离状态,而具有催化活性的离子基团仅是其中的一种特定的解离形式,因而随着pH的变化,具有催化活性的这种特殊的离子基团在总酶量中所占的比例就会不同,使酶所具有的催化能力也不同,最终影响酶反应的速度。
温度----酶大部分是由蛋白质组成的,而酶在起作用时一般需要一个结合位点和催化位点,这些位点的性能高低与酶本身结构有关,而酶的结构又受到温度的影响。
在较低温度范围内,反应活性随温度的升高而升高;当温度超过酶所允许的生理温度以上时,则随着温度的提高,酶的热变性失活速率会加快,导致酶的活性下降,故酶催化反应速率亦随温度的升高而降低。
*影响酶反应速率的因素:1)内部因素:酶的结构特定,底物的结构特性;2)外部因素:各种物质的浓度(如酶的浓度、底物的浓度、抑制剂的浓度等)和操作条件(如温度、压力、离子强度、pH等)。
2.固定化酶外扩散的有效因子主要受哪些因素的影响?3.什么叫细胞的倍增时间?它与细胞生长速度有何关系?答:分批培养时,在指数生长期内,细胞浓度增加一倍所需的时间。
倍增时间t=ln2/µmax ,为定值。
(个人认为与细胞生长速度无关)4.请解释什么是酶的半衰期。
答:在一不含底物、产物、抑制剂或调节剂的完全封闭体系,活性酶经过一不可逆的结构变化或化学变化而成为一无活性状态,当活性酶浓度变为初始活性酶浓度一半时所需的时间,称为酶的半衰期。
5.什么叫固体催化剂颗粒的临界半径和最大颗粒半径?答:对仅有内扩散限制的球形生物催化剂的零级反应,有临界半径Rc :无底物的最大核半径(在r<Rc 处无底物存在,也无反应发生)。
有最大颗粒半径Rmax :(当r =0时,CS =0对应的最大颗粒半径,即Rc =0)。
微机原理部分习题解答与复习重点(2013年秋).

【程序】方法2:用LOOP循环
TESTP: MOV MOV MOV MOV MOV
WRT: MOV
DX,4000H DS,DX AL,55H SI,0 CX,1000H [SI],AL
; 初始化数据段寄存器 ; 要写入的数据:55H ; 段内偏移(地址指针) ; 循环4K次 ; 写数据
INC SI
立即寻址 寄存器寻址 寄存器间接寻址 直接寻址 寄存器相对寻址 寄存器相对寻址
3
P134 习题 3.2 若1KB的数据存放在TABLE以下,试编程序将该数
据块搬到NEXT为首地址的内存区域中。
① 利用串操作指令。
② 不用串操作指令。
START: MOV DX,SEG TABLE MOV DS,DX MOV SI,OFFSET TABLE MOV DX,SEG NEXT MOV ES,DX MOV DI,OFFSET NEXT MOV CX,1024 CLD REP MOVSB ……
MEMR
OE
8088
系统总线 MEMW
MEMR
&
G1
Y0
A18
1
Y1 G2A
A19
A17
≥1
A16 A15
G2B
A14
A13 A12
C B
A11
A
74LS138
【程序】方法1:用串操作指令
TESTP: MOV MOV MOV MOV MOV CLD REP
DX,4000H ES,DX DI,0 CX,1000H AL,55H
LOOP WRT
MOV SI,0
MOV CX,1000H CHK: CMP [SI],AL
; 数据读出校验
2013习题解答4

10N9(
0 -0.036
)
)
B
0.015
8N9(
A-B
Ra 6.3
Ra 6.3
Ra 12.5
Ra 1.6
Ra 1.6
Ra 1.6
Ra 3.2
φ 32r6
φ 30k610N9φ30k68N9φ 24r6
Ra 6.3
Ra 6.3
Ra 12.5
仔细查看下图中的形位公差标注,指出标注错 误并改正
轴
读装配图6
1. 简答导杆为什么不随着手轮一起转动? 2. 拆画支座8的零件图。 导套9用固定螺钉紧固,导杆10装有 键12,它在导套9的槽内有导向作用,所以 导杆不随手轮一起转动。
读装配图7
1.说明此钻模装卸工件的过程。 2、拆画轴6的零件图。
装载时,放上工件,装上钻模板2,拧上 特制螺母5。 卸载时,拧下特制螺母5,那下钻模板2, 取出工件。
12.5
0.8 3.2
3.2 6.3
3.2
3.2
A
Ra 0.8 Ra 3.2 Ra 3.2
Ra 3.2
B
Ra 6.3
Ra 3.2
Ra 12.5
Ra 6.3
下图中未注表面的粗糙度Ra=6.3,请正确标注。
6.3
其余
下图中A表面的粗糙度Ra=3.2, A表面Ra=6.3, 其余表面Ra=12.5,请正确标注。
Φ10 -0.004 -0.019
Φ10
+0.020 +0.005
Φ10 -0.004 -0.019
Φ10
0
-0.009
1.看图后填空。 孔的公差代号 H7 ,轴的公差代号f6 。基本尺 寸 φ30 ;孔的最大极限尺寸φ30.021 , 最小极 限尺寸 φ30 ;轴的最大极限尺寸φ29.080 ,最 小极限尺寸φ29.067 ;孔的上偏差+0.021 ,孔 的下偏差 0 ;尺寸公差 0.021 ;轴的上偏差 -0.020 ,孔的下偏差 -0.033 ;尺寸公差0.013 ; 孔与轴的配合代号: φ30H7/f6 ; 配合种类 :间隙配合
王文玉主编《微观经济学》习题答案

1. 见教材释 2. 经济问题首先是稀缺资源的经济或节约利用问题。我们之所以有经济问题,是因为资源或手段 有限,而我们想要满足的需要更多,我们必须节约或慎重选择资源的用途。所以,只要资源是稀缺的,
我们就会有经济问题。由于人的需要或欲望(want)总是无限膨胀,稀缺现象即稀缺物品存在的现象就 是永恒的,所以我们总是有经济问题。
王文玉主编《微观经济学》(清华出版社 2013 年第 1 版)习题答案
即肉肠价格变化率是热狗价格变化率的 2 倍。所以, η肠 =肉肠需求量变化率/肉肠价格变化率 =热狗需求量变化率/(2×热狗价格变化率) =η/2.
即肉肠需求价格弹性是热狗需求价格弹性的 1/2。 (2)由于面包卷需求量总是等于肉肠需求量,面包卷对肉肠的交叉弹性就等于肉肠需求价格弹性。 (3)如果肉肠价格是面包卷价格的两倍,那么,肉肠价格等于热狗价格的 2/3,所以肉肠价格变化
王文玉主编《微观经济学》(清华出版社 2013 年第 1 版)习题答案
图 P
I J A BC
0
Q
线性需求函数的一般形式是 相应的需求价格弹性函数是
P = a + bQ,a > 0,b < 0
η= P dQ = a + bQ ⋅ 1 = a + bQ = 1 + a
2013.晶体缺陷习题答案

晶体缺陷习题1. 若fcc 的Cu 中每500个原子会失去一个,其晶格常数为0.3615nm ,试求Cu 的密度。
解:33/91.854.63)50011(4cm g N a A=⨯⨯-⨯=ρ 2. 由于H 原子可填入α-Fe 的间隙位置,若每200个铁原子伴随着一个H 原子,试求α-Fe 密度与致密度(已知α-Fe 的晶格常数0.286nm ,原子半径0.1241nm ;H 原子半径0.036nm )。
解:2339310*023.6*)10*286.0(100/0.1*185.552-+⨯=⨯⨯=A R N a A n ρ= 7.93 g/cm 3 68.001.0234333=⨯+⨯==ar r V nv K H Fe π 3. MgO 的密度为3.58 3g cm ,其晶格常数为0.42nm ,试求每个MgO 单位晶胞内所含的Schottky 缺陷之数目(Mg, O 的原子量分别为24.305,15.999)。
解:设单位晶胞中Schottky 缺陷之数目为x ,58.310*023.6*)10*42.0()999.15305.24()1(*423393=+⨯-=⨯⨯=-x N a A n A R ρ 4. Fcc 晶体中如下操作形成什么位错,Burgers 矢量是什么?(1)抽出(111)面的一个圆片;a/3 (111) 刃型位错(2)插入(110)半原子面,此面终止在(111)面上。
a/2 (110) 刃型位错5. 当刃型位错周围的晶体中含有(a)超平衡的空位、(b)超平衡的间隙原子、(c)低于平衡浓度的空位、(d)低于平衡浓度的间隙原子等四种情形时,该位错将怎样攀移?答:(a) 正攀移,(b )负攀移,(c )负攀移,(d) 正攀移6. 指出下图中位错环ABCDA 的各段位错线是什么性质的位错?它们在外应力τxy 作用下将如何运动?在外应力σyy 作用下将如何运动?解:7.下图是一个简单立方晶体,滑移系统是{100}<001>。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6-13检波电路如图所示,uS为已调波(大信号)。根据图示极性,画出RC两端、Cg两端、Rg两端、二极管两端的电压波形。
题6-13图
解6-13
各点波形如右图
6-14检波电路如图p6-12,其中 ,F=5kHz,fc=465kHz,rD=125Ω。试计算输入电阻Ri、传输系数Kd,并检验有无惰性失真及底部切割失真。
3、符合要求的基极回路为
P89页图3-27(C)图
3-13试回答下列问题:
(1)利用功放进行振幅调制时,当调制的音频信号加在基极或集电极时、应如何选择功放的工作状态?
(2)利用功放放大振幅调制信号时,应如何选择功放的工作状态?。
(3)利用功放放大等幅度的信号时,应如何选择功放的工作状态?
解3-13
(1)利用功放进行振幅调制时,当调制的音频信号加在基极时,选择工作欠压状态;当调制的音频信号加在集电极时、功放应选在过压状态。
解2-5:
总电容
串联频率
并联频率
品质因数
答:该晶体的串联和并联频率近似相等,为5kHz,Q值为 。
2-7求如图所示并联电路的等效噪声带宽和输出均方噪声电压值。设电阻R=10kΩ,C=200 pF,T=290 K。
题2-7图
解2-7:网络传输函数为
答:电路的等效噪声带宽为125kHz,和输出均方噪声电压值为19.865μV2.
3-7什么叫做高频功率放大器?它的功用是什么?应对它提出哪些主要要求?为什么高频功放一般在B类、C类状态下工作?为什么通常采用谐振回路作负载?
答3-7
高频功率放大器是一种能将直流电源的能量转换为高频信号能量的放大电路,其主要功能是放大高频信号功率,具有比较高的输出功率和效率。对它的基本要求是有选频作用、输出功率大、自身损耗小、效率高、所以为了提高效率,一般选择在B或C类下工作,但此时的集电极电流是一个余弦脉冲,因此必须用谐振电路做负载,才能得到所需频率的正弦高频信号。
题3-1图
解3-2:
根据已知条件可知,能够忽略中和电容和yre的影响。得:
品质因数
3dB带宽
(2)放大器的电压增益
中和电容
答:品质因数QL为40.4,带宽为11.51kHz,谐振时的电压增益为-309,中和电容值为1.615pF
3-3高频谐振放大器中,造成工作不稳定的王要因素是什么?它有哪些不良影响?为使放大器稳定工作,可以采取哪些措施?
3-10高频功率放大器中提高集电极效率的主要意义是什么?
答3-10
主要意义在于提高了电源的利用率,将直流功率的更多的转换为高频信号功率,减小晶体管的功率损耗。
3-11设一理想化的晶体管静特性如图所示,已知Ucc=24 V,Uc=21V,基极偏压为零偏,Ub=2.5V,试作出它的动特性曲线。此功放工作在什么状态?并计算此功放的θ、P1、P0、η及负载阻抗的大小。画出满足要求的基极回路。
2-2图P2-2为一电容抽头的并联振荡电路,振荡频率为1MHz,C1=400pF,C2=100pF。求回路电感L。若Q0=100,RL=2kΩ,求回路有载QL值。
解:接入系数 ,总电容 pF
根据 ,得到
kΩ
Q0=100,故 kΩ
R= KΩ
2-5一个5kHz的基频石英晶体谐振器, C0=6pF,,ro=15Ω。求此谐振器的Q值和串、并联谐振频率。
3-8高频功放的欠压、临界、过压状态是如何区分的?各有什么特点?当UC、UBB、Ub、RL四个外界因素只变化其中的一个时,高频功放的工作状态如何变化?
答3-8
当晶体管工作在线性区时的工作状态叫欠压状态,此时集电极电流随激励而改变,电压利用率相对较低。如果激励不变,则集电极电流基本不变,通过改变负载电阻可以改变输出电压的大,输出功率随之改变;该状态输出功率和效率都比较低。
已知:F=1kHz,mf=10,可求得Bs,所以
(4)单位电阻上的信号功率
不论是FM还是PM,都是等幅信号,其功率与载波功率相等,所以
(5)由于不知调制信号形式,因此仅从表达式无法确定此信号是FM波还是PM波。
P59 2-1.对于收音机的中频放大器,其中心频率f0=465kHz ,B0.707=8kHz,回路电容C=200pF,试计算回路电感和QL值。若电感线圈的Q0=100,问在回路上应并联多大的电阻才能满足要求。
反馈系数
4-11克拉泼和西勒振荡线路是怎样改进了电容反馈振荡器性能的?
答4-11
由于克拉波振荡器在回路中串行接入了一个小电容,使的晶体管的接入系数很小,耦合变弱,因此,晶体管本身的参数对回路的影响大幅度减小了,故使频率稳定度提高,但使的频率的调整范围变小,所以,西勒振荡器是在克拉波振荡器的基础上,在回路两端在并联一个可调电容,来增大频率调节范围。·
解:Uc=0.8V m=0.5
输入电阻
0.81
惰性失真的判断条件为
RC=
无惰性失真
底部切割失真判断条件
故无底部切割失真
6-15 在图P6-13的检波电路中,输入信号回路为并联谐振电路,其谐振频率f0=106Hz,回路本身谐振电阻R0=20Ω,检波负载为10kΩ,C1=0.01uF,rD=100Ω。
(1)若 mA,求检波器输入电压us(t)及检波器输出电压u0(t)的表达式;
(2)利用功放放大振幅调制信号时,功放应选在欠压状态,并为乙类工作。
(3) 利用功放放大等幅度的信号时,功放应选在过压状态,此时输出电压幅度比较稳定。
3-16改正图示线路中的错误,不得改变馈电形式,重新画出正确的线路。
题3-16图
解3-16:
3-18一高频功放以抽头并联回路作负载,振荡回路用可变电容调谐。工作频率f=5 MHZ,调谐时电容 C=200pF,回路有载品质因数QL=20,放大器要求的最佳负载阻抗RLr=50 Ω,试计算回路电感L和接入系数 P。
可以通过采取以下措施
1.减小激励Ub,集电极电流Ic1和电压振幅UC基本不变,输出功率和效率基本不变。
2.减小基极的负向偏置电压,集电极电流Ic1和电压振幅UC基本不变,输出功率和效率基本不变。
3.减小负载电阻RL,集电极电流Ic1增大,IC0也增大,但电压振幅UC减小不大,因此输出功率上升。
4.增大集电极电源电压,Ic1、IC0和UC增大,输出功率也随之增大,效率基本不变。
解3-18:
p152
4-1什么是振荡器的起振条件、平衡条件和稳定条件?振荡器输出信号的振幅和频率分别是由什么条件决定?
答4-1
4-3
图p4-2是一三回路振荡器的等效电路,设有下列四种情况:
(1) ;(2) ;(3) ;(4)
试分析上述四种是否都能振荡,振荡频率 与回路振荡频率有何关系?
串联谐振回路:当f<f0,容性;当f>f0,感性;
当晶体管工作在饱和区时的工作状态叫过压状态,此时集电极电流脉冲出现平顶凹陷,输出电压基本不发生变化,电压利用率较高。
过压和欠压状态分界点,及晶体管临界饱和时,叫临界状态。此时的输出功率和效率都比较高。
•当单独改变RL时,随着RL的增大,工作状态的变化是从欠压逐步变化到过压状态。
•当单独改变UC时,随着UC的增大,工作状态的变化是从过压逐步变化到欠压状态。
回路总电容为
反馈系数
固有谐振电导
接入系数
折合到ce两端的总电导为
起振条件为
其中 ,
故
4-9图示是一电容反馈振荡器的实际电路,已知C1=50 pF,C2=100 pF,C3= 10~260pF,要求工作在波段范围,即f=10~1OMHz,试计算回路电感L和电容C。设回路无载Q。=100,负载电阻R=1kΩ,晶体管输入电阻Ri=500Ω.若要求起振时环路增益K。KF=3,问要求的跨gs。和静态工作电流IcQ必须多大?
6-1已知载波电压uc=UCsinωCt,调制信号如图所示,fC>>1/TΩ。分别画出m=0.5及m=1两种情况下所对应的AM波波形以及DSB波波形。
题6-1图
解6-1,各波形图如下
6-2某发射机输出级在负载RL=100Ω上的输出信号为 。求总的输出功率Pav、载波功率Pc和边频功率P边频。
解:Uc=4V m=0.5
答3-3
集电结电容是主要引起不稳定的因素,它的反馈可能会是放大器自激振荡;环境温度的改变会使晶体管参数发生变化,如Coe、Cie、gie、goe、yfe、引起频率和增益的不稳定。
一般采取提高稳定性的措施为:
(1)选用 小的管子,使其容抗增大,反馈作用减弱。
(2)从电路上设法消除晶体管的反向作用,使它单向化,如采用中和法或失配法
2-10接收机等效噪声带宽近似为信号带宽,约10kHz,输出信噪比为12 dB,要求接收机的灵敏度为1PW,问接收机的噪声系数应为多大?
解2-10:
根据已知条件
答:接收机的噪音系数应为32dB。
3-1对高频小信号放大器的主要要求是什么?高频小信号放大器有哪些分类?
答:对高频小信号器的主要要求是:
1.比较高的增益
•当单独改变UBB时,随着UBB的负向增大,工作状态的变化是从过压逐步变化到欠压状态。
•当单独改变Ub时,随着Ub的增大,工作状态的变化是从欠压逐步变化到过压状态。
3-9已知高频功放工作在过压状态,现欲将它调整到临界状态,可以改变哪些外界因素来实现,变化方向如何?在此过程中集电极输出功率如何变化?
答3-9
并联谐振回路:当f>f0,容性;当f<f0,感性;
振荡器要能够振荡,需要满足“射同余异”的条件
故有两种可能情况,振荡器都能够振荡:
(1)回路1、2容性,回路3感性;
(2)回路1、2感性,回路3容性。
当f<f02,回路1呈容性,f>f01,回路2呈容性,f>f03,回路3呈感性;――f02>max(f01, f03)
