动点路径长训练
专题训练. 圆的基本性质--八大题型总结(拔尖篇)- 九年级数学上册 (浙教版)

专题3.12圆的基本性质章末八大题型总结(拔尖篇)【题型1动态图形的扫过的面积的计算】(2023秋·江苏·九年级专题练习)2.如图,半圆O的直径时停止滑动,若M是(2023·黑龙江鸡西·校考三模)3.在平面直角坐标系中,已知()2,0A ,()3,1B ,()1,3C ;(1)将ABC 沿x 轴负方向平移2个单位至111A B C △,画图并写出1C 的坐标____________;(2)以1A 点为旋转中心,将111A B C △逆时针方向旋转90︒得22A B C 1△,画图并写出2C 的坐标_____;(3)在平移和旋转过程中线段BC 扫过的面积为___________.(2023秋·浙江·九年级专题练习)4.如图所示,扇形OAB 从图①无滑动旋转到图②,再由图②到图③,60O ∠=︒,1OA =.(1)求O 点运动的路径长;(2)求O 点走过路径与射线l 围成的面积.【题型2圆周角定理有关的计算与证明】【方法点拨】圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.推论1:同弧或等弧所对的圆周角相等.推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径(2023秋·北京西城·九年级北京八中校考期中)5.如图,已知:过O 上一点A 作两条弦AB 、AC ,且45BAC ∠=︒,(AB ,AC 都不经过)O 过A 作AC 的垂线AF 交O 于D ,直线BD ,AC 交于点E ,直线BC ,DA 交于点F .(1)证明:BE BF =;(2)探索线段AB 、AE 、AF 的数量关系,并证明你的结论.(2023秋·湖北·九年级期末)6.已知ABC 内接于O ,BAC ∠的平分线交O 于点D ,连接DB ,DC .(1)如图①,当120BAC ∠=︒时,请直接写出线段(2)如图②,当90BAC ∠=︒时,试探究线段(1)求ADB ∠的度数;(2)求AC 的长度;(3)判定四边形AFBC 的形状,并证明你的结论.(2023秋·江苏盐城·九年级统考期中)8.如图,在O 的内接四边形(1)若75DAE ∠=︒,则(2)过点D 作DE AB ⊥(3)若62AB AE ==、【题型3垂径定理的实际应用】【方法点拨】垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.推论:平分弦(不是直径条弧.(2023秋·河北石家庄9.如图是一位同学从照片上剪切下来的海上日出时的画面,圆的半径为5厘米,上”太阳与海平线的位置关系是(2023秋·浙江台州·10.我市在创建全国文明城市检查中,发现一些破旧的公交车候车亭有碍观瞻,现已更换新的公交候车亭图2所示的是侧面示意图,FG为水平线段,PQ⊥FG,点H为垂足,FG=4m,FH=2.4m,点P在弧FG上,且弧FG所在的圆的圆心O到FG,PQ的距离之比为5:2,则PH的长约为多少米?(2023春·浙江台州·九年级台州市书生中学校考期中)11.如图这是我市某跨海大桥正侧面的照片,大桥的主桥拱为圆弧型,桥面AB长为800米,且与水面平行,小王用计算机根据照片对大桥进行了模拟分析,在桥正下方的水面上取一点P,在桥面AB上取点C,作射线PC交弧(主桥拱)于点D,右边画出了PC与PD关于AC长的函数图象,下列对此桥的判断不合理的是()A.桥拱的最高点与桥面AB的实际距离约为210米B.桥拱正下方的桥面EF的实际长度约为500米C.拍摄照片时,桥面离水面的实际高度约为110米D.桥面上BF段的实际长度约200米(1)求该圆的半径;(2)若水面上涨导致圆被水面截得的弦【题型4由点与圆的位置关系求求最值】【方法点拨】解决此类问题关键要记住若半径为当d=r时,点在圆上,当d<(2023秋·江苏苏州·九年级苏州市振华中学校校考期中)13.如图,在平面直角坐标系中,已知点为半径的圆上运动,且始终满足(2023秋·山东泰安·九年级校联考期末)15.如图,点()34P P ,,半径为大值是()A .32B .52(2023秋·河南驻马店·九年级平舆县第二初级中学校考期末)16.如图,Rt ABC 中,AB 的最小值为(2023秋·安徽淮北·九年级校考期末)的直径,18.如图,AB是O+的最小值为(点,则PC PDA.22B.2(2023秋·陕西渭南·九年级统考期末)19.如图,A、B是半圆O上的两点,的最小值为.(2023秋·广东广州·九年级校考期末)20.(1)如图①,在ABC 中,120A ∠= ,5AB AC ==.尺规作图:作ABC 的外接圆O ,并直接写出ABC 的外接圆半径R 的长.(2)如图②,O 的半径为13,弦24AB =,M 是AB 的中点,P 是O 上一动点,求PM 的最大值.(3)如图③所示,AB ,AC 、 BC是某新区的三条规划路,其中6km AB =,3km AC =,60BAC ∠= , BC 所对的圆心角为60 ,新区管委会想在 BC路边建物资总站点P ,在AB ,AC 路边分别建物资分站点E 、F ,也就是,分别在 BC、线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天都要将物资在各物资站点间按P E F P →→→的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷、环保和节约成本.要使得线段PE 、EF 、FP 之和最短,试求PE EF FP ++的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)【题型6动点的运动轨迹长度计算】(2023秋·江苏连云港·九年级校考阶段练习)22.如图,已知90ABC ∠=︒停止,圆心O 运动的路程是(2023秋·江苏徐州·九年级校考阶段练习)23.如图,有一块长为4cm 、宽为3cm 的矩形木板在桌面上按顺时针方向无滑动地翻滚,木板上顶点化为12A A A →→,其中,第二次翻滚时被桌面上一个小木块挡住,使木板边沿滚到点2A 的位置经过的路径长为()A .10cmB .3.5cm π(2023·浙江温州·校考三模)24.图1是挂桶式垃圾车的联动装置,通过钢轴先后作两次旋转移动垃圾桶,实现对垃圾桶提升和翻转,将垃圾桶内的垃圾自动收入车厢.图2,图110cm,AB =303cm,30cm BC CD ==【题型7正多边形与圆】【方法点拨】定义:正多边形的外接圆的圆心叫做这个正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心正多边形的一边的距离叫做正多边形的边心距.(2023秋·山东淄博·九年级统考期末)25.已知四个正六边形如图摆放在图中,顶点A ,B ,C ,D ,E ,F 在圆上.若两个大正六边形的边长均为小正六边形的边长是()A .33-B .2312-C .312+D .1312-(2023秋·河南驻马店·九年级统考期末)26.如图,已知O 的半径为4,则该圆内接正六边形ABCDEF 的边心距OG (① DF 的长为2π;②2DF OF =;③ODE 为等边三角形;④S 正八边形【题型8圆锥侧面积的相关计算】【方法点拨】解决此类问题掌握圆锥侧面积的计算公式是关键,并且能够灵活运用(2023秋·全国·九年级专题练习)29.小华的爸爸要用一块矩形铁皮加工出一个底面半径为缝(接缝忽略不计)()1你能求出这个锥形漏斗的侧面展开图的圆心角吗?()2如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?(2023秋·江苏·九年级专题练习)31.如图是一张直角三角形卡片,DE⊥AB.若将该卡片绕直线DE旋转一周,则形成的几何体的表面积为(2023秋·全国·九年级专题练习)32.如图,在一张四边形ABCD的纸片中,、交于点E、径的圆分别与AB AD(1)求证:DC与A的切线;(要求:尺规作图,不写作法,保留作图痕迹)(2)过点B作A(3)若用剪下的扇形AEF围成一个圆锥的侧面,能否从剪下的两块余料中选取一块,剪出一个圆作为这个圆锥的底面?。
最全初中数学几何动点问题专题分类归纳汇总训练

最全初中数学几何动点问题专题分类归纳汇总近几年有关“线段最值”的中考试题层出不穷,形式多样,往往综合了几何变换、函数等方面的知识,具有一定的难度,具有很强的探索性,通过研究发现,这些问题尽管形式多样、背景复杂、变化不断,但都可以通过几何变换转化为常见的基本问题.最值题目类型多:作图、计算;有求差最大,求和最小;求周长最小、求时间最短;求最值、已知最值求待定系数等;对称载体多:几乎涉及到初中全部的轴对称图形(角、线段、等腰三角形、等腰梯形、菱形、正方形、抛物线、圆、坐标轴).我们知道“对称、平移、旋转” 是三种保形变换。
通过这三种几何变换可以实现图形在保持形状、大小不变的前提下而使其位置发生变化,具有更紧凑的位置关系或组合成新的有利论证的基本图形.通过几何变换移动线段的位置是解决最值问题的有效手段,题目是千变万化的,但是运用几何变换把最值问题转化为基本问题却是不变的。
数学问题是千变万化的,几何变换的应用也不是单一的,有些问题需要多种变换的组合才能解决,看看以下策略对解决问题能否奏效。
(1)去伪存真。
刨去不变的线段,看清楚究竟是几段和的最小值问题,必须仔细研究题目的背景,搞清楚哪些是动点、哪些是定点、哪些是定长。
(2)科学选择。
捕捉题目的信号,探索变换的基础,选择变换的手段.平移把不“连”的线段“接”起来,旋转把“碰头”的线段“展”开来重“接”,对称把在同侧的线段翻折过去重组,因此“不连——平移、碰头——旋转、同侧——对称”是一般的思路;对称变换的基础是轴对称图形,平移变换的基础是平行线,旋转变换的基础是等线段,所以选择哪种几何变换还要看题目中具备何种变换的基础信息。
(3)怎么变换?对称变换一般以动点所在直线为对称轴,构建定点(直线)的对称点(直线),如有多个动点就必须作多次变换;平移一般是移动没有公共端点的两条线段中的某一条,与另一条对“接”;旋转变换一般以定点为旋转中心旋转60°或90°。
数学中考新题型注意求“从动点”运动路径长问题研究

数学中考新题型注意求“从动点”运动路径长问题研究发表时间:2020-11-30T14:08:53.030Z 来源:《中小学教育》2020年24期作者:李丽华[导读] 数学中考新题型的“从动点”运动路径长度问题李丽华营口市第三十一初级中学辽宁营口 115007摘要:数学中考新题型的“从动点”运动路径长度问题,从两个层面对学生的数学掌握水平进行综合考察,难度整体偏大。
本文对此类问题的难点产生原因进行了分析,提出注重对问题本质的思索,提升静态具象思维与动态抽象思维互相转化的能力等深度解决“从动点”运动路径长度问题的有效方式,以供参考。
关键词:从动点;运动路径长度;静态具象思维;动态抽象思维引言:初中数学中的从动点问题,在2010年以前的中考试卷中,出现的频率相对较低。
但随着教学的深入,出题者及广大教研人员发现,此类动态的“主从联动”问题(又被很多教师称之为瓜豆原理或旋转相似问题),对于考察学生们的抽象思维与逻辑思维能力具有良好的作用,故已成为了中学数学的“网红问题”。
一、数学中考新题型“从动点”与运动路径长度问题难点解析在初中数学有关几何问题的教学中,存在一种现象,即对于静止不动的几何问题,只要对基础规律有所了解的学生,都能够准确找到点、线、面之间的关系,对于周长、面积之间相互转化,求解目标项的问题,均能得出正确答案。
但当静态的“定量”转化为动态的“变量”时,很多学生由于欠缺逻辑思维能力,往往在求解时缺乏思路。
比如数学中考试卷中出现的热门新题型——“从动点”运动路径长度问题,几乎成为了“扣分专项”。
该类问题的难点如下:(1)题设条件与求解项之间存在“隔阂”,导致学生无法确认正确答案产生之前必须求得的关键条件。
如例题“在矩形ABCD中,AB (宽)=3,BC(长)=4,P是BC边上的一个动点,连接AP形成△ABP,沿AP边将其烦着,得到对称的△AQP,Q为点B翻折后的对称点,连接CQ,求CQ的最小值”。
2023年中考数学高频考点训练——圆-动点问题

2023年中考数学高频考点训练——圆-动点问题一、综合题1.如图,四边形OBCD 中的三个顶点在⊙O 上,A 是优弧BD 上的一个动点(不与点B 、D 重合).(1)当圆心O 在BAD ∠内部,∠ABO +∠ADO=70°时,求∠BOD 的度数;(2)当点A 在优弧BD 上运动,四边形OBCD 为平行四边形时,探究ABO ∠与ADO ∠的数量关系.2.如图,在每个小正方形的边长为1的网格中,ABO 的顶点A ,B ,O 均落在格点上,OB 为⊙O 的半径.(1)AOB ∠的大小等于(度);(2)将ABO 绕点O 顺时针旋转,得A B O '' ,点A ,B 旋转后的对应点为A ',B '.连接AB ',设线段AB '的中点为M ,连接A M '.当A M '取得最大值时,请在如图所示的网格中,用无刻度的直尺画出点B ',并简要说明点B '的位置是如何找到的(不要求证明).3.如图,AB 是O 的直径,CD 是O 的切线,切点为C ,过B 作BE CD ⊥,垂足为点E ,直线BE 交O 于点F.(1)判断ABC ∠与EBC ∠的数量关系,并说明理由.(2)若点C 在直径AB 上方半圆弧上运动,O 的半径为4,则①当CB 的长为时,以B 、O 、E 、C 为顶点的四边形是正方形;②当BE 的长为时,以B 、O 、F 、C 为顶点的四边形是菱形.4.先阅读材料,再解答问题:已知点00(:)P x y 和直线y kx b =+,则点P 到直线y kx b =+的距离d 可用公式d =计算.例如:求点(2,1)P -到直线23y x =+的距离.解:由直线23y x =+可知:2,3k b ==.所以点(2,1)P -到直线23y x =+的距离为255d ==.求:(1)求点P (2,-1)到直线y=x+1的距离.(2)已知直线21y x =+与25y x =-平行,求这两条平行线之间的距离;(3)如图已知直线443y x =--分别交,x y 轴于,A B 两点,☉C 是以(2,2)C 为圆心,2为半径的圆,P 为☉C 上的动点,试求PAB ∆面积的最大值.5.如图,⊙O 的半径为1,点A 是⊙O 的直径BD 延长线上的一点,C 为⊙O 上的一点,AD =CD ,∠A =30°.(1)求证:直线AC 是⊙O 的切线;(2)求△ABC 的面积;(3)点E 在 BND 上运动(不与B 、D 重合),过点C 作CE 的垂线,与EB 的延长线交于点F.①当点E 运动到与点C 关于直径BD 对称时,求CF 的长;②当点E 运动到什么位置时,CF 取到最大值,并求出此时CF 的长.6.一块含有30︒角的三角板ABC 如图所示,其中90C ∠=︒,30A ∠=︒,3BC cm =.将此三角板在平面内绕顶点A 旋转一周.(1)画出边BC 旋转一周所形成的图形;(2)求出该图形的面积.7.如图,在ABE 中,BE AE >,延长BE 到点D ,使DE BE =,延长AE 到点C ,使CE AE =.以点E 为圆心,分别以BE 、AE 为半径作大小两个半圆,连结CD .(1)求证:AB CD =;(2)设小半圆与BD 相交于点M ,24BE AE ==.①当ABE S 取得最大值时,求其最大值以及CD 的长;②当AB 恰好与小半圆相切时,求弧AM 的长.8.如图,A 是半径为12cm 的O 上的定点,动点P 从A 出发,以2πcm /s 的速度沿圆周逆时针运动,当点P 回到A 地立即停止运动.(1)如果90POA ∠= ,求点P 运动的时间;(2)如果点B 是OA 延长线上的一点,AB OA =,那么当点P 运动的时间为2s 时,判断直线BP 与O 的位置关系,并说明理由.9.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”。
运动路径长度问题

硬核:狙击2020中考数学重点/难点/热点想要对运动路径长度问题掌握得信手拈来,那么建议你对以下知识点进行提前学习会更好:1.《隐圆模型》2.《共顶点模型》-也可称“手拉手模型”3.《主从联动模型》-也可称“瓜豆原理模型”4.《旋转问题》—本系列的第二讲中所阐述的旋转相似模型此外,还需要明白的动点类型还有:5.线段垂直平分线——到线段两端点距离相等的动点一定在这条线段的垂直平分线上6.角平分线——到角两边距离相等的动点一定在这个角的角平分线上7.三角形中位线——动点到某条线的距离恒等于某平行线段的一半8.平行线分线段成比例——动点到某条线的距离与某平行线段成比例9.两平行线的性质——平行线间的距离,处处相等一、路径为圆弧型解题策略:①作出隐圆,找到圆心②作出半径,求出定长解题关键:通过《隐圆模型》中五种确定隐圆的基本条件作出隐圆,即可轻易得出结论.二、路径为直线型解题策略:①利用平行定距法或者角度固定法确定动点运动路径为直线型②确定动点的起点与终点,计算出路径长度即可解题关键:解题过程中常常出现中位线,平行线分线段成比例,相似证动角恒等于顶角等知识点三、路径为往返型解题策略:①通常为《主从联动模型》的衍生版②确定动点的起点与终点,感知运动过程中的变化③找出动点运动的最远点解题关键:解题过程中常常出现相似转线段长、《主从联动模型》中的滑动模型等【例题1】如图,等腰Rt△AOB中,∠AOB=90°,OA=,⊙O与AB相切,分别交OA、OB于N、M,以PB为直角边作等腰Rt△BPQ,点P在弧MN上由点M运动到点N,则点Q运动的路径长为()A.B.C.D.【例题2】已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度()A.πB.C.πD.2【例题3】如图,⊙O的半径为1,弦AB=1,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是.【例题4】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP 交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为()A. B. C.1 D.2【例题5】已知:如图1,平面直角坐标系中,点A的坐标是(0,6),点B在x轴上,且∠BAO=30°,点D是线段OA上的一点,以BD为边向下作等边△BDE.(1)如图2,当∠ODB=45°时,求证:OE平分∠BED.(2)如图3,当点E落在y轴上时,求出点E的坐标.(3)利用图1探究并说理:点D在y轴上从点A向点O滑动的过程中,点E也会在一条直线上滑动;并直接写出点E运动路径的长度.【例题6】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中,点C运动的路径长是.【例题7】如图1,已知抛物线y=x2+bx+c经过原点O,它的对称轴是直线x=2,动点P从抛物线的顶点A 出发,在对称轴上以每秒1个单位的速度向上运动,设动点P运动的时间为t杪,连结OP并延长交抛物线于点B,连结OA,AB.(1)求抛物线的函数解析式;(2)当△AOB为直角三角形时,求t的值;(3)如图2,⊙M为△AOB的外接圆,在点P的运动过程中,点M也随之运动变化,请你探究:在1≤t≤5时,求点M经过的路径长度.【例题8】如图,OM⊥ON,A、B分别为射线OM、ON上两个动点,且OA+OB=5,P为AB的中点.当B由点O向右移动时,点P移动的路径长为()A.2B.2C.D.5【例题9】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0),在整个运动过程中,求出线段PQ中点M所经过的路径长.【例题10】(1)如图1,已知AB=2,点D是等腰Rt△ABC斜边AC上一动点,以BD为一边向右下方作等边△BDE,当点D由点A运动到点C时,求点E运动的路径长;(2)如图2,已知AB=2,点D是等腰Rt△ABC斜边AC上一动点,以BD为一边向右下方作以E为直角顶点的等腰Rt△BDE,当点D由点A运动到点C时,求点E运动的路径长;(3)如图3,已知AB=2,点D是等腰Rt△ABC斜边AC上一动点,以BD为一边向右下方作以D为直角顶点的等腰Rt△BDE,当点D由点A运动到点C时,求点E运动的路径长;(4)如图4,已知AB=2,点D是等腰Rt△ABC斜边AC上一动点,以BD为一边向右下方作以D为直顶点的等腰△BDE,且∠BDE=120°,当点D由点A运动到点C时,求点E运动的路径长;【例题11】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是________.1.如图,在等腰Rt△ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是.2.已知线段AB=8,C、D是AB上两点,且AC=2,BD=4,P是线段CD上一动点,在AB同侧分别作等腰三角形APE和等腰三角形PBF,M为线段EF的中点,若∠AEP=∠BFP,则当点P由点C移动到点D时,点M移动的路径长度为.3.已知线段AB=10,P是线段AB上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点A移动到点B时,G点移动的路径长度为.4.如图,AB为⊙O的直径,AB=3,弧AC的度数是60°,P为弧BC上一动点,延长AP到点Q,使AP•AQ =AB2.若点P由B运动到C,则点Q运动的路径长为.5.如图,矩形ABCD中,AB=4,AD=6,点E在边AD上,且AE:ED=1:2.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F.设点M是线段EF的中点,则在点P运动的整个过程中,点M的运动路径长为________.6.等边三角形ABC的边长为2,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.(1)∠APB的度数;(2)当E从点A运动到点C时,试求点P经过的路径长;(3)连结CP,直接写出CP长度的最小值.7.如图,AB为半圆O的直径,AB=2,C,D为半圆上两个动点(D在C右侧),且满足∠COD=60°,连结AD,BC相交于点P若点C从A出发按顺时针方向运动,当点D与B重合时运动停止,则点P所经过的路径长为________.8.如图,A(﹣3,0),B(0,3),C(﹣1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C =90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.9.如图,矩形ABCD中,AB=6,BC=6,动点P从点A出发,以每秒个单位长度的速度沿线段AD 运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.(1)当t=1秒时,求动点P、Q之间的距离;(2)若动点P、Q之间的距离为4个单位长度,求t的值;(3)若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度为.10.(2019秋•江岸区校级月考)如图,正△ABC中,AB=2,AD⊥BC于D,P,Q分别是AB,BC上的动点,且PQ=AD,点M在PQ的右上方且PM=QM,∠M=120°,当P从点A运动到点B时,M运动的路径长为.(看成固定三角板滑动处理/或反其道而行之)11.如图,在四边形ABCD中,∠C=60°,∠A=30°,CD=BC.(1)求∠B+∠D的度数.(2)连接AC,探究AD,AB,AC三者之间的数量关系,并说明理由.(3)若BC=2,点E在四边形ABCD内部运动,且满足DE2=CE2+BE2,求点E运动路径的长度.12.已知在扇形AOB中,圆心角∠AOB=120°,半径OA=OB=8.(1)如图1,过点O作OE⊥OB,交弧AB于点E,再过点E作EF⊥OA于点F,则FO的长是,∠FEO=°;(2)如图2,设点P为弧AB上的动点,过点P作PM⊥OA于点M,PN⊥OB于点N,点M,N分别在半径OA,OB上,连接MN,则①求点P运动的路径长是多少?②MN的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;(3)在(2)中的条件下,若点D是△PMN的外心,直接写出点D运动的路经长.13.如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.14.(2019•兴化市模拟)正方形ABCD的边长为4,P为BC边上的动点,连接AP,作PQ⊥PA交CD边于点Q.当点P从B运动到C时,线段AQ的中点M所经过的路径长()A.2B.1C.4D.15.(2019•武汉模拟)如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P 向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为()A.πB.πC.πD.π16.如图,BC是⊙O的直径,BC=4,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在上从点M运动到点N时,点E运动的路径长是()A.B.C.D.17.(2020•河北模拟)如图,在正方形ABCD中,AB=1,P是边BC上的一个动点,由点B开始运动,运动到C停止.连接AP,以AP为直角边向右侧作等腰直角三角形,另一个顶点为Q.则点P从B运动到C的过程中,点Q的运动路径长为()A.πB.C.D.118.无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于.19.如图,已知点C是以AB为直径的半圆的中点,D为弧AC上任意一点,过点C作CE⊥BD于点E,连接AE,若AB=4,则AE的最小值为.20.如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是.21.如图,在平面直角坐标系中,点A(8,0),点P(0,m),将线段PA绕着点P逆时针旋转90°,得到线段PB,连接AB,OB,则BO+BA的最小值为.22.如图,P为边长为2的正方形ABCD的边BC上一动点,将线段DP绕P逆时针旋转90°得到线段PE (E为D的对应点),M为线段PE的中点,当点P从点C运动到点B的过程中,点M的运动路径长为____________.23.等边△ABC的边长为18,在AC,BC边上各取一点D,E,连接AE,BD相交于点P,若AE=BD,当D从点A运动到点C时,点P所经过的路径长为.24.(2020•武汉模拟)如图,定直线l经过圆心O,P是半径OA上一动点,AC⊥l于点C,当半径OA绕着点O旋转时,总有OP=OC,若OA绕点O旋转60°时,P、A两点的运动路径长的比值是.25.如图,已知正方形ABCD的边长为4,点P是AB边上一个动点,连接CP,过点P作PC的垂线交AD 于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O.(1)若AP=1,则AE=;(2)①求证:点O一定在△APE的外接圆上;②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.26.如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB﹣BC向终点C运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).设点E运动速度为每秒1个单位,运动的时间为x秒.(1)如图1,当点E在AB上时,求证:点G在直线BC上;(2)设正方形ABCD与正方形DEFG重叠部分的面积为S,求S与x之间的函数关系式;(3)直接写出整个运动过程中,点F经过的路径长.。
中考数学:点动产生路径长问题

点动产生的路径长问题近几年中考,和我们同学做的中考模拟试卷中,不断的出现了因动点计算路径长问题,这种题型因为隐藏的比较深,从而难以发现,计算比较繁琐。
在填空题选择题中比较多。
只要同学们在做题的过程中发现是这种题型,那么点所经过的路径一般就是就是两种结果。
一是线段。
二是圆弧。
为什么呢?因为只有这两图形是可以计算路径长的。
其它图形我们目前能计算路径长吗。
哈哈,这样解释印象有没有很深。
下面我们来看看我们会碰到的几种题型。
题型1:简单的图形翻转问题。
解法:这种题型比较简单。
只要找出旋转圆心,旋转时圆的半径,还有圆心角就可以了,然后利用扇形的弧长计算公式来计算。
注意,如果是圆弧旋转的话,圆心的路径是直线。
例题1:一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为___________试题分析:现将木板沿水平线翻滚, B点从开始至结束走过了4条弧,每条弧是一等边三角形的边为半径的扇形,圆心角为等边三角形的内角,所以 B点从开始至结束所走过的路程长度=4l=点评:本题考查扇形的弧长公式,关键是找出扇形的圆心角和半径,考查学生的空间想象能力例题2:矩形ABCD的边AB=8,AD=6,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置A1B1C1D1时(如图所示),则顶点A所经过的路线长是例题3:将半径为1、圆心角为60°的扇形纸片AOB,在直线l上向右作无滑动的滚动至扇形A’O’B’处,则顶点O经过的路线长为。
例题4:如图,一个圆心角为270°,半径为2m的扇形工件,未搬动前如图所示,A,B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止,则圆心O所经过的路线长是m.(结果保留π)例题5:已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是 m。
特殊四边形中的动点问题专项训练题

特殊四边形中的动点问题专项训练题一选择题1.如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=.点M是AD边的中点,点N是AB边上的一个动点.将△AMN沿MN所在的直线翻折到△A′MN,连接A′C.则线段A′C长度的最小值为()A.5 B.7 C.4D.52.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为()A.B. C.1﹣D.1﹣3.我们给出如下定义,顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH的形状是()A.平行四边形 B.矩形 C.菱形 D.正方形4.如图①,点P为矩形ABCD边上一个动点,运动路线是A→B→C→D→A,设点P运动的路径长为x,S△ABP=y,图②是y随x变化的函数图象,则矩形对角线AC的长是()A.2 B.6 C.12 D.245.如图,在菱形ABCD中,∠ABC=120°,AB=2.动点P从点A出发,以每秒2个单位的速度沿折线AD→DC运动到点C,同时动点Q也从点A出发,以每秒个单位的速度沿AC运动到点C,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是()A.B.C.D.6.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是()A.B.C.D.7.如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E,PF⊥CD于点F,连接EF,有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于.其中正确结论的个数是()A.2个B.3个C.4个D.5个8.如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF=CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M.P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM.有下列四个结论:①AE垂直平分DM;②PM+PN的最小值为3√2;③CF2=GE•AE;④S△ADM=6√2.其中正确的是()A.①②B.②③④C.①③④D.①③9.如图,在正方形ABCD中,点E为边CD的中点,连接AE,过点B作BF⊥AE于点F,连接BD交AE于点G,FH平分∠BFG交BD于点H.则下列结论中,正确的个数为()①AB2=BF•AE②S△BGF:S△BAF=2:3③当AB=a时,BD2﹣BD•HD=a2A.0个B.1个C.2个D.3个10.如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是()①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=2√2;⑤EP•DH=2AG•BH.A.①②③④⑤ B.①②③⑤ C.①②③ D.①②⑤二填空题11.在四边形ABCD中,AD∥BC,BC=6 cm,AD=9cm.点P以1cm/s的速度由A点向D点运动,同时点Q以2 cm/s的速度由C点向B点运动,当点P,Q运动s时,直线QP将四边形ABCD截出一个平行四边形.12.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为.13.如图,已知菱形ABCD的边长为8,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是.14.如图,在边长为6的菱形ABCD中,∠ABC=30°,P为BC上方一点,且S△PBC=S菱形,则PB+PC的最小值为.ABCDB C A M NP F E15.如图,在矩形OAHC 中,OC =8,OA =16,B 为CH 中点,连接AB .动点M 从点O 出发沿OA 边向点A 运动,动点N 从点A 出发沿AB 边向点B 运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM ,CN ,MN ,设运动时间为t (0<t <16)秒,则t=时,△CMN 为直角三角形.三 解答题16.如图,△ABC 中,点P 是边AC 上的一个动点,过P 作直线MN ∥BC ,设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F .(1)求证:PE =PF ;(2)当点P 在边AC 上运动时,四边形BCFE 可能是矩形吗?说明理由;(3)若在AC 边上存在点P ,使四边形AECF 是正方形,且 AP BC =32.求此时∠A 的大小.17.▱ABCD 的对角线AC ,BD 交于点O ,∠AOD=60°,∠ADO=90°,BD=12,点P 是AO 上一动点,点Q 是OC 上一动点(P ,Q 不与端点重合),且AP=OQ ,连接BQ ,DP .(1)线段PQ 的长为 ;(2)设△PDO 的面积为S 1,△QBO 的面积为S 2,S 1+S 2的值是否发生变化?若不变,求出这个不变的值;若变化,请说明随着AP 的增大,S 1+S 2的值是如何变化的;(3)DP+BQ 的最小值是 .18.如图,在矩形ABCD 中,AB =4,AD =10,直角尺的直角顶点P 在AD 上滑动时(点P 与A ,D 不重合),一直角边经过点C ,另一直角边AB 交于点E ,我们知道,结论“Rt △AEP ∽Rt △DPC ”成立.(1)当∠CPD =30°时,求AE 的长;(2)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.19.如图,在平面直角坐标系中,已知▱OABC的顶点A(10,0)、C(2,4),点D是OA的中点,点P在BC上由点B向点C运动.(1)求点B的坐标;(2)若点P运动速度为每秒2个单位长度,点P运动的时间为t秒,当四边形PCDA是平行四边形时,求t的值;(3)当△ODP是等腰三角形时,直接写出点P的坐标.20.如图,在口ABCD中,AB⊥AC,AB=1,,对角线BD、AC交于点O.将直线AC 绕点O顺时针旋转分别交BC、AD于点E、F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90⁰时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.21.如图①,将矩形纸片ABCD(AD>AB)折叠,使点C刚落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.(1)求证:四边形CEGF是菱形;(2)如图②,若AB=3,BC=9,当点G与点A重合时,求折痕EF的长.22.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.(1)若点F在边CD上,如图1.①证明:∠DAH=∠DCH;②猜想△GFC的形状并说明理由.(2)取DF中点M,连结MG.若MG=5,正方形边长为8,求BE的长.23.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD 的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.24.如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.(1)求△PCQ的面积S△PCQ=?(用t的代数式表示);(2)问:是否存在时刻t使S△DOP=S△PCQ?为什么?(3)当t为何值时,△DPQ是一个以DP为腰的等腰三角形?25.如图1,平行四边形ABCD中,AB=7,BC=10,点P是BC边上的点,连结AP,以AP 为对称轴作△ABP的轴对称图形△AQP.(1)如图1,连接CQ,若CQ∥AP,求BP的长;(2)如图2,当点P,Q,D三点共线时,恰有∠DCQ=∠DPC,求BP的长;(3)如图3,若点P在边BC运动的过程中,点Q到CD的最短距离为1,求BP的长.26.矩形ABCD的边长AB=18cm,点E在BC上,把△ABE沿AE折叠,使点B落在CD边的点F处,∠BAE=30°.(1)如图1,求DF的长度;(2)如图2,点N从点F出发沿FD以每秒1cm的速度向点D运动,同时点P从点A出发沿AF以每秒2cm的速度向点F运动,运动时间为t秒(0<t<9),过点P作PM⊥AD,于点M.①请证明在N、P运动的过程中,四边形FNMP是平行四边形;②连接NP,当t为何值时,△MNP为直角三角形?27.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE 交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.28.如图1,在正方形ABCD中,边长为2a,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:AF=BE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DG=2a;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.29.如图,点F在四边形ABCD的边AB上.(1)如图1,当四边形ABCD是正方形时,过点B作BE⊥CF,垂足为O,交AD于点E.求证:BE=CF;(2)当四边形ABCD是矩形,AD=6,AB=8时,①如图2,点P是BC上的一点,过点P作PE⊥CF,垂足为O,点O恰好落在对角线BD上,求的值;②如图3,点P是BC上的一点,过点P作PE⊥CF,垂足为O,点O恰好落在对角线BD上,延长EP、AB交于点G,当BG=2时,请直接写出DE的值.30.如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B⇒A,B⇒C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.(1)若a=4厘米,t=1秒,则PM=厘米;(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.。
求解动点路径长问题

运用“三点法”求解动点路径长问题初中数学中动点路径问题,一般有两种情况:线段或圆弧.本文提出一种求动点路径长的方法——三点法,“三点”指动点的起点,终点与过程点.该方法分为三步:(1)精准作图,运用刻度尺,圆规及量角器等工具作出位置较为精准的“三点”.(2)大胆猜测,若“三点”共线,则动点路径为线段;若“三点”不共线,则动点路径为圆弧.(3)小心验证,根据画出的“三点图”,运用相似三角形、“定角定长定圆”等方法对猜想进行严格的证明. 一、知识准备 1、基本概念如图1,在Rt ABC ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2tan 5DPE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .在图1中,点P 是“主动”在边AB 上开始动的点,称为“主动点”;点E 是跟着点P 在运动的点,称为“从动点”.又点P 从点A 运动到点B ,当点P 与点A 重合时记作点1P ,称为“主动点的起点”,此时1E 称为“从动点的起点”,此时作出符合要求的图形(如图2),称该图为“起点图”;当点P 与点B 重合时记作点2P ,称为“主动点的终点”,此时2E 称为“从动点的终点”,作出符合要求的图形(如图3),称该图为“终点图”.区别于起点1P ,终点2P ,将图1中的点P 称为“主动点的过程点”,此时E 称为“从动点的过程点”,相应地把图1称为“过程图”.将起点图,终点图,过程图放在同一个图形中,将这个图形称为“三点图”(如图4).2、定角定长定圆固定度数的角对着固定长度的线段时隐含着一个固定大小的圆,此时定线段为定圆的一条弦,定角为弦所对的一个圆周角.引例1 如图5,线段4AB =,点C 是平面上的一个动点,使90ACB ∠=︒,作出点C 的运动路径.由“90º角所对的弦是直径”可以得到点C 的运动路径是以AB 为直径的圆,且不与点A 、点B 重合(如图6).引例2 如图7,线段4AB =,点C 是平面上的一个动点,45ACB ∠=︒,作出顶点C 的运动路径.当点C 位置不同时,ACB ∠度数不变,根据“同弧或等弧所对的圆周角相等”,可以将ACB ∠看作弦AB 所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且290AOB ACB ∠=∠=︒,计算可得半径OA =所以,点C 的运动路径是优弧ACB ,且不与点A 、点B 重合(如图8).引例3 如图9,线段4AB =,点C 是平面上的一个动点,120ACB ∠=︒,作出顶点C 的运动路径.作出ACB ∠的补角'AC B ∠为60º,'AC B ∠的位置不同时度数为定值.类比引例2,可将'AC B ∠看作弦AB所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且2'120AOB AC B ∠=∠=︒,计算可得半径OA =.在所以点C 的运动路径是劣弧»AB ,且不与点A 、点B 重合(如图10). 二、方法归纳例l 如图11,在Rt ABC ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2tan 5DPE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .1.精准作图 因为2tan 5DPE ∠=,所以通过计算很难得到DPE ∠的度数(不借助计算器),但可以运用量角器测量图12中22DPE ∠≈︒.在图11的基础上,先作起点图.当点P 与点A 重合时记作点1P ,在图中作出122DPQ ∠=︒(如图12),过点D 作11DE PD ⊥交射线AQ 于点1E (如图13).当点P 与点B 重合时记作点2P ,运用类似的方法在图13的基础上作出终点图,并去掉多余部分,得到一幅完整的三点图(如图14).2、大胆猜测通过三点图发现点1E ,点E ,点2E 基本在一条直线上(如图14),所以可以大胆的猜测点E 的运动路径是一条线段,点E 运动的路径长就是线段12E E 的长度.于是提出猜想一“在三点图中,从动点的起点,终点,过程点三点共线时,从动点的运动路径为线段”.在三点图中,从动点的起点,终点,过程点三点不共线时,就初中数学而言,不共线的三点确定一个圆,这里提出猜想二“在三点图中,从动点的起点,终点,过程点三点不共线时,从动点的运动路径为圆弧”.当运动路径为圆弧时,考虑寻找固定度数的角与固定长度的线段,运用“定角定长定圆”的方法作出运动路径. 3.小心验证在图15中,因为1190E DE PDE ∠+∠=︒,1190PDP PDE ∠+∠=︒,∴11PDP E DE ∠=∠. 又∵1125DE DE DP DP ==, ∴11E DE PDP ∆∆:, ∴11DEE DPP ∠=∠.同理22E DE P DP ∆∆:,可得22DEE DPP ∠=∠. 又∵12180DPP DPP ∠+∠=︒, ∴12180DEE DEE ∠+∠=︒. ∴点1E ,点E ,点2E 三点共线.∵121290E DE PDE ∠+∠=︒,121290PDP PDE ∠+∠=︒, ∴1212PDP E DE ∠=∠. ∵121225DE DE DP DP ==, ∴1212E DE PDP ∆∆:, ∴121225E E PP =. ∵1210PP =, ∴124E E =.通过上述论证得到结论一:“当主动点在一条线段上运动,从动点也在一条线段上运动时,主动点的起点、终点、某个定点构成的三角形和从动点的起点、终点、某个定点构成的三角形相似”.因此可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长. 三、运用求解例2 如图16,在Rt COD ∆中,90COD ∠=︒,2OC OD ==,以O 为圆心,AB 为直径的圆经过点C ,点D .连结,AD BC 相交于点P ,将Rt COD ∆从OA 与OC 重合的位置开始,绕着点O 顺时针旋转90º,则交点P 所经过的路径长是.在图16的基础上先作起点图,当点C 与点A 重合时记作点1C ,此时点D 在点1D ,位置,1BC ,1AD ,交于点1P ,此时点1P ,与点A 重合(如图17).再作终点图,此时点C 与点1D 重合记作点2C ,点D 与点B 重合记作点2D ,2AD 与2BC 交于点2P ,点2P 与点B 重合(如图18).通过三点图,发现点1P ,点P ,点2P 三点不共线,考虑从动点的运动路径为圆弧,但需要运用“定角定长定圆”的方法加以证明.在PAB ∆中,4AB =为定长,因为90COD ∠=︒,所以90COA DOB ∠+∠=︒,又“同弧所对的圆周角的度数是圆心角度数的一半”, 得到190452CBA DAB ∠+∠=⨯︒=︒, 所以135APB ∠=︒为定角.所以点P 在以4AB =为弦,135APB ∠=︒为圆周角的定圆上运动.类比引例2,APB ∠的补角'45AP B ∠=︒也为定角,可将'AP B ∠看作弦AB 所对的一个圆周角,圆心'O 必在弦AB 的垂直平分线上,且2'90AOB AP B ∠=∠=︒.又因为“直径所对的圆周角为90º”,所以'O 是弦AB 的垂直平分线与圆O 的一个交点 所以半径'22O A =.所以点P 的运动路径是劣弧AB (如图19), 根据弧长公式得到90222180l ππ︒⨯==︒.通过上述论证可以发现,主动点1C ,点2C 与点O 构成的扇形12C OC 圆心角为90º,半径为2;从动点1P ,2P 与点0构成的扇形12POP 的圆心角为90º,半径为22.因为两个扇形的圆心角都为90º,所以扇形12C OC :扇形12POP ,相似比为1:2,因此扇形的弧长之比也为1:2.主动点C 的运动路径长为1902180l ππ︒⨯==︒,故从动点P 的运动路径长为122l l π==.于是得到结论二:“当主动点在一条圆弧上运动,从动点也在一条圆弧上运动时,主动点的起点、终点、某个定点构成的扇形和从动点的起点、终点、某个定点构成的扇形相似”.因此,可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长.巩固练习 1.如图,已知扇形AOB 中,OA =3,∠AOB =120°,C 是在上的动点.以BC 为边作正方形BCDE ,当点C 从【分析】如图,由此BO交⊙O于F,取的中点H,连接FH、HB、BD.易知△FHB是等腰直角三角形,HF =HB,∠FHB=90°,由∠FDB=45°=∠FHB,推出点D在⊙H上运动,轨迹是(图中红线),易知∠HFG=∠HGF=15°,推出∠FHG=150°,推出∠GHB=120°,易知HB=3,利用弧长公式即可解决问题.【解答】解:如图,由此BO交⊙O于F,取的中点H,连接FH、HB、BD.易知△FHB是等腰直角三角形,HF=HB,∠FHB=90°,∵∠FDB=45°=∠FHB,∴点D在⊙H上运动,轨迹是(图中红线),易知∠HFG=∠HGF=15°,∴∠FHG=150°,∴∠GHB=120°,易知HB=3,∴点D的运动轨迹的长为=2π.故答案为2π.【点评】本题考查轨迹、弧长公式、圆的有关知识、正方形的性质等知识,解题的关键是学会添加常用辅助线,正确寻找点D的运动轨迹,属于中考填空题中的压轴题.2.如图,边长为6的正方形ABCD的顶点A、B在一个半径为6的圆上,顶点C、D在圆内,将正方形ABCD沿圆【分析】作辅助线,首先求出∠D′AB的大小,进而求出旋转的角度,利用弧长公式问题即可解决.【解答】解:如图,分别连接OA、OB、OD′、OC、OC′;∵OA=OB=AB,∴△OAB是等边三角形,∴∠OAB=60°;同理可证:∠OAD′=60°,∴∠D′AB=120°;∵∠D′AB′=90°,∴∠BAB′=120°﹣90°=30°,由旋转变换的性质可知∠C′AC=∠B′AB=30°;∵四边形ABCD为正方形,且边长为6,∴∠ABC=90°,AC==6,∴当点D第一次落在圆上时,点C运动的路线长为:=π.以D或B为圆心滚动时,每次C点运动π,以A做圆心滚动两次,以B和D做圆心滚动三次,所以总路径=×2+π×3=(3+2)π.故答案为:(3+2)π.【点评】本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.3.将边长为4的正方形ABCD向右倾斜,边长不变,∠ABC逐渐变小,顶点A、D及对角线BD的中点N分别运动到A′、D′和N′的位置,若∠A′BC=30°,则点N到点N′的运动路径长为.【分析】根据题意可以画出相应的图形,可以求得∠NMN′的度数,然后根据弧长公式即可解答本题.【解答】解:作NM⊥BC于点M,连接MN′,∵点N′和点M分别为线段BD′和BC的中点,∴MN′==2,∴MN′=BM,∴∠MBN′=∠MN′B,∵∠A′BC=30°,∴∠MBN′=15°,∴∠N′MC=30°,∴∠NMN′=60°,∴点N到点N′的运动路径长为:,故答案为:.【点评】本题考查轨迹、正方形的性质,解题的关键是明确题意,找出所求问题需要的条件.。
初中数学动点路径长的问题解决策略

2017·05路径长问题的通常没有给出具体的动点运动轨迹,比较抽象,是学生难以把握的问题之一。
问题的解决策略是将动态问题转化为静态问题,寻找问题中的不变量,把抽象问题具体化,而初中阶段动点的运动轨迹一般只限于直线运动或圆弧运动,解决路径长问题关键在于确定动点运动的轨迹。
摘要关键词轨迹;运动;路径长;策略路径长问题是近几年中考的热点问题,它设计新颖,内涵丰富,既考查学生的基本画图能力,又考查学生逻辑推理能力。
它的难点在于题目中没有给出具体的动点运动轨迹,而且比较抽象,需要学生思考探究,很多学生对这类问题常常感到无从下手,产生畏难情绪。
为了解决这个问题,教师可以引导学生将动态问题转化为静态问题,寻找路径长问题中不变的量,把抽象问题具体化。
现结合例题探讨动点路径是线段与圆弧这两类问题轨迹的解题策略。
一、追根溯源,探究问题中不变的量教学过程中教师们常常发现学生在审题、析题方面不能抓住重点,遇到疑难问题,不懂得寻求解题的突破口,过度依赖教师的讲解,不能独立思考,学习处于被动状态。
新课程理念倡导以学生为主体,让学生积极、主动地参与课堂的探究活动,学生通过探究获得的解题经验往往比较直观,而且印象深刻,因此,教师传授新知识、新方法时,要让学生有充足的时间探究题目中隐含的条件,寻找解题的关键点,把复杂问题简单化。
学生在探究的过程得出解题经验,既获得成功的体验,又提高自身的综合解题能力。
1.动点到定直线距离保持不变,其轨迹是线段人教版七年级下册数学教科书采用这个例题来讲解无理数π如何在数轴上表示。
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点O 到达点O′,点O′的数值是___。
这是初中阶段教科书第一次讲解动点的轨迹问题,从图中可以看出O O′的长是这个圆的周长π,所以点O′在数轴上对应的数是π。
教师再让学生思考圆形车轮让乘坐者感觉舒适平稳的原因,学生探究后得出结论:圆心到水平面的距离相等。
七年级数学上册数轴上的动点问题专题训练(一)

七年级数学上册数轴上的动点问题专题训练(一)七年级数学上册数轴上的动点问题专题训练(一)前言:数轴上的动点问题离不开数轴上两点之间的距离。
为了便于我们对这类问题的分析,不妨先明确以下几个问题:1.数轴上两点间的距离,即为这两点所对应的坐标差,用右边的数减去左边的数的差。
即数轴上两点间的距离=右边点表示的数-左边点表示的数。
2.点在数轴上运动时,由于数轴向右的方向为正方向,因此向右运动的速度看作正速度,而向左运动的速度看作负速度。
在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标。
即一个点表示的数为a,向左运动b个单位后表示的数为a-b,向右运动b个单位后所表示的数为a+b。
3.数轴是数形结合的产物,分析数轴上点的运动要结合图形进行分析。
在数轴上运动形成的路径可看作数轴上线段的和差关系。
一、基础能力过关测试1.数轴上表示-5的点离原点的距离是5个单位长度,数轴上离原点6个单位长度的点有两个,它们表示的数是1和-1.2.数轴上的A点与表示-3的点距离4个单位长度,则A 点表示的数为-7.3.数轴上A、B两点离原点的距离分别为2和3,则AB 间距离是5.4.点A、B在数轴上对应的数分别是m、n,(n在m的右边)。
则AB间距离是n-m。
5.数轴上表示x和-2的两点间距离是|x+2|。
若|x+2|=5,则x=3或x=-7.6.若|a|=|b|,则a、b的关系是a=b或a=-b。
若|x−3|=|4−2x|,则x=2或x=5.7.若点A、点B表示的数分别是-2、6,则AB的中点为2.若点A、点B表示的数分别是a、b,则AB的中点为(a+b)/2.二、例题解析例1】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发,向数轴正方向运动,A的速度为a个单位长度/秒,B的速度为b个单位长度/秒,且a、b满足(a^2)2<b^2<5a^21)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动到3秒时的位置;2)若A、B两点在(1)中的位置,在数轴上存在一点C,且AC=2BC,求C点对应的数;3)若A、B两点从(1)中的位置同时按原速度向数轴负方向运动,几秒时,原点恰好在两个动点的正中间;4)若A、B两点从(1)中的位置同时按原速度向数轴负方向运动,问几秒后点A和点B相距2个单位长度;例2】已知数轴上有A、B两点,分别表示的数为-40和20.点A 以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动,设运动时间为t秒(t>0)。
运用“三点法”求解动点路径长问题

运用“三点法”求解动点路径长问题初中数学中动点路径问题,一般有两种情况:线段或圆弧.本文提出一种求动点路径长的方法——三点法,“三点”指动点的起点,终点与过程点.该方法分为三步:(1)精准作图,运用刻度尺,圆规及量角器等工具作出位置较为精准的“三点”.(2)大胆猜测,若“三点”共线,则动点路径为线段;若“三点”不共线,则动点路径为圆弧.(3)小心验证,根据画出的“三点图”,运用相似三角形、“定角定长定圆”等方法对猜想进行严格的证明.一、知识准备1、基本概念如图1,在Rt ABC ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2ta n 5D PE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .在图1中,点P 是“主动”在边AB 上开始动的点,称为“主动点”;点E 是跟着点P 在运动的点,称为“从动点”.又点P 从点A 运动到点B ,当点P 与点A 重合时记作点1P ,称为“主动点的起点”,此时1E 称为“从动点的起点”,此时作出符合要求的图形(如图2),称该图为“起点图”;当点P 与点B 重合时记作点2P ,称为“主动点的终点”,此时2E 称为“从动点的终点”,作出符合要求的图形(如图3),称该图为“终点图”.区别于起点1P ,终点2P ,将图1中的点P 称为“主动点的过程点”,此时E 称为“从动点的过程点”,相应地把图1称为“过程图”.将起点图,终点图,过程图放在同一个图形中,将这个图形称为“三点图”(如图4).2、定角定长定圆固定度数的角对着固定长度的线段时隐含着一个固定大小的圆,此时定线段为定圆的一条弦,定角为弦所对的一个圆周角.引例1 如图5,线段4AB =,点C 是平面上的一个动点,使90ACB ∠=︒,作出点C的运动路径.由“90º角所对的弦是直径”可以得到点C 的运动路径是以AB 为直径的圆,且不与点A 、点B 重合(如图6).引例2 如图7,线段4AB =,点C 是平面上的一个动点,45ACB ∠=︒,作出顶点C 的运动路径.当点C 位置不同时,ACB ∠度数不变,根据“同弧或等弧所对的圆周角相等”,可以将ACB ∠看作弦AB 所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且290AOB ACB ∠=∠=︒,计算可得半径OA =所以,点C 的运动路径是优弧ACB ,且不与点A 、点B 重合(如图8).引例3 如图9,线段4AB =,点C 是平面上的一个动点,120ACB ∠=︒,作出顶点C 的运动路径.作出ACB ∠的补角'AC B ∠为60º,'AC B ∠的位置不同时度数为定值.类比引例2,可将'AC B ∠看作弦AB 所对的一个圆周角,圆心O 必在弦AB 的垂直平分线上,且2'120AOB AC B ∠=∠=︒,计算可得半径OA =.在所以点C 的运动路径是劣弧»AB ,且不与点A 、点B 重合(如图10).二、方法归纳例l 如图11,在R t A B C ∆中,6,8AC BC ==,90C ∠=︒.点P 是边AB 上一动点,点D 是AC 延长线上的一个定点,连结PD ,过点D 作DE PD ⊥,连结PE ,且2tan 5DPE ∠=,当点P 从点A 运动到点B 时,点E 运动的路径长为 .1.精准作图因为2tan 5DPE ∠=,所以通过计算很难得到DPE ∠的度数(不借助计算器),但可以运用量角器测量图12中22DPE ∠≈︒.在图11的基础上,先作起点图.当点P 与点A 重合时记作点1P ,在图中作出122DPQ ∠=︒(如图12),过点D 作11DE PD ⊥交射线AQ 于点1E (如图13).当点P 与点B 重合时记作点2P ,运用类似的方法在图13的基础上作出终点图,并去掉多余部分,得到一幅完整的三点图(如图14).2、大胆猜测通过三点图发现点1E ,点E ,点2E 基本在一条直线上(如图14),所以可以大胆的猜测点E 的运动路径是一条线段,点E 运动的路径长就是线段12E E 的长度.于是提出猜想一“在三点图中,从动点的起点,终点,过程点三点共线时,从动点的运动路径为线段”.在三点图中,从动点的起点,终点,过程点三点不共线时,就初中数学而言,不共线的三点确定一个圆,这里提出猜想二“在三点图中,从动点的起点,终点,过程点三点不共线时,从动点的运动路径为圆弧”.当运动路径为圆弧时,考虑寻找固定度数的角与固定长度的线段,运用“定角定长定圆”的方法作出运动路径.3.小心验证在图15中,因为1190E DE PDE ∠+∠=︒,1190PDP PDE ∠+∠=︒, ∴11PDP E DE ∠=∠. 又∵1125DE DE DP DP ==, ∴11E DE PDP ∆∆:, ∴11DEE DPP ∠=∠.同理22E DE P DP ∆∆:,可得22DEE DPP ∠=∠.又∵12180DPP DPP ∠+∠=︒,∴12180DEE DEE ∠+∠=︒.∴点1E ,点E ,点2E 三点共线.∵121290E DE PDE ∠+∠=︒,121290PDP PDE ∠+∠=︒,∴1212PDP E DE ∠=∠. ∵121225DE DE DP DP ==, ∴1212E DE PDP ∆∆:, ∴121225E E PP =.∵1210PP =,∴124E E =.通过上述论证得到结论一:“当主动点在一条线段上运动,从动点也在一条线段上运动时,主动点的起点、终点、某个定点构成的三角形和从动点的起点、终点、某个定点构成 的三角形相似”.因此可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长.三、运用求解例2 如图16,在R t C O D ∆中,90COD ∠=︒,2OC OD ==,以O 为圆心,AB 为直径的圆经过点C ,点D .连结,AD BC 相交于点P ,将Rt COD ∆从OA 与OC 重合的位置开始,绕着点O 顺时针旋转90º,则交点P 所经过的路径长是 .在图16的基础上先作起点图,当点C 与点A 重合时记作点1C ,此时点D 在点1D ,位置,1BC ,1AD ,交于点1P ,此时点1P ,与点A 重合(如图17).再作终点图,此时点C 与点1D 重合记作点2C ,点D 与点B 重合记作点2D ,2AD 与2BC 交于点2P ,点2P 与点B 重合(如图18).通过三点图,发现点1P ,点P ,点2P 三点不共线,考虑从动点的运动路径为圆弧,但需要运用“定角定长定圆”的方法加以证明.在PAB ∆中,4AB =为定长,因为90COD ∠=︒,所以90COA DOB ∠+∠=︒,又“同弧所对的圆周角的度数是圆心角度数的一半”, 得到190452CBA DAB ∠+∠=⨯︒=︒,所以135APB ∠=︒为定角.所以点P 在以4AB =为弦,135APB ∠=︒为圆周角的定圆上运动.类比引例2,APB ∠的补角'45AP B ∠=︒也为定角,可将'AP B ∠看作弦AB 所对的一个圆周角,圆心'O 必在弦AB 的垂直平分线上,且2'90AOB AP B ∠=∠=︒.又因为“直径所对的圆周角为90º”,所以'O 是弦AB 的垂直平分线与圆O 的一个交点所以半径'O A =所以点P 的运动路径是劣弧AB (如图19),根据弧长公式得到90180l π︒⨯==︒. 通过上述论证可以发现,主动点1C ,点2C 与点O 构成的扇形12C OC 圆心角为90º,半径为2;从动点1P ,2P 与点0构成的扇形12POP 的圆心角为90º,半径为因为两个扇形的圆心角都为90º,所以扇形12C OC :扇形12POP ,相似比为,因此扇形的弧长之比也为1.主动点C 的运动路径长为1902180l ππ︒⨯==︒,故从动点P 的运动路径长为l =.于是得到结论二:“当主动点在一条圆弧上运动,从动点也在一条圆弧上运动时,主动点的起点、终点、某个定点构成的扇形和从动点的起点、终点、某个定点构成的扇形相似”.因此,可以先求出主动点的运动路径长再乘以相似比得到从动点的运动路径长.。
八年级数学动点问题专项训练(最新整理)
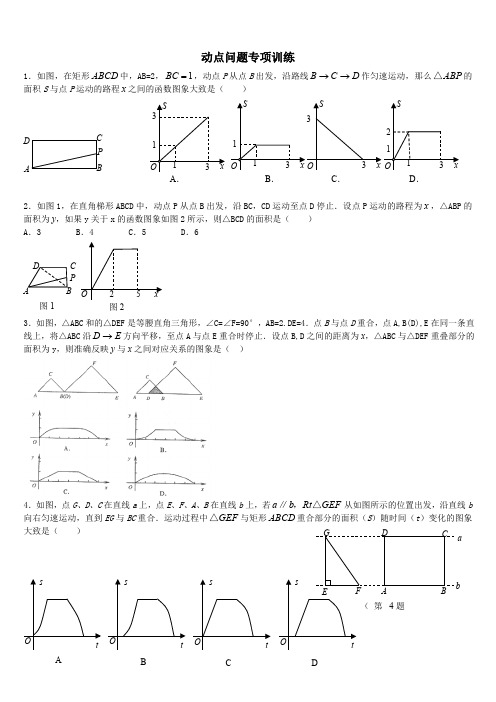
动点问题专项训练1.如图,在矩形中,AB=2,,动点P 从点B 出发,沿路线作匀速运动,那么的ABCD 1BC =B C D →→ABP △面积S 与点P 运动的路程之间的函数图象大致是( )xD C P BAA .B .C .D .2.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为,△ABP 的x 面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )A .3B .4C .5D .6图1ABCP D 图23.如图,△ABC 和的△DEF 是等腰直角三角形,∠C=∠F=90°,AB=2.DE=4.点B 与点D 重合,点A,B(D),E 在同一条直线上,将△ABC 沿方向平移,至点A 与点E 重合时停止.设点B,D 之间的距离为x ,△ABC 与△DEF重叠部分的D E →面积为y ,则准确反映y 与x 之间对应关系的图象是( )4.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若从如图所示的位置出发,沿直线b a b Rt GEF ∥,△向右匀速运动,直到EG 与BC 重合.运动过程中与矩形重合部分的面积(S )随时间(t )变化的图象GEF △ABCD 大致是( )aABCD5.(2009年牡丹江)如图,平面直角坐标系中,在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )6.如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止,设点P 运动的路程为,△ABP 的x 面积为y ,如果y 关于的函数图象如图2所示,则矩形ABCD 的面积是( )x A .10 8.16 C. 20 D .367.如图,三个大小相同的正方形拼成六边形ABCDEF ,一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动,最后到达点E .运动过程中PEF ∆的面积(s )随时间(t )变化的图象大致是( )8.如图8,点A 、B 、C 、D 为圆O 的四等分点,动点P 从圆心O 出发,沿O-C-D-O 的路线作匀速运动.设运动时间为秒, t ∠APB 的度数为y 度,则下列图象中表示y 与t 之间函数关系最恰当的是9. 13.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图4所示,设小矩形的长和宽分别为x 、y ,剪去部分的面积为20,若2≤x ≤10,则y 与x 的函数图象是:ABCDA .。
专题03 数轴上动点问题的答题技巧与方法(方法清单)(7个题型解读+提升训练)(原卷版)

专题03 数轴上动点问题的答题技巧与方法(方法清单)(7个题型解读+提升训练)【方法清单】【关键】化动为静,分类讨论。
抓住动点,化动为静,以不变应万变寻找破题点(边长、动点速度、角度以及所给图形的能建立等量关系等等) 建立所求的等量代数式,求出未知数等等。
动点问题定点化是主要思想。
比如以某个速度运动,设出时间后即可表示该点位置:再如函数动点,尽量设一个变量,y 尽量用来表示,可以把该点当成动点,来计算。
【步骤】1.画图形2.表线段3.列方程4.求正解1.数轴上两点间的距离,即为这两点所对应的坐标差的绝对值,也即用右边的数减去左边的数的差。
即数轴上两点间的距离=右边点表示的数一左边点表示的数2,点在数轴上运动时,由于数轴向右的方向为正方向,因此向右运动的速度看作正速度,而向作运动的速度看作负速度。
这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标。
即一个点表示的数为a,向左运动b 个单位后表示的数为 a b; 向右运动b个单位后所表示的数为a+b。
3,分析数轴上点的运动要是数形结合进行分析,点在数轴上运动形成的路径可看作数轴上线段的和差关系题型一、数轴上与速度、时间、距离有关问题【例1】.(2022秋•代县期中)如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,从图中可以看出,终点表示的数是﹣2,已知A,B是数轴上的点.请参照图并思考,完成下列填空:(1)如果点A表示数3,将点A向右移动7个单位长度,那么终点B表示的数是,A,B两点间的距离是.(2)如果点B表示数2,将点B向左移动9个单位长度,再向右移动5个单位长度,那么终点A表示的数是,A,B两点间的距离是.(3)如果点A表示的数是﹣4,将点A向右移动168个单位长度;再向左移动2个单位长度,那么终点B表示的数是,A,B两点间的距离是.(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是,A,B两点间的距离是.【变式1】.(2022秋•博罗县期中)如图,点A,B,C是数轴上三点,点C表示的数为6,BC=4,AB=12.(1)写出数轴上点A,B表示的数:,;(2)动点P,Q同时从A,C出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.①当t=2时,求出此时P,Q在数轴上表示的数;②t为何值时,点P,Q相距2个单位长度,并写出此时点P,Q在数轴上表示的数.【变式2】.(2022秋•历下区期中)为宣传健康知识,某社区居委会派车按照顺序为7个小区(分别记为A,B,C,D,E,F,G)分发防疫安全手册.社区工作人员乘车从服务点(原点)出发,沿东西向公路行驶,如果约定向东为正,向西为负,当天的行驶记录如下(单位:百米):+10,﹣18,+14,﹣30,+6,+22,﹣6(1)请你在数轴上标记出这D,E,F这三个小区的位置(在相应位置标记字母即可).(2)服务车最后到达的地方距离服务点多远?若该车辆油耗为0.01升/百米,则这次分发工作共耗油多少升?(3)为方便附近居民进行核酸检测,现居委会计划在这七个小区中选一个作为临时核酸检测点,为使七个小区所有居民步行到检测点的路程总和最小,假设各小区人数相等,那么检测点的位置应设在小区.题型二、数轴上点之间的位置关系问题【例2】(2022秋•余江区期中)如图,在一条不完整的数轴上,从左到右的点A,B,C把数轴分成①②③④四部分,点A,B,C对应的数分别是a,b,c,已知bc<0.(1)原点在第部分;(2)若AC=5,BC=3,b=﹣1,求a的值;(3)在(2)的条件下,数轴上一点D表示的数为d,若BD=2OC,直接写出d的值.【变式1】.(2022秋•南溪区期中)如图,在数轴上有三个点A,B,C,请回答下列问题:(1)将点B向左移动4个单位长度后,哪个字母所表示的数最小?是多少?(2)将点C向左移动6个单位长度后,这时点B表示的数比点C表示的数大多少?(3)怎样移动A、B、C中的两个点才能使三个点表示的数相同?有几种移法?【变式2】.(2022秋•惠济区期中)如图,在数轴上点A表示的数是8,若动点P从原点O出发,以2个单位/秒的速度向左运动,同时另一动点Q从点A出发,以4个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为t(秒).(1)当t=0.5时,求点Q到原点O的距离;(2)当t=2.5时求点Q到原点O的距离;(3)当点Q到原点O的距离为4时,求点P到原点O的距离.【变式3】.(2022秋•庐阳区校级期中)根据课堂所学知识我们知道:数轴上两点A、B对应的数分别为a,b(a<b),那么A,B两点之间距离可以用代数式b﹣a来表示.已知:如图,数轴上两点M、N对应的数分别为﹣8、4,点P为数轴上任意一点,其对应的数为x.(1)M,N两点之间的距离是;(2)当点P到点M、点N的距离相等时,求x的值;(3)当点P到点M、点N的距离之和是16时,求出此时x的值.题型三、数轴上动点定值问题【例3】.(2022秋•灞桥区校级期中)如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上,点A在数轴上表示的数是﹣12,点D在数轴上表示的数是15.(1)点B在数轴上表示的数是,点C在数轴上表示的数是;(2)若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度秒的速度也向左匀速运动,设运动时间为t秒,当t为何值时,点B与点C之间的距离为1个单位长度?(3)若线段AB、线段CD分别以1个单位长度/秒、2个单位长度/秒的速度同时向左匀速运动,与此同时,动点P从﹣15出发,以4个单位长度/秒的速度向右匀速运动.设运动时间为t秒,当0<t<5时,2AC﹣PD的值是否发生变化?若不变化,求出这个定值,若变化,请说明理由.【变式1】.(2022秋•河北区期中)在数轴上有三点A,B,C分别表示数a,b,c,其中b是最小的正整数,且|a+2|与(c﹣7)2互为相反数.(1)a=,b=,c=;(2)若将数轴折叠,使点A与点C重合,则点B与表示数的点重合;(3)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时点B和点C分别以每秒2个单位长度的速度和4个单位长度的速度向右运动,若点A与点B的距离表示为AB,点A 与点C的距离表示为AC,点B与点C的距离表示为BC,则t秒钟后,AB=,AC=,BC =;(用含t的式子表示)(4)请问:3BC﹣2AB的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请直接写出其值.【变式2】.(2022秋•上林县期中)已知点A、B在数轴上对应的数分别为a、b,且a=﹣2,b=10,点A、B之间的距离记作AB.(1)线段AB的长为;(直接写出结果)(2)若动点P在数轴上对应的数为x,①当点P是线段AB上一点,P A=2PB,则点P表示的数为;此时P A+PB=;(直接写出结果)②当P A+PB=14时,求x的值;③当动点P在点A的左侧,M、N分别是P A、PB的中点,在运动过程中的值是否发现变化?若不变,求出其值;若变化,请求出变化范围.题型四、数轴上折叠问题【例4】(2022秋•仁怀市期中)如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c﹣7)2=0.(1)a=,b=,c=;(2)若将数轴折叠,使得A点与C点重合,则点B与数对应的点重合;(3)若点A、B、C是数轴上的动点,点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,那么3BC﹣2AB的值是否随着运动时间t(秒)的变化而改变?若变化,请说明理由;若不变,请求出其值.【变式1】(2022秋•濮阳县期中)如图,已知在纸面上有一条数轴.操作一:折叠数轴,使表示1的点与表示﹣1的点重合,则表示﹣3的点与表示的点重合.操作二:折叠数轴,使表示1的点与表示3的点重合,在这个操作下回答下列问题:①表示﹣3的点与表示的点重合;②若数轴上A,B两点的距离为6(A在B的左侧),且折叠后A,B两点重合,则点A表示的数为,点B表示的数为.【变式2】.(2022秋•桓台县期中)如图所示的数轴中,点A表示1,点B表示﹣2,试回答下列问题:(1)A、B两点之间的距离是;(2)观察数轴,与点A的距离为5的点表示的数是;(3)若将数轴折叠,使点A与表示﹣3的点重合,则点B与表示数的点重合;(4)若数轴上M,N两点之间的距离为2022(点M在点N的左侧),且M,N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是和.【变式3】.(2022秋•南山区校级期中)学习完数轴以后,喜欢探索的小聪在纸上画了一个数轴(如图所示),并进行下列操作探究:(1)操作一:折叠纸面,使表示1的点与表示﹣1的点重合,则表示﹣4的点与表示的点重合.操作二:折叠纸面,使表示﹣3的点与表示1的点重合,回答以下问题:(2)表示2的点与表示的点重合;(3)若数轴上A、B两点之间距离是a(a>0)(A在B的左侧),且折叠后A、B两点重合.求A、B两点表示的数是多少?题型五、数轴上探究问题【例5】(2022秋•宛城区期中)【问题探索】如图,将一根木棒放在数轴(单位长度为lcm)上,木棒左端与数轴上的点A重合,右端与数轴上的点B重合.(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B时,它的右端在数轴上所对应的数为30:若将木棒沿数轴向左水平移动,则当它的右端移动到点A时,它的左端在数轴上所对应的数为6,由此可得这根木棒的长度为cm.(2)图中点A所表示的数是,点B所表示的数是.【实际应用】由(1)(2)的启发,请借助“数轴”这个工具解决下列问题:(3)一天,丽丽去问奶奶的年龄,奶奶说:“我若是你现在这么大,你还要32年才出生;你若是我现在这么大,我就106岁啦!”根据对话可知丽丽现在的岁数是,奶奶现在的岁数是.【变式】.(2022秋•和平区校级期中)阅读并解决相应问题:(1)问题发现:在数轴上,点A表示的数为﹣2,点B表示的数为3,若在数轴上存在一点P,使得点P到点A的距离与点P到点B的距离之和等于n,则称点P为点A、B的“n节点”.如图1,若点P表示的数为,有点P到点A的距离与点P到点B的距离之和为+=5,则称点P为点A、B的“5节点”.填空:①若点P表示的数为0,则n的值为.②数轴上表示整数的点称为整点,若整点P为A、B的“5节点”,请直接写出整点P所表示的数.(2)类比探究:如图2,若点P为数轴上一点,且点P到点A的距离为1,请你求出点P表示的数及n的值,并说明理由.(3)拓展延伸:在(1)(2)的条件下,若点P在数轴上运动(不与点A、B重合),满足点P到点B的距离等于点P到点A的距离的,且此时点P为点A、B的“n的节点”,求点P表示的数及n的值,并说明理由.题型六、数轴上新定义问题【例6】(2022秋•永安市期中)[阅读理解]点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离2倍,那么我们就称点C是{A,B}的关联点.例如,如图1,点A表示的数为﹣4,点B表示的数为2.表示0的点C到点A的距离是4,到点B的距离是2,那么点C是{A,B}的关联点;又如,表示﹣2的点D到点A的距离是2.到点B的距离是4,那么点D就不是{A,B}的关联点,但点D是{B,A}的关联点.[知识运用](1)如图2,M、N为数轴上两点,点M所表示的数为﹣4,点N所表示的数为5.数所表示的点是{M,N}的关联点;数所表示的点是{N,M}的关联点;[拓展提升](2)如图3,A、B为数轴上两点,点A所表示的数为﹣60,点B所表示的数为30.现有一动点从点P 出发向左运动.P点运动到数轴上的什么位置时,点P、点A和点B中恰有一个点为其余两点的关联点?【变式1】.(2022秋•衢州期中)点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇妙点,但点D是{B,A}的奇妙点.(1)点A表示的数为1,点B表示的数为2,点C表示的数为5,B是否为{C,A}的奇妙点?请说明理由.(2)如图2,M,N为数轴上的两点,点M所表示的数为﹣2,点N所表示的数为6.表示数的点是{M,N}的奇妙点;表示数的点是{N,M}的奇妙点;(3)如图3,A,B为数轴上的两点,点A所表示的数为﹣10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,B为其余两点的奇妙点?【变式2】.(2022秋•平遥县期中)阅读下列材料:我们给出一个新定义:数轴上给定不重合两点A,B,若数轴上存在一点M,使得点M到点A的距离等于点M到点B的距离,则称点M为点A与点B的“平衡点”.解答下列问题:(1)若点A表示的数为﹣3,点B表示的数为1,点M为点A与点B的“平衡点”,则点M表示的数为;(2)若点A表示的数为﹣3,点A与点B的“平衡点M”表示的数为﹣5,则点B表示数为;操作探究:如图,已知在纸面上有一条数轴.操作一:(3)折叠数轴,使表示1的点与表示﹣1的点重合,则表示﹣5的点与表示的点重合.操作二:(4)折叠数轴,使表示1的点与表示3的点重合,在这个操作下回答下列问题:①表示﹣2的点与表示的点重合;②若数轴上A,B两点的距离为7(A在B的左侧),且折叠后A,B两点重合,则点A表示的数为.【变式3】.(2022秋•高青县期中)数轴上有A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“关联点”.例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“关联点”.(1)若点A表示数﹣2,点B表示数1,下列各数﹣1,2,4,6所对应的点分别是C1,C2,C3,C4,其中是点A,B的“关联点”的是;(2)点A表示数﹣10,点B表示数15,P为数轴上一个动点:①若点P在点B的左侧,且点P是点A,B的“关联点”,求此时点P表示的数;②若点P在点B的右侧,点P,A,B中,有一个点恰好是其它两个点的“关联点”,请直接写出此时点P表示的数.【变式4】.(2022秋•朝阳区校级期中)已知数轴上两点A、B,若在数轴上存在一点C,使得AC+BC=nAB,则称点C为线段AB的“n倍点”.例如图1所示:当点A表示的数为﹣2,点B表示的数为2,点C表示的数为0,有AC+BC=2+2=4=AB,则称点C为线段AB的“1倍点”.请根据上述规定回答下列问题:已知图2中,点A表示的数为﹣3,点B表示的数为1,点C表示的数为x.(1)当﹣3≤x≤1时,点C(填“一定是”或“一定不是”或“不一定是”)线段AB的“1倍点”;(2)若点C为线段AB的“n倍点”,且x=﹣4,求n的值;(3)若点D是线段AB的“2倍点”,则点D表示的数为;(4)若点E在数轴上表示的数为t,点F表示的数为t+12,要使线段EF上始终存在线段AB的“3倍点”,求t的取值范围(用不等号表示)题型七:数轴上存在性问题【例7】(2022秋•蓝山县期中)已知数轴上三点A、B、C对应的数分别是﹣1,1,4,点P为数轴上任意一点,且表示的数是x.(1)点A到点B的距离AB为多少个单位长度?(2)点P到B的距离PB可以表示为;(3)如果点P到点A和到点C的距离相等,那么x的值是多少?(4)数轴上是否存在点P,使点P到点A与到点C的距离之和是8?若存在,请直接写出x的值;若不存在,请说明理由.【变式1】(2022春•南岗区校级期中)若数轴上A、B两点对应的数分别为﹣5、4,P为数轴上一点,对应数为x.(1)若P为线段AB的三等分点,直接写出P点对应的数.(2)数轴上是否存在点P,使P点到A点、B点的距离和为11?若存在,求出x值;若不存在,请说明理由.(3)若点P从点A出发向右运动,速度是2个单位/分,点Q从点B出发向左运动,速度是3个单位/分,它们同时出发,经过几分钟,Q、B、P三点中,其中一点是另外两点连成线段的中点?【变式2】(2022秋•定远县期中)对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“联盟点”.(1)若点A表示数﹣4,点B表示数5,点M是点A,B的“联盟点”,点M在A、B之间,且表示一个负数,则点M表示的数为;(2)若点A表示数﹣2,点B表示数2,下列各数,0,4,6所对应的点分别为C1,C2,C3,C4,其中是点A,B的“联盟点”的是;(3)点A表示数﹣15,点B表示数25,P为数轴上一点:①若点P在点B的左侧,且点P是点A,B的“联盟点”,此时点P表示的数是;②若点P在点B的右侧,点P,A,B中,有一个点恰好是其它两个点的“联盟点”,直接写出此时点P表示的数.【变式3】(2022秋•鱼台县期中)如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C 之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.(1)数轴上点A表示的数为,点B表示的数为;(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由.【提升训练】1.(2022秋•桥西区期中)在一条不完整的数轴上标出若干个点,每相邻两点相距一个单位长度,其中点A,B,C对应的分别是整数a,b,c.(1)若以B为原点,写出a,c的值;(2)若c﹣2a=14,判断并说明A,B,C中哪个点是数轴的原点;(3)在(2)的条件下,M点从A点以每秒0.5个单位的速度向右运动,点N从点C以每秒1.5个单位的速度向左运动,点P从点B以每秒2个单位的速度先向左运动碰到点M后立即返回向右运动,碰到点N后又立即返回向左运动,碰到点M后又立即返回向右运动,三个点同时开始运动,当三个点聚于一点时停止运动.直接写出点P在整个运动过程中,移动了多少个单位.2.(2022秋•肥西县校级期中)如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是﹣3,已知A、B是数轴上的点,请参照如图并思考,完成下列各题.(1)如果点A表示的数是﹣2,将点A向右移动5个单位长度到点B,那么点B表示的数是.A、B两点间的距离是.(2)如果点A表示的数是4,将点A向左移动8个单位长度,再向右移动3个单位长度到点B,那么点B表示的数是,A、B两点间的距离是.(3)如果点A表示的数是m,将点A向左移动n个单位长度,再向右移动p个单位长度到点B,那么点B表示的数是.3.(2022秋•沙坪坝区校级期中)数轴上给定两点A、B,点A表示的数为﹣1,点B表示的数为3,若数轴上有两点M、N,线段MN的中点在线段AB上(线段MN的中点可以与A或B点重合),则称M点与N 点关于线段AB对称,请回答下列问题:(1)数轴上,点O为原点,点C、D、E表示的数分别为﹣3、6、7,则点与点O关于线段AB对称;(2)数轴上,点F表示的数为x,G为线段AB上一点,若点F与点G关于线段AB对称,则x的最小值为,最大值为;(3)动点P从﹣9开始以每秒4个单位长度,向数轴正方向移动时,同时,线段AB以每秒1个单位长度,向数轴正方向移动,动点Q从5开始以每秒1个单位长度,向数轴负方向移动;当P、Q相遇时,分别以原速立即返回起点,回到起点后运动结束,设移动的时间为t,则t满足时,P 与Q始终关于线段AB对称.4.(2022秋•泊头市期中)如图是某一条东西方向直线上的公交线路的部分路段,西起A站,东至L站,途中共设12个上下车站点.某天,小明参加该路线上的志愿者服务活动,从C站出发,最后在某站结束服务活动.如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):+5,﹣3,+4,﹣5,+8,﹣2,+1,﹣3,﹣4,+1.(1)请通过计算说明结束服务的“某站”是哪一站?(2)若相邻两站之间的平均距离约为2.5千米,求这次小明志愿服务期间乘坐公交车行进的总路程约是多少千米?5.(2022秋•夏津县期中)已知数轴上三点M,O,N对应的数分别为﹣1,0,3,点P为数轴上任意一点,其对应的数为x.(1)MN的长为;(2)如果点P到点M、点N的距离相等,那么x的值是;(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.6.(2022秋•文成县期中)如图,在数轴上,点A表示﹣4,点B表示﹣1,点C表示8,P是数轴上的一个点.(1)求点A与点C的距离;(2)若PB表示点P与点B之间的距离,PC表示点P与点C之间的距离,当点P满足PB=2PC时,请求出在数轴上点P表示的数.7.(2022秋•新郑市期中)如图,已知在纸面上有一条数轴.操作一:(1)折叠纸面,使表示1的点与表示﹣1的点重合,则表示﹣2的点与表示的点重合.操作二:(2)折叠纸面,使表示﹣1的点与表示3的点重合,回答以下问题:①表示5的点与表示的点重合;②若数轴上A,B两点之间的距离为9(点A在点B的左侧),且A,B两点折叠后重合,求A,B两点表示的数.8.(2022秋•昆明期中)问题探究:(1)如图①,将两根长度为6cm的木棒放置在数轴(单位长度为1cm)上,第一根的两端分别与数轴上表示2的点和点A重合,第二根的两端分别与数轴上点A和点B重合,则图中点A所表示的数是,点B所表示的数是;(2)如图②,将一根未知长度的木棒放置在数轴(单位长度为1cm)上,木棒的左端与数轴上的点C重合,右端与数轴上的点D重合.若将木棒沿数轴向右移动,当它的左端移动到点D时,右端在数轴上所对应的数为26;若将木棒沿数轴向左移动,当它的右端移动到点C时,左端在数轴上所对应的数为2.由此可得这根木棒的长为cm;(3)在(2)的条件下,若数轴上有一点P,点P到木棒CD中点的距离为16个单位长度,则点P所表示的数是.9.(2022秋•嘉祥县期中)定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是【A,B】的美好点.例如:如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的美好点,但点D是【B,A】的美好点.如图2,M,N为数轴上两点,点M所表示的数为﹣7,点N所表示的数为2.(1)点E,F,G表示的数分别是﹣3,6.5,11,其中是【M,N】美好点的是;写出【N,M】美好点H所表示的数是.(2)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动.当t为何值时,P,M和N中恰有一个点为其余两点的美好点?10.(2022秋•承德期中)如图所示,在数轴上点A,B,C表示的数分别为﹣2,0,6.点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.(1)AB=,BC=,AC=;(2)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.①设运动时间为t,请用含有t的算式分别表示出AB,BC,AC;②在①的条件下,请问:BC﹣AB的值是否随着运动时间t的变化而变化?若变化,请说明理由;若不变,请求其值.11.(2022秋•霍邱县期中)如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)数轴上点B表示的数是,点P表示的数是(用含t的代数式表示);(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:①当点P运动多少秒时,点P与点Q相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?12.(2022秋•秦淮区校级期中)如图,将一根木棒放在数轴(单位长度为1cm)上,木棒左端与数轴上的点A重合,右端与数轴上的点B重合.(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B时,它的右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它的右端移动到点A时,它的左端在数轴上所对应的数为6,由此可得这根木棒的长为cm;(2)图中点A所表示的数是,点B所表示的数是;(3)由(1)(2)的启发,请借助“数轴”这个工具解决下列问题:一天,妙妙去问奶奶的年龄,奶奶说:“我若是你现在这么大,你还要37年才出生;你若是我现在这么大,我就119岁啦!”请问奶奶现在多少岁了?。
动点路径长专题

点的运动路径问题一、常见类型:1.线段 2.圆弧 3.组合型二、解题步骤:第一步,取动点在运动过程中特殊的三点(运动开始、运动中、运动结束)位置探索出动点运动的路径形状;三点共线线段三点不共线圆弧第二步,根据题目的已知条件求出动点运动的路径长;三点共线线段(勾股定理、两点间距离公式等)三点不共线圆弧(确定圆心、半径、圆心角)三、典例分析1.如图,已知AB=10,P 是线段AB 上的动点,分别以AP 、PB为边在线段AB 的同侧作等边△ACP 和△PDB ,连接CD ,设CD 的中点为G ,当点P 从点A 运动到点B 时,则点G 移动路径的长是 _________ .2.如图,边长为4的等边△AOB 的顶点O 在坐标原点,点A 在x 轴正半轴上,点B 在第一象限.一动点P 沿x 轴以每秒1个单位长度的速度由点O 向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间是t 秒.在点P 的运动过程中,线段BP 的中点为点E ,将线段PE 绕点P 按顺时针方向旋转60°得PC .(1)当点P 运动到线段OA 的中点时,点C 的坐标为 _________ ;(2)在点P 从点O 到点A 的运动过程中,用含t 的代数式表示点C 的坐标;(3)在点P 从点O 到点A 的运动过程中,求出点C 所经过的路径长.3如图,一块含有30º角的直角三角形ABC ,在水平桌面上绕点C 按顺时针方向旋转到 A ’B ’C ’的位置。
若BC 的长为15cm ,那么顶点A 从开始到结束所经过的路径长为 ( )A .π10cmB .π310cmC .π15cmD .π20cm4.如图,直线y=﹣x+4与两坐标轴交A 、B 两点,点P 为线段OA 上的动点,连接BP ,过点A 作AM 垂直于直线BP ,垂足为M ,当点P 从点O 运动到点A 时,则点M 运动路径的长为 _________ . 1122(,),(,)A x y B x y 若,则AB5在矩形ABCD 中,已知AB =2cm ,BC =3cm ,现有一根长为2cm 的木棒EF 紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF 的中点P 在运动过程中所经过的路径为 cm.6如图,一根长为2米的木棒AB 斜靠在墙角处,此时BC 为1米,当A 点下滑至A ′处并且A ′C=1米时,木棒AB 的中点P 运动的路径长为__________米.7如图,在Rt △ABC 纸片中,∠C=90°,AC=BC=4,点P 在AC 上运动,将纸片沿PB 折叠,得到点C 的对应点D (P 在C 点时,点C 的对应点是本身),则折叠过程对应点D 的路径长是 .B C E F。
2024年中考数学复习几何专项练习:动点运动路径之瓜豆原理(含答案解析)

2024年中考数学复习几何专项练习:动点运动路径之瓜豆原理(含答案解析)一、填空题1.如图,等边三角形ABC 中,AB =4,高线AHD 是线段AH 上一动点,以BD 为边向下作等边三角形BDE ,当点D 从点A 运动到点H 的过程中,点E 所经过的路径为线段CM ,则线段CM 的长为,当点D 运动到点H ,此时线段BE 的长为.【答案】2【分析】由“SAS ”可得△ABD ≌△CBE ,推出AD =EC ,可得结论,再由勾股定理求解2,BH =当,D H 重合时,2,BE BH ==从而可得答案.【详解】解:如图,连接EC .∵△ABC ,△BDE 都是等边三角形,∴BA =BC ,BD =BE ,∠ABC =∠DBE =60°,∴∠ABD =∠CBE ,在△ABD 和△CBE 中,BA BC ABD CBE BD BE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△CBE (SAS ),∴AD =EC ,∵点D 从点A 运动到点H ,∴点E的运动路径的长为CM AH ==,当,D H 重合,而BDE △(即BHE )为等边三角形,,BE BH \=4,,AB AH AH BC ==^Q2,BH ==2,BE ∴=故答案为:.【点睛】本题考查等边三角形的性质,全等三角形的判定和性质,动点的轨迹等知识,解题的关键是正确寻找全等三角形解决问题.2.如图,正方形ABCD 的边长为4,E 为BC 上一点,且1BE =,F 为AB 边上的一个动点,连接EF ,以EF 为边向右侧作等边EFG∆,连接CG ,则CG 的最小值为.【答案】52【分析】由题意分析可知,点F 为主动点,G 为从动点,所以以点E 为旋转中心构造全等关系,得到点G 的运动轨迹,之后通过垂线段最短构造直角三角形获得CG 最小值.【详解】由题意可知,点F 是主动点,点G 是从动点,点F 在线段上运动,点G 也一定在直线轨迹上运动将EFB ∆绕点E 旋转60︒,使EF 与EG 重合,得到EFB EHG ∆≅∆,从而可知EBH ∆为等边三角形,点G 在垂直于HE 的直线HN 上,作CM HN ⊥,则CM 即为CG 的最小值,作EP CM ⊥,可知四边形HEPM 为矩形,则1351222CM MP CP HE EC =+=+=+=.故答案为52.【点睛】本题考查了线段极值问题,分清主动点和从动点,通过旋转构造全等,从而判断出点G 的运动轨迹,是本题的关键.3.如图,等边ABC 中,8AB =,O 是BC 上一点,且14BO BC =,点M 为AB 边上一动点,连接OM ,将线段OM 绕点O 按逆时针方向旋转60︒至ON ,连接BN CN 、,则BCN △周长的最小值为.【答案】8+8【分析】过点N 作ND BC ⊥于点D ,过点O 作OH BM ⊥于点H ,则90OHM ODN ∠=∠=︒,证明HOM DNO ≌,可得DN OH =,从而得到点N 的运动轨迹是直线,且该直线与直线BC 平行,在BC 的左侧,与BCC 关于该直线的对称点E ,连接BE 交该直线于N ,即当点B ,N ,E 三点共线时,BCN △的周长最小,连接CE 交该直线于G ,则22CE CG DN ===CE BC ⊥,求出BE ,即可求解.【详解】解:如图,过点N 作ND BC ⊥于点D ,过点O 作OH BM ⊥于点H ,则90OHM ODN ∠=∠=︒,∵ABC 为等边三角形,∴60ABC ∠=︒,8BC AB ==,∴120BMO BOM ∠+∠=︒,根据题意得:60MON ∠=︒,OM ON =,∴120NOD BOM ∠+∠=︒,∴NOD BMO ∠=∠,∴HOM DNO ≌,∴DN OH =,∵14BO BC =,∴2BO =,∵60ABC ∠=︒,∴30BOH ∠=︒,∴112BH OB ==,∴DN OH ==∴点N 的运动轨迹是直线,且该直线与直线BC 平行,在BC 的左侧,与BC作点C 关于该直线的对称点E ,连接BE 交该直线于N ,即当点B ,N ,E 三点共线时,BCN △的周长最小,连接CE 交该直线于G ,则22CE CG DN ===,CE BC ⊥,∴BE =∴△ACN 的周长的最小值为8+故答案为:8+.【点睛】本题考查旋转变换,全等三角形的判定和性质,轴对称,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.4.如图,正方形ABCD 的边长为P 是CD 边上的一动点,连接AP ,将AP 绕点A 顺时针方旋转60︒后得到AQ ,连接CQ ,则点P 在整个运动过程中,线段CQ 所扫过的图形面积为.【答案】3-【分析】根据题意画出点P 在CD 上移动的过程,线段CQ 所扫过的面积就是COQ 的面积,根据正方形的性质,等边三角形的性质以及全等三角形的判定和性质,得出线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- ,再根据等边三角形,等腰直角三角形面积的计算方法进行计算即可.【详解】解:如图,当点P 在点D 时,相应的点Q 落在点O ,当点P 移动到点C 时,相应的点Q 在点Q ,CQ 扫过的面积就是COQ 的面积,由题意可知,AOD △、ACQ 都是等边三角形,AO DO AD ∴===AQ CQ AC ====,四边形ABCD 是正方形,AOD △是等边三角形,906030ODC ∴∠=︒-︒=︒,45ACD ∠=︒,OD CD = ,18030752DOC DCO ︒-︒∴∠=∠==︒,754530ACO ∴∠=︒-︒=︒,45607530QCO QCD DCO ∠=∠-∠=︒+︒-︒=︒,ACO QCO ∴∠=∠,AC QC = ,CO CO =,AOC ∴ ≌()SAS QOC ,AO QO ∴=,604515CQO CAO ∠=∠=︒-︒=︒,()3601801530290AOQ ∴∠=︒-︒-︒-︒⨯=︒,即AOQ △是等腰直角三角形,∴线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- 111222⎛=⨯⨯⨯ ⎝3=,故答案为:3.【点睛】本题考查正方形、等边三角形,等腰直角三角形以及全等三角形的判定和性质,掌握正方形、等边三角形,等腰直角三角形以及全等三角形的判定和性质是正确解答的前提.5.如图,点D 是等边ABC 边AB 上的一动点(不与端点重合),点D 绕点C 引顺时针方向旋转60 得点E ,所得的CDE 边DE 与BC 交于点F ,则CF DE的最小值为.【分析】由旋转的性质得CDE 为等边三角形,由CEF CAD ∽△△得到CF CE CD AC =,即CF CD DE AC =,从而得到当CD 最小时,比值最小,再由“垂线段最短”得到当CD AB ⊥时,CD 值最小,作出对应图形,利用“ACD 是含30︒角的直角三角形”求出CD AC,从而得解.【详解】解:由旋转的性质得:CD CE =,60DCE ∠=︒,CDE ∴ 为等边三角形,DE CD CE ∴==,60A DEC ∠=∠=︒60ACD DCB ∠+∠=︒60DCB ECF ∠+∠=︒ACD ECF∴∠=∠∵60A DEC ∠=∠= ,ACD ECF∠=∠CEF CAD∴ ∽CF CE CD AC ∴=,即CF CD DE AC=AC 为定值,∴当CD 最小时,比值最小.根据“垂线段最短”可知:当CD AB ⊥时,CD 值最小,过点C 作CD AB ⊥于D ,并补全图形如下:ABC 是等边三角形,CD AB ⊥,60ACB ∠=︒∴1302ACD ACB ∠=∠=︒设AC 2a =,则12AD AC a ==∴CD ==,∴此时CF CD DE AC ==即CF DE 的最小值为2.故答案为:2.【点睛】此题考查图形的旋转变化与性质,等边三角形的判定和性质,相似三角形的判定与性质,含30︒角的直角三角形的性质,垂线段最短,理解“垂线段最短”和利用相似三角形的性质将CF DE转化为CD AC 是解题的关键.6.如图,在ACB △中,60ACB ∠=︒,75BAC ∠=︒,12AC =,点D 是边BC 上的一动点,连接AD ,将线段AD 绕点A 按逆时针方向旋转75︒得到线段AE ,连接CE ,则线段CE 长度的最小值是.【答案】/-【分析】过点A 作AF BC ⊥于点F ,在AB 上取点N ,使12AN AC ==,连接DN ,过点N 作点NM BD ⊥于点M ,证明()SAS NAD DAE ≌,求出CE DN =,得出当DN 最小时,CE 最小,根据垂线段最短,得出当点D 与点M 重合时,DN 最小,则CE 最小,求出最小结果即可.【详解】解:过点A 作AF BC ⊥于点F ,在AB 上取点N ,使12AN AC ==,连接DN ,过点N 作点NM BD ⊥于点M ,如图所示:根据旋转可知,AD AE =,75DAE ∠=︒,∵75BAC DAE ==︒∠∠,∴BAC DAC DAE DAC ∠-∠=∠-∠,即NAD CAE =∠∠,∵AN AC =,AD AE =,∴()SAS NAD CAE ≌,∴CE DN =,∴当DN 最小时,CE 最小,∵垂线段最短,∴当点D 与点M 重合时,DN 最小,则CE 最小,∵90AFC ∠=︒,60BCA ∠=︒,∴906030CAF ∠=︒-︒=︒,∴162CF AC ==,∴AF ==,∵45BAF BAC CAF =-=︒∠∠∠,90AFB ∠=︒,∴904545B ∠=︒-︒=︒,∴B BAF ∠=∠,∴BF AF ==∴AB ==∴12BN AB AN =-=-,∵90BMN ∠=︒,45B ∠=︒,∴904545BNM =︒-︒=︒∠,∴B BNM =∠∠,∴BM NM =,∵222BN NM BM =+,∴()22212NM =-,解得:NM =-,∴CE 的最小值为-.故答案为:【点睛】本题主要考查了全等三角形的判定和性质,勾股定理,等腰三角形的判断和性质,直角三角形的性质,垂线段最短,解题的关键是作出辅助线,构造全等三角形,证明CE DN =.7.如图,点A 的坐标为3⎫⎪⎪⎝⎭,点B 是x 轴正半轴上的一点,将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC .若点C 的坐标为(,4)k ,则k 的值为.【分析】连接BC ,过A 点作AF x ⊥轴于F ,C 作CD x ⊥轴于点D ,CE AF ⊥于点E ,则四边形DCEF 是矩形,根据将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ,可得ABC 是等边三角形,AB AC BC ==,由点A 的坐标为,(,4)C k ,有AC ==,而BD ==FB ==OF BF BD OD k ++==,可得k =,解方程可得答案.【详解】解:连接BC ,过A 点作AF x ⊥轴于F ,C 作CD x ⊥轴于点D ,CE AF ⊥于点E ,则四边形DCEF 是矩形,如图:∵将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ,∴AB AC =,60BAC ∠=︒,∴ABC 是等边三角形,∴AB AC BC ==,∵点A 的坐标为,(,4)C k ,,∴3CE k FD =-=,4CD =,3AF =,∴1AE EF AF CD AF =-=-=,∴AC BC AB ====,在Rt BCD 中,BD =,在Rt AFB 中,FB =∵OF BF BD OD k ++==,∴3k =,设k x =x =,化简变形得:42346490x x -=-,解得21x =-(舍去)或2493x =,∴3x =或3x =-(不符合题意,舍去),∴k ,∴k =,.【点睛】本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含k 的代数式表示相关线段的长度.8.如图,在边长为6的等边ABC 中,直线AD BC ⊥,E 是AD 上的一个动点连接EC ,将线段EC 绕点C 逆时针方向旋转60︒得到FC ,连接DF ,则点E 运动过程中,DF 的最小值是.【答案】32【分析】取线段AC 的中点G ,连接EG ,根据等边三角形的性质可得出CD CG =以及FCD ECG Ð=Ð,由旋转的性质可得出EC FC =,由此即可利用全等三角形的判定定理SAS 证出FCD ≌ECG ,进而即可得出DF GE =,再根据点G 为AC 的中点,即可得出EG 的最小值,此题得解.【详解】解:取线段AC 的中点G ,连接EG ,如图所示.ABC 为等边三角形,6AC BC ==,且AD 为ABC 的对称轴,132CD CG AB ∴===,60ACD ∠=︒,60ECF =︒∠ ,FCD ECG \Ð=Ð.FCD ∴ ≌()ECG SAS ,DF GE ∴=.当EG BC ∥时,EG 最小,点G 为AC 的中点,∴此时1133222EG DF CD ===⨯=.故答案为:32.【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出DF GE =.9.如图,在ABC ∆中,90ACB ︒∠=,点D 在BC 边上,5BC =,2CD =,点E 是边AC 所在直线上的一动点,连接DE ,将DE 绕点D 顺时针方向旋转60︒得到DF ,连接BF ,则BF 的最小值为.【答案】72【分析】当E 与点C 重合时,点F 与等边三角形CDG 的点G 重合,当点F 开始运动时,△ECD ≌△FGD ,故点F 在线段GF 上运动,根据垂线段最短原理,当BF ⊥GF 时,BF 有最小值,根据直角三角形的性质计算即可.【详解】当E与点C重合时,点F与等边三角形CDG的点G重合,∵DE绕点D顺时针方向旋转60 得到DF,∴△DEF是等边三角形,∴∠GDC=∠FDE=60°,ED=FD,∴∠GDC-∠GDE=∠FDE-∠GDE,∴∠EDC=∠FDG,∵△DEF是等边三角形,∴CD=GD,∴△ECD≌△FGD,∴EC=GF,∠ECD=∠FGD=90°,∴点F在线段GF上运动,根据垂线段最短原理,当BF⊥GF时,BF有最小值,如图,当旋转到BF∥DG 时,BF⊥GF,垂足为F,过点D作DH⊥BF,垂足为H,∵∠FGD=90°,∴四边形FGDH是矩形,∴∠GDH=90°,GD=FH=2,∵∠GDC=60°,∴∠BDH=30°,∵BD=BC-CD=5-2=3,∴BH=1232 BD=,∴BF=FH+BH=2+32=72,故答案为:7 2.【点睛】本题考查了等边三角形的判定和性质,矩形的判定和性质,垂线段最短,直角三角形的性质,熟练掌握等边三角形的判定,灵活运用直角的判定和直角三角形的性质是解题的关键.10.如图,正方形ABCD的边长为4,E为BC上一点,且1BE=,F为AB边上的一个动点,连接EF,将EF 烧点E顺时什旋转60°得到EG,连接CG,则CG的最小值为.【答案】5 2【分析】由题意分析可知,点F为主动点,G为从动点,所以以点E为旋转中心构造全等关系,得到点G 的运动轨迹,之后通过垂线段最短构造直角三角形获得CG最小值.【详解】解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动,将△EFB绕点E旋转60°,使EF与EG重合,得到△EBH为等边三角形,△EBF≌△EHG,∴∠EHG=∠ABC=90°,HE=BE=1,∠BEH=60°,∴点G在垂直于HE的直线HN上.作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,∴∠CEP=180°-60°-90°=30°,∴CP=12CE=12×(4-1)=32,则CM=MP+CP=35122 HE PC+=+=,即CG的最小值为5 2.故答案为5 2.【点睛】本题考查了旋转的性质,线段最值问题,全等三角形的性质,正方形的性质,矩形的判定与性质,含30°角的直角三角形的性质,以及垂线段最短等知识,分清主动点和从动点,通过旋转构造全等,从而判断出点G的运动轨迹,是本题的关键,之后运用垂线段最短,构造图形计算,是极值问题中比较典型的类型.11.如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值【答案】.【分析】由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD ,由垂线段最短得到当CD ⊥AB 时,△BDE 的周长最小,于是得到结论.【详解】∵将△ACD 绕点C 逆时针方向旋转60°得到△BCE ,∴∠DCE=60°,DC=EC ,∴△CDE 是等边三角形,由旋转的性质得,BE=AD ,∴C △DBE =BE+DB+DE=AB+DE=4+DE ,∵△CDE 是等边三角形,∴DE=CD ,∴C △DBE =CD+4,由垂线段最短可知,当CD ⊥AB 时,△BDE 的周长最小,此时,∴△BDE 的最小周长,故答案为.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,三角形周长的计算,熟练掌握旋转的性质是解题的关键.12.如图,在ABC 中,8AC BC ==,60BCA ∠= ,直线AD BC ⊥,E 是AD 上的一个动点,连接EC ,将线段EC 绕点C 按逆时针方向旋转60 得到FC ,连接DF ,则点E 运动过程中,DF 的最小值是.【答案】2【分析】根据题意取线段AC 的中点G ,连接EG ,根据等边三角形的性质以及角的计算即可得出CD=CG 以及∠FCD=∠ECG ,由旋转的性质可得出EC=FC ,由此即可利用全等三角形的判定定理SAS 证出△FCD ≌△ECG ,进而即可得出DF=GE ,再根据点G 为AC 的中点,即可得出EG 的最小值.【详解】取线段AC 的中点G ,连接EG,如图所示.8AC BC == ,60BCA ∠= ,ABC ∴为等边三角形,且AD 为ABC 的对称轴,142CD CG AB ∴===,60ACD ∠= ,60ECF ∠= ,FCD ECG ∴∠=∠.在FCD 和ECG 中,FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩,FCD ∴ ≌()ECG SAS ,DF GE ∴=.当//EG BC 时,EG 最小,点G 为AC 的中点,∴此时11224EG DF CD BC ====.故答案为2.【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出.DF GE =本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边是关键.13.如图,等边△AOB 的边长为4,点P 从点O 出发,沿OA 以每秒1个单位的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间是t 秒.将线段BP 的中点绕点P 按顺时针方向旋转60°得点C ,点C 随点P 的运动而运动,连接CP 、CA .在点P 从O 向A 运动的过程中,当△PCA 为直角三角形时t 的值为.【答案】2或83【详解】如图(1)过点P 作PD ⊥OB 于点D ,过C 作CE ⊥OA 于E ,∴∠PDO=∠PEC=90°,∵∠O=60°,∴∠OPD=30°,∴OD=12t ,∴BD=4-12t ,,∵线段BP 的中点绕点P 按顺时针方向旋转60°得点C ,∴∠BPC=60°,BP=2PC ,∵∠OPD=30°,∴∠BPD+∠CPE=90°,∴∠DBP=∠CPE ,∴△PCE ∽△BPD ,∴CE PE PC PD BD PB==,11242PE t ==-,∴,PE=2-14t ,OE=2+34t ,如图(2)当∠PCA=90度时,作CF ⊥PA ,∴△PCF ∽△ACF ,∴△PCF ∽△ACF ,∴PF CF CF AF =,∴CF 2=PF•AF ,∵PF=2-14t ,AF=4-OF=2-34t ,,)2=(2-14t )(=2-34t ),∴t=2,这时P 是OA 的中点;如图(3)当∠CAP=90°时,此时OA=OE ,∴2+34t=4,∴t=83,故答案为2或83.【点睛】本题考查了相似三角形的判定与性质,勾股定理的运用,等边三角形的性质,直角三角形的性质,旋转的性质等,正确地添加辅助线,求出OE 的长是解题的关键.二、解答题14.在平面直角坐标系中,A (a ,0)、B (b ,0),且a ,b 满足26930a a b -+++=,C 、D 两点分别是y 轴正半轴、x 轴负半轴上的两个动点;(1)如图1,若C (0,4),求△ABC 的面积;(2)如图1,若C (0,4),BC =5,BD=AE ,且∠CBA=∠CDE ,求D 点的坐标;(3)如图2,若∠CBA =60°,以CD 为边,在CD 的右侧作等边△CDE ,连接OE ,当OE 最短时,求A ,E 两点之间的距离.【答案】(1)△ABC 的面积为12;(2)D 点的坐标为(-2,0);(3)A ,E 两点之间的距离为32【分析】(1)利用完全平方式和绝对值的性质求出a ,b ,然后确定A 、B 两点坐标,从而利用三角形面积公式求解即可;(2)根据题意判断出CBD DAE △≌△,从而得到CB AD =,然后利用勾股定理求出CB ,及可求出结论;(3)首先根据“双等边”模型推出DCB ECA ≌,得到120DBC EAC ∠=∠=︒,进一步推出AE BC ∥,从而确定随着D 点的运动,点E 在过点A 且平行于BC 的直线PQ 上运动,再根据点到直线的最短距离为垂线段的长度,确定OE 最短时,各点的位置关系,最后根据含30°角的直角三角形的性质求解即可.【详解】解:(1)∵26930a a b -+++=,∴()2330a b -++=,由非负性可知,3030a b -=⎧⎨+=⎩,解得:33a b =⎧⎨=-⎩,∴()3,0A ,()3,0B -,()336AB =--=,∵()0,4C ,∴4OC =,∴11641222ABC S AB OC ==⨯⨯= ;(2)由(1)知()3,0A ,()3,0B -,∴OA OB =,∵OC AB ⊥,∴90AOC BOC ∠=∠=︒,在AOC 和BOC 中,OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴()AOC BOC SAS △≌△,∴CBO CAO ∠=∠,∵CDA CDE ADE BCD CBA ∠=∠+∠=∠+∠,CBA CDE ∠=∠,∴ADE BCD ∠=∠,在BCD △和ADE V 中,BCD ADE CBD DAE BD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BCD ADE AAS ≌,∴CB AD =,∵()3,0B -,()0,4C ,∴3OB =,4OC =,∴5BC ==,∴5AD BC ==,∵()3,0A ,∴()2,0D -;(3)由(2)可知CB =CA ,∵∠CBA =60°,∴△ABC 为等边三角形,∠BCA =60°,∠DBC =120°,∵△CDE 为等边三角形,∴CD =CE ,∠DCE =60°,∵∠DCE =∠DCB +∠BCE ,∠BCA =∠BCE +∠ECA ,∴∠DCB =∠ECA ,在△DCB 和△ECA 中,CD CE DCB ECA CB CA =⎧⎪∠=∠⎨⎪=⎩∴()DCB ECA SAS ≌,∴120DBC EAC ∠=∠=︒,∵12060180EAC ACB ∠+∠=︒+︒=︒,∴AE BC ∥,即:随着D 点的运动,点E 在过点A 且平行于BC 的直线PQ 上运动,∵要使得OE 最短,∴如图所示,当OE ⊥PQ 时,满足OE 最短,此时∠OEA =90°,∵120DBC EAC ∠=∠=︒,60CAB ∠=︒,∴60OAE EAC CAB ∠=∠-∠=︒,30AOE ∠=︒,∵()3,0A ,∴3OA =,∴1322AE OA ==,∴当OE 最短时,A ,E 两点之间的距离为32.【点睛】本题考查坐标与图形,全等三角形的判定与性质,等腰三角形和等边三角形的判定与性质等,理解平面直角坐标系中点坐标的特征,掌握等腰或等边三角形的性质,熟练使用全等三角形的判定与性质是解题关键.15.在▱ABCD中,∠ABC=60°,AB=4,BC=6.点E'在BC边上且BE'=4,将B E'绕点B逆时针旋转a°得到BE(0°<a<180°).(1)如图1,当∠EBA=90°时,求S△BCE;(2)如图2,在旋转过程中,连接CE,取CE中点F,作射线BF交直线AD于点G.①求线段BF的取值范围;②当∠EBF=120°时,求证:BC﹣DG=2BF;(3)如图3.当∠EBA=90°时,点S为线段BE上一动点,过点E作EM⊥射线AS于点M,N为AM中点,直接写出BN的最大值与最小值.=6;【答案】(1)S△BCE(2)①1<BF<5;②证明见解答;(3)BNBN的最大值为【分析】(1)如图1,过点E 作EF ⊥BC 交CB 的延长线于点F ,根据题意求得∠EBF =180°-∠EBA -∠ABC =180°-90°-60°=30°,再根据特殊直角三角形的性质进而求得BC 上的高EF =2,代入面积公式算出结果;(2)①如图,在线段FG 上截取FK =BF ,连接EK 、CK ,可证得四边形BCKE 是平行四边形,得出:BE =CK =BE '=4,BC =6,再运用三角形三边关系即可求得答案;②可证△EKB ≌△BGA (AAS ),得出BK =AG ,由AG =AD -DG ,即可推出结论;(3)连接AE ,取AE 的中点P ,PA 的中点Q ,连接BP 、NP 、NQ 、BQ ,可证△ABE 是等腰直角三角形,得出:AE AB P 是AE 的中点,可得:BP ⊥AE ,且BP =AP =EP ,利用勾股定理得BQ,当B 、Q 、N 三点共线时,BN 的最小值=BQ -NQ,当点S 与点E 重合时,EM =0,PN =0,此时,BN 的最大值=BP 【详解】(1)解:如图1,过点E 作EH ⊥BC 交CB 的延长线于点H ,∴∠EHC =90°,∵∠ABC =60°,∠EBA =90°,∴∠EBH =180°-∠EBA -∠ABC =180°-90°-60°=30°,∵点E '在BC 边上且BE '=4,将B E '绕点B 逆时针旋转α°得到BE ,∴BE =B E '=4,∴EH =12BE =12×4=2,又∵BC =6,∴S △BCE =12BC •EH =12×6×2=6;(2)解:①如图,在线段FG 上截取FK =BF ,连接EK 、CK ,∵EF=FC,BF=FK,∴四边形BCKE是平行四边形,∴BE=CK=BE'=4,BC=6,在△BCK中,BC-CK<BK<BC+CK,∴6-4<BK<6+4,即2<2BF<10,∴1<BF<5;②证明:∵四边形ABCD是平行四边形,且∠ABC=60°,AB=4,∴∠A=180°-∠ABC=180°-60°=120°,AD∥BC,AD=BC,BE=AB,∵∠EBF=120°,即∠EBK=120°,∴∠EBK=∠A,∵EK∥BC,∴EK∥AD,∴∠EKB=∠BGA,在△EKB和△BGA中,EKB BGAEBK ABE AB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EKB≌△BGA(AAS),∴BK=AG,由①知:BK=2BF,又∵AG=AD-DG,∴2BF =BC -DG ;(3)解:连接AE ,取AE 的中点P ,PA 的中点Q ,连接BP 、NP 、NQ 、BQ ,∵∠ABE =90°,AB =BE =4,∴△ABE 是等腰直角三角形,∴AE ,∵点P 是AE 的中点,∴BP ⊥AE ,且BP =AP =EP ,∵N 是AM 的中点,P 是AE 的中点,∴PN 是△AEM 的中位线,∴PN ∥EM ,∴∠ANP =∠AME =90°,∵点Q 是AP 的中点,∴QN =PQ =12AP在Rt △BPQ 中,BQ =当B 、Q 、N 三点共线时,BN 的最小值=BQ -NQ 当点S 与点E 重合时,EM =0,PN =0,此时,BN 的最大值=BP 【点睛】本题是几何变换综合题,主要考查了旋转的性质,平行四边形的性质,等腰直角三角形的性质,全等三角形的判定与性质,三角形中位线定理及勾股定理等知识,解题的关键是灵活运用所学知识解决问题.16.如图,线段AB =10cm ,C 是线段AB 上的一个动点(不与A 、B 重合),在AB 上方分别以AC 、BC 为边作正△ACD 和正△BCE ,连接AE ,交CD 于M ,连接BD ,交CE 于N ,AE 、BD 交于H ,连接CH .(1)求sin ∠AHC ;(2)连接DE ,设AD =x ,DE =y ,求y 与x 之间的函数关系式;(3)把正△BCE 绕C 顺时针旋转一个小于60°的角,在旋转过程中H 到△DCE 的三个顶点距离和最小,即HC +HD +HE 的值最小,HC +HD +HE 的值总等于线段BD 的长.若AC =,旋转过程中某一时刻2AH =3DH ,此刻△ADH 内有一点P ,求PA +PD +PH 的最小值.【答案】(1)2;(2)y0<x <10);【分析】(1)过点C 作CT ⊥AE 于点T ,CR ⊥BD 于点R ,先证△ACE ≌△DCB 得∠CAM =∠HDM ,由直角三角函数可得sin sin =CT CA CAM CD HDM CR ∠=∠= ,从而得CH 平分∠AHB ,进而求得∠AHC =∠BHC =60°即可求解;(2)如图2中,如图,过点D 作DP ⊥CE 于点P ,先由三角函数求得CP =12CD =12x ,DP =2x ,又由AB =10cm ,得CE =CB =(10﹣x )cm ,进而得PE =|10﹣x ﹣12x |=|10﹣32x |,最后由勾股定理即可求得y 与x 之间的函数关系式;(3)如图3中,以AD 为边向外作等边△ADW ,连接WH ,由题意WH 是PA +PD +PH .过点D 作DS ⊥AH 于H ,过点W 作WG ⊥AD 于点G ,过点H 作HK ⊥AD 于K ,过点W 作WQ ⊥HK 于点Q .假设AH =3k ,DH =2k ,由勾股定理得AH =6,DH =4,DSHKDKWQ =KGGW =KWHQWH 的长即PA +PD +PH 的最小值.【详解】(1)解:过点C 作CT ⊥AE 于点T ,CR ⊥BD 于点R.∵△ADC ,△ECB 都是等边三角形,∴CA =CD ,CE =CB ,∠ACD =∠ECB =60°,∴∠ACE =∠DCB ,在△ACE 和△DCB 中,CA CD ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△DCB (SAS ),∴∠CAM =∠HDM ,∵CT ⊥AE ,CR ⊥BD ,∴sin sin =CT CA CAM CD HDM CR ∠=∠= ,∴CH 平分∠AHB ,∵∠AMC =∠DMH ,∴∠AHM =∠ACM =60°,∴∠AHC =∠BHC =60°,∴sin ∠AHC =2;(2)解:如图2中,如图,过点D 作DP ⊥CE 于点P .∵AC =CD =x (cm ),∠DCE =60°,∴CP =12CD =12x ,DP ,∵AB =10cm ,∴BC =AB ﹣AC =(10﹣x )cm ,∴CE =CB =(10﹣x )cm ,∴PE =|10﹣x ﹣12x |=|10﹣32x |,∴y =DE (0<x <10);(3)解:如图3中,以AD 为边向外作等边△ADW ,连接WH ,由题意WH 是PA +PD +PH .过点D 作DS ⊥AH 于H ,过点W 作WG ⊥AD 于点G ,过点H 作HK ⊥AD 于K ,过点W 作WQ ⊥HK 于点Q .∵2AH =3DH ,∴可以假设AH =3k ,DH =2k ,∵∠DHS =60°,DS ⊥AH ,∴SH =12DH =k ,DS ,AM =2k ,∵AD 2=AS 2+DS 2,∴()2=(2k )2+)2,∴k =2(负根已经舍弃),∴AH =6,DH =4,DS∵12•AH •DS =12•AD •HK ,∴HK =7,DK 7,∵AG =DG WQKG 是矩形,∴WQ =KG GW =KW∴HQ =KH +KQ =7,∴WH =∴PA +PD +PH 的最小值为【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,解直角三角形等知识,添加常用辅助线,构造直角三角形解决问题是解本题的关键.17.在学习了图形的旋转知识后,某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究.(1)问题梳理,问题呈现:如图1,点D 在等边ABC 的边BC 上,过点C 画AB 的平行线l ,在l 上取CE BD =,连接AE ,则在图1中会产生一对旋转图形.请结合问题中的条件,证明:ABD ACE ≌△△;(2)初步尝试:如图2,在ABC 中,AB AC =,点D 在BC 边上,且BD DC <,将ABD △沿某条直线翻折,使得AB 与AC 重合,点D 与BC 边上点F 重合,再将ACF △沿AC 所在直线翻折,得到ACE △,则在图2中会产生一对旋转图形.若30BAC ∠=︒,6AD =,连接DE ,求ADE V 的面积;(3)深入探究:如图3,在ABC 中,60ACB ∠=︒,75BAC ∠=︒,6AC =,点D 是边BC 上的任意一点,连接AD ,将线段AD 绕点A 按逆时针方向旋转75°,得到线段AE ,连接CE ,求线段CE 长度的最小值.【答案】(1)见解析;(2)9;(3)【分析】(1)根据△ABC 是等边三角形,可得AB =AC ,∠BAC =∠B =60°,进而利用SAS 可证明△ABD ≌△ACE .(2)如图2,过点E 作EH ⊥AD 于H ,由翻折可得△ACE ≌△ABD ≌△ACF ,可得AE =AD =6,EH =3,再运用S △ADE =12×AD ×EH ,即可求得答案.(3)如图3中,在AB 上截取AN =AC ,连接DN ,作NH ⊥BC 于H ,作AM ⊥BC 于M .利用SAS 证明△EAC ≌△DAN ,推出当DN 的值最小时,EC 的值最小,求出HN 的值即可解决问题.【详解】(1)如图1,∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠B =60°,∵CE ∥AB ,∴∠ACE =∠BAC =60°,∴∠B =∠ACE ,在△ABD 和△ACE 中,AB AC B ACE BD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS );(2)如图2,过点E 作EH ⊥AD 于H,∵由翻折可得:△ACF ≌△ABD ,△ACE ≌△ACF ,∴△ACE ≌△ABD ≌△ACF ,∴AE =AD =6,∠CAE =∠BAD ,∴∠DAE =∠BAC =30°,∵EH ⊥AD ,∴EH =12AE =3,∴S △ADE =12×AD ×EH =12×6×3=9;(3)如图3中,在AB 上截取AN =AC ,连接DN ,作NH ⊥BC 于H ,作AM ⊥BC 于M.∵∠CAB =∠DAE ,∴∠EAC =∠DAN ,∵AE =AD ,AC =AN ,∴△EAC ≌△DAN (SAS ),∴CE =DN ,∴当DN 的值最小时,EC 的值最小,在Rt △ACM 中,∵∠ACM =60°,AC =6,∴30CAM ∠=︒,∴132CM AC ==,∴AM∵∠MAB =∠BAC −∠CAM =75°−30°=45°,∴AMB 为等腰直角三角形,∴AB=,∴NB =AB −AN =−6,在Rt △NHB 中,∵∠B =45°,∴NBH △为等腰直角三角形,∴NH根据垂线段最短可知,当点D 与H 重合时,DN 的值最小,∴CE 的最小值为.【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.18.(一)发现探究在△ABC中AB=AC,点P在平面内,连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度,得到线段AQ,连接BQ;【发现】如图1如果点P是BC边上任意一点,则线段BQ和线段PC的数量关系是;【探究】如图2,如果点P为平面内任意一点.前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.请仅以图2所示的位置关系加以证明(或说明);(二)拓展应用【应用】如图3,在△DEF中,DE=6,∠EDF=60°,∠DEF=90°,P是线段EF上的任意一点连接DP,将线段DP绕点D顺时针方向旋转60°,得到线段DQ,连接EQ请求出线段EQ长度的最小值.【答案】【发现】BQ=PC;【探究】BQ=PC仍然成立,证明见解析;【应用】线段EQ长度的最小值为3.【分析】[发现]先判断出∠BAQ=∠CAP,进而用SAS判断出△BAQ≌△CAP,即可得出结论;[探究]结论BQ=PC仍然成立,理由同【发现】的方法;[应用]在DF上取一点H,使DH=DE,连接PH,过点H作HM⊥EF于M,构造出△DEQ≌△DHP,得出EQ=HP,当HP⊥EF(点P和点M重合)时,EQ最小,求HM即可.【详解】[发现]由旋转知,AQ=AP,∵∠PAQ=∠BAC,∴∠PAQ﹣∠BAP=∠BAC﹣∠BAP,∴∠BAQ=∠CAP,∵AB=AC,∴△BAQ≌△CAP(SAS),∴BQ=CP,故答案为:BQ=PC;【探究】结论:BQ=PC仍然成立,理由:由旋转知,AQ=AP,∵∠PAQ=∠BAC,∴∠PAQ﹣∠BAP=∠BAC﹣∠BAP,∴∠BAQ=∠CAP,∵AB=AC,∴△BAQ≌△CAP(SAS),∴BQ=CP,【应用】如图3,在DF上取一点H,使DH=DE,连接PH,过点H作HM⊥EF于M,由旋转知,DQ=DP,∠PDQ=60°,∵∠EDF=60°,∴∠PDQ=∠EDF,∴∠EDQ=∠HDP,∴△DEQ≌△DHP(SAS),∴EQ=HP,求EQ最小,就是求HP最小,当HP⊥EF(点P和点M重合)时,HP最小,最小值为HM,∵∠EDF=60°,∠DEF=90°,∴∠F=30°,∵DE=6,∴DF=2DE=12,∵DH=DE=6,∴FH=6,∵∠F=30°,∴HM=3.线段EQ长度的最小值为3..【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,含30°角的直角三角形的性质,恰当的作辅助线,把所求线段转化为与动点P有关的线段,根据垂线段最短确定线段位置是解本题的关键.。
初中数学几何动点训练题--三角形类(含答案)

几何动点训练题2一、单选题(共6题;共12分)1.(2020·芜湖模拟)如图,在等边△ABC中,AB=12,点D在AB边上,AD=4,E为AC中点,P为△ABC 内一点,且∠BPD=90°,则线段PE的最小值为()A. 3 ﹣2B.C. 2 ﹣4D. 4 ﹣82.(2020·秦安模拟)如图,边长为2的等边△ABC和边长为1的等边△A'B'C',它们的边B'C',BC位于同一条直线L上,开始时,点C'与B重合,△ABC固定不动,然后把△A'B'C'自左向右沿直线L平移,移出△ABC 外(点B'与C重合)停止,设△A'B'C'平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是()A. B. C. D.3.(2020八下·临汾月考)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的值不可能为( )A. 5B. 8C.D.4.(2019八下·滦南期末)如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边BC 上一动点,PE⊥AB 于E,PF⊥AC于F,M 为EF 中点,则AM 的最小值为()A. 1B. 1.3C. 1.2D. 1.55.(2019九下·桐乡月考)如图,正三角形纸片ABC中,D是BC的中点,P是AB边上的一个动点,将△BPD 沿PD翻折。
得到△QPD.当点P从点A向点B运动时,点Q也随之运动.若AB=6,则点Q经过的路径长是( )A. 3B. 6C. 3πD. 6π6.(2018九上·康巴什期中)如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为()A. S=t(0<t≤3)B. S= t2(0<t≤3)C. S=t2(0<t≤3)D. S= t2-1(0<t≤3)二、填空题(共4题;共4分)7.(2020·芜湖模拟)如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P是线段AD上一动点,当半径为5的⊙P与△ABC 的一边相切时,AP的长为________.8.(2020八下·锡山期中)E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD 并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为________.9.(2019七下·苏州期末)如图,中,.点从点出发沿路径向终点运动;点从点出发沿路径向终点运动.点和分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过和作于,于.则点运动时间等于________时,与全等。
正方形的动点问题 含答案

专题1.21正方形的动点问题(专项练习)一、单选题1.如图,在正方形ABCD 中,2,AB P =是AD 边上的动点,PE AC ⊥于点,E PF BD ⊥于点F ,则PE PF +的值为()A .4B .CD .22.如图,在边长为8的正方形ABCD 中,E 、F 分别是边AB 、BC 上的动点,且6EF =,M 为EF 中点,P 是边AD 上的一个动点,则CP PM +的最小值是()A .10B .3-C .3D .5+3.如图,动点M 在边长为2的正方形ABCD 内,且AM BM ⊥,P 是CD 边上的一个动点,E 是AD 边的中点,则线段PE PM +的最小值为()A 1-B 1+CD 1+二、填空题4.如图,已知2AB =,点D 是等腰Rt ABC ∆斜边AC 上的一动点,以BD 为一边向右下方作正方形BDEF ,当动点D 由点A 运动到点C 时,则动点F 运动的路径长为______.5.如图,正方形ABCD 的边长为4,点E 是AB 的中点,点P 是边BC 上的动点,点Q 是对角线AC 上的动点(包括端点A 、C ),则EP +PQ 的最小值是_________.6.如图,已知正方形ABCD 的边长是1,点E 是CD 边上的中点.P 为正方形ABCD 边上的一个动点,动点P 从A 点出发,沿A B C E →→→运动,到达点E .若点P 经过的路程为自变量x ,APE ∆的面积为因变量y ,则当15y =时,x 的值等于_________.7.已知正方形ABCD 的边长是1,E 为CD 边的中点,P 为正方形ABCD 边上的一个动点,动点P 从A 点出发,沿A B C D →→→运动,到达点E.若点P 经过的路程为自变量x ,△APE 的面积为函数y ,则当y =13时,x 的值等于_____________.8.如图,正方形ABCD 中,3AB =,点E 为对角线AC 上的动点,以DE 为边作正方形DEFG .点H 是CD 上一点,且23DH CD =,连接GH ,CG ,则DCG ∠=________度,运动变化过程中,GH 的最小值为________.9.如图,在正方形ABCD 中,AB =,点P 为边AB 上一个动点(不与A ,B 重合),过点A ,P 在正方形内部作正方形APEF ,交边AD 于F 点,连接DE ,EC ,当CDE △为等腰三角形时,AP =__________.10.如图,正方形ABCD 的边长为4,点E 是AB 边上一个动点,点F 是CD 边上一个动点,且AE =CF ,过点B 作BG ⊥EF 于点G ,连接AG ,则AG 长的最小值是_____.11.如图,正方形ABCD 的对角线AC 上有一动点P ,作PN CD ⊥于点N ,连接BP ,BN.若3AB =,BP =,则BN 的长为_________.12.如图,正方形ABCD 的边长是9,点E 是AB 边上的一个动点,点F 是CD 边上一点,4CF =,连接EF ,把正方形ABCD 沿EF 折叠,使点A ,D 分别落在点A ',D ¢处,当点D ¢落在线段BC 上时,线段AE 的长为__________.三、解答题13.(1)如图1,在正方形ABCD 中,点E 、F 分别是BC 、CD 边上的动点,且45EAF ∠=︒,求证:EF DF BE =+.(2)如图2,在正方形ABCD 中,如果点E 、F 分别是CB 、DC 延长线上的动点,且45EAF ∠=︒,则EF 、BE 、DF 之间数量关系是什么?请写出证明过程.(3)如图1,若正方形ABCD 的边长为6,35AE =AF 的长.14.如图,已知正方形ABCD 的边长是1,E 为CD 的中点,P 为正方形边上的一个动点,动点P 从A 出发沿A B C E ⇒⇒⇒运动,最终到达点E ,若点P 经过的路程AP x =,APE 的面积记为y ,问当x 等于何值时,y 的值等于13?15.如图,正方形ABCD 中,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边向正方形ABCD外作正方形GCEF ,连接DE ,连接BG 并延长交DE 于H .()1求证:BGC DEC ∠=∠.()2若正方形ABCD 的边长为1,试问当点G 运动到什么位置时,BH 垂直平分DE ?16.如图,已知ABC 中,90BAC ∠=︒,AB AC ==,点D 为边BC 上一动点,四边形ADEG 是正方形,连接GC ,正方形对角线AE 交BC 于点F .(1)求证:ABD ACG △≌△;(2)若4BD =,求AE 的值;(3)若5DF =,求BD 的值.17.已知:正方形ABCD 的对角线交于点O ,E 是线段OC 上的一动点,过点A 作AG BE ⊥交G ,交BD 于F .(1)若动点E 在线段OC 上(不含端点),如图(1),求证:OF OE =;(2)若动点E 在线段OC 的延长线上,如图(2),试判断OEF 的形状,并说明理由.18.(1)如图1,在正方形ABCD 中,点E 、F 分别是BC 、CD 边上的动点,且∠EAF =45°,求证:EF =DF+BE .(2)如图2,在正方形ABCD 中,如果点E 、F 分别是CB 、DC 延长线上的动点,且∠EAF =45°,则EF 、BE 、DF 之间数量关系是什么?请写出证明过程.(3)如图1,若正方形ABCD 的边长为6,AE =AF 的长.19.如图所示,E ,F 分别是正方形ABCD 的边AD ,CD 上的两个动点,且AE DF =,BE 交AF 于点H ,2AB =,连DH .求证:AF BE ⊥.20.已知,如图所示,正方形ABCD 的边长为1,G 为CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边向正方形ABCD 外作正方形GCEF ,连接DE 交BG 的延长线于点H .(1)求证:①BCG ∆≌△DCE .②BH DE ⊥.(2)当BH 平分DE 时,求GC 的长.21.在ABC ∆中,90ACB ∠=︒,分别以AB ,BC 为边向外作正方形ADEB 和正方形BCFH .(1)当BC m =时,正方形BCFH 的周长=_______(用含m 的代数式表示);(2)连接CE .试说明:三角形BEC 的面积等于正方形BCFH 面积的一半.(3)已知2AC BC ==,且点P 是线段DE 上的动点,点Q 是线段BC 上的动点,当P 点和Q 点在移动过程中,APQ ∆的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.22.如图,,M N 是正方形ABCD 的边CD 上的两个动点,满足,,CM DN AC BM =相交于点,E DE 与AN 相交于点F ,连接CF .(1)求证:DE AN ⊥;(2)若正方形ABCD 的边长为4,求CF 的最小值.23.已知正方形ABCD 的对角线AC 与BD 交于点O ,点E 、F 分别是OB 、OC 上的动点,(1)如果动点E 、F 满足BE=CF (如图):①写出所有以点E 或F 为顶点的全等三角形(不得添加辅助线);②证明:AE ⊥BF ;(2)如果动点E 、F 满足BE=OF (如图),问当AE ⊥BF 时,点E 在什么位置,并证明你的结论.24.在正方形ABCD中,点E是边CD的中点,点M是对角线AC上的动点,连接ME,⊥交正方形的边于点F;过点M作MF ME(1)当点F在边BC上时,①判断ME与MF的数量关系;∠=∠时,判断点M的位置;②当AEM DFM(2)若正方形的边长为2,请直接写出点F在BC边上时,AM的取值范围.参考答案1.C【分析】根据正方形的对角线互相垂直可得OA ⊥OD ,对角线平分一组对角可得∠OAD=45°,然后求出四边形OEPF 为矩形,△AEP 是等腰直角三角形,再根据矩形的对边相等可得PF=OE ,根据等腰直角三角形的性质可得PE=AE ,从而得到PE+PF=OA ,然后根据正方形的性质解答即可.解:在正方形ABCD 中,OA ⊥OB ,∠OAD=45°,∵PE ⊥AC ,PF ⊥BD ,∴四边形OEPF 为矩形,△AEP 是等腰直角三角形,∴PF=OE ,PE=AE ,∴PE+PF=AE+OE=OA ,∵正方形ABCD 的边长为2,∴11.22===OA AC 故选:C【点拨】本题考查了正方形的性质,矩形的判定与性质,等腰直角三角形的判定与性质,熟记各性质求出PE+PF=OA 是解题的关键.2.B【分析】延长CD 到C′,使C′D =CD ,CP +PM =C′P +PM ,当C′,P ,N 三点共线时,C′P +PM 的值最小,根据题意,点M 的轨迹是以B 为圆心,3为半径的圆弧上,圆外一点C′到圆上一点M 距离的最小值C′M =C′B−3,根据勾股定理即可得到结论.【详解】延长CD 到C′,使C′D =CD ,CP +PM =C′P +PM ,当C′,P ,M 三点共线时,C′P +PM 的值最小,根据题意,点M 的轨迹是以B 为圆心,3为半径的圆弧上,圆外一点C′到圆上一点M 距离的最小值C′M =C′B−3,∵BC =CD =8,∴CC′=16,∴C′B ==∴CP+PM的最小值是−3,故选B.【点拨】本题考查了轴对称−最短路线问题,正方形的性质,勾股定理,正确的找到P点的位置是解题的关键.3.A【分析】作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,由轴对称的性质及90°的圆周角所对的弦是直径,可知线段PE+PM的最小值为OE'的值减去以AB为直径的圆的半径OM,根据正方形的性质及勾股定理计算即可.解答:解:作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,如图:∵动点M在边长为2的正方形ABCD内,且AM⊥BM,∴点M在以AB为直径的圆上,OM=12AB=1,∵正方形ABCD的边长为2,∴AD=AB=2,∠DAB=90°,∵E是AD的中点,∴DE =12AD =12×2=1,∵点E 与点E '关于DC 对称,∴DE '=DE =1,PE =PE ',∴AE '=AD +DE '=2+1=3,在Rt △AOE '中,OE ',∴线段PE +PM 的最小值为:PE +PM=PE '+PM=ME '=OE '−OM−1.故选:A .【点拨】本题考查了轴对称−最短路线问题、圆周角定理的推论、正方形的性质及勾股定理等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.4.【分析】连接CF ,根据题意先证出BAD BCF ∆≅∆,然后得出AD CF =,所以点F 运动的路径长度即为点D 从A 到C 的运动路径,继而得出结论【详解】连接CF ,∵2AB =,ABC ∆是等腰直角三角形,∴AC =∠ABC=90°∵四边形BDEF 是正方形∴BD=BF ,∠DBF=∠ABC=90°,∴∠ABD=∠CBF,在△DAP 与△BAP 中AB BC ABD CBF BD BF =⎧⎪∠=∠⎨⎪=⎩∴BAD BCF∆≅∆,∴AD CF=,点F运动的路径长度即为点D从A到C的运动路径,为22CF=.故答案为22【点拨】本题主要考查的是等腰直角三角形的性质、等边三角形的性质、正方形的性质以及全等三角形的性质和判定,熟练掌握全等三角形的判定和性质是解题的关键.5.32【解析】试题解析:如图作点E关于BC的对称点E′,作E′Q′⊥AC于Q′交BC于P.∴PE=PE′,∴PQ+PE=PE′+PQ,当Q用Q′重合时,PE+PQ最小(垂线段最短),∵四边形ABCD是正方形,∴∠E′AQ′=45°,∵AE′=6,∴2∴PE+PQ的最小值为2.6.25或115或2110【解析】【分析】经过分析,点P 只有在AB 边,或者BC 边上,或DC 边上时,才有y=15.根据P 点的位置,由三角形面积公式表达出分段函数,在分段函数中,已知y 的值,求x .【详解】经过分析,点P 只有在AB 边,或者BC 边上,或DC 边上时,才有y=15,当点P 在AB 边上时,y=12•x•1=15,解得x=25,当点P 在BC 边上时,如图所示,y=12•(1+12)•1-12•(x-1)•1-12•12•(2-x )=15,解得x=115;当点P 在DC 边上时,y=12×(1+1+12-x )×1=15,解得:x=2110,综上所述,当y=15时,x 的值等于25或115或2110,故答案为:25或115或2110【点拨】此题考查了由动点的运动变化来列函数关系式,应注意自变量的变化范围分段来列.7.23或53【分析】根据P 点的运动轨迹,分析出当P 在AB 或BC 上均有可能,再根据APE ∆的面积为13分类讨论计算即可.【详解】(1)当P 在AB 上时,如图:11123y x ==∴23x =(2)当P 在BC 上时,如图:()()11111111112222223ABP EDC y S S S x x ∆∆⎛⎫=--=+--⋅--= ⎪⎝⎭ 梯ABCE ∴53x =故答案为:23或53【点拨】本题考查动点问题与三角形面积求算,不规则图形面积求算通常采用割补法,同时注意分类讨论.8.45°2【分析】连接CG .证明△ADE ≌△CDG (SAS ),推出∠DCG=∠DAE=45°,推出点G 的运动轨迹是射线CG ,根据垂线段最短可知,当GH ⊥CG 时,GH 的值最小.解:连接CG .∵四边形ABCD 是正方形,四边形DEFG 是正方形,∴DA=DC ,DE=DG ,∠ADC=∠EDG=90°,∠DAC=45°,∴∠ADE=∠CDG ,∴△ADE ≌△CDG (SAS ),∴∠DCG=∠DAE=45°,∴点G 的运动轨迹是射线CG ,根据垂线段最短可知,当GH ⊥CG 时,GH 的值最小,∵DH=23CD=2,∴CH=CD-DH=3-2=1,∴最小值=CH•sin45°=1×2222=.故答案为:45°;2.【点拨】此题考查正方形的性质,全等三角形的判定和性质,最短路径问题,关键是根据正方形的性质和三角形中位线定理解答.91或2【分析】分三种情形进行讨论:①当CE CD =时;②当CE DE =时;③当CD DE =时,E 与A 重合,不符合题意.然后根据等腰三角形的性质和勾股定理求出AE 即可解决问题.解:如图所示,连接AE∵四边形ABCD 和四边形APEF 都是正方形,且P 在AB 上,F 在AD 上∴∠CAB =∠EAB =∠DCE =45°,AB =BC ,AP =PE∴A ,E ,C 三点共线①当CE CD ==2AC ==,2AE AC CE =-=,2AE ==-1AP ==;②当CE DE =时,∵CE DE=∴∠CDE =∠DCE =45°∴∠DEC=90°∴CD ==∴1CE DE ==∵2AC ==∴1AE AC EC =-=,1AE ==∴22AP =;③当CD DE =时,E 与A 重合,不符合题意.综上所述,当CDE △为等腰三角形时,1AP =或2.1-或22.【点拨】本题考查正方形的性质,等腰三角形的定义,二次根式的运算,解题的关键是灵活运用相关知识点进行解题.10【分析】设正方形的中心为O ,可证EF 经过O 点.连结OB ,取OB 中点M ,连结MA ,MG ,则MA ,MG 为定长,利用两点之间线段最短解决问题即可.解:设正方形的中心为O ,可证EF 经过O 点.连结OB ,取OB 中点M ,连结MA ,MG ,则MA ,MG 为定长,过点M 作MH ⊥AB 于H .则MH=BH=1,AH=3,由勾股定理可得,MG=12,∵,当A,M,G三点共线时,AG最小.【点拨】本题主要考查了正方形的性质,解直角三角形,直角三角形斜边中线的性质等知识,解题的关键是求出AM,MG的值.11【分析】延长NP交AB于H.易知AH=PH,设AH=PH=x,则BH=3-x,在Rt△PBH中,根据PB2=PH2+BH2,可得x2+(3-x)2=2,推出x=1或2,接下来分两种情形分别求出BN即可.解:延长NP交AB于H.∵四边形ABCD是正方形,∴∠BAC=45°,AB∥CD,∵PN⊥CD,∴PN⊥AB,∴∠HAP=∠HPA=45°,∴AH=PH,设AH=PH=x,则BH=3-x,在Rt△PBH中,∵PB2=PH2+BH2,∴x2+(3-x)2=)2,∴x=1或2,当x=1时,BH=CN=2,在Rt△BCN中,==,当x=2时,BH=CN=1,在Rt△BCN中,==.综上所述,BN或.或.【点拨】本题考查了正方形的性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.12.2【分析】当D'落在线段BC上时,连接ED、ED'、DD',由折叠性质可知D'和D关于EF对称,即EF垂直平分DD',得出D E=D'E.求出DF=D'F=CD-CF=5,3CD'==.得出BD'=BC-CD'=6,设AE=x,则BE=9-x,在Rt△AED和Rt△BED'中,由勾股定理列方程解答即可.【详解】解:当D落在线段BC上时,如图1:连接ED、E D'.、DD'由折叠性质可知,D'和D关于EF对称,即EF垂直平分DD'.∴DE=D'E,∵正方形ABCD的边长是9,∴AB=BC=CD=AD=9.∵CF=4,∴DF=D'F=CD-CF=9-4=5CD'==∴3∴BD'=BC-CD'=6设AE=x,则BE=9-x,在Rt△AED和Rt△BED'中.由勾股定理得:2222222222DE AD AE x D E BE BD x9,(9)6''=+=+=+=-+92+x2=(9-x)2+62,解得:x=2,即AE=2.【点拨】本题主要考查了正方形的性质、折叠变换的性质、线段垂直平分线的性质、勾股定理等知识;掌握折叠变换的性质和利用勾股定理列方程是解答本题的关键.13.(1)见解析;(2)EF DF BE =-;证明见解析;(3)AF =.【分析】(1)把 ABE 绕点A 顺时针旋转90°至 ADG ,由“SAS”可证 EAF ≌ GAF ,可得出EF =FG ,则结论得证;(2)将 ABE 绕点A 顺时针旋转90°至△ADM ,根据SAS 可证明 EAF ≌ MAF ,可得EF =FM ,则结论得证;(3)由全等三角形的性质可得AE =AG =EF =FG ,BE =DG ,由勾股定理可求DG 的长,FD 的长,AF 的长.(1)证明:把ABE △绕点A 顺时针旋转90°至ADG ,如图1,∴BAE DAG ∠=∠,AE AG =,∵45EAF ∠=︒,∴45BAE FAD ∠+∠=︒,∴45DAG FAD ∠+∠=︒,∴EAF FAG ∠=∠,∵AF AF =,∴()△△≌EAF GAF SAS ,∴EF FG DF DG ==+,∴EF DF BE =+;(2)结论:EF DF BE =-;证明:如图2,将ABE △绕点A 顺时针旋转90°至ADM ,∴EAB MAD ∠=∠,AE AM =,90EAM =︒∠,BE DM =,∴45FAM EAF ∠=︒=∠,∵AF AF =,∴()△△≌EAF MAF SAS ,∴EF FM DF DM DF BE ==-=-;(3)解:由(1)可知AE AG ==∵正方形ABCD 的边长为6,∴6DC BC AD ===,∴3DG ==.∴3BE DG ==,∴633CE BC BE =-=-=,设DF x =,则3EF DG x ==+,6CF x =-,在Rt EFC △中,∵222+=CF CE EF ,∴222(6)3(3)x x -+=+,解得:2x =.∴2DF =,∴AF ===.【点拨】本题属于四边形综合题,主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行推导.14.当23x =或53x =时,APE 的面积为13【分析】利用面积公式求解即可.解:由题意可知:当动点P 从A 运动到B 时,111122ABE S =⨯⨯= ,当动点P 从B 运动到C 时,1111224ACE S =⨯⨯= ,由于111432<<,因此满足题意的点P 的位置只有两种情况①当01x <<时,即点P 在AB 边上运动时,如图a ,此时AP x =,11122APE S y x x ==⨯⨯= ,当13y =时,解得:()263x =②当12x <<时,即点P 在BC 边上运动,如图b ,此时折线1BP x =-,2PC x =-,()()1111311112222444APE ABP PEC ADE ABCD S y S S S S x x x ==---=--⨯--⨯-=- 正方形当13y =时,解得:53x =综上所述,当23x =或53x =时,APE 的面积为13【点拨】找出临界点是解题的关键.15.(1)证明见解析(2)当21CG =时,BH 垂直平分DE【分析】(1)根据正方形的边的性质和直角可通过SAS 判定△BCG ≌△DCE ,从而利用全等的性质得到∠BGC=∠DEC ;(2)连接BD ,解题关键是利用垂直平分线的性质得出BD=BE ,从而找到2,2-1,根据全等三角形的性质求解即可.解:()1证明:∵四边形ABCD 、GCEF 都是正方形,∴BC DC =,90BCG DCE ∠=∠= ,GC EC=∴BCG DCE ≅∴()2BGC DEC ∠=∠连接BD如果BH 垂直平分DE ,则有BD BE=∵1BC CD ==,∴2BD =∴21CE BE BC =-=-∴21CG CE ==即当21CG =-时,BH 垂直平分DE .【点拨】本题考查了全等三角形与线段垂直平分线的性质,解题的关键是熟练的掌握全等三角形的判定与性质以及线段垂直平分线的性质.16.(1)见详解;(2)45(3)3或4【分析】(1)根据同角的余角相等,证明BAD CAG ∠=∠,然后根据正方形的性质,得出边相等,由三角形全等的判定条件SAS 即可证明(2)由(1)中全等的性质以及勾股定理求出DG 的长,根据正方形的性质:对角线相等即可求解(3)根据SAS 证明DAF GAF △≌△,然后根据全等的性质,在直角△GFC 根据勾股定理即可求解(1)证明: 四边形ADEG 是正方形AD AG ∴=,90DAG =︒∠90BAC ∠=︒BAC DAG∴∠=∠BAD DAC DAC CAG∴∠+∠=∠+∠BAD CAG∴∠=∠在ABD △和ACG 中AB AC BAD CAG AD AG =⎧⎪∠=∠⎨⎪=⎩ABD ACG∴△△≌故答案为ABD ACG△≌△(2)90BAC ∠=︒ ,62AB AC ==,45B ACB ∴∠=∠=︒在Rt ABC △中22BC AB AC ∴=+=22(62)(62)12+=4BD = 1248DC BC BD ∴=-=-=由(1)知ABD ACG △≌△,4GC BD ∴==,45ACG B ∠=∠=︒454590ACB ACG ∴∠+∠=︒+︒=︒连接DG在Rt DCG △中22228445DG DC CG =+=+= 四边形ADEG 是正方形AE DG∴=45AE ∴=故答案为5(3)如图所示,连接FG四边形ADEG 是正方形AD DE ∴=,90ADE ∠=︒45DAE AED ∴∠=∠=︒90BAC ∠=︒BAD FAC BAC ∴∠+∠=∠-904545DAE ∠=︒-︒=︒由(1)知ABD ACG △≌△,BAD CAG ∴∠=∠,AD AG =,BD GC=45CAG FAC BAD FAC ∴∠+∠=∠+∠=︒45FAG ∴∠=︒FAG FAD∴∠=∠在DAF △和GAF 中AF AF FAG FAD AG AD =⎧⎪∠=∠⎨⎪=⎩(SAS)DAF GAF ∴△≌△GF DF∴=5DF = 5GF ∴=设BD x =,则1257FC x x=--=-由(2)知90FCG ∠=︒在Rt FCG △中222GC FC FG +=222(7)5x x ∴+-=13x ∴=,24x =BD ∴的值为3或4.故答案为3或4【点拨】本题主要考察三角形全等的判定和性质,正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键17.(1)见解析(2)△OEF 为等腰直角三角形,理由见解析【分析】(1)利用正方形的性质得OA =OB ,∠AOB =∠BOC =90°,则利用等角的余角相等得到∠GAE =∠OBE ,则可根据“ASA ”判断 AOF ≌ BOE ,从而得到OF =OE ;(2)同样方法证明△AOF ≌△BOE ,仍然得到OF =OE ,再结合90BOC ∠=°即可判定OEF 是等腰直角三角形.【详解】(1)证明:∵四边形ABCD 为正方形,∴OA OB =,AOB BOC∠=∠90=︒,∴∠OBE +∠OEG =90°,∵AG BE ⊥于点G ,∴90AGE ∠=︒,∴∠OAF +∠OEG =90°,∴GAE OBE ∠=∠,在AOF 和BOE △中,AOF BOE AO BO OAF OBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AOF BOE ASA △△≌,∴OF OE =;(2)解:OEF 是等腰直角三角形,理由如下:∵四边形ABCD 为正方形,∴OA OB =,AOB BOC∠=∠90=︒,∴∠OBE +∠OEG =90°,∵AG BE ⊥于点G ,∴90AGE ∠=︒,∴∠OAF +∠OEG =90°,∴GAE OBE ∠=∠,在AOF 和BOE △中,AOF BOE AO BO OAF OBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AOF BOE ASA △△≌∴OF OE =;又∵90BOC ∠=°,∴OEF 是等腰直角三角形.【点拨】此题考查了正方形的性质、全等三角形的判定与性质以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意证得AOF BOE ≌△△是解此题的关键.18.(1)见解析;(2)EF =DF ﹣BE ,见解析;(3)【分析】(1)把△ABE 绕点A 顺时针旋转90°至△ADG ,由“SAS”可证△EAF ≌△GAF ,可得出EF =FG ,则结论得证;(2)将△ABE 绕点A 顺时针旋转90°至△ADM ,根据SAS 可证明△EAF ≌△MAF ,可得EF =FM ,则结论得证;(3)由全等三角形的性质可得AE =AG=,EF =FG ,BE =DG ,由勾股定理可求DG 的长,FD 的长,AF 的长.【详解】(1)把△ABE 绕点A 顺时针旋转90°至△ADG ,如图1,∴∠BAE=∠DAG,AE=AG,∵∠EAF=45°,∴∠BAE+∠FAD=45°,∴∠DAG+∠FAD=45°,∴∠EAF=∠FAG,∵AF=AF,∴△EAF≌△GAF(SAS),∴EF=FG=DF+DG,∴EF=DF+BE;(2)结论:EF=DF﹣BE;证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,∴∠FAM=45°=∠EAF,∵AF=AF,∴△EAF≌△MAF(SAS),∴EF=FM=DF﹣DM=DF﹣BE;(3)如图,由(1)可得AE=AG=,EF=FG,BE=DG,=,∵DG3∴BE=DG=3,∴EC=BC﹣BE=3,∵EF2=EC2+CF2,∴(DF+3)2=9+(6﹣DF)2,∴DF=2,∴AF==.【点拨】本题考查了全等三角形的判定和性质,勾股定理,旋转等知识,此题为半角模型,∠EAF是∠BAD的一半,故命名半角模型,半角模型必旋转,再证全等即可.19.见解析【分析】根据正方形性质可得AB=DA,∠BAD=∠ADF=90°,又根据AE=DF,利用SAS可证得△ABE≌△DAF,于是∠ABE=∠DAF;由于∠DAF+∠BAH=∠ABE+∠BAH=90°,从而∠AHB=90°,于是证得结论证明:∵四边形ABCD是正方形,∴AB=DA,∠BAD=∠ADF=90°,又∵AE=DF,∴△ABE≌△DAF,∴∠ABE=∠DAF.∴∠DAF+∠BAH=∠ABE+∠BAH=90°,∴∠AHB=90°,∴AF⊥BE.【点拨】本题考查了正方形的性质、全等三角形的判定与性质.掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.20.(1)①见详解;②见详解;(2)1-【分析】①根据正方形确定BC=DC,CE=CG及∠BCD=∠ECG=900,即可证明全等;②根据(1)的全等得出∠BGC=∠DEC,再根据∠BGC+∠CBG=900,即可证得⊥BH DE(2)根据勾股定理求出线段BD的长,然后利用三角形全等证出BE=BD,再由BE-BC求出CE即CG的长.【详解】(1)①∵四边形ABCD与四边形GCEF均为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=900,∆≌△DCE∴BCG∆≌△DCE,②∵BCG∴∠BGC=∠DEC,∵∠BGC+∠CBG=900,∴∠DEC+∠CGB=900∴∠BHE=900⊥即BH DE(2)连接BD,∵四边形ABCD是正方形,边长为1,∴AB=AD=1,∠A=900,∴BD===∵BH平分DE,BH⊥DE,∴DH=EH,∠BHD=∠BHE,又∵BH=BH∴△BHD≌△BHE,∴,∴1.【点拨】此题考察正方形的性质运用,②中的垂直应有效利用①中全等的结论去证明,(2)中连接BD利用全等求得BE是解题的关键.21.(1)4m;(2)证明见解析;(3)△APQ的周长的最小值为【分析】(1)直接由正方形的性质得出答案即可;(2)连接AH,证明△BHA≌△BCE,利用△BHA的面积=△BCE的面积得出结论;(3)作点A关于DE的对称点A′,点A关于BC的对称点F,利用对称的性质得出△APQ 的周长的最小值为A′F,进一步求得问题即可.【详解】(1)∵四边形BCFH是正方形,∴BC=BH=FH=CF,∴当BC=m时,正方形BCFH的周长为4m,故答案为:4m;(2)如图1,连接AH,在△BHA和△BCE中,AB BE CBE ABH BC BH ⎪∠⎪⎩∠⎧⎨===∴△BHA ≌△BCE (SAS ),∵AF ∥BH ,∴BH 边上的高=正方形BCFH 的边∴△BHA 的面积等于12正方形BCFH 的面积.∴△AEC 的面积等于12正方形BCFH 的面积;(3)△APQ 的周长存在最小值.如图2,作点A 关于DE 的对称点A∴AP=A′P∵点A 关于BC 的对称点F ,∴AQ=QF ,∴△APQ 的周长的最小值为A′F ,过A′作A′M ⊥FA 交FA 的延长线于M ,∵2AC BC ==,90ACB ∠=︒∴∠BAC=45°,AB=2∴∠A′AM=45°,,∴△AA′M 为等腰直角三角形,,∴MA=MA′=4,∴MF=8,∴A′F=222284MF A M '+=+=45,∴△APQ 的周长的最小值为45.【点拨】此题综合考查正方形的性质,对称的性质,勾股定理的运用以及利用对称性求最短距离的问题,对于求最短距离的问题体现了建模思想的运用,注意辅助线的作法.22.(1)证明见解析;(2)CF 的最小值252-.【分析】(1)由正方形的四边相等,四个直角性质,证明()BCM ADN SAS ≌,再根据全等三角形的对应角相等,整理,证明()BCE DCE SAS ≌,最后整理出25∠∠、的数量关系即可;(2)取AD 中点P ,连接PF ,由(1)中结论,计算FP 的长,在Rt CPD △中,利用勾股定理求得CP 的长,最后根据三角形三边关系:两边之和大于第三边解题即可.(1)证明:ABCD 是正方形,90BC AD BCD ADC ∴∠∠︒=,==()CM DN BCM ADN SAS ∴ =,≌.12∴∠∠=又345ACD CE CE∠∠︒==,=()BCE DCE SAS ∴ ≌1424∴∠∠∴∠∠=.=.251590∴∠+∠∠+∠︒==.DE AN ∴⊥.(2)取AD 中点P ,连接PF由(1),得122FP AD ==在Rt CPD △中,由勾股定理,得224225CP =+=2+≥∴≥,CF FP CP CF∴CF的最小值2-.【点拨】本题考查几何综合,其中涉及正方形的性质、全等三角形的判定与性质、勾股定理、三角形的三边关系等知识,是重要考点,难度一般,掌握相关知识是解题关键.23.(1)①△ABE≌△BCF,△AOE≌△BOF,△ABF≌△DEA②见解析(2)见解析(1)①根据正方形性质及BE=CF即可得出全等的三角形,②根据全等三角形及正方形的性质即可得出结论.(2)根据正方形性质及已知条件由ASA得出△ABE≌△BCF,即可由等量代换得证.(1)①△ABE≌△BCF,△AOE≌△BOF,△ABF≌△DEA②证明:如图,延长AE交BF于点M,∵ABCD是正方形,∴AB=BC,∠BCF=∠ABE.∵BE=CF,∴△ABE≌△BCF(SAS).∴∠CBF=∠BAE∵∠ABE+∠EBM+∠CBF=90°,∴∠ABE+∠EBM+∠BAE=90°.∴∠AMB=90°.∴AE⊥BF.(2)点E是OB的中点.证明如下:∵ABCD是正方形,∴AB=BC,∠BCF=∠ABE.∵AE⊥BF,∴∠AMB=90°.∴∠ABE+∠EBM+∠BAE=90°.∴∠ABE+∠EBM+∠CBF=90°.∴∠CBF=∠BAE.∴△ABE≌△BCF(ASA).∴BE=CF.∵BE=OF,∴CF=OF.又∵OB=OC,∴BE=OE.∴点E是OB的中点.24.(1)①ME MF =,理由详见解析;②点M 位于正方形两条对角线的交点处(或AC 中点出),理由详见解析;(2)23222AM <<【分析】(1)①过点M 作MG CD ⊥于点G ,MH BC ⊥于点H ,通过证,MFH MGE ∆∆≌可得ME=MF ;②点M 位于正方形两条对角线的交点处时,,AE DF MFD MAE =∆∆≌,可得AEM DFM ∠=∠;(2)当点F 分别与B 重合时处和端点C 处时,可得M 的位置,进而得出AM 的取值范围.解:(1)ME MF =.理由是:过点M 作MG CD ⊥于点G ,MH BC ⊥于点H在正方形ABCD 中,90BCD ∠=︒45,ACD BCA ∠=∠=︒MH HC∴=∴矩形MHCG 为正方形90,HMG MH MG∴∠=︒=又,MF MG FMH EMG⊥∠=∠ ,MFH MGE ∴∆∆≌ME MF∴=②点M 位于正方形两条对角线的交点处(或AC 中点处)如图,ME 是ACD ∆的中位线,1,2ME AD ME AD ∴⊥=又ME MF = ,此时,F 是BC 中点,且AED CDF ∆∆≌,,AE DF MFD MAE ∴=∆∆≌,AEM DNF∴∠=∠(2)当点F 与B 重合时,M 在AC,BD 交点处时,此时AM 最小,AM=12AC=22;当点F 与点C 重合时,M 在AC,BD 交点到点C 的中点处,此时AM 最大,AM=322.故答案为23222AM <<【点拨】本题是运动型几何综合题,考查了全等三角形、正方形、命题证明等知识点.解题要点是:(1)明确动点的运动过程;(2)明确运动过程中,各组成线段、三角形之间的关系;(3)添加恰当的辅助线是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017春初三数学(路径)给力训练
1.等边三角形ABC ∆,点(3,0)B -,点(3,0)C ,点
A 在y 轴的正半轴上,点P 从点
B 出发,沿B
C 向点C 运动,AP 绕点A 逆时针旋转60o 得
到AQ ,点P 从点B 运动到点C 过程中,点Q 也随之运动.
(1)点Q 是 (是线段还是弧);(2)求点Q 运动的路径长.
2.如图,已知点A 是第一象限内横坐标为2的一个定点,AC ⊥x 轴于点M ,交直线y=﹣x 于点N .若点P 是线段ON 上的一个动点,
∠APB=30°,BA ⊥PA ,则点P 在线段ON 上运动时,A 点不变,B 点随之运动.求当点P 从点O 运动到点N 时,求点B 运动的路径长.
3.如图,以G (0,1)为圆心,半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为⊙G 上一动点,CF⊥AE 于F .当点E 从点B 出发顺时针运动到点D 时,求点F 所经过的路径长.
4.如图,半径为2cm ,圆心角为90°的扇形OAB 的AB 上有一运动的点
P .从点P 向半径OA 引垂线PH 交OA 于点H .设
△OPH 的内心为I ,当点P 在AB 上从点
A 运动到点
B 时,求内心I 所经过的路径长 .
5.如图,⊙O 是以原点为圆心,2为半径的圆,点P 是直线y=-x+6上的一点,过点P 作⊙O 的一条切线PQ ,Q 为切点,求切线长PQ
的最小值
6.如图,一根木棒(AB)长为2a ,斜靠在与地面(OM )垂直的墙壁(ON )上,与地面的倾斜角(∠ABO )为60°,当木棒A 端沿NO 向下滑动到A ′,AA ′=(23-)a ,求B 端沿直线OM 向右滑动到B ′,木棒中点从P 随之运动到P ′所经过的路径长.
7.如图,在直角坐标系中有一块三角板GEF 按图1放置,其中∠GEF=60°,∠G=90°,EF=4.随后三角板的点E 沿y 轴向点O 滑动,同时点F 在x 轴的正半轴上也随之滑动.当点E 到达点O 时,停止滑动.
(1)在图2中,利用直角三角形外接圆的性质说明点O 、E 、G 、F 四点在同一个圆上,并在图2中用尺规方法作出该圆,(不写作法,保留作图痕迹);
(2)滑动过程中直线OG 的函数表达式能确定吗?若能,请求出它的表达式;若不能,请说明理由; (3)求出滑动过程中点G 运动的路径的总长;
(4)若将三角板GEF 换成一块∠G=90°,∠GEF=α的硬纸板,其它条件不 变,试用含α的式子表示点G 运动的路径的总长.
8.点
A 在反比例函数6
(0)y x x
=>图象上的一个动点,AO OP ⊥,60OAP ∠=︒.点Q 是OA 的中点,点P 与Q 随点A 运动A
而变化,问点A 运动过程中,
(1)点Q 运动路径是什么函数图象,并说明理由. (2)点P 运动路径是什么函数图象,并说明理由. x
y
P
O
A
9.如图,在以O为圆心,2为半径的圆上任取一点A,过点A作AM⊥y轴于点M,AN⊥x轴于点N,点P为MN的中点,当点A沿着圆圈在第一象限内顺时针方向走完45°弧长时,求点P走过的路径长.
10.如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为2.函数y=-x+2图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点(包括端点).
(1)连接CO,求证:CO⊥AB;
(2)若△POA是等腰三角形,求点P的坐标;
(3)当直线PO与⊙C相切时,求∠POA的度数;
(4)当直线PO与⊙C相交时,设交点为E、F,点M为线段EF的中点,令PO=t,MO=s,求s
与t之间的函数关系,并写出t的取值范围;设点M为线段EF的中点,试写出点M的运动轨
迹,并直接写出点M运动轨迹的长度.
11.如图,△ABC在第一象限,其面积为16.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O 的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限.求点M随点P运动所形成的图形的面积.
12.如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原
点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限.求点C 随点A运动所形成的图形
的面积 .
13.如图1,已知点P在正三角形ABC的边BC上,以AP为边作正三角形APQ,连接CQ.①求证:△ABP≌△ACQ;
②若AB=6,点D是AQ的中点,求当点P由点B运动到点C时,点D运动路线的长.
14.边长为2的正方形ABCD的两条对角线交于点O,把BA与CD同时分别绕点B和C逆时针方向旋转,此时正方形ABCD随之变成四边形A′BCD′,设A′C,BD′交于点O,则旋转60°时,求点O运动到点O′所经
过的路径长
15.数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:
如图1,点P 为线段AB 上的一个动点,分别以AP 、BP 为边在同侧作正方形APDC 、BPEF .
(1)当点P 运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD 、DF 、AF ,AF 交DP 于点K ,当点P 运动时,在△APK、△ADK、△DFK 中,是否存在两个面积始终相等的三角形?请说明理由. 问题拓展:
(3)如图2,以AB 为边作正方形ABCD ,动点P 、Q 在正方形ABCD 的边上运动,且PQ=8.若点P 从点A 出发,沿A→B→C→D 的线路,向点D 运动,求点P 从A 到D 的运动过程中,PQ 的中点O 所经过的路径的长.
(4)如图3,在“问题思考”中,若点M 、N 是线段AB 上的两点,且AM=BN=1,点
G 、H 分别是边CD
、
EF 的中点,请直接写出点P 从M 到N 的运动过程中,GH 的中点O
所经过的路径的长及OM+OB 的最小值.
16.已知R t △ABC,∠ACB=90°,AC=BC=4,点O 是AB 中点,点P 、Q 分别从点A 、C 出发,沿AC 、CB 以每秒1个单位的速度运动,到达点C 、B 后停止。
连结PQ 、点D 是PQ 中点,连结CD 并延长交AB 于点E.
(1)试说明:△POQ 是等腰直角三角形;
(2)设点P 、Q 运动的时间为t 秒,试用含t 的代数式来表示△CPQ 的面积S ,并求出
S 的最大值;
(3)如图2,点P 在运动过程中,连结EP 、EQ ,问四边形PEQC 是什么四边形,并说明理由; (4)求点D 运动的路径长.
(图2)
(图1)
A
17.如图1,在Rt △ABC 中,∠C=90°,AC=6,BC=8,动点P 从点A 开始沿边AC 向点C 以1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD ∥BC ,交AB 于点D ,连接PQ 分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(t ≥0). (1)直接用含t 的代数式分别表示:QB= ,PD= .
(2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值;若不存在,说明理由.并探究如何改变Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度;
(3)如图2,在整个运动过程中,求出线段PQ 中点M 所经过的路径长.
18.Rt ABC ∆在平面直角坐标系中的初始位置如图1所示,90C ∠=︒,6AB =,3AC =,点A 在x 轴上由原点O 开始向右滑动,同时点B 在y 轴上也随之向点O 滑动,如图2所示;当点B 滑动至点O 重合时,运动结束。
在上述运动过程中, G 始终以AB 为直径。
(1)试判断在运动过程中,原点O 与⊙G 的位置关系,并说明理由;
(2)设点C 坐标为(x ,y ),试求出y 与x 的关系式,并写出自变量x 的取值范围; (3)根据对问题(1)、(2)的探究,请你求出整个过程中点C 运动的路径的长。
19.在平面直角坐标系x O y 中,点A 的坐标为(0,2),直线OP 经过原点,且位于一、三象限,∠AOP=45 °(如图1),设点A 关于直线
OP 的对称点为B .
(1)写出点B 的坐标 ;
(2)过原点O 的直线l 从直线OP 的位置开始,绕原点O 顺时针旋转, ①当直线l 顺时针旋转10°到直线l 1的位置时(如图1),点A 关于直线l 1的对称点为C ,则∠BOC 的度数是 ,线段OC 的长为 ; ②当直线l 顺时针旋转55°到直线l 2的位置时(如图2),点A 关于直线l 2的对称点为D ,则∠BOD 的度数是 ; ③直线l 顺时针旋转n °(0<n ≤90),在这个运动的过程中,点A 关于直线l 的对称点所经过的路径长为 (用含n 的代数式表示).
x y x y l 1
l 2第25题图
图2图1
A O A O P
P。
