信号与系统第一章答案
信号与系统第一章习题答案

t 0 > 0 函数式的信号的波形如图 1.2(b)所示. 。
3
cos ωt
1 … …
−
5π 2ω
−
3π 2ω
−
π 2ω
-1
π 2ω
(a)
3π 2ω
5π 2ω
t
cos ωtε (t )
1
ε (t )
1
…
π 2ω
3π 2ω
5π 2ω
t
t
(b)
-1 (c ) 图 1.1
cos ωtε (t − t 0 )
1
P = lim
E =∞
1 T → ∞ 2T
1 ∫ [ε (t )] dt = 2
T 2 −T
(2) ε (t ) − ε (t − 1) 是脉冲信号,其为能量信号,能量为:
E = lim
[ε (t ) − ε (t − 1)]2 dt = ∫0 [ε (t ) − ε (t − 1)]2 dt =1 T →∞ ∫−T
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
1 2T
2
∫
T
−T
9
cos 2(ω0 t + θ ) + 1 1 9 9 dt = lim ⋅ ⋅ 2T = T → ∞ 2 2T 2 2
T 2
2ω t 1 − cos 0 1 cos ω0 t + 1 9ω 0t ω t 5 dt = lim + sin − sin 0 + ∫ − T T →∞ 2T 2 20 20 2
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
信号与系统 第一章答案

P lim
所以 x[n] 为非能量信号非功率信号。 (6) x[n] cos( n/ 4)
E
P 1 7 1 cos 2 ( n/ 4) 8 n 0 2
所以 x[n] 为功率信号。 1.4 (1)错误,如指数信号。 (2)错误,一个能量信号与一个功率信号之和为功率信号。 (3)正确。 (4)错误,如 x(t) e , t 0 (5)错误,可能为非能量信号非功率信号。 (6)正确。 1.5
2
x[n] cos 2 ( n/ 8)
cos( n/ 4) 1 2
1
N
2
8
4
所以 x[n] 为周期信号,周期 N 8 。 (4) x[n] cos(n/ 2) cos( n/ 4)
T1 2 4 1 2
所以 x[n] 不是周期信号。 1.3 (1) x(t) e , t 0
2
x(t ) cos 2 t =
1+ cos(2 t) T 2 / 2 2
所以 x(t ) 为周期信号,周期 T 。 (4) x(t ) cos( t ) 2sin( 3 t)
T1 2 / 2 T2 2 / 3 2 / 3
所以 x(t ) 不是周期信号。 1.2 (1) x[n] e
T
1 100 3 50 2 T lim T T 2T 3 3
所以 x(t ) 为非能量信号非功率信号。 (3) x(t) 10cos(5t ) cos(10 t)
x(t) 10cos(5t ) cos(10 t) 5[cos(15 t) cos(5 t)]
E | e2t |2 dt
0 0
信号与系统答案1
∫
∞
e jω0t [δ (t +T) δ (t T)]dt = e jω0 (T ) e jω0 (T )
= 2 j sin(ω0T)
2-5: (4)
x(t)
2 0 2 3 5
t
2 -1 0
x(t+1)
1 2 4
t
2 -3 0
x(t/3+1)
3 6 12
t
2-9:
x(t) = et [u(t 1) u(t 2)] + tδ (t 3), 求 (1) (t), x '(t) x ∵x(t) = et [u(t 1) u(t 2)] + 3δ (t 3)
3-31:
5 1 y[k ] y[k 1] + y[k 2] = x[k ], y(1) = 0, y(2) = 1, 6 6 x[k ] = u[k ]
根据单位脉冲响应的定义,应满足方程 解: (1) 根据单位脉冲响应的定义 应满足方程: 应满足方程 5 1 h[k ] h[k 1] + h[k 2] = δ [k ] 6 6 第一步:求等效初始条件 第一步 求等效初始条件 :
t
3-4 已知离散时间 系统,输入 x1[k ] = δ [k 1] 时,输出 已知离散时间LTI系统 输入 输出; 系统 输出
1 k 1 y1[k ] = ( ) u[k 1], 求当输入x2 [k ] = 2δ [k ] + u[k ]时系统响应y2 [k ]. 2
x2 [k ] = 2 x1[k + 1] +
2-13:(3)
x[3k ]
2 1 1
2
k
-1 0 1 2
2-13:(4)
信号与系统课后习题答案—第1章

第1章 习题答案1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?解: ① 连续信号:图〔a 〕、〔c 〕、〔d 〕; ② 离散信号:图〔b 〕; ③ 周期信号:图〔d 〕; ④ 非周期信号:图〔a 〕、〔b 〕、〔c 〕; ⑤有始信号:图〔a 〕、〔b 〕、〔c 〕。
1-2 某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。
解: 设T 为此系统的运算子,由条件可知: y(t)=T[f(t)]=|f(t)|,以下分别判定此系统的线性和时不变性。
① 线性1〕可加性不失一般性,设f(t)=f 1(t)+f 2(t),那么y 1(t)=T[f 1(t)]=|f 1(t)|,y 2(t)=T[f 2(t)]=|f 2(t)|,y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|,而|f 1(t)|+|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下,不存在f 1(t)+f 2(t)→y 1(t)+y 2(t),因此系统不具备可加性。
由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。
2〕齐次性由条件,y(t)=T[f(t)]=|f(t)|,那么T[af(t)]=|af(t)|≠a|f(t)|=ay(t) 〔其中a 为任一常数〕即在f(t)→y(t)前提下,不存在af(t)→ay(t),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。
② 时不变特性由条件y(t)=T[f(t)]=|f(t)|,那么y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|,即由f(t)→y(t),可推出f(t-t 0)→y(t-t 0),因此,此系统具备时不变特性。
依据上述①、②两点,可判定此系统为一非线性时不变系统。
信号与系统第一章习题解答

Problems Solution
xn
1
1
0
-4 -3 -2 -1 0 1 2 3 4
n
(a)
xe n
n
x0 n
1
-4 -3 -2 -1 0 1 2 3 4
n
Chapter 1
2
Problems Solution
3
xn
3 xe n
12
-2
12
1
-1 0
7
Chapter 1
Problems Solution
作业: 1.14 1.15 1.16 1.17
1.21 (d) (e) (f)
1.22 (d) (g)
1.23
1.24 (a) (b) 1.26 (a) (b) 1.27 1.31
Chapter 1 1.14
1 , 0 t 1 xt T 2 -2, 1t 2
xt
1
2 1 0
1
xe t
1
t
-2 -1 0 1 2
t
(b)
x t
1
xo t
-2 -1
1/ 2
1
0
1
2
t
1/ 2
0
1 2
t
Chapter 1 1.24 Determine and sketch the even and odd parts of the signals.
1
-2 -1 0 1
Problems Solution
xt
gt
k
t 2k
2
3
2
信号与系统第一、二、三章自测题解答

第一章自测题答案1.已知)()4()(2t u t t f +=,则)(''t f =(t)4δ2u(t)'+ 2.2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
3.=-⎰∞∞-dt t t e tj )(0δωoj ωet 。
4.试画出下列各函数式表示的信号图形: (1)0 ),()(001>-=t t t u t f(2))]4()([3cos )(2--=t u t u t t f π在0到4区间内的6个周期的余弦波,余弦波的周期为2/3。
(3)][sin )(3t u t f π=5.已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形。
答:函数表达式:f(2-t) = [u(t)-u(t-1)]+2[u(t-1)-u(t-2)] f(6-2t)=[u(t-2)-u(t-2.5)]+2[u(t-2.5)-u(t-3)]6.信号f (5-3t )的波形如图1.2所示,试画出f (t )的波形。
答:f(5-3t)左移5/3得到f(-3t),然后再扩展3倍得到f(-t),最后反褶可得到f(t)7.对于下述的系统,输入为e (t ), 输出为r (t ),T [e (t )]表示系统对e (t )的响应,试判定下述系统是否为: (1) 线性系统;(2)非时变系统;(3)因果系统;(4)稳定系统:(a) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统9. 一线性非时变系统,当输入为单位阶跃信号u (t )时,输出r (t )为 )1()()(t u t u e t r t --+=-,试求该系统对图1.3所示输入e (t )的响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
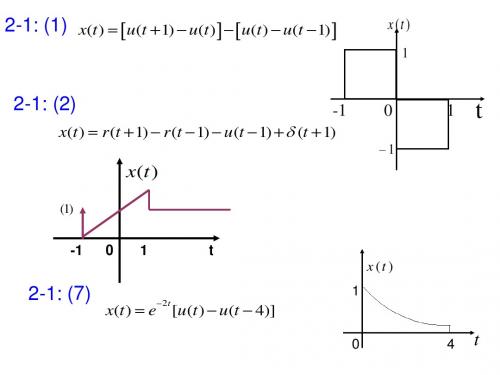
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=
(4))(sin )(t t f ε= (5))(sin )(t r t f =
(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为
(2)∞<<-∞=-t e t f t ,)(
(3))()sin()(t t t f επ=
(4))(sin )(t t f ε=
(5))(sin )(t r t f =
(7))(2)(k t f k ε=
(10))(])1(1[)(k k f k ε-+=
1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f
(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε
(11))]7()()[6sin()(--=k k k k f εεπ (12)
)]()3([2)(k k k f k ---=εε
解:各信号波形为
(1))2()1(3)1(2)(-+--+=t t t t f εεε
(2)
)2()1(2)()(-+--=t r t r t r t f (5)
)2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε
(11)
)]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε
1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=
解:
1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5)
)21(t f - (6))25.0(-t f
(7)dt
t df )
( (8)dx x f t ⎰∞-)( 解:各信号波形为
(1))()1(t t f ε-
(2)
)1()1(--t t f ε (5)
)21(t f - (6))25.0(-t f
(7)dt t df )
(
(8)dx x f t
⎰∞-)(
1-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
(1))()2(k k
f ε- (2))2()2(--k k f ε (3))]4()()[2(---k k k f εε (4))2(--k f
(5))1()2(+-+-k k
f ε (6))3()(--k f k f 解:
1-9 已知信号的波形如图1-11所示,分别画出)
(t f 和dt t df )(的波形。
解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对)23(t f -的波形展宽为原来的两倍而得)。
将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示。
再将)3(+t f 的波形右移3个单位,就得到了)(t f ,如图1-12(c)所示。
dt
t df )(的波形
如图1-12(d)所示。
1-10 计算下列各题。
(1)[]{})()2sin(cos 22
t t t dt
d ε+ (2))]([)1(t
e dt d t t δ-- (5)dt t t t )2()]4sin([2++⎰∞
∞-δπ (8)dx x x t
)(')1(δ⎰∞--
1-12 如图1-13所示的电路,写出
(1)以)(t u C 为响应的微分方程。
(2)以)(t i L 为响应的微分方程。
1-20 写出图1-18各系统的微分或差分方程。
1-23 设系统的初始状态为)0(x ,激励为)(⋅f ,各系统的全响应)(⋅y 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-t
t dx x xf x e t y 0)(sin )0()( (2)
⎰+=t dx x f x t f t y 0)()0()()( (3)⎰+=t
dx x f t x t y 0)(])0(sin[)( (4))2()()0()5.0()(-+=k f k f x k y k
(5)∑=+=k
j j f kx k y 0)()0()( 1-25 设激励为)(⋅f ,下列是各系统的零状态响应)(⋅zs y 。
判断各系统是否是线性的、时不变的、因果的、
稳定的?
(1)dt t df
t y zs )()(= (2))()(t f t y zs = (3))2cos()()(t t f t y zs π=
(4)
)()(t f t y zs -= (5))1()()(-=k f k f k y zs (6))()2()(k f k k y zs -=
(7)∑==k j zs j f k y 0)()( (8))1()(k f k y zs -=
1-28 某一阶LTI 离散系统,其初始状态为)0(x 。
已知当激励为)()(1
k k y ε=时,其全响应为 若初始状态不变,当激励为)(k f -时,其全响应为)(]1)5.0(2[)(2k k y k ε-=
若初始状态为)0(2x ,当激励为)(4k f 时,求其全响应。
