速度场模型
中国地壳运动整体速度场模型的建立方法研究

1 数 据 准 备
为建立 中国 地 壳 运 动 整 体 速 度场 模 型 , 据 根 所 能得 到 的 资料 , 将所 采 用 的 4 8点 ( 6 分布 在 北纬 l 。 0 、 经 7。 10之 间 ) 速 度 作 为 计 算 0~6 。东 0~ 4。 的 地 壳运 动 速度 场模 型 的起 算数 据 。
V0 . 7 No 4 12 . Au 2 0 g. 0 2
文章编号 :0 00 0 2 0 )40 3 —6 1 0 —5 X(0 2 0 —3 10
文献标识 码 : A
中 国地 壳 运 动 整 体 速 度 场 模 型 的建 立 方 法 研 究
刘 经 南 姚 宜斌 2 施 闯3
形变 , 相对于经典 的计算欧拉矢 量法 , 拟合 的方法 对块 体 的 刚 弹 性 没 有 要 求 。 目前 拟 合 的 方 法 很
多 , 多 项 式 拟 合 法 、 三 次样 条 函 数 拟合 法 等 , 有 双
但这 些 常 规 的拟合 方 法对 已知点 均匀 分 布 的要求
准而 不是 全球 运 动 基 准 的前 提 下求 解 位 移 , 以 可
体和 不细分块体 的情 况下建立 了中国地 壳运 动整体速度 场模 型 , 并对 其结果进行 了分析。结 果表 明, 对块 在 体介质 刚弹性 的认定 不明确 时 , 多面函数拟合 法 比计算 欧拉 矢量法 更适合 中国平 面地 壳运 动速 度场模 型 的
建立。
关键词 : 速度场模 型 ; 欧拉 矢量 ; 多面函数拟合 ; 壳运动 图像 地
量 的方 法 不 能较 细 致 地 反 映 其 形 变 特征 , 拟 合 而
的方 法可 以以任 意精 度逼 近 连续 的和非 连续 性 的
abaqus载荷、边界条件、预定义场的定义与区别

abaqus载荷、边界条件、预定义场的定义与区别下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!Abaqus载荷、边界条件、预定义场的定义与区别在有限元分析领域,Abaqus是一个被广泛使用的工具,用于模拟和分析各种工程问题。
绕方柱流速度场的数值模拟

大涡模拟( a eE d m li , L S 同其它基于雷诺平均 NS Lr dy i u tn 即 E ) g S ao - 方程( P N ) 即 A S 的模型相比, 前者 由于其具有较高的精度而更具吸引力。在 L S中, E 湍流的脉动运动除了那些 比滤波尺度小的小涡外, 其
余的大尺度涡都可以被 直接求解 , 而小尺度涡则用一 种基于涡粘模 型的亚格子尺度模型 ( ugd.a Shr - l i ̄ e
T NG O , Z 咖 , Z O B nka HU H U e—u n
( col f n .Si c , tt, s J o n nvrt, hn Sho g c e e S het i t gU i sy C e 60 3 , hn ) oE n m o a o ei 10 1 C ia
维普资讯
第3 7卷 第 2期
20 O2年 4月
J OUR L O 南O 交 通 T大AO ONG U 报 SIY NA西 F S UT HWES I 学 学 NI J T VER T
. 卯
N . o2
r O2 .2 0
文章 编号 : 5 -7 4 2 0 )20 2 - 0 822 (0 2 0 -1 1 4 2 0
M d1即 S S oe. G 模型) 来模拟。 雷诺数 ( e 为 2 0 h ) 200的绕方柱流的大涡模拟 , 由于其 中包含了许多复杂的流场现象如 流体的分离、
2 0 i o d c e .T eN— q ain i p i n on v t n s p 2 0 0 sc n u t d h Seu t o s ̄ l ti t d e i t ,df so tp a d p p g t n s p c o e iu in se n r a a o t f o i e
06-2013高级培训班_GeoEast解释速度建场方法原理

4.2 层位控制法速度建场
中国石油
平滑次数:10-50
网格间距:
Page 21
4.2 速度场质量检查
速度场剖面
中国石油
速度切片
速度体
Page 22
4.2 速度场质量检查
中国石油
Page 23
4.2 建场效果分析
ES2平均速度平面图
中国石油
Page 24
4.2 建场效果分析
中国石油
1 N
( T
i 1
Page 8
n
si
Ti )
基本概念:速度分析及构造成图基准面 基准面校正
中国石油
通过对CMP面为零线的叠加速 度进行基准面校正,得到以时 间剖面零线为准的叠加速度。
然后通过对叠加速度转换建立
和时间剖面零线相一致速度场, 用于构造成图。
基准面校正界面
Page 9
Page 7
基本概念:速度分析及构造成图基准面
中国石油
统一基准面 CMP面
Dact 值
解释层位
CMP参考面:叠加速度零线,通常是在贴近地表的CMP参考面进行叠加成 像、偏移处理,最后将成像结果校正到统一基准面。
统一基准面:时间剖面零线,这样作的目的是为了直观表征地下构造特
征,目前国内地震资料时间剖面基本都是以统一基准面为零线。
ES2平均速度平面图
中国石油
Page 36
4.4 建场效果分析(模型层析法)
中国石油
ES2深度平面图
Page 37
射线起始时间对模型层析精度影响分析
ES2反射层位对井误差分析(井校前)
起始
时间 井名
B65
高中物理关联速度模型

高中物理关联速度模型嘿,大家好!今天咱们聊聊一个让人又爱又恨的话题——速度模型。
别担心,不会让你们觉得像在上课,我会尽量让它轻松有趣。
速度,顾名思义,就是物体移动的快慢,简单来说,咱们日常生活中每次出门都在用到的。
想想你早上起床,赶着上学,那叫一个飞快,有时候感觉时间都不够用。
真是“光阴似箭”,一眨眼就得冲出家门。
说到速度模型,首先得介绍一下它的基本概念。
想象一下,咱们的车在马路上飞驰,车速就是速度的一个体现。
这车速快,那我们就能更快地到达目的地,省下不少时间。
可是,如果你在开车的时候突然遇到红灯,那可就“要么停,要么等”了。
哈哈,真是让人无奈。
这种情况就涉及到一个重要的概念:加速度。
你说说,这加速度就像是我们生活中的起伏,有时候顺风顺水,有时候却像是在逆风行驶。
再说说那“匀速运动”,也就是保持不变的速度,听起来挺简单,但实际上很少能做到。
想想你在校园里走路,有时候走得飞快,有时候却像在走迷宫,绕来绕去。
这就是生活的真实写照啊!很多时候,我们追求的就是那种匀速,稳定,没啥波折的感觉,但生活却偏偏给你来个惊喜,让你像小兔子一样跳来跳去。
真是“人生如戏,全靠演技”!还有个有趣的现象,就是“瞬时速度”。
这个词听起来挺高大上的,其实就是你在某一时刻的速度。
比如说,开车超车的那一瞬间,速度表上的数字跳动得飞快,仿佛在告诉你:“嘿,看我多牛!”这瞬间的刺激感,让人心跳加速,简直像是坐过山车一样刺激。
而咱们的生活中,瞬时速度又何尝不是呢?那一瞬间的决策,可能就会影响到接下来的道路。
就像古人说的“机不可失”,要抓住机会啊!在这里,还要提到一个经典的公式,速度等于距离除以时间。
这听起来像是老生常谈,但其实很有道理。
想象一下,你和朋友一起骑自行车,谁先到达终点,谁就是赢家。
但是,如果你们俩的距离不一样,那可就没得比了,对吧?这就像我们的人生,有时候走的路不同,结果也自然会不同。
有的人一步到位,有的人却可能慢半拍,这就是人生的差异所在。
部分4-时间域速度分析与CIP道集提取

椭圆展开叠加速度分析方法
速度交互拾取
椭圆展开法速度交互拾取界面
椭圆展开速度场模型叠加剖面
椭圆展开叠加速度分析方法
某2D测线椭圆展开叠加剖面
CDP 1-15408
CDP 1500-6000
椭圆展开叠加速度分析方法
某3D资料CMP道集和椭圆展开速度谱对比
CDP 5620位置处 CMP道集速度谱
CDP 5620位置处 椭圆展开速度谱 Nccs
由上两式得到等价偏移距 h : e
he x2 h2 ( 2 xh 2 ) vt
单平方根形式的散射点时距关系:
4he he2 2 t 2 2 2 v v 2
2 2
叠前时间偏移共散射点道集速度分析方法
2D CSP 道集速度分析方法改进工作: a)源程序 F -> C ,数据文件大小 2G -> 无限制; b)优化输入输出参数,更利于实际处理; c)实现并行。
ˆ 我们引入 x ˆ和 h
ˆ x ds dr 2
ˆ ds dr h 2
3D 等效偏移距表达式:
ˆˆ 2 2 xh 2 2 ˆ ˆ he x h ( ) vt
Байду номын сангаас
3D采集情况下散射点和 炮检点平面示意图
叠前时间偏移共散射点道集速度分析方法
某3D数据某测线CDP、CSP道集及速度谱
叠前时间偏移共散射点道集速度分析方法
CDP940 对比
基于CMP道集及速度谱
基于共散射点道集及速度谱
加振幅校正后共散射点道 集及速度谱
叠前时间偏移共散射点道集速度分析方法
CDP1060 对比
CMP道集及速度谱
共散射点道集及速度谱
汽车车身外流场计算模型及仿真

汽车车身外流场计算模型及仿真引言汽车在行驶的过程中不可避免的要与周边空气发生相互作用,随着车速的增加,这种相互作用会愈加的剧烈。
空气对在行驶中的汽车施加力和力矩,从而影响汽车的行驶。
所以,在汽车开发过程中,研究并优化汽车的空气动力性能非常重要。
另外,汽车的空气动力学性能不仅影响着汽车的燃油经济性,同时也对汽车的动力性、稳定性和操作性等方面有着巨大的影响,所以现代汽车设计越来越关注汽车的空气动力性能研究。
随着计算机技术的迅猛发展,对汽车结构分析的技术已基本成熟,且对更为复杂的流动问题的模拟计算也在不断的发展,其中计算流体力学( Computational Fluid Dynamics 简称CFD) 受到了越来越多的关注。
计算流体力学已从定性的分析发展到定量的计算,其应用也从最初的航空领域不断的扩展到包括汽车在内的多个领域[1-3] 。
新车型的开发过程中,空气动力性能分析是必不可少的。
利用数值模拟的方法对汽车行驶中的外流场进行分析能够用来预测或解决一些理论及实验都无法处理的复杂流动问题,并能取代部分实验环节。
但要求对问题的物理特性有足够的了解,才能建立合适的数学方程及相应的初始、边界条件等,这些都离不开实验和理论方法的支持。
目前,数值方法主要是应用欧拉方程和纳维-斯托克斯方程。
在汽车设计的研究分析领域,数值方法与传统的研究方法相结合,能够有效地改善汽车性能、节约研究资金、提高研究效率。
汽车车身外流场计算模型及仿真是计算流体力学在汽车外流场分析方面的应用研究之一[4-8] 。
本文通过建立汽车车身外流场的计算模型,利用计算流体力学方法和适当的矩阵代数算法,基于Fluent 仿真平台,分析研究汽车车身的空气动力性能。
1 汽车车身绕流的数学模型流场运动中,流场运动基本方程是根据基本物理定律质量守恒、动量守恒、能量守恒定律按一定的流体流动模型推导的。
对于空气来说,当风速小于三分之一声速时,也就是风速小于408km/h,可以认为是不可压缩气体。
【国家自然科学基金】_速度场模型_基金支持热词逐年推荐_【万方软件创新助手】_20140729

科研热词 近液相线铸造 相场法 多尺度模拟 激光技术 液/固相变 枝晶生长 数值模拟 半固态成形 飞行器控制、导航技术 非对角扩散项 随机场模型 铝合金 速度场模型 连续铸造 背景场模型 粉末流速度场 粉嘴 稳定性 碰撞检测 相场参数 界面形态演化 热噪声 激光重熔 温度场 液固相变 无迹卡尔曼滤波 数字粒子图像测速技术 控制算法 强迫对流 巡航导弹 对流速度 对流 定向凝固 多道搭接 地磁导航 地壳运动图像 国际地磁参考场 可观测性 半固态 侧枝 上游枝晶 三元合金 zl201合金 tial合金 itrf框架 6061合金
53 54 55 56 57 58 59 60 61 62 63
像素块 值模拟 人工冻土墙 主磁场 snake模型 simple算法 oseen-ivantsov理论 grace星间距离变率 gibbs随机场 champ al-1.2mg-0.7si合金
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 4 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
2000国家大地坐标系资料

按ITRF框架间转换关系进行转换
21
历元
(1)星表历元:由于岁差和章动以及自行的影响,
各种天体的天球坐标都随时变化。因此,星表所 列的各种天体的天球坐标,都只能是对应于某一 特定时刻的。 (2)观测历元:为了比较不同时刻的观测结果,需 要注明观测资料所对应的观测时刻,这种时刻称 为观测历元。 现在ITRF框架中使用的标准历元是J2000.0。前 缀“J”代表这是一个儒略历元。在使用J2000.0前 的标准历元是B1950.0,前缀“B” 代表这是一个 贝塞耳历元。贝塞耳历元在1984年前使用,现在 使用的是儒略历元。
17
ITRF 和IGS 的关系
使用的IGS产品 框架 ITRF92 ITRF93 ITRF94 ITRF96 ITRF97 IGS97 IGS00 IGS00b IGS05 GPS周 0730-0781 0782-0859 0860-0947 0948-1020 1021-1064 1065-1142 1143-1252 1253-1399 1400日期 1994年1月-1994年12月 1995年1月-1996年6月 1996年6月-1998年3月 1998年3月-1999年7月 1999年8月-2000年6月 2000年6月-2001年12月 2001年12月-2004年1月 2004年1月-2006年10月 2006年11月至今
& s (t = 2000.0) = s (1998.0) + s ⋅ (2000.0 − 1998.0)
基于当前历元、ITRF2005框架下站 坐标转换到CGCS2000示例
确定基准变化引起的站点位移
& Tx (t = 2000.0) = Tx (1998.0) + Tx ⋅ (2000.0 − 1998.0) & T (t = 2000.0) = T (1998.0) + T ⋅ (2000.0 − 1998.0)
【国家自然科学基金】_板块运动模型_基金支持热词逐年推荐_【万方软件创新助手】_20140802
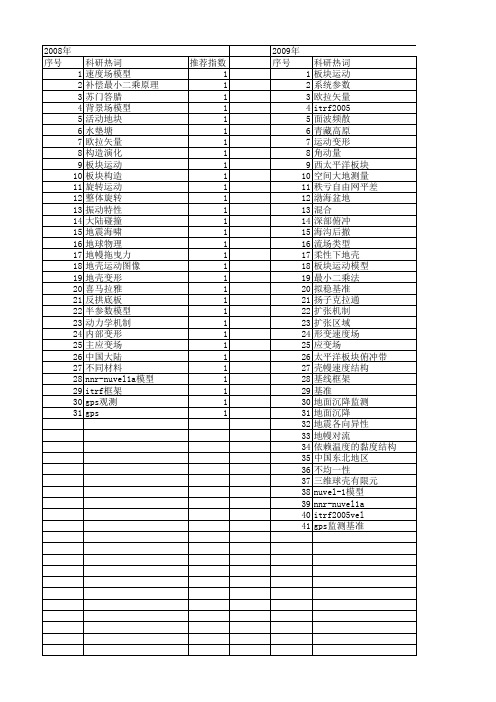
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Байду номын сангаас
sks波 gps资料
1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词 板块运动 系统参数 欧拉矢量 itrf2005 面波频散 青藏高原 运动变形 角动量 西太平洋板块 空间大地测量 秩亏自由网平差 渤海盆地 混合 深部俯冲 海沟后撤 流场类型 柔性下地壳 板块运动模型 最小二乘法 拟稳基准 扬子克拉通 扩张机制 扩张区域 形变速度场 应变场 太平洋板块俯冲带 壳幔速度结构 基线框架 基准 地面沉降监测 地面沉降 地震各向异性 地幔对流 依赖温度的黏度结构 中国东北地区 不均一性 三维球壳有限元 nuvel-1模型 nnr-nuvel1a itrf2005vel gps监测基准
53 54
2011年 科研热词 推荐指数 青藏高原 2 欧拉矢量 2 龙门山断裂带 1 颗粒物质 1 非线性 1 非平衡态 1 钢筋 1 鄂尔多斯块体 1 运动模型 1 车辆 1 超高压变质 1 自适应估计 1 联合仿真 1 石英-柯石英 1 石油地质 1 监测站 1 物理模拟实验 1 滞滑移动 1 深部断裂带延性应变集中 1 水垫塘 1 板块运动 1 板块深俯冲快折返 1 板块 1 最小二乘配置模型 1 断裂系统 1 断裂控油模式 1 数值模型 1 效用函数 1 接触状态 1 拟合推估 1 扩散动力学冷却速率法 1 悬架 1 快波方向 1 应变场 1 应力应变传播 1 巴彦喀拉块体 1 岩石圈变形 1 局域高压微区 1 姿态控制 1 地震预报 1 地震前兆 1 地壳运动 1 同位素定年法 1 压力与深度换算公式 1 动态挤压 1 动力分析 1 剪切作用 1 准噶尔盆地 1 中国大陆 1 中国地壳运动观测网 1 下地壳介质流动 1 上地幔各向异性 1
利用GPS资料采用非连续变形分析模型确定中国大陆地壳运动速度场

1 非 连续 变 形 分 析 方 法 ( D D A)
非连 续 变 形 分 析 (io t uu e r t n ds ni o sdf mai c n o o
a a s , A) 石 根 华博 士 在 1 9 年提 出 的一 n l i DD 是 ys 93
珥 目来源: 国家 自然基金资助项 目( 97 0 1 。 4 9 40 )
维普资讯
22 4
武 汉 大 学 学 报 一 息 科 学 版 信
20 0 2正
种全新 的数值方法。这种方法用位移作为 未知 数, 解平衡方程时则是用 与有限单元法中结构矩 阵分析相同的方法。非连续变形分析以严格遵循 经典力学规则为基础。它可用来分析块体系统的 力和位移的相互作用, 对各块体允许有位移 、 变形
内达到 了 1 的相 对精度 , 且在 中国太 陆 已测 0 并 定 了相 当数 量 的 G S站 点 的多期成 果 , P 可推算 出 这些点 的现今 运 动速 度 , 这就 必 然提 出 了如何 科 学地建立 中 国大 陆现今地 壳运 动速 度场模型 的 问 题, 以便 为地 质 、 学 、 球 物理学 等研究服 务 , 地震 地
和小应 变的逐 步 累 加 的结果 , 么 该地 区 的地 壳 那
运动 和 变 形 就 可 以用 球 面 非 连 续 变 形 分 析 ( D 方法 来模 拟 。基于此 , D A) 本文 采用 球 面 D DA 数值模 拟方法 , 中 国大陆 置 于一 个 非连 续块 体 把
力学系统 之 中 , 立 起 与实 际尽 量 符合 的中 国 大 建 陆动力 学模 型 , 以现有 的 G S测 站速度作 为控 并 P
和应 变 ; 整个块 体 系统 , 滑 动和块 体界 面间 对 允许 张 开或闭合 。如果 知道 每 个块 体 的几 何 形 状 、 荷 载、 材料特 性常数 以及块 体接 触 的摩擦 系数 、 着 粘
工程流体力学中的压力分布和速度场预测模型

工程流体力学中的压力分布和速度场预测模型在工程流体力学中,研究流体在管道、河流、飞行器、汽车等工程领域中的流动现象是非常重要的。
了解流体在不同场景中的压力分布和速度场是设计和优化工程系统的关键。
在本篇文章中,我们将探讨如何建立压力分布和速度场的预测模型,并介绍一些常用的方法和技术。
对于流体在工程中的流动问题,通常可以通过操控边界条件和使用数值模拟方法来进行分析。
压力分布和速度场的预测是其中重要的一部分。
首先,我们将重点讨论压力分布的预测模型。
在工程流动问题中,压力分布的预测通常可以通过求解流体力学的基本方程,如质量守恒方程和动量守恒方程来实现。
这些方程可以通过有限元法、有限差分法或有限体积法等数值方法离散化求解。
在实际应用中,我们通常会使用计算流体力学(CFD)软件来解决这些方程,并获得压力分布的预测结果。
除了数值模拟方法,压力分布的预测还可以通过实验测试来获得。
例如,我们可以利用压力传感器在管道或流体系统中进行测量,然后根据测量结果进行分析和预测。
实验测试通常更加准确和可靠,但也需要更多的时间和成本。
接下来,我们将讨论速度场的预测模型。
在工程流体力学中,速度场的预测有助于我们理解流体的流动规律和性质。
与压力分布预测类似,速度场的预测可以通过求解流体力学方程来实现。
不同的边界条件和流动场景会导致速度场的复杂性。
因此,我们需要选择适当的数值方法和模型来解决这些方程。
在工程流体力学中,常用的速度场预测模型包括雷诺平均N-S方程模型、湍流模型和多孔介质模型等。
这些模型可以通过数值模拟方法求解,从而预测速度场。
其中,雷诺平均N-S方程模型是最常用的模型之一,它基于雷诺应力的平均值来描述流体的运动。
湍流模型则用于描述湍流流动的统计性质,如湍流能量传递和湍流涡的发展。
多孔介质模型则适用于含有多孔介质的流动问题,如土壤中的地下水流动。
除了数值模拟方法,速度场的预测还可以通过实验测试来获得。
与压力分布的预测类似,我们可以使用各种测量设备和技术来获取流体的速度信息。
cems速度场系数

cems速度场系数
CEMS是Contour-based Environmental Modeling System的简写,该系统用于基于数值模型的环境流场建模。
在CEMS中,速
度场系数是用于确定流场速度分布的参数。
速度场系数的值可以根据具体的流场模型和实际情况进行调整和确定。
具体而言,在CEMS中,速度场系数可以根据以下几个方面
来确定:
1. 地理环境:地形、地貌、水文条件等会对流场速度分布产生影响。
速度场系数可以通过观测数据或者基于地理信息系统(GIS)的分析来确定。
2. 大气条件:气体密度、动力学粘性等大气条件会影响流场速度分布。
这些参数可以通过气象观测数据或者模型模拟来获得。
3. 边界条件:边界条件是指流场的边界处的速度分布情况。
根据具体情况,边界条件可以设定为固定速度、无滑移边界、自由边界等。
边界条件的选择将直接影响到速度场系数的确定。
需要注意的是,由于CEMS是基于数值模型的流场建模系统,速度场系数的准确性和合理性对模拟结果的准确性和可靠性至关重要。
因此,在使用CEMS进行环境流场建模时,需要根
据具体情况对速度场系数进行调整和确定,并进行模拟结果的验证和评估。
雷诺时均方程 湍流模型

雷诺时均方程是流体力学中描述湍流的数学方程之一,以法国工程师奥古斯特·雷诺(Augustin-Louis Cauchy-Louis Navier)的名字命名。
雷诺时均方程是通过对湍流进行平均来获得宏观流体动力学方程。
雷诺时均方程可以用于描述湍流中速度场的统计平均行为,其基本形式如下:
∂(ρūi)/∂t + ∂(ρūiuj)/∂xj = -∂(ρu'i'iūj)/∂xj + ∂(τij)/∂xj
其中:
-ρ是流体密度,
- ūi是速度场的时间平均值,
- ui是速度场的波动部分,
-τij是剪切应力张量(描述了流体内部的力与变形速率之间的关系)。
上述方程中第一项表示流体的加速度,第二项表示流体的对流,第三项表示涡度传输,第四项表示剪切应力的空间梯度。
湍流模型是为了解决雷诺时均方程中无法直接求解的湍流项而发展出来的,它通过对湍流的统计特性进行建模,将湍流项表示为其他已知物理量的函数。
常见的湍流模型包括Reynolds-Averaged Navier-Stokes (RANS) 模型、Large Eddy Simulation (LES) 模型和直接数
值模拟(DNS)。
RANS模型是最常用的湍流模型之一,它基于统计平均的假设,将湍流项表示为速度和长度尺度的函数。
LES模型则通过在时间和空间上对湍流进行滤波来解析大尺度涡旋,并对小尺度湍流进行模型化处理。
DNS模型则是对湍流的所有尺度进行直接数值求解,但由于计算复杂度很高,通常只适用于简单的几何情况和低雷诺数流动。
综上所述,雷诺时均方程和湍流模型是描述湍流行为的重要工具,它们在流体力学研究和工程应用中发挥着重要作用。
三种速度场模型在CORS基准站时间序列中的对比分析

三种速度场模型在CORS基准站时间序列中的对比分析
丑凡
【期刊名称】《测绘技术装备》
【年(卷),期】2024(26)1
【摘要】速度场建模方法研究对全球卫星导航坐标时间序列分析具有重要意义。
针对Ordinary Kriging法对分布稀疏点和区域边界点建模精度不高的问题,本文运用顾及高程因素影响的Ordinary Kriging单一改进模型和K-means-Ordinary Kriging组合模型对速度场进行建模。
结果表明,两种改进模型都可以提高Ordinary Kriging基础模型的建模精度。
其中,单一改进模型建模结果在SHK5点的改进最突出,高达8.66 mm/a;组合模型建模结果在NLIB点的最大改进达到8.22 mm/a。
从测区全部CORS点的STD值来看,组合模型对点密度相对低和边界点的速度场建模效果更好。
【总页数】8页(P30-37)
【作者】丑凡
【作者单位】甘肃省有色金属地质勘查局张掖矿产勘查院
【正文语种】中文
【中图分类】P228
【相关文献】
1.利用2015至2016年GNSS观测数据进行天津CORS基准站速度场分析
2.CORS基准站坐标时间序列周期性分析
3.CORS站高程非线性速度场及方差波动
模型构建方法4.安徽省CORS坐标时间序列噪声和速度场分析5.基于Mallat小波的厦门CORS基准站时间序列分析
因版权原因,仅展示原文概要,查看原文内容请购买。
常速度模型 状态方程

常速度模型状态方程
常速度模型(Constant Velocity Model)是一种简单的时间序列预测模型,假设时间序列的变化率是恒定的,即时间序列的值以固定的速度增长或下降。
常速度模型的数学表达式为:
(y_{t} = y_{t-1} + v)
其中 (y_t) 表示时间序列在时刻 (t) 的值,(y_{t-1})表示时间序列在时刻 (t-1) 的值,(v) 表示恒定的速度。
常速度模型的状态方程为:
(x_{t} = x_{t-1} + 1)
其中 (x_t) 表示时间序列在时刻 (t) 的状态,它是一个整数,表示 (y_t) 与 (y_{t-1}) 之间的差值。
因为 (v)是恒定的速度,所以 (x_t) 的变化速度也是恒定的。
请注意,这只是一个简化的模型,实际的时间序列数据可能受到许多其他因素的影响,因此需要更复杂的模型来准确预测时间序列的变化。
速度场系数的修改

速度场系数的修改在计算流体力学(CFD)中,速度场系数是表示流体流动速度的重要参数。
这些系数对于预测流体运动方向和速度非常重要。
在某些情况下,我们可能需要修改这些系数,以便更准确地模拟流动过程。
本文将重点介绍如何修改速度场系数,以便实现更好的流动预测。
1. 了解速度场系数首先,我们需要知道速度场系数是什么以及它们如何影响流动。
速度场系数包括雷诺数、马赫数、弗劳德数等。
这些系数反映了流体运动的不同特征。
例如,雷诺数表示流体惯性和粘性力作用的比例;马赫数表示流体流动速度相对于该介质声速的比值;弗劳德数表示流体通过管道时的不稳定性和涡流强度。
理解这些系数对于正确修改它们非常重要。
2. 根据实际情况建立模型要修改速度场系数,首先需要基于实际情况建立模型。
这通常涉及到对物理实验的观察和数据分析。
例如,在模拟乐高玩具汽车的风阻情况时,我们可以使用风洞模拟不同尺寸和形状的模型,以了解其流体阻力特征。
在建立模型时,我们需要考虑多种因素,如流体属性、流动速度、管道形状等。
3. 使用计算流体力学软件一旦建立了模型,我们可以使用计算流体力学(CFD)软件来分析和预测流体运动。
在CFD分析中,我们可以修改速度场系数以实现更准确的流动预测。
例如,当我们在飞行器上进行气动分析时,我们可以根据飞行器形状和飞行速度,修改雷诺数和马赫数以更好地反映实际情况。
使用CFD软件的好处在于,我们可以轻松地修改速度场系数,并根据修改结果进行分析和优化。
这使我们能够更好地理解流体运动的特性,并获得更准确的预测结果。
4. 使用实验验证最后,我们需要使用实验验证修改后的速度场系数是否正确。
在设计飞机或汽车时,我们可以进行多种实验来验证飞行或行驶过程中的流体运动特性。
这些实验可以包括风洞测试、液体模型实验等。
实验的结果可以在一定程度上验证我们修改速度场系数的正确性。
总结修改速度场系数可以帮助我们更好地了解流体运动的特性,并获得更准确的预测结果。
但是,为了正确修改这些系数,我们需要了解它们的基本知识和影响因素,并建立与实际情况相符合的模型。
速度模型算法

速度模型算法全文共四篇示例,供读者参考第一篇示例:速度模型算法是一种用来尽快找到解决方案的算法。
在计算机科学中,速度模型算法通常被用来解决优化问题,如最短路径问题、最小生成树问题等。
这些问题在现实生活中有着广泛的应用,比如在交通规划中找到最短路径,或者在通讯网络中找到最小生成树来建立网络拓扑。
在速度模型算法中,重点是要尽快找到一个可行解或者接近最优解的解。
速度模型算法一般不会保证找到最优解,但是会尽快找到一个满足要求的解。
常见的速度模型算法包括贪婪算法、分治算法、动态规划算法等。
贪婪算法是一种简单而高效的速度模型算法。
它的基本思想是每一步都选择局部最优解,最终得到全局最优解。
贪婪算法在很多问题中都有着良好的表现,比如霍夫曼编码、最小生成树等。
贪婪算法的缺点是有可能得到的不是最优解,但是实际应用中往往能够满足要求。
分治算法是一种将问题分解成子问题并分别求解的速度模型算法。
每个子问题的解会被合并成一个更大的问题的解。
分治算法在很多问题中有很好的表现,比如归并排序、快速排序等。
分治算法的优点是能够利用多线程或并行计算的方式加快求解速度。
动态规划算法是一种将问题分解成重叠子问题并存储子问题解的速度模型算法。
动态规划算法通常用来解决优化问题,比如最长公共子序列问题、最长递增子序列问题等。
动态规划算法的优点在于能够避免重复计算,加快求解速度。
但是动态规划算法的缺点是需要额外的存储空间来存储子问题解,因此在一些问题中可能不适用。
除了以上这三种速度模型算法,还有很多其他的速度模型算法,比如模拟退火算法、遗传算法、蚁群算法等。
这些算法在不同的问题中有着不同的表现,可以根据具体问题的特点选择合适的算法来求解。
速度模型算法是一种用来快速找到解决方案的算法。
在实际应用中,我们可以根据问题的特点选择合适的速度模型算法来求解,以提高运算效率和求解速度。
速度模型算法在各个领域都有着广泛的应用,是计算机科学中的重要研究方向之一。
kb值和速度场系数

kb值和速度场系数摘要:一、概念介绍1.kb 值2.速度场系数二、kb 值的应用1.地下水环境监测2.污染物迁移模拟三、速度场系数的应用1.水文水资源分析2.水利工程设计四、kb 值与速度场系数的关联1.数值模型2.参数关系五、总结1.意义与价值2.发展前景正文:kb 值和速度场系数在水文学和地下水环境研究中具有重要的意义。
kb 值是描述地下水动力学特性的一个参数,它反映了地下水在介质中的渗流能力。
速度场系数则是描述地下水运动状态的参数,它反映了地下水在介质中的运动速度。
本文将介绍这两个参数的概念、应用以及它们之间的关联。
kb 值在地下水环境监测中有着广泛的应用。
由于kb 值能够反映地下水在介质中的渗流能力,因此,通过测量kb 值,我们可以对地下水环境进行有效监测,为地下水污染治理提供科学依据。
此外,在污染物迁移模拟中,kb 值也是一个重要的参数。
通过对kb 值的合理运用,我们可以更好地模拟污染物在地下水中的迁移过程,从而为污染防控提供支持。
速度场系数在水文水资源分析和水利工程设计中具有重要应用。
在水文水资源分析中,速度场系数能够反映地下水的运动状态,为水文过程的研究提供重要信息。
在水利工程设计中,速度场系数则可以指导工程师们合理设计水利工程,以满足水资源的合理利用和调控需求。
kb 值与速度场系数之间存在密切的关联。
在数值模型中,这两个参数通常一起出现,共同描述地下水在介质中的运动状态。
同时,它们之间也存在一定的参数关系。
通过研究这种关系,我们可以更好地理解地下水在介质中的运动规律,从而为地下水研究提供理论支持。
总之,kb 值和速度场系数在水文学和地下水环境研究中具有重要意义和价值。
它们在监测地下水环境、模拟污染物迁移、分析水文水资源和指导水利工程设计等方面发挥着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间大地测量学作业学院:测绘科学与技术学院专业:测绘工程姓名:曹延虎学号:2014105542015年7月地壳运动速度场模型的建立方法一 模型实验分析1.1 多面函数法拟合水平速度场多面函数法是美国Hardy 教授于1977年提出的,它基于任何一个光滑的数学表面总可用一系列规则的数学函数以任意精度逼近的思想,利用已测点推估未测点。
由于具有设计灵活、可控性强等优点,多面函数法自提出以来,就被广泛用于与地学有关的插值问题。
设有m 个已测点s(x,y),s 为非随机信号,s(x,y)为点(x,y)上的水平运动速率,可用n 个核函数的总和去逼近任意点的水平运动速率。
式中n为所选的已知水平运动速率的点,称为结点;αi 为待定参数;Q 为核函数,一般选为对称距离型函数,δ为平滑因子。
本次模型取k=1/2,n=20,δ=0.01和δ=0.1的正双曲面函数为核函数。
平滑因子δ的作用是改变核函数的形状。
核函数一旦选定,平滑因子的改变同样也会影响内插与拟合的效果。
一般来讲,δ越大,核函数所表达的曲面越平缓;δ越小,曲面越陡峭。
不同的核函数对平滑因子的敏感度不同,显然,平滑因子的敏感度越低越好,这样的拟合效果将更趋于稳定。
本次实验拟合了30个数据,如下图红线所示。
k oi oi ni oi oi i y y x x yoi xoi y x Q y x y x Q y x v ])()[(),,,(),,,(),(2221δα+-+-=⋅=∑=Pv Q PQ Q v Q V Q v T T 1)(-=-=⋅=ααα图1 δ=0.01 效果图图2 δ=0.1 效果图图3 加入断层效果图1.1.1 Matlab源程序(原始数据及中间值见EXCEL表)%读入40个已知数据Jb2=xlsread('原始数据经纬度.xls',1,'B2:B41'); %读入经度Jl2=xlsread('原始数据经纬度.xls',1,'C2:C41'); %读入纬度%读入20个结点数据JJb2=xlsread('原始数据经纬度.xls',1,'I2:I21');%读入经度JJl2=xlsread('原始数据经纬度.xls',1,'J2:J21');%读入纬度how2=size(Jb2,1);vol2=size(JJb2,1);array2=[how2,vol2];for i2=1:how2for j2=1:vol2array2(i2,j2)=sqrt((Jb2(i2)-JJb2(j2))^2+(Jl2(i2)-JJl2(j2))^2+0.01^2); endend%读入已知点的速度值Vx2=xlsread('原始数据经纬度.xls',1,'D2:D41');Vy2=xlsread('原始数据经纬度.xls',1,'E2:E41');%计算拟合模型的参数Rx2=inv(array2'*array2)*array2'*Vx2;Ry2=inv(array2'*array2)*array2'*Vy2;xlswrite('原始数据经纬度.xls',Rx2,2,'A1');%将X方向的参数值输出xlswrite('原始数据经纬度.xls',Ry2,2,'B1');%将Y方向的参数值输出%计算改正数VVx2和VVy2VVx2=array2*Rx2-Vx2;VVy2=array2*Ry2-Vy2;%计算单位权中误差dx2=sqrt((VVx2'*VVx2)/(how2-vol2));dy2=sqrt((VVy2'*VVy2)/(how2-vol2));xlswrite('原始数据经纬度.xls',dx2,2,'C1'); %将X方向的中误差输入到excle中去xlswrite('原始数据经纬度.xls',dy2,2,'D1'); %将Y方向的中误差输入到excle中去%计算待估参数的协因数,两个协因数阵相同Qx2=inv(array2'*array2);Qy2=inv(array2'*array2);Dx2=sqrt(Qx2)*dx2;%计算方差Dy2=sqrt(Qy2)*dy2;%将参数的中误差输出xlswrite('原始数据经纬度.xls',Dx2,3,'E1'); %将X方向的参数中误差输入到excle中去xlswrite('原始数据经纬度.xls',Dy2,3,'E41'); %将Y方向的参数中误差输入到excle中去%用模型计算待定点的速度Unb2=xlsread('原始数据经纬度.xls',1,'D127:D157');%读入待求点的经度Unl2=xlsread('原始数据经纬度.xls',1,'E127:E157');%读入待求点的纬度Array_Un2=[size(Unb2,1),size(JJb2,1)];for k2=1:size(Unb2,1)for m2=1:size(JJb2,1)Array_Un2(k2,m2)=sqrt((Jb2(k2)-JJb2(m2))^2+(Jl2(k2)-JJl2(m2))^2+0.01^2);endendSpeed_X2=Array_Un2*Rx2; %计算南北方向(X方向)的速度Speed_Y2=Array_Un2*Ry2; %计算东西方向(Y方向)的速度%往excle中写数据%xlswrite(filename,A,sheet,range); % A就是待写的数据xlswrite('原始数据经纬度.xls',Speed_X2,1,'H127');xlswrite('原始数据经纬度.xls',Speed_Y2,1,'I127');1.2 局部多项式法拟合水平速度场多项式的形式有三种:一次多项式、二次多项式和三次多项式。
在插值时,寻找一个适合的函数并非易事,如多项式阶数太大的问题,其波动也会很大。
针对这个问题,局部多项式法是一个不错的选择。
它作为常用的拟合方法之一,能在给定搜索区域内对插值对象所有点插值出合理特定阶数的多项式,局部多项式插值产生的曲面根多依赖于局部的变异。
常见的多项式形式如下:33222222),(),(),(jY iX hXY Y X fY eX dXY cY bX a Y X F fY eX dXY cY bX a Y X F cYbX a Y X F +++++++++=+++++=++=本次拟合水平速度场所采用的数据与多面函数法的已知数据一样,本次实验也拟合了30个数据,如下图红线所示。
图4 拟合效果图1.2.1 Matlab 源程序(原始数据及中间值见EXCEL 表)%40个结点局部多项式拟合的预计模型clear,clc;Y=xlsread('原始数据经纬度.xls',1,'B2:B41'); %读入已知点数据,读入经度 Y X=xlsread('原始数据经纬度.xls',1,'C2:C41'); %读入纬度 X %读入40个结点数据Vy=xlsread('原始数据经纬度.xls',1,'D2:D41'); %读入东西方向的速度 Vy Vx=xlsread('原始数据经纬度.xls',1,'E2:E41'); %读入南北方向的速度 Vx how3=size(Y,1);array3=zeros(how3,10);for i3=1:how3for j3=1:10if j3==1array3(i3,j3)=1; % 1elseif j3==2array3(i3,j3)=X(i3); % Xelseif j3==3array3(i3,j3)=Y(i3); % Yelseif j3==4array3(i3,j3)=X(i3)*Y(i3); % X*Yelseif j3==5array3(i3,j3)=X(i3)^2; %X^2elseif j3==6array3(i3,j3)=Y(i3)^2; %Y^2elseif j3==7array3(i3,j3)=X(i3)^2*Y(i3); % X*Y^2elseif j3==8array3(i3,j3)=Y(i3)^2*X(i3); % Y*X^2elseif j3==9array3(i3,j3)=X(i3)^3; % X^3elseif j3==10array3(i3,j3)=Y(i3)^3; % Y^3endendend%计算拟合模型的参数Rx3=inv(array3'*array3)*array3'*Vx; %计算X方向的参数Ry3=inv(array3'*array3)*array3'*Vy; %计算Y方向的参数xlswrite('原始数据经纬度.xls',Rx3,2,'A1');%将X方向的参数值输出xlswrite('原始数据经纬度.xls',Ry3,2,'B1');%将Y方向的参数值输出%计算改正数VVx2和VVy2VVx3=array3*Rx3-Vx;VVy3=array3*Ry3-Vy;% %计算单位权中误差dx3=sqrt((VVx3'*VVx3)/(how3-10));dy3=sqrt((VVy3'*VVy3)/(how3-10));xlswrite('原始数据经纬度.xls',dx3,2,'C1'); %将X方向的中误差输入到excle中去 xlswrite('原始数据经纬度.xls',dy3,2,'D1'); %将Y方向的中误差输入到excle中去% %计算待估参数的协因数,两个协因数阵相同Qx3=inv(array3'*array3);Qy3=inv(array3'*array3);% %计算参数的中误差Dx3=sqrt(Qx3)*dx3;Dy3=sqrt(Qy3)*dy3;% %将参数的中误差输出xlswrite('原始数据经纬度.xls',Dx3,3,'A1'); %将X方向的参数中误差输入到excle 中去xlswrite('原始数据经纬度.xls',Dy3,3,'B1'); %将X方向的参数中误差输入到excle 中去% %用模型计算待定点的速度% %计算南北方向(X方向)的速度Unb3_Y=xlsread('原始数据经纬度.xls',1,'D127:D157');%读入待求点的经度 YUnl3_X=xlsread('原始数据经纬度.xls',1,'E127:E157');%读入待求点的纬度 XOritation=zeros(size(Unb3_Y),10);for k=1:size(Unb3_Y)for n=1:10if n==1Oritation(k,n)=1; % 1elseif n==2Oritation(k,n)=Unl3_X(k); % Xelseif n==3Oritation(k,n)=Unb3_Y(k); % Yelseif n==4Oritation(k,n)=Unl3_X(k)*Unb3_Y(k); % X*Yelseif n==5Oritation(k,n)=Unl3_X(k)^2; %X^2elseif n==6Oritation(k,n)=Unb3_Y(k)^2; %Y^2elseif n==7Oritation(k,n)=Unl3_X(k)^2*Unb3_Y(k); % X*Y^2elseif n==8Oritation(k,n)=Unb3_Y(k)^2*Unl3_X(k); % Y*X^2elseif n==9Oritation(k,n)=Unl3_X(k)^3; % X^3elseif n==10Oritation(k,n)=Unb3_Y(k)^3; % Y^3endendendX_Speed=Oritation*Rx3; %计算相应点的X 方向速度Y_Speed=Oritation*Ry3; %计算相应点的Y 方向速度xlswrite('原始数据经纬度.xls',X_Speed,1,'F127'); %将X 方向的参数中误差输入到excle 中去xlswrite('原始数据经纬度.xls',Y_Speed,1,'G127'); %将Y 方向的参数中误差输入到excle 中去1.3 反距离加权法拟合水平速度场反距离加权法是一个加权平均插值法,又称为谢别德法。
