单缝夫琅禾费衍射强度
夫琅禾费衍射实验报告

[实验题目]
夫琅禾费衍射的定量研究
[实验目的]
1、掌握在光学平台上组装、调整光路的基本方法; 2、观察并定量测定不同衍射元件产生的光衍射图样; 3、学习微机自动控制和测量衍射光强的分布及其相关参量。
[实验内容]
1、掌握在光学平台上组装、调试产生夫琅禾费衍射的光路; 2、 定量研究单缝衍射图样分布规律 (光强比、 对称性、 缝宽等) , 统一取第二排第四列的单狭缝(缝.宽 b=175μm) ; 3、定量研究三缝衍射光强分布,计算缝间距和缝宽(缝宽 b=40 μm,缝间距 d=90μm),定性分析干涉和衍射的相互关系; 4、定性观察 10 个不同衍射屏衍射的光强分布。
2
2
表示衍射光场任意方向的相对光强。
单缝衍射光强分布的特点: 单缝的夫琅禾费衍射图样的中心有一 个主极强(零级衍射斑),两侧都有一系列次极强和暗斑。主极强出现 在 sin
0 的地方, 原因是到这里的各条衍射光线有相同的
相位,它们相干叠加的结果具有最大的光强。 几何光学中的光线就是零级衍射线, 几何光学中的象点就是零级 衍射斑的中心。 在单缝衍射因子具有极大值的地方, 即在
一、单缝衍射 计算光强比: 背景光: I p
I 3 I 4 4 15 9.5 2 2
I1 I 2 175 172 1.83%( 10%) . 对称性要求: I I 172 175 1 2 Ip 9.5 2 2
4
主极强位置与缝数目 N 无关,但 N 越大,主极强宽度越小;相 邻主极强之间有 N-1 个暗纹和 N-2 个次极强;光强分布的外部轮廓 (包络线型)与单缝衍射的形状相同,这是单缝衍射因子的作用。
夫琅禾费单缝衍射光强分布的研究

夫琅禾费单缝衍射光强分布的研究(Research Of Fraunhofer Single Slot Diffraction Of LightIntensity Distribution)摘要:我们在光学中学习了有关夫琅禾费单缝衍射和圆孔衍射的内容,本文主要是对夫琅禾费单缝衍射光强的计算公式进行数学推导以及拓展,并且根据推导的数学公式对夫琅禾费单缝衍射光强分布情况进行讨论,对夫琅禾费单缝衍射的特点进行分析介绍。
关键词:夫琅禾费单缝衍射(Fraunhofer single slot diffraction)、光强(Light intensity)、光强分布(Light intensity distribution)、最大值(Maximum)引言:光的衍射是光的波动性的重要现象之一。
衍射现象即波在传播过程中不沿直线传播,而是向各方向绕射的现象。
而光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强分布不均匀的现象,称为光的衍射。
在衍射现象中,把平行光束的衍射现象,称为夫琅禾费衍射。
夫琅禾费衍射在光学研究中有着重要意义,它主要包括单缝衍射、圆孔衍射。
这里我重点介绍夫琅禾费单缝衍射的光强分布特点。
一、夫琅禾费单缝衍射实验装置与衍射图样的特点。
所谓夫琅禾费衍射是指光源、衍射屏和观察屏三者之间都是相距无限远的衍射情况。
即相当于入射光和衍射光都是平行的情况。
在这种情况下计算衍射花样中光强的分布时,数学运算就比较简单。
所谓光源在无限远,实际上就是把光源置于第一个透镜的焦平面上,使之成为平行光束;所谓观察角在无限远,实际上是在第二个透镜的焦平面上观察衍射花样。
由于透镜的会聚,衍射花样的光强将比菲涅耳衍射花样的光强大大增加。
夫琅禾费单缝衍射包含着衍射现象的许多主要特征。
夫琅禾费单缝衍射光路图如下图所示:夫琅禾费单缝衍射图样的主要特点如下:(1)中央有一条特别明亮的亮条纹,其宽度是其他亮条纹的两倍;其他亮条纹的宽度相等,亮度逐渐下降。
单缝衍射光强的分布测量实验报告

竭诚为您提供优质文档/双击可除单缝衍射光强的分布测量实验报告篇一:衍射光强分布测量衍射光强分布测量***,物理学系摘要:本实验利用激光为光源研究激光经过单缝与单丝时的衍射光强度分布情况。
激光的高准直性符合夫琅和费远场条件,且高单色性保证测量时没有不同波长光的叠加影响。
光感应器方面使用光栅尺与电脑连接做0.02毫米/点的高精度自动扫描。
通过巴比涅原理迂回得到了没有直射光时单丝的衍射光强分布,完整验证了运用衍射光强分布来测量小微物体的长度的方法和可行性,并实际运用此法测量了铜丝和头发丝的直径。
关键词:衍射分布巴比涅原理单缝直径测量ThemeasurementoftheDistributionofLightDiffraction YixiongKeYiLin,DepartmentofphysicsAbstarct:Thisexperimentmadeuseoflaserasthelightsourcetoverif yaseriesofdiffractionpatternsof633nmlaserviadiffere ntsingleslitsandmonofilaments.Thecollimationfeature ofthelasermeetstheconditionofFraunhoferdiffraction, themonochromicfeatureoflaserprovideabetterexperimen talenvironmentthatthediffractionpatternwon`tbeinter ferebythelightofotherwavelength.weuselinearencorder connectedtopcviauLI(universalLaboratoryInterface)as thesensortoautomaticallyscanthediffractionpatternwi ththeratioof0.02mmperdot.weusebabinet’sprincipletogetthediffractionpatternofamonofilament p letelyverifiedthemethodandfeasibilityofmeasuringati nyobjectwithitsdiffractionpattern.Inaddition,wetryt omeasurethediameterofacopperwireandpeople’shairinthiswayKeywords:Diffractiondistributionbabinet`sprinciplesingleslitsmeasureDiameterofthewire1一、引言衍射是波遇到障碍物时便利直线传播的现象。
20.2 单缝的夫琅禾费衍射

B
A C
·P
0
f
AC = a sinϕ = (2k +1)
(3) OP间有几条暗纹? 间有几条暗纹? 间有几条暗纹
λ
2 0 1 1 2
= 2.5λ
∴ k =2
2
两条暗纹
单缝可分成几个半波带? (4) 单缝可分成几个半波带?
5个半波带
点为第二级暗纹,则缝可分成几个半波带? (5) 若P点为第二级暗纹,则缝可分成几个半波带? 缝可分成4 AC = a sinϕ = 2k ⋅ = 4⋅ 缝可分成4个半波带 2 2
§20.2 单缝的夫琅禾费衍射
一、实验装置 二、 用半波带法分析条纹的形成 三、用旋矢法求解强度分布 四、条纹分析 五、其他衍射现象 六、光学仪器的分辨本领
1
第20章光的衍射
2
第20章光的衍射
一、实验装置
P
O
*
f′
ϕ
B
ϕ
A
·x
0
正一级 中央亮纹 负一级
C
f
( 单缝夫琅和费衍射 )
单缝处波面看作无穷多个相干波源 P点是 (无穷)多光束干涉的结果 点是 无穷)
λ
D
物点 一一对应 物点
第20章光的衍射
像点 像斑
ϕ1
可分辨
ϕ1 > δϕ
ϕ2
刚可分辨
ϕ2 = δϕ
ϕ3 < δϕ
ϕ3
不可分辨
瑞利判据: 对于两个等光强的非相干物点,如果一个像斑中心 瑞利判据 对于两个等光强的非相干物点 如果一个像斑中心 恰好落在另一像斑的边缘(第一暗纹处 第一暗纹处),则此两像被认为是刚 恰好落在另一像斑的边缘 第一暗纹处 则此两像被认为是刚 好能分辨。 好能分辨。此时两像斑中心角距离为最小分辨角
ch2-3 夫琅禾费单缝衍射

一 实验装置和衍射图样的特点
缝平面 透镜L′ ′ 装置如图 透镜L
观察屏
·p
0 A
f
S
*
f′
b
图样特点 中央有一条特别明亮的亮条纹
两侧排列着强度极小的亮条纹, 两侧排列着强度极小的亮条纹,相邻两两 条问纹间还有一条暗纹。 条问纹间还有一条暗纹。 两侧的亮条纹等宽, 两侧的亮条纹等宽,中央亮条纹的宽度是 两侧的二倍。 两侧的二倍。
二.强度的计算
菲涅尔半波带法 惠更斯-菲涅尔积分公式 惠更斯-菲涅尔积分公式
K(θ ) E = ∫ dE = ∫ C dS cos(wt −ϕ) r
λ
a
δ
P
θ
θ 为衍射角
•
f
P点的光强取决于狭缝上各子波源 点的光强取决于狭缝上各子波源 到此的光程差。光强分布? 到此的光程差。光强分布?
δ 为缝边缘两条光线在 p 点的光程差
二者常常同时存在。 二者常常同时存在。
例如,不是极细缝情况下的双缝干涉, 例如,不是极细缝情况下的双缝干涉,就应 情况下的双缝干涉 该既考虑双缝的干涉,又考虑每个缝的衍射。 该既考虑双缝的干涉,又考虑每个缝的衍射。
菲涅耳半波带的数目决定于
δ = b sin θ
P•
•
•
•
λ
2
f
1、k 由 b、λ、θ 确定。 、 确定。 2、k 不一定是整数。 、 不一定是整数。
对应沿 θ 方向衍射 b sin θ 的平行光狭缝, 的平行光狭缝,波 k = λ 阵面可分半波带数
2
三、单缝衍射明暗条纹条件
由半波带法可得明暗纹条件为: 由半波带法可得明暗纹条件为:
b sin θ = kλ , ( k = +1,+2LL)
§7夫琅禾费单缝和矩孔衍射
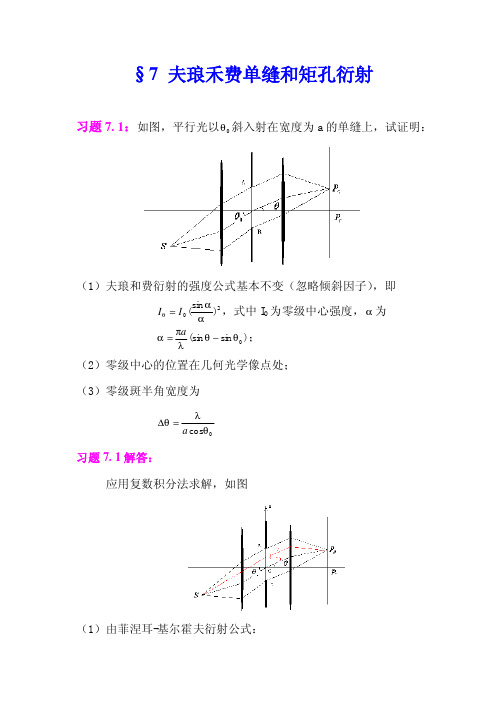
折射光:
n = 1.5, a = 1cm, λ = 0.6µm,θ0 = arc(sin 75o / n)
∆θ =
λ
≈ 5.2 ×10−4 rad
(na) cosθ0
(3)入射角为 850
反射光: n = 1, a = 1cm, λ = 0.6µm,θ0 = 85o
∆θ =
λ
≈ 3.4 ×10−4 rad
∆θ = λ a
线宽度为
∆l = 2 f∆θ = 2 f λ a
则
a=2f λ ∆l
代入数值,得
a = 63µm
Σ0 = Σa + Σb
则
U~0 (P) = U~a (P) +U~b (P)
在夫琅和费衍射中,除几何像
点外,自由传播场
~ U0
(
P)
=
0
,故
除几何像点外,有 U~a (P) = −U~b (P)
所以
Ia (P) = Ib (P) 即产生相同的夫琅和费衍射图样。
习题 7. 4:衍射细丝测径仪就是把单缝夫琅和费衍射装置中的单缝用
(na) cosθ0
折射光:
n = 1.5, a = 1cm, λ = 0.6µm,θ0 = arc(sin 85o / n)
∆θ =
λ
≈ 5.4 ×10−4 rad
(na) cosθ0
习题 7. 3:试用巴俾涅原理证明:互补的衍射屏产生的夫琅和费衍射 图样相同。
习题 7. 3 解答: 巴俾涅原理:若 a 和 b 为互补的衍射屏,即
α =0
即
α
=
πa λ
(sin θ
−
sinθ0 )
=
0
光学之夫琅禾费单缝衍射的强度和条纹

由于Δφ很小,所以sinΔφ = Δφ,因此
A
A0
sinu u
单缝 L A
y F
其中A0 = nΔA,u = πasinθ/λ。
θ
O
F点的 光强为
I I0(siunu)2 其中I0 = A02。
aB
C Δδ
当θ→0时,u→0,因此I→I0。I0是最大光强,称为主极大。
几何路程不同,却有相同的光程。
从而干涉互相加强。
单缝中心O处出现一条与单缝平行的亮条纹,即中央明条纹。
{范例7.5} 夫琅禾费单缝衍射的强度和条纹
波长为λ的单色光,平行通过宽度为a的单缝,产生的衍射称为
夫琅禾费单缝衍射。(1)说明半波带理论,分析衍射明暗条纹的
分布规律。在什么地方光强最大? 单缝 L
[解析](1)如图所示,单缝AB的宽度 A
F
为a,其长度方向垂直于屏幕。
平行光垂直入射到狭缝上,
a
O
通过单缝之后,光线经过透
B
镜L会聚在屏幕上某点F。
单缝内AB间各点的子波源都具有同一 单缝上各子波源发出
相位,由于透镜不产生附加的光程差, 的子波到达O点后仍 从单缝上各点到达O点的光线所经过的 然具有相同的位相,
(k = 1,2,3,…)
如果衍射角不满足上面两式,也就是说:在这些方向上单缝既 不能分割成偶数个半波带,也不能分割成奇数个半波带,
则屏幕上对应位置的的光强介于极大和极小 之间,使得明条纹在屏幕上延伸一定的宽度。
这是因为 条纹形成
两个公式给出的分别是明条纹和暗条纹的中心位置。 的理论不
明条纹的宽度就是两条暗条纹之间的距离。
单缝衍射的光强分布及缝宽测定

单缝衍射的光强分布及缝宽测定周鹏1(武汉大学 物理科学与技术学院,湖北,武汉,430072)摘要:本实验利用光电转化法研究单缝夫琅禾费衍射的光强分布,并利用衍射花样测定单缝的宽度,加深了对光的衍射理论的理解。
关键词:单缝衍射;光强分布;光电检流计1作者:周鹏(1994.11—),男,山东济宁人,武汉大学2011级物理弘毅班本科生,学号:20113010200061.引言为了计算衍射图必须取一定的近似,通常取菲涅尔近似和夫琅禾费近似,相应的衍射区光波的行为分别为菲涅尔衍射和夫琅禾费衍射。
夫琅禾费衍射要求光源级接受屏到衍射屏的距离都是无限远或相当于无限远,其衍射图样不随距离的增加而改变。
夫琅禾费衍射的计算较菲涅尔衍射简单,在傅里叶光学中具有重要的意义。
2.实验原理图 1 夫琅禾费衍射原理图夫琅和费衍射是平行光的衍射,在实验中可借助两个透镜来实现,如图1所示。
与光轴平行的衍射光会聚于屏上0P 处,是中央亮纹的中心,其光强设为0I ;与光轴成θ 角的衍射光束会聚于P θ 处,可以证明, P θ处的光强I θ为202sin ,s n i u I I u a u θλπθ==(1)式中,a 为狭缝宽度,λ为单色光的波长。
理论上可以证明,激光发散角(rad 53101~101--⨯⨯)很小,可当做平行光入射.不加透镜,若满足2/8L a λ>>,单缝衍射就处于夫琅禾费衍射区域。
根据该式可以对L 的取值范围进行估算:实验时,若取4110a m -≈⨯,入射光是He-Ne 激光,其波长为632.80nm ,2/ 1.62a cm cm λ=≈,所以只要取cm L 20≥,就可满足夫琅禾费衍射的远场条件.但实验证明,取80L cm ≈,结果较为理想由(1)式可知:当0u =时,衍射光强有最大值;当(1,2, 3...)u k k π±±==±时,衍射光强有极小值,对应于屏上的暗纹,由于θ值实际上很小,因此可近似地认为暗纹对应的衍射角为/k a θλ≈。
基于MATLAB的矩孔、单缝、圆孔夫琅和费衍射概诉

课程设计任务书学生姓名:专业班级:指导教师:工作单位:信息工程学院题目: 夫琅和费矩孔、单缝、圆孔衍射图样一、设计目的了解MA TLAB软件的基本知识,基本的程序设计,软件在高等数学和工程数学中的应用,学会使用软件进行数值计算和控制工程中的应用。
二、设计内容和要求1.绘制弗朗禾费矩孔、单缝和圆孔衍射图样,可以是二维的或三维的,也可以两种都有。
改变矩孔、单缝和圆孔的参数,比较衍射条纹的变化。
2. 学习Matlab语言的概况和Matlab语言的基本知识。
3.学习Matlab语言的程序设计。
三、初始条件计算机;Matlab软件。
四、时间安排1、2015年01月19日,任务安排,课设具体实施计划与课程设计报告格式的要求说明。
2、2015年01月20日,查阅相关资料,学习Matlab语言的基本知识,学习MATLAB语言的应用环境、调试命令,绘图功能函数等。
3、2015年01月21日至2015年01月22日,Matlab课程设计制作和设计说明书撰写。
4、2015年01月23日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:2015年01 月19日系主任(或负责教师)签名:2015年01 月19日目录摘要 (I)1.设计的内容及要求 (1)1.1设计的目的 (1)1.2设计任务要求 (1)2.设计原理及设计思路 (1)2.1夫琅和费干涉理论 (1)2.1.1夫琅和费圆孔衍射 (2)2.1.2夫琅和费矩孔衍射 (2)2.1.3夫琅和费单缝衍射 (2)2.2设计思路 (3)3.仿真及分析 (4)4.心得和体会 (8)参考文献 (8)摘要物理光学理论较为复杂抽象,实验现象的演示对条件要求高。
采用MATLAB7.0强大的函数作图功能对矩孔、单缝、圆孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。
从而加深对夫琅和费原理、概念、和图像的理解。
通过使用MATLAB编写程序,不仅理解了物理思想,而且了解了运用软件解决物理问题的方法。
单缝衍射光强分布实验报告

单缝衍射光强分布【实验目的】1.定性观察单缝衍射现象和其特点。
2.学会用光电元件测量单缝衍射光强分布,并且绘制曲线。
【实验仪器】【实验原理】光波遇到障碍时,波前受到限制而进入障碍后方的阴影区,称为衍射。
衍射分为两类:一类是中场衍射,指光源与观察屏据衍射物为有限远时产生的衍射,称菲涅尔衍射;一类是远场衍射,指光源与接收屏距衍射物相当于无限远时所产生的衍射,叫夫琅禾费衍射,它就是平行光通过障碍的衍射。
夫琅禾费单缝衍射光强;其中 λ;a 为缝宽,为衍射角,λ为入射光波长。
上图中 为衍射角,a 为缝宽。
【实验内容】(一)定性观察衍射现象1.按激光器、衍射板、接收器(屏)的顺序在光节学导轨上放置仪器,调节光路,保证等高共轴。
衍射板与接收器的间距不小于1m。
2.观察不同形状衍射物的衍射图样,记录其特点。
(二)测量单缝衍射光强分布曲线1.选择一个单缝,记录缝宽,测量-2到+2级条纹的光强分布。
要求至少测30个数据点。
2.测量缝到屏的距离L。
3.以为横坐标,I/I0为纵坐标绘制曲线,在同一张图中绘出理论曲线,做比较。
【实验步骤】1.摆好实验仪器,布置光路如下图顺序为激光器—狭缝—接收器—数字检流计,其中狭缝与出光口的距离不大于10cm,狭缝与接收器的距离不小于1m。
2.调节激光器水平,即可拿一张纸片,对准接收器的中心,记下位置,然后打开激光器,沿导轨移动纸片,使激光器的光点一直打纸片所记位置,即光线打过来的高度要一致。
3.再调节各光学元件等高共轴,先粗调,即用眼睛观察,使得各个元件等高;再细调,用尺子量取它们的高度(狭缝的高度,激光器出光口的高度,接收器的中心),调节升降旋钮使其等高,随后用一纸片,接到光源发出的光,以其上的光斑位置作为参照,依次移动到各个元件前,调节他们的左右(即调节接收器底座的平移螺杆,狭缝底座的平移螺杆)高低,使光线恰好垂直照到元件的中心。
4.调节狭缝宽度,使光束穿过,可见衍射条纹,调节宽度,使条纹中心亮纹的宽度约为5mm,且使得条纹最亮,而数字检流计的读数最大,经过上述调节后,上述任何一个旋钮的改变都会使读数变小。
物理实验居家单缝夫琅禾费衍射实验数据及完整实验报告和结论

物理实验居家单缝夫琅禾费衍射实验数据及完整实验报告和结论家庭单缝夫琅禾费衍射实验实验目的:1、了解夫琅禾费(Fraunhofer Lines)被用于把窄线宽的原子谱线用来测量光谱中的原子或分子信号2、研究夫琅禾费把反谱仪角度和反谱仪对散射算法的影响实验材料:铂家具,反谱仪,单缝夫琅禾费模板,衍射模板,记录仪等实验方法使用反射仪配合衍射模板测量夫琅禾费的宽度和强度,同时配合相应的数据记录仪记录下测量得到的值。
首先,我们调整反射仪角度,使其与衍射模板对齐,然后将反射仪射线对准夫琅禾费模板,根据数据记录仪记录的测量值,推算出窄线宽的夫琅禾费。
然后,我们可以确定单缝夫琅禾费模板反射仪角度和反射仪对散射算法的影响。
最后,我们可以使用夫琅禾费把反谱仪角度和反谱仪对散射算法进行测量,记录数据,并比较结果。
实验结果通过实验,我们测量出夫琅禾费窄线宽的宽度,测量结果如下所示:第一组:夫琅禾费宽度为0.64 nm。
第二组:夫琅禾费宽度为0.62 nm。
第三组:夫琅禾费宽度为0.61 nm。
另外,我们还研究了反谱仪角度和反谱仪对散射算法的影响,研究结果如下:1、随着反谱仪角度的增大,夫琅禾费的宽度也会增大;2、反谱仪对夫琅禾费的散射算法的影响很大,当反谱仪的偏差角度较大时,夫琅禾费的宽度和强度会减小,且变化趋势不断。
结论本次实验通过配合衍射模板测量夫琅禾费的宽度和强度,我们可以推算出窄线宽的夫琅禾费。
另外,我们也研究了反谱仪角度和反谱仪对散射算法的影响,结果表明:随着反谱仪角度的增大,夫琅禾费的宽度也会增大;反谱仪对夫琅禾费的散射算法的影响很大,当反谱仪的偏差角度较大时,夫琅禾费的宽度和强度会减小,且变化趋势不断。
本次实验为理解夫琅禾费的原理,及其对光谱中原子或分子信号的测量提供了重要的实验经验。
Matlab演示夫琅禾费单缝衍射强度分布

Matlab演示夫琅禾费单缝衍射强度分布作者:王晶宜等来源:《科学与财富》2015年第27期摘要:研究单缝夫琅禾费衍射条纹强度分布及各参量之间的关系是光学领域非常重要的研究内容。
本文基于光的衍射理论,用Matlab软件程序实现了单缝夫琅禾费衍射中各相关参量之间的关系,并可视化不同缝宽和不同入射波长条件下的衍射条纹强度分布。
关键词:Matlab;单缝夫琅禾费衍射;衍射强度分布1.引言鉴于夫琅禾费单缝衍射的物理规律较为抽象、难以理解及数学表达式求解复杂、耗费时间,故利用MATLAB软件进行仿真演示,实现数据及物理现象的可视化,促进对物理规律更深层次的理解。
遵循MATLAB平台程序设计特性,编制MATLAB平台正确运行的程序。
需要的软件运行环境也很简单:1、硬件平台:计算机处理器主频要求为528MHz 以上;2、内存要求256MB RAM 以上;3、软件平台:操作系统:Windows XP Professional Edition;4、编程平台:MATLAB R2009a。
2.夫琅禾费单缝衍射理论与MATLAB编程障碍物、孔或缝的大小与波长相当是,光通过这一障碍物时,其后空间会发生光的衍射,衍射屏上能接收到有规律光强分布的衍射条纹。
按照光源、障碍物和观察屏三者的位置关系,障碍物到光源和观察屏距离为无限远的,称为夫琅禾费衍射,属于远场衍射,它的分析计算比较简单,同时又有很多实际应用。
衍射光强分布公式为:(1)其中中间因子u为:(2)a=8e-6;lambda=5e-7;theta=(-0.1*pi:0.00001:0.1*pi);u=pi*a*sin(theta)./lambda;I=sinc(u).^2;根据可得描述次级条纹的超越方程:(3)k=3;um=(k+1)*pi;uu=linspace(0,um,1000);figureplot([0;um],[0;0],uu,uu,'k')hold onplot(uu,tan(uu),'LineWidth',2)不同缝宽的单缝夫琅禾费衍射强度与衍射角关系曲线及干涉条纹可视化 lambda=400e-9;a1=0.001*1e-3;a2=0.01*1e-3;theta=(-0.1*pi:0.00001:0.1*pi);u1=pi*a1/lambda.*sin(theta);u2=pi*a2/lambda.*sin(theta);I1=sinc(u1).^2;I2=sinc(u2).^2;figureColorMap([r,r*0,r*0])image(I1*3000)axis off3. 总结基于光的衍射理论,计算单缝夫琅禾费衍射中各相关参量之间的关系,具体包括超越方程u=tanu求解,衍射相对光强与中间因子u的关系,不同缝宽条件下的衍射光强,不同入射波长的单缝夫琅禾费衍射强度与衍射角的关系,最后可视化不同颜色的衍射条纹。
夫琅禾费单缝衍射
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝(设宽度分别为a、b) 衍射光在x, y方向的衍射角分别为
x, y
衍射光场:两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角:
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛(正常人眼) a=D/2=1mm,n=1,n'=1.336,
0=550nm,f '=2.2cm
角分辨极限: m=0.610/n'a ≈2.511×10-4 rad
线分辨极限:
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
2.3 夫琅禾费单缝衍射
bsin j
实验 衍射光强的定量研究与单缝的测量

实验 衍射光强的定量研究与单缝的测量【实验目的】1.掌握在光具座上组装、调整光路的实验技能;学习微机自动控制进行测量时相关参量的设定。
2.了解光强测量的一种方法,观察并定量测定衍射元件产生的光衍射图样;掌握一种单缝宽度的测量方法。
【实验原理】1.衍射光强分布谱光的衍射是人所共知的一种自然现象,光衍射的实验光路主要由光源、衍射元件和观察屏等三要素,在光具座或光学平台上组装而成。
根据三者间距离的大小,将光衍射效应大致分成两种典型的光衍射图样,一种是衍射元件与光源和观察屏都相距无穷远,产生这种类型的光衍射叫夫琅禾费衍射,另一种是上述三者间相距有限远,产生的光衍射叫做菲涅耳衍射。
由于激光光束平行度较佳,且三者间距离远大于元件的线度,故本实验着重研究更具有实际意义的夫琅禾费衍射。
根据光衍射理论分析,不同衍射元件产生的光衍射图样和光强分布是不同的。
在理想条件下,理论研究不同衍射元件产生的衍射效应,得到对应的夫琅禾费衍射光强计算公式为:⑴ 单缝夫琅禾费衍射光强理论计算公式λθπθsin ,sin 20a u u u I I =⎪⎭⎫ ⎝⎛=上式表示在衍射角θ时,观测点的光强I θ值与光波波长λ值和单缝宽度a 相关,[]2sin()/u u 被叫做单缝衍射因子,表征衍射光场内任一点相对强度(I 0/I θ)的大小。
若sin θ为横坐标,(I 0/I θ)为纵坐标,可得到单缝衍射光强分布谱(如图14-1)。
从图14-1可见,零衍射斑即主极大在中心,高级衍射斑即次极大,它们顺序出现在sin θ=±1.43a λ,±2.46a λ,±3.47aλ,…的位置,各级次极强的光强与入射光强比值分别是I 1/I 0≈4.7%,I 2/I 0≈1.7%,I 3/I 0≈0.08%,…。
此外,在单缝衍射光强分布谱上还有暗斑,依次出现在sin θ=±a λ,±2a λ,±3aλ,…的位置,分别称为±1、±2、±3、…级。
单缝夫琅禾费衍射强度

单缝夫琅禾费衍射强度夫琅禾费衍射是描述光线通过一个或多个狭缝时发生的衍射现象的一种现象。
在夫琅禾费衍射中,当单缝宽度与入射光波长的数量级相同或更小时,将产生非常明显的弯曲和交叉条纹,这些条纹是由光的干涉效应产生的。
夫琅禾费衍射的强度分布及其数学表达可以通过洛伦兹和费涅尔两种方法来解释。
洛伦兹衍射理论适用于宽缝夫琅禾费衍射,而费涅尔衍射理论适用于窄缝夫琅禾费衍射。
在此我们主要关注窄缝夫琅禾费衍射。
夫琅禾费衍射的强度分布可以用到达屏幕上某一点的光波的相位差来解释。
当光线通过狭缝时,它会弯曲并扩散,形成一个曲线状的波前。
然后,这些波前将在屏幕上重新汇聚,形成一系列明暗交替的条纹。
夫琅禾费衍射的强度分布公式为:I(x) = I_0 * (sin(kx) / (kx))^2其中,I(x)表示在距离狭缝x处的强度,I_0表示入射光的强度,k表示光波数(2π/λ),x表示距离狭缝的垂直距离。
这个公式表明,强度的分布取决于弦波的相位和幅度,即x的正弦函数。
当sin(kx)为0时,I(x)为最小值,表示出现弱光斑。
当sin(kx)的数值为整数倍时,I(x)为最大值,表示出现强光斑。
这些强弱光斑构成了明暗相间的衍射图样。
夫琅禾费衍射的强度分布进一步说明了缝隙宽度对衍射图样的影响。
当缝隙宽度小于入射光波长的数量级时,衍射图样中会出现更多的明暗条纹,且条纹之间的间距更紧密。
当缝隙宽度大于入射光波长的数量级时,衍射图样中的明暗条纹将变得更宽,并且间距变得更大。
夫琅禾费衍射的强度分布还受到屏幕与狭缝的距离以及观察点的位置的影响。
当屏幕与狭缝的距离变大时,衍射图样会变得模糊,条纹的间距也会变大。
当观察点接近狭缝时,衍射图样的明暗条纹更加集中,明亮部分更亮,暗部分更暗。
在实际应用中,夫琅禾费衍射广泛用于光学中的波导、探测器、太阳能电池等领域。
通过对衍射图样的分析,可以提取出有关光波特性以及物体的形状和尺寸等信息。
因此,深入了解夫琅禾费衍射的强度分布对于光学设计和精密测量有重要意义。
2_6夫琅禾费单缝衍射

屏幕 屏幕
S
*
3
2.6.2 强度的计算 x
屏幕
dx
r
θ
r0
P
B
S
F1
x
λ
Δ = x sin θ
M N 0 D B′
P0
θ
宽度dx窄带所发次波振幅
将波前 BB′分割成许多等宽窄带dx, 初位相 ϕ0 = 0
A0 dx A0 整个狭缝所发次波振幅; b A0 dx cos ωt M点所发次波的振动 dE0 = b
πb sin θ λ
λ
次最大光强的角位 置近似为:
sin θ k 0
2
2k + 1 λ ≈± 2 b
⎛ sin u ⎞ 代入单缝衍射因子 I = ⎜ ⎟ I 0 各次最大的光强为: ⎝ u ⎠
I10 = 0.0472 I 0
I 20 = 0.0165 I 0
I 30 = 0.0083I 0
10
可见,衍射级次越高,光强就越小。次最大的光 强最大不到中央最大值的1/20,并且随着级数的增 加而很快减小。 光强曲线
1.0
I I0
− 3π
− 2π
−π
0
π
2π
u
11
2.6.4 单缝衍射图案的特点
(1)、各级最大值的光强不相等,随着级数k的增 大而减小。中央最大值的光强最大(主最大), 次最大值远小于中央最大值 I10< 0.05I0 (2)、角宽度 规定以相邻暗纹的角距离作为其间条纹的角宽度。 在近轴条件下, θ很小, sinθ ≈θ , 由暗纹的角位置公式 sin θ k ≈ θ = k
~ A0 dx 其复振幅为 dE = e b
i
2π
夫琅禾费单缝衍射光强分析与探讨 修改

夫琅禾费单缝衍射光强分析与探讨摘要:在夫琅禾费单缝衍射实验中,如果在透镜的物方焦面内沿着某一圆周改变光源S的位置,让透镜出射的单色平面光波都以相同的入射角H0入射到单缝衍射屏上,则单缝衍射光强分布均会发生改变,说明衍射图样的光强分布不仅和入射角H0以及衍射角H有关,而且和光源S的位置有关;考虑单缝衍射屏上光波相位的分布和平面光波的入射方位(即光源S的位置)的关系,采用矢量图解法对单缝衍射因子进行分析及计算,得到了全面的夫琅禾费单缝衍射光强公式。
关键词:单缝衍射;光强;光程差;斜入射目录1 夫琅禾费单缝衍射(一) (1)的物方焦点时的装置及现象 (1)1.1 单色点光源S位于透镜L11.2 用积分法来求夫琅禾费单缝衍射的光强………………………………()1.3 衍射光强的极值分布条件及特点………………………………………()2 夫琅禾费单缝衍射(二)……………………………………………………()2.1 单色点光源S位于透镜L的物方焦面上时的装置……………………()12.2 单缝衍射因子分析及计算………………………………………………()3 总结…………………………………………………………………………()1 夫琅禾费单缝衍射(一)1.1 单色点光源S位于透镜L的物方焦点时的装置及现象1如图1所示,单色点光源S置于凸透镜L1的物方焦平面上,从点光源发出的光经过透镜以后变成平行光,垂直射到宽度约为十分之几毫米的狭缝上。
缝后置一凸透镜L2,在L2象方焦平面上放置接收屏,则屏上显现出由一系列不连续的明亮短线组成的衍射图样,如图1[1]所示。
改变缝的宽度,衍射图样也发生变化,缝越宽,衍射图样越收缩,当缝宽足够大时(远大于波长),则衍射图样缩成一点,这就是点光源S在透镜中所成的象。
狭缝对光波在方向上的限制,使光在x方向上产生衍射,生成一系列沿x方向排列的明亮的短线,这些短线好像是点光源的一个扩展开的象。
如果用氮生在光器作为光源,则可以把透镜L1去掉,使激光直接照射在单缝上,并且去掉L2,在缝后足够远处(几米)屏上可观察到夫琅禾费衍射图样。
夫琅禾费单缝衍射光强分布MATLAB分析毕业论文

夫琅禾费单缝衍射光强分布MATLAB分析毕业论文摘要衍射为人们所熟悉的现象,对于光的这种特殊现象在很多方面有着应用。
在光的衍射的基础上,介绍了什么是夫琅禾费衍射,几种实现夫琅禾费衍射的方法和原理及光强分布特点,以基尔霍夫积分定理为基础,利用衍射公式的近似对基尔霍夫衍射公式进行了推导,从理论上得出了夫琅禾费单缝衍射的光强公式,利用Matlab软件进行了光强分布的图样仿真,并用实验采集到的图样对理论和仿真的结论进行了验证,采用对观察屏上各点的光强进行计算的方法,对衍射条纹分析对比研究,重点研究了夫琅禾费单缝衍射光强分布以及衍射的条纹分析,计算结果与实验结果得到了很好的吻合。
关键词:夫琅禾费单缝衍射;光强分布;衍射条纹;对比分析AbstractDiffraction to people familiar with the phenomenon, the light of this unique phenomenon has applications in many areas.In the diffraction of light on the basis of what is on the Fraunhofer diffraction, the realization of several Fraunhofer diffraction methods and principles and distribution of light intensity to Kirchhoff integral theorem based on the formula used diffraction Kirchhoff diffraction similar to the formula derived from the theory that the Fraunhofer single-slit diffraction of light formula, using the Matlab software Light simulation of the design and use of the images collected on theory Simulation and the conclusions were verified by on-screen to observe the strong points of light to the method of calculation, the diffraction fringes of comparative study, focused on the Fraunhofer single-slit diffraction intensity distribution and diffraction analysis of the fringe The results with the experimental results have been very good anastomosis.Key words:Fraunhofer single-slit diffraction;light distribution;diffraction fringes ; comparative analysis目录第1章概述 (1)1.1 光的衍射 (1)1.2 研究的内容与目的 (2)第2章夫琅禾费衍射原理 (3)2.1 惠更斯—菲涅耳原理 (3)2.2 夫琅禾费衍射 (4)2.3 实现夫琅禾费衍射的几种方法 (5)2.4 菲涅耳半波带分析法 (7)2.5 夫琅禾费衍射光强图样特点 (10)2.6 本章小结 (13)第3章光强分布的推导 (14)3.1 基尔霍夫积分定理 (14)3.2 基尔霍夫衍射公式 (16)3.3 基尔霍夫衍射公式的近似 (18)3.4 夫琅禾费单缝衍射光强分布 (20)3.5 本章小结 (21)第4章条纹分析 (22)4.1 理论分析 (22)4.2 仿真分析 (24)4.3 实验分析 (27)4.4 对比分析 (30)4.5 本章小结 (31)结论 ......................................................................................... 错误!未定义书签。
2.3 夫琅禾费单缝衍射解析

平行衍射光
平行衍射光 光线系1,光线系2,光线系 3…构成无穷多束平行衍射光。
A
3 3 3
2
2
1
1
O
K
2 θ 1 O/ 3 2 1 L 3 2 1
B
光学
§ 2.3 夫琅禾费单缝衍射
平行衍射光的方向
衍射角 每一束平行光与单缝 法线方向之间的夹角 θ 称为衍射角,变化 范围 0→±π /2 (向 上为正,向下为负)。
(3)波长 越大,条纹越宽。 白光:中央特亮,其余呈彩色分布。
如何解释这些实验规律?
光学
§ 2.3 夫琅禾费单缝衍射
三、惠更斯-菲涅耳原理分析衍射过程
平行衍射光
衍射光 如图中A点的1,2,3…光线 都是衍射光线。
A
3 3 3
2
2
1
1
O
K
2 θ 1 O/ 3 2 1 L 3 2 1
B
光学
§ 2.3 夫琅禾费单缝衍射
x P
复振幅:
B
f
A0 dx ik dE e (xsin r' ) b
光学
§ 2.3 夫琅禾费单缝衍射
A dx (xsin r' ) 0 复振幅: dE eik b
P点处的合振幅:
P点处的光强:
bsin sin( ) bsin 2 i ( r ' ) b A0 ikr' ikxsin EP dE e e dx A0e 0 bsin b ( )
光学
§ 2.3 夫琅禾费单缝衍射
六、条纹宽度
中央明纹角宽度:中央亮纹对透镜中心的张角。 由暗纹条件: b sin k 当θ很小,有 k k 中央明纹角宽度:2 0 2
单缝和圆孔的夫琅禾费衍射介绍

二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等,设为A1,相邻
窄带所发子波在P点引起的振
动的光程差
δ = (asin)/N
B
相位差 2 2 asin
N
屏上P点的合振幅 AP就是各子波的振幅矢量和的 模,这是多个同方向、同频率,同振幅、初相依 次差一个恒量的简谐振动的合成。
对于屏中心o点
衍射角为零,各子波的相位相同
A
1
…
A 0
o点的合振动振幅 A0 = N A1
中央明纹的光强 I0 A02
对于屏上其它点P,由
于屏上位置不同,对应的衍
射角就不同,Ap的大小也
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
(1) 衍射条纹与狭缝平行。 (2)中心条纹很亮,两侧明条纹对称分布, 亮度减弱。 (3)中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理:
单缝处波面看作无穷多个相干波源,屏上一点是 (无穷)多光束干涉的结果。
由 a sin1
有
sin1
a
30 mm 0.20 m
0.15
d
a
θ1
L
β
150
1 8.63°
如图: 15°1 23.63° 15°1 6.37°
L d(ctg ctg )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单缝夫琅禾费衍射强度
摘要:
1.单缝衍射概述
2.夫琅禾费衍射原理
3.衍射强度的计算方法
4.夫琅禾费衍射的应用
正文:
1.单缝衍射概述
单缝衍射是一种光的波动现象,当光线通过一个缝隙时,会在其后方形成一系列明暗交替的条纹。
这些条纹是由于光波在传播过程中遇到缝隙,发生衍射现象而产生的。
单缝衍射的研究对于理解光的波动性质以及发展光纤通信、光学仪器等技术具有重要意义。
2.夫琅禾费衍射原理
夫琅禾费衍射,又称为夫琅禾费衍射公式,是由德国物理学家夫琅禾费(Fraunhofer)在19 世纪初提出的。
夫琅禾费衍射原理描述了单缝衍射条纹的亮度分布规律,其基本公式为:
I = (b / a) * (L / d)^2 * sin^2(α)
其中,I 表示衍射强度,b 表示光源到缝的距离,a 表示缝到观察屏的距离,L 表示光源到观察屏的距离,d 表示缝的宽度,α表示入射光线与缝的中心线的夹角。
3.衍射强度的计算方法
根据夫琅禾费衍射原理,我们可以通过测量衍射条纹的亮度来计算衍射强度。
具体方法是,在实验中改变光源到缝的距离、缝到观察屏的距离以及入射光线与缝的中心线的夹角,观察不同条件下衍射条纹的亮度变化,然后利用夫琅禾费衍射公式计算衍射强度。
4.夫琅禾费衍射的应用
夫琅禾费衍射在实际应用中具有重要价值。
例如,在光纤通信中,夫琅禾费衍射原理可以用于计算光纤的传输性能,以提高通信质量和传输距离;在光学仪器的研制中,夫琅禾费衍射可以用于评估仪器的分辨率和成像质量。
此外,夫琅禾费衍射还在物理、光学等领域的科研和教学中具有广泛的应用。
总之,夫琅禾费衍射作为一种重要的光学现象,对于理解光的波动性质以及发展光纤通信、光学仪器等技术具有重要意义。
