大学物理静电场习题集答案解析
大学物理题库-第5章 静电场习题(含答案解析)

真空中的静电场一 选择题1.两个等量的正电荷相距为2a ,P 点在它们的中垂线上,r 为P 到垂足的距离。
当P 点电场强度大小具有最大值时,r 的大小是:[ ](A )42a r =(B )32a r = (C )22ar = (D )a r 2= 2.如图5-1所示,两个点电荷的电量都是q +,相距为a 2,以左边点电荷所在处为球心,以a 为半径作一球形高斯面,在球面上取两块相等的小面积1S 和2S ,设通过1S 和2S 的电通量分别为1Φ和2Φ,通过整个球面的电通量为Φ,则[ ](A )021εq=ΦΦ>Φ,(B )0212,εq=ΦΦ<Φ(C )021εq=ΦΦ=Φ,(D )021εq=ΦΦ<Φ,3.在静电场中,高斯定理告诉我们 [ ](A )高斯面内不包围电荷,则高斯面上各点E的量值处处相等;(B )高斯面上各点E只与面内电荷有关,与面外电荷无关;(C )穿过高斯面的E(D )穿过高斯面的E 通量为零,则高斯面上各点的E必为零; 4.如图5-2所示,两个“无限长”的同轴圆柱面,半径分别为1R 和2R ,其上均匀带电,沿轴线方向单位长度上的带电量分别为1λ和2λ,则在两圆柱面之间、距轴线为r 的P 点处的场强大小为:[ ](A )r 012πελ (B )r 0212πελλ+ (C )()r R -2022πελ (D )()1012R r -πελ5.电荷面密度为+σ和-σ的两块“无限大”均匀带电平行平板,放在与平面垂直的x2-5 图1 - 5 图轴上a +和a -位置,如图5-3所示。
设坐标圆点o 处电势为零,则在a x a +<<-区域的电势分布曲线为: ( )6.真空中两个平行带电平板A 、B ,面积均为S ,相距为)(S d d <<2,分别带电量q +和q -,则两板间相互作用力的大小为:[ ](A )204d q πε (B )Sq 0ε (C )Sq 022ε (D )不能确定7.静电场中,下列说法哪一个是正确的?[ ](A )正电荷的电势一定是正值; (B )等势面上各点的场强一定相等;(C )场强为零处,电势也一定为零; (D )场强相等处,电势梯度矢量一定相等。
大学物理(第四版)课后习题及答案 静电场

证2:如图所示,取无限长带电细线为微元,各微元在点P激发的电场强 度dE在Oxy平面内且对x轴对称,因此,电场在y轴和z轴方向上的分量之 和,即Ey、Ez均为零,则点P的电场强度应为
积分得 电场强度E的方向为带电平板外法线方向。 上述讨论表明,虽然微元割取的方法不同,但结果是相同的。
(2)由于正、负电荷分别对称分布在y轴两侧,我们设想在y轴上能 找到一对假想点,如果该带电环对外激发的电场可以被这一对假想点上 等量的点电荷所激发的电场代替,这对假想点就分别称作正、负等效电 荷中心。等效正负电荷中心一定在y轴上并对中心O对称。由电偶极矩p 可求得正、负等效电荷中心的间距,并由对称性求得正、负电荷中心。 解:(1)将圆环沿y轴方向分割为一组相互平行的元电偶极子,每一元 电偶极子带电
行,对电场强度通量贡献为零。整个高斯面的电场强度通量为 由于,圆柱体电荷均匀分布,电荷体密度,处于高斯面内的总电荷 由高斯定理可解得电场强度的分布, 解:取同轴柱面为高斯面,由上述分析得 题7.16:一个内外半径分别R1为R2和的均匀带电球壳,总电荷为Q1,球 壳外同心罩一个半径为 R3的均匀带电球面,球面带电荷为Q2。求电场 分布。电场强度是否是场点与球心的距离r的连续函数?试分析。
题7.16分析:以球心O为原点,球心至场点的距离r为半径,作同心球面 为高斯面。由于电荷呈球对称分布,电场强度也为球对称分布,高斯面 上电场强度沿径矢方向,且大小相等。因而,在确定高斯面内的电荷 后, 利用高斯定理 即可求的电场强度的分布 解:取半径为r的同心球面为高斯面,由上述分析 r < R1,该高斯面内无电荷,,故
E=0 在距离圆孔较远时x>>r,则 上述结果表明,在x>>r时。带电平板上小圆孔对电场分布的影响可以忽 略不计。 题7.15:一无限长、半径为R的圆柱体上电荷均匀分布。圆柱体单位长 度的电荷为,用高斯定理求圆柱体内距轴线距离为r处的电场强度。
大学物理习题参考解答上静电场环路定理_电势能_电势和电势差

02. 如图所示, CDEF 是一矩形,边长分别为 l 和 2l 。在 DC 延长线上 CA l 处的 A 点有点电荷 q ,在 CF 的中点 B 点有点电荷 q ,若使单位正电荷从 C 点沿 CDEF 路径运动到 F 点,则电场
力所作的功等于:
【D】
(A)
q 4ol
5 1; 5l
(B)
q 4ol
三 判断题
09. 静电场中某点电势值的正负取决于电势零点的选取。
【对】
10. 在已知静电场分布的条件下,任意两点 P1 和 P2 之间的电势差决定于 P1 和 P2 两点的位置。【 对 】
11. 正电荷在电势高的地方,电势能也一定高。 12. 电场强度的方向总是指向电势降落最快的方向。
【对】 【对】
1 4 0
4 r12 r1
1 4 0
4 r22 r2
0
——
r1 ' r2 0
XCH
第3页
20XX-3-24
大学物理教程_上_习题集参考解答
r1 r2
—— 外球面带负电
外球面应放掉电荷: Q Q Q Q 4 r22 4 r22
Q
(1
r1 r2
)
4
r22
将 r1 10 cm and r2 20 cm , 8.85 109C / m2 代入上式得到:
13. 静电场的保守性体现在电场强度的环流等于零。
【对】
四 计算题
14. 如图所示, AB 2L , OCD 是以 B 为中心 L 为半径的半圆, A 和 B 两处分别有正负电荷 q 和 q ,试问:
1) 把单位正电荷从 O 沿 OCD 移动到 D ,电场力对它作了多少功?
XCH
大学物理第五章 静电场部分的习题及答案

第五章 静电场一、简答题1、为什么在无电荷的空间里电场线不能相交?答案:由实验和理论知道,静电场中任一给定点上,场强是唯一确定的,即其大小和方向都是确定的.用电场线形象描述静电场的空间分布时,电场线上任一点的切线方向表示该点的场强方向.如果在无电荷的空间里某一点上有几条电场线相交的话,则过此交点对应于每一条电场线都可作出一条切线,这意味着交点处的场强有好几个方向,这与静电场中任一给定点场强具有唯一确定方向相矛盾,故无电荷的空间里电场线不能相交.2、简述静电场中高斯定理的文字内容和数学表达式。
答案:在真空中的静电场内,通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S Sq S d E3、写出静电场的环路定理,并分别说明其物理意义。
答案:静电场中,电场强度的环流总是等于零(或0l=⋅⎰l d E ),静电场是保守场。
4、感生电场与静电场有哪些区别和联系?二、选择题1、如图所示,两个同心均匀带电球面,内球面半径为1R 、带有电荷1Q ,外球面半径为2R 、带有电荷2Q ,则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A.20214r Q Q επ+ B.()()2202210144R r Q R r Q -π+-πεε C.()2120214R R Q Q -+επ D.2024r Q επ 2、半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为:( B )3、图示一均匀带电球体,总电荷为Q +,其外部同心地罩一内、外半径分别为1r 、2r 的金属球壳.设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势为: ( D )A.204r QE επ=,r Q U 04επ= B.0=E ,104r Q U επ= C. 0=E ,r Q U 04επ=D.0=E ,204r Q U επ= 4、图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:( D )A.C B A E E E >>,C B A U U U >>B.C B A E E E <<,C B A U U U <<C.C B A E E E >>,C B A U U U <<D.C B A E E E <<,C B A U U U >>5、面积为S 的空气平行板电容器,极板上分别带电量q ±,若不考虑边缘效应,则两极板间的相互作用力为 ( B )A.S q 02εB.S q 022εC.2022S q εD.202Sq ε 6、一均匀带电球面在球面内各处产生的场强 ( A )A.处处为零B.不一定为零C.一定不为零D.是常数7、已知一高斯面所包围的体积内电量代数和0=∑i q ,则可肯定:( C )A.高斯面上各点场强均为零B.穿过高斯面上每一面元的电通量均为零C.穿过整个高斯面的电通量为零D.以上说法都不对8、下列说法中正确的是 ( D )A.电场强度为0的点,电势也一定为0.B.电场强度不为0的点,电势也一定不为0.C.电势为0的点,则电场强度也一定为0.D.电势在某一区域为常数,则电场强度在该区域也必定为0.9、如图所示,一个带电量为q 的点电荷位于正立方体的中心上,则通过其中一侧面的电场强度通量等于 ( B ):A.04εqB.06εqC.06πεqD.04πεq 三、计算题1、两无限长同轴圆柱面,半径分别为1R 和2R (21R R < ),带有等量异号电荷,单位长度的电量为λ和λ-,求:(1) 1R r <;(2)21R r R <<;(3)r R <2处各点的场强。
大学物理学 第10章_静电场 习题解答 [王玉国 康山林 赵宝群]
![大学物理学 第10章_静电场 习题解答 [王玉国 康山林 赵宝群]](https://img.taocdn.com/s3/m/d8d02e12650e52ea55189898.png)
q 6 0 q ;如果它包含 q 所在 24 0
2 2
对于边长 a 的正方形,如果它不包含 q 所在的顶点,则 e 顶点则 e 0 .
(3) 因为通过半径为 R 的圆平面的电通量等于通过半径为 R x 的球冠面的电通 量,而球冠面积*
S 2π( R 2 x 2 )[1
P R q r P'
2q a O a 3q a
+Q q a
R
d
∞
题 10-10 图
题 10-11 图
题 10-12 图
10-12 如图所示.试验电荷 q , 在点电荷 Q 产生的电场中,沿半径为 R 的整个圆弧 的 3/4 圆弧轨道由 a 点移到 d 点的过程中电场力做功多大?从 d 点移到无穷远处的过程中, 电场力做功为多少? 解:因为在点电荷 Q 产生的电场中, U a U d 。故试验电荷 q 在点电荷 Q 产生的电 场中, 沿半径为 R 的整个圆弧的 3/4 圆弧轨道由 a 点移到 d 点的过程中电场力做功 Aad 0 ; 从 d 点移到无穷远处的过程中,电场力做功为
q0 2.0 105 C .试求该点电荷所受的电场力。
点电荷所在处产生场强为: d E
dx
4 0 d x
2 l
。整个杆上电荷在该点的场强为:
E
4 0
d x
0
dxLeabharlann 2l4 0 d d l
点电荷 q0 所受的电场力大小为:
F
方向:沿 x 轴负向
A q U d U qU d
[或另解: A
qQ 4 0 R
]
R
qE d r
大学大学物理习题解答参考答案-一、真空中的静电场

20XX年复习资料大学复习资料专业:班级:科目老师:一、日期:真空中的静电场一、 选择题:1.下列几个说法哪一个是正确的?(A ) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向。
(B ) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同。
(C ) 场强方向可由/F E =q 定出,其中q 为试验电荷的电量,q 可正可负,F 为试验电荷所受的电场力。
(D ) 以上说法都不正确。
[ ]2.关于静电场中某点电势值的正负,下列说法中正确的是:(A ) 电势值的正负取决于置于该点的试验电荷的正负。
(B ) 电势值的正负取决于电场力对试验电荷作功的正负。
(C ) 电势值的正负取决于电势零点的选取。
(D ) 电势值的正负取决于产生电场的电荷的正负。
[ ]3、某电场的电力线分布情况如图所示。
一负电荷从M 点移到N 点。
有人根据这个图作出下列几点结论,其中哪点是正确的?(A ) 电场强度N M E E <。
(B )电势N M U U <。
(C )电势能N M W W <。
(D )电场力的功A>0。
[ ]4、将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处,测得它所受的力为F .若考虑到电量q 0不是足够小,则(A)F /q 0 比P 点处原先的场强数值大.(B)F /q 0 比P 点处原先的场强数值小.(C)F /q 0 等于原先P 点处场强的数值.(D)F /q 0 P 点处场强数值关系无法确定,[ ]5、一电偶极子放在均匀电场中,当电偶极矩的方向与场强方向不一致时,其所受的合力F 和合力矩M 为:(A) F =0,M =0, (B) F =0,M ≠0,(C) F ≠0,M =0, (D) F ≠0,M ≠0, [ ]6、已知一高斯面所包围的体积内电量代数和∑i q =0,则可肯定:(A ) 高斯面上各点场强均为零。
(B ) 穿过高斯面上每一面元的电通量均为零。
《大学物理学》习题解答静电场中的导体和电介质

根据球形电容器的电容公式,得:
C
4 0
R1R2 R2 R1
4.58102 F
【12.7】半径分别为 a 和 b 的两个金属球,球心间距为 r(r>>a,r>>b),今用一根电容可忽略的细导线将 两球相连,试求:(1)该系统的电容;(2)当两球所带的总电荷是 Q 时,每一球上的电荷是多少?
【12.7 解】由于 r a , r b ,可也认为两金属球互相无影响。
以相对电容率 r ≈1 的气体。当电离粒子通过气体时,能使其电离,若两极间有电势差时,极间有电流,
从而可测出电离粒子的数量。若以 E1 表示半径为 R1 的长直导体附近的电场强度。(1)求两极间电势差的
关系式;(2)若 E1 2.0 106 V m1 , R1 0.30 mm , R2 20.00 mm , 两极间的电势差为多少?
, (R2
r) ;
外球面的电势 内外球面电势差
VR2
R2
E3 dr
Q1 Q2 4 0 R2
U
VR2
VR1
R2 R1
E2
dr
Q1 4 0
(1 R1
1) R2
可得:
Q1 6 109 C , Q2 4 109 C
【12.4】如图所示,三块平行导体平板 A,B,C 的面积均为 S,其中 A 板带电 Q,B,C 板不带电,A 和 B 间相距为 d1,A 和 C 之间相距为 d2,求(1)各导体板上的电荷分布和导体板间的电势差;(2)将 B,C 导体 板分别接地,再求导体板上的电荷分布和导体板间的电势差。
第 12 章 静电场中的导体和电介质
【12.1】半径为 R1 的金属球 A 位于同心的金属球壳内,球壳的内、外半径分别为 R2、R3 ( R2 R3 )。
大学物理第7章真空中的静电场答案解析

第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7-1图0 dqξd ξ习题7-2 图a204r dxdE πελ=θπελcos 420rdxdE y =, θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===, 代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y+--πελ,方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy ==2204Ly y L+πελ7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7-2 图byx习题7-3图2022R q επ=,如图,方向沿x 轴正向。
大学物理静电场习题答案

第12章 静电场P35.12.3 如图所示,在直角三角形ABCD 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强.[解答]根据点电荷的场强大小的公式22014q qE k r r ==πε, 其中1/(4πε0) = k = 9.0×109N·m 2·C -2.点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯, 方向向下.点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯,方向向右.C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.12.4 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元 d s = R d θ,电荷元为d q = λd s ,在O 点产生的场强大小为220001d 1d d d 444q s E R R R λλθπεπεπε===, 场强的分量为d E x = d E cos θ,d E y = d E sin θ.对于带负电的圆弧,同样可得在O 点的场强的两个分量.由于弧形是对称的,x 方向的合场强为零,总场强沿着y 轴正方向,大小为2d sin y LE E E ==⎰θ/6/60000sin d (cos )22R R==-⎰ππλλθθθπεπε0(1)22R=-λπε.12.5 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C·m -1,求:(1)棒的延长线上与棒的近端d 1 = 8cm 处的场强;(2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强.[解答](1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m).在细棒上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产图13.1生的场强的大小为1220d d d 4()q lE k r x l ==-λπε场强的方向沿x 轴正向.因此P 1点的总场强大小通过积分得120d 4()L L l E x l λπε-=-⎰014LLx lλπε-=-011()4x L x Lλπε=--+ 220124L x L λπε=-. ①将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯- = 2.41×103(N·C -1),方向沿着x 轴正向.(2)建立坐标系,y = d 2. 在细棒上取一线元d l ,所带的电量为 d q = λd l ,在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE kr r λπε==, 由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ.由图可知:r = d 2/sin θ,l = d 2cot θ, 所以 d l = -d 2d θ/sin 2θ, 因此 02d sin d 4y E d λθθπε-=,总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==. ②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N·C -1). 方向沿着y 轴正向.[讨论](1)由于L = a /2,x = L+d 1,代入①式,化简得1011011144/1a E d d a d d a λλπεπε==++,保持d 1不变,当a →∞时,可得1014E d λπε→, ③这就是半无限长带电直线在相距为d 1的延长线上产生的场强大小.(2)由②式得y E ==,当a →∞时,得 022y E d λπε→, ④这就是无限长带电直线在线外产生的场强公式.如果d 1=d 2,则有大小关系E y = 2E 1.12.6 一均匀带电无限长细棒被弯成如图所示的对称形状,试问θ为何值时,圆心O 点处的场强为零.[解答]设电荷线密度为λ,先计算圆弧的电荷在圆心产生的场强.在圆弧上取一弧元 d s =R d φ, 所带的电量为d q = λd s ,在圆心处产生的场强的大小为2200d d d d 44q s E kr R Rλλϕπεπε===, 由于弧是对称的,场强只剩x 分量,取x 轴方向为正,场强为d E x = -d E cos φ. 总场强为2/20/2cos d 4x E R πθθλϕϕπε--=⎰2/20/2sin 4Rπθθλϕπε--=0sin 22R λθπε=,方向沿着x 轴正向.再计算两根半无限长带电直线在圆心产生的场强.根据上一题的公式③可得半无限长带电直线在延长上O 点产生的场强大小为`04E Rλπε=,由于两根半无限长带电直线对称放置,它们在O 点产生的合场强为``02coscos 222x E E R θλθπε==,方向沿着x 轴负向.当O 点合场强为零时,必有`x x E E =,可得 tan θ/2 = 1, 因此 θ/2 = π/4, 所以 θ = π/2.12.7 一宽为b 的无限长均匀带电平面薄板,其电荷密度为σ,如图所示.试求:(1)平板所在平面内,距薄板边缘为a处的场强.(2)通过薄板几何中心的垂直线上与薄板距离为d 处的场强.[解答](1)建立坐标系.在平面薄板上取一宽度为d x 的带电直线,电荷的线密度为d λ = σd x , 根据直线带电线的场强公式02E rλπε=, 得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-,其方向沿x 轴正向.由于每条无限长直线在P 点的产生的场强方向相同,所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ /20/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+. ①图13.4图13.5.场强方向沿x 轴正向.(2)为了便于观察,将薄板旋转建立坐标系.仍然在平面薄板上取一宽度为d x 的带电直线,电荷的线密度仍然为d λ = σd x ,带电直线在Q 点产生的场强为221/200d d d 22()xE rb x λσπεπε==+,沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+,设x = d tan θ,则d x = d d θ/cos 2θ,因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰ 0arctan()2bdσπε=. ② 场强方向沿z 轴正向.[讨论](1)薄板单位长度上电荷为λ = σb ,①式的场强可化为0ln(1/)2/b a E a b aλπε+=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02E aλπε→, ③ 这正是带电直线的场强公式.(2)②也可以化为0arctan(/2)2/2z b d E d b dλπε=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02z E dλπε→,这也是带电直线的场强公式.当b →∞时,可得2z E σε→, ④ 这是无限大带电平面所产生的场强公式.12.8 (1)点电荷q 位于一个边长为a 的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?(2)如果将该场源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?[解答]点电荷产生的电通量为Φe = q/ε0.(1)当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1 = Φe /6 = q /6ε0.(2)当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1 = Φe /24 = q /24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零.12.9 面电荷密度为σ的均匀无限大带电平板,以平板上的一点O 为中心,R 为半径作一半球面,如图所示.求通过此半球面的电通量.[解答]设想在平板下面补一个半球面,与上面的半球面合成一个球面.球面内包含的电荷为q = πR 2σ, 通过球面的电通量为图13.7Φe = q /ε0, 通过半球面的电通量为Φ`e = Φe /2 = πR 2σ/2ε0.12.10 两无限长同轴圆柱面,半径分别为R 1和R 2(R 1 > R 2),带有等量异号电荷,单位长度的电量为λ和-λ,求(1)r < R 1;(2) R 1 < r < R 2;(3)r > R 2处各点的场强.[解答]由于电荷分布具有轴对称性,所以电场分布也具有轴对称性.(1)在内圆柱面内做一同轴圆柱形高斯面,由于高斯内没有电荷,所以E = 0,(r < R 1).(2)在两个圆柱之间做一长度为l ,半径为r 的同轴圆柱形高斯面,高斯面内包含的电荷为 q = λl , 穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ,根据高斯定理Φe = q /ε0,所以02E rλπε=, (R 1 < r < R 2). (3)在外圆柱面之外做一同轴圆柱形高斯面,由于高斯内电荷的代数和为零,所以E = 0,(r > R 2).12.11 一厚度为d 的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法.(1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E = E`.在板内取一底面积为S ,高为2r 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E S2d d d S S S =⋅+⋅+⋅⎰⎰⎰E S E S E S 1`02ES E S ES =++=,高斯面内的体积为 V = 2rS , 包含的电量为 q =ρV = 2ρrS , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρr/ε0,(0≦r ≦d /2).①(2)穿过平板作一底面积为S ,高为2r 的圆柱形高斯面,通过高斯面的电通量仍为 Φe = 2ES , 高斯面在板内的体积为V = Sd , 包含的电量为 q =ρV = ρSd , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρd /2ε0,(r ≧d /2). ②方法二:场强叠加法. (1)由于平板的可视很多薄板叠而成的,以r 为界,下面平板产生的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层d y ,面电荷密度为d σ = ρd y ,产生的场强为 d E 1 = d σ/2ε0, 积分得100/2d ()222rd y dE r ρρεε-==+⎰,③ 同理,上面板产生的场强为/2200d ()222d ry d E r ρρεε==-⎰,④ r 处的总场强为E = E 1-E 2 = ρr/ε0.(2)在公式③和④中,令r = d /2,得E 2 = 0、E = E 1 = ρd /2ε0,E 就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.1212.13 一半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为R`<R的小球体,如图所示,试求两球心O 与O`处的电场强度,并证明小球空腔内的电场为均强电场.[解答]挖去一块小球体,相当于在该处填充一块电荷体密度为-ρ的小球体,因此,空间任何一点的场强是两个球体产生的场强的叠加.对于一个半径为R ,电荷体密度为ρ的球体来说,当场点P 在球内时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r r ππρε=P 点场强大小为3E r ρε=.当场点P 在球外时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r R ππρε=P 点场强大小为3203R E rρε=. O 点在大球体中心、小球体之外.大球体在O 点产生的场强为零,小球在O 点产生的场强大小为320`3O R E aρε=, 方向由O 指向O `.O`点在小球体中心、大球体之内.小球体在O`点产生的场强为零,大球在O 点产生的场强大小为`03O E a ρε=, 方向也由O 指向O `.[证明]在小球内任一点P ,大球和小球产生的场强大小分别为 03r E r ρε=, `0`3r E r ρε=,方向如图所示.设两场强之间的夹角为θ,合场强的平方为222``2cos r r r r E E E E E θ=++2220()(`2`cos )3r r rr ρθε=++, 根据余弦定理得222`2`c o s ()a r rr r πθ=+--, 所以 03E a ρε=, 可见:空腔内任意点的电场是一个常量.还可以证明:场强的方向沿着O 到O `的方向.因此空腔内的电场为匀强电场.12.14 如图所示,在A 、B 两点处放有电量分别为+q 和-q 的点电荷,AB 间距离为2R ,现将另一正试验电荷q 0从O 点经过半圆弧路径移到C点,求移动过程中电场力所做的功.[解答]正负电荷在O 点的电势的和为零:U O = 0;图13.10图13.11在C 点产生的电势为0004346C q q q U RRRπεπεπε--=+=,电场力将正电荷q 0从O 移到C 所做的功为W = q 0U OD = q 0(U O -U D ) = q 0q /6πε0R .12.15 真空中有两块相互平行的无限大均匀带电平面A 和B .A 平面的电荷面密度为2σ,B 平面的电荷面密度为σ,两面间的距离为d .当点电荷q 从A 面移到B 面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为E A = 2σ/2ε0 = σ/ε0,E B = σ/2ε0,两平面在它们之间产生的场强方向相反,因此,总场强大小为E = E A - E B = σ/2ε0, 方向由A 平面指向B 平面.两平面间的电势差为U = Ed = σd /2ε0,当点电荷q 从A 面移到B 面时,电场力做的功为W = qU = qσd /2ε0.12.16 一半径为R 的均匀带电球面,带电量为Q .若规定该球面上电势值为零,则无限远处的电势为多少?[解答]带电球面在外部产生的场强为204Q E rπε=,由于d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=,当U R = 0时,04Q U Rπε∞=-.12.17 电荷Q 均匀地分布在半径为R 的球体内,试证明离球心r (r <R )处的电势为2230(3)8Q R r U Rπε-=. [证明]球的体积为343V R π=, 电荷的体密度为 334Q QV R ρπ==. 利用13.10题的方法可求球内外的电场强度大小为30034QE r r R ρεπε==,(r ≦R ); 204Q E rπε=,(r ≧R ).取无穷远处的电势为零,则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrRQ Qr r r R r πεπε∞=+⎰⎰230084R rRQQ rRrπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r Rπε-=. 12.18 在y = -b 和y = b 两个“无限大”平面间均匀充满电荷,电荷体密度为ρ,其他地方无电荷.(1)求此带电系统的电场分布,画E-y 图;(2)以y = 0作为零电势面,求电势分布,画E-y 图.[解答]平板电荷产生的场强的方向与平板垂直且对称于中心面:E = E`,但方向相反.(1)在板内取一底面积为S ,高为2y 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E Sd d d 2S S S ES =⋅+⋅+⋅=⎰⎰⎰E S E S E S 12.高斯面内的体积为 V = 2yS ,包含的电量为 q = ρV = 2ρSy , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρy/ε0, (-b ≦y ≦b ).穿过平板作一底面积为S ,高为2y 的圆柱形高斯面,通过高斯面的电通量仍为地Φe = 2ES ,高斯面在板内的体积为 V = S 2b , 包含的电量为 q = ρV = ρS 2b , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρb/ε0, (b ≦y );E = -ρb/ε0, (y ≦-b ).E-y 图如左图所示.(2)对于平面之间的点,电势为d d yU y ρε=-⋅=-⎰⎰E l 202y C ρε=-+,在y = 0处U = 0,所以C = 0,因此电势为22y U ρε=-,(-b ≦y ≦b ). 这是一条开口向下的抛物线.当y ≧b 时,电势为d d nqbnqbU y y C εε=-⋅=-=-+⎰⎰E l ,在y = b 处U = -ρb 2/2ε0,所以C = ρb 2/2ε0,因此电势为2002b b U y ρρεε=-+,(b ≦y ). 当y ≦-b 时,电势为00d d b bU y y C ρρεε=-⋅==+⎰⎰E l ,在y = -b 处U = -ρb 2/2ε0,所以C = ρd 2/2ε0,因此电势为2002b b U y ρρεε=+, 两个公式综合得200||2b b U y ρρεε=-+,(|y |≧d ). 这是两条直线.U-y 图如右图所示.U-y 图的斜率就形成E-y 图,在y = ±b 点,电场强度是连续的,因此,在U-y 图中两条直线与抛物线在y = ±b 点相切.[注意]根据电场求电势时,如果无法确定零势点,可不加积分的上下限,但是要在积分之后加一个积分常量.根据其他关系确定常量,就能求出电势,不过,线积分前面要加一个负号,即d U =-⋅⎰E l这是因为积分的起点位置是积分下限.12.19 两块“无限大”平行带电板如图所示,A 板带正电,B 板带负电并接地(地的电势为零),设A 和B 两板相隔5.0cm ,板上各带电荷σ=3.3×10-6C·m -2,求: (1)在两板之间离A板1.0cm 处P 点的电势;(2)A 板的电势.[解答]两板之间的电场强度为E=σ/ε0,方向从A 指向B .以B 板为原点建立坐标系,则r B = 0,r P = -0.04m ,r A = -0.05m . (1)P 点和B 板间的电势差为d d BBPPr r P B r r U U E r -=⋅=⎰⎰E l()B P r r σε=-, 由于U B = 0,所以P 点的电势为6123.3100.048.8410P U --⨯=⨯⨯=1.493×104(V). (2)同理可得A 板的电势为()A B A U r r σε=-=1.866×104(V).12.20 电量q 均匀分布在长为2L 的细直线上,试求:(1)带电直线延长线上离中点为r 处的电势;(2)带电直线中垂线上离中点为r 处的电势;(3)由电势梯度算出上述两点的场强. [解答]电荷的线密度为λ = q/2L . (1)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的电势公式,它在P 1点产生的电势为101d d 4lU r lλπε=-总电势为10d 4L L l U r lλπε-=-⎰ 0ln()4Ll Lr l λπε=--=-0ln8q r LLr Lπε+=-. (2)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,在线的垂直平分线上的P 2点产生的电势为2221/20d d 4()lU r l λπε=+, 积分得2221/201d 4()LLU l r l λπε-=+⎰)4Ll Ll λπε=-=0ln8q Lπε=0ln4q LLrπε=.(3)P 1点的场强大小为11U E r∂=-∂ 011()8qL r L r L πε=--+22014qr L πε=-, ①方向沿着x 轴正向.P 2点的场强为22U E r∂=-∂01[4qL r πε==, ②方向沿着y 轴正向.[讨论]习题13.3的解答已经计算了带电线的延长线上的场强为1220124L E x L λπε=-, 由于2L λ = q ,取x = r ,就得公式①.(2)习题13.3的解答还计算了中垂线上的场强为y E =取d 2 = r ,可得公式②. 由此可见,电场强度可用场强叠加原理计算,也可以用电势的关系计算.12.21 如图所示,一个均匀带电,内、外半径分别为R 1和R 2的均匀带电球壳,所带电荷体密度为ρ,试计算:(1)A ,B 两点的电势;(2)利用电势梯度求A ,B 两点的场强.[解答](1)A 点在球壳的空腔内,空腔内的电势处处相等,因此A 点的电势就等于球心O 点的电势.在半径为r 的球壳处取一厚度为d r 的薄壳,其体积为d V = 4πr 2d r ,包含的电量为 d q = ρd V = 4πρr 2d r ,在球心处产生的电势为00d d d 4O q U r r rρπεε==, 球心处的总电势为2122210d ()2R O R U r r R R ρρεε==-⎰, 这就是A 点的电势U A .过B 点作一球面,B 的点电势是球面外的电荷和球面内的电荷共同产生的.球面外的电荷在B 点产生的电势就等于这些电荷在球心处产生的电势,根据上面的推导可得22120()2B U R r ρε=-. 球面内的电荷在B 点产生的电势等于这些电荷集中在球心处在B 点产生的电势.球壳在球面内的体积为3314()3B V r R π=-, 包含的电量为 Q = ρV ,这些电荷集中在球心时在B 点产生的电势为332100()43B BBQ U r R r r ρπεε==-. B 点的电势为U B = U 1 + U 2322120(32)6B BR R r r ρε=--. (2)A 点的场强为0AA AU E r ∂=-=∂. B 点的场强为3120()3B B B B BU R E r r r ρε∂=-=-∂.图13.18[讨论] 过空腔中A 点作一半径为r 的同心球形高斯面,由于面内没有电荷,根据高斯定理,可得空腔中A 点场强为E = 0, (r ≦R 1).过球壳中B 点作一半径为r 的同心球形高斯面,面内球壳的体积为3314()3V r R π=-,包含的电量为 q = ρV ,根据高斯定理得方程 4πr 2E = q/ε0, 可得B 点的场强为3120()3R E r rρε=-, (R 1≦r ≦R 2).这两个结果与上面计算的结果相同.在球壳外面作一半径为r 的同心球形高斯面,面内球壳的体积为33214()3V R R π=-,包含的电量为 q = ρV ,根据高斯定理得可得球壳外的场强为33212200()43R R qE r rρπεε-==,(R 2≦r ). A 点的电势为d d AAA r r U E r ∞∞=⋅=⎰⎰E l12131200d ()d 3AR R r RR r r r r ρε=+-⎰⎰2332120()d 3RR R r r ρε∞-+⎰ 22210()2R R ρε=-. B 点的电势为d d BBB r r U E r ∞∞=⋅=⎰⎰E l23120()d 3BR rR r r r ρε=-⎰2332120()d 3R R R r r ρε∞-+⎰ 322120(32)6B BR R r r ρε=--.A 和B 点的电势与前面计算的结果相同.12.21 (1)设地球表面附近的场强约为200V·m -1,方向指向地球中心,试求地球所带有的总电量.(2)在离地面1400m 高处,场强降为20V·m -1,方向仍指向地球中心,试计算在1400m 下大气层里的平均电荷密度.[解答]地球的平均半径为R =6.371×106m .(1)将地球当作导体,电荷分布在地球表面,由于场强方向指向地面,所以地球带负量.根据公式 E = -σ/ε0, 电荷面密度为 σ = -ε0E ; 地球表面积为 S = 4πR 2, 地球所带有的总电量为Q = σS = -4πε0R 2E = -R 2E /k ,k 是静电力常量,因此电量为629(6.37110)200910Q ⨯⨯=-⨯=-9.02×105(C). (2)在离地面高为h = 1400m 的球面内的电量为2()``R h E Q k+=-=-0.9×105(C),大气层中的电荷为q = Q - Q` = 8.12×105(C).由于大气层的厚度远小于地球的半径,其体积约为V = 4πR 2h = 0.714×1018(m 3), 平均电荷密度为ρ = q /V = 1.137×10-12(C·m -3).。
大学物理第六章静电场习题答案

第六章 静电场习题6-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解:(1)如图任选一点电荷为研究对象,分析其受力有1230F F F F =++=合 y 轴方向有()()21322002032cos 242433304q qQ F F F a a q q Q aθπεπεπε=+=+=+=合得 33Q q =-(2)这种平衡与三角形的边长无关。
6-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如图所示。
设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量。
解:对其中任一小球受力分析如图所示,有⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 6-3 在氯化铯晶体中,一价氯离子Cl -与其最邻近的八个一价铯离子Cs +构成如图所示的立方晶格结构。
(1)求氯离子所受的库仑力;(2)假设图中箭头所指处缺少一个铯离子(称作晶格缺陷),求此时氯离子所受的库仑力。
(1)由对称性可知 F 1= 0(2)291222200 1.9210N 43q q e F r aπεπε-===⨯ 方向如图所示6-4 长l =15.0 cm 的直导线AB 上均匀地分布着线密度95.010C m λ-=⨯的正电荷。
试求:(1)在导线的延长线上与导线B 端相距1 5.0cm a =处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2 5.0d cm =处Q 点的场强。
解:(1)如图所示,在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε2220)(d π4d x a x E E llP P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l -=ελ 用15=l cm ,9100.5-⨯=λ1m C -⋅,5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)同理 2220d d π41d +=x xE Q λε 方向如图所示由于对称性可知⎰=l QxE 0d ,即Q E只有y 分量22222220dd d d π41d ++=x x xE Qyλε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d l l x x 2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅ 方向沿y 轴正向*6-5 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量。
大学物理第05章 静电场习题解答

第5章 静电场习题解答5.1一带电体可作为点电荷处理的条件是( C ) (A )电荷必须呈球形分布。
(B )带电体的线度很小。
(C )带电体的线度与其它有关长度相比可忽略不计。
(D )电量很小。
5.2图中所示为一沿 x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x >0)和 -λ(x < 0),则 oxy 坐标平面上点(0,a )处的场强 E 为:( B ) ( A ) 0 ( B )02aλπεi ( C )04a λπεi ( D ) ()02aλπε+i j 5.3 两个均匀带电的同心球面,半径分别为R 1、R 2(R 1<R 2),小球带电Q ,大球带电-Q ,下列各图中哪一个正确表示了电场的分布 ( d )(C) (D)5.4 如图所示,任一闭合曲面S 内有一点电荷q ,O 为S 面上任一点,若将q 由闭合曲面内的P 点移到T 点,且OP =OT ,那么 ( d )(A) 穿过S 面的电通量改变,O 点的场强大小不变; (B) 穿过S 面的电通量改变,O 点的场强大小改变; (C) 穿过S 面的电通量不变,O 点的场强大小改变;(D) 穿过S 面的电通量不变,O 点的场强大小不变。
5.5如图所示,a 、b 、c 是电场中某条电场线上的三个点,由此可知 ( c ) (A) E a >E b >E c ; (B) E a <E b <E c ; (C) U a >U b >U c ; (D) U a <U b <U c 。
5.6关于高斯定理的理解有下面几种说法,其中正确的是 ( c )(A) 如果高斯面内无电荷,则高斯面上E处处为零;(B) 如果高斯面上E处处不为零,则该面内必无电荷; (C) 如果高斯面内有净电荷,则通过该面的电通量必不为零;(D) 如果高斯面上E处处为零,则该面内必无电荷。
5.7 下面说法正确的是 [ D ](A)等势面上各点场强的大小一定相等; (B)在电势高处,电势能也一定高; (C)场强大处,电势一定高;(D)场强的方向总是从电势高处指向低处.5.8 已知一高斯面所包围的体积内电量代数和0i q =∑ ,则可肯定:[ C ] (A )高斯面上各点场强均为零。
(完整版)大学物理静电场练习题及答案
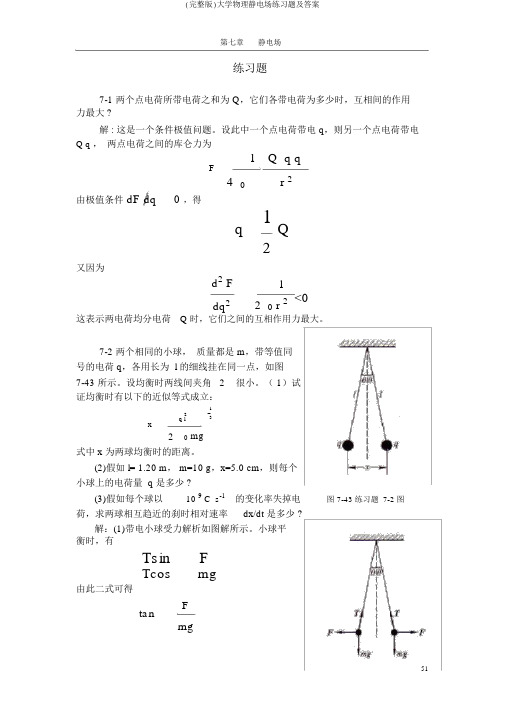
练习题7-1 两个点电荷所带电荷之和为 Q,它们各带电荷为多少时,互相间的作用力最大 ?解 : 这是一个条件极值问题。
设此中一个点电荷带电 q,则另一个点电荷带电Q q ,两点电荷之间的库仑力为1Q q qFr 24 0由极值条件 dF dq0 ,得q 1 Q 2又因为d2 F1dq2 2 0 r 2<0这表示两电荷均分电荷Q 时,它们之间的互相作用力最大。
7-2 两个相同的小球,质量都是 m,带等值同号的电荷 q,各用长为 l 的细线挂在同一点,如图7-43 所示。
设均衡时两线间夹角 2很小。
( 1)试证均衡时有以下的近似等式成立:123q lx0 mg2式中 x 为两球均衡时的距离。
(2)假如 l= 1.20 m, m=10 g,x=5.0 cm,则每个小球上的电荷量 q 是多少 ?(3)假如每个球以10 9 C s-1的变化率失掉电图 7-43 练习题 7-2 图荷,求两球相互趋近的刹时相对速率dx/dt 是多少 ?解:(1)带电小球受力解析如图解所示。
小球平衡时,有FTsinTcos mg由此二式可得tanFmg因为 很小,可有 tanx 2l ,再考虑到Fq20 x 24可解得21xq l 32 0mg(2)由上式解出3120 mgx22.38 108 Cql(3) 因为1 1dx l3 2 dq 2x dq3dt2 0 mgqdt3q dt3带入数据解得1.4010 3 m s-1合力的大小为F F x 2F 1cos212e 2x224d0 x2x 2d22132e 2 x44 x2d 2 3 2令 dF dx0 ,即有8e 2138x 24x2d23 22 4x 2d25 2由此解得 粒子受力最大的地点为xd2 2第七章静电场7-4 由相距较近的等量异号电荷构成的系统称电偶极子,生物细胞膜及土壤颗粒表面的双电层可视为好多电偶极子的会集。
所以,电偶极子是一个十分重要的物理模型。
大学物理静电场习题答案

第12章 静电场P35.12.3 如图所示,在直角三角形ABCD 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强.[解答]根据点电荷的场强大小的公式22014q qE k r r ==πε, 其中1/(4πε0) = k = 9.0×109N·m 2·C -2.点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯, 方向向下.点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯,方向向右.C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.12.4 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元 d s = R d θ,电荷元为d q = λd s ,在O 点产生的场强大小为220001d 1d d d 444q s E R R R λλθπεπεπε===, 场强的分量为d E x = d E cos θ,d E y = d E sin θ.对于带负电的圆弧,同样可得在O 点的场强的两个分量.由于弧形是对称的,x 方向的合场强为零,总场强沿着y 轴正方向,大小为2d sin y LE E E ==⎰θ/6/60000sin d (cos )22R R==-⎰ππλλθθθπεπε0(1)22R=-λπε.12.5 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C·m -1,求:(1)棒的延长线上与棒的近端d 1 = 8cm 处的场强;(2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强.[解答](1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m).在细棒上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产图13.1生的场强的大小为1220d d d 4()q lE k r x l ==-λπε场强的方向沿x 轴正向.因此P 1点的总场强大小通过积分得120d 4()L L l E x l λπε-=-⎰014LLx lλπε-=-011()4x L x Lλπε=--+ 220124L x L λπε=-. ①将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯- = 2.41×103(N·C -1),方向沿着x 轴正向.(2)建立坐标系,y = d 2. 在细棒上取一线元d l ,所带的电量为 d q = λd l ,在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE kr r λπε==, 由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ.由图可知:r = d 2/sin θ,l = d 2cot θ, 所以 d l = -d 2d θ/sin 2θ, 因此 02d sin d 4y E d λθθπε-=,总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==. ②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N·C -1). 方向沿着y 轴正向.[讨论](1)由于L = a /2,x = L+d 1,代入①式,化简得1011011144/1a E d d a d d a λλπεπε==++,保持d 1不变,当a →∞时,可得1014E d λπε→, ③这就是半无限长带电直线在相距为d 1的延长线上产生的场强大小.(2)由②式得y E ==,当a →∞时,得 022y E d λπε→, ④这就是无限长带电直线在线外产生的场强公式.如果d 1=d 2,则有大小关系E y = 2E 1.12.6 一均匀带电无限长细棒被弯成如图所示的对称形状,试问θ为何值时,圆心O 点处的场强为零.[解答]设电荷线密度为λ,先计算圆弧的电荷在圆心产生的场强.在圆弧上取一弧元 d s =R d φ, 所带的电量为d q = λd s ,在圆心处产生的场强的大小为2200d d d d 44q s E kr R Rλλϕπεπε===, 由于弧是对称的,场强只剩x 分量,取x 轴方向为正,场强为d E x = -d E cos φ. 总场强为2/20/2cos d 4x E R πθθλϕϕπε--=⎰2/20/2sin 4Rπθθλϕπε--=0sin 22R λθπε=,方向沿着x 轴正向.再计算两根半无限长带电直线在圆心产生的场强.根据上一题的公式③可得半无限长带电直线在延长上O 点产生的场强大小为`04E Rλπε=,由于两根半无限长带电直线对称放置,它们在O 点产生的合场强为``02coscos 222x E E R θλθπε==,方向沿着x 轴负向.当O 点合场强为零时,必有`x x E E =,可得 tan θ/2 = 1, 因此 θ/2 = π/4, 所以 θ = π/2.12.7 一宽为b 的无限长均匀带电平面薄板,其电荷密度为σ,如图所示.试求:(1)平板所在平面内,距薄板边缘为a处的场强.(2)通过薄板几何中心的垂直线上与薄板距离为d 处的场强.[解答](1)建立坐标系.在平面薄板上取一宽度为d x 的带电直线,电荷的线密度为d λ = σd x , 根据直线带电线的场强公式02E rλπε=, 得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-,其方向沿x 轴正向.由于每条无限长直线在P 点的产生的场强方向相同,所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ /20/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+. ①图13.4图13.5.场强方向沿x 轴正向.(2)为了便于观察,将薄板旋转建立坐标系.仍然在平面薄板上取一宽度为d x 的带电直线,电荷的线密度仍然为d λ = σd x ,带电直线在Q 点产生的场强为221/200d d d 22()xE rb x λσπεπε==+,沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+,设x = d tan θ,则d x = d d θ/cos 2θ,因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰ 0arctan()2bdσπε=. ② 场强方向沿z 轴正向.[讨论](1)薄板单位长度上电荷为λ = σb ,①式的场强可化为0ln(1/)2/b a E a b aλπε+=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02E aλπε→, ③ 这正是带电直线的场强公式.(2)②也可以化为0arctan(/2)2/2z b d E d b dλπε=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02z E dλπε→,这也是带电直线的场强公式.当b →∞时,可得2z E σε→, ④ 这是无限大带电平面所产生的场强公式.12.8 (1)点电荷q 位于一个边长为a 的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?(2)如果将该场源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?[解答]点电荷产生的电通量为Φe = q/ε0.(1)当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1 = Φe /6 = q /6ε0.(2)当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1 = Φe /24 = q /24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零.12.9 面电荷密度为σ的均匀无限大带电平板,以平板上的一点O 为中心,R 为半径作一半球面,如图所示.求通过此半球面的电通量.[解答]设想在平板下面补一个半球面,与上面的半球面合成一个球面.球面内包含的电荷为q = πR 2σ, 通过球面的电通量为图13.7Φe = q /ε0, 通过半球面的电通量为Φ`e = Φe /2 = πR 2σ/2ε0.12.10 两无限长同轴圆柱面,半径分别为R 1和R 2(R 1 > R 2),带有等量异号电荷,单位长度的电量为λ和-λ,求(1)r < R 1;(2) R 1 < r < R 2;(3)r > R 2处各点的场强.[解答]由于电荷分布具有轴对称性,所以电场分布也具有轴对称性.(1)在内圆柱面内做一同轴圆柱形高斯面,由于高斯内没有电荷,所以E = 0,(r < R 1).(2)在两个圆柱之间做一长度为l ,半径为r 的同轴圆柱形高斯面,高斯面内包含的电荷为 q = λl , 穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ,根据高斯定理Φe = q /ε0,所以02E rλπε=, (R 1 < r < R 2). (3)在外圆柱面之外做一同轴圆柱形高斯面,由于高斯内电荷的代数和为零,所以E = 0,(r > R 2).12.11 一厚度为d 的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法.(1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E = E`.在板内取一底面积为S ,高为2r 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E S2d d d S S S =⋅+⋅+⋅⎰⎰⎰E S E S E S 1`02ES E S ES =++=,高斯面内的体积为 V = 2rS , 包含的电量为 q =ρV = 2ρrS , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρr/ε0,(0≦r ≦d /2).①(2)穿过平板作一底面积为S ,高为2r 的圆柱形高斯面,通过高斯面的电通量仍为 Φe = 2ES , 高斯面在板内的体积为V = Sd , 包含的电量为 q =ρV = ρSd , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρd /2ε0,(r ≧d /2). ②方法二:场强叠加法. (1)由于平板的可视很多薄板叠而成的,以r 为界,下面平板产生的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层d y ,面电荷密度为d σ = ρd y ,产生的场强为 d E 1 = d σ/2ε0, 积分得100/2d ()222rd y dE r ρρεε-==+⎰,③ 同理,上面板产生的场强为/2200d ()222d ry d E r ρρεε==-⎰,④ r 处的总场强为E = E 1-E 2 = ρr/ε0.(2)在公式③和④中,令r = d /2,得E 2 = 0、E = E 1 = ρd /2ε0,E 就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.1212.13 一半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为R`<R的小球体,如图所示,试求两球心O 与O`处的电场强度,并证明小球空腔内的电场为均强电场.[解答]挖去一块小球体,相当于在该处填充一块电荷体密度为-ρ的小球体,因此,空间任何一点的场强是两个球体产生的场强的叠加.对于一个半径为R ,电荷体密度为ρ的球体来说,当场点P 在球内时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r r ππρε=P 点场强大小为3E r ρε=.当场点P 在球外时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r R ππρε=P 点场强大小为3203R E rρε=. O 点在大球体中心、小球体之外.大球体在O 点产生的场强为零,小球在O 点产生的场强大小为320`3O R E aρε=, 方向由O 指向O `.O`点在小球体中心、大球体之内.小球体在O`点产生的场强为零,大球在O 点产生的场强大小为`03O E a ρε=, 方向也由O 指向O `.[证明]在小球内任一点P ,大球和小球产生的场强大小分别为 03r E r ρε=, `0`3r E r ρε=,方向如图所示.设两场强之间的夹角为θ,合场强的平方为222``2cos r r r r E E E E E θ=++2220()(`2`cos )3r r rr ρθε=++, 根据余弦定理得222`2`c o s ()a r rr r πθ=+--, 所以 03E a ρε=, 可见:空腔内任意点的电场是一个常量.还可以证明:场强的方向沿着O 到O `的方向.因此空腔内的电场为匀强电场.12.14 如图所示,在A 、B 两点处放有电量分别为+q 和-q 的点电荷,AB 间距离为2R ,现将另一正试验电荷q 0从O 点经过半圆弧路径移到C点,求移动过程中电场力所做的功.[解答]正负电荷在O 点的电势的和为零:U O = 0;图13.10图13.11在C 点产生的电势为0004346C q q q U RRRπεπεπε--=+=,电场力将正电荷q 0从O 移到C 所做的功为W = q 0U OD = q 0(U O -U D ) = q 0q /6πε0R .12.15 真空中有两块相互平行的无限大均匀带电平面A 和B .A 平面的电荷面密度为2σ,B 平面的电荷面密度为σ,两面间的距离为d .当点电荷q 从A 面移到B 面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为E A = 2σ/2ε0 = σ/ε0,E B = σ/2ε0,两平面在它们之间产生的场强方向相反,因此,总场强大小为E = E A - E B = σ/2ε0, 方向由A 平面指向B 平面.两平面间的电势差为U = Ed = σd /2ε0,当点电荷q 从A 面移到B 面时,电场力做的功为W = qU = qσd /2ε0.12.16 一半径为R 的均匀带电球面,带电量为Q .若规定该球面上电势值为零,则无限远处的电势为多少?[解答]带电球面在外部产生的场强为204Q E rπε=,由于d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=,当U R = 0时,04Q U Rπε∞=-.12.17 电荷Q 均匀地分布在半径为R 的球体内,试证明离球心r (r <R )处的电势为2230(3)8Q R r U Rπε-=. [证明]球的体积为343V R π=, 电荷的体密度为 334Q QV R ρπ==. 利用13.10题的方法可求球内外的电场强度大小为30034QE r r R ρεπε==,(r ≦R ); 204Q E rπε=,(r ≧R ).取无穷远处的电势为零,则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrRQ Qr r r R r πεπε∞=+⎰⎰230084R rRQQ rRrπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r Rπε-=. 12.18 在y = -b 和y = b 两个“无限大”平面间均匀充满电荷,电荷体密度为ρ,其他地方无电荷.(1)求此带电系统的电场分布,画E-y 图;(2)以y = 0作为零电势面,求电势分布,画E-y 图.[解答]平板电荷产生的场强的方向与平板垂直且对称于中心面:E = E`,但方向相反.(1)在板内取一底面积为S ,高为2y 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E Sd d d 2S S S ES =⋅+⋅+⋅=⎰⎰⎰E S E S E S 12.高斯面内的体积为 V = 2yS ,包含的电量为 q = ρV = 2ρSy , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρy/ε0, (-b ≦y ≦b ).穿过平板作一底面积为S ,高为2y 的圆柱形高斯面,通过高斯面的电通量仍为地Φe = 2ES ,高斯面在板内的体积为 V = S 2b , 包含的电量为 q = ρV = ρS 2b , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρb/ε0, (b ≦y );E = -ρb/ε0, (y ≦-b ).E-y 图如左图所示.(2)对于平面之间的点,电势为d d yU y ρε=-⋅=-⎰⎰E l 202y C ρε=-+,在y = 0处U = 0,所以C = 0,因此电势为22y U ρε=-,(-b ≦y ≦b ). 这是一条开口向下的抛物线.当y ≧b 时,电势为d d nqbnqbU y y C εε=-⋅=-=-+⎰⎰E l ,在y = b 处U = -ρb 2/2ε0,所以C = ρb 2/2ε0,因此电势为2002b b U y ρρεε=-+,(b ≦y ). 当y ≦-b 时,电势为00d d b bU y y C ρρεε=-⋅==+⎰⎰E l ,在y = -b 处U = -ρb 2/2ε0,所以C = ρd 2/2ε0,因此电势为2002b b U y ρρεε=+, 两个公式综合得200||2b b U y ρρεε=-+,(|y |≧d ). 这是两条直线.U-y 图如右图所示.U-y 图的斜率就形成E-y 图,在y = ±b 点,电场强度是连续的,因此,在U-y 图中两条直线与抛物线在y = ±b 点相切.[注意]根据电场求电势时,如果无法确定零势点,可不加积分的上下限,但是要在积分之后加一个积分常量.根据其他关系确定常量,就能求出电势,不过,线积分前面要加一个负号,即d U =-⋅⎰E l这是因为积分的起点位置是积分下限.12.19 两块“无限大”平行带电板如图所示,A 板带正电,B 板带负电并接地(地的电势为零),设A 和B 两板相隔5.0cm ,板上各带电荷σ=3.3×10-6C·m -2,求: (1)在两板之间离A板1.0cm 处P 点的电势;(2)A 板的电势.[解答]两板之间的电场强度为E=σ/ε0,方向从A 指向B .以B 板为原点建立坐标系,则r B = 0,r P = -0.04m ,r A = -0.05m . (1)P 点和B 板间的电势差为d d BBPPr r P B r r U U E r -=⋅=⎰⎰E l()B P r r σε=-, 由于U B = 0,所以P 点的电势为6123.3100.048.8410P U --⨯=⨯⨯=1.493×104(V). (2)同理可得A 板的电势为()A B A U r r σε=-=1.866×104(V).12.20 电量q 均匀分布在长为2L 的细直线上,试求:(1)带电直线延长线上离中点为r 处的电势;(2)带电直线中垂线上离中点为r 处的电势;(3)由电势梯度算出上述两点的场强. [解答]电荷的线密度为λ = q/2L . (1)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的电势公式,它在P 1点产生的电势为101d d 4lU r lλπε=-总电势为10d 4L L l U r lλπε-=-⎰ 0ln()4Ll Lr l λπε=--=-0ln8q r LLr Lπε+=-. (2)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,在线的垂直平分线上的P 2点产生的电势为2221/20d d 4()lU r l λπε=+, 积分得2221/201d 4()LLU l r l λπε-=+⎰)4Ll Ll λπε=-=0ln8q Lπε=0ln4q LLrπε=.(3)P 1点的场强大小为11U E r∂=-∂ 011()8qL r L r L πε=--+22014qr L πε=-, ①方向沿着x 轴正向.P 2点的场强为22U E r∂=-∂01[4qL r πε==, ②方向沿着y 轴正向.[讨论]习题13.3的解答已经计算了带电线的延长线上的场强为1220124L E x L λπε=-, 由于2L λ = q ,取x = r ,就得公式①.(2)习题13.3的解答还计算了中垂线上的场强为y E =取d 2 = r ,可得公式②. 由此可见,电场强度可用场强叠加原理计算,也可以用电势的关系计算.12.21 如图所示,一个均匀带电,内、外半径分别为R 1和R 2的均匀带电球壳,所带电荷体密度为ρ,试计算:(1)A ,B 两点的电势;(2)利用电势梯度求A ,B 两点的场强.[解答](1)A 点在球壳的空腔内,空腔内的电势处处相等,因此A 点的电势就等于球心O 点的电势.在半径为r 的球壳处取一厚度为d r 的薄壳,其体积为d V = 4πr 2d r ,包含的电量为 d q = ρd V = 4πρr 2d r ,在球心处产生的电势为00d d d 4O q U r r rρπεε==, 球心处的总电势为2122210d ()2R O R U r r R R ρρεε==-⎰, 这就是A 点的电势U A .过B 点作一球面,B 的点电势是球面外的电荷和球面内的电荷共同产生的.球面外的电荷在B 点产生的电势就等于这些电荷在球心处产生的电势,根据上面的推导可得22120()2B U R r ρε=-. 球面内的电荷在B 点产生的电势等于这些电荷集中在球心处在B 点产生的电势.球壳在球面内的体积为3314()3B V r R π=-, 包含的电量为 Q = ρV ,这些电荷集中在球心时在B 点产生的电势为332100()43B BBQ U r R r r ρπεε==-. B 点的电势为U B = U 1 + U 2322120(32)6B BR R r r ρε=--. (2)A 点的场强为0AA AU E r ∂=-=∂. B 点的场强为3120()3B B B B BU R E r r r ρε∂=-=-∂.图13.18[讨论] 过空腔中A 点作一半径为r 的同心球形高斯面,由于面内没有电荷,根据高斯定理,可得空腔中A 点场强为E = 0, (r ≦R 1).过球壳中B 点作一半径为r 的同心球形高斯面,面内球壳的体积为3314()3V r R π=-,包含的电量为 q = ρV ,根据高斯定理得方程 4πr 2E = q/ε0, 可得B 点的场强为3120()3R E r rρε=-, (R 1≦r ≦R 2).这两个结果与上面计算的结果相同.在球壳外面作一半径为r 的同心球形高斯面,面内球壳的体积为33214()3V R R π=-,包含的电量为 q = ρV ,根据高斯定理得可得球壳外的场强为33212200()43R R qE r rρπεε-==,(R 2≦r ). A 点的电势为d d AAA r r U E r ∞∞=⋅=⎰⎰E l12131200d ()d 3AR R r RR r r r r ρε=+-⎰⎰2332120()d 3RR R r r ρε∞-+⎰ 22210()2R R ρε=-. B 点的电势为d d BBB r r U E r ∞∞=⋅=⎰⎰E l23120()d 3BR rR r r r ρε=-⎰2332120()d 3R R R r r ρε∞-+⎰ 322120(32)6B BR R r r ρε=--.A 和B 点的电势与前面计算的结果相同.12.21 (1)设地球表面附近的场强约为200V·m -1,方向指向地球中心,试求地球所带有的总电量.(2)在离地面1400m 高处,场强降为20V·m -1,方向仍指向地球中心,试计算在1400m 下大气层里的平均电荷密度.[解答]地球的平均半径为R =6.371×106m .(1)将地球当作导体,电荷分布在地球表面,由于场强方向指向地面,所以地球带负量.根据公式 E = -σ/ε0, 电荷面密度为 σ = -ε0E ; 地球表面积为 S = 4πR 2, 地球所带有的总电量为Q = σS = -4πε0R 2E = -R 2E /k ,k 是静电力常量,因此电量为629(6.37110)200910Q ⨯⨯=-⨯=-9.02×105(C). (2)在离地面高为h = 1400m 的球面内的电量为2()``R h E Q k+=-=-0.9×105(C),大气层中的电荷为q = Q - Q` = 8.12×105(C).由于大气层的厚度远小于地球的半径,其体积约为V = 4πR 2h = 0.714×1018(m 3), 平均电荷密度为ρ = q /V = 1.137×10-12(C·m -3).。
大学物理静电场练习题带答案
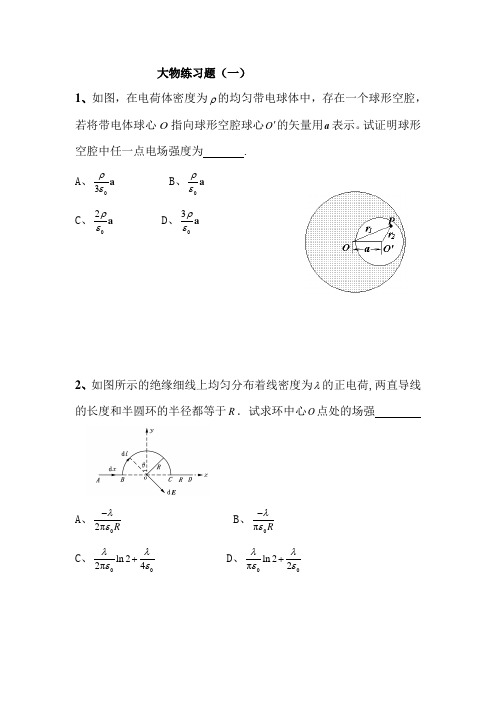
大物练习题(一)1、如图,在电荷体密度为ρ的均匀带电球体中,存在一个球形空腔,若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示,一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ,求导体球和球壳之间的电势差 (填写A 、B 、C 或D ,从下面的选项中选取)。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭4.如图所示,电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ,今测得导体表面靠近P 点处的电荷面密度为2σ。
求:(1)P 点处的场强 ;(2)导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5.如图,在一带电量为Q 的导体球外,同心地包有一各向同性均匀电介质球壳,其相对电容率为r ε,壳外是真空,则在壳外P 点处(OP r =)的场强和电位移的大小分别为[ ](A )2200,44r Q QE D rr εεε==ππ; (B )22,44r Q QE D r r ε==ππ; (C )220,44Q QE D r r ε==ππ; (D )2200,44Q QE D r r εε==ππ。
6、在一点电荷产生的静电场中,一块电介质如图放置,以点电荷所在处为球心作一球形闭合面,则对此球形闭合面: (A )高斯定理成立,且可用它求出闭合面上各点的场强;(B )高斯定理成立,但不能用它求出闭合面上各点的场强; (C )由于电介质不对称分布,高斯定理不成立; (D )即使电介质对称分布,高斯定理也不成立。
大学物理静电场习题问题详解

第12章 静电场P35.12.3 如图所示,在直角三角形ABCD 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强.[解答]根据点电荷的场强大小的公式22014q qE kr r ==πε, 其中1/(4πε0) = k = 9.0×109N ·m 2·C -2.点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯, 方向向下.点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε 994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯,方向向右.C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.12.4 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元 d s = R d θ,电荷元为d q = λd s ,在O 点产生的场强大小为220001d 1d d d 444q s E R R R λλθπεπεπε===,场强的分量为d E x = d E cos θ,d E y = d E sin θ.对于带负电的圆弧,同样可得在O 点的场强的两个分量.由于弧形是对称的,x 方向的合场强为零,总场强沿着y 轴正方向,大小为2d sin y LE E E ==⎰θ/6/6000sin d (cos )22R R ==-⎰ππλλθθθπεπε0(12R=λπε.12.5 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C ·m -1,求:(1)棒的延长线上与棒的近端d 1 = 8cm 处的场强;(2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强.[解答](1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m).在细棒上取一线元d l ,图13.1所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产生的场强的大小为1220d d d 4()q lE k r x l ==-λπε场强的方向沿x 轴正向.因此P 1点的总场强大小通过积分得120d 4()L L l E x l λπε-=-⎰ 014LLx lλπε-=-011()4x L x Lλπε=--+ 220124L x Lλπε=-. ① 将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯-= 2.41×103(N ·C -1),方向沿着x 轴正向.(2)建立坐标系,y = d 2. 在细棒上取一线元d l ,所带的电量为 d q = λd l ,在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE kr rλπε==, 由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ.由图可知:r = d 2/sin θ,l = d 2cot θ,所以 d l = -d 2d θ/sin 2θ,因此 02d sin d 4y E d λθθπε-=,总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==. ②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N ·C -1). 方向沿着y 轴正向.[讨论](1)由于L = a /2,x = L+d 1,代入①式,化简得1011011144/1a E d d a d d a λλπεπε==++,保持d 1不变,当a →∞时,可得1014E d λπε→, ③这就是半无限长带电直线在相距为d 1的延长线上产生的场强大小.(2)由②式得y E ==,当a →∞时,得 022y E d λπε→, ④这就是无限长带电直线在线外产生的场强公式.如果d 1=d 2,则有大小关系E y = 2E 1.12.6 一均匀带电无限长细棒被弯成如图所示的对称形状,试问θ为何值时,圆心O 点处的场强为零.[解答]设电荷线密度为λ,先计算圆弧的电荷在圆心产生的场强.在圆弧上取一弧元 d s =R d φ, 所带的电量为d q = λd s ,在圆心处产生的场强的大小为2200d d d d 44q s E kr R Rλλϕπεπε===, 由于弧是对称的,场强只剩x 分量,取x 轴方向为正,场强为d E x = -d E cos φ. 总场强为2/20/2cos d 4x E R πθθλϕϕπε--=⎰2/20/2sin 4Rπθθλϕπε--=0sin 22R λθπε=,方向沿着x 轴正向.再计算两根半无限长带电直线在圆心产生的场强.根据上一题的公式③可得半无限长带电直线在延长上O 点产生的场强大小为`04E Rλπε=,由于两根半无限长带电直线对称放置,它们在O 点产生的合场强为``02coscos 222x E E R θλθπε==,方向沿着x 轴负向.当O 点合场强为零时,必有`x x E E =,可得 tan θ/2 = 1, 因此 θ/2 = π/4, 所以 θ = π/2.12.7 一宽为b 的无限长均匀带电平面薄板,其电荷密度为σ,如图所示.试求:(1)平板所在平面内,距薄板边缘为a 处的场强.(2)通过薄板几何中心的垂直线上与薄板距离为d 处的场强.[解答](1)建立坐标系.在平面薄板上取一宽度为d x 的带电直线,电荷的线密度为d λ = σd x , 根据直线带电线的场强公式02E rλπε=, 得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-,其方向沿x 轴正向.由于每条无限长直线在P 点的产生的场强方向相同,所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ 图13.4图13.5/20/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+. ① 场强方向沿x 轴正向.(2)为了便于观察,将薄板旋转建立坐标系.仍然在平面薄板上取一宽度为d x 的带电直线,电荷的线密度仍然为d λ = σd x ,带电直线在Q 点产生的场强为221/200d d d 22()xE rb x λσπεπε==+,沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+,设x = d tan θ,则d x = d d θ/cos 2θ,因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰ 0arctan()2bdσπε=. ② 场强方向沿z 轴正向.[讨论](1)薄板单位长度上电荷为λ = σb ,①式的场强可化为0ln(1/)2/b a E a b aλπε+=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02E aλπε→, ③ 这正是带电直线的场强公式.(2)②也可以化为0arctan(/2)2/2z b d E d b dλπε=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02z E dλπε→,这也是带电直线的场强公式.当b →∞时,可得2z E σε→, ④ 这是无限大带电平面所产生的场强公式.12.8 (1)点电荷q 位于一个边长为a 的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?(2)如果将该场源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?[解答]点电荷产生的电通量为Φe = q/ε0.(1)当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1 = Φe /6 = q /6ε0.(2)当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1 = Φe /24 = q /24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零.12.9 面电荷密度为σ的均匀无限大带电平板,以平板上的一点O 为中心,R 为半径作一半球面,如图所示.求通过此半球面的电通量.[解答]设想在平板下面补一个半球面,与上面的半球面合成一个球面.球面内包含的电荷为q = πR 2σ, 通过球面的电通量为Φe = q /ε0, 通过半球面的电通量为Φ`e = Φe /2 = πR 2σ/2ε0.12.10 两无限长同轴圆柱面,半径分别为R 1和R 2(R 1 > R 2),带有等量异号电荷,单位长度的电量为λ和-λ,求(1)r < R 1;(2) R 1 < r < R 2;(3)r > R 2处各点的场强.[解答]由于电荷分布具有轴对称性,所以电场分布也具有轴对称性.(1)在内圆柱面内做一同轴圆柱形高斯面,由于高斯内没有电荷,所以E = 0,(r < R 1).(2)在两个圆柱之间做一长度为l ,半径为r 的同轴圆柱形高斯面,高斯面内包含的电荷为 q = λl , 穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ,根据高斯定理Φe = q /ε0,所以02E rλπε=, (R 1 < r < R 2). (3)在外圆柱面之外做一同轴圆柱形高斯面,由于高斯内电荷的代数和为零,所以E = 0,(r > R 2).12.11 一厚度为d 的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法.(1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E = E`.在板内取一底面积为S ,高为2r 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E S2d d d S S S =⋅+⋅+⋅⎰⎰⎰E S E S E S 1`02ES E S ES =++=,高斯面内的体积为 V = 2rS ,包含的电量为 q =ρV = 2ρrS , 根据高斯定理 Φe = q/ε0, 可得场强为 E = ρr/ε0,(0≦r ≦d /2).①(2)穿过平板作一底面积为S ,高为2r 的圆柱形高斯面,通过高斯面的电通量仍为 Φe = 2ES , 高斯面在板内的体积为V = Sd ,包含的电量为 q =ρV = ρSd , 根据高斯定理 Φe = q/ε0, 可得场强为 E = ρd /2ε0,(r ≧d /2). ②方法二:场强叠加法. (1)由于平板的可视很多薄板叠而成的,以r 为界,下面平板产生的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层d y ,面电荷密度为d σ = ρd y ,产生的场强为 d E 1 = d σ/2ε0, 积分得100/2d ()222rd y dE r ρρεε-==+⎰,③ 同理,上面板产生的场强为图13.7/2200d ()222d ry dE r ρρεε==-⎰,④ r 处的总场强为E = E 1-E 2 = ρr/ε0.(2)在公式③和④中,令r = d /2,得E 2 = 0、E = E 1 = ρd /2ε0,E 就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.1212.13 一半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为R`<R 的小球体,如图所示,试求两球心O 与O`处的电场强度,并证明小球空腔内的电场为均强电场.[解答]挖去一块小球体,相当于在该处填充一块电荷体密度为-ρ的小球体,因此,空间任何一点的场强是两个球体产生的场强的叠加.对于一个半径为R ,电荷体密度为ρ的球体来说,当场点P 在球内时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r r ππρε=P 点场强大小为3E r ρε=. 当场点P 在球外时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r R ππρε=P 点场强大小为3203R E rρε=. O 点在大球体中心、小球体之外.大球体在O 点产生的场强为零,小球在O 点产生的场强大小为320`3O R E aρε=, 方向由O 指向O `.O`点在小球体中心、大球体之内.小球体在O`点产生的场强为零,大球在O 点产生的场强大小为`03O E a ρε=, 方向也由O 指向O `.[证明]在小球内任一点P ,大球和小球产生的场强大小分别为 03r E r ρε=,`0`3r E r ρε=,方向如图所示.设两场强之间的夹角为θ,合场强的平方为222``2cos r r r r E E E E E θ=++2220()(`2`cos )3r r rr ρθε=++, 根据余弦定理得222`2`cos()a r r rr πθ=+--, 所以 03E a ρε=, 可见:空腔内任意点的电场是一个常图13.10量.还可以证明:场强的方向沿着O 到O `的方向.因此空腔内的电场为匀强电场.12.14 如图所示,在A 、B 两点处放有电量分别为+q 和-q 的点电荷,AB 间距离为2R ,现将另一正试验电荷q 0从O 点经过半圆弧路径移到C点,求移动过程中电场力所做的功.[解答]正负电荷在O 点的电势的和为零:U O = 0;在C 点产生的电势为0004346C q q q U RRRπεπεπε--=+=,电场力将正电荷q 0从O 移到C 所做的功为W = q 0U OD = q 0(U O -U D ) = q 0q /6πε0R .12.15 真空中有两块相互平行的无限大均匀带电平面A 和B .A 平面的电荷面密度为2σ,B 平面的电荷面密度为σ,两面间的距离为d .当点电荷q 从A 面移到B 面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为E A = 2σ/2ε0 = σ/ε0,E B = σ/2ε0, 两平面在它们之间产生的场强方向相反,因此,总场强大小为E = E A - E B = σ/2ε0, 方向由A 平面指向B 平面.两平面间的电势差为U = Ed = σd /2ε0,当点电荷q 从A 面移到B 面时,电场力做的功为W = qU = q σd /2ε0.12.16 一半径为R 的均匀带电球面,带电量为Q .若规定该球面上电势值为零,则无限远处的电势为多少?[解答]带电球面在外部产生的场强为204Q E r πε=,由于d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=,当U R = 0时,04Q U Rπε∞=-.12.17 电荷Q 均匀地分布在半径为R 的球体内,试证明离球心r (r <R )处的电势为2230(3)8Q R r U Rπε-=. [证明]球的体积为343V R π=, 电荷的体密度为 334Q QV Rρπ==. 利用13.10题的方法可求球内外的电场强度大小为30034Q E r r Rρεπε==,(r ≦R ); 204Q E r πε=,(r ≧R ).取无穷远处的电势为零,则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrRQ Q r r r Rrπεπε∞=+⎰⎰图13.11230084RrRQ Q rRrπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r Rπε-=.12.18 在y = -b 和y = b 两个“无限大”平面间均匀充满电荷,电荷体密度为ρ,其他地方无电荷.(1)求此带电系统的电场分布,画E-y 图;(2)以y = 0作为零电势面,求电势分布,画E-y 图.[解答]平板电荷产生的场强的方向与平板垂直且对称于中心面:E = E`,但方向相反.(1)在板内取一底面积为S ,高为2y 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E Sd d d 2S S S ES=⋅+⋅+⋅=⎰⎰⎰E S E S E S 12.高斯面内的体积为 V = 2yS ,包含的电量为 q = ρV = 2ρSy , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρy/ε0, (-b ≦y ≦b ).穿过平板作一底面积为S ,高为2y 的圆柱形高斯面,通过高斯面的电通量仍为地Φe = 2ES ,高斯面在板内的体积为 V = S 2b , 包含的电量为 q = ρV = ρS 2b , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρb/ε0, (b ≦y );E = -ρb/ε0, (y ≦-b ).E-y 图如左图所示.(2)对于平面之间的点,电势为d d yU y ρε=-⋅=-⎰⎰E l 202y C ρε=-+,在y = 0处U = 0,所以C = 0,因此电势为22y U ρε=-,(-b ≦y ≦b ). 这是一条开口向下的抛物线.当y ≧b 时,电势为00d d nqb nqbU y y Cεε=-⋅=-=-+⎰⎰E l ,在y = b 处U = -ρb 2/2ε0,所以C = ρb 2/2ε0,因此电势为2002b b U y ρρεε=-+,(b ≦y ). 当y ≦-b 时,电势为00d d b bU y y C ρρεε=-⋅==+⎰⎰E l ,在y = -b 处U = -ρb 2/2ε0,所以C = ρd 2/2ε0,因此电势为2002b b U y ρρεε=+, 两个公式综合得200||2b b U y ρρεε=-+,(|y |≧d ). 这是两条直线.U-y 图如右图所示.U-y 图的斜率就形成E-y 图,在y = ±b 点,电场强度是连续的,因此,在U-y 图中两条直线与抛物线在y = ±b 点相切.[注意]根据电场求电势时,如果无法确定零势点,可不加积分的上下限,但是要在积分之后加一个积分常量.根据其他关系确定常量,就能求出电势,不过,线积分前面要加一个负号,即d U =-⋅⎰E l这是因为积分的起点位置是积分下限.12.19 两块“无限大”平行带电板如图所示,A 板带正电,B 板带负电并接地(地的电势为零),设A 和B 两板相隔5.0cm ,板上各带电荷σ=3.3×10-6C ·m -2,求: (1)在两板之间离A 板1.0cm 处P 点的电势;(2)A 板的电势.[解答]两板之间的电场强度为E=σ/ε0,方向从A 指向B .以B 板为原点建立坐标系,则r B = 0,r P = -0.04m ,r A = -0.05m . (1)P 点和B 板间的电势差为d d BBPPr r P B r r U U E r -=⋅=⎰⎰E l()B P r r σε=-, 由于U B = 0,所以P 点的电势为6123.3100.048.8410P U --⨯=⨯⨯=1.493×104(V).(2)同理可得A 板的电势为()A B A U r r σε=-=1.866×104(V).12.20 电量q 均匀分布在长为2L 的细直线上,试求:(1)带电直线延长线上离中点为r 处的电势;(2)带电直线中垂线上离中点为r 处的电势;(3)由电势梯度算出上述两点的场强. [解答]电荷的线密度为λ = q/2L . (1)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的电势公式,它在P 1点产生的电势为101d d 4lU r lλπε=-总电势为10d 4L L l U r lλπε-=-⎰ln()4Ll Lr l λπε=--=-0ln8q r LLr Lπε+=-. (2)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,在线的垂直平分线上的P 2点产生的电势为2221/20d d 4()lU r l λπε=+,积分得2221/201d 4()LLU l r l λπε-=+⎰)4Ll Ll λπε=-=08q Lπε=04q Lπε=.(3)P 1点的场强大小为11U E r∂=-∂ 011()8qL r L r L πε=--+22014qr L πε=-, ①方向沿着x 轴正向.P 2点的场强为22U E r∂=-∂01[4qL r πε==, ②方向沿着y 轴正向.[讨论]习题13.3的解答已经计算了带电线的延长线上的场强为1220124L E x L λπε=-, 由于2L λ = q ,取x = r ,就得公式①.(2)习题13.3的解答还计算了中垂线上的场强为y E =取d 2 = r ,可得公式②.由此可见,电场强度可用场强叠加原理计算,也可以用电势的关系计算.12.21 如图所示,一个均匀带电,内、外半径分别为R 1和R 2的均匀带电球壳,所带电荷体密度为ρ,试计算:(1)A ,B 两点的电势;(2)利用电势梯度求A ,B 两点的场强.[解答](1)A 点在球壳的空腔内,空腔内的电势处处相等,因此A 点的电势就等于球心O 点的电势.在半径为r 的球壳处取一厚度为d r 的薄壳,其体积为d V = 4πr 2d r ,包含的电量为 d q = ρd V = 4πρr 2d r ,在球心处产生的电势为00d d d 4O q U r r rρπεε==, 球心处的总电势为2122210d ()2R O R U r r R R ρρεε==-⎰, 这就是A 点的电势U A .过B 点作一球面,B 的点电势是球面外的电荷和球面内的电荷共同产生的.球面外的电荷在B 点产生的电势就等于这些电荷在球心处产生的电势,根据上面的推导可得图13.1822120()2B U R r ρε=-.球面内的电荷在B 点产生的电势等于这些电荷集中在球心处在B 点产生的电势.球壳在球面内的体积为3314()3B V r R π=-, 包含的电量为 Q = ρV ,这些电荷集中在球心时在B 点产生的电势为332100()43B BBQ U r R r r ρπεε==-. B 点的电势为U B = U 1 + U 2322120(32)6B BR R r r ρε=--. (2)A 点的场强为0AA AU E r ∂=-=∂. B 点的场强为3120()3B B B B BU R E r r rρε∂=-=-∂. [讨论] 过空腔中A 点作一半径为r 的同心球形高斯面,由于面内没有电荷,根据高斯定理,可得空腔中A 点场强为E = 0, (r ≦R 1).过球壳中B 点作一半径为r 的同心球形高斯面,面内球壳的体积为3314()3V r R π=-,包含的电量为 q = ρV ,根据高斯定理得方程 4πr 2E = q/ε0, 可得B 点的场强为3120()3R E r rρε=-, (R 1≦r ≦R 2).这两个结果与上面计算的结果相同.在球壳外面作一半径为r 的同心球形高斯面,面内球壳的体积为33214()3V R R π=-,包含的电量为 q = ρV ,根据高斯定理得可得球壳外的场强为33212200()43R R qE r r ρπεε-==,(R 2≦r ). A 点的电势为d d AAA r r U E r ∞∞=⋅=⎰⎰E l12131200d ()d 3AR R r RR r r r r ρε=+-⎰⎰2332120()d 3RR R r r ρε∞-+⎰ 22210()2R R ρε=-. B 点的电势为d d BBB r r U E r ∞∞=⋅=⎰⎰E l23120()d 3BR r R r r r ρε=-⎰2332120()d 3R R R r r ρε∞-+⎰ 322120(32)6B BR R r r ρε=--.A 和B 点的电势与前面计算的结果相同.12.21 (1)设地球表面附近的场强约为200V ·m -1,方向指向地球中心,试求地球所带有的总电量.(2)在离地面1400m 高处,场强降为20V ·m -1,方向仍指向地球中心,试计算在1400m 下大气层里的平均电荷密度.[解答]地球的平均半径为R =6.371×106m .(1)将地球当作导体,电荷分布在地球表面,由于场强方向指向地面,所以地球带负量.根据公式 E = -σ/ε0,电荷面密度为 σ = -ε0E ;地球表面积为 S = 4πR 2, 地球所带有的总电量为Q = σS = -4πε0R 2E =-R 2E /k ,k 是静电力常量,因此电量为629(6.37110)200910Q ⨯⨯=-⨯=-9.02×105(C).(2)在离地面高为h = 1400m 的球面内的电量为2()``R h E Q k+=-=-0.9×105(C), 大气层中的电荷为q = Q - Q` = 8.12×105(C).由于大气层的厚度远小于地球的半径,其体积约为V = 4πR 2h = 0.714×1018(m 3), 平均电荷密度为ρ = q /V = 1.137×10-12(C ·m -3).。
静电场习题答案及小结

2 0 a
qቤተ መጻሕፍቲ ባይዱ
a
a
O
QU o
3 3q Uo 2 0 a
a
2q
10
6.如图所示 ,半径为 R的导体球原来带电为 Q,现将 一点电荷 q 放在球外离球心距离为 x(>R) 处 , 导体球 上的电荷在P点(OP = R/2)产生的场强和电势.
+
解:由于静电感应,使电荷重 + 新分布 , 球内处处场强为零 . 因 + R O .R/2P. 此P点总的电场强度也为零. + + q + E 0 EP P 2 4 0 ( x R / 2)
E内 0 2、均匀带电球面 q E外 4 r 2
q E 2 4 r U q 4 r
q U内 4 R U q 外 4 r
E内 0 3、“无限长”均匀带电柱面 E外 2 r
8. 有两个点电荷电量都是 +q,相距为2a。今以左边的点 电荷所在处为球心,以a为半径作一球形高斯面, 在球 面上取两块相等的小面积S1和S2, 其位臵如图所示。设通 过S1 和 S2的电场强度通量分别为1和2,通过整个球面 的电场强度通量为S,则 A. Φ Φ , Φ q /
S2
we E 2
二、静电场的基本规律 l E dl 0 s D ds q 静电 导体 静电感应 E内 0;U 常数 场中 电介质 电极化 端面出现q束 , 引入D
各向均匀电介质,有 D E
三、重要结论
1、点电荷
I II
III
x
4.半径为R1和R2的两个同轴金属圆筒,其间充 满着相对介电常数为r的均匀介质,设两筒上单 位长度带电量分别为+ 和-,则介质中的电位移 / 20 r r . / 2 r ,电场强度大小E= 矢量的大小D=
《大学物理》真空中的静电场练习题及答案解析

《大学物理》真空中的静电场练习题及答案解析一 选择题1. 下列几个说法中哪一个是正确的 (B )(A )电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向(B )电场中某点的场强大小与试验电荷无关。
(C )场强大小由 E =F /q 可知,某点的场强大小与试验电荷受力成正比,与电量成反比。
(D )在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同2. 如图所示为一沿 x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ、-λ,则 oxy坐标平面上点(0,a )处的场强E 的方向为( A )( A )x 正方向 (B ) x 负方向 (C )y 正方向(D )y 负方向3.如图所示,一个带电量为q 的点电荷位于正立方体的中心上,则通过其中一侧面的电场强度通量等于:( B )(A)04εq (B)06εq (C) 024εq (D) 027εq第2题图 第3题图 4.关于高斯定理0ε∑⎰⎰=⋅=Φi s e q s d E ,下列说法中正确的是( C )(A )如果高斯面无电荷,则高斯面上的电场强度处处为零(B )如果高斯面上的电场强度处处为零,则高斯面内无电荷(C )如果高斯面上的电场强度处处为零,则通过高斯面的电通量为零(D )若通过高斯面的电通量为零,则高斯面上的电场强度处处为零5.如图所示,闭合曲面S 内有一点电荷q ,P 为S 面上一点,在S 面外A 点有一点电荷,q ,将其移到B 点,则( B )(A )通过S 面的电通量不变,P 点的电场强度不变。
(B )通过S 面的电通量不变,P 点的电场强度变化。
(C )通过S 面的电通量改变,P 点的电场强度不变。
(D )通过S 面的电通量改变,P 点的电场强度变化。
6.下列说法中正确的是( D )(A )场强为0的点电势也为0 (B )场强不为0的点电势也不为0(C )电势为0的点,则电场强度也一定为0(D )电势在某一区域为常数,则电场强度在该区域必定为01.B2.A3.B4.C5.D 、6D二 填空题1、在点电荷的q +,q -电场中,作如图所示的三个高斯面,求通过321S S 、、S ,球面的电通量分别为________________、_______________、______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12章 静电场P35.12.3 如图所示,在直角三角形ABCD 的A 点处,有点电荷q 1 =1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC =4cm ,试求C 点的场强.[解答]根据点电荷的场强大小的公式22014q qE kr r ==πε, 其中1/(4πε0) = k = 9.0×109N ·m 2·C -2.点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯, 方向向下.点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯,方向向右.C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.12.4 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元d s = R d θ, 电荷元为d q = λd s ,在O 点产生的场强大小为220001d 1d d d 444q s E R R R λλθπεπεπε===,场强的分量为d E x = d E cos θ,d E y =d E sin θ.对于带负电的圆图13.1弧,同样可得在O 点的场强的两个分量.由于弧形是对称的,x 方向的合场强为零,总场强沿着y 轴正方向,大小为2d sin y LE E E ==⎰θ/6/60000sin d (cos )22R R==-⎰ππλλθθθπεπε0(12R=-λπε.12.5 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C ·m -1,求:(1)棒的延长线上与棒的近端d 1 = 8cm 处的场强;(2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强.[解答](1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m).在细棒上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产生的场强的大小为1220d d d 4()q lE kr x l ==-λπε 场强的方向沿x 轴正向.因此P 1点的总场强大小通过积分得120d 4()L L l E x l λπε-=-⎰ 014LLx lλπε-=-011()4x L x Lλπε=--+ 220124L x L λπε=-. ①将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯-= 2.41×103(N ·C -1),方向沿着x 轴正向.(2)建立坐标系,y = d 2.在细棒上取一线元d l ,所带的电量为d q = λd l ,在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE kr r λπε==, 由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ.由图可知:r = d 2/sin θ,l = d 2cot θ, 所以 d l = -d 2d θ/sin 2θ, 因此 02d sin d 4y E d λθθπε-=,总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==. ②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N ·C -1).方向沿着y 轴正向.[讨论](1)由于L = a /2,x = L+d 1,代入①式,化简得1011011144/1a E d d a d d a λλπεπε==++,保持d 1不变,当a →∞时,可得1014E d λπε→, ③这就是半无限长带电直线在相距为d 1的延长线上产生的场强大小.(2)由②式得y E ==,当a →∞时,得 022y E d λπε→, ④这就是无限长带电直线在线外产生的场强公式.如果d 1=d 2,则有大小关系E y = 2E 1.12.6 一均匀带电无限长细棒被弯成如图所示的对称形状,试问θ为何值时,圆心O 点处的场强为零.[解答]设电荷线密度为λ,先计算圆弧的电荷在圆心产生的场强.图13.4在圆弧上取一弧元 d s =R d φ, 所带的电量为 d q = λd s ,在圆心处产生的场强的大小为2200d d d d 44q s E kr R Rλλϕπεπε===, 由于弧是对称的,场强只剩x 分量,取x 轴方向为正,场强为 d E x = -d E cos φ. 总场强为2/20/2cos d 4x E R πθθλϕϕπε--=⎰2/20/2sin 4Rπθθλϕπε--=0sin 22R λθπε=,方向沿着x 轴正向.再计算两根半无限长带电直线在圆心产生的场强.根据上一题的公式③可得半无限长带电直线在延长上O 点产生的场强大小为`04E Rλπε=,由于两根半无限长带电直线对称放置,它们在O 点产生的合场强为``02coscos 222x E E R θλθπε==,方向沿着x 轴负向.当O 点合场强为零时,必有`x x E E =,可得 tan θ/2 = 1, 因此 θ/2 = π/4, 所以 θ = π/2.12.7 一宽为b的无限长均匀带电平面薄板,其电荷密度为σ,如图所示.试求:(1)平板所在平面内,距薄板边缘为a 处的场强.(2)通过薄板几何中心的垂直线上与薄板距离为d 处的场强.[解答](1)建立坐标系.在平面薄板上取一宽度为d x 的带电直线,电荷的线密度为图13.5d λ = σd x ,根据直线带电线的场强公式02E rλπε=, 得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-,其方向沿x 轴正向.由于每条无限长直线在P 点的产生的场强方向相同,所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ /20/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+. ① 场强方向沿x 轴正向.(2)为了便于观察,将薄板旋转建立坐标系.仍然在平面薄板上取一宽度为d x 的带电直线,电荷的线密度仍然为d λ = σd x ,带电直线在Q 点产生的场强为221/200d d d 22()xE rb x λσπεπε==+,沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+, 设x = d tan θ,则d x = d d θ/cos 2θ,因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰ 0arctan()2bdσπε=. ② 场强方向沿z 轴正向.[讨论](1)薄板单位长度上电荷为λ = σb ,①式的场强可化为0ln(1/)2/b a E a b aλπε+=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02E aλπε→, ③ 这正是带电直线的场强公式.(2)②也可以化为0arctan(/2)2/2z b d E d b dλπε=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02z E dλπε→,这也是带电直线的场强公式.当b →∞时,可得2z E σε→, ④ 这是无限大带电平面所产生的场强公式.12.8 (1)点电荷q 位于一个边长为a 的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?(2)如果将该场源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?[解答]点电荷产生的电通量为Φe = q/ε0.(1)当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1 = Φe /6 = q /6ε0.(2)当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1 = Φe /24 = q /24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零.12.9 面电荷密度为σ的均匀无限大带电平板,以平板上的一点O 为中心,R 为半径作一半球面,如图所示.求通过此半球面的电通量.[解答]设想在平板下面补一个半球面,与上面的半球面合成一个球面.球面内包含的电荷为q = πR 2σ,通过球面的电通量为Φe = q /ε0,通过半球面的电通量为Φ`e = Φe /2 = πR 2σ/2ε0.12.10 两无限长同轴圆柱面,半径分别为R 1和R 2(R 1 > R 2),带有等量异号电荷,图13.7单位长度的电量为λ和-λ,求(1)r < R 1;(2) R 1 < r < R 2;(3)r > R 2处各点的场强.[解答]由于电荷分布具有轴对称性,所以电场分布也具有轴对称性.(1)在内圆柱面内做一同轴圆柱形高斯面,由于高斯内没有电荷,所以E = 0,(r < R 1).(2)在两个圆柱之间做一长度为l ,半径为r 的同轴圆柱形高斯面,高斯面内包含的电荷为 q = λl , 穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ,根据高斯定理Φe = q /ε0,所以02E rλπε=, (R 1 < r < R 2). (3)在外圆柱面之外做一同轴圆柱形高斯面,由于高斯内电荷的代数和为零,所以E = 0,(r > R 2).12.11 一厚度为d 的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法. (1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E = E`.在板内取一底面积为S ,高为2r 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E S2d d d S S S =⋅+⋅+⋅⎰⎰⎰E S E S E S 1`02ES E S ES =++=,高斯面内的体积为 V = 2rS , 包含的电量为 q =ρV = 2ρrS , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρr/ε0,(0≦r ≦d /2).①(2)穿过平板作一底面积为S ,高为2r 的圆柱形高斯面,通过高斯面的电通量仍为 Φe = 2ES ,高斯面在板内的体积为V = Sd , 包含的电量为 q =ρV = ρSd , 根据高斯定理 Φe = q/ε0, 可得场强为 E = ρd /2ε0,(r ≧d /2). ②方法二:场强叠加法. (1)由于平板的可视很多薄板叠而成的,以r 为界,下面平板产生的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层d y ,面电荷密度为d σ = ρd y ,产生的场强为 d E 1 = d σ/2ε0, 积分得100/2d ()222rd y dE r ρρεε-==+⎰,③ 同理,上面板产生的场强为/2200d ()222d ry d E r ρρεε==-⎰,④ r 处的总场强为E = E 1-E 2 = ρr/ε0.(2)在公式③和④中,令r = d /2,得E 2 = 0、E = E 1 = ρd /2ε0,E 就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.12 12.13 一半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为R`<R 的小球体,如图所示,试求两球心O 与O`处的电场强度,并证明小球空腔内的电场为均强电场.[解答]挖去一块小球体,相当于在该处填充一块电荷体密度为-ρ的小球体,因此,空间任何一点的场强是两个球体产生的场强的叠加.对于一个半径为R ,电荷体密度为ρ的球体来说,当场点P 在球内时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程图13.102301443E r r ππρε=P 点场强大小为3E r ρε=. 当场点P 在球外时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r R ππρε=P 点场强大小为3203R E rρε=. O 点在大球体中心、小球体之外.大球体在O 点产生的场强为零,小球在O 点产生的场强大小为320`3O R E aρε=, 方向由O 指向O `.O`点在小球体中心、大球体之内.小球体在O`点产生的场强为零,大球在O 点产生的场强大小为`03O E a ρε=, 方向也由O 指向O `.[证明]在小球内任一点P ,大球和小球产生的场强大小分别为3r E r ρε=, `0`3r E r ρε=, 方向如图所示.设两场强之间的夹角为θ,合场强的平方为222``2cos r r r r E E E E E θ=++2220()(`2`cos )3r r rr ρθε=++, 根据余弦定理得222`2`cos()a r r rr πθ=+--, 所以 03E a ρε=, 可见:空腔内任意点的电场是一个常量.还可以证明:场强的方向沿着O 到O `的方向.因此空腔内的电场为匀强电场.12.14 如图所示,在A 、B 两点处放有电量分别为+q 和-q 的点电荷,AB 间距离为2R ,现将另一正试验电荷q 0从O 点经过半圆弧路径移到C 点,求移动过程中电场力所做的功.[解答]正负电荷在O 点的电势的和为零:U O = 0;在C 点产生的电势为0004346C q q q U RRRπεπεπε--=+=,电场力将正电荷q 0从O 移到C 所做的功为W = q 0U OD = q 0(U O -U D ) = q 0q /6πε0R .12.15 真空中有两块相互平行的无限大均匀带电平面A 和B .A 平面的电荷面密度为2σ,B 平面的电荷面密度为σ,两面间的距离为d .当点电荷q 从A 面移到B 面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为E A = 2σ/2ε0 = σ/ε0,E B = σ/2ε0,两平面在它们之间产生的场强方向相反,因此,总场强大小为E = E A - E B = σ/2ε0, 方向由A 平面指向B 平面.两平面间的电势差为U = Ed = σd /2ε0,当点电荷q 从A 面移到B 面时,电场力做的功为W = qU = q σd /2ε0.12.16 一半径为R 的均匀带电球面,带电量为Q .若规定该球面上电势值为零,则无限远处的电势为多少?[解答]带电球面在外部产生的场强为204Q E rπε=,由于d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=,当U R = 0时,04Q U Rπε∞=-.12.17 电荷Q 均匀地分布在半径为R的球体内,试证明离球心r (r <R )处的电势为2230(3)8Q R r U Rπε-=. [证明]球的体积为343V R π=,电荷的体密度为 334Q QV R ρπ==. 利用13.10题的方法可求球内外的电场强度大小为30034QE r r Rρεπε==,(r ≦R ); 204Q E r πε=,(r ≧R ).取无穷远处的电势为零,则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrR Q Q r r r R rπεπε∞=+⎰⎰ 230084R rRQQ rR rπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r R πε-=.12.18 在y = -b 和y = b 两个“无限大”平面间均匀充满电荷,电荷体密度为ρ,其他地方无电荷.(1)求此带电系统的电场分布,画E-y 图;(2)以y = 0作为零电势面,求电势分布,画E-y 图.[解答]平板电荷产生的场强的方向与平板垂直且对称于中心面:E = E`,但方向相反.(1)在板内取一底面积为S ,高为2y 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E Sd d d 2S S S ES =⋅+⋅+⋅=⎰⎰⎰E S E S E S 12.高斯面内的体积为 V = 2yS ,包含的电量为 q = ρV = 2ρSy , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρy/ε0, (-b ≦y ≦b ).穿过平板作一底面积为S ,高为2y 的圆柱形高斯面,通过高斯面的电通量仍为地Φe = 2ES , 高斯面在板内的体积为 V = S 2b , 包含的电量为 q = ρV = ρS 2b , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρb/ε0, (b ≦y );E = -ρb/ε0, (y ≦-b ).E-y 图如左图所示.(2)对于平面之间的点,电势为d d yU y ρε=-⋅=-⎰⎰E l 22yC ρε=-+, 在y = 0处U = 0,所以C = 0,因此电势为22y U ρε=-,(-b ≦y ≦b ). 这是一条开口向下的抛物线.当y ≧b 时,电势为 0d d nqbnqbU y y C εε=-⋅=-=-+⎰⎰E l ,在y = b 处U = -ρb 2/2ε0,所以C = ρb 2/2ε0,因此电势为2002b b U y ρρεε=-+,(b ≦y ). 当y ≦-b 时,电势为00d d b bU y y C ρρεε=-⋅==+⎰⎰E l , 在y = -b 处U = -ρb 2/2ε0,所以C = ρd 2/2ε0,因此电势为2002b b U y ρρεε=+, 两个公式综合得200||2b b U y ρρεε=-+,(|y |≧d ). 这是两条直线.U-y 图如右图所示.U-y 图的斜率就形成E-y 图,在y = ±b 点,电场强度是连续的,因此,在U-y 图中两条直线与抛物线在y =±b 点相切.[注意]根据电场求电势时,如果无法确定零势点,可不加积分的上下限,但是要在积分之后加一个积分常量.根据其他关系确定常量,就能求出电势,不过,线积分前面要加一个负号,即d U =-⋅⎰E l这是因为积分的起点位置是积分下限.12.19 两块“无限大”平行带电板如图所示,A 板带正电,B 板带负电并接地(地的电势为零),设A 和B 两板相隔5.0cm ,板上各带电荷σ=3.3×10-6C ·m -2,求:(1)在两板之间离A 板1.0cm 处P 点的电势;(2)A 板的电势.[解答]两板之间的电场强度为E=σ/ε0,方向从A 指向B .以B 板为原点建立坐标系,则r B = 0,r P = -0.04m ,r A = -0.05m .(1)P 点和B 板间的电势差为d d BBPPr r P B r r U U E r -=⋅=⎰⎰E l0()B Pr r σε=-, 由于U B = 0,所以P 点的电势为 6123.3100.048.8410P U --⨯=⨯⨯=1.493×104(V). (2)同理可得A 板的电势为()A B A U r r σε=-=1.866×104(V).12.20 电量q 均匀分布在长为2L 的细直线上,试求:(1)带电直线延长线上离中点为r 处的电势;(2)带电直线中垂线上离中点为r 处的电势;(3)由电势梯度算出上述两点的场强.[解答]电荷的线密度为λ = q/2L .(1)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的电势公式,它在P 1点产生的电势为101d d 4lU r lλπε=-总电势为10d 4L L l U r lλπε-=-⎰ln()4Ll Lr l λπε=--=-0ln8q r LLr Lπε+=-. (2)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,在线的垂直平分线上的P 2点产生的电势为2221/20d d 4()lU r l λπε=+, 积分得 2221/201d 4()LLU l r l λπε-=+⎰)4Ll Ll λπε=-=08q Lπε=0ln4q LLrπε=.(3)P 1点的场强大小为11U E r∂=-∂011()8qL r L r Lπε=--+22014q r L πε=-, ①方向沿着x 轴正向.P 2点的场强为22U E r∂=-∂01[4qL r πε==, ②方向沿着y 轴正向.[讨论]习题13.3的解答已经计算了带电线的延长线上的场强为1220124L E x L λπε=-, 由于2L λ = q ,取x = r ,就得公式①.(2)习题13.3的解答还计算了中垂线上的场强为y E =取d 2 = r ,可得公式②.由此可见,电场强度可用场强叠加原理计算,也可以用电势的关系计算.12.21 如图所示,一个均匀带电,内、外半径分别为图13.18R 1和R 2的均匀带电球壳,所带电荷体密度为ρ,试计算:(1)A ,B 两点的电势;(2)利用电势梯度求A ,B 两点的场强.[解答](1)A 点在球壳的空腔内,空腔内的电势处处相等,因此A 点的电势就等于球心O 点的电势.在半径为r 的球壳处取一厚度为d r 的薄壳,其体积为d V = 4πr 2d r ,包含的电量为 d q = ρd V = 4πρr 2d r , 在球心处产生的电势为00d d d 4O q U r r rρπεε==, 球心处的总电势为2122210d ()2R O R U r r R R ρρεε==-⎰, 这就是A 点的电势U A .过B 点作一球面,B 的点电势是球面外的电荷和球面内的电荷共同产生的.球面外的电荷在B 点产生的电势就等于这些电荷在球心处产生的电势,根据上面的推导可得22120()2B U R r ρε=-. 球面内的电荷在B 点产生的电势等于这些电荷集中在球心处在B 点产生的电势.球壳在球面内的体积为3314()3B V r R π=-, 包含的电量为 Q = ρV ,这些电荷集中在球心时在B 点产生的电势为332100()43B BBQ U r R r r ρπεε==-. B 点的电势为U B = U 1 + U 2322120(32)6B BR R r r ρε=--. (2)A 点的场强为0AA AU E r ∂=-=∂. B 点的场强为3120()3B B B B BU R E r r r ρε∂=-=-∂.[讨论] 过空腔中A 点作一半径为r 的同心球形高斯面,由于面内没有电荷,根据高斯定理,可得空腔中A 点场强为E = 0, (r ≦R 1).过球壳中B 点作一半径为r 的同心球形高斯面,面内球壳的体积为3314()3V r R π=-,包含的电量为 q = ρV , 根据高斯定理得方程 4πr 2E = q/ε0,可得B 点的场强为3120()3R E r rρε=-, (R 1≦r ≦R 2).这两个结果与上面计算的结果相同.在球壳外面作一半径为r 的同心球形高斯面,面内球壳的体积为33214()3V R R π=-,包含的电量为 q = ρV ,根据高斯定理得可得球壳外的场强为33212200()43R R q E r rρπεε-==,(R 2≦r ). A 点的电势为d d AAA r r U E r ∞∞=⋅=⎰⎰E l12131200d ()d 3AR R r RR r r r r ρε=+-⎰⎰2332120()d 3RR R r r ρε∞-+⎰ 22210()2R R ρε=-. B 点的电势为d d BBB r r U E r ∞∞=⋅=⎰⎰E l23120()d 3BR rR r r r ρε=-⎰2332120()d 3R R R r r ρε∞-+⎰ 322120(32)6B BR R r r ρε=--.A 和B 点的电势与前面计算的结果相同.12.21 (1)设地球表面附近的场强约为200V ·m -1,方向指向地球中心,试求地球所带有的总电量.(2)在离地面1400m 高处,场强降为20V ·m -1,方向仍指向地球中心,试计算在1400m 下大气层里的平均电荷密度.[解答]地球的平均半径为R =6.371×106m .(1)将地球当作导体,电荷分布在地球表面,由于场强方向指向地面,所以地球带负量.根据公式 E = -σ/ε0, 电荷面密度为 σ = -ε0E ; 地球表面积为 S = 4πR 2, 地球所带有的总电量为Q = σS = -4πε0R 2E = -R 2E /k ,k 是静电力常量,因此电量为629(6.37110)200910Q ⨯⨯=-⨯=-9.02×105(C).(2)在离地面高为h = 1400m 的球面内的电量为2()``R h E Q k+=-=-0.9×105(C),大气层中的电荷为q = Q - Q` = 8.12×105(C).由于大气层的厚度远小于地球的半径,其体积约为V = 4πR 2h = 0.714×1018(m 3),平均电荷密度为ρ = q /V = 1.137×10-12(C ·m -3).。
