线性代数与数学模型(第二版)(电子科技大学成都学院大学数学教研室 编)思维导图
考研复习辅导书 2

数学:基础阶段(3月——5月)0.2013年研究生入学考试数学考试大纲1.《高等数学(第六版)》同济大学主编高等教育出版社(上下册)《高等数学习题全解指南(第六版)》同济大学主编高等教育出版社(上下册)2.《工程数学—线性代数(第五版)》同济大学主编高等教育出版社《线性代数附册学习辅导与习题全解(第五版)》同济大学主编高等教育出版社或《线性代数(第二版)》居余马主编清华大学出版社《线性代数学习指南(第二版)》居余马主编清华大学出版社3.《概率论与数理统计(第四版)》浙江大学主编高等教育出版社《概率论与数理统计习题全解指南(第四版)》浙江大学主编高等教育出版社4.《考研数学焦点概念与性质》徐兵主编高等教育出版社5.《考研数学基础核心核心讲义(经济类)》陈文灯主编北京理工大学出版社(高等数学部分)6.《线性代数辅导讲义》李永乐主编西安交通大学出版社7.《概率论与数理统计讲义(基础篇)》姚孟臣主编机械工业出版社8.《数学基础过关660题(数学三)》李永乐主编西安交通大学出版社强化阶段(6月——8月)1.《数学复习全书(数学三)》李永乐李正元主编国家行政学院出版社或《数学复习全书(数学三)》李永乐王式安主编西安交通大学出版社2.《考研数学复习指南(经济类)》陈文灯主编北京理工大学出版社(微分中值定理等高等数学部分)3.《考研数学单选题解题方法与技巧》陈文灯主编北京理工大学出版社总结提高阶段(9月——11月)1.《数学十年真题解析(数学三)》李永乐主编国家行政学院出版社2.《数学全真模拟经典400题(数学三)》李永乐主编国家行政学院出版社模拟冲刺阶段(12月)1.《数学决胜冲刺6+2(数学三)》李永乐主编西安交通大学出版社2.《五年真题十套模拟(经济类)》陈文灯主编北京理工大学出版社3.《合肥工业大学超越考研最后五套题(数学三)》近三年英语:基础阶段(3月——5月)1.《新概念英语3(技能培养)》亚历山大何其莘主编外语教学与研究出版社《新概念英语3之全新全绎》周成刚主编西安交通大学出版社2.《考研英语词汇词根+联想记忆法(乱序版)》俞敏洪主编群言出版社3.《考研英语词汇速记宝典》徐绽主编海豚出版社4.《考研英语阅读理解150篇(基础训练)》曾鸣张剑主编世界图书出版中心强化阶段(6月——8月)1.《历年考研英语真题解析及复习思路(试卷版)》曾鸣张剑主编世界图书出版中心2.《考研英语阅读Part B全突破》张锦芯主编中国人民大学出版社3.《考研英语拆分与组合翻译法》唐静主编群言出版社4.《考研英语万能作文》王若平主编中航出版传媒有限责任公司总结提高阶段(9月——11月)1.《考研英语阅读理解150篇(提高冲刺)》曾鸣张剑主编世界图书出版中心2.《考研英语完形填空与填空式阅读:新题型》张销民主编群言出版社3.《考研英语冲刺热点作文50篇(狂背板)》曾鸣张剑主编世界图书出版中心模拟冲刺阶段(12月)1.《考研英语最后预测五套题》曾鸣张剑主编世界图书出版中心2.《考研英语最后冲刺五套题》新东方研发中心西安交通大学出版社政治:预习阶段(暑假)1.《考研政治序列之一要点精编》任汝芬主编西安交通大学出版社基础阶段(9月——10月)1.《考研政治考试大纲解析》(红宝书)教育部考试中心主编高等教育出版社2.《考研政治命题人1000题》肖秀荣主编北京航空航天大学出版社强化阶段(11月)1.《风中劲草考研政治冲刺背诵核心考点》杨杰主编学林出版社2.《政治基础过关2000题》陈先奎主编北京理工大学出版社(马克思主义哲学部分)3.《考研政治真题考点分析解析解题秘诀》米鹏主编中国政法大学出版社总结提高阶段阶段(12月)1.《考研政治命题人形式与政策及当代世界经济与政治核心预测》肖秀荣主编北京航空航天大学出版社2.《考研政治序列四之最后四套题》任汝芬主编西安交通大学出版社3.《考研政治命题人终极预测4套卷》肖秀荣主编北京航空航天大学出版社冲刺阶段(1月)1.《启航考研政治20天20题》北京启航主编中国市场出版社2.《考研政治分析题深度预测10题》田维彬主编北京航空航天大学出版社3.各个辅导班最后押题的分析题专业课准备阶段(3月——暑假前)1.《微观经济学(第七版)》平狄克主编中国人民大学出版社《微观经济学学习指导(第七版)》乔纳森汉密尔顿主编中国人民大学出版社《微观经济学(第7版)》平狄克主编清华大学出版社2.《微观经济学:现代观点(第八版)》范里安主编格致出版社《微观经济学:现代观点(第八版)练习册》伯格斯特尤主编格致出版社3.《管理学(第九版)》罗宾斯主编中国人民大学出版社《管理学学习指导(第九版)》考克斯主编中国人民大学出版社基础阶段(暑假——9月份)1.《管理学》张玉利主编南开大学出版社2004年2.《管理学》周三多主编复旦大学出版社3.《现代西方经济学教程(第二版)》微观经济学部分魏埙主编南开大学出版社4.《西方经济学(第一版)》微观经济学部分高鸿业主编中国人民大学出版社When you are old and grey and full of sleep,And nodding by the fire, take down this book,And slowly read, and dream of the soft lookYour eyes had once, and of their shadows deep;How many loved your moments of glad grace,And loved your beauty with love false or true,But one man loved the pilgrim soul in you,And loved the sorrows of your changing face;And bending down beside the glowing bars,Murmur, a little sadly, how love fledAnd paced upon the mountains overheadAnd hid his face amid a crowd of stars.The furthest distance in the worldIs not between life and deathBut when I stand in front of youYet you don't know thatI love you.The furthest distance in the worldIs not when I stand in front of youYet you can't see my loveBut when undoubtedly knowing the love from both Yet cannot be together.The furthest distance in the worldIs not being apart while being in loveBut when I plainly cannot resist the yearningYet pretending you have never been in my heart. The furthest distance in the worldIs not struggling against the tidesBut using one's indifferent heartTo dig an uncrossable riverFor the one who loves you.。
(完整版)线性代数教案(正式打印版)

特征值与特征向量的求解方法
注意事项
在求解过程中,需要注意特征多项式f(λ)的根可能为重根,此时需要验证 是否满足定义中的条件。
在求解特征向量时,需要注意齐次线性方程组的基础解系的求法。
特征值与特征向量的应用举例
01
应用一
判断矩阵是否可对角化。若矩阵A有n个线性无关的特征向 量,则A可对角化。
02
图像处理
在图像处理中,经常需要对图像进行旋转、缩放等操作,这些操作可以通过矩阵对角化来实现。例如,将一个图像矩 阵与一个旋转矩阵相乘,就可以实现图像的旋转。
数据分析
在数据分析中,经常需要对数据进行降维处理,以提取数据的主要特征。通过对数据的协方差矩阵进行对角化,可以 得到数据的主成分,从而实现数据的降维。
REPORTING
线性代数课程简介
线性代数是数学的一个重要分支,主 要研究向量空间、线性变换及其性质 。
本课程将系统介绍线性代数的基本概 念、理论和方法,包括向量空间、矩 阵、线性方程组、特征值与特征向量 、线性变换等内容。
它是现代数学、物理、工程等领域的 基础课程,对于培养学生的抽象思维 、逻辑推理和问题解决能力具有重要 作用。
工具。
2023
PART 04
线性方程组与高斯消元法
REPORTING
线性方程组概念及解法
线性方程组定义
由n个未知数和m个线性方程组成的方程组,形如Ax=b,其中A为系数矩阵,x为未知数 列向量,b为常数列向量。
解的存在性与唯一性
当系数矩阵A的秩等于增广矩阵(A,b)的秩,且等于未知数个数n时,方程组有唯一解;当 秩小于n时,方程组有无穷多解;当秩大于n时,方程组无解。
要作用。
向量空间与子空间
(完整版)成都电子科技大学自动化专业本科培养方案

自动化专业本科人才培养方案一、专业代码与名称专业代码:080602专业名称:自动化二、学制与学位修业年限:四年授予学位:工学学士三、培养目标经过系统的教育和教学活动,使学生具有扎实的基础、宽广的知识面和较强的实践动手能力,培养学生的创新精神和团队意识,使其在掌握自动化和控制工程领域先进技术的基础上,具有提出和解决带有挑战性问题的能力,不断提高自身的综合素质。
同时,发展学生个性,培养学生具有健全人格,使其成为德智体美全面发展的高素质人才。
四、基本要求本专业学生主要学习自动控制原理、计算机控制系统、传感器原理、过程控制系统、线性系统理论、电力电子技术、系统工程导论等专业知识,并接受1~2个学科专业方向的基本训练。
毕业后可从事国民经济、国防和科研各部门的运动控制、过程控制、机器人智能控制、导航制导与控制,现代集成制造系统、模式识别与智能系统、系统工程理论与实践、新型传感器、电子与自动检测系统、复杂网络与计算机应用系统等领域的科学研究、技术开发、教学及管理等工作。
毕业生应获得以下几个方面的知识和能力:1.扎实的数理基础,较好的人文社会科学和管理科学基础,以及外语综合能力;2.系统掌握本学科领域必需的技术基础理论知识,包括电路理论、电子技术、信号与系统、自动控制理论、计算机软硬件、电力电子学、电力系统自动化等。
3.较强的工程实践能力,较熟练的计算机应用能力;4.本学科领域内1~2个专业方向的知识与技能,了解本学科前沿的发展趋势;5.较强的工作适应能力,一定的科学研究、技术开发和组织管理的实际工作能力。
五、专业特色1、在科研、教学、实验和毕业设计环节与计算机技术、网络通信等专业有机结合,培养适应面宽广的“多才”专业;2、理论与实践并重,培养学生的实际动手能力,不断提高学生的工程素质和专业基础,训练工程型人才;3、开展各类竞赛辅助教学,培养学生的团队意识,引导学生发现问题并寻找解决问题的办法,不断提升学生的创新能力。
高等代数课程教学大纲.总结

精品文档高等代数( 1)课程教学大纲第一部分前言一、课程基本信息1.课程类别:专业基础课2.开课单位:数学与财经系3.适用专业:数学与应用数学专业4. 备选教材:《高等代数(第三版)》,北京大学数学系几何与代数教研室前代数组编.高等教育出版社,2003.二、课程性质和目标高等代数是数学与应用数学专业的一门重要基础课程。
本课程的主要内容是多项式理论和线性代数理论。
通过本课程的教学,使学生掌握代数基本理论和基本方法,培养学生代数方面的科学的思维、抽象的思维,逻辑推理、提高运算以及解决实际应用的能力,为进一步学习专业后续课程奠定坚实的代数基础。
本课程的教学目的是使学生获得一元多项式,行列式,线性方程组,矩阵等方面的系统知识 , 为进一步学习近世代数,复变函数、等后续课程打下坚实的基础,也为深入理解初等数学、指导中学数学教学提供了高等的专业知识与重要的方法论。
通过本门课程系统的学习与严格的训练,全面掌握高等代数的基本理论知识;培养抽象的逻辑思维能力与推理论证能力;具备熟练的运算能力与技巧;提高建立数学模型,并应用代数学的理论知识解决实际应用问题的能力。
三、课程学时与学分教学时数:96 学时,其中理论教学81 学时,实践教学15 学时学分数: 6 学分教学时数具体分配:教学内容理论教学实践教学合计(学时)(学时)(学时)第一章多项式26632第二章行列式16319第三章线性方程组22325第四章矩阵17320合计811596第二部分教学内容及其要求第一章多项式1.教学目标:要求学生理解数域的概念;掌握一元多项式的概念、运算及基本性质;掌握带余除法与整除性的关系,会进行相关运算;会求多项式的最大公因式;理解不可约多项式的概念,掌握求重因式的方法;理解多项式在不同的数域的因式分解形式;掌握Eisenstein判别法,会求有理系数多项式的根。
2.教学重点:整除概念,带余除法及整除的性质,最大公因式、互素、辗转相除法、不可约多项式概念、性质,k 重因式与 k 重根的关系。
大学《线性代数》第2版(清华大学出版社、居余马)课后习题详细答案-较完整

1 a2 a3 1 0
0
( )( ) ( )( ) 22、解法 1: 1 b2 b3 = 1 b2 − a2 b3 − a3 = b2 − a2 c3 − a3 − c2 − a2 b3 − a3
1 c2 c3 1 c2 − a2 c3 − a3
整理得 = (ab + bc + ca)(b − a)(c − a)(c −b)
1 1 11 1 1 1 1
−2 1 0
1 −1 2 1
1 −1 2 1 0 −2 1 0
13、
第1,4行交换 −
=−
= − −3 −2 −4 = −7
4 1 20
4 1 2 0 0 −3 −2 −4
−1 −5 −3
1 1 11
5 0 4 2 0 −1 −5 −3
14、先将第 1 行与第 5 行对换,第 3 行与第 4 行对换(反号两0 0 1 3 第3,5行对换 − 0 1 0 1 1 = − 6 7 8
= −10*2 = −20
43
00024
00024 010
01 01 1
00 01 3
17、根据课本 20 页公式(1.22)
0 0 1 −1 2
0030 0024 1 240
2
1 −1 2
0 = (−1)2×3 3
2 2 3 L 2 2 第3行 − 第1行 1 0 1 L 0 0
28、
L L L L L L LLLLLL L L L L L L
2 2 2 L n −1 2 第n行 − 第1行 1 0 0 L n − 3 0
−5 0 0 0 0
所以
* A = (−1)3*5 | A || B |= −3!5!
《线性代数》课程教学大纲
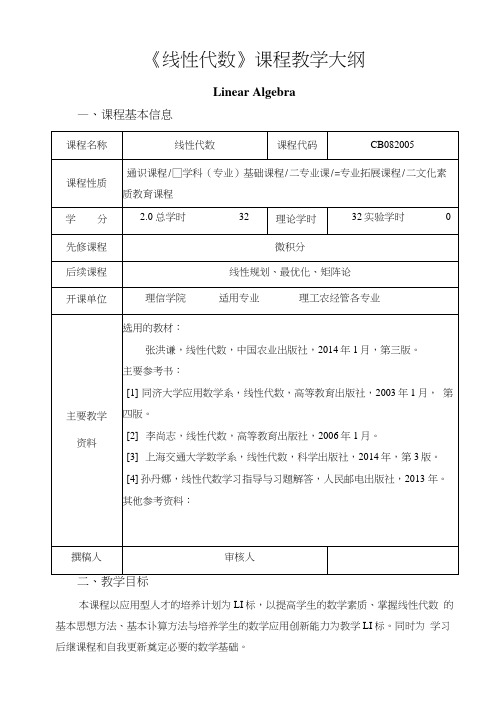
《线性代数》课程教学大纲Linear Algebra—、课程基本信息二、教学目标本课程以应用型人才的培养计划为LI标,以提高学生的数学素质、掌握线性代数的基本思想方法、基本讣算方法与培养学生的数学应用创新能力为教学LI标。
同时为学习后继课程和自我更新奠定必要的数学基础。
(一)知识LI标线性代数将使学生获得行列式、n维向量、矩阵、线性方程组、特征值和特征向量、二次型等相关的基本知识,同时接受基本运算技能的训练,为今后学习各类后继课程和进一步扩大数学知识面奠定必要的数学基础。
(二)能力LI标线性代数培养学生抽象思维能力和逻辑推理的理性思维能力,综合运用所学知识分析问题和解决问题的能力以及较强的自主学习能力,进而培养学生的创新意识和能力。
(三)素质□标随着社会的发展,线性代数的内容更为丰富、方法更为综合、应用更为广泛。
线性代数不仅是一种工具,而且是一种思维模式;它不仅是一种知识, 而且是一种素养;它不仅是一种科学,而且是一种文化。
本课程将培养学生的思维能力、数学素养及数学文化,在应用型高素质人才培养中起到不可替代的作用。
培养学生科学思维的能力。
为今后学习各类后继课程和进一步扩大数学知识面奠定必要的数学基础。
三、基本要求本课程是理工等学科各专业的一门重要基础理论课程。
要求学生掌握行列式、n 维向量、矩阵、线性方程组、特征值和特征向量、二次型等基本知识和基本计算方法, 并能利用所学知识解决一些实际问题。
(-)了解克莱姆法则及应用;向量组线性相关、线性无关的有关性质及判别法; 初等矩阵的性质和矩阵等价的概念;线性方程组的基本概念;二次型秩的概念、二次型的标准型的概念及惯性定理。
(二)理解矩阵的等价、相似与合同,矩阵的初等变换和秩;向量的线性相关性, 极大无关组与向量组的秩;齐次线性方程组的基础解系,线性方程组的通解:矩阵的特征值与特征向量,矩阵的相似对角化;二次型与标准形。
(三)掌握矩阵与行列式的运算;向量组线性相关性的判定,向量组的极大无关组和秩的计算;线性方程组的解法;矩阵的特征值与特征向量的计算,矩阵的相似对角化的判定;化二次型为标准形的方法。
电子科大 数理方程(谷超豪)第二章

入 、冫 k=G争
h1厂 丶
二 `
‘
¨
,
丨 n、 1)
知 哂攵亡 奋冫‘、 (0.9亏
三Κutx)= Dk ‘i^Jt匕 冫二Bk sin姥 x
k:丨
`
`2'灬
λ /弋 (z`Υ )`J岑 (号
Tκ ⑴=Ck e~o∴、苎
k=l,2,灬 ′
a廴 可锡她。9+(-扬 廴垃 果冻亻午):
(2,♂ )
(2d‘ 9
ut ˉo· uxx ˉo 丿 :t、 O,o〈 X<艾 '
㈣
二 u|t∞ tP tx)`
⑶
u |y冫o = 0 9
㈣
常敛 h)0匙 1tx十 hu|x:\=〓 0 )
' 弘
) 艹
丶
△ 彳Δ、 、、 '^、 14‘xl乇 ) =
(x) Tt七) ,
``号
` t2、
玉lx|可 k七)=矿 r(㈥ T⑴
√
§1 戴 讠禚k材 之岛i问 迈钙扌廴1 ^t慝 1.〖Ιt1讠 徉钙冕泷
堪 本忌诞 。(%㈤妙恝孥)蜘|时 问内通△L良裁旬甑乜号`正 wfs9|:吻直
该 冢洵上锅踢卫 莨硖车 知钺劬勋银 ,⊥迎伎追讠向与温宝轩高眈 臼衤皈·
甚小叻砣罾`u(x)b,△ ,θ :蝴 碎 枉砬遗“x♂ )0,B讠 lq t hJ锈 烛灾
“+lS⒃
-弓仅q炱铋 ,Klk而
ut× 政冫当乇>0叮
叭α9t)伫 惫 呔
祟aX人 删 之
砑ξˉ由S觥 肫 htl′℃`铷 悫,次 可 軎.文 Qu‘ “浅)
土匀氵芋殄廴(2d)`(小 D印 卜0`弘^钰 bk u巛 l弋 )春 窭、
group theory 2

■ 等价表示: 设群G在线性空间V上的两个表示B和A通过一个 相似变换相联系, 即对于任意gα∈G, 有B(gα)=SA(gα)S-1, 其 中S是V上的一个非奇异矩阵, 则称这两个表示为等价表示. ■ 可约表示: 设A是群G在表示空间V上的一个表示, 如果V 存在一个G的不变真子空间W,即对任意 w∈W和任意gα∈G, 有A(gα) w ∈W. 则称表示A是可约的. ■ 完全可约表示: 设群G的表示A的表示空间V可以分解为子 空间W1和W2的直和, 即V=W1⊕W2, 且W1和W2都是G的不 变真子空间, 即对于任意w1∈W1, w2∈W2和任意gα∈G,有 A(gα) w1 ∈W1, A(gα) w2 ∈W2 则称表示A是完全可约的.
v = ∑ xi ei = ∑ e' j ( S 1 ) ji xi = ∑ x' j e' j
i i, j j
x' = ( S 1 ) x
则V中任一线性变换A在上述两组基下的矩阵由下式联系
Ae' j = ∑ Ae j S ji = ∑ Aij ei S ji
i i, j i i, j
= ∑ A'ij e'i =∑ A'ij e j S ji = ∑ A' ji ei Sij
i i
满足
x + y = ∑ ( xi + yi )g i
i
, ax = ∑ (axi ) g i
i
则所有元素 x ≡ ∑ xi g i 的集合构成一个线性空间, 称为群空间. i 记作VG. 群元称为群空间的自然基底.
■ 群代数定义: 设x,y是群空间VG 中的任意两个向量, 即
x = ∑ xi g i , y = ∑ yi g i ∈ VG
线性代数教学大纲

《线性代数》课程目录Linear Algebra课程编号:学时:36课程性质:必修选课对象:理工类各专业,经济管理学类各专业先修课程:高中数学内容提要:第一章的内容以行列式为中心,介绍行列式的概念、性质与计算及克莱默法则求解线性方程组的方法。
第二章介绍了矩阵这一十分有用的工具,讨论了矩阵的运算、初等变换及矩阵的相关性质。
第三章以矩阵为工具,进一步讨论了线性方程组的求解及解的结构。
第四章介绍了矩阵的特征值理论。
第五章介绍了二次型理论。
建议选用教材:《线性代数》第二版,彭玉芳尹福源沈亦一编,高教出版社,1999年主要参考书:《线性代数》第三版,同济大学数学教研室编,高教出版社, 1999 年《线性代数习题集》上海财经大学应用数学系编,上海财大出版社,2004 年《线性代数》居余马等编,清华大学出版社, 1995 年《线性代数解题指导》王中良编,北京大学出版社,2004年《线性代数》课程教学大纲一、课程的目的和任务《线性代数》是一门基础理论课,由于线性问题广泛存在于经济科学、管理科学及技术科学的各个领域,特别是在计算机日益普及的今天,解大型线性方程组,求矩阵的特征向量等已经成为工程技术人员经常遇到的课题,因此课程所介绍的方法广泛地应用于这个学科,这就要求工科学生必须具备有关的基本理论知识,并熟练地掌握它的方法。
通过这门课程的学习,使学生获得线性代数的基本知识和必要的基本运算技能,提高学生的抽象思维能力、逻辑推理能力、实际应用能力以及解题的技能与技巧,同时使学生在运用数学方法分析问题和解决问题的能力方面得到进一步的培养和训练,从而为学生学习后续课程及进一步提高打下必要的数学基础。
二、课程基本要求《线性代数》是高等学校数学教学的重要组成部分,是现代工程科学和经济管理中必备的数学基本理论和基本知识,是进一步学习其它数学分支的基础课程。
要求学生能掌握线性代数中行列式、向量空间、矩阵、线性方程组、二次型的基本理论,学会解线性方程组。
西安电子科技大学线性代数试卷及参考答案3

α1 = (1,1, 0 ) ,
T
α 2 = ( 0, 0,1)
T
同理,当 λ2 = 0 时,得线性无关的特征向量为 α 3 = ( −1,1, 0 ) .
T
将 α1 , α 2 , α 3 单位化得
η1 =
1 1 T T T (1,1, 0 ) ,η2 = ( 0, 0,1) ,η3 = ( −1,1, 0 ) 2 2
n
0 0
L
0 0
L L
n −1 1− n
L
三、 (12 分)问 a, b 为何值时,线性方程组
⎧ x1 + x2 + 2 x3 + 3 x4 = 1; ⎪ x + 3 x + 6 x + x = 3; ⎪ 1 2 3 4 ⎨ ⎪3 x1 − x2 − ax3 + 15 x4 = 3; ⎪ ⎩ x1 − 5 x2 − 10 x3 + 12 x4 = b.
故 λ1 = −1 为 A 的三重特征值.
⎛ −3 1 −2 ⎞ ⎛ 1 0 1 ⎞ ⎜ ⎟ ⎜ ⎟ 解 (λ1 E − A) X = 0 .因 − E − A = −5 2 −3 → 0 1 1 ⎜ ⎟ ⎜ ⎟ ⎜ 1 0 1 ⎟ ⎜ 0 0 0⎟ ⎝ ⎠ ⎝ ⎠
得其基础解系中只含一个解向量 α = (−1, −1,1) ,从而属于 λ1 = −1 的线性无关的特征向
⎛1 ⎜ 0 初等行 三 解: A ⎯⎯⎯ →⎜ ⎜0 ⎜ ⎜0 ⎝
( −1) 或
2
n −1
( n + 1)! )
1 2 3 −1 1 2 0 2−a 2 0 0 3
1 ⎞ ⎟ 1 ⎟ = A1 4 ⎟ ⎟ b+5 ⎟ ⎠
线性代数第二版陈维新

第一章 行列式H2733-PKGKD-DTBW8-6B8R9-CP32P习题1.11. 证明:(1)首先证明)3(Q 是数域。
因为)3(Q Q ⊆,所以)3(Q 中至少含有两个复数。
任给两个复数)3(3,32211Q b a b a ∈++,我们有3)()3()3)(3(3)()()3()3(3)()()3()3(2121212122112121221121212211b a a b b b a a b a b a b b a a b a b a b b a a b a b a +++=++-+-=+-++++=+++。
因为Q 是数域,所以有理数的和、差、积仍然为有理数,所以)3(3)()3()3)(3()3(3)()()3()3()3(3)()()3()3(2121212122112121221121212211Q b a a b b b a a b a b a Q b b a a b a b a Q b b a a b a b a ∈+++=++∈-+-=+-+∈+++=+++。
如果0322≠+b a ,则必有22,b a 不同时为零,从而0322≠-b a 。
又因为有理数的和、差、积、商仍为有理数,所以 )3(33)(3)3()3)(3()3)(3(332222212122222121222222112211Q ba b a a b ba b b a a b a b a b a b a b a b a ∈--+--=-+-+=++。
综上所述,我们有)3(Q 是数域。
(2)类似可证明)(p Q 是数域,这儿p 是一个素数。
(3)下面证明:若q p ,为互异素数,则)()(q Q p Q ⊄。
(反证法)如果)()(q Q p Q ⊆,则q b a p Q b a +=⇒∈∃,,从而有q abqb a p p 2)()(222++==。
由于上式左端是有理数,而q 是无理数,所以必有02=q ab 。
电子科技大学矩阵理论!

1.上三角矩阵R 的逆 R 1 也是上三角矩阵,且对角 元是R 对角元的倒数;
2.两个上三角矩阵 R1、R2 的乘积 R1R2也是上三角
矩阵,且对角元是 R1与R2对角元之积; 3.酉矩阵U 的逆 U 1也是酉矩阵; 4.两个酉矩阵之积 U1U2也是酉矩阵.
返回
返回
返回
返回
(3 )三角 |A | 不 B | ||A ||等 ||B || |式 ,A ,B P m n .
则称映 |||射 |为pmn上的矩阵 . 范数
返回
例 1 设APmn, 则
nm
|| A||m1
| aij |
j1i1
nm
1
|| A||m2(
| aij |2)2
j1i1
|A ||m | m i,j{a a i||j} x 1 i m 1 j n
返回
定义 2 设 |||a | : P m l R ,|||b | : P l n R ,
||||c:Pmn R是 矩 阵 范 数 , 如 果 ||A|c B | ||A |a |||B |b |
则 称 矩 |||a |阵 ,|||b |和 范 |||c |数 相. 容 如果 ||A|B |||A ||||B ||
0 0 0 0 0 0
返回
定理 2 设 A C r m n ,且 A B 1 D 1 B 2 D 2 均 为 A 的最大秩分解,则
(1) 存在 r阶可逆Q, 矩使 阵得 B 1 B 2 Q D 1 Q 1 D 2
( 2 ) D 1 H ( D 1 D 1 H ) 1 ( B 1 H B 1 ) 1 B 1 H D 2 H (D 2 D 2 H ) 1 (B 2 H B 2 ) 1 B 2 H
intro1数学课程简介

课程号:20100440 课程名:泛函分析课程英文名:Functional Analysis学时:68 学分:4先修课程:实变函数、高等代数基本面向:数学学院教材:《泛函分析》江泽坚、孙善利编高等教育出版社1998 一版参考书:1.《实变函数与泛函分析》(下册)夏道行等等教育出版社1984 一版2.《实变函数与泛函分析》(下册)曹广福、严从荃编人民教育出版社第2版3. W.Rudin,Functional Analysis,McGraw_HillBook Company,1973课程简介:线性赋范空间,Banach空间,Hilbert空间(包括有界,紧集,列紧集,完全有界集等)。
Banach 空间上有界线性算子(包括算子范数,有界性,连续性,Hahn-Banach定理,闭图象定理,逆算子定理,谱理论,紧算子Riesz-Schauder理论等)Hilbert 空间上的有界线性算子(射影定理、Riesz表示定理)。
课程号:20100640 课程名:概率统计课程英文名Probability and Statistics学时:68 学分:4先修课程:数学分析、线性代数基本面向:数学学院各专业教材:《概率论基础》(第二版)李贤平高等教育出版社1997参考书:1.《概率论》(第一册概率论基础)复旦大学高等教育出版社,1979。
2.《概率论引论》汪仁官北京大学出版社19943.《概率论及数理统计》(第二版)(上)梁之舜等高等教育出版社1988课程简介:事件与概率,条件概率与统计独立性,随机变量与分布函数,数字特征与特征函数,极限定理。
课程号:20100850 课程名:高等代数-1课程英文名:Advanced Algebra-1学时:102 学分:5先修课程:高中数学基本面向:数学数院各专业教材:《Advanced Algebra》彭国华、李德琅高等教育出版社-Springer(计划2004年出版参考书:1。
《高等代数》北京大学数学系几何代数教研空编高等教育出版社2.《高等代数》张禾瑞、郝锅新高等教育出版社3.《Linear Slgebra》B。
线代 (1)

a22 a32
a12
b2 . b3
b1
例4
解 由于方程组的系数行列式为 D 2 1
x1 2 x 2 x 3 2 , 2 x 1 x 2 3 x 3 1, x x x 0. 1 2 3
解线性方程组
1
2 1 1
且 D 1 1 1 2 3 1 1 2 1
求行列式 D 4 5 6 7 8 9
1 2 3
1 1
例3
求解方程
解 D 3 x 2 4 x 18 9 x 2 x 2 12 2 x 5x 6 0 所以 x 2 或 x 3
4 9
2 3
1
x2
x 0
a11 x1 a12 x2 a13 x3 b1 , 应用:三元线性方程组 a21 x1 a22 x2 a23 x3 b2 , a x a x a x b ; 31 1 32 2 33 3 3
a1 al a b b1 bm
a1 al b a b1 bm
欲 a1 al a b1 bm b c1 cn 设排列为 2) 即 a1 al a b1 bm b c1 cn
对换 a , b
a1 al b b1 bm a c1 cn a1 al a b b1 bm c1 cn
如:2级排列共有2种:12
123 132 213 231 312 321 3级排列共有6种:
21
我们规定n个不同的自然数,按由小到大次序组 成的排列,称为n级标准排列. 2、逆序数 定义 在一个排列中,若某两个数的先后次序与标准 排列不同,则称这两个数组成一个逆序。 一个排列中所有逆序的总数称为此排列的逆序 数.记为 ( i1i2 in )或N ( i1i2 in ) 逆序 逆序 排列32514中, 逆序
组合数学(西安电子科技大学(第二版))习题4答案

习题四(容斥原理)1.试求不超过200的正整数中素数的个数。
解:因为2215225,13169==,所以不超过200的合数必是2,3,5,7,11,13的倍数,而且其因子又不可能都超过13。
设i A 为数i 不超过200的倍数集,2,3,5,7,11,13i =,则22001002A ⎢⎥==⎢⎥⎣⎦,3200663A ⎢⎥==⎢⎥⎣⎦,5200405A ⎢⎥==⎢⎥⎣⎦,7200287A ⎢⎥==⎢⎥⎣⎦, 112001811A ⎢⎥==⎢⎥⎣⎦,132001513A ⎢⎥==⎢⎥⎣⎦,232003323A A ⎢⎥==⎢⎥⨯⎣⎦, 252002025A A ⎢⎥==⎢⎥⨯⎣⎦,272001427A A ⎢⎥==⎢⎥⨯⎣⎦,2112009211A A ⎢⎥==⎢⎥⨯⎣⎦, 2132007213A A ⎢⎥==⎢⎥⨯⎣⎦,352001335A A ⎢⎥==⎢⎥⨯⎣⎦,37200937A A ⎢⎥==⎢⎥⨯⎣⎦, 3112006311A A ⎢⎥==⎢⎥⨯⎣⎦,3132005313A A ⎢⎥==⎢⎥⨯⎣⎦,57200557A A ⎢⎥==⎢⎥⨯⎣⎦, 5112003511A A ⎢⎥==⎢⎥⨯⎣⎦,5132003513A A ⎢⎥==⎢⎥⨯⎣⎦,7112002711A A ⎢⎥==⎢⎥⨯⎣⎦, 7132002713A A ⎢⎥==⎢⎥⨯⎣⎦,111320011113A A ⎢⎥==⎢⎥⨯⎣⎦,2352006235A A A ⎢⎥==⎢⎥⨯⨯⎣⎦, 2372004237A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,231120032311A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,231320022313A A A ⎢⎥==⎢⎥⨯⨯⎣⎦ 2572002257A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,251120012511A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,251320012513A A A ⎢⎥==⎢⎥⨯⨯⎣⎦, 271120012711A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,271320012713A A A ⎢⎥==⎢⎥⨯⨯⎣⎦, 21113200021113A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,3572001357A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,351120013511A A A ⎢⎥==⎢⎥⨯⨯⎣⎦351320013513A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,371120003711A A A ⎢⎥==⎢⎥⨯⨯⎣⎦,…, 235720002357A A A A ⎢⎥==⎢⎥⨯⨯⨯⎣⎦,…,23571113200023571113A A A A A A ⎢⎥==⎢⎥⨯⨯⨯⨯⨯⎣⎦, 所以 23571113200(1006640281815)(3320149713965533221)(6432211110111i i j i j k i j k lii ji j ki j k li j k l m i j k l m ni j k l mi j k l m nA A A A A A S A A A A A A A A A A A A A A A A A A A A A <<<<<<<<<<<<<<<=-+-+-+=-++++++++++++++++++++-+++++++++++++∑∑∑∑∑∑0)00041+-+=但这41个数未包括2,3,5,7,11,13本身,却将非素数1包含其中, 故所求的素数个数为:416146+-=2.问由1到2000的整数中:(1)至少能被2,3,5之一整除的数有多少个? (2)至少能被2,3,5中2个数同时整除的数有多少个? (3)能且只能被2,3,5中1个数整除的数有多少个? 解:设i A 为1到2000的整数中能被i 整除的数的集合,2,3,5i =,则2200010002A ⎢⎥==⎢⎥⎣⎦,320006663A ⎢⎥==⎢⎥⎣⎦,520004005A ⎢⎥==⎢⎥⎣⎦, 23200033323A A ⎢⎥==⎢⎥⨯⎣⎦,25200020025A A ⎢⎥==⎢⎥⨯⎣⎦,35200013335A A ⎢⎥==⎢⎥⨯⎣⎦, 235200066235A A A ⎢⎥==⎢⎥⨯⨯⎣⎦, (1)即求235A A A ++,根据容斥原理有:235235232535235()1000666400(333200133)661466A A A A A A A A A A A A A A A ++=++-+++=++-+++=(2)即求232535A A A A A A ++,根据容斥原理有:232535232535235235235235()333200133266534A A A A A A A A A A A A A A A A A A A A A A A A ++=++-+++=++-⨯=(3)即求[1]N ,根据Jordan 公式有:1112233235232535235[1]2()310006664002(333200133)366932N q C q C q A A A A A A A A A A A A =-+=++-⨯+++⨯=++-⨯+++⨯=3.求从1到500的整数中能被3和5整除但不能被7整除的数的个数。
