平行轴定理及垂直轴定理
平行轴及垂直轴定理
平行轴定理转动惯量与转动轴的位置有关。
绕着一个固定轴转动的物体的动能是2z I 21K ω= 之前我们可以将动能用质心的动能和相对于质心的内能之和的形式表示出来： int 2cm K Mv 21K +=一个刚体上的两个平行轴。
Z 轴是固定的，质心轴绕着z 轴运动。
相对于任意一个轴物体都处于运动状态。
考虑绕不经过质心的固定轴（假设是z 轴）的转动。
质心绕着这个固定轴转动，设它与轴之间的距离为d ：因此 ωd v cm =222cm Md 21Mv 21ω= 一个物体以角速度ω绕固定轴z 轴的转动同样可以视为以同样的角速度绕平行于z 轴且通过质心的固定轴的转动。
也就是说，绕z 轴的转动等同于绕过质心的平行轴的转动与质心的转动的叠加。
绕通过质心的固定轴转动的动能为：2cm int I 21K ω=所以 222cm Md 21I 21K ωω+= 22cm 2z ]Md I [21I 21ωω+= 两相比较可得：2cm z Md I I +=，这就是平行轴定理。
例：木棒细木棒绕着它长度的中点转动，转动惯量为：2cm ML 121I = ——那么，当木棒绕着它的一端转动时，它的转动惯量是多少？3ML I )2L (M 12ML I 2Ld 222=+== 垂直轴定理一个薄平板，它可以绕着三个坐标轴中的任意一个转动。
表明了一个平板状物体绕着它的三个互相垂直的坐标轴转动的转动惯量之间的关系。
考虑一个薄板，它可以绕着它的三个垂直的坐标轴中的任意一个转动。
设与之相对应的转动惯量分别为z y x I I ,I 和假设平板处于xy 平面上，从z 轴到参考点P 的垂直距离为22y x R +=∫∫+==dV )y x (dV R I 222z ρρ∫=dV y I 2x ρ∫=dV x I 2y ρ所以 ，这便是垂直轴定理。
y x z I I I +=例：1） 圆盘•处于xy 平面上的一个圆盘，其转动惯量为2z MR 21I = 由对称性可知，y x I I =因此由垂直轴定理即可得到：x z 2I I =4MR 2I I I 2z y x === 2） 正方形平板•正方形的变长为a通过对称性可知，y x I I =因此由垂直轴定理即可得到：2z x Ma 61I 2I == 例：当圆柱体转动时，绳子开始释放，物体m 向下落。
转动惯量公式表
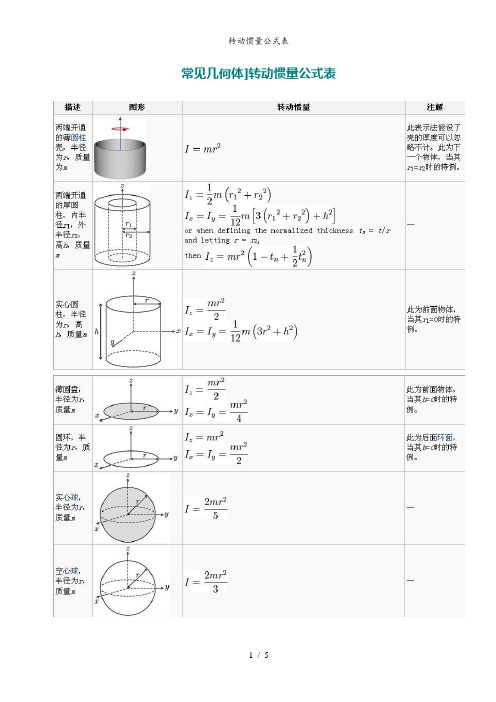
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。
当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。
对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些（绕定轴转动时）的刚体动力学公式。
角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。
只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。
由这一公式，可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
刚体定轴转动定律
o
P
x
2.角位移
描写刚体位置变化的物理量。
角坐标的增量：
称为刚体的角位移
y v2 p v1
P
3.角速度
R
x
描写刚体转动快慢和方向
的物理量。
角速度 lim d
t0 t dt 方向：满足右手定则，沿刚体转动方向右旋大拇指指向。
角速度是矢量，但对于刚体定轴 转动角速度的方向只有两个，在表 示角速度时只用角速度的正负数值 就可表示角速度的方向，不必用矢 量表示。
11mb 2
例4、半径为 R 质量为 M 的 圆环，绕垂直于圆环平面的 质心轴转动，求转动惯量J。
解： J R2dm MR 2
M o R dm
例5、半径为 R 质量为 M 的圆盘，绕垂直于圆盘 平面的质心轴转动，求转动惯量 J。
解：分割圆盘为圆环
dm
M
R2
2
rdr
J r2dm
M
dr
R
0
t 细杆绕一端的转动惯量
J 1 ml 2 3
摩擦阻力
t
例8、质量为 m1 和m2 两个物体， 跨在定滑轮上 m2 放在光滑的桌 面上，滑轮半径为 R，质量为 M，求：m1 下落的加速度，和 绳子的张力 T1、T2。
解：m1 g T1 m1a （1）
T2 m2a
b)作圆周运动的质点的角动量 L＝ r m v
c)角动量是描述转动状态的物理量；
P L
d)质点的角动量又称为动量矩。
or
dL
d (r mv)
dr
mv
r
d (mv)
r
F
dt
运动生物力学复习资料
●运动生物力学是生物力学的一个重要分支，是研究体育运动中人体机械运动规律的科学。
它是将体育运动中人体（或器械）复杂的运动形式及变化规律结合力学和生物学的原理进行研究的一门科学。
●根据力学观点，人体运动可以描述为：在神经系统控制下，以肌肉收缩为动力，以关节位支点，以骨骼为杠杆的机械运动。
●运动生物力学的任务：1.改进运动技术。
根据人体的形态机能特点，研究最合理、最有效的运动技术，以求达到最好的运动成绩。
2.改善训练手段。
通过改善训练手段可增加运动训练的适应性，并能提高运动成绩。
2.预防运动损。
预防运动损伤是生物力学研究的一大基本任务，从运动损伤发生的机制，到其检测与研究方法，相关应用研究越来越普及与深入。
3.运动康复与健康促进。
运动损伤的性质和康复治疗有赖于生物学、运动手段和力学的综合知识，而运动生物力学恰恰能够很好地提供完整的视角。
3.设计与改革运动器材。
运动生物力学理论与方法的运用在改革运动器材方面起着举足轻重的作用，它通过改良各项运动器材来帮助运动员实现运动成绩的提高。
●运动生物力学的测量方法有：运动学测量、动力学测量、人体测量及肌电图测量。
运动学测量参数---肢体的（角）位移、（角）速度、（角）加速度等。
运动学参数---主要界定在力的测量。
人体测量参数----人体环节的长度、围度及惯性参数如质量、转动惯量。
肌电图参数----测量肌肉收缩时的神经支配特性。
●人体动作结构--运动时所组成的各动作间相互联系、相互作用的方式或顺序称为动作结构。
●人体动作结构特征1.运动学特征---时间特征、空间特征、时空特征。
2.动力学特征---力的特征、能量特征、惯性特征。
●动作系统---大量单一动作按一定规律组成为成套的动作技术，这些成套的动作技术称为动作系统。
●动作系统的分类及特点1.周期性动作系统---是指以周期性循环的规律出现的动作组合的成套连续动作。
跑，泳特点---反复性和连贯性、节律性、交互性、惯性作用。
平行轴定理和垂直轴定理的讲解
三. 转动动能定理 —— 合力矩功的效果
dA Md (J
对于一有限过程
d )d
dt
Jd
d( 1 2
J 2 )
dEk
A
2 dA
1
2 1
d( 1 2
J 2 )
1 2
J22
1 2
J12
Ek
绕定轴转动刚体在任一过程中动能的增量，等于在该过程中
作用在刚体上所有外力所作功的总和。 —— 动能定理
刚体的机械能 刚体重力势能
1)
l' 2l 3
Nx 0
N y mg
质心运动定理与转动定律联用
§6.2 绕定轴转动刚体的动能 动能定理
一. 转动动能
z
设系统包括有 N 个质量元
m1, m2
r1, r2,..., ri,
,.......,
..., rN
mi,......,mN
v1,v2,...,vi ,...,v N
取第 i 个质元 ,其动能为
Ny
J 1 ml，2 现有一水平力作用于距轴为 l' 处
O
3
求 轴对棒的作用力（也称轴反力）。
Nx
解 设轴对棒的作用力为 N
Nx, Ny
由转动定律 Fl' J
由质心运 动定理
F
Nx
macx
m
l 2
Ny
mg
macy
ml 2
2
0
l' C F mg
质点系
打击中心
Nx
ml 2
Fl ' J
F
F (3l ' 2l
d
O
r' ri
转动惯量公式表
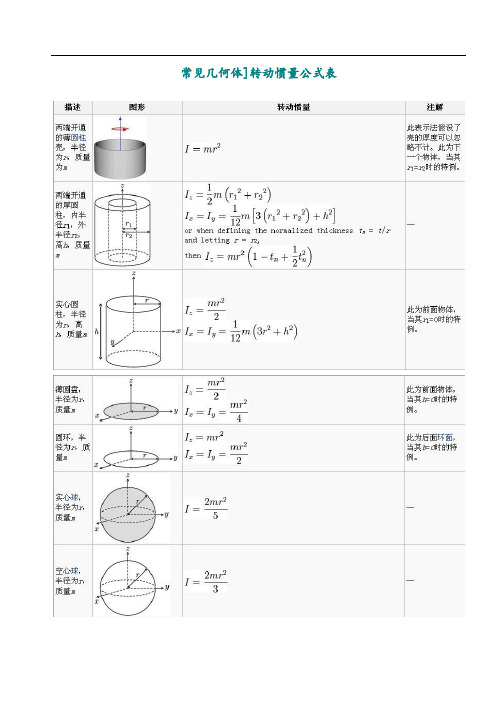
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。
当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。
对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些（绕定轴转动时）的刚体动力学公式。
角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。
只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。
由这一公式，可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
最新《力学》漆安慎(第二版)答案07章
力学（第二版）漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义：∑⎰⎰==dm dm r r mr m r c i i c //求质心方法：对称分析法，分割法，积分法。
⒉刚体对轴的转动惯量定义：∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理∑==c c a m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：∑∑==c c c c I a m F βτ（不必考虑惯性力矩）动能：221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F， 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动？答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。
若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。
但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。
7.2 对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动？答：对静止的刚体施以外力作用，当合外力为了零，即0i c F ma ==∑时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以，对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。
由刚体的转动定律M J α=可知，刚体将发生转动。
比如，置于光滑水平面上的匀质杆，对其两端施以大小相同、方向相反，沿水平面且垂直于杆的两个作用力时，杆所受的外力的合力为零，其质心虽然保持静止，但由于所受合外力矩不为零，将作绕质心轴的转动。
平行轴定理及垂直轴定理
1 2
mi
ri
2
2
各质元速度不同，
刚体对定轴的总动能为
但角速度相同
Eki
(
1 2
mi
ri 2
2
)
1 2
miri2 2
Ek
1 2
J 2
结论 定轴转动刚体的动能等于转动惯量与其角速度平方乘积的一半
转动物体具有储能、稳速等作用：……
二.
力矩的功
dA
F
dr
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
例 一根长为 l ，质量为 m 的均匀细直棒，可绕轴 O 在竖直平
面内转动，初始时它在水平位置
求 它由此下摆 角时的 和
O
m
l
x
解 M 1 mglcos
Fl ' J
F
F (3l' 2l
1)
l' 2l 3
N y mg
质心运动定理与转动定律联用
Nx 0
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
§6.2 绕定轴转动刚体的动能 动能定理
一. 转动动能
z
设系统包括有 N 个质量元
m1,
m2
,.......,
mi,......,mN
r1, r2,..., ri,..., rN v1,v2,...,vi ,...,v N
取第 i 个质元 ,其动能为
转动惯量公式表
常见几何体]转动惯量公式表关于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。
当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。
关于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。
关于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径关于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径关于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2别离为其内外半径。
关于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。
关于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径关于立方体当回为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。
只明白转动惯量的计算方式而不能利用是没成心义的。
下面给出一些（绕定轴转动时）的刚体动力学公式。
角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外，β为。
能够看出那个式子与牛顿第二定律是对应的。
角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。
只用E=（1/2）mv^2不行分析转动刚体的问题，是因为其中不包括刚体的任何转动信息，里面的速度v只代表刚体的质心运动情形。
由这一公式，能够从能量的角度分析刚体动力学的问题。
惯量(Moment of Inertia)是绕轴转动时惯性（回转物体维持其或静止的特性）的，用字母I或J表示。
刚体动力学2
J = ∑ mi ri 2
转动惯量
转动定律
M = Jβ
刚体是特殊质点系，转动定律和质心运 动定律非常相似：
G G M = Jβ
G G F = mac
4
§3.3 转动惯量
一、转动惯量的物理意义 转动惯量特点
J = ∑ mi ri = ∑ J i
2
第 第三 三章 章
转动惯量是转 动惯性的量度
质量是平动 惯性的量度
桌面支持力对轴不产生力矩，摩 擦力矩使圆盘转动停止。 设转动方向为正，转动定律
o
ω0
R
dω −M f = J β = J dt
14
第三 三章 章 设圆盘的体密度 ρ ，厚度 l，在圆盘上 第 半径r处，取宽为dr的细圆环为质元。 质量dm=ρdV=2πrlρdr ，摩擦力df=μN=μgdm G G G 2 d M = 2 πμρ glr dr 力矩 dM f = r × df 大小 f
转 动 定 律
第 第三 三章 章
o x 1 2 M = Fy = J β = ml β 3 y F = F = ma x方向上的质心运动定理 ∑ x cx c
【解】只有F的力矩引起转动，转动定律
线量和角量关系，细杆的质心在l/2处
F y
l acx = ac = β 2
解得
2 y= l 3
17
【例】 如图所示，两物体的质量
J = ∑ mi ri
2
2
J = ∫r dm
质量体分布 dm ρ= dV J = ∫V r 2 ρ d V
6
一些常见刚体的转动惯量 一些常见刚体的转动惯量
第 第三 三章 章
细杆
1 2 J = ml 12
两条直线的位置关系-平行和垂直
直线的方程及其性质
直线的方程：一般形式为 Ax+By+C=0，其中A、B不同时为0。
直线的性质
直线上的任意两点确定的直线方程是 唯一的。
两条不重合的直线，如果斜率相等，则它们平 行；如果斜率之积为-1，则它们垂直。
两条平行线之间的距离是常数，可以 通过公式计算。
两条垂直线的斜率互为相反数的倒数， 即k1*k2=-1。
01
两条垂直相交直线的交角为90度 。
02
在同一平面内，两条直线的交角 的平分线与这两条直线所形成的 四个角中，有一个角是直角。
垂直直ቤተ መጻሕፍቲ ባይዱ在坐标系中的表示
在平面直角坐标系中，两条垂直相交直线的斜 率互为相反数的倒数。即，如果一条直线的斜 率为k，那么与它垂直的直线的斜率为-1/k。
一条直线与y轴垂直，那么它的斜率为 0，可以表示为y=b(b为常数)的形式。
利用方程联立求解交点坐标
01
02
03
04
将两条直线的方程联立，解出 交点坐标；
若方程组无解，则两直线平行 ；
若方程组有唯一解，则两直线 相交于该点；
若方程组有无穷多解，则两直 线重合。
结合图形分析实际问题
在平面直角坐标系中， 画出两条直线的图形；
结合实际问题的背景 和意义，分析两直线 位置关系对问题的影 响。
在三角形 ABC 中，已知 A(0,0)， B(4,0)，C(0,3)。若直线 DE 与 AB 边平行且过点 C，求 DE 所在 直线的方程。
解答
由题意知 AB 边所在直线的方程为 x/4 + y/3 = 1。因为 DE 与 AB 边平行，所以 DE 所在直线的斜率 也为 -3/4。设 DE 所在直线的方 程为 y = -3/4x + b，将点 C(0,3) 代入得 b = 3。所以，DE 所在直 线的方程为 y = -3/4x + 3。
转动惯量公式表
转动惯量公式表 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12其中m是杆的质量，L是杆的长度。
当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3其中m是杆的质量，L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。
对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些（绕定轴转动时）的刚体动力学公式。
角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外，β为。
可以看出这个式子与牛顿第二定律是对应的。
角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。
只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v只代表刚体的质心运动情况。
由这一公式，可以从能量的角度分析刚体动力学的问题。
初中证明直线垂直、平行的方法
证明两条直线垂直（直角）的常用方法（一）相交线与平行线1.定义法：两条直线相交成直角则两直线垂直。
2.两条平行线中有一条垂直第三直线，则另一条也垂直第三直线。
即：若a‖b，a⊥c，则b⊥c。
3.邻补角的平分线互相垂直。
4.到线段两端的距离相等的点在线段的垂直平分线上。
（二）三角形5.证直角三角形：直角三角形的两直角边互相垂直。
①三角形的两内角互余，则第三个内角为直角。
②三角形一边上的中线等于这条边的一半，则这边所对的内角为直角。
③勾股定理的逆定理：三角形一边的平方等于其他两边的平方和，则这边所对的内角为直角。
6.三线合一法：等腰三角形的顶角平分线或底边的中线垂直于底边。
7.三角形相似法：证一个三角形与直角三角形相似。
8.三角形全等法：证一个三角形与直角三角形全等。
（三）四边形9.矩形的两邻边互相垂直。
10.菱形的两条对角线互相垂直平分，且平分每一组对角。
（四）圆12.半圆或直径所对的圆周角是直角。
13.圆的切线垂直于过切点的半径。
（五）图形变换法14.轴对称图形的对称轴垂直平分对应点之间的连线。
15.同一法或反证法（不要求掌握）证明直线平行的常用方法（一）平行线与相交线：1.在同一平面内，两条不相交的直线互相平行。
2.在同一平面内，垂直于同一直线的两直线互相平行。
3.平行于同一直线的两直线互相平行。
4.平行线的判定方法：（1）同位角相等，两直线平行；（2）内错角相等，两直线平行；（3）同旁内角互补，两直线平行。
（二）三角形5.三角形中位线定理：三角形的中位线平行且等于第三边的一半。
6.一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，则这条直线平行于三角形的第三边。
（三）四边形7.平行四边形的两组对边互相平行。
8.梯形的两底边平行。
9.梯形的中位线平行于两底。
（四）同一法或反证法（不要求掌握）证明两线段相等的常用方法（一）三角形1.等角对等边：两线段在同一三角形中，证明等腰或等边三角形。
转动惯量的测量
转动惯量的测量摘要:本文是对转动惯量问题的讨论。
首先介绍了转动惯量及其重要性。
接着对转动惯量的大小进行了讨论，规则均匀物体的转动惯量可由积分公式直接求得，而不规则、不均匀物体的转动惯量则需要用实验测得。
实验测量转动惯量的方法有多种，其中用三线摆测量转动惯量是常用测量转动惯量的方法之一，本文主要讨论了用三线摆测量转动惯量，对这个实验的原理，数据，误差等做了详细的分析。
关键词：转动惯量圆环三线摆目录引言 (1)1 转动惯量简介 (1)2 公式法测算转动惯量 (2)2.1 转动惯量的计算公式 (2)2.2 圆盘转动惯量的计算 (3)2.3 公式法测算圆环转动惯量 (4)3 三线摆法测量转动惯量 (5)3.1 仪器和用具 (5)3.2 实验原理 (6)3.3 实验内容 (8)3.4 实验数据与结果 (9)3.5 误差分析 (10)4 结论 (11)参考文献 (11)引言转动惯量是刚体力学中描述刚体转动性质的物理量，是大学物理课程中一个学习重点。
在科学技术日新月异的今天，转动惯量在越来越多的领域受到重视，在科学实验、工程技术、航空航天、体育运动等多个领域都是一个重要参量。
所以研究转动惯量，分析用什么方法能够相对精准、便捷地测出物体转动惯量的数值大小非常必要。
角动量上式中ω表示角速度，L表示角动量。
这个公式与质点直线运动中mvp=相当。
2 公式法测算转动惯量对转动惯量有了一个初步的了解之后，转动惯量的大小又和哪些量有关呢？能否精确量化呢？怎样知道一个物体的转动惯量呢？是否所有物体的转动惯量都可以计算得到呢？2.1 转动惯量的计算公式按转动惯量的定义有i i m r I ∆∑=2 (2.1)也就是说，刚体对转轴的转动惯量等于各质点到转轴的距离的二次方2i r 与各质点的质量i m ∆相乘再求和。
由此可得，是）（1刚体的总质量；）（2质量的分布；）（3转轴的位置，这三个量决定了转动惯量的大小。
对于任何一个刚体，必须指出所转轴，这样转动惯量才能确定的。
08级运动生物力学讲稿（第二章1、2）
3、质量与重量的关系是：W = MG（G = Mg） 4、绝对质量与相对质量：
人体各环节的质量叫做各环节的绝对质量；各环节的绝对质量与人体总 质量之比叫做各环节相对质量。 （二）重量
重量通常指重力的大小，包括人体总重量和人体环节重量。人体环节的 重量称为环节绝对重量，环节绝对重量与人体总重量之比叫做环节相对重 量。
第二节 人体惯性参数 一、人体惯性参数的概念和意义 （一）概念：人体惯性参数是描述人体整体或环节惯性的基本物理量，包括 人体整体及环节的质量、质心（重心）位置、转动惯量及转动半径等。 （二）确定人体惯性参数的意义：
是建立人体模型，进行人体运动力学及运动损伤与预防方法研究的基础 参数，在体育、国防工业、医学、康复等领域具有广泛的应用价值。
唐山师范学院体育系理论课讲稿
2、物理意义：I 是量度转动物体惯性大小的物理量，用以描述物体保持原
有转动状态的能力。
I 是标量，单位是 kg·m2 3、影响转动惯量大小的因素：
（1）全部质量（m 越大，I 越大）。 （2）质量分布（形状，mi 与轴的距离）
（3）转轴位置（对同一刚体，转轴不同，I 不同） 指出物体转动惯量的大小时，必须同时指明是相对哪一转动轴而言。
例如跳高运动员的踏跳时间与跳起高度的关系，最大相对起跳力与踏跳 时间的关系。
四、人体功能代偿和运动能力极限指标的不可计测性特征 （一）人体生理功能代偿能力是指人体某些组织器官在部分损伤后，其正常 部分的细胞、组织可完成整个组织器官的正常生理机能。
例如：1/5 肝脏、一只肾、2/5 肺叶，一个大脑半球等可维持正常生理 活动。说明正常人体的生理活动只保持在一定水平上，尚有相当一部分潜能 没有发挥出来。
刚体转动惯量计算方法
刚体绕轴转动惯性的度量。
其数值为J=∑ mi*ri^2，式中mi表示刚体的某个质点的质量，ri表示该质点到转轴的垂直距离。
；求和号（或积分号）遍及整个刚体。
转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。
规则形状的均质刚体，其转动惯量可直接计得。
不规则刚体或非均质刚体的转动惯量，一般用实验法测定。
转动惯量应用于刚体各种运动的动力学计算中。
描述刚体绕互相平行诸转轴的转动惯量之间的关系，有如下的平行轴定理：刚体对一轴的转动惯量，等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。
由于和式的第二项恒大于零，因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
还有垂直轴定理：垂直轴定理一个平面刚体薄板对于垂直它的平面轴的转动惯量，等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
表达式:Iz=Ix+Iy刚体对一轴的转动惯量，可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离，称为刚体绕该轴的回转半径κ，其公式为_____，式中M为刚体质量；I为转动惯量。
转动惯量的量纲为L^2M，在SI单位制中，它的单位是kg·m^2。
刚体绕某一点转动的惯性由更普遍的惯量张量描述。
惯量张量是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。
补充对转动惯量的详细解释及其物理意义：先说转动惯量的由来，先从动能说起大家都知道动能E=(1/2)mv^2，而且动能的实际物理意义是：物体相对某个系统（选定一个参考系）运动的实际能量，（P势能实际意义则是物体相对某个系统运动的可能转化为运动的实际能量的大小）。
E=(1/2)mv^2 （v^2为v的2次方）把v=wr代入上式(w是角速度,r是半径，在这里对任何物体来说是把物体微分化分为无数个质点，质点与运动整体的重心的距离为r,而再把不同质点积分化得到实际等效的r)得到E=(1/2)m(wr)^2由于某一个对象物体在运动当中的本身属性m和r都是不变的，所以把关于m、r的变量用一个变量K代替,K=mr^2得到E=(1/2)Kw^2K就是转动惯量，分析实际情况中的作用相当于牛顿运动平动分析中的质量的作用，都是一般不轻易变的量。
转动惯量公式表
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。
当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。
对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些（绕定轴转动时）的刚体动力学公式。
角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。
只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。
由这一公式，可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
刚体转动惯量及其计算方法
刚体转动惯量及其计算方法刚体转动惯量，又称为转动惯性矩或转动惯量，是刚体在绕一些轴旋转时所表现出的惯性特性，表示刚体的转动惯性大小。
刚体转动惯量的计算方法取决于刚体的形状和绕轴的方向。
以下将介绍一些常见的刚体形状及其转动惯量的计算方法。
1.点质量对于一个具有质量m的质点，其转动惯量I可以简化为I=m*r^2，其中r是质点到旋转轴的距离。
2.细长棒对于一个质量为m、长度为L且绕其一端点O转动的细长棒，其转动惯量I=(1/3)*m*L^23.圆盘对于一个质量为m、半径为R的圆盘绕其垂直于圆盘平面的轴转动，其转动惯量I=(1/2)*m*R^24.球体对于一个质量为m、半径为R的球体绕其直径转动，其转动惯量I=(2/5)*m*R^25.长方体对于一个质量为m、边长分别为a、b、c的长方体绕其长边转动，其转动惯量I=(1/12)*m*(a^2+b^2)+(1/3)*m*c^26.圆环对于一个质量为m、外半径为R、内半径为r的圆环绕其中心垂直于环面的轴转动，其转动惯量I=m*(R^2+r^2)/2以上是一些简单常见形状刚体的转动惯量计算公式，实际上，对于更复杂的刚体形状，计算其转动惯量可能需要使用积分方法。
这涉及到刚体的质量分布情况以及积分计算的具体步骤，在毕业论文中可以详细描述。
此外，当刚体绕不通过其质心的轴转动时，其转动惯量的计算需要利用平行轴定理或垂直轴定理。
平行轴定理认为，刚体绕任意平行于通过其质心的轴转动的转动惯量等于其绕通过质心的轴转动惯量加上刚体质量乘以轴与质心之间的距离的平方。
垂直轴定理认为，刚体绕通过其质心的垂直轴转动的转动惯量等于其绕通过质心的任意轴转动的转动惯量减去刚体质量乘以质心到垂直轴的距离的平方。
总结起来，刚体转动惯量的计算方法依赖于刚体的形状和绕轴的方向。
对于简单形状的刚体，可以使用已知的转动惯量公式进行计算。
对于复杂形状的刚体，可能需要使用积分方法来计算转动惯量。
在计算转动惯量时，还需要考虑平行轴定理和垂直轴定理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
University Physics
例 一根长为 l ，质量为 m 的均匀细直棒，可绕轴 O 在竖直平 m l x 面内转动，初始时它在水平位置 O 求 它由此下摆 角时的 和 1 C 解
M mglcos 2 l 由动能定理 A Md mgcosd 0 0 2 lmg 1 2 sin 0 J 0 2 2 3 gsin 3gsin 1/ 2 2 ( )
mgr 2 常量 a 2 mr J Z
2 mgr h 1 at 2 1 2 t2 2 2 mr J Z
2 gt J Z mr 2 ( 1) 2h
若滑轮质量不可忽略，怎样？
Xu Zhongfeng, Xi’an Jiaotong University, 2010
l d 3gcos d 2 dt l dt l
mg
1 2 J ml 3
d 3gcos dt 2l 1 2 1 J mglsin 0 此题也可用机械能守恒定律方便求解 2 2
Xu Zhongfeng, Xi’an Jiaotong University, 2010
Xu Zhongfeng, Xi’an Jiaotong University, 2010
Nx 0
University Physics
§6.2 绕定轴转动刚体的动能 动能定理
z
一. 转动动能
设系统包括有 N 个质量元
m1 , m2 ,......., mi ,......, mN
r1 , r2 ,..., ri , ..., rN v1 ,v 2 ,...,v i ,...,v N
University Physics
例 图示装置可用来测量物体的转动惯量。待测物体A装在转 动架上，转轴Z上装一半径为r 的轻鼓轮，绳的一端缠绕 在鼓轮上，另一端绕过定滑轮悬挂一质量为 m 的重物。 重物下落时，由绳带动被测物体 A 绕 Z 轴转动。今测得 重物由静止下落一段距离 h，所用时间为t， 求 物体A对Z 轴的转动惯量Jz。设绳子
i
i i
C
mi
m
C
质心的势能
hc
hi EP 0
刚体的 机械能
1 2 E J mghC 2
刚体的机械能守恒
1 2 J mghC C 2
对于包括刚体的系统，功能原理和机械能守恒定律仍成立
Xu Zhongfeng, Xi’an Jiaotong University, 2010
Xu Zhongfeng, Xi’an Jiaotong University, 2010
绕定轴转动刚体在任一过程中动能的增量，等于在该过程中 作用在刚体上所有外力所作功的总和。 —— 动能定理
University Physics
刚体的机械能 刚体重力势能
E Ek E p
Ep
i
m gh m h mg mgh
C
z
M
z
L
Jz Jx Jy
—— (薄板)垂直轴定理
xy 轴 —— 在薄板内 z 轴 —— 垂直于薄板 例如:
1 J z mR 2 2 Jz Jx Jy 1 J x J y mR2 Jx Jy 4
z
z
m C x
圆盘
R
y
x
y
薄板
Xu Zhongfeng, Xi’an Jiaotong University, 2010
O
取第 i 个质元 ,其动能为 1 1 2 2 Eki miv i mi ri 2 2 2 各质元速度不同， 但角速度相同 刚体对定轴的总动能为 1 2 Ek J 1 1 2 2 2 2 2 Eki ( 2 mi ri ) 2 mi ri 结论 定轴转动刚体的动能等于转动惯量与其角速度平方乘积的一半
例 一轻绳绕在半径 r =20 cm 的飞轮边缘，在绳端施以F=98 N 的拉力，飞轮的转动惯量 J=0.5 kg· m2，飞轮与转轴间的摩擦 不计，绳与滑轮间无相对滑动，(见图)
求 (1) 飞轮的角加速度; (2) 如以重量P =98 N 的物体挂在绳端，试计算飞轮的角加速度. 解 (1) Fr J
J z ML2 2MLxc
J z ' J z ML
2
(m x L)
i i
M (mi xi ) L M
MxC L
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
四. 转动定律的应用举例
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
例 匀质圆盘以 0 在水平桌面上转动,受摩擦力而静止 求 到圆盘静止所需时间 解 取一质元 dm ds 2π rdr 摩擦力矩
R 0
dM z rdf r gdm
University Physics
机械能守恒
mgh v 2 (mr 2 J Z ) / (2r 2 ) 0
2 v mgh 2 (mr 2 J Z ) 2r mg dh 2v dv 1 2 (mr 2 J Z ) dt dt 2r
dh dv v， a dt dt
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
例 一个刚体系统，如图所示，已知，转动惯量
1 2 J ml，现有一水平力作用于距轴为 l' 处 3
求 轴对棒的作用力（也称轴反力）。 解 设轴对棒的作用力为 N 由转动定律 由质心运 动定理
1 1
i i i
(2) 内力矩作功之和为零。
三. 转动动能定理 —— 合力矩功的效果 d 1 dA Md ( J )d Jd d( J 2 ) dEk
dt 2 对于一有限过程 2 2 1 1 1 2 2 2 A dA d( J ) J2 J1 Ek 1 1 2 2 2
University Physics
ri ri ro
ri ri ro 2ri ro
2 2 2
J z'
x
z'
r i'
Jz mi
z
ri L 2 xi L
2
2
r
o
L
ri
O C M
2 2 2 m r m ( r L 2 xi L) ii i i i i
不可伸缩，绳子、各轮质量及轮轴 处的摩擦力矩忽略不计。
解 分析（机械能）： Ek 1 0
Ek 2 mv 2 / 2 J Z 2 / 2
v 2 (mr 2 J Z ) / (2r 2 ) E p EP 2 EP1 mgh
Xu Zhongfeng, Xi’an Jiaotong University, 2010
R
M z dM z
R
2 2gr dr mgR 0 3 d 由转动定律 M z J
2
3R 0 dt 0 4gd 3R 0 t 4g
0
t
2 1 d mgR mR 2 3 2 dt dt 4 g 2 1 2 mgR mR 3R 3 2 4 g 0 t t 0 4 g t 3R 3R
University Physics
平行轴定理及垂直轴定理
J z' J z ML
2 ——
平行轴定理
(Parallel-Axis Theorem)
z' L
z M
ቤተ መጻሕፍቲ ባይዱ
Jz —— 刚体绕通过质心轴的转动惯量 例如: 2 1 1 1 L J Z M ML2 ML2 ML2 JZ 4 3 2 12
Fr 98 0.2 39.2 rad/s 2 J 0.5
mgr J mr 2
两者区别
rO
T mg
(2) mg T ma
T F
Tr J a r
98 0.2 2 21 . 8 rad/s 0.5 10 0.22
Xu Zhongfeng, Xi’an Jiaotong University, 2010
xdm mxC
C
mg
dm
重力对整个棒的合力矩等于重力全部集中于质心所产生的力矩
Mz 1 3 3g cos d d 3g cos mgl cos 2 dt d 2l J 2 ml 2l ω θ 3 gcos 3 gsin 0 d 0 2l d l
r' vi F dr ri • m P i
d
转动物体具有储能、稳速等作用：……
二. 力矩的功 dA F dr Fcosds Frcosd F rd Md
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
dA Md
对一有限过程
(力矩的功就是力的功)
若M=C
A Md (
1
2
积分形式 ）
A M ( 2 1 )
1
讨论 2 2 2 (1) 合力矩的功 A Md ( M i )d M i d Ai
Ny
O
Nx
Nx, N y
Fl ' J
l F N x macx m 2 l 2 N y mg macy m 0 2