电桥灵敏度的研究(1)
惠斯通电桥测电阻——实验报告

2.考察电压与电桥灵敏度的关系 3..用箱式电桥测电阻 选择倍率分别为 1:1,1:10,10:1,测量待测电阻.调节 R3,使检流计偏转 一格,记下 R3,将数据记录下来,表格自制。 (四)列数据表格 表(1) 考察比率臂与电桥灵敏度的关系 U (V) G R1 (Ω ) 2000 200 1.5V 200 200 20 2 R2 (Ω ) 2000 200 R3 (Ω )
实验十五
实验目的
惠斯通电桥测电阻
1、掌握惠斯通电桥测电阻的原理和方法。 2、学会正确使用箱式电桥测电阻的方法。 3、了解提高电桥灵敏度的几种途径
实验器材
1.箱式惠斯通电桥(QJ23 型) 、 2.电阻箱(ZX21 型两只,ZX36 型 一只) 、 3.电阻板、4.检流计、5.滑线变阻器、6.直流稳压电源。
2
x
R1 R
Rs
度。所谓电桥灵敏度,就是在已经平衡的电桥里,当调节比较臂的电阻 RS, 使改变一个微小量△RS,使检流计指针离开平衡位置△d 格,则定义电桥灵 敏度 S 为
S d R S / R S
(1
5-3) 式中:RS 是电桥平衡时比较臂的电阻值,△RS/RS 是比较臂的相对改变量。 因此,电桥灵敏度 S 表示电桥平衡时,比较臂 RS 改变一个相对值时,检流计 指针偏转的格数。S 的单位是“格” 。例如,S=100 格=1 格/(1/100),则电 桥平衡后,只要 RS 改变 1%,检流计就会有 1 格的偏转。一般讲,检流计指 针偏转 1/10 格时,就可以被觉察,也就是说,此灵敏度的电桥,在它平衡 后,RS 只要改变 0.1%,我们就能够觉察出来,这样由于电桥灵敏度的限制 所导致的误差不会大于 0.1%。这也正是我们研究电桥灵敏度的目的。 电桥灵敏度与下面诸因素有关: (1)与检流计的电流灵敏度 Si 成正比。 (2)与电源的电动势 E 成正比。 (3)与电源的内阻 rE 和串联的限流电阻 RE 之和有关。 (4)与检流计的内阻和串联的限流电阻 RG 之和有关。越小,电桥灵敏度 S 越高,反之则低。 (5)与检流计和电源所接的位置有关。 因此,实验中要使电桥具有较高的灵敏度,以保证电桥平衡的可靠性, 从而保证测量的准确性。 3.实验装置 (1)箱式电桥:其面板和电路结构见图15-3。
惠斯通电桥灵敏度与检测毫伏表内阻的关系研究

惠斯通电桥是一种用于测量电阻、电感和电容的仪器。
而在这个仪器的使用中,对于毫伏表内阻的检测尤为重要。
本文将探讨惠斯通电桥的灵敏度与检测毫伏表内阻的关系,并深入分析这一关系对于电子测量领域的重要意义。
**一、惠斯通电桥的基本原理与概念**让我们简单回顾一下惠斯通电桥的基本原理与概念。
惠斯通电桥由英国物理学家惠斯通于1833年发明,是一种用来测量未知电阻值的仪器。
其基本结构包括四个电阻,分别为R1、R2、R3和未知电阻Rx,它们构成了一个平衡的电桥电路。
当电桥平衡时,滑动变阻器位于中点,则滑动变阻器两端的电压为零。
而当电桥出现不平衡时,滑动变阻器两端会产生电压差。
**二、电桥灵敏度与内阻检测的关系**接下来,我们将重点讨论电桥的灵敏度与内阻检测的关系。
在电桥测量中,灵敏度是一个重要的参数,它决定了电桥能够测量的电阻变化范围。
而对于毫伏表内阻的检测来说,灵敏度则成为了一个关键因素。
当我们希望测量的电阻值较小时,需要较高的灵敏度。
惠斯通电桥的灵敏度与电桥的电阻值有关。
在惠斯通电桥中,灵敏度可以用下式表示:S = R3 / (R1 + R2)其中,S是灵敏度,R1、R2和R3分别为电桥中的三个已知电阻。
从这个公式可以看出,当R1和R2的数值接近时,电桥的灵敏度就会变得非常高。
因此在实际测量中,为了提高惠斯通电桥的灵敏度,我们通常会采用比较接近的电阻值。
**三、惠斯通电桥在毫伏表内阻检测中的应用**那么,惠斯通电桥的灵敏度与检测毫伏表内阻有何关系呢?事实上,毫伏表是一种用于测量电压的仪器,而其内阻则会影响到其测量的准确性。
当我们使用惠斯通电桥来检测毫伏表的内阻时,灵敏度的高低将直接影响到检测结果的精确度。
高灵敏度的电桥可以更精确地检测出毫伏表的内阻值。
因为当电桥的灵敏度较低时,对于内阻的微小变化可能无法被准确地检测出来,从而影响了测量的精度。
而高灵敏度的电桥则能够更加灵敏地发现内阻的变化,从而提高了内阻检测的准确性。
实验十八直流电桥测电阻实验报告

Rx 的变化量 δRx 。电桥灵敏阈 δRx 反映了电桥平衡判断中可能包含的误差,故
∆n 0.2 S= =
∆Rx δRx
Rx
Rx
又有
δRx
=
0.2∆Rx ∆n
=
0.2R1∆R0 ∆nR2
由(18.3)和(18.6)可得到 Rx 的不确定度
1
( ) σ Rx
⎡ =⎢
⎢⎣
δRx
2
+
⎛ ⎜⎜ ⎝
R0 R2
(1)桥臂电阻的误差。
Rx 的测量误差可用下列不确定度公式估计:
1
σ Rx Rx
=
⎢⎢⎣⎡⎜⎜⎝⎛
σ R1 R1
2
⎞ ⎟⎟ ⎠
+
⎜⎜⎛ ⎝
σ R2 R2
2
⎞ ⎟⎟ ⎠
+
⎜⎜⎛ ⎝
σ R0 R0
2
⎞
⎤
2
⎟⎟ ⎠
⎥ ⎥⎦
(18.3)
式中σ R1 ,σ R2 ,σ R0 分别是 R1, R2 , R0 的不确定度。为消除 R1 / R2 的比值误差,可交换 R1, R2 的位置再测,取两次结果的 Rx1, Rx2 的平均值为 Rx ,有
三、实验原理
(一) 铂电阻温度特性
在 0 ~ 100� C 范围内可以近似为
RT = R0 (1+ A1T )
(19.1)
RT , R0 , A1,T 分别表示温度 T 时的阻值、0 摄氏度时的阻值、正温系数和温度。
图 19-1 非平衡电桥电路原理图
(二)用非平衡电桥测量铂电阻温度系数
如图 19-1 所示,I 为恒流电源; R1, R2 为固定电阻, Rp 为可调电阻,用作平衡电
基础物理实验研究性报告 惠斯通电桥测量中电阻及灵敏度的分析与探究

①平衡电桥采用了零示法——根据示零器的“零”或“非零”的指标,即可判断电桥是否平衡而不涉及数值的大小。因此,只需示零器足够灵敏,就可以使电桥达到很高的灵敏度,从而为提高它的测量精度提供了条件。
用平衡电桥测量电阻的实质是拿已知的电阻和未知的电阻进行比较,这种比较测量法简单而精确,如果采用精确电阻作为桥臂,则可以使测量的结果达到很高的精确度。
.读数过程中出现的误差。
6.电桥灵敏度的分析研究
6.1电桥灵敏度的物理意义
与课本上所学习到的绝对灵敏度不同,电桥(相对)灵敏度的定义为
表示当电桥平衡后桥臂电阻 的相对改变 引起检流计的偏转格数为 ,一定的 所引起 愈大,电桥灵敏度越大。
例如, ,它表示电桥平衡后,某一桥臂电阻改变万分之一,检流计就会显示 的偏转,这恰恰是通常情况下,人眼所能判断的最大偏转。所以该电桥灵敏度限制所带来的测量误差小于万分之一。
基础物理实验研究性报告
惠斯通电桥法测量中电阻及灵敏度的分析与探究
第一作者
胡子晗14131088
院系
交通科学与工程学院
第二作者
张彤昊14131082
院系
交通科学与工程学院
第三作者
张鸿曜14131031
院系
交通科学与工程学院
2015年12月15日
摘要:
本报告以惠斯通电桥法测量中等数值电阻的实验为出发点,在测量中电阻的过程中深入思考了电桥平衡条件以及实验操作中的一些问题。同时对电桥灵敏度进行了较为透彻的分析与研究,对该实验的正确操作与严格的数据处理具有重要的意义。并根据操作实验的经历对本实验的实验仪器和操作提出了自己的想法。
2.实验仪器
电阻箱、 型电子检流计、固定电阻两个(标称值相同,但不知准确值)、直流稳压电源、滑线变阻器( )、待测中电阻、开关等、 型箱式电桥。
探究惠斯通电桥灵敏的影响因素

探究惠斯通电桥灵敏的影响因素郭 超200802050234 08物理(2)班 红河学院摘要:电阻的测量是电磁学中的重要实验,测量方法很多其中以电桥发通常采用惠斯通电桥法,因为该方法从根本上消除了采用伏安法测电阻时由于电表内阻的接入而带来的系统误差,从而提高了准确度。
而“电桥”是很重要的电磁学基本测量仪器之一,它主要用来测量电阻器的阻值,线圈的电感和电容器的电容及其损耗,电桥的灵敏度直接影响测电阻的精确值,其灵敏读与诸多因素有关。
关键词:惠斯通电桥;灵敏度;因素一. 电桥原理惠斯通电桥的原理如(图一)所示,图中ab.bc.cd 和da 四条支路分别由电阻1R )(X R .2R .3R 和4R 组成,称为电桥的桥臂。
通常,桥臂ab 接待侧)(X R 电阻,其余各比电阻都市可以调节的标准电阻。
在ab 对角线之间连接检流计、开关、和限流电阻GR 。
在ac 两对角见连接电池、开关和限流电阻E R ,当接通开关E S 和GS 后,各支路中军有电流通过,检流计支路起了沟通abd 和adc 两条之路的作用,可以使比较bd 两点的电势,点桥之名由此而来。
适当调整各支臂的电阻阻值,可以使流过检流计的电流为零,即=G I 。
这时,称电桥达到了平衡。
平衡时 b.d两点的电势相等。
根据分压器原理可知:212R R R U U abbc += (1)433R R R U U acdb += (2)平衡时,dc bc U U =即433212R R R R R R +=+ (3)整理化简后得到 X R R R R R ==4321 (4)由(3)式可知:待测电阻1R )(X R 等于32R R 与4R 的乘积。
通常,称2R 、3R 为比例臂,与此相应的4R 为比较臂。
所以电桥由四臂(测量臂、比较臂、和比例臂)、检流计和电源三部分组成。
电桥灵敏度的引入及由于电桥灵敏度引入的被测量的相对系统误差2.1电桥灵敏度的引入在用天平秤称质量是已知,测得质量的精度住要取决于天平的灵敏度。
(整理)惠斯通电桥实验

实验3 惠斯通电桥测量电阻常用伏安法和电桥法。
由于伏安法测量中电表的内阻会对测量带来附加误差,测量精度受到限制。
电桥是用比较法测量电阻的仪器,电桥测量的特点是灵敏、准确和使用方便。
电桥分为直流电桥和交流电桥两大类。
电桥不但可以测量电阻、电容、电感,还可以通过测量传感器的电阻变化,间接测量温度、压力、应变、真空度和加速度等非电学量,所以被广泛应用于现代工业自动控制,非电量电测法中。
直流电桥又可分为平衡电桥和非平衡电桥。
平衡电桥采样调节电桥平衡测量待测电阻值,主要用于测量处于稳定状态的物理量;非平衡电桥直接测量电桥的输出,通过计算得到物理量的值,非平衡电桥主要用于测量处于变化状态的物理量。
本实验的惠斯通电桥为直流电桥,又名直流单臂电桥,主要用于测量中等数量级电阻(161010Ω-Ω量级),虽然它的这种功能在生产和科研的大多数场合中已被其他仪器(如万用表)所取代,但是电桥电路却在自动检测,自动控制等多个领域得到广泛应用。
因此,本实验不仅是要学会组装电桥测量电阻,了解基本实验方法——平衡法和比较法,更重要的是通过测量电阻掌握调整电桥平衡方法,从而了解平衡电桥的基本特性,为在自动控制以及检测电路中应用电桥电路打下一个良好基础。
对于低电阻(611010-Ω-Ω量级)的测量,要考虑其接触电阻、导线电阻的影响,应使用开尔文电桥即直流双臂电桥,对于高电阻(710Ω量级)则可考虑用冲击电流计等方法。
【实验目的】1. 掌握惠斯通电桥的结构特点和测量电阻的原理。
2. 练习按电路图连接线路。
3. 掌握调整电桥平衡的方法。
4. 研究电桥灵敏度。
5. 学习系统误差的分析方法,初步掌握消除和减小部分系统误差的方法。
【实验原理】1. 惠斯通电桥的结构及测量原理 (1)惠斯通电桥的结构图1是惠斯通桥的结构图。
4个电阻120,,,x R R R R 连成四边形,称为电桥的4个臂,其中12,R R 称为比例臂,x R 为待测臂,0R 为比较臂。
电桥灵敏度与桥臂阻值关系的研究
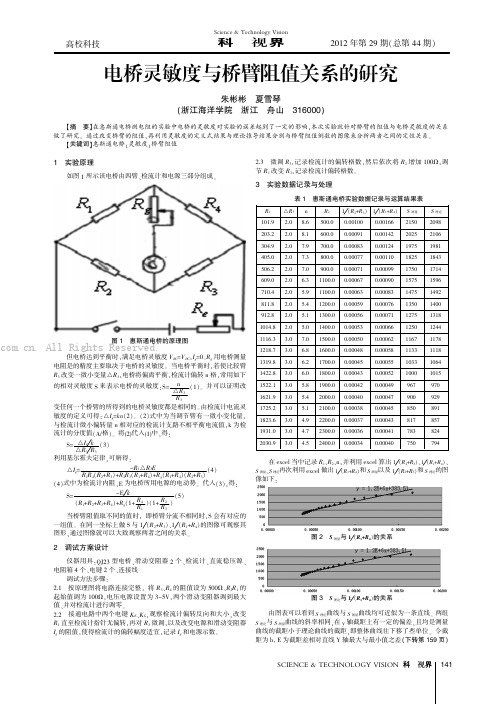
1实验原理如图1所示该电桥由四臂、检流计和电源三部分组成。
图1惠斯通电桥的原理图但电桥达到平衡时,满足电桥灵敏度V BC =V DC ,I g =0。
R g 用电桥测量电阻是的精度主要取决于电桥的灵敏度。
当电桥平衡时,若使比较臂R 3改变一微小变量△R 3,电桥将偏离平衡,检流计偏转n 格,常用如下的相对灵敏度S 来表示电桥的灵敏度:S=n △R 3R 3(1)。
并可以证明改变任何一个桥臂的所得到的电桥灵敏度都是相同的。
由检流计电流灵敏度的定义可得:△I g =kn (2)。
(2)式中为当调节臂有一微小变化量,与检流计微小偏转量n 相对应的检流计支路不相平衡电流值,k 为检流计的分度值(A/格)。
将(2)代入(1)中,得:S=△I g k △R 3R 3(3)利用基尔霍夫定律,可解得:△I g =-R 1△R 3E R 1R 4(R 2+R 3)+R 2R 3(R 1+R 4)+R g (R 1+R 4)(R 2+R 3)(4)(4)式中为检流计内阻,E 为电桥所用电源的电动势。
代入(3),得:S=-E k 1+R 2+R 3+R 4g R 4R 1R 2R 3(5)当桥臂阻值取不同的值时,即桥臂分流不相同时,S 会有对应的一组值。
在同一坐标上做S 与1(R 2+R 3)、1(R 1+R 4)的图像可观察其图形,通过图像就可以大致观察两者之间的关系。
2调试方案设计仪器用具:QJ23型电桥、滑动变阻器2个、检流计、直流稳压源、电阻箱4个、电键2个、连接线调试方法步骤:2.1按原理图将电路连接完整,将R 3、R 4的阻值设为500Ω、R 2R 1的起始值调为100Ω,电压电源设置为3~5V,两个滑动变阻器调到最大值、并对检流计进行调零。
2.2接通电路中两个电键K E 、K G ,观察检流计偏转反向和大小,改变R 1直至检流计指针无偏转,再对R 3微调,以及改变电源和滑动变阻器I g 的阻值,使得检流计的偏转幅度适宜,记录I g 和电源示数。
探究惠斯通电桥灵敏度的影响因素

探究惠斯通电桥灵敏度的影响因素实验者: 同组实验者: 指导教师:【摘要】用惠斯通电桥测电阻时,其精度主要取决于电桥的灵敏度。
电桥的灵敏度S 越大,由电桥灵敏度引入的误差越小。
要提高测量电阻的精度,就应该从电桥灵敏度的影响因素中入手。
该实验基于此思想,通过调试改变试验中的各相关数据和仪器,探究影响电桥灵敏度的几个具体因素,从而设法找出提高电桥灵敏度的方法。
【关键词】惠斯通电桥 灵敏度 因素 【实验原理】惠斯通电桥的原理图如右图所示,其中1R 、2R 、3R 和4R )(X R 组成了电桥的桥壁。
当满足0==g DC BC I V V ,时,电桥处于平衡,使调节3R 有一微小变化量3R δ,从而会引起检流计指针有一微小偏转n 。
通常定义电桥的绝对灵敏度S 为3R nS δ=(1) 电桥的相对灵敏度为:33R R nS δ=相 (2)可以证明,改变任何一个桥壁,其所得的电桥灵敏度都相同。
由检流计电流灵敏度的定义很容易导出:G I I S n ∆= (3)其中,I S 为检流计的电流灵敏度,G I ∆为改变桥壁3R 一个微小变化量3R δ时,检流计微小偏转n 格相对应的检流计支路的不平衡电流。
再利用基尔霍夫定理解得))(()()(32414132324131R R R R R R R R R R R R R ER R I G G ++++++-=∆δ (4)将(4)式带入(2)式,可得:)1)(1()(k/32144321R RR R R R R R R E S g ++++++-=(5)由(2)式可知,如果检流计的最小可辨偏转量为n ∆(一般认为0.2n ∆=格),则由电桥灵敏度引入的被测电阻值的相对不确定度为:R nR S∆∆=(6) 表明电桥的灵敏度S 越大,由电桥灵敏度引入的误差越小。
【调试方案设计】1、 仪器用品:直流稳压电源1个、检流计1个、滑动变阻器1个、万用表1个、电阻箱5个、电键1个、连接线若干 2、 调试方法步骤:2.1 按原理图连接电路,先使50G R =Ω,设置桥臂比为1:1,电源电压在3~5V 之间取值,滑动变阻器取最大值。
惠斯通电桥测电阻——实验报告

实验十五惠斯通电桥测电阻实验目的1、掌握惠斯通电桥测电阻的原理和方法。
2、学会正确使用箱式电桥测电阻的方法。
3、了解提高电桥灵敏度的几种途径实验器材1.箱式惠斯通电桥(QJ23型)、2.电阻箱(ZX21型两只,ZX36型一只)、3.电阻板、4.检流计、5.滑线变阻器、6.直流稳压电源。
实验原理电桥法测量是一种很重要的测量技术。
由于电桥法线路原理简明,仪器结构简单,操作方便,测量的灵敏度和精确度较高等优点,使它广泛应用于电磁测量,也广泛应用于非电量测量。
电桥可以测量电阻、电容、电感、频率、压力、温度等许多物理量。
同时,在现代自动控制及仪器仪表中,常利用电桥的这些特点进行设计、调试和控制。
电桥分为直流电桥和交流电桥两大类。
直流电桥又分为单臂电桥和双臂电桥,单臂电桥又称为惠斯通电桥,主要用于精确测量中值电阻。
双臂电桥又称为开尔文电桥,主要用于精确测量低值电阻。
本次实验主要是学习应用惠斯通电桥测电阻。
1.惠斯通电桥的线路原理惠斯通电桥的线路原理如图15-1所示。
四个电阻R1,R2,R x和R S联成一个四边形,每一条边称作电桥的一个臂,其中:R1,R2组成比例臂,R x为待测臂,R S 为比较臂,四边形的一条对角线AC中接电源E,另一条对角线BD中接检流计G。
所谓“桥”就是指接有检流计的BD这条对角线,检流计用来判断B,D两点电位是否相等,或者说判断“桥”上有无电流通过。
电桥没调平衡时,“桥”上有电流通过检流计,当适当调节各臂电阻,可使“桥”上无电流,即B,D两点电位相等,电桥达到了平衡。
此时的等效电路如图15-2所示。
根据图15-2很容易证明sx R R R R =21s21x R R R R ⨯=(15-1)此式即电桥的平衡条件。
如果已知R 1,R 2,R S ,则待测电阻R x 可求得。
设式(15-1)中的R 1/R 2=K ,则有R x =K ·R S (15-2)式中的K 称为比例系数。
惠斯通电桥测检流计灵敏度

惠斯通电桥测检流计灵敏度电桥种类较多,用途各异。
按其工作状态,可分为平衡电桥和非平衡电桥;按其工作电源可分为交流电桥和直流电桥两大类。
直流电桥又有单臂电桥和双臂电桥之分,即常说的惠斯通电桥和开尔文电桥。
惠斯通电桥适用于测量中等大小阻值的电阻,测量范围为10~106 。
一、实验目的:(1)了解惠斯通电桥的结构和测量原理。
(2)掌握用自搭惠斯通电桥测量电阻。
(3)学习电桥测电阻的不确定度计算方法。
二、实验仪器:直流稳压电源,检流计,滑线变阻器,电阻箱(三个),待测电阻,导线三、实验原理1.惠斯通电桥的线路原理图5-1为惠斯通电桥的原理图,待测电阻Rx和R1、R2、R0四个电阻构成电桥的四个“臂”,检流计G连通的CD称为“桥”。
当AB端加上直流电源时,桥上的检流计用来检测其间有无电流及比较“桥”两端(即CD端)的电位大小。
调节R1、R2和R0,可使CD 两点的电位相等,检流计G 指针指零(即Ig=0),此时,电桥达到平衡。
电桥平衡时,UAC=UAD ,UBC=UBD ,即I1R1=I2R2,IxRx=I0R0。
因为G 中无电流,所以,I1=Ix,,I2=I0,。
上列两式相除,得:21R R Rx R (5-1)则Rx=021R R R =CR0(5-2)式(5-2)即为电桥平衡条件。
显然,惠斯通电桥测电阻的原理,就是采用电压比较法。
由于电桥平衡须由检流计示零表示,故电桥测量方法又称为零示法。
当电桥平衡时,已知三个桥臂电阻,就可以求得另一桥臂得待测电阻值。
通常称R0为比较臂,R1/R2(即C )为比率(或倍率),Rx 为电桥未知臂。
在测量时,要先知道Rx 得估测值,根据Rx 的大小,选择合适的比率系数,把R0调在预先估计的数值上,再细调R0使电桥平衡。
利用惠斯通电桥测电阻,从根本上消除了采用伏安法测电阻时由于电表内阻接入而带来的系统误差,因而准确度也就提高了。
E12电桥的灵敏度公式(5-2)是在电桥平衡的条件下推导出的,而电桥是否平衡,实验时是看检流计有无偏转来判断的。
电桥性能实验

直流电桥原理在进行金属箔式应变片单臂、半桥、全桥性能实验之前,我们有必要先来介绍一下直流电桥的相关知识。
电桥电路有直流电桥和交流电桥两种。
电桥电路的主要指标是桥路灵敏度、非线性和负载特性。
下面具体讨论有关直流电路和与之相关的这几项指标。
一、 平衡条件直流电桥的基本形式如图1—1所示.R 1, R 2,R 3 , R 4 为电桥的桥臂电阻,R L 为其负载(可以是测量仪表内阻或其他负载)。
当R L∞时,电桥的输出电压V 0应为V 0=E (433211R R R R R R +-+) 当电桥平衡时,V0=0,由上式可得到R 1R 4=R 2R 3 或4321R R R R = (1-1)图1—1式(1-1)秤为电桥平衡条件。
平衡电桥就是桥路中相邻两桥臂阻值之比应相等,桥路相邻两臂阻值之比相等方可使流过负载电阻的电流为零。
二、 平衡状态 1.单臂直流电桥所谓单臂就是电桥中一桥臂为电阻式传感器,且其电阻变化为△R ,其它桥臂为阻值固定不变,这时电桥输出电压V 0≠0(此时仍视电桥为开路状态),则不平衡电桥输出电压V 0为V 0=E R R R R R R R R R R ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+∆+⎪⎪⎭⎫ ⎝⎛∆⎪⎭⎫ ⎝⎛341211114113 (1—2) 设桥臂比n=12R R ,由于△R 1《R 1,分母中11R R ∆可忽略,输出电压便为V ”0=E R R R R R R R R ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛∆⎪⎭⎫ ⎝⎛3412114113 这是理想情况,式(1—2)为实际输出电压,由此可求出电桥非线性误差。
实际的非线性特性曲线与理想线性曲线的偏差秤为绝对非线性误差。
则其相对线性误差r 为:r=''000V V V -= ⎪⎪⎭⎫ ⎝⎛+∆+⎪⎪⎭⎫ ⎝⎛∆-1211111R R R R R R =⎪⎪⎭⎫ ⎝⎛+∆+⎪⎪⎭⎫ ⎝⎛∆-n R R R R 11111 (1—3)由此可见,非线性误差与电阻相对变化11R R ∆有关,当11R R ∆较大时,就不可忽略误差了。
惠斯通电桥测电阻实验报告 (1)

肇 庆 学 院肇 庆 学 院电子信息与机电工程 学院 普通物理实验 课 实验报告级 班 组 实验合作者 实验日期姓名: 学号 老师评定实实验原理:1.桥式电路的基本结构。
电桥的构成包括四个桥臂(比例臂R 2和R 3,比较臂R 4,待测臂R x ),“桥”——平衡指示器(检流计)G 和工作电源E 。
在自组电桥线路中还联接有电桥灵敏度调节器R G (滑线变阻器)。
2.电桥平衡的条件。
惠斯通电桥(如图1所示)由四个“桥臂”电阻(R 2、R 3、R 4、和R x )、一个“桥”(b 、d 间所接的灵敏电流计)和一个电源E 组成。
b 、d 间接有灵敏电流计G 。
当b 、d 两点电位相等时,灵敏电流计G 中无电流流过,指针不偏转,此时电桥平衡。
所以,电桥平衡的条件是:b 、d 两点电位相等。
此时有U ab =U ad ,U bc =U dc , 由于平衡时0=g I ,所以b 、d 间相当于断路,故有I 4=I 3 I x =I 2所以 44R I R I x x = 2233R I R I =可得x R R R R 324= 或 432R R R R x = 一般把K R R =32称为“倍率”或“比率”,于是 R x =KR 4要使电桥平衡,一般固定比率K ,调节R 4使电桥达到平衡。
3.自组电桥不等臂误差的消除。
实验中自组电桥的比例臂(R 2和R 3)电阻并非标准电阻,存在较大误差。
当取K=1时,实际上R 2与R 3不完全相等,存在较大的不等臂误差,为消除该系统误差,实验可采用交换测量法进行。
先按原线路进行测量得到一个R 4值,然后将R 2与R 3的位置互相交换(也可将R x 与R 4的位置交换),按同样方法再测一次得到一个R ’4值,两次测量,电桥平衡后分别有:432R R R R x ⋅='423R R R R x ⋅= 联立两式得: '44R R R x ⋅=由上式可知:交换测量后得到的测量值与比例臂阻值无关。
直流单臂电桥实验报告

直流单臂电桥实验报告一、实验原理:1.直流单臂电桥适用范围:直流单臂电桥主要是用来测量中等阻值(10~105Ω)电阻的。
2.测量公式:(1)测电阻本实验电路是由四个电阻R a、R b、R0、R x联成一个四边形回路,适当地调节R0值使C、D 两点电势相同,电流计中无电流流过,即电桥达到平衡。
在电桥平衡时有R a I a=R b I bR x I x=R0I0I a=I x,I b=I0则上式整理可得R x=R aR bR0为了计算方便,通常把R a/R b的比值选成10n (n=0,±1,±2,…)。
令C=R a/R b,则R x=CR0可见电桥平衡时,由已知的R a、R b及R0值便可算出R x。
(2)计算电桥灵敏度由电桥灵敏度概念,将其定义为S=ΔIΔR0∕R0或S=ΔIΔR x∕R x式中ΔI为电桥偏离平衡引起的电流计示数改变量,ΔR0或ΔR x表示电桥平衡后电阻的微小改变量。
电桥灵敏度也可以由基尔霍夫定律给出:S=EK[(R a+R b+R0+R x)+(2+R bR0+R xR a)R g]式中K和R g为电流计的常量。
(3)待测电阻的相对误差由(2)中公式可直接得到:ΔR x R x =ΔIs(4)换臂法计算公式R x=√R0′R0′′≈12(R0′+R0′′)3.实验电路图:4.比例臂倍率如何适当选取:通过比较臂R0调节的有效位数多少来判断,R0调节的有效位数越多,C的选取越恰当。
比如:给定一个四旋钮电阻箱(调节范围为1~9999Ω),如果待测电阻阻值大约为230Ω,代入为了使R0调节电桥由非平衡态达到平衡态的位数最多,即四个旋钮都用上,需选取倍率为0.1。
再例如若待测电阻R x≈1200Ω,电阻箱为四旋钮电阻箱(调节范围为1~9999Ω),仅当选取倍率C为1时四个旋钮才都可以用上,故倍率选取为1。
给出一般结论则为:应选倍率为电阻箱最大有效位数与待测电阻所占位数之差的倒数。
用单臂电桥测电阻带实验数据处理电桥灵敏度实验数据

本科实验报告实验名称: 用单臂电桥测电阻实验13 用单臂电桥测电阻(略写)【实验目的】(1)掌握用单臂电桥测量电阻的原理和方法。
(2)学习用交换法减小和消除系统误差。
(3)初步研究电桥的灵敏度。
【实验原理】单臂电桥,也叫惠斯登电桥,适用于精确测量中值电阻(10~的测量装置。
电桥法测电阻,其实质是把被测电阻与标准电阻相比较,已确定其值。
由于电阻的制造可以达到很高的精度,所以用电桥法测电阻也可以达到很高的精度。
电桥分为直流电桥和交流电桥两大类。
直流电桥又分为单臂电桥和双臂电桥。
惠斯登电桥是直流电桥中的单臂电桥;双臂电桥又称为开尔文电桥,适用于测量低电阻(~10Ω)。
单臂电桥的线路原理单臂电桥的基本线路如图所示。
它是由四个电阻R1,R2,Rs,Rx连成一个四边形ACBD,在对角线AB上接上电源E,在对角线CD上接上检流计P组成。
接入检流计(平衡指示)的对角线称为“桥”,四个电阻称为“桥臂”。
在一般情况下,桥路上检流计中有电流通过,因而检流计的指针偏转。
若适当调节某一电阻值,例如改变Rs的大小可使C,D两点的电位相等,此时流过检流计P的电流Ip=0,称为电桥平衡。
则有(1)(2)(3)由欧姆定律知= 2 (4)=s (5)由以上两式可得(6)此式即为电桥的平衡条件。
若R1,R2,Rs已知,Rx即可由上式求出。
通常取R1,R2为标准电阻,称为比率臂,将称为桥臂比;Rs为可调电阻,成为比较臂。
改变Rs使电桥达到平衡,即检流计P中无电流流过,便可测出被测电阻Rx的值。
用交换法减小和消除系统误差分析电桥线路和测量公式可知,用单臂电桥测量Rx的误差,除其他因素外,还与标准电阻R1,R2的误差有关。
可以用交换法来消除这一系统误差,方法是:先连接好电桥线路,调节Rs使P中无电流,可求出Rs,然后将R1与R2交换位置,再调节Rs使P中无电流,记下此时的Rs',可得,相乘可得Rx=,这样就消除了由R1,R2本身的误差引起的对Rx引入的测量误差。
电桥灵敏度

电桥灵敏度与比例臂倍率、电源电动势的关系研究物理学院谷大贤110801107指导老师:朱路扬电桥•电桥使用比较法进行测量,具有较高的灵敏度和准确度,在自动控制和检测中得到广泛的应用。
根据用途不同,电桥有多种类型,其中,惠斯通电桥是最基本的一种。
它是惠斯通1843年发明的,通常用来准确测量10—106Ω的中值电阻,惠斯通电桥又称直流单臂电桥。
当电桥平衡时,BD支路电流为零。
则满足0021CR R R R R X ==B C A R 1R x R PR 2E K 图1 惠斯通电桥测电阻原理图Ro I 1I 2G电桥灵敏度S 的计算•电桥平衡后,R 0改变△R 0引起检流计指针偏转△n 格。
0/R R n S ∆∆=B C A R 1R xR PR 2E K 图1 惠斯通电桥测电阻原理图RoI 1I 2G•电桥灵敏度的高低对测量结果的准确度影响很大。
很多实验和理论都证明,电桥灵敏度影响因素主要有:检流计的灵敏度、电源电动势、比例臂的倍率、回路总电阻。
)2()11()11(111xx g x i R R R R R R C R C ES S ++++++=表1R1/ΩR2/Ωr R0/Ω△R0/Ω△n/格S 500500.146.6 1.15211.8 5001500.3139.8 1.7 4.8394.7 5003000.6279.635466 5004000.8372.7 4.25443.7 500550 1.1512.565427.1 500750 1.5698.89.25379.8 500950 1.9884.813.15337.6 500150031398.327.65253.3 50050001046652285102.3表2R1/ΩR2/Ωr R0/Ω△R0/Ω△n/格S 500100.02100.8 3.85132.6 500300.06302.38.15186.6 500440.088443.511.15199.8 500550.11554.213.75202.3 500600.12604.514.75205.6 500700.14705.217.35203.8 5001000.2100825.65196.9 5002000.42015575176.8 500500150321975127.7表3R1/ΩR2/Ωr R0/Ω△R0/Ω△n/格S 30180.6279.835466.3 50300.6279.6 2.95482.1 100600.6279.5 2.85499.1 2001200.6279.6 2.85499.3 2501500.6279.6 2.85499.3 3001800.6279.5 2.95481.9 5003000.6279.635466 10006000.6279.8 3.65388.6 200012000.6279.8 4.95285.5表4V/v R0/Ω△R0/Ω△n/格S 1466155155.3 2465.99.35250.5 4465.8 4.55517.6 7465.7 2.75862.4 10465.7 1.851293.6 13465.6 1.3 4.91755 16465.5 1.152115.9 18465.50.9 4.92534.4 20465.40.9 5.12637.3。
惠斯登电桥(探究性实验报告范文)

惠斯登电桥(探究性实验报告范文)一实验目的:1.使用自组电桥测电阻。
2.探究影响电桥灵敏度的因素有哪些,以及他们是如何影响电桥灵敏度的。
二仪器说明:电阻箱(5个:R1R2R0RLR’)直流稳压电源检流计开关(2个)待测电阻(3个:20±1Ω,510±25.5Ω,1800±90Ω)若干导线三实验原理:1.惠斯登电桥的原理图5.1为惠斯登电桥的基本线路:图5.1四个电阻R某、R0、R1、R2组成电桥的四个臂,在两组对角线上分别连上检流计和电源,线路BGD就是所谓的“桥”。
检流计的指针有偏转时,电桥不平衡;当I1I某,I2I0,检流计指针指零时,电桥达到平衡,B和D两点的电位相等,有:I1R1I2R2,I某R某I0R0,由此可得:R1R2R2R0R1R某,即R某R0此式为惠斯登电桥的平衡条件,也是测电阻的原理。
其中R某为待测臂,R0为比较臂,R1和R2为比例臂,2.电桥的灵敏度R1R2=K为倍率。
当电桥平衡时,若将比较臂R0改变一小量..R0,检流计偏转n格,定义电桥的灵敏度S为:SnR0R0。
所谓“电桥平衡”,从理论上讲应是通过检流计的电流为零,但实际上是靠观察检流计的指针偏转与否来确定的,当偏转很小时人眼难以分辨,以至我们认为电桥是平衡的,这样会带来测量误差。
设检流计偏转n格(一般n0.2格)人眼刚能分辨出,则由电桥灵敏度引入的被测量R某的相对误差为R某R某nS,绝对误差为R某nSR某。
可见S值越大,电桥越灵敏,因此带来的误差就越小。
理论可知:SESG(R某R0R1R2)(2R某R1R2R0)Rg,式中E为电源电动势,SG为检流计灵敏度,Rg为检流计内阻。
电桥的灵敏度与下列因素有关:(1)与检流计的灵敏度SG成正比。
但检流计灵敏度不能太大,否则电桥平衡不易调节,应选取灵敏度适当的检流计。
(2)与电源的电动势E成正比。
(3)与检流计的内阻Rg有关。
检流计的内阻越小,电桥越灵敏;但内阻较大时,电桥易调节平衡。
惠斯通电桥静态灵敏度的研究

(
-
此,
为△a, 于电桥灵敏度限制所引起的最大相对 则由
误差为: △
R () 4 /
由以上讨论可知, 若检流计偏转格数 的分辨率 帆 … 率
O
4 6 0
/
三 t
8 。/
/ 。 ・0 0
o0 } ・ 0 / } / /
/
5 ) A( 4c Ra 0
R= l H 5DO O ( R I t=, 0∞ f 爿 0 3
s // : 2” /I , 1 i 0 … 1 i { 。 _ / /一’ 0
, ,
R}5 O
5 0
” I 姗 ) ∞ 0
摘 要 : 文通过 理论 分析 , 讨 了决定 惠斯 通 电桥 静 态灵敏 度 的 因素 , 后用 Ma e t a软件进 一步 本 探 然 t mac h i
探讨 了惠斯通 电桥桥臂 电阻在各定值平衡条件附近 的变化规律 , 出了单臂 电阻变化( 找 静态) 时电桥高灵敏
度 的条 件。
关键 词 : 电阻; 电桥 ; 态; 静 灵敏度 中图分类 号 : 4 . O4 11 文献标 识码 : B 文章编 号 :6 1 7 2(0 110 9-3 17- 9. 1)—140 4 2
R :O1 1 1 f 0 0 1 0 00
R }O , f, O , 0C O 0 m ¥ f 5 O
, m 1
R  ̄ 50 【 50 0 ) (0 n 00 1.
R 5n 5 l , 铷 I l R c 0 】 R 0l
k R 0 3 00 I n 0 0 1 5 0
l
l l 0 I0 5 5 I t (  ̄ x O
15 a70 × 451 0 jl × l 19 x }6l{,: 8 . 1 8×。6l O * m6 0 【9 × 19 。 0182 9 s 4 Io o x‘ 6 3 8 l 】 4
电桥灵敏度与检流计内阻关系的分析

电桥灵敏度与检流计内阻关系的分析作者:周慕王杭秋尹会听来源:《绿色科技》2014年第10期摘要:指出了在自搭式惠斯通电桥实验中,检流计内阻是电桥灵敏度一个重要影响因素。
首先从理论上推导出了电桥灵敏度与检流计内阻关系式,然后在实验中取检流计内阻不同值进行了分析,结果表明:检流计内阻Rg远远大于其他桥臂电阻时,电桥灵敏度很低,Rg在0~5000Ω范围中,随着Rg减小,电桥灵敏度会增加明显。
关键词:惠斯通电桥;灵敏度;检流计内阻中图分类号:O441.1文献标识码:A文章编号:16749944(2014)100235021引言惠斯通电桥采用比较法测量未知电阻,具有操作简便、测量精度高的特点,广泛地应用于科学测量技术诸多领域[1]。
高等学校大学物理实验中惠斯通电桥实验多采用自搭式。
学生实验时除完成基本测量外,还会探究电桥灵敏度与电源电动势、桥臂电阻[2~4]、桥臂比例之间的关系。
其实,为保护检流计,在“桥”上会和检流计串联一保护电阻,它对电桥灵敏度的影响学生们往往不会深入探究。
本文中将保护电阻和检流计内阻合称为检流计内阻,从理论推导和数值分析两方面探究检流计内阻对电桥灵敏度的影响。
4结论(1)实验结果表明,Rg取大于5000Ω的较大阻值时,电桥灵敏度普遍很低,检流计内阻对实验影响较大,主要原因是电桥不平衡时通过检流计的电流非常小,不利于检测。
(2)Rg取小于5000Ω的阻值时,当桥臂比例相同,检流计的内阻Rg越小,S电桥灵敏度越高。
Rg取值主要有串联的保护电阻决定,保护电阻一般先取最大值,随着逐渐趋近平衡,Rg应当减小到0。
(3)Rg 取小于5000Ω的阻值时,随着Rg的减小,各桥臂比例下,电桥灵敏度均逐渐增大,且桥臂1∶1条件下增大最明显。
采用自搭式惠斯通电桥测量电阻,为保护检流计,实验初保护电阻Rg需要设置较大的阻值,经过分析检流计内阻Rg应随着实验电桥趋于平衡逐渐减小,取Rg值越小,对电桥灵敏度提高越有利。
单臂电桥、半桥电路、全桥电路的灵敏度关系推导

单臂电桥、半桥电路、全桥电路的灵敏度关系推导该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
单臂电桥、半桥电路、全桥电路的灵敏度关系推导该文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注。
文档下载说明Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document 单臂电桥、半桥电路、全桥电路的灵敏度关系推导can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!单臂电桥、半桥电路、全桥电路是电子电路领域常见的三种电桥电路。
单臂直流电桥灵敏度的研究

单臂直流电桥灵敏度的研究-电气论文单臂直流电桥灵敏度的研究吴宪郎陈华(上海工程技术大学)摘要:用单臂直流电桥(又称惠斯通电桥)测电阻时,其精度主要取决于电桥的灵敏度。
电桥的灵敏度S 越大,由电桥灵敏度引入的误差越小。
要提高测量电阻的精度,就应该从电桥灵敏度的影响因素入手。
实验基于此思想,通过调试改变试验中的各相关数据和仪器,探究影响电桥灵敏度的几个具体因素。
关键词:单臂直流电桥灵敏度因素0 引言单臂直流电桥是一种用比较法测电阻的精密仪器,可测电阻范围为几十到几十万欧姆。
而电桥的平衡是依据检流计的指针是否为零来判断的,由于判断时受到眼睛分辨能力的限制而存在差异,会给测量结果带来误差,影响测量的准确性。
这个影响的大小取决于电桥的灵敏度。
惠斯通电桥在科学测量技术中应用广泛,随着科学技术的发展,对测量精度的要求越来越高,而惠斯通电桥灵敏度的高低关系到测量结果的精确度问题,影响惠斯通电桥灵敏度的因素有哪些,它们是如何影响灵敏度的。
近年来,许多作者对这些问题进行了一些定性的探讨,没有定量化研究和从理论上进行解释。
本文从定量的角度对惠斯通电桥的灵敏度进行了探讨,并从理论上进行了分析和解释,目的是为了更好地提高电桥的测量精度。
1 单臂直流电桥单臂直流电桥是一种常用测量电路,如图1。
直流电桥将桥臂电阻的变化转变为电压或电流变化。
若供给电桥的电源为交流电,电桥成为交流电桥。
对直流电桥,当电桥各桥臂电阻满足桥路对臂电阻乘积相等的条件时,电桥平衡,电桥输出电压为零。
Rx 是待测电阻,R1、R3、R4 是电阻箱,电源电压记为E,G 是检流计,实验电路图如图2 示。
检流计本身的灵敏度是通过的单位电流下指针偏转这四组实验数据很好地说明了当四个电阻阻值满足该比例关系时,电桥灵敏度最大。
4 当电阻阻值一定的情况下电阻位置与灵敏度的关系不妨设比例系数k= R0R11 即R1R0 同时又有R2Rx此时交换R0 和R2(直观上说是将阻值较大的两个电阻接在同一侧),得到另一种电路图如下所示:令s1-s2=M*(Rx-R1)(Rx*R1-R02),其中M 是大于0的常数因为无论是交换前还是交换后都有RxR1=R2R0,所以s1-s2=M*R0 (Rx-R1)(R2-R0)对导出的关系式进行分析:当Rx=R1;R2=R0 时,即4 个电阻阻值相等时有s1=s2,此时采用两者中的任何一个方法都可以;当RxR1;R2R0 或RxR1;R2R0 时,s1s2 采用交换前的连接法,即让阻值大的两个电阻接在一块,让阻值小的两个电阻接在一块,这样能使灵敏度增大;当RxR1;R2R0 或RxR1;R2R0 时,s1s2 采用交换后的连接法,也是让阻值大的两个电阻接在一块,让阻值小的两个电阻接在一块,这样能使灵敏度增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)
为电桥的相对灵敏度.
如果 I g 是检流计中的电流, 则 S a =
S
i
Ig
∃R
=
S iS c,
Sr=
S
i
Ig
∃R
R
=
S iS c∃, S i 为检流计的电流灵敏度, S c 为
电桥线路灵敏度, S c∃ 为电桥线路相对灵敏度. 由于在通
常情况下待测电阻 R 的阻值是不能改变的, 因此不能用
(1) 式或 (2) 式计算电桥灵敏度.
Sa =
(R 1 + R 2) R +
ES i (R 1 R 2 +
2R + R 0) R g ,
(18)
Sr=
(R 1 + R 2) +
ES i (2 + R 1
R2 +
R2
R
2)R
.
1
(19)
设检流计是采用 A C15 2 型光点检流计, 通常考虑 (R 1 + R 3) ∥ (R 2 + R 4) = R 临, 所以
S c∃1 = S c∃0; 如果 ∃ r = o (R 2) , 则电桥的绝对灵敏度亦与桥臂无关, 并且有
S c∃ = R S c 或 S r = R S a,
(12)
即电桥的相对灵敏度是其绝对灵敏度的 R 倍, R 为待测电阻的大小. 当 ∃ r = o (R ) 时,
Sa =
S iIg
∃R
=
ES i (R 0 + R + R 1 + R 2) R + (R 1 R 2 +
0
- R0 R2 + R0 + Rg
K 1 = [R R 0 + (R 2 + R g) (R 0 + R g) ] = con stan t, 且 K 1 < ∃ ,
所以
S c1 =
E R 0∃R 1 (∃ + ∃Α) ∃R
=
E
(∃ + K 1∃R 1)
1 R2
,
(8)
S c∃1 =
E R 0∃R 2 (∃ + ∃Α) ∃R
The research on sen s itiv ity of br idge
YANG Chang-quan ,M ENG Gu i- ju
(D ep t. of p hysics, H uanggang N o rm a l U n iversity, H uangzhou 438000, H ubei)
(7)
现讨论如下:
1° 当电桥平衡, R 1 改变至 R 1 + ∃R 1 时,
∃ ’= ∃ + ∃Α, ∃ ’1 = E R 0∃R 1,
∃’及 ∃’1 为 ∃ 及 ∃1 对应的系数行列式, 这里
∃R 1
0
R2
∃Α= 0 R + R 0
- R0
= [R R 0 + (R 2 + R g) (R 0 + R g ) ]∃R 1 = K 1∃R 1,
(3)
回路 EadcKE
(R 0 + R ) I 2 - R 0 I g = E ,
(4)
回路 bcdb
R 2 I 1 - R 0 I 2 + (R 2 + R 0 + R g) I g = 0.
(5)
对 (3) ~ (5) 式运用克莱姆法则, 有
这里
Ig = ∃1 ∃,
R1 + R2
0
E
∃1 =
0
第 21 卷第 5 期 2001 年 10 月
黄 冈 师 范 学 院 学 报 Jou rna l of H uanggang N o rm a l U n iversity
V o l. 21 N o. 5 O ct. 2001
电桥灵敏度的研究
杨昌权 , 孟桂菊
(黄冈师范学院 物理系, 湖北 黄州 438000)
Abstract: T he au tho rs ob ta ined the W ien B ridge’s rela t ion s betw een the ab so lu te sen sit ivity (S a) and the rela t ive sen sit ivity (S r) by ana ly sising the W hena t stone B ridge’s rela t ion s of S a and S r and u sing ∃ 2 Y a lterna t ion. W e a lso d iscu ssed tha t the d ifferen t cho ices of W ien B ridge’s p ropo rt iona l a rm s can affect the b ridge sen sit ivity. Key words: b ridge; sen sit ivity; W hena t stone B ridge; W ien B ridge; p ropo rt iona l a rm s
于 R 1, R 2, R 3, R 4 的阻值远比接触 (或接线) 电阻大, 所以只考虑R N 与R X 之间的接触 (或接线) 电阻, 设此
电阻大小为 r (一般很小).
对图 2 利用 ∃2Y 变换, 即可化为与图 1 相同的电路, 即
R0 =
RN +
R 4r R3 + R4 +
r=
RN +
R
R4 3+
1
=
∃R
Α
2R
.
2
(13)
为了便于计算由于灵敏度不合理带来的误差, 我们认为电阻的变化量很小, 所以
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
R g = R 3 ∥ R 4 = R 临 2.
从 (18) 式和 (19) 式可以得到:
1°R 3 和 R 4 的选择对电桥灵敏度的影响很大.
2°双电桥的绝对灵敏度比相对灵敏度大.
综上所述, 用双电桥测量低值电阻时应特别注意 R 1, R 2, R 3, R 4 的选择, 对检流计除了考虑其灵敏度
外, 应强调其临界外阻的选择.
参考文献:
[ 1 ] 杨介信, 陈国美. 普通物理实验: 第二册[M ]. 北京: 高等教育出版社, 1985. 83~ 86. [ 2 ] 李继凡, 罗远瑜, 陶时澍等. 精密电气测量[M ]. 北京: 计量出版社, 1984. 124~ 141.
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
1 R 0R 1
,
(11)
其中 K 2 = con stan t, 且 K 2 < ∃. 为讨论方便, 不妨令各次改变量都相同, 比较 (8) ~ (11) 式, 有
K 1 ≠ K 2, S c1 ≠ S c0, S c∃1 ≠ S c∃0.
但是在通常情况下改变量 ∃ r = o (R 1R 0) 的条件很容易满足, 因此, 电桥的相对灵敏度与桥臂无关, 即
2R + R 0) R g ,
Sr=
(R 0 +
R
+
R1 +
ES i R 2) + (2 +R1Βιβλιοθήκη R+R
R
2)R
.
g
由此亦可以看出提高电桥灵敏度的努力方向. 在实验中常常研究电桥的相对灵敏度, 方法是将平衡的桥
任一桥臂改变一微量, 读出此时检流计的偏转, 即
Sr=
Α ∃R R
=
∃R
Α
0R
0
=
∃R
Α
1R
(16)
∃R =
R3
1 +
R4
+
R3 (R 3 + R 4) 2
r∃R 3,
(17)
由 (16) 式和 (17) 式可以看出R 3, R 4 的改变对检流计中的电流影响很小, 即调节平衡时应重点注意R 1 与
R 2. 设 R 1 变为 R 1 + ∃R 1 (相应地 R 3 变为 R 3 + ∃R 3) , 考虑 R 1, R 0 都很小. 当 ∃R 1 = o[m ax (R 2, R R 0) ] 时
图 1 是惠斯登电桥的电路原理图 (设不考虑电源的内阻). 由于要研究测量结果的误差, 所以必须考 虑 I g = 0 的可信程度, 它通常由灵敏度这个物理量来反映.
当电桥平衡时, 设待测电阻 R 变化一个微量 ∃ r, 引起检流计的偏转为角 Α, 则
S
a
≡
Α ∃R
(1)
为电桥的绝对灵敏度;
S
r
≡
Α ∃R R
R 3r R3 + R4 +
) r
或RX
=
R R
1R
2
N
+
R 4r R3+ R4+
(R rR
1 2
-
R R
3 4
).
(15)
由 (15) 式可看出, 只有当电桥平衡, 即R 1 =
R2
R R
3 4
或
r
很小时,
才能方便地测量 R
X.
∃R 0 =
R3
1 +
R4
+
