空间向量复习精选例题(含答案解析)

合集下载

(完整版)高中数学空间向量训练题

高中数学空间向量训练题（含解析）一．选择题1．已知 M 、N 分别是周围体 OABC的棱 OA，BC的中点，点 P 在线 MN 上，且 MP=2PN，设向量= ，= ，= ，则=（）A．+ +B．+ +C．+ +D．+ +2．已知=（ 2，﹣ 1，2），=（﹣ 1， 3，﹣ 3），=（13，6，λ），若向量，，共面，则λ=（）A．2B．3C． 4D．63．空间中，与向量同向共线的单位向量为（）A．B．或C．D．或4．已知向量，且，则x的值为（）A．12 B．10 C．﹣ 14D． 145．若 A，B，C 不共线，对于空间任意一点O 都有=++，则P，A，B，C四点（）A．不共面B．共面C．共线D．不共线6．已知平面α的法向量是（ 2，3，﹣ 1），平面β的法向量是（ 4，λ，﹣ 2），若α∥β，则λ的值是（）A．B．﹣ 6 C．6D．7．已知，则的最小值是（）第 1页（共 40页）8．有四个命题：①若 =x +y ，则与、共面；②若与、共面，则 =x +y ；③若 =x +y，则 P，M ，A，B 共面；④若 P，M， A，B 共面，则=x +y ．其中真命题的个数是（）A．1 B．2 C． 3 D．49．已知向量 =（2，﹣1，1）， =（1，2，1），则以，为邻边的平行四边形的面积为（）A．B．C．4 D． 810．以以下图，在长方体ABCD﹣A1B1C1D1中， AD=AA1=1，AB=2，点 E 是棱 AB 的中点，则点 E 到平面 ACD1的距离为（）A．B．C．D．11．正方体 ABCDA1B1C1D1中，直线 DD1与平面 A1BC1所成角的正弦值为（）A．B．C．D．二．填空题（共 5 小题）12．已知向量=（ k， 12，1）， =（4，5，1），=（﹣ k， 10，1），且 A、 B、 C 三点共线，则 k=．13．正方体 ABCD﹣ A1B1C1D1的棱长为 1，MN 是正方体内切球的直径，P 为正方体表面上的动点，则?的最大值为．14．已知点 P 是平行四边形 ABCD所在的平面外一点，若是=（ 2，﹣ 1，﹣ 4），=（4，2，0），=（﹣ 1， 2，﹣ 1）．对于结论：① AP⊥AB；② AP⊥ AD；③是平面ABCD的法向量；④∥．其中正确的选项是．15．设空间任意一点 O 和不共线三点 A，B，C，且点 P 满足向量关系，若P，A，B，C 四点共面，则 x+y+z=．16．已知平面α⊥平面β，且α∩β =l，在 l 上有两点 A，B，线段 AC? α，线段 BD? β，并且 AC ⊥ l，BD⊥l， AB=6，BD=24， AC=8，则 CD=．17．如图，在四棱锥P﹣ABCD中， PA丄平面 ABCD， AB 丄 BC，∠ BCA=45°，PA=AD=2，AC=1，DC=（Ⅰ）证明 PC丄 AD；（Ⅱ）求二面角 A﹣PC﹣ D 的正弦值；（Ⅲ）设 E 为棱 PA上的点，满足异面直线BE与 CD所成的角为 30°，求 AE的长．18．如图，在四棱锥 P﹣ABCD中，底面 ABCD为直角梯形， AD∥BC，∠ ADC=90°，平面PAD⊥底面 ABCD， Q 为 AD 的中点， M 是棱 PC上的点， PA=PD=2，BC= AD=1，CD= ．（Ⅰ）求证：平面 PQB⊥平面 PAD；（Ⅱ）若 M 为棱 PC的中点，求异面直线AP 与 BM 所成角的余弦值．19．如图，在四棱锥S﹣ABCD中， SD⊥底面 ABCD，底面 ABCD是正方形，且 SD=AD，E 是 SA 的中点．（1）求证：直线 BA⊥平面 SAD；（2）求直线 SA与平面 BED的夹角的正弦值．20．如图，四棱锥 P﹣ABCD中，底面 ABCD是直角梯形，∠ DAB=90°AD∥BC， AD⊥侧面 PAB，△ PAB是等边三角形， DA=AB=2， BC=，E是线段AB的中点．（Ⅰ）求证： PE⊥CD；（Ⅱ）求 PC与平面 PDE所成角的正弦值．21．如图，在四棱锥 P﹣ABCD中，平面 PAD⊥平面 ABCD，E 为 AD 的中点， PA⊥AD，BE∥CD，BE⊥AD，PA=AE=BE=2，CD=1．（Ⅰ）求证：平面 PAD⊥平面 PCD；（Ⅱ）求二面角 C﹣PB﹣ E 的余弦值；（Ⅲ）在线段 PE上可否存在点 M ，使得 DM∥平面 PBC？若存在，求出点M 的地址；若不存在，说明原由．22．如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直． AB∥CD，AB⊥BC，AB=2CD=2BC， EA⊥EB．（Ⅰ）求证： AB⊥DE；（Ⅱ）求直线 EC与平面 ABE所成角的正弦值；（Ⅲ）线段 EA 上可否存在点 F，使 EC∥平面 FBD？若存在，求出；若不存在，说明原由．23．如图，三棱柱 ABC﹣A1B1C1中，AB=AC=CC1，平面 BAC1⊥平面 ACC1A1，∠ACC1=∠BAC1=60°， AC1∩ A1C=O．（Ⅰ）求证： BO⊥平面 AA1C1C；（Ⅱ）求二面角 A﹣BC1﹣B1的余弦值．24．如图，在四棱锥P﹣ ABCD中， PA⊥平面，四边形ABCD为正方形，点M， N 分别为线段PB，PC上的点， MN⊥PB．（Ⅰ）求证： MN⊥平面 PAB；（Ⅱ）当 PA=AB=2，二面角 C﹣AN﹣D 大小为时，求PN的长．上的点，且 CD=DE=，CE=2EB=2．（Ⅰ）证明： DE⊥平面 PCD（Ⅱ）求二面角 A﹣PD﹣ C 的余弦值．26．如图，在几何体 ABCDE中，四边形 ABCD是矩形， AB⊥平面 BEC，BE⊥ EC，AB=BE=EC=2，G， F 分别是线段 BE，DC的中点．（1）求证： GF∥平面 ADE；（2）求平面 AEF与平面 BEC所成锐二面角的余弦值．27．如图，在四棱锥P﹣ABCD中， PD⊥平面 ABCD，四边形 ABCD是菱形， AC=2，BD=2，E 是 PB 上任意一点．（Ⅰ）求证： AC⊥DE；（Ⅱ）已知二面角 A﹣PB﹣D 的余弦值为，若E为PB的中点，求EC与平面PAB所成角的正弦值．28．如图，三棱柱 ABC﹣ A1B1C1中，侧面 BB1C1C 为菱形， AB⊥B1C．（Ⅰ）证明： AC=AB1；（Ⅱ）若 AC⊥ AB1，∠ CBB1=60°， AB=BC，求二面角 A﹣A1B1﹣ C1的余弦值．29. 已知四棱锥P— ABCD ， PB⊥ AD，侧面 PAD 为边长等于 2 的正三角形，底面ABCD 为菱形，侧面PAD 与底面 ABCD 所成的二面角为120°.（1）求点 P 到平面 ABCD 的距离；（2）求面 APB 与面 CPB 所成二面角的余弦值.PCDBA30 如图，在三棱柱ABC ﹣ A 1B 1C1中， AA 1⊥底面ABC ，∠ ACB=90°，AC=BC=1 ， AA 1=2，D 是棱AA 1的中点．（Ⅰ）求证：B1C 1∥平面 BCD ；（Ⅱ）求三棱锥B﹣ C1CD 的体积；（Ⅲ）在线段BD 上可否存在点Q，使得 CQ ⊥ BC 1？请说明原由．31 如图，在三棱锥A﹣ BCD中， O、 E 分别为 BD、 BC中点， CA=CB=CD=BD=4，AB=AD=2（1）求证： AO⊥面 BCD（2）求异面直线 AB 与 CD所成角的余弦值（3）求点 E 到平面 ACD的距离．32 在三棱柱ABC﹣ A1B1C1中，侧面ABB1A1为矩形， AB=2， AA1=2，D是AA1的中点，BD与AB1交于点O，且CO⊥ABB1A1平面．（1）证明： BC⊥AB 1；（2）若 OC=OA，求直线 CD与平面 ABC所成角的正弦值．2018 年 01 月 20 日 shu****e168的高中数学组卷参照答案与试题解析一．选择题（共11 小题）1．已知 M 、N 分别是周围体 OABC的棱 OA，BC的中点，点 P 在线 MN 上，且 MP=2PN，设向量= ，= ，= ，则=（）A．+ +B．+ +C．+ +D．+ +【解答】解：以以下图，= +，=（+），=，=﹣，=．∴= += +=+ （﹣）=+=×（ + ） + ×=++=+ + ．应选： C．2．已知=（ 2，﹣ 1，2），=（﹣ 1， 3，﹣ 3），=（13，6，λ），若向量，，共面，则λ=（）A．2B．3C． 4D．6【解答】解：∵=（2，﹣ 1， 2），=（﹣ 1，3，﹣ 3），=（13，6，λ），三个向量共面，∴，∴（ 2，﹣ 1，2）=x（﹣ 1，3，﹣ 3）+y（13，6，λ）∴解得：应选： B．3．空间中，与向量同向共线的单位向量为（）A．B．或C．D．或【解答】解：∵，∴与同向共线的单位向量向量，第10页（共 40页）4．已知向量，且，则x的值为（）A．12 B．10 C．﹣ 14D． 14【解答】解：由于向量，且，属于=﹣8﹣6+x=0，解得 x=14；应选： D．5．若 A，B，C 不共线，对于空间任意一点O 都有=++，则P，A，B，C四点（）A．不共面B．共面C．共线D．不共线【解答】解： A，B，C 不共线，对于空间任意一点O 都有=x +y +z，则 P，A，B，C 四点共面的充要条件是x+y+z=1，而=++，因此P，A，B，C四点不共面．应选： A．6．已知平面α的法向量是（ 2，3，﹣ 1），平面β的法向量是（ 4，λ，﹣ 2），若α∥β，则λ的值是（）A．B．﹣ 6 C．6D．【解答】解：∵α∥β，且平面α的法向量是 =（2，3，﹣ 1），平面β的法向量是 =（ 4，λ，﹣ 2），∴即存在实数μ使得，即（ 2，3，﹣ 1）=（4μ，λμ，﹣ 2μ），解得μ=，λ=6应选 C．7．已知，则的最小值是（）A．B．C．D．【解答】解：=（﹣ 1﹣t， t﹣1，﹣ t），∴==≥，当且仅当t=0时取等号．∴的最小值是．应选： A．8．有四个命题：①若 =x +y ，则与、共面；②若与、共面，则=x +y；③若=x +y，则 P，M ，A，B 共面；④若 P，M， A，B 共面，则=x +y．其中真命题的个数是（）A．1B．2C． 3D．4【解答】解：若=x +y ，则与，必然在同一平面内，故①对；若=x +y ，则、、三向量在同一平面内，∴ P、M、A、B 共面．故③对；若=x +y ，则与、共面，但若是，共线，就不用然能用、来表示，故②不对；同理④也不对．∴真命题的个数为 2 个．应选： B．9．已知向量=（2，﹣1，1）， =（1，2，1），则以，为邻边的平行四边形的面积为（）A．B．C．4D． 8【解答】解：设向量，的夹角为θ，=，=，∴ cosθ===．∴ sin θ==．∴以，为邻边的平行四边形的面积S=??sin θ==，应选： B．10．以以下图，在长方体ABCD﹣A1B1C1D1中， AD=AA1=1，AB=2，点 E 是棱 AB 的中点，则点 E 到平面 ACD1的距离为（）A．B．C．D．【解答】解：如图，以 D 为坐标原点，直线DA，DC， DD1分别为 x，y，z 轴建立空间直角坐标系，则D1（ 0， 0，1），E（1，1，0）， A（ 1， 0， 0），C（0，2，0）．=（ 1， 1，﹣ 1）， =（﹣ 1，2，0），=（﹣ 1， 0， 1），设平面 ACD1的法向量为=（a，b，c），则，取 a=2，得=（ 2， 1， 2），点 E 到平面 ACD1的距离为：h===．应选： C．11．正方体 ABCDA1B1C1D1中，直线 DD1与平面 A1BC1所成角的正弦值为（）A．B．C．D．【解答】解：∵△ A1BC1是等边三角形， A1B1=BB1=B1C1，∴B1在平面 A1BC1上的射影为△ A1 BC1的中心 O，设正方体棱长为 1，M 为 A1C1的中点，则 A1B= ，∴ OB= BM==，∴ OB1==，∴ sin∠B1BO==，即BB1与平面A1BC1所成角的正弦值为，∵DD1∥BB1，∴直线 DD1与平面11 所成角的正弦值为．A BC应选： A．二．填空题（共 5 小题）12．已知向量=（ k， 12，1），=（4，5，1），=（﹣ k， 10，1），且 A、 B、 C 三点共线，则 k=．【解答】解：∵向量=（ k， 12，1）， =（4，5，1），=（﹣ k，10，1），∴=（4﹣k，﹣ 7，0）， =（﹣ 2k，﹣ 2， 0）．又 A、B、C 三点共线，∴存在实数λ使得，∴，解得．故答案为：﹣．13．正方体 ABCD﹣ A1B1C1D1的棱长为 1，MN 是正方体内切球的直径，P 为正方体表面上的动点，则?的最大值为．【解答】解：连接 PO，可得? ==++=﹣，当获取最大值时，?获取最大值为=．故答案为：．14．已知点 P 是平行四边形 ABCD所在的平面外一点，若是=（ 2，﹣ 1，﹣ 4），=（4，2，0），=（﹣ 1， 2，﹣ 1）．对于结论：① AP⊥AB；② AP⊥ AD；③是平面 ABCD的法向量；④∥．其中正确的选项是①②③ ．【解答】解：由 =（2，﹣ 1，﹣ 4），=（ 4， 2， 0）， =（﹣ 1，2，﹣ 1），知：在①中，=﹣2﹣2+4=0，∴⊥，∴ AP⊥AB，故①正确；在②中，? =﹣4+4+0=0，∴⊥，∴ AP⊥AD，故②正确；在③中，由 AP⊥AB， AP⊥ AD，AB∩AD=A，知是平面 ABCD的法向量，故③正确；在④中，=（ 2， 3， 4），假设存在λ使得 =，则，无解，∴∥．故④不正确；综上可得：①②③正确．故答案为：①②③．15．设空间任意一点 O 和不共线三点 A，B，C，且点 P 满足向量关系，若 P，A，B，C 四点共面，则 x+y+z= 1 ．【解答】若空间任意一点 O 和不共线的三点 A，B，C，满足向量关系式：，则 P，A，B，C 四点共面的充要条件是： x+y+z=1，故答案为： 1．16．已知平面α⊥平面β，且α∩β =l，在 l 上有两点 A，B，线段 AC? α，线段 BD? β，并且 AC ⊥l，BD⊥l， AB=6，BD=24， AC=8，则 CD= 26 ．【解答】解：∵平面α⊥平面β，且α∩β=l，在 l 上有两点 A，B，线段 AC? α，线段 BD? β，AC⊥l， BD⊥ l，AB=6，BD=24，AC=8，∴=，∴=（）2==64+36+576=676，∴CD=26．故答案为： 26．三．解答题（共12 小题）17．如图，在四棱锥P﹣ABCD中， PA丄平面 ABCD， AB 丄 BC，∠ BCA=45°，PA=AD=2，AC=1，DC=（Ⅰ）证明 PC丄 AD；（Ⅱ）求二面角 A﹣PC﹣ D 的正弦值；（Ⅲ）设 E 为棱 PA上的点，满足异面直线BE与 CD所成的角为 30°，求 AE的长．【解答】（本小分 13 分）明：（Ⅰ）∵在△ ADC中， AD=2，AC=1，DC=222∴ AC +AD =CD ，∴ AD⊥ AC，⋯（1 分）如，以点 A 原点建立空直角坐系，依意得 A（0，0，0）， D（ 2， 0， 0），C（0，1，0），B（，，0），P（0，0，2），得=（0，1， 2）， =（2，0，0），∴=0，∴ PC⊥AD．⋯（4 分）解：（Ⅱ），，平面 PCD的一个法向量=（ x， y， z），，不如令 z=1，得=（1，2，1），可取平面 PAC的一个法向量=（1，0，0），于是 cos＜＞==，从而 sin＜＞=，因此二面角 A PC D 的正弦．⋯（8分）（Ⅲ）点 E 的坐（ 0， 0， h），其中 h∈[ 0，2] ，由此得=（），由=（2， 1，0），故，∵ 足异面直BE与 CD所成的角 30°，∴=cos30°=，解得h=，即AE=．⋯（13分）18．如，在四棱 P ABCD中，底面 ABCD直角梯形， AD∥BC，∠ ADC=90°，平面 PAD⊥底面ABCD， Q AD 的中点， M 是棱 PC上的点， PA=PD=2，BC= AD=1，CD= ．（Ⅰ）求：平面 PQB⊥平面 PAD；（Ⅱ）若 M 棱 PC的中点，求异面直AP 与 BM 所成角的余弦．【解答】解：（Ⅰ）∵ AD∥ BC，BC= AD，Q AD 的中点，∴四形 BCDQ平行四形，可得CD∥BQ．∵∠ ADC=90°，∴∠ AQB=90°即QB⊥AD．又∵平面 PAD⊥平面 ABCD，平面 PAD∩平面 ABCD=AD，∴BQ⊥平面 PAD．∵ BQ? 平面 PQB，∴平面 PQB⊥平面 PAD．（Ⅱ）∵ PA=PD，Q 为 AD 的中点，∴ PQ⊥ AD．∵平面 PAD⊥平面 ABCD，且平面 PAD∩平面 ABCD=AD，∴ PQ⊥平面 ABCD．（注：不证明 PQ⊥平面 ABCD直接建系扣 1 分）因此，以 Q 为原点、 QA、QB、QP 分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系，以以下图则 Q（0，0，0）， A（1，0， 0），P（0，0，），B（0，，0）， C（﹣ 1，， 0）∵ M 是 PC中点，∴ M （﹣，，）∴=（﹣ 1，0，），=（﹣，﹣，）设异面直线 AP 与 BM 所成角为θ，则 cosθ=|cos＜，＞| ==．∴异面直线 AP 与 BM 所成角的余弦值为．19．如图，在四棱锥S﹣ABCD中， SD⊥底面 ABCD，底面 ABCD是正方形，且 SD=AD，E 是 SA 的中点．（1）求证：直线 BA⊥平面 SAD；（2）求直线 SA与平面 BED的夹角的正弦值．【解答】（本分 12 分）解：（ 1）明：∵ SD⊥平面 ABCD，∴ SD⊥AB，又 AD⊥AB，AD∩SD=D，∴ AB⊥平面 SAD，⋯（6 分）（2）以 D 原点，分以 DA、DC、 DS x，y， z 建立空直角坐系，如，AB=2， A（ 2， 0，0），S（0，0，2），B（1，2，0），E（1，0，0），故=（2，0， 2），=（2， 2， 0），=（1，0， 1），⋯（ 8 分）平面 BED的一个法向量=（x，y，z），由得，取=（1， 1， 1），⋯（10 分）直 SA与平面 BED所成角θ，因 cos==，因此 sin θ=，即直 SA与平面 BED所成角的正弦⋯（ 12 分）20．如，四棱 P ABCD中，底面 ABCD是直角梯形，∠ DAB=90°AD∥BC， AD⊥ 面 PAB，△ PAB是等三角形， DA=AB=2， BC=，E是段AB的中点．（Ⅰ）求： PE⊥CD；（Ⅱ）求 PC与平面 PDE所成角的正弦．【解答】解：（Ⅰ）∵ AD⊥ 面 PAB，PE? 平面 PAB，∴ AD⊥EP．又∵△ PAB是等三角形， E 是段 AB 的中点，∴ AB⊥EP．∵AD∩ AB=A，∴ PE⊥平面 ABCD．∵CD? 平面 ABCD，∴ PE⊥ CD．⋯（ 5 分）（Ⅱ）以 E 原点， EA、EP分 y、 z ，建立如所示的空直角坐系．E（0，0，0）， C（ 1， 1， 0），D（ 2，1，0），P（0，0，）．=（2， 1， 0），=（0，0，），=（1， 1，）．=（x，y，z）平面 PDE的一个法向量．由，令 x=1，可得=（ 1， 2，0）．⋯（ 9 分）PC与平面 PDE所成的角θ，得=因此 PC与平面 PDE所成角的正弦．⋯（12分）21．如，在四棱 P ABCD中，平面 PAD⊥平面 ABCD，E AD 的中点， PA⊥AD，BE∥CD，BE⊥AD，PA=AE=BE=2，CD=1．（Ⅰ）求：平面 PAD⊥平面 PCD；（Ⅱ）求二面角 C PB E 的余弦；（Ⅲ）在段 PE上可否存在点 M ，使得 DM∥平面 PBC？若存在，求出点 M 的地址；若不存在，明原由．【解答】解：（Ⅰ）明：由已知平面 PAD⊥平面 ABCD，PA⊥ AD，且平面PAD∩平面 ABCD=AD，因此 PA⊥平面 ABCD．因此 PA⊥CD．又因BE⊥AD，BE∥CD，因此 CD⊥AD．因此 CD⊥平面 PAD．因 CD? 平面PCD，因此平面 PAD⊥平面 PCD．⋯（4 分）（Ⅱ）作 Ez⊥AD，以 E 原点，以的方向分x，y的正方向，建立如所示的空直角坐系 E xyz，点 E（0，0，0）， P（ 0， 2，2）， A（0， 2， 0），B（2，0，0）， C（ 1， 2， 0），D（0，2，0）．因此，，．平面 PBC的法向量=（ x，y，z），因此即令 y=1，解得=（ 2， 1， 3）．平面 PBE的法向量=（a，b，c），因此即令 b=1，解得=（ 0， 1， 1）．因此 cos＜＞=．由可知，二面角 C PB E 的余弦．⋯（10分）（Ⅲ）“ 段 PE上存在点 M，使得 DM∥平面 PBC”等价于“”．因，，λ∈（0，1），M （0，2λ 2，2 2λ），．由（Ⅱ）知平面 PBC的法向量=（ 2， 1， 3），因此．解得．因此段 PE上存在点 M ，即 PE中点，使得 DM∥平面 PBC．⋯（ 14 分）22．如，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直． AB∥CD，AB⊥BC，AB=2CD=2BC， EA⊥EB．（Ⅰ）求： AB⊥DE；（Ⅱ）求直 EC与平面 ABE所成角的正弦；（Ⅲ）段 EA 上可否存在点 F，使 EC∥平面 FBD？若存在，求出；若不存在，明原由．【解答】（Ⅰ ）明：取 AB 中点 O，接 EO，DO．因 EB=EA，因此 EO⊥ AB．⋯（1 分）因四形 ABCD直角梯形， AB=2CD=2BC， AB⊥ BC，因此四形 OBCD正方形，因此 AB⊥OD．⋯（2 分）因 EO∩OD=O因此 AB⊥平面 EOD．⋯（3 分）因 ED? 平面 EOD因此 AB⊥ED．⋯（4 分）（Ⅱ）解：因平面 ABE⊥平面 ABCD，且 EO⊥AB，平面 ABE∩平面 ABCD=AB因此 EO⊥平面 ABCD，因 OD? 平面 ABCD，因此 EO⊥OD．由 OB，OD，OE两两垂直，建立如所示的空直角坐系O xyz．⋯（5 分）因△ EAB等腰直角三角形，因此 OA=OB=OD=OE， OB=1，因此 O（0，0，0）， A（ 1，0，0），B（1，0，0）， C（ 1， 1， 0），D（0，1，0），E（ 0， 0， 1）．因此，平面 ABE的一个法向量．⋯（7 分）直 EC与平面 ABE所成的角θ，因此，即直 EC与平面 ABE所成角的正弦．⋯（ 9 分）（Ⅲ）解：存在点 F，且，有 EC∥平面 FBD．⋯（10 分）明以下：由，，因此．平面 FBD的法向量=（a，b，c），有因此取 a=1，得 =（ 1，1，2）．⋯（ 12 分）因=（1，1， 1）?（1，1，2）=0，且 EC?平面 FBD，因此 EC∥平面 FBD．即点 F 足，有 EC∥平面 FBD．⋯（ 14 分）23．如，三棱柱 ABC A1B1C1中，AB=AC=CC1，平面 BAC1⊥平面 ACC1A1，∠ACC1=∠BAC1=60°，AC1∩ A1C=O．（Ⅰ）求： BO⊥平面 AA1C1C；（Ⅱ）求二面角 A BC1B1的余弦．【解答】明：（Ⅰ ）依意，四形 AA1C1C 菱形，且∠ AA1C1=60°∴△ AA1C1正三角形，又∠ BAC1=60°，∴△ BAC1正三角形，又 O AC1中点，∴BO⊥ AC1，∵平面 ABC1⊥平面 AA1C1C，平面 ABC1∩平面 AA1C1C=AC1，∵BO? 平面 AA1CC1，∴ BO⊥平面 AA1C1C．⋯（4 分）解：（Ⅱ）以 O 坐原点，建空直角坐系，如，令 AB=2，，C1（，，）010∴，平面 BB1 1的一个法向量，C由得，取 z=1，得⋯（9分）又面 ABC1的一个法向量∴⋯（11 分）故所求二面角的余弦⋯（ 12 分）24．如，在四棱P ABCD中， PA⊥平面，四形ABCD正方形，点M， N 分段PB，PC上的点， MN⊥PB．（Ⅰ）求： MN⊥平面 PAB；（Ⅱ）当 PA=AB=2，二面角 C AN D 大小，求PN的．【解答】（Ⅰ ）明：在正方形ABCD中， AB⊥BC，∵PA⊥平面 ABCD， BC? 平面 ABCD，∴ PA⊥ BC．∵AB∩PA=A，且 AB，PA? 平面 PAB，∴BC⊥平面 PAB， BC⊥PB，∵MN⊥PB，∴ MN∥BC，则 MN⊥平面 PAB；（Ⅱ）解：∵ PA⊥平面 ABCD，AB，AD? 平面 ABCD，∴ PA⊥AB，PA⊥ AD，又 AB⊥AD，如图，以 A 为原点， AB，AD，AP 所在直线为 x，y，z 轴，建立空间直角坐标系A﹣xyz，则C（2，2，0）， D（ 0， 2， 0），B（2，0，0），P（0，0，2）．设平面 DAN 的一个法向量为 =（x，y，z），平面 CAN的一个法向量为 =（a，b，c），设 =λ，λ∈[ 0， 1] ，∵=（2，2，﹣2），∴=（2λ，2λ，2﹣2λ），又 =（0，2，0），∴，取 z=1，得=（，0，1），∵=（0，0，2）， =（2，2，0），∴，取 a=1 得，到=（1，﹣ 1，0），∵二面 C﹣ AN﹣ D 大小为，∴ | cos＜，＞| =cos=，∴ | cos＜，＞| =|| =|| =，解得λ=，∴，则 PN=．25．如题图，三棱锥 P﹣ABC中，PC⊥平面 ABC，PC=3，∠ ACB=．D，E分别为线段AB，BC 上的点，且 CD=DE=，CE=2EB=2．（Ⅰ）证明： DE⊥平面 PCD（Ⅱ）求二面角 A﹣PD﹣ C 的余弦值．【解答】（Ⅰ ）证明：∵ PC⊥平面 ABC，DE? 平面 ABC，∴ PC⊥DE，∵CE=2，CD=DE= ，∴△CDE为等腰直角三角形，∴ CD⊥DE，∵ PC∩CD=C，DE垂直于平面 PCD内的两条订交直线，∴DE⊥平面 PCD（Ⅱ）由（Ⅰ）知△ CDE为等腰直角三角形，∠ DCE=，过点 D 作 DF 垂直 CE于 F，易知 DF=FC=FE=1，又由已知 EB=1，故 FB=2，由∠ ACB=得DF∥AC，，故AC= DF=，以 C 为原点，分别以，，的方向为xyz轴的正方向建立空间直角坐标系，则C（0，0，0）， P（ 0， 0， 3），A（， 0， 0），E（0，2，0）， D（1， 1，0），∴ =（1，﹣ 1，0）， =（﹣ 1，﹣ 1，3）， =（，﹣ 1， 0），设平面 PAD的法向量=（ x， y， z），由，故可取=（2， 1， 1），由（Ⅰ）知 DE⊥平面 PCD，故平面 PCD的法向量可取=（1，﹣ 1，0），∴两法向量夹角的余弦值cos＜，＞==∴二面角 A﹣PD﹣ C 的余弦值为．26．如图，在几何体 ABCDE中，四边形 ABCD是矩形， AB⊥平面 BEC，BE⊥ EC，AB=BE=EC=2，G， F 分别是线段 BE，DC的中点．（1）求证： GF∥平面 ADE；（2）求平面 AEF与平面 BEC所成锐二面角的余弦值．【解答】解法一：（ 1）如图，取 AE 的中点 H，连接 HG，HD，∵G 是 BE的中点，∴ GH∥ AB，且 GH= AB，又∵ F 是 CD中点，四边形ABCD是矩形，∴DF∥AB，且 DF= AB，即 GH∥DF，且 GH=DF，∴四边形 HGFD是平行四边形，∴ GF∥ DH，又∵ DH? 平面 ADE，GF?平面 ADE，∴ GF∥平面 ADE．（ 2）如图，在平面BEG内，过点 B 作 BQ∥ CE，∵BE⊥EC，∴ BQ⊥BE，又∵ AB⊥平面 BEC，∴ AB⊥BE，AB⊥ BQ，以 B 为原点，分别以的方向为x轴，y轴，z轴的正方向建立空间直角坐标系，则 A（0，0，2）， B（ 0， 0， 0），E（2，0，0）， F（ 2， 2， 1）∵ AB⊥平面 BEC，∴为平面BEC的法向量，设=（x，y，z）为平面 AEF的法向量．又=（2，0，﹣ 2），=（2，2，﹣ 1）由垂直关系可得，取 z=2 可得．∴ cos＜，＞==∴平面 AEF与平面 BEC所成锐二面角的余弦值为．解法二：（1）如图，取 AB 中点 M ，连接 MG，MF，又G 是 BE的中点，可知 GM∥AE，且 GM= AE又AE? 平面 ADE，GM?平面 ADE，∴GM∥平面 ADE．在矩形 ABCD中，由 M， F 分别是 AB， CD的中点可得 MF∥AD．又AD? 平面 ADE，MF?平面 ADE，∴ MF∥平面ADE．又∵ GM∩MF=M，GM? 平面 GMF，MF? 平面GMF∴平面 GMF∥平面 ADE，∵GF? 平面 GMF，∴ GF∥平面 ADE（ 2）同解法一．第30页（共 40页）27．如，在四棱P ABCD中， PD⊥平面 ABCD，四形 ABCD是菱形， AC=2，BD=2，E 是 PB 上任意一点．（Ⅰ）求： AC⊥DE；（Ⅱ）已知二面角 A PB D 的余弦，若 E PB的中点，求 EC与平面 PAB所成角的正弦．【解答】（I）明：∵ PD⊥平面 ABCD，AC? 平面 ABCD∴PD⊥AC又∵ ABCD是菱形，∴ BD⊥ AC，BD∩PD=D∴AC⊥平面 PBD，∵ DE? 平面 PBD∴AC⊥DE⋯（6 分）（ II）解：分以OA， OB， OE 方向x， y， z 建立空直角坐系，PD=t，由（ I）知：平面 PBD的法向量，令平面PAB 的法向量，根据得∴因二面角 A PB D 的余弦，，即，∴⋯（9 分）∴EC与平面 PAB所成的角θ，∵，∴⋯（12 分）28．如，三棱柱 ABC A1B1C1中，面 BB1C1C 菱形， AB⊥B1C．（Ⅰ）明： AC=AB1；（Ⅱ）若 AC⊥ AB1，∠ CBB1=60°， AB=BC，求二面角 A A1B1C1的余弦．【解答】解：（1）连接 BC1，交 B1C 于点 O，连接 AO，∵侧面 BB1 C1C 为菱形，∴BC1⊥B1C，且 O 为 BC1和 B1C 的中点，又∵ AB⊥ B1 C，∴ B1C⊥平面 ABO，∵ AO? 平面 ABO，∴ B1C⊥ AO，又B10=CO，∴ AC=AB1，（2）∵ AC⊥ AB1，且 O 为 B1C 的中点，∴ AO=CO，又∵ AB=BC，∴△ BOA≌△ BOC，∴ OA⊥OB，∴ OA， OB，OB1两两垂直，以 O 为坐标原点，的方向为x轴的正方向，|| 为单位长度，的方向为 y 轴的正方向，的方向为z轴的正方向建立空间直角坐标系，∵∠ CBB1°，∴△ 1 为正三角形，又，=60CBB AB=BC∴ A（ 0， 0，）， B（ 1， 0， 0，）， B （，，），（，，）00 C 001∴=（0，，），= =（1，0，），==（﹣ 1，，0），设向量=（x，y，z）是平面 AA1B1的法向量，则，可取=（1，，），同理可得平面 A1 B1C1的一个法向量=（1，﹣，），∴ cos＜，＞== ，∴二面角 A﹣A1B1﹣ C1的余弦值为29. 已知四棱锥P— ABCD ， PB⊥ AD，侧面PAD为边长等于 2 的正三角形，底面ABCD为菱形，侧面PAD 与底面ABCD所成的二面角为120°.（ 1）求点P 到平面ABCD的距离；（ 2）求面APB与面CPB所成二面角的大小.PCDBA（传统法）解（ 1）：以以下图，作 PO⊥平面 ABCD ，垂足为点 O. 连接 OB、 OA、OD ， OB 与 AD 交于点 E，连接 PE.PDCEO BA∵AD ⊥ PB，∴ AD⊥ OB.∵P A=PD ，∴ OA=OD .于是 OB 均分 AD ，点 E 为 AD 的中点，∴ PE ⊥AD. 由此知∠ PEB 为面 PAD 与面 ABCD 所成二面角的平面角，∴∠ PEB=120°，∠ PEO=60°. 由已知可求得 PE= 3，33，即点 P 到平面 ABCD 的距离为3 .∴PO=PE·sin60°=3×=222（2）（空间向量法）解法一：以以下图建立直角坐标系，其中O 为坐标原点， x 轴平行于 DA .zPGCDOEyBAxP（ 0，0，333， 0）， PB 中点 G 的坐标为（ 0，33，3），连接 AG.）， B（ 0，2244又知 A（ 1，3，0）， C（－ 2，3 3，0） . 22由此获取 GA =（1，－3，－3），44PB =（0，3 3，－3）， BC =（－2，0，0）.22于是有 GA · PB =0， BC · PB =0，∴ GA ⊥ PB ， BC ⊥ PB . GA ， BC 的夹角 θ 等于所求二面角的平面角.于是 cos θ=GA BC|GA || BC |=－2 7，7由于题目中的二面角为钝角，因此所求二面角的大小为－2 7 。

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.如图，长方体中，分别为中点，（1）求证：．（2）求二面角的正切值．【答案】（1）见解析（2）【解析】（1）由长方体及E、F分别为AB、C1D1的中点知，AE平行且等于C1F，所以AEC1F是平行四边形，所以C1E∥AF，由线面平行的判定定理知，C1E∥面ACF；（2）易证FG⊥面ABCD，过F作FH⊥AC于H，连结HG，因为FG⊥面ABCD，则FG⊥AC，所以∠FHG为二面角F—AC—G的平面角，然后通过解三角形，求出FG、GH的长，即可求出∠FHG的正切值，即为二面角F-AC-G的正切值.试题解析：(1)证明：在长方体中，分别为中点，且四边形是平行四边形3分，5分(2)．长方体中，分别为中点，7分过做于，又就是二面角的平面角 9分，在中， 11分直角三角形中 13分二面角的正切值为 14分考点:线面平行的判定定理；二面角的计算；逻辑推理能力2.如图，在直三棱柱A1B1C1－ABC中，AB⊥AC，AB＝AC＝2，A1A＝4，点D是BC的中点．(1)求异面直线A1B与C1D所成角的余弦值；(2)求平面ADC1与平面ABA1夹角的正弦值．【答案】（1）（2）【解析】解：(1)以A为坐标原点，建立如图所示的空间直角坐标系A－xyz，则A(0,0,0)，B(2,0,0)，C(0,2,0)，D(1,1,0)，A1(0,0,4)，C1(0,2,4)，∴＝(2,0，－4)，＝(1，－1，－4)．∵cos〈，〉＝＝＝，∴异面直线A1B与C1D所成角的余弦值为.(2)设平面ADC1的法向量为n1＝(x，y，z)，∵＝(1,1,0)，＝(0,2,4)，∴n1·＝0，n 1·＝0，即x＋y＝0且2y＋4z＝0，取z＝1，得x＝2，y＝－2，∴n1＝(2，－2,1)是平面ADC1的一个法向量．取平面AA1B的一个法向量为n2＝(0,1,0)，设平面ADC1与平面ABA1夹角的大小为θ.由cosθ＝＝＝，得sinθ＝.因此，平面ADC1与平面ABA1夹角的正弦值为.3.已知正方体ABCD－A1B1C1D1中，点E为上底面A1C1的中心，若＝＋x＋y，则x、y的值分别为()A．x＝1，y＝1B．x＝1，y＝C．x＝，y＝D．x＝，y＝1【答案】C【解析】如图，＝＋＝＋＝＋ (＋)．4.如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：(1)·；(2)·；(3)EG的长；(4)异面直线AG与CE所成角的余弦值．【答案】（1）（2）－（3）（4）【解析】解：设＝a，＝b，＝c.则|a|＝|b|＝|c|＝1，〈a，b〉＝〈b，c〉＝〈c，a〉＝60°.＝BD＝c－a，＝－a，＝b－c，(1)·＝(c－a)·(－a)＝a2－a·c＝；(2)·＝ (c－a)·(b－c)＝ (b·c－a·b－c2＋a·c)＝－；(3)＝＋＋＝a＋b－a＋c－b＝－a＋b＋ c.||2＝a2＋b2＋c2－a·b＋b·c－c·a＝.即||＝，所以EG的长为.(4)设、的夹角为θ.＝b＋c，＝＋＝－b＋a，cosθ＝＝－，由于异面直线所成角的范围是(0°，90°]，所以异面直线AG与CE所成角的余弦值为.5.在如图所示的空间直角坐标系中，一个四面体的顶点坐标分别是（0,0,2），（2,2,0），（1,2，1），（2,2,2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（）A．①和②B．③和①C．④和③D．④和②【答案】D【解析】设，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②，故选D.【考点】空间由已知条件，在空间坐标系中作出几何体的形状，再正视图与俯视图，容易题.6.如图，直四棱柱底面直角梯形，∥，，是棱上一点，，，，，.（1）求异面直线与所成的角；（2）求证：平面.【答案】(1);（2）证明见解析.【解析】（1）本题中由于有两两垂直，因此在求异面直线所成角时，可以通过建立空间直角坐标系，利用向量的夹角求出所求角；（2）同（1）我们可以用向量法证明线线垂直，以证明线面垂直，，，，易得当然我们也可直线用几何法证明线面垂直，首先，这由已知可直接得到，而证明可在直角梯形通过计算利用勾股定理证明，，，因此，得证.（1）以原点，、、分别为轴、轴、轴建立空间直角坐标系.则，，，. 3分于是,,,异面直线与所成的角的大小等于. 6分（2）过作交于，在中，，，则，，，， 10分，.又，平面. 12分【考点】（1）异面直线所成的角；（2）线面垂直.7.（2013•天津）如图，四棱柱ABCD﹣A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，AA1=AB=2，E为棱AA1的中点．（1）证明B1C1⊥CE；（2）求二面角B1﹣CE﹣C1的正弦值．（3）设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为，求线段AM的长．【答案】（1）见解析（2）（3）【解析】（1）证明：以点A为原点建立空间直角坐标系，如图，依题意得A（0，0，0），B（0，0，2），C（1，0，1），B1（0，2，2），C1（1，2，1），E（0，1，0）．则，而=0．所以B1C1⊥CE；（2）解：，设平面B1CE的法向量为，则，即，取z=1，得x=﹣3，y=﹣2．所以．由（1）知B1C1⊥CE，又CC1⊥B1C1，所以B1C1⊥平面CEC1，故为平面CEC1的一个法向量，于是=．从而==．所以二面角B1﹣CE﹣C1的正弦值为．（3）解：，设0≤λ≤1，有．取为平面ADD1A1的一个法向量，设θ为直线AM与平面ADD1A1所成的角，则==．于是．解得．所以．所以线段AM的长为．8.如图，四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB≌△DCB，EA=EB=AB=1，PA=，连接CE并延长交AD于F.（1）求证：AD⊥平面CFG；（2）求平面BCP与平面DCP的夹角的余弦值.【答案】（1）见解析（2）【解析】（1）因为△DAB ≌△DCB，EA=EB=AB=1，所以△ECB是等边，,（2）建立空间坐标系如图，取向观点的坐标为, 向量设平面PBC的法向量平面PDC的法向量则【考点】本题主要考查空间垂直关系的证明、平行关系的运用，考查空间角的求解方法，考查空间想象能力、推理论证能力、计算能力.9.如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.（1）证明：PA⊥BD；（2）若PD=AD，求二面角A-PB-C的余弦值。

空间向量练习及答案解析

空间向量练习一、选择题(共15小题，每小题4.0分,共60分)1.已知平面α的一个法向量是(2，－1,1)，α∥β，则下列向量可作为平面β的一个法向量的是() A． (4,2，－2) B． (2,0,4) C． (2，－1，－5) D． (4，－2,2)2.如图，过边长为1的正方形ABCD的顶点A作线段EA⊥平面AC，若EA＝1，则平面ADE与平面BCE所成的二面角的大小是()A． 120° B． 45° C． 150° D． 60°3.已知＝(1,2,3)，＝(2,1,2)，＝(1,1,2)，点Q在直线OP上运动，则当·取得最小值时，点Q的坐标为()A． B． C． D．4.将正方形ABCD沿对角线BD折成直二面角A－BD－C，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD所成的角为60°；④AB与CD所成的角为60°.其中错误的结论是()A．① B．② C．③ D．④5.如图所示，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB＝BC＝AA1，∠ABC＝90°，点E，F分别是棱AB，BB1的中点，则直线EF和BC1的夹角是()A． 45° B． 60° C． 90° D． 120°6.已知在空间四面体O－ABC中，点M在线段OA上，且OM＝2MA，点N为BC中点，设＝a，＝b，＝c，则等于()A．a＋b－ c B．－a＋b＋ c C．a－b＋ c D．a＋b－c7.已知在棱长为2的正方体ABCD－A1B1C1D1中，E是DC的中点，建立如图所示的空间直角坐标系，则AB1与D1E所成角的余弦值为()A． B． C．－ D．－8.如图所示，在正方体ABCD－A1B1C1D1中，M，N，P分别是棱CC1，BC，A1B1上的点，若∠B1MN＝90°，则∠PMN的大小()A．等于90° B．小于90° C．大于90° D．不确定9.如图，S是正三角形ABC所在平面外一点，M，N分别是AB和SC的中点，SA＝SB＝SC，且∠ASB＝∠BSC＝∠CSA＝90°，则异面直线SM与BN所成角的余弦值为()A．－ B． C．－ D．10.已知平面α内两向量a＝(1,1,1)，b＝(0,2，－1)且c＝ma＋nb＋(4，－4,1)．若c为平面α的法向量，则m ，n 的值分别为( ) A ．－1,2 B ． 1，－2 C ． 1,2 D ．－1，－211.如图，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，底面ABC 是等腰直角三角形，∠ACB ＝90°，侧棱AA 1＝2，D ，E 分别是CC 1与A 1B 的中点，点E 在平面ABD 上的射影是△ABD 的重心G ，则A 1B 与平面ABD 所成角的正弦值为( )A ．√23B ．√73C ．√32D ．√3712.如图，在直三棱柱ABC －A 1B 1C 1中，∠ACB ＝90°，2AC ＝AA 1＝BC ＝2，若二面角B 1－DC －C 1的大小为60°，则AD 的长为( ) A ．√2 B ．√3 C ． 2 D ．√2213.三棱锥A －BCD 中，平面ABD 与平面BCD 的法向量分别为n 1，n 2，若〈n 1，n 2〉＝π3，则二面角A －BD －C 的大小为( ) A ．π3 B ．2π3 C ．π3或2π3D ．π3或－π314.已知AB ⃗⃗⃗⃗⃗ ＝(1,5，－2)，BC ⃗⃗⃗⃗⃗ ＝ (3,1，z )，若AB ⃗⃗⃗⃗⃗ ⊥BC ⃗⃗⃗⃗⃗ ，BP ⃗⃗⃗⃗⃗ ＝(x －1，y ，－3)，且BP ⊥平面ABC ，则BP ⃗⃗⃗⃗⃗ 等于( ) A ．(407,157,−3) B ．(337,157,−3) C ．(−407,−157,−3) D ．(337,−157,−3)15.如图，在平行六面体ABCD －A 1B 1C 1D 1中，点M ，P ，Q 分别为棱AB ，CD ，BC 的中点，平行六面体的各棱长均相等．给出下列结论：①A 1M ∥D 1P ；②A 1M ∥B 1Q ；③A 1M ∥平面DCC 1D 1；④A 1M ∥平面D 1PQB 1.这四个结论中正确的个数为( ) A ． 1 B ． 2 C ． 3 D ． 4二、填空题(共6小题，每小题4.0分,共24分)16.如图所示，已知正四面体A-BCD 中，AE ＝AB ，CF ＝CD ，则直线DE 和BF 所成角的余弦值为________．17.已知a ＝(3，－2，－3)，b ＝(－1，x －1,1)，且a 与b 的夹角为钝角，则x 的取值范围是________．18.如图，平面PAD ⊥平面ABCD ，ABCD 为正方形，∠PAD ＝90°，且PA ＝AD ＝2，E ，F 分别是线段PA ，CD 的中点，则异面直线EF 与BD 所成角的余弦值为________． 19.如图，在三棱柱ABC －A 1B 1C 1中，所有棱长均为1，且AA 1⊥底面ABC ，则点B 1到平面ABC 1的距离为________．20.如下图所示，PD 垂直于正方形ABCD 所在平面，AB ＝2，E 为PB 的中点，cos 〈DP⃗⃗⃗⃗⃗ ，AE ⃗⃗⃗⃗⃗ 〉＝√33，若以DA ，DC ，DP 所在直线分别为x ，y ，z 轴建立空间直角坐标系，则点E 的坐标为________．21.已知点P 是平行四边形ABCD 所在的平面外一点，如果AB⃗⃗⃗⃗⃗ ＝(2，－1，－4)，AD ⃗⃗⃗⃗⃗ ＝(4,2,0)，AP ⃗⃗⃗⃗⃗ ＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③AP ⃗⃗⃗⃗⃗ 是平面ABCD 的法向量；④AP ⃗⃗⃗⃗⃗ ∥BD ⃗⃗⃗⃗⃗⃗ .其中正确的是____________．三、解答题(共6小题，每小题11.0分,共66分) 22.如图所示，已知四棱锥P －ABCD 的底面为直角梯形，AB ∥DC ，∠DAB ＝90°，PA ⊥底面ABCD ，且PA ＝AD ＝DC ＝12AB ＝1，M 是PB 的中点．(1)证明：面PAD ⊥面PCD ；(2)求AC 与PB 所成角的余弦值； (3)求面AMC 与面BMC 所成二面角的余弦值．23.如下图所示，在三棱锥P －ABC 中，PA ⊥底面ABC ，PA ＝AB ，∠ABC ＝60°，∠BCA ＝90°，点D ，E 分别在棱PB ，PC 上，且DE ∥BC . (1)求证：BC ⊥平面PAC ；(2)当D 为PB 的中点时，求AD 与平面PAC 所成的角的正弦值； (3)是否存在点E ，使得二面角A －DE －P 为直二面角？并说明理由．24.如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，点E ，F 是棱BC ，CD 的中点，求：(1)直线DF 与B 1F 所成角的余弦值；(2)二面角C 1－EF －A 的余弦值．25.如图，在四棱锥S－ABCD中，底面ABCD是直角梯形，AB垂直于AD和BC，侧棱SB⊥平面ABCD，且SB＝AB＝AD＝1，BC＝2.(1)求SA与CD所成的角；(2)求平面SCD与平面SAB所成的锐二面角的余弦值．26.如下图，四棱柱ABCD－A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA1＝AB＝2，E为棱AA1的中点．(1)证明B1C1⊥CE；(2)求二面角B1－CE－C1的正弦值．27.如下图，在正四棱柱ABCD－A1B1C1D1中，AB＝2，AA1＝4，E为BC的中点，F为CC1的中点．(1)求EF与平面ABCD所成的角的余弦值；(2)求二面角F－DE－C的余弦值．空间向量练习答案解析1.【答案】D【解析】∵α∥β，∴β的法向量与α的法向量平行，又∵(4，－2,2)＝2(2，－1,1)，故选D.2.【答案】B【解析】以A为坐标原点，分别以AB，AD，AE所在直线为x轴，y轴，z轴，建立如图所示的空间直角坐标系Axyz，则E(0,0,1)，B(1,0,0)，C(1,1,0)，＝(1,0，－1)，＝(1,1，－1)．设平面BCE的法向量为n＝(x，y，z)，则即可取n＝(1,0,1)．又平面EAD的法向量为＝(1,0,0)，所以cos〈n，〉＝＝，故平面ADE与平面BCE所成的二面角为45°.3.【答案】C【解析】设Q(x，y，z)，因Q在上，故有∥，设＝λ(λ∈R)，可得x＝λ，y＝λ，z＝2λ，则Q(λ，λ，2λ)，＝(1－λ，2－λ，3－2λ)，＝(2－λ，1－λ，2－2λ)，所以·＝6λ2－16λ＋10＝62－，故当λ＝时，·取最小值，此时Q.4.【答案】C【解析】如图所示，取BD的中点O，以点O为坐标原点，OD，OA，OC所在直线分别为x轴，y轴，z轴，建立空间直角坐标系Oxyz，设正方形ABCD边长为，则D(1,0,0)，B(－1,0,0)，C(0,0,1)，A(0,1,0)，所以＝(0，－1,1)，＝(2,0,0)，·＝0，故AC⊥BD.①正确．又||＝，||＝，||＝，所以△ACD为等边三角形．②正确．对于③，为面BCD的一个法向量，cos〈，〉＝＝＝＝－.所以AB与OA所在直线所成的角为45°，所以AB与平面BCD所成角为45°.故③错误．又cos〈，〉＝＝＝－.因为异面直线所成的角为锐角或直角，所以AB与CD所成角为60°.故④正确．5.【答案】B【解析】不妨设AB＝BC＝AA1＝1，则＝－＝(－)，＝＋，∴||＝|－|＝，||＝，·＝(－)·(＋)＝，∴cos〈，〉＝＝＝，∴〈，〉＝60°，即异面直线EF与BC1的夹角是60°.6.【答案】B【解析】＝－＝(＋)－＝b＋c－a.7.【答案】A【解析】∵A(2,2,0)，B1(2,0,2)，E(0,1,0)，D1(0,2,2)，∴＝(0，－2,2)，＝(0,1,2)，∴||＝2，||＝，·＝0－2＋4＝2，∴cos〈，〉＝＝＝，又异面直线所成角的范围是，∴AB1与ED1所成角的余弦值为.8.【答案】A【解析】A1B1⊥平面BCC1B1，故A1B1⊥MN，·＝(＋)·＝·＋·＝0，∴MP⊥MN，即∠PMN＝90°.9.【答案】B【解析】不妨设SA＝SB＝SC＝1，以S为坐标原点，，，所在直线分别为x轴，y轴，z 轴，建立空间直角坐标系Sxyz，则相关各点坐标为A(1,0,0)，B(0,1,0)，C(0,0,1)，S(0,0,0)，M，N.因为＝，＝，所以||＝，||＝，·＝－，cos〈，〉＝＝－，因为异面直线所成的角为锐角或直角，所以异面直线SM 与BN 所成角的余弦值为.10.【答案】A【解析】 c ＝ma ＋nb ＋(4，－4,1)＝(m ，m ，m )＋(0,2n ，－n )＋(4，－4,1)＝(m ＋4，m ＋2n －4，m －n ＋1)，由c 为平面α的法向量，得即解得11.【答案】A【解析】∵侧棱与底面垂直，∠ACB ＝90°，所以分别以CA ，CB ，CC 1所在直线为x 轴、y 轴、z 轴，建立如图空间直角坐标系，设CA ＝CB ＝a ，则A (a,0,0)，B (0，a,0)，A 1(a,0,2)，D (0,0,1)， ∴E (a 2,a2,1)，G (a 3,a 3,13)，GE ⃗⃗⃗⃗⃗ ＝(a 6,a 6,23)，BD ⃗⃗⃗⃗⃗⃗ ＝(0，－a,1)， ∵点E 在平面ABD 上的射影是△ABD 的重心G ，∴GE ⃗⃗⃗⃗⃗ ⊥平面ABD ，∴GE ⃗⃗⃗⃗⃗ ·BD ⃗⃗⃗⃗⃗⃗ ＝0，解得a ＝2，∴GE ⃗⃗⃗⃗⃗ ＝(13,13,23)，BA 1⃗⃗⃗⃗⃗⃗⃗ ＝(2，－2,2)，∵GE ⃗⃗⃗⃗⃗ ⊥平面ABD ，∴GE ⃗⃗⃗⃗⃗ 为平面ABD 的一个法向量，又cos 〈GE ⃗⃗⃗⃗⃗ ，BA 1⃗⃗⃗⃗⃗⃗⃗ 〉＝GE ⃗⃗⃗⃗⃗ ·BA 1⃗⃗⃗⃗⃗⃗⃗⃗ |GE ⃗⃗⃗⃗⃗ ||BA 1⃗⃗⃗⃗⃗⃗⃗⃗ |＝43√63×2＝√23，∴A 1B 与平面ABD 所成角的正弦值为√23，故选A.12.【答案】A【解析】如下图，以C 为坐标原点，CA ，CB ，CC 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则C (0,0,0)，A (1,0,0)，B 1(0,2,2)，C 1(0,0,2)设AD ＝a ，则D 点坐标为(1,0，a )，CD ⃗⃗⃗⃗⃗ ＝(1,0，a )，CB 1⃗⃗⃗⃗⃗⃗⃗ ＝(0,2,2)，设平面B 1CD 的一个法向量为m ＝(x ，y ，z )，则{m ·CB 1⃗⃗⃗⃗⃗⃗⃗ =0,m ·CD⃗⃗⃗⃗⃗ =0⇒{2y +2z =0,x +az =0,令z ＝－1，得m ＝(a,1，－1)，又平面C 1DC 的一个法向量为n ＝(0,1,0)，则由cos 60°＝m·n|m ||n |，得1√a 2+1＝12，即a ＝√2，故AD ＝√2. 13.【答案】C【解析】如图所示，当二面角A －BD －C 为锐角时，它就等于〈n 1，n 2〉＝π3；当二面角A －BD －C 为钝角时，它应等于π－〈n 1，n 2〉＝π－π3＝2π3. 14.【答案】D【解析】因为AB ⃗⃗⃗⃗⃗ ⊥BC ⃗⃗⃗⃗⃗ ，所以AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ ＝0，即1×3＋5×1＋(－2)z ＝0，所以z ＝4，因为BP ⊥平面ABC ，所以BP⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ，且BP ⃗⃗⃗⃗⃗ ⊥BC ⃗⃗⃗⃗⃗ ，即1×(x －1)＋5y ＋(－2)×(－3)＝0，且3(x －1)＋y ＋(－3)×4＝0.解得x ＝407，y ＝－157，于是BP ⃗⃗⃗⃗⃗ ＝(337,−157,−3).15.【答案】C【解析】因为A 1M ⃗⃗⃗⃗⃗⃗⃗⃗ ＝A 1A ⃗⃗⃗⃗⃗⃗⃗ ＋AM ⃗⃗⃗⃗⃗⃗ ＝A 1A ⃗⃗⃗⃗⃗⃗⃗ ＋12AB ⃗⃗⃗⃗⃗ ，D 1P ⃗⃗⃗⃗⃗⃗⃗ ＝D 1D ⃗⃗⃗⃗⃗⃗⃗⃗ ＋DP ⃗⃗⃗⃗⃗ ＝A 1A ⃗⃗⃗⃗⃗⃗⃗ ＋12AB ⃗⃗⃗⃗⃗ ，所以A 1M ⃗⃗⃗⃗⃗⃗⃗⃗ ∥D 1P ⃗⃗⃗⃗⃗⃗⃗ ，从而A 1M ∥D 1P ，可得①③④正确．又B 1Q 与D 1P 不平行，故②不正确．故选C. 16.【答案】【解析】＝＋＝＋，＝＋＝＋，所以cos 〈，〉＝＝＝＝.17.【答案】 B【解析】若两向量的夹角为钝角，则a ·b ＜0，且a 与b 不共线，故3×(－1)＋(－2)×(x －1)＋(－3)×1＜0，且x ≠，解得x ＞－2，且x ≠，故选B. 18.【答案】【解析】以A 为坐标原点，AB ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示空间直角坐标系Axyz ，则E (0,0,1)，F (1,2,0)，B (2,0,0)，D (0,2,0)．＝(1,2，－1)，＝(－2,2,0)，故cos 〈，〉＝＝.19.【答案】√217【解析】建立如图所示的空间直角坐标系，则A (√32,12,0)，B (0,1,0)，B 1(0,1,1)，C 1(0,0,1)，则C 1A ⃗⃗⃗⃗⃗⃗⃗ ＝(√32,12,−1)，C 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝(0,1,0)，C 1B ⃗⃗⃗⃗⃗⃗⃗ ＝(0,1，－1)，设平面ABC 1的一个法向量为n ＝(x ，y,1)，则有{C 1A ⃗⃗⃗⃗⃗⃗⃗ ·n =√32x +12y −1=0,C 1B ⃗⃗⃗⃗⃗⃗⃗ ·n =y −1=0.解得n ＝(√33,1,1)，则所求距离为|C 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·n |n ||＝1√13+1+1＝√217.20.【答案】(1,1,1)【解析】设PD ＝a (a ＞0)，则A (2,0,0)，B (2,2,0)，P (0,0，a )，E (1,1,a2).∴DP ⃗⃗⃗⃗⃗ ＝(0,0，a )，AE⃗⃗⃗⃗⃗ ＝(−1,1,a2)，∵cos 〈DP ⃗⃗⃗⃗⃗ ，AE ⃗⃗⃗⃗⃗ 〉＝√33，∴a 22＝a √2+a 24·√33，∴a ＝2.∴E 的坐标为(1,1,1)．21.【答案】①②③【解析】由于AP ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ ＝－1×2＋(－1)×2＋(－4)×(－1)＝0， AP ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ ＝4×(－1)＋2×2＋0×(－1)＝0，所以①②③正确． 22.【答案】因为PA ⊥AD ，PA ⊥AB ，AD ⊥AB ，以A 为坐标原点，AD 长为单位长度，如图建立空间直角坐标系，则各点坐标为A (0,0,0)，B (0,2,0)，C (1,1,0)，D (1,0,0)，P (0,0,1)，M (0,1,12)， (1)∵AP ⃗⃗⃗⃗⃗ ＝(0,0,1)，DC ⃗⃗⃗⃗⃗ ＝(0,1,0)，故AP ⃗⃗⃗⃗⃗ ·DC ⃗⃗⃗⃗⃗ ＝0，∴AP ⃗⃗⃗⃗⃗ ⊥DC ⃗⃗⃗⃗⃗ ，∴AP ⊥DC ，又由题设知：AD ⊥DC ，且AP 与AD 是平面PAD 内的两条相交直线，由此得DC ⊥面PAD ，又DC 在面PCD 上，故面PAD ⊥面PCD ； (2)∵AC⃗⃗⃗⃗⃗ ＝(1,1,0)，PB ⃗⃗⃗⃗⃗ ＝(0,2，－1)， ∴|AC ⃗⃗⃗⃗⃗ |＝√2，|PB ⃗⃗⃗⃗⃗ |＝√5，AC ⃗⃗⃗⃗⃗ ·PB⃗⃗⃗⃗⃗ ＝2，∴cos 〈AC ⃗⃗⃗⃗⃗ ，PB ⃗⃗⃗⃗⃗ 〉＝√105，由此得AC 与PB 所成角的余弦值为√105；(3)在MC 上取一点N (x ，y ，z )，则存在λ∈R ，使NC ⃗⃗⃗⃗⃗ ＝λMC ⃗⃗⃗⃗⃗⃗ ，NC ⃗⃗⃗⃗⃗ ＝(1－x,1－y ，－z )，MC ⃗⃗⃗⃗⃗⃗ ＝(1,0,−12)，∴x ＝1－λ，y ＝1，z ＝12λ.要使AN ⊥MC ，只需AN ⃗⃗⃗⃗⃗⃗ ·MC ⃗⃗⃗⃗⃗⃗ ＝0，即x －12z ＝0，解得λ＝45，可知当λ＝45时，N 点坐标为(15,1,25)，能使AN ⃗⃗⃗⃗⃗⃗ ·MC⃗⃗⃗⃗⃗⃗ ＝0，此时，AN ⃗⃗⃗⃗⃗⃗ ＝(15,1,25)，BN ⃗⃗⃗⃗⃗⃗ ＝(15,−1,25)，由AN ⃗⃗⃗⃗⃗⃗ ·MC ⃗⃗⃗⃗⃗⃗ ＝0，BN ⃗⃗⃗⃗⃗⃗ ·MC ⃗⃗⃗⃗⃗⃗ ＝0，得AN ⊥MC ，BN ⊥MC ， ∴∠ANB 为所求二面角的平面角，∵|AN⃗⃗⃗⃗⃗⃗ |＝√305，|BN ⃗⃗⃗⃗⃗⃗ |＝√305，AN ⃗⃗⃗⃗⃗⃗ ·BN ⃗⃗⃗⃗⃗⃗ ＝－45，∴cos 〈AN ⃗⃗⃗⃗⃗⃗ ，BN ⃗⃗⃗⃗⃗⃗ 〉＝－23，故所求的二面角的余弦值为－23.23.【答案】以A 为原点，AB ⃗⃗⃗⃗⃗ ，AP ⃗⃗⃗⃗⃗ 分别为y 轴、z 轴的正方向，过A 点且垂直于平面PAB 的直线为x 轴，建立空间直角坐标系Axyz ，设PA ＝a ，由已知可得：A (0,0,0)，B (0，a ，0)，C (√34a,34a,0)，P (0,0，a )．(1)AP⃗⃗⃗⃗⃗ ＝(0,0，a )，BC ⃗⃗⃗⃗⃗ ＝(√34a,−a 4,0)，∴BC ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ ＝0，∴BC ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ ，∴BC ⊥AP ，又∵∠BCA ＝90°，∴BC ⊥AC ，∴BC ⊥平面PAC .(2)∵D 为PB 的中点，DE ∥BC ，∴E 为PC 的中点，∴D (0,a 2,a2)，E (√38a,38a,a 2)，∴由(1)知，BC ⊥平面PAC ，∴DE ⊥平面PAC ，垂足为点E ， ∴∠DAE 是AD 与平面PAC 所成的角，∵AD ⃗⃗⃗⃗⃗ ＝(0,a 2,a 2)，AE ⃗⃗⃗⃗⃗ ＝(√38a,38a,a 2)，∴cos ∠DAE ＝AD ⃗⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗|AD ⃗⃗⃗⃗⃗⃗ ||AE ⃗⃗⃗⃗⃗ |＝√144， ∴AD 与平面PAC 所成的角的正弦值为√24.(3)∵DE ∥BC ，又由(1)知BC ⊥平面PAC ，∴DE ⊥平面PAC ，又∵AE ⊂平面PAC ，PE ⊂平面PAC ，∴DE ⊥AE ，DE ⊥PE ，∴∠AEP 为二面角A －DE －P 的平面角． ∵PA ⊥底面ABC ，∴PA ⊥AC ，∴∠PAC ＝90°，∴在棱PC 上存在一点E ，使得AE ⊥PC ，这时∠AEP ＝90°，故存在点E ，使得二面角A －DE －P 是直二面角．24.【答案】如图，以A 为坐标原点，建立空间直角坐标系Axyz ，则D (0,2,0)，E (2,1,0)，F (1,2,0)，B 1(2,0,2)，C 1(2,2,2)，(1)因为DE ⃗⃗⃗⃗⃗ ＝(2，－1,0)，B 1F ⃗⃗⃗⃗⃗⃗⃗ ＝(－1,2，－2)，所以cos 〈DE ⃗⃗⃗⃗⃗ ，B 1F ⃗⃗⃗⃗⃗⃗⃗ 〉＝DE ⃗⃗⃗⃗⃗⃗ ·B 1F ⃗⃗⃗⃗⃗⃗⃗⃗ |DE ⃗⃗⃗⃗⃗⃗ ||B 1F ⃗⃗⃗⃗⃗⃗⃗⃗ |＝−43√5＝－4√515，所以直线DE 与B 1F 所成角的余弦值为4√515； (2)因为C 1E ⃗⃗⃗⃗⃗⃗⃗ ＝(0，－1，－2)，EF ⃗⃗⃗⃗⃗ ＝(－1,1,0)，设平面C 1EF 的一个法向量为n ＝(x ，y,1)，则由{n ·C 1E ⃗⃗⃗⃗⃗⃗⃗ =0,n ·EF ⃗⃗⃗⃗⃗ =0,可得{−y −2=0,−x +y =0, 解得x ＝y ＝－2，所以n ＝(－2，－2,1)，又AA 1⃗⃗⃗⃗⃗⃗⃗ ＝(0,0,2)是平面AEF 的一个法向量，所以cos 〈AA 1⃗⃗⃗⃗⃗⃗⃗ ，n 〉＝n·AA1⃗⃗⃗⃗⃗⃗⃗⃗ |n ||AA 1⃗⃗⃗⃗⃗⃗⃗⃗ |＝22×3＝13，观察图形，可知二面角C 1－EF －A 为钝角，所以二面角C 1－EF －A 的余弦值为－13. 25.【答案】(1)建立如图所示的空间直角坐标系，则B (0,0,0)，S (0,0,1)，A (1,0,0)，C (0,2,0)，D (1,1,0)，SA ⃗⃗⃗⃗⃗ ＝(1,0，－1)， CD⃗⃗⃗⃗⃗ ＝(1，－1,0)，因为cos 〈SA ⃗⃗⃗⃗⃗ ，CD ⃗⃗⃗⃗⃗ 〉＝SA ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗|SA⃗⃗⃗⃗⃗ ||CD ⃗⃗⃗⃗⃗ |＝12，所以SA 与CD 所成的角为60°； (2)设平面SCD 的法向量为n 1＝(x ，y ，z )，又SC⃗⃗⃗⃗ ＝(0,2，－1)，{n 1·SC⃗⃗⃗⃗ =0,n 1·CD⃗⃗⃗⃗⃗ =0,所以{2y −z =0,x −y =0, 令x ＝1，则n 1＝(1,1,2)，因为BC ⊥平面SAB ，第 11 页共 11 页所以平面SAB 的一个法向量为n 2＝(0,1,0)，cos 〈n 1，n 2〉＝√66，所以平面SCD 与平面SAB 所成的锐二面角的余弦值为√66. 26.【答案】如下图，以点A 为原点建立空间直角坐标系，依题意得A (0,0,0)，B (0,0,2)，C (1,0,1)，B 1(0,2,2)，C 1(1,2,1)，E (0,1,0)．(1)易得B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝(1,0，－1)，CE ⃗⃗⃗⃗⃗ ＝(－1,1，－1)，于是B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·CE⃗⃗⃗⃗⃗ ＝0，所以B 1C 1⊥CE ；(2)B 1C ⃗⃗⃗⃗⃗⃗⃗ ＝(1，－2，－1)，设平面B 1CE 的法向量m ＝(x ，y ，z )，则{m ·B 1C ⃗⃗⃗⃗⃗⃗⃗ =0,m ·CE ⃗⃗⃗⃗⃗ =0,即{x −2y −z =0,−x +y −z =0, 消去x ，得y ＋2z ＝0，不妨令z ＝1，可得一个法向量为m ＝(－3，－2,1)，由(1)，B 1C 1⊥CE ，又CC 1⊥B 1C 1，可得B 1C 1⊥平面CEC 1，故B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝(1,0，－1)为平面CEC 1的一个法向量，于是cos 〈m ，B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ 〉＝m·B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |m ||B 1C 1|＝−4√14×√2＝－2√77，从而sin 〈m ，B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ 〉＝√217，所以二面角B 1－CE －C 1的正弦值为√217. 27.【答案】建立如下图所示的空间直角坐标系D-xyz ，则D (0,0,0)，A (2,0,0)，C (0,2,0)，B (2,2,0)，E (1,2,0)，F (0,2,2)，(1)EF⃗⃗⃗⃗⃗ ＝(－1,0,2)，易得平面ABCD 的一个法向量为n ＝(0,0,1)，设EF ⃗⃗⃗⃗⃗ 与n 的夹角为θ，则cos θ＝EF ⃗⃗⃗⃗⃗ ·n |EF ⃗⃗⃗⃗⃗ ||n|＝25√5，∴EF 与平面ABCD 所成的角的余弦值为2√55； (2)EF ⃗⃗⃗⃗⃗ ＝(－1,0,2)，DF ⃗⃗⃗⃗⃗ ＝(0,2,2)，设平面DEF 的一个法向量为m ，则m ·DF ⃗⃗⃗⃗⃗ ＝0，m ·EF⃗⃗⃗⃗⃗ ＝0，可得m ＝(2，－1,1)，∴cos 〈m ，n 〉＝m·n|m ||n |＝√66，∴二面角F －DE －C 的余弦值为√66.。

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.如图，在四棱锥中，底面，，，，，点为棱的中点.（Ⅰ）证明：；（Ⅱ）若为棱上一点，满足，求二面角的余弦值.【答案】（Ⅰ）详见解析；（Ⅱ）余弦值为.【解析】思路一：坐标法.依题意，以点为原点建立空间直角坐标系（如图），写出各点的坐标，利用空间向量即可解决问题.思路二：几何法.（Ⅰ）如图，取中点，连接，.易得四边形为矩形，从而使问题得证.（Ⅱ）由于，那么BF在平面ABCD内的射影与AC垂直，故考虑作出BF在平面ABCD 内的射影.在中，过点作交于点.由题设可得，从而得，.在平面内，作交于点，于是.显然为二面角的平面角. 在三角形PAG中，由余弦定理可得二面角的余弦值.试题解析：解法一：坐标法.依题意，以点为原点建立空间直角坐标系（如图），可得，，，.由为棱的中点，得.（Ⅰ）向量，，故. 所以，.（Ⅱ）向量，，，.由点在棱上，设，.故.由，得，因此，，解得.即.设为平面的法向量，则即不妨令，可得为平面的一个法向量取平面的法向量，则.易知，二面角是锐角，所以其余弦值为.解法二：几何法.（Ⅰ）如图，取中点，连接，.由于分别为的中点，故，且，又由已知，可得且，故四边形为平行四边形，所以.因为底面，故，而，从而平面，因为平面，于是，又，所以.（Ⅱ）如图，在中，过点作交于点.因为底面，故底面，从而.又，得平面，因此.在底面内，可得，.在平面内，作交于点，于是.由于，故，所以四点共面.由，，得平面，故.所以为二面角的平面角.在中，，，，由余弦定理可得，在三角形PAG中，由余弦定理得.所以，二面角的余弦值为.【考点】1、空间直线的垂直关系；2、二面角.2.在如图所示的多面体中，四边形和都为矩形.（Ⅰ）若，证明：直线平面；（Ⅱ）是否存在过的平面，使得直线平行，若存在请作出平面并证明，若不存在请说明理由.【答案】（Ⅰ）见解析；（Ⅱ）存在，证明见解析【解析】（Ⅰ）由四边形和都为矩形知，⊥AB，⊥AC，由线面垂直判定定理知⊥面ABC，由线面垂直定义知⊥BC，又因为AC⊥BC，由线面垂直判定定理知，BC⊥面；（Ⅱ）取AB的中点为M，连结交于D，连结DE，显然E是的中点，根据三角形中位线定理得，DE∥，又由于DE在面过的平面内，根据线面平行的判定定理知和该平面平行.试题解析：（Ⅰ）证明：因为四边形和都是矩形，所以 2分因为为平面内的两条相交直线，所以 4分因为直线平面，所以又由已知，为平面内的两条相交直线，所以平面 7分（Ⅱ）存在 8分连接，设，取线段AB的中点M，连接.则平面为为所求的平面. 1１分由作图可知分别为的中点，所以 13分又因为因此 14分考点: 空间线面垂直垂直的判定与性质；线面平行的判定；推理论证能力3.平面α经过三点A(－1,0,1)，B(1,1,2)，C(2，－1,0)，则下列向量中与平面α的法向量不垂直的是()A．(，－1，－1)B．(6，－2，－2)C．(4,2,2)D．(－1,1,4)【答案】D【解析】设平面α的法向量为n，则n⊥，n⊥，n⊥，所有与 (或、)平行的向量或可用与线性表示的向量都与n垂直，故选D.4.如图所示，已知空间四边形OABC中，|OB|＝|OC|，且∠AOB＝∠AOC，则、夹角θ的余弦值为()A．0B．C．D．【答案】A【解析】设＝a，＝b，＝c.由已知条件∠AOB＝∠AOC，且|b|＝|c|，·＝a·(c－b)＝a·c－a·b＝|a||c|cos∠AOC－|a||b|cos∠AOB＝0，∴cosθ＝0.故选A.5.若向量a＝(1,1，x)，b＝(1,2,1)，c＝(1,1,1)，满足条件(c－a)·(2b)＝－2，则x＝________.【答案】2【解析】c－a＝(0,0,1－x)，2b＝(2,4,2)，由(c－a)·(2b)＝－2，得(0,0,1－x)·(2,4,2)＝－2，即2(1－x)＝－2，解得x＝2.6.如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：(1)·；(2)·；(3)EG的长；(4)异面直线AG与CE所成角的余弦值．【答案】（1）（2）－（3）（4）【解析】解：设＝a，＝b，＝c.则|a|＝|b|＝|c|＝1，〈a，b〉＝〈b，c〉＝〈c，a〉＝60°.＝BD＝c－a，＝－a，＝b－c，(1)·＝(c－a)·(－a)＝a2－a·c＝；(2)·＝ (c－a)·(b－c)＝ (b·c－a·b－c2＋a·c)＝－；(3)＝＋＋＝a＋b－a＋c－b＝－a＋b＋ c.||2＝a2＋b2＋c2－a·b＋b·c－c·a＝.即||＝，所以EG的长为.(4)设、的夹角为θ.＝b＋c，＝＋＝－b＋a，cosθ＝＝－，由于异面直线所成角的范围是(0°，90°]，所以异面直线AG与CE所成角的余弦值为.7.已知点A(1，t，－1)关于x轴的对称点为B，关于xOy平面的对称点为C，则BC中点D的坐标为________．【答案】(1,0,1)【解析】因为A(1，t，－1)关于x轴的对称点为B(1，－t,1)，关于xOy平面的对称点为C(1，t,1)，所以BC中点D的坐标为(，，)，即D(1,0,1)．8.直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成的角的余弦值为（）A．B．C．D．【答案】C【解析】以C为原点，直线CA为x轴，直线CB为y轴，直线为轴，则设CA=CB=1，则，，A（1，0，0），，故，，所以，故选C.【考点】本小题主要考查利用空间向量求线线角，考查空间向量的基本运算，考查空间想象能力等数学基本能力，考查分析问题与解决问题的能力.9.如图，已知四棱锥P-ABCD的底面ABCD是菱形，且PC⊥平面ABCD，PC＝AC＝2,E是PA 的中点。

(完整版)空间向量小题(答案)

第3章（考试时间90分钟，满分120分）、选择题（本大题共10小题，每小题5分，共50分•在每小题给出的四个选项中，只有一项是符合题目要求的）1 .设 a = （x, 2y, 3） , b = （1,1,6），且 a // b ,则 x + y 等于（）1A. 2C.23解析： T a // b ,「. x = 2y = 6,3•••x +y= 4.答案： B2 .若 a = （0,1，- 1）, b = （1,1,0），且（a +入b ）丄a ,则实数入的值是（A . - 1 D.— 2解析： a + 入 b = （0,1 , — 1） + （入，入，0）=（入，1 + 入，一 1）, 因为（a + 入b ） • a =（入，1+ 入，一1） • （0,1，— 1） =1 + 入 + 1 = 2 + 入=0, 所以X = — 2. 答案： D23 .若向量（1,0 , z ）与向量（2,1,0）的夹角的余弦值为——，则z 等于（）A . 0B . 12 ______ 1 + z 2 •1 = . 1 + z 2,「. z = 0. 答案： A4.若 a =e 1 + e 2+ e 3, b = e 1 — e 2— e 3, c = e 1 — e 2, d = 3e 1 + 2e 2 + e 3（｛e 1, e 2, e 3｝为空间的一■解析：由题知——2,寸1+ Z 2.^5yJ 5C.— 1D. 2 B .4 D. 2B . 0C. 1x= 21个基底），且d = xa + yb + zc ,贝U x , y , z 分别为（)5 B. J ，A C = X B+B CT CC=AB+ B C- c T C,所以 x = 1,2 y = 1,3 z =— 1, 1 1所以 x = 1, y = 2 z = — 3,C -2,i 2, 1D .5，解析:d =xa + yb + zc = x (e i + e ?+ e 3)+ y (e i — e 2— e 3)+ z (e i — e 2).f5 3••• {x + y + z = 3, x — y — z = 2, x — y = 1,/• x =㊁, y = 2， z =— 1答案： A5.若直线l 的方向向量为a = （1 , — 1,2），平面a 的法向量为U = （ — 2,2 , — 4），则（） A . l //a C. l ?aB . l 丄 a D. I 与a 斜交解析： ■/ u =— 2a ,「. u // a ,• l 丄 a ，故选B. 答案：BABC — A B' C' D 中，若 AC = x XB+ 2y B C > 3zC ^ C,贝U x + y + z 等A . 17 B.7C.6解析:如图,6 .在平行六面休答案：B成的角的余弦值为(A』10C迈.10答案：C8.已知空间四个点A(1,1,1),耳一4,0,2) , q —3, - 1,0),D( —1,0,4)，则直线AD与平面ABC所成的角为()A. 60°C. 30°解析：设门=(x, y, 1)是平面ABC的一个法向量.1 3一4x - 2y—2= 0, • x = 2，y=- 2,72 1 ,贝U sin 0 == 7 = 2, - 0= 30° .故选 C.I AD I n| 7 2答案：C9•在正方体ABC—ABCD中，平面ABD与平面CBD所成二面角的余弦值为1A.—2解析:2 3• n= 2，一2, 1 .••• AB= ( - 5, - 1,1) ,AC= (—4,—2，一1),又AD= ( —2, —1,3) ，设AD与平面ABC所成的角为0 ,7 .已知正四棱柱ABC B ABCD中，AA= 2AB E为AA的中点，则异面直线BE与CD所1B.53D.—5解析：以DA DC DD所在直线为x轴, y轴，z轴建立空间直角坐标系，则B(1,1,0),曰1,0,1) ，C(0,1,0)，D(0,0,2).•- Bfe= (0，- 1,1) ,CD= (0，- 1,2).• cos〈BE CD〉BL CDI B E i CD| .2x )5B. 45°D. 90°••• { —5x—y + 1 = 0,I AD •叫1B.-3—— 14,/：/A以点D 为原点，DA DC DD 为x 轴，y 轴，z 轴建立空间直角坐标系，设正方体的棱长为1 则 AC= ( — 1,1 , - 1) , AC = ( — 1,1,1).又可以证明 AC 丄平面BCD, AG 丄平面ABD,又cos 〈AC , AC 〉=亍结合图形可知平面31ABD 与平面CBD 所成二面角的余弦值为故选B.答案： B10.如右图所示，在棱长为 1的正方体ABC — ABCD 中，E 、F 分别为棱AA 、BB 的中点，G 为棱AB 上的一点，且 A G= X (0 w 入w 1 )，则点G 到平面DEF 的距离为()A. .''3B 冷解析：因为 A 1B 1// EF, G 在 AB 上，所以G 到平面DEF 的距离即为 A 到平面DEF 的距离, 即是A 到DE 的距离，DE^V ：5,答案： D二、填空题(本大题共4小题，每小题5分，共20分•请把正确答案填在题中横线上 )11•若 a = (2 , - 3,5) , b = ( — 3,1 , - 4)，则 | a - 2b | = ___________ . 解析：因为 a — 2b = (8 , — 5,13), 所以 | a — 2b | = ；82 + — 5 2 + 132= ,-'258. 答案：.'25812.设 a = (2 , — 3,1) , b = ( — 1 , — 2,5) , d = (1,2 , — 7) , c 丄 a , c 丄 b ,且 c • d =10 ,则c =解析：设 c = (x , y , z ),D. '5 ~5由三角形面积可得所求距离为f.故选D.11X22根据题意得｛2x — 3y + z = 0, x — 2y + 5z = 0, x + 2y — 7z = 10.-5 -13•直角△ ABC 勺两条直角边 BC= 3, AC= 4, P®平面ABC PC=舟，则点P 到斜边AB 的5距离是 ________解析：则 A (4,0,0) ，B (0,3,0) ，P 0，0，5 ,所以 AB= ( — 4,3,0),T 9 AP= — 4, 0, 5 ,1 1 7因此 x + y + z = 1 + ^ — 3 = 6*所以AP 在AB 上的投影长为I Ak AB I AB16~5，所以P 到AB 的距离为答案： 325625=3. 65 解得x =祛答案:65 12,15 5 15以C 为坐标原点,。

(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、在直三棱柱111C B A ABC -中，090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。

求证：AM B A ⊥1练习：棱长为a 的正方体ABCD —A 1B 1C 1D 1中，在棱DD 1上是否存在点P 使B 1D ⊥面P AC ？例2 如图，已知矩形ABCD 和矩形ADEF 所在平面互相垂直，点N M ,分别在对角线AE BD ,上，且AE AN BD BM 31,31==,求证：//MN 平面CDE练习1、在正方体1111D C B A ABCD -中,E,F 分别是BB 1,,CD 中点，求证：D 1F ⊥平面ADE2、如图，在底面是菱形的四棱锥P —ABCD 中, ︒=∠60ABC ，,2,a PD PB a AC PA ====点E 在PD 上,且PE :ED = 2: 1.在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.二、利用空间向量求空间的角的问题例1 在正方体1111D C B A ABCD -中,E 1，F 1分别在A 1B 1,,C 1D 1上，且E 1B 1=41A 1B 1，D 1F 1=41D 1C 1，求BE 1与DF 1所成的角的大小。

例2 在正方体1111D C B A ABCD -中, F 分别是BC 的中点，点E 在D 1C 1上,且=11E D 41D 1C 1,试求直线E 1F 与平面D 1AC例3 在正方体1111D C B A ABCD -中,求二面角1C BD A --的大小。

zx1CFD CBA例4 已知E,F分别是正方体1111DCBAABCD-的棱BC和CD的中点，求：（1）A1D与EF所成角的大小；（2）A1F与平面B1EB所成角的大小；（3）二面角BBDC--11的大小。

三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1，底面ΔAB C求点B1到平面A1B C的距离。

空间向量练习及答案解析

空间向量练习及答案解析1.已知平面α的一个法向量为(2,-1,1)，且α∥β，则平面β的一个可能的法向量是哪个？A。

(4,2,-2) B。

(2,0,4) C。

(2,-1,-5) D。

(4,-2,2)2.在如图所示的正方形ABCD中，过点A作线段EA垂直于平面AC，若EA=1，则平面ADE和平面BCE所成的二面角大小是多少？A。

120° B。

45° C。

150° D。

60°3.已知向量a=(1,2,3)，向量b=(2,1,2)，向量c=(1,1,2)，点Q在直线OP上移动，当a·Q+b·Q取得最小值时，点Q的坐标是多少？A。

B。

C。

D.4.将正方形ABCD沿对角线BD折成直角二面角A-BD-C，以下哪个结论是错误的？A。

AC⊥BDB。

△ACD是等边三角形C。

∠ABC与平面BCD所成的角为60°D。

∠ABD与CD所成的角为60°5.在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=BC=AA1，∠ABC=90°，点E和F分别是棱AB和BB1的中点，直线EF和BC1的夹角是多少？A。

45° B。

60° C。

90° D。

120°6.在空间四面体O-ABC中，点M在线段OA上，且OM=2MA，点N为BC中点，设∠AOM=a，∠BOM=b，∠CON=c，则a+b-c等于多少？A。

a+b-c B。

-a+b+c C。

a-b+c D。

a+b-c7.在棱长为2的正方体ABCD-A1B1C1D1中，E是DC的中点，建立如图所示的空间直角坐标系，AB1和D1E所成角的余弦值是多少？A。

B。

C。

- D。

-8.在正方体ABCD-A1B1C1D1中，M、N、P分别是棱CC1、BC和A1B1上的点，若∠B1MN=90°，则∠PMN的大小是多少？A。

等于90° B。

小于90° C。

(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、在直三棱柱111C B A ABC -中，090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。

三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1，底面ΔAB C求点B1到平面A1B C的距离。

高中数学空间向量经典例题及解析

高中数学空间向量经典例题及解析一、引言空间向量是高中数学的一个重要知识点，它涉及到三维空间中向量的加法、数乘、数量积和向量积等运算。

这些运算在解决实际问题中有着广泛的应用，因此学好空间向量对于学生来说至关重要。

本篇文章将通过经典例题的方式，对空间向量的相关知识点进行深入解析，以期帮助学生更好地掌握这一知识点。

二、经典例题及解析【例题1】在空间四边形中，已知两个向量，，求异面直线的夹角(锐角或直角)。

【解析】本题考查空间向量的夹角问题，需要利用两个向量的夹角公式。

【解答】首先根据向量的定义，可得到向量，的坐标分别为(, )。

根据向量的加法，可得向量的坐标为(, )。

又因为两个向量垂直，所以它们的数量积为0，即，所以。

根据异面直线夹角公式，可得异面直线的夹角为。

【例题2】在长方体中，已知三个向量，，求异面直线的夹角(锐角或直角)。

【解析】本题除了需要用到向量的加法、数乘、数量积和向量积等运算，还需要用到长方体的性质。

【解答】首先根据向量的定义，可得到向量的坐标分别为(, , )。

又因为长方体中，所以可以表示为和的线性组合，即或。

设所在直线的方向向量，所在平面的法向量，则的坐标分别为(, )。

根据向量夹角公式和向量垂直的条件，可得垂直于平面，所以。

又因为两个向量垂直，所以它们的数量积为0，即，所以。

根据异面直线夹角公式，可得异面直线AB与CD的夹角为。

【例题3】已知长方体，设点，求与平面之间的距离。

【解析】本题需要利用长方体的性质和向量的数量积求解。

【解答】设平面的法向量，则所在直线的方向向量。

因为点在平面内，所以点在平面外，所以向量，即。

又因为向量与平面共线，所以向量，即。

根据向量的数量积和点到平面的距离公式，可得与平面之间的距离为。

三、总结空间向量是高中数学的一个难点也是重点，通过经典例题的解析，我们可以更好地掌握空间向量的相关知识点。

在解决实际问题时，我们需要灵活运用向量的加法、数乘、数量积和向量积等运算，同时还要注意向量的表示和坐标的确定。

空间向量基本定理(经典练习及答案详解)

1.2 空间向量基本定理课后篇巩固提升1.如图,在平行六面体ABCD -A 1B 1C 1D 1中,AC 与BD 的交点为M ,AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =b ,AA 1⃗⃗⃗⃗⃗⃗⃗ =c ,则下列向量中与C 1M ⃗⃗⃗⃗⃗⃗⃗⃗ 相等的向量是( ) A.-12a +12b +cB.12a +12b +cC.-12a -12b -cD.-12a -12b +cC 1M ⃗⃗⃗⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ −AC 1⃗⃗⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )-(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ +CC 1⃗⃗⃗⃗⃗⃗⃗ )=-12a -12b -c .2.(2020广东汕头金山中学高二上期中)已知正方体ABCD -A 1B 1C 1D 1,点E 为上底面A 1C 1的中心,若AE ⃗⃗⃗⃗⃗ =AA 1⃗⃗⃗⃗⃗⃗⃗ +x AB ⃗⃗⃗⃗⃗ +y AD ⃗⃗⃗⃗⃗ ,则x ,y 的值分别为( ) A.1,1B.1,12C.12,12D.12,1AE ⃗⃗⃗⃗⃗ =12(AA 1⃗⃗⃗⃗⃗⃗⃗ +AC 1⃗⃗⃗⃗⃗⃗⃗ )=12(AA 1⃗⃗⃗⃗⃗⃗⃗ +AA 1⃗⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )=AA 1⃗⃗⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ ,所以x=12,y=12.故选C .3.在空间四边形OABC 中,OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,OC ⃗⃗⃗⃗⃗ =c ,点M 在线段AC 上,且AM=2MC ,N 是OB 的中点,则MN ⃗⃗⃗⃗⃗⃗⃗ = ( )A.23a +12b -23cB.23a -12b +23cC.-13a +12b -23cD.13a +12b -13cMA ⃗⃗⃗⃗⃗⃗ =23CA ⃗⃗⃗⃗⃗ =23(OA ⃗⃗⃗⃗⃗ −OC ⃗⃗⃗⃗⃗ ),ON⃗⃗⃗⃗⃗⃗ =12OB ⃗⃗⃗⃗⃗ , MN ⃗⃗⃗⃗⃗⃗⃗ =MO ⃗⃗⃗⃗⃗⃗ +ON ⃗⃗⃗⃗⃗⃗ =MA ⃗⃗⃗⃗⃗⃗ +AO ⃗⃗⃗⃗⃗ +ON⃗⃗⃗⃗⃗⃗ =23(a -c )-a +12b =-13a +12b -23c .4.在正方体ABCD -A 1B 1C 1D 1中,设AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =b ,AA 1⃗⃗⃗⃗⃗⃗⃗ =c ,A 1C 1与B 1D 1的交点为E ,则BE⃗⃗⃗⃗⃗ = .,BE ⃗⃗⃗⃗⃗ =BB 1⃗⃗⃗⃗⃗⃗⃗ +B 1E ⃗⃗⃗⃗⃗⃗⃗ =AA 1⃗⃗⃗⃗⃗⃗⃗ +12(B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ +B 1A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ )=AA 1⃗⃗⃗⃗⃗⃗⃗ +12(AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=-12a +12b +c .-12a +12b +c5.已知三棱柱ABC -A 1B 1C 1的侧棱垂直于底面,∠BAC=90°.求证:AB ⊥AC 1.AB ⃗⃗⃗⃗⃗ =a ,AC ⃗⃗⃗⃗⃗ =b ,AA 1⃗⃗⃗⃗⃗⃗⃗ =c ,则AC 1⃗⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +CC 1⃗⃗⃗⃗⃗⃗⃗ =b +c .所以AB ⃗⃗⃗⃗⃗ ·AC 1⃗⃗⃗⃗⃗⃗⃗ =a ·(b +c )=a ·b +a ·c , 因为AA 1⊥平面ABC ,∠BAC=90°, 所以a ·b =0,a ·c =0, 得AB ⃗⃗⃗⃗⃗ ·AC 1⃗⃗⃗⃗⃗⃗⃗ =0,故AB ⊥AC 1. 6.如图所示,在平行四边形ABCD 中,AD=4,CD=3,∠ADC=60°,PA ⊥平面ABCD ,PA=6,求线段PC 的长.ABCD 中,∠ADC=60°,所以∠BAD=120°.又PA ⊥平面ABCD , 所以PA ⊥AB ,PA ⊥AD.因为PC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AP ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ −AP ⃗⃗⃗⃗⃗ , 所以|PC ⃗⃗⃗⃗⃗ |=√(AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ -AP⃗⃗⃗⃗⃗ )2= √|AB ⃗⃗⃗⃗⃗ |2+|AD ⃗⃗⃗⃗⃗ |2+|AP ⃗⃗⃗⃗⃗ |2+2AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ -2AB ⃗⃗⃗⃗⃗ ·AP ⃗⃗⃗⃗⃗ -2AD ⃗⃗⃗⃗⃗ ·AP⃗⃗⃗⃗⃗=√9+16+36+2×3×4×(-12)-0-0=7,即线段PC 的长为7.关键能力提升练7.(2020安徽淮北一中高二上期中)已知M ,N 分别是四面体OABC 的棱OA ,BC 的中点,点P 在线段MN 上,且MP=2PN ,设向量OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,OC ⃗⃗⃗⃗⃗ =c ,则OP ⃗⃗⃗⃗⃗ =( ) A.16a+16b+16cB.13a+13b+13cC.16a+13b+13c D.13a+16b+16cOP ⃗⃗⃗⃗⃗ =OM ⃗⃗⃗⃗⃗⃗ +MP ⃗⃗⃗⃗⃗⃗ =OM ⃗⃗⃗⃗⃗⃗ +23(ON ⃗⃗⃗⃗⃗⃗ −OM ⃗⃗⃗⃗⃗⃗ )=23ON ⃗⃗⃗⃗⃗⃗ +13OM ⃗⃗⃗⃗⃗⃗ =23×12(OB⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ )+13×12OA ⃗⃗⃗⃗⃗ =13b +13c +16a ,故选C .8.在四面体O -ABC 中,G 1是△ABC 的重心,G 是OG 1上的一点,且OG=3GG 1,若OG ⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗ ,则(x ,y ,z )为( ) A.(14,14,14) B.(34,34,34) C.(13,13,13) D.(23,23,23)如图所示,连接AG 1交BC 于点E ,则E 为BC 的中点,AE⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=12(OB ⃗⃗⃗⃗⃗ -2OA ⃗⃗⃗⃗⃗ +OC⃗⃗⃗⃗⃗ ), AG 1⃗⃗⃗⃗⃗⃗⃗ =23AE ⃗⃗⃗⃗⃗ =13(OB ⃗⃗⃗⃗⃗ -2OA ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ ). 因为OG ⃗⃗⃗⃗⃗ =3GG 1⃗⃗⃗⃗⃗⃗⃗ =3(OG 1⃗⃗⃗⃗⃗⃗⃗ −OG ⃗⃗⃗⃗⃗ ),所以OG ⃗⃗⃗⃗⃗ =34OG 1⃗⃗⃗⃗⃗⃗⃗ .则OG ⃗⃗⃗⃗⃗ =34OG 1⃗⃗⃗⃗⃗⃗⃗ =34(OA ⃗⃗⃗⃗⃗ +AG 1⃗⃗⃗⃗⃗⃗⃗ )=34(OA ⃗⃗⃗⃗⃗ +13OB ⃗⃗⃗⃗⃗ −23OA ⃗⃗⃗⃗⃗ +13OC ⃗⃗⃗⃗⃗)=14OA ⃗⃗⃗⃗⃗ +14OB ⃗⃗⃗⃗⃗ +14OC⃗⃗⃗⃗⃗ .9.(多选题)在三棱锥P-ABC 中,三条侧棱PA ,PB ,PC 两两垂直,且PA=PB=PC=3,G 是△PAB 的重心,E ,F 分别为棱BC ,PB 上的点,且BE ∶EC=PF ∶FB=1∶2,则下列说法正确的是( ) A.EG ⊥PG B.EG ⊥BC C.FG ∥BC D.FG ⊥EF,设PA ⃗⃗⃗⃗⃗ =a ,PB ⃗⃗⃗⃗⃗ =b ,PC ⃗⃗⃗⃗⃗ =c ,则{a ,b ,c }是空间的一个正交基底,则a ·b=a ·c=b ·c=0.取AB 的中点H , 则BC⃗⃗⃗⃗⃗ =c-b , PG⃗⃗⃗⃗⃗ =23PH ⃗⃗⃗⃗⃗⃗ =23×12(a+b )=13a+13b , PE ⃗⃗⃗⃗⃗ =PB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =PB ⃗⃗⃗⃗⃗ +13(PC ⃗⃗⃗⃗⃗ −PB ⃗⃗⃗⃗⃗ )=23b+13c ,则EG ⃗⃗⃗⃗⃗ =PG ⃗⃗⃗⃗⃗ −PE ⃗⃗⃗⃗⃗ =13a+13b-23b-13c=13a-13b-13c ,BC⃗⃗⃗⃗⃗ =c-b , FG ⃗⃗⃗⃗⃗ =PG ⃗⃗⃗⃗⃗ −PF ⃗⃗⃗⃗⃗ =13a+13b-13b=13a ,EF ⃗⃗⃗⃗⃗ =PF⃗⃗⃗⃗⃗ −PE ⃗⃗⃗⃗⃗ =13b-13c+23b =-13c-13b. EG ⃗⃗⃗⃗⃗ ·PG ⃗⃗⃗⃗⃗ =0,故A 正确;EG ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0,故B 正确;FG ⃗⃗⃗⃗⃗ ≠λBC ⃗⃗⃗⃗⃗ (λ∈R ),故C 不正确;FG ⃗⃗⃗⃗⃗ ·EF ⃗⃗⃗⃗⃗ =0,故D 正确.故选ABD .10.若a=e 1+e 2,b=e 2+e 3,c=e 1+e 3,d=e 1+2e 2+3e 3,若e 1,e 2,e 3不共面,当d =α a +β b +γ c 时,α+β+γ=.d =(α+γ)e 1+(α+β)e 2+(γ+β)e 3,所以{α+γ=1,α+β=2,γ+β=3,故有α+β+γ=3.11.(2020浙江杭州学军中学高二上期中)在棱长为a 的正四面体ABCD 中,E ,F 分别为棱AD ,BC 的中点,则异面直线EF 与AB 所成角的大小是 ,线段EF 的长度为 .AB ⃗⃗⃗⃗⃗ =a ,AC ⃗⃗⃗⃗⃗ =b ,AD ⃗⃗⃗⃗⃗ =c ,则{a ,b ,c }是空间的一个基底,|a|=|b|=|c|=a ,a ·b=a ·c=b ·c =12a 2.∴EF ⃗⃗⃗⃗⃗ =AF ⃗⃗⃗⃗⃗ −AE ⃗⃗⃗⃗⃗ =12(a+b )-12c ,∴EF ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ =12a 2+12a ·b-12a ·c =12a 2,|EF⃗⃗⃗⃗⃗ |=√(12a +12b -12c) 2=√22a. ∴cos <EF ⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ >=EF ⃗⃗⃗⃗⃗ ·AB⃗⃗⃗⃗⃗ |EF ⃗⃗⃗⃗⃗ ||AB ⃗⃗⃗⃗⃗|=12a 2√22a×a =√22, ∴异面直线EF 与AB 所成的角为π4.√22a 12.如图所示,在平行六面体ABCD -A 1B 1C 1D 1中,MA ⃗⃗⃗⃗⃗⃗ =-13AC ⃗⃗⃗⃗⃗ ,ND ⃗⃗⃗⃗⃗⃗ =13A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ ,设AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =b ,AA 1⃗⃗⃗⃗⃗⃗⃗ =c ,试用a ,b ,c 表示MN⃗⃗⃗⃗⃗⃗⃗ .AN ,则MN⃗⃗⃗⃗⃗⃗⃗ =MA ⃗⃗⃗⃗⃗⃗ +AN ⃗⃗⃗⃗⃗⃗ . 由已知可得四边形ABCD 是平行四边形,从而可得AC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =a +b ,MA ⃗⃗⃗⃗⃗⃗ =-13AC ⃗⃗⃗⃗⃗ =-13(a +b ),又A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −AA 1⃗⃗⃗⃗⃗⃗⃗ =b -c ,故AN ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ +DN ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −ND ⃗⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −13A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =b -13(b -c ),所以MN⃗⃗⃗⃗⃗⃗⃗ =MA⃗⃗⃗⃗⃗⃗ +AN ⃗⃗⃗⃗⃗⃗ =-13(a +b )+b -13(b -c )=13(-a +b +c ). 13.在正方体ABCD -A 1B 1C 1D 1中,已知E ,F ,G ,H 分别是CC 1,BC ,CD 和A 1C 1的中点.证明: (1)AB 1∥GE ,AB 1⊥EH ; (2)A 1G ⊥平面EFD.设正方体棱长为1,AB ⃗⃗⃗⃗⃗ =i ,AD ⃗⃗⃗⃗⃗ =j ,AA 1⃗⃗⃗⃗⃗⃗⃗ =k ,则{i ,j ,k }构成空间的一个单位正交基底. AB 1⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ =i +k ,GE ⃗⃗⃗⃗⃗ =GC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ =12i +12k =12AB 1⃗⃗⃗⃗⃗⃗⃗ ,∴AB 1∥GE.EH ⃗⃗⃗⃗⃗⃗ =EC 1⃗⃗⃗⃗⃗⃗⃗ +C 1H ⃗⃗⃗⃗⃗⃗⃗ =12k +(-12)(i +j )=-12i -12j +12k , ∵AB 1⃗⃗⃗⃗⃗⃗⃗ ·EH ⃗⃗⃗⃗⃗⃗ =(i +k )·(-12i -12j +12k)=-12|i |2+12|k |2=0,∴AB 1⊥EH.(2)A 1G ⃗⃗⃗⃗⃗⃗⃗ =A 1A ⃗⃗⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +DG ⃗⃗⃗⃗⃗ =-k +j +12i ,DF ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ +CF ⃗⃗⃗⃗⃗ =i -12j ,DE ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ =i +12k .∴A 1G ⃗⃗⃗⃗⃗⃗⃗ ·DF ⃗⃗⃗⃗⃗ =(-k +j +12i)·(i -12j)=-12|j |2+12|i |2=0,∴A 1G ⊥DF.A 1G ⃗⃗⃗⃗⃗⃗⃗ ·DE ⃗⃗⃗⃗⃗ =(-k +j +12i)·(i +12k)=-12|k |2+12|i |2=0,∴A 1G ⊥DE.又DE ∩DF=O ,∴A 1G ⊥平面EFD.学科素养创新练14.如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,D 1B 1的中点,求证:EF ⊥平面B 1AC.AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =c ,AA 1⃗⃗⃗⃗⃗⃗⃗ =b ,有a ·b =0,a ·c =0,b ·c =0,则EF ⃗⃗⃗⃗⃗ =EB 1⃗⃗⃗⃗⃗⃗⃗ +B 1F ⃗⃗⃗⃗⃗⃗⃗ =12(BB 1⃗⃗⃗⃗⃗⃗⃗ +B 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ )=12(AA 1⃗⃗⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ )=12(AA 1⃗⃗⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=12(-a +b +c ),AB 1⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AA 1⃗⃗⃗⃗⃗⃗⃗ =a +b .∴EF ⃗⃗⃗⃗⃗ ·AB 1⃗⃗⃗⃗⃗⃗⃗ =12(-a +b +c )·(a +b )=12(|b |2-|a |2)=0.∴EF ⃗⃗⃗⃗⃗ ⊥AB 1⃗⃗⃗⃗⃗⃗⃗ ,即EF ⊥AB 1.同理EF ⊥B 1C. ∵AB 1∩B 1C=B 1,∴EF ⊥平面B 1AC.。

空间向量的习题及答案

空间向量的习题及答案空间向量是线性代数中的重要概念之一，它在解决几何问题时起到了关键作用。

本文将通过一些典型的习题来探讨空间向量的性质和应用，并给出详细的答案解析。

1. 习题一：已知向量a = (1, 2, -3)，向量b = (-2, 1, 4)，求向量a与向量b的数量积和向量积。

解析：向量a与向量b的数量积为：a·b = 1*(-2) + 2*1 + (-3)*4 = -2 + 2 - 12 = -12。

向量a与向量b的向量积为：a×b = (2*(-3) - 1*4, 1*(-3) - (-2)*4, 1*1 - (-2)*(-3)) = (-6 - 4, -3 + 8, 1 + 6) = (-10, 5, 7)。

2. 习题二：已知向量a = (2, -1, 3)，向量b = (3, 4, -2)，求向量a与向量b的夹角的余弦值。

解析：向量a与向量b的夹角的余弦值为：cosθ = (a·b) / (|a| * |b|)。

其中，a·b为向量a与向量b的数量积，|a|为向量a的模，|b|为向量b的模。

计算得到：a·b = 2*3 + (-1)*4 + 3*(-2) = 6 - 4 - 6 = -4，|a| = √(2^2 + (-1)^2+ 3^2) = √(4 + 1 + 9) = √14，|b| = √(3^2 + 4^2 + (-2)^2) = √(9 + 16 + 4)= √29。

代入公式得到：cosθ = (-4) / (√14 * √29)。

3. 习题三：已知向量a = (1, 2, 3)，向量b = (4, 5, 6)，求向量a与向量b的和、差和模长。

解析：向量a与向量b的和为：a + b = (1 + 4, 2 + 5, 3 + 6) = (5, 7, 9)。

向量a与向量b的差为：a - b = (1 - 4, 2 - 5, 3 - 6) = (-3, -3, -3)。

空间向量及其运算(习题及答案)

空间向量及其运算(习题及答案)例1：在正方体ABCD-A1B1C1D1中，E为上底面A1B1C1D1的中心，若AE=AA1+xAB+yAD，则x，y的值分别为（）。

解析：由于E为上底面A1B1C1D1的中心，所以AE的长度为A1E的长度的一半，即AE=1/2A1E。

又因为A1E的方向向量为1/2(AB+AD)，所以AE=1/2(AA1+AB+AD)。

将AE=AA1+xAB+yAD代入，得到x=1/2，y=1/2，故选D。

例2：在平行六面体ABCD-A1B1C1D1中，AB=2，AA1=2，AD=1，且AB，AD，AA1两两之间的夹角都是60°，则AC1·BD1=（）。

解析：由于AB，AD，AA1两两之间的夹角都是60°，所以它们构成一组正交基底。

设AB=a，AD=b，AA1=c，则AC1=AB+BC1+CA1=a+b/2+c/2，BD1=BD=AD+DC1+CB1=b+a/2+c/2.将AC1·BD1代入，得到AC1·BD1=(a+b/2+c/2)·(b+a/2+c/2)=ab+ac/2+bc/2+a^2/4+b^2/4+c^2/4+ac/4+bc/4，化简得到AC1·BD1=ab+ac+bc+1/4(a^2+b^2+c^2)，代入数值计算得到AC1·BD1=5/2，故选B。

例3：在正方体ABCD-A1B1C1D1中，E，F分别是A1B1，C1D1的一个四等分点，求BE与DF所成角的余弦值。

解析：以DA，DC。

设正方体ABCD-A1B1C1D1的棱长为1，则B(1，1，0)，E(1，1/2，1)，D(0，0，0)，F(0，1/2，1)。

由于BE的方向向量为(0,-1,1)，DF的方向向量为(0,1,1)，所以BE·DF=0*(-1)+(-1)*1+1*1=0，即BE与DF所成角的余弦值为0，故选A。

1.在三棱锥O-ABC中，设OA=a，OB=b，OC=c，用a，b，c表示MN，则MN=1/2√(2a^2+2b^2-2c^2)。

空间几何与向量练习题及解析

空间几何与向量练习题及解析一、选择题1. 已知向量A = 3A + 2A− A，向量A= −2A + A + 3A，求A与A的数量积A·A的值为：A. 1B. -1C. -10D. 10解析：数量积公式为：A·A = AAAA + AAAA + AAAA，其中AA、AA、AA分别表示向量A和A的A、A、A分量的乘积。

带入已知的A和A的分量进行计算：A·A = (3)(-2) + (2)(1) + (-1)(3) = -6 + 2 - 3 = -7答案：选项A. 12. 在空间直角坐标系中，已知点A(2, 1, 3)和点A(-1, 4, 2)，向量A的末端与向量A的起点重合，A·A的值为：A. 3B. 17C. 11D. -9解析：点A(2, 1, 3)和点A(-1, 4, 2)可以确定唯一的向量A和A。

根据数量积A·A的定义，可以先求出A和A的分量，然后进行运算：A·A = (2)(-1) + (1)(4) + (3)(2) = -2 + 4 + 6 = 8答案：选项B. 17二、填空题1. 设向量A = 2A + 3A− A，向量A = 4A + A，若A = A + AAA，则A和A分别为______、______。

解析：根据已知条件，A的A分量为-1，而A的A分量为1。

因此A = 4，A = -1。

答案：4、-12. 已知点A(1, 2, 3)和点A(4, -1, -2)，则向量AA的大小为________。

解析：向量AA可以由终点坐标减去起点坐标得到，即AA = (4-1)A + (-1-2)A + (-2-3)A = 3A - 3A - 5A。

根据向量的模的定义，可以得到：|AA| = √((3)^2 + (-3)^2 + (-5)^2) = √(9 + 9 + 25) = √43答案：√43三、计算题1. 已知向量A = 3A - 2A + 4A，向量A = A + A，求向量A与向量A 的夹角A的余弦值cos A。

空间向量典型例题

空间向量典型例题空间向量与立体几何一、非坐标系向量法1.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心，则AB1与底面ABC所成角的正弦值等于（）。

答案：（B）2/3.2.等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D的余弦值为1/3，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值等于。

答案：3/4.3.已知正四面体ABCD中，E、F分别在AB，CD上，且CF=CD，AE=AB/4，则直线DE和BF所成角的余弦值为（）。

答案：（C）-13/13.4.如图，已知四棱柱ABCD-A1，CB=CD，∠C1CB=∠C1CD，证明：C1C垂直于BD；当∠C1CB的值为多少时，能使A1CB1D是菱形且A1C垂直于平面C1BD？请给出证明。

二、坐标系向量法1.如图，在直三棱柱ABCD-A1B1C1D1中，点M是AC的中点，点N是BD的中点，求异面直线AN和B1M所成角的余弦值，以及平面A1B1C1和平面ABC所成二面角的正弦值。

2.如图，在直棱柱ABCD-A1B1C1D1中，AB=BC=1，AC=BD=√2，点M是AC的中点，点N是BD的中点。

证明：（1）MN⊥平面A1B1C1D1；（2）直线MN和平面A1B1C1D1所成二面角的正弦值为1/√10.3.如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC。

求证：PC⊥AB；求二面角B-AP-C的大小。

4.如图，已知点P在正方体ABCD-A1B1C1D1的对角线BD1上，∠PDA=60°。

求（1）DP与CC1所成角的大小；（2）DP与平面A1AD1所成角的大小。

5.如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，∠ABC=90°，OA⊥底面ABCD，OA=2，M为OA的中点。

求（1）异面直线AB与MD所成角的大小；（2）点B到平面OCD的距离。

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.在如图所示的多面体中，四边形和都为矩形.（Ⅰ）若，证明：直线平面；（Ⅱ）是否存在过的平面，使得直线平行，若存在请作出平面并证明，若不存在请说明理由.【答案】（Ⅰ）见解析；（Ⅱ）存在，证明见解析【解析】（Ⅰ）由四边形和都为矩形知，⊥AB，⊥AC，由线面垂直判定定理知⊥面ABC，由线面垂直定义知⊥BC，又因为AC⊥BC，由线面垂直判定定理知，BC⊥面；（Ⅱ）取AB的中点为M，连结交于D，连结DE，显然E是的中点，根据三角形中位线定理得，DE∥，又由于DE在面过的平面内，根据线面平行的判定定理知和该平面平行.试题解析：（Ⅰ）证明：因为四边形和都是矩形，所以 2分因为为平面内的两条相交直线，所以 4分因为直线平面，所以又由已知，为平面内的两条相交直线，所以平面 7分（Ⅱ）存在 8分连接，设，取线段AB的中点M，连接.则平面为为所求的平面. 1１分由作图可知分别为的中点，所以 13分又因为因此 14分考点: 空间线面垂直垂直的判定与性质；线面平行的判定；推理论证能力2.如图，平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形，AF∥DE，AF⊥FE，AF＝AD＝2DE＝2，M为AD的中点．(1)证明：MF⊥BD；(2)若二面角A－BF－D的平面角的余弦值为，求AB的长．【答案】（1）见解析（2）【解析】(1)证明由已知得△ADF为正三角形，所以MF⊥AD，因为平面ABCD⊥平面ADEF，平面ABCD∩平面ADEF＝AD，MF⊂平面ADEF，所以MF⊥BD.(2)设AB＝x，以F为原点，AF，FE所在直线分别为x轴，y轴建立如图所示的空间直角坐标系，则F(0,0,0)，A(－2,0,0)，D(－1，，0)，B(－2,0，x)，所以＝(1，－，0)，＝(2,0，－x)．因为EF⊥平面ABF，所以平面ABF的法向量可取n1＝(0,1,0)．设n2＝(x1，y1，z1)为平面BFD的法向量，则可取n2＝.因为cos〈n1，n2〉＝＝，得x＝，所以AB＝.3.已知向量＝(2,4,5)，＝(3，x，y)，若∥，则() A．x＝6，y＝15B．x＝3，y＝C．x＝3，y＝15D．x＝6，y＝【答案】D【解析】∵＝＝，∴x＝6，y＝，选D项．4.如图，正方体ABCD－A1B1C1D1中，E，F分别在A1D，AC上，且A1E＝A1D，AF＝AC，则()A．EF至多与A1D，AC之一垂直B．EF⊥A1D，EF⊥ACC．EF与BD1相交D．EF与BD1异面【答案】B【解析】以D点为坐标原点，以DA，DC，DD1所在直线分别为x，y，z轴建立空间直角坐标系，设正方体棱长为1，则A1(1,0,1)，D(0,0,0)，A(1,0,0)，C(0,1,0)，E(，0，)，F(，，0)，B(1,1,0)，D1(0,0,1)，＝(－1,0，－1)，＝(－1,1,0)，＝(，，－)，＝(－1，－1,1)，＝－，·＝·＝0，从而EF∥BD1，EF⊥A1D，EF⊥AC.故选B.5.已知2a＋b＝(0，－5,10)，c＝(1，－2，－2)，a·c＝4，|b|＝12，则以b，c为方向向量的两直线的夹角为________．【答案】60°【解析】由题意得(2a＋b)·c＝0＋10－20＝－10.即2a·c＋b·c＝－10，又∵a·c＝4，∴b·c＝－18，∴cos〈b，c〉＝＝＝－，∴〈b，c〉＝120°，∴两直线的夹角为60°.6.已知点A(1，t，－1)关于x轴的对称点为B，关于xOy平面的对称点为C，则BC中点D的坐标为________．【答案】(1,0,1)【解析】因为A(1，t，－1)关于x轴的对称点为B(1，－t,1)，关于xOy平面的对称点为C(1，t,1)，所以BC中点D的坐标为(，，)，即D(1,0,1)．7.如图，四棱柱中，底面.四边形为梯形，,且.过三点的平面记为，与的交点为.（1）证明：为的中点；（2）求此四棱柱被平面所分成上下两部分的体积之比；（3）若，，梯形的面积为6，求平面与底面所成二面角大小.【答案】（1）为的中点；（2）；（3）.【解析】（1）利用面面平行来证明线线平行∥，则出现相似三角形，于是根据三角形相似即可得出，即为的中点.（2）连接.设，梯形的高为，四棱柱被平面所分成上下两部分的体积分别为和，，则.先表示出和，就可求出，从而.（3）可以有两种方法进行求解.第一种方法，用常规法，作出二面角.在中，作，垂足为，连接.又且，所以平面，于是.所以为平面与底面所成二面角的平面角.第二种方法，建立空间直角坐标系，以为原点，分别为轴和轴正方向建立空间直角坐标系.设.因为，所以.从而，，所以，.设平面的法向量，再利用向量求出二面角.（1）证：因为∥，∥,，所以平面∥平面.从而平面与这两个平面的交线相互平行，即∥.故与的对应边相互平行，于是.所以，即为的中点.（2）解：如图，连接.设，梯形的高为，四棱柱被平面所分成上下两部分的体积分别为和，，则.，，所以，又所以，故.（3）解法1如第（20）题图1，在中，作，垂足为，连接.又且，所以平面，于是.所以为平面与底面所成二面角的平面角.因为∥，，所以.又因为梯形的面积为6，，所以.于是.故平面与底面所成二面角的大小为.解法2如图，以为原点，分别为轴和轴正方向建立空间直角坐标系.设.因为，所以.从而，，所以，.设平面的法向量，由得，所以.又因为平面的法向量，所以，故平面与底面所成而面积的大小为.【考点】1.二面角的求解；2.几何体的体积求解.8.如图，正方形与梯形所在的平面互相垂直，，∥，，，为的中点．（1）求证：∥平面；（2）求证：平面平面；（3）求平面与平面所成锐二面角的余弦值.【答案】（1）证明过程详见解析；（2）证明过程详见解析；（3）.【解析】本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力.第一问，作出辅助线MN，N为中点，在中，利用中位线得到，且，结合已知条件，可证出四边形ABMN为平行四边形，所以，利用线面平行的判定，得∥平面；第二问，利用面面垂直的性质，判断面，再利用已知的边长，可证出，则利用线面垂直的判定得平面BDE，再利用面面垂直的判定得平面平面；第三问，可以利用传统几何法证明二面角的平面角，也可以利用向量法建立空间直角坐标系，求出平面BEC和平面ADEF的法向量，利用夹角公式计算即可.（1）证明：取中点，连结．在△中，分别为的中点，所以∥，且．由已知∥，，所以∥，且．所以四边形为平行四边形，所以∥．又因为平面，且平面，所以∥平面． 4分（2）证明：在正方形中，．又因为平面平面，且平面平面，所以平面．所以． 6分在直角梯形中，，，可得．在△中，，所以． 7分所以平面． 8分又因为平面，所以平面平面． 9分（3）（方法一）延长和交于．在平面内过作于,连结．由平面平面，∥，，平面平面=，得，于是．又，平面，所以，于是就是平面与平面所成锐二面角的平面角. 12分由，得.又，于是有.在中，.所以平面与平面所成锐二面角的余弦值为． 14分（方法二）由（2）知平面，且．以为原点，所在直线分别为轴，建立空间直角坐标系．易得.平面的一个法向量为.设为平面的一个法向量，因为，所以，令，得．所以为平面的一个法向量．１２分设平面与平面所成锐二面角为．则．所以平面与平面所成锐二面角的余弦值为． 14分【考点】中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角.9.如图，直四棱柱底面直角梯形，∥，，是棱上一点，，，，，.（1）求异面直线与所成的角；（2）求证：平面.【答案】(1);（2）证明见解析.【解析】（1）本题中由于有两两垂直，因此在求异面直线所成角时，可以通过建立空间直角坐标系，利用向量的夹角求出所求角；（2）同（1）我们可以用向量法证明线线垂直，以证明线面垂直，，，，易得当然我们也可直线用几何法证明线面垂直，首先，这由已知可直接得到，而证明可在直角梯形通过计算利用勾股定理证明，，，因此，得证.（1）以原点，、、分别为轴、轴、轴建立空间直角坐标系.则，，，. 3分于是,,,异面直线与所成的角的大小等于. 6分（2）过作交于，在中，，，则，，，， 10分，.又，平面. 12分【考点】（1）异面直线所成的角；（2）线面垂直.10.在如图所示的几何体中，平面，∥，是的中点，，．（1）证明：∥平面；（2）求二面角的大小的余弦值．【答案】（1）详见解析；（2）【解析】（1）要证明直线和平面平行，只需证明直线和平面内的一条直线平行，取中点，连接，则，且，由已知得，且，故，则四边形是平行四边形，可证明，进而证明∥平面，或可通过建立空间直角坐标系，用坐标表示相关点的坐标，证明直线的方向向量垂直于平面的法向量即可；（2）先求半平面和的法向量的夹角的余弦值，再观察二面角是锐二面角还是钝二面角，来决定二面角的大小的余弦值的正负，从而求解．（1）因为，∥，所以平面．故以为原点，建立如图所示的空间直角坐标系，则相关各点的坐标分别是，，，，，．所以，因为平面的一个法向量为，所以，又因为平面，所以平面． 6分（2）由（1）知，，，．设是平面的一个法向量，由得，取，得，则设是平面的一个法向量，由得，取，则，则设二面角的大小为，则，故二面角的大小的余弦值为．【考点】1、直线和平面平行的判断；2、二面角的求法.11.如图，在四棱锥中，底面是直角梯形，,，平面平面,若，，,，且．（1）求证：平面；（2）设平面与平面所成二面角的大小为，求的值．【答案】（1）参考解析；（2）【解析】（1）由，所以.又,.在三角形PAO中由余弦定理可得.所以.即.又平面平面且平面平面=AD，平面PAD.所以平面.（2）由题意可得建立空间坐标系，写出相应点的坐标，平面PAD的法向量易得，用待定系数写出平面PBC的法向量，根据两向量的法向量夹角的余弦值，求出二面角的余弦值.（1）因为，，所以， 1分在中，由余弦定理，得， 3分，， 4分， 5分又平面平面，平面平面,平面，平面． 6分（2）如图，过作交于，则，，两两垂直，以为坐标原点，分别以，，所在直线为轴，建立空间直角坐标系， 7分则，，8分，， 9分设平面的一个法向量为，由得即取则，所以为平面的一个法向量． 11分平面,为平面的一个法向量．所以， 12分． 13分【考点】1.线面垂直的证明.2.二面角.3.空间坐标系的表示.4.向量的夹角.12.如图，在直三棱柱中，已知，，．（1）求异面直线与夹角的余弦值；（2）求二面角平面角的余弦值．【答案】（1），（2）．【解析】（1）利用空间向量求线线角，关键在于正确表示各点的坐标. 以为正交基底，建立空间直角坐标系．则，，，，所以，,因此，所以异面直线与夹角的余弦值为．（2）利用空间向量求二面角，关键在于求出一个法向量. 设平面的法向量为，则即取平面的一个法向量为；同理可得平面的一个法向量为；由两向量数量积可得二面角平面角的余弦值为．试题解析：如图，以为正交基底，建立空间直角坐标系．则，，，，所以，，，．（1）因为，所以异面直线与夹角的余弦值为． 4分（2）设平面的法向量为，则即取平面的一个法向量为；所以二面角平面角的余弦值为． 10分【考点】利用空间向量求线线角及二面角13.如图，在正四棱锥P－ABCD中，PA＝AB＝，点M，N分别在线段PA和BD上，BN＝BD．（1）若PM＝PA，求证：MN⊥AD；（2）若二面角M－BD－A的大小为，求线段MN的长度．【答案】（1）详见解析;（2）．【解析】（1）由于这是一个正四棱锥，故易建立空间坐标系，易得各点的坐标，由，得，由，得，即可求得向量的坐标：．不难计算出它们的数量积，问题得证;（2）利用在上，可设，得出点的坐标，表示出，进而求出平面的法向量n＝(λ－1，0，λ)，由向量的夹角公式可得，解得，从而确定出，由两点间距离公式得.试题解析：证明：连接交于点，以为轴正方向，以为轴正方向，为轴建立空间直角坐标系．因为，则．（1）由，得，由，得，所以．因为．所以. 4分（2）因为在上，可设，得．所以．设平面的法向量，由得其中一组解为，所以可取n＝(λ－1，0，λ). 8分因为平面的法向量为，所以，解得，从而，所以. 10分【考点】1.线线垂直的证明;2.二面角的计算14.如图，已知四棱锥的底面的菱形，，点是边的中点，交于点，（1）求证：；（2）若的大小；（3）在（2）的条件下，求异面直线与所成角的余弦值。

空间向量典型习题含详解

1.如图1，矩形ABCD中，AB=12，AD=6，E、F分别为CD、AB边上的点，且DE=3，BF=4，将△BCE沿BE折起至△PBE位置（如图2所示），连结AP、PF，其中PF=2．（1）求证：PF⊥平面ABED；（2）求点A到平面PBE的距离．2.如图，在正三棱柱中，，点P，Q分别为，BC的中点．求异面直线BP与所成角的余弦值；求直线与平面所成角的正弦值．3.如图，四棱锥P-ABCD的底面ABCD是菱形，AC与BD交于点O，OP⊥底面ABCD，点M为PC中点，AC=4，BD=2，OP=4．（1）求直线AP与BM所成角的余弦值；（2）求平面ABM与平面PAC所成锐二面角的余弦值．4.如图，在三棱柱ABC-A1B1C1中，平面A1B1C⊥平面AA1C1C，∠BAC=90°．（1）证明：AC⊥CA1；（2）若△A1B1C是正三角形，AB=2AC=2，求二面角A1-AB-C的大小．5.如图，四棱锥P-ABCD中，AB∥DC，DC⊥BC，AB=2，CD=DP=1，PA=PB=BC=3，侧棱PC上点E满足PE=2EC．（1）求证PA∥平面BED；（2）求二面角A-PB-C的余弦值．6.如图，在正方体ABCD-A1B1C1D1中，E，F分别为底面A1B1C1D1和侧面B1C1CB的中心．求证：(1)EF∥A1B；(2)EF∥平面A1BD；(3)平面B1EF∥平面A1BD．7.如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面；（2）求与平面所成角的正弦值.答案和解析1.【答案】解：（1）连结EF，由翻折不变性可知，PB=BC=6，PE=CE=9，在△PBF中，PF2+BF2=20+16=36=PB2，所以PF⊥BF，在图1中，利用勾股定理，得EF==，在△PEF中，EF2+PF2=61+20=81=PE2，∴PF⊥EF，又∵BF∩EF=F，BF⊂平面ABED，EF⊂平面ABED，∴PF⊥平面ABED．（2）解：由（1）知PF⊥平面ABED，∴PF为三棱锥P-ABE的高．设点A到平面PBE的距离为h，由等体积法得V A-PBE=V P-ABE，即∴h=，即点A到平面PBE的距离为．【解析】本题考查直线与平面垂直的证明，考查点到平面距离的求法，解题时要注意空间思维能力的培养，要注意等积法的合理运用．（1）连结EF，由翻折不变性可知，PB=BC=6，PE=CE=9，由已知条件，利用勾股定理推导出PF⊥BF，PF⊥EF，由此能够证明PF⊥平面ABED．（2）由PF⊥平面ABED，知PF为三棱锥P-ABE的高，利用等积法能求出点A 到平面PBE的距离．2.【答案】解：如图，在正三棱柱ABC-A1B1C1中，设AC，A1C1的中点分别为O，O1，则，OB⊥OC，OO1⊥OC，OO1⊥OB，故以{，，}为基底，建立空间直角坐标系O-xyz，∵AB=AA1=2，A（0，-1，0），B（，0，0），C（0，1，0），A1（0，-1，2），B1（，0，2），C1（0，1，2）．（1）点P为A1B1的中点．∴，，，∴，，，，，．|cos＜，＞|===．∴异面直线BP与AC1所成角的余弦值为：；（2）∵Q为BC的中点．∴Q（，，）∴，，，，，，，，，设平面AQC1的一个法向量为=（x，y，z），由，可取=（，-1，1），设直线CC1与平面AQC1所成角的正弦值为θ，sinθ=|cos＜，＞|==，∴直线CC1与平面AQC1所成角的正弦值为．【解析】本题考查了向量法求空间角，属于中档题．设AC，A1C1的中点分别为O，O1，以{}为基底，建立空间直角坐标系O-xyz，（1）由|cos|=可得异面直线BP与AC1所成角的余弦值；（2）求得平面AQC 1的一个法向量为，设直线CC1与平面AQC1所成角的正弦值为θ，可得sinθ=|cos|=，即可得直线CC1与平面AQC1所成角的正弦值．3.【答案】解：（1）因为ABCD是菱形，所以AC⊥BD．又OP⊥底面ABCD，以O为原点，直线OA，OB，OP分别为x轴，y轴，z轴，建立如图所示空间直角坐标系．则A（2，0，0），B（0，1，0），P（0，0，4），C（-2，0，0），M（-1，0，2）．=（-2，0，4），=（01，-1，2），cos＜，＞===．故直线AP与BM所成角的余弦值为．（2）=（-2，1，0），=（-1，-1，2）．设平面ABM的一个法向量为=（x，y，z），则，令x=2，得=（2，4，3）．又平面PAC的一个法向量为=（0，1，0），∴cos＜，＞===．故平面ABM与平面PAC所成锐二面角的余弦值为．【解析】（1）以O为原点，直线OA，OB，OP分别为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出直线AP与BM所成角的余弦值．（2）求出平面ABM的一个法向量和平面PAC的一个法向量，利用向量法能求出平面ABM与平面PAC所成锐二面角的余弦值．本题考查异面直线所成角的余弦值的求法，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．4.【答案】证明：（Ⅰ）过点B1作A1C的垂线，垂足为O，由平面A1B1C⊥平面AA1C1C，平面A1B1C∩平面AA1C1C=A1C，得B1O⊥平面AA1C1C，又AC⊂平面AA1C1C，得B1O⊥AC．由∠BAC=90°，AB∥A1B1，得A1B1⊥AC．又B1O∩A1B1=B1，得AC⊥平面A1B1C．又CA1⊂平面A1B1C，得AC⊥CA1．（Ⅱ）以C为坐标原点，的方向为x轴正方向，||为单位长，建立空间直角坐标系C-xyz．由已知可得A（1，0，0），A1（0，2，0），B1（0，1，）．所以=（1，0，0），=（-1，2，0），==（0，-1，）．设n=（x，y，z）是平面A1AB的法向量，则，即可取=（2，，1）．设=（x，y，z）是平面ABC的法向量，则，即，可取=（0，，1）．则cos⟨ ，＞==．又因为二面角A1-AB-C为锐二面角，所以二面角A1-AB-C的大小为．【解析】（Ⅰ）过点B1作A1C的垂线，推导出B1O⊥平面AA1C1C，从而B1O⊥AC．由∠BAC=90°，AB∥A1B1，得A1B1⊥AC．从而AC⊥平面A1B1C．由此能证明AC⊥CA1．（Ⅱ）以C为坐标原点，的方向为x轴正方向，||为单位长，建立空间直角坐标系C-xyz．利用向量法能求出二面角A1-AB-C的大小．本题考查线线垂直的证明，考查二面角的求法，考查推理论证能力、运算求解能力，考查函数与方程思想，是中档题．5.【答案】（12分）（1）证明：连接AC，交BD于F，连接EF，因为AB∥DC，所以，即AF=2FC，又PE=2EC，所以AP∥FE，又FE⊆平面BDE，AP⊄平面BDE，所以PA∥平面BED．（4分）（2）解：取AB中点M，连接PM，DM，过点P作PN⊥MD，垂足为N．因为PA=PB，所以PM⊥AB，又MB=DC且MB=DC，则四边形BCDM是平行四边形，所以MD∥BC，所以MD⊥AB，又PM∩MD=M，所以AB⊥平面PMD，又AB⊂平面ABCD，所以平面PMD⊥平面ABCD，又平面PMD∩平面ABCD=MD及PN⊥MD，所以PN⊥平面ABCD．由MB=1，PB=3得，则有PM2+PD2=DM2，即PM⊥PD，所以，所以，（8分）如图建立空间直角坐标系C-xyz，则D（1，0，0），，，，B（0，3，0），A （2，3，0），，，，，，，，，设平面PAB法向量，，，由得，取，可得，，．设平面PBC法向量，，，由得，取，可得，，．．所以＜，＞=．二面角A-PB-C的余弦值为：．（12分）【解析】（1）连接AC，交BD于F，连接EF，通过AB∥DC，证明AP∥FE，即可证明PA∥平面BED．（2）取AB中点M，连接PM，DM，过点P作PN⊥MD，垂足为N．建立空间直角坐标系C-xyz，求出平面PAB法向量，平面PBC法向量，利用空间向量的数量积求解二面角A-PB-C的余弦值即可．本题考查直线与平面平行的判断定理的应用，二面角的平面角的求法，考查空间想象力以及计算能力．6.【答案】证明：以点D为原点，DA,DC,DD1分别为x轴、y轴、z轴，建立空间直角坐标系，令正方体的棱长为2，则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,0),E(1,1,2),F(1,2,1)，（1）,因为，所以,所以EF//A1B；（2）设平面A1BD的一个法向量为，则，即2y-2z=0，2x+2y=0，令x=1，则,因为，所以EF∥平面A1BD；（3）由（2），同理求出平面EFB1的一个法向量，所以平面B1EF∥平面A1BD．【解析】本题主要考查利用空间向量判断线线、线面、面面之间的平行. 建立空间直角坐标系，求出线面的方向向量与法向量，(1)由两条直线的方向向量共线，即可判断出结论；(2)由直线的方向向量与平面的法向量垂直，即可得出结论；(3)由两个平面的法向量共线，即可得出结论.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

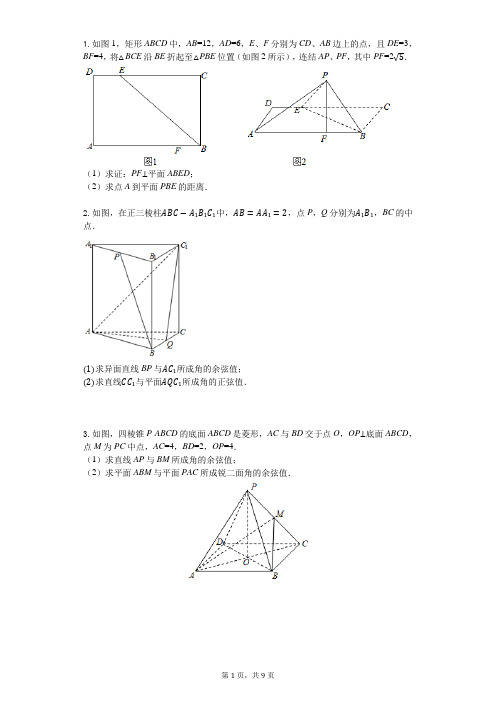
∴二面角 B1-BE-F 的大小为 arccos(
2 )。 3
（4）∵ GD1 =(-1，0，2)，而 GD1 n1 =-2+0+2=0，
z D1 A1 F E B1 C1
∴直线 GD1∥平面 BEFD。（5） DD1 =(0，0，2)， | n1 | 4 4 1 3 ， ∴ n1 的单位向量为(
空间向量
2 2 2 0， 0 0 0， 0 设 AB a ，则 A 2 a，，B 0，2 a，，C 2 a，．设 OP h ，则 P(0， 0，h) ． 2 1 a ， 0 ， h ． ∵ D 为 PC 的中点，∴ OD 4 2 2 1 PA 0， h 2 a，，∴ OD 2 PA ．
∵ PA n1 2 2 0, PA n1，又PA 平面BDE, PA // 平面BDE. （2）由（Ⅰ）知 n1 (1, 1,1) 是平面 BDE 的一个法向量，又 n 2 DA (2,0,0) 是平面 DEC 的一个法向量. 设二面角 B—DE—C 的平面角为，由图可知 n1 , n 2
（2） DA =（2，0，0），设 DA 与面 EFG 所成的角为θ，则 sin
∴直线 C1D 与平面 A1C1B 的所成角为 arcsin
| DA n | 4 21 4 21 = ，∴ arcsin 21 21 | DA || n |
（2）平面 A1C1B 的法向量 n =(2，1，2)，平面 AA1C1C 的法向量 n ' =(2，1，0)，设二者夹角为θ ，∴ cos
∴ cos PA ，n PA ·n PA n 210 ． 30
d
OC n n
(
2 2 , , 0) ( 2, 2,1) 2 2 ( 2, 2,1)
设 PA 与平面 PBC 所成的角为， 210 ，n 则 sin cos PA ． 30
210 ． 30 2 2 1 2 2 1 h a， a， h （3） △PBC 的重心 G ，∴ OG ， 6 a，6 a， 3 6 3 6
（3）∵ PB (2,2,2), DE (0,1,1)
假设棱 PB 上存在点 F，使 PB⊥平面 DEF，设 PF PB(0 1) ，则 PF (2 ,2 ,2 ), DF DP PF (2 ,2 ,2 2 ) ，
2 2 由 PF DF 0得4 4 2 (2 2 ) 0
DD 上的点，且 CF=2GD=2.求：（1） C 到面 EFG 的距离；
∴ PB DE 0 2 2 0, PB DE. （2）DA 与面 EFG 所成的角；（3）在直线 BB 上是否存在点 P，使得 DP//面 EFG?,若存在，找出点 P 的位置，若不存在，试说明理由。
（3）存在点 P，在 B 点下方且 BP=3，此时 P(2，2，－3)
| n n' | 5 5 ， 3 | n | | n' | 3 5
1 5 （或用二倍角公式得 arccos ）。 9 3
DP =(2，2，－3)，∴ DP n =0，∴DP//面 EFG
∴二面角 D-A1C1-B 的大小为 2arccos

2 5 2 2 2 5 ( 2) ( 2) 1
11 0
∴ PA 与平面 PBC 所成的角为 arcsin
。
OP 底面 ABC ．练 4 在三棱锥 P ABC 中，AB BC ，AB BC kPA ，点 O，D 分别是 AC，PC 的中点，（1）求证： OD ∥ 平面 PAB ； 1 （2）当 k 时，求直线 PA 与平面 PBC 所成角的大小； 2 （3）当 k 为何值时， O 在平面 PBC 内的射影恰好为 △PBC 的重心？
n1 · BE =-a+2c=0， n1 · BD =2a+2b=0，
【解析】（1）以 D 为坐标原点，分别以 DA、DC、DP 所在直线为 x 轴、 y 轴、z 轴建立空间直角坐标系，设 PD=DC=2，则 A（2，0，0）， P（0，0，2），E（0，1，1），B（2，2，0），
PA (2,0,2), DE (0,1,1), DB (2,2,0)
空间向量
空间向量
例 1 在空间直角坐标系 D-xyz 中，在正方体 ABCD-A1B1C1D1 中，E、 F、G 分别是 B1C1、C1D1、AD 的中点。求：（1）异面直线 AD1 与 BE 的所成角的大小；（2）直线 AD1 与平面 BEFD 所成角的大小；（3）二面角 B1-BE-F 的大小；（4）求证：直线 GD1∥平面 BEFD；（5）求直线 GD1 与平面 BEFD 的距离。解：设正方体的棱长为 2。则正方体各顶点的坐标分别为：A(2， 0，0)，B(2，2，0)，C(0，2，0)，D(0，0，0)，A1(2，0，2)，B1(2， 2，2)，C1(0，2，2)，D1(0，0，2)。 ∴E(1，2，2)，F(0，1，2)，G(1，0，0)。（1）直线 AD1 的一个法向量为 AD1 =(-2，0，2)，直线 BE 的一个法向量为 BE =(-1，0，2)。设异面直线 AD1 与 BE 的所成角为θ1， ∴cosθ1= |
AD1 n1
(2) 2 0 (2) 2 1
设 n1 ( x, y, z ) 是平面 BDE 的一个法向量，
∴直线 AD1 与平面 BDFE 所成角为 arcsin
2 。 6
则由
n 1 DE 0 y z 0 得取y 1, 得n 1 (1, 1,1). n 1 DB 0 2 x 2 y 0
（法二）∵平面 BEFD 的方程为 4 x 4 y 2 z 0 ， ∴平面 BEFD 的一个法向量为 n1 =(2，-2，1)。（下同法一）（3）∵平面 BDFE 的一个法向量为 n1 =(2，-2，1)。平面 B1BE 的一个法向量为 n2 =(0，1，0)。设 n1 与 n2 的夹角为φ3，∴cosφ3=
取 a=2，得 b=-2，c=1，∴平面 BDFE 的一个法向量为 n1 =(2，-2，1)。设直线 AD1 与平面 BDFE 所成角θ2， AD1 与 n1 所成的角为φ2，则
2 sinθ2=|cosφ2|= | ， | =| |= 2 2 2 2 1 6 | AD1 | | n1 | 2 0 2 2 2 1
AD1 BE | AD1 | | BE |
|=|
(2) (1) 0 0 2 2 2 02 1 02
2 2 1 2
|=
3 10 ， 10
∴异面直线 AD1 与 BE 的所成角为 arccos
3 10 。 10
（ 2）（法一）设平面 BDFE 的一个法向量为 n1 =(a，b，c)，
∵ OG 平面 PBC ，∴OG PB ． 2 1 1 0 ， a ， h · PB a 2 h 2 0 ．又 PB 2 ，∴ OG 6 3
∴OD ∥ PA ，∴ OD ∥平面 PAB ． 1 7 （2） k ，即 PA 2a ，∴ h a， 2 2 2 7 ∴ PA 0， a 2 a， 2 1 1 ， 1 ，可求得平面 PBC 的法向量 n ． 7
分析：建立如图所示的直角坐标系，则 2 2 2 2 A ( , ,0) B ( , , 0) 2 2 2 2 ，，
C ( 2 2 2 2 2 2 , ,0) D ( , , 0) S (0, 0, 2) DB ( 2, 2, 0) CS ( , , 2) 2 2 2 2 2 2 ，，。，。
解：长方体各顶点的坐标分别为：A(1，0，0)， C(0，2，0)，D(0，0，0)，A1(1，0，1)，B1(1，2， 1)，D1(0，0，1)。
D x A
EF n =0， FG n =0， x=2z，z=-2y，取 y=1，
得 n =（－4，1，－2）（1）∵ CF =（0，0，－1）， ∴C 到面 EFG 的距离为 d
∴
(0,1)，此时PF PB
PF 1 3 PB，使得 PB⊥平面 DEF
1 3
1 3
即在棱 PB 上存在点 F，
练 1 在空间直角坐标系 D-xyz 中，长方体 ABCD-A1B1C1D1 中，AB=2，AD=AA1=1，求：（1）直线 C1D 与平面 A1C1B 的所成角；（2）二面角 D-A1C1-B 的大小；（3）顶点 B1 到平面 A1C1B 的距离；
z A1 1 D1 1 C1 B1 C y 2 B
解：如图，以 D 为原点建立空间直角坐标系则 E(1，2，0)，F（0，2，2），G（0，0，1） ∴ EF =（－1，0，2）， FG =（0，－2，－1），设 n =（x，y，z）为面 EFG 的法向量，则 B(1 ， 2 ， 0) ， 1)，C1(0，2，
练 3 如图，正四棱锥 S-ABCD 的高 SO=2，底边长 AB= 2 。求异面直线 BD 和 SC 之间的距离？
（3）在平面 A1C1B 上取点 B，∴ BB1 =(0，0，1)， ∴点 B1 到平面 A1C1B 的距离 d
| n BB1 | |n|
=
2 。 3
练 2 如图，正四棱柱 ABCD ABCD 中，底面边长为 2，侧棱长为 3，E 为 BC 的中点，FG 分别为 CC 、
2 2 1Байду номын сангаас，， )， 3 3 3
D A x B
C
y
2 2 1 2 ∴直线 GD1 与平面 BEFD 的距离 d=(0，0，2)· ( ，， )= 。▋ 3 3 3 3