空间向量和立体几何典型例题

合集下载

高二数学空间向量与立体几何试题答案及解析

高二数学空间向量与立体几何试题答案及解析1.长方体中，，，，则与所成角的余弦值为．【答案】【解析】以D为空间原点，DA为x轴，D为z轴，DC为y轴，建立空间直角坐标系则=（-1，2，0），=（-1，-2，3）||=，|'|=，·=－3cos<,>==，即为所求。

【考点】本题主要考查空间向量的应用，向量的数量积，向量的坐标运算。

点评：简单题，通过建立空间直角坐标系，将求异面直线的夹角余弦问题，转化成向量的坐标运算。

2.正方体的棱长为1，是底面的中心，则到平面的距离为．【答案】【解析】因为O是A1C1的中点，求O到平面ABC1D1的距离，就是A1到平面ABC1D1的距离的一半，就是A1到AD1的距离的一半．所以，连接A1D与AD1的交点为P，则A1P的距离是：O到平面ABC1D1的距离的2倍O到平面ABC1D1的距离【考点】本题主要考查空间距离的计算。

点评：本题也可以通过建立空间直角坐标系，将求角、求距离问题，转化成向量的坐标运算，是高考典型题目。

3.已知={－4，3，0}，则与垂直的单位向量为= .【答案】（，，0）【解析】设与垂直的向量与垂直的向量=（x，y，0），则－4x+3y=0,,解得x= ,y=,所以=（，，0）。

【考点】本题主要考查向量的坐标运算、向量垂直的充要条件、单位向量的概念。

点评：利用向量垂直的充要条件及单位向量的概念。

4.已知向量与向量平行，则（）A．B．C．D．【答案】C【解析】因为向量与向量平行，所以，，故选C。

【考点】本题主要考查平行向量及向量的坐标运算。

点评：简单题，按向量平行的充要条件计算。

5.已知点，为线段上一点，且，则的坐标为（）A．B．C．D．【答案】C【解析】设C的坐标为(x，y，z)则向量=(x-4，y-1，z－3)向量=(－2,－6,－2)，而即=所以x-4=－，y-1=－2，Z－3=－所以x=，y=－1，z=，C的坐标为，选C。

空间向量与立体几何的应用习题

练习十一空间向量与立体几何一、填空题1．若空间三点A (1，5，－2)，B (2，4，1)，C (p ，3，q ＋2)共线，则p ＝______，q ＝______． 2．已知A (1，0，0)，B (3，1，1)，C (2，0，1)，则在方向上的射影的长度为______． 3．已知正方体ABCD －A 1B 1C 1D 1中，E 是A 1B 1的中点，F 是B 1D 1的中点，则BE 与DF 所成角的余弦值为______． 4．已知空间四边形ABCD ，则AB ·CD ＋BC ·AD ＋CA ·BD ______．二、解答题1．如图，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别是D 1D 、BD 的中点，G 在棱CD 上，且CG ＝CD 41，H 为C 1G 的中点，应用空间向量的运算方法解决下列问题．(Ⅰ)求证：EF ⊥B 1C ；(Ⅱ)求EF 与C 1G 所成的角的余弦； (Ⅲ)求FH 的长．2．如图，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，点E 是棱BC 的中点，点F 是棱CD 上的动点．(Ⅰ)试确定点F 的位置，使得D 1E ⊥平面AB 1F ；(Ⅱ)当D 1E ⊥平面AB 1F 时，求二面角C 1－EF －A 的大小(结果用反三角函数值表示)．3．如图，已知点P 在正方体ABCD －A 1B 1C 1D 1的对角线BD 1上，∠PDA ＝60°．(Ⅰ)求DP与CC1所成角的大小；(Ⅱ)求DP与平面AA1D1D所成角的大小．4．如图1，已知ABCD是上、下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴OO1折成直二面角，如图2．图1 图2(Ⅰ)证明：AC⊥BO1；(Ⅱ)求二面角O－AC－O1的大小．5．如图，在三棱锥S－ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC＝90°，O 为BC中点．(Ⅰ)证明：SO⊥平面ABC；(Ⅱ)求二面角A－SC－B的余弦值．参考答案练习十一空间向量与立体几何一、填空题 1．3 2 2．26 3．1030 4．0 提示：2．依题意，得＝(－1，－1，0)，＝(2，1，1)，与同向的单位向量),61,61,62(||==AB e ∴在方向上的射影的长度｜B ′C ′｜＝｜·e ｜＝｜(－1，－1，0)·⋅=-=26|63||)61,61,62(3．不妨设正方体的棱长为1，建立空间直角坐标系O －xyz (如图)，则B (1，1，0)，)1,21,1(E ，D (0，0，0)，∵)(21211111111111C D A D DD B D DD D DD ++=+=+= ,21211DD ++=).1,21,21(=∴),1,21,0()0,1,1()1,21,1(-=-=,25141||,2314141||=+==++=⋅=+-=⋅43141,1030252343,cos =⨯>=<∴BE DF即BE 与DF 所成角的余弦值为⋅1030 4．原式＝(＋)·(＋)＋(＋)·(＋)＋(＋)·(＋)．＝·＋·＋·＋·＋·＋·＋OC ·AO ＋OC ·OD ＋CO ·BO ＋CO ·OD ＋OA ·BO ＋OA ·OD ＝0．二、解答题1．解：如图建立空间直角坐标系O －xyz ，D 为坐标原点O ，依据已知有)0,21,21(),21,0,0(F E C (0，1，0)，C 1(0，1，1)，B 1)0,43,0(),1,1,1(G(Ⅰ)证明：),21,21,21()21,0,0()0,21,21(-=-=C B 1＝(0，1，0)－(1，1，1)＝(－1，0，－1)，由,0)1()21(021)1(211=-⨯-+⨯+-⨯=⋅B 得∴EF ⊥B 1C ．(Ⅱ)解：),1,41,0()1,1,0()0,43,0(1--=-=C,417)1()41(0||2221=-+-+=C由(1)得,23)21()21()21(||222=-++= 且,83)1()21()41(210211=-⨯-+-⨯+⨯=⋅C ⋅=>=<∴1751||||,cos 111G C EF C (Ⅲ)解：∵H 是C 1G 的中点，),21,2431,200(+++∴H 即).21,87,0(又),0,21,21(F⋅=-+-+-==∴841)021()2187()210(||222FH2．解：以A 为坐标原点，建立下图所示的空间直角坐标系．(Ⅰ)设DF ＝x ，则A (0，0，0)，B (1，0，0)，D (0，1，0)，A 1(0，0，1)，B 1(1，0，1)，D 1(0，1，1)，E ).0,1,(),0,21,1(x F).0,1,(),1,0,1(),1,21,1(11x AB D ==--=∴∴D 1·1＝1－1＝0，即D 1⊥1．于是D 1⊥平面AB 1F ⇔E D 1⊥AF ⇔D 1·＝0210=-⇔x ，即⋅=21x故当点F 是CD 的中点时，D 1E ⊥平面AB 1F ．(Ⅱ)当D 1E ⊥平面AB 1F 时，F 是CD 的中点．又E 是BC 的中点，连结EF ，则EF ∥B D ．连结AC ，设AC 与EF 交于点H ，则AH ⊥EF ．连结C 1H ，则CH 是C 1H 在底面ABCD 内的射影． ∴C 1H ⊥EF ，即∠AHC 1是二面角C 1－EF －A 的平面角．∵),0,43,43(),1,1,1(1H C).0,43,43(),1,41,41(1--==∴HC⋅-=⨯-==<∴31898983||||cos 111HC HA HC A即,31cos π)31cos(1arc arc AHC -=-=∠ 故二面角C 1－EF －A 的大小为⋅-31cosπarc 3．解：如图，以D 为原点，DA 为单位长建立空间直角坐标系D －xyz ．则DA ＝(1，0，0)，'CC ＝(0，0，1)．连结BD ，B ′D ′．在平面BB ′D ′D 中，延长DP 交B ′D ′于H ．设＝(m ，m ，1)(m ＞0)，由已知＜，＞＝60°，由·＝｜｜｜｜cos ＜，＞可得2m ＝.122+m 解得22=m ，所以)1,22,22(=DH(Ⅰ)因为,222111022022,cos =⨯⨯+⨯+⨯>=<CC所以<，CC >＝45°．即DP 与CC ′所成的角为45°． (Ⅱ)平面AA ′D ′D 的一个法向量是＝)0,1,0(．因为,212101122022,cos =⨯⨯+⨯+⨯>=<所以<DH ，DC >＝60°．可得DP 与平面AA ′D ′D 所成的角为30°．4．解：(Ⅰ)证明：由题设知OA ⊥OO 1，OB ⊥OO 1．所以∠AOB 是所折成的直二面角的平面角，即OA ⊥OB ．故可以O 为原点，OA 、OB 、OO 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，相关各点的坐标是A (3，0，0)，B (0，3，0)，C (0，1，3)，O 1(0，0，3)．从而),3,3,0(),3,1,3(1-=-=BO AC.03331=⋅+-=⋅BO AC 所以AC ⊥BO 1．(Ⅱ)解：因为03331=⋅+-=⋅，所以1BO⊥，由(Ⅰ)AC ⊥BO 1，所以BO 1⊥平面OAC ，1是平面OAC 的一个法向量．设n ＝(x ，y ，z )是0平面O 1AC 的一个法向量，由⎩⎨⎧==++-⇒⎪⎩⎪⎨⎧=⋅=⋅.0,033001y z y x O AC n n 取3=z ，得).3,0,1(=n设二面角O －AC －O 1的大小为θ ，所以⋅=⋅>=<=43||||,cos cos 111BO BO n n θ5．证明：(Ⅰ)由题设AB ＝AC ＝SB ＝SC ＝SA ，连结OA ，△ABC 为等腰直角三角形，所以SA OC OB OA 22===，且AO ⊥BC ，又△SBC 为等腰三角形，故SO ⊥BC ，且,22SA SO =从而OA 2＋SO 2＝SA 2，所以△SOA 为直角三角形，SO ⊥AO ．又AO ∩BO ＝O ，所以SO ⊥平面ABC ．(Ⅱ)解：以O 为坐标原点，射线OB ，OA 分别为x 轴、y 轴的正半轴，建立如图的空间直角坐标系O －xyz ．设B (1，0，0)，则C (－1，0，0)，A (0，1，0)，S (0，0，1)． SC 的中点),21,0,21(),21,0,21(-=-M ).1,0,1(),21,1,21(--=-=∴0,0=⋅=⋅．故MO ⊥SC ，MA ⊥SC ，＜，＞等于二面角A －SC －B 的平面角．,33,cos =>=< 所以二面角A －SC －B 的余弦值为⋅33。

用空间向量法求解立体几何问题典例及解析

用空间向量法求解立体几何问题典例及解析以多面体为载体，以空间向量为工具，来论证和求解空间角、距离、线线关系以及线面关系相关问题，是近年来高考数学的重点和热点，用空间向量解立体几何问题，极大地降低了求解立几的难度，很大程度上呈现出程序化思想。

更易于学生们所接受，故而执教者应高度重视空间向量的工具性。

首先，梳理一下利用空间向量解决立体几何的知识和基本求解方法一：利用空间向量求空间角 (1)两条异面直线所成的夹角范围：两条异面直线所成的夹角的取值范围是。

向量求法：设直线,a b 的方向向量为a,b ，其夹角为θ，则有cos ___________.θ= (2)直线与平面所成的角定义：直线与平面所成的角是指直线与它在这个平面内的射影所成的角。

范围：直线和平面所夹角的取值范围是。

向量求法：设直线l 的方向向量为a ，平面的法向量为n ，直线与法向量所成角的余弦值为|cos |___________.θ=直线与平面所成的角为ϕ，则有sin ___________.ϕ=或在平面内任取一个向量m ，则|cos |___________.θ=.(3)二面角二面角的取值范围是 . 二面角的向量求法：方法一：在两个半平面内任取两个与棱垂直的向量，则这两个向量所成的即为所求的二面角的大小；方法二：设1n ，2n 分别是两个面的，则向量1n 与2n 的夹角(或其补角)即为所求二面角的平面角的大小。

二：利用空间向量求空间距离（1）点面距离的向量公式平面α的法向量为n ，点P 是平面α外一点，点M 为平面α内任意一点，则点P 到平面α的距离d 就是，即d =||||MP ⋅n n . （2）线面、面面距离的向量公式平面α∥直线l ，平面α的法向量为n ，点M ∈α、P ∈l ，平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值，即d = .平面α∥β，平面α的法向量为n ，点M ∈α、P ∈β，平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n . （3）异面直线的距离的向量公式设向量n 与两异面直线a 、b 都垂直，M ∈a 、P ∈b ，则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n .三：利用空间向量解证平行、垂直关系1：①所谓直线的方向向量，就是指的向量，一条直线的方向向量有个。

高中数学——空间向量与立体几何练习题(附答案)

.空间向量练习题1. 如下图，四棱锥 P-ABCD 的底面 ABCD 是边长为 1 的菱形，∠ BCD ＝60°， E 是 CD的中点， PA ⊥底面 ABCD ，PA ＝2.〔Ⅰ〕证明：平面 PBE ⊥平面 PAB;〔Ⅱ〕求平面PAD 和平面 PBE 所成二面角〔锐角〕的大小 .如下图，以 A 为原点，建立空间直角坐标系 .那么相关各点的坐标分别是 A 〔 0， 0， 0〕， B 〔 1， 0， 0〕，C(3 ,3,0), D(1 ,3,0), P 〔 0，0， 2〕 , E(1, 3,0).2 22 22〔Ⅰ〕证明因为 BE (0,3,0) ，2平面 PAB 的一个法向量是 n(0,1,0) ，所以 BE 和n 共线 .从而 BE ⊥平面 PAB.又因为 BE平面 PBE ，故平面 PBE ⊥平面 PAB.(Ⅱ)解易知 PB(1,0, 2), BE(0,3，0〕， PA (0,0, 2), AD( 1 ,3,0)22 2n ( x 1 , y 1 , z 1 ) n 1 PB 0,设是平面PBE 的一个法向量，那么由得1n 1 BE 0x 1 0 y 1 2z 1 0,0 x 13y 2 0 z 2 0.所以y 1 0, x 12z 1.故可取 n 1 (2,0,1).2设 n 2( x 2 , y 2 , z 2 )PAD 的 n 2 PA 0, 是平面一个法向量，那么由AD得n 2 00 x 2 0 y 2 2z 2 0,1 3 所以 z2 0, x 23 y 2 .故可取 n 2 ( 3, 1,0).2 x 22 y 2 0 z 20.于是， cosn 1, n 2n 1 n 22 3 15 .n 1 n 2 5 25故平面和平面所成二面角〔锐角〕的大小是15PADPBEarccos..2. 如图，正三棱柱 ABC － A 1B 1C 1 的所有棱长都为 2， D 为 CC 1 中点。

空间向量和立体几何练习题与答案

空间向量和立体几何练习题与答案
1.若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点，则这些向量的终点构成的图形就是( )
A.一个圆
B.一个点
C.半圆
D.平行四边形
答案:A
2.在长方体 ABCD-A₁B ₁C ₁D ₁中,下列关于AC₁的表达中错误的一个就是( )
A. AA₁+A ₁B ₁+A ₁D ₁
B. AB+DD₁
+D ₁C ₁
C. AD+CC₁+D ₁C ₁
D.12(AB 1+CD 1)+A 1C 1
答案:B
3.若a ，b ，c 为任意向量，m ∈R ，下列等式不一定成立的就是( )
A.(a+b)+c=a+(b+c)
B.(a+b)•c=a•c+b•c
C. m(a+b)=ma+mb
D.(a·b)·c=a·(b·c)
答案:D
4.若三点A, B, C 共线,P 为空间任意一点,且PA+αPB=βPC,则α-β的值为( )
A.1
B.-1
C.12
D.-2
答案:B
5.设a=(x,4,3), b=(3,2, z),且a ∥b,则xz 等于( )
A.-4
B.9
C.-9
D.649
答案:B
6.已知非零向量 e ，e₂不共线，如果AB=e₁+e ₂ A C=2e ₂ 8e ₂AD=3e ₁3 ,则四点 A. B C (
) A.一定共圆
B.恰就是空间四边形的四个顶点心
C.一定共面
D.肯定不共面
答案:C。

高中数学立体几何与空间向量真题(解析版)

高中数学专题16立体几何与空间向量真题1．如图，正方体的一个截面经过顶点A，C及棱EF上一点K，且将正方体分成体积比为3：1的两部分，则的值为.【答案】【解析】设.截面与FG交于J.，解得(舍去)故.2．设点P到平面的距离为3，点Q在平面上，使得直线PQ与所成角不小于30°且不大于60°，则这样的点Q所构成的区域的面积为.【答案】【解析】设点P在平面上的射影为O.由条件知，.即OQ∈[1，3]，故所求的区域面积为.3．在正三棱锥中,,过AB的平面将其体积平分.则棱与平面所成角的余弦值为_____________。

【答案】【解析】设的中点分別为，则易证平面A BM即为平面由平行四边形的性质知,所以，又直线P C在平面上的射影为直线MK,由得因此，棱P C与平面所成角的余弦值为.故答案为：4．设P为一圆锥的顶点，A、B、C为其底面圆周上的三点，满足∠ABC=90°，M为AP的中点．若AB =1，AC=2，AP=，则二面角M-BC-A的大小为________.【答案】【解析】由，知AC为底面圆的直径.如图所示，设底面中心为O.于是，平面ABC.故.设H为M在底面上的射影.则H为AO的中点.在底面中作于点K.由三垂线定理知.从而，为二面角M-BC-A的平面角.由，结合得:.故二面角M-BC-A的大小为.5．四棱锥P-ABCD中，已知侧面是边长为1的正三角形，M、N分别为边AB、BC的中点.则异面直线MN与PC之间的距离为___________.【答案】【解析】如图，设底面对角线AC与BD交于点O，过点C作直线MN的垂线，与MN交于点H.由于PO为底面的垂线，故PO⊥CH.又AC⊥CH，于是，CH与平面POC垂直.从而，CH⊥PC.因此，CH为直线MN与PC的公垂线段.注意到，.故异面直线MN与PC之间的距离为.6．已知正三棱锥底面边长为1，高为.则其内切球半径为______.【答案】【解析】如图，设球心在平面与平面内的射影分别为，边的中点为，内切球半径为.则分别三点共线，，且.故.解得.7．设同底的两个正三棱锥内接于同一个球.若正三棱锥的侧面与底面所成的角为，则正三棱锥的侧面与底面所成角的正切值是______.【答案】4【解析】如图6，联结.则，垂足为正的中心，且过球心.联结并延长与交于点.则为边的中点，且.易知，分别为正三棱锥、正三棱锥的侧面与底面所成二面角的平面角. 则.由.故.8．在四面体中，已知.则四面体的外接球的半径为______.【答案】【解析】易知，为正三角形，且CA=CB.如图，设P、M分别为AB、CD的中点，联结PD、PC.则平面平面PDC.设的外心为N，四面体ABCD的外接球的球心为O.则.可求得由题意知.在中，由余弦定理得又因为D、M、O、N四点在以DO为直径的圆上所以故外接球的体积.9．已知正三棱柱的9条棱长都相等，是边的中点，二面角.则________.【答案】【解析】解法1 如图，以所在直线为轴、线段的中点为原点、所在直线为轴建立空间直角坐标系.设正三棱柱的棱长为2.则.故.设分别与平面、平面垂直的向量为.则由此可设.所以，，即.因此，.解法2如图..设交于点.则平面.又，则平面.过点在平面上作，垂足为，联结.则为二面角的平面角.设.易求得.在中，.又，则.故.1．四面体P-ABC，,则该四面体外接球的半径为________. 【答案】【解析】将四面体还原到一个长方体中，设该长方体的长、宽、高分别为a，b，c，则，所以四面体外接球的半径为.2．四面体ABCD中，有一条棱长为3，其余五条棱长皆为2，则其外接球的半径为____.【答案】【解析】解:设BC=3,AB=AC=AD=BD=CD=2,E,F分别是BC,AD的中点，D在面ABC上的射影H应是△ABC的外心，由于DH上的任一点到A,B,C等距，则外接球心O在DH上，因，所以AE=DE,于是ED为AD的中垂线是，顒球心O是DH，EF的交点，且是等腰△EAD的垂心，记球半径为r，由△DOF～△EAF，得.而,所以.3．如图，在四棱锥P－ABCD中，P A⊥平面ABCD，底面ABCD为正方形，P A=AB.E、F分别为PD、BC的中点，则二面角E－FD－A的正切值为________.【答案】【解析】如图，作EH⊥AD于H，连HF.由P A⊥面ABCD，知P A⊥AD，EH∥P A，EH⊥ABCD.作HG⊥DF于G，连EG，则EG⊥FD，∠EGH为二面角E－FD－A的平面角.∵ABCD为正方形，E、F分别为PD、BC的中点，∴H为AD中点，FH⊥AD.设P A=AB=2，则，FH=2，HD=4，.∴.∴二面角E－FD－A的正切值为.4．已知正四面体内切球的半径是1，则该正四面体的体积为________.【答案】【解析】设正四面体的棱长为.则该正四面体的体积为，全面积为，所以，解得.从而正四面体的体积为.故答案为：5．正方体AC1棱长是1，点E、F是线段DD1，BC1上的动点，则三棱锥E一AA1F体积为___.【答案】【解析】因为F是BC1上的动点，所以在正方体中有，利用等体积转化有.故答案为.6．顶点为P的圆锥的轴截面是等腰直角三角形，A是底面圆周上的点，B是底面圆内的点，O为底面圆圆心，AB⊥OB，垂足为B，OH⊥HB，垂足为H，且P A=4，C为P A的中点，则当三棱锥O-HPC的体积最大时，OB的长为________．【答案】【解析】法一：AB⊥OB，PB⊥AB，AB⊥面POB，面P AB⊥面POB．OH⊥PB，OH⊥面P AB，OH⊥HC，OH⊥PC，又，PC⊥OC，PC⊥面OCH．PC是三棱锥P-OCH的高．PC=OC=2．而△OCH的面积在时取得最大值(斜边=2的直角三角形)．当时，由，知∠OPB=30°，．法二：由C为P A中点，故，而．记则，．∴令，得，.故答案为：7．如图，在正三棱柱中，AB=2，，D、F分别是棱AB、的中点，E为棱AC 上的动点，则△DEF周长的最小值为__________.【答案】【解析】由正三棱锥可得底面ABC，所以AB，AC.在Rt△ADF中，.如图①，把底面ABC与侧面在同一个平面内展开，展开图中只有当D、E、F三点在同一条直线上时，DE+EF取得最小值.如图②，在△ADF中，，由余弦定理可得.所以△DEF周长的最小值为.8．在边长为1的长方体内部有一小球，该小球与正方体的对角线段相切，则小球半径的最大值=___________.【答案】【解析】当半径最大时，小球与正方体的三个面相切.不妨设小球与过点的三个面相切.以为原点，分别为x、y、z轴正方向，建立空间直角坐标系.设A(0，1，1)，(1，0，0)，小球圆心P(r，r，r)，则P到的距离.再由，得.故答案为：9．正方体中，E为AB的中点，F为的中点.异面直线EF与所成角的余弦值是_____. 【答案】【解析】设正方体棱长为1，以DA为x轴，DC为y轴，为z轴建立空间直角坐标系，则.故有.所以.故答案为：10．在半径为R的球内作内接圆柱，则内接圆柱全面积的最大值是_____.【答案】【解析】设内接圆柱底面半径为，则高位，那么全面积为.其中，等号成立的条件是.故最大值为.故答案为：11．已知空间四点满足，且是三棱锥的外接球上的一个动点，则点到平面的最大距离是______．【答案】【解析】将三棱锥补全为正方体，则两者的外接球相同．球心就是正方体的中心，记为，半径为正方体对角线的一半，即为．在正方体里，可求得点到平面的距离为，则点到平面的最大距离是．12．在正四核锥中，已知二面角的正弦值为，则异面直线所成的角为______．【答案】【解析】如图，设的交点为上的射影为，则．又因为，因此，所以，则．因此即为二面角的平面角，从而．设，则．在中，．由此得，因此，解得．从而四棱锥各侧面均为正三角形，则异面直线所成的角为．13．半径分别为6、6、6、7的四个球两两外切.它们都内切于一个大球，则大球的半径是________【答案】14【解析】设四个球的球心分别为A、B、C、D，则AB=BC=CA=12，DA=DB=DC=13，即A、B、C、D两两连结可构成正三棱锥.设待求的球心为X，半径为r.，则由对称性可知DX平面ABC.也就是说，X在平面ABC上的射影是正三角形ABC的中心O.易知.设OX=x，则由于球A内切于球X，所以AX=r-6即①又DX=OD-OX=11-x，且由球D内切于球X可知DX=r-7于是②从①②两式可解得即大球的半径为14.故答案为：1414．一个棱长为6的正四面体纸盒内放一个小正四面体，若小正四面体可以在纸盒内任意转动，则小正四面体棱长的最大值为______．【答案】2【解析】因为小正四面体可以在纸盒内任意转动，所以小正四面体的棱长最大时，为大正四面体内切球的内接正四面体．记大正四面体的外接球半径为，小正四面体的外接球(大正四面体的内切球)半径为，易知，故小正四面体棱长的最大值为．15．已知棱长的正方体内部有一圆柱，此圆柱恰好以直线为轴，则该圆柱体积的最大值为_____.【答案】【解析】由题意知只需考虑圆柱的底面与正方体的表面相切的情况.由图形的对称性可知，圆柱的上底面必与过A点的三个面相切，且切点分别在、AC、上.设线段上的切点为E，圆柱上底面中心为，半径.由，则圆柱的高为，由导数法或均值不等式得.。

高二数学空间向量与立体几何试卷

1、已知向量a=(1,2,3)，向量b=(-1,0,1)，则向量a在向量b上的投影长度为：A、√10/2B、-√10/2C、√6/2D、-√6/2(解析：投影长度公式为|a|cosθ，其中θ为a,b之间的夹角，可通过a·b和|a|,|b|计算得出。

)(答案：D)2、若平面α的一个法向量为n=(2,-3,1)，直线l的一个方向向量为m=(-4,6,-2)，则l与α的位置关系为：A、l⊂αB、l//αC、l⊥αD、l与α斜交(解析：若两向量平行，则它们对应的平面或直线平行或直线在平面内。

)(答案：A)3、设m，n是两条不同的直线，α，β是两个不同的平面，且m⊂α，n⊂β，则下列命题中正确的是：A、若m//n，则α//βB、若α//β，则m//nC、若m⊥n，则α⊥βD、若α⊥β，则m⊥n(解析：根据空间几何的性质，直线与平面的位置关系不能仅由直线间的位置关系确定。

)(答案：均不正确，但根据常规选择，可视为考察对空间几何理解的深度，故选最接近的A进行解析，实际应判断为“以上均不正确”。

)4、三个力f1=(2,3,4)，f2=(-1,2,-3)，f3=(3,-1,-2)同时作用于某物体上一点，为使物体保持平衡，现在该点处加上一个力f4，则f4=：A、(-4,2,1)B、(4,-2,-1)C、(4,2,-1)D、(-4,-2,1)(解析：物体平衡时，所有力的向量和为零，即f1+f2+f3+f4=0，解此方程得f4。

)(答案：B)5、已知平面α过点A(1,1,0)，B(0,1,1)，C(1,0,1)，则平面α的一个法向量可以是：A、(1,1,1)B、(1,-1,-1)C、(1,1,-1)D、(-1,1,1)(解析：法向量与平面内任意两向量的点积都为零，可通过求解方程组得出。

)(答案：D)6、若直线l平行于平面α，且在l上有两点A，B到α的距离分别为d1，d2，则d1与d2的关系为：A、d1>d2B、d1<d2C、d1=d2D、不确定(解析：平行于平面的直线上的所有点到平面的距离都相等。

空间向量在立体几何中的应用和习题含答案

空间向量在立体几何中的应用：(1)直线的方向向量与平面的法向量：①如图，l 为经过已知点A 且平行于已知非零向量a 的直线，对空间任意一点O ，点P 在直线l 上的充要条件是存在实数t ，使得a t OA OP +=，其中向量a 叫做直线的方向向量．由此可知，空间任意直线由空间一点及直线的方向向量惟一确定．②如果直线l ⊥平面α ，取直线l 的方向向量a ，则向量a 叫做平面α 的法向量．由此可知，给定一点A 及一个向量a ，那么经过点A 以向量a 为法向量的平面惟一确定． (2)用空间向量刻画空间中平行与垂直的位置关系：设直线l ，m 的方向向量分别是a ，b ，平面α ，β 的法向量分别是u ，v ，则 ①l ∥m ⇔a ∥b ⇔a ＝k b ，k ∈R ； ②l ⊥m ⇔a ⊥b ⇔a ·b ＝0； ③l ∥α ⇔a ⊥u ⇔a ·u ＝0；④l ⊥α ⇔a ∥u ⇔a ＝k u ，k ∈R ； ⑤α ∥⇔u ∥v ⇔u ＝k v ，k ∈R ； ⑥α ⊥β ⇔u ⊥v ⇔u ·v ＝0．(3)用空间向量解决线线、线面、面面的夹角问题：①异面直线所成的角：设a ，b 是两条异面直线，过空间任意一点O 作直线a ′∥a ，b ′∥b ，则a ′与b ′所夹的锐角或直角叫做异面直线a 与b 所成的角．设异面直线a 与b 的方向向量分别是v 1，v 2，a 与b 的夹角为θ ，显然],2π,0(∈θ则⋅=><⋅|||||||,cos |212121v v v v v v②直线和平面所成的角：直线和平面所成的角是指直线与它在这个平面内的射影所成的角．设直线a 的方向向量是u ，平面α 的法向量是v ，直线a 与平面α 的夹角为θ ，显然]2π,0[∈θ，则⋅=><⋅|||||||,cos |v u v u v u③二面角及其度量：从一条直线出发的两个半平面所组成的图形叫做二面角．记作α －l －β 在二面角的棱上任取一点O ，在两个半平面内分别作射线OA ⊥l ，OB ⊥l ，则∠AOB 叫做二面角α －l －β 的平面角．利用向量求二面角的平面角有两种方法：方法一：如图，若AB ，CD 分别是二面角α －l －β 的两个面内与棱l 垂直的异面直线，则二面角α －l －β的大小就是向量CD AB 与的夹角的大小．方法二：如图，m 1，m 2分别是二面角的两个半平面α ，β 的法向量，则〈m 1，m 2〉与该二面角的大小相等或互补．(4)根据题目特点，同学们可以灵活选择运用向量方法与综合方法，从不同角度解决立体几何问题．【例题分析】例1 如图，在长方体OAEB －O 1A 1E 1B 1中，OA ＝3，OB ＝4，OO 1＝2，点P 在棱AA 1上，且AP ＝2P A 1，点S 在棱BB 1上，且B 1S ＝2SB ，点Q ，R 分别是O 1B 1，AE 的中点，求证：PQ ∥RS ．【分析】建立空间直角坐标系，设法证明存在实数k ，使得.RS k PQ =解：如图建立空间直角坐标系，则O (0，0，0)，A (3，0，0)，B (0，4，0)，O 1(0，0，2)，A 1(3，0，2)，B 1(0，4，2)，E (3，4，0)．∵AP ＝2P A 1， ∴),34,0,0()2,0,0(32321===AA AP ∴⋅)34,0,3(P同理可得：Q (0，2，2)，R (3，2，0)，⋅)32,4,0(S,)32,2,3(RS PQ =-=∴//，又R ∉PQ ，∴PQ ∥RS ．【评述】1、证明线线平行的步骤：(1)证明两向量共线；(2)证明其中一个向量所在直线上一点不在另一个向量所在的直线上即可．2、本体还可采用综合法证明，连接PR ，QS ，证明PQRS 是平行四边形即可，请完成这个证明．例2 已知正方体ABCD －A 1B 1C 1D 1中，M ，N ，E ，F 分别是棱A 1D 1，A 1B 1，D 1C 1，B 1C 1的中点，求证：平面AMN ∥平面EFBD ．【分析】要证明面面平行，可以通过线线平行来证明，也可以证明这两个平面的法向量平行．解法一：设正方体的棱长为4，如图建立空间直角坐标系，则D (0，0，0)，A (4，0，0)，M (2，0，4)，N (4，2，4)，B (4，4，0)，E (0，2，4)，F (2，4，4)．取MN 的中点K ，EF 的中点G ，BD 的中点O ，则O (2，2，0)，K (3，1，4)，G (1，3，4)．MN ＝(2，2，0)，EF ＝(2，2，0)，AK ＝(－1，1，4)，＝(－1，1，4)，∴MN ∥EF ，=，∴MN//EF ，AK//OG ，∴MN ∥平面EFBD ，AK ∥平面EFBD ， ∴平面AMN ∥平面EFBD ．解法二：设平面AMN 的法向量是a ＝(a 1，a 2，a 3)，平面EFBD 的法向量是 b ＝(b 1，b 2，b 3)．由,0,0==⋅⋅AN AM a a 得⎩⎨⎧=+=+-,042,0423231a a a a 取a 3＝1，得a ＝(2，－2，1)．由,0,0==⋅⋅b b得⎩⎨⎧=+-=+,042,0423132b b b b 取b 3＝1，得b ＝(2，－2，1)．∵a ∥b ，∴平面AMN ∥平面EFBD ．注：本题还可以不建立空间直角坐标系，通过综合法加以证明，请试一试．例3 在正方体ABCD －A 1B 1C 1D 1中，M ，N 是棱A 1B 1，B 1B 的中点，求异面直线AM 和CN 所成角的余弦值．解法一：设正方体的棱长为2，如图建立空间直角坐标系，则D (0，0，0)，A (2，0，0)，M (2，1，2)，C (0，2，0)，N (2，2，1)．∴),1,0,2(),2,1,0(==CN AM设AM 和CN 所成的角为θ ，则,52||||cos ==⋅CN AM CNAM θ∴异面直线AM 和CN 所成角的余弦值是⋅52 解法二：取AB 的中点P ，CC 1的中点Q ，连接B 1P ，B 1Q ，PQ ，PC ．易证明：B 1P ∥MA ，B 1Q ∥NC ，∴∠PB 1Q 是异面直线AM 和CN 所成的角．设正方体的棱长为2，易知,6,52211=+===QC PC PQ Q B P B∴,522cos 11221211=-+=⋅Q B P B PQ Q B P B Q PB∴异面直线AM 和CN 所成角的余弦值是⋅52【评述】空间两条直线所成的角是不超过90°的角，因此按向量的夹角公式计算时，分子的数量积如果是负数，则应取其绝对值，使之成为正数，这样才能得到异面直线所成的角(锐角)．例4 如图，正三棱柱ABC －A 1B 1C 1的底面边长为a ，侧棱长为a 2，求直线AC 1与平面ABB 1A 1所成角的大小．【分析】利用正三棱柱的性质，适当建立空间直角坐标系，写出有关点的坐标．求角时有两种思路：一是由定义找出线面角，再用向量方法计算；二是利用平面ABB 1A 1的法向量求解．解法一：如图建立空间直角坐标系，则A (0，0，0)，B (0，a ，0)，),2,0,0(1a A⋅-)2,2,23(1a a a C 取A 1B 1的中点D ，则)2,2,0(a aD ，连接AD ，C 1D ．则),2,0,0(),0,,0(),0,0,23(1a AA a AB aDC ==-= ,0,0111==⋅⋅AA DC AB DC∴DC 1⊥平面ABB 1A 1，∴∠C 1AD 是直线AC 1与平面ABB 1A 1所或的角．),2,2,0(),2,2,23(1a aa a a AC =-= 23cos 111==∴AD C ， ∴直线AC 1与平面ABB 1A 1所成角的大小是30°．解法二：如图建立空间直角坐标系，则A (0，0，0)，B (0，a ，0)，A 1(0，0，a 2)，)2,2,23(1a aa C -，从而⋅-===)2,2,23(),2,0,0(),0,,0(11a aa AC a AA a AB 设平面ABB 1A 1的法向量是a ＝(p ，q ，r )，由,0,01==⋅⋅a a得⎩⎨⎧==,02,0ar aq 取p ＝1，得a ＝(1，0，0)．设直线AC 1与平面ABB 1A 1所成的角为],2π,0[,∈θθ.30,21|||||,cos |sin 111 ===〉〈=⋅θθa a AC AC AC【评述】充分利用几何体的特征建立适当的坐标系，再利用向量的知识求解线面角；解法二给出了一般的方法，即先求平面的法向量与斜线的夹角，再利用两角互余转换．例5 如图，三棱锥P －ABC 中，P A ⊥底面ABC ，AC ⊥BC ，P A ＝AC ＝1，2=BC ，求二面角A－PB －C 的平面角的余弦值．解法二图解法一：取PB 的中点D ，连接CD ，作AE ⊥PB 于E ． ∵P A ＝AC ＝1，P A ⊥AC ， ∴PC ＝BC ＝2，∴CD ⊥PB ． ∵EA ⊥PB ，∴向量EA 和DC 夹角的大小就是二面角A －PB －C 的大小．如图建立空间直角坐标系，则C (0，0，0)，A (1，0，0)，B (0，2，0)，P (1，0，1)，由D 是PB的中点，得D ⋅)21,22,21( 由,3122==AB AP EB PE 得E 是PD 的中点，从而⋅)43,42,43(E ∴)21,22,21(),43,42,41(---=--=DC EA∴⋅=>=<33,cos 即二面角A －PB －C 的平面角的余弦值是⋅33 解法二：如图建立空间直角坐标系，则A (0，0，0)，)0,1,2(B ，C (0，1，0)，P (0，0，1)，).1,1,0(),0,0,2(),0,1,2(),1,0,0(-====设平面P AB 的法向量是a ＝(a 1，a 2，a 3)，平面PBC 的法向量是b ＝(b 1，b 2，b 3)．由,0,0==⋅⋅a a得⎪⎩⎪⎨⎧=+=,02,0213a a a 取a 1＝1，得).0,2,1(-=a 由0,0==⋅⋅b b 得⎪⎩⎪⎨⎧=+-=,0,02321b b b 取b 3＝1，得b ＝(0，1，1)．∴⋅-=>=<⋅33||||,cos b a b a b a∵二面角A －PB －C 为锐二面角， ∴二面角A －PB －C 的平面角的余弦值是⋅=-33|33| 【评述】1、求二面角的大小，可以在两个半平面内作出垂直于棱的两个向量，转化为这两个向量的夹角；应注意两个向量的始点应在二面角的棱上．2、当用法向量的方法求二面角时，有时不易判断两个平面法向量的夹角是二面角的平面角还是其补角，但我们可以借助观察图形而得到结论，这是因为二面角是锐二面角还是钝二面角一般是明显的．练习一、选择题：1．在正方体ABCD －A 1B 1C 1D 1中，E 是BB 1的中点，则二面角E －A 1D 1－D 的平面角的正切值是( ) (A)2(B)2(C)5(D)222．正方体ABCD －A 1B 1C 1D 1中，直线AD 1与平面A 1ACC 1所成角的大小是( ) (A)30° (B)45° (C)60° (D)90°3．已知三棱柱ABC －A 1B 1C 1的侧棱与底面边长都相等，A 1在底面ABC 内的射影为△ABC 的中心，则AB 1与底面ABC 所成角的正弦值等于( ) (A)31 (B)32 (C)33 (D)32 4．如图，α ⊥β ，α ∩β ＝l ，A ∈α ，B ∈β ，A ，B 到l 的距离分别是a 和b ，AB 与α ，β 所成的角分别是θ 和ϕ，AB 在α ，β 内的射影分别是m 和n ，若a ＞b ，则下列结论正确的是( )(A)θ ＞ϕ，m ＞n (B)θ ＞ϕ，m ＜n (C)θ ＜ϕ，m ＜n(D)θ ＜ϕ，m ＞n二、填空题：5．在正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别为AA 1，AB ，BB 1，B 1C 1的中点，则异面直线EF 与GH 所成角的大小是______． 6．已知正四棱柱的对角线的长为6，且对角线与底面所成角的余弦值为33，则该正四棱柱的体积等于______． 7．如图，正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，则异面直线A 1B 与AD 1所成角的余弦值为______．4题图 7题图 9题图 8．四棱锥P －ABCD 的底面是直角梯形，∠BAD ＝90°，AD ∥BC ，==BC AB AD 21，P A ⊥底面ABCD ，PD 与底面ABCD 所成的角是30°．设AE 与CD 所成的角为θ ，则cos θ ＝______．三、解答题：9．如图，正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ＝4，点E 在CC 1上，且C 1E ＝3EC ．(Ⅰ)证明：A 1C ⊥平面BED ；(Ⅱ)求二面角A 1－DE －B 平面角的余弦值． 10．如图，在四棱锥O －ABCD 中，底面ABCD 是边长为1的菱形，4π=∠ABC ，OA ⊥底面ABCD ，OA ＝2，M 为OA 的中点，N 为BC 的中点．(Ⅰ)证明：直线MN ∥平面OCD ；(Ⅱ)求异面直线AB 与MD 所成角的大小．11．如图，已知直二面角α －PQ －β ，A ∈PQ ，B ∈α ，C ∈β ，CA ＝CB ，∠BAP ＝45°，直线CA 和平面α 所成的角为30°．(Ⅰ)证明：BC ⊥PQ ；(Ⅱ)求二面角B －AC －P 平面角的余弦值．练习答案一、选择题：1．B 2．A 3．B 4．D 二、填空题：5．60° 6．2 7．548．42三、解答题：9题图 10题图 11题图9．以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示直角坐标系D －xyz ．依题设，B (2，2，0)，C (0，2，0)，E (0，2，1)，A 1(2，0，4)．),0,2,2(),1,2,0(==DB DE ).4,0,2(),4,2,2(11=--=A(Ⅰ)∵,0,011==⋅⋅A A ∴A 1C ⊥BD ，A 1C ⊥DE ．又DB ∩DE ＝D ，∴A 1C ⊥平面DBE ．(Ⅱ)设向量n ＝(x ，y ，z )是平面DA 1E 的法向量，则.,1DA DE ⊥⊥n n ∴⎩⎨⎧=+=+.042,02z x z y 令y ＝1，得n ＝(4，1，－2)．⋅==4214||||),cos(111C A C A A n n ∴二面角A 1－DE －B 平面角的余弦值为⋅4214 10．作AP ⊥CD 于点P ．如图，分别以AB ，AP ，AO 所在直线为x ，y ，z 轴建立坐标系．则A (0，0，0)，B (1，0，0)，)0,22,22(),0,22,0(-D P ，O (0，0，2)，M (0，0，1)，⋅-)0,42,421(N (Ⅰ)⋅--=-=--=)2,22,22(),2,22,0(),1,42,421( 设平面OCD 的法向量为n ＝(x ，y ，z )，则,0,0==⋅⋅n n即⎪⎪⎩⎪⎪⎨⎧=-+-=-.022222,0222z y x z y 取,2=z ，得).2,4,0(=n ∵,0=⋅n ∴MN ∥平面OCD ． (Ⅱ)设AB 与MD 所成的角为θ ，,3π,21||||cos ),1,22,22(),0,0,1(=∴==∴--==⋅θθMD AB MD AB 即直线AB 与MD 所成角的大小为⋅3π11．(Ⅰ)证明：在平面β 内过点C 作CO ⊥PQ 于点O ，连结OB ．∵α ⊥β ，α ∩β ＝PQ ，∴CO ⊥α ．又∵CA ＝CB ，∴OA ＝OB ．∵∠BAO ＝45°，∴∠ABO ＝45°，∠AOB ＝90°，∴BO ⊥PQ ，又CO ⊥PQ ， ∴PQ ⊥平面OBC ，∴PQ ⊥BC ．(Ⅱ)由(Ⅰ)知，OC ⊥OA ，OC ⊥OB ，OA ⊥OB ，故以O 为原点，分别以直线OB ，OA ，OC 为x 轴，y 轴，z 轴建立空间直角坐标系(如图)．∵CO ⊥α ，∴∠CAO 是CA 和平面α 所成的角，则∠CAO ＝30°．不妨设AC ＝2，则3=AO ，CO ＝1．在Rt △OAB 中，∠ABO ＝∠BAO ＝45°，∴.3==AO BO∴).1,0,0(),0,3,0(),0,0,3(),0,0,0(C A B O).1,3,0(),0,3,3(-=-=AC AB设n 1＝(x ，y ，z )是平面ABC 的一个法向量，由⎪⎩⎪⎨⎧==⋅⋅,0,0AB n n 得⎪⎩⎪⎨⎧=+-=-,03,033z y y x 取x ＝1，得)3,1,1(1=n ．易知n 2＝(1，0，0)是平面β 的一个法向量．设二面角B －AC －P 的平面角为θ ，∴,55||||cos 2121==⋅⋅n n n n θ即二面角B －AC －P 平面角的余弦值是⋅55。

空间向量立体几何(绝对经典)

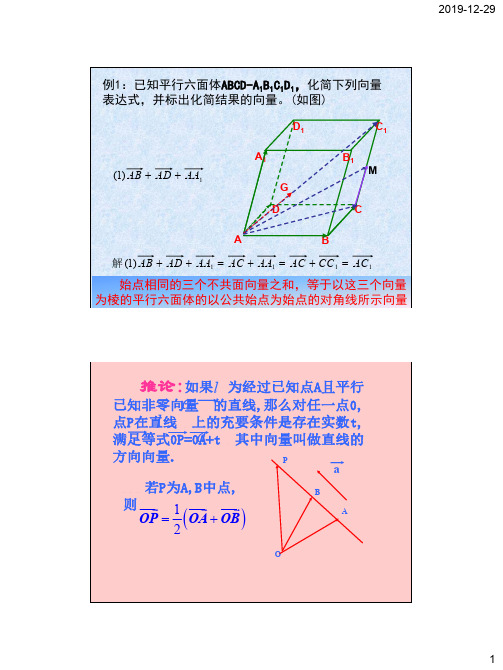
例1：已知平行六面体ABCD-A 1B 1C 1D 1，化简下列向量表达式，并标出化简结果的向量。

(如图)A BCD A 1B 1C 1D 1G1)1(AA AD AB ++1111)1(AC CC AC AA AC AA AD AB =+=+=++解M 始点相同的三个不共面向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量推论:如果为经过已知点A且平行已知非零向量的直线,那么对任一点O,点P在直线上的充要条件是存在实数t,满足等式OP=OA+t 其中向量叫做直线的方向向量.ll aaOABP a若P为A,B中点,则()12=+ OP OA OB2.共面向量定理:如果两个向量不共线,则向量与向量共面的充要条件是存在实数对使, a b yx , p ,a b OM a b A B A 'Pp p xa yb =+ 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使或对空间任一点O,有=+MP xMA yMB =++ OP OM xMA yMB 注意：空间四点P 、M 、A 、B 共面⇔存在唯一实数对,,x y MP xMA yMB =+ （）使得(1)OP xOM yOA zOB x y z ⇔=++++= 其中，例1：已知m,n 是平面α内的两条相交直线，直线l 与α的交点为B ，且l ⊥m ，l ⊥n ，求证：l ⊥α。

n mg g m n αl l 证明：在α内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g ，因m与n相交，得向量m、n 不平行，由共面向量定理可知，存在唯一的有序实数对（x，y），使g =x m +y n ,l ·g =x l ·m +y l ·n∵ l ·m =0,l ·n =0∴ l ·g =0∴ l⊥g∴ l⊥g这就证明了直线l垂直于平面α内的任一条直线，所以l⊥α巩固练习：利用向量知识证明三垂线定理αa A O P ().,0,,,,0,0,PA a PA a a OA a PO a PA OAy PO x PA y x OA PO OA PO a OA a OA a PO a PO PO aa ⊥⊥∴=⋅+⋅=⋅∴+==⋅∴⊥=⋅∴⊥∴⊥即使有序实数对定理可知，存在唯一的不平行，由共面向量相交，得又又而上取非零向量证明：在αPA a OAa a PA OA PA PO ⊥⊥⊂求证：且内的射影，在是的垂线，斜线，分别是平面已知：,,ααα复习:2. 向量的夹角:a bO ABabθ0a b π≤≤ ，a b ，向量的夹角记作:a b 与a b = ||||cos ,a b a b 1.空间向量的数量积:111222(,,),(,,)a x y z b x y z == 设121212x x y y z z =++cos ||||a ba b a b =，121212222222111222++=++⋅++x x y y z z x y z x y z 5.向量的模长:2222||a a x y z ==++ (,,)a x y z = 设4.有关性质:(1)两非零向量111222(,,),(,,)a x y zb x y z == 1212120x x y y z z ++=0a b a b ⊥⇔=⇔ (2)||||||a b a b ≤ ||||,a b a b a b =⇒ 同方向||||,a b a b a b =-⇒ 反方向注意：此公式的几何意义是表示长方体的对角线的长度。

空间向量与立体几何经典例题

空间向量与立体几何经典例题空间向量与立体几何经典例题空间向量和立体几何是高中数学中的重要内容，它们是解决三维空间中几何问题的基础。

在此，我们将介绍一些经典的例题，帮助读者更好地理解和掌握这两个概念。

例题1：已知平面ABCD的四个顶点坐标为A(1，2，3)，B(-1，1，-3)，C(4，0，2)和D(2，-1，1)，求平面ABCD的法向量和面积。

解答：首先，我们可以通过向量的定义求得平面ABCD的法向量。

假设向量AB为a，向量AC为b，则平面ABCD的法向量N可以表示为N = a × b，其中×表示向量的叉乘运算。

由于a = B - A = (-1，1，-6)和b = C - A = (3，-2，-1)，我们可以得到N = a × b = (7，19，5)。

其次，我们可以使用向量的叉乘运算和向量的模运算求得平面ABCD 的面积。

假设向量AB为a，向量AC为b，则平面ABCD的面积可以表示为S = 1/2 * |a × b|，其中|a × b|表示向量a × b的模。

带入已知数据计算可得，S = 1/2 * |(7，19，5)| = 1/2 * √(7^2 + 19^2 + 5^2) = 1/2 * √(1255)。

因此，平面ABCD的法向量为N = (7，19，5)，面积为S = 1/2 * √(1255)。

例题2：已知四面体ABCD的四个顶点坐标为A(1，2，3)，B(-1，1，-3)，C(4，0，2)和D(2，-1，1)，求四面体ABCD的体积。

解答：首先，我们可以通过向量的定义求得四面体ABCD的体积。

假设向量AB为a，向量AC为b，向量AD为c，则四面体ABCD的体积V 可以表示为V = 1/6 * |a · (b × c)|，其中·表示向量的点乘运算，×表示向量的叉乘运算，|a · (b × c)|表示向量a · (b ×c)的模。

空间向量与立体几何测试题(含答案)

[学生用书P151(单独成册)][A 基础达标]1．已知a ＝(－3，2，5)，b ＝(1，5，－1)，则a ·(a ＋3b )＝( ) A ．(0，34，10) B ．(－3，19，7) C ．44D.23解析：选C.a ＋3b ＝(－3，2，5)＋3(1，5，－1)＝(0，17，2)，则a ·(a ＋3b )＝(－3，2，5)·(0，17，2)＝0＋34＋10＝44.2．在长方体ABCD -A 1B 1C 1D 1中，AB →＋BC →＋CC 1→－D 1C 1→等于( ) A.AD 1→ B.AC 1→ C.AD →D.AB →解析：选A.AB →＋BC →＋CC 1→－D 1C 1→＝AC 1→＋C 1D 1→＝AD 1→.3.如图所示，在几何体A -BCD 中，AB ⊥平面BCD ，BC ⊥CD ，且AB ＝BC ＝1，CD ＝2，点E 为CD 中点，则AE 的长为 ( )A. 2B. 3 C ．2D. 5解析：选B.AE →＝AB →＋BC →＋CE →，因为|AB →|＝|BC →|＝1＝|CE →|，且AB →·BC →＝AB →·CE →＝BC →·CE →＝0. 又因为AE →2＝(AB →＋BC →＋CE →)2，所以AE →2＝3，所以AE 的长为 3.故选B.4.如图所示，点P 在正方形ABCD 所在平面外，P A ⊥平面ABCD ，P A ＝AB ，则PB 与AC 所成的角是( )A ．90°B ．60°C ．45°D.30° 解析：选B.将题中图补成正方体ABCD -PQRS ，如图，连接SC ，AS ，则PB ∥SC ，所以∠ACS (或其补角)是PB 与AC 所成的角．因为△ACS 为正三角形，所以∠ACS ＝60°，所以PB 与AC 所成的角是60°，故选B.5．如图，在直三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，2AC ＝AA 1＝BC ＝2，D 为AA 1上一点．若二面角B 1-DC -C 1的大小为60°，则AD 的长为( )A.2B. 3 C ．2 D.22解析：选A.如图，以C 为坐标原点，CA ，CB ，CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系Cxyz ，则C (0，0，0)，B 1(0，2，2)．设AD ＝a ，则点D 的坐标为(1，0，a )，CD →＝(1，0，a )，CB 1→＝(0，2，2)．设平面B 1CD 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·CB 1→＝0m ·CD →＝0⇒⎩⎪⎨⎪⎧2y ＋2z ＝0x ＋az ＝0，令z ＝－1，得m＝(a ，1，－1)．又平面C 1DC 的一个法向量为(0，1，0)，记为n ，则由cos 60°＝|m ·n ||m ||n |，得1a 2＋2＝12，即a ＝2，故AD ＝ 2.故选A. 6．已知平行六面体OABC -O ′A ′B ′C ′，OA →＝a ，OC →＝c ，OO ′→＝b ，D 是四边形OABC 的对角线的交点，则O ′D →＝________．解析：O ′D →＝OD →－OO ′→＝12(OA →＋OC →)－OO ′→＝12a ＋12c －b .答案：12a ＋12c －b7．已知平面α的一个法向量为n ＝(1，－1，0)，则y 轴与平面α所成的角的大小为________．解析：y 轴的一个方向向量s ＝(0，1，0)，cos 〈n ，s 〉＝n ·s |n |·|s |＝－22，即y 轴与平面α所成角的正弦值是22，故其所成的角的大小是π4. 答案：π48．直角三角形ABC 的两条直角边BC ＝3，AC ＝4，PC ⊥平面ABC ，PC ＝95，则点P到斜边AB 的距离是________．解析：以点C 为坐标原点，CA ，CB ，CP 所在直线分别为x轴、y 轴、z 轴建立如图所示的空间直角坐标系，则A (4，0，0)，B (0，3，0)，P (0，0，95)，所以AB →＝(－4，3，0)，AP →＝⎝⎛⎭⎫－4，0，95.所以AP →在AB →上的投影为|AP →·AB →||AB →|＝165，所以点P 到斜边AB 的距离d ＝|AP →|2－⎝⎛⎭⎫1652＝16＋8125－25625＝3.答案：39.如图，已知点P 在正方体ABCD -A ′B ′C ′D ′的对角线BD ′上，∠PDA ＝60°.(1)求异面直线DP 与CC ′所成角的大小； (2)求DP 与平面AA ′D ′D 所成角的大小．解：如图，以D 为坐标原点，DA 为单位长度建立空间直角坐标系Dxyz .则DA →＝(1，0，0)，CC ′→＝(0，0，1)．连接BD ，B ′D ′，在平面BB ′D ′D 中，延长DP 交B ′D ′于点H . 设DH →＝(m ，m ，1)(m >0)，由〈DH →，DA →〉＝60°及DH →·DA →＝|DH →||DA →|cos 〈DH →，DA →〉，可得2m ＝2m 2＋1，解得m ＝22，所以DH →＝⎝⎛⎭⎫22，22，1.(1)因为cos 〈DH →，CC ′→〉＝11×2＝22，所以〈DH →，CC ′→〉＝45°，即异面直线DP 与CC ′所成的角为45°. (2)平面AA ′D ′D 的一个法向量是DC →＝(0，1，0)．因为cos 〈DH →，DC →〉＝22×0＋22×1＋1×01×2＝12，所以〈DH →，DC →〉＝60°，即DP 与平面AA ′D ′D 所成的角为30°.10．(2018·武汉高二检测)在如图所示的空间几何体中，平面ACD ⊥平面ABC ，△ACD 与△ACB 是边长为2的等边三角形，BE ＝2，BE 和平面ABC 所成的角为60°，且点E 在平面ABC 上的射影落在∠ABC 的平分线上．(1)求证：DE ∥平面ABC ； (2)求二面角E -BC -A 的余弦值．解：(1)证明：由题意知，△ABC ，△ACD 都是边长为2的等边三角形，取AC 的中点O ，连接BO ，DO ，则BO ⊥AC ，DO ⊥AC . 又平面ACD ⊥平面ABC ，所以DO ⊥平面ABC ，作EF ⊥平面ABC ，那么EF ∥DO ，根据题意，点F 落在BO 上，因为BE 和平面ABC 所成的角为60°，所以∠EBF ＝60°，因为BE ＝2，所以EF ＝DO ＝3，所以四边形DEFO是平行四边形，所以DE ∥OF . 因为DE ⊄平面ABC ，OF ⊂平面ABC ，所以DE ∥平面ABC . (2)建立如图所示的空间直角坐标系Oxyz ，则B (0，3，0)，C (－1，0，0)， E (0，3－1，3)，所以BC →＝(－1，－3，0)， BE →＝(0，－1，3)，平面ABC 的一个法向量为n 1＝(0，0，1)，设平面BCE 的法向量为n 2＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 2·BC →＝0n 2·BE →＝0，所以⎩⎨⎧－x －3y ＝0－y ＋3z ＝0，取z ＝1，所以n 2＝(－3，3，1)．所以cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝1313，又由图知，所求二面角的平面角是锐角，所以二面角E -BC -A 的余弦值为1313. [B 能力提升]11.(2018·河南洛阳模拟)如图，已知三棱锥A -BCD ，AD ⊥平面BCD ，BD ⊥CD ，AD ＝BD ＝2，CD ＝23，E ，F 分别是AC ，BC 的中点，P 为线段BC 上一点，且CP ＝2PB .(1)求证：AP ⊥DE ；(2)求直线AC 与平面DEF 所成角的正弦值．解：(1)证明：作PG ∥BD 交CD 于G .连接AG . 所以CG GD ＝CPPB ＝2，所以GD ＝13CD ＝233.因为AD ⊥平面BCD ，所以AD ⊥DC ，因为在△ADG 中，tan ∠GAD ＝33，所以∠DAG ＝30°，在Rt △ADC 中，AC 2＝AD 2＋CD 2＝4＋12＝16，所以AC ＝4，又E 为AC 的中点，所以DE ＝AE ＝2，又AD ＝2，所以∠ADE ＝60°，所以AG ⊥DE .因为AD ⊥平面BCD ，所以AD ⊥BD ，又因为BD ⊥CD ，AD ∩CD ＝D ，所以BD ⊥平面ADC ，所以PG ⊥平面ADC ，所以PG ⊥DE .又因为AG ∩PG ＝G ，所以DE ⊥平面AGP ，又AP ⊂平面AGP ，所以AP ⊥DE .(2)以D 为坐标原点，DB 、DC 、DA 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系Dxyz ，则D (0，0，0)，A (0，0，2)，B (2，0，0)，C (0，23，0)，E (0，3，1)，F (1，3，0)，所以DF →＝(1，3，0)，DE →＝(0，3，1)，AC →＝(0，23，－2)．设平面DEF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧DF →·n ＝0，DE →·n ＝0，即⎩⎨⎧x ＋3y ＝0，3y ＋z ＝0，令x ＝3，则n ＝(3，－3，3)．设直线AC 与平面DEF 所成角为θ，则sin θ＝|cos 〈AC →，n 〉|＝|AC →·n ||AC →|·|n |＝|－6－6|421＝217，所以AC 与平面DEF 所成角的正弦值为217.12．(2017·高考山东卷)如图，几何体是圆柱的一部分，它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的，G 是DF ︵的中点．(1)设P 是CE ︵上的一点，且AP ⊥BE ，求∠CBP 的大小； (2)当AB ＝3，AD ＝2时，求二面角E -AG -C 的大小．解：(1)因为AP ⊥BE ，AB ⊥BE ， AB ，AP ⊂平面ABP ，AB ∩AP ＝A ，所以BE ⊥平面ABP ，又BP ⊂平面ABP ，所以BE ⊥BP ，又∠EBC ＝120°，因此∠CBP ＝30°. (2)法一：取EC ︵的中点H ，连接EH ，GH ，CH . 因为∠EBC ＝120°，所以四边形BEHC 为菱形，所以AE ＝GE ＝AC ＝GC ＝32＋22＝13. 取AG 中点M ，连接EM ，CM ，EC ，则EM ⊥AG ，CM ⊥AG ，所以∠EMC 为所求二面角的平面角．又AM ＝1，所以EM ＝CM ＝13－1＝2 3. 在△BEC 中，由于∠EBC ＝120°，由余弦定理得EC 2＝22＋22－2×2×2×cos 120°＝12，所以EC ＝23，因此△EMC 为等边三角形，故所求的角为60°. 法二：以B 为坐标原点，分别以BE ，BP ，BA 所在的直线为x ，y ，z 轴，建立如图所示的空间直角坐标系．由题意得A (0，0，3)，E (2，0，0)，G (1，3，3)，C (－1，3，0)，故AE →＝(2，0，－3)，AG →＝(1，3，0)，CG →＝(2，0，3)，设m ＝(x 1，y 1，z 1)是平面AEG 的一个法向量．由⎩⎪⎨⎪⎧m ·AE →＝0，m ·AG →＝0，可得⎩⎨⎧2x 1－3z 1＝0，x 1＋3y 1＝0.取z 1＝2，可得平面AEG 的一个法向量m ＝(3，－3，2)．设n ＝(x 2，y 2，z 2)是平面ACG 的一个法向量．由⎩⎪⎨⎪⎧n ·AG →＝0，n ·CG →＝0，可得⎩⎨⎧x 2＋3y 2＝0，2x 2＋3z 2＝0.取z 2＝－2，可得平面ACG 的一个法向量n ＝(3，－3，－2)．所以cos 〈m ，n 〉＝m ·n |m |·|n |＝12.因此所求的角为60°.13．(选做题)如图，在三棱锥P -ABC 中，AB ＝AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知BC ＝8，PO ＝4，AO ＝3，OD ＝2.(1)证明：AP ⊥BC ；(2)在线段AP 上是否存在点M ，使得二面角A -MC -B 为直二面角？若存在，求出AM 的长；若不存在，请说明理由．解：(1)证明：如图，以O 为坐标原点，建立空间直角坐标系Oxyz .则A (0，－3，0)，B (4，2，0)，C (－4，2，0)，P (0，0，4)，所以AP →＝(0，3，4)，BC →＝(－8，0，0)，由此可得AP →·BC →＝0，所以AP →⊥BC →，即AP ⊥BC . (2)假设存在满足题意的点M ，设PM →＝λP A →，0≤λ<1，则PM →＝λ(0，－3，－4)，所以BM →＝BP →＋PM →＝(－4，－2，4)＋λ(0，－3，－4) ＝(－4，－2－3λ，4－4λ)， AC →＝(－4，5，0)．设平面BMC 的一个法向量为n 1＝(x 1，y 1，z 1)，平面APC 的一个法向量为n 2＝(x 2，y 2，z 2)．由⎩⎪⎨⎪⎧BM →·n 1＝0BC →·n 1＝0，得⎩⎪⎨⎪⎧－4x 1－（2＋3λ）y 1＋（4－4λ）z 1＝0－8x 1＝0即⎩⎪⎨⎪⎧x 1＝0z 1＝2＋3λ4－4λy 1，可取n 1＝⎝ ⎛⎭⎪⎫0，1，2＋3λ4－4λ.由⎩⎪⎨⎪⎧AP →·n 2＝0AC →·n 2＝0，得⎩⎪⎨⎪⎧3y 2＋4z 2＝0－4x 2＋5y 2＝0，即⎩⎨⎧x 2＝54y 2z 2＝－34y2，可取n 2＝(5，4，－3)．由n 1·n 2＝0，得4－3×2＋3λ4－4λ＝0，解得λ＝25，故AM ＝35|AP →|＝35×32＋42＝3.综上所述，线段AP 上存在点M 符合题意，此时AM ＝3.。

高中数学《空间向量与立体几何》练习题(含答案解析)

高中数学《空间向量与立体几何》练习题（含答案解析）一、单选题1．在空间直角坐标系Oxyz 中，与点()1,2,1-关于平面xOz 对称的点为（）A ．()1,2,1--B ．()1,2,1-C ．()1,2,1---D ．()1,2,1--2．在空间直角坐标系内，平面α经过三点(1,0,2),(0,1,0),(2,1,1)A B C -，向量(1,,)n λμ=是平面α的一个法向量，则λμ+=（）A ．7-B ．5-C ．5D ．73．已知点()3,1,0A -，若向量()2,5,3AB =-，则点B 的坐标是（）．A ．()1,6,3-B ．()5,4,3-C ．()1,6,3--D ．()2,5,3-4．如图，O A B '''△是水平放置的OAB 的直观图，6A O ''=，2''=B O ，则OAB 的面积是（）A ．6B ．12C ．D ．5．平面α的一个法向量是1(2n =,1-,1)3，平面β的一个法向量是(3m =-,6,2)-，则平面α与平面β的关系是（）A ．平行B ．重合C ．平行或重合D ．垂直6．已知某圆柱的内切球半径为92，则该圆柱的侧面积为（） A ．492π B ．49π C ．812π D ．81π7．O 、A 、B 、C 为空间四点，且向量OA 、OB 、OC 不能构成空间的一个基底，则下列说法正确的是（） A ．OA 、OB 、OC 共线B ．OA 、OB 共线C ．OB 、OC 共线D ．O 、A 、B 、C 四点共面8．在正方体1111ABCD A B C D -中，E 为线段11A B 的中点，则异面直线1D E 与1BC 所成角的余弦值为（）A B C D9．已知△ABC O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为（）AB ．32C ．1D 10．在正方体1111ABCD A B C D -中，P ，Q 分别为AB ，CD 的中点，则（）A ．1AB ⊥平面11A BCB ．异面直线1AB 与11AC 所成的角为30° C ．平面11ABD ∥平面1BC Q D ．平面1B CD ⊥平面1B DP二、填空题11．已知角α和角β的两边分别平行且一组边方向相同，另一组边的方向相反，若α＝45°，则β＝________. 12．若直线l 的方向向量(),1,2m x =-，平面α的法向量()2,2,4n =--，且直线l ⊥平面α，则实数x 的值是______.13．词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术・商功》，是古代人对一些特殊锥体的称呼．在《九章算术・商功》中，把四个面都是直角三角形的四面体称为“鳖臑”．现有如图所示的“鳖臑”四面体P ABC ，其中PA ⊥平面ABC ，2PA AC ==，BC =则四面体P ABC 的外接球的表面积为______．14．设空间向量,,i j k 是一组单位正交基底，若空间向量a 满足对任意的,,x y a xi y j --的最小值是2，则3a k +的最小值是_________．三、解答题15．如图，在三棱柱111ABC A B C 中，点D 是AB 的中点．(1)求证：1AC △平面1CDB ．(2)若1AA ⊥平面ABC ，AC BC =，求证：CD ⊥平面11ABB A ．16．如图，空间四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：（1）EH △平面BCD ；（2）BD △平面EFGH .17．如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，底面ABCD 是正方形，AC 与BD 交于点O ，E 为PB 的中点.(1)求证：EO平面PDC ；(2)求证：平面PAC ⊥平面PBD .18．如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.参考答案与解析1．A【分析】根据空间直角坐标系的对称点坐标特点直接求解即可.【详解】解：因为点()1,2,1-，则其关于平面xOz 对称的点为()1,2,1--.故选：A.2．D【解析】求出(1,1,2)AB =--，(2,0,1)BC =-，利用与(1,,)n λμ=数量积为0，求解即可.【详解】(1,1,2)AB =--，(2,0,1)BC =-120n AB λμ⋅=-+-=20n BC μ⋅=-+=可得2μ=，5λ=，7λμ+=故选：D3．B【分析】利用空间向量的坐标运算求得B 的坐标.【详解】设O 为空间坐标原点，()()()3,1,02,5,35,4,3OB OA AB =+=-+-=-.故选：B4．B【分析】由直观图和原图的之间的关系，和直观图画法规则，还原OAB 是一个直角三角形，其中直角边6,4OA OB ==，直接求解其面积即可．【详解】解：由直观图画法规则，可得OAB 是一个直角三角形，其中直角边6,4OA OB ==， △11641222OAB S OA OB =⋅=⨯⨯=．故选：B ．5．C【分析】由题设知6m n =-，根据空间向量共线定理，即可判断平面α与平面β的位置关系. 【详解】平面α的一个法向量是1(2n =,1-,1)3，平面β的一个法向量是(3m =-,6,2)-， ∴6m n =-，∴平面α与平面β的关系是平行或重合．故选：C ．6．D 【分析】由题意可得该圆柱底面圆的半径为92，圆柱的高为9，从而可求出其侧面积【详解】由题意得，该圆柱底面圆的半径为92，圆柱的高为9，所以该圆柱的侧面积为929812ππ⨯⨯=. 故选：D7．D【解析】根据向量OA 、OB 、OC 不能构成空间的一个基底知向量共面，即可得出结论.【详解】因为O 、A 、B 、C 为空间四点，且向量OA 、OB 、OC 不能构成空间的一个基底，所以OA 、OB 、OC 共面，所以O 、A 、B 、C 四点共面，故选：D8．B【分析】连接1AD ，AE ，得到11//AD BC ，把异面直线1D E 与1BC 所成角转化为直线1D E 与1AD 所成角，取1AD 的中点F ，在直角1D EF 中，即可求解.【详解】在正方体1111ABCD A B C D -中，连接1AD ，AE ，可得11//AD BC ，所以异面直线1D E 与1BC 所成角即为直线1D E 与1AD 所成角，即1AD E ∠为异面直线1D E 与1BC 所成角，不妨设12AA =，则1AD =1D E AE =取1AD 的中点F ，因为1D E AE =，所以1EF AD ⊥，在直角1D EF中，可得111cos D F AD E D E ∠==. 故选：B.9．C【分析】根据球O 的表面积和ABC 的面积可求得球O 的半径R 和ABC 外接圆半径r ，由球的性质可知所求距离d =【详解】设球O 的半径为R ，则2416R ππ=，解得：2R =.设ABC 外接圆半径为r ，边长为a ，ABC212a ∴=，解得：3a =，2233r ∴==∴球心O 到平面ABC 的距离1d =.故选：C.【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.10．D【分析】A 项反证法可得；B 项由平移法计算异面直线所成角；C 项由面面平行的判断和性质可得结果；D 项建立空间直角坐标系可得结果.【详解】对于选项A ，假设1AB ⊥面11A BC ，则111AB AC ⊥，这与已知1AB 与11A C 不垂直相矛盾，所以假设不成立.故选项A 错误；对于选项B ，连接1DC ，1DA ，因为11AB DC ∥，所以11DC A ∠为异面直线1AB 与11A C 所成的角或补角，又因为△11AC D 为等边三角形，所以1160DC A ∠=︒，故选项B 错误；对于选项C ，因为11B D BD ∥，11AD BC ∥，由面面平行的判定定理可得平面11AB D ∥平面1BDC ，而平面1BQC 与平面1BDC 相交，所以平面11AB D 与平面1BC Q 也相交，故选项C 错误；对于选项D ，以D 为坐标原点，DA ，DC ，1DD 所在的直线分别为x ，y ，z 轴，建立空间直角坐标系，如图所示，设正方体的棱长为1，则()0,0,0D ，()11,1,1B ，()0,1,0C ，11,,02P ⎛⎫ ⎪⎝⎭，可得()11,1,1DB =，()0,1,0DC =，11,,02DP ⎛⎫= ⎪⎝⎭，设平面1B CD 的法向量为()1,,n x y z =，则11100n DB x y z n DC y ⎧⋅=++=⎪⎨⋅==⎪⎩，可取1x =，则0y =，1z =-，即()11,0,1n =-，设平面1B DP 的法向量为()2,,b c n a =，则2120102n DB a b c n DP a b ⎧⋅=++=⎪⎨⋅=+=⎪⎩，可取1a =，则2b =-，1c =，可得平面1B DP 的一个法向量为()21,2,1n =-，由121010n n ⋅=+-=，所以12n n ⊥，即平面1B CD ⊥平面1B DP ，故选项D 正确. 故选：D.11．135°【分析】首先根据题意将图画出，然后根据α＝45°，AB △CD ，可得180BCD α︒∠=-，进而得出结论.【详解】解：如图，由题意知α＝45°，AB △CD ，180135BCD α︒︒∴∠=-=，即135β︒=.故答案为：135°.【点睛】本题考查了平行线的性质，结合图会使问题变得简单，属于基础题.12．-1【分析】利用法向量的定义和向量共线的定理即可.【详解】直线l 的方向向量(),1,2m x =-，平面α的法向量()2,2,4n =--，直线l ⊥平面α，必有//m n ，即向量m 与向量n 共线，m n λ∴= ，△11222x -==--，解得=1x -；故答案为：-1.13．16π 【分析】确定外接球球心求得球半径后可得表面积．【详解】由于PA ⊥平面ABC ，因此PA 与底面上的直线,,AC AB BC 都垂直，从而AC 与AB 不可能垂直，否则PBC 是锐角三角形，由于<AC BC ，因此有AC BC ⊥，而PA 与AC 是平面PAC 内两相交直线，则BC ⊥平面PAC ，PC ⊂平面PAC ，所以BC PC ⊥，所以PB 的中点O 到,,,P A B C 四个点的距离相等，即为四面体P ABC 的外接球球心．2222222222216PB PA AB PA AC BC =+=++=++=，4PB =，所以所求表面积为224()42162PB S πππ=⨯=⨯=．故答案为：16π．14．1【分析】以,i j 方向为,x y 轴，垂直于,i j 方向为z 轴建立空间直角坐标系，根据条件求得a 坐标，由3a k +的表达式即可求得最小值.【详解】以,,i j k 方向为,,x y z 轴建立空间直角坐标系，则()1,0,0i =，()0,1,0j =，()0,0,1k = 设(),,a r s t = 则(a xi y j r x --=-当,r x s y ==时a xi y j --的最小值是2，2t ∴=±取(),,2a x y = 则()3,,5a k x y += 23a k x ∴+=+又因为,x y 是任意值，所以3a k +的最小值是5.取(),,2a x y =- 则()3,,1a k x y += 23a k x ∴+=+又因为,x y 是任意值，所以3a k +的最小值是1.故答案为：1.15．(1)证明见解析；(2)证明见解析.【分析】(1)连接1BC ，交1B C 于点E ，连接ED ，用中位线证明1ED AC ∥即可；(2)证明CD △AB ，CD △1AA 即可.【详解】（1）连接1BC ，交1B C 于点E ，连接.ED△111ABC A B C 是三棱柱，△四边形11BCC B 为平行四边形，△E 是1BC 的中点.△点D 是AB 的中点，△ED 是1ABC 的中位线，△1ED AC ∥，又ED ⊂平面1CDB ，1AC ⊄平面1CDB ，△1AC △平面1CDB .（2）△1AA ⊥平面ABC ，AB ⊂平面ABC ，△1AA AB ⊥，△AC BC =，AD BD =，△CD AB ⊥，△1AA AB A =，1,AA AB ⊂平面11ABB A ，△CD ⊥平面11ABB A .16．（1）见解析（2）见解析【分析】（1）推导出EH △BD ，由此能证明EH △平面BCD ；（2）由BD △EH ，由此能证明BD △平面EFGH .【详解】（1）△EH 为△ABD 的中位线，△EH △BD .△EH △平面BCD ，BD △平面BCD ，△EH △平面BCD ；（2）△FG 为△CBD 的中位线，△FG △BD ，△FG △EH ，△E 、F 、G 、H 四点共面，△BD △EH ，BD △平面EFGH ，EH △平面EFGH ，△BD △平面EFGH .【点睛】本题考查线面平行的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查化归与转化思想，是中档题.17．(1)证明见解析(2)证明见解析【详解】（1）证明：△四边形ABCD 为正方形，△O 为BD 的中点，△E 为PB 的中点，△OE PD ∥，又△OE ⊄平面,PDC PD ⊂平面PDC ，△OE 平面PDC ；（2）证明：△四边形ABCD 为正方形，△AC BD ⊥，△PD ⊥平面ABCD ，且AC ⊂平面ABCD ，所以PD AC ⊥，又△,PD BD ⊂平面PBD ，且PD BD D ⋂=，△AC ⊥平面PBD ，又△AC ⊂平面PAC ，△平面PAC ⊥平面PDB .18．(1)证明见解析；【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可.【详解】（1）因为AB AD =，O 是BD 中点，所以OA BD ⊥，因为OA ⊂平面ABD ，平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =，所以OA ⊥平面BCD ．因为CD ⊂平面BCD ，所以OA CD ⊥.（2）[方法一]：通性通法—坐标法如图所示，以O 为坐标原点，OA 为z 轴，OD 为y 轴，垂直OD 且过O 的直线为x 轴，建立空间直角坐标系O xyz -，则1,0),(0,1,0),(0,1,0)2C D B -，设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,,0)3322EB m BC =--=，设(),,n x y z =为平面EBC 的法向量，则由00EB n EC n ⎧⋅=⎨⋅=⎩可求得平面EBC 的一个法向量为2(3,1,)n m =--．又平面BCD 的一个法向量为()0,0,OA m =，所以cos ,n OA ==1m =．又点C 到平面ABD 112132A BCD C ABD V V --==⨯⨯⨯=，所以三棱锥A BCD - [方法二]【最优解】：作出二面角的平面角如图所示，作EG BD ⊥，垂足为点G ．作GF BC ⊥，垂足为点F ，连结EF ，则OA EG ∥．因为OA ⊥平面BCD ，所以EG ⊥平面BCD ，EFG ∠为二面角E BC D --的平面角．因为45EFG ∠=︒，所以EG FG =．由已知得1OB OD ==，故1OB OC ==．又30OBC OCB ∠=∠=︒，所以BC =因为24222,,,,133333GD GB FG CD EG OA ======，111122(11)13332A BCD BCD BOC V S O S OA A -==⨯⨯=⨯⨯⨯⨯⨯=． [方法三]：三面角公式考虑三面角B EDC -，记EBD ∠为α，EBC ∠为β，30DBC ∠=︒，记二面角E BC D --为θ．据题意，得45θ=︒．对β使用三面角的余弦公式，可得cos cos cos30βα=⋅︒，化简可得cos βα=．△使用三面角的正弦公式，可得sin sin sin αβθ=，化简可得sin βα=．△ 将△△两式平方后相加，可得223cos 2sin 14αα+=，由此得221sin cos 4αα=，从而可得1tan 2α=±．如图可知π(0,)2α∈，即有1tan 2α=，根据三角形相似知，点G 为OD 的三等分点，即可得43BG =，结合α的正切值，可得2,13EG OA ==从而可得三棱锥A BCD - 【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.。

(完整版)空间向量和立体几何典型例题

∵PC 平面PCD，
∴PC⊥AB.
（Ⅱ）∵AC=BC,AP=BP,
∴△APC≌△BPC.
又PC⊥AC，
∴PC⊥BC.
又∠ACB＝90°，即AC⊥BC，
且AC∩PC=C，
∴AB＝BP，
∴BE⊥AP.
∵EC是BE在平面PAC内的射影，
∴CE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
在△BCE中，∠BCE=90°,BC=2,BE= ，
空间向量与立体几何典型例题
一、选择题：
1．(2008全国Ⅰ卷理)已知三棱柱的侧棱与底面边长都相等，在底面内的射影为的中心，则与底面所成角的正弦值等于（C）
A． B． C． D．
1.解：C．由题意知三棱锥为正四面体，设棱长为，则，棱柱的高（即点到底面的距离），故与底面所成角的正弦值为 .
（Ⅱ）连结BO，在直角梯形ABCD中、BC∥AD，AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形，
所以OB∥DC.
由（Ⅰ）知，PO⊥OB,∠PBO为锐角，
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中，AB=1,AO=1,
所以OB＝，
，，
，．
是二面角的平面角．
，，，
．
二面角的大小为．
（Ⅲ），
在平面内的射影为正的中心，且的长为点到平面的距离．
如（Ⅱ）建立空间直角坐标系．
，
点的坐标为．．
点到平面的距离为．
5．(2008福建文)如图，在四棱锥中，侧面PAD⊥底面ABCD,侧棱PA=PD= ,底面ABCD为直角梯形，其中BC∥AD,AB⊥CD,AD=2AB=2BC=2,O为AD中点。（1）求证：PO⊥平面ABCD;

高中数学空间向量与立体几何经典题型与答案

空间向量与立体几何经典题型与答案1 已知四棱锥P ABCD -的底面为直角梯形，//AB DC ,⊥=∠PA DAB ,90底面ABCD ,且12PA AD DC ===，1AB =,M 是PB 的中点 (Ⅰ）证明：面PAD ⊥面PCD ; （Ⅱ）求AC 与PB 所成的角;（Ⅲ)求面AMC 与面BMC 所成二面角的大小证明:以A 为坐标原点AD 长为单位长度，如图建立空间直角坐标系,则各点坐标为1(0,0,0),(0,2,0),(1,1,0),(1,0,0),(0,0,1),(0,1,)2A B C D P M(Ⅰ）证明：因.,0),0,1,0(),1,0,0(DC AP DC AP DC AP ⊥=⋅==所以故由题设知AD DC ⊥,且AP 与AD 是平面PAD 内的两条相交直线,由此得DC ⊥面PAD 又DC 在面PCD 上,故面PAD ⊥面PCD（Ⅱ）解:因),1,2,0(),0,1,1(-==PB AC.510||||,cos ,2,5||,2||=⋅⋅>=<=⋅==PB AC PBAC PB AC PB AC PB AC 所以故（Ⅲ)解:在MC 上取一点(,,)N x y z ，则存在,R ∈λ使,MC NC λ=..21,1,1),21,0,1(),,1,1(λλ==-=∴-=---=z y x MC z y x NC要使14,00,.25AN MC AN MC x z λ⊥=-==只需即解得),52,1,51(),52,1,51(,.0),52,1,51(,54=⋅-===⋅=MC BN BN AN MC AN N 有此时能使点坐标为时可知当λANB MC BN MC AN MC BN MC AN ∠⊥⊥=⋅=⋅所以得由.,0,0为所求二面角的平面角30304||,||,.5552cos(,).3||||2arccos().3AN BN AN BN AN BN AN BN AN BN ===-∴==-⋅-故所求的二面角为2 如图，在四棱锥V ABCD -中，底面ABCD 是正方形，侧面VAD 是正三角形,平面VAD ⊥底面ABCD（Ⅰ)证明:AB ⊥平面VAD ；(Ⅱ）求面VAD 与面DB 所成的二面角的大小证明:以D 为坐标原点，建立如图所示的坐标图系（Ⅰ)证明:不防设作(1,0,0)A ，则(1,1,0)B ， )23,0,21(V , )23,0,21(),0,1,0(-==VA AB由,0=⋅VA AB 得AB VA ⊥，又AB AD ⊥,因而AB 与平面VAD 内两条相交直线VA ,AD 都垂直∴AB ⊥平面VAD(Ⅱ）解:设E 为DV 中点，则)43,0,41(E ， ).23,0,21(),43,1,43(),43,0,43(=-=-=DV EB EA由.,,0DV EA DV EB DV EB ⊥⊥=⋅又得因此，AEB ∠是所求二面角的平面角,,721||||),cos(=⋅⋅=EB EA EB EA EB EA 解得所求二面角的大小为.721arccos3 如图，在四棱锥P ABCD -中,底面ABCD 为矩形，侧棱PA ⊥底V面ABCD ，3AB =，1BC =,2PA =, E 为PD 的中点（Ⅰ)求直线AC 与PB 所成角的余弦值;(Ⅱ）在侧面PAB 内找一点N ,使NE ⊥面PAC ，并求出点N 到AB 和AP 的距离解:(Ⅰ)建立如图所示的空间直角坐标系，则,,,,,A B C D P E 的坐标为(0,0,0)A 、(3,0,0)B 、(3,1,0)C 、(0,1,0)D 、(0,0,2)P 、1(0,,1)2E ,从而).2,0,3(),0,1,3(-==PB AC 设PB AC 与的夹角为θ，则,1473723||||cos ==⋅⋅=PB AC PB AC θ ∴AC 与PB 所成角的余弦值为1473 (Ⅱ)由于N 点在侧面PAB 内，故可设N 点坐标为(,0,)x z ，则)1,21,(z x NE --=,由NE ⊥面PAC 可得,⎪⎩⎪⎨⎧=+-=-⎪⎪⎩⎪⎪⎨⎧=⋅--=⋅--⎪⎩⎪⎨⎧=⋅=⋅.0213,01.0)0,1,3()1,21,(,0)2,0,0()1,21,(.0,0x z z x z x AC NE AP NE 化简得即 ∴⎪⎩⎪⎨⎧==163z x 即N 点的坐标为)1,0,63(，从而N 点到AB 和AP 的距离分别为31,64 如图所示的多面体是由底面为ABCD 的长方体被截面1AEC F 所截面而得到的，其中14,2,3,1AB BC CC BE ====(Ⅰ）求BF 的长；（Ⅱ）求点C 到平面1AEC F 的距离解:（Ｉ）建立如图所示的空间直角坐标系，则(0,0,0)D ,(2,4,0)B1(2,0,0),(0,4,0),(2,4,1),(0,4,3)A C E C 设(0,0,)F z∵1AEC F 为平行四边形，.62,62||).2,4,2().2,0,0(.2),2,0,2(),0,2(,,11的长为即于是得由为平行四边形由BF BF EF F z z EC AF F AEC =--=∴∴=∴-=-=∴∴(ＩI)设1n 为平面1AEC F 的法向量，)1,,(,11y x n ADF n =故可设不垂直于平面显然 ⎩⎨⎧=+⨯+⨯-=+⨯+⨯⎪⎩⎪⎨⎧=⋅=⋅02020140,0,011y x y x AF n AE n 得由 ⎪⎩⎪⎨⎧-==∴⎩⎨⎧=+-=+.41,1,022,014y x x y 即 111),3,0,0(n CC CC 与设又=的夹角为α,则 .333341161133||||cos 1111=++⨯=⋅⋅=n CC n CC α ∴C 到平面1AEC F 的距离为.11334333343cos ||1=⨯==αCC d５如图,在长方体1111ABCD A B C D -,中,11,2AD AA AB ===,点E 在棱AD 上移动（１)证明:11D E A D ⊥;（2）当E 为AB 的中点时,求点E 到面1ACD 的距离； (3)AE 等于何值时,二面角1D EC D --的大小为4π 解：以D 为坐标原点,直线1,,DA DC DD 分别为,,x y z 轴,建立空间直角坐标系,设AE x =,则11(1,0,1),(0,0,1),(1,,0),(1,0,0),(0,2,0)A D E x A C(1）.,0)1,,1(),1,0,1(,1111E D DA x E D DA ⊥=-=所以因为(2）因为E 为AB 的中点,则(1,1,0)E ，从而)0,2,1(),1,1,1(1-=-=AC E D ，)1,0,1(1-=AD ，设平面1ACD 的法向量为),,(c b a n =,则⎪⎩⎪⎨⎧=⋅=⋅,0,01AD n AC n 也即⎩⎨⎧=+-=+-002c a b a ,得⎩⎨⎧==c a ba 2，从而)2,1,2(=n ，所以点E 到平面1ACD 的距离为.313212||||1=-+=⋅=n n E D h （３)设平面1D EC 的法向量),,(c b a n =,∴),1,0,0(),1,2,0(),0,2,1(11=-=-=DD C D x CE由⎩⎨⎧=-+=-⇒⎪⎩⎪⎨⎧=⋅=⋅.0)2(02,0,01x b a c b CE n C D n 令1,2,2b c a x =∴==-， ∴).2,1,2(x n -= 依题意.225)2(222||||||4cos211=+-⇒=⋅⋅=x DD n DD n π∴321+=x (不合,舍去）,322-=x∴23AE =-时，二面角1D EC D --的大小为4π6 如图,在三棱柱111ABC A B C -中，AB ⊥侧面11BB C C ,E 为棱1CC 上异于1,C C 的一点,1EA EB ⊥，已知112,2,1,3AB BB BC BCC π===∠=,求:（Ⅰ）异面直线AB 与1EB 的距离;（Ⅱ）二面角11A EB A --的平面角的正切值解:（I)以B 为原点,1BB 、BA 分别为,y z 轴建立空间直角坐标系ﻩ由于，112,2,1,3AB BB BC BCC π===∠=ﻩ在三棱柱111ABC A B C -中有1(0,0,0),(0,0,2),(0,2,0)B A B ,)0,23,23(),0,21,23(1C C -设即得由,0,),0,,23(11=⋅⊥EB EA EB EA a E)0,2,23()2,,23(0a a --⋅--= ,432)2(432+-=-+=a a a a .,04343)02323()0,21,23()0,21,23(),(2321,0)23)(21(11EB BE EB BE E a a a a ⊥=+-=⋅⋅-⋅=⋅===--即故舍去或即得又AB ⊥侧面11BB C C ，故AB BE ⊥ 因此BE 是异面直线1,AB EB 的公垂线，则14143||=+=BE ，故异面直线1,AB EB 的距离为1 （I Ｉ）由已知有,,1111EB A B EB EA ⊥⊥故二面角11A EB A --的平面角θ的大小为向量EA A B 与11的夹角.22tan ,32||||cos ),2,21,23(),2,0,0(111111==⋅=--===θθ即故因A B EA A B EA EA BA A B７如图，在四棱锥P ABCD -中，底面ABCD 为矩形,PD ⊥底面ABCD ，E 是AB 上一点，PF EC ⊥ 已知,21,2,2===AE CD PD 求（Ⅰ）异面直线PD 与EC 的距离；（Ⅱ)二面角E PC D --的大小解:(Ⅰ）以D 为原点,DA 、DC 、DP 分别为,,x y z 轴建立空间直角坐标系由已知可得(0,0,0),(0,0,2),(0,2,0)D P C则(2EF =-由0EF PC ⋅=得又由F 在PC 上得,(2222EF =-因,,EF PC DG PC ⊥⊥故E -的大小为向量EF DG 与的夹角22||||DG EF DG EF ⋅=4。

空间向量典型例题

空间向量典型例题空间向量与立体几何一、非坐标系向量法1.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心，则AB1与底面ABC所成角的正弦值等于（）。

答案：（B）2/3.2.等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D的余弦值为1/3，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值等于。

答案：3/4.3.已知正四面体ABCD中，E、F分别在AB，CD上，且CF=CD，AE=AB/4，则直线DE和BF所成角的余弦值为（）。

答案：（C）-13/13.4.如图，已知四棱柱ABCD-A1，CB=CD，∠C1CB=∠C1CD，证明：C1C垂直于BD；当∠C1CB的值为多少时，能使A1CB1D是菱形且A1C垂直于平面C1BD？请给出证明。

二、坐标系向量法1.如图，在直三棱柱ABCD-A1B1C1D1中，点M是AC的中点，点N是BD的中点，求异面直线AN和B1M所成角的余弦值，以及平面A1B1C1和平面ABC所成二面角的正弦值。

2.如图，在直棱柱ABCD-A1B1C1D1中，AB=BC=1，AC=BD=√2，点M是AC的中点，点N是BD的中点。

证明：（1）MN⊥平面A1B1C1D1；（2）直线MN和平面A1B1C1D1所成二面角的正弦值为1/√10.3.如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC。

求证：PC⊥AB；求二面角B-AP-C的大小。

4.如图，已知点P在正方体ABCD-A1B1C1D1的对角线BD1上，∠PDA=60°。

求（1）DP与CC1所成角的大小；（2）DP与平面A1AD1所成角的大小。

5.如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，∠ABC=90°，OA⊥底面ABCD，OA=2，M为OA的中点。

求（1）异面直线AB与MD所成角的大小；（2）点B到平面OCD的距离。

2024年高考真题分类汇编九空间向量与立体几何

且 ⊥ ，以为坐标原点，, , 分别为, , 轴建立空间直角坐标系，
则 0,
可得⃗
1,0 , 1,
0,
1,
1,0 , 1,0,0 , 0,2,0 , 0,0,2 ，
2 , ⃗
1,
1,
2 , ⃗
1,0,
2 , ⃗
0,2,
2 ,
6 / 14
, , ，则
则 0,0,0 , 0,0,2 3 , 0,3 3, 0 , 3,3 3, 0 , 2,0,0 , 0,
，
2 3, 0 ，
因为是的中点，所以 4,2 3, 0 ，
所以⃗
3,3 3,
2 3 , ⃗
0,3 3,
2 3 , ⃗
4,2 3,
2 3 , ⃗
2,0,
1 1 0
分别取1
2
1，则1
⃗⋅⃗
|⃗|⋅|⃗|
则 cos⃗, ⃗
3、1
1、2
2 22
22 0
，
0，即⃗
1,3,1 、⃗
0,0,2 ，平面1 的法向量为⃗
1,3,1 ，
1 3
1 9 1⋅ 1 1
1，2
0
1,1,0 ，
2 22
，
11
故平面1 与平面1 1 的夹角余弦值为2 22；
设平面的法向量为⃗
令
1，则取
2，可得⃗
0,
2，则
则 cos⟨⃗, ⃗⟩

2,1 ，
1
5
2 0 ，
2 2 0
2,1,1 ，
1，可得⃗
⃗⋅⃗
|⃗|⋅|⃗|
0,
⃗
, , ，则 ⃗ ⋅
⃗ ⋅ ⃗

人教版高中数学选修2-1第三章-空间向量与立体几何练习题及答案

第三章空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1. 下列命题中不正确的命题个数是( ) ①若A 、B 、C 、D 是空间任意四点，则有AB +BC + CD +DA =0；②对空间任意点O 及不共线的三点A 、B 、C ，若OP =x OA +y OB +z OC （其中x 、y 、z ∈R ），则P 、A 、B 、C 四点共面；③若a 、b 共线，则a 及b 所在直线平行。

A .1 B .2 C .3 D .42.设OABC 是四面体，G 1是△ABC 的重心，G 是OG 1上一点，且OG =3GG 1，若OG =x OA +y OB +z OC ，则（x ，y ，z ）为( )A .（41，41，41） B .（43，43，43） C .（31，31，31） D .（32，32，32） 3．在平行六面体ABCD －EFGH 中，AG xAC y AF z AH =++，________.x y z ++=则4.已知四边形ABCD 中，AB =a －2c ，CD =5a +6b －8c ，对角线AC 、BD 的中点分别为E 、F ，则EF =_____________.5.已知矩形ABCD ，P 为平面ABCD 外一点，且PA ⊥平面ABCD ，M 、N 分别为PC 、PD 上的点，且M 分PC 成定比2，N 分PD 成定比1，求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中，1AA =2AB ，E 为1AA 重点，则异面直线BE 及1CD 所形成角的余弦值为( )A .1010 B . 15C .31010 D . 352．如图，设A ，B ，C ，D 是空间不共面的四点，且满足0AB AC ⋅=，0AC AD ⋅=，0AB AD ⋅=，则△BCD 的形状是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定的3．已知ABCD －A 1B 1C 1D 1 为正方体，则下列命题中错误的命题为__________．4．如图，已知：平行六面体ABCD －A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB =∠C 1CD =∠BCD =60° （1）证明：C 1C ⊥BD ；_C_D_A_P_ N_B_M（2）当1CDCC 的值为多少时，能使A 1C ⊥平面C 1BD ？请给出证明． §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1．已知向量(2，2，3)OA =-，(，1，4)OB x y z =-，且平行四边形OACB 的对角线的中点坐标为M 31(0，，)22-，则(，，)x y z =( ) A ．(2，4，1)--- B ．(2，4，1)-- C ．(2，4，1)-- D ．(2，4，1)--2．已知(2，2，4)a=-，(1，1，2)b =-，(6，6，12)c =--，则向量、、a b c ( )A ．可构成直角三角形B ．可构成锐角三角形C ．可构成钝角三角形D ．不能构成三角形3．若两点的坐标是A （3cosα，3sinα，1），B （2cosθ，2sinθ，1），则|AB |的取值范围是( ) A ．[0，5] B ．[1，5] C ．（1，5） D ．[1，25]4.设点C （2a +1，a +1，2）在点P （2，0，0）、A （1，－3，2）、B （8，－1，4）确定的平面上，则a 的值为 .5.如图，正三棱柱ABC -A 1B 1C 1的底边长为a ，侧棱长为2a .建立适当的坐标系，⑴写出A ，B ，A 1，B 1的坐标；⑵求AC 1及侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1．到一定点（1，0，1）的距离小于或等于2的点的集合为( ) A ．222{(,,)|(1)(1)4}x y z x y z -++-≤ B ．222{(,,)|(1)(1)4}x y z x y z -++-= C ．222{(,,)|(1)(1)2}x y z x y z -++-≤ D ．222{(,,)|(1)(1)2}x y z x y z -++-=2. 正方体ABCD —A 1B 1C 1D 1中，直线BC 1及平面A 1BD 所成角的余弦值为( ) A ．42 B ．32 C ．33 D ．23 3. 已知斜三棱柱111ABC A B C -，90BCA ∠=，2AC BC ==，1A 在底面ABC 上的射影恰为AC 的中点D ，又知11BA AC ⊥.（1）求证：1AC ⊥平面1A BC ；D 1C 1B 1A 1DABCC 1 B 1 A 1B A（2）求1C 到平面1A AB 的距离；（3）求二面角1A A B C --余弦值的大小.B 4. 如图，在直三棱柱111ABC A B C -中， AB =1，1AC AA ==(1)证明：1ABA C ⊥；（2）求二面角A —1A C —B 的大小.5. 如右图，四棱锥S-ABCD 棱S D 上的点. （1）求证：AC ⊥SD ；（2）若SD ⊥平面PAC ，求二面角P-AC-D 的大小（3）在（2）的条件下，侧棱S C 上是否存在一点E ，使得BE ∥平面PAC .若存在，求S E ：EC 的值；若不存在，试说明理由.参考答案第三章空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b －5c5.如图所示，取PC 的中点E ，连结NE ，则MN EN EM =-. 连结AC ，则§3.1.3空间向量的数量积运算1.C2.B3. ③④4.（1）设1,,CB a CD b CC c === ，则||||a b =，BD CD CB b a =-=- ，所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ，11BD CC BD CC ∴⊥⊥即；（2）1,2,CD x CD CC ==1设则 2CC =x，设1,,A A a AD b DCc ===，11,A C a b c C D a c =++=-，2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-，令24260xx +-=，则2320x x --=，解得1x =，或23x =-（舍去），_C_D _A_P_ N _B _M _EA 1§3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示 1.A 2.D 3.B 4.165. （1）建系如图，则A （0，0，0） B （0，a ，0）A 1（0，0，2a )，C 1（-23a ，a 2,2a) (2)解法一：在所建的坐标系中，取A 1B 1的中点M ，于是M （0，a 2,2a），连结AM ，MC 1则有所以，MC 1⊥平面ABB 1A 1.因此，AC 1及AM 所成的角就是AC 1及侧面ABB 1A 1所成的角.∴2194a AC AM ⋅=，而|13||3,||2AC a AM a ==，由cos<1,AC AM >=1132||||AC AM AC AM ⋅=，∴ <1,AC AM >=30°. ∴AC 1及侧面ABB 1A 1所成的角为30°. 3.2立体几何中的向量方法新课标第一网1.A2.C3. （1）如右图，取AB 的中点E ，则//DE BC ，因为BC AC ⊥，所以DEAC ⊥，又1A D ⊥平面ABC ，以1,,DE DC DA 为,,x y z 轴建立空间坐标系，则()0,1,0A -，()0,1,0C ，()2,1,0B ，()2,0,0CB =，由10AC CB ⋅=，知1A C CB ⊥，又11BA AC ⊥，从而1AC ⊥平面1A BC .（2）由1AC ⋅2130BA t =-+=，得t =.设平面1A AB 的法向量为(),,n x y z =，(1AA =，()2,2,0AB =，所以10220n AA y n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩，设1z =，则()3,n =-，所以点1C 到平面1A AB 的距离1AC n d n⋅==7. （3）再设平面1A BC 的法向量为(),,m x y z =，(10,CA =-，()2,0,0CB =，所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩，设1z =，则()0,3,1m =，故cos ,m n m n m n⋅<>==⋅77-，根据法向量的方向，可知二面角1A A B C --的余弦值大小为77. 4.（1）三棱柱111ABC A B C -为直三棱柱，由正弦定理030ACB∠=.如右图，建立空间直角坐标系，则1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量，设平面1A BC 的法向量为(,,)n l m n =，则10,0,130BC n AC n BC ⋅=⋅==-又（，，），不妨取1,(3,1,1)mn ==则，1A AC BD ∴--15二面角的大小为arccos 5. 5. （1）连结BD ，设AC 交于BD 于O ，由题意知SO ABCD ⊥平面.以O 为坐标原点，OB OC OS ，，分别为x 轴、y 轴、z 轴正方向，建立坐标系O xyz -如右图.设底面边长为a ，则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -，2(0,,0)2C a ，2(0,,0)2OC a =，26(,0,)22SD a a =--，0OC SD ⋅= ，故OC SD ⊥.从而 AC SD ⊥. (2)由题设知，平面PAC 的一个法向量26()2DSa =，平面DAC 的一个法向量600aOS =（，，，设所求二面角为θ，则3cos OS DS OS DSθ⋅==，得所求二面角的大小为30°._C_A_S_F_BO（3）在棱SC 上存在一点E 使//BE PAC 平面.由（2）知DS 是平面PAC 的一个法向量，且),(0,)DS CS ==.设,CEtCS = 则((1)BE BC CE BC tCS t =+=+=-，而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时，BE DS ⊥.而BE 不在平面PAC 内，故//BE PAC 平面. 作者于华东责任编辑庞保军。

高考必刷大题空间向量与立体几何

故 2λ＝－2,2λ＋2μ－μt＝0， 3μt＝ 3，
解得
t＝23，从而D→F＝0，43，2
3
3.
123456
所以直线AE与DF所成角的余弦值为
|cos〈A→E，D→F〉|＝|AA→→EE|·|DD→→FF|＝
2 7×2
7＝37. 3
123456
4.(2023·成都模拟)如图所示，直角梯形ABDE和三角形ABC所在平面互相垂直，DB⊥AB，ED∥AB，AB＝2DE＝2BD＝2，AC＝BC，异面直线DE 与AC所成角为45°，点F，G分别为CE，BC的中点，点H是线段EG上靠近点G的三等分点.
则有nn··B—C→CC→＝1 ＝x＋－x＋3y＝30z，＝0，
可取 n＝( 3，－1,1)，又—BA→1 ＝(1,0， 3)，
—→
所以点
A1 到平面
BCC1B1 的距离为| BA|n1|·n|＝2
3＝2 5
515，
所以所求距离为2 515.
123456
3.(2024·丹东模拟)如图，平行六面体ABCD－A1B1C1D1的所有棱长都相等，平面CDD1C1⊥平面ABCD，AD⊥DC，二面角D1－AD－C的大小为120°， E为棱C1D1的中点.
(1)求证：A，B，F，H四点共面；
123456
如图，取AB的中点O，连接OC，OE，因为AC＝BC，故∠BAC为锐角，又ED∥AB，故∠BAC即为异面直线DE与AC所成角，则∠BAC＝45°，则∠ACB＝90°，即AC⊥CB，因为直角梯形ABDE和三角形ABC所在平面互相垂直，DB⊥AB，平面ABDE∩平面ABC＝AB，DB⊂平面ABDE，
123456
设平面PBD的法向量为n＝(x，y，z)，则nn··PP→→DB＝＝22xy－－22zz＝＝00，，取 x＝1，得 n＝(1,1,1)， ∵A→M＝n，∴AM⊥平面 PBD.