高中数学-空间直角坐标系与空间向量典型例题
空间向量复习精选例题(含答案解析)

∴二面角 B1-BE-F 的大小为 arccos(
2 )。 3
(4)∵ GD1 =(-1,0,2),而 GD1 n1 =-2+0+2=0,
z D1 A1 F E B1 C1
∴直线 GD1∥平面 BEFD。 (5) DD1 =(0,0,2), | n1 | 4 4 1 3 , ∴ n1 的单位向量为(
空间向量
2 2 2 0, 0 0 0, 0 设 AB a ,则 A 2 a, ,B 0,2 a, ,C 2 a, . 设 OP h ,则 P(0, 0,h) . 2 1 a , 0 , h . ∵ D 为 PC 的中点,∴ OD 4 2 2 1 PA 0, h 2 a, ,∴ OD 2 PA .
∵ PA n1 2 2 0, PA n1,又PA 平面BDE, PA // 平面BDE. (2)由(Ⅰ)知 n1 (1, 1,1) 是平面 BDE 的一个法向量, 又 n 2 DA (2,0,0) 是平面 DEC 的一个法向量. 设二面角 B—DE—C 的平面角为 ,由图可知 n1 , n 2
(2) DA =(2,0,0) ,设 DA 与面 EFG 所成的角为θ, 则 sin
∴直线 C1D 与平面 A1C1B 的所成角为 arcsin
| DA n | 4 21 4 21 = ,∴ arcsin 21 21 | DA || n |
(2)平面 A1C1B 的法向量 n =(2,1,2),平面 AA1C1C 的法向量 n ' =(2,1,0), 设二者夹角为θ ,∴ cos
∴ cos PA ,n PA ·n PA n 210 . 30
高中数学第一章空间向量与立体几何 空间直角坐标系课后提能训练新人教A版选择性必修第一册

第一章 1.3 1.3.1A级——基础过关练1.已知点A(-3,1,4),则点A关于x轴对称的点的坐标为( )A.(-3,-1,-4) B.(-3,-1,4)C.(3,1,4) D.(3,-1,-4)【答案】A【解析】关于x轴对称的点,横坐标相同,纵坐标、竖坐标均互为相反数,所以A(-3,1,4)关于x轴的对称点坐标为(-3,-1,-4).2.在空间直角坐标系中,已知点P(1,2,3),过点P作平面Oyz的垂线PQ,则垂足Q 的坐标为( )A.(0,2,0) B.(0,2,3)C.(1,0,3) D.(1,2,0)【答案】B【解析】由于垂足Q在Oyz平面内,可设Q(0,y,z),因为直线PQ⊥Oyz平面,所以P,Q两点的纵坐标、竖坐标都相等.因为点P的坐标为(1,2,3),所以y=2,z=3,可得Q(0,2,3).3.在如图所示的长方体ABCD-A1B1C1D1中,已知点B1(1,0,3),D(0,2,0),则点C1的坐标为( )A.(1,2,3) B.(1,3,2)C.(2,3,1) D.(3,2,1)【答案】A【解析】观察图形可知点C1的坐标为(1,2,3).4.在如图所示的空间直角坐标系中,单位正方体顶点A的坐标是( )A .(-1,-1,-1)B .(1,-1,1)C .(1,-1,-1)D .(-1,1,-1)【答案】C【解析】依据空间点的坐标定义可知,点A 的坐标是(1,-1,-1).5.如图,在正方体OABC -O 1A 1B 1C 1中,棱长为2,E 是B 1B 上的点,且|EB |=2|EB 1|,则点E 的坐标为( )A .(2,2,1)B .⎝ ⎛⎭⎪⎫2,2,23C .⎝ ⎛⎭⎪⎫2,2,13D .⎝⎛⎭⎪⎫2,2,43 【答案】D【解析】因为EB ⊥Oxy 平面,而B (2,2,0),故设E (2,2,z ).又因为|EB |=2|EB 1|,所以|BE |=23|BB 1|=43,故点E 的坐标为⎝⎛⎭⎪⎫2,2,43.6.(2021年绵阳月考)在空间直角坐标系中,已知点A (-1,1,3),则点A 关于xOz 平面的对称点的坐标为( )A .(1,1,-3)B .(-1,-1,-3)C .(-1,1,-3)D .(-1,-1,3)【答案】D【解析】根据空间直角坐标系的对称性可得点A (-1,1,3)关于xOz 平面的对称点的坐标为(-1,-1,3).故选D .7.(多选)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =5,AD =4,AA 1=3,以直线DA ,DC ,DD 1分别为x 轴、y 轴、z 轴,建立空间直角坐标系,则( )A .点B 1的坐标为(4,5,3)B .点C 1关于点B 对称的点为(5,8,-3) C .点A 关于直线BD 1对称的点为(0,5,3) D .点C 关于平面ABB 1A 1对称的点为(8,5,0) 【答案】ACD【解析】根据题意知,点B 1(4,5,3),A 正确;B (4,5,0),C 1(0,5,3),故点C 1关于点B 对称的点为(8,5,-3),B 错误;点A 关于直线BD 1对称的点为C 1(0,5,3),C 正确;点C (0,5,0)关于平面ABB 1A 1对称的点为(8,5,0),D 正确.故选ACD .8.如图,在长方体OABC -O 1A 1B 1C 1中,OA =2,AB =3,AA 1=2,M 是OB 1与BO 1的交点,则点M 的坐标是________.【答案】⎝ ⎛⎭⎪⎫1,32,1 【解析】因为OA =2,AB =3,AA 1=2,所以A (2,0,0),A 1(2,0,2),B (2,3,0),故B 1(2,3,2).所以点M 的坐标为⎝⎛⎭⎪⎫22,32,22,即点M 的坐标为⎝⎛⎭⎪⎫1,32,1. 9.在空间直角坐标系中,点M (-2,4,-3)在Ozx 平面上的射影为点M ′,则点M ′关于原点对称点的坐标是________.【答案】(2,0,3)【解析】点M 在Oxz 平面上的射影为点M ′(-2,0,-3),所以点M ′关于原点对称点的坐标为(2,0,3).10.已知点P 的坐标为(3,4,5),试在空间直角坐标系中作出点P ,并写出求解过程. 解:如图,由P (3,4,5)可知点P 在x 轴上的射影为点A (3,0,0),在y 轴上的射影为点B (0,4,0),以OA ,OB 为邻边的矩形OACB 的顶点C 是点P 在Oxy 坐标平面上的射影C (3,4,0).过点C 作直线垂直于Oxy 坐标平面,并在此直线的Oxy 平面上方截取5个单位长度,得到的点就是P.B级——能力提升练11.在空间直角坐标系中,点M的坐标是(4,7,6),则点M关于y轴对称的点在Ozx平面上的射影的坐标为( )A.(4,0,6) B.(-4,7,-6)C.(-4,0,-6) D.(-4,7,0)【答案】C【解析】点M关于y轴对称的点是M′(-4,7,-6),点M′在Ozx平面上的射影的坐标为(-4,0,-6).12.(多选)已知点M(x,y,z)是空间直角坐标系Oxyz中的一点,则( )A.与点M关于x轴对称的点是(x,-y,-z)B.与点M关于原点对称的点是(-x,-y,-z)C.与点M关于xOy平面对称的点是(x,y,-z)D.与点M关于yOz平面对称的点是(x,-y,z)【答案】ABC【解析】与点M关于yOz平面对称的点是(-x,y,z),D错误,A,B,C均正确.故选ABC.13.直三棱柱ABC-A1B1C1的所有棱长都是2,以A为坐标原点建立如图所示的空间直角坐标系,则顶点B1关于平面xAz对称的点的坐标是________.【答案】(3,-1,2)【解析】∵直三棱柱ABC-A1B1C1的所有棱长都是2,∴B(3,1,0),∴顶点B1的坐标是(3,1,2),则其关于平面xAz的对称点为(3,-1,2).14.在空间直角坐标系Oxyz中,z=1的所有点构成的图形是________________;点P(2,3,5)到平面xOy的距离为________.【答案】过点(0,0,1)且与z轴垂直的平面 5【解析】z =1表示一个平面,其与平面Oxy 平行且距离为1,故z =1的所有点构成的图形是过点(0,0,1)且与z 轴垂直的平面.点P (2,3,5)到平面Oxy 的距离与其横纵坐标无关,只与其竖坐标有关.由于平面Oxy 的方程为z =0,故点P (2,3,5)到平面Oxy 的距离为|5-0|=5.15.在空间直角坐标系中有一个点P (1,3,-2),求: (1)点P 关于坐标原点O 的对称点P 1的坐标; (2)点P 关于x 轴的对称点P 2的坐标; (3)点P 关于坐标平面Oyz 的对称点P 3的坐标.解:(1)设点P 1的坐标为(x 1,y 1,z 1),因为点P 和P 1关于坐标原点O 对称, 所以O 为线段PP 1的中点.由中点坐标公式,得⎩⎪⎨⎪⎧x 1=-1,y 1=-3,z 1=2,所以点P 1的坐标为(-1,-3,2). (2)设点P 2的坐标为(x 2,y 2,z 2), 因为点P 和P 2关于x 轴对称,所以⎩⎪⎨⎪⎧x 2=1,3+y 22=0,-2+z 22=0,即⎩⎪⎨⎪⎧x 2=1,y 2=-3,z 2=2,则点P 2的坐标为(1,-3,2). (3)设点P 3的坐标为(x 3,y 3,z 3), 因为点P 和P 3关于平面yOz 对称,所以⎩⎪⎨⎪⎧x 3+12=0,y 3=3,z 3=-2,即⎩⎪⎨⎪⎧x 3=-1,y 3=3,z 3=-2,故点P 3的坐标为(-1,3,-2).。
高中数学立体几何与空间向量真题(解析版)

高中数学专题16立体几何与空间向量真题1.如图,正方体的一个截面经过顶点A,C及棱EF上一点K,且将正方体分成体积比为3:1的两部分,则的值为.【答案】【解析】设.截面与FG交于J.,解得(舍去)故.2.设点P到平面的距离为3,点Q在平面上,使得直线PQ与所成角不小于30°且不大于60°,则这样的点Q所构成的区域的面积为.【答案】【解析】设点P在平面上的射影为O.由条件知,.即OQ∈[1,3],故所求的区域面积为.3.在正三棱锥中,,过AB的平面将其体积平分.则棱与平面所成角的余弦值为_____________。
【答案】【解析】设的中点分別为,则易证平面A BM即为平面由平行四边形的性质知,所以,又直线P C在平面上的射影为直线MK,由得因此,棱P C与平面所成角的余弦值为.故答案为:4.设P为一圆锥的顶点,A、B、C为其底面圆周上的三点,满足∠ABC=90°,M为AP的中点.若AB =1,AC=2,AP=,则二面角M-BC-A的大小为________.【答案】【解析】由,知AC为底面圆的直径.如图所示,设底面中心为O.于是,平面ABC.故.设H为M在底面上的射影.则H为AO的中点.在底面中作于点K.由三垂线定理知.从而,为二面角M-BC-A的平面角.由,结合得:.故二面角M-BC-A的大小为.5.四棱锥P-ABCD中,已知侧面是边长为1的正三角形,M、N分别为边AB、BC的中点.则异面直线MN与PC之间的距离为___________.【答案】【解析】如图,设底面对角线AC与BD交于点O,过点C作直线MN的垂线,与MN交于点H.由于PO为底面的垂线,故PO⊥CH.又AC⊥CH,于是,CH与平面POC垂直.从而,CH⊥PC.因此,CH为直线MN与PC的公垂线段.注意到,.故异面直线MN与PC之间的距离为.6.已知正三棱锥底面边长为1,高为.则其内切球半径为______.【答案】【解析】如图,设球心在平面与平面内的射影分别为,边的中点为,内切球半径为.则分别三点共线,,且.故.解得.7.设同底的两个正三棱锥内接于同一个球.若正三棱锥的侧面与底面所成的角为,则正三棱锥的侧面与底面所成角的正切值是______.【答案】4【解析】如图6,联结.则,垂足为正的中心,且过球心.联结并延长与交于点.则为边的中点,且.易知,分别为正三棱锥、正三棱锥的侧面与底面所成二面角的平面角. 则.由.故.8.在四面体中,已知.则四面体的外接球的半径为______.【答案】【解析】易知,为正三角形,且CA=CB.如图,设P、M分别为AB、CD的中点,联结PD、PC.则平面平面PDC.设的外心为N,四面体ABCD的外接球的球心为O.则.可求得由题意知.在中,由余弦定理得又因为D、M、O、N四点在以DO为直径的圆上所以故外接球的体积.9.已知正三棱柱的9条棱长都相等,是边的中点,二面角.则________.【答案】【解析】解法1 如图,以所在直线为轴、线段的中点为原点、所在直线为轴建立空间直角坐标系.设正三棱柱的棱长为2.则.故.设分别与平面、平面垂直的向量为.则由此可设.所以,,即.因此,.解法2如图..设交于点.则平面.又,则平面.过点在平面上作,垂足为,联结.则为二面角的平面角.设.易求得.在中,.又,则.故.1.四面体P-ABC,,则该四面体外接球的半径为________. 【答案】【解析】将四面体还原到一个长方体中,设该长方体的长、宽、高分别为a,b,c,则,所以四面体外接球的半径为.2.四面体ABCD中,有一条棱长为3,其余五条棱长皆为2,则其外接球的半径为____.【答案】【解析】解:设BC=3,AB=AC=AD=BD=CD=2,E,F分别是BC,AD的中点,D在面ABC上的射影H应是△ABC的外心,由于DH上的任一点到A,B,C等距,则外接球心O在DH上,因,所以AE=DE,于是ED为AD的中垂线是,顒球心O是DH,EF的交点,且是等腰△EAD的垂心,记球半径为r,由△DOF~△EAF,得.而,所以.3.如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD为正方形,P A=AB.E、F分别为PD、BC的中点,则二面角E-FD-A的正切值为________.【答案】【解析】如图,作EH⊥AD于H,连HF.由P A⊥面ABCD,知P A⊥AD,EH∥P A,EH⊥ABCD.作HG⊥DF于G,连EG,则EG⊥FD,∠EGH为二面角E-FD-A的平面角.∵ABCD为正方形,E、F分别为PD、BC的中点,∴H为AD中点,FH⊥AD.设P A=AB=2,则,FH=2,HD=4,.∴.∴二面角E-FD-A的正切值为.4.已知正四面体内切球的半径是1,则该正四面体的体积为________.【答案】【解析】设正四面体的棱长为.则该正四面体的体积为,全面积为,所以,解得.从而正四面体的体积为.故答案为:5.正方体AC1棱长是1,点E、F是线段DD1,BC1上的动点,则三棱锥E一AA1F体积为___.【答案】【解析】因为F是BC1上的动点,所以在正方体中有,利用等体积转化有.故答案为.6.顶点为P的圆锥的轴截面是等腰直角三角形,A是底面圆周上的点,B是底面圆内的点,O为底面圆圆心,AB⊥OB,垂足为B,OH⊥HB,垂足为H,且P A=4,C为P A的中点,则当三棱锥O-HPC的体积最大时,OB的长为________.【答案】【解析】法一:AB⊥OB,PB⊥AB,AB⊥面POB,面P AB⊥面POB.OH⊥PB,OH⊥面P AB,OH⊥HC,OH⊥PC,又,PC⊥OC,PC⊥面OCH.PC是三棱锥P-OCH的高.PC=OC=2.而△OCH的面积在时取得最大值(斜边=2的直角三角形).当时,由,知∠OPB=30°,.法二:由C为P A中点,故,而.记则,.∴令,得,.故答案为:7.如图,在正三棱柱中,AB=2,,D、F分别是棱AB、的中点,E为棱AC 上的动点,则△DEF周长的最小值为__________.【答案】【解析】由正三棱锥可得底面ABC,所以AB,AC.在Rt△ADF中,.如图①,把底面ABC与侧面在同一个平面内展开,展开图中只有当D、E、F三点在同一条直线上时,DE+EF取得最小值.如图②,在△ADF中,,由余弦定理可得.所以△DEF周长的最小值为.8.在边长为1的长方体内部有一小球,该小球与正方体的对角线段相切,则小球半径的最大值=___________.【答案】【解析】当半径最大时,小球与正方体的三个面相切.不妨设小球与过点的三个面相切.以为原点,分别为x、y、z轴正方向,建立空间直角坐标系.设A(0,1,1),(1,0,0),小球圆心P(r,r,r),则P到的距离.再由,得.故答案为:9.正方体中,E为AB的中点,F为的中点.异面直线EF与所成角的余弦值是_____. 【答案】【解析】设正方体棱长为1,以DA为x轴,DC为y轴,为z轴建立空间直角坐标系,则.故有.所以.故答案为:10.在半径为R的球内作内接圆柱,则内接圆柱全面积的最大值是_____.【答案】【解析】设内接圆柱底面半径为,则高位,那么全面积为.其中,等号成立的条件是.故最大值为.故答案为:11.已知空间四点满足,且是三棱锥的外接球上的一个动点,则点到平面的最大距离是______.【答案】【解析】将三棱锥补全为正方体,则两者的外接球相同.球心就是正方体的中心,记为,半径为正方体对角线的一半,即为.在正方体里,可求得点到平面的距离为,则点到平面的最大距离是.12.在正四核锥中,已知二面角的正弦值为,则异面直线所成的角为______.【答案】【解析】如图,设的交点为上的射影为,则.又因为,因此,所以,则.因此即为二面角的平面角,从而.设,则.在中,.由此得,因此,解得.从而四棱锥各侧面均为正三角形,则异面直线所成的角为.13.半径分别为6、6、6、7的四个球两两外切.它们都内切于一个大球,则大球的半径是________【答案】14【解析】设四个球的球心分别为A、B、C、D,则AB=BC=CA=12,DA=DB=DC=13,即A、B、C、D两两连结可构成正三棱锥.设待求的球心为X,半径为r.,则由对称性可知DX平面ABC.也就是说,X在平面ABC上的射影是正三角形ABC的中心O.易知.设OX=x,则由于球A内切于球X,所以AX=r-6即①又DX=OD-OX=11-x,且由球D内切于球X可知DX=r-7于是②从①②两式可解得即大球的半径为14.故答案为:1414.一个棱长为6的正四面体纸盒内放一个小正四面体,若小正四面体可以在纸盒内任意转动,则小正四面体棱长的最大值为______.【答案】2【解析】因为小正四面体可以在纸盒内任意转动,所以小正四面体的棱长最大时,为大正四面体内切球的内接正四面体.记大正四面体的外接球半径为,小正四面体的外接球(大正四面体的内切球)半径为,易知,故小正四面体棱长的最大值为.15.已知棱长的正方体内部有一圆柱,此圆柱恰好以直线为轴,则该圆柱体积的最大值为_____.【答案】【解析】由题意知只需考虑圆柱的底面与正方体的表面相切的情况.由图形的对称性可知,圆柱的上底面必与过A点的三个面相切,且切点分别在、AC、上.设线段上的切点为E,圆柱上底面中心为,半径.由,则圆柱的高为,由导数法或均值不等式得.。
高中数学高考总复习立体几何空间向量空间直角坐标系习题及详解

高考总复习含详解答案高中数学高考总复习立体几何空间向量空间直角坐标系习题及详解一、选择题1.已知四边形ABCD 满足:AB →·BC →>0,BC →·CD →>0,CD →·DA →>0,DA →·AB →>0,则该四边形为()A .平行四边形B .梯形C .平面四边形D .空间四边形[答案]D [解析]∵AB →·BC →>0,∴∠ABC>π2,同理∠BCD>π2,∠CDA>π2,∠DAB >π2,由内角和定理知,四边形ABCD 一定不是平面四边形,故选 D. 2.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB →的值为()A .0B .1C .0或1D .任意实数[答案]C [解析]AP →可为下列7个向量:AB →,AC →,AD →,AA 1→,AB 1→,AC 1→,AD 1→,其中一个与AB →重合,AP →·AB →=|AB →|2=1;AD →,AD 1→,AA 1→与AB →垂直,这时AP →·AB →=0;AC →,AB 1→与AB →的夹角为45°,这时AP →·AB →=2×1×cos π4=1,最后AC 1→·AB →=3×1×cos ∠BAC 1=3×13=1,故选 C. 3.如图,在平行六面体ABCD -A 1B 1C 1D 1中,M 为AC 与BD 的交点,N 为BB 1的靠近B 的三等分点,若A 1B 1→=a ,A 1D 1→=b ,A 1A →=c ,则MN →等于()A .-12a +12b +13c B.12a +12b -13c C.12a -12b -13c D .-12a -12b +23c [答案] C。
最新题型空间向量证明立体几何问题

C
B
0 AB ' • A'C 3 1 h2, h2 2.
A
AB ' • BC ' 0 2 h2 0. BC ' AB '
题型四:线面平行
例.在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1E
证明:如图建立坐标系D xyz,
A1
D1 z
F
C1 设AD 2.则
A1(2,0,2), C1(0,2,2), E(0,0,1)
|
即所求二面角的余弦值是 6 。
6, 3
3
题型七:面面平行
例:在正方体ABCD-A1B1C1D1中,求证:面A1BD∥面CB1D1
证明: 如图分别以D1 A1、D1C1、D1D 三边所在的直线为x, y, z轴建立空间
直角坐标系.设正方体的棱长为1,则
Z
A1(1, 0, 0), B1(1,1, 0), C(0, 0,1), D(0, 0,1)
或先求平面BDE的法向量 n 再证明 A' F n
题型六:面面角
例、已知,ABCD是一直角梯形,ABC 900, SA 平面ABCD,
SA AB BC 1, AD 1 ,求面SCD与面SBA所成的二面角的余弦值。
2 解:建立直角坐系A - xyz如所示,
z
A (0,0,0),C (- 1,1,0),D(0, 1 ,0), S(0,0,1) S
n
2、根据n·a = 0且n·b = 0可列出方程组
x1x x2 x
y1 y2
y y
z1z z2 z
0 0
ab
3、取某一个变量为常数(当然取得越简单越好), 便得到平面法向量n的坐标.
空间向量立体几何(绝对经典)
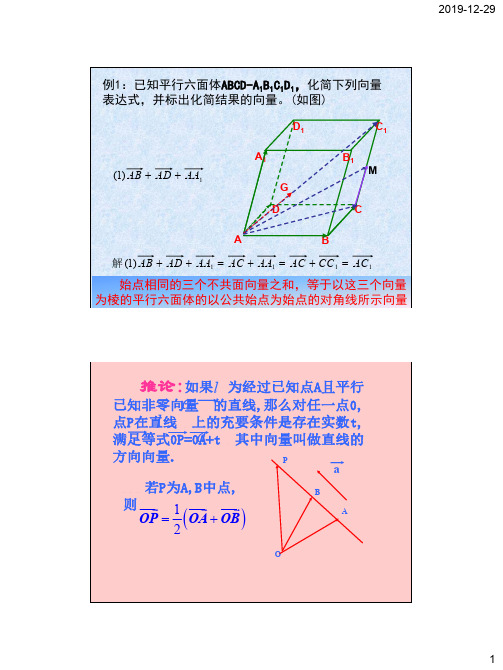
例1:已知平行六面体ABCD-A 1B 1C 1D 1,化简下列向量表达式,并标出化简结果的向量。
(如图)A BCD A 1B 1C 1D 1G1)1(AA AD AB ++1111)1(AC CC AC AA AC AA AD AB =+=+=++解M 始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式OP=OA+t 其中向量叫做直线的方向向量.ll aaOABP a若P为A,B中点,则()12=+ OP OA OB2.共面向量定理:如果两个向量 不共线,则向量 与向量 共面的充要条件是存在实数对 使, a b yx , p ,a b OM a b A B A 'Pp p xa yb =+ 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使或对空间任一点O,有=+MP xMA yMB =++ OP OM xMA yMB 注意:空间四点P 、M 、A 、B 共面⇔存在唯一实数对,,x y MP xMA yMB =+ ()使得(1)OP xOM yOA zOB x y z ⇔=++++= 其中,例1:已知m,n 是平面α内的两条相交直线,直线l 与α的交点为B ,且l ⊥m ,l ⊥n ,求证:l ⊥α。
n mg g m n αl l 证明:在α内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g ,因m与n相交,得向量m、n 不平行,由共面向量定理可知,存在唯一的有序实数对(x,y),使g =x m +y n ,l ·g =x l ·m +y l ·n∵ l ·m =0,l ·n =0∴ l ·g =0∴ l⊥g∴ l⊥g这就证明了直线l垂直于平面α内的任一条直线,所以l⊥α巩固练习:利用向量知识证明三垂线定理αa A O P ().,0,,,,0,0,PA a PA a a OA a PO a PA OAy PO x PA y x OA PO OA PO a OA a OA a PO a PO PO aa ⊥⊥∴=⋅+⋅=⋅∴+==⋅∴⊥=⋅∴⊥∴⊥即使有序实数对定理可知,存在唯一的不平行,由共面向量相交,得又又而上取非零向量证明:在αPA a OAa a PA OA PA PO ⊥⊥⊂求证:且内的射影,在是的垂线,斜线,分别是平面已知:,,ααα复习:2. 向量的夹角:a bO ABabθ0a b π≤≤ ,a b ,向量 的夹角记作:a b 与a b = ||||cos ,a b a b 1.空间向量的数量积:111222(,,),(,,)a x y z b x y z == 设121212x x y y z z =++cos ||||a ba b a b =,121212222222111222++=++⋅++x x y y z z x y z x y z 5.向量的模长:2222||a a x y z ==++ (,,)a x y z = 设4.有关性质:(1)两非零向量111222(,,),(,,)a x y zb x y z == 1212120x x y y z z ++=0a b a b ⊥⇔=⇔ (2)||||||a b a b ≤ ||||,a b a b a b =⇒ 同方向||||,a b a b a b =-⇒ 反方向注意:此公式的几何意义是表示长方体的对角线的长度。
人教B版高中同步学案数学选择性必修第一册精品课件 第一章 空间向量的坐标与空间直角坐标系 分层作业册

,- 2 ,0
2
B.(0,1,0)
C.
2 2
,
,0
2 2
D.(-1,-1,0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
解析 对 A,存在实数 λ=- 2,使(1,1,0)=- 2((−
2
2
, − , 0)
2
2
=
1
2
+
1
=1,故
2
2 2
,- ,0),且
2 2
A 正确;
不垂直,故 B 不正确; = − =(4,2,0)-(-2,1,4)=(6,1,-4),
∴| |= 62 + 12 + (-4)2 = 53,故 C 正确;
1 = 6,
假设=k (k∈R),则 -2 = , 无解,因此假设不成立,即 AP 与 BC 不平行,
1 = -4,
(2)求a与b的夹角;
(3)若ka+b与ka-2b互相垂直,求实数k的值.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
(1) =(-3,0,4)-(-1,1,2)=(-2,-1,2).
因为 c∥ ,所以 c=λ ,所以 c=λ(-2,-1,2)=(-2λ,-λ,2λ).
∴cos< , >=
·
| || |
=
1 2 + 2 +(1-)2
=cos
由 0<λ<1,解得 λ= 2-1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1
60°=2.
14. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面
高中试卷-专题03 空间向量的应用(含答案)

专题03 空间向量的应用一、单选题1.(2020·贵州省铜仁第一中学高二开学考试)已知两个异面直线的方向向量分别为a r ,b r ,且|a r |=|b r|=1,a r •12b r =-,则两直线的夹角为( )A .30°B .60°C .120°D .150°【答案】B【解析】设两直线的夹角为θ,则由题意可得1×1×cos a r <,12b =-r >,∴cos a r <,12b =-r >,∴a r <,23b p =r >,∴θ3p =,故选:B .2.(2019·穆棱市第一中学高二期末)若平面,a b 的法向量分别为1,1,3,(1,2,6)2a b æö=-=--ç÷èør r ,则( )A .//a bB .a 与b 相交但不垂直C .a b^D .//a b 或a 与b 重合【答案】D【解析】因为12a b =-r r ,所以平面,a b 的法向量共线,故//a b 或a 与b 重合.故选:D.3.(2020·北京高二期末)已知直线l 的方向向量为m u r ,平面a 的法向量为n r ,则“0m n ×=u r r”是“l ∥a ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】B【解析】Q 0m n ×=u r r \m n^u r r Q 0m n ×=u r r ,即m n ^u r r ,不一定有l ∥a ,也可能l aÌ\“0m n ×=u r r ”是“l ∥a ”的不充分条件Q l ∥a ,可以推出m n ^u r r ,\“0m n ×=u r r ”是“l ∥a ”是必要条件,综上所述, “0m n ×=u r r ”是“l ∥a ”必要不充分条件.故选:B.4.(2019·山东省济南一中高二期中)在平面ABCD 中,(0,1,1)A ,(1,2,1)B ,(1,0,1)C --,若(1,,)a y z =-v ,且a v 为平面ABCD 的法向量,则2y 等于( )A .2B .0C .1D .无意义【答案】C【解析】由题得,(1,1,0)AB =uuu r ,(1,1,2)AC =--uuu r ,又a r 为平面ABCD 的法向量,则有00a AB a AC ì×=í×=îuuu v v uuu v v ,即10120y y z -+=ìí-+=î,则1y =,那么21y =.故选:C5.(2019·四川省双流中学高三月考)已知点P 是正方体1111ABCD A B C D -的棱CD 的中点,给出以下结论:①11A P C D ^;②1A P BD ^;③11A P BC ^;④1AP ^平面1BC D 其中正确命题的序号是( )A .①B .②C .③D .④【答案】C【解析】设正方体边长为2,建立如图空间直角坐标系.则()12,1,2A P =--uuur .对①, ()10,2,2C D =--uuuu r ,因为110242A P C D ×=-+=uuur uuuu r ,故①错误.对②, ()2,2,0BD =--uuu r ,因为1422A P BD ×=-=uuur uuu r ,故②错误.对③, ()12,0,2BC =-uuuu r ,因为1440A P BD ×=-=uuur uuu r ,故③正确.对④,由②有1A P BD ^不成立,故1AP ^平面1BC D 不成立.故④错误.故选:C6.(2019·穆棱市第一中学高二期末)如图,在正方体ABCD 1111A B C D 中,以D 为原点建立空间直角坐标系,E 为B 1B 的中点,F 为11A D 的中点,则下列向量中,能作为平面AEF 的法向量的是( )A .(1,-2,4)B .(-4,1,-2)C .(2,-2,1)D .(1,2,-2)【答案】B【解析】设正方体棱长为2,则A (2,0,0),E (2,2,1),F (1,0,2),∴AE uuu r =(0,2,1),AF uuu r =(﹣1,0,2)设向量n r=(x ,y ,z )是平面AEF 的一个法向量则2020n AE y z n AF x z ì×=+=ïí×=-+=ïîuuu r r uuu r r ,取y=1,得x=﹣4,z=﹣2∴n r =(﹣4,1,﹣2)是平面AEF 的一个法向量因此可得:只有B 选项的向量是平面AEF 的法向量故选:B .7.(2019·包头市第四中学高二期中)在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M l l =<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )ABCD【答案】D【解析】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,则M (2,λ,2),D 1(0,0,2),E (2,0,1),F (2,2,1),1ED uuuu v =(﹣2,0,1),EF uuu r =(0,2,0),EM uuuu r =(0,λ,1),设平面D 1EF 的法向量n r=(x ,y ,z ),则1·20·20n ED x z n EF y ì=-+=í==îuuuu v v uuuv v ,取x =1,得n r =(1,0,2),∴点M 到平面D 1EF=N 为EM 中点,所以N ,选D .8.(2020·湖南省高二期末)已知直三棱柱111ABC A B C -中,底面边长和侧棱长都相等,则异面直线1AB 与1BC 所成的角的余弦值为( )A .12B .18C .14D .34【答案】C【解析】立空间坐标系如图,设边长为2,得到A (2,0,0),1B (12),B (10),1C (0,0,2)向量()()112,1,2AB BC =-=uuuv uuuu v 设异面直线夹角为q ,则1111cos =||||AB BC AB BC q ×=×uuuv uuuu v uuuv uuuu v 14故答案为C9.(2018·山西省山西大附中高二期中)过正方形ABCD 的顶点A ,作PA ^平面ABCD ,若PA BA =,则平面ABP 和平面CDP 所成的锐二面角的大小是A .30°B .45°C .60°D .90°【答案】B【解析】法一:建立如图(1)所示的空间直角坐标系,不难求出平面APB 与平面PCD 的法向量分别为n 1=(0,1,0),n 2=(0,1,1),故平面ABP 与平面CDP 所成二面角的余弦值为1212n n n n=,故所求的二面角的大小是45°.法二:将其补成正方体.如图(2),不难发现平面ABP 和平面CDP 所成的二面角就是平面ABQP 和平面CDPQ 所成的二面角,其大小为45°.10.(2020·山东省章丘四中高二月考)在正方形1111ABCD A B C D -中,棱AB ,11A D 的中点分别为E ,F ,则直线EF 与平面11AA D D 所成角的余弦值为( )A B C D 【答案】D【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设正方体1111ABCD A B C D -的棱长为2,则()2,1,0E , ()1,0,2F , ()1,1,2EF =--uuu r ,平面11AA D D 的法向量()0,1,0n =r ,设直线EF 与平面11AA D D 所成角为q ,0,2p éùqÎêúëû,则||sin ||||EF n EF n q ===uuu r r g uuu r r g .所以cos q ==\直线EF 与平面11AA D D 故选:D .二、多选题11.(2020·山东省高二期末)已知ν为直线l 的方向向量,1n ,2n 分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )A .12////n n a bÛB .12n n a b^Û^C .1////n l n aÛD .1//n l n a ^Û【答案】AB【解析】A 选项,平面α,β不重合,所以平面α,β的法向量平行等价于平面α,β平行,正确;B 选项,平面α,β不重合,所以平面α,β的法向量垂直等价于平面α,β垂直,正确;C 选项,直线的方向向量平行于平面的法向量等价于直线垂直于平面,错误;D 选项,直线的方向向量垂直于平面的法向量等价于直线平行于平面或直线在平面内,错误.故选:AB12.(2019·山东省高三)正方体1111ABCD A B C D -的棱长为1,,,E F G 分别为11,,BC CC BB 的中点.则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为98D .点C 和点G 到平面AEF 的距离相等【答案】BC【解析】对选项A :(方法一)以D 点为坐标原点,DA 、DC 、1DD 所在的直线分别为x 、y 、z 轴,建立空间直角坐标系,则(0,0,0)D 、(1,0,0)A 、1(1,0,1)A 、1,1,02E æöç÷èø、10,1,2F æöç÷èø、11,1,2G æöç÷èø.从而1(0,0,1)DD =uuuu r ,11,1,2AF æö=-ç÷èø,从而1102DD AF ×=¹uuuu r uuu r ,所以1DD 与直线AF 不垂直,选项A 错误;(方法二)取1DD 的中点N ,连接AN ,则AN 为直线AF 在平面11ADD A 内的射影,AN 与1DD 不垂直,从而AF 与1DD 也不垂直,选项A 错误;取BC 的中点为M ,连接1A M 、GM ,则1A M AE ∥,GM EF ∥,易证1A MG AEF 平面∥平面,从而1A G AEF ∥平面,选项B 正确;对于选项C ,连接1AD ,1D F ,易知四边形1AEFD 为平面,且1D H AH ==,1A D =132AD H S D ==,而113948AD H AEFD S S ==四边形△,从而选项C 正确;对于选项D :(方法一)由于111111112222224GEF EBG BEFG S S S D D æö=-=+´-´´=ç÷èø梯形,而11112228ECF S D =´´=,而13A GEF EFG V S AB -D =×,13A ECF ECF V S AB -D =×,所以2A GEF A ECF V V --=,即2G AEFC AEF V V --=,点G 到平面AEF 的距离为点C 到平面AEF 的距离的二倍.从而D 错误.(方法二)假设点C 与点G 到平面AEF 的距离相等,即平面AEF 将CG 平分,则平面AEF 必过CG 的中点,连接CG交EF于点O ,易知O 不是CG 的中点,故假设不成立,从而选项D 错误.13.(2020·福建省高二期末)正方体1111ABCD A B C D -中,E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点,则下列结论正确的是( )A .1B G BC^B .平面AEF I 平面111AA D D AD =C .1//A H 面AEFD .二面角E AF C --的大小为4p 【答案】BC【解析】由题可知,1B G 在底面上的射影为BG ,而BC 不垂直BG ,则1B G 不垂直于BC ,则选项A 不正确;连接1AD 和1BC ,E 、F 、G 、H 分别为1CC 、BC 、CD 、BB 、1BB 的中点,可知11////EF BC AD ,所以AEF D Ì平面1AD EF ,则平面AEF I 平面111AA D D AD =,所以选项B 正确;由题知,可设正方体的棱长为2,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,则各点坐标如下:()()()()()()12,0,0,0,2,0,0,2,1,2,0,2,2,2,1,1,2,0A C E A H F ()()()()110,2,1,1,2,0,1,0,1,0,0,2A H AF EF AA =-=-=-=uuuu r uuu r uuu r uuur ,设平面AEF 的法向量为(),,n x y z =r ,则00n AF n EF ì×=í×=îuuu v v uuu v v ,即200x y x z -+=ìí-=î,令1y =,得2,2x z ==,得平面AEF 的法向量为()2,1,2n =r ,所以10A H n ×=uuuu r r ,所以1//A H 平面AEF ,则C选项正确;由图可知,1AA ^平面AFC ,所以1AA uuur是平面AFC 的法向量,则1112cos ,3AA n AA n AA n×<>===×uuur r uuur r uuur r .得知二面角E AF C --的大小不是4p ,所以D 不正确.故选:BC.三、填空题14.(2019·山东省济南一中高二期中)若平面a的一个法向量为(n =v,直线l的一个方向向量为a =v ,则l 与a 所成角的正弦值为________.【答案】15【解析】由题,设l 与a 所成角为q,可得||1sin 5||||n a n a q ×===v v v v .故答案为:1515.(2019·陕西省西北大学附中高二期中)如图,在正三棱柱111ABC A B C -中,12,AB AC AA === ,E F 分别是,BA11A C 的中点.设D 是线段11B C 上的(包括两个端点)动点,当直线BD 与EF,则线段BD 的长为_______.【答案】【解析】以E 为原点,EA,EC 为x,y轴建立空间直角坐标系,如下图.1(0,0,0),,2),(0,1,0),(0,,2)(11)2E F B D t t --££1,2),(0,1,2)2EF BD t ==+uuu v uuuv cos q =解得t=1,所以BD =,填.点睛:利用空间向量求解空间角与距离的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.16.(2019·浙江省宁波市鄞州中学高二期中)正方体1111ABCD A B C D -中,,E F 分别是1,AA AB 的中点,则EF 与直线1AC 所成角的大小为______ ;EF 与对角面11BDD B 所成角的正弦值是 __________.【答案】2p 12【解析】如图所示建立空间直角坐标系,设正方体的边长为2,则()2,0,1E ,()2,1,0F ,()2,0,0A ,()10,2,2C ,故()0,1,1EF =-uuu r ,()12,2,2AC =-uuuu r .故10EF AC ×=uuu r uuuu r ,故EF 与直线1AC 所成角的大小为2p .易知对角面11BDD B 的一个法向量为()1,1,0n =-r ,设EF 与对角面11BDD B 所成角为q ,故1sin cos ,2EF n EF n EF n q ×===×uuu r r uuu r r uuu r r .故答案为:2p ;12.17.(2019·江西省会昌中学高二月考)已知正方体1111ABCD A B C D -的棱长为a ,点E ,F ,G 分别为棱A B ,1AA ,11C D 的中点,下列结论中,正确结论的序号是___________.①过E ,F ,G 三点作正方体的截面,所得截面为正六边形;②11//B D 平面EFG ;③1BD ^平面1ACB ;④异面直线EF 与1BD ;⑤四面体11ACB D 的体积等于312a .【答案】①③④【解析】延长EF 分别与1l B A ,1B B 的延长线交于N ,Q ,连接GN 交11A D 于H ,设HG 与11B C 的延长线交于P ,连接P Q 交1CC 于I ,交BC 于M ,连FH ,HG ,GI ,IM ,ME ,EF ,如图:则截面六边形EFHGIM 为正六边形,故①正确:因为11B D 与HG 相交,故11B D 与平面EFG 相交,所以②不正确:1,BD AC BD AC ^\^Q (三垂线定理),1111,BC B C BD B C ^\^Q (三垂线定理),且AC 与1B C 相交,所以1BD ^平面1ACB ,故③正确;以D 为原点,1,,DA DC DD 分别为,,x y z 轴建立空间直角坐标系,则1(0,0,0),(,,0),(,0,),(,,0),(0,0,)22a a D E a F a B a a D a ,则(0,,)22a a EF =-uuu r ,1(,,)BD a a a =--uuuu r ,所以111cos ,||||EF BD EF BD EF BD ×<>=uuu r uuuu r uuu r uuuu r uuu r uuuur ===所以1sin ,EF BD <>==uuu r uuuu r=所以111sin ,tan ,cos ,EF BD EF BD EF BD <><>=<>uuu r uuuu r uuu r uuuu r uuu r uuuur ==,所以异面直线EF 与1BD,故④正确;因为四面体11ACB D 的体积等于正方体的体积减去四个正三棱锥的体积,即为3331114323a a a -´´=,故⑤不正确.故答案为:①③④四、解答题18.(2019·广西壮族自治区田东中学高二期中)已知三棱柱111ABC A B C -的侧棱垂直于底面,90BAC Ð=°,12AB AA ==,1AC =,M ,N 分别是11A B ,BC 的中点.(1)求证:1AB AC ^;(2)求证://MN 平面11ACC A .【答案】(1)证明见解析 (2) 证明见解析【解析】Q 三棱柱为直三棱柱 1AA \^平面ABC 1AA AC \^,1AA AB ^又90BAC Ð=o ,则1,,AB AC AA 两两互相垂直,可建立如下图所示的空间直角坐标系则()0,0,0A ,()0,2,0B ,()1,0,0C -,()11,0,2C -,()0,1,2M ,1,1,02N æö-ç÷èø(1)()0,2,0AB =uuu r Q ,()11,0,2AC =-uuuu r ()10120020AB AC \×=´-+´+´=uuu r uuuu r 1AB AC \^(2)由题意知:AB uuu r是平面11ACC A 的一个法向量()0,2,0AB =uuu r Q ,1,0,22MN æö=--ç÷èøuuuu r ()10200202AB MN æö\×=´-+´+´-=ç÷èøuuu r uuuu r AB MN \^uuu r uuuu r MN ËQ 平面11ACC A //MN \平面11ACC A 19.(2020·陕西省高二期末)如图,在棱长为2的正方体1111ABCD A B C D -中E ,F 分别为AB ,1A C的中点.(1)求EF ;(2)求证://EF 平面11AA D D【答案】(1;(2)证明见解析【解析】(1)由题知,(2,1,0)E ,(1,1,1)F ,∴(1,0,1)EF =-uuu r ,∴||EF ==uuu r (2)由题知,(2,0,0)A ,1(0,0,2)D ,∴1(2,0,2)AD =-uuuu r ,∴12AD EF =uuuu r uuu r ,故//AD EF ,又1AD Ì平面11AA D D ,EF Ë平面11AA D D∴EF ∥平面11AA D D .20.(2020·北京高二期末)如图,在直三棱柱111ABC A B C -中,3AC =,4BC =,5AB =,14AA =,点D 是AB 的中点.(1)求异面直线AC 与1BC 所成的角;(2)求证:1//AC 平面1CDB .【答案】(1)2p (2)证明见解析【解析】(1)因为3AC =,4BC =,5AB =,所以222AC BC AB +=,所以ABC D 是直角三角形,所以2ACB p=,所以AC BC^因为三棱柱111ABC A B C -为直三棱柱,所以1C C ^平面ABC ,所以1C C AC ^,1C C BC^以C 为原点,分别以CA 、CB 、1CC 为x 轴、y 轴、z 轴,建立空间直角坐标系,则(0C ,0,0),(3A ,0,0),(0B ,4,0),1(0C ,0,4)所以直线AC 的方向向量为(3,0,0)CA =uuu r ,直线1BC 的方向向量为1(0,4,4)BC =-uuuu r ,设异面直线AC 与1BC 所成的角为q ,因为10CA BC =uuu r uuuu r g ,所以cos 0q =,所以异面直线AC 与1BC 所成的角为2p.(2)由(1)可知3,2,02D æöç÷èø,1(0B ,4,4),则3,2,02CD æö=ç÷èøuuu r ,1(0,4,4)CB =uuur 设平面1CDB 的法向量为(,,)n x y z =r ,则1·0·0CD n CB n ì=ïí=ïîuuu v v uuuv v ,所以3202440x y y z ì+=ïíï+=î令4x =,则3y =-,3z =,所以(4,3,3)n =-r直线1AC 的方向向量为1(3,0,4)AC =-uuuu r ,因为10AC n =uuuu r r g ,1AC Ë平面1CDB , 所以1//AC 平面1CDB .21.(2020·银川三沙源上游学校高二期末)如图,在直三棱柱111ABC A B C -中,AB AC ^,2AB AC ==,1AA =,D 为棱BC 的中点.(1)求直线1DB 与平面11AA C C 所成角的正弦值;(2)求平面11AA C C 与平面1ADB 所成二面角的余弦值.【答案】(12).【解析】则(0,0,0)A ,1(0,0,A ,(2,0,0)C ,(0,2,0)B ,(1,1,0)D ,1(0,2,B ,所以(2,0,0)AC =uuu r ,1(0,0,AA =uuur ,(1,1,0)AD =uuu r ,1(1,1,DB =-uuuu r ,如下图:(1)设平面11AA C C 的一个法向量为(,,)m x y z =u r ,则100AC m AA m ì×=ïí×=ïîuuu v v uuuv v,即00ìïí=ïî,取(0,1,0)m =u r ,所以1cos ,DB m <=uuuu r u r ,所以直线1DB 与平面11AA C C(2)设平面1ADB 的一个法向量为111(,,)n x y z =r ,则100AD n DB n ì×=ïí×=ïîuuu v v uuuu v v,即1111100x y x y +=ìïí-++=ïî,取(1,n =-r ,所以cos ,m n <=u r r ,所以求平面11AA C C 与平面1ADB所成二面角的余弦值.22.(2019·江苏省苏州实验中学高一月考)直四棱柱1111ABCD A B C D -中,2AB BC ==,90ABC Ð=°,E 、F 分别为棱AB 、11B C 上的点,2AE EB =,112C F FB =.求证:(1)//EF 平面11AA C C ;(2)线段AC 上是否存在一点G ,使面EFG ^面11AA C C .若存在,求出AG 的长;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,AG =【解析】(1)如图所示:以1A 为原点,11A D ,11A B ,1A A 分别为,,x y z 轴建立空间直角坐标系:则1(0,0,0)A ,1(0,2,0)B ,1(2,2,0)C ,设(0,0,)A a ,则4(0,,)3E a ,2(,2,0)3F ,所以22(,,)33EF a =-uuu r ,1(0,0,)A A a =uuur ,11(2,2,0)AC =uuuu r ,因为11113EF A A A C =-+uuu r uuur uuuu r ,所以EF uuu r ,1A A uuur ,11AC uuuu r 共面,又EF 不在平面11AA C C 内,所以//EF 平面11AA C C(2)线段AC 上存在一点G ,使面EFG ^面11AA C C ,且AG =证明如下:在三角形AGE 中,由余弦定理得EG ====,所以222AG EG AE +=,即EG AG ^,又1A A ^平面ABCD ,EG Ì平面ABCD ,所以1A A EG ^,而1AG A A A Ç=,所以EG ^平面11AA C C ,因为EG Ì平面EFG ,所以EFG ^面11AA C C .23.(2020·北京高二期末)如图,在底面是正方形的四棱锥P ABCD -中,PA ^平面ABCD ,2AP AB ==,,,E F G 是,,BC PC CD 的中点.(1)求证:BG ^平面PAE ;(2)在线段BG 上是否存在点H ,使得//FH 平面PAE ?若存在,求出BH BG 的值;若不存在,说明理由.【答案】(1)证明见解析;(2)存在,35.【解析】(1)证明:因为四棱锥P ABCD -底面是正方形,且PA ^平面ABCD ,以点A 为坐标原点,,,AB AD AP所在直线分别为,,x y z 轴建立如图所示空间直角坐标系.则(0,0,0),(2,0,0),(0,0,2),A B P ,(2,2,0),(0,2,0)C D ,因为,,E F G 是,,BC PC CD 的中点,所以(2,1,0),(1,1,1),(1,2,0)E F G ,所以(1,2,0)BG =-uuu v ,(0,0,2),(2,1,0),AP AE ==uuu v uuu v 所以0BG AP ×=uuu v uuu v ,且0BG AE ×=uuu v uuu v . 所以BG AP ^,BG AE ^,且AE AP A =I .所以BG ⊥平面PAE .(2)假设在线段BG 上存在点H ,使得FH //平面PAE . 设BH BG l =uuuv uuu v (01)l ££,则(1,21,1)FH FB BH AB AF BG l l l =+=-+=---uuuv uuu v uuuv uuu v uuu v uuu v .因为FH //平面PAE ,BG ⊥平面PAE ,所以(1)(12(21)0(1)530FH GB l l l ×=-×-+-+´-=-=uuuv uuu v . 所以35l =. 所以,在线段BG 上存在点H ,使得FH //平面PAE .其中35BH BG =.。
高考数学空间向量例题

1(2019辽宁理19))已知三棱锥P -ABC 中,PA ⊥面ABC ,AB ⊥AC ,PA=AC=,N 为AB 上一点,AB=4AN,M,S分别为PB,BC 的中点.证明:CM ⊥SN ;审题要津:本题空间坐标系易建立,可用坐标法.证明:设PA=1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图,则P (0,0,1),C (0,1,0),B (2,0,0),M (1,0,12),N(12,0,0),S (1,12,0)因为110022CM SN •=-++=, 所以CM ⊥SN .【点评】对坐标系易建立的空间线线垂直判定(证明)问题,常用向量法,即通过证明所证直线的方向向量的数量积为0证明两直线垂直.例2(2019天津理19) 在长方体1111ABCD A B C D -中,E 、F 分别是棱BC ,1CC 上的点,CF =AB =2CE , 1::AB AD AA = 1:2:4.证明AF ⊥平面1A ED审题要津:本题空间坐标系易建立,可用坐标法.解析:如图所示,建立空间直角坐标系,点A 为坐标原点,设1AB =,依题意得(0,2,0)D ,(1,2,1)F , 1(0,0,4)A ,31,,02E ⎛⎫⎪⎝⎭已知(1,2,1)AF =,131,,42EA ⎛⎫=--⎪⎝⎭,11,,02ED ⎛⎫=- ⎪⎝⎭于是AF ·1EA =0,AF ·ED =0.因此,1AF EA ⊥,AF ED ⊥,又1EA ED E ⋂=所以AF ⊥平面1A ED【点评】对坐标系易建立的空间线面垂直问题,通常用向量法,先求出平面的法向量和直线的方向向量,证明平面法向量与直线的方向向量平行或者直接用向量法证明直线与平面内两条相交直线垂直,再用线面垂直判定定理即可. 例 3 (2019年山东文)在如图所示的几何体中,四边形ABCD 是正方形,MA ⊥平面ABCD ,//PD MA ,E 、G 、F 分别为MB 、PB 、PC 的中点,且2AD PD MA ==.求证:平面EFG ⊥平面PDC .审题要津:本题空间坐标系易建立,可用坐标法.解析:以A 为原点,向量DA ,AB ,AM 分别为x 轴、y 轴、z 轴的正方向,如图建立坐标系,设AM=1,则AD=AB=PD=2,则B(0,2,0),C(-2,2,0),D(-2,0,0),P(-2,0,2), M(0,0,1),则E(0,1,12),G(-1,1,1),F(-2,1,1),∴EG =(-1,0,12),GF =(-1,0,0),设平面EFG 的法向量m =(x ,y ,z ),则 EG •m =12x z -+=0且GF •m =x -=0,取y =1,则x =z =0,∴m =(0,1,0),易证面PDC 的法向量为DA=(2,0,0), ∵DA •m =200100⨯+⨯+⨯=0,∴m ⊥DA , ∴平面EFG ⊥平面PDC【点评】对于易建立空间坐标系的面面垂直问题,常向量法,即先建立坐标系,求出两个平面的法向量,通过证明这两个平面的法向量垂直,即得面面垂直.考点2.利用空间向量处理空间平行关系空间线线、线面、面面平行关系问题是高考考查的另一个重点内容,考查的形式灵活多样,常与探索性问题、垂直问题、空间角问题结合,可以是小题,也可以是解答题的一个小题,题目的难度一般不大,是高考中的得分点之一.例4(2019 湖南理18)在正方体1111ABCD A B C D -,E 是棱1DD 的中点。
空间向量典型例题

空间向量典型例题空间向量与立体几何一、非坐标系向量法1.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于()。
答案:(B)2/3.2.等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为1/3,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于。
答案:3/4.3.已知正四面体ABCD中,E、F分别在AB,CD上,且CF=CD,AE=AB/4,则直线DE和BF所成角的余弦值为()。
答案:(C)-13/13.4.如图,已知四棱柱ABCD-A1,CB=CD,∠C1CB=∠C1CD,证明:C1C垂直于BD;当∠C1CB的值为多少时,能使A1CB1D是菱形且A1C垂直于平面C1BD?请给出证明。
二、坐标系向量法1.如图,在直三棱柱ABCD-A1B1C1D1中,点M是AC的中点,点N是BD的中点,求异面直线AN和B1M所成角的余弦值,以及平面A1B1C1和平面ABC所成二面角的正弦值。
2.如图,在直棱柱ABCD-A1B1C1D1中,AB=BC=1,AC=BD=√2,点M是AC的中点,点N是BD的中点。
证明:(1)MN⊥平面A1B1C1D1;(2)直线MN和平面A1B1C1D1所成二面角的正弦值为1/√10.3.如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC。
求证:PC⊥AB;求二面角B-AP-C的大小。
4.如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°。
求(1)DP与CC1所成角的大小;(2)DP与平面A1AD1所成角的大小。
5.如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=90°,OA⊥底面ABCD,OA=2,M为OA的中点。
求(1)异面直线AB与MD所成角的大小;(2)点B到平面OCD的距离。
备战高考数学一轮复习讲义第36讲 空间直角坐标系与空间向量

第36讲 空间直角坐标系与空间向量激活思维1. (人A 选必一P22练习1改)已知a =(-3,2,5),b =(1,5,-1),则3a -b = (-10,1,16) , a ·b = 2 .解析: 因为a =(-3,2,5),b =(1,5,-1),所以3a -b =(-9,6,15)-(1,5,-1)=(-10,1,16),a ·b =-3+10-5=2.2. (人A 选必一P22练习2)已知a =(2,-1,3),b =(-4,2,x ),且a ⊥b ,则x 的值为 103 .解析: 因为a ⊥b ,即a ·b =0,所以2×(-4)+(-1)×2+3x =0,解得x =103. 3. (人A 选必一P22练习3改)已知点M 在z 轴上,且点M 到点A (1,0,2)与到点B (1,-3,1)的距离相等,则点M 的坐标是( D )A. (0,0,3)B. (0,0,2)C. (0,0,-2)D. (0,0,-3)解析: 设点M (0,0,m ),因为点M 到点A (1,0,2)与到点B (1,-3,1)的距离相等,所以12+02+(m -2)2=12+32+(m -1)2,解得m =-3,所以点M 的坐标为(0,0,-3).4. (人A 选必一P7例2改)如图,在平行六面体ABCD -A ′B ′C ′D ′中,AB =4,AD =3,AA ′=5,∠BAD =90°,∠BAA ′=∠DAA ′=60°,则AA ′→·AB →= 10 ,AC ′的长为85 .(第4题)解析: AA ′→·AB →=|AA ′→|·|AB →|·cos60°=5×4×12=10.因为AC ′→=AC →+CC ′→=AB →+AD →+AA ′→,所以AC ′→2=(AB →+AD →+AA ′→)2=AB →2+AD →2+AA ′→2+2(AB →·AD →+AB →·AA ′→+AD →·AA ′→)=16+9+25+2⎝ ⎛⎭⎪⎫0+5×4×12+3×5×12=85,所以|AC ′→|=85,即AC ′的长为85.基础回归1. 空间向量中的有关定理 (1) 共线向量定理空间中两个向量a 与b (b ≠0)共线的充要条件是存在实数λ,使得 a =λb . (2) 共面向量定理共面向量定理的向量表达式: p =x a +y b ,其中x ,y ∈R ,a ,b 为不共线的向量.(3) 空间向量基本定理如果三个向量a ,b ,c 不共面,那么对空间中任一向量p ,存在有序实数组{x ,y ,z },使得 p =x a +y b +z c ,{a ,b ,c }叫做空间中的 一组基底 .2. 空间向量的数量积(1) 两向量的夹角:若两个非零向量a ,b ,在空间中任取一点O ,作OA →=a ,OB →=b ,则∠AOB 叫做向量a ,b 的夹角,记做〈a ,b 〉,其范围是0≤〈a ,b 〉≤π.若〈a ,b 〉=π2,则称a 与b 互相垂直,记做a ⊥b .(2) 两向量的数量积:若空间中两个非零向量a ,b ,则|a |·|b |cos 〈a ,b 〉叫做向量a ,b 的数量积,记做a ·b ,即a ·b =|a ||b |cos 〈a ,b 〉.3. 空间向量的坐标表示及其应用 设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3).向向量 的方向向量有 无数 个平面的法向量直线l ⊥平面α,取直线l 的方向向量,则这个向量叫做平面α的法向量.显然一个平面的法向量有无数个,它们是共线向量5. 空间位置关系的向量表示位置关系向量表示 直线l 1,l 2的方向向量分别为n 1,n 2l 1∥l 2 n 1∥n 2⇔n 1=λn 2 l 1⊥l 2 n 1⊥n 2⇔n 1·n 2=0 直线l 的方向向量为n ,平面α的法向量为ml ∥α n ⊥m ⇔m ·n =0 l ⊥αn ∥m ⇔n =λm 平面α,β的法向量分别为n ,m α∥β n ∥m ⇔n =λm α⊥βn ⊥m ⇔n ·m =06. 常用结论(1) 在空间中,P ,A ,B ,C 四点共面的充要条件是OP →=xOA →+yOB →+zOC →(其中x +y +z =1),O 为空间中任意一点.(2) 在利用MN →=xAB →+yAC →证明MN ∥平面ABC 时,必须说明点M 或点N 不在平面ABC 内.举题说法空间向量的线性运算例1 如图,在空间四边形OABC 中,OA→=a ,OB →=b ,OC →=c .点M 在OA上,OM =2MA ,N 是BC 的中点,则MN →= -23a +12b +12c (用a ,b ,c 表示).(例1)解析: 因为ON→=12c +12b ,所以MN →=ON →+MO →=-23a +12b +12c .用已知向量表示未知向量的解题策略:(1) 要结合图形,以图形为指导是解题的关键;(2) 要正确理解向量加法、减法与数乘运算的几何意义; (3) 三角形法则、向量加法的平行四边形法则在空间中仍然成立.变式 (人A 选必一P15习题1.2T4)如图,在三棱柱ABC -A ′B ′C ′中,已知AA ′→=a ,AB →=b ,AC →=c ,点M ,N 分别是BC ′,B ′C ′的中点,试用基底{a ,b ,c }表示向量AM→,AN →.(变式)【解答】 如图,连接A ′N ,则AM →=AB →+12BC ′→=AB →+12(BC →+CC ′→)=AB→+12BC →+12CC ′→=AB →+12(AC →-AB →)+12AA ′→=12AB →+12AC →+12AA ′→=12a +12b +12c =12(a +b +c ),AN →=AA ′→+A ′N →=AA ′→+12(A ′B ′→+A ′C ′→)=AA ′→+12(AB →+AC →)=a +12b +12c .(变式)空间向量的数量积的运算及应用例2 如图,在平行六面体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,∠BAA 1=∠DAA 1=45°,∠BAD =60°,则|AC 1→|=__3__.(例2)解析: AC 1→=AC →+AA 1→=AB →+AD →+AA 1→,由题知,|AB →|=|AD →|=1,|AA 1→|=2,AB →与AD →的夹角为∠BAD =60°,AB →与AA 1→的夹角为∠BAA 1=45°,AD →与AA 1→的夹角为∠A 1AD =45°,所以|AC 1→|2=(AB →+AD →+AA 1→)2=|AB →|2+|AD →|2+|AA 1→|2+2AB →·AD →+2AB →·AA 1→+2AD →·AA 1→=1+1+2+2×1×1×cos60°+2×1×2×cos45°+2×1×2×cos45°=9,所以|AC 1→|=3.利用向量解决立体几何问题时,也可以将几何问题转化成向量问题,或通过建立空间直角坐标系利用向量的坐标进行求解,然后代入向量数量积公式进行相关计算和证明.变式 (人A 选必一P14练习2)如图,在平行六面体ABCD -A ′B ′C ′D ′中,AB =2,AD =2,AA ′=3,∠BAD =∠BAA ′=∠DAA ′=60°,则BC ′与CA ′所成角的余弦值为__0__.(变式)解析: 取基底{AB →,AD →,AA ′→},BC ′→=BC →+BB ′→=AD →+AA ′→,CA ′→=CA →+AA ′→=CB →+CD →+AA ′→=-AD →-AB →+AA ′→,所以BC ′→·CA ′→=(AD →+AA ′→)·(-AD →-AB →+AA ′→)=-AD →2-AD →·AB →+AD →·AA ′→-AD →·AA ′→-AB →·AA ′→+AA ′→2=-4-2-3+9=0.设BC ′与CA ′的夹角为θ,则cos θ=|cos 〈BC ′→,CA ′→〉|=|BC ′→·CA ′→||BC ′→||CA ′→|=0,所以BC ′与CA ′所成角的余弦值为0.利用空间向量证明平行问题例3 (2022·江苏百校联考)已知△ABC 为等腰直角三角形,AC =BC =4,E ,F 分别为AC 和AB 上的点,且AE =1,EF ∥BC ,如图(1).沿EF 将△AEF 折起使平面AEF ⊥平面BCEF ,连接AC ,AB ,如图(2).已知M 为棱AC 上一点,试确定M 的位置,使EM ∥平面ABF .图(1) 图(2)(例3)【解答】 因为平面AEF ⊥平面BCEF ,AE ⊥EF ,所以AE ⊥EC ,又CE ⊥EF ,所以建立如图所示的空间直角坐标系,则A (0,0,1),B (3,4,0),C (3,0,0),F (0,1,0),所以AC→=(3,0,-1).设AM →=λAC →,EM →=EA →+AM →=EA →+λAC →=(3λ,0,1-λ).设n =(x ,y ,z )为平面ABF 的法向量,则⎩⎪⎨⎪⎧n ·FB →=0,n ·F A →=0,即⎩⎨⎧3x +3y =0,-y +z =0,因此可取n =(1,-1,-1),所以n ·EM →=(1,-1,-1)·(3λ,0,1-λ)=4λ-1.因为EM ∥平面ABF ,所以n ·EM →=0,即λ=14,所以当AM →=14AC →时,EM ∥平面ABF .(例3)证明直线与平面平行,只需证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,或证直线的方向向量与平面内某直线的方向向量平行,然后说明直线在平面外即可.利用空间向量证明垂直问题例4 如图,已知四棱锥P -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =PB =PC =2CD ,侧面PBC ⊥底面ABCD .(例4)(1) 求证:P A ⊥BD ;【解答】 如图,取BC 的中点O ,连接PO ,因为△PBC 为等边三角形,所以PO ⊥BC .因为平面PBC ⊥底面ABCD ,平面PBC ∩底面ABCD =BC ,PO ⊂平面PBC ,所以PO ⊥底面ABCD .以BC 的中点O 为坐标原点,以BC 所在的直线为x 轴,过点O 与AB 平行的直线为y 轴,OP 所在的直线为z 轴,建立如图所示的空间直角坐标系.不妨设CD =1,则AB =BC =2,PO =3,所以A (1,-2,0),B (1,0,0),D (-1,-1,0),P (0,0,3),所以BD →=(-2,-1,0),P A →=(1,-2,-3).因为BD →·P A →=(-2)×1+(-1)×(-2)+0×(-3)=0,所以P A →⊥BD →,所以P A ⊥BD .(例4)(2) 求证:平面P AD ⊥平面P AB .【解答】 如图,取P A 的中点M ,连接DM ,则M ⎝ ⎛⎭⎪⎫12,-1,32.因为DM→=⎝ ⎛⎭⎪⎫32,0,32,PB →=(1,0,-3),所以DM →·PB→=32×1+0×0+32×(-3)=0,所以DM →⊥PB →,即DM ⊥PB .因为DM →·P A →=32×1+0×(-2)+32×(-3)=0,所以DM →⊥P A →,即DM ⊥P A .又因为P A ∩PB =P ,P A ,PB ⊂平面P AB ,所以DM ⊥平面P AB .因为DM ⊂平面P AD ,所以平面P AD ⊥平面P AB .用向量证明垂直的方法:(1) 线线垂直:证明两直线所在的方向向量互相垂直;(2) 线面垂直:证明直线的方向向量与平面的法向量共线;(3) 面面垂直:证明两个平面的法向量互相垂直.随堂内化1. 若向量a ,b 的坐标满足a +b =(-2,-1,2),a -b =(4,-3,-2),则a ·b 等于( B )A. 5B. -5C. 7D. -1解析: 因为a +b =(-2,-1,2),a -b =(4,-3,-2),两式相加得2a =(2,-4,0),解得a =(1,-2,0),b =(-3,1,2),所以a ·b =1×(-3)+(-2)×1+0×2=-5.2. 已知向量a =(1,1,0),b =(1,-2,2),且k a -b 与a +b 互相垂直,则k 的值为( B )A. 2B. 8C. -1D. -63. 已知A (4,1,3),B (2,3,1),C (3,7,-5),点P (x ,-1,3)在平面ABC 内,则x 的值为( D )A. -4B. 1C. 10D. 11解析: 因为点P (x ,-1,3)在平面ABC 内,所以存在实数λ,μ,使得等式AP →=λAB→+μAC →成立,所以(x -4,-2,0)=λ(-2,2,-2)+μ(-1,6,-8),所以⎩⎨⎧x -4=-2λ-μ,-2=2λ+6μ,0=-2λ-8μ,消去λ,μ,解得x =11.4. 如图,在三棱锥A -BCD 中,DA ,DB ,DC 两两垂直,且DB =DC =DA =2,E 为BC 的中点.(第4题)(1) 求证:AE ⊥BC ;【解答】 因为AE →=DE →-DA →=12(DB →+DC →)-DA →,BC →=DC →-DB →,所以AE →·BC→=⎝ ⎛⎭⎪⎫12DB →+12DC →-DA →·(DC →-DB →)=12DB →·DC →-12DB →·DB →+12DC →·DC →-12DC →·DB→-DA →·DC →+DA →·DB →=0-2+2-0-0+0=0,所以AE →⊥BC →,即AE ⊥BC .(2) 求直线AE 与DC 所成角的余弦值.【解答】 因为AE →·DC →=⎝ ⎛⎭⎪⎫12DB →+12DC →-DA →·DC →=12DB →·DC →+12DC →·DC →-DA →·DC →=0+2-0=2, |AE →|=(2)2+22=6,所以cos 〈AE →,DC →〉=AE →·DC →|AE →||DC →|=26×2=66,即直线AE 与DC 所成角的余弦值为66.练案❶ 趁热打铁,事半功倍. 请老师布置同学们及时完成《配套精练》. 练案❷ 1. 补不足、提能力,老师可增加训练《抓分题·高考夯基固本天天练》(分基础和提高两个版本)对应内容,成书可向当地发行咨询购买.2. 为提高高考答卷速度及综合应考能力,老师可适时安排《一年好卷》或《抓分卷·高考保分增效天天练》,成书可向当地发行咨询购买.。
高中数学第1章空间向量与立体几何章末核心素养整合新人教版选择性必修第一册

= ,
则
解得
= .
· = -- + = ,
取 x=1,则 y=1,z=2,于是 n=(1,1,2)是平面 PCF 的一个法向量.
设点 A 到平面 PCF 的距离为 d,又=(a,a,0),
|·|
则 d=
||
=
×+×+×
求证:
(1)A1B1⊥平面AA1C;
(2)AB1∥平面A1C1C.
证明:∵二面角A1-AB-C是直二面角,
∴平面A1ABB1⊥平面ABC.
又四边形A1ABB1是正方形,∴AA1⊥AB.
∴AA1⊥平面ABC.∴AA1⊥AC.
又AB=AC,BC= AB,
∴∠CAB=90°,即AC⊥AB.∴AB,AC,AA1两两互相垂直.
(2)=(0,2,2), =(1,1,0), =(2,0,-2).
设平面 A1C1C 的法向量为 m=(a,b,c),
+ = ,
· = ,
则
即
∴ = -,
- = , = .
· = ,
令 a=1,则 b=-1,c=1.∴m=(1,-1,1)为平面 A1C1C 的一个法向量.
设点A到平面PBC的距离为h,
∵AD∥BC,AD⊄平面PBC,∴AD∥平面PBC,
∴h为AD到平面PBC的距离,
|· |
∴h=
| |
=
=
a.
规律总结
1.求点到平面的距离,常常利用向量法,转化为平面外一点与
平面内一点构成的向量在平面的法向量方向上的投影向量的
长度.
2.求直线到平面的距离,往往转化为点到平面的距离求解,且
【高中数学】1.3.1空间直角坐标系 1.3.2 空间向量运算的坐标表示

1.3 空间向量及其运算的坐标表示1.3.1 空间直角坐标系 1.3.2 空间向量运算的坐标表示基础过关练题组一 空间向量的坐标表示1.在空间直角坐标系中,点P(1,2,3)关于平面Oyz 对称的点的坐标为( ) A.(1,-2,-3) B.(-1,-2,3) C.(-1,2,3) D.(-1,2,-3)2.空间直角坐标系中,已知A(1,-2,3),B(3,2,-5),则线段AB 的中点坐标为( ) A.(-1,-2,4) B.(-2,0,1) C.(2,0,-2) D.(2,0,-1)3.在直三棱柱ABO-A 1B 1O 1中,∠AOB=π2,AO=4,BO=2,AA 1=4,D 为A 1B 1的中点,则在空间直角坐标系中(O 为坐标原点),DO ⃗⃗⃗⃗⃗⃗ 的坐标是 ,A 1B ⃗⃗⃗⃗⃗⃗⃗ 的坐标是 . 题组二 空间向量线性运算的坐标表示4.(2020黑龙江牡丹江第一高级中学高二上期中)已知O 为原点,a=(1,-2,1),a-b=(-1,2,-1),则b 等于( ) A.(2,-4,2) B.(-2,4,-2) C.(-2,0,-2) D.(2,1,-3)5.已知向量a=(1,2,3),b=(-1,0,1),则a+2b=( ) A.(-1,2,5) B.(-1,4,5) C.(1,2,5)D.(1,4,5)6.(2020湖南长沙明德中学高二上月考)若a =(1,λ,2),b=(2,-1,2),c=(1,4,4),且a,b,c 共面,则λ= .7.(2020湖南师范大学附属中学高二上期中)已知a=(x,1,3),b=(-1,3,9),若a 与b 共线,则x 的值是 .8.已知O 是坐标原点,且A,B,C 三点的坐标分别是(2,-1,2),(4,5,-1),(-2,2,3),求适合下列条件的点P 的坐标:(1)OP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ );(2)AP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ -AC⃗⃗⃗⃗⃗ ).题组三 空间向量数量积的坐标表示9.已知a=(1,1,0),b=(0,1,1),c=(1,0,1),p=a-b,q=a+2b-c,则p ·q=( ) A.-1 B.1 C.0 D.-210.直三棱柱ABC-A 1B 1C 1的底面是边长为2的正三角形,侧棱为3,M,N 分别为A 1C 1,BC 的中点,则AB ⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗⃗ =( ) A.2 B.-2 C.√10D.-√1011.(2020重庆高二上期中)如图,建立空间直角坐标系Oxyz.单位正方体ABCD-A'B'C'D'的顶点A 位于坐标原点,其中B(1,0,0),D(0,1,0),A'(0,0,1).(1)若E 是棱B'C'的中点,F 是棱B'B 的中点,G 是侧面CDD'C'的中心,分别求出向量OE ⃗⃗⃗⃗⃗ ,OG ⃗⃗⃗⃗⃗ ,FG⃗⃗⃗⃗⃗ 的坐标; (2)在(1)的条件下,分别求出(OE ⃗⃗⃗⃗⃗ +OG ⃗⃗⃗⃗⃗ )·FG ⃗⃗⃗⃗⃗ ,|EG⃗⃗⃗⃗⃗ |的值.12.已知向量a=(2,1,-2),c=(-1,0,1),向量b同时满足下列三个条件:①a·b=-1;②|b|=3;③b⊥c.(1)求a+2c的模;(2)求向量b的坐标.题组四 利用空间向量的坐标运算解决平行和垂直问题13.设x,y ∈R,向量a=(x,1,1),b=(1,y,1),c=(2,-4,2),且a ⊥c,b ∥c,则x+y 的值为( ) A.-1 B.1 C.2 D.314.(2020山西大同第一中学高二上期中)如图,在正方体ABCD-A 1B 1C 1D 1中,M,N 分别是BC 1,CD 1的中点,则下列说法错误的是( )A.MN 与CC 1垂直B.MN 与AC 垂直C.MN 与BD 平行D.MN 与A 1B 1平行15.已知AB ⃗⃗⃗⃗⃗ =(1,5,-2),BC ⃗⃗⃗⃗⃗ =(3,1,z),若AB ⃗⃗⃗⃗⃗ ⊥BC ⃗⃗⃗⃗⃗ ,BP ⃗⃗⃗⃗⃗ =(x-1,y,-3),且BP ⊥平面ABC,则BP⃗⃗⃗⃗⃗ = . 题组五 利用空间向量求夹角和距离(长度)16.在空间直角坐标系中,已知M(-1,0,2),N(3,2,-4),则MN 的中点P 到坐标原点O 的距离为( ) A.√3 B.√2C.2D.317.(2020四川绵阳中学高二上期中)空间直角坐标系中的点A(3,3,1)关于平面Oxy 的对称点A'与点B(-1,1,5)间的距离为( ) A.6 B.2√6C.4√3D.2√1418.(2020北京十二中高二上期中)已知点A(0,1,2),B(1,-1,3),C(1,5,-1). (1)若D 为线段BC 的中点,求线段AD 的长;(2)若AD ⃗⃗⃗⃗⃗ =(2,a,1),且AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =1,求a 的值,并求此时向量AB ⃗⃗⃗⃗⃗ 与AD ⃗⃗⃗⃗⃗ 夹角的余弦值.19.(2020山西太原第五中学高二上月考)如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在线段AB上,点Q在线段DC上.(1)当PB=2AP,且点P关于y轴的对称点为M时,求|PM|的长度;(2)当点P是面对角线AB的中点,点Q在面对角线DC上运动时,探究|PQ|的最小值.深度解析能力提升练题组一空间向量运算的坐标表示1.(2020山东泰安第一中学高二上期末,)已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若{a,b,c}不能构成空间的一个基底,则实数λ的值为()A.0B.357C.9 D.6572.(2020北京东直门中学高二上期中,)已知O 为原点,OA ⃗⃗⃗⃗⃗ =(1,2,3),OB ⃗⃗⃗⃗⃗ =(2,1,2),OP ⃗⃗⃗⃗⃗ =(1,1,2),点Q 在直线OP 上运动,则QA ⃗⃗⃗⃗⃗ ·QB ⃗⃗⃗⃗⃗ 取得最小值时,点Q 的坐标为( ) A.(12,34,13) B.(12,23,34)C.(43,43,83) D.(43,43,73) 3.(多选)(2020陕西西北大学附属中学高二上期中,)设几何体ABCD-A 1B 1C 1D 1是棱长为a 的正方体,A 1C 与B 1D 相交于点O,则( ) A.A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =a 2 B.AB ⃗⃗⃗⃗⃗ ·A 1C ⃗⃗⃗⃗⃗⃗⃗ =√2a 2C.CD ⃗⃗⃗⃗⃗ ·AB 1⃗⃗⃗⃗⃗⃗⃗ =-a 2D.AB ⃗⃗⃗⃗⃗ ·A 1O ⃗⃗⃗⃗⃗⃗⃗ =12a4.(多选)()已知向量a ·b=b ·c=a ·c,b=(3,0,-1),c=(-1,5,-3),下列等式中正确的是( )A.(a ·b)·c=b ·cB.(a+b)·c=a ·(b+c)C.(a+b+c)2=a 2+b 2+c 2D.|a+b+c|=|a-b-c|5.()已知点P 是棱长为1的正方体A 1B 1C 1D 1-ABCD 的底面A 1B 1C 1D 1上一点(包括边界),则PA ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 的取值范围是 . 题组二 利用空间向量的坐标运算解决平行、垂直问题 6.(2020江苏启东中学高二上期中,)已知两个向量a=(2,-1,3),b=(4,m,n),且a ∥b,则m+n 的值为 (深度解析) A.1 B.2 C.4 D.8 7.()在三棱柱A 1B 1C 1-ABC 中,侧棱AA 1⊥底面A 1B 1C 1,∠BAC=90°,AB=AC=AA 1=1,D 是棱CC 1的中点,P 是AD 的延长线与A 1C 1的延长线的交点.若点Q 在直线B 1P 上,则下列结论正确的是( ) A.当点Q 为线段B 1P 的中点时,DQ ⊥平面A 1BD B.当点Q 为线段B 1P 的三等分点时,DQ ⊥平面A 1BDC.在线段B1P的延长线上,存在一点Q,使得DQ⊥平面A1BDD.不存在点Q,使DQ与平面A1BD垂直8.()已知a=(3,2λ-1,1),b=(μ+1,0,2μ).若a⊥b,则μ=;若a∥b,则λ+μ=.9.(2020浙江绍兴高二上期末阶段测试,)如图,已知四棱柱ABCD-A1B1C1D1,AA1⊥平面ABCD,四边形ABCD是正方形,点E在线段A1D上,且A1E=2ED.(1)证明:BD1⊥AC;(2)证明:BD1∥平面ACE.题组三利用空间向量的坐标运算解决长度和夹角问题10.(2020安徽芜湖高二上期末,)如图,在三棱锥P-ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则异面直线AC与PD所成角的余弦值为(深度解析)A.14B.√24C.√34D.1211.(2020湖北武汉高二期末联考,)在棱长为1的正方体ABCD-A 1B 1C 1D 1中,P 是底面ABCD(含边界)上一动点,满足A 1P ⊥AC 1,则线段A 1P 长度的取值范围是( ) A.[√62,√2] B.[√62,√3]C.[1,√2]D.[√2,√3]12.(多选)(2020山东莱州第一中学高二上期末,)正方体A 1B 1C 1D 1-ABCD 的棱长为2,M 为B 1C 1的中点,下列命题中正确的是( ) A.AB 1与BC 1成60°角B.若CN ⃗⃗⃗⃗⃗ =13NC 1⃗⃗⃗⃗⃗⃗⃗ ,面A 1MN 交CD 于点E,则CE=13C.P 点在正方形ABB 1A 1边界及内部运动,且MP ⊥DB 1,则P 点的轨迹长等于√2D.E,F 分别在DB 1,A 1C 1上,且DE EB 1=A 1FFC 1=2,直线EF 与AD 1,A 1D 所成角分别是α,β,则α+β=π2答案全解全析 基础过关练1.C 点P 关于平面Oyz 对称的点的坐标与点P 的横坐标相反,故选C.2.D 设中点坐标为(x,y,z),根据中点坐标公式得x=1+32=2,y=-2+22=0,z=3−52=-1.3.答案 (-2,-1,-4);(-4,2,-4)解析 如图建系,则O(0,0,0),A 1(4,0,4),B 1(0,2,4),B(0,2,0),∴A 1B ⃗⃗⃗⃗⃗⃗⃗ =(-4,2,-4).∵D 为A 1B 1的中点,∴D(2,1,4),∴DO⃗⃗⃗⃗⃗⃗ =(-2,-1,-4).4.A ∵a-b=(-1,2,-1),∴b=a-(-1,2,-1)=(1,-2,1)-(-1,2,-1)=(2,-4,2),故选A.5.A a+2b=(1,2,3)+2(-1,0,1)=(1,2,3)+(-2,0,2)=(-1,2,5),故选A.6.答案 1解析 ∵a,b,c 共面,∴存在实数m,n,使得c=ma+nb, ∴{1=m +2n,4=λm -n,4=2m +2n,解得λ=1. 7.答案 -13解析 ∵a 与b 共线,∴∃λ∈R,使b =λa, ∴{-1=λx,3=λ,9=3λ,解得{λ=3,x =−13.8.解析 由题得AB ⃗⃗⃗⃗⃗ =(2,6,-3),AC⃗⃗⃗⃗⃗ =(-4,3,1). (1)∵OP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ -AC⃗⃗⃗⃗⃗ )=12(2+4,6-3,-3-1)=12(6,3,-4)=(3,32,-2), ∴P (3,32,-2).(2)∵AP ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ -AC⃗⃗⃗⃗⃗ ) =12(2+4,6-3,-3-1)=12(6,3,-4)=(3,32,-2), ∴OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +AP⃗⃗⃗⃗⃗ =(2,-1,2)+(3,32,-2) =(5,12,0),∴P (5,12,0).9.A p=a-b=(1,0,-1),q=a+2b-c=(1,1,0)+(0,2,2)-(1,0,1)=(0,3,1), ∴p ·q=1×0+0×3+(-1)×1=-1,故选A. 10.B 如图,建立空间直角坐标系,则A(0,0,0),B(2,0,0),M (12,√32,3),N (32,√32,0),∴AB ⃗⃗⃗⃗⃗ =(2,0,0),NM⃗⃗⃗⃗⃗⃗⃗ =(-1,0,3), ∴AB ⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗⃗ =2×(-1)+0+0=-2,故选B.11.解析 (1)由题图知,O(0,0,0),E (1,12,1),G (12,1,12),F (1,0,12),∴OE ⃗⃗⃗⃗⃗ =(1,12,1),OG ⃗⃗⃗⃗⃗ =(12,1,12),OF ⃗⃗⃗⃗⃗ =(1,0,12),∴FG ⃗⃗⃗⃗⃗ =OG ⃗⃗⃗⃗⃗ -OF ⃗⃗⃗⃗⃗ =(12,1,12)-1,0,12=(-12,1,0).(2)(OE ⃗⃗⃗⃗⃗ +OG ⃗⃗⃗⃗⃗ )·FG ⃗⃗⃗⃗⃗ =(32,32,32)·(-12,1,0)=34,EG ⃗⃗⃗⃗⃗ =OG ⃗⃗⃗⃗⃗ -OE ⃗⃗⃗⃗⃗ =(-12,12,-12),∴|EG ⃗⃗⃗⃗⃗ |=√EG⃗⃗⃗⃗⃗ 2=√32. 12.解析 (1)∵a=(2,1,-2),c=(-1,0,1),∴a+2c=(2,1,-2)+(-2,0,2)=(0,1,0), ∴|a+2c|=√0+1+0=1.(2)设b=(x,y,z),则a ·b=2x+y-2z=-1①,|b|=√x 2+y 2+z 2=3②,b ·c=-x+z=0③, 由①②③得{x =2,y =−1,z =2或{x =−2,y =−1,z =−2,∴b=(2,-1,2)或b=(-2,-1,-2).13.A ∵a ⊥c,∴a ·c=2x-4+2=0,解得x=1,又b ∥c,∴12=y-4=12,解得y=-2,则x+y=-1,故选A.14.D 设正方体的棱长为1,如图,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A 1(1,0,1),B 1(1,1,1),C 1(0,1,1),M (12,1,12),N (0,12,12),∴MN ⃗⃗⃗⃗⃗⃗⃗ =(-12,-12,0),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,1),AC ⃗⃗⃗⃗⃗ =(-1,1,0),BD ⃗⃗⃗⃗⃗⃗ =(-1,-1,0),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,1,0),∴MN ⃗⃗⃗⃗⃗⃗⃗ ·CC 1⃗⃗⃗⃗⃗⃗⃗ =0,∴MN ⊥CC 1,A 说法正确;MN⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =12-12=0,∴MN ⊥AC,B 说法正确;易知BD ⃗⃗⃗⃗⃗⃗ =2MN ⃗⃗⃗⃗⃗⃗⃗ ,且M,N ∉BD,∴MN ∥BD,C 说法正确;设MN ⃗⃗⃗⃗⃗⃗⃗ =λA 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ,得{-12=0×λ,-12=λ,0=0×λ,无解,所以MN 与A 1B 1不平行,D 说法错误.故选D.15.答案 (337,-157,-3)解析 因为AB ⃗⃗⃗⃗⃗ ⊥BC ⃗⃗⃗⃗⃗ ,所以AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0, 即1×3+5×1+(-2)z=0,所以z=4.因为BP ⊥平面ABC, 所以BP ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ,且BP ⃗⃗⃗⃗⃗ ⊥BC⃗⃗⃗⃗⃗ , 即{1×(x -1)+5y +(−2)×(−3)=0,3(x -1)+y +4×(−3)=0, 解得{x =407,y =−157,所以BP⃗⃗⃗⃗⃗ =(337,-157,-3). 16.A 由中点坐标公式,得P(1,1,-1),所以OP⃗⃗⃗⃗⃗ =(1,1,-1),|OP ⃗⃗⃗⃗⃗ |=√1+1+1=√3.故选A. 17.D 由题意得,A'(3,3,-1),所以A'B ⃗⃗⃗⃗⃗⃗ =(-4,-2,6),所以|A'B ⃗⃗⃗⃗⃗⃗ |=√16+4+36=2√14,故选D.18.解析 (1)由题意得,D(1,2,1),∴AD ⃗⃗⃗⃗⃗ =(1,1,-1),|AD ⃗⃗⃗⃗⃗ |=√1+1+1=√3,即线段AD 的长为√3.(2)易知AB ⃗⃗⃗⃗⃗ =(1,-2,1),∴AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =2-2a+1=1,解得a=1,∴AD ⃗⃗⃗⃗⃗ =(2,1,1).∴cos<AB ⃗⃗⃗⃗⃗ ,AD ⃗⃗⃗⃗⃗ >=AB ⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗ |AB ⃗⃗⃗⃗ ||AD ⃗⃗⃗⃗ |=√6×√6=16,即向量AB ⃗⃗⃗⃗⃗ 与AD ⃗⃗⃗⃗⃗ 夹角的余弦值为16.19.解析 由题意知A(1,0,1),B(1,1,0),C(0,1,0),D(1,1,1). (1)由PB=2PA 得P (1,13,23),所以M (-1,13,-23),所以|PM|=2√133.(2)当点P 是面对角线AB 的中点时,P (1,12,12),点Q 在面对角线DC 上运动,设点Q(a,1,a),a ∈[0,1], 则|PQ|=√(a -1)2+(1−12)2+(a -12)2=√2a 2-3a+32=√2(a -34)2+38,所以当a=34时,|PQ|取得最小值√64,此时点Q (34,1,34). 方法归纳 利用向量坐标求空间中线段长度的一般步骤:(1)建立适当的空间直角坐标系;(2)求出线段端点的坐标(或线段对应向量的坐标);(3)利用两点间的距离公式求出线段的长(或利用向量模的坐标公式求出对应向量的模).能力提升练1.D ∵{a,b,c}不能构成空间的一个基底,∴a,b,c 共面,则c=xa+yb,其中x,y ∈R,则(7,5,λ)=(2x,-x,3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y), ∴{7=2x -y,5=−x +4y,λ=3x -2y,解得{x =337,y =177,λ=657.故选D.2.C 点Q 在直线OP 上运动,设OQ ⃗⃗⃗⃗⃗⃗ =λOP ⃗⃗⃗⃗⃗ =(λ,λ,2λ)(λ∈R),则QA ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ -OQ ⃗⃗⃗⃗⃗⃗ =(1-λ,2-λ,3-2λ),QB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ -OQ⃗⃗⃗⃗⃗⃗ =(2-λ,1-λ,2-2λ), ∴QA ⃗⃗⃗⃗⃗ ·QB ⃗⃗⃗⃗⃗ =6(λ-43)2-23,当λ=43时,QA ⃗⃗⃗⃗⃗ ·QB ⃗⃗⃗⃗⃗ 最小,此时,Q (43,43,83),故选C.3.AC 如图,建立空间直角坐标系,则A(a,0,0),B(a,a,0),C(0,a,0),D(0,0,0),A 1(a,0,a),B 1(a,a,a),O (a 2,a 2,a2),∴A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,a,0),AC⃗⃗⃗⃗⃗ =(-a,a,0),AB ⃗⃗⃗⃗⃗ =(0,a,0),A 1C ⃗⃗⃗⃗⃗⃗⃗ =(-a,a,-a),CD ⃗⃗⃗⃗⃗ =(0,-a,0),AB 1⃗⃗⃗⃗⃗⃗⃗ =(0,a,a),A 1O ⃗⃗⃗⃗⃗⃗⃗ =(-a 2,a 2,-a2). ∴A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =a 2,A 对;AB ⃗⃗⃗⃗⃗ ·A 1C ⃗⃗⃗⃗⃗⃗⃗ =a 2,B 错;CD ⃗⃗⃗⃗⃗ ·AB 1⃗⃗⃗⃗⃗⃗⃗ =-a 2,C 对;AB ⃗⃗⃗⃗⃗ ·A 1O ⃗⃗⃗⃗⃗⃗⃗ =12a 2,D 错.故选AC.4.BCD 易得a ·b=a ·c=b ·c=-3+0+3=0.(a ·b)·c=0,b ·c=0,所以A 选项错误;(a+b)·c-a ·(b+c)=a ·c+b ·c-a ·b-a ·c=0,所以(a+b)·c=a ·(b+c),所以B 选项正确; (a+b+c)2=a 2+b 2+c 2+2a ·b+2b ·c+2a ·c=a 2+b 2+c 2,所以C 选项正确; (a-b-c)2=a 2+b 2+c 2-2a ·b+2b ·c-2a ·c=a 2+b 2+c 2,即(a+b+c)2=(a-b-c)2,|a+b+c|=|a-b-c|,所以D 选项正确. 故选BCD. 5.答案 [12,1]解析 如图所示,建立空间直角坐标系,则A 1(0,0,0),A(0,0,1),C(1,1,1). 设P(x,y,0)(x,y ∈[0,1]).则PA ⃗⃗⃗⃗⃗ =(-x,-y,1),PC ⃗⃗⃗⃗⃗ =(1-x,1-y,1), ∴PA ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ =-x(1-x)-y(1-y)+1 =(x -12)2+(y -12)2+12. ∵x,y ∈[0,1],∴当x=12,y=12时,PA ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 有最小值12.当点P 取(0,0,0),(1,0,0),(1,1,0),(0,1,0)时,PA ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ 有最大值1. ∴PA ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 的取值范围是[12,1]. 6.C 因为a ∥b,所以∃λ∈R,使得b =λa,得{4=2λ,m =−λ,n =3λ,解得{λ=2,m =−2,n =6,所以m+n=4,故选C.解题反思 在解决有关平行的问题时,通常需要引入参数,如本题中已知a ∥b,引入参数λ,使b =λa,转化为方程组求解;本题也可以利用坐标成比例求解,即由a ∥b,得42=m-1=n3,求出m,n.7.D 如图,建立空间直角坐标系,则A 1(0,0,0),B 1(1,0,0),B(1,0,1),D (0,1,12),P(0,2,0),所以B 1P ⃗⃗⃗⃗⃗⃗⃗ =(-1,2,0),B 1D ⃗⃗⃗⃗⃗⃗⃗ =(-1,1,12),A 1B ⃗⃗⃗⃗⃗⃗⃗ =(1,0,1),A 1D ⃗⃗⃗⃗⃗⃗⃗ =(0,1,12). 设存在点Q,使DQ 与平面A 1BD 垂直,设B 1Q ⃗⃗⃗⃗⃗⃗⃗ =λB 1P ⃗⃗⃗⃗⃗⃗⃗ (0≤λ≤1),则DQ ⃗⃗⃗⃗⃗⃗ =B 1Q ⃗⃗⃗⃗⃗⃗⃗ -B 1D ⃗⃗⃗⃗⃗⃗⃗ =λB 1P ⃗⃗⃗⃗⃗⃗⃗ -B 1D ⃗⃗⃗⃗⃗⃗⃗ =(-λ,2λ,0)--1,1,12=(1−λ,2λ-1,-12).由{DQ ⃗⃗⃗⃗⃗⃗ ⊥A 1B ⃗⃗⃗⃗⃗⃗⃗ ,DQ ⃗⃗⃗⃗⃗⃗ ⊥A 1D ⃗⃗⃗⃗⃗⃗⃗ ,得{1−λ-12=0,2λ-1-14=0,无解,故选D.8.答案 -35;710解析 由a ⊥b,得a ·b =3(μ+1)+2μ=0,解得μ=-35.由a ∥b,得μ+13=2μ1,且2λ-1=0,解得μ=15,λ=12,所以λ+μ=710.9.证明 (1)设AC 与BD 交于点O,A 1C 1与B 1D 1交于点O 1,连接OO 1,设AB=a,AA 1=b.如图,建立空间直角坐标系,则O(0,0,0),A (0,−√22a,0),B (√22a,0,0),C (0,√22a,0),D (-√22a,0,0),A 1(0,−√22a,b),D 1(-√22a,0,b),∴BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(-√2a,0,b),AC ⃗⃗⃗⃗⃗ =(0,√2a,0), ∴BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =0,∴BD 1⊥AC.(2)设E(x,y,z),∵A 1E=2ED,∴A 1E ⃗⃗⃗⃗⃗⃗⃗ =2ED ⃗⃗⃗⃗⃗ ,即x,y+√22a,z-b =2(-√22a -x,-y,-z),解得x=-√23a,y=-√26a,z=b3,即E (-√23a,-√26a,13b),∴AE⃗⃗⃗⃗⃗ =(-√23a,√23a,13b). 设BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ +μAE ⃗⃗⃗⃗⃗ (λ,μ∈R),则(-√2a,0,b)=λ(0,√2a,0)+μ(-√23a,√23a,13b), 即{-√2a =0−√23μa,0=√2λa +√23μa,b =0+13μb,解得{λ=−1,μ=3,即BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =-AC ⃗⃗⃗⃗⃗ +3AE ⃗⃗⃗⃗⃗ .∴BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ,AE ⃗⃗⃗⃗⃗ 共面,又BD 1⊄平面ACE,∴BD 1∥平面ACE.10.B 取AC 的中点O,连接OP,OB, ∵PA=PC,∴AC ⊥OP,∵平面PAC ⊥平面ABC,平面PAC ∩平面ABC=AC, ∴OP ⊥平面ABC,又∵AB=BC,∴AC ⊥OB,以O 为坐标原点,建立如图所示的空间直角坐标系,∵△PAC 是等腰直角三角形,PA=PC=4,△ABC 为等边三角形, ∴A(2√2,0,0),C(-2√2,0,0),P(0,0,2√2),D(√2,√6,0), ∴AC⃗⃗⃗⃗⃗ =(-4√2,0,0),PD ⃗⃗⃗⃗⃗ =(√2,√6,-2√2), ∴cos<AC ⃗⃗⃗⃗⃗ ,PD ⃗⃗⃗⃗⃗ >=AC ⃗⃗⃗⃗ ·PD⃗⃗⃗⃗ |AC ⃗⃗⃗⃗ ||PD ⃗⃗⃗⃗ |=√=-√24.∴异面直线AC 与PD 所成角的余弦值为√24.故选B.解题反思 用坐标法求解立体几何问题,关键是建立适当的空间直角坐标系.建系时,关键是寻找线面垂直的条件,将垂线所在直线作为z 轴,利用底面的图形特点建立x 轴和y 轴.11.A 如图,建立空间直角坐标系,则A(0,0,0),A 1(0,0,1),C 1(1,1,1), ∵P 是底面ABCD(含边界)上一动点, ∴设P(x,y,0)(0≤x ≤1,0≤y ≤1), 则A 1P ⃗⃗⃗⃗⃗⃗⃗ =(x,y,-1),AC 1⃗⃗⃗⃗⃗⃗⃗ =(1,1,1), ∵A 1P ⊥AC 1,∴A 1P ⃗⃗⃗⃗⃗⃗⃗ ·AC 1⃗⃗⃗⃗⃗⃗⃗ =x+y-1=0,∴A 1P ⃗⃗⃗⃗⃗⃗⃗ 2=x 2+y 2+1=x 2+(1-x)2+1=2x 2-2x+2=2(x -12)2+32, ∴当x=12时,A 1P ⃗⃗⃗⃗⃗⃗⃗ 2取最小值32,此时线段A 1P 的长度为√62;当x=0或x=1时,A 1P ⃗⃗⃗⃗⃗⃗⃗ 2取最大值2,此时线段A 1P 的长度为√2,∴线段A 1P 长度的取值范围是[√62,√2].故选A.12.ACD 如图,建立空间直角坐标系,则A(2,0,2),B(2,2,2),C(0,2,2),D(0,0,2),A 1(2,0,0),B 1(2,2,0),C 1(0,2,0),D 1(0,0,0),M(1,2,0).对于A,AB 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,-2),BC 1⃗⃗⃗⃗⃗⃗⃗ =(-2,0,-2),cos<AB 1⃗⃗⃗⃗⃗⃗⃗ ,BC 1⃗⃗⃗⃗⃗⃗⃗ >=AB 1⃗⃗⃗⃗⃗⃗ ·BC 1⃗⃗⃗⃗⃗⃗ |AB 1⃗⃗⃗⃗⃗⃗ ||BC 1⃗⃗⃗⃗⃗⃗ |=√√=12,∴AB 1与BC 1成60°角,A 对;对于B,∵CN ⃗⃗⃗⃗⃗ =13NC 1⃗⃗⃗⃗⃗⃗⃗ ,∴N (0,2,32),设E(0,m,2),则A 1M ⃗⃗⃗⃗⃗⃗⃗⃗ =(-1,2,0),A 1N ⃗⃗⃗⃗⃗⃗⃗⃗ =(-2,2,32),A 1E ⃗⃗⃗⃗⃗⃗⃗ =(-2,m,2),由已知得A 1,M,N,E 四点共面, ∴∃λ,μ∈R,使得A 1M ⃗⃗⃗⃗⃗⃗⃗⃗ =λA 1N ⃗⃗⃗⃗⃗⃗⃗⃗ +μA 1E ⃗⃗⃗⃗⃗⃗⃗ , 得{-1=-2λ-2μ,2=2λ+mμ,0=32λ+2μ,解得{λ=2,μ=−32,m =43,∴E (0,43,2),∴CE ⃗⃗⃗⃗⃗ =(0,−23,0),|CE⃗⃗⃗⃗⃗ |=23,B 错; 对于C,设P(2,y,z)(0≤y ≤2,0≤z ≤2),则MP ⃗⃗⃗⃗⃗⃗ =(1,y-2,z),DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =(2,2,-2), 由MP ⃗⃗⃗⃗⃗⃗ ·DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =2+2y-4-2z=0,得y-z=1.∴点P 的轨迹长为线段y-z=1(1≤y ≤2)的长度,为√2,C 对; 对于D,∵E,F 分别在DB 1,A 1C 1上,且DE EB 1=A 1FFC 1=2,∴DE ⃗⃗⃗⃗⃗ =23DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =23(2,2,-2)=(43,43,-43),A 1F ⃗⃗⃗⃗⃗⃗⃗ =23A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =23(-2,2,0)=(-43,43,0),则E (43,43,23),F (23,43,0),则EF⃗⃗⃗⃗⃗ =(-23,0,-23), 则cos α=|cos<EF ⃗⃗⃗⃗⃗ ,D 1A ⃗⃗⃗⃗⃗⃗⃗ >|=|-43-43√(-3)2+(-3)2×√4+4|=832√23×2√2=1,故α=0,cos β=|cos<EF ⃗⃗⃗⃗⃗ ,DA 1⃗⃗⃗⃗⃗⃗⃗⃗ >|=|-43+43√(-3)+(-3)×√4+4=0,故β=π2,即α+β=π2,故D 正确.高考数学:试卷答题攻略一、“六先六后”,因人因卷制宜。
高二数学空间向量基本定理与坐标运算试题

高二数学空间向量基本定理与坐标运算试题1.已知向量,,则以,为邻边的平行四边形的面积为( )A.B.C.4D.8【答案】B.【解析】首先由向量的数量积公式可求与夹角的余弦值,然后根据同角三角函数的关系得,最后利用正弦定理表示平行四边形的面.【考点】向量模的运算;利用正弦定理表示三角形的面积.2.点关于原点对称的点的坐标是.【答案】【解析】空间直角坐标系中点的对称关系:,可得.【考点】空间直角坐标系中点的对称关系.3.在空间直角坐标系中,点P(1,3,-5)关于平面xoy对称的点的坐标是( )A.(-1,3,-5)B.(1,3,5)C.(1,-3,5)D.(-1,-3,5)【答案】B【解析】根据空间直角坐标系坐标的对称的结论:点(x,y,z)关于平面xoy对称的点坐标为(x,y,-z),可知答案是B.【考点】空间直角坐标系点的对称问题.4.已知向量,且∥,则实数的值为.【答案】.【解析】由已知得=(k+1,2k+2,k+2),=(-1,-2,-3),再由两向量共线的充要条件知=,建立方程解得k=.【考点】(1)向量的坐标运算;(2)向量共线的充要条件.5.已知向量,,且,那么等于()A.B.C.D.【答案】A【解析】因为,所以,所以,所以,解得,所以,选答案A.【考点】空间向量平行的坐标关系.6.已知空间四边形,其对角线为,分别是边的中点,点在线段上,且使,用向量表示向量是()A.B.C.D.【答案】A【解析】解:因为,选A7.已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为()A.2B.3C.4D.5【答案】B【解析】由已知中△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),利用中点公式,求出BC边上中点D的坐标,代入空间两点间距公式,即可得到答案.解:∵B(4,-3,7),C(0,5,1),则BC的中点D的坐标为(2,1,4)则AD即为△ABC中BC边上的中线故选B.【考点】空间中两点之间的距离点评:本题考查的知识点是空间中两点之间的距离,其中根据已知条件求出BC边上中点的坐标,是解答本题的关键.8.为空间的两个不同的点,且,空间中适合条件的点的集合表示的图形是 .【答案】经过点且与垂直的平面【解析】设点M(x,y,z),那么可知设A(0,0,0),B(0,0,1),,由则可知(x,y,z)(0,0,1)=1,z=1,可知表示的图形为过点B的与AB垂直的平面。
高二数学空间向量基本定理与坐标运算试题答案及解析

高二数学空间向量基本定理与坐标运算试题答案及解析1.在直三棱柱中,底面ABC为直角三角形,,. 已知G与E分别为和的中点,D与F分别为线段和上的动点(不包括端点). 若,则线段的长度的最小值为。
【答案】为z轴,则【解析】建立直角坐标系,以A为坐标原点,AB为x轴,AC为y轴,AA1(),,,()。
所以,。
因为,所以,由此推出。
又,,从而有。
【考点】(1)空间向量的坐标运算及空间两点间距离公式的应用;(2)利用二次函数思想求最值。
2.是坐标原点,设,若,则点的坐标应为( )A.B.C.D.【答案】B【解析】根据题意,设点B(x,y,z),由于,且,故可知点的坐标应为,故选B.【考点】空间向量的坐标运算点评:主要是考查了空间中向量的坐标的代数运算,属于基础题。
3.已知向量,若,则______。
【答案】【解析】因为,所以,显然所以【考点】本小题主要考查共线向量的数量关系,考查学生运用公式的能力.点评:向量共线是空间向量的常考内容,记清楚关系直接代入计算即可,难度不大.4.已知,,则的最小值是A.B.C.D.【答案】C【解析】解:因为,,则则利用二次函数的性质得到最小值为,选C5.在直三棱柱中,,已知G与E分别为和的中点,D与F分别为线段AC和AB上的动点(不包括端点).若,则线段DF长度的取值范围为( )A.B.C.D.【答案】C【解析】解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1,1 2 ),G( 1 2 ,0,1),F(x,0,0),D(0,y,0)∴ GD =(-,y,-1), EF =(x,-1,- )∵GD⊥EF,∴x+2y-1=0,∴x=1-2yDF2= x2+y2 = (1-2y)2+y2 = 5y2-4y+1 =" 5(y-2" 5 )2+1 5 ∵0<y<1∴当y="2" 5 时,线段DF长度的最小值是又y=1时,线段DF长度的最大值是 1而不包括端点,故y=1不能取;故线段DF的长度的取值范围是:[ ,1).故选A.6.已知a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是().A.1B.C.D.【答案】D【解析】因为,所以7.空间直角坐标系中,O为坐标原点,已知两点A(3,1,0),B(-1,3,0),若点C满足=α+β,其中α,βR,α+β=1,则点C的轨迹为()A.平面B.直线C.圆D.线段【答案】D【解析】解:因为A(3,1,0),B(-1,3,0),若点C满足=α+β,其中α,βR,α+β=1,则说明A,B,C三点共线,解:设点C的坐标为(x,y,z ),由题意可得(x,y,z )=(3α-β,α+3β,0 ),再由α+β="1" 可得x=3α-β=3-4β,y=α+3β=1+2β,故有 x+2y-5=0,故点C的轨迹方程为x+2y-5=0,则点C的轨迹为直线,故选B.8.在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的是以BC为斜边的直角三角形,则实数x的值为。
高二数学空间向量基本定理与坐标运算试题答案及解析

高二数学空间向量基本定理与坐标运算试题答案及解析1.三棱锥中,两两垂直且相等,点分别是线段和上移动,且满足,,则和所成角余弦值的取值范围是()A.B.C.D.【答案】C.【解析】以为原点,分别,,为, , 轴建立如图所示的空间直角坐标系.不妨设,, ,则由,得出,,,.于是向量,,所以,令,,则.因为对称轴为,所以关于为递增函数,关于为递增函数.又因为与独立取值,所以,所以和所成角余弦值的取值范围为,即为所求.【考点】立体几何与空间向量.2.点关于原点对称的点的坐标是.【答案】【解析】空间直角坐标系中点的对称关系:,可得.【考点】空间直角坐标系中点的对称关系.3.已知,,,三角形的面积为()A.B.C.D.【答案】B【解析】,所以,所以,故选B.【考点】1.空间向量夹角公式;2.三角形面积公式.4.已知=(2,4,5),=(3,x,y),若∥,则()A.x=6,y=15B.x=3,y=C.x=3,y=15D.x=6,y=【答案】D【解析】因为∥,所以,所以x=6,y=.【考点】空间向量的平行.5.设是正三棱锥,是的重心,是上的一点,且,若,则为()A.B.C.D.【答案】A【解析】由是上一点,且,可得又因为是的重心,所以而,所以,所以,选A.【考点】1.空间向量的加减法;2.空间向量的基本定理.6.已知,当取最小值时,的值等于()A.B.-C.19D.【答案】A【解析】根据空间中两点间的距离公式可得设,,故,根据二次函数的图像可知,该函数的最小值在对称轴上取到,所以当取最小值时,的值等于,选A.【考点】1.空间中两点间的距离问题;2.二次函数的图像与性质.7.设点关于原点的对称点为,则等于()A.B.C.D.【答案】A【解析】关于原点对称的两个点的坐标之间横坐标、纵坐标、坚坐标的数都是相反数,故,所以,故选A.【考点】1.关于原点对称的两个点的坐标;2.空间中两点间的距离公式.8.已知向量,,且,那么等于()A.B.C.D.【答案】A【解析】因为,所以,所以,所以,解得,所以,选答案A.【考点】空间向量平行的坐标关系.9.已知,则的最小值是_______________.【答案】【解析】根据题意,由于,则可知,结合二次函数性质可知当t=时,根号下取得最小值,即可知答案为【考点】向量的数量积点评:主要是考查了运用向量的数量积来求解向量的模长的运用,属于基础题。
高二数学空间向量试题答案及解析

高二数学空间向量试题答案及解析1.如图,在三棱锥中,直线平面,且,又点,,分别是线段,,的中点,且点是线段上的动点.(1)证明:直线平面;(2)若,求二面角的平面角的余弦值.【答案】(1)见解析;(2)3.(3)【解析】(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明线面平行,需证线线平行,只需要证明直线的方向向量平行;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.试题解析:(1)连结QM 因为点,,分别是线段,,的中点所以,所以平面, 平面因为,所以平面∥平面 ,平面所以∥平面(2)方法1:过M作MH⊥AN于H,连QH,则∠QHM即为二面角的平面角, 令即QM=AM=1所以此时,MH=,记二面角的平面角为则tan=,所以COS=即为所求.方法2:以B为原点,以BC、BA所在直线为x轴y轴建空间直角坐标系,设则A(0,2,0),M(0,1,0),N(1,0,0),p(0,2,2),Q(0,1,1),=(0,-1,1),记,则取又平面ANM的一个法向量,所以cos=即为所求.【考点】空间几何体的线面平行以及二面角.2.如图,正三棱柱中,是的中点,.(Ⅰ)求证:平面;(Ⅱ)求二面角的平面角的余弦值.【答案】(Ⅰ)见解析;(Ⅱ).【解析】(Ⅰ)想要解决这个问题,需要构造平行线,连结交于,连结,则又平面平面(Ⅱ)解决本题的关键是构造二面角的平面角,过作的垂线,过作的垂线,则就是二面角的平面角,然后根据条件计算出 .试题解析:(Ⅰ)连结交于,连结,则分别是,的中点,又平面平面(Ⅱ)过作的垂线,垂足为,则,且面,过作的垂线,垂足为,则,连结,则就是二面角的平面角,且,即二面角的余弦值为【考点】线面平行的判定,二面角.3.如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.(Ⅰ)求证:PA⊥平面ABCD;(Ⅱ)求EF和平面ABCD所成的角α的正切;(Ⅲ)求异面直线EF与BD所成的角β的余弦.【答案】(1)由已知PA⊥AD,AB⊥AD,所以为平面PAD与平面ABCD所成二面角的平面角.由已知平面PAD⊥平面ABCD得,PA⊥AB,又AB平面ABCD,AD平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD;(2)所求的角α的正切值为;(3)异面直线EF与BD所成角β的余弦值为.【解析】(1)根据两个平面垂直的性质定理可得PA⊥平面ABCD;(2)连接AF,则即为α,在直角三角形EAF中,根据计算求得结果即可;(3))欲求异面直线EF与BD所成的角β的大小,只需平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成的锐角或直角,就是异面直线所成角,再放入三角形中,通过解三角形,求出此角.试题解析:(1)由已知PA⊥AD,AB⊥AD,所以为平面PAD与平面ABCD所成二面角的平面角.由已知平面PAD⊥平面ABCD得,PA⊥AB,又AB平面ABCD,AD平面ABCD,且AB∩AD=A,所以PA⊥平面ABCD.(2)连接AF,因为PA⊥平面ABCD,则AF是EF在平面ABCD上的射影,即=α.设PA=AD=a,FD=,则.在中,,所以所求的角的正切值为.(3)取BC的中点M,连接EM、FM,则FM∥BD,∴∠EFM(或其补角)就是异面直线EF 与BD所成的角.可求得,同理,,又,∴在△MFE中,,故异面直线EF与BD所成角β的余弦值为.【考点】异面直线及其所成的角;直线与平面平行、垂直的判定;直线与平面所成的角.4.如图,分别是正三棱柱的棱、的中点,且棱,.(1)求证:平面;(2)在棱上是否存在一点,使二面角的大小为,若存在,求的长,若不存在,说明理由。
高二数学空间向量的应用试题

高二数学空间向量的应用试题1.如图,底面是直角梯形的四棱锥,,底面,,,求面与面所成的二面角的余弦值.【答案】面与面所成的二面角的余弦值为.【解析】解:如图所示建立空间直角坐标系,则,,,.设平面与平面的法向量分别为,则由得即又由得即不妨令,,则,,,,,.故面与面所成的二面角的余弦值为.【考点】本题主要考查空间向量的应用,向量的数量积,向量的坐标运算。
点评:典型综合题。
通过建立空间直角坐标系,将求二面角余弦问题,转化成向量的坐标运算。
2.已知是边长为1的正三角形所在平面外一点,且,分别是的中点,则异面直线与所成角的余弦值为()A.B.C.D.【答案】B【解析】由已知,这是一个正四面体,由平面几何知识,||=||=。
如图,因为分别是的中点,所以=,==,=·===-所以C==,故选B。
【考点】本题主要考查空间向量的应用,向量的数量积。
点评:典型综合题。
通过综合应用几何图形的特征,将问题转化成向量的数量积运算,达到解题目的。
3.长方体中,,为与的交点,为与的交点,又,则长方体的高等于()A.B.C.D.【答案】C【解析】如图所示,分别以DA,DC,DD为x,y,z轴,建立空间直角坐标系,则A(4,0,0),B(4,4,0),E(2,2,h),F(2,4,)。
所以=(-2,4,),=(-2,-2,h),而,所以=(-2,4,)·(-2,-2,h)=4-8+=0,解得h=。
故选C。
【考点】本题主要考查空间向量的应用,向量的垂直,向量的数量积。
点评:典型题。
通过综合应用几何图形的特征,将问题转化成向量的坐标运算,达到解题目的。
4.如图,直三棱柱中,,,侧棱,侧面的两条对角线交点为,则面与面所成二面角的余弦值等于()A.B.C.D.【答案】D【解析】如图以C为原点建立坐标系.B(,0,0),B1(,1,0),A1(0,1,1),D(,,),M(,1,0),=(,,),=(,-1,-1),=(0,,),设BD中点为G,连接B1G,则G(,,),=(-,,),=(-,-,),∴·=0,∴BD⊥B1G,又CD⊥BD,∴与的夹角θ等于所求二面角的平面角,利用向量的夹角公式得cosθ=,故选D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学-空间直角坐标系与空间向量一、建立空间直角坐标系的几种方法 构建原则:遵循对称性,尽可能多的让点落在坐标轴上。
作法:充分利用图形中的垂直关系或构造垂直关系来建立空间直角坐标系. 类型举例如下:(一)用共顶点的互相垂直的三条棱构建直角坐标系例1 已知直四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,底面ABCD 是直角梯形,∠A 为直角,AB ∥CD ,AB =4,AD =2,DC =1,求异面直线BC 1与DC 所成角的余弦值.解析:如图1,以D 为坐标原点,分别以DA 、DC 、DD 1所在直线为x 、y 、z 轴建立空间直角坐标系,则C 1(0,1,2)、B (2,4,0), ∴1(232)BC =--,,,(010)CD =-,,.设1BC 与CD 所成的角为θ, 则11317cos 17BC CD BC CDθ==. (二)利用线面垂直关系构建直角坐标系例2 如图2,在三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,EA ⊥EB 1.已知2AB =,BB 1=2,BC =1,∠BCC 1=3π.求二面角A -EB 1-A 1的平面角的正切值.解析:如图2,以B 为原点,分别以BB 1、BA 所在直线为y 轴、z 轴,过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系. 由于BC =1,BB 1=2,AB =2,∠BCC 1=3π,∴在三棱柱ABC -A 1B 1C 1中,有B (0,0,0)、A (0,0,2)、B 1(0,2,0)、31022c ⎛⎫- ⎪ ⎪⎝⎭,,、133022C ⎛⎫ ⎪ ⎪⎝⎭,,.设302E a ⎛⎫ ⎪ ⎪⎝⎭,,且1322a -<<, 由EA ⊥EB 1,得10EAEB =,即3322022a a ⎛⎫⎛⎫---- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭,,,,233(2)2044a a a a =+-=-+=,∴13022a a ⎛⎫⎛⎫--= ⎪⎪⎝⎭⎝⎭,即12a =或32a =(舍去).故31022E ⎛⎫ ⎪ ⎪⎝⎭,,. 由已知有1EA EB ⊥,111B A EB ⊥,故二面角A -EB 1-A 1的平面角θ的大小为向量11B A 与EA 的夹角.因11(002)B A BA ==,,,31222EA ⎛⎫=-- ⎪ ⎪⎝⎭,, 故11112cos 3EA B A EA B A θ==,即2tan 2θ=(三)利用面面垂直关系构建直角坐标系例3 如图3,在四棱锥V -ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD . (1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的余弦值.解析:(1)取AD 的中点O 为原点,建立如图3所示的空间直角坐标系.设AD =2,则A (1,0,0)、D (-1,0,0)、B (1,2,0)、V (0,0,3),∴AB =(0,2,0),VA =(1,0,-3).由(020)(103)0AB VA =-=,,,,,得 AB ⊥VA .又AB ⊥AD ,从而AB 与平面VAD 内两条相交直线VA 、AD 都垂直,∴ AB ⊥平面VAD ;(2)设E 为DV 的中点,则13022E ⎛⎫- ⎪ ⎪⎝⎭,,∴33022EA ⎛⎫=-⎪ ⎪⎝⎭,,,33222EB ⎛⎫=- ⎪ ⎪⎝⎭,,,(103)DV =,,. ∴332(103)022EB DV ⎛⎫=-= ⎪ ⎪⎝⎭,,,,, ∴EB ⊥DV .又EA ⊥DV ,因此∠AEB 是所求二面角的平面角.∴21cos 7EA EB EAEB EA EB==,. 故所求二面角的余弦值为217. (四)利用正棱锥的中心与高所在直线构建直角坐标系例4 已知正四棱锥V -ABCD 中,E 为VC 中点,正四棱锥底面边长为2a ,高为h . (1)求∠DEB 的余弦值;(2)若BE ⊥VC ,求∠DEB 的余弦值.解析:(1)如图4,以V 在平面AC 的射影O 为坐标原点建立空间直角坐标系,其中O x ∥BC ,O y ∥AB ,则由AB =2a ,OV =h ,有B (a ,a ,0)、C (-a ,a ,0)、D (-a ,-a ,0)、V (0,0,h )、222a a h E ⎛⎫-⎪⎝⎭,, ∴3222a h BE a ⎛⎫=-- ⎪⎝⎭,,,3222a h DE a ⎛⎫= ⎪⎝⎭,,.∴22226cos 10BE DEa h BE DE a h BE DE-+==+,, 即22226cos 10a h DEB a h -+=+∠;(2)因为E 是VC 的中点,又BE ⊥VC ,所以0BEVC =,即3()0222a h a a a h ⎛⎫----= ⎪⎝⎭,,,,,∴22230222a h a --=,∴2h a =. 这时222261cos 103a h BE DE a h -+==-+,,即1cos 3DEB =-∠. 引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.下面以高考考题为例,剖析建立空间直角坐标系的三条途径.(五)利用图形中的对称关系建立坐标系图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.例5已知两个正四棱锥P -ABCD 与Q -ABCD 的高都为2,AB =4. (1)证明:PQ ⊥平面ABCD ; (2)求异面直线AQ 与PB 所成的角; (3)求点P 到面QAD 的距离. 简解:(1)略;(2)由题设知,ABCD 是正方形,且AC ⊥BD .由(1),PQ ⊥平面ABCD ,故可分别以直线CA DB QP ,,为x ,y ,z 轴建立空间直角坐标系(如图1),易得(2202)(0222)AQ PB =--=-,,,,,,1cos 3AQ PB AQ PB AQ PB<>==,. 所求异面直线所成的角是1arccos3. (3)由(2)知,点(0220)(22220)(004)D AD PQ -=--=-,,,,,,,,设n =(x ,y ,z )是平面QAD 的一个法向量,则00AQ AD ⎧=⎪⎨=⎪⎩,,n n 得200x z x y ⎧+=⎪⎨+=⎪⎩,,取x =1,得(112)--,,n =.点P 到平面QAD 的距离22PQ d ==n n.点评:利用图形所具备的对称性,建立空间直角坐标系后,相关点与向量的坐标应容易得出.第(3)问也可用“等体积法”求距离.二、向量法解立体几何 (一)知识点向量的数量积和坐标运算b a,是两个非零向量,它们的夹角为θ,则数θcos ||||⋅⋅b a 叫做a 与b 的数量积(或内积),记作b a ⋅,即.cos ||||θ⋅⋅=⋅b a b a 其几何意义是a 的长度与b 在a 的方向上的投影的乘积. 其坐标运算是:若),,(),,,(222111z y x b z y x a ==,则①212121z z y y x x b a ++=⋅;②222222212121||,||z y x b z y x a ++=++=;③212121z z y y x x b a ++=⋅④222222212121212121,cos z y x z y x z z y y x x b a ++⋅++++>=<(二)例题讲解 题型:求角度相关1. 异面直线n m ,所成的角分别在直线n m ,上取定向量,,b a则异面直线n m ,所成的角θ等于向量b a ,所成的角或其补角(如图1所示),则.||||||cos b a b a⋅⋅=θ 2. 直线L 与平面α所成的角在L 上取定AB ,求平面α的法向量n (如图2所示),再求||||cos n AB n AB ⋅=θ,则θπβ-=2为所求的角.3. 二面角方法一:构造二面角βα--l 的两个半平面βα、的法向量21n n 、(都取向上的方向,如图3所示),则图1图①若二面角βα--l 是“钝角型”的如图3甲所示,那么其大小等于两法向量21n n 、的夹角的补角,即||||cos 2121n n n n ⋅=θ② 若二面角βα--l 是“锐角型”的如图3乙所示,那么其大小等于两法向量21n n 、的夹角,即||||cos 2121n n ⋅=θ.方法二:在二面角的棱l 上确定两个点B A 、,过B A 、分别在平面βα、内求出与l 垂直的向量21n n 、(如图4所示),则二面角βα--l 的大小等于向量21n n 、的夹角,即 ||||cos 2121n n ⋅=θ题型:求距离相关1. 异面直线n m 、的距离分别在直线n m 、上取定向量,,b a求与向量b a 、都垂直的向量n ,分别在n m 、上各取一个定点B A 、,则异面直线n m 、的距离d 等于AB 在n 上的射影长,即||n n AB d=.证明:设CD 为公垂线段,取b DB a CA==,||||)(n AB n CD n BD AB CA n CD BD AB CA CD ⋅=⋅∴⋅++=⋅∴++= ||||n n AB CD d ==∴设直线n m ,所成的角为θ,显然.||||||cos b a b a⋅⋅=θ 2. 平面外一点p 到平面α的距离n 图图4图1求平面α的法向量n,在面内任取一定点A,点p到平面α的距离d等于AP在n上的射影长,即d=.|n|图5三、法向量 例题解析题型:求空间角1、运用法向量求直线和平面所成角设平面α的法向量为n =(x, y, 1),则直线AB 和平面α所成的角θ的正弦值为 sin θ= cos(2π-θ) = |cos<AB , n >| = AB AB n n••2、运用法向量求二面角设二面角的两个面的法向量为12,n n ,则<12,n n >或π-<12,n n >是所求角。
这时要借助图形来判断所求角为锐角还是钝角,来决定<12,n n >是所求,还是π-<12,n n >是所求角。
题型:求空间距离1、求两条异面直线间的距离设异面直线a 、b 的公共法向量为(,,)n x y z =,在a 、b 上任取一点A 、B ,则异面直线a 、b 的距离:d =AB ·cos ∠BAA '=||||AB n n •略证:如图,EF 为a 、b 的公垂线段, a '为过F 与a 平行的直线, 在a 、b 上任取一点A 、B , 过A 作AA '//EF ,交a '于A ',则¡¯//AAn ,所以∠BAA '=<,BA n >(或其补角)∴异面直线a 、b 的距离d =AB ·cos ∠BAA '=||||AB n n • * 其中,n 的坐标可利用a 、b 上的任一向量,a b (或图中的,AE BF ),及n 的定义得0n a n a n b n b ⎧⎧⊥•=⎪⎪⇒⎨⎨⊥•=⎪⎪⎩⎩ ① 解方程组可得n 。
