基于Matlab仿真PID校正
基于MATLAB软件“PID校正控制”教学研究

目前国内很多高校如吉林大学、中国民航大学、 将区间算法与粒子群算法分别引入基本遗传算法初始
收稿日期:2017 10 10 作者简介:肖理庆(1981 ),男,山东平度人,副教授,博士,研究方向:自动控制原理与无损检测.
66
德州学院学报 第34卷
种群生成与变异操作中,同时在算法迭代过程中采取
制系统、电烤箱恒温控制系统、水池液位控制系统等 动化专业控制系统 MATLAB 仿真实验课程中唯一
实际系统,无法合理调整 PID 控制器参数.
的设计性实验.根 据 上 述 情 况,笔 者 整 合 了 “PID 校
为了提高“PID 校正控制”课堂教学效 果以 及学 正控制”的教学内容与教学目标为:
生课 程 设 计、毕 业 设 计 质 量,在 反 思 传 统 PID 教 学
“PID 校正控制”理论性强、内容抽象,学 生掌 握情况 不同知识点之间的联系;
并不理想,又使其成 为“自 动 控 制 原 理”课 程 教 学 的
(2)所提供的控 制 系 统 传 递 函 数 缺 少 实 际 工 程
难点.另外,根 据 学 生 课 程 设 计 论 文 与 毕 业 设 计 论 背景的介绍;
课堂教学中,为后续课程的教学以及课程设计、毕业 3 PID 校正控制软件
设计奠定了良好的基础.
2 传 统 PID 教 学 方 法 反 思 与 课 程 教 学内容、教学目标整合
3.1 改 进 遗 传 算 法 典 型 函 数 测 试 由于 PID控制器参数整定属于低维优化问题,因
此可引入区间算法.本软件所采用的改进遗传算法是
中图分类号:G642.0 文献标识码:A 文章编号:1004 9444(2018)02 0065 05
1 引言
基于MATLAB的PID控制器参数整定及仿真

基于MATLAB的PID控制器参数整定及仿真摘要: PID控制器结构和算法简单应用广泛,但参数整定方法复杂,通常用凑试法来确定。
文中探讨利用MATLAB实现PID参数整定及仿真的方法,并分析、比较比例控制、比例积分控制和比例微分控制,探讨了Kp, Ti, Td 3个参数对PID 控制规律的影响。
关镇词: MATLAB ; PID控制器;参数整定;仿真Parameter tuning and emulation of PID controller based on MATLAB Ahstratct; The control structure and algorithm of PID is easy and widely applicable,but its setting meth-ods of parameter are multifarious. Generally utilize guessing and trying to fix. This artical is convenient to tune PID parameters and emulate through MATLAB experiment. Analyze and compare the proportion control, the proportion integral control and the proportion differential control. Discuss the influence of three parameters KP ,Ti and Td to the PID control rules.Key words ; MATLAB;PID controller; parameter tuning; emulation引言PID控制器又称为PID调节器,是按偏差的比例P( Proportional )、积分I(Integxal)、微分D ( Differential orDerivative)进行控制的调节器的简称,它主要针对控制对象来进行参数调节。
PID控制算法及MATLAB仿真分析

题目:以PID控制进行系统仿真学院自动化学院专业班级工业自动化111班学生姓名黄熙晴目录1 引言 (1)1.1本论文研究内容 (1)2 PID控制算法 (1)2.1模拟PID控制算法 (1)2.2数字式PID控制算法 (3)2.3PID控制算法的改进 (5)2.3.1微分项的改进 (5)2.3.2积分项的改进 (9)2.4模糊PID控制算法 (11)2.4.1模糊推理的系统结构 (12)2.4.2 PID参数在线整定原则 (12)2.5PID控制器研究面临的主要问题 .................................. 错误!未定义书签。
3 MATLAB编程和仿真 (13)3.1PID控制算法分析 (13)3.2MATLAB仿真 (15)4结语 (20)参考文献...................................................................................... 错误!未定义书签。
1 引言PID控制器以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。
光学表面等离子共振生物传感技术受温度影响很大,因此设计高精度的温度控制器对于生物分析仪十分重要。
研究PID的控制算法是PID控制器整定参数优化和设定的关键技术之一。
在工业过程控制中,目前采用最多的控制方式依然是PID方式。
它具有容易实现、控制效果好、鲁棒性强等特点,同时它原理简单,参数物理意义明确,理论分析体系完整,并为工程界所熟悉,因而在工业过程控制中得到了广泛应用。
在实际的应用中,许多被控过程机理复杂,具有高度非线性、时变不确定性和纯滞后等特点,特别是在噪声、负载扰动等因素的影响下,参数复杂烦琐的整定过程一直困扰着工程技术人员。
为了减少参数整定的工作量,克服因环境变化或扰动作用造成系统性能的降低,就要提出一种PID控制参数的自动整定。
1.2本论文研究内容本文在介绍传统的PID控制算法,并对传统算法改进后,在学习的基础上提出一种模糊参数自整定方法,这种模糊控制的PID算法必须精确地确定对象模型。
基于MATLAB的PID参数调整方法的仿真研究

整 定 方 法 :基 于稳 定 性 分析 的经 验 整 定法 ,工 程 整 定法 一 扩 充 临 界 比例 度 法 做 了仿 真 研 究 ,取 得 了好 的仿 真 结果 ,对 研
究各种 实际过程控制系统 PD参数在线调整具有理论指导意义 。 I
关键 词 :PD参 数 整 定 ;MA L B;仿 真 I TA 中 图分 类 号 :T 2 3 文 献 标 识码 :A 文 章 编 号 : 17 -4 0 f0 1 1 0 一O P 7 6 2 8 12 1) 一O 4 4 0
相关应 用研 究能达到 事倍功 半的效 果L。 2 j
运行如 下整定程 序 ,可 以得 出整定后 的根轨迹 图
及 整定前 后系统 的伯特 图( 图 2 图 3所 示) 如 、 :
% P D n r lr s d o ig e - c o s I Co to e e n Z e lrNih l Ba
ce ral la l;
1 PD 参 数 整 定方 法 的 MA L B 仿 真 I TA
11 经验整 定法( ige- c os ) MA L . Ze l Ni l 法 的 r h T AB 仿真 Ze l - c os 法是 基于 稳定 性分 析 的PD i e Ni l gr h 方 I 整定方法[。
PD ( rp ro a it r1 e v t e I po ot n 1ne a d r ai )作 为经 i . g . i v
K d= 0. 5 , K =1 . 6 47 6 927 5。
典 的控制 理 论 ,P D 制 中一 个关 键 的 问题 便 是 I控 PD参数 的整定 。 实际 的应用 中 , 多被 控过程 I 在 许 机 理复杂 ,具有 高度 非线性 、时变 不确定性 和纯 滞后 等特 点。在噪 声、负 载扰动等 因素 的影 响下 , 过程 参数甚 至模型 结构均 会 随时间和 工作环 境 的 变化 而变化 。这 就要求在PD控制 中 ,不仅PD参 I I 数 的整 定不依赖 于对象 数学模 型 , 且P D 数能 并 I参 够在线 调整 ,以满足 实时控制 的要求 L。 l J MA L B是一 款 高 性 能数 值 计 算 和 可 视 化 TA
PID控制和其MATLAB仿真

序号,k=1,2,……,e (k-1)和e (k)分别为第(k-
1)和第k时刻所得旳偏差信号。
1.3.1 位置式PID控制算法
• 位置式PID控制系统
1.3.1 位置式PID控制算法
根据位置式PID控制算法得 到其程序框图。
在仿真过程中,可根据实 际情况,对控制器旳输出 进行限幅:[-10,10]。
• 变速积分旳基本思想是,设法变化积分项旳累加 速度,使其与偏差大小相相应:偏差越大,积分 越慢;反之则越快,有利于提升系统品质。
• 设置系数f(e(k)),它是e(k)旳函数。当 ∣e(k)∣增大时,f减小,反之增大。变速积分 旳PID积分项体现式为:
ui (k )
ki
k
1
e(i)
f
e(k )e(k )T
i0
1.3.8 变速积分算法及仿真
• 系数f与偏差目前值∣e(k)∣旳关系能够是线性 旳或是非线性旳,例如,可设为
1
f
e(k
)
A
e(k A
)
B
0
e(k) B B e(k) A B e(k) A B
1.3.8 变速积分算法及仿真
• 变速积分PID算法为:
u(k)
k
p e(k )
ki
1.3.4 增量式PID控制算法及仿真
• 增量式PID阶跃跟踪成果
1.3.5 积分分离PID控制算法及仿真
• 在一般PID控制中,引入积分环节旳目旳主要是为了 消除静差,提升控制精度。但在过程旳开启、结束或 大幅度增减设定时,短时间内系统输出有很大旳偏差 ,会造成PID运算旳积分积累,致使控制量超出执行机 构可能允许旳最大动作范围相应旳极限控制量,引起 系统较大旳振荡,这在生产中是绝对不允许旳。
控制系统pid参数整定方法的matlab仿真

控制系统PID参数整定方法的MATLAB仿真1. 引言PID控制器是一种常见的控制算法,广泛应用于自动控制系统中。
其通过调节三个参数:比例增益(Proportional gain)、积分时间常数(Integral time constant)和微分时间常数(Derivative time constant),实现对被控对象的稳态误差、响应速度和稳定性等性能指标的调节。
PID参数的合理选择对控制系统的性能至关重要。
本文将介绍PID控制器的经典整定方法,并通过MATLAB软件进行仿真,验证整定方法的有效性。
2. PID控制器的整定方法2.1 手动整定法手动整定法是根据经验和试错法来选择PID参数的方法。
具体步骤如下:1.将积分时间常数和微分时间常数设为零,仅保留比例增益,将比例增益逐渐增大直至系统产生较大的超调现象。
2.根据超调响应的情况,调整比例增益,以使系统的超调量接近所需的范围。
3.逐步增加微分时间常数,观察系统的响应速度和稳定性。
4.增加积分时间常数,以减小系统的稳态误差。
手动整定法的优点是简单易行,但需要经验和反复试验,对控制系统要求较高。
2.2 Ziegler-Nichols整定法Ziegler-Nichols整定法是一种基于试探和试错法的自整定方法,该方法通过调整系统的输入信号,观察系统的输出响应,从而确定PID参数。
具体步骤如下:1.将I和D参数设为零,仅保留P参数。
2.逐步增大P参数,直到系统的输出出现大幅度的振荡。
3.记录下此时的P参数值,记为Ku。
4.根据振荡的周期Tp,计算出系统的临界增益Kc = 0.6 * Ku。
5.根据系统的类型选择相应的整定法则:–P型系统:Kp = 0.5 * Kc,Ti = ∞,Td = 0–PI型系统:Kp = 0.45 * Kc,Ti = Tp / 1.2,Td = 0–PID型系统:Kp = 0.6 * Kc,Ti = Tp / 2,Td = Tp / 82.3 Cohen-Coon整定法Cohen-Coon整定法是基于频域曲线拟合的方法,主要应用于一阶和二阶系统的整定。
基于matlab仿真的PID控制研究

基于matlab仿真的PID控制研究目录摘要.....................................................ⅡAbstract.................................................Ⅲ一、设计任务 (1)二、设计要求 (2)三、方案论证 (3)四、基于MATLAB下的系统模型搭建与仿真 (4)五、收获与总结 (15)参考文献 (17)附录 (18)摘要PID控制,又称PID调节,是比例(proportional)、积分(intergral)、微分(differential)调节的简称。
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。
在自动控制的发展历程中,PID调节是历史悠久、控制性能最强的基本调解方式。
PID调节原理简单,易于整定,使用方便;按PID调节功能工作的各类调节器广泛应用于国民经济所有工业生产部门,适用性特强;PID的调节性能指标对于受控对象特性的少许变化不是很灵敏,这就极大的保证了调节的有效性;PID调节可用于补偿系统使之达到大多数品质指标的要求。
直到目前为止,PID调节仍然是最广泛应用的基本控制方式。
关键词:PID调节AbstractPID control, also known as PID regulation is proportional (proportional), points (intergral), differential (differential) adjusted for short. PID controllers come out has been nearly 70 years of history, with its simple structure, good stability, reliable, easy to adjust and become one of the major technology industry control. In the development of the automatic control, PID regulation is a long history, the strongest performance of the basic control mediation. PID regulator principle is simple, easy tuning, easy to use; the work of the PID regulation function is widely used in various types of regulators in all industrial production sectors of the national economy, particularly strong applicability; PID regulation controlled object performance characteristics for a little change is not very sensitive, which greatly ensure the effectiveness of the regulation; PID regulator can be used to compensate the system so as to meet the requirements of most quality indicators. Until now, PID regulation is still the basic control the most widely used.Keyword:PID regulator一、设计任务PID 控制器具有结构简单、容易实现、控制效果好、鲁棒性强等特点,是迄今为止最稳定的控制方法。
《MATLAB控制系统仿真》PID控制系统校正设计

《MATLAB控制系统仿真》PID控制系统校正设计引言1.PID校正装置PID校正装置也称为PID控制器或PID调节器。
这里P,I,D分别表示比例、积分、微分,它是最早发展起来的控制方式之一。
2.PID校正装置的主要优点原理简单,应用方便,参数整定灵活。
适用性强,在不同生产行业或领域都有广泛应用。
鲁棒性强,控制品质对受控对象的变化不太敏感,如受控对象受外界扰动时,无需经常改变控制器的参数或结构。
在科学技术迅速发展的今天,出现了许多新的控制方法,但PID由于其自身的的优点仍然在工业过程控制中得到最广泛的应用。
PID控制系统校正设计1.设计目的1.1 熟悉常规PID控制器的设计方法1.2掌握PID参数的调节规律1.3学习编写程序求系统的动态性能指标2.实验内容2.1在SIMULINK窗口建立方框图结构模型。
2.2设计PID控制器,传递函数模型如下。
()⎪⎭⎫⎝⎛++=s T s T k s G d i p c 112.3修改PID 参数p K 、i T 和d T ,讨论参数对系统的影响。
3.4利用稳定边界法对PID 参数p K 、i T 和d T 校正设计。
2.5根据PID 参数p K 、i T 和d T 对系统的影响,调节PID 参数实现系统的超调量小于10%。
3. 实验操作过程3.1在SIMULINK 窗口建立模型图1 设计模型方框图3.2设计PID 控制器图2 PID控制器模型3.3利用稳定边界法对PID参数p K、i T和d T校正设计: 表1 PID稳定边界参数值校正后的响应曲线图3(a)校正后的响应曲线图3(b)校正后的响应曲线3.4调节PID参数实现系统的超调量小于10%:表2 PID 参数图4 响应曲线图4.规律总结1.P控制规律控制及时但不能消除余差,I控制规律能消除余差但控制不及时且一般不单独使用,D控制规律控制很及时但存在余差且不能单独使用。
2.比例系数越小,过渡过程越平缓,稳态误差越大;反之,过渡过程振荡越激烈,稳态误差越小;若p K过大,则可能导致发散振荡。
计算机控制基于MATLAB的PID参数调整方法的仿真研究

Hefei University计算机控制技术基于MATLAB的PID参数调整方法的仿真研究专业及班级_____ 09级自动化(1)班____ __姓名______ _____ __________ ___学号_______ __________ __授课老师_______ ____丁健__________ __完成时间____ ______2012-6-2________ _ __基于MATLAB的PID参数调整方法的仿真研究摘要:应用MATLAB 软件的MATLAB 语言编程和Simulink 仿真工具箱相结合的方式对过程控制中的PID参数整定方法:基于稳定性分析的经验整定法,工程整定法—扩充临界比例度法做了仿真研究,取得了好的仿真结果,对研究各种实际过程控制系统PID 参数在线调整具有理论指导意义。
关键词:PID参数整定;MATLAB;仿真PID(proportional-integral-derivative)作为经典的控制理论,PID 控制中一个关键的问题便是PID 参数的整定。
在实际的应用中,许多被控过程机理复杂,具有高度非线性、时变确定性和纯滞后等特点。
在噪声、负载扰动等因素的影响下,过程参数甚至模型结构均会随时间和工作环境的变化而变化。
这就要求在PID 控制中,不仅PID 参数的整定不依赖于对象数学模型,并且PID参数能够在线调整,以满足实时控制的要求。
MATLAB是一款高性能数值计算和可视化软件,MATLAB 语言作为一种科学计算语言,具有极强的适应能力,它用简洁的代码和函数库为编程研究人员提供了直观简单的程序开发环境;Simulink 工具箱为工程领域研究人员提供了仿真研究环境,应用该软件进行自动控制系统方面的相关应研究能达到事倍功半的效果。
1 PID 参数整定方法的MATLAB 仿真1.1 经验整定法(Ziegler-Nichols 法)的MATLAB仿真Ziegler-Nichols 方法是基于稳定性分析的PID 整定方法。
基于matlab的智能PID控制器设计和仿真毕业设计论文

基于MATLAB的智能PID控制器设计与仿真摘要在工业生产中应用非常广泛的是PID控制器,是最早在经典控制理论基础上发展起来的控制方法,应用也十分广泛。
传统的PID控制器原理十分简单,即按比例、积分、微分分别控制的控制器,但是他的核心也是他的难点就是三个参数(比例系数Kp、积分系数Ki、微分系数Kd)的整定。
参数整定的合适,那么该控制器将凭借结构简单、鲁棒性好的优点出色的完成控制任务,反之则达不到人们所期望的控制效果。
人工神经网络模拟人脑的结构和功能而形成的信息处理系统,是一门十分前沿高度综合的交叉学科,并广泛应用于工程领域。
神经网络控制是把自动控制理论同他模仿人脑工作机制的数学模型结合起来,并拥有自学习能力,能够从输入—输出数据中总结规律,智能的处理数据。
该技术目前被广泛应用于处理时变、非线性复杂的系统,并卓有成效。
关键词自适应PID控制算法,PID控制器,神经网络Design and simulation of Intelligent PID Controllerbased on MATLABAbstractPID controller ,the control method which is developed on the basis of classical control theory, is widely used in industrial production.The Principle of traditional PID controller is very simple, which contains of the proportion, integral, differential three component, but its core task and difficulties is three parameter tuning(proportional coefficient Kp, integral coefficient Ki and differential coefficient KD).If the parameter setting is suitable, the controller can accomplish the control task with the advantages of simple structure and good robustness;but on the contrary, it can not reach the desired control effect which we what.Artificial neural network , the formation of the information processing system which simulate the structure and function of the human brain , is a very high degree of integration of the intersection of disciplines, and widely used in the field of engineering. Neural network control ,combining automatic control theory and the imitate mathematical model of the working mechanism of human brain , has self-learning ability, and can summarize the law of the input-output data , dealing with data intelligently .This technique has been widely used in the process of time-varying, nonlinear and complex system, and it is very effective.Key W ord:Adaptive PID control algorithm,PID controller,Neural network目录摘要 (I)Abstract (II)第一章绪论 (1)1.1 课题研究背景及意义 (1)第二章 PID控制器 (2)2.1 PID控制原理 (2)2.2常规PID控制器的算法理论 (3)2.2.1 模拟PI D控制器 (3)2.2.2 数字P I D控制算法 (3)2.2.3常规PID控制的局限 (5)2.2.4 改进型PID控制器 (5)第三章人工神经网络 (8)3.1 人工神经网络的原理 (8)3.2神经网络PID控制器 (8)3.2.1神经元PID控制器 (8)3.2.2 单神经元自适PID应控制器 (9)3.3 BP神经网络参数自学习的PID控制器 (12)第四章MATAB仿真 (16)4.1 仿真过程 (16)第五章结论与展望 (24)致谢 (25)参考文献 (25)华东交通大学毕业设计(论文)第一章绪论1.1 课题研究背景及意义在工业生产中应用非常广泛的是PID控制器,是最早在经典控制理论基础上发展起来的控制方法,应用也十分广泛。
基于MATLAB的PID控制器参数整定及仿真

基于MATLAB的PID控制器参数整定及仿真PID控制器是一种经典的控制器,在工业自动化控制系统中广泛应用。
其主要功能是根据系统的误差信号,通过调整输出信号的比例、积分和微分部分来减小误差,并达到系统的稳定控制。
PID控制器参数整定是指确定合适的比例常数Kp、积分常数Ki和微分常数Kd的过程。
本文将介绍基于MATLAB的PID控制器参数整定及仿真的方法。
首先,在MATLAB中建立一个包含PID控制器的模型。
可以通过使用MATLAB的控制系统工具箱来实现这一过程。
在工具箱中,可以选择合适的建模方法,如直接设计模型、积分节点模型或传输函数模型。
通过这些工具,可以方便地建立控制系统的数学模型。
其次,进行PID控制器参数整定。
PID控制器参数整定的目标是通过调整比例常数Kp、积分常数Ki和微分常数Kd,使系统的响应特性达到最佳状态。
常用的PID参数整定方法有经验法、试误法、Ziegler-Nichols方法等。
1.经验法:根据系统的特性和经验,选择合适的PID参数。
这种方法常用于初步整定,但可能需要根据实际情况调整参数。
2.试误法:通过逐步试验和调整PID参数,使系统的输出响应逐渐接近期望值,从而达到最佳控制效果。
3. Ziegler-Nichols方法:该方法是一种经典的系统辨识方法,通过测试系统的临界稳定性,得到系统的传递函数参数,并据此计算出合适的PID参数。
最后,进行PID控制器参数整定的仿真。
在MATLAB中,可以通过使用PID模块进行仿真。
可以输入相应的输入信号和初始参数,观察系统的输出响应,并通过调整参数,得到最佳的控制效果。
总结起来,基于MATLAB的PID控制器参数整定及仿真的过程包括:建立控制系统模型、选择PID参数整定方法、进行PID参数整定、进行仿真实验。
PID控制器参数整定的好坏直接影响控制系统的工作性能。
通过基于MATLAB的仿真实验,可以方便地调整和优化控制系统的PID参数,提高系统的响应速度、稳定性和抗干扰性能。
基于matlab的数字pid直流电机调速系统的实现毕业论文[管理资料]
![基于matlab的数字pid直流电机调速系统的实现毕业论文[管理资料]](https://img.taocdn.com/s3/m/2a305c99af1ffc4ffe47acfe.png)
基于MATLAB的数字PID直流电机调速系统的实现作者系(院)专业电气工程及其自动化年级学号指导教师日期学生诚信承诺书本人郑重承诺:所呈交的论文是我个人在导师指导下进行的研究工作及取得的研究成果。
尽我所知,除了文中特别加以标注和致谢的地方外,论文中不包含其他人已经发表或撰写的研究成果,也不包含为获得安阳师范学院或其他教育机构的学位或证书所使用过的材料。
与我一同工作的同志对本研究所做的任何贡献均已在论文中作了明确的说明并表示了谢意。
签名:日期:论文使用授权说明本人完全了解安阳师范学院有关保留、使用学位论文的规定,即:学校有权保留送交论文的复印件,允许论文被查阅和借阅;学校可以公布论文的全部或部分内容,可以采用影印、缩印或其他复制手段保存论文。
签名:导师签名:日期基于MATLAB的数字PID直流电机调速系统的实现摘要:本文主要研究了直流电机的数学模型、直流电动机调速系统工作原理、电机调速系统的常规PID控制器的设计方法及其参数的常规控制原理。
通过MATLAB来仿真PID控制器的参数对控制性能的影响,来进一步研究数字PID控制器的设计方法及其在直流调速系统的的应用。
关键词:直流电机;直流电动机调速系统;PID;MATLAB;数字PID;1 引言计算机仿真技术是应用电子计算机对研究对象的数学模型进行计算和分析的方法。
对于从事控制系统研究与设计的技术人员而言,MATLAB 是目前控制系统计算机辅助设计实用有效的工具。
这不仅是因为它能解决控制论中大量存在的矩阵运算问题更因为它提供了强有力的工具箱支持。
与控制系统直接相关的工具箱有控制系统、系统辨识、信息处理、优化等。
还有一些先进和流行的控制策略工具箱,如鲁棒控制、u —分析与综合、神经网络、模糊预测控制、非线性控制设计、模糊逻辑等。
可以说目前理论界和工业界广泛应用和研究的控制算法,几乎都可以在 MATLAB中找到相应的工具箱。
同时MATLAB软件中还提供了新的控制系统模型输入与仿真工具SIMULINK,它具有构造模型简单、动态修改参数实现系统控制容易、界面友好、功能强等优点,成为动态建模与仿真方面应用最广泛的软件包之一。
基于MATLAB的PID控制器参数整定及仿真

基于MATLAB的PID控制器参数整定及仿真基于MATLAB的PID控制器参数整定及仿真摘要:PID控制器结构和算法简单,应⽤⼴泛,但参数整定⽐较复杂,在此我探讨利⽤MATLAB实现PID参数整定及其仿真的⽅法,并分析⽐较⽐例、⽐例积分、⽐例微分控制,探讨K p,T i,T d三个参数对PID控制规律的影响关键字:PID控制器,MATLAB,参数整定,仿真Parameter tuning and emulation of controller based on MATLAB Abstract:The control structure and algorithm of PID is easy and widely applicable,but its setting methods of are multifarious,Generally utilize guessing and trying to fix.It is convenient to tune PID parameters and emulate through MATLAB experiment.Analyze and compare the proportion、the proportion integral and the proportion differential control.Discuss the influence of three parameters K p,Ti and T d to the PID control rules.Key words:PID controller,MATLAB,parameter turning,emulation⼀PID控制的简介及其发展1.1PID控制简介PID(P,proportion⽐例;I,integration积分;D,differentiation)⽤于控制精度,⽐例是必须的,它直接影响精度,影响控制的结果;积分相当于⼒学的惯性能使震荡趋于平缓;微分控制提前量,它相当于⼒学的加速度,影响控制的反应速度,太⼤会导致⼤的超调量使系统极不稳定;太⼩会使反应缓慢。
基于Matlab的控制系统PID校正的仿真总结

1.2 连续系统的基本PID仿真
1.2.1
基本的PID控制
1.2.2
线性时变系统的PID控制
1.2 连续系统的基本PID仿真
s
G(s)
K e s Ts 1
表 1 调节器Ziegler-Nichols整定公式
为实现用Ziegler-Nichols整定公式计算系统P、
PI、PID校正器的参数,作者给出函数zn01 ()。
用Ziegler-Nichols整定公式计算系统P、PI、
PID校正器的参数的函数zn01.m。调用格式 为:[Gc,Kp,Ti,Td]=zn01(PID,vars) 其中PID是校正器类型,当PID=1时,为计算 P调节器的参数;当PID=2时,为计算PI调节 器的参数;当PID=3时,为计算PID调节器的 参数。输入参量vars为带延迟—惯性环节模 型的 KT 已知三参数:K=vars(1);T=vars (2);tau=vars(3)。输入参量Gc为校正 器传递函数,Kp为校正器的比例系数;Ti为 校正器的积分时间常数;Td为校正器的微分 时间常数。
function [Gc,Kp,Ti,Td]=zn01(PID,vars) K=vars(1);T=vars(2);tau=vars(3); Kp=[];Ti=[];Td=[]; if PID ==1, Kp=T/(K*tau); elseif PID==2, Kp=0.9*T/(K*tau); Ti=3.33*tau; elseif PID==3, Kp=1.2*T/(K*tau); Ti=2*tau;Td=tau/2; end switch PID case 1,Gc=Kp; case 2,Gc=tf([Kp*Ti Kp],[Ti 0]); case 3,nn=[Kp*Ti*Td Kp*Ti Kp]; dd=[Ti 0]; Gc=tf(nn,dd) end
基于MATLABSimulink的PID参数整定

基于MATLABSimulink的PID参数整定基于MATLAB/Simulink的PID参数整定摘要:针对PID参数整定过程的复杂性,基于MATLAB/Simulink仿真环境,模拟临界⽐例度法PID参数整定的⽅法和步骤,给出了⼀种简单有效的PID参数整定⽅法。
与通常的整定⽅法⽐较,其优点是⾮常直观、可以随意修改仿真参数,节省了⼤量的计算和编程⼯作量。
通过仿真实例验证了该⽅法的有效性。
关键词:PID控制;参数整定;MATLAB/Simulink;临界⽐例度法Abstract:The PID tuning is a complicated process.To solve the problem,a method of critical gain is presented based on the MATLAB/Simulink simulationenvironment.The simulation examples are also given.Key words:PID control;parameter tuning;MATLAB/Simulink;critical gain method 1 引⾔PID控制是最早发展起来且⽬前在⼯业过程控制中仍然是应⽤最为⼴泛的控制策略之⼀。
据统计,在⼯业过程控制中95%以上的控制路都具有PID结构,⽽且许多⾼级控制都是以PID控制为基础的。
PID控制能被⼴泛应⽤和发展,根本原因在于PID控制具有以下优点:原理简单,使⽤⽅便,PID参数K p、T i和T d可以根据过程动态特性及时调整,适应性强。
鲁棒性强,即其控制品质对控对象特性的变化不太敏感。
采⽤不同的PID参数,对控制系统的性能将会不—样,因此PID参数的调节和优化决定了控制系统最终能达到的控制性能,PID参数整定是控制系统设计的核⼼内容。
综观各种PID参数整定⽅法,可以有如下分类:根据研究⽅法来划分,可分为基于频域的PID参数整定⽅法和基于时域的PID参数整定⽅法;根据发展阶段来划分,可分为常规PID参数整定⽅法和智能PID 参数整定⽅法根据被控对象个数来划分,可分为单变量PID参数整定⽅法和多变量PID参数整定⽅法;根据控制量的组合形式来划分,可分为线性PID参数整定和⾮线性PID参数整定⽅法。
基于Matlab的控制系统PID校正的仿真总结

四、结论
PID控制系统结构简单、稳定性好、 工作可靠、调整方便。PID校正响应速 度比P校正和PI校正都要快,但是超调 量比较大。
控制工程与控制理论课程设计讲座
先进PID控制及 其MATLAB仿真
主讲人 付冬梅 自动化系
第1章 数字PID控制
1.1
PID控制原理 连续系统的模拟PID仿真 数字PID控制
程序运行以后,还得到经P、PI、PID校正(用Ziegler-Nichols整定公式计算)系统阶跃给 定响应曲线,如图所示。
图 3-1 Ziegler-Nichols的P、PI、PID控制阶跃响应曲线
由图可见,用Ziegler-Nichols整定公式计算的P、PI、PID校正器对系统 校正后,其阶跃给定响应曲线中的P、PI校正两者响应速度基本相同。 因为这两种校正求出的Kp不同,所以两种校正的被调量终了值不同。PI 校正的超调量比P校正的要小些。PID校正的比前两者的响应速度都要快, 但是超调量最大。
D I
C P
I
C
P
D
D
C
P
I
P
D
I
C
P
D
I
1 G ( s ) K P (1 TD s ) TI s
(2-2)
由式(2-2)可以看出,PID控制是通过三个
参量起作用的。这三个参量取值的大小不同, 就是比例、积分、微分作用强弱的变化。为 了说明每个参数单独变化时对于系统较正时 的影响,特列举以下实例。
1.3.2 连续系统的数字PID控制 仿真
本方法可实现D/A及A/D的功能,符合数字实
时控制的真实情况,计算机及DSP的实时 PID控制都属于这种情况。 采用MATLAB语句形式进行仿真。被控对象 为一个电机模型传递函数: 1
matlab实验十 控制系统的PID校正设计及仿真

实验十 控制系统的PID 校正设计及仿真一、实验目的1.学会用MA TLAB 对系统进行仿真;2.应用频率综合法对系统进行PID 校正综合。
二、设计原理与步骤1.设计原理超前校正的主要作用是增加相角裕量,改善系统的动态响应特性。
滞后校正的作用是改善系统的静态特性,两种校正结合起来就能同时改善系统的动态和静态特性。
滞后超前校正(亦称PID 校正)综合了前两种校正的功能。
滞后超前校正(亦称PID 校正)的传递函数为:)(,)1()1)(1()1)(1()(121212T T S T S T S T S T S G C ααββα>>≥++++=它相当于一个滞后校正与一个超前校正相串联,其对数频率特性如图10-1所示:2.设计步骤基于频率法综合滞后-超前校正的步骤是:(1)根据静态指标要求,确定开环比例系数K ,并按已确定的K 画出系统固有部分的Bode 图;(2)根据动态指标要求确定c ω,检查系统固有部分在c ω的对数幅频特性的斜率是否为-2,如果是,求出c ω点的相角;(3)按综合超前校正的步骤(3)~(6)综合超前部分G C1(S )(注意在确定m θ时要计入滞后校正带来的0012~5的相角滞后量)。
在第(6)步时注意,通常)()(c c c g L L ωω+比0高出很多,所以要引进滞后校正;(4)令βlg 20=)()(c c c g L L ωω+求出β;(5)按综合滞后校正的步骤(4)~(5)综合滞后部分)(2S G c ;(6)将滞后校正与超前校正串联在一起,构成滞后超前校正:)()()(21S G S G S G c c c ⋅=三、实验内容练习10-1反馈控制系统的开环传递函数为:)105.0)(11.0()(++=S S S K S G 要求:(1)速度偏差系数Kv 50≥(2)相位裕度γ%5400±=(3)增益穿越频率%510±=c ω要求:(1)设计满足上述要求的滞后-超前控制器;(2)用Simulink 进行仿真;(3)画出校正前后的Bode 图(4)分析讨论设计过程及结果。
基于Matlab仿真PID校正汇总
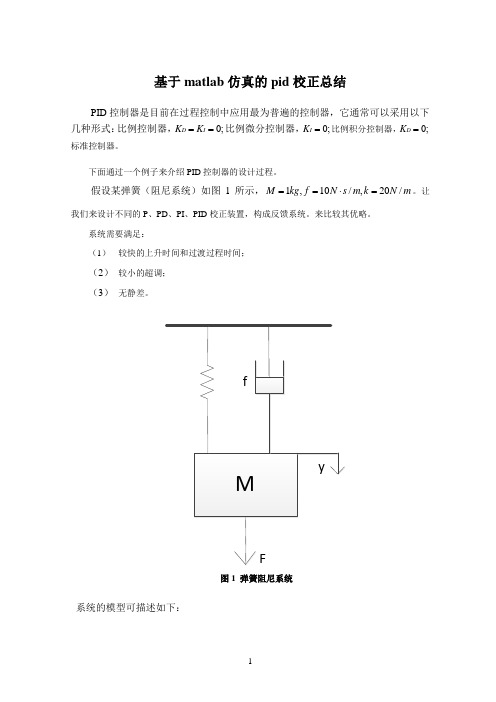
基于matlab 仿真的pid 校正总结PID 控制器是目前在过程控制中应用最为普遍的控制器,它通常可以采用以下几种形式:比例控制器,0;D I K K ==比例微分控制器,0;I K =比例积分控制器,0;D K =标准控制器。
下面通过一个例子来介绍PID 控制器的设计过程。
假设某弹簧(阻尼系统)如图1所示,1,10/,20/M kg f N s m k N m ==⋅=。
让我们来设计不同的P 、PD 、PI 、PID 校正装置,构成反馈系统。
来比较其优略。
系统需要满足:(1) 较快的上升时间和过渡过程时间;(2) 较小的超调; (3) 无静差。
图1 弹簧阻尼系统系统的模型可描述如下:控制系统建模与仿真论文( 2011)()2()1()X s G s F s Ms fs k==++(1)、绘制未加入校正装置的系统开环阶跃响应曲线。
根据系统的开环传递函数,程序如下:clear; t=0:0.01:2; num=1; den=[1 10 20]; c=step(num,den,t); plot(t,c);xlabel('Time-Sec'); ylabel('y');title('Step Response'); grid;系统的阶跃响应曲线如图2图2 未加入校正时系统的开环阶跃响应曲线(2)、加入P 校正装置我们知道,增加p K 可以降低静态误差,减少上升时间和过渡时间,因此首先选择P 校正,也就是加入一个比例放大器。
此时,系统的闭环传递函数为:2()10(20)pc p K G s s s K =+++此时系统的静态误差为120pp K K -+。
所以为了减少静差,可以选择系统的比例增益为300p K =。
这样就可以把静差缩小到0.0625。
虽然系统的比例系数越大,静差越小,但是比例系数也不能没有限制地增大,它会受到实际物理条件和放大器实际条件的限制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于matlab 仿真的pid 校正总结PID 控制器是目前在过程控制中应用最为普遍的控制器,它通常可以采用以下几种形式:比例控制器,0;D I K K ==比例微分控制器,0;I K =比例积分控制器,0;D K =标准控制器。
下面通过一个例子来介绍PID 控制器的设计过程。
假设某弹簧(阻尼系统)如图1所示,1,10/,20/M kg f N s m k N m ==⋅=。
让我们来设计不同的P 、PD 、PI 、PID 校正装置,构成反馈系统。
来比较其优略。
系统需要满足:(1) 较快的上升时间和过渡过程时间;(2) 较小的超调; (3) 无静差。
图1 弹簧阻尼系统系统的模型可描述如下:控制系统建模与仿真论文( 2011)()2()1()X s G s F s M s fs k==++(1)、绘制未加入校正装置的系统开环阶跃响应曲线。
根据系统的开环传递函数,程序如下:clear; t=0:0.01:2; num=1; den=[1 10 20]; c=step(num,den,t); plot(t,c);xlabel('Time-Sec'); ylabel('y');title('Step Response'); grid;系统的阶跃响应曲线如图2图2 未加入校正时系统的开环阶跃响应曲线(2)、加入P 校正装置我们知道,增加p K 可以降低静态误差,减少上升时间和过渡时间,因此首先选择P 校正,也就是加入一个比例放大器。
此时,系统的闭环传递函数为:2()10(20)pc p K G s s s K =+++此时系统的静态误差为120pp K K -+。
所以为了减少静差,可以选择系统的比例增益为300p K =。
这样就可以把静差缩小到0.0625。
虽然系统的比例系数越大,静差越小,但是比例系数也不能没有限制地增大,它会受到实际物理条件和放大器实际条件的限制。
一般取几十到几百即可。
增大比例增益还可以提高系统的快速性。
加入P 校正后,程序如下:clear; t=0:0.01:2; Kp=300; num=[Kp]; den=[1 10 (20+Kp)]; c=step(num,den,t); plot(t,c);xlabel('Time-Sec'); ylabel('y');title('Step Response'); gird;加入P 校正后系统的闭环阶跃响应曲线如图3控制系统建模与仿真论文( 2011)图3 加入P校正后系统的闭环阶跃响应曲线从图3中可以看出,系统的稳定值在0.94左右,静差约为0.06。
基本符合系统的需要。
并且,曲线的形状从过阻尼转变为衰减震荡。
系统的快速性也得到了改善。
系统的上升时间不超过0.2s,调节时间不超过0.7s。
不过转变为衰减震荡后又出现了新的问题。
系统的超调量比较大,达到了38%。
第一个峰值振荡频率过大,需要寻找新的方法继续校正。
(3)、PD校正装置设计在P校正后虽然有效地减小了静差、改善了系统的响应速度,但出现了超调过K可以降低大的现象。
有自控原理的知识我们知道,加入微分调节,也就是增大D超调量,减小调节时间,对上升时间和静差影响不大。
因此,可以选择PD校正,也就是在系统中加入一个比例放大器和一个微分放大器。
此时,系统的闭环传函为:2()(10)(20)D pc D p K s K G s s K s K +=++++这里仍然选择300p K =,D K 的选择一般为系统震荡频率的8倍左右。
所以经过调试我们选择10D K =。
编辑程序如下: clear;t=0:0.01:2; Kp=300; Kd=10;num=[Kd Kp];den=[1 (10+Kd) (20+Kp)]; c=step(num,den,t); plot(t,c);xlabel('Time-Sec'); ylabel('y');title('Step Response'); grid;加入PD 校正后系统的阶跃响应曲线如图4:图4 加入PD 校正后系统的闭环阶跃响应曲线控制系统建模与仿真论文( 2011)由图4中可以看出,加入PD 校正,系统的曲线仍然是呈衰减震荡,但衰减次数显著减少,比且超调量也降低了不少。
而且对系统的上升时间和静差来说影响不大。
剩下的问题就是如何实现无静差。
(4)、PI 校正装置设计消除静差,可以通过加入积分环节。
当在原系统的基础上加入一个比例放大器和一个积分放大器时,系统的闭环传递函数为:32()10(20)p Ic p IK s K G s s s K s K +=++++加入PI 校正后,系统的阶跃响应曲线如图5所示:图5 PI 校正后系统的闭环阶跃响应曲线由图可见,加入PI 校正后,系统的稳态值为1,也就是实现了无静差。
系统的输出量可以无误差地跟踪设定值的变化。
然而,这样的系统调节时间稍长,响应速度不够快。
为了满足这些要求,我们接下来引入经典的PID 校正。
(5)、PID 校正装置设计加入p K 、I K 、D K 。
通过调节这三个参数,并使用Matlab 绘图进行逐步校正。
此处省略调试过程。
最终取450P K =,300I K =,40D K =。
系统的闭环传递函数如下:232()(10)(20)D p Ic D p IK s K s K G s s K s K s K ++=+++++编写程序如下: clear;t=0:0.01:2; Kp=450; Ki=300; Kd=40;num=[Kd Kp Ki];den=[1 (10+Kd) (20+Kp) Ki]; c=step(num,den,t); plot(t,c);xlabel('Time-Sec'); ylabel('y');title('Step Response'); grid;所得图形如图6所示:控制系统建模与仿真论文( 2011)图6 PID校正后系统的闭环阶跃响应曲线4.1 PID参数整定法概述1.PID参数整定方法(1)Relay feedback :利用Relay 的on-off 控制方式,让系统产生一定的周期震荡,再用Ziegler-Nichols调整法则去把PID值求出来。
(2)在线调整:实际系统中在PID控制器输出电流信号装设电流表,调P值观察电流表是否有一定的周期在动作,利用Ziegler-Nichols把PID求出来,PID值求法与Relay feedback 一样。
(3)波德图&跟轨迹:在MA TLAB里的Simulink绘出反馈方块图。
转移函数在用系统辨识方法辨识出来,之后输入指令算出PID值。
[13]2.PID调整方式图4-1 PID 调整方式如上描述之PID 调整方式分为有转函数和无转移函数,一般系统因为不知转移函数,所以调PID 值都会从Relay feedback 和在线调整去着手。
波德图及根轨迹则相反,一定要有转移函数才能去求PID 值,那这技巧就在于要用系统辨识方法,辨识出转移函数出来,再用MA TLAB里的Simulink 画出反馈方块图,调出PID 值。
[15]所以整理出来,调PID 值的方法有在线调整法、Relay feedback 、波德图法、根轨迹法。
前提是要由系统辨识出转移函数才可以使用波德图法和根轨迹法,如下图4-2所示。
4.2 针对无转移函数的PID 调整法在一般实际系统中,往往因为过程系统转移函数要找出,之后再利用系统仿真找出PID 值,但是也有不需要找出转移函数也可调出PID 值的方法,以下一一介绍。
4.2.1 Relay feedback 调整法控制系统建模与仿真论文( 2011)图4-3 Relay feedback调整法如上图4-3所示,将PID控制器改成Relay,利用Relay的On-Off控制,将系统扰动,可得到该系统于稳定状态时的震荡周期及临界增益(T u及Ku),在用下表4-4 的Ziegler-Nichols 第一个调整法则建议PID调整值,即可算出该系统之Kp、T i、T v之值。
表4-4 Ziegler-Nichols第一个调整法则建议PID调整值[9]4.2.2 Relay feedback在计算机做仿真Step 1:以MA TL AB里的Simulink绘出反馈方块,如下图4-5所示。
Step 2:让Relay做On-Of f动作,将系统扰动(On-Off动作,将以±1做模拟),如下图4-6所示。
图4-6Step 3:即可得到系统的特性曲线,如下图4-7所示。
图4-7 系统震荡特性曲线Step 4:取得Tu及a,带入公式3-1,计算出Ku。
以下为Relay feedback临界震荡增益求法控制系统建模与仿真论文( 2011)ad Ku ⨯=π4公式(4-1)a:振幅大小 d:电压值4.2.3 在线调整法图4-8 在线调整法示意图在不知道系统转移函数的情况下,以在线调整法,直接于PID 控制器做调整,亦即PID 控制器里的I 值与D 值设为零,只调P 值让系统产生震荡,这时的P 值为临界震荡增益Kv ,之后震荡周期也可算出来,只不过在线调整实务上与系统仿真差别在于在实务上处理比较麻烦,要在PID 控制器输出信号端在串接电流表,即可观察所调出的P 值是否会震荡,虽然比较上一个Relay feedback 法是可免除拆装Relay 的麻烦,但是就经验而言在实务上线上调整法效果会较Relay feedback 差,在线调整法也可在计算机做出仿真调出PID 值,可是前提之下如果在计算机使用在线调整法还需把系统转移函数辨识出来,但是实务上与在计算机仿真相同之处是PID 值求法还是需要用到调整法则Ziegler-Nichols 经验法则去调整,与Relay feedback 的经验法则一样,调出PID 值。
4.2.4 在线调整法在计算机做仿真Step 1:以MA TLAB 里的Simulink 绘出反馈方块,如下图4-9所示图4-9反馈方块图PID方块图内为图4-10 PID方块图Step 2:将Td调为0,Ti无限大,让系统为P控制,如下图4-11所示。
图4-11Step 3:调整K P使系统震荡,震荡时的K P即为临界增益K U,震荡周期即为T V。
(使在线调整时,不用看a求K U),如下图4-12所示。
控制系统建模与仿真论文( 2011)图4-12 系统震荡特性图Step 4:再利用Ziegler-Nichols调整法则,即可求出该系统之Kp、T i,T d之值。
