AP 微积分BC 选择题样卷一
ap微积分真题答案

ap微积分真题答案【篇一:ap 微积分bc 选择题样卷一】version - section i - part a calculators are not permitted on this portion of the exam28 questions - 55 minutes1) givenfind dy/dx. a) b) c) d) e)2) give the volume of the solid generated by revolving the region bounded by the graph of y = ln(x), the x-axis, the lines x = 1 and x = e, about the y-axis. a) b) c) d)e)3) the graph of the derivative of fis shown below.find the area bounded between the graph of f and the x-axis over the interval [-2,1], given that f(0) = 1. a) b) c) d) e)4) determine dy/dt, given thatanda)b)c)d)e)5) the function-1is invertible. give the slope of the normal line to the graph of f atx = 3.a) b) c)d)e)6) determinea) b)c) d) e)7) give the polar representation for the circle of radius 2 centered at ( 0 , 2 ). a)b)c)d)e)8) determinea)b)c) d)e)9) determinea) b) c) d) e)10) give the radius of convergence for the seriesa)b)c) d)e)11) determinea)b)【篇二:ap 微积分bc选择题样卷二】17 questions - 50 minutes1) the limit of the sequenceas n approaches is -3. what is the value of c? a)b)c)d)e)2) ifand y = 3 when x = -2, then what is y? a) b) c)d) e)3) the graph of the derivative of fis given below.which of the following is false about the function f?a) f is increasing on [1,4].b) f is concave down on [1,5/2].c) f is concave down on [-3,0).d) f is not differentiable at 0. e) the funciton is constant on (-,-3].4) determinea)b)c) d) e)5) give the area that lies below the x-axis and is contained within theregion bounded by the polar curvea) b) c) d) e)6) give the error that occurs when the area between the curve and the x-axis over the interval [0,1] is approximated by the trapezoid rule with n = 4. a)b)c)d)e)7) letdetermine f(2/3). a)b)c) d) e)8) give the length of the curve determined byfor t from 0 to 2. a)b)c)d)e)9) particles a and b leave the origin at the same time and move along the y-axis. their positions are determined by the functionsfor t between 0 and 8. what is the velocity of particle b when particlea stops for the first time? a) b)c)d) e)10) the base of a solid is the region in the xy plane enclosed by thecurvesover the interval[0,/4]. cross sections of the solid perpendicular to the x-axis are squares. determine the volume of the solid. a)b)c)d)e)11) give the minimum value of the functionfor x 0. a)b)c)d)e)12) select the true statement associated with the function【篇三:ap微积分考试详解】>微积分ap课程包括微积分ab (calculus ab) 和微积分bc(calculus bc)两门课。
AP微积分BC模考卷2023

AP 微积分 BC 模考卷 2023一、选择题(每题1分,共5分)1. 若函数f(x)在点x=a处可导,则f'(a)表示的是()A. f(x)在x=a处的斜率B. f(x)在x=a处的函数值C. f(x)在x=a处的切线方程D. f(x)在x=a处的曲率A. lim(x→∞) f(x) = LB. lim(x→0) f(x) = LC. lim(x→a) f(x) = ∞D. lim(x→∞) f'(x) = L3. 若函数f(x) = x^3 3x在x=1处的导数为0,则()A. x=1是f(x)的极大值点B. x=1是f(x)的极小值点C. x=1是f(x)的拐点D. x=1是f(x)的驻点A. ∫(0,1) x dxB. ∫(1,∞) 1/x^2 dxC. ∫(∞,∞) e^(x^2) dxD. ∫(0,2π) sin(x) dx5. 若f(x) = e^(2x),则f''(x)是()A. 2e^(2x)B. 4e^(2x)C. e^(2x)D. 2e^x二、判断题(每题1分,共5分)6. 若函数在闭区间上连续,则该函数在该区间上一定可积。
()7. 若f'(x) > 0,则f(x)是单调递增函数。
()8. 泰勒公式可以用来近似任何可导函数。
()9. 第一类间断点处的函数一定不可导。
()10. 两个函数的导数相等,则这两个函数一定相同。
()三、填空题(每题1分,共5分)11. 函数f(x) = x^2在x=0处的导数f'(0) = ______。
12. 若f(x) = 3x^3 4x^2 + 2x,则f'(x) = ______。
13. ∫(0,π) sin(x) dx = ______。
14. 函数f(x) = e^x的n阶导数f^(n)(x) = ______。
15. 曲线y = x^3在点(1,1)处的切线方程是______。
历年AP微积分真题

历年AP微积分真题Introduction:微积分是数学的一个重要分支,被广泛应用于科学、工程、经济学等领域。
AP微积分考试是美国高中学生常参加的一项重要考试,通过该考试可以获得大学学分。
本文将回顾历年AP微积分真题,帮助读者了解该考试的内容和难度。
Section 1: Differential CalculusDifferential calculus is concerned with the study of rates of change and slopes of curves. This section of the AP Calculus exam tests students' understanding and application of derivative concepts.1. Example question:Find the derivative of the function f(x) = 3x^2 + 2x - 5.Solution:Using the power rule, we differentiate term by term to obtain f'(x) = 6x + 2.2. Example question:A particle moves along a straight line with position function s(t) = 4t^3 - 6t^2 + 2t + 1. Find the velocity function.Solution:To find the velocity function, we differentiate the position function with respect to time. Thus, v(t) = s'(t) = 12t^2 - 12t + 2.Section 2: Integral CalculusIntegral calculus focuses on the accumulation of quantities and finding areas under curves. This section of the AP Calculus exam examines students' ability to calculate definite and indefinite integrals.3. Example question:Evaluate the definite integral ∫(4x^3 + 2x - 1)dx from x = 1 to x = 3.Solution:Using the power rule and the constant rule, we integrate term by term and evaluate the integral to obtain 110.4. Example question:Fin d the indefinite integral ∫(5e^x + 3/x)dx.Solution:Integrating term by term, we obtain the indefinite integral as 5e^x +3ln|x| + C, where C is the constant of integration.Section 3: Applications of CalculusCalculus is widely used in various real-world applications such as physics, economics, and biology. This section of the AP Calculus exam assesses students' ability to apply calculus concepts to solve practical problems.5. Example question:A tank contains 500 liters of water with a salt concentration of 0.2 grams per liter. Brine with a concentration of 1 gram per liter enters the tank at a rate of 5 liters per minute. The mixture is continuously stirred and drained at a rate of 3 liters per minute. Find the salt concentration in the tank after 10 minutes.Solution:Using the principles of differential equations, we set up a rate of change equation and solve it to find the salt concentration to be approximately 0.439 grams per liter after 10 minutes.Conclusion:The AP Calculus exam covers a wide range of topics in both differential and integral calculus. By reviewing past exam questions, students can gain a better understanding of the exam format and level of difficulty. Mastering calculus concepts and their applications is crucial for success in this exam and for a deeper understanding of the field of mathematics.。
AP-微积分BC-选择题样卷一

13) Determine
a)
b)
c)
d)
e)
14) Determine they-intercept of the tangent line to the curve
atx= 4.
a)
b)
c)
d)
e)
15) The functionfis graphed below.
Give the number of values ofcthat satisfy the conclusion of the Mean Value Theorem for derivatives on the interval [2,5].
At which of the following values oftwill the particle change direction?
I)t= 1/8
II)t= 1/6
III)t= 1
IV)t= 2
a) I, II and III
b) I and II
c) I, III and IV
d) II, III and IV
a)
b)
c)
d)
e)
26) Give the first 3 nonzero terms in the Taye function
a)
b)
c)
d)
e)
27) Determine
a)
b)
c)
d)
e)
28) Which of the following series converge(s)?
a)
b)
c)
d)
e)
10) Give the radius of convergence for the series
AP考试模拟试题与答案1-微积分BC- AP Calculus-BC

(A) III only (B) I and II only
(C) II and III only (D) I and III only (E) I, II, and III
y f
a
0
x b
Figure 1T-3
7.
∞
1
=
n = 1 (2n − 1)(2n + 1)
(C) e 2
x
a
0
b
(A)
y
Figure 1T-1 A possible graph of f is (see Figure 1T-2):
(B)
y
(C)
y
a
b
x
a0
b
xa
0
bx
(D)
y
(E)
y
a0
b
x
a
0
bx
Figure 1T-2
GO ON TO THE NEXT PAGE
374 STEP 5. Build Your Test-Taking Confidence
This page intentionally left blank
AP Calculus BC Practice Exam 1 373
Section I—Part A
Number of Questions 28
Time 55 Minutes
Use of Calculator No
Directions:
ap考试模拟试题与答案1微积分bcapcalculusbc
AP Calculus BC Practice Exam 1 371
AP Calculus BC Practice Exam 1
AP微积分BC 2023年真题 附答案和评分标准 AP Calculus BC 2023 Real

AP微积分BC 2023年真题附答案和评分标准 AP Calculus BC2023 Real一、选择题1. 问题描述这个问题是关于……2. 解答过程解答过程如下: - 第一步:…… - 第二步:…… - 第三步:……3. 答案和评分标准答案为:A评分标准如下: - 如果只给出了答案,得0分。
- 如果给出了正确的解答过程,得1分。
二、填空题1. 问题描述这个问题是关于……2. 解答过程解答过程如下: - 第一步:…… - 第二步:…… - 第三步:……3. 答案和评分标准答案为:50评分标准如下: - 如果只给出了答案,得0分。
- 如果给出了正确的解答过程,得1分。
三、解答题1. 问题描述这个问题是关于……2. 解答过程解答过程如下: - 第一步:…… - 第二步:…… - 第三步:……3. 答案和评分标准答案为:解答过程如下:解答步骤1解答步骤2解答步骤3评分标准如下: - 如果只给出了答案而没有解答步骤,得0分。
- 如果给出了解答步骤但部分错误,得1分。
- 如果给出了正确的解答步骤,得2分。
四、简答题1. 问题描述这个问题是关于……2. 解答过程解答过程如下: - 第一步:…… - 第二步:…… - 第三步:……3. 答案和评分标准答案为:……评分标准如下: - 如果只给出了答案而没有解答步骤,得0分。
- 如果给出了解答步骤但部分错误,得1分。
- 如果给出了正确的解答步骤,得2分。
五、解决问题1. 问题描述这个问题是关于……2. 解答过程解答过程如下: - 第一步:…… - 第二步:…… - 第三步:……3. 答案和评分标准答案为:……评分标准如下: - 如果只给出了答案而没有解答步骤,得0分。
- 如果给出了解答步骤但部分错误,得1分。
- 如果给出了正确的解答步骤,得2分。
六、总结通过完成这道AP微积分BC 2023年真题的解答,我们学习了……总体而言,这道题目涵盖了……Markdown文本格式的输出使得我们能够清晰地呈现问题描述、解答过程、答案和评分标准,这对于学生来说非常有帮助。
2003AP微积分BC真题
2003 AP 微积分BC 真题17题.223,4102/3/24Let x t t t dy dy dt t dx dx dt t =−−+=⇒===−此时发现 导数不存在,即切线为垂直与x 轴的直线。
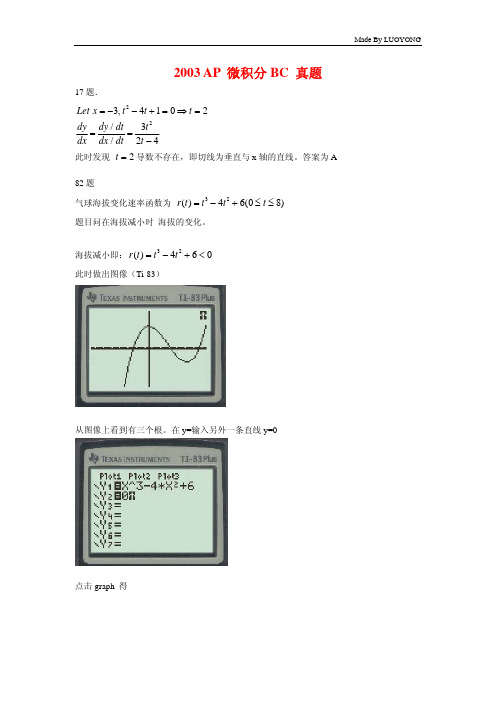
答案为A2t =82题气球海拔变化速率函数为32()46(08)r t t t t =−+≤≤题目问在海拔减小时 海拔的变化。
海拔减小即:32()460r t t t =−+<此时做出图像(Ti-83)从图像上看到有三个根。
在y=输入另外一条直线y=0点击graph 得接着按2nd 、trace 选择intersec(交点)出下面对话框。
让输入第一条曲线的x值,点击右导航键,移到零点附近,此时可以看到x=1.36……,按enter ,接着让选第二条曲线值,同样按enter。
Guess?(让你猜零点),按enter。
计算器自动算出x=1.36……附近的零点x=1.572。
同样的方法算出右边的零点x=3.514。
然后积分即可。
2008 AP 微积分BC 真题22题[]1111000011001100'()()()()()()()()'()()(1)(1)(0)(0)()'()()'()(1)(1)(0)(0)'()()15f xg x dx g x df x g x f x f x dg x f x g x dx g f g f f x g x dx f x g x dx g f g f f x g x dx ==−=−−⇒=−−∫∫∫∫∫∫∫= 88题()f x 单调递减大于0,所以图像只能在x 轴上方。
根据定积分几何意义求面积,有: 1221()()0f x dx f x dx =−<∫∫,所以答案CDE 都错。
2312()()0f x dx f x dx >∫∫>,所以答案A 对。
2021 ap微积分bc选择题

2021年AP微积分BC选择题是考察学生对微积分知识掌握程度的重要一环。
这份选择题目包含了各个知识点和难度等级的题目,通过分析和解答这些题目,可以全面了解学生对微积分的掌握情况。
本篇文章将按照以下结构进行分析和解答。
一、导言2021年AP微积分BC选择题的重要性和意义本文将通过分析和解答2021年AP微积分BC选择题,全面了解学生对微积分知识的掌握情况。
微积分作为数学中的重要分支,对学生的逻辑思维能力和数学分析能力有着重要的促进作用。
对AP微积分BC选择题进行分析和解答能够帮助学生巩固知识,提高解题能力。
二、分析题目1. 对2021年AP微积分BC选择题的整体印象2. 难度较大的题目分析3. 难度较小的题目分析2021年AP微积分BC选择题的整体难度如何?哪些题目的难度较大,需要特别注意?哪些题目的难度较小,适合作为基础练习?三、解答题目1. 难题的解答方法和步骤2. 基础题的解答方法和步骤通过解答2021年AP微积分BC选择题,指导学生掌握解题方法,培养解决问题的能力,帮助学生更好地掌握微积分知识。
四、总结对学习微积分的启示通过对2021年AP微积分BC选择题的分析和解答,怎样总结对学生学习微积分的启示,如何更好地提高学生的解题能力。
在完成以上结构后,文章将会全面而严谨地分析和解答2021年AP微积分BC选择题,为学生提供深入的学习参考和指导。
五、分析题目1. 对2021年AP微积分BC选择题的整体印象在整体印象方面,2021年AP微积分BC选择题依然保持着较高的难度和严谨的命题水准。
题目涵盖范围广泛,包括了微分和积分的应用、曲线的性质、微分方程和级数等各个方面的知识点。
整体难度确实较高,对考生的数学基础要求较高。
2. 难度较大的题目分析一些考生普遍反映,2021年AP微积分BC选择题中的一些多项式的级数展开以及微分方程的题目难度较大。
这些题目需要考生对级数收敛性和微分方程的解法有着较深入的理解和掌握。
ap微积分bc 2017简答题

主题:AP微积分BC 2017简答题解析一、问题一:求曲线y=x^4-2x^3的所有拐点。
1. 答案:我们需要求出曲线的二阶导数。
根据求导法则,对y=x^4-2x^3进行求导,得到y'=4x^3-6x^2。
再对y'进行求导,得到y''=12x^2-12x。
接下来,我们需要找到拐点,即y''=0的点。
解方程12x^2-12x=0,得到x=0和x=1。
曲线的拐点为(0,0)和(1,-1)。
二、问题二:求由曲线y=x^3-3x^2+5x和直线y=4x-3所围成的图形的面积。
2. 答案:我们需要找到两条曲线的交点。
解方程x^3-3x^2+5x=4x-3,得到x^3-3x^2+x+3=0。
利用数值方法或者代数方法求得曲线的交点为x=1和x=3。
我们需要求出两条曲线之间的面积。
利用定积分,求解∫[1,3](x^3-3x^2+5x-(4x-3))dx,得到8.5。
由曲线y=x^3-3x^2+5x和直线y=4x-3所围成的图形的面积为8.5。
三、问题三:已知y=e^x,求y''+2y'+y的表达式。
3. 答案:我们需要求出y'和y''。
对y=e^x分别求一阶和二阶导数,得到y'=e^x和y''=e^x。
将y''+2y'+y的表达式带入,得到e^x+2e^x+e^x=4e^x。
所求表达式为4e^x。
四、问题四:求由两个不相交的圆x^2+y^2=4和(x-2)^2+y^2=1所围成的区域的面积。
4. 答案:我们需要找到两个圆的交点坐标。
解方程x^2+y^2=4和(x-2)^2+y^2=1,得到x=1和x=3。
我们需要求出两个圆围成的区域的面积。
利用定积分,求解∫[1,3]sqrt(4-x^2)-sqrt(1-(x-2)^2)dx,得到4.694。
所求区域的面积为4.694。
ap微积分bc考试原题

AP微积分BC考试原题及答案一、选择题1.下列函数中,在区间(0, +∞)上是减函数的是( ) A. y = x^2 B. y = 1/x C. y =x^3 D. y = 2/x 答案:D2.若f(x) = ∫ (x^2 + 2x - 5) dx,则f'(x) = ( ) A. x^2 + 2x - 5 B. x^2 + 2x - 4 C.x^2 + 2x - 3 D. x^2 + 2x - 6 答案:D3.已知f(x) = sin x + cos x,则f'(x) = ( ) A. -cos x - sin x B. cos x - sin x C. sinx + cos x D. cos x + sin x 答案:B二、填空题4.若f(x) = (x - 1)/(x^2 + 1),则f'(x) = _______.答案:f'(x) = \frac{x^2 +1}{(x^2 + 1)^2}5.设f(x) = x^3 + 4x^2 + x,则f'(x) = _______.答案:f'(x) = 3x^2 + 8x + 1三、解答题6.求函数f(x) = (sin x + cos x)^5 的导数.答案:f'(x) = (5\sin{x} \cdot (\sin{x}+ \cos{x})^4 \cdot (\cos{x} - \sin{x}) - 5\cos{x} \cdot (\sin{x} + \cos{x})^4 \cdot (\sin{x} - \cos{x})) / (\sin{x} + \cos{x})^2$7.求函数f(x) = x^3 - 3x^2 在区间(-∞, a) 上的最小值.答案:f'(x) = 3x^2- 6x = 3x(x - 2),令,令f'(x) > 0,解得,解得x < 0或或0 < x < 2,因此,函数,因此,函数f(x)在在( - \infty,0)上单调递增,在上单调递增,在(0,2)上单调递减,在上单调递减,在(2, + \infty)上单调递增,又上单调递增,又f(0) = 0,f( - 1) = 4,f(1) = -2,f(4) = 16,故当,故当a < 0时,函数时,函数f(x)在区间在区间( - \infty,a)上的最小值为上的最小值为0;当;当0 \leqslant a < 1时,函数时,函数f(x)在区间在区间( - \infty,a)上的最小值为上的最小值为f(a);当;当a > 1时,函数时,函数f(x)在区间在区间( - \infty,a)上的最小值为上的最小值为- 2$.。
AP微积分_calculus_BC真题答案-048

0
3
1 1 3 f '(t )dt 1 1 2 2 2 2 2
f (3) f (0)
3 9 2 2
4 1 f (4) f (0) f '(t )dt (8 2 2 ) 8 2 0 2 f (4) f (0) 8 2 5 2
2003 AP calculus BC EXAM 答案
1-5 ECADC 6-10 CCBAC 11-15 DEAEB 16-20 CACDD 21-25 BEBDD 26-28 DED 76-80 EACDA 81-85 AAECA 86-90 CCCDB 91-92 BC
Free-response
dx is not positive because x(t ) is decreasing along the arc BD as t increase. dt
(b)
t t 1 dx =0; cos( ) 0 or sin( )0 dt 6 2
t
6
2
or
t 1
2
; t 3 for both.
QUESTION1 Point of intersection e 3 x x at (T, S) =(0.238734, 0.488604)
(a) Area =
1
T
( x e 3 x )dx 0.442 or 0.443
1
(b) Volume = ((1 e 3 x )2 (1 x )2 )dx 1.423 or 1.424
4.52 2.52 5.147 or 5.148
9
(d) x(9) x (0)
AP考试模拟试题与答案1-微积分BC- AP Calculus-BC

6. The graph of the function f is shown in Figure 1T-3. Which of the following statements is/are true?
I. f (0) = 0
II. f has an absolute maximum value on [a , b]
Use the answer sheet provided on the previous page. All questions are given equal weight. Points are not deducted for incorrect answers and no points are given to unanswered questions. Unless otherwise indicated, the domain of a function f is the set of all real numbers. The use of a calculator is not permitted in this part of the exam.
GO ON TO THE NEXT PAGE
(C) e 2
x
a
0
b
(A)
y
Figure 1T-1 A possible graph of f is (see Figure 1T-2):
(B)
y
(C)
y
a
b
x
a0
b
xa
0
bx
(D)
y
(E)
y
a0
b
x
a
0
bx
Figure 1T-2
微积分考试题目及答案

微积分考试题目及答案一、选择题(每题2分,共20分)1. 函数 \( f(x) = x^2 - 4x + 4 \) 的导数是:A. \( 2x - 4 \)B. \( 2x + 4 \)C. \( x^2 - 4 \)D. \( x - 2 \)2. 曲线 \( y = x^3 - 6x^2 + 9x \) 在 \( x = 3 \) 处的切线斜率是:A. 0B. 3C. 6D. 93. 若 \( f(x) = 3x^3 + 2x^2 - 5x + 7 \),求 \( f'(1) \) 的值是:A. 12B. 10B. 8D. 64. 定积分 \( \int_{0}^{1} x^2 dx \) 的值是:A. \( \frac{1}{3} \)B. \( \frac{1}{2} \)C. \( \frac{2}{3} \)D. \( \frac{3}{4} \)5. 函数 \( g(x) = \sin(x) + \cos(x) \) 的原函数 \( G(x) \) 是:A. \( -\cos(x) + \sin(x) + C \)B. \( \sin(x) - \cos(x) + C \)C. \( \sin(x) + \cos(x) + C \)D. \( \cos(x) + \sin(x) + C \)6. 函数 \( h(x) = \ln(x) \) 的导数是:A. \( \frac{1}{x} \)B. \( \frac{1}{x^2} \)C. \( \frac{1}{x+1} \)D. \( \frac{1}{x-1} \)7. 若 \( F(x) = \int_{1}^{x} e^t \, dt \),求 \( F'(x) \) 的值是:A. \( e \)B. \( e^x \)C. \( e^1 \)D. \( e^{-1} \)8. 函数 \( p(x) = e^x - x - 1 \) 在 \( x = 0 \) 处的泰勒展开式是:A. \( e^x - x - 1 \)B. \( 1 - x \)C. \( e^x \)D. \( 1 \)9. 函数 \( q(x) = \frac{1}{x} \) 在 \( x = 1 \) 处的导数是:A. 1B. -1C. 0D. 无穷大10. 函数 \( r(x) = \frac{x^2}{x-1} \) 在 \( x = 2 \) 处的导数是:A. 4B. 5C. 6D. 7二、简答题(每题10分,共30分)11. 求函数 \( f(x) = x^3 - 3x^2 + 2 \) 在区间 \( [0, 3] \) 上的定积分。
ap微积分试题

ap微积分试题1. 计算 $\displaystyle \lim _{x\rightarrow 2}\frac{x^{2}-4}{x-2}$解答: 当 $x \neq 2$ 时,可以将分子因式分解为 $x^{2}-4=(x-2)(x+2)$,因此原式化简为 $\displaystyle \lim _{x\rightarrow 2}(x+2)=4$2. 计算 $\displaystyle \lim _{x\rightarrow 0}\frac{\sin x}{x}$解答: 当 $x \neq 0$ 时,使用极限定义可以得到 $\displaystyle \lim _{x\rightarrow 0}\frac{\sin x}{x}=1$3. 计算 $\displaystyle \lim _{x\rightarrow\infty}\left(1+\frac{1}{x}\right)^{x}$解答: 将极限中的式子取自然对数,得到 $\ln \left(\lim_{x\rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}\right)$进一步利用对数的性质有 $\ln \left(\lim _{x\rightarrow\infty}\left(1+\frac{1}{x}\right)^{x}\right)=\lim _{x\rightarrow\infty}x\ln \left(1+\frac{1}{x}\right)$再次利用极限性质有 $\lim _{x\rightarrow \infty}\ln\left(1+\frac{1}{x}\right)^{x}=\lim _{x\rightarrow \infty}x\ln\left(1+\frac{1}{x}\right)=\lim _{x\rightarrow \infty}\frac{\ln\left(1+\frac{1}{x}\right)}{\frac{1}{x}}$利用极限的基本性质即可得到 $\ln \left(\lim _{x\rightarrow\infty}\left(1+\frac{1}{x}\right)^{x}\right)=\ln (e)=1$因为 $\ln (e)=1$,所以 $\displaystyle \lim _{x\rightarrow\infty}\left(1+\frac{1}{x}\right)^{x}=e$这些是一些常见的微积分试题,请根据自己的能力和时间来进行适当的练习和复习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AP Calculus Practice Exam
BC Version - Section I - Part A
Calculators ARE NOT Permitted On This Portion Of The Exam
28 Questions - 55 Minutes
1) Given
Find dy/dx.
a)
b)
c)
d)
e)
2) Give the volume of the solid generated by revolving the region bounded by the graph of y = ln(x), the x-axis, the lines x = 1 and x = e, about the y-axis.
a)
b)
c)
d)
e)
3) The graph of the derivative of f is shown below.
Find the area bounded between the graph of f and the x-axis over the interval [-2,1], given that f(0) = 1.
a)
b)
c)
d)
e)
4) Determine dy/dt, given that
and
a)
b)
c)
d)
e)
5) The function
is invertible. Give the slope of the normal line to the graph of f -1 at x = 3.
a)
b)
c)
d)
e)
6) Determine
a)
b)
c)
d)
e)
7) Give the polar representation for the circle of radius 2 centered at ( 0 , 2 ).
a)
b)
c)
d)
e)
8) Determine
a)
b)
c)
d)
e)
9) Determine
a)
b)
c)
d)
e)
10) Give the radius of convergence for the series
a)
b)
c)
d)
e)
11) Determine
a)
b)
c)
d)
e)
12) The position of a particle moving along the x-axis at time t is given by
At which of the following values of t will the particle change direction I) t = 1/8
II) t = 1/6
III) t = 1
IV) t = 2
a) I, II and III
b) I and II
c) I, III and IV
d) II, III and IV
e) III and IV
13) Determine
a)
b)
c)
d)
e)
14) Determine the y-intercept of the tangent line to the curve
at x = 4.
a)
b)
c)
d)
e)
15) The function f is graphed below.
Give the number of values of c that satisfy the conclusion of the Mean Value Theorem for derivatives on the interval [2,5].
a)
b)
c)
d)
e)
16) Give the average value of the function
on the interval [1,3].
a)
b)
c)
d)
e)
17) A rectangle has both a changing height and a changing width, but the height and width change so that the area of the rectangle is always 20 square feet. Give the rate of change of the width (in ft/sec) when the height is 5 feet, if the height is decreasing at that moment at the rate of 1/2 ft/sec.
a)
b)
c)
d)
e)
18) The graph of the derivative of f is shown below.
Give the number of values of x in the interval [-3,3] where the graph of f has inflection.
a)
b)
c)
d)
e)
19) A rectangle has its base on the x-axis and its vertices on the positive portion of the parabola
What is the maximum possible area of this rectangle
a)
b)
c)
d)
e)
20) Compute
a)
b)
c)
d)
e)
21) Determine
a)
b)
c)
d)
e)
22) Determine
a)
b)
c)
d)
e)
23) Give the exact value of
a)
b)
c)
d)
e)
24) Determine
a)
b)
c)
d)
e)
25) Give the derivative of
a)
b)
c)
d)
e)
26) Give the first 3 nonzero terms in the Taylor series expansion about x = 0 for the function
a)
b)
c)
d)
e)
27) Determine
a)
b)
c)
d)
e)
28) Which of the following series converge(s)
a) B only
b) A, B and C
c) B and C
d) A and B
e) A and C
1) d)
2) e)
3) b)
4) b)
5) e)
6) a)
7) c)
8) c)
9) b)
10) d)
11) c)
12) c)
13) c)
14) e)
15) a)
16) d)
17) a)
18) b)
19) a)
20) d)
21) b)
22) b)
23) a)
24) c)
25) d)
26) b)
27) b)
28) c)。
