匝道线元法

合集下载

怎样计算不完整缓和曲线起点及终点的坐标及切线方位角资料

通过弧长计算出园心角,通过园心角计算出弦长,以及这段园曲线的弦切角,直线的方位角加上(左转减,右转加)这个弦切角就是弦的方位角,这样就可以求出园曲线的终点(也就是下一段曲线的直缓点)的坐标.怎样计算不完整缓和曲线起点及终点的坐标及切线方位角以上为一条匝道的曲线图及要素表。

第一缓和段长度根据公式c=R*L及C=A*A，图中A=100，R=150,可算出第一缓和段的长度为66.667米。

而HY里程减去YH里程为60.902米。

因此此段缓和曲线是在离其起点5.765米的地方与前段圆曲线相交。

图上标为YH点。

固此YH点并非第一缓和段起点。

第二缓和段也有同样的问题，DZD点亦非第二缓和段终点。

问题：怎样计算第一缓和段真正起点的坐标和第二缓和段真正终点的坐标。

及切线方位角。

本人水平有限，苦苦思索未得其解。

在此劳烦各位同仁给予小弟支援。

不胜感谢！测量路上诚与仁兄们携手同行，让我们的测量之路多一丝欣慰，少一分苦闷。

QQ26889412E-mail: yujuying@ 注：曲线要素表可能看不清楚。

但可以把图片另存为一个文件。

然打开此文件就非常清楚了。

1.计算出Y1H的坐标及方位角；2.计算出过渡段缓和曲线在Y1H点的支距dx,dy及偏角β；3.由Y1H的方位角及偏角β可反算出过渡缓和曲线虚起点的方位角。

4.由Y1H的坐标、dx,dy及方位角可反算出过渡缓和曲线起点的坐标。

(用支距到大地坐标的变换公式反算。

关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线，实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算，这就牵涉到线元的起点终点曲率半径判断的问题，一般的直线元，圆曲线元的起点终点半径判断，比较容易，可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题，缓和曲线有时候判断算对了，有时候却坐标算不对，究其原因，其实问题出于该缓和曲线是否是完整缓和曲线引起的。

Casio5800交点法与线元法(积木法)匝道坐标正反算放样程序

Casio5800交点法与线元法（积木法）匝道坐标正反算放样程序1主程序名：ZBZFS（功能：进入计算主程序）65→Dimz↙Deg:Fix 3↙＂1.JD ZFS 2. ZHADAO ZFS＂? I: I→Z[61]: ＂1.ZHONG SHU JS 2. JS＂? I↙If I=1: Then Goto1: Else Goto2:IfEnd↙LbI 1 :If Z[61]=1: Then Prog＂JDYS＂:Else Cls:＂K0＂?A:＂KN＂?L :＂X0＂?U :＂Y0＂?V :＂F0＂?W :＂R0＂?P :＂RN＂?Q:＂ZX:-1,+1,0＂?G:IfEnd↙LbI 2 :Prog＂JS＂2子程序名：JS（功能：选择正算或反算模式）Cls:＂XC＂?H:＂YC＂?Z↙Cls:＂1.ZS 2.FS＂? I: I=2=>Goto 3↙LbI 1 : Cls: If Z[61]=1: Then＂JD ZS KX+XXX＂?K :Prog＂4＂: Else ＂ZHADAO ZS KX+XXX＂?K :IfEnd↙LbI 2: Cls:90→B: Cls:＂RJ Or 0 To K＂?B:B=0 =>Goto 1:＂Z＂?T↙Prog ＂XY-A＂↙X+Tcos(M+B)→X↙Y+Tsin(M+B)→Y↙360Frac((M+360)÷360→M↙Pol(X-H,Y-Z : 360Frac((J+360)÷360→J↙2→O: Prog ＂XY-B＂:Goto 2↙LbI 3 : Cls: If Z[61]=1: Then＂JD FS KN+＂?K:＂X＂?C:＂Y＂?D:Prog＂4＂:Else Cls: ＂ZHADAO FS＂:＂X＂?C:＂Y＂?D:IfEnd↙LbI 4 :Prog ＂XY-A＂↙(D-Y)sin(M)+(C-X)cos(M)→H↙If Abs(H)＞X10-3 :Then K+H→K:Goto 4:IfEnd↙(D-Y)÷cos(M)→T↙3→O: Prog ＂XY-B＂:Goto 3↙3子程序名：XY-A（功能：坐标计算程序）5→N: G(Q-1-P-1)÷Abs（L-A）→F: Abs（K-A）÷N→R: 90R÷π→S:W+(FNR+2GP-1)NS→M:1→E↙U+R÷6×(Cos (W)+Cos (M) +4∑（Cos (W+((E+0.5)FR+2GP-1)×(E+0.5)S),E,0,(N-1)）+2∑（Cos (W+((EFR+2GP-1)ES,E,1,(N-1))）→X ↙V+R÷6×(sin (W)+sin (M) +4∑（sin (W+((E+0.5)FR+2GP-1)×(E+0.5)S),E,0,(N-1)）+2∑（sin (W+((EFR+2GP-1)ES,E,1,(N-1))）→Y↙4子程序名：XY-B（功能：显示正算或反算结果）If O=2:Then↙Cls :＂K×××=＂:＂Z=＂:＂X=＂:＂Y=＂: Locate 6,1, K : Locate 4, 2, T : Locate 4,3, X : Locate 4,4, Y◢If T=0 :Then Cls :＂QF(Z)=＂: Locate 8,1, M:M▼DMS◢IfEnd↙Cls :＂K×××=＂:＂S=＂: Locate 6,1, K : Locate 4, 2, I :＂F=＂:J:J▼DMS◢IfEnd↙If O=3:Then ＂X=＂:＂Y=＂:＂K×××=＂:＂Z=＂: Locate 4,1,C: Locate 4, 2, D : Locate 6,3,K :Locate 4,4,T◢IfEnd:Cls↙5子程序名:4（功能：将交点参数转为线元计算参数）LbI 1: IF Z[48]＜0 :Then -1→Z[62] : Else:1→Z[62]:IfEndLbI 2: If K≥Z[57]:Then Z[57]→A:Z[1]→L:Z[23]→U:Z[24]→V : Z[31]→W : 10^45→P:10^45→Q : 0→G:IfEnd↙LbI 3:If K≥Z[1]:Then Z[1]→A : Z[2]→L : Z[19]→U : Z[20]→V:Z[29]→W : 10^45→P:Z[46]→Q : Z[62]→G: IfEnd↙LbI 4:If K≥Z[2]:Then Z[2]→A : Z[4]→L:Z[25]→U : Z[26]→V:Z[32]→W : Z[46]→P : Z[46]→Q : Z[62]→G: IfEnd↙LbI 5:f K≥Z[4]:Then Z[4]→A : Z[5]→L : Z[27]→U:Z[28]→V : Z[33]→W : Z[46]→P : 10^45→Q : Z[62]→G: IfEnd↙LbI 6:If K≥Z[5]:Then Z[5]→A : Z[5]+1000→L:Z[21]→U : Z[22]→V : Z[30]→W:10^45→P :10^45→Q : 0→G : IfEnd↙6子程序名：JDYS（功能：输入交点要素、显示交点要素及主点坐标）Cls : ＂BP＂?H:H→Z[57]：＂K（JD）＂?K:K→Z[41] :＂X（JD）＂?X :X→Z[42]:＂Y （JD）＂?Y:Y →Z[43]:＂LS1＂?B:B→Z[44] :＂LS2＂?C:C →Z[45]: ?R:R →Z[46]:＂（ZH）FWJ°＂?M:M→Z[47] : ＂α（Z-,Y+）°＂?O:O→Z[48] : Z[47]+Z[48]→Z[49]: Prog ＂1＂:Prog ＂2＂↙Cls :＂T1=＂:＂T2=＂:＂L=＂:＂LY=＂: Locate 4,1, Z[50] : Locate 4,2, Z[51]: Locate 4,3, Z[52] : Locate 4,4, Z[53]◢Cls :＂E=＂: Locate 7,1, Z[54]Cls :＂K（QD）=＂: ＂X=＂: ＂Y=＂: ＂FWJ=＂Locate 7,1,Z[57] :Locate 7,2, Z[23] :Locate 7,3, Z[24] :Locate 7,4, Z[31] ◢Cls :＂K（ZH）=＂: ＂X=＂: ＂Y=＂: ＂FWJ=＂:Locate 7,1,Z[1] : Locate 7,2, Z[19] :Locate 7,3, Z[20] :Locate 7,4, Z[29]◢Cls : ＂K（HY）=＂: ＂X=＂: ＂Y=＂: ＂FWJ=＂: Locate 7,1,Z[2] : Locate 7,2, Z[25] :Locate 7,3, Z[26] :Locate 7,4, Z[32]◢Cls :＂K（QZ）=＂: Locate 7,1,Z[3]◢Cls :＂K（YH）=＂: ＂X=＂: ＂Y=＂: ＂FWJ=＂: Locate 7,1,Z[4] : Locate 7,2, Z[27] :Locate 7,3, Z[28] :Locate 7,4, Z[33]◢Cls :＂K（HZ）=＂: ＂X=＂: ＂Y=＂: ＂FWJ=＂: Locate 7,1,Z[5] : Locate 7,2, Z[21] :Locate 7,3, Z[22] :Locate 7,4, Z[30]◢7子程序名：1（功能：计算交点要素）If Z[48]＜0 :Then -1→Z[55] : Else 1→Z[55] : IfEnd : Z[55]* Z[48]→Z[56] ↙Z[44] 2 ÷24÷Z[46]- Z[44]^(4)÷2688÷Z[46] ^(3) →Z[6] ↙Z[45] 2 ÷24÷Z[46]- Z[45]^(4)÷2688÷Z[46] ^(3) →Z[7] ↙Z[44]÷2-Z[44]^(3)÷240÷Z[46]2 →Z[8] ↙Z[45]÷2-Z[45]^(3)÷240÷Z[46]2 →Z[9] ↙Z[8]+(( Z[46]+Z[7]-( Z[46]+Z[6])cos(Z[56]))÷sin(Z[56]))→Z[50]↙Z[9]+(( Z[46]+Z[6]-( Z[46]+Z[7])cos(Z[56]))÷sin(Z[56]))→Z[51]↙Z[46]* Z[56]π÷180+( Z[44]+ Z[45]) ÷2→Z[52]↙Z[46]* Z[56]π÷180-( Z[44]+ Z[45]) ÷2→Z[53]↙(Z[46]+(Z[6]+Z[7])÷2)÷cos(Z[56]÷2)- Z[46]→Z[54]↙Z[41]-Z[50]→Z[1] ↙↙Z[1]+Z[44]→Z[2] ↙↙Z[2]+Z[53]÷2→Z[3]↙Z[1]+Z[52]-Z[45]→Z[4]↙Z[4]+Z[45]→Z[5]↙8子程序名：2（功能：计算主点坐标及切线方位角）Z[42]-Z[50]cos(Z[47])→Z[19]: (直缓坐标)Z[43]-Z[50]sin(Z[47])→Z[20]↙Z[47]→Z : 360Frac((Z+360)÷360→Z[29] （方位角）Z[42]+Z[51]cos(Z[49])→Z[21]: (缓直坐标)Z[43]+Z[51]sin(Z[49])→Z[22]↙Z[49]→Z: 360Frac((Z+360)÷360→Z[30] （方位角）Z[1]-Z[57]→L↙（H→Z[57]为前直线起点桩号）Z[42]-( Z[50]+L)cos(Z[47])→Z[23]↙(前直线起点坐标)Z[43]-( Z[50]+L)sin(Z[47])→Z[24]↙Z[47]→Z : 360Frac((Z+360)÷360→Z[31]↙（方位角）Z[44]→Z[12]:Z[44]→Z[13]:Prog＂3＂↙Z[4]-Z[1]→L:90(2L-Z[44])÷Z[46]÷π→Z[11]↙Z[46]sin(Z[11])+Z[8]→Z[14]:Z[46](1-cos(Z[11]))+Z[6]→Z[15]↙Z[19]+Z[14]cos(Z[47])-Z[55]Z[15]sin(Z[47])]→Z[27]↙（圆缓点坐标）Z[20]+Z[14]sin(Z[47])+Z[55]Z[15]cos(Z[47])]→Z[28]↙Z[47]+Z[55]Z[11]→Z: 360Frac((Z+360)÷360→Z[33]↙（方位角）Z[2]-Z[1]→L:90(2L-Z[44])÷Z[46]÷π→Z[58]↙Z[46]sin(Z[58])+Z[8]→Z[14]:Z[46](1-cos(Z[58]))+Z[6]→Z[15]↙Z[19]+Z[14]cos(Z[47])-Z[55]Z[15]sin(Z[47])]→Z[25]↙（缓圆点坐标）Z[20]+Z[14]sin(Z[47])+Z[55]Z[15]cos(Z[47])]→Z[26]↙Z[47]+Z[55]Z[58]→Z: 360Frac((Z+360)÷360→Z[32]↙（方位角）9子程序名：3（主点坐标计算辅助程序）If Z[12]=0 :Then 0→Z[14]: 0→Z[15]:Else↙Z[12]- Z[12]^(5)÷40÷(Z[46]*Z[13])2+ Z[12]^(9)÷3456÷(Z[46]*Z[13])^(4) →Z[14]↙Z[12]^(3)÷6÷(Z[46]*Z[13])-Z[12]^(7)÷336÷(Z[46]*Z[13])^(3)+ Z[12]^(11) ÷42240÷(Z[46]*Z[13])^(5)→Z[15] ↙IfEnd↙程序说明：1、进入程序：1.JD ZFS 2. ZHADAO ZFS? 选1为交点法正反算（以后操作均为交点法计算），选2为线元法正反算（以后操作均为线元法计算）2、ZHONG SHU JS 2. JS?选1重输参数，选2直接进入交点法或线元法正反算（参数为已输过的参数）3、参数输入：一、交点法已知数据输入：BP？上一交点ZH桩号K（JD）?交点桩号X（JD）?交点X坐标Y（JD）?交点Y坐标LS1 ?第一缓和曲线长度LS2 ?第二缓和曲线长度R ? 圆曲线半径（ZH）FWJ°?交点前（即前交点至本交点也即ZH点）的正切线方位角α（Z-,Y+）?本交点处线路转角（左转为负，右转为正，度分秒输入）交点法计算要素显示：T1=第一切线长T2=第二切线长L=曲线总长LY=圆曲线长E=曲线外距K(ZH)=直缓点桩号K(HY)=缓圆点桩号K(QZ)=曲中点桩号K(YH)=圆缓点桩号K(HZ)=缓直点桩号二、线元法已知数据输入：K0？KN? R0? RN?F0?X0? Y0?ZX? 分别为线元起点桩号、终点桩号、起点半径、终点半径、起点切线方位角、起点X坐标、起点Y坐标、线元转向。

fx-9750GⅡ操作说明

免责申明：免费提供；仅供参考。

卡西欧(上海)贸易有限公司不对用户使用本程序发生的任何问题负责。

读者对本程序的问题请发电子邮件到775403338@ 邮箱咨询。

fx-9750GⅡ公路测量程序使用说明一、程序使用流程本程序数据和主程序是分开的，编程时将不同的工程数据存放到不同的数据文件里，如A匝道，文件名为A，将匝道A所有的曲线线元参数输入A文件里。

运行时只要运行文件名A的程序就可以了，具体运行流程见下图：二、数据文件的编写（一）交点法数据文件编辑交点法编写数据文件必须是对称型的，即直线段→缓和曲线段→圆曲线段→缓和曲线段→直线段，（如果任意一端没有直线段，则把直线段长度看做是0），另外圆曲线两侧缓和曲线的旋转常数必须相等，并且和直线段连接处的半径必须是无穷大。

交点法数据文件编写一般是根据设计图纸提供的平面曲线参数一览表提供的参数来编写，每个弯道包括：弯道起点方位角（C），交点X坐标（D），交点Y坐标（E），缓和曲线长度（F，当没有设缓和曲线时，F=0），交点转交（G，向左转弯，G为负值，向右转弯，G取正值），交点桩号（H），弯道圆曲线半径（R）。

下图是一段市政道路设计参数数据。

根据上图提供的数据，可以编辑成如下的数据文件：文件名:CHLNR在上图中，有两个条件转移语句即If L>0：Then 98°39°35.12°→C:4774.384→D: 2415.861→E:140→F:31°17°23°→G:410.007→H:600→R:IfEndIf L>1060：Then 129°56°58.19°→C:4206.421→D: 3093.946→E:70→F:-33°50°48°→G:1285.437→H:600→R:IfEnd……如果还有其他弯道，可以继续完后加。

在这些存放设计参数的语句前后的程序表达式是固定的。

道路平曲线概念讲解

道路平曲线概念讲解道路平曲线是什么意思呢？其实可以理解不同坡度的道路之间，用于过渡的曲线，防止坡度突然变化影响车辆的平稳，坡度变化过大且没有平曲线的话车辆容易腾空或者挂碰车辆底盘，造成危险。

所以在道路测量中就离不开道路平曲线这个概念了。

但是很许多刚入门的测量新手对道路平曲线的概念还不是很了解，今天就为大家讲解一下道路平曲线的概念。

首先是道路中线的组成，道路的中线，包括立交匝道的中线，无论多么复杂的线形，都是由直线、圆曲线和缓和曲线三个基本线元组成，如图所示：、直线概念：直线：具有固定的曲率半径，且曲率为0（半径无穷大），可理解为一种特殊的圆曲线。

特点：1）两点之间以直线为最短。

2）笔直的道路给人以短捷、直达的良好印象。

3）汽车在直线上行驶受力简单，方向明确，驾驶操作简易。

4）测设施工方便。

二、缓和曲线概念：缓和曲线:为了使路线的平面线形更加符合汽车的行驶轨迹、离心力逐渐变化，确保行车的安全和舒适，需要在直线和圆曲线之间或半径相差较大的两个同向圆曲线之间设置一段曲率连续变化的曲线，此曲线称为缓和曲线。

目前我国公路设计中，以回旋线作为缓和曲线。

缓和曲线类型：1•完整缓和曲线：判断标准：A2=RxLs2、非完整缓和曲线：判断标准：A2/RxLsA=缓和曲线参数在道路及立交匝道设计中，实际采用的线形往往是直线、圆曲线、缓和曲线中的一种或几种组合而成。

主要有以下几种:(1)基本型曲线是按“直线-回旋曲线-圆曲线-回旋曲线-直线”的顺序组合起来的线型。

基本型中，又可以根据其中两个回旋曲线参数相等与否而分为对称式和不对称式两种。

(2)S 型曲线把两个反向圆曲线用回旋曲线连接起来的线型,GQ 处R=8。

两个反向回旋曲线的参数可以相等，也可以不相等。

-II) 【【ti8 (3)C 型曲线同向曲线的两回旋曲线在曲率为0处径相衔接的形式。

C 型曲线连接处的曲率为0,即GQ 处R=8，相当于两同向曲线中间直线长度为0,对行车和线形都有一定影响，所以C 型曲只有在特殊地形条件下方可使用。

fx9750卡西欧9750公路线元法计算程序

新版程序把线元法和交点法已经集成在一个模块中了，用户只需修改JD程序和ZA程序中的数据部分即可,其余不需作任何的改动。

2.因为每条路高程计算不尽相同，且比较复杂，现在可利用PC机EXCEL计算好打印成表格带到工地上使用，所以本版程序未对线路高程序进行专门的编程计算，而是利用统计计算模式中来输入桩号（第一列X）及左、右高程（第二、三列Y，Freq），这种输入数据的方式最为直观，易发现错误，也易修改，输入完毕后运行S 程序对数据按桩号进行排序，在程序中通过调用GG程序来进行内插计算，SG=-1得左标高，SG=1得右标高（若SG输入0,则可进行一般的线性内插计算）。

3.在JD程序和XY程序中，先将一个计算单元的数据置入矩阵F中（1行8列或1行9列），这样程序可读性极好。

4．相比原CASIO4850程序操作习惯，作了一点小小的改动，测站坐标存在Z[10]，N中，X坐标原存在M中容易被误操作修改，而设计标高存在M中，这样易于修改，因为CASIO5800没有IN，OUT功能，很不方便。

4.程序利用Z[2]变量值来判断是采用交点法还是线元法模型计算，Z[2]＝0为线元法，否则为交点法。

一、PQX程序：计算中边桩坐标及近似的桩号反算，在运行模式直接调用。

① Z*10+→S:”XO”?S:S→Z*10+:”YO”?N:Prog “AU”② Lbl 2:?L:Prog “Z”:Prog “E”:1n→O:90→S③ Lbl 4:”JJ”?S:”YC”?O:SO=0 =>Goto 2‘原来lbl 后没有标号４的。

④ O=-1 =>Goto 6⑤ “X,Y”:R+OCos(Z+S)→X▲U+OSin(Z+S)→Y▲Prog“D”:Goto 4⑥ Lbl 6:Z*7+→X:Z*8+→Y:”XF”?X:”YF”?Y:XY=0 =>Goto 4⑦ X→Z*7+:Y→Z*8+:Pol(X-R,Y-U+1p):Z+S-J→J:”YC,DL,L”:ICos(J)→O▲ISin(J)→I▲L+I▲Goto 6二、P程序：在程序中提供一个自由运算的模式。

计算器中的测量软件----道路之星操作手册 (1)

柃路园柃路园9860计算器与道路之星销售靠的是诚信与服务来经营店铺，店铺诚信服务、服务第一。

在本店铺购买后包教会道路之星安装与使用，并解决购买者任何测量问题，同时赠送各种常用软件及测量文件案例，并对新手及老手测量人员提供测量服务。

柃路园—(服务淘宝第一、价格淘宝最低）购买者请看准测量服务：网店网址：按住Ctrl并点击鼠标“柃路园—(淘宝网址)”以跟踪连接教程网址：按住Ctrl并点击鼠标“（道路之星软件视频讲解_道路之星软件使用教程 - )”以跟踪连接QQ测量服务群：128528455 电话138****4860基于Casio计算器的中文测量计算系统道路之星V1.22操作手册目录第一章概述- 1 - 第二章系统安装- 3 - 第一节电脑端程序- 3 - 第二节计算器与电脑交换数据- 5 - 第三节计算器程序- 7 - 第四节计算器程序基本操作- 11 - 第五节简易操作指南- 14 - 第三章常规计算- 16 - 第四章水准网记录及平差- 20 - 第五章控制测量记录与平差- 26 - 第六章道路测设- 30 - 第一节项目管理- 30 - 第二节道路正反算- 36 - 第三节路基路面控制- 44 - 第四节边坡计算- 49 - 第五节结构物及桥梁计算及检测- 53 - 第六节隧道超欠挖计算- 60 - 第七章计算器数据输入- 68 -道路之星用户手册第一章概述第一章概述一、功能和特点道路之星适用于公路、铁路、城市道路主线、立交匝道、隧道的勘测设计与施工放样工作。

软件分为两个部分：a.电脑端数据处理负责设计输入输出、设计成果的复核、现场采集数据的分析计算以及与计算器进行文件传输；b.计算器端施工现场计算基于Casio fx9750、fx9860、fxCG20计算器设计，负责现场的施工指导和相关数据的采集。

（一）、道路全线测设系统：将道路全线或一个标段所有数据一次性输入，主线、匝道可以存入一个文件，用路线名进行标识，一个项目文件可以包含任意多条路线。

计算器中的测量软件----道路之星操作手册 (1)

柃路园柃路园9860计算器与道路之星销售靠的是诚信与服务来经营店铺，店铺诚信服务、服务第一。

立交匝道计算案例——又一个高速公路立交匝道的计算

立交匝道计算案例-又一个高速公路立交匝道的计算该问题是上个月网友“快乐的我”提出的，我一直未引起重视，今晚一细看，再次对设计单位无语了，真是：没有最“那个”，只有更“那个”。

设计文件图片质量较差，但绝对会很严重地挑战各位的计算能力，网友自己也声称：“叫了好几个哥们帮忙看都说有问题”，我今晚也暂时未能琢磨出来。

看各路高手有何良策？————————————————————————————————————————————————————————————现在是作一个总结的时候了。

分析F匝道，该匝道设计文件的特殊之处在于，没有标注缓和曲线参数A，同时匝道的起、终点的半径有待确定。

设计单位“偷懒”，但同时也为锻炼一线测量员的计算能力提供了又一个很好的实例。

F匝道共四个线元，为表达方便，分别用1~4来指代。

线元1、3、4为缓和曲线，线元2为圆曲线，其中线元1明显为不完整缓和曲线，线元3、4为完整缓和曲线，要顺利进行F匝道的逐桩坐标计算，需要确定的参数是：1．匝道起点的切线方位角；2．匝道起点的半径；3．匝道终点的半径。

幸运的是，这里，设计单位给出了各曲线的交点坐标，因此，很容易地根据线元1的交点（HJD1）坐标与线元1起点坐标，求得线元1起点切线方位角（也是匝道起点切线方位角）为：236°01′46.95″。

类似地，根据线元1的终点坐标与线元1的交点(HJD)坐标，求得线元1的终点切线方位角为：318°08′13.66″。

这样，线元1的起点、终点切线方位角之差即为线元1的转角：82°06′26.71″。

这里设线元1的起点半径为R1，终点半径为R2，线元1的长度为L，这里已知R2=40m，L=107.341m，根据缓和曲线的相关几何特性，可列方程组如下：根据以上方程组，可求解得：A=67.875m，R1=587.962m。

现在只剩下最后一个问题，就是计算线元4终点半径，即匝道终点半径。

开车驾驶时压斑马线的处罚方法

开车驾驶时压斑马线的处罚方法在开车驾驶的过称中我们可能会不小心的压到一些交通标志线，那么对于汽车压到这些交通标志线，我们会被怎么处罚呢?以下是店铺为你整理的开车压斑马线处罚方法，希望能帮到你。

开车压斑马线处罚方法机动车驾驶人在行车时遇到前方路面上有白色菱形预告标识或看到避让行人的警示牌时，应该提前主动降低车速，如果人行横道上有行人正在通过，机动车必须停车让行人先通过。

根据《中华人民共和国道路交通安全法》第四十七条规定，机动车行经人行横道时，应当减速行驶;遇行人正在通过人行横道，应当停车让行。

机动车行经没有交通信号的道路时，遇行人横过道路，应当避让。

对遇行人正在通行人行横道时未停车让行的行为，交警将依法处以罚款100元，记3分的处罚，造成交通事故的，罚款200元，记3分。

开车哪些线不能压1、白色实线白色实线的作用是分隔同向车道，通常施划在交叉路口的交通灯前，不少人开车压线违章被拍，压的基本上就是这种标线。

2、黄色禁止停车实线当单黄实线被施划在道路一侧边上时，其身份便转变为“禁止停车标线”，表示在该路段禁止任何车辆停放。

3、黄色虚实线黄色虚实线通常施划在桥梁前后及允许掉头的路段，也能起到分隔双方向车道的作用，黄色实线一侧禁止车辆越线或压线行驶，虚线一侧准许车辆暂时越线或转弯。

4、单黄实线单黄实线的作用是分隔双向车道，禁止双方向车辆越线或压线行驶，单黄实线一般施划于单方向只有一条车道或一条机动车道和一条非机动车道道路，这类道路路幅本身就窄，如果车辆压过单黄实线，很容易与对向车辆迎头相撞，十分危险，此外，有其他危险需要禁止超车的路段一般也会设置单黄实线。

5、双黄实线双黄实线的作用和单黄实线一样，同样是禁止双方向车辆越线或压线行驶，双黄实线一般施划于单方向有两条或两条以上机动车道，而且没有设置实体中央分隔带的道路上，一般这样的道路路幅较宽，往来车辆较多，如果越线行驶，同样容易撞上迎面而来的车辆。

6、禁停网格线一片让人看得眼花缭乱的黄色网格就是禁停网格线，这种标志标线较少看到，通常施划于易发生因临时停车造成堵塞的交叉路口、重要单位出入口及其他需要设置的路口等，任何车辆在禁停网格线上停车(包括停车等候交通灯)，都属于违章行为。

C匝道线元法坐标计算双心版

C匝道线元法坐标计算（双心版）一、示例图纸
主点坐标表
逐桩坐标表
线位数据图
二、图纸分析
根据主点坐标表和线位数据图分析出下图：
BP—HY为一段缓和曲线，A=70,LS=41.585，由于A²≠LS*R，70²≠41.585*60，所以该段缓和曲线为非完整缓和曲线，起点半径为：
有两个数据值，在用“测量员”或者“轻松测量”时输入哪一个都可以。

此处是双心软件计算不需要考虑。

HY—YH为一段圆曲线，R=60；YH—EP为一段缓和曲线，由于A²=LS*R，90²=135*60，所以该段缓和曲线为完整的，终点半径为无穷大。

三、双心软件输入参数
四、坐标计算结果
五、生成CAD脚本图。

立交匝道中线坐标的线元法计算

在图１中有：
Ｊ
Ｉ一ｄ பைடு நூலகம்ｌ
将式（）入式（）得：２代３，
一
（３）
（）４
“ 直线曲线及转角一览表 ” 其中线坐标的计算不宜，
使用基本型曲线的计算公式，是使用线元法。而
ｌ线元法中线坐标的计算公式
ｆ— ＰＤ＾＋（）２
｛一ｆｉｄ＝ｌｘｄＳ＇ｉ，ｃｏｓｌｆ
ｆ一ｏ，ｚｊｓ１ｃｄｌｆ
（７）
式中：Ｌ—ＤＫＢ —ＤＫＡ为回旋曲线长度； —ＤＫ，ｚ —
（８）
ＤＫ，为任意点距回旋曲线起点的长度。
曲线右偏时，Ａ为正；偏时，ＡＰｐ、左ｐ、Ｂ为负。
１一ｄｚ
设回旋曲线起点在路线坐标系下的坐标为Ａ
维普资讯
１４７
ｖ运ｔｏｓＨｉｈｙ路ｔｍｏｉｅｇ公ｗａｓ＆Ａｕ与ｔ汽ｐｉａｉｎｏＡｐｌｃ
广．￡
．— ＡＩＳｚ：Ｘ＋‘ａｆＸＣ＇Ｏｄ
ｌＹ— ＋Ｉｓａｄ ‘ｉｚｎ
ＬＪ０
㈤
Ｒ” ” Ｒ１：Ｒ— Ｏ＞一０：＝Ａ ≠ Ａ一１Ｒ ÷
Ｔ” ” Ｒ２：Ｔ— Ｏ＞＝Ｂ一０ ≠ Ｂ一１Ｔ： ÷
｛：Ｌ—Ｐ— ＳＰ｝
总第１６期２
Ｈｉｈｙｇｗａｓ＆ＡｕｏｔｖｐｌｃｔｏｓｔｍｏｉｅＡｐｉａｉｎ

fx-5800p全线坐标正反算带高程计算程序(线元法

曲线任意里程中边桩坐标正反算(CASIO fx-5800P计算器)程序一、程序功能及原理1.功能说明：本程序由一个主程序(TYQXJS)和五个子程——正算子程序(SUB-ZS)、反算子程序(SUB-FS)等构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

本修改版程序既可实现正算全线贯通，亦可实现反算全线贯通。

本程序在CASIO fx-5800P计算器运行。

2．计算原理：利用Gauss-Legendre 5点通用公式正算线路中边桩坐标、线外测点至曲线元起点和终点的垂距的符号是否相异（即Dca×Dcb<0=>该测点在其线元内）进行判断并利用该线元要素反算中桩里程、支距，最后计算出放样数据。

二、源程序1.主程序(TYQXJS)Deg:fix 3119→DimZ“INPUT(0) Or DATA(Else)”?ILbl 0:“1.SZ=>XY,2.XY=>SZ，3.TF=>CK,4.SD=>FY，5.TW=>FY”?NIf N=1 Or N=5:Then Goto 1Else If N=2 Or N=3 Or N=4:Then Goto 2Else Goto 3IfEnd:IfEndLbl 1:“K(m)=”?SIf S<0:Then Goto 0:IfEnd“JL(m)=”?ZIf Z≠0:Then “ANGLE→R(Deg)=”?M:IfEndIf I=0:Then Prog “DAT1”:Else Prog “DAT2”:IfEndS-O→W:If W<0:Then Goto 0:Else If W>H:Then Goto 0:IfEnd:IfEndProg “SUB-ZS”:Prog “SUB-GC”If Z<0:Then“XL(m)=”:X◢“YL(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse If Z>0:Then “XR(m)=”:X◢“YR(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse “X(m)=”:X◢“Y(m)=”:Y◢“Hs(m)=”:L◢“FWJ=”: F►DMS◢IfEnd:IfEndGoto 1Lbl 2:“X(m)=”?X:If X<0:Then Goto 0:IfEnd“Y(m)=”?YIf N=3 Or N=4:Then “H(m)=”?→Z[2]:IfEndX→Z[4]:Y→Z[5]:90→MIf I=0:Then Prog “DAT1”G+QEH(C+HD)→F:1→J:U→Z[8J]:V→Z[8J+1]G-M→A:F-M→B:Prog “SUB-ZX1”:Goto BG+M→A:F+M→B:Prog “SUB-ZX1”:Goto B:IfEnd0→J:Lbl A: Isz JZ[8J+3]-M→A:Z[8(J+1)+3]-M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog“DAT1” :Goto B:IfEndZ[8J+3]+M→A:Z[8(J+1)+3]+M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog “DAT1” :Goto B:Else Goto A:IfEndLbl B:Prog“SUB-FS”O+W→S:Prog “SUB-GC”“K(m)=”:S◢“Hs(m)=”:L◢“JL(m)=”:Z◢If N=3:Then Prog “WIDE”:IfEndIf N=4:Then Prog “SDFY”:IfEndGoto 2Lbl 3:“TYQXJS→END”2. 正算子程序(SUB-ZS)0.1184634425→A: 0.2393143352→B:0.2844444444→Z[1]:0.0469100770→K:0.2307653449→L:0.5→Z[3]U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Z[1]cos(G+QEZ[3]W(C+Z[3]WD))+Bcos(G+QE(1 -L)W(C+(1-L)WD))+Acos(G+QE(1-K)W(C+(1-K)WD)))→XV+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Z[1]sin(G+QEZ[3]W(C+Z[3]WD))+Bsin(G+QE(1-L)W(C+(1-L)WD))+Asin(G+QE(1-K)W(C+(1-K)WD)))→YG+QEW(C+WD)+M→FX+Zcos(F)→X:Y+Zsin(F)→YF-M→F:If F<0:Then F+360→F:IfEndReturn3. 反算子程序(SUB-FS)G-M→T:Abs((Y-V)cos(T)-(X-U)sin(T))→W:0→ZLbl C:Prog “SUB-ZS”T+QEW(C+WD)→L:(Z[5]-Y)cos(L)-(Z[4]-X)sin(L)→ZIf Abs（Z）<10-6:Then Goto D:Else W+Z→W：Goto C:IfEndLbl D:0→Z:Prog “SUB-ZS”:(Z[5]-Y)÷cos(F)→Z:Return4．高程计算子程序（SUB-GC）Prog “DAT3”0．5RAbs(0.01(E-D))→TIf E>D:Then 1→C:Else -1→C:IfEndIf S<A:Then -0.01D→W:Else 0.01E→W:IfEndAbs(A-S)→LIf L>T:Then B+WL→L:Else B+WL+C(T-L)2÷2÷R→L:IfEndReturn5. 垂距计算子程序(SUB-ZX1)(Z[5]-Z[8J+1])cos(A)-(Z[4]-Z[8J])sin(A)→Z[6](Z[5]-Z[8(J+1)+1])cos(B)-(Z[4]-Z[8(J+1)])sin(B)→Z[7]Return6.曲线元要素数据库：DAT1(两条线路，可扩充为多条线路)If I=0:Then Goto E: Else If I=2:Then Goto F:IfEnd:IfEndJ=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]：IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd………………………………………………..Goto HLbl F: J=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]：IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd(注：如有多个曲线元要素继续添加入数据库DAT1中)Goto GLbl E:“X0=”?U:“Y0=”?V:“S0=”?O:“F0=”?G:“LS=”?H:“R0=”?P:“RN=”?R:“Q=”?Q Lbl G:1÷P→C:(P-R)÷(2HPR)→D:180÷π→E:Return7．隧道放样子程序：SDFY5.5→A:8.5→B:L+1.5→CIf I=1:Then -1→K:Else 1→K:IfEnd 给左右隧道符号赋值1.25K→F:4.25K→L:7.25K→K 给各圆心距路线的偏距赋值Z[2]-C→D 计算测点至圆心的高差D，If D>A:Then Goto 1:Else If D<0:Then Goto 2:IfEnd:IfEndZ-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E，实测半径W“R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C:E-√(A2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(A2-D2)→L“DL(m)=”:L◢IfEnd:ReturnLbl 1Z-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E，实测半径W“R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C“Dh(m)=”:C◢IfEnd:ReturnLbl 2:Abs(D)→D:Abs(Z)→Z:Abs(K)→K:Abs(F)→FIf Z>K:Then Z-F→E:Else Z+K→E:IfEnd√(D2+E2)→W:W-B→T“R(m)=”:W◢“Rc(m)=”:T◢If E≤B:Then D-√(B2-E2)→C:E-√(B2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(B2-D2)→L“DL(m)=”:L◢显示测点水平偏移量LIfEnd:Return8．曲线元要素判断数据库：DAT2(两条线路，可扩充为多条线路)If I=2:Then Goto A:IfEndIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程：Then 5→J：Prog “DAT1”：Return .................................Else If S<第n线元里程：Then n→J：Prog “DAT1”：ReturnIfEnd:IfEnd:IfEnd:IfEndLbl AIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程：Then 5→J：Prog “DAT1”：Return Else If S<第n线元里程：Then n→J：Prog “DAT1”：ReturnIfEnd:IfEnd:IfEnd:IfEnd .................................9．高程数据库子程序：DAT3（两条线路，可扩充为多条线路）If I=0:Then Goto A:Else If I=2:Then Goto B:IfEnd:IfEndIf S≤46500:Then 46150→A:361.26→B:40000→R:-0.3→D:-1.2→E:ReturnElse If S≤47200:Then 46800→A:353.46→B:20000→R:-1.2→D:1→E:ReturnElse If S≤48400:Then 47500→A:360.46→B:20000→R:1→D:-1.6→E:ReturnElse If S≤49600:Then 48700→A:341.26→B:10000→R:-1.6→D:2.45→E:Return IfEnd:IfEnd:IfEnd:IfEndIf S>49600 And S≤50300:Then 49840→A:369.19→B:100000→R:2.45→D:2.8→E:Return Else If I=2:Then49800→A:368.21→B:150000→R:2.45→D:2.7→E:ReturnIfEnd:IfEndLbl A:“C PEG(m)=”?→A“C H(m)=”?→B“R(m)=”?→R“I1=”?→D“I2=”?→EReturnLbl B49800→A:368.21→B:150000→K:2.45→D:2.7→E:Return10.填方路基宽度检查子程序（WIDE）“WIDTH CHECK”◢“H→MID(m)=”?→A 起坡点与中桩高差常数“DIST→MID(m)=”?→B 起坡点与中桩距离常数“i=”?→C 路基填筑坡度CAbs(Z[2]-L+A)→DAbs(Z)-B-D→E“DL(m)=”:E◢显示实有宽度与应有宽度之差值Return11.坡口坡脚线坐标计算子程序:SUB-TW“TIANWA LINE”◢“DIST→MID(m)=”?A 起坡点与中桩距离常数“H→MID(m)=”?B 起坡点与中桩高差常数“T(1) Or W(Else)=”?C 填方边坡为1，其它为挖方边坡“i=”?E 填方或挖方边坡坡度Abs(Z)-A→D: DE→KIf C=1:Then L-B-K→W:Else L+B+K→W:IfEnd“JS H(m)=”:W◢计算出应有高程“SC H(m)=”？→D 输入实测高程D-W→T“GC(m)=”:T◢显示实测高程与计算高程的差异Return三、使用说明1、规定(1) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。

关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法

关于这点，相关的课本教材上没有明确的讲述，网上对此问题的解释也是散见于不同的论文著作中，对于测量新手来说，线元法程序是非常适用上手的，但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误，的确是件令人恼火的事情，在此我就把自己的判断经验做一论述，给用线元法程序的测友们一同分享，当然高手们请一笑而过，也可留下你的经验与大家一起分享交流学习。

第一：先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题，以免混为一谈.1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类；当对于一个单交点内的两段缓和曲线（即常说的第一缓和曲线和第二缓和曲线而言）又有对称缓和曲线与不对称缓和曲线之分。

由此看来，完整与对称与否是针对缓和曲线两个方面来看待区分的。

2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线，也可以知道缓和曲线上：各个点的半径是不同的，起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从ZH向HY方向；或者是从所接圆曲线半径值向正无穷大过度的，如从YH向HZ 方向。

那么由此可以不难判断出来，完整缓和曲线就是符合上述特征的，那么不完整的缓和曲线就是不符合上述特征的，但是线路上的平曲线设计时候一般缓和曲线不单独存在的，整体上缓和曲线前或后一般都是要连接一个圆曲线的，那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段，一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。

道路平曲线概念讲解

所以在道路测量中就离不开道路平曲线这个概念了。

但是很许多刚入门的测量新手对道路平曲线的概念还不是很了解，今天就为大家讲解一下道路平曲线的概念。

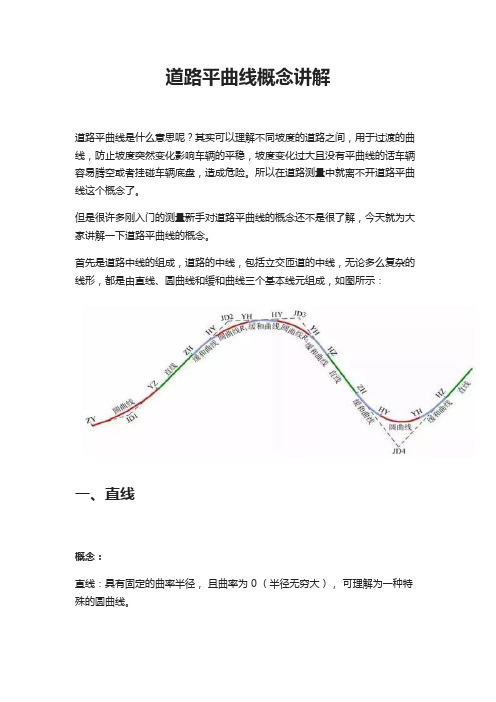
首先是道路中线的组成，道路的中线，包括立交匝道的中线，无论多么复杂的线形，都是由直线、圆曲线和缓和曲线三个基本线元组成，如图所示：一、直线概念：直线：具有固定的曲率半径，且曲率为 0 （半径无穷大），可理解为一种特殊的圆曲线。

特点：1）两点之间以直线为最短。

2）笔直的道路给人以短捷、直达的良好印象。

3）汽车在直线上行驶受力简单，方向明确，驾驶操作简易。

4）测设施工方便。

二、缓和曲线概念：缓和曲线 :为了使路线的平面线形更加符合汽车的行驶轨迹、离心力逐渐变化，确保行车的安全和舒适，需要在直线和圆曲线之间或半径相差较大的两个同向圆曲线之间设置一段曲率连续变化的曲线，此曲线称为缓和曲线。

目前我国公路设计中，以回旋线作为缓和曲线。

缓和曲线类型：1.完整缓和曲线 :判断标准： A²=R x Ls2、非完整缓和曲线：判断标准： A²≠R x LsA= 缓和曲线参数缓和曲线三、圆曲线概念：圆曲线：即圆的一部分（圆弧），具有固定的曲率半径。

特点1、曲线上任一点曲率半径R为常数2、大半径的圆曲线线形美观、顺适、行车舒适，是公路上常采用的线形。

四、道路中常见的线形组合在道路及立交匝道设计中，实际采用的线形往往是直线、圆曲线、缓和曲线中的一种或几种组合而成。

主要有以下几种：(1)基本型曲线是按“直线－回旋曲线－圆曲线－回旋曲线－直线”的顺序组合起来的线型。

基本型中，又可以根据其中两个回旋曲线参数相等与否而分为对称式和不对称式两种。

(2)S 型曲线把两个反向圆曲线用回旋曲线连接起来的线型,GQ处R=∞。

计算器中的测量软件----道路之星操作手册

道路之星V1.22操作手册目录第一章概述- 1 - 第二章系统安装- 3 - 第一节电脑端程序- 3 - 第二节计算器与电脑交换数据- 5 - 第三节计算器程序- 7 - 第四节计算器程序基本操作- 11 - 第五节简易操作指南- 14 - 第三章常规计算- 16 - 第四章水准网记录及平差- 20 - 第五章控制测量记录与平差- 26 - 第六章道路测设- 30 - 第一节项目管理- 30 - 第二节道路正反算- 36 - 第三节路基路面控制- 44 - 第四节边坡计算- 49 - 第五节结构物及桥梁计算及检测- 53 - 第六节隧道超欠挖计算- 60 - 第七章计算器数据输入- 68 -道路之星用户手册第一章概述第一章概述一、功能和特点道路之星适用于公路、铁路、城市道路主线、立交匝道、隧道的勘测设计与施工放样工作。

统一计算中边桩平面坐标及高程，进行一致的查询、放样等计算。

1、支持任意多级断链，支持任意道路断面形式。

2、平面。

支持点法或线元法，都可适用于对称或不对称基本形、S或C形、拱（凸）形、复曲线、卵形线、回头曲线等各种线形。

提供的成果主要有：直曲表、线元一览表、逐桩坐标计算表。

3、纵断面。

可以进行纵断面的设计、计算。

竖曲线计算方式可以选择传统或精确算法。

4、超高加宽。

采用按板块进行超高、加宽的计算。

加宽方式有：线性过渡、三次抛物线、四次抛物线过渡；超高过渡方式：线性过渡、三次抛物线过渡。

5、结构物计算。

匝道程序

匝道计算程序立交匝道中边桩坐标放样正反算程序ramp（0911改进版）一、前言本人编著《casio fx-5800p计算与道路坐标放样计算》中，有关立交匝道坐标放样计算程序有三个：1．p132，立交匝道坐标放样计算程序ramp-1，它的特点是手工输入线元基础数据，可计算该线元范围内的中、边桩坐标和极坐标放样数据，无坐标反算功能；2．p136，道路（立交）坐标反算计算程序ramp-2，它的特点是手工输入线元基础数据，可在该线元范围内根据坐标反算对应中桩及据中桩距离。

3．p147，立交匝道坐标放样计算程序ramp-3，它的特点是采用了数据库子程序保存立交匝道的各线元的基础数据，而不需要手工输入了，运行一次程序可计算一条匝道而不只是一个线元的中、边桩坐标和极坐标放样数据，同样无坐标反算功能。

2009年3月22日，我在qq空间中发布了ramp-3程序的更新版，并取名为ramp-4，该程序的特点是在ramp-3功能的基础上，增加了坐标反算功能，参见链接：/qqblog/595077/1237737328.htm。

今天发布的立交匝道中边桩坐标放样正反算程序ramp（0911版）是我的立交匝道计算的最新成果，具备前面所有版本程序的全部功能。

与ramp-4 程序比较，ramp（0911版）程序的主要改进之处有：1．鉴于卡西欧编程计算器积分函数计算误差的争议（参见日志：/qqblog/595077/1242886367.htm），本程序坐标积分计算改为采用gauss-legendre积分法（四节点）进行计算，计算速度与采用计算器内部积分函数相比，速度无明显区别，但程序代码相对多一些；2．匝道线元数据库子程序改为矩阵变量的形式，使数据组织更加简洁，数据输入更加快捷；3．计算结果显示输出采用了满屏四行输出的形式，一屏可同时显示四个计算结果（或关键数据）；4．可调用数据库子程序，也可手工输入线元基础数据进行计算（参见程序运行框图）；5．考虑到立交匝道各线元基础数据数量大、不易根据设计图表准确确定等特点，特编写了在计算机上运行的“立交匝道参数辅助计算excel程序”，帮助用户准确、快速编写匝道数据库子程序。

(整理)互通式立交匝道中线偏移及其距离的确定.

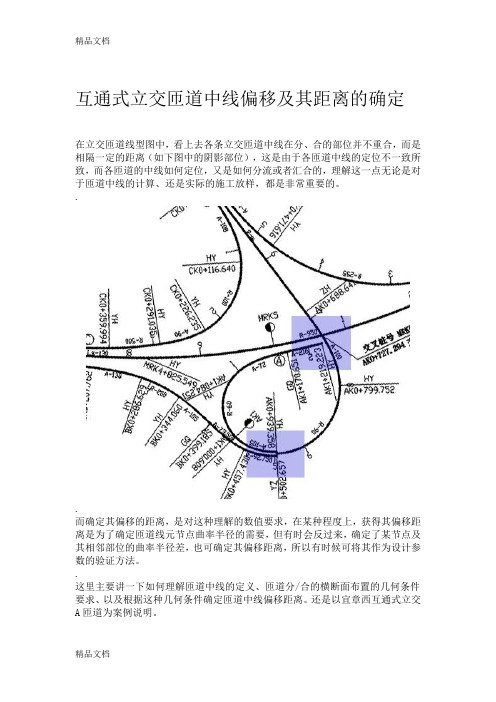
互通式立交匝道中线偏移及其距离的确定在立交匝道线型图中，看上去各条立交匝道中线在分、合的部位并不重合，而是相隔一定的距离（如下图中的阴影部位），这是由于各匝道中线的定位不一致所致，而各匝道的中线如何定位，又是如何分流或者汇合的，理解这一点无论是对于匝道中线的计算、还是实际的施工放样，都是非常重要的。

..而确定其偏移的距离，是对这种理解的数值要求，在某种程度上，获得其偏移距离是为了确定匝道线元节点曲率半径的需要，但有时会反过来，确定了某节点及其相邻部位的曲率半径差，也可确定其偏移距离，所以有时候可将其作为设计参数的验证方法。

.这里主要讲一下如何理解匝道中线的定义、匝道分/合的横断面布置的几何条件要求、以及根据这种几何条件确定匝道中线偏移距离。

还是以宜章西互通式立交A匝道为案例说明。

如下图，A匝道在K0+939.358处由双向车流匝道分为两条单向车流匝道，其中右向偏移的单向匝道继续定义为A匝道，而左向偏移的单向匝道定位为B匝道，偏移后的那一点定义为B匝道的起点。

A匝道在K1+219.223处以一个与高速公路主线转向相同的缓和曲线汇合到高速主线中，而且与主线有一个很明显距离较大的偏移距离。

..确定这个偏移距离首先对线元节点的曲率半径的确定非常重要，因为在立交匝道线形设计时考虑到线形的连续型有个比较重要的原则，我称之为“同心圆”原则，怎么理解呢，我们假想在偏移的地方，偏移前后两点半径之差等于其偏移距离，也就是两点所在的圆弧有一个共同的圆心。

比如，根据图上标注，A匝道偏移前是一个半径为90米的圆曲线，而外侧偏移（A匝道左侧）后，即B匝道的第一个线元是一个半径为92.75米的圆曲线，这时可以认为偏移距离为2.75米，当然这个是否为真，需要进一步验证（经过验证后也确实如此）。

同样，A匝道内侧偏移（A匝道右侧）后，是一个缓曲参数为105米的缓和曲线，同样根据同心圆原则，可假设（这里只能先假设，因为图形上没有明确的标注）这个缓和曲线线元起点的半径为90米减去偏移距离。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

任意里程中边桩坐标正反算(CASIO
fx-4800P计算器)程序
时间:2007-12-18 13:13:15 来源:工测员网作者:未知
1. 加编数据库作为主程序 , 计算中不必逐项输入 " 线元要素 ", 提高运算速度，避免现场忙中出错
2. 将原来的主程序并入数据库
3. 计算直观 , 人性化
4. 正算直接输入里程和边距 , 反算输入近似里程便可
5. 增加了“ 计算点与测站点” 的距离和方位角计算语句，方便直接放样
6. 愿收获与大家共享
7. 核心计算程序摘自“yshf”
1. 正算子程序 (SUB1)
A=0.1739274226 ： B=0.3260725774 ： K=0.0694318442 ： L=0.3300094782 ：F=1-L ：
M=1-K ：
X=U+W(Acos(G+57.2958QKW(1/P+KWD))+Bcos(G+57.2958QLW(1/P+LWD))+Bcos(G+ 57.2958QFW
(1/P+FWD))+Acos(G+57.2958QMW(1/P+MWD))) ：
Y=V+W(Asin(G+57.2958QKW(1/P+KWD))+Bsin(G+
57.2958QLW(1/P+LWD))+Bsin(G+57.2958QFW(1/P+FWD))+Asin(G+57.2958QMW(1/ P+MWD))) ： F=G+57.2958QW(1/P+
WD)+90 ： X=X+ZcosF ： Y=Y+ZsinF
2. 反算子程序 (SUB2)
T=G-90 ： W=Abs((Y-V)cosT-(X-U)sinT) ： Z=0 ： Lbl 0 ： Prog "SUB1" ：L=T+57.2958QW(1/P+
WD) ： Z=(J-Y)cosL-(I-X)sinL ： AbsZ<1E-6=>Goto1 ：≠>W=W+Z ： Goto 0Δ←┘
Lbl 1 ： Z=0 ： Prog "SUB1" ： Z=(J-Y)÷sinF
3、 . 增设数据库程序（ＳＪＫ主程序）
Lb1 4 ： "1.SZ => XY" ： "2.XY => SZ" ：｛ NS ｝：S ∠ 下一线元起点里程＝＞O = 本线元起点里程： U= 本线元起点 X ： V= 本线元起点 Y ： G= 本线元起算方位角： H= 本线元长度： P= 起点曲率半径： R= 终点曲率半径： Q=0 或 1 、 -1 ： Goto0Δ←┘( 第一线元数据要素)
S ∠ 下一线元起点里程＝＞O = 本线元起点里程： U= 本线元起点 X ： V= 本线元起点 Y ： G= 本线元起算方位角： H= 本线元长度： P= 起点曲率半径： R= 终点曲率半径： Q=0 或 1 、 -1 ： Goto0Δ←┘( 第二线元数据要素)
S ∠ 下一线元起点里程＝＞O = 本线元起点里程： U= 本线元起点 X ： V= 本线元起点 Y ： G= 本线元起算方位角： H= 本线元长度： P= 起点曲率半径： R= 终点曲率半径： Q=0 或 1 、 -1 ： Goto0Δ←┘( 第三线元数据要素)。

Goto0Δ←┘( 第 N-1 线元数据要素) 。

Goto0Δ←┘( 第 N 线元数据要素)
LB1 0 ： D=(P-R)÷(2HPR) ： N=1=>Goto 1 ：≠>Goto 2Δ←┘
Lbl 1 ： {Z} ： Z ： W=Abs(S-O) ： Prog "SUB1" ：X"XS"=X ◢ Y"YS"=Y ◢
F"FS"=F-90 ◢
C“XC” ：E“YC” ： I=0 ： J=0 ： Pol （ X-C ， Y-E ）：I“I=” ◢ J ∠ 0 ＝＞J“J=”+360 ◢
≠ ＞J“J=” ◢
ΔGoto4←┘
Lbl 2 ： {XY} ： XY ： I=X ： J=Y ： Prog "SUB2" ： S"S"=O+W ◢
Z"Z "=Z ◢
Goto4
三、使用说明
1 、规定
(1). 把所有相关的” 线元要素“ 依次输入”SJK“
(2). 运算时直接调用“SJK” 运行，程序提示输入里程“S” ？时，正算直接输入待求点里程，反算输入所求点“ 近似“ 里程
(3). 程序中“XC 、 YC 、” 为测站坐标，“ Ｉ＝” 、“ Ｊ＝” 为放样距离和方位角
(4) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1 ；当线元往右偏时， Q=1 ；当线元为直线时， Q=0 。

(5) 当所求点位于中线时， Z=0 ；当位于中线左铡时， Z 取负值；当位于中线中线右
侧时， Z 取正值。

(6) 当线元为直线时，其起点、止点的曲率半径为无穷大，以 10 的 45 次代替。

(7) 当线元为圆曲线时，无论其起点、止点与什么线元相接，其曲率半径均等于圆
弧的半径。

(8) 当线元为完整缓和曲线时，起点与直线相接时，曲率半径为无穷大，以 10 的45
次代替；与圆曲线相接时，曲率半径等于圆曲线的半径。

止点与直线相接时，曲率半
径为无穷大，以 10 的 45 次代替；与圆曲线相接时，曲率半径等于圆曲线的半径。

(9) 当线元为非完整缓和曲线时，起点与直线相接时，曲率半径等于设计规定的值；与圆曲线相接时，曲率半径等于圆曲线的半径。

止点与直线相接时，曲率半径等
于设计规定的值；与圆曲线相接时，曲率半径等于圆曲线的半径。

2 、输入与显示说明
输入部分：
1. SZ => XY
2. XY = > SZ
N ? 选择计算方式，输入 1 表示进行由里程、边距计算坐标；输入 2 表示由坐标反算
里程和边距。

显示部分：
XS=××× 正算时，计算得出的所求点的 X 坐标
YS=××× 正算时，计算得出的所求点的 Y 坐标
FS=××× 正算时，所求点对应的中线点的切线方位角
S=××× 反算时，计算得出的所求点的里程
Z=××× 反算时，计算得出的所求点的边距。

匝道线元法

怎样计算不完整缓和曲线起点及终点的坐标及切线方位角资料

Casio5800交点法与线元法(积木法)匝道坐标正反算放样程序

fx-9750GⅡ操作说明

道路平曲线概念讲解

fx9750卡西欧9750公路线元法计算程序

计算器中的测量软件----道路之星操作手册 (1)

最新Qh2-8线元法任意路线与匝道曲线坐标正、反算程序

计算器中的测量软件----道路之星操作手册 (1)

立交匝道计算案例——又一个高速公路立交匝道的计算

开车驾驶时压斑马线的处罚方法

C匝道线元法坐标计算双心版

立交匝道中线坐标的线元法计算

fx-5800p全线坐标正反算带高程计算程序(线元法

关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法

道路平曲线概念讲解

计算器中的测量软件----道路之星操作手册

匝道程序

(整理)互通式立交匝道中线偏移及其距离的确定.