微商的概念

导函数与原函数的对照表

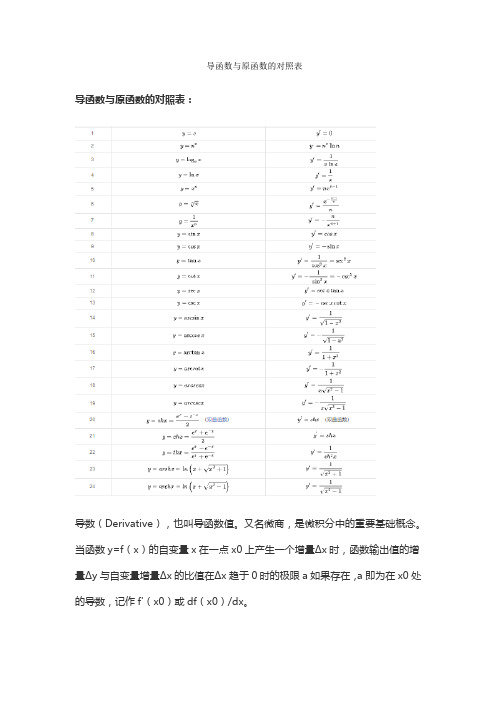
导函数与原函数的对照表
导函数与原函数的对照表：
导数（Derivative），也叫导函数值。

又名微商，是微积分中的重要基础概念。

当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

导数是函数的局部性质。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

导数的求导法则
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。

基本的求导法则如下：
1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合（即①式）。

2、两个函数的乘积的导函数：一导乘二+一乘二导（即②式）。

3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方（即
③式）。

4、如果有复合函数，则用链式法则求导。

导数的定义

x x0
x0
x
二、导数概念
1.导数定义
定义: 设y f (x)在点x0的某邻域内有定义, 若存在极限
y lim
lim
f ( x0 x ) f ( x0 )
x0 x x0
x
则称此函数在x0可导，极限值为函数 f 在点 x0 处
的导数或微商 , 记作
因此，在x =2处函数y =x的导数
f (2) lim y lim f (2 x) f (2) lim x
x0 x x0
x
x0 x
=1
用（2）式.
f (2) lim f (x) f (2)
x2 x 2
x

f
2
( x0
)

lim
x x0

1 2
g(t
2 0
2t0
t
t 2 )
1 2
gt
2 0
t
s(t0 )
s
s(t0 t)

g 2
(2t0
t).
令
t 0 ，得瞬时速度
v(t0 )

lim
t 0
g(t0 2
t)

gt0
2.切线问题割线的极限位置——切线位置
切线
切线可看作曲线上过某定点的一系列割线的极限位置。
f ( x) f ( x0 ) . x x0
lim =1
x2 x 2
练习：求函数 y
f (x)
1在
x
x2
的导数
2.单侧导数
若 lim x x0
f (x) f (x0) x x0

电商与微商的区别

电商与微商的区别电商与微营销是两个概念微商电商：通俗地说，就是做淘宝、天猫、京东，你不能把淘宝店往微信上一搬家就称自己换了行业，由做电商的变成做微营销的了，换个马甲就出来继续混，这两者是截然不同的。

虽然都是网上玩的，但性质却大大不同。

那区别在哪里呢?区别不在地面或网络的售卖形式上，而在人的行为习惯上。

在淘宝天猫，我们的行为惯性就是选购，寻求最大化的边际利益。

而在微信、微博、陌陌上，我们的行为惯性就是社交。

在一个社交惯性的平台上，达成自己的商业目的，这才叫微商。

在一个购物平台上卖东西，这叫电商。

这么定义的话，那我确实看到过做微营销的：一个朋友早几年就在微博上推销商品，轰轰烈烈地干上一场，也确确实实亏了几十万。

微商用电商的思路去做微营销，注定是要一败涂地的。

微信的微店具备了淘宝搬家功能，这是一种误导，让做电商的人误以为按原来的套路搬个家就可以做微营销了。

这也说明走在前端进行平台开发的微信团队，自己也不是特别清楚什么是微营销。

他们是成熟的软件开发者，却是半熟的人性研究者。

感情和生意之间有道鸿沟腾讯叫好不叫座，看着阿里巴巴哗啦哗啦地收银子，也是急得冒汗，所以可劲地往购物上靠，拉京东、搞微店、买大众点评、派，无所不用其极。

可是人的行为惯性是那么难改，人们就爱在微信上聊天扯淡，就是不太喜欢花钱。

微商虽然微信耗去了我们70%的时间，可是在微信上，我们就是“宁说千句话，不舍一文钱”。

手机淘宝不常打开，可打开就购物花钱。

这种感觉我想对于小马哥来说，如同跟一个女子精神恋爱，跟你谈情，却总跟别人上床，如此恋爱得越深，小马哥就越痛苦。

可是换过来讲，小马哥也不用伤心。

瘦马哥(马云)也有精神上的失落，我们天天在淘宝天猫上购物，也没有交到一个朋友不是?他也就是个首富了，穷得就剩钱了。

微商我们的天性里，就是生意归生意，朋友归朋友。

阿里的就是生意，腾讯的就是朋友，做微商难就难在，你要把这两个搞在一块儿就搞混了。

当你发现一个朋友开始向你卖东西时，你就开始归类：这家伙到底是朋友还是商人?在微博上卖东西，完全没有情感牵绊，烦了可以让他“滚粗”;而在微信上，熟人跟你推介东西，你碍于面子总得买一点儿，买多了，感情就淡薄了，这个家伙就从朋友的归类爬进了商人的归类。

微商与微分

函数，和的复合函数对的导数为
或
链式法则的物理意义：
在单位时间由决定的变化率
=（在单位时间内的变化率）*（在单位时间内的变化率）
(6)幂函数在的微商。
，
基本初等函数的微商公式：
(1) ；
(2) ；，，；
(3) ，；
(4) ，；
(5) ；
(6) ；
(7) ；
(8) ；
抽去实际意义，在数学上有共同的数量关系：
函数的增量比自变量的增量当的极限
定义4．1设函数在点附近有定义．对于自变量在点的任一增量，函数在该点的相应改变量为
＝．
若极限＝
存在，则称函数在点可导，并称极限值为在的微商(differential quotient)或导数(derivative)，记为
证明(i)因为
＝
＝，
所以＝＝。
(ii)由于
＝＋
＝＋
注意到可导必连续，则
＝
＝
(iii)由于
＝
＝
＝
同样利用可导必连续得
定理4.2证完。
利用商的微商运算法则，立得
反函数的求导法则
定理4.3若函数在点附近连续且严格单调，又，则其反函数在点＝可导，且
＝
证明由在附近连续且严格单调，则反函数在点附近连续且严格单调．因此，
(9) ；
(10) ；
(11) ；
(12)
其次，我们有微商的运算法则：
(1) ＝；
(2) ＝；四则运算法则
(3) ＝；
(4) ＝反函数求导法则
(5) ＝链式法则
根据这张微商表和微商法则．

微商的概念及其计算

这些公式一般运用后面所讲的方法进行推导. 30
4. 对数函数 y ln x (x 0)
lim y lim ln(x x) ln x
x0 x x0
x 等价无穷小替代
lim
ln 1
x x
lim
x x
1
x0
x
x0 x x
(ln x) 1
x
31
例8
y loga x (a 0, x 0) , 求y .
(3)
u( x) u( x)v( x) u( x)v( x)
v(
x)
v2 ( x)
( v(x) 0)
36
在证明这些公式时, 用到下列表达式：
u u(x x) u(x)
u(x x) u(x) u
37
(1) 证明 (u(x) v(x)) u(x) v(x)
(u(x) v(x)) lim (u(x x) v(x x)) (u(x) v(x))
x0 x x0
x
6
二.导数的概念
1. 导数的定义
定义设函数f (x)在 U(x0) 有定义,且 x0+x U(x0).
如果极限 lim f (x0 x) f (x0 ) lim y a 存在,
x0
x
x0 x
则称函数 f (x) 在点 x0 处可导, 极限值 a 称为 f (x) 在
点 x0 处的导数. 记为 f (x0 ) a， y'|xx0 a,
x)
1 x ln
a
ae
(ln x) 1 x
33
5. 指数函数 y ax (a 0)
lim y lim a xx a x a x lim ax 1

导数的本质是函数

导数的本质是函数导数是函数的局部性质。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。

导数（Derivative），也叫导函数值。

又名微商，是微积分中的重要基础概念。

当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

导数是函数的局部性质。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。

然而，可导的函数一定连续；不连续的函数一定不可导。

对于可导的函数f(x)，x→f'(x)也是一个函数，称作f(x)的导函数（简称导数）。

寻找已知的函数在某点的导数或其导函数的过程称为求导。

实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。

反之，已知导函数也可以反过来求原来的函数，即不定积分。

微积分基本定理说明了求原函数与积分是等价的。

求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

“极限”是数学中的分支——微积分的基础概念，广义的“极限”是指“无限靠近而永远不能到达”的意思。

积分是微积分学与数学分析里的一个核心概念。

通常分为定积分和不定积分两种。

微分是一个变量在某个变化过程中的改变量的线性主要部分。

导数（Derivative），也叫导函数值。

h) h)
u(x) v()
h 0
h
h 0
h
h l i0 m u(xhh) u(x)vv((x x ) h u)v (x()x)v(xhh)v(x)
u(xh)vu(x(x)) uv(u (xx(v))xv2 )((vxxu())(xx )vh()x)
故结论成立.
推论h: v(xCvh )v(xvC)2v ( C为常数 )
( 1 )[ u ( x ) v ( x ) ] u ( x ) v ( x ) ( 2 ) [ u ( x ) v ( x ) ] u ( x ) v ( x ) u ( x ) v ( x ) (3) u v((x x)) u(x)v(x v)2 (x u )(x)v(x) (v(x)0)
例 ,(u 如 v w ) u v w
(2) (uv)uvuv
证: 设 f(x ) u (x )v (x ),则有
f(x)lim f(xh)f(x) liu m (x h )v (x h ) u (x )v (x )
h 0
h
h 0
h
hl im 0u(xhh)u(
x)
v(xh)u(
x)
v(xh)v(x) h
x x 0
x 0
x
右导数若单侧极限limfx0xfx0
x 00
x
存在 ,则称之为 fx在 x0的右导数记为 fx00.
左导数若单侧极限limfx0xfx0
x 00
x
存在 ,则称之为 fx在 x0的左导数记为 fx00.
显然: 函数在一点可导其左右导数都保存并相等.
第二章微积分的基本概念 2-1 微商的概念

8个超经典微商招代理牛逼文案(或许你正需要)

8个超经典微商招代理牛逼文案（或许你正需要)关于微商的概念真正的公式：微商＝微信电商＋微博电商.然而，大多数人提起微商,一般指的就是微信朋友圈的产品销售.由于微信大多数加的是比较亲近的朋友、家人，而这些朋友又在朋友圈大规模地推广毒面膜、假冒产品，拉代理,拉下线，使微商被称为“杀熟营销”。

以下为网上广泛流传的微商经常拿来征集会员的8句经典语录，好与坏，相信大众的眼睛是雪亮的，自有评判。

此处，只是怀着一种取其精华的心态,从心理角度来剖析其中的价值与高明之处，不代表支持或反对大家去做微商的概念。

1.要抱怨你的朋友圈都是微商,那说明你的朋友都很上进，总比都是怨妇强。

跟着苍蝇会找到厕所，跟着蜜蜂会找到花朵,跟着千万赚百万，跟着乞丐会要饭.活鱼逆流而上，死魚随波逐流。

总有一天,你会发现微商能带给你意想不到的收获,或是思想上,或是财富上!如果你现在还在嘲笑别人做微商，5年后你会更后悔！就像当初没有人看好马云一样！点评：这句话，说真的是不错的文案！击中人性的痛点:经常抱怨与讨厌抱怨的矛盾心理、缺乏方向感与寻找上进的心理、嘲笑别人与反而被人嘲笑的矛盾。

在人性的底线上挂了一块肉,让人有欲望，也能够得着，高度恰到好处，的确有迷惑人心的功效.2。

一直不明白，想赚钱又死要面子人的自尊是哪里来的,你一个月就3000多块钱的工资能维护你多少的尊严？我承认，我会刷屏，连孟非、老郭、吴昕都在卖产品，你有什么拉不下脸的？自己挣钱自己花才是最牛的，你能挣钱给别人花你就更NB！最可怕的事就是比你优秀的人还比你努力。

点评：这句话,直击人内心的硬伤.工资低但又害怕被人瞧不起，每个人都会有这种感觉，后面用明星作为例证，犹如，给人重重地一击,进而来抚慰，鼓动群众将自己内心的真正情怀释放出来，匹配产品的功能需求，煽动性的话语，的确是步步为营，最终让大家都能信服，做微商就是真理，至于真的算不上真理，只是在精致的蜜语中，让人忘记了痛感。

3。

不要问我,跟我做代理，能挣多少，当你问这句话的时候,你的思想还停留在给别人打工的阶段,能挣多少，你得问你自己想挣多少，boss都是很有野心的，思想决定行动,行动决定收入,收入决定你生活的品质，你必须调整你的思想，你就是boss，你不是跟我在做，我只是你的仓库，而你是boss…点评:这句话，上升到思想的高度,玩逼格。

浅谈微商的法律地位

E-business电子商务0122017年5月浅谈微商的法律地位大连理工大学史泽众摘要：进入21世纪以来，互联网得到了极大地发展，由此产生了互联网经济，电子商务在互联网经济当中的作用举足轻重，近十几年来也是愈发繁荣，涌现出了一批诸如阿里巴巴、京东一类的电子商务企业，并且在国际上也享有盛誉。

2011年以来，伴随着互联网、电子商务的强势引爆，社会上出现了一种叫“微商”的商业形式，这是一种新鲜的事物，人们对此可能还不太熟悉，而且有时候微商又游离于法律的真空地带，一不小心就会和传销等违法犯罪行为挂上钩，所以在这种情形下，有必要对微商的法律地位进行一下探讨和研究，一方面避免不明真相的“吃瓜群众”误入歧途，另一方面也能够为日后将微商纳入法律监管渠道提供一定的理论支持。

关键词：微商法律地位概念界定法律规制中图分类号：F724.6 文献标识码：A 文章编号：2096-0298(2017)05(a)-012-03近几年来，互联网发展迅速，“提速降费”“互联网+行动计划”等政策出现了重大利好，基于互联网技术而产生的电子商务也是方兴未艾，可以说在电子商务领域，中国已经走在了世界的前列。

那么，这几年来人们也经常听到这么一个词“微商”，那究竟什么是微商，微商和传统的商业主体有什么区别，对于微商目前有没有纳入监管轨道，本文就从这几个方面进行讨论，探究微商的法律地位。

1 微商的概念以前也存在“微商”这么一种说法，但是此微商非彼微商，以前的微商按照一些百科上的解释其实是一种数学上的概念，而这里的微商则是依托互联网技术而产生的一种新型的电子商务营销模式。

微商，英文名叫WeChat Business，从英文名称来看，其中有一个单词“WeChat”，而“WeChat”是微信的英文名称，由此可见，微商肯定和2011年诞生的即时通讯工具微信有关，而事实上也的确如此。

微商的概念最开始是由微盟CEO孙涛勇提出的，指一种社会化移动社交电商模式，是企业或者个人基于社会化媒体开店的新型电商。

第四节微商与微分

y x
反例:
在 x = 0 处连续 , 但不0可导.
xo
x
不可导
点
4. 微商的计算
原料
基本初等函数的微商公式
加工
四则运算复合运算
微商法则
产品
初等函数的微商
基本初等函数的微商公式
（1）常值函数 y c '
c' 0 （2） y xn : 其中 n 是正整数
(xn ) ' nxn1 （3）正弦函数 y sin x 与余弦函数 y cos x
第四章微商与微分
微商概念来自一个连续量随另一个速度量变化的“瞬时”变化率。
§1 微商的概念及其计算
例1 变速直线运动的速度
设描述质点运动位置的函数为
则到的平均速度为
v f (t) f (t0 ) t t0
而在时刻的瞬时速度为
v lim
t t0
f (t) f (t0 ) t t0
特别：
x ' 1 2x
1 x
'
1 x2
总结：
ln x ' 1
x
98页微商公式表和运算法则。要求：熟记
例7 y sin x2 ，求 y '
解： y sin x2 可视为y sin u 和 u x2 的复合，故
y ' sin u ' x2 ' cos u 2x 2x cos x2
例13
设
f
x
x sin
0,
1 x
,
x0 x0
当 x 0 时，函数 f x 是可导的：
f
'x
sin
1 x
1 x

导数的定义及其应用

导数的定义及其应用在数学中，导数是一个十分常见的概念，它的定义和应用范围都非常广泛。

本文将分别从导数的定义和应用这两个方面进行详细探讨。

一、导数的定义导数，又称微商，是数学中一个十分基础的概念。

它表示函数在某一点处的变化速率，具体定义如下：设函数 f(x) 在点 x0 处连续，则函数 f(x) 在点 x0 处的导数f’(x0) 定义为：f’(x0) = lim f(x) - f(x0)x→x0 ----------------x - x0其中，x0 是任意实数，x 与 x0 之间的差值可以趋近于0但不能等于0。

这个定义可以简单解释为：在函数的某一点处，如果微小的变化量 dx 对应的函数变化量为 dy，那么导数f’(x) 就是 dy/dx 的极限值。

二、导数的应用导数具有许多实际应用，下面我们将就导数在各个领域中的应用进行探讨。

1. 极值问题在微积分中，一个函数在某一点的导数可以告诉我们该函数在该点处是否有极值。

换句话说，如果一个函数在某一点处的导数为0，则该点就是函数的一个可能的极值点。

我们可以通过对该函数导数的符号进行分析来确定是极大值或极小值。

2. 斜率问题导数也可以用来描述曲线的斜率。

当我们求出一条曲线在某一点的导数时，这个导数就可以告诉我们该点处该曲线的切线的斜率。

切线的斜率在几何学的角度来讲，就代表了曲线在该点处的斜率。

3. 最速下降线导数还可以用于求解物理问题，如最速下降线。

假设一个物体在空气中落下时受到阻力，那么它将在空气中以一个最快的速度下落。

这个速度可以通过求解物体所受阻力的函数的导数来得到，这个导数的零点就表示物体以最快速度下落时的速度。

4. 泰勒级数最后，导数还可以用于计算函数的泰勒级数。

泰勒级数是一个多项式，它可以代表一个周期性函数，并且可以用无限个次数的导数来确定。

总的来说，导数是微积分中一个重要的概念，它不仅可以用来解决极值问题和斜率问题，还可以用于计算最速下降线和泰勒级数等。

《高等数学》课件2-1微商的概念

02 可导函数的极值点满足一阶导数为零，二阶导数不为零。
03 可导函数的拐点满足一阶导数变号，二阶导数不为零。
导数的计算方法
定义法
通过导数的定义公式计算导数。
链式法则
对于复合函数的导数，使用链式法则进行计算。
乘积法则
对于两个函数的乘积的导数，使用乘积法则进行计算。
幂函数求导法则
对于幂函数的导数，使用幂函数求导法则进行计算。
微积分基本定理的应用非常广泛，它可以用来计算定积分、解决一些微分方程以及证明一些重要的数学定理。
微积分的应用实例
在物理学中，微积分被广泛应用于解决力学、热学、光学等问题，例如计算物体运动的速度和加速度、求解热传导方程等。
在工程学中，微积分是解决各种实际问题的必备工具，例如在电路分析、流体动力学、控制理论等领域中，都需要用到微积分的知识。
在具体运算中，微商的符号表示可以与其他数学符号进行运
算，如乘法、加法等。
微商的符号表示形式简洁明了，能够直观地反映函数在某一
点处的变化趋势。
微商的几何意义
微商在几何上表示曲线在某一点处的切线斜率。
若函数在某一点处可导，则该点处存在切线，切线的斜率即
为函数在该点的微商。
对于不可导的函数，微商无法给出切线斜率的具体值，但在可导区间内，微商可以描述函数在该点附近的局部变化趋势。
04
微商与积分的关系
导数与积分的关系
01
导数是函数在某一点的变化率，而积分则是一种求和运算，两者在概念上存在明显差异。
02
导数和积分在微积分中具有密切的联系，通过微积分基本定理，我们可以将一个函数的积分转化为其导数的积分之和，从而将求
积分的问题转化为求导数的问题。

微商的调研报告

微商的调研报告1. 背景介绍随着互联网和移动互联网的迅速发展，微商成为了一个风口，越来越多的人选择加入微商行业。

微商的兴起带来了无数商机，但也引发了一系列问题。

针对这些问题，市场调研显得尤为重要。

本文将从微商的概念、市场情况、调研结果和对策等方面进行分析和研究。

2. 微商的概念和市场情况2.1 微商的定义微商是指以社交网络平台为主要销售渠道，以个体或小团体为经营主体，以个人信誉为销售支撑的适度规模的电子商务模式。

2.2 微商的市场情况目前，微商市场的规模已经非常庞大，已成为国内的一种新型零售模式。

根据第三方数据显示，我国的微商从业人员超过1000万，微商销售额占全国网上购物市场的比例高达20%以上。

同时，由于微商门槛较低，各类人群都可以参与，市场还有较大的增长空间。

3. 调研结果3.1 微商从业人员的特征调研显示，微商从业人员以女性为主，多数为30岁以下的年轻人。

其中，女性的比例高达70%以上。

此外，微商从业人员大多数为白领和学生，学历高于大专。

3.2 微商营销方式目前，微商营销方式主要分为线上和线下两种。

线上主要通过微信、微博、QQ空间等社交平台进行推广，线下则通过朋友圈、家庭和朋友的圈子进行推荐。

此外，还有一部分微商会通过举行微商会议、派发宣传单等方式进行推广。

3.3 微商销售方式微商销售方式主要分为直销和间接销售两种。

直销就是销售员通过社交平台等渠道直接向客户销售产品，间接销售则是几个销售员组成一个小团队，然后共同销售产品，每个销售员都有自己的客户。

此外，还有一种整合营销方式，即销售员不仅销售产品，还会为客户提供相关服务，如教学视频、培训课程等。

3.4 微商市场的现状调研显示，微商市场竞争激烈，价格战频繁。

微商从业人员的产品品质和服务质量良莠不齐，存在一定的信任危机。

同时，微商也因此受到了一定的监管压力，国家相关法律法规的制定和落实是一项亟待解决的问题。

4. 对策建议4.1 建立行业标准为了保障消费者权益，建立行业标准是十分必要的。

微商的概念

微商的概念Usually，说到微信营销，大家很自然就想到了朋友圈里各种面膜、丰胸产品;说起微信卖货，大家就觉得那简直是将市场搬去了朋友圈一直卖广告。

我们把那些在朋友圈上卖货的人统称“微商”。

但这就是微商了吗?如果对微信营销缺乏一些常识性的了解，一腔热血就扎了进去，结局注定是悲伤的。

所以首先让我们了解微商的定义。

“微商”微商，顾名思义，就是在用微信赚钱，更多人认为是在朋友圈买东西。

做微商，确实是可以赚很多钱的，但是前提是你对微信营销有一定的了解，并且要会应用。

不然的话，你只用热情和梦想去做，那你的微商生意一定是失败的。

Part 1：什么是朋友圈营销?朋友圈营销，其实很大程度上已经和朋友没有关系了。

在现实生活中的朋友其实都不是我们的意向客户，在我们天天刷屏的时候，说不定早就拉黑我们了。

微信营销，如果你认为只有这一种玩法，那你就输了!做营销有两种模式：代理模式和零售模式。

根据我对市场的观察，99%的微商其实都是走代理模式，说白了也就是想办法把货甩给下家，至于另一种模式——实际的零售，其实是没有几个人会去关心的。

其实我们都知道，做微商的目的都是为了赚钱，如何去赚更多的钱才是我们应该关心的。

微信上的生意和传统生意都是一样的，所以，如果你真的想做微信营销的话，你必须要好好考虑一下，是以代理模式还是以零售模式进入微商这个行业。

不同的模式，就要有不同思维，最后需要用不同的方式去行动。

Part 2：微商的模式有两种1、代理模式选择做微商的人，基本上都学到过或多或少微商方面的知识，这样的人，在加入微商的时候，他就不再是一个纯粹的消费者了，更多的是从一个商家的角度去看待问题。

也就是说是否符合代理商的口味，产品的卖点是否适合微信营销的特点是他首先考虑的。

如果你想以代理模式去做微商，那你选择目标产品和运营项目的前提，是你的产品能不能吸引代理商的加盟，那就意味着你不能考虑消费者人群的需求，因为消费者人群不再是你的目标客户。

高三导数的概念知识点总结

高三导数的概念知识点总结导数是高中数学中一个重要的概念，它在微积分中占据着重要的地位。

它不仅在高中阶段的数学学习中起着重要的作用，而且在后续的高等数学中也扮演着关键角色。

本文将对高三导数的概念、性质和计算方法进行总结。

一、导数的概念导数，亦称微商或斜率，是函数在某一点的变化率。

对于函数y=f(x)，它在点x处的导数可以用数学符号表示为f'(x)或dy/dx。

导数可以解释函数的局部性质，即函数在某一点的斜率。

二、导数的几何意义导数的几何意义主要体现在切线与曲线的关系上。

对于函数y=f(x)，如果在点(x，y)处存在导数f'(x)，则此时曲线y=f(x)在该点与切线的斜率相等。

换句话说，导数是切线的斜率。

三、导数的性质1. 对于常数函数y=c，其导数为0，即f'(x)=0。

2. 若函数y=f(x)可导，那么在其导函数f'(x)存在的区间内，函数连续。

3. 若函数y=f(x)可导，则在其定义域内，函数一定是单调的。

4. 若函数y=f(x)在某一点x处可导，那么在该点左右两侧的导数相等。

四、导数的计算法则1. 常数法则：若f(x) = c，其中c为常数，则f'(x) = 0。

2. 基本初等函数法则：a) 若f(x) = x^n，其中n为常数，则f'(x) = nx^(n-1)。

b) 若f(x) = e^x，则f'(x) = e^x。

c) 若f(x) = ln(x)，其中x>0，则f'(x) = 1/x。

d) 若f'(x) = sin(x)，则f'(x) = cos(x)；如果f(x) = cos(x)，则f'(x) = -sin(x)。

3. 和差法则：若f(x) = u(x) ± v(x)，其中u(x)和v(x)是可导函数，则f'(x) = u'(x) ± v'(x)。

微商的概念

微商的概念微商一直以来是一个数学概念，但是随着时间，经济的发展对微商的定义有一个全新的感念，它不但但是一个数学上的感念。

微：微小的意思。

商：自古以来都是对商人，经济的一种解说。

在现实生活中每个人都是一个微小的商人。

微商新的解说符合现代人，更能符合现代社会的发展。

微商的数学含义：微商就是在某函数结点上的导数为函数，其因变量的改变量与自变量的改变量两者相除的商。

由速度问题和切线问题抽象出来的数学概念。

又称变化率。

如一辆汽车在10小时内走了600千米，它的平均速度是60千米/小时，但在实际行驶过程中，是有快慢变化的，不都是60千米/小时。

为了较好地反映汽车在行驶过程中的快慢变化情况，可以缩短时间间隔，设汽车所在位置x与时间t的关系为x=f（t），那么汽车在由时刻t0变到t1这段时间内的平均速度是：[f(t1)-f(t0)] / [t1-t0]，当t1与t0很接近时，汽车行驶的快慢变化就不会很大，平均速度就能较好地反映汽车在t0 到t1这段时间内的运动变化情况，自然就把极限：[f(t1)-f(t0)] / [t1-t0]作为汽车在时刻t0的瞬时速度，这就是通常所说的速度微商的新定义：微商乃一人制企业主。

社会的细胞是由人作为分子组成的，最小的单位是一个人，只要这个人会发生商业信息或产品的交换或交易买卖就可以称作商人，这是区别于其他人的类别的明显标志。

纵观古今，横贯世界，商业经济的发展和繁荣就是由众多的微商企业主不断的发展壮大，同时有更多的微商分子集结形成了大量的市场经济主体，才形成了所谓的商业。

所以微商是商业经济的细胞，由众多的微商组合而成的微商群，即形成了如今的全球商业市场经济。

独木难成林，聚沙成丘就是这个道理。

所以不可忽视微的力量。

[此文档可自行编辑修改，如有侵权请告知删除，感谢您的支持，我们会努力把内容做得更好]最新可编辑word文档。

log2x求导等于多少

log2x求导等于多少1/xln2。

导数,也叫导函数值。

又名微商,是微积分中的重要基础概念。

当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx 趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。

导数与函数的性质单调性(1)如果导数大于零，它将单调增加；如果导数小于零，则单调递减；导数等于零是函数的驻点，不一定是极值点。

需要通过代入入口点左右两边的值来计算导数正负判断的单调性。

(2)如果已知函数是增函数，导数大于等于零；如果已知函数是减函数，导数小于或等于零。

根据微积分基本定理，对于可导的函数，有：如果函数的导函数在某个区间内总是大于零(或小于零)，那么函数在这个区间内单调递增(或单调递减)，也称为函数的单调区间。

函数的导数等于零的点称为函数的驻点，在该点函数可能得到最大值或最小值(即极值可疑点)。

进一步判断需要知道附近导函数的符号。

对于一个满足的点，如果有一个点在前一个区间大于等于零，在后一个区间小于等于零，则为最大值点，否则为最小值点。

x变化时函数（蓝色曲线）的切线变化。

函数的导数值就是切线的斜率，绿色代表其值为正，红色代表其值为负，黑色代表值为零。

凹凸性导函数的凹凸性与其导数的单调性有关。

如果函数的导数在某个区间内单调递增，那么这个区间内的函数是向下凹的，反之亦然。

如果二阶导函数存在，也可以通过它的正负来判断。

如果在某个区间内总是大于零，那么这个区间内的函数是向下凹的，反之这个区间内的函数是向上凸的。

曲线的凹凸分界点称为曲线的拐点。

sinx 平方的导数

sinx 平方的导数
sinx平方的导数是sin2x。

导数（Derivative），也叫导函数值。

又名微商，是微积分中的重要基础概念。

当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a
如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

导数是函数的局部性质。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。

然而，可导的函数一定连续；不连续的函数一定不可导。

对于可导的函数f(x)，x↦f'(x)也是一个函数，称作f(x)的导函数（简
称导数）。

寻找已知的函数在某点的导数或其导函数的过程称为求导。

实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。

反之，已知导函数也可以反过来求原来的函数，即不定积分。

微积分基本定理说明了求原函数与积分是等价的。

求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。