第11章 多重线性回归分析思考与练习参考答案
(完整版)多元线性回归模型习题及答案

多元线性回归模型一、单项选择题1.在由30n =的一组样本估计的、包含3个解释变量的线性回归模型中,计算得多重决定系数为0.8500,则调整后的多重决定系数为( D )A. 0.8603B. 0.8389C. 0.8655D.0.8327 2.下列样本模型中,哪一个模型通常是无效的(B ) A.iC (消费)=500+0.8iI (收入)B. di Q (商品需求)=10+0.8i I (收入)+0.9i P (价格) C. si Q (商品供给)=20+0.75i P (价格)D. iY (产出量)=0.650.6i L (劳动)0.4i K (资本)3.用一组有30个观测值的样本估计模型01122t t t ty b b x b x u =+++后,在0.05的显著性水平上对1b 的显著性作t 检验,则1b 显著地不等于零的条件是其统计量t 大于等于( C )A.)30(05.0t B.)28(025.0t C.)27(025.0t D.)28,1(025.0F4.模型tt t u x b b y ++=ln ln ln 10中,1b 的实际含义是( B )A.x 关于y 的弹性B. y 关于x 的弹性C. x 关于y 的边际倾向D. y 关于x 的边际倾向5、在多元线性回归模型中,若某个解释变量对其余解释变量的判定系数接近于1,则表明模型中存在( C )A.异方差性B.序列相关C.多重共线性D.高拟合优度6.线性回归模型01122......t t t k kt t y b b x b x b x u =+++++ 中,检验0:0(0,1,2,...)t H b i k ==时,所用的统计量服从( C )A.t(n-k+1)B.t(n-k-2)C.t(n-k-1)D.t(n-k+2)7. 调整的判定系数 与多重判定系数之间有如下关系( D )A.2211n R R n k -=-- B. 22111n R R n k -=---C. 2211(1)1n R R n k -=-+-- D. 2211(1)1n R R n k -=----8.关于经济计量模型进行预测出现误差的原因,正确的说法是( C )。
回归思考与练习参考答案

第18章Logistic回归思考与练习参考答案一、最佳选择题1. Logistic回归与多重线性回归比较,( A )。
A.logistic回归的因变量为二分类变量B.多重线性回归的因变量为二分类变量C.logistic回归和多重线性回归的因变量都可为二分类变量D.logistic回归的自变量必须是二分类变量E.多重线性回归的自变量必须是二分类变量2. Logistic回归适用于因变量为( E )。
A.二分类变量B.多分类有序变量C.多分类无序变量D.连续型定量变量E.A、B、C均可3. Logistic回归系数与优势比OR的关系为( E )。
A.0等价于OR>1 B.0等价于OR<1 C.=0等价于OR=1 D.<0等价于OR<1 E.A、C、D均正确4. Logistic回归可用于( E )。
A.影响因素分析B.校正混杂因素C.预测D.仅有A和C E.A、B、C均可5. Logistic回归中自变量如为多分类变量,宜将其按哑变量处理,与其他变量进行变量筛选时可用( D )。
A.软件自动筛选的前进法B.软件自动筛选的后退法C.软件自动筛选的逐步法D.应将几个哑变量作为一个因素,整体进出回归方程E.A、B、C均可二、思考题1. 为研究低龄青少年吸烟的外在因素,研究者采用整群抽样,在某中心城区和远城区的初中学校,各选择初一年级一个班的全部学生进行调查,并用logistic回归方程筛选影响因素。
试问上述问题采用logistic回归是否妥当?答:上述问题采用logistic回归不妥当,因为logistic回归中参数的极大似然估计要求样本结局事件相互独立,而研究的问题中低龄青少年吸烟行为不独立。
2. 分类变量赋值不同对logistic回归有何影响? 分析结果一致吗?答:(1)若因变量交换赋值,两个logistic回归方程的参数估计绝对值相等,符号相反;优势比互为倒数,含义有所区别,实质意义一样;模型拟合检验与回归系数的假设检验结果相同。
【分析】应用回归分析课后习题参考答案全部版何晓群刘文卿

【关键字】分析第一章回归分析概述1.2 返回分析与相关分析的联系与区别是什么?答:联系有返回分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在返回分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在返回分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而返回分析不仅可以揭示变量x对变量y的影响大小,还可以由返回方程进行预测和控制。
1.3 返回模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性返回模型的基本假设是什么?答:线性返回模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip 是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性返回分析思考与练习参考答案2.1 一元线性返回有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)= 2 i=1,2, …,nCov(εi, εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(Xi, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, 2 ) i=1,2, …,n2.3 证明(2.27式),ei =0 ,eiXi=0 。
《应用回归分析》课后题答案要点

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
管理统计学习题参考答案第十一章

十一章1. 解:回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;在线性回归中,按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多元线性回归分析。
相关分析,相关分析是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的相关关系的一种统计方法。
相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。
既可以从描述统计的角度,也可以从推断统计的角度来说明。
所谓相关分析,就是用一个指标来表明现象间相互依存关系的密切程度。
所谓回归分析,就是根据相关关系的具体形态,选择一个合适的数学模型,来近似地表达变量间的平均变化关系。
它们具有共同的研究对象,在具体应用时,相关分析需要依靠回归分析来表明现象数量相关的具体形式,而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。
只有当变量之间存在着高度相关时,进行回归分析寻求其相关的具体形式才有意义。
由于相关分析不能指出变量间相互关系的具体形式,所以回归分析要对具有相关关系的变量之间的数量联系进行测定,从而为估算和预测提供了一个重要的方法。
在有关管理问题的定量分析中,推断统计加具有更加广泛的应用价值。
需要指出的是,相关分析和回归分析只是定量分析的手段。
通过相关与回归分析,虽然可以从数量上反映现象之间的联系形式及其密切程度,但是现象内在联系的判断和因果关系的确定,必须以有关学科的理论为指导,结合专业知识和实际经验进行分析研究,才能正确解决。
因此,在应用时要把定性分析和定量分析结合起来,在定性分析的基础上开展定量分析。
计量经济学(完整版)多元线性回归模型习题及答案

多元线性回归模型一、单项选择题1.在由30n =的一组样本估计的、包含3个解释变量的线性回归模型中,计算得多重决定系数为0.8500,则调整后的多重决定系数为( ) A. 0.8603 B. 0.8389 C. 0.8655 D.0.83272.下列样本模型中,哪一个模型通常是无效的() A. i C (消费)=500+0.8i I (收入) B. d i Q (商品需求)=10+0.8i I (收入)+0.9i P (价格)C. s i Q (商品供给)=20+0.75i P (价格)D. i Y (产出量)=0.650.6i L (劳动)0.4i K (资本)3.用一组有30个观测值的样本估计模型01122t t t t y b b x b x u =+++后,在0.05的显著性水平上对1b 的显著性作t 检验,则1b 显著地不等于零的条件是其统计量t 大于等于( ) A. )30(05.0t B. )28(025.0t C. )27(025.0t D. )28,1(025.0F4.模型t t t u x b b y ++=ln ln ln 10中,1b 的实际含义是( )A.x 关于y 的弹性B. y 关于x 的弹性C. x 关于y 的边际倾向D. y 关于x 的边际倾向 5、在多元线性回归模型中,若某个解释变量对其余解释变量的判定系数接近于1,则表明模型中存在( )A.异方差性B.序列相关C.多重共线性D.高拟合优度6.线性回归模型01122......t t t k kt t y b b x b x b x u =+++++ 中,检验0:0(0,1,2,...)t H b i k ==时,所用的统计量 服从( )A.t(n-k+1)B.t(n-k-2)C.t(n-k-1)D.t(n-k+2)7. 调整的判定系数与多重判定系数 之间有如下关系( ) A.2211n R R n k −=−− B. 22111n R R n k −=−−− C. 2211(1)1n R R n k −=−+−− D. 2211(1)1n R R n k −=−−−− 8.关于经济计量模型进行预测出现误差的原因,正确的说法是( )。
《计量经济学》多媒体课件-多元线性回归模型习题参考解答

《计量经济学》多媒体课件-多元线性回归模型习题参考解答自己整理的《计量经济学》多媒体课件-多元线性回归模型习题参考解答相关文档,希望能对大家有所帮助,谢谢阅读!为了研究我国各地区入境旅游情况,建立了旅游外汇收入(Y,百万美元)、旅行社从业人数(X1,人)、国际游客人数(X2,万人)模型。
利用某年31个省市的横断面数据对结果进行了估计,具体如下:t=(-3.066806)(6.652983)(3.378064)R2=0.934331华氏度=191.1894牛顿=31 (1)从经济意义上考察估计模型的合理性。
(2)在5%显著性水平上,分别检验参数的显著性。
(3)在5%显著性水平下,模型的总体显著性得到检验。
3.2试根据以下数据估算偏回归系数、标准误差、可确定系数和修正可确定系数:经研究发现,家庭书刊的消费受几位户主受教育年限的影响。
该表显示了从某一地区一些家庭的抽样调查中获得的样本数据:家庭书刊年消费支出(元)y家庭月平均收入(元)x户主受教育年限(年)t家庭书刊年消费支出(元)y家庭月平均收入(元)x户主受教育年限(年)t450 1027.2 8 793.2 1998.6 14 507.7 1045.2 9 660.8 2196 10 613。
12 792.7 2105.4 12 563.4 1312.2 9 580.8 2147.4 8 501.5 1316.4 7 612.7 2154 10 781.5 1442.4 15 890.8 2231.4 14 541.8 1641 9 1121 2611.8 18 611.1 1768.8 10 1099(2)利用样本数据估计模型参数;(3)检查户主受教育年限对家庭书刊消费是否有显著影响;(4)分析估算模型的经济意义和作用。
3.4考虑以下“预期-扩大菲利普斯曲线”模型:其中:=实际通货膨胀率(%);=失业率(%);=预期通货膨胀率(%)下表是某国的相关数据。
多元线性回归(习题答案)

第3章练习题参考解答3.1为研究中国各地区入境旅游状况,建立了各省市旅游外汇收入(Y ,百万美元)、旅行社职工人数(X1,人)、国际旅游人数(X2,万人次)的模型,用某年31个省市的截面数据估计结果如下:ii i X X Y 215452.11179.00263.151ˆ++-= t=(-3.066806) (6.652983) (3.378064)(1) 从经济意义上考察估计模型的合理性。
(2) 在5%显著性水平上,分别检验参数21,ββ的显著性。
(3) 在5%显著性水平上,检验模型的整体显著性。
3.1参考解答:由模型估计结果可看出:旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。
平 均说来,旅行社职工人数增加1人,旅游外汇收入将增加0.1179百万美元;国际旅游人数增加1万人次,旅游外汇收入增加1.5452百万美元。
取0.05α=,查表得0.025t (313) 2.048-=因为3个参数t 统计量的绝对值均大于048.2)331(025.0=-t ,说明经t 检验3个参数均显著不为0,即旅行社职工人数和国际旅游人数分别对旅游外汇收入都有显著影响。
取0.05α=,查表得0.05(1,)(2,28) 3.34F k n k F α--==由于34.3)28,2(1894.19905.0=>=F F ,说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响,线性回归方程显著成立。
3.2根据下列数据试估计偏回归系数、标准误差,以及可决系数与修正的可决系数:3.2参考解答:由已知,偏回归系数21221222221212ˆ()i iii ii i iii iy x x y x x xx x x x β-=-∑∑∑∑∑∑∑274778.346280.0004250.9004796.00084855.096280.0004796.000⨯-⨯=⨯- 0.726594= 22111232221212ˆ()i iii ii i iii iy x x y x x xx x x x β-=-∑∑∑∑∑∑∑24250.90084855.09674778.3464796.00084855.096280.0004796.000⨯-⨯=⨯- 2.73628=12132ˆˆˆY X X βββ=-+ 367.6930.726594402.760 2.736288.0=-⨯-⨯ 53.1598=可决系数 213222ˆˆi i i iiy x y x R yββ+=∑∑∑0.72659474778.346 2.736284250.966042.269⨯+⨯=0.998832=修正的可决系数2211(1)n R R n k-=--- 1511(10.998832)153-=--- 0.998637=标准误差 由于 2∑i e =21RSSR TSS=- 即22(1)ieR TSS =-∑(10.998832)66042.269=-⨯ 77.1374= F 统计量2211n k R F k R -=--=1530.9988323110.998832---=5130.986标准误差22ˆie n kσ=-∑77.1374153=-6.4281=所以标准误差ˆ 2.5354σ=3.3参考解答:(1)建立家庭书刊消费的计量经济模型: i i i i u T X Y +++=321βββ其中:Y 为家庭书刊年消费支出、X 为家庭月平均收入、T 为户主受教育年数 (2)估计模型参数,结果为Dependent Variable: Y Method: Least Squares Date: 10/20/13 Time: 18:32 Sample: 1 18Included observations: 18Variable Coefficient Std. Error t-Statistic Prob. C -50.01638 49.46026 -1.011244 0.3279 X 0.086450 0.029363 2.944186 0.0101 T52.370315.202167 10.067020.0000 R-squared0.951235 Mean dependent var 755.1222 Adjusted R-squared 0.944732 S.D. dependent var 258.7206 S.E. of regression60.82273 Akaike info criterion11.20482Sum squared resid 55491.07 Schwarz criterion 11.35321 Log likelihood -97.84334 Hannan-Quinn criter. 11.22528 F-statistic 146.2974 Durbin-Watson stat 2.605783 Prob(F-statistic)0.000000即 ˆ50.01640.086552.3703i i iY X T =-++ (49.46026)(0.02936) (5.20217)t= (-1.011244) (2.944186) (10.06702) R 2=0.951235 944732.02=R F=146.2974(3)检验户主受教育年数对家庭书刊消费是否有显著影响:由估计检验结果, 户主受教育年数参数对应的t 统计量为10.06702, 明显大于t 的临界值131.2)318(025.0=-t ,(户主受教育年数参数所对应的P 值为0.0000,明显小于05.0=α)可判断户主受教育年数对家庭书刊消费支出确实有显著影响;同理可以判断,家庭月平均收入对家庭书刊消费支出的影响也是显著的。
第11章 多重线性回归分析思考与练习参考答案

第11章多重线性回归分析思考与练习参考答案一、最佳选择题1.逐步回归分析中,若增加自变量的个数,则(D)。
A.回归平方和与残差平方和均增大B.回归平方和与残差平方和均减小C.总平方和与回归平方和均增大D.回归平方和增大,残差平方和减小E.总平方和与回归平方和均减小2.下面关于自变量筛选的统计学标准中错误的是(E)。
A.残差平方和(SS残差)缩小B.确定系数(R)增大2C.残差的均方(MS残差)缩小D.调整确定系数(Rad)增大2E.Cp统计量增大3.多重线性回归分析中,能直接反映自变量解释因变量变异百分比的指标为(C)。
A.复相关系数B.简单相关系数C.确定系数D.偏回归系数E.偏相关系数4.多重线性回归分析中的共线性是指(E)。
A.Y关于各个自变量的回归系数相同B.Y关于各个自变量的回归系数与截距都相同C.Y变量与各个自变量的相关系数相同D.Y与自变量间有较高的复相关E.自变量间有较高的相关性5.多重线性回归分析中,若对某一自变量的值加上一个不为零的常数K,则有(D)。
A.截距和该偏回归系数值均不变B.该偏回归系数值为原有偏回归系数值的K 倍C.该偏回归系数值会改变,但无规律D.截距改变,但所有偏回归系数值均不改变E.所有偏回归系数值均不会改变二、思考题1.多重线性回归分析的用途有哪些?答:多重线性回归在生物医学研究中有广泛的应用,归纳起来,可以包括以下几个方面:定量地建立一个反应变量与多个解释变量之间的线性关系,筛选危险因素,通过较易测量的变量估计不易测量的变量,通过解释变量预测反应变量,通过反应变量控制解释变量。
2.多重线性回归模型中偏回归系数的含义是什么?答:偏回归系数的含义是:在控制其他自变量的水平不变的情况下,该自变量每改变一个单位,反应变量平均改变的单位数。
3.请解释用于多重线性回归参数估计的最小二乘法的含义。
答:最小二乘法的含义是:残差的平方和达到最小。
4.如何判断和处理多重共线性?答:如果自变量之间存在较强的相关,则存在多重共线性。
第11章 多重线性回归分析思考与练习参考答案

第11章 多重线性回归分析 思考与练习参考答案一、 最佳选择题1. 逐步回归分析中,若增加自变量的个数,则( D )。
A. 回归平方和与残差平方和均增大B. 回归平方和与残差平方和均减小C. 总平方和与回归平方和均增大D. 回归平方和增大,残差平方和减小E. 总平方和与回归平方和均减小2. 下面关于自变量筛选的统计学标准中错误的是( E )。
A. 残差平方和(残差SS )缩小B. 确定系数(2R )增大C. 残差的均方(残差MS )缩小D. 调整确定系数(2ad R )增大E. p C 统计量增大3. 多重线性回归分析中,能直接反映自变量解释因变量变异百分比的指标为 ( C )。
A. 复相关系数B. 简单相关系数C.确定系数D. 偏回归系数E. 偏相关系数 4. 多重线性回归分析中的共线性是指( E )。
A.Y 关于各个自变量的回归系数相同B.Y 关于各个自变量的回归系数与截距都相同C.Y 变量与各个自变量的相关系数相同D.Y 与自变量间有较高的复相关E. 自变量间有较高的相关性5. 多重线性回归分析中,若对某一自变量的值加上一个不为零的常数K ,则有( D )。
A. 截距和该偏回归系数值均不变B. 该偏回归系数值为原有偏回归系数值的K 倍C. 该偏回归系数值会改变,但无规律D. 截距改变,但所有偏回归系数值均不改变E. 所有偏回归系数值均不会改变二、思考题1. 多重线性回归分析的用途有哪些?答:多重线性回归在生物医学研究中有广泛的应用,归纳起来,可以包括以下几个方面:定量地建立一个反应变量与多个解释变量之间的线性关系,筛选危险因素,通过较易测量的变量估计不易测量的变量,通过解释变量预测反应变量,通过反应变量控制解释变量。
2. 多重线性回归模型中偏回归系数的含义是什么?答:偏回归系数的含义是:在控制其他自变量的水平不变的情况下,该自变量每改变一个单位,反应变量平均改变的单位数。
3. 请解释用于多重线性回归参数估计的最小二乘法的含义。
管理统计学习题参考答案第十一章

一章1. 解:回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;在线性回归中,按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多元线性回归分析。
相关分析,相关分析是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的相关关系的一种统计方法。
相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。
既可以从描述统计的角度,也可以从推断统计的角度来说明。
所谓相关分析,就是用一个指标来表明现象间相互依存关系的密切程度。
所谓回归分析,就是根据相关关系的具体形态,选择一个合适的数学模型,来近似地表达变量间的平均变化关系。
它们具有共同的研究对象,在具体应用时,相关分析需要依靠回归分析来表明现象数量相关的具体形式,而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。
只有当变量之间存在着高度相关时,进行回归分析寻求其相关的具体形式才有意义。
由于相关分析不能指出变量间相互关系的具体形式,所以回归分析要对具有相关关系的变量之间的数量联系进行测定,从而为估算和预测提供了一个重要的方法。
在有关管理问题的定量分析中,推断统计加具有更加广泛的应用价值。
需要指出的是,相关分析和回归分析只是定量分析的手段。
通过相关与回归分析,虽然可以从数量上反映现象之间的联系形式及其密切程度,但是现象内在联系的判断和因果关系的确定,必须以有关学科的理论为指导,结合专业知识和实际经验进行分析研究,才能正确解决。
因此,在应用时要把定性分析和定量分析结合起来,在定性分析的基础上开展定量分析。
多元线性回归模型习题及答案

多元线性回归模型一、单项选择题1.在由30n =的一组样本估计的、包含3个解释变量的线性回归模型中,计算得多重决定系数为0.8500,则调整后的多重决定系数为( D )2.下列样本模型中,哪一个模型通常是无效的(B )A. i C (消费)=500+0.8i I (收入)B. d i Q (商品需求)=10+0.8i I (收入)+0.9i P (价格)C. s i Q (商品供给)=20+0.75i P (价格)D. i Y (产出量)=0.650.6i L (劳动)0.4i K (资本)3.用一组有30个观测值的样本估计模型01122t t t t y b b x b x u =+++后,在0.05的显著性水平上对1b 的显著性作t 检验,则1b 显著地不等于零的条件是其统计量t 大于等于( C )A. )30(05.0tB. )28(025.0tC. )27(025.0tD. )28,1(025.0F4.模型t t t u x b b y ++=ln ln ln 10中,1b 的实际含义是( B )A.x 关于y 的弹性B. y 关于x 的弹性C. x 关于y 的边际倾向D. y 关于x 的边际倾向5、在多元线性回归模型中,若某个解释变量对其余解释变量的判定系数接近于1,则表明模型中存在( C )A.异方差性B.序列相关C.多重共线性D.高拟合优度6.线性回归模型01122......t t t k kt t y b b x b x b x u =+++++ 中,检验0:0(0,1,2,...)t H b i k ==时,所用的统计量 服从( C )A.t(n-k+1)B.t(n-k-2)C.t(n-k-1)D.t(n-k+2)7. 调整的判定系数与多重判定系数 之间有如下关系( D ) A.2211n R R n k -=-- B. 22111n R R n k -=--- C. 2211(1)1n R R n k -=-+-- D. 2211(1)1n R R n k -=---- 8.关于经济计量模型进行预测出现误差的原因,正确的说法是( C )。
《应用回归分析》课后题答案[整理版]
![《应用回归分析》课后题答案[整理版]](https://img.taocdn.com/s3/m/603529c1f242336c1eb95eca.png)
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
统计学第十一章课后习题答案

11。
1(1)绘制产量与生产费用的散点图,判断二者之间的关系形态。
散点图如下:从上图,可以看出产量与生产费用的关系为正的线性相关关系。
(2)计算产量与生产费用之间的线性相关系数.r=0.920232(3)对相关系数的显著性进行检验(a=0。
05),并说明二者之间的关系系数。
假设:H o :ρ=0,H 1:ρ≠0 计算检验的统计量:t=|r|√n−21−r²=|0。
92—232|√12−21−0.920232²=7.435当a=0。
05时,t 0.052⁄(12-2)=2.228。
由于检验统计量t=7。
435>t a 2⁄=2.228,拒绝原假设。
表明产量与生产费用之间的线性关系显著.11.2(1)散点图如下:(2)r=0.8621,正相关11。
3(1)0ˆβ=10表示当X=0时Y 的期望值为10 (2)1ˆβ=—0.5表示X 每增加1个单位,Y 平均下降0.5个单位。
(3)X=6时,E (Y )=10—0。
5x6=711.4.(1)%90436362=+=+==SSE SSR SSR SST SSR R ,%902=R 表示,在因变量y 取值的变差中,有90%可以由x 与y 之间的线性关系来解释. (2)5.021842n =--=SSE S e 。
5.0=e S 表示,当用x 来预测y 时,平均的预测误差为0.5。
11.5(1)散点图如下:(2)r=0。
9489,因为r>0.8,所以运送时间与运送距离有较强的正线性关系。
(3)利用最小二乘法求出估计的回归方程,并解释回归系数的实际意义。
得到的回归方程为x 003585.0118129.0y ˆ+=,回归系数003585.0ˆ=β表示运送距离每增加1公里,运送时间平均增加0.003585天.11.6(1)散点图如下:从上图可知,人均gdp 和人均消费水平为正相关关系(2)r=0.998128,具有非常强的正线性关系。
第11章多重线性回归分析案例辨析及参考答案
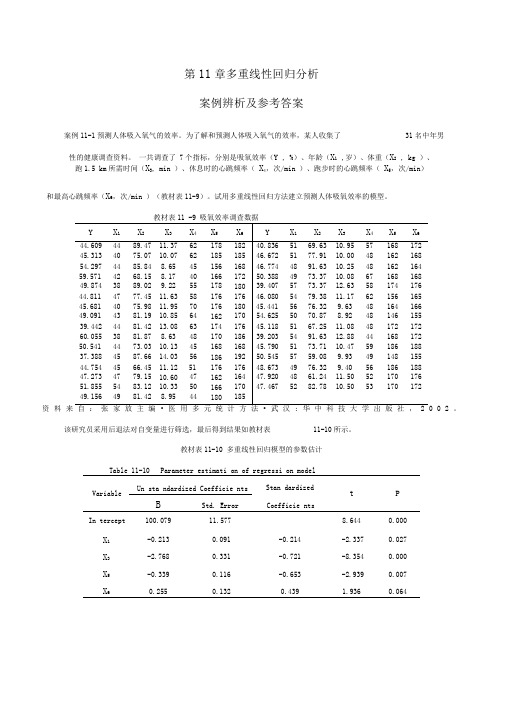
第11章多重线性回归分析案例辨析及参考答案案例11-1预测人体吸入氧气的效率。
为了解和预测人体吸入氧气的效率,某人收集了31名中年男性的健康调查资料。
一共调查了 7个指标,分别是吸氧效率(Y , %)、年龄(X1,岁)、体重(X2, kg )、跑1.5 km所需时间(X3, min )、休息时的心跳频率(X4,次/min )、跑步时的心跳频率(X5,次/min)和最高心跳频率(X6,次/min )(教材表11-9)。
试用多重线性回归方法建立预测人体吸氧效率的模型。
教材表11 -9 吸氧效率调查数据Y X1 X2X3 X4 X5 X6 Y X1 X2X3 X4 X5 X644.609 44 89.47 11.37 62 178 182 40.836 51 69.63 10.95 57 168 17245.313 40 75.07 10.07 62 185 185 46.672 51 77.91 10.00 48 162 16854.297 44 85.84 8.65 45 156 168 46.774 48 91.63 10.25 48 162 16459.571 42 68.15 8.17 40 166 172 50.388 49 73.37 10.08 67 168 16849.874 38 89.02 9.22 55 178 180 39.407 57 73.37 12.63 58 174 17644.811 47 77.45 11.63 58 176 176 46.080 54 79.38 11.17 62 156 16545.681 40 75.98 11.95 70 176 180 45.441 56 76.32 9.63 48 164 16649.091 43 81.19 10.85 64 162 170 54.625 50 70.87 8.92 48 146 15539.442 44 81.42 13.08 63 174 176 45.118 51 67.25 11.08 48 172 17260.055 38 81.87 8.63 48 170 186 39.203 54 91.63 12.88 44 168 17250.541 44 73.03 10.13 45 168 168 45.790 51 73.71 10.47 59 186 18837.388 45 87.66 14.03 56 186 192 50.545 57 59.08 9.93 49 148 15544.754 45 66.45 11.12 51 176 176 48.673 49 76.32 9.40 56 186 18847.273 47 79.15 10.60 47 162 164 47.920 48 61.24 11.50 52 170 17651.855 54 83.12 10.33 50 166 170 47.467 52 82.78 10.50 53 170 17249.156 49 81.42 8.95 44 180 185资料来自:张家放主编•医用多元统计方法•武汉:华中科技大学出版社,2002。
回归分析练习题及参考答案
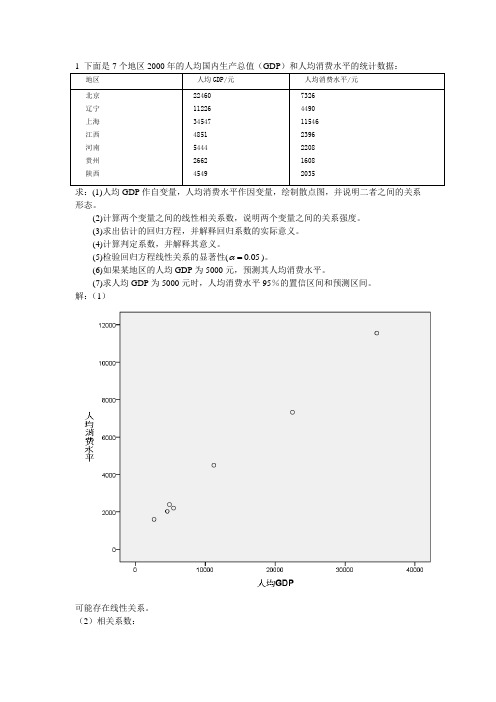
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
多重共线性习题及答案

多重共线性一、单项选择题1、当模型存在严重的多重共线性时,OLS估计量将不具备()A、线性B、无偏性C、有效性D、一致性2、经验认为某个解释与其他解释变量间多重共线性严重的情况是这个解释变量的VIF()A、大于B、小于C、大于5D、小于53、模型中引入实际上与解释变量有关的变量,会导致参数的OLS估计量方差()A、增大B、减小C、有偏D、非有效4、对于模型y t=b0+b1x1t+b2x2t+u t,与r12=0相比,r12=0.5时,估计量的方差将是原来的()A、1倍B、1.33倍C、1.8倍D、2倍5、如果方差膨胀因子VIF=10,则什么问题是严重的()A、异方差问题B、序列相关问题C、多重共线性问题D、解释变量与随机项的相关性6、在多元线性回归模型中,若某个解释变量对其余解释变量的判定系数接近于1,则表明模型中存在( )A 异方差B 序列相关C 多重共线性D 高拟合优度7、存在严重的多重共线性时,参数估计的标准差()A、变大B、变小C、无法估计D、无穷大8、完全多重共线性时,下列判断不正确的是()A、参数无法估计B、只能估计参数的线性组合C、模型的拟合程度不能判断D、可以计算模型的拟合程度二、多项选择题1、下列哪些回归分析中很可能出现多重共线性问题()A、资本投入与劳动投入两个变量同时作为生产函数的解释变量B、消费作被解释变量,收入作解释变量的消费函数C、本期收入和前期收入同时作为消费的解释变量的消费函数D、商品价格、地区、消费风俗同时作为解释变量的需求函数E、每亩施肥量、每亩施肥量的平方同时作为小麦亩产的解释变量的模型2、当模型中解释变量间存在高度的多重共线性时()A、各个解释变量对被解释变量的影响将难以精确鉴别B、部分解释变量与随机误差项之间将高度相关C、估计量的精度将大幅度下降D、估计对于样本容量的变动将十分敏感E、模型的随机误差项也将序列相关3、下述统计量可以用来检验多重共线性的严重性()A、相关系数B、DW值C、方差膨胀因子D、特征值E、自相关系数4、多重共线性产生的原因主要有()A、经济变量之间往往存在同方向的变化趋势B、经济变量之间往往存在着密切的关联C、在模型中采用滞后变量也容易产生多重共线性D、在建模过程中由于解释变量选择不当,引起了变量之间的多重共线性E、以上都正确5、多重共线性的解决方法主要有()A、保留重要的解释变量,去掉次要的或替代的解释变量B、利用先验信息改变参数的约束形式C、变换模型的形式D、综合使用时序数据与截面数据E、逐步回归法以及增加样本容量6、关于多重共线性,判断错误的有()A、解释变量两两不相关,则不存在多重共线性B、所有的t检验都不显著,则说明模型总体是不显著的C、有多重共线性的计量经济模型没有应用的意义D、存在严重的多重共线性的模型不能用于结构分析7、模型存在完全多重共线性时,下列判断正确的是()A、参数无法估计B、只能估计参数的线性组合C、模型的判定系数为0D、模型的判定系数为1三、简述1、什么是多重共线性?产生多重共线性的原因是什么?2、什么是完全多重共线性?什么是不完全多重共线性?3、完全多重共线性对OLS估计量的影响有哪些?4、不完全多重共线性对OLS估计量的影响有哪些?5、从哪些症状中可以判断可能存在多重共线性?6、什么是方差膨胀因子检验法?四、判断(1)如果简单相关系数检测法证明多元回归模型的解释变量两两不相关,则可以判断解释变量间不存在多重共线性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章 多重线性回归分析 思考与练习参考答案
一、 最佳选择题
1. 逐步回归分析中,若增加自变量的个数,则( D )。
A. 回归平方和与残差平方和均增大
B. 回归平方和与残差平方和均减小
C. 总平方和与回归平方和均增大
D. 回归平方和增大,残差平方和减小
E. 总平方和与回归平方和均减小
2. 下面关于自变量筛选的统计学标准中错误的是( E )。
A. 残差平方和(残差SS )缩小
B. 确定系数(2
R )增大
C. 残差的均方(残差MS )缩小
D. 调整确定系数(2
ad R )增大
E. p C 统计量增大
3. 多重线性回归分析中,能直接反映自变量解释因变量变异百分比的指标为 ( C )。
A. 复相关系数
B. 简单相关系数
C.确定系数
D. 偏回归系数
E. 偏相关系数 4. 多重线性回归分析中的共线性是指( E )。
A.Y 关于各个自变量的回归系数相同
B.Y 关于各个自变量的回归系数与截距都相同
C.Y 变量与各个自变量的相关系数相同
D.Y 与自变量间有较高的复相关
E. 自变量间有较高的相关性
5. 多重线性回归分析中,若对某一自变量的值加上一个不为零的常数K ,则有( D )。
A. 截距和该偏回归系数值均不变
B. 该偏回归系数值为原有偏回归系数值的K 倍
C. 该偏回归系数值会改变,但无规律
D. 截距改变,但所有偏回归系数值均不改变
E. 所有偏回归系数值均不会改变
二、思考题
1. 多重线性回归分析的用途有哪些?
答:多重线性回归在生物医学研究中有广泛的应用,归纳起来,可以包括以下几个方面:定量地建立一个反应变量与多个解释变量之间的线性关系,筛选危险因素,通过较易测量的变量估计不易测量的变量,通过解释变量预测反应变量,通过反应变量控制解释变量。
2. 多重线性回归模型中偏回归系数的含义是什么?
答:偏回归系数的含义是:在控制其他自变量的水平不变的情况下,该自变量每改变一个单位,反应变量平均改变的单位数。
3. 请解释用于多重线性回归参数估计的最小二乘法的含义。
答:最小二乘法的含义是:残差的平方和达到最小。
4. 如何判断和处理多重共线性?
答:如果自变量之间存在较强的相关,则存在多重共线性。
可以通过分析自变量之间的相关系数、计算方差膨胀因子和容忍度等指标判断是否存在多重共线性。
如果自变量间存在多重共线性,最简单的处理办法是删除变量,即在相关性较强的变量中删除测量误差大的、缺失数据多的、从专业上看意义不是很重要的或者在其他方面不太满意的变量。
其次,也可采用主成分回归方法。
5. 如何判断、分析自变量间的交互作用?
答:基于专业背景知识,构造可能的交互作用项,并检验交互作用项是否有统计学意义。
6. 多重线性回归模型的基本假定有哪些?如何判断资料是否满足这些假定?如果资料不满足假定条件,常用的处理方法有哪些?
答:多重线性回归的前提条件是线性、独立性、正态性和等方差性,可以借助残差分析等方法判断资料是否满足条件。
如果资料不满足前提条件,可以采用变量变换和非线性回归等方法处理。
三、计算题
为确定老年妇女进行体育锻炼还是增加营养会减缓骨骼损伤,一名研究者用光子吸收法测量了骨骼中无机物含量,对三根骨头主侧和非主侧记录了测量值,结果见教材表11-20。
分别用两种桡骨测量结果作为反应变量对其他骨骼测量结果作多重线性回归分析,提出并拟合适当的回归模型,分析残差。
解:答案提示,需要对自变量进行筛选,而且要考虑是否存在多重共线性,如果存在,应进行适当的处理。
教材表11-20 骨骼中无机物的含量
受试者编号主侧桡骨桡骨主侧肱骨肱骨主侧尺骨尺骨
1 1.103 1.05
2 2.139 2.238 0.87
3 0.872
2 0.842 0.859 1.87
3 1.741 0.590 0.744
3 0.925 0.873 1.887 1.809 0.767 0.713
4 0.857 0.744 1.739 1.547 0.706 0.674
5 0.795 0.809 1.734 1.715 0.549 0.654
6 0.78
7 0.779 1.509 1.474 0.782 0.571
7 0.933 0.880 1.695 1.656 0.737 0.803
8 0.799 0.851 1.740 1.777 0.618 0.682
9 0.945 0.876 1.811 1.759 0.853 0.777
10 0.921 0.906 1.954 2.009 0.823 0.765
11 0.792 0.825 1.624 1.657 0.686 0.668
12 0.815 0.751 2.204 1.846 0.678 0.546
13 0.755 0.724 1.508 1.458 0.662 0.595
14 0.880 0.866 1.786 1.811 0.810 0.819
15 0.900 0.838 1.902 1.606 0.723 0.677
16 0.764 0.757 1.743 1.794 0.586 0.541
17 0.733 0.748 1.863 1.869 0.672 0.752
18 0.932 0.898 2.028 2.032 0.836 0.805
19 0.856 0.786 1.390 1.324 0.578 0.610
20 0.890 0.950 2.187 2.087 0.758 0.718
21 0.688 0.532 1.650 1.378 0.533 0.482
22 0.940 0.850 2.334 2.225 0.757 0.731
23 0.493 0.616 1.037 1.268 0.546 0.615
24 0.835 0.752 1.509 1.422 0.618 0.664
25 0.915 0.936 1.971 1.869 0.869 0.868
资料来源:《实用多元统计分析》(第4版),Richard A. Johnson & Dean W. Wichern,陆璇译,清华大学出版社。
(郝元涛张岩波)。
