北师大统计学基础习题答案5
《统计学基础》第三版习题答案

各位老师读者好:《统计学基础》(王瑞卿主编,北京大学出版社,2016年8月第3版)每个项目后面设置了技能训练题库,由于统计学教材很多,不同的老师在编写时内容描述会有些许差异,所以有些习题答案可能有差异,答案以本教材为准。
祝各位工作、学习顺利。
真诚欢迎各位提出您的宝贵意见!王瑞卿2016年9月12日项目1 统计概论一、填空题1.现代统计的含义包括三个方面: 、 和 。
2.一个完整的统计工作过程可以划分为 、 、 、 四个阶段。
3.总体是由许多具有 的个别事物组成的整体;总体单位是 的组成单位。
4.标志是说明总体单位的特征的名称,按表现形式不同分为 和 两种。
5.统计指标按其所说明的总体现象内容的不同,可分为 和 。
参考答案1.统计工作统计资料统计学2. 统计设计统计调查统计整理统计分析3.共同属性总体4.数量标志品质标志5.数量指标质量指标二、单项选择题1.统计总体的同质性是指(B )。
A.总体各单位具有某一共同的品质标志或数量标志B.总体各单位具有某一共同的品质标志属性或数量标志值C.总体各单位具有若干互不相同的品质标志或数量标志D.总体各单位具有若干互不相同的品质标志属性或数量标志值2.某地区有800家工业企业,要研究这些企业的产品生产情况,总体是( A ),总体单位是( B )。
A.全部工业企业B.每一家工业企业C.每一件产品D.800家工业企业的全部工业产品3.要了解某班50名学生的学习情况,则总体是( A ),总体单位是( C )。
A.50名学生B.50个学生的学习成绩C.每一个学生D.每一个学生的学习成绩4.一个统计总体( B )。
A.只能有一个标志B.可以有多个标志C.只能有一个指标D.可以有多个指标5.张明的月工资为4560元,工资是( B ),4550是( C )。
A.品质标志B.数量标志C.变量值D.指标6.在调查设计时,学校作为总体,每个班作为总体单位,各班学生人数是( A )。
统计学 第五章习题 正确答案

第五章 概论与概率分布重点知识1.样本、样本空间、随机事件的定义;2.事件的运算:交、并、对立事件、互斥事件;3.概论的定义:古典定义、统计定义、经验定义;4.概率的计算:加法公式,乘法公式,条件概率,事件的独立性,全概率公式,贝叶斯公式; 5.随机变量的定义,有几种类型;6.离散型随机变量及其分布的定义与性质,数学期望与方差:重点了解二项分布及其简单性质; 7.连续型随机变量及其分布的定义与性质,数学期望与方差:重点了解正态分布及其简单性质,会根据标准正态分布计算任何正态分布随机变量的概率;复习题一、填空1.用古典法求算概率.在应用上有两个缺点:①它只适用于有限样本点的情况;②它假设 。
2.若事件A 和事件B 不能同时发生,则称A 和B 是 事件。
3.在一副扑克牌中单独抽取一次,抽到一张红桃或爱司的概率是 ;在一副扑克牌中单独抽取一次,抽到一张红桃且爱司的概率是 。
4.甲、乙各射击一次,设事件A 表示甲击中目标,事件B 表示乙击中目标,则甲、乙两人中恰好有一人不击中目标可用事件 表示.5.已知甲、乙两个盒子里各装有2个新球与4个旧球,先从甲盒中任取1个球放入乙盒,再从乙盒中任取1个球,设事件A 表示从甲盒中取出新球放入乙盒,事件B 表示从乙盒中取出新球,则条件概率P(B A )=__.6.设A,B 为两个事件,若概率P (A )=41,P(B)=32,P(AB)=61,则概率P(A+B)=__.7.设A,B 为两个事件,且已知概率P(A)=0.4,P(B)=0.3,若事件A,B 互斥,则概率P(A+B)=__. 8.设A,B 为两个事件,且已知概率P(A)=0.8,P(B)=0.4,若事件A ⊃B ,则条件概率P(B A )=__. 9.设A,B 为两个事件,若概率P(B)=103,P(B A )=61,P(A+B)=54,则概率P(A)=__.10.设A,B 为两个事件,且已知概率P(A )=0.7,P(B)=0.6,若事件A,B 相互独立,则概率P(AB)=__. 11.设A,B 为两个事件,且已知概率P(A)=0.4,P(B)=0.3,若事件A,B 相互独立,则概率P(A+B)=__. 12.设A,B 为两个事件,若概率P(B)=0.84,P(A B)=0.21,则概率P(AB)=__. 13.设离散型随机变量X 的概率分布如下表ccccPX 4322101-则常数c =__.14.已知离散型随机变量X 的概率分布如下表414121P321X则概率P {3<X }=__.15.已知离散型随机变量X 的概率分布如下表6632P213-X11则数学期望)(X E =__.16.设离散型随机变量X 服从参数为p 的两点分布,若离散型随机变量X 取1的概率p 为它取0的概率q 的3倍,则方差)(X D =__.17.设连续型随机变量的概率X 密度为⎪⎩⎪⎨⎧<<-=其他,0210,1)(2x x k x ϕ 则常数k =__.18.设连续型随机变量X 的概率密度为⎩⎨⎧≤≤=其他,00,24)(2rx x x ϕ 则常数r =__.19.已知连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧≥=-其他,00,2)(2x xex xϕ 则概率}11{<<-X P =__.20.已知连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧≤≤=其他,021,2)(2x x x ϕ 则数学期望)(X E =_____.21.设X 为随机变量,若数学期望1)12(=-X E ,则数学期望)(X E =__.22.设X 为随机变量,若方差3)63(=-X D ,则方差)(X D =__.二、单项选择1.设A,B 为两个事件,若事件A ⊃B ,则下列结论中( )恒成立.(a)事件A,B 互斥 (b)事件A,B 互斥 (c)事件A ,B 互斥 (d)事件A ,B 互斥 2.设A,B 为两个事件,则事件B A +=( ).(a)A +B (b)A-B (c)A B (d)AB3.投掷两颗均匀骰子,则出现点数之和等于6的概率为( ).(a)111 (b)115 (c)361 (d)3654.盒子里装有10个木质球与6个玻璃球,木质球中有3个红球、7个黄球,玻璃球中有2个红球、4个黄球,从盒子里任取1个球.设事件A 表示取到玻璃球,事件B 表示取到红球,则条件概率P(A B )=( ).(a)114 (b)74 (c)83 (d)535.设A,B 为两个事件,若概率P(A)=31,P(A B )=32,P(A B )=53,则概率P(B)=__.(a)51 (b)52 (c)53 (d)546.设A,B 为两个事件,且已知概率P(A)>O ,P(B)>0,若事件A ⊃B,下列等式中( )恒成立.(a)P(A+B)=P(A)+P(B) (b)P(A-B)=P(A)-P(B)(c)P(AB)=P(A)P(B) (d)P(B A )=17.设A,B 为两个事件,则概率P(A+B)=( ).(a)P(A)+P(B) (b)P(A)+P(B)-P(A)P(B)(c)1-P (B A ) (d)1-P( A )P(B ) 8.设A,B 为两个事件,若概率P(A)=31,P(B)=41,P(AB)=121,则( ).(a)事件A 包含B (b)事件A ,B 互斥但不对立 (c)事件A ,B 对立 (d)事件A ,B 相互独立 9.设A,B 为两个事件,且已知概率P(A)=53,P(A+B)=107,若事件A,B 相互独立,则概率P(B)=( ).(a)161 (b)101 (c)41 (d)5210.设A,B 为两个事件,且已知概率P(A)>O ,P(B)>O ,若事件A,B 相互独立,则下列等式中( )恒成立.(a)P(A+B)=P(A)+P(B) (b)P(A+B)=P(A) (c)P(A-B)=P(A)-P(B) (d)P(A-B)=P(A)P(B )11.中( )可以作为离散型随机变量X 的概率分布.(a)6321-P321X11 (b)653-21P321X1(c)6321P321X 11 (d)65321P321X 112.已知离散型随机变量X 的概率分布如下表52511015110142101PX-则下列概率计算结果中( )正确.(a)0}3{==X P (b)0}0{==X P . (c)1}1{=->X P (d)1}4{=<X P13.设离散型随机变量X 的所有可能取值为-1与l ,且已知离散型随机变良X 取-1的概率为)10(<<p p ,取1的概率为q ,则数学期望=)(2X E ( ).(a)O (b)l (c)p q - (d)2)(p q - 14.设连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧≥+=其他,00,1)(2x x kx ϕ 则常数k =( ).(a)π1(b)π (c)π2(d)2π15.下列函数中( )不能作为连续型随机变量X 的概率密度.(a)⎩⎨⎧≤≤-=其他,001,3)(2x x x f (b)⎪⎩⎪⎨⎧≤≤-=其他,021,2)(x x x g(c)⎪⎩⎪⎨⎧≤≤=其他,020,cos )(πx x x h (d)⎪⎩⎪⎨⎧≤≤=其他,02,sin )(ππx x x h 16.设X 为连续型随机变量,若b a ,皆为常数,则下列等式中( )非恒成立.(a)}{}{a X P a X P ==≥ (b)}{}{b X P b X P <=≤ (c)1}{=≠a X P (d)0}{==b X P 17.已知连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他,040,81)(x x x ϕ 则数学期望)(X E =( ).(a)21 (b)2 (c)83 (d)3818.设X 为随机变量,若数学期望)(X E 存在,则数学期望))((X E E =( ).(a)O (b))(X E (c))(2X E (d)2))((X E 19.设X 为随机变量,若方差)(X D =4,则方差)43(+X D =( ).(a)12 (b)16 (c)36 (d)4020.设X ,Y 为随机变量,已知随机变量X 的标准差等于4,随机变量Y 的标准差等于3,若随机变量X ,Y 相互独立,则随机变量X -Y 的标准差等于( ).(a)1 (b)7 (c)5 (d)7四、名词解释1、 数学期望:2、 对立事件:3、 随机事件:4、 事件和:5、 事件积:6、 互斥事件:7、 互相独立事件:五、判断题1.对于连续型随机变量,讨论某一点取值的概率是没有意义的。
统计学第五章作业参考答案

第五章 统计指数一、单项选择1、按指数的性质不同,指数可分为 ( B ) A 、个体指数和总指数 B 、数量指标指数和质量指标指数 C 、综合指数和平均数指数 D 、定基指数和环比指数2、按指数研究的范围不同,指数可分为 ( A ) A 、个体指数和总指数 B 、数量指标指数和质量指标指数 C 、综合指数和平均数指数 D 、定基指数和环比指数3、综合指数是计算总指数 ( C ) A 、唯一的方法 B 、最科学的方法 C 、最基本的方法 D 、最不理想的方法4、用综合指数编制总指数的关键问题在于 ( B ) A 、确定被比对象 B 、确定同度量因素及其固定时期 C 、确定对比基期D 、计算个体指数5、数量指标指数和质量指标指数划分的依据是 ( D ) A 、说明现象的范围不同 B 、指数表现的形式不同 C 、指数采用的基期不同 D 、统计指标的内容不同6、下列指数中,属于质量指标指数的有 ( D ) A 、农产品产量总指数 B 、商品销售量总指数 C 、粮食播种面积总指数 D 、职工劳动生产率总指数7、下列指数中,属于质量指标指数的有 ( A ) A 、粮食平均亩产量总指数 B 、职工人数总指数 C 、股票流通量总指数 D 、房屋销售量总指数8、下列指数中,属于数量指标指数的有 ( D ) A 、某种工业产品单位成本总指数 B 、全部商品批发价格指数 C 、农产品收购价格指数 D 、职工人数总指数9、下列指数中,属于数量指标指数的有 ( D ) A 、居民消费价格指数 B 、农副产品收购价格指数 C 、股票价格指数 D 、农产品产量总指数10、编制数量指标综合指数时,其同度量因素最好固定在 ( B ) A 、报告期 B 、基期 C 、计划期 D 、任意时期11、编制质量指标综合指数时,其同度量因素最好固定在 ( A ) A 、报告期 B 、基期 C 、计划期 D 、任意时期 12、数量指标指数10q p q p∑∑变形为加权算术平均数指数时的权数是 ( B )A 、11q pB 、00q pC 、10q pD 、01q p 13、质量指标指数1101p q p q∑∑变形为加权调和平均数指数时的权数是 ( A )A 、11q pB 、00q pC 、10q pD 、01q p14、在由三个指数所组成的指数体系中,两个因素指数的同度量因素通常( C ) A 、都固定在基期 B 、都固定在报告期C 、一个固定在基期,一个固定在报告期D 、采用基期和报告期的平均数 15、某厂生产费用今年比去年增长50%,产量比去年增长25%,则单位成本比去年上升 ( C ) A 、25% B 、37.5% C 、20% D 、12.5%16、某企业的职工工资水平今年比去年提高了5%,职工人数增加了2%,则该企业工资总额增长了 ( B ) A 、10% B 、7.1% C 、7% D 、11%17、单位成本报告期比基期下降8%,产量增加8%,在这种条件下,生产总费用 ( B ) A 、增加 B 、减少 C 、没有变动 D 、难以确定 18、某商品价格发生变动,现在的100元只值原来的90元,则价格指数为( D ) A 、10% B 、90% C 、110% D 、111%二、多项选择1、下列属于质量指数的有 ( CDE ) A 、工资总额指数 B 、商品销售量指数 C 、劳动生产率指数 D 、原材料单耗指数 E 、产品价格指数2、产品单位成本指数∑∑=1011qz q z K 是 ( ACDE )A 、质量指标指数B 、数量指标指数C 、总指数D 、综合指数E 、派氏指数3、我国居民消费价格指数是 ( BDE ) A 、个体指数 B 、总指数 C 、综合法指数 D 、平均法指数 E 、动态指数4、若以q 表示出口数量,p 表示出口价格,则 ( ABD ) A 、∑∑0011pq p q 表示出口额的相对变动程度B 、∑∑001pq p q 表示出口量的变动而使出口额变动的程度C 、0111p q p q ∑∑-表示出口量的绝对变动量D 、0111p q p q ∑∑-表示由于出口价格的变动而使出口额变动的绝对量E 、0011p q p q ∑∑-表示由于出口量的变动而使出口额变动的绝对量 5、某农产品报告期的收购额为120万元,比基期增加了20%,按基期收购价格计算的报告期假定收购额为115万元,,则计算结论正确的有 ( ABCD ) A 、收购量增长15%B 、收购价格提高了4.35%C 、由于收购价的提高使农民增收5万元D 、由于收购量的增加使收购额增加15万元E 、报告期收购额比基期增加了15万元三、计算②计算两种商品销售价格总指数及由于销售价格变动对销售额的影响绝对额。
北京师范大学《统计学》课后习题答案
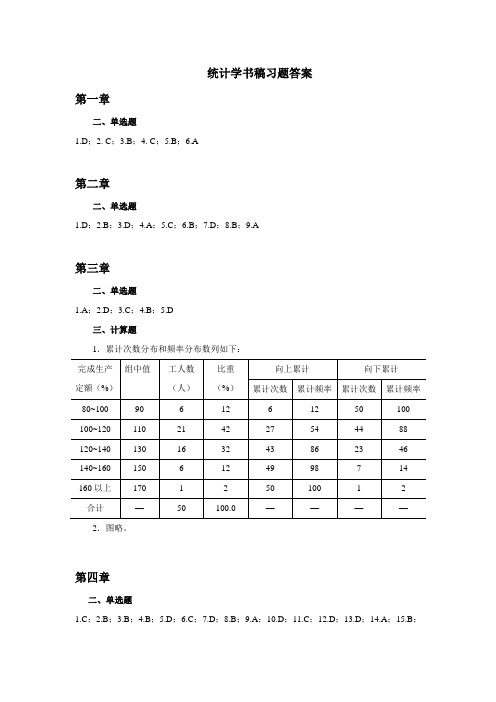
统计学书稿习题答案第一章二、单选题1.D;2. C;3.B;4. C;5.B;6.A第二章二、单选题1.D;2.B;3.D;4.A;5.C;6.B;7.D;8.B;9.A第三章二、单选题1.A;2.D;3.C;4.B;5.D三、计算题1.累计次数分布和频率分布数列如下:2.图略。
第四章二、单选题1.C;2.B;3.B;4.B;5.D;6.C;7.D;8.B;9.A;10.D;11.C;12.D;13.D;14.A;15.B;16.A ;17.C ;18.C ;19.B ;20.C ;21.D ;22.B ;23.C ;24.B ;25.B ;26.B ;27.A ;28.B ; 29.A ;30.C ;31.B ;32.A ;33.C 三、计算题 1. 101.82% 2. 97.83% 3.(3)、(5)为结构相对指标,(6)为计划完成程度相对指标,(7)为动态相对指标。
5. 产品产量计划完成程度为108%,提前完成五年计划的时间为三个季度。
6. 3.64级7. 十月份平均每人日生产量为57件/人,十一月份平均每人日生产量为64件/人。
8. 甲市场的平均价格1.2元/kg ,乙市场的平均价格1.18元/kg 。
9. 76.1X =分,e M =76.09分,o M =75.88分10. 20个商店的平均完成销售计划指标为101.75%,20个商店的平均流通费用率12.38%。
11. 54.75X =,σ=2.8512. 甲企业:633X =元,σ=112.3,V σ=17.74% 乙企业:613X =元,σ=111.05,V σ=18.12% 13. 甲品种:999X =斤,σ=68.91斤,V σ=6.9% 乙品种:998X =斤,σ=162.71斤,V σ=16.3%14. 零件合格率=93.84%,标准差=24.04%第五章二、单选题1.A ;2.B ;3.C ;4.A ;5.D ;6.B ;7.D ;8.A三、计算题1.(1)(93.11%,98.89%);(2)43件2. 97户;为原来的9倍3.(1)1600X =元,46.35X μ=元;(2)月平均工资的估计区间为()1507.3,1692.7元,工资总额的估计区间为()2260950,2539050元。
统计学第五章课后题及答案解析

第五章一、单项选择题1.抽样推断的目的在于()A.对样本进行全面调查B.了解样本的基本情况C.了解总体的基本情况D.推断总体指标2.在重复抽样条件下纯随机抽样的平均误差取决于()A.样本单位数B.总体方差C.抽样比例D.样本单位数和总体方差3.根据重复抽样的资料,一年级优秀生比重为10%,二年级为20%,若抽样人数相等时,优秀生比重的抽样误差()A.一年级较大B.二年级较大C.误差相同D.无法判断4.用重复抽样的抽样平均误差公式计算不重复抽样的抽样平均误差结果将()A.高估误差B.低估误差C.恰好相等D.高估或低估5.在其他条件不变的情况下,如果允许误差缩小为原来的1/2,则样本容量()A.扩大到原来的2倍B.扩大到原来的4倍C.缩小到原来的1/4D.缩小到原来的1/26.当总体单位不很多且差异较小时宜采用()A.整群抽样B.纯随机抽样C.分层抽样D.等距抽样7.在分层抽样中影响抽样平均误差的方差是()A.层间方差B.层内方差C.总方差D.允许误差二、多项选择题1.抽样推断的特点有()A.建立在随机抽样原则基础上 B.深入研究复杂的专门问题C.用样本指标来推断总体指标 D.抽样误差可以事先计算E.抽样误差可以事先控制2.影响抽样误差的因素有()A.样本容量的大小 B.是有限总体还是无限总体C.总体单位的标志变动度 D.抽样方法E.抽样组织方式3.抽样方法根据取样的方式不同分为()A.重复抽样 B.等距抽样 C.整群抽样D.分层抽样 E.不重复抽样4.抽样推断的优良标准是()A.无偏性 B.同质性 C.一致性D.随机性 E.有效性5.影响必要样本容量的主要因素有()A.总体方差的大小 B.抽样方法C.抽样组织方式 D.允许误差范围大小E.要求的概率保证程度6.参数估计的三项基本要素有()A.估计值 B.极限误差C.估计的优良标准 D.概率保证程度E.显著性水平7.分层抽样中分层的原则是()A.尽量缩小层内方差 B.尽量扩大层内方差C.层量扩大层间方差 D.尽量缩小层间方差E.便于样本单位的抽取三、填空题1.抽样推断和全面调查结合运用,既实现了调查资料的_______性,又保证于调查资料的_______性。
统计学基础课后全部详细答案及讲解

统计学第一至四章答案第一章一、思考题1.统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。
统计方法可分为描述统计和推断统计。
2.统计数据的分类:按计量尺度:分类数据、顺序数据和数值型数据按获取数据的方式:观测数据和实验数据按数据与时间的关系:截面数据和时间序列数据特点:分类数据各类别之间是平等的并列关系,各类别之间的顺序可以任意改变;顺序数据的分类是有序的;数值型数据说明的是现象的数量特征,是定量数据;观测数据是通过调查或观测而收集到的数据,是在没有对事物进行人为控制的条件下得到的;实验数据是在实验中控制实验对象而收集到的数据;截面数据也称静态数据,描述的是现象在某一时刻的变化情况;时间序列数据也称动态数据,描述的是现象随时间的变化情况。
3.对武昌分校的全体教师进行工资调查,那么全体教师就是总体,从中抽取五十名教师进行调查,这五十名教师的集合就是样本,全体教师工资的总体平均值和总体标准差等描述特征的数值就是参数,五十名教师工资的样本平均值和样本标准差等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说教师的工资。
4.有限总体:指总体的范围能够明确确定,而且元素的数目是有限可数的。
例如:武昌分校10级金融专业学生无限总体:指总体所包含的元素是无限的、不可数的。
例如:整个宇宙的星球5.变量可分为分类变量、顺序变量、数值型变量。
同时数值型变量可分为离散型变量和连续型变量。
6.离散型变量只能取有限个值,而且其取值都以整位数断开,可以一一列举,例如“产品数量”、“企业数”。
连续型变量的取值指连续不断的,不能一一列举。
例如“温度”、“年龄”。
二、练习题1.(1)数值型变量(2)分类变量(3)数值型变量(4)顺序变量(5)分类变量2.(1)这一研究的总体是IT从业者,样本是从IT从业者中抽取的1000人,样本量是1000(2)“月收入”是数值型变量(3)“消费支付方式”是分类变量3.(1)这一研究的总体是所有的网上购物者(2)“消费者在网上购物的原因”是分类变量第二章一、思考题1:答:1:普查的特点:①:普查通常是一次性的或周期性的;②:普查一般需要规定统一的调查时间;③:普查的数据一般比较准确;4:普查的使用范围比较狭窄,只能调查一些最基本的、特定的现象。
《统计学基础》课后习题答案

《统计学基础》课后习题答案第一章课后练习题答案二、单项选择题1.C2.D3.D4.C5.C6.B7.C8.A9.D 10.B三、多项选择题1.ACE 2.AC 3.ABC 4.CD 5.BDE 6.ABCE 7.DE8.ACD 9.AE 10.BCDE四、判断题1.√2.√3.√4.√5.×6.×7.√8. √9. √第二章课后练习题答案二、案例分析题调查方案一般包括以下几个方面的内容。
一、确定调查目的调查目的是指某项调查需要摸清的情况和解决的问题。
明确地规定调查目的,是统计调查中最根本的问题。
二、确定调查对象与调查单位调查对象是指要调查的社会经济现象的总体,它是由性质相同的许多单位组成的集合体。
调查单位就是构成调查对象总体的个体单位,即标志的承担者。
确定调查对象,就是要确定被研究现象总体的范围,调查对象确定后,调查单位也就随之确定了。
除确定调查单位外,还需确定填报单位(又称报告单位)。
调查单位是调查登记标志的承担者,填报单位则是负责填写调查报告的单位。
确定调查单位,就是明确所要搜集的资料落实、依附于谁。
确定填报单位,则是为了明确谁来负责执行登记、填写、上报资料的工作。
三、确定调查项目和调查表(一)调查项目调查项目是指需要向调查单位调查的内容,也就是确定向调查单位登记些什么问题。
制定调查项目应注意以下几点:1.所选择的调查项目,必须是能够取得确切资料的,那些无法取得资料的项目就不能作为调查项目。
2.对每一调查项目应该有确切的涵义和统一的解释,以免调查人员或被调查者按照各自不同的理解进行回答。
3.各个调查项目之间应尽可能相互联系,彼此衔接,以便研究现象之间的相互联系和从动态上研究现象的发展变化规律。
还应该设置为了核对资料所必要的项目。
调查项目确定后,将各个调查项目按照一定的顺序排列在一定的表格上,就形成了调查表。
调查表是统计工作中搜集资料的基本工具。
(二)调查表调查表一般有表头、表体和表脚三部分组成。
统计学第五章答案

标准差或者离散系数。
(2)如果选择风险小的股票进行投资,应该选择商业类股票还是高科技类股票?
选择离散系数小的股票,则选择商业股票。
(3)如果进行股票投资,你会选择商业类股票还是高科技类股票?
考虑高收益,则选择高科技股票;考虑风险,则选择商业股票。
(
(3)粗略地估计一下,男生中有百分之几的人体重在55kg一65kg之间?
计算标准分数:
Z1= = =-1;Z2= = =1,根据经验规则,男生大约有68%的人体重在55kg一65kg之间。
(4)粗略地估计一下,女生中有百分之几的人体重在40kg~60kg之间?
计算标准分数:
Z1= = =-2;Z2= = =2,根据经验规则,女生大约有95%的人体重在40kg一60kg之间。
4.1一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:
要求:
(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:
(1)(2)(3)
(4)
4.2随机抽取25个网络用户,得到他们的年龄数据如下:
ZA= = =1;产线平均每天的产量为3 700件,标准差为50件。如果某一天的产量低于或高于平均产量,并落人士2个标准差的范围之外,就认为该生产线“失去控制”。下面是一周各天的产量,该生产线哪几天失去了控制?
时间
周一周二周三周四周五周六周日
(1)两位调查人员所得到的样本的平均身高是否相同?如果不同,哪组样本的平均身高较大?
(2)两位调查人员所得到的样本的标准差是否相同?如果不同,哪组样本的标准差较大?
统计学第五章课后题及答案解析教学文案

第五章一、单项选择题1.抽样推断的目的在于()A.对样本进行全面调查 B.了解样本的基本情况C.了解总体的基本情况 D.推断总体指标2.在重复抽样条件下纯随机抽样的平均误差取决于()A.样本单位数 B.总体方差C.抽样比例 D.样本单位数和总体方差3.根据重复抽样的资料,一年级优秀生比重为10%,二年级为20%,若抽样人数相等时,优秀生比重的抽样误差()A.一年级较大 B.二年级较大C.误差相同 D.无法判断4.用重复抽样的抽样平均误差公式计算不重复抽样的抽样平均误差结果将()A.高估误差 B.低估误差C.恰好相等 D.高估或低估5.在其他条件不变的情况下,如果允许误差缩小为原来的1/2,则样本容量()A.扩大到原来的2倍 B.扩大到原来的4倍C.缩小到原来的1/4 D.缩小到原来的1/26.当总体单位不很多且差异较小时宜采用()A.整群抽样 B.纯随机抽样C.分层抽样 D.等距抽样7.在分层抽样中影响抽样平均误差的方差是()A.层间方差 B.层内方差C.总方差 D.允许误差二、多项选择题1.抽样推断的特点有()A.建立在随机抽样原则基础上 B.深入研究复杂的专门问题C.用样本指标来推断总体指标 D.抽样误差可以事先计算E.抽样误差可以事先控制2.影响抽样误差的因素有()A.样本容量的大小 B.是有限总体还是无限总体C.总体单位的标志变动度 D.抽样方法E.抽样组织方式3.抽样方法根据取样的方式不同分为()A.重复抽样 B.等距抽样 C.整群抽样D.分层抽样 E.不重复抽样4.抽样推断的优良标准是()A.无偏性 B.同质性 C.一致性D.随机性 E.有效性5.影响必要样本容量的主要因素有()A.总体方差的大小 B.抽样方法C.抽样组织方式 D.允许误差范围大小E.要求的概率保证程度6.参数估计的三项基本要素有()A.估计值 B.极限误差C.估计的优良标准 D.概率保证程度E.显著性水平7.分层抽样中分层的原则是()A.尽量缩小层内方差 B.尽量扩大层内方差C.层量扩大层间方差 D.尽量缩小层间方差E.便于样本单位的抽取三、填空题1.抽样推断和全面调查结合运用,既实现了调查资料的_______性,又保证于调查资料的_______性。
《统计学基础版》详细答案

【习题与实践训练】答案第一章判断题1.×2.×3.×4.×5.×6.×7.√8.×9.× 10.√单项选择题1.B2.D3.D4.D5.A6.C7.D8.B9.A 10.C多项选择题1.BCDE2.ABCD3.ACD4.ADE5.ABC6.ABCDE7.ADE8.BCE9.ABCDE 10.BCD填空题1.工作过程与结果理论与实践2.统计设计、统计调查、统计整理和统计分析3.大量观察法、统计分组法、综合指标法4. 变动的数量标志5.总体单位数量标志品质标志统计总体数量指标质量指标6.指标条件指标名称、指标数值、指标单位7.一系列相互联系的统计指标所组成的有机整体基本专题8. 定性数据定量数据9.母体子样 10.连续型变量离散型变量应用能力训练题1.略2.略3. ⑴总体:持有该公司信用卡的所有顾客;总体单位:持有该公司信用卡的每一位顾客;样本:300名顾客;样本量:300名;品质标志:过去六个月是否购买产品;数量标志:每位顾客购买金额;数量指标:300名顾客购买总额;质量指标:平均购买额为1782.67元;统计量:300名顾客平均购买额为1782.67元;参数:持有该公司信用卡的所有顾客购买总额。
⑵本案例采用的统计方法属推断统计。
4.轿车生产总量,旅游收入是数量指标;经济发展速度,人口出生率,安置再就业人数,城镇居民人均可支配收入,恩格尔系数是质量指标。
区分数量指标与质量指标的方法是:数量指标用绝对数表示,质量指标用相对数和平均数表示。
5.总体:中国农民;样本:全国31个省(区、市)6.8万户农村住户的农民;变量:现金收入、工资性收入、出售农产品的收入、家庭二、三产业生产经营收入、财产性收入、转移性收入。
6.略。
第二章判断题1.×2.×3.×4. √5.×6.×7. ×8. √9.× 10. ×单项选择题1.C2.A3.A4.C5.B6.D7.A8.C9.B 10.D多项选择题1.BDE2.ACD3.BCD4.ADE5.BCE6.ABCE7.ABCE8.BDE9.BDE 10.ABC填空题1.单一表一览表2.普查抽样调查重点调查典型调查3.全面调查非全面调查4.直接观察法5.有意识随机6.统计调查方案7.表头表体表脚8. 访问法(采访法、询问法)9. 开放式问题封闭式问题 10.网上直接调查网上间接调查应用能力训练题1.略2.略3. ⑴全面调查一次性调查直接调查统计报表⑵全面调查一次性调查直接调查普查⑶非全面调查经常性调查直接调查抽样调查⑷非全面调查经常性调查直接调查重点调查⑸非全面调查经常性调查直接调查典型调查4. ⑴直接观察法直接调查⑵实验法直接调查⑶访问法直接调查⑷网上调查直接调查5.略6.略第三章一、判断题1.× 2. × 3. × 4. × 5. √ 6. √ 7. × 8. × 9. √ 10. √二、选择题1.B 2. B 3. C 4.A 5. D 6.A 7.D 8.B 9.D 10.A 三、多项选择题1.ACD 2.BCD 3.ABDE 4.CD 5.ACE 6.BCE 7.BCD 8.ABE 9.BCDE 10.BC 四、填空题1.选择分组标志和划分各组界限2.类型分组、结构分组和分析分组3.品质分配数列变量分配数列4.组限每个组的最大值每个组的最小值组中值5.反比6.上组限不在内7.等距分组异距分组8.按某标志分的组各组相应的分配次数或频率或标志值频数频率9.钟型分布、U型分布和J型分布。
(完整版)北大版统计学原理课后习题答案简版

(10)国民经济统计指标体系、科技统计指标体系、社会统计指标体系
2、多选题:
(1)b.e (2)a.d (3)a.b.c.e (4)a.c.e (5)b.d (6)a.b.c (7)c.d (8)a.b.c.d (9)a.b.c.d.e
3、判断题:
(1)√(2)√(3)×(4)√(5)√
2、计算题:
(1)2005年粮食产量=167.330772亿斤
粮食产量每年平均增长速度=
(2)①
年份
1995
1996
1997
1998
1999
2000
产量(万件)
500
550
604
664.4
700
735
逐期增长量(万件)
-
50
54
60.4
35.6
35
累计增长量(万件)
-
50
104
164.4
200
235
第一章总论
1、单选题:
(1)b (2)c (3)a (4)b (5)a (6)d (7)d (8)b (9)d (10)d (11)c (12)a (13)c (14)d (15)d
2、多选题:
(1)a.c.e (2)a.b.d (3)b.e (4)c.e (5)b.d.e (6)a.b.c (7)a.c.e (8)a.b.c.e (9)b.c.e
276
315
合计
192
219
258
189
858
季平均
64
73
89
73
71.5
季节比率(%)
89.51
102.1
120.28
《统计学》-第5章-习题答案

第五章方差分析思考与练习参考答案1.试述方差分析的基本思想。
解答:方差分析的基本思想是,将观察值之间的总变差分解为由所研究的因素引起的变差和由随机误差项引起的变差,通过对这两类变差的比较做出接受或拒绝原假设的判断的。
2.方差分析有哪些基本假设条件?如何检验这些假设条件? 解答:(1)在各个总体中因变量都服从正态分布;(2 )在各个总体中因变量的方差都相等;(3)各个观测值之间是相互独立的。
正态性检验:各组数据的直方图/峰度系数、偏度系数/Q-Q图,K-S检验*等方差齐性检验:计算各组数据的标准差,如果最大值与最小值的比例小于2:1,则可认为是同方差的。
最大值和最小值的比例等于 1.83<2。
也可以采用Levene检验方法。
独立性检验:检查样本数据获取的方式,确定样本之间无相关性。
3.对三个不同专业的学生的统计学成绩进行比较研究,每个专业随机抽取6人。
根据数据得到的方差分析表的部分内容如表5-21。
请完成该表格。
如果显著性水平a=0.05,能认为三个专业的考试成绩有显著差异吗?表5-21不同专业考试成绩的方差分析表解答:表不同专业考试成绩的方差分析表查f分布可知,p(F< 0.9067964)= 0.7952296,在显著性水平a=0.05时,不能拒绝原假设,认为三个专业的成绩无显著差异。
根据以下背景资料和数据回答4-7题。
为测试A、B、C、D、E五种节食方案,一位营养学家选择了50名志愿者随机分成五组,每组采用一种方案测量两个月后每个人的降低的体重,得到的实验数据如表5-22。
表5-22不同节食方案的降低的体重(公斤)序号 万案A 万案B 万案C 万案D 万案E1 6.5 2.9 8 5.1 11.52 11.6 5.5 11.9 2.5 13.23 7.7 4.3 8.5 1.5 114 8.7 3.6 8.9 2.2 13.15 8.4 3.9 9.1 1.4 13.86 4.1 6.7 11.4 3.1 12.8 7 8.7 4.5 12.6 5.4 12 8 6.6 1.7 12.4 1.9 11.5 9 7.1 6.59.4 4.1 14.6 108.9 5.4 10.6 3.6 13.74.不同节食方案的实验效果的描述统计资料如表5-23。
统计学基础课后答案

尊敬的老师(读者)好:首先感谢使用本教材,由于时间仓促,教材存在一些错误,给您带来不便请您谅解,现对部分错误及添加内容做了修改,同时提供部分习题答案,习题有超出课本范围可直接忽略。
多媒体课件我会陆续发给大家!本教材出版社已经重新修改再次印刷,相信错误基本没有了。
欢迎您批评指正!祝您工作愉快!王瑞卿2009年11月24日教材修改:小错误直接修改在教材上了。
原教材106页,思考与技能训练在原来习题基础上添加如下内容:要求:在原来对应同类习题前加上如下内容一、填空题1.绝对数是说明总体特征的指标。
2.按绝对数的计量单位不同可分为、、三类指标。
3.总体单位总数和标志值总数随着变化而可能转化。
4.相对数是由两个有联系的指标计算得到。
5.结构相对数和比例相对数都是在基础上计算的。
6.计划指标的表现形式可以是绝对数,也可以是和。
7.强度相对数的正指标数值越大,表示现象的强度和密度越8.系数和倍数是将对比的基数定为而计算的相对数。
9.实物指标能够直接反映产品的量,价值指标反映产品的量。
10.我国汉族人口占总人口的91,59%,则少数民族人口占总人口的百分比为。
11.续接原来的填空题二、单项选择题1.下面属于时期指标的是( )A.商场数量B.营业员人数C.商品价格D.商品销售量2.某大学10个分院共有学生5000人、教师300人、设置专业27个。
若每个分院为调查单位,则总体单位总数是( )A.分院数B.学生数C.教师数D.专业数3.下面属于结构相对数的有( )A.人口出生率B.产值利润率C.恩格尔系数D.工农业产值比4.用水平法检查长期计划完成程度,应规定( )A.计划期初应达到的水平B.计划期末应达到的水平C.计划期中应达到的水平D.整个计划期应达到的水平5.属于不同总体的不同性质指标对比的相对数是( )A.动态相对数B. 比较相对数C.强度相对数D.比例相对数6.数值可以直接相加总的指标是( )A.绝对数B.相对数C.时点数D.时期数7.第五次人口普查结果,我国每10万人中具有大学程度的为3611人。
统计学基础练习题库及参考答案

第一章定量资料的统计描述1第一部分一、单选题1、甲乙丙三位研究者评价人们对四种方便面的喜好程度。
甲让评定者先挑选出最喜欢的品牌,然后挑出剩余三种最喜欢的,最后挑出剩余两种比较喜欢的。
研究者乙让评定者把四种品牌分别给予1~5的等级评定(1表示最不,5表示最喜欢),研究者丙只是让评定者挑出自己最喜欢的品牌。
三位研究者所使用的数据类型是:BA.称名数据-顺序数据-计数数据B.顺序数据-等距数据-称名数据C.顺序数据-等距数据-顺序数据D.顺序数据-等比数据-计数数据2、调查200名不同年龄组的被试对手表的偏好程度如下:表1 200名不同年龄组的被试对手表的偏好程度该题自变量和因变量的数据类型是:DA.称名数据-顺序数据B.计数数据-等比数据C.顺序数据-等距数据D.顺序数据-称名数据3、157.5的实上限是:CA.157.75 B.157.65 C.157.55 D.158.54、随机现象的数量化表示称为:BA.自变量B.随机变量C.因变量 D.相关变量5、实验或研究对象的全体称为:AA.总体B.样本点C.个体D.元素6、下列数据中,哪个数据是顺序变量:CA.父亲月收入2400元B.迈克的语文成绩是80分C.约翰100米短跑得第2名D.玛丽某项技能测试得了5分。
二、概念题数据类型、变量、观测值、随机变量、总体、样本、个体、次数、比率、概率、参数、统计量、μ、ρ、r、σ、S、β、n。
第一章定量资料的统计描述2一、单选题1、一批数据中各个不同数据值出现的次数情况是:AA.次数分布B.概率密度C.累积概率密度D.概率2、以下各种图形中,表示连续数据频次分布的是:CA.条图B.圆图C.直方图D.散点图3、特别适用于描述具有百分比结构的分类数据的统计图:BA.散点图B.圆图C.条图D.线图5、以下各种统计图中,表示离散数据频次分布的:AA.圆图B.直方图C.散点图D.线形图6、相关变量的统计图是:AA.散点图B.圆图C.条图D.线图7、适用于描述某种事物在时间上的变化趋势,以及一事物随另外一事物的发展变化的趋势,还适用于比较不同人物群体在心理或教育现象上的变化特征以及相互联系的统计图是:D A.散点图B.圆图C.条图D.线图二、多选题1、频次分布可以为:ABCDA.简单次数分布B.分组次数分布C.相对次数分布D.累积次数分布2、以下各种图形中,表示连续数据频次分布的是:BDA.圆图B.直方图C.条图D.线图3、累加曲线的形状大约有:ABDA.正偏态B.负偏态C.F分布D.正态分布4、统计图按照形状划分为:ABCDA.直方图B.曲线图C.圆图D.散点图三、简答题1、简述条图、直方图、圆图、线图、散点图的用途。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Exercise 51. P201: 4.59.Let 54321Y Y Y Y Y <<<<be the order statistics of a random sample of size n from a distribution with p.d.f. ∞<<=-x e x f x 0,)(,zero elsewhere..Show that 21Y Z =and 242Y Y Z -=are independent. Solution: Since ∞<<=-x e x f x 0,)(, so ∞<<-=-x e x F x 0,1)()()()]()][()()][([!1!1!1!5),(424242424,2y f y f y F y F y F y F y y g -=424422))()(1(120y y y y y y e e e e e e --------= Since 12Z Y =,214Z Z Y +=,11101==J . 22111211212112421)1)(1(120))(1(120),(z z z z z z z z z z z z z e e e e ee eee e z z g ---------------=--=)1(20)()]'([)](1)][([!3!1!5)()(11424322211z z e e y f y F y F y F y g z g ---=-== ⎰⎰∞----∞--==01240121222211)1)(1(120),()(dz e e e e dz z z g z g z z z z222211222205042)1(6)1(201120)|5|4()1(120z z z z z z z z e e e e e e ee----∞-∞----=-⋅=----= Thus, =),(21z z g )()(2211z g z g .So 1Z and 2Z are independent.P274: 6.15. Let X be the mean of a random sample of size n from adistribution that is )9,(μN . Find n such that 90.0)11Pr(=+<<-X X μ, approximately.Solution: Since ~X )9,(n N μ,)1,0(~3)(N X n μ-.90.01)3(2)3|3)(Pr(|)1|Pr(|)11Pr(=-Φ=<-=<-=+<<-nn X n X X X μμμ Thus )3(n Φ=0.95, 645.13=nand 35.24≈n . Because n must be an integer, so n=24 or 25.P275: 6.18. Let 121,,,+n n X X X X be a random sample of size 9 from adistribution that is ),(2σμN .(a) If σis known, find the length of a 95 percent confidence interval for if this interval is based on the random variable.(b) If σis unknown, find the expected value of the length of a 95 percent confidence interval for if this interval is based on the random variable S X /)(8μ-. (c) Compare these two answers. Solution:(a) Since ~991∑==i iXX )9,(2σμN ,thus)1,0(~)(9N X σμ-.Pr(|σμ)(9-X |<1.96)=0.9595.0)96.1)(396.1Pr(=<-<-⇔σμX95.0)396.1396.1Pr(=+<<-⇔σμσX X . The 95 percent confidence interval for μis )396.1,396.1(σσ+-X X and the length of it isσσ31.17598≈ (b) Since σ is unknown, then )8(~)(81/t SX n S X T μμ-=--=975.0)P r (95.01)Pr(295.0))(8Pr(=≤⇒=-≤⇒=<-<-b T b T b S X b μFrom TABLE IV of Appendix B, we know b=2.306, thus95.0)8306.28306.2Pr(=+<<-σμσX X . The 95 percent confidence interval for μ is )8306.2,8306.2(σσ+-X X with the length S L 8612.4=⎰∞-Γ===02342121222)4(183612.4))/9((38612.4)(8612.4)(dx e x x S E S E L E xσσσ)29(22)4(183612.422)4(183612.42)4(183612.429402729402274ΓΓ=Γ=Γ=⎰⎰∞-∞-σσσdy e y dx e x y xThen σ49.1)(≈L E(c) From (a) we know the answer is σ31.1, from (b) we know the answer isσ49.1. The two methods yield results that are in substantial agreement, which shows the length of the confidence interval for μ is almost the same with the parameter σ known or unknown.P279: 6.30.Let two independent random samples, each of size 10, from two normal distributions ),(21σμN and ),(22σμN yield 8.4=x ,64.821=s ,6.5=y ,88.722=s . Find a 95 percent confidence interval for.Solution: Let 1021,,X X X and 1021,,Y Y Y denote, respectively, independent random samples from the two distributions ),(21σμN and),(22σμN , then ~10101∑==i iXX )10,(21σμN and ~10101∑==i iYY )10,(22σμN .)5,(~221σμμ--N Y X .)18(~/)1010(222221χσS S +)18(~9)()()()101101(18)(10)()(222121222121t S S Y X S S Y X T +---=++---=μμμμ.101.295.0)Pr(=⇒=<<-b b T b and95.0))(3)()(3)Pr((2221212221=++-<-<+--S S b Y X S S b Y X μμ So the random intervalis )3101.2)(,3101.2)((22212221S S Y X S S Y X ++-+--. Let 8.4=x ,64.821=s ,6.5=y ,88.722=s , we get a 95 percent confidenceinterval (-3.6,2.0).2. Use Splus or R software to compute the mean, standard deviation, skewness and kurtosis of the following dataset.-0.4292, 0.0064, 0.1181, -0.6282, 2.2010, -1.7623, 0.0921,1.8742, 1.4538, 0.3575, -1.5848, 0.4993, 0.7762, -0.2638, -1.1003, -2.2480, 0.5419, -0.4018, -0.3562, -0.5872. Solution: > x<-c(-0.4292,0.0064,0.1181,-0.6282,2.2010,-1.7623,0.0921,1.8742,1.4538,0.3575,-1.5848,0.4993,0.7762,-0.2638,-1.1003,-2.2480,0.5419,-0.4018,-0.3562,-0.5872) > a=mean(x) > a[1] -0.072065 > b=sd(x) > b[1] 1.143067> c=mean(((x-a)/b)^3) > c[1] 0.1234913> d=mean(((x-a)/b)^4)-3 > d[1] -0.5280221So the mean of the dataset is -0.072065, the standard deviation is 1.143067, the skewness is 0.1234913 and the kurtosis is -0.5280221.3*. P203: 4.73. Let n Y Y Y <<< 21be the order statistics of a random sample of size n from the exponential distribution with p.d.f.∞<<=-x e x f x 0,)(,zero elsewhere..(a) Show that 11nY Z =,))(1(122Y Y n Z --=,))(2(233Y Y n Z --=,…1--=n n n Y Y Z , are independent and that each i Z has the exponential distribution.Solution: Since n y y y n e e e n y y y g ---= 21!),,(21, andn n n Z Z n Zn Z Y n Z n Z Y n Z Y ++-+=-+==-21,,1,12121211 and the Jacobian is!1121111021111011101n n n n n n n n J =---=nn z z z z n z n z n z n z nz n n e e e eee y y y g J z z z g ---++-+--+--=== 2121211)1()1(2121),,(||),,(k z n k k n k k e dz dz dz dz z z z g z g -+-∞∞∞∞==⎰⎰⎰⎰ 11012100),,()(So )()()(),,(221121n n n z g z g z g z z z g = and ∞<<=-k z k k z e z g k 0,)( Which shows that n z z z ,,21are independent and that each i z has the exponential distribution.(b) Demonstrate that all linear functions of n Y Y Y ,,,21 , such as ∑ni i Y a 1, canbe expressed as linear functions of independent random variables. Solution:)())(1())(1(11122112211---++---++--+=+++n n n k k k n n Y Y b Y Y k n b Y Y n b nY b Y a Y a Y a n n Z b Z b Z b +++= 2211. Then ,)2()1(,)1(232121a n b n n b a n b n b =---=-- n n n n n k k k a b a b b a k n b k n b ==-=--+---+)1(,)1()2(,,)()1(,111 . Then n n nk k n n a b k n a a b n a a a b n a a a b =+-++=-++=++=,1,,1,322211So1,11+-+==∑∑==i n a a b Z b Y a ni i ni i i ni i i .Since n Z Z Z ,,,21 are independent, thenn n Z b Z b Z b ,,,2211 are independent. So∑=ni i i Y a 1can be expressed as linearfunctions of independent random variables.P275: 6.19.Let 121,,,+n n X X X X be a random sample of size n+1, n>1, from a distribution that is ),(2σμN . Let n X X ni /1∑= andn X X S ni /)(212-=∑. Find the constant c so that the statisticσ1+-n X X chas a t-distribution. If n=8, determine k suchthat 80.0)Pr(=+<<-kS X kS X μ. The observed interval is ),(ks x ks x +- often called an 80 percent prediction interval for 9X . Solution: )/,(~2n N X σμ,),(~21σμN X n +,),1,0(~21σnn N X X n +-+ ).1(~11)1(1),1(~).1,0(~112212221--⋅+⋅-=-+--+-+++n t SX X n nn n n nS n n X X n nS N nn X X n n n σσχσσTherefore 11+-=n n c . 80.0)9797Pr()Pr()Pr(999=<-=<-=+<<-k S X X k S X X kS X x kS X 60.1,415.197==k k . So k=1.60.。
