三次样条插值课后题集
第三章 插值法 三次样条插值

问题
分段低次插值
在处理实际问题时,总是希望将所得到的数据点用得越多越好。
最简单的方法是用直线将函数值点直接连接。
分段低次插值
基本思想:用分段低次多项式来代替单个多项式。
具体作法:(1) 把整个插值区间分割成多个小区间;
(2) 在每个小区间上作低次插值多项式;
(3) 将所有插值多项式拼接整一个多项式。
优点:公式简单、运算量小、稳定性好、收敛性…
缺点:节点处的导数不连续,失去原函数的光滑性。
三次样条函数
样条函数
由一些按照某种光滑条件分段拼接起来的多项式组成的函数。
最常用的样条函数为三次样条函数,即由三次多项式组成,满足处处有二阶连续导数。
定义设节点a =x 0< x 1 < …< x n -1 < x n =b ,若函数
在每个小区间[x i , x i +1 ]上是三次多项式,则称其为三次样条函数。
如果同时满足s (x i ) = f (x i ) (i = 0, 1, 2, …, n ),则称s (x ) 为f (x ) 在[a , b ]上的三次样条函数。
],[)(2b a C x s ∈
利用线性插值公式,即可得的表达式:
求导得:
即:
:第一类边界条件(缺省边界条件)。
练习题三 插值法
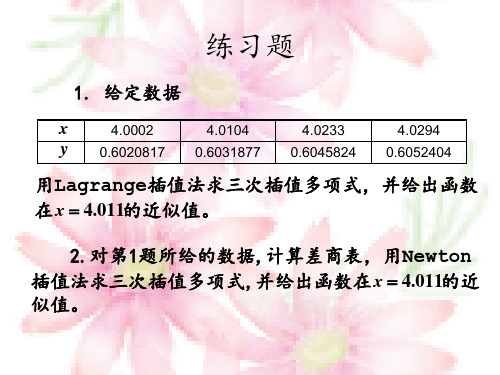
用Lagrange插值法求三次插值多项式,并给出函数 插值法求三次插值多项式, 插值法求三次插值多项式 的近似值。 在 x = 4.011的近似值。 2.对第1题所给的数据,计算差商表, 2.对第1题所给的数据,计算差商表,用Newton 对第 插值法求三次插值多项式, 插值法求三次插值多项式,并给出函数在 x = 4.011的近 似值。 似值。
(4)用 的近似值, (4)用3次样条插值求 f ( x ) 在 x = 0.425的近似值, 并与准确值作比较; 并与准确值作比较; 取值如下, 5. 已知函数 f ( x )取值如下,试求
x f (x) 0 .25 0 .5000 0 . 30 0 .5477 0 . 39 0 .6245 0 .45 0 .6708 0 .53 0 .7280
对第1题所给的数据计算差商表用newton插值法求三次插值多项式并给出函数在对函数在区间选取不同个数的等距插值节点用分段线性插值代替次插值函数观察插值节点增多时误差的变化情况
练习题
1. 给定数据
x y
4.0002 0.6020817 4.0104 0.6031877 4.0233 0.6045824 4.0294 0.6052404
1 − 3. 对函数 2 在区间 [−4,4] 选取不同个数的等 1+ x 距插值节点, 次插值函数, 距插值节点,用分段线性插值代替 n 次插值函数,观
察插值节点增多时误差的变化情况。 察插值节点增多时误差的变化情况。 4. 给出 f ( x ) = sin x 在 xk = 0.1k , k = 0,1,L,10 的函 数值 f ( xk ) = yk 。 (1)用9次Lagrange插值多项式求 f ( x ) 在 x = 0.425 (1)用 插值多项式求 的近似值,并与准确值作比较; 的近似值,并与准确值作比较; (2)用 (2)用9次Newton插值多项式计算 f ( x ) 在 x = 0.425 插值多项式计算 的近似值,并与准确值作比较; 的近似值,并与准确值作比较; (3)用分段线性插值求 的近似值, (3)用分段线性插值求 f ( x ) 在 x = 0.425的近似值, 并与准确值作比较; 并与准确值作比较;
matlab三次样条插值例题解析

文章标题:深度解析Matlab三次样条插值1. 前言在数学和工程领域中,插值是一种常见的数值分析技术,它可以用来估计不连续数据点之间的值。
而三次样条插值作为一种常用的插值方法,在Matlab中有着广泛的应用。
本文将从简单到复杂,由浅入深地解析Matlab中的三次样条插值方法,以便读者更深入地理解这一技术。
2. 三次样条插值概述三次样条插值是一种利用分段三次多项式对数据点进行插值的方法。
在Matlab中,可以使用spline函数来进行三次样条插值。
该函数需要输入数据点的x和y坐标,然后可以根据需要进行插值操作。
3. 三次样条插值的基本原理在进行三次样条插值时,首先需要对数据点进行分段处理,然后在每个分段上构造出一个三次多项式函数。
这些多项式函数需要满足一定的插值条件,如在数据点处函数值相等、一阶导数相等等。
通过这些条件,可以得到一个关于数据点的插值函数。
4. Matlab中的三次样条插值实现在Matlab中,可以使用spline函数来进行三次样条插值。
通过传入数据点的x和y坐标,可以得到一个关于x的插值函数。
spline函数也支持在已知插值函数上进行插值点的求值,这为用户提供了极大的灵活性。
5. 三次样条插值的适用范围和局限性虽然三次样条插值在许多情况下都能够得到较好的插值效果,但也存在一些局限性。
在数据点分布不均匀或有较大噪音的情况下,三次样条插值可能会出现较大的误差。
在实际应用中,需要根据具体情况选择合适的插值方法。
6. 个人观点和总结通过对Matlab中三次样条插值的深度解析,我深刻地理解了这一插值方法的原理和实现方式。
在实际工程应用中,我会根据数据点的情况选择合适的插值方法,以确保得到准确且可靠的结果。
我也意识到插值方法的局限性,这为我在实际工作中的决策提供了重要的参考。
通过以上深度解析,相信读者已经对Matlab中的三次样条插值有了更加全面、深刻和灵活的理解。
在实际应用中,希望读者能够根据具体情况选择合适的插值方法,以提高工作效率和准确性。
中南大学matlab课后习题(1)

%用循环结构实现
a=0;
for i=1:n
a=a+1/(i^2);
end
disp(a);
j=1:n;
%用 sum 函数实现
b=sum(1./(j.^2)); 输入一个数:34
b=
(2)( )( )( ) (
) (= )
clear n=input('输入一个数:'); a=1; for i=1:n a=((2*i*i*2)/((2*i-1)*(2*i+1)))*a; end disp(a); 输入一个数:8
1/5 1/6 1/7 1/8
1/5
1/6
1/7
1/8
1/9
P=pascal(5)
P= 1 1 1 1 1
1
1
1
1
2
3
4
5
3
6
10
15
4
10
20
35
5
15
35
70
Hh=det(H)
Hh = 1/0000
Hp=det(P)
Hp = 1
Th=cond(H)
Th = 476607
Tp=cond(P)
Tp = 178868/21 P 矩阵性能更好,因为 Tp 更接近 1. 5.已知 A,求 A 的特征值及特征向量,并分析其数学意义。 A=[-29,6,18;20,5,12;-8,8,5]
min=a(i); end end max min 请输入二十个数[ 3 4 6 5 3 44 5 5 5 6 6 5 5 4 3 32 2 2 2 6]
max =
44
min =
2
4.
,当 a 取、、、…、、、时,求各点的函数值。要求分别用顺序结
三次样条插值算法详解知识讲解

mn
Mn
18
稍加整理得
2m0m13y1h0y0h20M0 g0 m n12m n3ynh n y 1n1hn 21M n gn
联合基本方程组得一个n+1阶三对角方程组, 化成矩阵形式为:仍然是严格对角占优
2 1
1
2
1
m0 m1
g0 g1
2 2 2
3 2
m 2 g2
x [ x i,x i 1 ]h i, x i 1 x i,i 0 , 1 , ,n 1
( x ) ( 2 x 1 )x ( 1 ) 2 ,1 ( x ) x ( x 1 ) 2 12
对Si(x)求二阶,导 并数 整理后得
Si(x)6(xix hii3 12x)(yi1yi) 6 x 2 x h ii2 4 x i 1m i6 x 4 x h ii2 2 x i 1m i 1
3
(1)因为s(x)在每个小区间上是一个次小于三次的多 项式,故有四个未知系数; (2)因为s(x)有n分段,从而共有4n个未知系数! (3)但插值条件与样条条件仅给出4n-2个条件,无法 定出4n个未知系数,还差2个条件!这2个条件我们用 边界条件给出!
4
通常我们对插值多项式在两端点的状态加以要求也就是 所谓的边界条件:
6
第三类又称周期边界条件: 由区间端点处的函数值或导数值满足周期条件给出
s3 (x0 0) s3 (xn 0)
s3
(
x0
0)
s3 ( xn
0)
s3(x0 0) s3(xn 0)
这样三次样条插 值问题就分成三 类!其实不止这
三类!
7
样条函数的例子
容易验证: (11x326x215x)15 0x1
计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
(1)
这里共有了 3n-3 个条件,再加上条件(2)中的 n+1 个插值条件,共有 4n-2 个条件,
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
(6)
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式(1)内点拼接条件,可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
(3) (4)
其中
i
hi 1 hi1
, hi
i
hi hi 1
三次样条插值作业题

例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%============================= % 本段代码解决作业题的例1 %============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2;RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1);for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i);end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i)); end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepVar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1); for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) ); S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-',num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=1和x=2两个横轴点作垂线 %line([1, 1], [2.5, -0.5], 'LineStyle', '--');line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x轴和y轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ...'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
科学计算实习题二 三次样条插值
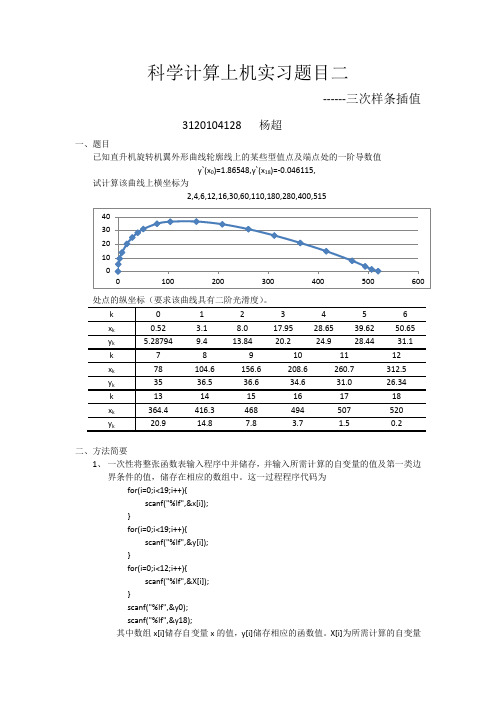
for(i=0;i<12;i++){ for(k=1;k<19;k++){
if((X[i]>x[k-1])&&(X[i]<x[k]))
S[i]=M[k-1]/(6*h[k])*pow(x[k]-X[i],3)+M[k]/(6*h[k])*pow(X[i]-x[k-1],3)+(y[k-1]-M[k-1]/ 6*pow(h[k],2))*(x[k]-X[i])/h[k]+(y[k]-M[k]/6*pow(h[k],2))*(X[i]-x[k-1])/h[k];
} 3、 利用解三对角线方程组的追赶法解出在结处的二阶导数值,这一过程程序代码如
下 bt[0]=1.0/2; for(i=1;i<=17;i++){ bt[i]=v[i]/(2-u[i]*bt[i-1]); } f[0]=g[0]*1.0/2; for(i=1;i<=18;i++){ f[i]=(g[i]-u[i]*f[i-1])/(2-u[i]*bt[i-1]); } M[18]=f[18]; for(i=17;i>=0;i--){ M[i]=f[i]-bt[i]*M[i+1];
的值。 2、 按照课本第 92 页的公式(4.44)计算确定 M 的线性方程组的系数数组 u、v、g,
并储存在相应的数组中。这一过程程序代码为 for(i=1;i<19;i++){ h[i]=x[i]-x[i-1]; } for(i=1;i<18;i++){ u[i]=h[i]/(h[i]+h[i+1]); v[i]=1-u[i]; } g[0]=6/h[1]*((y[1]-y[0])/h[1]-y0); g[18]=6/h[18]*(y18-(y[18]-y[17])); for(i=1;i<18;i++){ g[i]=6/(h[i]+h[i+1])*((y[i+1]-y[i])/h[i+1]-(y[i]-y[i-1])/h[i]);
计算方法大作业——三次样条插值

计算方法上机报告
此完成所有数据的输入。继续按 Enter 键会出现提示“选择封闭方程组的边界条件: 第 一类边界条件输入 1,第二类边界条件输入 2,第三类边界条件输入 3。 ”根据已知情况 选择相应的边界条件,若为自然三次样条插值,则选 1,并将插值区间两端点的二阶导 数值设置为 0。输入完成之后按 Enter 开始求解,程序运行结束后命令窗口会显示要求 的三次样条插值函数,同时会出现该插值函数以及插值节点的图像,便于直接观察。 2.3 算例及计算结果 (1) 《数值分析》课本第 137 页的例题 4.6.1,已知函数 y=f(x)的数值如下表,求它 的自然三次样条插值函数。 xi yi -3 7 -1 11 0 26 3 56 4 29
2 三次样条插值
2 三次样条插值
2.1 算法原理及程序框图 设在区间[a, b]上给定 n+1 个节点 xi(a ≤ x0 < x1 < … < xn ≤ b),在节点 xi 处的函数 值为 yi = f(xi) (i = 0,1,…,n)。若函数 S(x)满足以下三个条件: (1) 在每个子区间[xi-1, xi] (i = 0,1,…,n)上,S(x)是三次多项式; (2) S(xi) = yi (i = 0,1,…,n); (3) 在区间[a, b]上,S(x)的二阶导数 S”(x)连续, 则称 S(x)为函数 yi = f(x) 在区间[a, b]上的三次样条插值函数。 由定义可知 S(x)共有 4n 个待定参数,根据条件(3)可得如下 3n-3 个方程,
S x
x x i
6hi
3
M i 1
x xi 1
6hi
3
x x hi2 M i yi 1 M i 1 i 6 hi
(完整word版)数值分析作业-三次样条插值..0001

数值计算方法作业实验4.3三次样条差值函数实验目的:掌握三次样条插值函数的三弯矩方法实验函数:求和的近似值实验内容:(1) 编程实现求三次样条插值函数的算法,分别考虑不同的边界条件;(2) 计算各插值节点的弯矩值;(3) 在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲线比较插值结果。
实验4.5三次样条差值函数的收敛性实验目的:多项式插值不一定是收敛的,即插值的节点多,效果不一定好。
对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。
实验内容:按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。
实验要求:(1)随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情况,分析所得结果并与拉格朗日插值多项式比较;(2)三次样条插值函数的思想最早产生于工业部门。
作为工业应用的例子,考虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线, 其中一 段数据X k 0 1 23 4 5678910y k 0.00.79 1.532.19 2.713.03 3.27 2.89 3.06 3.19 3.29y k0.80.2算法描述:拉格朗日插值:错误!未找到引用源。
n(x _ X ) 其中错误!未找到引用源。
是拉格朗日基函数,其表达式为:h(x)」j=0 (x i- X j )牛顿插值:N n (x) =f (X g ) f[X o ,X i ](X -xO) f[X o ,X i ,X 2〕(X - xO)(x - X i ) •…f[X g ,X i ...X n ] =(f[X i ,X 2,...X n ] - f [ X 。
,为,..人」)/(X . - X g )三样条插值:所谓三次样条插值多项式Sn(x)是一种分段函数,它在节点Xi(a<X0<X1……<Xn<b)分成的每个小区间[x i-i ,x i ]上是三次多项式,其在此区间 上的表达式如下:f[X °,X i ,X 2,...X n ](X -X °)(X -X i )...(X-Xn J )f [X i , X j ]f (X i ) - f (X j ) X i -X jf [X i , X j ,X k]=其中*.f[X j ,X k ] - f[K ,X j ]X k -X iS(x)二 M 3(X i -x) 6h i.Mi (x —Xy )3 . [ y i - y i4 h i (M i - My)6h i h i 6 h ih i M i 4 h i M iy i- 6)( 6*,皿"]因此,只要确定了 Mi 的值,就确定了整个表达式,Mi 的计算方法如下:i 4式中 Mi= S (X i ).则Mi 满足如下n-1个方程:7 M i 」■ 2M i …冷 M i i = di , i =1,2,...n —'1 常用的边界条件有如下几类:(1)给定区间两端点的斜率 m o ,m n ,即s(x 0) = y 0 =m 0,S(x n ) = y n = m n(2) 给定区间两端点的二阶导数 MO ,Mn,即S (XcH y 。
三次样条插值作业题

例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%=============================% 本段代码解决作业题的例1%============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2; RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度 h = zeros(1, length(IndVar) - 1); for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i); end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i));end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepV ar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1);for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) );S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-', num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=1和x=2两个横轴点作垂线%line([1, 1], [2.5, -0.5], 'LineStyle', '--');line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x轴和y轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ...'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
数值分析课后答案(4)

数值分析课后答案(4)习题四1.已知ln(2.0)=0.6931;ln(2.2)=0.7885,ln(2.3)=0.8329, 试用线性插值和抛物插值计算.ln2.1的值并估计误差解:线形插值:取02.0x = 00.6931y = 12.2x = 10.7885y = 22.3x = 20.8329y = 110 2.1 2.3 2.1 2.0(0)(1)0.69310.832901102.0 2.32.3 2.0x x x x L f x f x x x x x ----=+=+----=0.7410抛物线插值:12200102()()()()x x x x l x x x x --=-- 02211012()()()()x x x x l x x x x --=-- 01222021()()()()x x x x l x x x x --=--2200211222L l y l y l y =++=0.7422.已知x=0,2,3,5对应的函数值分别为y=1,3,2,5.试求三次多项式的插值解:解:取00x = 12x = 23x = 35x = 12330010203()()()()()()x x x x x x l x x x x x x ---=--- 023********()()()()()()x x x x x x l x x x x x x ---=---01332202123()()()()()()x x x x x x l x x x x x x ---=--- 01233303132()()()()()()x x x x x x l x x x x x x ---=---3300311322333L l y l y l y l y =+++=1156261310323++-x x x3.设函数f(x)在[a,b]上具有直到二阶的连续导数,且f(a)=f(b)=0, 求证:2"1m ax |()|()m ax |()|8a x ba x bf x b a f x ≤≤≤≤≤-解:取01;x a x b ==,1()()0x a x b L f a f b a bb a--=+=--''''211()()()|()()||()()|||||224f f b a R f x L x x a x b εε-=-≤--≤∴''21()()|()||()|||||24f b a f x L x ε-≤+''1()|()||||()|8f L x b a ε=+-|||8)("|a b f -=ε4.证明n 次Lagrange 插值多项式基函数满足∑==ni ki n ki x x l x 0,)(, n k ≤≤0解:取()kf x x = 则n 0()nki i Ln lx x ==∑(1)()()()!n nii fx f x Ln Rn x x n +=-==-∑(1)0()()!k n nii x x x n +==-∑=0所以()()f x Ln x = 即证 5.证明 )(')()()(,xi x x x x l n i n i n ωω-=证明:、01110111()()()()()ln ()()()()()i i n i i i i i i i n x x x x x x x x x x i x x x x x x x x x x -+-+-----= -----01110111()()()()()()()()()()i i ni i ii i i i i nix x x x x x x x x x x x x x x x x x x x x x x x -+-+------=------取 0111()()()()()()n i ii n x x xx xxxx x x x x ω-+=------则 '1020111011()()()())()()()()()()()()()n nn i in n x x x x x x x x x x x x x xx xx x x x x x x x x xxω-+-=--+---+-----++--- ('0111()()()()()()n i i i i i i i i n x x x x x x x x x x x ω-+=-----所以,'()ln ()()n i n i x i x x x ωω=-6.设nn x a x a a x f ++=10)(有n 个不同的实根.,,21n x x x证明:=-=∑11,0)('n ni i kia x f x证明:取()kx x ?= 1()()n n x x xx ω=-- 而,0()nn f x a a x =++ 有n 个不同的实根。
习题六(Matlab数值计算)课后习题

习题六(Matlab数值计算)课后习题1、利⽤MATLAB 提供的randn 函数⽣成符合正态分布的10×5随机矩阵A,进⾏如下操作:(1)A 各列元素的均值和标准⽅差。
(2)A 的最⼤元素和最⼩元素。
(3)求A 每⾏元素的和以及全部元素之和。
(4)分别对A 的每列元素按升序、每⾏元素按降序排序。
A=randn(10,5);disp('各列元素的均值:');mean(A)disp('各列元素的标准⽅差:');std(A)disp('A 的最⼤元素:');max(max(A))disp('A 的最⼩元素:');min(min(A))disp('A 每⾏元素之和:');sum(A,2)disp('全部元素之和:');sum(sum(A))disp('每列元素按升序:');Y=sort(A)disp('每⾏元素按降序:');Y=sort(A,2,'descend')各列元素的均值:ans =-0.1095 0.1282 -0.2646 0.3030 -0.2464各列元素的标准⽅差:ans =0.9264 1.2631 0.8129 0.8842 1.3151A 的最⼤元素:ans =2.5855A 的最⼩元素:ans =-1.9330A 每⾏元素之和:ans =-2.29701.25450.06615.0489-0.69881.1002-2.9310-2.0595-1.68780.3112全部元素之和:ans =-1.8932每列元素按升序:Y =-1.2141 -1.4916 -1.4224 -1.1658 -1.9330-1.1135 -1.0891 -1.4023 -0.8045 -1.7947-0.8637 -1.0616 -0.7648 -0.2437 -1.1480-0.7697 -0.7423 -0.6156 0.1978 -0.6669-0.2256 0.0326 -0.1961 0.2157 -0.4390-0.0068 0.0859 -0.1924 0.2916 -0.08250.0774 0.5525 -0.1774 0.6966 0.10490.3714 1.1006 0.4882 0.8351 0.18731.1174 1.5442 0.7481 1.4193 0.72231.53262.3505 0.8886 1.5877 2.5855每⾏元素按降序:Y =1.4193 -0.6156 -0.8637 -1.0891 -1.14800.7481 0.2916 0.1049 0.0774 0.03260.7223 0.5525 0.1978 -0.1924 -1.21412.5855 1.5877 1.1006 0.8886 -1.11351.5442 -0.0068 -0.6669 -0.7648 -0.80451.5326 0.6966 0.1873 0.0859 -1.40230.8351 -0.0825 -0.7697 -1.4224 -1.49160.4882 0.3714 -0.2437 -0.7423 -1.93300.2157 -0.1774 -0.2256 -0.4390 -1.06162.3505 1.1174 -0.1961 -1.1658 -1.79472、按要求对指定函数进⾏插值和拟合。
(完整word版)数值分析作业-三次样条插值..
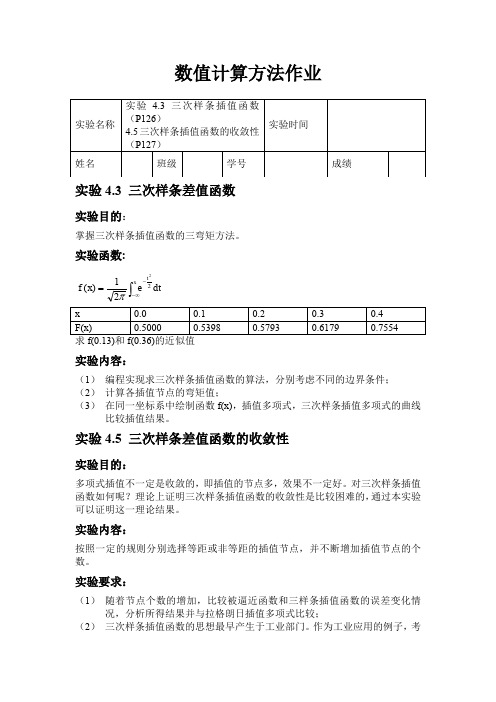
数值计算方法作业实验4.3 三次样条差值函数实验目的:掌握三次样条插值函数的三弯矩方法。
实验函数:dt ex f xt ⎰∞--=2221)(πx 0.0 0.1 0.2 0.3 0.4 F(x) 0.5000 0.5398 0.57930.61790.7554求f(0.13)和f(0.36)的近似值实验内容:(1) 编程实现求三次样条插值函数的算法,分别考虑不同的边界条件; (2) 计算各插值节点的弯矩值;(3) 在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲线比较插值结果。
实验4.5 三次样条差值函数的收敛性实验目的:多项式插值不一定是收敛的,即插值的节点多,效果不一定好。
对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。
实验内容:按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。
实验要求:(1) 随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情况,分析所得结果并与拉格朗日插值多项式比较;(2) 三次样条插值函数的思想最早产生于工业部门。
作为工业应用的例子,考实验名称 实验 4.3三次样条插值函数(P126)4.5三次样条插值函数的收敛性(P127) 实验时间姓名班级学号成绩虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线,其中一段数据如下: k x 0 1 2 3 4 5 6 7 8 9 10 k y 0.0 0.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29 ky ' 0.80.2算法描述:拉格朗日插值:错误!未找到引用源。
其中错误!未找到引用源。
是拉格朗日基函数,其表达式为:()∏≠=--=ni j j j i ji x x x x x l 0)()(牛顿插值:))...()(](,...,,[....))(0](,,[)0](,[)()(1102101210100----++--+-+=n n n x x x x x x x x x x f x x x x x x x f x x x x f x f x N其中⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧--=--=--=-)/(]),...,[],...,[(]...,[..],[],[],,[)()(],[01102110x x x x x f x x x f x x x f x x x x f x x f x x x f x x x f x f x x f n n n n i k j i k j k j i ji j i j i三样条插值:所谓三次样条插值多项式Sn(x)是一种分段函数,它在节点Xi(a<X0<X1……<Xn<b)分成的每个小区间[x i-1,x i ]上是三次多项式,其在此区间上的表达式如下:],[),6()6(]6)([6)(6)()(111113131i i ii i i i i i i i i i i i i i i i i i x x x h yM h M h h y x M M h h y y h x x Mi h x x M x S -------∈-+-+---+-+-=式中Mi=)(i x S ''.因此,只要确定了Mi 的值,就确定了整个表达式,Mi 的计算方法如下:令⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=---+=+=+=+--++++++],,[6)(6111111111i i i i i i i i i i i i i i i i i i i ix x x f h y y h y y h h d h h h h h h λμ则Mi 满足如下n-1个方程:1,...2,1,211-==+++-n i d M M M i i i i i i λμ 常用的边界条件有如下几类:(1) 给定区间两端点的斜率m 0,m n ,即n n n m y x S m y x S ='='='=')(,)(000 (2) 给定区间两端点的二阶导数M0,Mn,即n n n M y x S M y x S =''=''=''='')(,)(000 (3) 假设y=f(x)是以b-a 为周期的周期函数,则要求三次样条插值函数S (x )也为周期函数,对S (x )加上周期条件2,1,0),0()0()(0)(=-=+p x S x S n p p对于第一类边界条件有⎪⎪⎩⎪⎪⎨⎧--=+--=+--)(62)(6211001110n n n n n n i h y y mn h M M m h y y h M M对于第二类边界条件有⎩⎨⎧=+=+-n n n n d M M d M M 221100μλ其中n n n n nnn M u x x f m h d M m x x f h d )1(2]),[(6)1(2)],[(6100001010-+-=-+-=-μλλ那么解就可以为⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----n n n n n n n d d d d d M M M M M 1210121011...2...............2............................1..2.1......0..2μλμλμλ 对于第三类边界条件,)0()0(,,000-=+==n n n x S x S M M y y ,由此推得0010012d M M M n =-++μλ,其中]),1[],[(6,,101010110n n nn n n x x f x x f h h d h h h h h h --+=+=+=μλ,那么解就可以为: ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------1221012101221100...2.............2..............................2..,,.......,..22n n n n n n n d d d d d M M M M M n μλλμλμμλ 程序代码: 1拉格朗日插值函数Lang.mfunction f=lang(X,Y,xi) %X 为已知数据的横坐标 %Y 为已知数据的纵坐标 %xi 插值点处的横坐标%f 求得的拉格朗日插值多项式的值 n=length(X); f=0; for i=1:n l=1; for j=1:i-1l=l.*(xi-X(j))/(X(i)-X(j)); end ; for j=i+1:nl=l.*(xi-X(j))/(X(i)-X(j)); end ;%拉格朗日基函数 f=f+l*Y(i); endfprintf('%d\n',f) return2 牛顿插值函数newton.mfunction f=newton(X,Y,xi) %X 为已知数据的横坐标 %Y 为已知数据的纵坐标 %xi 插值点处的横坐标%f 求得的拉格朗日插值多项式的值 n=length(X);newt=[X',Y'];%计算差商表for j=2:nfor i=n:-1:1if i>=jY(i)=(Y(i)-Y(i-1))/(X(i)-X(i-j+1));else Y(i)=0;endendnewt=[newt,Y'];end%计算牛顿插值f=newt(1,2);for i=2:nz=1;for k=1:i-1z=(xi-X(k))*z;endf=f+newt(i-1,i)*z;endfprintf('%d\n',f)return3三次样条插值第一类边界条件Threch.mfunction S=Threch1(X,Y,dy0,dyn,xi)% X为已知数据的横坐标%Y为已知数据的纵坐标%xi插值点处的横坐标%S求得的三次样条插值函数的值%dy0左端点处的一阶导数% dyn右端点处的一阶导数n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:n%求函数的一阶差商h(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:n%求函数的二阶差商f2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=6*(f1(1)-dy0)/h(1);d(n+1)=6*(dyn-f1(n-1))/h(n-1);%¸赋初值A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=1;A(n+1,n)=1;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;syms x;for i=1:nSx(i)=collect(Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x-X(i))...+M(i)/2*(x-X(i))^2+(M(i+1)-M(i))/(6*h(i))*(x-X(i))^3);digits(4);Sx(i)=vpa(Sx(i));%三样条插值函数表达式endfor i=1:ndisp('S(x)=');fprintf('%s (%d,%d)\n',char(Sx(i)),X(i),X(i+1));endfor i=1:nif xi>=X(i)&&xi<=X(i+1)S=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(xi-X(i))+M(i)/2*(xi-X(i))^2+(M (i+1)-M(i))/(6*h(i))*(xi-X(i))^3;endenddisp('xi S');fprintf('%d,%d\n',xi,S);return4 三次样条插值第二类边界条件Threch2.mfunction [Sx]=Threch2(X,Y,d2y0,d2yn,xi)X为已知数据的横坐标%Y为已知数据的纵坐标%xi插值点处的横坐标%S求得的三次样条插值函数的值%d2y0左端点处的二阶导数% d2yn右端点处的二阶导数n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:n%求一阶差商h(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:n%求二阶差商f2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=2*d2y0;d(n+1)=2*d2yn;%赋初值A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=0;A(n+1,n)=0;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;syms x;for i=1:nSx(i)=collect(Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x-X(i))... +M(i)/2*(x-X(i))^2+(M(i+1)-M(i))/(6*h(i))*(x-X(i))^3);digits(4);Sx(i)=vpa(Sx(i));endfor i=1:ndisp('S(x)=');fprintf('%s (%d,%d)\n',char(Sx(i)),X(i),X(i+1));endfor i=1:nif xi>=X(i)&&xi<=X(i+1)S(i)=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(xi-X(i))+M(i)/2*(xi-X(i))^2 +(M(i+1)-M(i))/(6*h(i))*(xi-X(i))^3;endenddisp('xi S');fprintf('%d,%d\n',xi,S);return5插值节点处的插值结果main3.mclearclcX=[0.0,0.1,0.2,0.3,0.4];Y=[0.5000,0.5398,0.5793,0.6179,0.7554];xi=0.13;%xi=0.36;disp('xi=0.13');%disp('xi=0.36');disp('拉格朗日插值结果');lang(X,Y,xi);disp('牛顿插值结果');newton(X,Y,xi);disp('三次样条第一类边界条件插值结果');Threch1(X,Y,0.40,0.36,xi);%0.4,0.36分别为两端点处的一阶导数disp('三次样条第二类边界条件插值结果');Threch2(X,Y,0,-0.136,xi);%0,-0.136分别为两端点处的二阶导数6将多种插值函数即原函数图像画在同一张图上main2.mclearclcX=[0.0,0.1,0.2,0.3,0.4];Y=[0.5000,0.5398,0.5793,0.6179,0.7554];a=linspace(0,0.4,21);NUM=21;L=zeros(1,NUM);N=zeros(1,NUM);S=zeros(1,NUM);B=zeros(1,NUM);for i=1:NUMxi=a(i);L(i)=lang(X,Y,xi);% 拉格朗日插值N(i)=newton(X,Y,xi);%牛顿插值B(i)=normcdf(xi,0,1);%原函数S(i)=Threch1(X,Y,0.4,0.36,xi);%三次样条函数第一类边界条件endplot(a,B,'--r');hold on;plot(a,L,'b');hold on;plot(a,N,'r');hold on;plot(a,S,'r+');hold on;legend('原函数','拉格朗日插值','牛顿插值','三次样条插值',2);hold off7增加插值节点观察误差变化main4.mclear;clc;N=5;%4.5第一问Ini=zeros(1,1001);a=linspace(-1,1,1001);Ini=1./(1+25*a.^2);for i=1:3 %节点数量变化次数N=2*N;t=linspace(-1,1,N+1);%插值节点ft=1./(1+25*t.^2);%插值节点函数值val=linspace(-1,1,101);for j=1:101L(j)=lang(t,ft,val(j));S(j)=Threch1(t,ft,0.074,-0.074,val(j));%三样条第一类边界条件插值endplot(a,Ini,'k')%原函数图象hold onplot(val,L,'r')%拉格朗日插值函数图像hold onplot(val,S,'b')%三次样条插值函数图像str=sprintf('插值节点为%d时的插值效果',N);title(str);legend('原函数','拉格朗日插值','三次样条插值');%显示图例hold offfigureend8车门曲线main5.mclearclcX=[0,1,2,3,4,5,6,7,8,9,10];Y=[0.0,0.79,1.53,2.19,2.71,3.03,3.27,2.89,3.06,3.19,3.29]; dy0=0.8;dyn=0.2;n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:nh(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:nf2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=6*(f1(1)-dy0)/h(1);d(n+1)=6*(dyn-f1(n-1))/h(n-1); A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=1;A(n+1,n)=1;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;x=zeros(1,n);S=zeros(1,n);for i=1:nx(i)=X(i)+0.5;S(i)=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x(i)-X(i))+M(i)/2*(x(i)-X(i ))^2+(M(i+1)-M(i))/(6*h(i))*(x(i)-X(i))^3;endplot(X,Y,'k'); hold on;plot(x,S,'o');title('三次样条插值效果图');legend('已知插值节点','三次样条插值');hold off实验结果:4.31计算插值节点处的函数值xi=0.13时Xi=0.36时2将多种插值函数即原函数图像画在同一张图上4.5.1增加插值节点观察误差变化4.5.2 车门曲线。
三次样条插值作业题

例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%============================= % 本段代码解决作业题的例1 %============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2;RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1);for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i);end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i)); end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepVar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1); for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) ); S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-',num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=1和x=2两个横轴点作垂线 %line([1, 1], [2.5, -0.5], 'LineStyle', '--');line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x轴和y轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ...'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
数值分析作业-三次样条插值
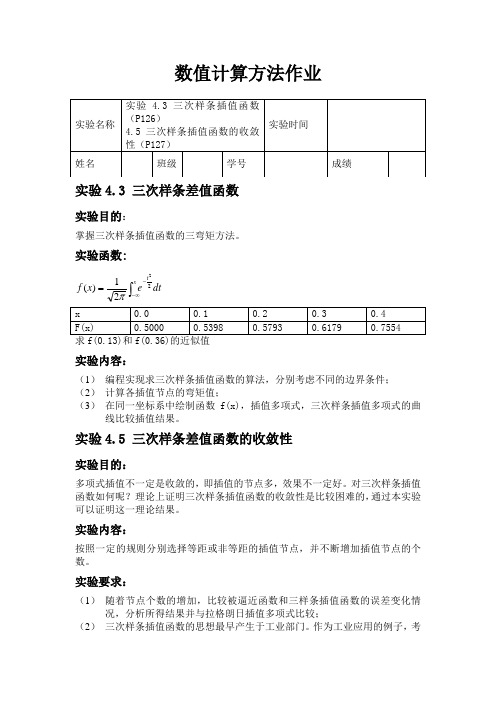
数值计算方法作业实验4.3 三次样条差值函数实验目的:掌握三次样条插值函数的三弯矩方法。
实验函数:dt ex f xt ⎰∞--=2221)(π实验内容:(1) 编程实现求三次样条插值函数的算法,分别考虑不同的边界条件; (2) 计算各插值节点的弯矩值;(3) 在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲线比较插值结果。
实验4.5 三次样条差值函数的收敛性实验目的:多项式插值不一定是收敛的,即插值的节点多,效果不一定好。
对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。
实验内容:按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。
实验要求:(1) 随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情况,分析所得结果并与拉格朗日插值多项式比较;(2) 三次样条插值函数的思想最早产生于工业部门。
作为工业应用的例子,考虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线,其中一段数据如下:kx012345678910 ky0.00.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29ky'0.80.2算法描述:拉格朗日插值:其中是拉格朗日基函数,其表达式为:()∏≠=--=nijj jiji xxxxxl)()(牛顿插值:))...()(](,...,,[....))(](,,[)0](,[)()(11211211----++--+-+=nnnxxxxxxxxxxfxxxxxxxfxxxxfxfxN其中⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧--=--=--=-)/(]),...,[],...,[(]...,[..],[],[],,[)()(],[11211xxxxxfxxxfxxxfxxxxfxxfxxxfxxxfxfxxfnnnnikjikjkjijijiji三样条插值:所谓三次样条插值多项式Sn(x)是一种分段函数,它在节点Xi(a<X0<X1……<Xn<b)分成的每个小区间[xi-1,xi]上是三次多项式,其在此区间上的表达式如下:],[),6()6(]6)([6)(6)()(111113131iiiiiiiiiiiiiiiiiiiiixxxhyMhMhhyxMMhhyyhxxMihxxMxS-------∈-+-+---+-+-=式中Mi=)(ixS''.因此,只要确定了Mi 的值,就确定了整个表达式,Mi 的计算方法如下:令⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=---+=+=+=+--++++++],,[6)(6111111111i i i i i i i i i i i i i i i i i i i ix x x f h y y h y y h h d h h h h h h λμ则Mi 满足如下n-1个方程:1,...2,1,211-==+++-n i d M M M i i i i i i λμ 常用的边界条件有如下几类:(1) 给定区间两端点的斜率m 0,m n ,即n n n m y x S m y x S ='='='=')(,)(000 (2) 给定区间两端点的二阶导数M0,Mn,即n n n M y x S M y x S =''=''=''='')(,)(000 (3) 假设y=f(x)是以b-a 为周期的周期函数,则要求三次样条插值函数S (x )也为周期函数,对S (x )加上周期条件2,1,0),0()0()(0)(=-=+p x S x S n p p对于第一类边界条件有⎪⎪⎩⎪⎪⎨⎧--=+--=+--)(62)(6211001110n n n n n n i h y y mn h M M m h y y h M M对于第二类边界条件有⎩⎨⎧=+=+-n n n n d M M d M M 221100μλ其中n n n n nnn M u x x f m h d M m x x f h d )1(2]),[(6)1(2)],[(6100001010-+-=-+-=-μλλ那么解就可以为⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----n n n n n n n d d d d d M M M M M 1210121011...2...............2............................1..2.1......0..2μλμλμλ对于第三类边界条件,)0()0(,,000-=+==n n n x S x S M M y y ,由此推得0010012d M M M n =-++μλ,其中]),1[],[(6,,101010110n n nn n n x x f x x f h h d h h h h h h --+=+=+=μλ,那么解就可以为: ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------1221012101221100...2.............2..............................2..,,.......,..22n n n n n n n d d d d d M M M M M n μλλμλμμλ 程序代码: 1拉格朗日插值函数Lang.mfunction f=lang(X,Y,xi) %X 为已知数据的横坐标 %Y 为已知数据的纵坐标 %xi 插值点处的横坐标%f 求得的拉格朗日插值多项式的值 n=length(X); f=0; for i=1:n l=1; for j=1:i-1l=l.*(xi-X(j))/(X(i)-X(j)); end ; for j=i+1:nl=l.*(xi-X(j))/(X(i)-X(j)); end ;%拉格朗日基函数 f=f+l*Y(i); endfprintf('%d\n',f) return2 牛顿插值函数newton.mfunction f=newton(X,Y,xi) %X 为已知数据的横坐标 %Y 为已知数据的纵坐标%xi插值点处的横坐标%f求得的拉格朗日插值多项式的值n=length(X);newt=[X',Y'];%计算差商表for j=2:nfor i=n:-1:1if i>=jY(i)=(Y(i)-Y(i-1))/(X(i)-X(i-j+1));else Y(i)=0;endendnewt=[newt,Y'];end%计算牛顿插值f=newt(1,2);for i=2:nz=1;for k=1:i-1z=(xi-X(k))*z;endf=f+newt(i-1,i)*z;endfprintf('%d\n',f)return3三次样条插值第一类边界条件Threch.mfunction S=Threch1(X,Y,dy0,dyn,xi)% X为已知数据的横坐标%Y为已知数据的纵坐标%xi插值点处的横坐标%S求得的三次样条插值函数的值%dy0左端点处的一阶导数% dyn右端点处的一阶导数n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:n%求函数的一阶差商h(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:n%求函数的二阶差商f2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=6*(f1(1)-dy0)/h(1);d(n+1)=6*(dyn-f1(n-1))/h(n-1);%¸赋初值A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=1;A(n+1,n)=1;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;syms x;for i=1:nSx(i)=collect(Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x-X(i))...+M(i)/2*(x-X(i))^2+(M(i+1)-M(i))/(6*h(i))*(x-X(i))^3);digits(4);Sx(i)=vpa(Sx(i));%三样条插值函数表达式endfor i=1:ndisp('S(x)=');fprintf('%s (%d,%d)\n',char(Sx(i)),X(i),X(i+1));endfor i=1:nif xi>=X(i)&&xi<=X(i+1)S=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(xi-X(i))+M(i)/2*(xi-X(i))^2+(M(i+1)-M(i))/(6 *h(i))*(xi-X(i))^3;endenddisp('xi S');fprintf('%d,%d\n',xi,S);return4 三次样条插值第二类边界条件Threch2.mfunction [Sx]=Threch2(X,Y,d2y0,d2yn,xi)X为已知数据的横坐标%Y为已知数据的纵坐标%xi插值点处的横坐标%S求得的三次样条插值函数的值%d2y0左端点处的二阶导数% d2yn右端点处的二阶导数n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:n%求一阶差商h(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:n%求二阶差商f2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=2*d2y0;d(n+1)=2*d2yn;%赋初值A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=0;A(n+1,n)=0;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;syms x;for i=1:nSx(i)=collect(Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x-X(i))... +M(i)/2*(x-X(i))^2+(M(i+1)-M(i))/(6*h(i))*(x-X(i))^3);digits(4);Sx(i)=vpa(Sx(i));endfor i=1:ndisp('S(x)=');fprintf('%s (%d,%d)\n',char(Sx(i)),X(i),X(i+1));endfor i=1:nif xi>=X(i)&&xi<=X(i+1)S(i)=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(xi-X(i))+M(i)/2*(xi-X(i))^2+(M(i+1)-M(i)) /(6*h(i))*(xi-X(i))^3;endenddisp('xi S');fprintf('%d,%d\n',xi,S);return5插值节点处的插值结果main3.mclearclcX=[0.0,0.1,0.2,0.3,0.4];Y=[0.5000,0.5398,0.5793,0.6179,0.7554];xi=0.13;%xi=0.36;disp('xi=0.13');%disp('xi=0.36');disp('拉格朗日插值结果');lang(X,Y,xi);disp('牛顿插值结果');newton(X,Y,xi);disp('三次样条第一类边界条件插值结果');Threch1(X,Y,0.40,0.36,xi);%0.4,0.36分别为两端点处的一阶导数disp('三次样条第二类边界条件插值结果');Threch2(X,Y,0,-0.136,xi);%0,-0.136分别为两端点处的二阶导数6将多种插值函数即原函数图像画在同一张图上main2.mclearclcX=[0.0,0.1,0.2,0.3,0.4];Y=[0.5000,0.5398,0.5793,0.6179,0.7554];a=linspace(0,0.4,21);NUM=21;L=zeros(1,NUM);N=zeros(1,NUM);S=zeros(1,NUM);B=zeros(1,NUM);for i=1:NUMxi=a(i);L(i)=lang(X,Y,xi);% 拉格朗日插值N(i)=newton(X,Y,xi);%牛顿插值B(i)=normcdf(xi,0,1);%原函数S(i)=Threch1(X,Y,0.4,0.36,xi);%三次样条函数第一类边界条件endplot(a,B,'--r');hold on;plot(a,L,'b');hold on;plot(a,N,'r');hold on;plot(a,S,'r+');hold on;legend('原函数','拉格朗日插值','牛顿插值','三次样条插值',2);hold off7增加插值节点观察误差变化main4.mclear;clc;N=5;%4.5第一问Ini=zeros(1,1001);a=linspace(-1,1,1001);Ini=1./(1+25*a.^2);for i=1:3 %节点数量变化次数N=2*N;t=linspace(-1,1,N+1);%插值节点ft=1./(1+25*t.^2);%插值节点函数值val=linspace(-1,1,101);for j=1:101L(j)=lang(t,ft,val(j));S(j)=Threch1(t,ft,0.074,-0.074,val(j));%三样条第一类边界条件插值endplot(a,Ini,'k')%原函数图象hold onplot(val,L,'r')%拉格朗日插值函数图像hold onplot(val,S,'b')%三次样条插值函数图像str=sprintf('插值节点为%d时的插值效果',N);title(str);legend('原函数','拉格朗日插值','三次样条插值');%显示图例hold offfigureend8车门曲线main5.mclearclcX=[0,1,2,3,4,5,6,7,8,9,10];Y=[0.0,0.79,1.53,2.19,2.71,3.03,3.27,2.89,3.06,3.19,3.29]; dy0=0.8;dyn=0.2;n=length(X)-1;d=zeros(n+1,1);h=zeros(1,n-1);f1=zeros(1,n-1);f2=zeros(1,n-2);for i=1:nh(i)=X(i+1)-X(i);f1(i)=(Y(i+1)-Y(i))/h(i);endfor i=2:nf2(i)=(f1(i)-f1(i-1))/(X(i+1)-X(i-1));d(i)=6*f2(i);endd(1)=6*(f1(1)-dy0)/h(1);d(n+1)=6*(dyn-f1(n-1))/h(n-1); A=zeros(n+1,n+1);B=zeros(1,n-1);C=zeros(1,n-1);for i=1:n-1B(i)=h(i)/(h(i)+h(i+1));C(i)=1-B(i);endA(1,2)=1;A(n+1,n)=1;for i=1:n+1A(i,i)=2;endfor i=2:nA(i,i-1)=B(i-1);A(i,i+1)=C(i-1);endM=A\d;x=zeros(1,n);S=zeros(1,n);for i=1:nx(i)=X(i)+0.5;S(i)=Y(i)+(f1(i)-(M(i)/3+M(i+1)/6)*h(i))*(x(i)-X(i))+M(i)/2*(x(i)-X(i))^2+(M(i+1)-M (i))/(6*h(i))*(x(i)-X(i))^3;endplot(X,Y,'k'); hold on;plot(x,S,'o');title('三次样条插值效果图');legend('已知插值节点','三次样条插值');hold off实验结果:4.31计算插值节点处的函数值xi=0.13时Xi=0.36时2将多种插值函数即原函数图像画在同一张图上4.5.1增加插值节点观察误差变化从上面三张图可以看出增加插值节点并不能改善差之效果4.5.2 车门曲线(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
数值逼近蒋尔雄3样条插值和曲线拟合答案

第三章 样条插值和曲线拟合1.x y =有如下的函数表试用一次、二次、三次、四次多项式插值函数求8,看哪一个最接近8。
解 先作差商表4167121013934201511008160124601316111100-⨯---故:8.2)48(512)8(1=-+=p819047619.2)98)(48(2101)48(512)8(2=----+=p844444.2)98)(48)(18(34201)48)(18(601)18(311)8(3=---⨯+----+=p6222.2)1(47810081478601)18(861)08(10)8(4=-⨯⨯⨯-⨯⨯+---⨯+=p 已知828427.28=,因此选定)8(,16,9,42321p x x x ===最接近8。
利用Neville 方法得:xi8-xif(xi) 2.828427188171-1.333333333.3333333 2.4 4422.866666667 2.62222222.8 2.84444449-1 32.8190476192.8571429 16 -8 4f(8)= 2.828427125 xi8-xif(xi)88171-1 1/33 1/3 2 2/5 4422 13/15 2 28/452 4/5 2 38/45 9-1 32 86/1052 6/7 16 -8 4已知 828427.28=,故选定)8(,16,9,42321p x x x ====2.819047619最接近8.11101201011121213434342121------ 所以:)())(1())(1()1(1)(21213421344-++-++++-=x x x x x x x x x p , 故:0232.0)1.0(4=p 与f (0.1)=0.1不相等。
(2)若采用分段插值,则在],0[21上,x x f x f x L =--+--=00)(0)0()(21212121,所以: )1.0(1.0)1.0(f L ==,结果一样。
第五章(3)三次样条插值

6( xi xi 1 2 x ) ( yi 1 yi ) 3 hi 1
而
2 4 6 S ( xi 0) mi 1 mi 2 ( yi yi 1 ) hi hi hi 4 2 6 S ( xi 0) mi m i 1 2 ( yi 1 yi ) hi 1 hi 1 hi 1
n
当n 时,Ln ( x )只在 | x | 3.63 内收敛,而在该区间外 是发散的。
从图中可以看出,在 0 附近插值效果是好的,即余项较 小,另一种现象是插值多项式随节点增多而振动。这种插值 多项式当节点增加时反而不能更好地接近被插值函数的现象, 称为龙格现象。
上述现象告诉我们用高次插值多项式是不 妥当的,从数值计算上可解释为高次插值多项 式的计算会带来舍入误差的增大,从而引起计 算失真。因此,实践上作插值时一般只用一次、 二次最多用三次插值多项式。
式中x [ xi 1 , xi ] (i 1,2,, n)
第(2)步
为了确定mi,需要用到S ( x )的二阶导数在节点连续 的条件, S ( x )在[ xi 1 , xi ]和[ xi , xi 1 ]上的二阶导数分别为
Si( x ) 6 x 2 xi 1 4 xi 6 x 4 xi 1 2 xi mi 1 mi 2 2 hi hi ( x [ xi 1 , xi ])
若记hi xi xi 1,则上式可写为
( x x i ) 2 hi 2( x x i 1 ) ( x x i 1 ) 2 hi 2( x i x ) Si ( x) y i 1 yi 3 3 hi hi ( x x i ) 2 ( x x i 1 ) ( x x i 1 ) 2 ( x x i ) m i 1 mi 2 2 hi hi
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j j j j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%============================= % 本段代码解决作业题的例1%============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2;RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1);for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i);end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i));% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepVar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1); for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) );S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ),'-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-', num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14) hold on end% 过x=1和x=2两个横轴点作垂线 % line([1, 1], [2.5, -0.5], 'LineStyle', '--'); line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x 轴和y 轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ... 'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j j j j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%============================= % 本段代码解决作业题的例2%============================= clear all clc% 自变量x 与因变量y 的取值 IndVar = [1, 2, 4, 5]; DepVar = [1, 3, 4, 2];% 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1);for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i);end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 0;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 0;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i));end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 0;for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 0;% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) );S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i, polyval(Part_1, 5), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ),'-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-', num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=2和x=4两个横轴点作垂线 % line([2, 2], [4.5, 0.5], 'LineStyle', '--'); line([4, 4], [4.5, 0.5], 'LineStyle', '--');% 为x 轴和y 轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ... 'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次自然样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+--∈-+-+----∈-+-+--=.5,4,)4(2)5(375.4)5(375.0,4,2,)2(75.2)4(75.1)2(1875.0)4(0625.0,2,1,)1(125.3)2()1(125.0)(3333x x x x x x x x x x x x x x s曲线的图像如图所示:[][][][]⎪⎪⎩⎪⎪⎨⎧∈-+-+--∈-+-+----∈-+-+----∈-+-+--=.53.0,45.0,)45.0(1.9)53.0(3987.8)53.0(1442.2,45.0,39.0,)39.0(1903.11)45.0(417.10)39.0(859.2)45.0(399.2,39.0,30.0,)3.0(9518.6)39.0(1137.6)3.0(5993.1)39.0(4806.3,30.0,25.0,)25.0(9697.10)3.0(10)25.0(2652.6)(333333x x x x x x x x x x x x x x x x x x x s试求在区间[0.25,0.53]上满足上述函数表所给出的插值条件的三次自然样条插值函数s(x)求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j jjj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++本题采用和例2基本相同的Matlab 代码,只改变初始条件。
