统计分析与SPSS的应用薛薇第四版的第六章课后习题:第一题
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.016.817.921.223.926.822.4第二组24.921.322.630.229.922.520.7第三组16.020.117.320.922.026.820.8第四组17.518.220.217.719.118.416.5第五组25.226.226.929.330.429.728.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
ANOVA销售额平方和df均方F显著性组之间405.5344101.38411.276.000组内269.737308.991总计675.27134概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量:销售额LSD(L)95%置信区间平均差(I)组别(J)组别(I-J)标准错误显著性下限值上限第一组第二组-3.30000 *1.60279.048-6.5733-.0267第三组.728571.60279.653-2.54484.0019第四组3.057141.60279.066-.21626.3305第五组-6.70000 *1.60279.000-9.9733-3.4267*1.60279.048.02676.5733第二组第一组3.30000第三组4.02857 *1.60279.018.75527.3019*1.60279.0003.08389.6305第四组6.35714*第五组-3.400001.60279.042-6.6733-.1267第三组第一组-.728571.60279.653-4.00192.5448第二组-4.02857 *1.60279.018-7.3019-.7552第四组2.328571.60279.157-.94485.6019第五组-7.42857 *1.60279.000-10.7019-4.1552第四组第一组-3.057141.60279.066-6.3305.2162第二组-6.35714 *1.60279.000-9.6305-3.0838第三组-2.328571.60279.157-5.6019.9448第五组-9.75714 *1.60279.000-13.0305-6.4838*1.60279.0003.42679.9733第五组第一组6.70000*1.60279.042.12676.6733第二组3.40000*1.60279.0004.155210.7019第三组7.42857*1.60279.0006.483813.0305第四组9.75714*.均值差的显著性水平为0.05。
最新《统计分析与SPSS的应用(第五版)》课后练习答案(第4章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第4章SPSS基本统计分析1、利用第2章第7题数据采用SPSS频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析——描述统计——频率,选择“常住地”,“职业”和“年龄”到变量中,然后,图表——条形图——图表值(频率)——继续,勾选显示频率表格,点击确定。
Statistics户口所在地职业年龄N Valid 282 282 282Missing 0 0 0户口所在地Frequency Percent ValidPercentCumulativePercentValid 中心城市200 70.9 70.9 70.9 边远郊区82 29.1 29.1 100.0 Total 282 100.0 100.0职业Frequency Percent ValidPercentCumulativePercentValid 国家机关24 8.5 8.5 8.5 商业服务业54 19.1 19.1 27.7 文教卫生18 6.4 6.4 34.0公交建筑业15 5.3 5.339.4 经营性公司18 6.4 6.445.7学校155.3 5.351.1一般农户3512.4 12.4 63.5 种粮棉专业户4 1.4 1.4 64.9 种果菜专业户10 3.5 3.5 68.4 工商运专业户34 12.1 12.1 80.5 退役人员17 6.0 6.0 86.5 金融机构35 12.4 12.4 98.9现役军人 3 1.11.1 100.0Total 282 100.0 100.0年龄Frequency Percent ValidPercent Cumulative PercentValid 20岁以下 4 1.4 1.4 1.4 20~35岁146 51.8 51.8 53.2 35~50岁91 32.3 32.3 85.5 50岁以上41 14.5 14.5 100.0 Total 282 100.0 100.0分析:本次调查的有效样本为282份。
薛薇SPSS统计分析方法及应用第六章方差分析精品文档

单因素方差分析的进一步分析
进一步 分析
方差相等时的一些多重比较方法
LSD方法
最小显著性差异法。用T检验完成组间成对均值的 比较。检验的敏感度较高,即使是各个水平间的均 值存在细微差别也有可能被检验出来,但此方法对 第一类弃真错误不进行控制和调整。
Bonferroni方法
修正最小显著性差异法。用T检验完成组间成对均值的比 较,但通过设置每个检验的误差率来控制整个误差率。因此 采用此方法看到的显著值是多重比较完成后的调整值。
1)
MSA MSAB
FB
SSB/(r 1) SSAB/(k 1)(r 1)
MSA MSAB
计算检验统计量观测值和概率P值
给出显著性水平 ,并作出统计决策
(1)若FA的概率p< ,则拒绝原假设,即认为控制
变量A的不同水平对观测变量产生了显著影响。
(2)FB的概率p< ,则拒绝原假设,即认为控制变
(4)给定显著性水平,得出结论。
当 p 时,拒绝原假设,即认为控制变量
不同水平下观测变量各总体的均值存在显著差异;
当 p 时,则不能拒绝原假设,即认为控
制变量不同水平下观测变量各总体的均值没有显 著差异
单因素方差分析的基本操作及应用
举例
广告形式对销售额的单因素方差分析
以广告城市与销售额.sav为例
多因素方差分析的其他功能
均值检验 模型分析
多因素方差分析的进一步分析的操 作
建立 非饱和
模型
均值比较的操作
练习
某教学实验中,采用不同的教学方法和不同的 教材进行教学实验,获得一系列数据,现在分析不 同教学方法和不同教材对教改成绩的影响,数据附 在文件夹教改成绩.sav。要求:进行均值的多重比 较,方法选用LSD法,得出教改成绩多因素方差分 析的饱和模型表和非饱和模型表,并得出教学方法 和教材的交互作用图。
《统计分析与SPSS的应用(第五版)》课后练习标准答案(第6章)

《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)————————————————————————————————作者:————————————————————————————————日期:《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5第五组25.2 26.2 26.9 29.3 30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组-3.30000* 1.60279 .048 -6.5733 -.0267 第三组.72857 1.60279 .653 -2.5448 4.0019第四组 3.05714 1.60279 .066 -.2162 6.3305第五组-6.70000* 1.60279 .000 -9.9733 -3.4267 第二组第一组 3.30000* 1.60279 .048 .0267 6.5733 第三组 4.02857* 1.60279 .018 .7552 7.3019第四组 6.35714* 1.60279 .000 3.0838 9.6305第五组-3.40000* 1.60279 .042 -6.6733 -.1267 第三组第一组-.72857 1.60279 .653 -4.0019 2.5448 第二组-4.02857* 1.60279 .018 -7.3019 -.7552第四组 2.32857 1.60279 .157 -.9448 5.6019第五组-7.42857* 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.05714 1.60279 .066 -6.3305 .2162第二组-6.35714* 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714* 1.60279 .000 -13.0305 -6.4838第五组第一组 6.70000* 1.60279 .000 3.4267 9.9733 第二组 3.40000* 1.60279 .042 .1267 6.6733第三组7.42857* 1.60279 .000 4.1552 10.7019第四组9.75714* 1.60279 .000 6.4838 13.0305*. 均值差的显著性水平为 0.05。
《统计分析与SPSS的应用》课后练习答案(第3章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第3章SPSS数据的预处理1利用第2章第7题数据,采用SPSS数据筛选功能将数据分成两份文件。
其中,第一份数据文件存储常住地是“沿海或中心繁华城市”且本次存款金额在1000至5000 之间的调查数据;第二份数据文件是按照简单随机抽样所选取的70%的样本数据。
第一份文件:选取数据数据——选择个案——如果条件满足——存款>=1000& 存款<5000& 常住地=沿海或中心繁华城市。
第二份文件:选取数据数据——选择个案——随机个案样本——输入70。
2、利用第2章第7题数据,将其按常住地(升序)、收入水平(升序)、存款金额(降序)进行多重排序。
排序数据——排序个案——把常住地、收入水平、存款金额作为排序依据分别设置排列顺序。
3、利用第2章第9题的完整数据,对每个学生计算得优课程数和得良课程数,并按得优课程数的降序排序。
计算转换——对个案内的值计数输入目标变量及目标标签,把所有课程选取到数字变量,定义值——设分数的区间,之后再排序。
4、利用第2章第9题的完整数据,计算每个学生课程的平均分以及标准差。
同时,计算男生和女生各科成绩的平均分。
方法一:利用描述性统计,数据——转置学号放在名称变量,全部课程放在变量框中,确定后,完成转置。
分析——描述统计——描述,将所有学生变量全选到变量框中,点击选项——勾选均值、标准差。
先拆分数据——拆分文件按性别拆分,分析——描述统计——描述,全部课程放在变量框中,选项——均值。
方法二:利用变量计算,转换——计算变量分别输入目标变量名称及标签——均值用函数mean完成平均分的计算,标准差用函数SD完成标准差的计算。
数据----------------- 分类汇总--- 性别作为分组变量、全部课程作为变量摘要、(创建只包含汇总变量的新数据集并命名)——确定5、利用第2章第7题数据,大致浏览存款金额的数据分布状况,并选择恰当的组限和组距进行组距分组。
统计分析与SPSS的应用(第五版)课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
可知,1和2、1和5、2和3,2和4,2和5,3和5,4和5有显著差异。
2、从两个总体中分别抽取n 1 =7 和和n 2 =6 的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格“A”和单元格“B”内的计算结果。
答:已知组内均方=组内偏差平方和/自由度,所以A=26.4/11=2.4F 统计量=组间均方/组内均方所以B=7.5/2.4=3.1253、为研究某种降血压药的适用特点,在五类具有不同临床特征的高血压患者中随机挑选了若干志愿者进行对比试验,并获得了服用该降压药后的血压变化数据。
现对该数据进行单因素方差分析,所得部分分析结果如下表所示。
1)请根据表格数据说明以上分析是否满足方差分析的前提要求,为什么?2)请填写表中空缺部分的数据结果,并说明该降压药对不同组患者的降压效果是否存在显著差异。
3)如果该降压药对不同组患者的降压效果存在显著差异,那么该降压药更适合哪组患者?(1)因F检验的概率P值小于显著性水平(0.05),拒绝原假设,方差不齐,不满足方差分析的前提假设。
《统计分析与SPSS的应用》课后练习答案(第1章)

《统计分析与SPSS的应用》课后练习答案(第1章)《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第1章SPSS统计分析软件概述1、SPSS的中文全名和英文全名是什么SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是:Statistical Package for the Social Science.(StatisticalProduct and Service Soluti ons)2、SPSS有哪两个主要窗口它们的作用和特点各是什么SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据;结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、什么是SPSS的数据集什么是SPSS的活动数据集SPSS的数据集:SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
活动数据集:其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS有哪三种主要使用方式各自的特点是什么SPSS的三种基本运行方式:完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
程序运行方式:是指在使用SPSS的过程中,统计分析人员根据自己的需要,手工编写SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式:是前两者的综合。
5、.sav、.spo、.sps分别是SPSS哪类文件的扩展名sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps 是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在哪些菜单中统计绘图和分析功能主要集中在哪些菜单中SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
《统计分析与SPSS的应用》课后练习答案(第4章)

统计分析与SPSS 的应用(第五版)》课后练习答案第4 章SPSS 基本统计分析1 、利用第2 章第7 题数据采用SPSS 频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析——描述统计——频率,选择“常住地” ,“职业”和“年龄”到变量中,然后,图表——条形图——图表值(频率)——继续,勾选显示频率表格,点击确定。
户口所在地职业年龄分析:本次调查的有效样本为282 份。
常住地的分布状况是:在中心城市的人最多,有200 人,而在边远郊区只有82 人;职业的分布状况是:在商业服务业的人最多,其次是一般农户和金融机构;年龄方面:在35-50 岁的人最多。
由于变量中无缺失数据,因此频数分布表中的百分比相同。
2、利用第2 章第7 题数据,从数据的集中趋势、离散程度以及分布形状等角度,分析被调查者本次存款金额的基本特征,并与标准正态分布曲线进行对比。
进一步,对不同常住地储户存款金额的基本特征进行对比分析。
分析——描述统计——描述,选择存款金额到变量中。
点击选项,勾选均值、标准差、方差、最小值、最大值、范围、偏度、峰度、按变量列表,点击继续——确定。
分析:由表中可以看出,有效样本为282 份,存(取)款金额的均值是4738.09 ,标准差为10945.09 ,峰度系数为33.656 ,偏度系数为5.234 。
与标准正态分布曲线进行对比,由峰度系数可以看出,此表的存款金额的数据分布比标准正态分布更陡峭;由偏度系数可以看出,此表的存款金额的数据为右偏分布,表明此表的存款金额均值对平均水平的测度偏大。
分析:由表中可以看出,中心城市有200 人,边远郊区为82 人。
两部分样本存取款金额均呈右偏尖峰分布,且边远郊区更明显。
3、利用第2 章第7 题数据,如果假设存款金额服从正态分布,能否利用本章所讲解的功能,找到存款金额“与众不同”的样本,并说明理由。
分析——描述统计——描述,选择存款金额到变量中。
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)
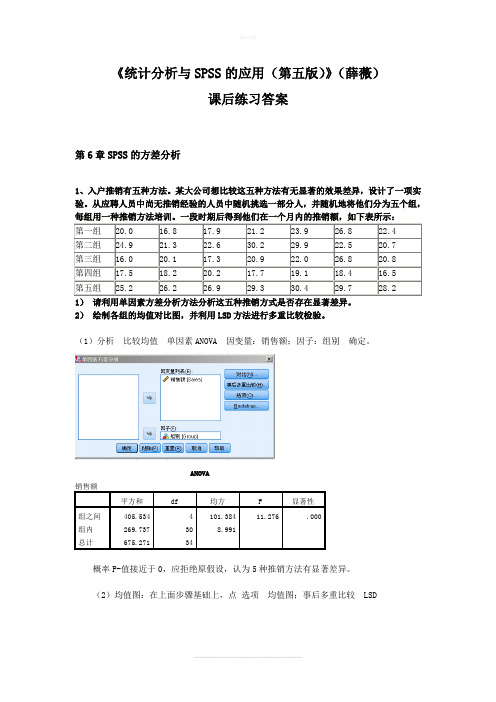
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.016.817.921.223.926.822.4第二组24.921.322.630.229.922.520.7第三组16.020.117.320.922.026.820.8第四组17.518.220.217.719.118.416.5第五组25.226.226.929.330.429.728.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
ANOVA销售额平方和df均方F显著性组之间405.5344101.38411.276.000组内269.737308.991总计675.27134概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J)标准错误显著性95% 置信区间下限值上限第一组第二组-3.30000* 1.60279.048-6.5733-.0267第三组.72857 1.60279.653-2.5448 4.0019第四组 3.05714 1.60279.066-.2162 6.3305第五组-6.70000* 1.60279.000-9.9733-3.4267第二组第一组 3.30000* 1.60279.048.0267 6.5733第三组 4.02857* 1.60279.018.75527.3019第四组 6.35714* 1.60279.000 3.08389.6305第五组-3.40000* 1.60279.042-6.6733-.1267第三组第一组-.72857 1.60279.653-4.0019 2.5448第二组-4.02857* 1.60279.018-7.3019-.7552第四组 2.32857 1.60279.157-.9448 5.6019第五组-7.42857* 1.60279.000-10.7019-4.1552第四组第一组-3.05714 1.60279.066-6.3305.2162第二组-6.35714* 1.60279.000-9.6305-3.0838第三组-2.32857 1.60279.157-5.6019.9448第五组-9.75714* 1.60279.000-13.0305-6.4838第五组第一组 6.70000* 1.60279.000 3.42679.9733第二组 3.40000* 1.60279.042.1267 6.6733第三组7.42857* 1.60279.000 4.155210.7019第四组9.75714* 1.60279.000 6.483813.0305*. 均值差的显著性水平为 0.05。
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)
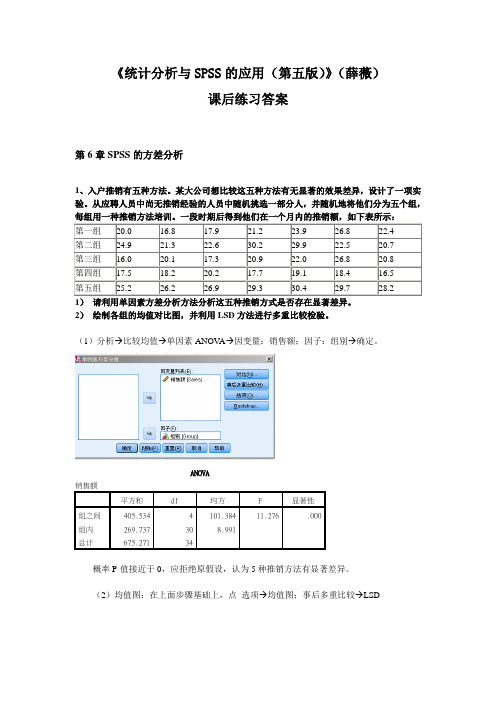
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5第五组25.2 26.2 26.9 29.3 30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额 LSD(L)(I) 组别 (J) 组别 平均差(I-J) 标准 错误 显著性95% 置信区间下限值 上限 第一组第二组 -3.30000*1.60279 .048 -6.5733 -.0267 第三组 .72857 1.60279 .653 -2.5448 4.0019 第四组3.05714 1.60279 .066 -.2162 6.3305 第五组-6.70000* 1.60279 .000 -9.9733 -3.4267 第二组第一组 3.30000* 1.60279 .048 .0267 6.5733 第三组 4.02857* 1.60279 .018 .7552 7.3019 第四组 6.35714* 1.60279 .000 3.0838 9.6305 第五组-3.40000* 1.60279 .042 -6.6733 -.1267 第三组第一组 -.72857 1.60279 .653 -4.0019 2.5448 第二组 -4.02857* 1.60279 .018 -7.3019 -.7552 第四组 2.32857 1.60279 .157 -.9448 5.6019 第五组-7.42857* 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.057141.60279.066-6.3305.2162第二组-6.35714* 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714* 1.60279 .000 -13.0305 -6.4838第五组第一组 6.70000* 1.60279 .000 3.4267 9.9733 第二组 3.40000* 1.60279 .042 .1267 6.6733第三组7.42857* 1.60279 .000 4.1552 10.7019第四组9.75714* 1.60279 .000 6.4838 13.0305*. 均值差的显著性水平为 0.05。
《统计分析与SPSS的应用》课后练习答案(第6章)

《统计分析与SP SS的应用(第五版)》课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.0 16. 8 17. 9 21. 2 23.9 26.8 22.4第二组24.9 21. 3 22.6 30.2 29.9 22.5 20.7第三组16.0 20. 1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19. 1 18.4 16. 5第五组25.2 26.2 26.9 29.3 (30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
[勰ib融巴]卫£也r「匪抽I普型ANOVA 销售额平方和df 均方 F 显著性组之间405. 534 4 101. 384 11.276 .000组内269. 737 30 8. 991总计675. 271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSDV LSDs-ffj-k"alii^Du^carii1 gqnfWTn- i二口呛achsk:IL 鉴 F*b .Dumrt1 5=11 卅 Djncan:节.Thll : ! Ise-屮1 R'E G AF_ Hochhsras GT2七赴 --------------- 1 R-E-iS-A q0 lb riel潑哎I 叫口辱■带1—lHiihar^/ !T2□ ISjFtt®」(fllTWWIWiiEI 1曲匡I 町K 柱竝圭WI Brctwn~*orEylheI 昌业hDynrisittTi=创 nwsH* ■询 IDjJrruKtC就夕值創玦1研JTI*附探曲□朗闽耶H ■■宅IL” [两II 药耐丨Aj ni M(D 组别J)组别平均差(I-J) 标准错误显著性95%置信区间下限值上限第一组第二组 -3. 30000 *1. 60279 .048 -6.5733 0267第三组.72857 1. 60279 .653 -2.54484.0019第四组3.05714 1. 60279 .066 2162 6. 3305第五组-6.70000 * 1. 60279 .000 -9.9733-3. 4267 第二组第一组 3. 30000 * 1. 60279 .048 .0267 6. 5733第三组4. 02857* 1. 60279 .018 .7552 7. 3019第四组6. 35714* 1. 60279 .000 3. 0838 9.6305第五组-3. 40000 *1. 60279 .042 -6.6733 1267 第三组第一组 72857 1. 60279 .653 -4.0019 2.5448第二组-4.02857 * 1. 60279 .018 -7. 30197552第四组2. 32857 1. 60279 .157 9448 5. 6019第五组-7. 42857 ♦ 1. 60279 .000 -10. 7019 -4.1552笫四组第一组-3. 057141. 60279.066-6. 3305.2162多重比较LSD (L)0.05可知,1和纟.1和5、2和3, 2和4, 2和5, 3和5, 4和5有显著差异。
《统计分析与SPSS的应用(第五版)》课后练习答案(第4章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第4章SPSS基本统计分析1、利用第2章第7题数据采用SPSS频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析——描述统计——频率,选择“常住地”,“职业”和“年龄”到变量中,然后,图表——条形图——图表值(频率)——继续,勾选显示频率表格,点击确定。
Statistics户口所在地职业年龄N Valid 282 282 282Missing 0 0 0户口所在地Frequency Percent ValidPercentCumulativePercentValid 中心城市200 70.9 70.9 70.9 边远郊区82 29.1 29.1 100.0 Total 282 100.0 100.0职业Frequency Percent ValidPercentCumulativePercentValid 国家机关24 8.5 8.5 8.5 商业服务业54 19.1 19.1 27.7 文教卫生18 6.4 6.4 34.0 公交建筑业15 5.3 5.3 39.4 经营性公司18 6.4 6.4 45.7 学校15 5.3 5.3 51.1 一般农户35 12.4 12.4 63.5 种粮棉专业户4 1.4 1.4 64.9种果菜专业户10 3.5 3.5 68.4 工商运专业户34 12.1 12.1 80.5 退役人员17 6.0 6.0 86.5 金融机构35 12.4 12.4 98.9 现役军人 3 1.1 1.1 100.0 Total 282 100.0 100.0年龄Frequency Percent ValidPercent Cumulative PercentValid 20岁以下 4 1.4 1.4 1.4 20~35岁146 51.8 51.8 53.2 35~50岁91 32.3 32.3 85.5 50岁以上41 14.5 14.5 100.0 Total 282 100.0 100.0分析:本次调查的有效样本为282份。
数据分析与SPSS软件应用(微课版)-课后习题答案1-10章全书章节练习题答案

第1章统计分析与SPSS软件概述习题与思考题(一)填空题1.定性数据,定序数据,定距数据,定比数据2.主成分分析,因子分析,聚类分析,判别分析,对应分析等3.数据清理,数据转换,缺失数据插补,数据的合并汇总拆分4.完全窗口菜单运行方式,程序运行方式5.SPSS Base(二)选择BADAD(三)判断√√×√×(四)简答题1.目前常用的统计分析工具或软件有哪些?你使用过哪些?它们之间的区别在哪里?解:常用的统计分析工具有SPSS、SAS、STATA、Python等。
2.试检查自己的SPSS软件共有几个模块,其中包括了哪些基本功能,并思考平时的统计分析需要哪些模块才能满足需要。
解:SPSS软件共有11个模块,分别是SPSS Base、SPSS Advance、SPSS Categories、SPSS Complex Sample、SPSS Conjoint、SPSS Exact Test、SPSS Maps、SPSS Missing Value Analysis、SPSS Regression、SPSS Tables和SPSS Trends。
其中SPSS Base是必需的,SPSS的整体框架、基本数据的获取、数据准备和整理等基本功能都集中在这一模块上,其他模块必须在该模块的基础上才能工作。
3.阐述定性、定序、定距、定比数据,并各举1例。
解:定性变量又称为名义变量。
这是一种测量精度最低、最粗略的基于“质”因素的变量,它的取值只代表观测对象的不同类别,如“班级”。
定序变量又称为有序变量、顺序变量,它取值的大小能够表示观测对象的某种顺序关系(等级、方位或大小等),也是基于“质”因素的变量,如“满意度”。
定距变量又称为间隔变量,它的取值之间可以比较大小,可以用加减法计算出差异的大小,如“重量”。
定比变量又称为比率变量,它与定距变量意义相近,差别在于定距变量中的“0”值只表示某一取值,定比数据变量表示“没有”,如“年龄”。
统计分析与SPSS的应用(第五版)课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,第一组第二组第三组第四组第五组1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间 4 .000组内30总计34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组*.048第三组.72857 .653第四组.066第五组*.000第二组第一组*.048 .0267第三组*.018 .7552第四组*.000第五组*.042第三组第一组.653第二组*.018第四组.157第五组*.000第四组第一组.066 .2162第二组*.000第三组.157 .9448第五组*.000第五组第一组*.000第二组*.042 .1267第三组*.000第四组*.000*. 均值差的显著性水平为。
可知,1和2、1和5、2和3,2和4,2和5,3和5,4和5有显著差异。
2、从两个总体中分别抽取n 1 =7 和和n 2 =6 的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格“A”和单元格“B”内的计算结果。
答:已知组内均方=组内偏差平方和/自由度,所以A=11=F 统计量=组间均方/组内均方所以B==3、为研究某种降血压药的适用特点,在五类具有不同临床特征的高血压患者中随机挑选了若干志愿者进行对比试验,并获得了服用该降压药后的血压变化数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.
(1)H0:五种推销方法不存在显著差异。
由以上结果可知,观测变量推销额的离差平方总和为675.271;如果仅考虑推销方法单个因素的影响,则推销额总变差中,不同推销方法可解释的变差为405.534,抽样误差引起的变差为269.737,它们的方差分别为101.384和8.991,相除所得的F统计量的观测值为11.276,对应的概率P值近似为0.如果在统计性水平α为0.05,由于概率P值小于显著性水平α,应拒绝原假设,认为不同推销方式对推销额产生了显著影响,不同推销方式的推销额的影响效应不全为0。
(2)H0:各水平(不同推销方法)下各总体方差无显著差异.
上表是推销方法对推销额的单因素方差分析结果。
可以看到:不同推销方法下推销额的方差齐性检验值为2.048,概率P-值为0.113大于显著性水平0.05,不应拒绝原假设,认为不同推销方法下推销额的总体方差无显著差异,满足方差分析的前提要求。
H0:不同推销方式没有对推销额产生显著影响,即:不同水平下控制因素的影响不显著。
由第一题可得:
在此之后检验:
在LSD方法中,第一组和第三组的效果没有明显的差异(概率P值为0.653),第一组和第四组的效果没有明显的差异(概率P值为0.066);与第二组和第五组有明显的差异(概率P 值分别为0.048,接近0)。
