1-10000常用对数表
常用对数表——精选推荐

一.常用對數表:(1)科學記號:每個正數A,都可以唯一地表示成,10n a A ⨯=其中101<≤a ,n 為整數,這種形式稱為A 的科學記號,例如:210587.27.258⨯=。
(2)首數與尾數: A 表成科學記號,10n a A ⨯=則a n A log log +=,其中1log 0<≤a ,則n 稱為此對數的首數,loga 稱為尾數。
例如:(1)log2340=3+log2.34 ∴log2340的首數為3,尾數為log2.34(2)log0.0234=-2+log2.34 ∴log234的首數為-2,尾數為log2.34(3)首數的性質: (可估計幾位數)(i)若logA 的首數為n,則A 的整數部分為n+1位數。
(ii)若logA 的首數為-n,則A 在小數點後第n 位數開始不為0。
(4)尾數的性質: (可估計首位數字)若logA 的尾數為loga,且5log log 4log <≤a ,則A 的首位數字為4,餘類推。
例1.已知log1.98=0.2967,則 (1)log198000=? (2)log0.0000198=?(3)若logx=2.2967,x=? (4)若logy= -2.7033,則y=?例2.若log3.14=0.4969,log3.15=0.4983,則log3.142=?例3.已知log4.37=0.6405,log43.8=1.6415,若logx= -0.3593,則x=?(求至小數點後第四位)<類>1.已知log199=2.2989,則 (1)log1.99=? (2)若logx= -2+0.2989,則x=?2.已知log1.965=0.2931,則 (1)若logx= 5.2931,則x=?若logy= -2.7069,則y=?3.若log5.38=0.7308,log5.39=0.7316,則log538.65=?4.已知log62.2=1.7938,log623=2.7945,若logx= 3.7940,則x=?(求至小數點後第一位)答案:1.(1)0.2989 (2)0.0199 2.(1)196500 (2)0.0019653. 2.73134. 6222.9例4.若56.23.883=x ,試利用下列對數表,求出x 的近似值為何?A:2.784例5.,,N b a ∈若loga=3.28,logb=5.88,分別求a,b 是幾位正整數?又最高位數字分別是多少?(已知log2=0.301,log3=0.4771,log7=0.8451)例6.(1)1002為 位數,其首位數字為 ,個位數字為 。
log常用对数表

log常用对数表常用对数表是一种常见的数学工具,用于将指数形式的数值转换为对数形式。
在科学、工程和商业领域中,常用对数表被广泛应用于各种计算和测量中,例如声学、光学、电磁学、化学和经济学等。
常用对数表通常包括自然对数表和常用对数表两种。
自然对数表以e(约等于2.71828)为底,常用对数表则以10 为底。
下面是常用对数表的一些基本信息和应用示例。
1. 基本信息常用对数表通常以10 的幂次方为间隔进行排列,例如10^0、10^1、10^2、10^3 等。
每个数值对应一个对数值,即以10 为底数的指数形式。
例如,在常用对数表中,10^2 对应的对数值是2,表示100 的以10 为底的对数值是2。
2. 应用示例常用对数表在各种领域中有广泛的应用。
例如:声学中,声音的频率和声压级之间的关系可以用对数来表示,因此常用对数表在声学测量中非常有用。
光学中,光的强度和曝光时间之间的关系也可以用对数来表示,因此常用对数表在摄影和电影制作中有重要的应用。
电磁学中,无线电波的功率和频率之间的关系可以用对数来表示,因此常用对数表在无线电通信中有广泛的应用。
化学中,pH 值是一种常见的对数测量单位,因此常用对数表在化学实验中有重要的应用。
经济学中,货币的汇率和通货膨胀率之间的关系可以用对数来表示,因此常用对数表在经济学研究中也有广泛的应用。
除了在各个专业领域中的应用,常用对数表还有一些有趣的数学性质和实际应用。
1. 对数的换底公式对数的换底公式是指可以用任意正实数作为底数来表达对数值。
换底公式为log_b(a) = log_c(a) / log_c(b),其中a、b、c 均为正实数,且b 和c 均不为1。
这个公式表明,如果我们知道以任意正实数为底的对数值,就可以求出以其他正实数为底的对数值。
2. 对数的运算性质对数具有一些重要的运算性质,例如对数的乘积法则、商数法则和幂次法则等。
这些法则可以帮助我们方便地进行对数计算,简化复杂的问题。
对数查表方法

查表、内插法1.对数表把一些正整数或有限小数的对数近似值制成一个对照表, 依据这个表再配合对数运算律, 我们就可估计所有正实数的对数值.2.常用对数以10为底数的对数, 我们称它为常用对数, 并且用log 来代替log10.自然对数以无理数e = 2.71828…的对数, 我们称它为自然对数.3.对数查表法则(1)设1x≤<10, 且x含小数点以下二位数字 ( 如:x = 8.72, x = 4.52 ), 则可由对数表查出log x, 其法如下:例:log 8.72 = .解:利用对数表中, 从最左一行( 直行) N底下找出87 ( 代表8.7 ),其次在最上面一列( 横列) N的右侧找到2, 然后在87之横列与2的直行交会处找到一数9405 ( 代表0.9405 ), 则log 8.72 = 0.9405.N0123456789表尾差12345678955 87|||–––––––9405––––––––————————–|||——————3 (2)表尾差:若1≤x <10, x含小数三位数字( 如:x = 8.726, x = 4.237 ), 则如下表之求法.例:log 8.726 = .解:(i) 先查出前三个数字8.72的对数值log8.72 = 0.9405.(ii) 在87的横列与表尾差数字6的直行交会处找到数字3,log 8.726 = 0.9405 + 0.0003 = 0.9408例1.(1) 利用对数表, 求log 8.83的值.(2) 利用对数表, 求( 8.72 )11.2的近似值. 96.5例2.(1) 利用对数表, 求5375.8587.2375.9⨯. 9.856(2) 利用对数表计算( 4.32 )2⨯( 125.2 )2÷32)51.31(之值. 29330类题.请用对数表, 求15346.1的近似值到小数点下二位. ( 四舍五入 ) 1.02乙 .首数与尾数1. 科学记号:每一个正实数a 都可以写成 a = b ‧10n 其中 n ∈ Z, 1≤ b < 10,则称 b ‧10n 为a 的科学记号. 2. 首数、尾数:设 a = b ‧10n ⇒ log a = n + log b, ( n ∈Z, 0≤ log b < 1 ).我们称 ” 整数n ”为log a 的首数, “ log b ”为log a 的尾数. <Notes:>尾数相同的条件: 设x > 0, y > 0,log x 与log y 的尾数相等 ⇔ x = y ‧10n ( n ∈Z).3. 首数性质:(1) 对数 = 首数 + 尾数 ( 首数是整数, 0≤ 尾数 < 1 ).(2) 真数 a ≥ 1,log a 的首数为n ( n ≤ log a < n + 1) ⇔ a 的整数部分为 n + 1位数. (3) 真数 a < 1 ( 0 < a < 1 )log a 的首数为 – n ( - n ≤ log a < - n + 1 )⇔ a 在小数点后第n 位数字始不为0. 例3.利用对数表, 求log 543.7及log 0.000123的值. 2.7354, 4.0899类题.利用对数表, 求log3208000及log 00123.0的值. 4.841,2.5449例4.已知 log x = 4.7835, 求x 的近似值. 60740类题.已知 log x = -2.7073, 求x 的近似值. 0.001962. 例5.已知 log 1965 = 3.2931, 则 (1) log 19.65 = . 1.2931(2) log 0.00001965 = . –4.7069(3) 若log x = 5.2931, 则x = . 196500 (4) log y = -2.7069, 则 y = . 0.001965类题.已知 log 199 = 2.2989, log x = -2 + 0.2989, 求 x = . 0.0199例6. 试问:(1) 340是几位数? 20 (2) (73)20在小数点后第几位开始出现不为0的数字? 8( log 3 = 0.4771, log 7 = 0.8451 )类题.(1) 230是几位数? 10 (2) (21)30在小数点后第几位数始不为0? 10例7.(1) 设 log a = 4.531, 试求 log a 的首数和尾数, a 的整数部分是几位数?4, 0.531, 5(2) 设 log b = 4.531, 试求 log b 的首数和尾数, b 在小数点后第几位始出现不为0的数字? -4, 0.531, 4 (3) 求下列对数的首数(a) log 3652.78 (b) log 7.29 (c) log 0.007 3, 0, -3例8.已知 log 2 = 0.3010, log 3 = 0.4771, log 7 = 0.8451:求 3100为 位数,且其最高位( 首位 )数字为 . 48, 5类题.27100÷5200的整数部分为 位数, 且最高位数字为 . 4, 2例9.设47100为168位数时, 则4717为 位数.29类题.若7100为85位数, 11100为105位数, 则7730为 位数. 57 例10.已知 log 2 = 0.3010, log 3 = 0.4771, log 7 =0.8451, 将 (76)50表为纯小数时,从小数点后第n 位起开始出现不为0的数字, 令此数字为α,则(1) n = , (2) α= . 4, 4类题.已知 log 2 = 0.3010, log 3 = 0.4771, log 7 =0.8451, 试问65)108(7的近似值在 小数点后第 位才出现不为0的数字, 且该数字为 . 13, 9 例11.(1) 设10 < x < 100, 又log x 2与 log x 1之尾数相等, 试求x. 1034, 1035(2) A, B 为三位数, 而B > 900, 若B 之常用对数尾数2倍于A 之常用对数之尾数, 则A = . 310类题.(1) 已知 0.1 < x < 1, 若 log x 3与 log x 1之尾数相等, 试求x. 1041-, 1021-, 1043-(2) 设A, B ∈N, 且200 < A < 300, B 为四位数, 若log A 的尾数是log B 尾数的两倍, 则A, B 各为多少? 225, 1500,256, 1600, 289, 1700例12.已知 log 2 = 0.30103, log 3 = 0.47712, (1) 比较2106与366的大小. 2106 > 366(2) 2106+366为几位数? 33应用问题例13.假设定期存款的年利率为6 %, 复利计息. 李先生存进10000元言明定期5年, 求期满后的本利和. 13460类题. 设年利率为12.5%, 若依复利计算, 则至少要 年( 取整数年数 ), 本利和才 会超过本金的2倍. 6丙 .内插法原理:实数 x 的微小变量, 跟其所对应的对数 y 的变量近似值成比例. 1. 作法:a b a f b f --)()( = ax a f x f --)()(<Notes:>表尾差查不到时, 再用内插法直接计算.例14.查对数表知:log 1.346 = 0.1290, log 1.347 = 0.1294, 那么log 1.3467该是多少? 0.12928类题.用内插法 log 7.4142的值. 0.87002例15.(1) 已知 log 728 = 2.8621, log 0.0729 = -1.1373, 则 log 728300 = . 5.8623(2) 设106776.0= 4.76, 106785.2= 477且10x = 4766, 则x 之近似值为 . 3.6781( 用四舍五入求进似值到小数点第四位 ) 类题.(1)由 log 72800 = 4.8621, log 0.000729 = -3.1373, 求出log 7283 = . 3.8623(2)log 1.35 = 0.1303, log 1.34 = 0.1271, 则log 1346 = . 3.1290 (请用内插法计算)。
对数表(1)

对数表什么是对数?在数学中,对数是一种指数运算的逆运算。
对数能够帮助我们解决指数运算中的问题,例如寻找未知指数的指数。
常见的对数有自然对数(以常数e为底的对数,记作ln)和常用对数(以常数10为底的对数,记作log)。
对数的定义如下:对于任意正实数a和正整数b,如果满足aⁿ = b,则我们说n是以a为底数的对数函数,记作logₐb。
其中,a称为底数,b称为真数,n称为对数。
对数的性质对数函数具有一些重要的性质,它们有助于我们更好地理解和使用对数:1.对数函数的定义域为正实数,值域为实数。
2.对数的底数必须大于0且不等于1,真数必须大于0。
3.对于任意的正实数a,有logₐa = 1,即以自身为底的对数等于1。
4.对于任意的正实数a,有logₐ1 = 0,即以任意正实数为底的对数等于0。
5.对于任意的正整数a,有log₁ₐa = 0,即以1为底数的对数等于0。
6.对于任意的正整数a,有logₐa = logₐb当且仅当a = b,即以相同底数的两个数的对数相等,当且仅当这两个数相等。
对数表对数表是一种用来存储对数值的表格。
它是一个将底数和真数组合在一起的表格,每个组合对应着一个对数值。
对数表的制作可以通过计算,也可以通过查找现有的对数表来获取对数值。
通常,对数表按顺序列出一系列底数和真数的组合,并标记它们的对数值。
例如,下面是一个常见对数表的示例:底数真数对数值2 1 02 2 12 4 22 8 32 16 42 32 5上述示例是以底数为2的常用对数表,它列出了2的幂次方对应的对数值。
从表中可以看出,当真数是2的幂次方时,对数值刚好等于幂次方的值。
常用对数表往往由计算机程序或计算器存储,以便在需要时高效地进行对数计算。
这些表通常会提供对数的近似值,因为计算精确的对数是一项复杂的计算任务。
另外,还有一些特殊的对数表,如对底数为e的自然对数表、对底数为10的常用对数表等,它们在某些领域的计算中具有特殊的应用。
1至1万中英语数字对照
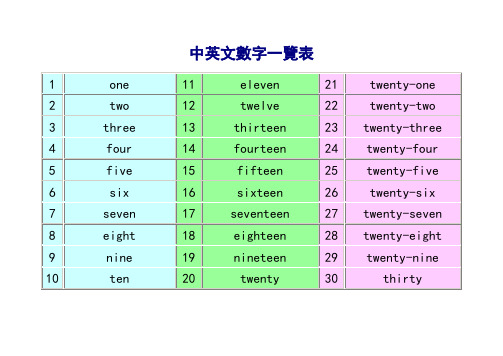
中英文數字一覽表英文数字英文数字和中文一样都是十进制(decimal):有一到十有一种形式(pattern),十一到二十形式重复,二十一到三十再重复。
基数(cardinal numbers)一到十一到十都是单个音节:onetwothreefourfivesixseveneightnineten几十20、30(tens)是在1-10基数后面加上“ty”(=×10):20 = twenty30 = thirty40 = forty50 = fifty60 = sixty70 = seventy80 = eighty90 = ninety[编辑]十几“十几”(teens)在数字后加个“teen”,代表+10 例:4 = four14 = fourteen6 = six16 = sixteen(加了个“teen”,代表+10)不规则但是,11和12的不符合以上规则:1 = one11 = eleven2 = two12 = twelve有些的拼法有改变,要注意:3 = three13 = thirteen30 = thirty4 = four40 = forty(没有“u”)但是fourteen(14)正常8 = eight18 = eighteen(一个t而已)二十几、三十几在数字前加个“twenty-”,代表+20(见#×10)注意,一定要在twenty 和单数之间写个连字符(-)。
例:4 = four24 = twenty-four6 = six26 = twenty-six同样的,在数字前加个“thirty”,代表+30(见#×10)例:4 = four34 = thirty-four(加了个“thirty”,代表+30)6 = six36 = thirty-six(加了个“thirty”,代表+30)加“forty”,代表+40,等等大的数字一百多的数前面加上“one hundred and”“a hundred and”比较口语。
