Matlab偏微分方程工具箱应用简介

偏微分方程—matlab

基础知识偏微分方程的定解问题各种物理性质的定常（即不随时间变化）过程，都可用椭圆型方程来描述。

其最典型、最简单的形式是泊松(Poisson)方程),(2222y x f yux u u =∂∂+∂∂=∆ （1）特别地，当 f ( x , y ) ≡ 0 时，即为拉普拉斯(Laplace)方程，又称为调和方程02222=∂∂+∂∂=∆yux u u （2）带有稳定热源或内部无热源的稳定温度场的温度分布，不可压缩流体的稳定无旋流动及静电场的电势等均满足这类方程。

Poisson 方程的第一边值问题为⎪⎩⎪⎨⎧Ω∂=Γ=Ω∈=∂∂+∂∂=∆Γ∈),(),(),(),(),(2222y x y x u y x y x f y ux u u y x ϕ （3）其中 Ω 为以 Γ 为边界的有界区域， Γ 为分段光滑曲线， Ω U Γ 称为定解区域，f (x, y),ϕ(x, y) 分别为 Ω,Γ 上的已知连续函数。

第二类和第三类边界条件可统一表示成)0(0),(>=⎪⎭⎫⎝⎛+∂∂Γ∈a u n u y x α （4）其中 n 为边界 Γ 的外法线方向。

当α = 0 时为第二类边界条件，α ≠ 0 时为第三类边界条件。

在研究热传导过程，气体扩散现象及电磁场的传播等随时间变化的非定常物理问题时，常常会遇到抛物型方程。

其最简单的形式为一维热传导方程)0(022>=∂∂-∂∂a xua t u （5）方程（5）可以有两种不同类型的定解问题：初值问题（也称为 Cauchy 问题）⎪⎩⎪⎨⎧+∞<<∞-=+∞<<-∞>=∂∂-∂∂x x x u x t x ua tu )()0,(,0022ϕ （6）初边值问题⎪⎪⎪⎩⎪⎪⎪⎨⎧<<===<<<<=∂∂-∂∂lx t g t l u t g t u x x u l x T t x ua t u 0),(),(),(),0()()0,(0,002122ϕ （7）其中ϕ)(),(),(21x g x g x ϕ为已知函数，且满足连接条件 )0()(),0()0(21g l g ==ϕϕ问题（7）中的边界条件)(),(),(),0(21t g t l u t g t u ==称为第一类界条件。

(完整版)偏微分方程的MATLAB解法

引言偏微分方程定解问题有着广泛的应用背景。

人们用偏微分方程来描述、解释或者预见各种自然现象，并用于科学和工程技术的各个领域fll。

然而，对于广大应用工作者来说，从偏微分方程模型出发，使用有限元法或有限差分法求解都要耗费很大的工作量，才能得到数值解。

现在，MATLAB PDEToolbox已实现对于空间二维问题高速、准确的求解过程。

偏微分方程如果一个微分方程中出现的未知函数只含一个自变量，这个方程叫做常微分方程，也简称微分方程；如果一个微分方程中出现多元函数的偏导数，或者说如果未知函数和几个变量有关，而且方程中出现未知函数对几个变量的导数，那么这种微分方程就是偏微分方程。

常用的方法有变分法和有限差分法。

变分法是把定解问题转化成变分问题，再求变分问题的近似解；有限差分法是把定解问题转化成代数方程，然后用计算机进行计算；还有一种更有意义的模拟法，它用另一个物理的问题实验研究来代替所研究某个物理问题的定解。

虽然物理现象本质不同，但是抽象地表示在数学上是同一个定解问题，如研究某个不规则形状的物体里的稳定温度分布问题，由于求解比较困难，可作相应的静电场或稳恒电流场实验研究，测定场中各处的电势，从而也解决了所研究的稳定温度场中的温度分布问题。

随着物理科学所研究的现象在广度和深度两方面的扩展，偏微分方程的应用范围更广泛。

从数学自身的角度看，偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各方面进行发展。

从这个角度说，偏微分方程变成了数学的中心。

一、MATLAB方法简介及应用1.1 MATLAB简介MATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

1.2 Matlab主要功能数值分析数值和符号计算工程与科学绘图控制系统的设计与仿真数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程1.3 优势特点1) 高效的数值计算及符号计算功能，能使用户从繁杂的数学运算分析中解脱出来；2) 具有完备的图形处理功能，实现计算结果和编程的可视化；3) 友好的用户界面及接近数学表达式的自然化语言，使学者易于学习和掌握；4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ，为用户提供了大量方便实用的处理工具。

(完整版)偏微分方程的MATLAB解法

引言偏微分方程定解问题有着广泛的应用背景。

人们用偏微分方程来描述、解释或者预见各种自然现象，并用于科学和工程技术的各个领域fll。

然而，对于广大应用工作者来说，从偏微分方程模型出发，使用有限元法或有限差分法求解都要耗费很大的工作量，才能得到数值解。

现在，MATLAB PDEToolbox已实现对于空间二维问题高速、准确的求解过程。

偏微分方程如果一个微分方程中出现的未知函数只含一个自变量，这个方程叫做常微分方程，也简称微分方程；如果一个微分方程中出现多元函数的偏导数，或者说如果未知函数和几个变量有关，而且方程中出现未知函数对几个变量的导数，那么这种微分方程就是偏微分方程。

常用的方法有变分法和有限差分法。

变分法是把定解问题转化成变分问题，再求变分问题的近似解；有限差分法是把定解问题转化成代数方程，然后用计算机进行计算；还有一种更有意义的模拟法，它用另一个物理的问题实验研究来代替所研究某个物理问题的定解。

虽然物理现象本质不同，但是抽象地表示在数学上是同一个定解问题，如研究某个不规则形状的物体里的稳定温度分布问题，由于求解比较困难，可作相应的静电场或稳恒电流场实验研究，测定场中各处的电势，从而也解决了所研究的稳定温度场中的温度分布问题。

随着物理科学所研究的现象在广度和深度两方面的扩展，偏微分方程的应用范围更广泛。

从数学自身的角度看，偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各方面进行发展。

从这个角度说，偏微分方程变成了数学的中心。

一、MATLAB方法简介及应用1.1 MATLAB简介MATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

1.2 Matlab主要功能数值分析数值和符号计算工程与科学绘图控制系统的设计与仿真数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程1.3 优势特点1) 高效的数值计算及符号计算功能，能使用户从繁杂的数学运算分析中解脱出来；2) 具有完备的图形处理功能，实现计算结果和编程的可视化；3) 友好的用户界面及接近数学表达式的自然化语言，使学者易于学习和掌握；4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ，为用户提供了大量方便实用的处理工具。

pde工具介绍

也可以用动画来表示杆上的温度随时间的变化,在上面的程序后面加上如下语句 figure h=plot(xx’,js(1,:)) set(h,’erasemode’,’xor’); for j=2:10 set(h,’ydata’,js(j,:)); drawnow; pause(0.1) end 上图右面是其中的一个画面，所有的画面按时间排列起来，就形成上一幅瀑布图. 例4. 讨论有限长的细杆在第一类边界条件下的热传导问题.可以将这个结果与无限长细杆的热传导问题对比. 无限长细杆的热传导的定解问题是 2 ut = a uxx u(0, t) = 0, u(l, t) = 0 u(x, t = 0) = ϕ(x) 其中0 ≤ x ≤ 20,即l = 20,取a = 10且 ϕ (x ) = 所得的解为 2 10nπ 11nπ − n2π2a2 t nπ u(x, t) = cos − cos e 400 sin x nπ 20 20 20 n=1 再画出前50个分波的合成图形,在程序中用子函数来计算各个分波,然后在主函数中调用.所用的程序是 function jxj
1.1 可解问题的分类
偏微分方程工具箱将问题分成8种类型来设置解法， Generic Scalar 一般标量场 Generic system 一般的偏微分方程组 Structual Mechnics,Plane Stress 结构力学−平面应力场 Structual Mechnics,Plane Strain 结构力学−平面应变场 Electrostatics 静电场 Magnetostatics 静磁场 Ac Power Electromagnetics 交流电磁场 Conductive Media DC 直流导电介质问题 Heat Transfer 热传导问题 Diﬀusion 扩散问题

电磁场中matlab仿真实现工具箱

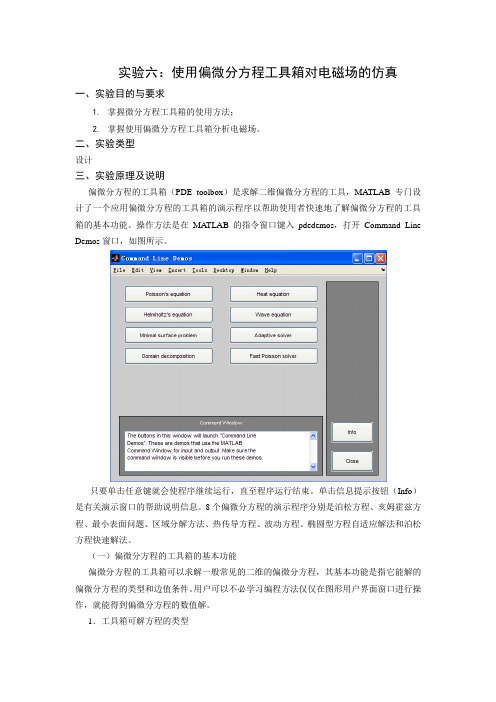
实验六：使用偏微分方程工具箱对电磁场的仿真一、实验目的与要求1.掌握微分方程工具箱的使用方法；2.掌握使用偏微分方程工具箱分析电磁场。

二、实验类型设计三、实验原理及说明偏微分方程的工具箱（PDE toolbox）是求解二维偏微分方程的工具，MA TLAB专门设计了一个应用偏微分方程的工具箱的演示程序以帮助使用者快速地了解偏微分方程的工具箱的基本功能。

操作方法是在MA TLAB的指令窗口键入pdedemos，打开Command Line Demos窗口，如图所示。

只要单击任意键就会使程序继续运行，直至程序运行结束。

单击信息提示按钮（Info）是有关演示窗口的帮助说明信息。

8个偏微分方程的演示程序分别是泊松方程、亥姆霍兹方程、最小表面问题、区域分解方法、热传导方程、波动方程、椭圆型方程自适应解法和泊松方程快速解法。

（一）偏微分方程的工具箱的基本功能偏微分方程的工具箱可以求解一般常见的二维的偏微分方程，其基本功能是指它能解的偏微分方程的类型和边值条件。

用户可以不必学习编程方法仅仅在图形用户界面窗口进行操作，就能得到偏微分方程的数值解。

1．工具箱可解方程的类型定义在二维有界区域Ω上的下列形式的偏微分方程，可以用偏微分方程工具箱求解：椭圆型()f au u c =+∇∙∇- 抛物型()f au u c tu d =+∇∙∇-∂∂ 双曲型()f au u c tu d =+∇∙∇-∂∂22 本征值方程()du au u c λ=+∇∙∇-式中，u 是偏微分方程的解；c 、a 、d 、f 是标量复函数形式的系数，在抛物型和双曲型方程中，它们也可以是t 的函数，λ是待求的本征值。

当c 、a 、f 是u 的函数时，称之为非线性方程，形式为()()()()u f u u a u u c =+∇∙∇-也可以用偏微分方程工具箱求解。

2．工具箱可解方程的边值条件解偏微分方程需要的边值条件一般为下面两种之一：狄里赫利(Diriclet)边值条件 hu=r广义诺曼(Generalized Neumann)边值条件 ()g qu u c n =+∇∙式中，n为边界外法向单位向量；h 、q 、r 、g 是在边界上定义的复函数。

matlab求解初边值问题的偏微分方程

偏微分方程是描述自然界中动态过程的重要数学工具，在工程领域中，求解偏微分方程是很多实际问题的重要一步。

MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来求解各种类型的偏微分方程。

本文将介绍使用MATLAB求解初边值问题的偏微分方程的方法和步骤。

一、MATLAB中的偏微分方程求解工具MATLAB提供了几种可以用来求解偏微分方程的工具和函数，主要包括：1. pdepe函数：用于求解偏微分方程初边值问题的函数，可以处理各种类型的偏微分方程，并且可以自定义边界条件和初始条件。

2. pdepeplot函数：用于绘制pdepe函数求解得到的偏微分方程的解的可视化图形，有助于直观地理解方程的解的特性。

3. pdetool工具箱：提供了一个交互式的图形用户界面，可以用来建立偏微分方程模型并进行求解，适用于一些复杂的偏微分方程求解问题。

二、使用pdepe函数求解偏微分方程初边值问题的步骤对于给定的偏微分方程初边值问题，可以按照以下步骤使用pdepe函数进行求解：1. 定义偏微分方程需要将给定的偏微分方程转化为标准形式，即将偏微分方程化为形式为c(x,t,u)∂u/∂t = x(r ∂u/∂x) + ∂(p∂u/∂x) + f(x,t,u)的形式。

2. 编写边界条件和初始条件函数根据实际问题的边界条件和初始条件，编写相应的函数来描述这些条件。

3. 设置空间网格选择合适的空间网格来离散空间变量，可以使用linspace函数来产生均匀分布的网格。

4. 调用pdepe函数求解偏微分方程将定义好的偏微分方程、边界条件和初始条件函数以及空间网格作为参数传递给pdepe函数，调用该函数求解偏微分方程。

5. 可视化结果使用pdepeplot函数绘制偏微分方程的解的可视化图形，以便对解的性质进行分析和理解。

三、实例分析考虑一维热传导方程初边值问题：∂u/∂t = ∂^2u/∂x^2, 0<x<1, 0<t<1u(0,t) = 0, u(1,t) = 0, u(x,0) = sin(πx)使用MATLAB求解该初边值问题的步骤如下：1. 定义偏微分方程将热传导方程化为标准形式，得到c(x,t,u) = 1, r = 1, p = 1, f(x,t,u) = 0。

matlab偏微分方程组求解

matlab偏微分方程组求解摘要：一、引言1.介绍Matlab 在偏微分方程组求解中的应用2.阐述偏微分方程组的重要性和应用领域3.说明Matlab 在偏微分方程组求解中的优势二、Matlab 偏微分方程组求解方法1.有限差分法2.有限元法3.边界元法4.其他求解方法三、Matlab 偏微分方程组求解步骤1.准备模型和参数2.选择适当的求解方法3.编写求解脚本4.分析结果四、Matlab 偏微分方程组求解案例分析1.二维热传导方程2.二维亥姆霍兹方程3.三维波动方程五、结论1.总结Matlab 在偏微分方程组求解中的应用2.强调Matlab 在偏微分方程组求解中的重要性3.展望Matlab 在偏微分方程组求解领域的发展前景正文：一、引言Matlab 是一款功能强大的数学软件，广泛应用于科学计算、数据分析、建模等领域。

偏微分方程组是描述众多自然现象和工程问题的数学模型，求解偏微分方程组对于理解这些现象和问题具有重要意义。

Matlab 提供了丰富的工具箱和函数，可以方便地求解偏微分方程组，为科研和工程应用提供了强大的支持。

二、Matlab 偏微分方程组求解方法Matlab 提供了多种求解偏微分方程组的方法，包括有限差分法、有限元法、边界元法等。

有限差分法是一种常用的数值求解方法，通过离散化方程组，将偏微分方程转化为离散形式的代数方程组，从而求解。

有限元法和边界元法是另外两种常用的数值求解方法，分别通过将偏微分方程转化为有限个单元的加权积分和边界上的加权积分，从而求解。

除了上述方法外，Matlab 还支持其他求解方法，如有限体积法、谱方法等。

有限体积法是将偏微分方程组的控制区域划分为有限个体积单元，通过对单元内的值进行插值，得到离散形式的偏微分方程组。

谱方法则是利用傅里叶变换将偏微分方程组转化为频域问题，从而求解。

三、Matlab 偏微分方程组求解步骤求解偏微分方程组的过程主要包括准备模型和参数、选择适当的求解方法、编写求解脚本和分析结果四个步骤。

Matlab偏微分方程工具箱应用简介

Matlab偏微分方程工具箱应用简介1．概述本文只给出该工具箱的函数列表，读者应先具备偏微分方程的基本知识，然后根据本文列出的函数查阅Matlab的帮助，便可掌握该工具箱的使用。

2．偏微分方程算法函数列表adaptmesh 生成自适应网络及偏微分方程的解assemb 生成边界质量和刚度矩阵assema 生成积分区域上质量和刚度矩阵assempde 组成偏微分方程的刚度矩阵及右边hyperbolic 求解双曲线型偏微分方程parabolic 求解抛物线型偏微分方程pdeeig 求解特征型偏微分方程pdenonlin 求解非线性型微分方程poisolv 利用矩阵格式快速求解泊松方程3．图形界面函数pdecirc 画圆pdeellip 画椭圆pdemdlcv 转化为版本1.0式的*.m文件pdepoly 画多边形pderect 画矩形pdetool 偏微分方程工具箱的图形用户界面4．几何处理函数csgchk 检查几何矩阵的有效性csgdel 删除接近边界的小区decsg 将固定的几何区域分解为最小区域initmesh 产生最初的三角形网络jigglemesh 微调区域内的三角形网络poimesh 在矩形区域上产生规则的网络refinemesh 细化三角形网络wbound 写一个边界描述文件wgeom 写一个几何描述文件pdecont 画轮廓图pdemesh 画偏微分方程的三角形网络pdeplot 画偏微分方程的三角形网络pdesurf 画表面图命令5．通用函数pdetriq 三角形单元的品性度量poiasma 边界点对快速求解泊松方程的“贡献”矩阵poicalc 规范化的矩阵格式的点索引poiindex 规范化的矩阵格式的点索引sptarn 求解一般的稀疏矩阵的特征值问题tri2grid 由三角形格式转化为矩形格式。

matlab偏微分方程工具箱使用手册

MATLAB偏微分方程工具箱使用手册一、Matlab偏微分方程工具箱介绍Matlab偏微分方程工具箱是Matlab中用于求解偏微分方程（PDE）问题的工具。

它提供了一系列函数和工具，可以用于建立、求解和分析PDE问题。

PDE是许多科学和工程领域中的重要数学模型，包括热传导、扩散、波动等现象的数值模拟、分析和优化。

Matlab偏微分方程工具箱为用户提供了丰富的功能和灵活的接口，使得PDE问题的求解变得更加简单和高效。

二、使用手册1. 安装和启用在开始使用Matlab偏微分方程工具箱前，首先需要确保Matlab已经安装并且包含了PDE工具箱。

确认工具箱已经安装后，可以通过以下命令启用PDE工具箱：```pdetool```这将打开PDE工具箱的图形用户界面，用户可以通过该界面进行PDE 问题的建立、求解和分析。

2. PDE建模在PDE工具箱中，用户可以通过几何建模工具进行PDE问题的建立。

用户可以定义几何形状、边界条件、初值条件等，并选择适当的PDE方程进行描述。

PDE工具箱提供了各种几何建模和PDE方程描述的选项，用户可以根据实际问题进行相应的设置和定义。

3. 求解和分析一旦PDE问题建立完成，用户可以通过PDE工具箱提供的求解器进行求解。

PDE工具箱提供了各种数值求解方法，包括有限元法、有限差分法等。

用户可以选择适当的求解方法，并进行求解。

求解完成后，PDE工具箱还提供了丰富的分析功能，用户可以对结果进行后处理、可视化和分析。

4. 结果导出和应用用户可以将求解结果导出到Matlab环境中，并进行后续的数据处理、可视化和分析。

用户也可以将结果导出到其他软件环境中进行更进一步的处理和应用。

三、个人观点和理解Matlab偏微分方程工具箱是一个非常强大的工具，它为科学和工程领域中的PDE问题提供了简单、高效的解决方案。

通过使用PDE工具箱，用户可以快速建立、求解和分析复杂的PDE问题，从而加快科学研究和工程设计的进程。

利用Matlab中的PDE工具箱进行偏微分方程求解！

利用Matlab中的PDE工具箱进行偏微分方程求解！在科学技术各领域中，有很多问题都可以归结为偏微分方程问题。

在物理专业的力学、热学、电学、光学、近代物理课程中都可遇见偏微分方程。

偏微分方程，再加上边界条件、初始条件构成的数学模型，只有在很特殊情况下才可求得解析解。

随着计算机技术的发展，采用数值计算方法，可以得到其数值解。

下面的几个简单例子，将为大家介绍如何利用Matlab中的PDE 工具箱进行偏微分方程的求解！抛物线型受热金属块的热传导问题：一块受热的有矩形裂纹的金属块。

金属块的左侧被加热到100℃，右侧热量则以恒定速率降低到周围空气的温度，所有其他边界都是独立的，于是边界条件为：初始温度为0℃。

指定起始时间为0，研究5s的热扩散问题。

求解结果如下：具体步骤：1.建模。

先画一个起点为(-0.5,-0.8)，终点为(0.5,0.8)的矩形，再建另一个矩形，起点(-0.05,-0.4)，终点(0.05,0.4)，然后在设置公式中输入R1-R2；2.设置边界条件；3.PDE中设置参数，d=1,c=1,a=0,f=0；4.初始化网格并细化一次；5.在Solve Parameter中，设置u0=0，时间为[0:0.5:5]，然后求解。

注意到金属块的温度升高很快，可试着改变时间列表的表达式为logspace(-2,0.5,20)以便观察。

双曲线型方形薄膜横向波动问题（波动方程）：薄膜左侧和右侧固定（u=0），上端和下端自由：满足边界条件的初值为：求解结果如下：具体步骤：1.建模，画出起点(-1,-1)，终点(1,1)的矩形；2.确定边界条件；3.PDE Specification对话框中选择双曲线型，参数设为c=1,a=0,f=0,d=1；4.初始化网格，并细化一次；5.在Solve Parameters对话框的时间中输入linspace(0,5,31)，u的初值为atan(cos(pi/2*x))，一次偏导的初值为3*sin(pi*x).*exp(sin(pi/2*y))，然后求解。

《偏微分方程概述及运用matlab求解偏微分方程常见问题》.

北京航空航天大学偏微分方程概述及运用matlab求解微分方程求解常见问题姓名徐敏学号57000211班级380911班2011年6月偏微分方程概述及运用matlab求解偏微分方程常见问题徐敏摘要偏微分方程简介，matlab偏微分方程工具箱应用简介，用这个工具箱解方程的过程是：确定待解的偏微分方程；确定边界条件；确定方程所在域的几何形状；划分有限元；解方程关键词MATLAB 偏微分方程程序如果一个微分方程中出现的未知函数只含有一个自变量，这个方程叫做常微分方程，也简称微分方程：如果一个微分方程中出现多元函数的偏导数，或者说如果未知函数和几个变量有关，而且方程中出现未知函数对几个变量的导数，那么这种微分方程就是偏微分方程。

一，偏微分方程概述偏微分方程是反映有关的未知变量关于时间的导数和关于空间变量的导数之间制约关系的等式。

许多领域中的数学模型都可以用偏微分方程来描述，很多重要的物理、力学等学科的基本方程本身就是偏微分方程。

早在微积分理论刚形成后不久，人们就开始用偏微分方程来描述、解释或预见各种自然现象，并将所得到的研究方法和研究成果运用于各门科学和工程技术中，不断地取得了显著的成效，显示了偏微分方程对于人类认识自然界基本规律的重要性。

逐渐地，以物理、力学等各门科学中的实际问题为背景的偏微分方程的研究成为传统应用数学中的一个最主要的内容，它直接联系着众多自然现象和实际问题，不断地提出和产生出需要解决的新课题和新方法，不断地促进着许多相关数学分支(如泛函分析、微分几何、计算数学等)的发展，并从它们之中引进许多有力的解决问题的工具。

偏微分方程已经成为当代数学中的一个重要的组成部分，是纯粹数学的许多分支和自然科学及工程技术等领域之间的一座重要的桥梁。

在国外，对偏微分方程的应用发展是相当重视的。

很多大学和研究单位都有应用偏微分方程的研究集体，并得到国家工业、科学部门及军方、航空航天等方面的大力资助。

比如在国际上有重大影响的美国的Courant研究所、法国的信息与自动化国立研究所等都集中了相当多的偏微分方程的研究人员，并把数学模型、数学方法、应用软件及实际应用融为一体，在解决实际课题、推动学科发展及加速培养人才等方面都起了很大的作用。

偏微分方程工具箱能解二阶三阶

偏微分方程工具箱能解二阶三阶
【原创实用版】
目录
1.偏微分方程工具箱的概述
2.二阶和三阶偏微分方程的解法
3.偏微分方程工具箱的实际应用
正文
偏微分方程工具箱是一种数学工具，可以用来解决偏微分方程问题。

偏微分方程是一种涉及多个自变量的微分方程，它在许多领域都有应用，如物理学、工程学和经济学等。

二阶和三阶偏微分方程是偏微分方程中的两种类型。

二阶偏微分方程指的是包含两个自变量的偏微分方程，而三阶偏微分方程则包含三个自变量。

这两种方程的解法都有一定的复杂性，需要使用偏微分方程工具箱来解决。

偏微分方程工具箱中包含了许多数学工具，如偏微分方程求解器、偏微分方程符号计算器和偏微分方程可视化工具等。

这些工具可以帮助用户解决各种偏微分方程问题，包括二阶和三阶偏微分方程。

例如，使用偏微分方程求解器，用户可以输入二阶或三阶偏微分方程，并求解出方程的解。

偏微分方程符号计算器则可以帮助用户进行符号计算，如求导、积分和求和等。

偏微分方程可视化工具则可以将方程的解绘制成图形，方便用户进行观察和分析。

偏微分方程工具箱的实际应用非常广泛，它在各种领域都有重要的作用。

例如，在物理学中，偏微分方程可以用来描述物体的运动和力学系统的行为；在工程学中，偏微分方程可以用来解决电路和机械系统的问题；在经济学中，偏微分方程可以用来描述经济系统的动态行为。

总之，偏微分方程工具箱是一种重要的数学工具，它可以帮助用户解决各种偏微分方程问题，包括二阶和三阶偏微分方程。

pdetool，特殊函数，guide

也可以用动画来表示杆上的温度随时间的变化,在上面的程序后面加上如下语句
figure h=plot(xx’,js(1,:)) set(h,’erasemode’,’xor’); for j=2:10
set(h,’ydata’,js(j,:)); drawnow; pause(0.1) end
上图右面是其中的一个画面，所有的画面按时间排列起来，就形成上一幅瀑布图.
热传导方程
例3. 无限长细杆的热传导的定解问题是1
ut = a2uxx u(x, t = 0) = ϕ(x)
利用付里叶变换求得问题的解是
1梁昆淼.数学物理方法.北京: 高等教育出版社,1998,第三版,407
+∞
u(x, t) =
ϕ(ξ)
√1
e−
(x−ξ)2 4a2t
dξ
−∞
2a πt
在其中取初始温度分布如下，这是在区间0 ∼ 1之间高度为1的一个
始状态所画出的图形与差分方程的解有一定的偏差.
2梁昆淼.数学物理方法.北京: 高等教育出版社,1998,第三版,215
(a)整体图 (b)初始状态 (c)最后状态
图非齐次方程的输运问题的解析解
所用的程序是,在这里a2 = 50, b = 5, l = 1,为了方便比较,两个计算是采用了相同的数据.
一种近似.
再用PDETOOL来解这个问题. 求解区域为−10 ≤ x ≤ 10, −0.2 ≤ y ≤ 0.2,矩形的上下边界为诺伊曼边界条件, 取q = 0, g = 0,左右边界为Dirichlet边界条件,取h = 1, r = 0. 方程类型应该选抛物型(Parabolic). 求解参数time取0 : 0.005 : 0.2,初条件u(t0)为10 ∗ tanh(10000 ∗ x) − 10 ∗ tanh(10000(x − 0.05)),这个初始温度分布近似于定解问题中初始条件.这个设置是为了用函数而不是用语句来描述初始温度. 作图选择的参数为Color,Heigh(3-D plot)和Animation.上图右面是其中一个画面. 例5. 定解问题是2

matlab 求解偏微分方程

matlab 求解偏微分方程求解偏微分方程是数学中的一种重要问题，而MATLAB是一种功能强大的数学软件，可以用于求解各种数学问题，包括偏微分方程。

在本文中，我们将探讨如何使用MATLAB求解偏微分方程，并介绍一些常用的求解方法和技巧。

偏微分方程是描述自然界中许多现象的数学模型，例如热传导、扩散、波动等。

求解偏微分方程的目标是找到满足方程条件的未知函数。

MATLAB提供了许多内置函数和工具箱，可以方便地进行偏微分方程的求解。

我们需要定义偏微分方程的边界条件和初始条件。

边界条件是指在求解区域的边界上给定的条件，而初始条件是指在求解区域内给定的初始状态。

这些条件将帮助我们确定偏微分方程的解。

接下来，我们可以使用MATLAB中的偏微分方程求解函数来求解方程。

MATLAB提供了几种常用的求解方法，例如有限差分法、有限元法和谱方法等。

通过选择合适的求解方法，我们可以得到偏微分方程的数值解。

在使用MATLAB求解偏微分方程时，我们还可以使用一些技巧和优化方法来提高求解效率。

例如，可以使用网格剖分方法来将求解区域划分为若干小区域，从而减少计算量。

此外，还可以使用迭代方法来逐步逼近偏微分方程的解，从而提高求解精度。

除了求解偏微分方程，MATLAB还可以用于可视化偏微分方程的解。

通过使用MATLAB的绘图函数，我们可以将数值解以图形的形式展示出来，从而更直观地理解偏微分方程的解。

需要注意的是，在使用MATLAB求解偏微分方程时，我们需要考虑计算资源的限制。

由于偏微分方程的求解通常需要大量的计算和存储资源，因此我们需要合理安排计算机的内存和处理器的使用，以避免计算过程中的错误或崩溃。

总结起来，MATLAB是一种强大的数学软件，可以用于求解偏微分方程。

通过选择合适的求解方法和优化技巧，我们可以得到偏微分方程的数值解，并用图形的形式展示出来。

使用MATLAB求解偏微分方程可以帮助我们更好地理解和解决实际问题，是数学研究和工程应用中的重要工具之一。

matlab中求解偏微分方程

文章标题：深入探讨 Matlab 中求解偏微分方程的方法和应用一、引言在现代科学和工程中，偏微分方程是一种重要的数学工具，用于描述各种自然现象和物理过程，如热传导、流体力学、电磁场等。

Matlab 是一个用于科学计算和工程应用的强大工具，提供了丰富的数值计算和数据可视化功能，其中包括求解偏微分方程的工具箱，本文将深入探讨在Matlab中求解偏微分方程的方法和应用。

二、基本概念偏微分方程（Partial Differential Equation, PDE）是关于多个变量的函数及其偏导数的方程。

在物理学和工程学中，PDE广泛应用于描述空间变量和时间变量之间的关系。

在Matlab中，求解PDE通常涉及到确定PDE类型、边界条件、初始条件和求解方法等步骤。

三、求解方法1. 有限差分法（Finite Difference Method）有限差分法是求解PDE的常用数值方法之一，它将PDE转化为差分方程组，并通过迭代求解得到数值解。

在Matlab中，可以使用pdepe 函数来求解具有一维、二维或三维空间变量的PDE，该函数可以直接处理边界条件和初始条件。

2. 有限元法（Finite Element Method）有限元法是另一种常用的数值方法，它将求解区域离散化为有限数量的单元，并通过单元之间的插值来逼近PDE的解。

Matlab提供了pdenonlin函数来求解非线性PDE，该函数支持各种复杂的几何形状和非线性材料参数。

3. 特征线法（Method of Characteristics）特征线法适用于一维双曲型PDE的求解，该方法基于特征线方程的性质来构造数值解。

在Matlab中，可以使用pdegplot函数来展示特征线，并通过构造特征线网格来求解PDE。

四、实际应用1. 热传导方程的求解假设我们需要求解一个长条形的材料中的热传导方程，可以通过在Matlab中定义边界条件和初始条件，然后使用pdepe函数来求解得到温度分布和热流线。

MATLAB偏微分方程工具箱PDEToolbox

❖ （ 2）用 M 文件编程求解． ❖ 本章首先对可视化方法（ G U I）求解作初步介绍，
然后详细介绍用 M文件编程解几类基本偏微分方程，并对典型偏微分的解的静态（或动态）显示曲线分布进行了讨论。
MATLAB偏微分方程工具箱PDEToolbox
22.1 用偏微分方程工具箱求解微分方程
直接使用图形用户界面（Graphical User Interface，简记作GUI）求解．
MATLAB偏微分方程工具箱PDEToolbox
例 22.1.1 解热传导方程 ut u f
边界条件是齐次类型，定解区域自定。
计算机仿真
【解】第一步：启动MATLAB，键入命令pdetool并回
MATLAB偏微分方程工具箱PDEToolbox
图2MA2TL.A1B偏所微分讨方程论工具定箱PD解EToo问lbox题的区域
第三步：选取边界首先选择Boundary菜单中Boundary Mode命
令，进入边界模式．然后单击Boundary菜单中 Remove All Subdomain Borders选项，从而去掉子域边界，如图22.2．单击Boundary菜单中Specify Boundary Conditions选项，打开Boundary Conditions对话框，输入边界条件．本例取默认条件，即将全部边界设为齐次Dirichlet条件，边界显示为红色．如果想将几何与边界信息存储，可选择 Boundary菜单中的Export Decomposed Geometry,Boundary Cond’s命令，将它们分别存储在g、b变量中，并通过MATLAB形成M文件．
22.2 计算机仿真编程求解偏微分方程

matlab 偏微分方程拟合

matlab 偏微分方程拟合摘要：1.偏微分方程概述2.MATLAB 在偏微分方程中的应用3.使用MATLAB 拟合偏微分方程的步骤4.实例：双曲线型偏微分方程的拟合5.总结正文：一、偏微分方程概述偏微分方程是数学中的一个重要分支，广泛应用于物理、工程和生物学等领域。

偏微分方程描述了某些变量在空间和时间上的变化规律，通常包括三个或更多的变量。

在工程和科学研究中，准确地拟合偏微分方程对于预测和控制这些变量的变化具有重要意义。

二、MATLAB 在偏微分方程中的应用MATLAB 是一种强大的数学软件，可以方便地用于解决偏微分方程问题。

MATLAB 提供了许多用于拟合偏微分方程的函数和工具箱，如PDE Toolbox、Finite Element Toolbox 等。

这些工具箱为偏微分方程的求解提供了高效的算法和灵活的编程环境。

三、使用MATLAB 拟合偏微分方程的步骤1.准备数据：首先需要收集或创建适当的数据集，用于描述偏微分方程的解。

这些数据通常包括实验数据、观测数据或理论数据。

2.选择适当的工具箱和函数：根据问题类型和数据类型，选择适当的MATLAB 工具箱和函数，如PDE Toolbox、Finite Element Toolbox 等。

3.建立数学模型：使用MATLAB 中的函数和工具箱，将偏微分方程转化为数值问题。

这通常包括离散化、网格划分、选择适当的数值方法等。

4.编写MATLAB 程序：根据数学模型，编写MATLAB 程序，以执行数值计算并生成解的近似值。

5.分析结果：对计算结果进行分析，检查解的准确性和稳定性，并根据需要调整模型或方法。

四、实例：双曲线型偏微分方程的拟合双曲线型偏微分方程是一种常见的非线性偏微分方程，其解通常具有双曲线形状。

下面是一个双曲线型偏微分方程的拟合实例：假设我们有以下双曲线型偏微分方程：u/x - u/y = 1我们可以使用MATLAB 中的PDE Toolbox 和Finite Element Toolbox 来拟合这个方程。

用MATLAB偏微分方程工具箱PDE-Box求解空载磁场

作业：电机电磁场有限元分析——用MA TLAB偏微分方程工具箱求解空载磁场电机与电器 2009级张华一、电机数据的选取：电机的设计数据选自Ansoft Rmxprt 11软件中自带的电机实例，数据文件位于该软件主程序文件夹下的Examples\rmxprt5\syng3\bjs7-6-1.pjt中。

该实例是一台6极同步发电机。

从Rmxprt的Design Output中可以找出该电机的一系列的工作参数。

为了得到空载磁场，要从中找出空载励磁电流--No-Load Exciting Current (A)：735.793为绘制求解区域其机构，要得到其尺寸数据，其迭片结构如图1所示。

（具体尺寸在打开文件bjs7-6-1.pjt后可以看到）图1 求解电机的迭片图二、确定求解区域为了简化分析，选用一个极下的区域进行求解，根据半周期条件，可以求得整个区域的解。

三、使用有限元软件进行求解这里采用MA TLAB PDE toolbox进行空载磁场的有限元求解，求解后并与Ansoft 2D所生成的同一电机的解进行了一致性的比较。

1．MA TLAB PDE toolbox的介绍。

MA TLAB的偏微分工具箱提供了图形用户界面的解法工具，此优点使偏微分方程工具箱在实际中得到了很多的应用。

图形用户界面可以画出二维图形,从而定义偏微分方程的边界条件,可以定义偏微分方程,建立、细分网格,并通过计算在计算机上显示最终结果。

2．求解区域的绘制。

根据电机的结构数据和迭片结构，编写MA TLAB程序在PDE toolbox的GUI中精确绘制出求解区域。

①绘制电机轮廓图利用基本封闭曲线（如椭圆、多变形）的绘图函数绘制出电机的轮廓如图2所示。

图2 PDE toolbox 中的电机轮廓图将求解问题确定为Magnetostatics(静磁场求解)，再把Set formula改为：REC1*(DELTA1+S1+S2+R2+R1+R3 +POLEBODY+P1+P2+P3+P4+P5+P6+P7+P8+P9+P10+P11+P12+D1+D2+D3+D4+D5+D6+P13+P14+P15+P16+P17+P18)即可得到求解区域范围。

matlab simulation 偏微分

matlab simulation 偏微分一、简介Matlab是一款广泛应用于数值模拟和数学计算的软件，其强大的矩阵运算能力使其在偏微分方程的仿真中具有很高的应用价值。

本篇文章将介绍如何使用Matlab进行偏微分方程的仿真模拟。

二、准备工作在开始仿真之前，需要准备以下工具和环境：1.安装Matlab软件：确保已经安装了Matlab软件，并具备相应的操作权限和技能。

2.安装所需的Matlab工具箱：如数值分析工具箱、图形绘制工具箱等，以支持偏微分方程的仿真模拟。

3.建立仿真模型：根据实际问题，建立相应的偏微分方程模型，并确定控制方程的形式和数学性质。

三、Matlab仿真模拟过程使用Matlab进行偏微分方程的仿真模拟，需要按照以下步骤进行：1.导入必要的库和函数：使用Matlab自带的函数库和工具箱，以及第三方库，如SciPy等。

2.定义变量和初始条件：根据实际问题，定义相应的变量和初始条件，如扩散系数、边界条件等。

3.建立边界条件函数：根据实际问题，建立相应的边界条件函数，如对流项、扩散项等。

4.选择算法求解偏微分方程：使用Matlab自带的算法求解函数，如fzero、fsolve等，对偏微分方程进行求解。

5.绘制结果图像：使用Matlab的绘图功能，绘制结果图像，以便观察和分析。

四、案例应用以下是一个简单的偏微分方程仿真模拟案例：考虑一维扩散方程，其中x为空间坐标，u为未知函数，v为扩散系数。

设定初值为u(0)=1,u(L)=0,L=1,时间间隔为dt=0.01。

使用Matlab进行仿真模拟，可以得到随时间变化的扩散系数v(x)的图像。

通过调整参数和边界条件，可以进一步探索偏微分方程在不同场景下的应用。

五、总结通过Matlab进行偏微分方程的仿真模拟，可以方便地进行数值计算和图形绘制，对于解决实际问题具有很高的应用价值。

本文介绍了使用Matlab进行偏微分方程仿真模拟的基本步骤和方法，并结合案例应用进行了说明。