例题工程力学.
工程力学---材料力学第七章-梁弯曲时位移计算与刚度设计经典例题及详解

P
B C
l 2 l 2
A
x
P 解:AC段:M ( x ) x 2 y P EIy x 2 A P 2 EIy x C x 4 l 2 P 3 EIy x Cx D 12
P
B C
l 2
x
由边界条件: x 0时,y 0
l 由对称条件: x 时,y 0 2
梁的转角方程和挠曲线方程分别为:
最大转角和最大挠度分别为:
11qa max A 1 x1 0 6 EI 19qa 4 ymax y2 x2 2 a 8EI
3
例5:图示变截面梁悬臂梁,试用积分法
求A端的挠度 P
I
2I
l
fA 解: AC段 0 x l
B
P 3 2 EIy x C2 x D2 6
由边界条件: x l时,y=0, =0
得:
C2
1 1 Pl 2 , D2 Pl 3 2 3
l x 时,yC左 =yC右 , C左 = C右 由连续条件: 2
5 3 2 C1 Pl , D1 Pl 3 16 16
由连续条件: x1 x2 a时, y1 y2 , y1 y2
由边界条件: x1 0时, y1 0
0 x 2 a 时 , y 由对称条件: 2 2
得 D1 0
C1 C2 得 D1 D2
11 3 得 C2 qa 6
qa 1 (11a 2 3 x12 ) 0 x1 a 6 EI q 2 [3ax2 2 ( x2 a)3 11a 3 a x2 2a 6 EI qa y1 (11a 2 x1 x13 ) 0 x1 a 6 EI q y2 [4ax23 ( x2 a) 4 44a 3 x2 ] a x2 2a 24 EI
工程力学(例题)

1.如图2-4所示为一曲柄摇杆机构。
机构中各构件自重不计,圆轮上的销子A 在摇杆BC 的光滑导槽内,圆轮上作用一力偶,其力偶矩大小为M 1=2kN·m,OA =r =0.5m 。
在图示位置时OA 与OB 相互垂直,α=30°,且系统处于平衡状态。
求作用于在摇杆BC 上的力偶矩M 2及铰链O 、B 处的约束力。
解(1)取圆轮为研究对象,画受力图如图2-4b 所示。
A 点的约束力FA 与摇杆的导槽垂直,根据力偶只能用力偶平衡的性质,铰链O 处的约束力FO 必定与FA 形成一个力偶,其转向与M 1转向相反,由此可以确定FA 指向如图2-4b 所示。
ΣMi =0 M 1-FAr sin α=0(2)取摇杆BC 为研究对象,画受力图如图2-4c 所示。
F'A (与FA 互为作用力与反作用力)和FB 形成一力偶,且与M 2平衡。
解之得 M 2=4 M 1=8 kN·m 由此求得2.在图4-8a 所示的杆件中,已知F 1=20kN ,F 2=50kN ,AB 段的直径d 1=20mm ,BC 段的直径d 2=30mm ,试计算各段杆件横截面上的正应力。
解 (1)采用轴力图的简易画法,从左至右作图,可以在不求出固定端约束力和情况下,直接根据外力情况画出轴力图。
(2)确定各横截面的轴力F N 。
采用轴力图的简易画法直接画出轴力图如图解得1sin 30A M F r =ΣM i =020sin ArM F α-+=18kNsin 30O A B M F F F r ====4-8b 所示。
从轴力图上可以看出,各横截面的轴力分别为F N1=20kN ,F N2=-30kN 。
(3)计算各横截面上的正应力。
由式(4-3),AB 段横截面上的正应力为BC 段横截面上的正应力为3.如图4-14a 所示,杆件受轴向载荷作用。
已知:F 1=30kN ,F 2=10kN ,AC 段横截面 面积A 1=500mm2,CD 段横截面面积A 2=200mm2,材料的弹性模量E =200GPa试计算各段杆件横截面上的应力和杆的 总变形Δl 。
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得: D 0
Pl 2 得: C 16
AC段梁的转角方程和挠曲线方程分别为:
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为:
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16:图示梁B处为弹性支座,弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解:(1)梁不变形,仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件: x 0时,y 0
x l时,y 0
得:
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
工程力学

4kN
BC段:
x Fs ( x ) 4kN
M ( x ) 4(l x )
2kN M x
3)作Fs、M 图
4kNm
【例6.3】 图示结构中,AB为圆截面钢杆,已知F=18kN,钢材的许用 应力[]=160MPa,试设计AB杆的直径。
杆端
左侧
例5.7 简支梁AB的C点处作用一集中力偶m,作该梁的Fs、M 图。 m 解: m R R 1)求约束力
a b
A B
x B
l
A
x
l
C
2)列切力、弯矩方程
建立坐标轴 x AC段: m Fs ( x ) RA
l
RA
Fs
RB
m l x
( 0 < x ≤ a)
M ( x ) RA x
(2)计算许用载荷 根据杆①的强度条件
1 A 100´ 200 = =38.6´ 103 N=38.6kN 0.518 0.518
解得
F£
根据杆②的强度条件
解得
结构的许用载荷
[F]=38.6kN。
FN2=0.732F≤[]2A
2 A 160´ 200 F£ = =43.7´ 103 N=43.7kN 0.732 0.732
左上右下错动外力为正
集中力作用点的左、右邻截面上的切力不相等,相差集中 M= m ( P ) 上凹弯曲
一侧 力的大小;弯矩相等。 所以,不考虑集中力作用点的切力。 外力( 偶 ) 矩为正 O
一侧
O为截面的形心
例:求1、2、3、4、5各截面的内力。
m=qa2 A
工程力学材料力学-知识点-及典型例题
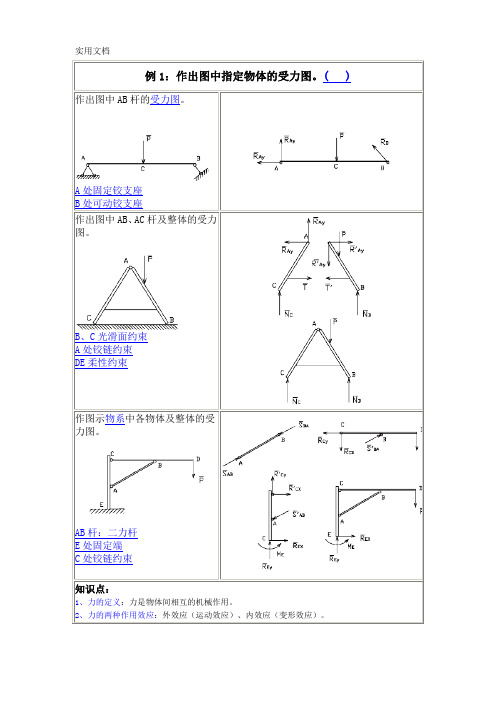
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
工程力学讲义1-3章例题

F CB
C
F 'BA
ϕ [例] 已知: F、a 、b、 , 求:MB (F) 和 例 已知:
解:①用力对点之矩求解
M A (F ) .
a
A
F
ϕ
M B ( F ) = F ⋅ d = Fb cos ϕ
②应用合力矩定理求
M B ( F ) = M B ( Fy ) + M B ( Fx )
= 0 + F cos ϕ ⋅ b
2)摇杆BC:
C
NA
A
NO
α
M2
NB
B
NA ⋅r ∑ M = 0 : sin 30 − M 2 = 0. ∴ M 2 = 8 kNm.
23
M 2 , N A ', N B
思考题 试求机构的滑块在图示位置保持平衡时两主动力偶的关系
解: 1) AB杆为平衡对象。 AB杆为平衡对象。 滑块与杆之间为光滑面约束,因 此D处的约束力FD必垂直于AB。 处的约束力F 必垂直于AB。
P A B
NA
A
或:
P
B
4)A点的约束反力 N A ) 点的约束反力 5)A点的约束反力也可以用两个分力 ) 点的约束反力也可以用两个分力 表示 FAX , FAY 。
NB P
B
FAY
A
FAX
注:作业的书写格式 。
NB
1
第一章 静力学基本公理和物体的受力分析 [例1] 试分析杆 的受力 例 试分析杆AB的受力 的受力。 注:作业的书写格式 。 解:1.杆 AB .
17
A
简易吊车如图所示,滑轮大小忽略不计, 例:简易吊车如图所示,滑轮大小忽略不计,杆自 重不计, 求杆AB、 所受的力。(P= 所受的力。( 重不计, 求杆 、BC所受的力。( =20kN) )
工程力学受力分析

受力分析一、例题1、在图1-22(a)所示的平面系统中,匀质圆盘A重G1,借本身重量和摩擦不计的理想滑轮C和柔绳维持在仰角是α的光滑斜面上,绳的一端挂着重G2的物块B。
试分析圆盘A 和滑轮C的受力情况,并分别画出平衡时两物体的量力图。
解:(1)取圆盘为研究对象,画出其简图。
(2)在其简图上画出主动力。
(3)画约束力。
圆盘A和滑轮C的受力图分别为图1-22(b)和图1-22(c),由于满足三力平衡汇交定理条件,两受力图都可画为三力汇交形式,图1-22(d)为滑轮C三力汇交形式的受力图。
2、简易支架的结构如图1-23(a)所示,图中A、B、C三点为铰链连接。
悬挂物的重量为G,横梁AD和斜杆BC的重量不计。
试分别画出横梁AD和斜杆BC的受力图。
解:(1)先取斜杆BC(二力杆)为研究对象,假设为受拉杆,画受力图见图1-23(b)。
(2)再取横梁AD为研究对象,根据固定铰支座和柔绳约束,画受力图如图1-23(c)所示,注意B点处反作用力方向不能重新假定,要与图1-23(b)中FB方向相反。
3、如图1-24(a)所示的三铰拱桥,由左右两拱桥铰接而成。
设各拱桥的自重不计,在左拱上作用有载荷F,试分别画出左拱和右拱的受力图。
解:(1)先取右拱(二力杆)为研究对象,假设为受压,画受力图[见图1-24(c)]。
(2)取左拱为研究对象,受力图见图1-24(b)。
4、如图1-25(a)所示,梯子的两部分AB和AC在A点铰接,又在D、E两点用水平绳连接。
梯子放在光滑水平面上,若其自重不计,但在AB的中点处作用一铅直载荷F。
试分别画出梯子的AB、AC部分以及整个系统的受力图。
解:分别取梯子的AB、AC部分以及整个系统为研究对象,画分离体的受力图,如图1-25(b)、(c)、(d)所示。
注意:梯子整体的受力图中不要画AB与AC之间的相互作用力,因为对梯子整体来说这是内力。
由于内力成对出现,对梯子整体来说是平衡力系,因此不必画出,只需画出全部外力。
工程力学例题

例 题
例4-1
已知: AC=CB= l, P=10kN; 求:铰链A和DC杆受力. (用平面任意力系方法求解)
解: 取AB梁,画受力图.
Fx 0
FAx Fc cos 45 0
FAy Fc sin 45 F 0
Fy 0
M
A
0
Fc cos 45 l F 2l 0
5 FA 2 2l P l 0 2
解得
5 2 FA P 8
Fix 0
解得
FEx FA cos 450 0
5 FEx P 8
iy
F
解得
0
FEy P FA sin 450 0
13 FEy P 8
取DCE杆,画受力图.
0 M 0 F cos 45 2l FK l FEx 2l 0 C DB
q 20 kN
求: 固定端A处约束力.
, l 1m; F 400kN, m
解: 取T型刚架,画受力图. 1 其中 F1 q 3l 30kN 2 Fx 0 FAx F1 F sin 600 0 解得 FAx 316.4kN
F Ay P F cos 60 0 Fy 0 解得 FAy 300kN
M A 10.37kN
例4-8 已知: P1, P2, P=2P1, r, R=2r, 200 ; 求: 物C 匀速上升时,作用于轮I 上的力偶矩M;轴承A,B处的 约束力.
解: 取塔轮及重物C,画受力图.
M
由
B
0
Pr F R 0
解得
Pr F 10 P 1 R Fr tan 20 0 F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程常见的约束
1、柔绳、链条、胶带构成的约束
P
P
柔索只能受拉力,又称张力。用 FT 表示。 柔索对物体的约束力沿着柔索背向被约束物体。
F1
F2
胶带对轮的约束力沿轮缘的切线方向,为拉力。
2、刚性光滑面约束
P P
P P
光滑支承接触对非自由体的约束力,作用 在接触处;方向沿接触处的公法线并指向受力
连线,但指向不定。
FA
C
A
P
A
B
FB
B
§1–4 受力分析和受力图
受力图的画法步骤:
1.确定研究对象,取分离体。 2.画出研究对象所受的全部主动力。 3.在存在约束的地方,按约束类型逐一画出约 束反力。
注意:
1.首先确定物体系统中是否存在二力构件,如果有先画 二力构件的受力图。 2.当分析物体系统受力时,要分清内力与外力,内力成 对可不画。 3.作用力与反作用力之间的相互关系,作用力一经假定, 反作用力与之大小相等方向相反。
FC
FG
受力分析例题
分别画出图中滑 轮B、杆AC和DC
FE
FBy
的受力图。
B
FBx
FH
FAy
FAx
A
FB' x
FD
D
C
FC
FC
B
C
FB' y
受力分析例题
分别画出图中杆AB、
BC和DE的受力图。
FBy FBx
FD y
FD x
FDx
FDy
FB y
FB x
FAy FAx
FH
FH
FCx
P
FCy
受力分析例题
2、力系的等效替换(或简化):用一个简单力系等效代
替一个复杂力系。
3、建立各种力系的平衡条件:建立各种力系的平衡条件,
并应用这些条件解决静力学实际问题。
第一章 静力学公理和物体受力分析
§1-1基本概念
力:物体间的相互机械作用,这种作用使物体运
动状态发生变化(外效应),或使物体变形(内效应)。
按力的作用点分: 集中力和分布力。
受力分析例题
受力分析例题
已知球A重W1,借本身重量和摩擦不计的理想滑轮C和柔
绳维持在仰角是的光滑斜面上,绳的一端挂着重W2的物
体B。试分析物体B、球A和滑轮C的受力。
解:
1.物体B受力图。
FD
D
B
2.球A受力图。 3.滑轮C的受力图。
W2
FE
E AF
W1 FF
HG
E
C
AF
D B
W1
I H
FH
G
C
公理3 力的平行四边形法则
合力 FR F1 F2
(矢量和)
亦可用力三角形求得合力矢
此公理表明了最简单力系的简化规律,是复杂 力系简化的基础。
推理2 三力平衡汇交定理
作用在刚体上的三个力,若构成平衡力系,且其 中两个力的作用线汇交于一点,则三个力必在同一平面内, 而且第三个力的作用线一定通过汇交点。
二力构件
二力构件:只在两个力作用下处于平衡的构件。 二力构件的受力特点:力必沿作用点的连线。
思考题
P
FA A
FB B
受力图正确吗?
FB B
FA A
公理2 加减平衡力系原理
在作用于刚体的力系中,加上或减去任意 对平衡力系不改变原力系对刚体的作用效应。
加减平衡力系原理是力系简化的重要依据。
推理1 力的可传性
作用在刚体上的力可沿作用线滑移至刚体内 任意点而不改变力对刚体的作用效应。
推理1 力的可传性
作用在刚体上的力是滑动矢量,力的三要素 为大小、方向和作用线。
公理3 力的平行四边形法则
作用在刚体上同一点的两个力,可以合成 为一个合力。合力的作用点也在该点,合力的大小 和方向,由这两个力为边构成的平行四边形的对角 线确定,合力矢等于这两个力矢的几何和。
课程简介
工程力学(或者应用力学)是:将力学原理 应用实际工程系统的科学。
其目的是:了解工程系统的性态并为其设计提 供合理的规则。
工程力学
理论力学:研究物体机械运动
一般规律。
材料力学:研究构件正常工作
应满足的要求。
工
理论力学
刚体
程
平衡、运动(外效应)
力
材料力学
变形固体
学
变形、内力(内效应)
技术基础课。研究物体受力后的效应
§ 1-2 静力学公理
公理1 二力平衡条件
刚体在两个力作用下平衡的充分必要条件 是二力沿着同一直线,大小相等,方向相反。 使刚体平衡的充分必要条件
最简单力系的平衡条件
柔性体(受拉力平衡) (仍平衡)
刚化为刚体
二力平衡条件是刚体平衡的充分必要条件,是 变形体平衡的必要非充分条件。
刚体(受压平衡)
柔性体(受压不能平衡)
物体,故称为法向约束力,用 FN 表示。
3、刚性光滑铰链约束(固定铰链支座、径向轴 承、圆柱铰链等)
(1)固定铰链支座
A
F A
由左边A、B构件之一与
B
B
地面或机架固定而成。
(2)光滑圆柱铰链
约束特点:由两个各穿孔的构件及圆柱销 钉组成,如剪刀。
(3)向心轴承(径向轴承)
约束力: 当不计摩擦时,轴与孔在接触处为光 滑接触约束——法向约束力。约束力作用在接触处, 沿径向指向轴心。
约束特点: 轴在轴承孔内, 轴为非自由体、 轴承孔为约束。
4、辊轴约束
约束特点:在铰支座与光滑固定平面之间装有光滑 辊轴而成。 约束力:构件受到⊥光滑面的约束力。向上或向下
5、二力杆(或二力构件)
两端用光滑铰链与其他物体相接,杆的自重不
计,中间不受力作用的杆件(直杆或曲杆)构成的
约束。二力杆的约束反力必沿着二力杆两端铰链的
柔性体(受拉力平衡) 刚化为刚体(仍平衡)
刚体(受压平衡)
柔性体(受压不能平衡)
注意:刚体平衡条件只是变形体平衡的必要条件非充分条件。
§1-3 约束和约束力
自由体:运动不受其他物体直接制约的物体。 非自由体:运动受到其他物体直接制约的物体。 约束:对非自由体的位移起限制作用的物体。 约束力:约束对非自由体(被约束体)的作用力。 主动力:约束力以外的力。
平衡时 F3 必与 F12 共线则三力必汇交O 点,且共面。
公理4 作用和反作用定律
作用力和反作用力总是同时存在,两个力 大小相等、方向相反,沿着同一直线,分别作用在 两个相互作用的物体上。
在画物体受力图时要注衡,如将已 平衡的变形体刚化为刚体,其平衡状态不变。
刚体:绝对不变形的物体,或物体内任意两点间的距离
不改变的物体。一个物体能否视为刚体,不仅取决于变 形的大小,而且和问题本身的要求有关。
第一部分 静力学
静力学是研究物体的受力分析、力系的等效
替换(或简化)、建立各种力系的平衡条件的一门 科学。
1、物体的受力分析:分析物体(或物体系)受哪些力,每
个力的作用位置和方向,并画出物体的受力图。
