数学建模灰色预测程序代码
灰色预测模型公式

灰色预测模型公式灰色预测模型是一种基于历史数据和现有数据的预测方法,它可以用来预测未来某个事件或指标的发展趋势。
灰色预测模型的核心思想是利用系统自身的信息和规律,通过建立灰色微分方程来进行预测。
灰色预测模型的公式可以表示为:$$\hat{X}_{0}^{(k)} = (X_{0}^{(1)} + X_{0}^{(2)} + ... + X_{0}^{(k)}) / k$$$$\hat{X}_{i}^{(k)} = (X_{0}^{(1)} + X_{0}^{(2)} + ... + X_{0}^{(k)}) / k$$$$\hat{X}_{i+1}^{(1)} = aX_{i}^{(1)} + b$$$$\hat{X}_{i+1}^{(k+1)} = aX_{i}^{(k+1)} + b$$其中,$X_{0}^{(k)}$表示观测数据的累加生成序列,$\hat{X}_{i}^{(k)}$表示预测值,$a$和$b$为待确定的系数。
灰色预测模型的核心思想是将数据分为两个部分:系统的发展规律部分和随机波动部分。
系统的发展规律部分可以通过灰色微分方程进行建模和预测,而随机波动部分则通过随机项来表示。
灰色预测模型的建模步骤如下:1. 数据预处理:对原始数据进行平滑处理,消除随机波动的影响,得到累加生成序列。
2. 确定发展规律:根据累加生成序列,建立灰色微分方程,估计系统的发展规律。
3. 模型参数估计:通过最小二乘法估计模型的参数,确定$a$和$b$的值。
4. 模型检验和优化:对模型进行检验和优化,确保预测结果的准确性和可靠性。
5. 模型预测:利用建立好的灰色预测模型,对未来的数据进行预测。
灰色预测模型在实际应用中具有广泛的应用价值。
它可以用来预测各种经济指标、环境数据、自然灾害等,为决策提供科学依据。
同时,灰色预测模型还可以用于评估和分析系统的可持续发展能力,帮助企业和机构合理规划和管理资源。
灰色预测模型是一种基于历史数据和现有数据的预测方法,它通过利用系统自身的信息和规律,建立灰色微分方程来进行预测。
灰色预测程序

利用MATLAB编程预测2003年中国蔬菜产量,并对预测结果做残差检验和后验差检验,程序如下:function [X,c,error1,error2]=GM11(X0,k)% 建立函数[X,c,error1,error2]=GM11(X0,k)% 其中X0为输入序列,k为预测长度,% X为预测输出序列,c为后验差检验数,error1为残差,error2为相对误差format long;n=length(X0);X1=[];X1(1)=X0(1);for i=2:nX1(i)=X1(i-1)+X0(i); %计算累加生成序列endfor i=1:n-1B(i,1)=-0.5*(X1(i)+X1(i+1)); %计算B,Y nB(i,2)=1;Y(i)=X0(i+1);endalpha=(B'*B)^(-1)*B'*Y'; %做最小二乘估计a=alpha(1,1);b=alpha(2,1);d=b/a; %计算时间响应函数参数c=X1(1)-d;X2(1)=X0(1);X(1)=X0(1);for i=1:n-1X2(i+1)=c*exp(-a*i)+d;X(i+1)=X2(i+1)-X2(i); %计算预测序列endfor i=(n+1):(n+k)X2(i)=c*exp(-a*(i-1))+d; %计算预测序列X(i)=X2(i)-X2(i-1);endfor i=1:nerror(i)=X(i)-X0(i);error1(i)=abs(error(i)); %计算残差error2(i)=error1(i)/X0(i); %计算相对误差endc=std(error1)/std(X0); %计算后验差检验数作业陕西省农业总产值数据如下年份 1985 1986 1987 1888 1989 1990 1991 1992 1993 1994 总产值 62.9 58.8 61.4 87.2 104.9 124.8 110.7 129.0 155.3 219.03请建立灰色系统GM (1,1)模型,并预测1995-1997三年的农业总产值 在命令行输入:X0=[62.9 58.8 61.4 87.2 104.9 124.8 110.7 129.0 155.3 219.03]; k=3;[X,c,error1,error2]=GM11(X0,k) plot(1985: 1994,X0,'g*-') hold onplot(1985:1997,X)1984198619881990199219941996199850100150200250300350奥运会金牌中国预测 X0=[15,5,16,16,28,32,51,38];[X,c,error1,error2]=GM11(X0,k) plot(1:8,X0,'g*-') hold on plot(1:9,X)123456789X0=[5,16,16,28,32,51,38]; k=1;[X,c,error1,error2]=GM11(X0,k) plot(1:7,X0,'g*-') hold on plot(1:8,X)12345678X0=[16,16,28,32,51,38]; k=1;[X,c,error1,error2]=GM11(X0,k) plot(1:6,X0,'g*-') hold onplot(1: 7,X)1234567X0=[16,28,32,51,38]; k=1;[X,c,error1,error2]=GM11(X0,k) plot(1:5,X0,'g*-') hold on plot(1:6,X)1 1.52 2.53 3.54 4.555.56X0=[28,32,51,38]; k=1;[X,c,error1,error2]=GM11(X0,k) plot(1:4,X0,'g*-') hold on plot(1:5,X)1 1.52 2.53 3.54 4.55X0=[32,51,38]; k=1;[X,c,error1,error2]=GM11(X0,k) plot(1:3,X0,'g*-') hold on plot(1:4,X)1 1.52 2.53 3.54。
灰色预测MATLAB程序

作用:求累加数列、求a b的值、求预测方程、求残差clc %清屏,以使结果独立显示x=[ ];format long; %设置计算精度if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换 x=x';endn=length(x); %取输入数据的样本量z=0;for i=1:n %计算累加值,并将值赋予矩阵bez=z+x(i,:);be(i,:)=z;endfor i=2:n %对原始数列平行移位y(i-1,:)=x(i,:);endfor i=1:n-1 %计算数据矩阵B的第一列数据c(i,:)=*(be(i,:)+be(i+1,:));endfor j=1:n-1 %计算数据矩阵B的第二列数据e(j,:)=1;endfor i=1:n-1 %构造数据矩阵BB(i,1)=c(i,:);B(i,2)=e(i,:);endalpha=inv(B'*B)*B'*y; %计算参数矩阵即a b的值for i=1:n+1 %计算数据估计值的累加数列,如改为n+1为n+m可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha(2,:)/alpha(1,: );%显示输出预测值的累加数列endvar(1,:)=ago(1,:) %显示输出预测值for i=1:n %如改n为n+m-1,可预测后m-1个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下一预测值endfor i=1:nerror(i,:)=x(i,:)-var(i,:); %计算残差endc=std(error)/std(x); %调用统计工具箱的标准差函数计算后验差的比值c ago %显示输出预测值的累加数列alpha %显示输出参数数列var %显示输出预测值error %显示输出误差c %显示后验差的比值作用:数据处理判断是否可以用灰色预测、求级比、求累加数列、求a b的值、求预测方程clc,clearx0=[ ]'; %注意这里为列向量n=length(x0);lamda=x0(1:n-1)./x0(2:n) %计算级比range=minmax(lamda') %计算级比的范围x1=cumsum(x0) %累加运算B=[*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];Y=x0(2:n);u=B\Y %拟合参数u(1)=a,u(2)=bx=dsolve('Dx+a*x=b','x(0)=x0'); %求微分方程的符号解x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)}) %代入估计参数值和初始值yuce1=subs(x,'t',[0:n-1]); %求已知数据的预测值y=vpa(x,6) %其中的6表示显示6位数字yuce=[x0(1),diff(yuce1)] %差分运算,还原数据。
灰色预测模型matlab程序精确版

%x=[1019,1088,1324,1408,1601];gm1(x); 测试数据%二次拟合预测GM(1,1)模型function gmcal=gm1(x)if nargin==0x=[1019,1088,1324,1408,1601]endformat long gsizex=length(x);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加生成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,用于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=length(z1);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置%YNB=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';%B,au0,auafor = au(1);ufor = au(2);ua = au(2)./au(1);%afor,ufor,ua%输出预测的 a u 和 u/a的值constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';%constant1,afor1,x1t1,estr,tstr,leftbra,rightbrastrcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+ ',leftbra,num2str(ua),rightbra)%输出时间响应方程%******************************************************%二次拟合k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endend%ze1sizeze1=length(ze1);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';%z4,X1,G,au20Aval = au2(1);Bval = au2(2);%Aval,Bval%输出预测的 A,B的值strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',lef tbra,num2str(Bval),rightbra)%输出时间响应方程nfinal = sizex-1 + 1;(其中+1可改为+5等其他数字,即可预测更多的数字)%决定预测的步骤数5 这个步骤可以通过函数传入%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%x3fcast%一次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%一次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%二次拟合预测值%***精度检验p C************////////////////////////////////// k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexelseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexelses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizex;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的方差 s1sqrt 为x方差的平方根S1 k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexelses2total = s2total + (err1(k5) - err1avg)^2; endends2suqare = s2total ./ sizex;%s2suqare 残差数列err1的方差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizex;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进行改进运行结果x =1019 1088 1324 1408 1601ans =x1(t+1)=8908.4929exp(0.11871t)+(-7889.4929)ans =x1(t+1)=8945.2933exp(0.11871t)+(-7935.7685)x31fcast =Columns 1 through 31019 1122.89347857097 1264.43142178303 Columns 4 through 61423.80987235488 1603.27758207442 1805.36675232556 x41fcast =Columns 1 through 31019 1118.05685435129 1269.65470492098 Columns 4 through 61429.69153740195 1609.90061644041 1812.82460377782 x =1019 1088 1324 1408 1601Cval =0.139501578334155 pval =1。
灰色预测MATLAB程序

灰色预测专设工⑼他QA—叫吋)为原始数列.其1次累❖加生成数列为恥=妙①曲⑵,…卅何),其中X° 仇)二工* ° (0.址=1=2= -:n5-1卷定义卫的决导数为d(k) = *町(上)=x 叫咼-x cl)(Jt-l).令为数列工①的邻值生成数列.即却(去)=^(*) + (1- a)x0)(t-lX于是定义GM (L 1)的灰微分方程模型为d(k)-血⑴住)=K即或严>(£) + “尹⑻=人⑴在式(1)中』。
>(灼称为灰导数,我称为发展系数, 弧称为白化背景值,b称为灰作用量乜将时刻表殳二2「3「/代入(1)式有V!1「—ay=代⑶ B =Ib*- :X闵0)-Z,:](K)1于是G\I <1»1)複至可表示为Y = Bu.現在问题归结为求sb 在值。
用一元线性回归・即最小二秦法求它们的活计值 为注二实陌上回归分析中求估计值是用软件计尊的・有标准程序求解,iOmaClab 等。
GM <1» 1>的白化晏対于G\I <1> 1)的灰微分方程(1) >如果将灰导数打(Q 的时刻 视为连绫变里"则x°)视为时问(函数卅⑺,于是*〉(Q 対血于导数里级 心2 >白化背臬值申的对应于导数卅⑴。
于是G\I (1,1)的坝徽 分方樂対应于的白微分方程为内・则数堀列X©可以塗互G\I <19 1) 且可以进行页色预测。
否朋,対数摄做适当的克换处理■如平移叢换:取C 使得鞍据列严伙)=工⑴伙)+ G 上=1,2,…,的级比都華住可吝禎盖内。
心⑴⑴ + o?i> (r)二◎ dr<2)GM mi )质色预测的步骤1 •教摇的枪绘与处連为了ftilGAl (1,1)建複方法的可行性,亲要为已知期S 做必要的检蛉处理。
设原始教据列为了 逛=(乂°(1)*6(2)严炉00; >计算数列的级比如果所有的级比都落在可容覆盖区间 • fc =A-2,3"・如果対所有的|p 伙)|<0・1 -则认为达到较高的要求,否则 若旳所有的|。
灰色预测MATLAB程序

灰色预测心设尹曲⑴#为原始数列,其1次累<加生成数列为炉=(孝①宀2\S,其中©=2^°:⑺卫=12…止i-1尋定文沙的灰导数为d(Jt)=玄㈣(Jt)=尤⑴的-工⑴(*-1).令尹为数列壬⑴的邻值生成数列,即尹)(町=加小(町十(1—a)x山(k-1).于是定文GM(1T1)的灰微分方程模型为d(k)+az①(上)=&_即或.严⑹+盘⑴懐)=乩⑴在式(1)中口①的称为灰导数’熬称为发展系数'弧称为白化背景值,b称为灰作用量。
将时刻表庄=23…用代入(O式有j<0)(2)-az⑴(2)=工®⑶—俺叫巧=»于是GMIL)樫型可表示为r=现在问题归结为求巧h在值。
用一元绒性回归,即最小二垂進求它们的估计值住=[]卜护跖护F奕厢上回归分析中求诂计值是用软件计算的,有标淮程博求解,如山訥甜等。
GM(1.1)的白化型对于的(1-1)的获微分方程⑴,如果将解导教矿悶的时報=%…屮观対连续叢里"则工⑴衩为时间i函敕卅®,于是-<'W耐应于导敕重级必%),白化背杲值刃(時对应于导數申⑴。
于是GM(1,1)的换微分方嗨对应于的白微分方程为写®4曲%「)=也⑵GAI(1>1)换色预刪的步叢1-數堀的椅噓弓处理为了保证©M(B1)屋複方达的可行性・需要対已却皴堀锁必要的检峻处Ho 设療皓数攥列为了-计算埶列的级比如果所有的级比都落在可容覆盖区间盂-內・则數摒列X糾可咲建立G*ICL-1)複型且可以避行页色预测。
否则,丙軌据懺适当的叢换处理,如平移銮换:取C使得敕培列严⑹二工蚀盘)+匚用二12…”的级比都落在可啓禎盖内。
(1)残差檢验:计算相对薙差Z 建立GM (L T 1)複型不妬设少弋以m 叫唠霸足上面的要求,以它芮議堀列建立GM(1>1)型蛊(仍(i)+血C1\A)=b ・用回归分祈求得目上的估计值"于是相应的白化模型为 气^十小卄工解为工叱)=0)①—勺中1-色-⑶ 应Q于是停到预测值壬⑴(上+1)=0叫1)一勺>加+仝血二12…卫一1=aa伙而相应地得到预«=x co \t +1)=x 0)(t+l)-x a)(i)3i =1,2,-?n-l ?如果对所有的^<0.1・则认为达到鞭嵩的要求:否则,若耐所有的|^)1<0^,则认対达到一般要求©(2)级比偏差値桧验:计算能)=1-呂学©如果对所有的|,则认为达列较高的要求孑吾则若对斫有的,则认为达到一般要求O灰色预测计算实例^…;=:=-■■■■昏例北方某城市1986—1992年道路交通噪声平均声级数据见表6序号年吶寺表拆市近年来交通噪声数据[眶(应)]二諾;二319S872.4第—爭:级比检验建立丢通噪屛均声级数锯时间序列如下:4198972.1j 1990?1.4 619?17201199771.6艸=(•严①卫购(2)厂卅⑺) =(711,72.4.71.4,72.1.71.4,7UQ.71.6)些(1)求级比k(k)忠防护住T)2=(几⑵山⑶.…也⑺)g=(0.982JJ.0042J.0098-0.9917J.0056)(2)级比判断由于所有的X.(10e[0.982J.009S],k=2,3.6故可以用双0)作满意的GM(1,1)建模’第二步:GM(1,1)建模(1)对原始数据X®作一次累加,即卞⑴=(71.L143.5215.9.288359.4.431.4,503)(2)构造数据矩阵B及数据向量Y-2)—H 弋3/>1⑶讦算1T心求解得F'⑴=(工倒〔1〉_-)e 弋Q f+-1*^+1)=0<l,U)--)£-t +-=-3092^--^+31000⑶求生咸数列值歸型齊看:n令“is 那血由上面的碉醯数可甲得,其中取菱由龙⑴(i}=恥壮曲5加得丁I —"炉閃=进悶-进德-尊(71儿72.4.72.2:72.1:71.9:71.7,71.6)^}=(s"a >亍⑴⑵,…,网⑺A<第三步;模型检验•>模型的各种检验指标值的计算结果见表工 •t*表7GM(1检验表<序号年俯原始值模型值残差相对误差级比偏差•>1 19S6 71.1 71.1<219S7 72.4 72.4 -0.0057 0.01%0.0023 <3 19S S 72.4 72.2 0.163S 0.23%0.0203 •>4 19S9 72.1 72.1 0.0329 0.05%-O.(K H8 •>5199071.4 71.9 -0-49S4 0.7%-0.0074 <61991 72.0 71.7 0.21599 037%0.0107<71992 71.6 71.6 0.037S0.05%-0.0032于是得到目=山的餡,立欖型7-B)'1B TY=(dt0.0023 72.6573dt+0.002ix (1>=72.657^心经验证・该模型的精度较高.可进行预测和预报计算的Matlab 程序如下:仃坝测和预报n=length(x); z=0;%取输入数据的样本量for i=1:nz=z+x(i,:)be(i,:)=z; %计算累加值,并将值赋予矩阵beend for i=2:n %对y(i-1,:)=x(i,:)%对原始数列平行移位 endfor i=1:n-1%计算数据矩阵B 的第一列数据c(i,:)=-0.5*(be(i,:)+be(i+1,:)); clCjdearxO=[71H 72.472A 72J71477m c n.lengthtxO);*'b%注意这里为列帖lamda =xD(l :n-1),A0(2:n)%计算级比range =minmaxflamda f )%计算级比的范阖 X1=cumsum(xO);%累加运算B=['0,5*(xl(l ;n ^l)+xl(2:n))t ones(n -1,1)]TY 二甸(2:町;口=B\Y%拟合参数u(l>=a .u(2)=bx=dsolve (+a 'x =b\f x(0)-xO^J ;%求徴分方程的特号解x =subs(xJ*a\,b r /xO ,Mu(l)P u(2)t xO(l)|)i%代入荷计痹擞值和初蜡值yucel =subs %求巳知数擁的扳测位y-vpa(x,6)奄其中的石表示显不白位数字yuce=[x0(l)T diff(yucel)]%羔分运算,还原数据 epsiIon=-yuce%计算战羞作用:求累加数列、求ab 的值、求预测方程、求残差clc %清屏,以使结果独立显示x=[71.172.472.472.171.472.071.6]; format long ;%设置计算精度if length(x(:,1))==1%对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x endM.I-JTVorhlllst 模型endfor j=1:n-1%计算数据矩阵B的第二列数据e(j,:)=1;endfor i=1:n-1%构造数据矩阵BB(i,1)=c(i,:);B(i,2)=e(i,:);endalpha=inv(B'*B)*B'*y;%计算参数矩阵即ab的值for i=1:n+1%计算数据估计值的累加数列,如改为n+1为n+m可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha( 2,:)/alpha(1,:);%显示输出预测值的累加数列endvar(1,:)=ago(1,: )for i=1:n%显示输出预测值%如改n为n+m-1,可预测后m-1个值var(i+1,:)=ago(i+1,:)-ago(i,:);%估计值的累加数列的还原,并计算出下一预测值endfor i=1:nerror(i,:)=x(i,:)-var(i,:);%计算残差endc=std(error)/std(x);%调用统计工具箱的标准差函数计算后验差的比值cago alpha var%显示输出预测值的累加数列%显示输出参数数列%显示输出预测值error %显示输出误差c %显示后验差的比值作用:数据处理判断是否可以用灰色预测、求级比、求累加数列、求ab的值、求预测方程clc,clearx0=[71.172.472.472.171.472.071.6]';%注意这里为列向量n=length(x0);lamda=x0(1:n-1)./x0(2:n)%计算级比range=minmax(lamda')%计算级比的范围x1=cumsum(x0)%累加运算B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];Y=x0(2:n);u=B\Y%拟合参数u(1)=a,u(2)=bx=dsolve('Dx+a*x=b','x(0)=x0');%求微分方程的符号解x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)})%代入估计参数值和初始值yuce1=subs(x,'t',[0:n-1]);%求已知数据的预测值y=vpa(x,6)%其中的6表示显示6位数字yuce=[x0(1),diff(yuce1)]%差分运算,还原数据。
MATLAB实现灰色预测程序

MATLAB实现灰色预测程序function [y,p,e]=huise_1_1(X,k) %灰色模型的malab程序%Example [y,p]=gm_1_1([200 250 300 350],2)%接口描述:X的预测的初始数列,|X|>4,K是指向后进行预测的个数%命令格式:程序保存的文件名,eg:huise.m 则命令是:huise([579.8 547.5 527.0 492.3 437.0],5) if nargout>3;error('Too many output argument.');endif nargin==1,k=1;x_orig=X;elseif nargin==0|nargin>2error('Wrong number of input arguments.');endx_orig=X;predict=k; %AGO 处理,即是对初始数列进行一阶累加x=cumsum(x_orig); %计算系数(a 和u)------------------------n=length(x_orig); %生成矩阵Bfor i=1:(n-1);B(i)=-(x(i)+x(i+1))/2;endB=[B' ones(n-1,1)]; %生成矩阵Yfor i=1:(n-1);y(i)=x_orig(i+1);endY=y'; %计算系数a=au(1) u=au(2)au=(inv(B'*B))*(B'*Y); %--------------------------------------------------------%把huise模型公式转换成符号coef1=au(2)/au(1);coef2=x_orig(1)-coef1;coef3=0-au(1);costr1=num2str(coef1);costr2=num2str(abs(coef2));costr3=num2str(coef3);eq=strcat(costr1,'+',costr2,'e^',costr3,'*(t-1))'); %计算每一个值for t=1:(n+predict)mcv(t)=coef1+coef2*exp(coef3*(t-1));endx_mcv0=diff(mcv);x_mcve=[x_orig(1) x_mcv0] %输出图形中的各点x_mcv=diff(mcv(1:end-predict));x_orig_n=x_orig(2:end);x_c_error=x_orig_n-x_mcv;x_error=mean(abs(x_c_error./x_orig_n));if x_error>0.2 %相对误差的均值disp('model disqualification!');elseif x_error>0.1disp('model check out');elsedisp('model is perfect!');endplot(1:n,x_orig,'o',1:n+predict,x_mcve);p=x_mcve(end-predict+1:end); %画出预测模型和初始数列的点xlabel('年份(从第一个数据年份起)');ylabel('产水量(万吨)');title('灰度模型GM(1,1)');grid ony=eq;e=x_error;p=x_mcve(end-predict+1:end);。
灰色预测的matlab实现,代码大全

disp('确定的模型为:x1(k+1)=(x(1)-u_a)*exp(-k*a)+u_a') 改进灰色模型代码: for i=1:inf if i==1
e(i)=input('输入数据:'); else if e(i-1)==0 break; else end
e(i)=input('输入数据:');
6
1
x2(k+1)=(x0(1)-u_a)*exp(-k*a)+u_a; end %求出新数列的模拟值 x2 x3=x2; x3(m2+k0)=[]; x4=[0 x3]; x5=x2-x4;%利用累减生成法求出原始数据的模拟值 x5 disp('3.一次累加(1-AGO)生成的数据的模拟值:') Y=''; for z=1:m2+k0 Y=strcat(Y,'(',num2str(x2(z)),')'); end disp(Y); disp('4.原始数据的模拟值:') Y=''; for z=1:m2+k0 Y=strcat(Y,'(',num2str(x5(z)),')'); end disp(Y); % 4. 模型检验(算出的值到等级参照表中检查其精度等级) %计算后验差比 C 和残差序列 Q x6=x5(1:m2); Q=x0-x6;%Q 为残差序列 s1=std(Q);%s1 为残差序列 Q 的标准差 s2=std(x0);%s2 为初始序列 x0 的标准差 C=s1/s2;%后验差比 C(越小越好) w1=1:m2; w1=[ones(m2,1) w1']; w2=Q'; [bb,bint,r1,rint,stats]=regress(w2,w1); rcoplot(r1,rint) C1=strcat('5.后验差比(均方差比值): C=',num2str(C));disp(C1); if C<=0.35 disp(' 由于 C<=0.35,则此模型精度等级为 1 级(好) 。'); else if C<=0.5 disp(' 由于 0.35<C<=0.5,则此模型精度等级为 2 级(合格) 。'); else if C<=0.65 disp(' 由于 0.5<C<=0.65,则此模型精度等级为 3 级(勉强) 。'); else disp(' 由于 C>0.65,则此模型精度等级为 4 级(不合格) 。'); end end end
数学建模灰色预测程序代码

数学建模灰色预测程序代码这里写了四个函数,方便在Matl ab里面调用,分别是GM(1,1),残差GM (1,1),新陈代谢GM(1,1),Verhu st自己写得难免有所疏忽,需要的朋友自己找本书本来试验一下。
Gm(1,1)funct ion [px0,a b,rel]=gm11(x0,numbe r)%[px0,a b,rel]=gm11(x0,numbe r)%p x0为预测数列,re l为平均相对误差,r el为平均相对误差(为百分比)%默认的numbe r参数为原数组大小if na rgin==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换 nu mber=max(s ize(x0));endn=max(size(x0));%取输入数据的样本量x1=z eros(size(x0));fork=1:nfor i=1:k x1(k)=x1(k)+x0(i); %计算累加值,并将值赋予矩阵beende ndz=zeros(size(x0));for k=2:n z(k)=0.5*(x1(k)+x1(k-1)); %计算数据矩阵B的第一列数据endy=x0';y(1)=[];b(:,1)=-z';b(:,2)=1;b(1,:)=[];ab=inv(b'*b)*b'*y; %计算参数矩阵a=ab(1);b=ab(2);p x0(1)=x0(1);%求还原值系列fork=1:n umber-1 px0(k+1)=(1-e xp(a)) * ( x0(1)-b/a ) *exp(-a*k);endtemp=px0(1:n);x0;t emp=(temp-x0)./x0; %相对误差temp(1)=[]; %删除第一个为零的误差tem p=abs(temp);re l=sum(temp)/(n-1)*100;残差Gm(1,1)f uncti on [p x0,ab,rel]=ccgm11(x0,numb er)%[px0,ab,re l]=gm11(x0,numb er)%px0为残差预测数列,ab为求得的系数,rel为平均相对误差(为百分比) %默认的numb er参数为原数组大小if n argin==1 nu mber=max(s ize(x0));endn=max(size(x0));%数组大小..[px0,ab,rel]=gm11(x0,nu mber);wuc ha=x0-px0(1:n);i=n;%求后面的同号的数目.wh ile(w ucha(i)*wu cha(i-1)>0 & i>=2) i=i-1;ends tart=i;le ngth=n-i+1;new=wuch a(sta rt:n);iflengt h>=4p wucha=gm11(new);px0(star t:n)=px0(s tart:n)+pw uchaclea r wuc ha;w ucha=px0-x0;wu cha=w ucha./x0; %相对误差w ucha=abs(w ucha);rel=sum(wucha)/(n-1)*100;en dve rhustfunc tion[px0,ab,re l]=ve rhust(x1,n umber)%[p x0,ab,rel]=verh ust(x0,num ber)%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比)%默认的num ber参数为原数组大小ifnargi n==1n umber=max(size(x1));endn=max(size(x1));x0(1)=x1(1);for k=2:nx0(k)=x1(k)-x1(k-1);z(k)=0.5*(x1(k)+x1(k-1));endx0;z;B=[-(z(2:n))'(z(2:n).^2)'];B;Y=(x0(2:n))';Y;ab=in v(B'*B)*B'*Y;a=ab(1);b=a b(2);fork=1:n umberpx0(k)=(a*x1(1))/(b*x1(1)+(a-b*x1(1)).*e xp(a*(k-1)));e ndte mp=px0(1:n);x1;tem p=(te mp-x1)./x1; %相对误差te mp(1)=[]; %删除第一个为零的误差temp=abs(t emp);rel=sum(t emp)/(n-1)*100;新陈代谢Gm(1,1)f uncti on [p x0,ab,rel]=xcdx gm11(x0,nu mber,step)%[px0,ab,rel]=xcdxg m11(x0,num ber,s tep)%x0为原系列,nu mber为要预测的数目,ste p为基本步长%px0为预测数列,rel为平均相对误差,re l为平均相对误差(为百分比)%默认的n umber参数为原数组大小%模型假设预测的数据和原始数据都要大于等于5ifnargi n==1n umber=max(size(x0));step=max(s ize(x0));endi f nar gin==2 step=max(size(x0));endn=max(size(x0));ifn<ste p | n<5 err or('此模型要求至少有五个原始数据,并且原始数据个数要大于新陈代谢的步长.');end[px0,ab,r el]=g m11(x0,n);last=n;x0;px0;wh ile l ast<n umberbegin=last-step+1; te mp=px0(beg in:la st);t emp=g m11(t emp,s tep+1); las t=las t+1;p x0(la st)=t emp(s tep+1);en d 。
数学建模算法:灰色预测模型GM(1,1)及Python代码
数学建模算法:灰⾊预测模型GM(1,1)及Python代码灰⾊预测模型GM(1,1)灰⾊预测模型\(GM(1,1)\)是在数学建模⽐赛中常⽤的预测值⽅法,常⽤于中短期符合指数规律的预测。
其数学表达与原理分析参考⽂章尾部⽹页与⽂献资料。
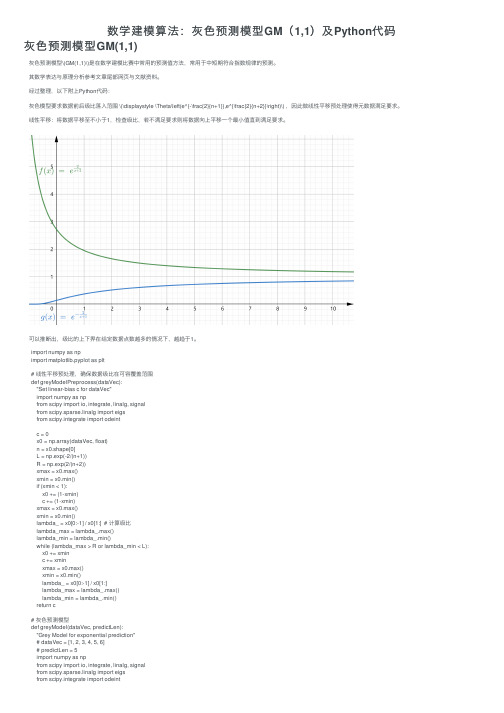
经过整理,以下附上Python代码:灰⾊模型要求数据前后级⽐落⼊范围 \(\displaystyle \Theta\left(e^{-\frac{2}{n+1}},e^{\frac{2}{n+2}}\right)\) ,因此做线性平移预处理使得元数据满⾜要求。
线性平移:将数据平移⾄不⼩于1,检查级⽐,若不满⾜要求则将数据向上平移⼀个最⼩值直到满⾜要求。
可以推断出,级⽐的上下界在给定数据点数越多的情况下,越趋于1。
import numpy as npimport matplotlib.pyplot as plt# 线性平移预处理,确保数据级⽐在可容覆盖范围def greyModelPreprocess(dataVec):"Set linear-bias c for dataVec"import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintc = 0x0 = np.array(dataVec, float)n = x0.shape[0]L = np.exp(-2/(n+1))R = np.exp(2/(n+2))xmax = x0.max()xmin = x0.min()if (xmin < 1):x0 += (1-xmin)c += (1-xmin)xmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:] # 计算级⽐lambda_max = lambda_.max()lambda_min = lambda_.min()while (lambda_max > R or lambda_min < L):x0 += xminc += xminxmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:]lambda_max = lambda_.max()lambda_min = lambda_.min()return c# 灰⾊预测模型def greyModel(dataVec, predictLen):"Grey Model for exponential prediction"# dataVec = [1, 2, 3, 4, 5, 6]# predictLen = 5import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintx0 = np.array(dataVec, float)n = x0.shape[0]x1 = np.cumsum(x0)B = np.array([-0.5 * (x1[0:-1] + x1[1:]), np.ones(n-1)]).TY = x0[1:]u = linalg.lstsq(B, Y)[0]def diffEqu(y, t, a, b):return np.array(-a * y + b)t = np.arange(n + predictLen)sol = odeint(diffEqu, x0[0], t, args=(u[0], u[1]))sol = sol.squeeze()res = np.hstack((x0[0], np.diff(sol)))return res# 输⼊数据x = np.array([-18, 0.34, 4.68, 8.49, 29.84, 50.21, 77.65, 109.36])c = greyModelPreprocess(x)x_hat = greyModel(x+c, 5)-c# 画图t1 = range(x.size)t2 = range(x_hat.size)plt.plot(t1, x, color='r', linestyle="-", marker='*', label='True')plt.plot(t2, x_hat, color='b', linestyle="--", marker='.', label="Predict")plt.legend(loc='upper right')plt.xlabel('xlabel')plt.ylabel('ylabel')plt.title('Prediction by Grey Model (GM(1,1))')plt.show()误差分析部分:可就绝对误差、相对误差、级⽐、残差做数据分析,以下⽰例为最⼩⼆乘法线性回归分析。
灰色模型预测GM(1,1)MATLAB程序代码

灰色模型预测GM(1,1)MATLAB程序代码版权所有引用请注明出处function gmcal=gm1(x)%% 二次拟合预测GM(1,1)模型%x = [5999,5903,5848,5700,7884];sizexd2 = size(x,2);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加生成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,用于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=size(z1,2);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置B=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';afor = au(1);ufor = au(2);ua = au(2)./au(1);constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1 ),tstr,rightbra,'+',leftbra,num2str(ua),rightbra) %输出时间响应方程k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endendsizeze1 = size(ze1,2);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';Aval = au2(1);Bval = au2(2);strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,ri ghtbra,'+',leftbra,num2str(Bval),rightbra) %输出时间响应方程nfinal = sizexd2-1 + 1; %决定预测的步骤数5 这个步骤可以通过函数传入%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%一次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%一次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%二次拟合预测值%***精度检验p C************////////////////////////////////// k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexd2elseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizexd2;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的方差 s1sqrt 为x方差的平方根S1k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses2total = s2total + (err1(k5) - err1avg)^2; endends2suqare = s2total ./ sizexd2;%s2suqare 残差数列err1的方差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrt pnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizexd2;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进行改进。
灰色预测及MATLAB实现

3.1灰色预测基础知识
什么是灰色预测?
灰色预测是就灰色系统所做的预测。所谓灰色系统是介于白 色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一 系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部 分信息已知,部分信息未知,那么这一系统就是灰色系统。一般 地说,社会系统、经济系统、生态系统都是灰色系统。例如物价 系统,导致物价上涨的因素很多,但已知的却不多,因此对物价 这一灰色系统的预测可以用灰色预测方法。 灰色系统理论认为对既含有已知信息又含有未知或非确定信 息的系统进行预测,就是对在一定方位内变化的、与时间有关的 灰色过程的预测。尽管过程中所显示的现象是随机的、杂乱无章 的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规 律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预 测。
ˆ (4)用最小二乘法求解灰参数 a ( a, ) ( B B )
T T
1
B Yn 。
T
ˆ (5)将灰参数 a 代入
ˆ x dy
(1)
dx
(1)
ax
(1)
,求解得
(1)
dt
(t 1) ( x
(0)
a
)e
at
a
dx ˆ ˆ (1) 由于 a 是通过最小二乘法求出的近似值,因此 x (t 1) 事近似表达
(1)
ˆ 序列,得到近似数据序列 x ˆ x
(0)
(0)
ˆ (t 1) x
(1)
ˆ (t 1) x
(t )
(7)建立灰色预测模型进行检验,步骤如下:
① 计算 x
(0)
与x
(0)
(t ) 之间的残差和相对误差 (t ) x
分数灰色预测matlab代码详解

分数灰色预测matlab代码详解分数灰色预测(Fractional Grey Model,FGM)是以函数的非线性分数阶微分方程为基础的一种新型时间序列预测方法。
在FGM中,将已知的数值序列$X(k),k=1,2,\cdots,n$ 作为被预测序列,通过构造二阶单位根非线性微分方程,建立起包含一阶导数、二阶导数、初值以及终值的模型,进而计算模型参数并根据模型实现对未来数值的预测。
该方法对中小样本序列具有良好的预测效果,且其原理简单、易于理解,因此在实际预测中得到了广泛应用。
以下是FGM的matlab代码和具体解释。
首先,导入数据,例如一组销售数据:```matlabY = [42 59 72 88 114 138 157 186 212];```接下来,可以通过以下函数将数据转换为一阶、二阶累加数据:```matlabX = cumsum(Y); % 一阶累加n = length(X);for i = 1:n-1DX(i) = X(i+1)-X(i); % 二阶累加end```然后,可以定义分数阶微分方程。
FGM的分数阶微分方程为:$$_{0}D_{t}^{\alpha}X(t)=a_{1}\cdot X(t)+a_{2}$$其中 $a_{1}$、$a_{2}$ 为待求参数,$\alpha$ 为分数阶微分阶次。
根据变换公式,$a_{1}$ 和 $a_{2}$ 可以通过以下函数求得:```matlabsyms a1 a2eq1 = DX(1) - a1*X(1) - a2;eq2 = DX(2) - a1*X(2) - a2;eq3 = DX(3) - a1*X(3) - a2;eq4 = DX(4) - a1*X(4) - a2;eq5 = DX(5) - a1*X(5) - a2;eq6 = DX(6) - a1*X(6) - a2;eq7 = DX(7) - a1*X(7) - a2;eq8 = DX(8) - a1*X(8) - a2;eqn = DX(n-1) - a1*X(n-1) - a2;[eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8,eqn][A,B] = equationsToMatrix([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8,eqn],[a1,a2]); X = linsolve(A,B);a1 = X(1)a2 = X(2)```这里使用了符号计算工具箱,利用上述方程组解出 $a_{1}$ 和 $a_{2}$。
(完整word版)灰色预测代码(word文档良心出品)

例一function predate=greypred(ddata,lenn,stepnum)predata=[];llen=length(ddata);sumdata(1:llen)=l;for k=1:llensumdata(k)=sum(ddata(1:k));endyn=ddata(2:llen)';B(1:llen-l,1:2)=1;for k=l:lien-lB(k,1)=-0.5*(sumdata(k)+sumdata(k+1));endcoeff=inv(B'*B)*B'*yn %用最小二乘拟合系数for k=l:lenn+llenanser=(ddata(1)-coeff(2)/coeff(1))*exp(coeff(1)*(k-1))+coeff(2)/coeff(1); predata=[predata anser];endpredata(2:lenn+lien)=predata(2:lenn+lien)-predata(1:lenn+lien-1);step=1;X=2002:2009;Y=[2724.8 3126.1 3664.8 4193.4 4792.1];len=8,num=5;%已知5个原始数据reg= Y(1:num);predlen=len-num;%需要预测的数据个数predy= greypred(reg,predlen,step);figure(1)hold onplot(x(1:5),y,'-b');plot(x,predy,'-ro');legend('真实值','预测值'),title('预测效果');xlabel('年'),ylabel('收入增加值');hold offep=Y-predy(1:num);%残差eeq=ep./y;%相对残差figure(2)plot(x(1:5),Y,'-b.',x(1:5),predy(1:5),'-ro');legend('真实值','预测值')title('真实值与预测值的接近程度');xlabel('年'),ylabel('收人增加值')figure(3)plot(x(1:5),ep,'-b',x(1:5),eeq,'-ro');legend('残差','相对误差');axis square例2y=[48.7 57.17 68.76 92.15]n=length(y);yy=ones(n,1);yy(1)=y(1);for i=2:nyy(i)=yy(i-1)+y(i);endB=ones(n-1,2);for i=1:(n-1)B(i,1)=-(yy(i)+yy(i+1))/2;B(i,2)=1;endBT=B';for j=1:n-1YN(j)=y(j+1);endYN=YN';A=inv(BT*B)*BT*YN;a=A(1);u=A(2);t=u/a;t_test=10;i=1:t_test+n;yys(i+1)=(y(1)-t).*exp(-a.*i)+t;yys(1)=y(1);for j=n+t_test:-1:2ys(j)=yys(j)-yys(j-1);endx=1:n;xs=2:n+t_test;yn=ys(2:n+t_test);plot(x,y,'^r',xs,yn,'*-b');det=0;for i=2:ndet=det+abs(yn(i)-y(i));enddet=det/(n-1);disp(['百分绝对误差为:',num2str(det),'%']); disp(['预测值为:',num2str(ys(n+1:n+t_test))]);。
灰色模型的R代码

灰⾊模型的R代码This post was kindly contributed by - go there to comment and to read最近帮朋友写了⼀个灰⾊模型GM(1,1)的R实现,参考⽹上现有的matlab代码,⽐较容易就可以弄出来。
下⾯是具体过程,主函数是GM(),建⽴的模型是⼀个S3类,搭配两个⾃定义的泛型函数print和plot可以得到结果输出和图形。
# 本代码⽤来计算GM(1,1)灰度模型# 输⼊:x 原始数据,adv为外推预测步长# 输出:actual 原始数据,fit 拟合数据,degree 拟合精度,# C 后验差⽐值,P ⼩概率误差,predict 外推预测值# 主函数GM <- (x,adv=0) {x0 <- xk = (x0)# AGOx1 = (x0)# construct matrix B & YB = (-0.5*(x1[-k]+x1[-1]),(1,times=k-1))Y = x0[-1]# compute BtB...BtB = (B)%*%BBtB.inv = (BtB)BtY = (B)%*%Y# estimatealpha = BtB.inv%*%BtY# 建⽴预测模型<- (k) {y = (x0[1] - alpha[2]/alpha[1])*(-alpha[1]*k)+alpha[2]/alpha[1](y)}pre <- (X=0:(k-1),FUN=)prediff <- (pre[1],(pre))# 计算残差error <- ((prediff-x0),digits=6)emax <- (error)emin <- (error)# 模型评价incidence <- (x) {((emin + 0.5*emax)/(x+0.5*emax))}degree <- ((error,incidence))s1 <- (((x0-(x0))^2)/5)s2 <- (((error-(error))^2)/5)<- s2/s1e <- (error-(error))p <- (e<0.6745)/length(e)result <- (actual = x0,fit = prediff,degree = degree,= ,P = p)# 外推预测第k+adv项if (adv > 0) {pre.adv <- (k+adv-1)-(k+adv-2)result$predict <- pre.adv}(result) <- 'GM1.1'(result)}# 增加对应gm1.1类的泛型函数 print & plotprint.GM1.1 <- (mod){('the result of GM(1,1)\n')('Actual Data:', '\n',mod$actual ,'\n')('Fit Data:', '\n',(mod$fit,2) ,'\n')('Degree:', (mod$degree,3) ,'\n')('C:', (mod$C,3) ,'\n')('P:', (mod$P,3) ,'\n')if (!(mod$predict)) {('Predict Data:', (mod$predict,2), '\n')}}plot.GM1.1 <- (mod,adv=5){prex <- (adv)x <- mod$actualfor (k in 1:adv){prex[k] <- GM(x,k)$predict}value = (x,prex)res <- (index = 1:(value),value = value,type = (((1,(x)),(2,(prex)))))()p <- (res,aes(x=index,y= value))p + geom_point(aes(color=type),size=3)+ geom_path(linetype=2) +theme_bw()}# 原始数据x = (26.7,31.5,32.8,34.1,35.8,37.5)# 预测第7项res <- GM(x,1)(res)(res,3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i=n; %ຫໍສະໝຸດ 后面的同号的数目. while(wucha(i)*wucha(i-1)>0 & i>=2)
i=i-1;
end
start=i;
length=n-i+1;
new=wucha(start:n);
if length>=4
x1;
temp=(temp-x1)./x1; %相对误差
temp(1)=[]; %删除第一个为零的误差
temp=abs(temp);
rel=sum(temp)/(n-1)*100;
新陈代谢Gm(1,1)
function [px0,ab,rel]=xcdxgm11(x0,number,step)
number=max(size(x1));
end
n=max(size(x1));
x0(1)=x1(1);
for k=2:n
x0(k)=x1(k)-x1(k-1);
z(k)=0.5*(x1(k)+x1(k-1));
end
x0;
z;
B=[-(z(2:n))' (z(2:n).^2)'];
error('此模型要求至少有五个原始数据,并且原始数据个数要大于新陈代谢的步长.');
end
[px0,ab,rel]=gm11(x0,n);
last=n;
x0;
px0;
while last<number
begin=last-step+1;
temp=px0(begin:last);
temp(1)=[]; %删除第一个为零的误差
temp=abs(temp);
rel=sum(temp)/(n-1)*100;
残差Gm(1,1)
function [px0,ab,rel]=ccgm11(x0,number)
%[px0,ab,rel]=gm11(x0,number)
temp=gm11(temp,step+1);
last=last+1;
px0(last)=temp(step+1);
end
a=ab(1);
b=ab(2);
px0(1)=x0(1);
%求还原值系列
for k=1:number-1
px0(k+1)=(1-exp(a)) * ( x0(1)-b/a ) * exp(-a*k);
end
temp=px0(1:n);
x0;
temp=(temp-x0)./x0; %相对误差
%[px0,ab,rel]=xcdxgm11(x0,number,step)
%x0为原系列,number为要预测的数目,step为基本步长
%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比)
%
默认的number参数为原数组大小
end
end
z=zeros(size(x0));
for k=2:n
z(k)=0.5*(x1(k)+x1(k-1)); %计算数据矩阵B的第一列数据
end
y=x0';
y(1)=[];
b(:,1)=-z';
b(:,2)=1;
b(1,:)=[];
ab=inv(b'*b)*b'*y; %计算参数 矩阵
数学建模灰色预测程序代码
这里写了四个函数,方便在Matlab里面调用,分别是GM(1,1),残差GM(1,1),新陈代谢GM(1,1),Verhust自己写得难免有所疏忽,需要的朋友自己找本书本来试验一下。。
B;
Y=(x0(2:n))';
Y;
ab=inv(B'*B)*B'*Y;
a=ab(1);b=ab(2);
for k=1:number
px0(k)=(a*x1(1))/(b*x1(1)+(a-b*x1(1)).*exp(a*(k-1)));
end
temp=px0(1:n);
%模型假设预测的数据和原始数据都要大于等于5
if nargin==1
number=max(size(x0));
step=max(size(x0));
end
if nargin==2
step=max(size(x0));
end
n=max(size(x0));
if n<step | n<5
verhust
function [px0,ab,rel]=verhust(x1,number)
%[px0,ab,rel]=verhust(x0,number)
%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比)
%默认的number参数为原数组大小
if nargin==1
Gm(1,1)
function [px0,ab,rel]=gm11(x0,number)
%[px0,ab,rel]=gm11(x0,number)
%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比)
%默认的number参数为原数组大小
if nargin==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换
%px0为残差预测数列,ab为求得的系数,rel为平均相对误差(为百分比)
%默认的number参数为原数组大小
if nargin==1
number=max(size(x0));
end
n=max(size(x0)); %数组大小..
[px0,ab,rel]=gm11(x0,number);
number=max(size(x0));
end
n=max(size(x0)); %取输入数据的样本量
x1=zeros(size(x0));
for k=1:n
for i=1:k
x1(k)=x1(k)+x0(i); %计算累加值,并将值赋予矩阵be
pwucha=gm11(new);
px0(start:n)=px0(start:n)+pwucha
clear wucha;
wucha=px0-x0;
wucha=wucha./x0; %相对误差
wucha=abs(wucha);
rel=sum(wucha)/(n-1)*100;
end
