简单组合体ppt课件
合集下载
高中数学必修二课件:基本立体图形 简单组合体

思考题1 (1)说出下面的两个几何体分别是由哪些简单的几何体构成的?
【解析】 ①四棱台挖去一个圆柱. ②三棱柱和四棱柱.
(2)如图①②所示的图形绕虚线旋转一周后形成的立体图形分别是由哪些简 单几何体组成的?
【解析】 旋转后的图形如图所示.其中③是由一个圆柱O1O2和两个圆台 O2O3,O4O3组成的;④是由一个圆锥O5O4,一个圆柱O3O4及一个圆台O1O3中挖 去圆锥O2O1组成的.
8.1 基本立体图形(第3课时) 简单组合体
要点1 简单组合体的定义 由_柱__体_、__锥_体__、_台__体_、__球_体___等简单几何体组合而成的几何体叫做简单组合体. 要点2 简单组合体的构成形式
(1)___由_简__单_几__何_体__拼_接__而_成______,如图1所示. (2)____由__简_单__几_何__体_截__去_或__挖_去__一_部__分_而__成_____,如图2所示.
【解析】 (1)底面为正方形的四棱锥(如图①). (2)如图②,需要3个,分别为四棱锥A1-ABCD,A1-CDD1C1,A1- BCC1B1.
题型三 组合体中的简单计算
例3 一个圆锥底面半径为1 cm,高为 2 cm,其中有一个内接正方体,则
2
这个内接正方体的棱长为___2__c_m__.
【解析】 设该圆锥的轴截面为SEF,正方体的对角面为ACC1A1.
探究2 几何体的割补过程,实质上就是组合体的研判过程,灵活地割补, 是计算、判断的有力工具.
思考题2 如下图,甲为一几何体的展开图.
(1)沿图甲中虚线将它们折叠起来,是哪一种几何体?试用文字描述并画出 示意图;
(2)需要多少个这样的几何体才能拼成一个棱长为6 cm的正方体?请在图乙中的 棱长为6 cm的正方体ABCD-A1B1C1D1中指出这几个几何体的名称.(用字母表示)
简单组合体
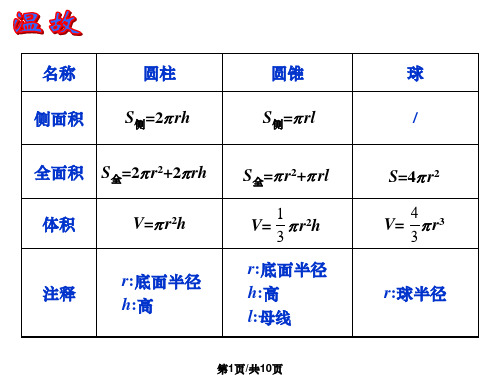
解:六角螺帽的体积是六棱柱的体积 与圆柱体积之差,即:
V 3 122 610 3.14 (10 )2 10
4
2
2956 (mm3) 2.956 (cm3 )
所以螺帽的个数为 5.81000 (7.8 2.956) 252(个) 答:这堆螺帽大约有252个.
第2页/共10页
已知球 O 的面上有四点 A、B、C、D,DA⊥平面 ABC, AB⊥BC,DA=AB=BC= 2,求球 O 的体积.
A
A
A
B
DB
D
M
OM
C
C
第8页/共10页
➢今天学到了哪些数学知识? ➢今天你认为何处值得注意?
第9页/共10页
感谢您的欣赏
第10页/共10页
BF=8,CG=12时,回答下列问题:
(1)四边形EFGH是什么图形?证明之;
G
(2)求DH的长; (3)求这个几何体的体积.
H
PN
F
E
M
D
C
A
B
第6页/共10页
如图所示,长方体的相邻三条棱的长度分别是3、3、6,将 一个长方体截去一部分,求这个几何体的体积.
第7页/共10页
如图,已知正四面体 ABCD 的棱长为 a, (1)求二面角 A-CD-B; (2)以 A 为顶点,△BCD 的外接圆为底面作圆锥,求圆锥 的表面积; (3)求此圆锥内接正方体的体积 (正方体的下底面在圆锥 的底面上,四个顶点在侧面上).
名称 侧面积
圆柱
S侧=2 rh
圆锥
S侧= rl
全面积 S全=2 r2+2rh
体积
V= r2h
注释
r:底面半径 h:高
高中数学 第一章 立体几何初步 1.3.1 简单组合体的三视图课件12高一数学课件

第十五页,共十八页。
简单组合体的作图要点:
1.利用空间想象力,分析、判断出三个视图的基本形状(xíngzhuàn)。 2.利用长对正、高平齐、宽相等的规律,借助参考线画出三视图的轮廓线 3.在三视图中看的见的轮廓线画实线,被挡住的轮廓线画虚线。
2021/12/11
第十六页,共十八页。
谢谢 使用 (xiè xie)
2021/12/11
四、三视图之间的对应(duìyìng)规律
主视图
左视图(shìtú) 高 平 齐
长对正
俯视图
宽 相
等
第九页,共十八页。
2021/12/11
主视图
左视图(shìtú)
高 平 齐
长对正 俯视图
宽 相
等
第十页,共十八页。
例1 螺栓是棱柱和圆柱(yuánzhù)构成的组合体,如图画出 它的三视图。
2021/12/11
第十七页,共十八页。
内容(nèiróng)总结
简单几何体的三视图。3.从几何体的上面向下面(xià mian)正投影,得到的投影图 ——。几何体的主视图、 左视图、俯视图合称为几何体的三视图.。例1 螺栓是棱柱和圆柱构成的组合体,如图画出它的三视图。例3 画出如图所示物体的三视图.。2.根据下列几何体的视图方向,画出它的三视图。2.利用长对正、高平齐、宽
3、圆锥(yuánzhuī)的三视图
2021/12/11
第七页,共十八页。
三、简单组合体的三视图 下面我们来看几组组合体,看一看它们有什么(shén me)
特征?
将基本( jīběn)几何体拼接成的组合体.
从基本( jīběn)几何体中切掉或挖掉部分构成的组合体.
2021/12/11
简单组合体的作图要点:
1.利用空间想象力,分析、判断出三个视图的基本形状(xíngzhuàn)。 2.利用长对正、高平齐、宽相等的规律,借助参考线画出三视图的轮廓线 3.在三视图中看的见的轮廓线画实线,被挡住的轮廓线画虚线。
2021/12/11
第十六页,共十八页。
谢谢 使用 (xiè xie)
2021/12/11
四、三视图之间的对应(duìyìng)规律
主视图
左视图(shìtú) 高 平 齐
长对正
俯视图
宽 相
等
第九页,共十八页。
2021/12/11
主视图
左视图(shìtú)
高 平 齐
长对正 俯视图
宽 相
等
第十页,共十八页。
例1 螺栓是棱柱和圆柱(yuánzhù)构成的组合体,如图画出 它的三视图。
2021/12/11
第十七页,共十八页。
内容(nèiróng)总结
简单几何体的三视图。3.从几何体的上面向下面(xià mian)正投影,得到的投影图 ——。几何体的主视图、 左视图、俯视图合称为几何体的三视图.。例1 螺栓是棱柱和圆柱构成的组合体,如图画出它的三视图。例3 画出如图所示物体的三视图.。2.根据下列几何体的视图方向,画出它的三视图。2.利用长对正、高平齐、宽
3、圆锥(yuánzhuī)的三视图
2021/12/11
第七页,共十八页。
三、简单组合体的三视图 下面我们来看几组组合体,看一看它们有什么(shén me)
特征?
将基本( jīběn)几何体拼接成的组合体.
从基本( jīběn)几何体中切掉或挖掉部分构成的组合体.
2021/12/11
简单组合体的三视图课件

谢谢大家
•
1.批评对作品的意义不言而喻。好的 批评如 同灯光 ,指引 着作品 从暗处 走向前 台。近 些年的 诗歌批 评中, 不乏这 样的经 典或中 肯之作 。
•
2.但与此同时,诗歌批评庸俗化的趋 势越来 越明显 ,不少 诗歌批 评为了 应酬需 要,违 心而作 ,学术 含量可 疑,甚 至堕落 为诗人 小圈子 里击鼓 传花的 游戏道 具。这 类批评 对诗歌 创作来 说类同 饮鸩止 渴,还 不如索 性没有 的好。
•
7.诗歌批评庸俗化趋势亟须扭转。文 学批评 的职业 公信力 需要树 立,批 评家需 要贡献 学术良 知。果 真如此 ,对诗 歌和读 者,都 将是福 音。
•
8.中国音乐在发展过程中,不断承传 自我, 吸收各 地音乐 ,器乐 发达, 演奏形 式丰富 。金、 石、土 、革、 丝、木 、匏、 竹,皆 可作乐 器。乐 曲类型 已有祭 神乐、 宴乐、 军乐、 节庆乐 等区别 。玄宗 时已有 超百人 的大型 交响乐 团,其 演员按 艺术水 平分为 “坐部 伎”与 “立部 伎”。
Y
水平投影 (俯视图)
首先,观察从长方体的正前方的正投影
主视图
P
其次,观察从长方体的正左方的正投影
主视图
左视图
P
Q
再次,观察从长方体的正上方的正投影
主视图
左视图
V
俯视图
W
球的三视图
圆柱的三视图
从上面看
俯视图
从左面看 左视图
从正面看 主视图
主视图
左视图
俯视图
下图中哪一幅是左视图?
俯视图:光左视图:光线自物体的左面向右投射
所得的投影称左视图;
简单组合体
• (1)将基本几何体拼接 而成
高中数学必修二教学课件:简单组合体的三视图 (共23张PPT)

俯视 左视
主视图
对
左视图 错
主视
俯视图
错
D1
C1 B1 A 1
D1
C1 B1
A 1
D A
左视
C
B
D A B
C
正方体
D1
A 1
B1
A
左视图
D1
C1 B1 A 1
D1
C1 B1 1
A 1
D A
左视
C
B A
D B
C
正方体
左视图
D1
C1 B1 A 1
D1
C1 B1
A 1
D A
左视
C
B A
D B
C
正方体
教材:普通高中课程标准实验教科书(北师大版)(必修2)
授课教师:玉山一中
吴移东
汽车设计图纸
主视图
知识
回顾
左 视 图
俯视图
知识
三视图之间的投影规律
主 视 图 左 视 图 主 视 图 反 映 了 物 体 的 高 度 和 长 度 左 视 图 反 映 了 物 体 的 高 度 和 宽 度
回顾
俯 视 图 反 映 了 物 体 的 长 度 和 宽 度
组合体的生成方式
(1)将基本几何体拼接成的组合体 (2)从基本几何体中切掉 或挖掉部分构成组合体
教材:普通高中课程标准实验教科书(北师大版)(必修2)
例2 画出这个组合体的三视图.
主视
例3 请画出立白洗洁精塑料 瓶的视图
主视图
左视图
俯视图
某同学画下图物体的三视图,对吗?若 有错,请指出并改正。
左视图
挑战自我
下图是一个工业轴承架的模 型,画出它的三视图(通孔)
主视图
对
左视图 错
主视
俯视图
错
D1
C1 B1 A 1
D1
C1 B1
A 1
D A
左视
C
B
D A B
C
正方体
D1
A 1
B1
A
左视图
D1
C1 B1 A 1
D1
C1 B1 1
A 1
D A
左视
C
B A
D B
C
正方体
左视图
D1
C1 B1 A 1
D1
C1 B1
A 1
D A
左视
C
B A
D B
C
正方体
教材:普通高中课程标准实验教科书(北师大版)(必修2)
授课教师:玉山一中
吴移东
汽车设计图纸
主视图
知识
回顾
左 视 图
俯视图
知识
三视图之间的投影规律
主 视 图 左 视 图 主 视 图 反 映 了 物 体 的 高 度 和 长 度 左 视 图 反 映 了 物 体 的 高 度 和 宽 度
回顾
俯 视 图 反 映 了 物 体 的 长 度 和 宽 度
组合体的生成方式
(1)将基本几何体拼接成的组合体 (2)从基本几何体中切掉 或挖掉部分构成组合体
教材:普通高中课程标准实验教科书(北师大版)(必修2)
例2 画出这个组合体的三视图.
主视
例3 请画出立白洗洁精塑料 瓶的视图
主视图
左视图
俯视图
某同学画下图物体的三视图,对吗?若 有错,请指出并改正。
左视图
挑战自我
下图是一个工业轴承架的模 型,画出它的三视图(通孔)
北师大版高中数学必修二 3.1简单组合体的三视图课件(共21张PPT)

(1)将基本几何体拼接成组合体, 如图. (2)从基本几何中切掉或挖 掉部分构成组合体, 如图.
一般地, 组合体是由上述两种方式综合生成的, 如下图
三视图分析2.exe
探究活动1
下图的几何体是由怎样的简单几何体 组合的?它的三视图对吗?
俯视
左视
主视图 对 左视图 错
主视
俯视图 错
探究活动2
以长方体为载体,你能画出下图中组
左视
D1
A1
B1
D
A 长方体 B
C1 A1
左视
C A
D1
C1
B1
D
C
B
左视图
探究活动3:
数学来源于生活,又服务于生活, 下面是工人师傅的一些零件,你能按照 要求完成它的视图吗?
练习1.下图所示物体的俯视图对吗?
俯视
俯视图
练习2.下图所示物体的主视图对吗?
主视
主视图
练习3.画出下图所示组合体的三视图.
合体的左视图吗?
D1
C1
B1
左视
D
C
A
B
D1
A1
B1
D
A
B
长方体
A1
C1 A1
左视
C
D1
A
B1
D1
C1
B1
D
C
B
A
左视图
探究活动2
以长方体为载体,你能画出下图中组 合体的左视图吗?D1A1Fra bibliotek左视B1
D
C
A
B
D1
A1
B1
D
A 长方体 B
C1 A1
左视
C A
D1
一般地, 组合体是由上述两种方式综合生成的, 如下图
三视图分析2.exe
探究活动1
下图的几何体是由怎样的简单几何体 组合的?它的三视图对吗?
俯视
左视
主视图 对 左视图 错
主视
俯视图 错
探究活动2
以长方体为载体,你能画出下图中组
左视
D1
A1
B1
D
A 长方体 B
C1 A1
左视
C A
D1
C1
B1
D
C
B
左视图
探究活动3:
数学来源于生活,又服务于生活, 下面是工人师傅的一些零件,你能按照 要求完成它的视图吗?
练习1.下图所示物体的俯视图对吗?
俯视
俯视图
练习2.下图所示物体的主视图对吗?
主视
主视图
练习3.画出下图所示组合体的三视图.
合体的左视图吗?
D1
C1
B1
左视
D
C
A
B
D1
A1
B1
D
A
B
长方体
A1
C1 A1
左视
C
D1
A
B1
D1
C1
B1
D
C
B
A
左视图
探究活动2
以长方体为载体,你能画出下图中组 合体的左视图吗?D1A1Fra bibliotek左视B1
D
C
A
B
D1
A1
B1
D
A 长方体 B
C1 A1
左视
C A
D1
组合体说课正式版PPT课件

组合体说课正式版ppt课件
目
CONTENCT
录
• 组合体的概念 • 组合体的设计 • 组合体的制造 • 组合体的应用案例 • 组合体的未来发展
01
组合体的概念
定义与特点
定义
组合体是由两个或两个以上的基本几何体通过叠加、挖切等方式 组合而成的立体。
特点
组合体可以是复杂的,也可以是简单的,其形状和结构取决于组 成它的基本几何体及其组合方式。
案例二:某建筑结构的组合体应用
总结词:结构优化
详细描述:该建筑结构采用组合体的设计理念,将不同的建筑材料和结构形式进行优化组合,实现了 建筑的功能需求和美学要求。组合体设计提高了建筑的结构安全性和稳定性,减少了材料浪费和环境 污染。
案例三:某交通工具的组合体制造
总结词
轻量化与强度
详细描述
该交通工具采用先进的组合体制造技术,通过将不同的材料和结构进行优化组 合,实现了轻量化和高强度。组合体制造技术提高了交通工具的性能和安全性, 降低了能耗和排放,符合可持续发展的要求。
组合体的分类
叠加型
由两个或多个基本几何体按一定顺序叠加而成。
挖切型
在某个基本几何体内挖去另一几何体而形成。
综合型
由叠加和挖切两种方式综合而成。
组合体的应用场景
80%
工程设计
在机械、建筑、船舶、航空航天 等工程领域中,经常需要使用组 合体来设计和分析各种结构和装 置。
100%
科学研究
在物理学、化学、生物学等科学 领域中,为了研究物质的性质和 变化规律,常常需要构建各种组 合体模型来进行实验和模拟。
根据需求分析,形成初步的设计概念,包括形状、结 构、颜色、材质等方面的设想。
03
目
CONTENCT
录
• 组合体的概念 • 组合体的设计 • 组合体的制造 • 组合体的应用案例 • 组合体的未来发展
01
组合体的概念
定义与特点
定义
组合体是由两个或两个以上的基本几何体通过叠加、挖切等方式 组合而成的立体。
特点
组合体可以是复杂的,也可以是简单的,其形状和结构取决于组 成它的基本几何体及其组合方式。
案例二:某建筑结构的组合体应用
总结词:结构优化
详细描述:该建筑结构采用组合体的设计理念,将不同的建筑材料和结构形式进行优化组合,实现了 建筑的功能需求和美学要求。组合体设计提高了建筑的结构安全性和稳定性,减少了材料浪费和环境 污染。
案例三:某交通工具的组合体制造
总结词
轻量化与强度
详细描述
该交通工具采用先进的组合体制造技术,通过将不同的材料和结构进行优化组 合,实现了轻量化和高强度。组合体制造技术提高了交通工具的性能和安全性, 降低了能耗和排放,符合可持续发展的要求。
组合体的分类
叠加型
由两个或多个基本几何体按一定顺序叠加而成。
挖切型
在某个基本几何体内挖去另一几何体而形成。
综合型
由叠加和挖切两种方式综合而成。
组合体的应用场景
80%
工程设计
在机械、建筑、船舶、航空航天 等工程领域中,经常需要使用组 合体来设计和分析各种结构和装 置。
100%
科学研究
在物理学、化学、生物学等科学 领域中,为了研究物质的性质和 变化规律,常常需要构建各种组 合体模型来进行实验和模拟。
根据需求分析,形成初步的设计概念,包括形状、结 构、颜色、材质等方面的设想。
03
8.1基本立体图形第二课时 旋转体与简单组合体PPT课件(人教版)

1.思考辨析,判断正误 (1)圆锥有无数条母线,它们有公共点即圆锥的顶点,且长度相等.( √ ) (2)过圆锥的轴的截面是全等的等边三角形.( × ) (3)圆台有无数条母线,且它们相等,但延长后不相交于一点.( × ) (4)过圆台任意两条母线的截面是等腰梯形.( √ ) 提示 (2)不一定是等边三角形,但一定是等腰三角形. (3)延长后相交于一点.
【训练3】 用一个平行于圆锥底面的平面截这个圆锥,截得的圆台上、下底面 的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台的母线长. 解 设圆台的母线长为l cm,截得圆台的上底面的半径为r cm. 根据题意,得圆台的下底面的半径为4r cm. 根据相似三角形的性质,得3+3 l=4rr.解得 l=9. 所以圆台的母线长为9 cm.
球常用表示 球心的字母 来表示,左 图可表示为 __球__O__
2.棱柱和圆柱统称为柱体,棱锥和圆锥统称为锥体,棱台和圆台统称为台体. 3.简单组合体
(1)定义:由_简__单__几__何__体___组合而成的几何体叫做简单组合体. (2)简单组合体的构成情势:一种是由简单几何体_拼__接___而成的;另一种是 由简单几何体__截__去__或__挖__去__一部分而成的.
课堂小结
1.圆柱、圆锥、圆台的关系如图所示.
2.球面、球体的区分和联系 区分
球的表面是球面,球面是旋转形成 球面
的曲面 球体是几何体,包括球面及所围的 球体 空间部分
联系 球面是球体的表面
3.处理台体问题常采用还台为锥的补体思想,处理组合体问题常采用分割思想. 4.重视圆柱、圆锥、圆台的轴截面在解决几何量中的特殊作用,切实体会空间
1
课前预习
知识探究
1.圆柱、圆锥、圆台、球
简单组合体的空间几何体的结构 课件

简单组合体的结构特征
上节课我们学习了柱、锥、台、 球等简单几何体的结构特征.
在我们的生活周围, 有不少有特色的建筑物, 它们有丰富多彩的结构.
现实世界中的物体表示的几 何体,除柱体、锥体、台体和球 体等简单几何体外,还有大量的 几何体是由简单几何体组合而成 的,这些几何体叫做简单组合体.
思路1:
例1 指出左下图中的柜子(只看外形) 是由哪些简单几何体构成的?
左图的柜子 只看外形可 以画成右图 的形式.
思路2:
其他思路如左图(此处不一一 列举),有兴趣可以课后再探讨.
例2 下面这个瓶子是由哪些简单几 何体构成的?
例1和例2都是由几种简单几何体拼接而成的.
由此我们总结出: 简单组合体的构成,第一种基本形式是由几
由一个圆柱挖去一 个圆台而成.
至此,我们发现,简单组合体的构成有 两种基本形式: 1.由简单几何体拼接而成; 2.简单几何体挖去一部分而成.
1.下面这个几何体是由哪些简单几何体构成的?
由一个四棱柱和一 个圆柱拼接而成.
2.下面这个几何体是由哪些简单几何体构成的?
由一单几何体构成的?
种简单几何体拼接而成.
例3 下面这个几何体是由哪些简单几 何体构成的?
这个零件的外观 是一个大圆柱挖掉了 一个小圆柱.
例4 下面这个几何体是由哪些简单 几何体构成的?
这个几何体的外观是一个大棱 柱挖掉了一个小棱柱.
例3和例4都是由简单几何体挖去一部分而成. 由此我们总结出:
简单组合体的构成,第二种基本形式是由简 单几何体挖去一部分而成.
上节课我们学习了柱、锥、台、 球等简单几何体的结构特征.
在我们的生活周围, 有不少有特色的建筑物, 它们有丰富多彩的结构.
现实世界中的物体表示的几 何体,除柱体、锥体、台体和球 体等简单几何体外,还有大量的 几何体是由简单几何体组合而成 的,这些几何体叫做简单组合体.
思路1:
例1 指出左下图中的柜子(只看外形) 是由哪些简单几何体构成的?
左图的柜子 只看外形可 以画成右图 的形式.
思路2:
其他思路如左图(此处不一一 列举),有兴趣可以课后再探讨.
例2 下面这个瓶子是由哪些简单几 何体构成的?
例1和例2都是由几种简单几何体拼接而成的.
由此我们总结出: 简单组合体的构成,第一种基本形式是由几
由一个圆柱挖去一 个圆台而成.
至此,我们发现,简单组合体的构成有 两种基本形式: 1.由简单几何体拼接而成; 2.简单几何体挖去一部分而成.
1.下面这个几何体是由哪些简单几何体构成的?
由一个四棱柱和一 个圆柱拼接而成.
2.下面这个几何体是由哪些简单几何体构成的?
由一单几何体构成的?
种简单几何体拼接而成.
例3 下面这个几何体是由哪些简单几 何体构成的?
这个零件的外观 是一个大圆柱挖掉了 一个小圆柱.
例4 下面这个几何体是由哪些简单 几何体构成的?
这个几何体的外观是一个大棱 柱挖掉了一个小棱柱.
例3和例4都是由简单几何体挖去一部分而成. 由此我们总结出:
简单组合体的构成,第二种基本形式是由简 单几何体挖去一部分而成.
简单组合体
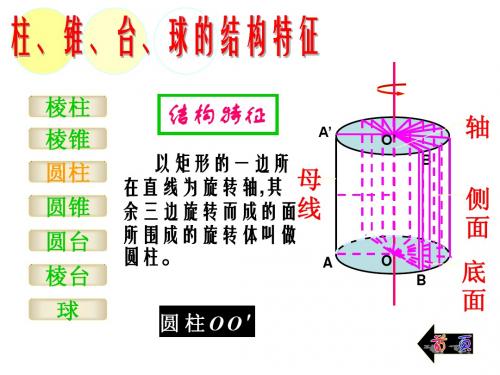
棱柱 棱锥 圆柱 圆锥 圆台 棱台 球
(1)棱柱与圆柱统 称为柱体。 称为柱体。 (2)棱锥与圆锥统 称为锥体。 称为锥体。 (3)棱台与圆 ) 台统称为台体
实例 归纳小结
棱柱 棱锥 圆柱 圆锥 圆台 棱台 球
结构特征
以半圆的直径所在直 线为旋转轴,半圆面旋 线为旋转轴 半圆面旋 转一周形成的旋转体. 转一周形成的旋转体
棱柱 棱锥 圆柱 圆锥 圆台 棱台 球
结构特征
A’ O’ B’
轴 侧 面
以矩形的一边所 在直线为旋转轴,其 在直线为旋转轴 其 母 余三边旋转而成的面线 所围成的旋转体叫做 圆柱。 圆柱。 A
O B
圆柱OO ′
底 面
棱柱 棱锥 圆柱 圆锥 圆台 棱台 球
结构特征
以直角三角形的 一条直角边所在直线 为旋转轴,其余两边旋 为旋转轴 其余两边旋 转形成的曲面所围成 的几何体叫做圆锥。 的几何体叫做圆锥。 A
O
半 径 球 心
球O
直径
A D’ D A’
上底面 侧棱
C’ B’ C
顶点
侧 B 面 下底面
棱台ABCD − A′ B′C ′D′
思考题: .平行于圆柱, 思考题:1.平行于圆柱, 圆锥, 圆锥,圆台的底面的截面是 什么图形? 什么图形? 过圆柱, 2.过圆柱,圆锥 , 圆台的旋转轴的截面是什么 实 验 图形? 图形?
包
性质1: 性质 :平行于底面的截面 都是圆。 都是圆。 性质2:过轴的截面(轴截面) 性质 :过轴的截面(轴截面) 分别是全等的矩形, 分别是全等的矩形,等腰 三角形,等腰梯形。 三角形,等腰梯形。
S
母 线
O B
顶 点
轴 侧 面 底 面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 左视图反映:上、下 、前、后
三视图能反映物体真实的形状和长、宽、高。
50
基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
51
棱柱的三视图
俯
左
六棱柱
52
棱锥的三视图
俯
左
正三棱锥
53
棱锥的三视图
俯
左
正四棱锥
54
棱台的三视图
俯
左
正四棱台
55
一些螺母、带盖螺母又是有什么主要的几何结构特征 呢?
4
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何 结构特征是什么?
5
简单组合体
居民的住宅又有什么主要几何结构特征?
6
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主 要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成 的吗?
到的投影称为主视图或正视图. 2.自上向下的称为俯视图. 3. 自左向右的称为左视图.
30
三视图的形成
V
V正立投影面 H水平投影面 W侧立投影3面1
三视图的形成
V
H
W
V正视图 H俯视图 W侧视图
32
三视图的形成
正 视 图
左视图
俯视图
33
三视图表达的意义
从前面正对着物体观察,画出正视图,正视 图反映了物体的长和高及前后两个面的实形.
正视图和俯视图 ----长对正 正视图和左视图 ----高平齐
俯视图和左视图 ----宽相等
36
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆 柱、圆锥、球的三视图.
37
正方体的三视图
俯 左
38
长方体的三视图
俯
左
长方体
39
圆柱的三视图
俯
左
圆柱
40
圆锥的三视图
俯
左 圆锥
41
球的三视图
从上向下正对着物体观察,画出俯视图,布 置在主视图的正下方,俯视图反映了物体的长和 宽及上下两个面的实形.
从左向右正对着物体观察,画出左视图,布 置在主视图的正右方,左视图反映了物体的宽和 高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
34
三视图的特点
高平齐 长对正
宽相等
35
三视图的对应规律
A
B
10
C
D
正方体的表面展开图
11
6、下图不是棱柱的展开图的是( C )
A
B
12
7、正方体的六个面分别涂有红,蓝,黄,绿,黑,白六种颜色, 根据下图所示,绿色面的相对面是_______色 蓝色
红
绿
黄
黄
黑
蓝
13
8、一个长,宽,高分别为5cm,4cm,3cm的长方体木 块,有一只蚂蚁经木快表面从顶点A爬行到C,最短的路 程是多少?
1.1.2简单组合体的结构特征
1
简单组合体
日常生活中我们常用到的日用品,比如:消毒液、暖 瓶、洗洁精等的主要几何结构特征是什么?
由柱、锥、台、球组成了一些简单的组合体.认识 它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
2
简单组合体
走在街上会看到一些物体,它们的主要几何结构特征 是什么?
3
简单组合体
7
旋转体
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的 呢?这个轮胎呢?
8
生活与数学
数学在生活中无处不在,培养在生活中不断的用数 学的眼光看问题,会逐渐激发学数学的兴趣,增强数 学地分析问题、解决问题的能力.
9
5、下列图中,不是正方体的表面展开图的是( C )
28
知识小结
中心投影:投射线交于一点.
投影的分类: 平行投影
斜投影
正投影(本节主要学习利用正投影绘制
空间图形的三视图,并能根据所给的三视图
了解该空间图形的基本特征.)
29
那什么是空间图形的三视图呢?
概念:视图是指将物体按正投影向投影面 投射所得到的图形.
1.光线自物体的前面向后投射所得
三 视 图
俯
左
球体
42
小节三视图有关概念
“视图”是将物体按正投影法向投影面投射时 所得到的投影图.
光线自物体的前面向后投影所得的投影图称 为“正视图” ,自左向右投影所得的投影图称 为“侧视图”,自上向下投影所得的投影图称 为“俯视图”.
用这三种视图即可刻划空间物体的几何结构, 这种图称之为“三视图”.即向三个互相垂直 的投影面分别投影,所得到的三个图形摊平在 一个平面上,则就是三视图.
24
摄影作品
25
美术作品
26
在一束平行光线的照射下形成的投射,叫做平行投影。 平行投影分正投影和斜投影两种。
D A
C B
D ABC
a
d
c b
d a
b
c
投射线与投影面 相倾斜的平行投 影法 -----斜投影法
平行投影法
投射线与投影面相互垂 直的平行投影法
----------正投影法。
27
中心投影形成的直观图能非常逼真地反映原来的物 体,主要运用于绘画领域。 平行投影形成的直观图则能比较精确地反映原来物体 的形状和特征。因此更多应用于工程制图或技术图样
43
那怎样画一个空间几何体的三 视图呢?请同学们看底下图的三视图.
V
44
1. 在主视图、俯 视图中都体现形体的长 度,且长度在竖直方向 上是对正的,我们称之 为长对正。
45
2. 在主视图、左视图上都体现形体的高 度,且高度在水平方向上是平齐的,我们称之 为高平齐。
46
3. 在左视图、俯视图上都体现形体的宽 度,且是同一形体的宽度,是相等的,我们称 之为宽相等。
47
三视图表达的意义
从前面正对着物体观察,画出主视图,主 视图反映了物体的长和高及前后两个面的实 形。
• 主视图反映:上、下 、左、右
48
从上向下正对着物体观察,画出俯视 图,布置在主视图的正下方,俯视图反映 了物体的长和宽及上下两个面的实形。
• 俯视图反映:前、后 、左、右
49
从左向右正对着物体观察,画出左视图, 布置在主视图的正右方,左视图反映了物体的 宽和高及左右两个面的实形。
的面(投影面)投射,并在该面上得到图形的方法.
22
把光由一点向外散射形成的投影,叫
做中心投影。 中心投影法
投射中心 物体
投影面
投射线 投影
物体位置改变,投
影大小也改变
23
在中心投影下,空间的点的投影是点,直线的投影是直线。 S
D
A B
C
da cbFra bibliotek中心投影法
人的视觉,照片,美术作品等都是中心投影。
74cm
C
A
14
1.2空间几何体的三视图和直观图
15
皮影戏表演
16
手影表演
17
手影表演
18
手影表演
19
手影表演
20
请同学们看下面几个常见的自然 现象,考虑它们是怎样得到的?
21
这种现象我们把它称为是投影.
通过观察和自己的认识 , 你是怎 样来理解投影的含义的?
投影是光线(投射线)通过物体,向选定
三视图能反映物体真实的形状和长、宽、高。
50
基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
51
棱柱的三视图
俯
左
六棱柱
52
棱锥的三视图
俯
左
正三棱锥
53
棱锥的三视图
俯
左
正四棱锥
54
棱台的三视图
俯
左
正四棱台
55
一些螺母、带盖螺母又是有什么主要的几何结构特征 呢?
4
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何 结构特征是什么?
5
简单组合体
居民的住宅又有什么主要几何结构特征?
6
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主 要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成 的吗?
到的投影称为主视图或正视图. 2.自上向下的称为俯视图. 3. 自左向右的称为左视图.
30
三视图的形成
V
V正立投影面 H水平投影面 W侧立投影3面1
三视图的形成
V
H
W
V正视图 H俯视图 W侧视图
32
三视图的形成
正 视 图
左视图
俯视图
33
三视图表达的意义
从前面正对着物体观察,画出正视图,正视 图反映了物体的长和高及前后两个面的实形.
正视图和俯视图 ----长对正 正视图和左视图 ----高平齐
俯视图和左视图 ----宽相等
36
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆 柱、圆锥、球的三视图.
37
正方体的三视图
俯 左
38
长方体的三视图
俯
左
长方体
39
圆柱的三视图
俯
左
圆柱
40
圆锥的三视图
俯
左 圆锥
41
球的三视图
从上向下正对着物体观察,画出俯视图,布 置在主视图的正下方,俯视图反映了物体的长和 宽及上下两个面的实形.
从左向右正对着物体观察,画出左视图,布 置在主视图的正右方,左视图反映了物体的宽和 高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
34
三视图的特点
高平齐 长对正
宽相等
35
三视图的对应规律
A
B
10
C
D
正方体的表面展开图
11
6、下图不是棱柱的展开图的是( C )
A
B
12
7、正方体的六个面分别涂有红,蓝,黄,绿,黑,白六种颜色, 根据下图所示,绿色面的相对面是_______色 蓝色
红
绿
黄
黄
黑
蓝
13
8、一个长,宽,高分别为5cm,4cm,3cm的长方体木 块,有一只蚂蚁经木快表面从顶点A爬行到C,最短的路 程是多少?
1.1.2简单组合体的结构特征
1
简单组合体
日常生活中我们常用到的日用品,比如:消毒液、暖 瓶、洗洁精等的主要几何结构特征是什么?
由柱、锥、台、球组成了一些简单的组合体.认识 它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
2
简单组合体
走在街上会看到一些物体,它们的主要几何结构特征 是什么?
3
简单组合体
7
旋转体
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的 呢?这个轮胎呢?
8
生活与数学
数学在生活中无处不在,培养在生活中不断的用数 学的眼光看问题,会逐渐激发学数学的兴趣,增强数 学地分析问题、解决问题的能力.
9
5、下列图中,不是正方体的表面展开图的是( C )
28
知识小结
中心投影:投射线交于一点.
投影的分类: 平行投影
斜投影
正投影(本节主要学习利用正投影绘制
空间图形的三视图,并能根据所给的三视图
了解该空间图形的基本特征.)
29
那什么是空间图形的三视图呢?
概念:视图是指将物体按正投影向投影面 投射所得到的图形.
1.光线自物体的前面向后投射所得
三 视 图
俯
左
球体
42
小节三视图有关概念
“视图”是将物体按正投影法向投影面投射时 所得到的投影图.
光线自物体的前面向后投影所得的投影图称 为“正视图” ,自左向右投影所得的投影图称 为“侧视图”,自上向下投影所得的投影图称 为“俯视图”.
用这三种视图即可刻划空间物体的几何结构, 这种图称之为“三视图”.即向三个互相垂直 的投影面分别投影,所得到的三个图形摊平在 一个平面上,则就是三视图.
24
摄影作品
25
美术作品
26
在一束平行光线的照射下形成的投射,叫做平行投影。 平行投影分正投影和斜投影两种。
D A
C B
D ABC
a
d
c b
d a
b
c
投射线与投影面 相倾斜的平行投 影法 -----斜投影法
平行投影法
投射线与投影面相互垂 直的平行投影法
----------正投影法。
27
中心投影形成的直观图能非常逼真地反映原来的物 体,主要运用于绘画领域。 平行投影形成的直观图则能比较精确地反映原来物体 的形状和特征。因此更多应用于工程制图或技术图样
43
那怎样画一个空间几何体的三 视图呢?请同学们看底下图的三视图.
V
44
1. 在主视图、俯 视图中都体现形体的长 度,且长度在竖直方向 上是对正的,我们称之 为长对正。
45
2. 在主视图、左视图上都体现形体的高 度,且高度在水平方向上是平齐的,我们称之 为高平齐。
46
3. 在左视图、俯视图上都体现形体的宽 度,且是同一形体的宽度,是相等的,我们称 之为宽相等。
47
三视图表达的意义
从前面正对着物体观察,画出主视图,主 视图反映了物体的长和高及前后两个面的实 形。
• 主视图反映:上、下 、左、右
48
从上向下正对着物体观察,画出俯视 图,布置在主视图的正下方,俯视图反映 了物体的长和宽及上下两个面的实形。
• 俯视图反映:前、后 、左、右
49
从左向右正对着物体观察,画出左视图, 布置在主视图的正右方,左视图反映了物体的 宽和高及左右两个面的实形。
的面(投影面)投射,并在该面上得到图形的方法.
22
把光由一点向外散射形成的投影,叫
做中心投影。 中心投影法
投射中心 物体
投影面
投射线 投影
物体位置改变,投
影大小也改变
23
在中心投影下,空间的点的投影是点,直线的投影是直线。 S
D
A B
C
da cbFra bibliotek中心投影法
人的视觉,照片,美术作品等都是中心投影。
74cm
C
A
14
1.2空间几何体的三视图和直观图
15
皮影戏表演
16
手影表演
17
手影表演
18
手影表演
19
手影表演
20
请同学们看下面几个常见的自然 现象,考虑它们是怎样得到的?
21
这种现象我们把它称为是投影.
通过观察和自己的认识 , 你是怎 样来理解投影的含义的?
投影是光线(投射线)通过物体,向选定
