第五节简单拉压超静定问题
拉压超静定

简单的拉、压超静定问题
第1页/共38页
§7—7 简单的 拉、压超静定问题
一、静定与超静定问题 1、静定问题: 杆件的轴力可以用静力平衡条件求出,这种情况 称作静定问题。 2、超静定问题: 只凭静力平衡方程已不能解出全部未知力, 这种情况称做超静定问题。
3、超静定的次数: 未知力个数与独立平衡方程的数目之差, 称作超静定的次数。
F
A F N 3(l cos )
E3 A3
第15页/共38页
D
A
A
FN3
3、补充方程
B
D
C
3
1
FN3
2
A A
F
(F F N 3)l
2 EA cos 2
F
N 3(l cos )
E3 A3
第16页/共38页
D
B
D
C
3
1
FN3
2
A
A
A A
F
FN3
FN3 1 2
F EA
cos3
E3 A3
第17页/共38页
二、超静定问题的基本解法
例题1:两端固定的等直杆AB横截面积为A,弹性模量为E,在C
点处承受轴力 F 的作用,如图 所示 。计算约束反力。
A a
C
F
B
第4页/共38页
A a
C
F
B
FA
A
C
F
B
FB
这是一次超静定问题
第5页/共38页
A a
C
F
B
A
A
C
F
B
基本系统
C
F
B
FB
相当系统
拉压超静定

1 2
F
FN 1 FN 2 FN 3
y
A
x
列出变形几何关系 将A点的位移分量向各杆投 影.得
l1 y sin x cos
y
x
A x
整理得
l2 x l3 y sin x cos
变形关系为 l3 l1 2l2 cos
l1
l2
l3
4、补充方程
FN 1l FN 3l cos EA cos EA
FN 1 FN 3 cos 2
5、求解方程组得 F F cos 2 F FN 1 FN 2 N3 1 2 cos 3 1 2 cos 3 3
拉、压超静定问题
木制短柱的4个角用4个40mm×40mm×4mm的等边角钢加固, 已知角钢的许用应力[σst]=160MPa,Est=200GPa;木材的许 用应力[σW]=12MPa,EW=10GPa,求许可载荷F。 F 解: 平衡方程: F FW Fst (1) F 变形协调关系: l st l w FW l FW 物理关系: lW EW AW Fst Fst l lst Est Ast 补充方程:
2
拉、压超静定问题
超静定结构的求解方法: 1、列出独立的平衡方程 Fx 0 FN1 FN 2
y
F
0 2FN1 cos FN 3 F
2、变形几何关系 l1 l2 l3 cos 3、物理关系
FN 1l FN 3l l1 l3 EA cos EA
F
根据角钢许用应力,确定F
0.283F st st F 698 kN Ast 根据木柱许用应力,确定F 0.717F W W AW
拉压超静定问题

4、联立静力方程与力的补充方程求出所有的未知力。
三、注意的问题 拉力——伸长变形相对应;压力——缩短变形相对应。
例 设 1、2、3三杆用铰链连接如图,已知:各杆长为:
l1=l2、 l3=l;各杆面积为 A1=A2、 A3 ;各杆弹性模量为: E1=E2、E3。外力沿铅垂方向,求各杆的内力。
B
DC
1
3
2
l
A G
(a)
B
DC
解:、平衡方程:
1 32
l3
A
l1
E
A
(c)
Fx 0 FN1 sin FN 2 sin 0 Fy 0 FN1 cos FN 2 cos FN3 G 0
、几何方程——变形协调方程:
L1 L3 cos
补充方程:由力与变形的物理条件得:
FN1 FN 3
工程力学
拉压超静定问题
一、概念
1、静定:结构或杆件的未知力个数等于有效静力方程的个数, 只利用有效静力方程就可以求出所有的未知力。
2、超静定:结构或杆件的未知力个数大于有效静力方程的个数, 只利用有效静力方程不能求出所有的未知力。
3、多余约束:在超静定系统中多余维 持结构几何不变性所需要的杆或支座。
4、多余约束反力:多余约束对应的反力。
BDC
1
3
2
A G
5、超静定的分类(按超静定次数划分): 超静定次数=多余约束个数=未知力个数-有效静力方程个数。 二、求解超静定(关键——变形几何关系的确定) 步骤:1、根据平衡条件列出平衡方程(确定超静定的次数)。
2、根据变形协调条件列出变形几何方程。 3、根据力与变形的物理条件,列出力的补充方程。
FN 2
6.1拉压超静定问题

A 简图 N A
C P
P 为什么画轴力图? 应注意什么? + x
轴力的简便求法: 轴力的简便求法: 以x点左侧部分为对象,x点的内力N(x)由下式计算:
N ( x ) = ∑ P (←) − ∑ P (→)
其中“ΣP( )”与“ΣP( )”均为x点左侧与右侧部分的 所有外力。
例11 设1、2、3三杆用铰链连接如图,已知:各杆长为: L1=L2、 L3 =L ;各杆面积为A1=A2=A、 A3 ;各杆弹性模量 为:E1=E2=E、E3。外力沿铅垂方向,求各杆的内力。 解: 、平衡方程: B 3 1 D C 2 N3
∑X
= N 1 sin α − N 2 sin α = 0
[σ ] 1 A1 N1 ≤ P= 0 .07 0 .07
160× 308.6 = 705.4kN = 0.07
另外:若将钢的面积增大 倍 怎样? 另外:若将钢的面积增大5倍,怎样? 若将木的边长变为25mm,又怎样? 若将木的边长变为 边长变为 , 怎样? 结构的最大载荷永远由钢控制着。 结构的最大载荷永远由钢控制着。
Α1=5cm2 , Α2=10cm2,当温度升至T2
=25℃时,求各杆的温度应力。 a (线膨胀系数α =12.5× 10 −6 / oC N1 a 弹性模量E=200GPa) 解: 、平衡方程: ;
∑Y = N − N
1
2
=0
、几何方程: a
∆L = ∆LT − ∆LN = 0
N2
、物理方程
∆ LT = 2 a ∆ Tα ;
1 A 3 D
2
B 1
α α
C 2
∑ ∑Y = N1 cosα + N2 cosα − N3 = 0
材料力学 简单的超静定问题

FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程:由几何方程和物理方程得:
F N 1l1 E1 A1
2
cos a
(5)联解(1)、(2)、(3)式,得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
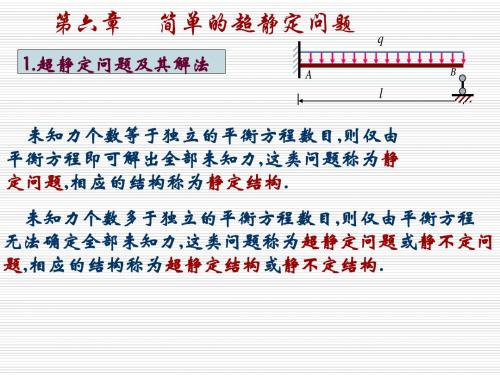
1.单纯依靠静力平衡方程能够确定全部未知力(支反 力、内力)的问题,称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力(支反 力、内力)的问题,称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固,角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa,弹性模量分别为E1=200GPa 和 E2 =10GPa;求许可载荷P。 解:(1)以压头为研究对象, 设每 个角钢受力为FN1,木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
拉伸、压缩超静定问题

定结构的变形受到部分或全部约束, 温度变化时,
在图中, AB杆代表蒸汽锅炉与原动机间的管道。
与锅炉和原动机相比, 管道刚度很小, 故可把A, B两端简化成固定端。
固定于枕木或基础上的钢轨也类似于这种情况。
当管道中通过高压蒸汽, 或因季节变化引起钢轨温度变化时, 就相当于上述两端固定杆的温度发生了变化。
因为固定端限制杆
件的膨胀或收缩, 所以
势必有约反力F R A和
F R B作用于两端。
这将
引起杆件内的应力, 这
种应力称为热应力或
温度应力。
必须再补充一个变形协调方
这就是补充的变形协调方程。
拉压超静定

A 1 B 2
FN1
D
FN2 F
D
3 C h
FN3
F
平衡方程为
( FN1 FN3 ) cos FN2 F cos 0 FN1 sin FN3 sin F sin 0
这是一次超静定问题
A 1 B 2
1 D
E
l3
D3
l2
( FN1 FN3 ) cos FN2 F cos 0 FN1 sin FN3 sin F sin 0 l1 l3 2 l2 cos
A 1 B 2
D
物理方程为
FN1l1 FN1h l1 EA EA cos FN2l2 FN2h l2 EA EA FN3l3 FN3h l3 EA EA cos
2.10 拉伸、压缩超静定问题 一、超静定问题及求解方法 静定问题: 杆件的轴力可以用静力平衡条件求出, 这种情况称作静定问题。 超静定问题: 只凭静力平衡方程已不能解出全部 未知力, 这种情况称做超静定问题。
超静定的次数: 未知力数超过独立平衡方程数 的数目, 称作超静定的次数。
2.10 拉伸、压缩超静定问题 变形协调方程: 在静不定问题中, 各部分变形之 间必存在相互制约的条件, 这种条件称为变形相 容条件(变形协调方程)。
2 FN1 3 FN2 6 F
这是一次超静定问题
(2) 画变形几何关系图 建立变形几何方程
变形协调条件为: 梁 ABCD 绕 铰 链 A 转 动 , ①、② 两杆仍与其铰接
d C 2d B
②
A a
60º B
超静定问题
l >
B端必接触
C
40kN 1.2m
静力平衡方程
RA RB 100kN
B
变形协调条件为 l
RB
RA
A
60kN 2.4m 1.2m
轴 力 图
15kN
85kN
⊕ 25kN
C
40kN 1.2m
B
RA 103 1.2 ( RA 60) 103 2.4 RB 103 1.2 l 9 6 9 6 9 6 210 10 600 10 210 10 600 10 210 10 300 10
3
FC
A
FC
C
L
2
L
B
2
P
例题 6.10
当系统的温度升高时,下列结构中的____不会 A 产生温度应力.
A
B
C
D
例题 6.11
图示静不定梁承受集中力F和集中力偶Me作用, 梁的两端铰支,中间截面C处有弹簧支座.在下列 关于该梁的多余约束力与变形协调条件的讨论 中,___是错误的. C
RB
RA 85kN
RB 15kN
三、扭转超静定问题 扭转变形计算公式
Tl GI p
T ( x) dx GI p l
例3.两端固定的圆截面等直杆AB,在截面
C受外力偶矩m作用,求杆两端的支座反力
偶矩。
m
A C B
a
b
解:
A
m
ɑ
mA
C
B
b
m
静力平衡方程为: m A mB m 变形协调条件为:
5 ql 8
B
L
q
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五节简单拉压超静定问题
在前面几节讨论的问题中,杆件的约束反力和杆件的内力可以用静力平衡方程求出,这类问题称为静定问题。
例如图5-25a所示的杆AB,在C处受到集中力P,则AC、CB段的内力可由平衡方程求出;同样,图5-26a所示的构架,是由AB及AC两杆组成,在A点受到载荷G的作用,求AB和AC杆的两个未知内力时,因能列出两个平衡方程,所以是静定问题。
(a) (b)
图5-25
图5-26
在工程实际中,有时为了增加构件和结构物的强度和刚度,或者由于构造上的需要,往往要给构件增加一些约束,或在结构物中增加一些杆件,这时构件的约束反力或杆件的数目多于刚体静力学平衡方程的数目,因而仅用静力平衡方程不能求解。
这类问题称为超静定问题或称静不定问题。
未知力个数与独立的平衡方程数之差称为静不定次数或称超静定次数。
例如图5-25b所示的杆,A、B两端有未知的约束力R1、R2,y方向静力平衡方程数只有1个,故属于一次超静定问题;图5-26b所示的构架,是由AB、AC、AD三杆组成,若取节点A研究,其所受力组成平面汇交力系,可列出2个静力平衡方程,但未知力有3个(N1、N2、N3),属于一次超静定问题。
显然仅由静力平衡方程不能求出全部未知内力。
求解超静定问题,除了根据静力平衡条件列出平衡方程外,还必须根据杆件变形之间的相互关系(称为变形协调条件),列出变形的几何方程,再由力和变形之间的物理条件(虎克定律)建立所需的补充方程。
下面通过例题说明超静定问题的解法。
例5-8图5-27a所示为两端固定的杆。
在C、D两截面处有一对力P作用,杆的横截面面积为A,弹性模量为E,求A、B处支座反力,并作轴力图。
图5-27 解:取AB 杆为研究对象,设A 、B 处的约束反力为压力,如图5-27b 所示,由平衡方程
0,0=-+-=∑X B A R P P R
得 B A R R = (a )
上式中只知道两个未知约束反力相等,不能解出具体值,故还需要列一个补充方程。
显然,杆件各段变形后,由于约束的限制,总长度保持不变,故变形协调条件为
0=∆+∆+∆DB CD AC l l l
根据虎克定律,得到AC l ∆=EA l R A -,=∆CD l EA l R P A )(-,=∆DB l EA l R B
-,代入上式得到变形的几何方程为
0)(=--+-EA l R EA l R P EA l R B A A
整理后得
P R R B A =+2 (b ) 将式(a )代入式(b ),可解得
3P R R B A =
=
作出杆的轴力图,如图5-27c 所示。
例5-9 图5-28a 所示结构中,已知杆1、杆2和杆3的抗拉刚度均为EA ,角030=α, 重物G=38kN ,试求各
杆所受的拉力。
(a) (b) (c)
图5-28
解:(1)列平衡方程
在重力G 作用下,三根杆均被拉长,故可设三杆均受拉力,节点A 的受力图如图5-28b 所示,列平衡方程: ΣX=0, 0sin sin 21=+-ααN N F F
ΣY=0, 0cos cos 321=-++G F F F N N N αα
整理得到
⎪⎩⎪⎨⎧=-+=033121G F F F F N N N N (1)
(2)变形几何关系
由图5-28c 可以看到,由于结构左右对称,杆1、2的抗拉刚度相同,所以节点A 只能垂直下移。
设变形后各杆汇交于A’点,则3l A A ∆='。
以B 点为圆心,杆1的原长BA 为半径作圆弧并与BA’相交,BA’在圆弧以外的线段即为杆1的伸长1l ∆,由于变形很小,可用垂直于BA’的直线AE 代替上述弧线,且仍可以认为030=='∠αD A B 。
于是
αcos 31l l ∆=∆ (2)
(3)物理关系
由虎克定律,得到
EA l F l EA l F l N N 3
33111,=∆=∆ (3)
(4)补充方程
将物理关系式(3)代入几何方程(2),得到解该超静定问题的补充方程
αcos 3311EA l F EA l F N N =
将αcos 13l l =代入上式,整理得到α231cos N N F F =,即
3175.0N N F F = (4)
(5)求解各杆轴力
联立求解补充方程(4)和平衡方程(1),可得
kN
5.16175.033=+⨯=G
F N ,
21N N F F ==
对于超静定结构,由于制造误差会造成装配应力,温度变化会造成温度应力。
我们知道,所有构件在制造中或多或少都会有一些误差,这种误差,在静定结构中不会引起任何内力及应
力。
而在超静定结构中则有不同的特点。
例如图5-29所示的三杆桁架结
图5-29
构,如果杆3制造时短了δ,为了将三根杆装配在一起,则必须将杆3拉长,杆1、2压短,这种强行装配使杆3中产生拉应力,杆1、2中产生压应力。
这种由于装配而引起的杆内应力,称为装配应力。
装配应力是在载荷作用前结构中已经具有的应力,因而是一种初应力。
这种应力的存在,有时是不利的,它会降低构件承受载荷的能力,但有时又可以利用它来达到一定的目的。
例如轮毂和轴的紧配合就是有意识地利用与装配应力相应的变形,来防止轮毂和轴的相对转动;预应力钢筋混凝土构件,也是利用装配应力来提高其承受载荷的能力。
在工程实际中,构件往往会遇到温度变化,从而引起构件热胀冷缩的温度变形。
在静定结构中,构件可以自由
变形,故温度改变不会在构件内产生应力。
例如图5-25a 、图5-26a 所示的杆,如果全杆各点处温度均上升了ΔT 0C ,
则杆件因热胀而伸长,但不会产生应力。
然而在图5-30a 所示的超静定结构中,如果杆AB 的温度发生变化,由于有了多余的约束,在杆内将出现温度应力。
设温度变化前杆AB 长度正好合适,如果全杆各点处温度均上升了
图5-30
ΔT 0C ,设想此时只有一个支座A ,则杆应伸长L T L t ⋅∆=∆α,其中α为材料的线膨胀系数。
但由于两端均受到刚性支座的约束,杆的长度不能改变。
因此,杆的两端必受到来自支座的轴向压力P ,使杆缩短了ΔL P (t L ∆=)而回到原长L (图5-30c )。
同时在杆内产生了应力
L L E P T ∆=σ。
这种由于温度改变而在杆件内产生的应力称为温度应
力,其计算式为 T E T ∆=ασ (5-11)
碳钢的C /1105.1206-⨯=α,E=200GP a 。
所以
a a 96MP 2.5P 10200105.12T T T ∆=∆⨯⨯⨯=-σ
可见当温度变化T ∆较大时,T σ的数值便非常可观。
为了避免过高的温度应力,在送热管道中可以增加伸缩节
(图5-31);在铁路钢轨各段之间留有伸缩缝,以削弱对钢轨膨胀的约束,降低温度应力;铁路桥梁一端用固定铰链支座,另一端采用可动铰链支座(图5-32),可以避免桥梁水平方向的温度应力。
图5-31 图5-32。
